Manual Dev
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 484 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- !!!!!!!!!! ALL USERS MUST READ !!!!!!!!!!
- Linux and Mac OS USERS MUST READ
- About the manual
- 1 Overview
- 2 General information
- 3 Functions
- 3.2 Showing molecular structure and viewing orbitals / isosurfaces (0)
- 3.3 Outputting all properties at a point (1)
- 3.4 Outputting and plotting specific property in a line (3)
- 3.5 Outputting and plotting specific property in a plane (4)
- 3.6 Outputting and plotting specific property within a spatial region (5)
- 3.7 Custom operation, promolecular and deformation properties (subfunction 0, -1, -2 in main function 3, 4, 5)
- 3.8 Checking & Modifying wavefunction (6)
- 3.9 Population analysis and atomic charges (7)
- 3.9.1 Hirshfeld population (1)
- 3.9.2 Voronoi deformation density (VDD) population (2)
- 3.9.3 Mulliken atom & basis function population analysis (5)
- 3.9.4 Löwdin population (6)
- 3.9.5 Modified Mulliken population defined by Ros & Schuit (SCPA) (7)
- 3.9.6 Modified Mulliken population defined by Stout & Politzer (8)
- 3.9.7 Modified Mulliken population defined by Bickelhaupt (9)
- 3.9.8 Becke atomic charge with atomic dipole moment correction (10)
- 3.9.9 Atomic dipole moment corrected Hirshfeld charges (ADCH, 11)
- 3.9.10 CHELPG (Charges from electrostatic potentials using a grid based method, 12)
- 3.9.11 Merz-Kollmann charge (13)
- 3.9.12 AIM charge (14)
- 3.9.13 Hirshfeld-I population (15)
- 3.9.14 CM5 charge (16)
- 3.9.15 Electronegativity Equalization Method (EEM) (17)
- 3.10 Orbital composition analysis (8)
- 3.10.1 Output basis function, shell and atom composition in a specific orbital by Mulliken, Stout-Politzer and SCPA approaches (1, 2, 3)
- 3.10.2 Define fragment 1 and 2 (-1, -2)
- 3.10.3 Output composition of fragment 1 and inter-fragment composition by Mulliken, Stout-Politzer and SCPA approaches (4, 5, 6)
- 3.10.4 Orbital composition analysis by natural atomic orbital approach (7)
- 3.10.5 Calculate atom and fragment contributions by Hirshfeld or Hirshfeld-I method (8,10)
- 3.10.6 Calculate atom and fragment contributions by Becke method (9)
- 3.10.7 Evaluate oxidation state by LOBA method
- 3.11 Bond order analysis (9)
- 3.11.1 Mayer bond order analysis (1)
- 3.11.2 Multi-center bond order analysis (2, -2, -3)
- 3.11.3 Wiberg bond order analysis in Löwdin orthogonalized basis (3)
- 3.11.4 Mulliken bond order analysis (4) and decomposition (5)
- 3.11.5 Orbital occupancy-perturbed Mayer bond order (6)
- 3.11.6 Fuzzy bond order (7)
- 3.11.7 Laplacian bond order (8)
- 3.11.8 Decompose Wiberg bond order in NAO basis as atomic orbital pair contributions (9)
- 3.12 Plotting total, partial, and overlap population density-of-states (10)
- 3.13 Plotting IR/Raman/UV-Vis/ECD/VCD spectrum (11)
- 3.14 Topology analysis (2)
- 3.15 Quantitative analysis of molecular surface (12)
- 3.16 Process grid data (13)
- 3.16.0 Visualize isosurface of present grid data (-2)
- 3.16.1 Output present grid data to Gaussian cube file (0)
- 3.16.2 Output all data points with value and coordinate (1)
- 3.16.3 Output data points in a XY/YZ/XZ plane (2, 3, 4)
- 3.16.4 Output average data of XY/YZ/XZ planes in a range of Z/X/Y (5,6,7)
- 3.16.5 Output data points in a plane defined three atom indices or three points (8,9)
- 3.16.6 Output data points in specified value range (10)
- 3.16.7 Grid data calculation (11)
- 3.16.8 Map values of a cube file to specified isosurface of present grid data (12)
- 3.16.9 Set value of the grid points that far away from / close to some atoms (13)
- 3.16.10 Set value of the grid points outside overlap region of two fragments (14)
- 3.16.11 If data value is within certain range, set it to a specified value (15)
- 3.16.12 Scale data range (16)
- 3.16.13 Show statistic data of the points in specific spatial and value range (17)
- 3.16.14 Calculate and plot integral curve in X/Y/Z direction (18)
- 3.17 Adaptive natural density partitioning (AdNDP) analysis (14)
- 3.18 Fuzzy atomic space analysis (15)
- 3.18.0 Basic concepts
- 3.18.1 Integration of a real space function in fuzzy atomic spaces (1)
- 3.18.2 Integration of a real space function in overlap spaces (8)
- 3.18.3 Calculate atomic multipole moments (2)
- 3.18.4 Calculate atomic overlap matrix (3)
- 3.18.5 Calculate localization and delocalization index (4)
- 3.18.6 Calculate PDI (5)
- 3.18.7 Calculate FLU and FLU-π (6,7)
- 3.18.8 Calculate condensed linear response kernel (9)
- 3.18.9 Calculate para linear response index (10)
- 3.18.10 Calculate multi-center delocalization index (11)
- 3.19 Charge decomposition analysis and plotting orbital interaction diagram (16)
- 3.20 Basin analysis (17)
- 3.21 Electron excitation analysis (18)
- 3.21.1 Analyze and visualize hole-electron distribution, transition dipole moment and transition density (1)
- 3.21.2 Plot transition density matrix as color-filled map (2)
- 3.21.3 Analyze charge-transfer based on density difference grid data (3)
- 3.21.4 Calculate (r index to measure charge-transfer length (4)
- 3.21.5 Calculate transition dipole moments between all excited states (5)
- 3.21.6 Generate natural transition orbitals (NTOs) (6)
- 3.21.7 Calculate ghost-hunter index (7)
- 3.21.8 Calculate interfragment charge transfer in electronic excitation (8)
- 3.100 Other functions part 1 (100)
- 3.100.1 Draw scatter graph between two functions and generate their cube files
- 3.100.2 Export .pdb, .xyz, .wfn, .wfx, .molden, .fch, NBO .47 or input file of mainstream quantum chemistry codes
- 3.100.3 Calculate molecular van der Waals volume
- 3.100.4 Integrate a function in whole space
- 3.100.5 Show overlap integral between alpha and beta orbitals
- 3.100.6 Monitor SCF convergence process of Gaussian
- 3.100.7 Generate Gaussian input file with initial guess from converged wavefunction
- 3.100.8 Generate Gaussian input file with initial guess from fragment wavefunctions
- 3.100.9 Evaluate coordination number for all atoms
- 3.100.11 Calculate overlap and centroid distance between two orbitals
- 3.100.13 Calculate HOMA and Bird aromaticity index
- 3.100.14 Calculate LOLIPOP (LOL Integrated Pi Over Plane)
- 3.100.15 Calculate intermolecular orbital overlap
- 3.100.18 Yoshizawa's electron transport route analysis
- 3.100.19 Generate promolecular .wfn file from fragment wavefunctions
- 3.100.20 Calculate Hellmann-Feynman forces
- 3.100.21 Calculate properties based on geometry information for specific atoms
- 3.100.22 Detect π orbitals and set occupation numbers
- 3.100.23 Fit function distribution to atomic value
- 3.100.24 Obtain NICS_ZZ for non-planar system
- 3.100.25 Calculate area and perimeter for a ring
- 3.200 Other functions part 2 (200)
- 3.200.1 Weak interaction analysis for fluctuation environment by RDG method
- 3.200.2 Calculate atomic and bond dipole moments in Hilbert space
- 3.200.3 Generate cube file for multiple orbital wavefunctions
- 3.200.4 Generate iso-chemical shielding surfaces (ICSS) and related quantities
- 3.200.5 Plot radial distribution function for a real space function
- 3.200.6 Analyze correspondence between orbitals in two wavefunctions
- 3.200.7 Parse output of (hyper)polarizability task of Gaussian
- 3.200.8 Calculate (hyper)polarizability by sum-over-states (SOS) method
- 3.200.9 Calculate average bond length and average coordinate number
- 3.200.10 Output various kinds of integral between orbitals
- 3.200.11 Calculate center, the first and second moments of a real space function
- 3.200.12 Calculate energy index (EI) or bond polarity index (BPI)
- 3.200.13 Pipek-Mezey orbital localization
- 3.200.14 Perform integration within isosurfaces of a real space function
- 3.200.15 Calculate electron correlation index
- 3.200.16 Generate natural orbitals based on the density matrix in .fch/.fchk file
- 4 Tutorials and Examples
- Prologue and generation of input files
- 4.0 View orbitals and structure
- 4.1 Calculate properties at a point
- 4.2 Topology analysis
- 4.3 Plot properties in a line
- 4.4 Plot properties in a plane
- 4.4.1 Color-filled map of electron density of hydrogen cyanide
- 4.4.2 Shaded surface map with projection of localized orbital locator in a plane of monofluoroethane
- 4.4.3 Contour map of electron density Laplacian of uracil without contributions from some atoms
- 4.4.4 Contour map of electrostatic potential of chlorine trifluoride
- 4.4.5 Contour map of two orbital wavefunctions
- 4.4.6 Gradient+contour map with topology paths of electron density of hydrogen peroxide
- 4.4.7 Deformation map of electron density of acetyl chloride
- 4.5 Generate grid data and view isosurface
- 4.5.1 Electron localization function of chlorine trifluoride
- 4.5.2 Laplacian of electron density of 1,3-butadiene
- 4.5.3 Calculate ELF-α and ELF-π to study aromaticity of benzene
- 4.5.4 Use Fukui function and dual descriptor to study favorable site for electrophilic attack of phenol
- 4.5.5 Plot difference map of electron density to study electron transfer of imidazole coordinated magnesium porphyrin
- 4.5.6 Study electron delocalization range function EDR(r;d) of anionic water dimer
- 4.5.7 Study orbital overlap distance function D(r) of thioformic acid
- 4.6 Modify wavefunction
- 4.7 Population analysis and atomic charge calculation
- 4.7.1 Calculate Hirshfeld and CHELPG charges for chlorine trifluoride
- 4.7.2 Calculate and compare ADCH charges with Hirshfeld charges for acetamide
- 4.7.3 Calculate condensed Fukui function and condensed dual descriptor
- 4.7.4 Illustration of computing Hirshfeld-I charges
- 4.7.5 Calculating EEM charges for ethanol-water cluster
- 4.8 Molecular orbital composition analysis
- 4.9 Bond order analysis
- 4.10 Plot density of states (DOS)
- 4.11 Plot spectrums
- 4.11.1 Plot infrared spectrum for NH3BF3
- 4.11.2 Plot UV-Vis spectrum and the contributions from individual transitions for acetic acid
- 4.11.3 Plot electronic circular dichroism spectrum for asparagine
- 4.11.4 Plot conformational weighted spectrum for plumericin
- 4.11.5 Plot Raman spectrum for 2-methyloxirane based on Raman intensity
- 4.11.6 Simultanously plot multiple systems
- 4.12 Quantitative analysis of molecular surface
- 4.12.1 Electrostatic potential analysis on phenol molecular surface
- 4.12.2 Average local ionization energy analysis on phenol molecular surface
- 4.12.3 Local molecular surface analysis for acrolein
- 4.12.4 Fukui function distribution on local molecular surface of phenol
- 4.12.5 Becke surface analysis on guanine-cytosine base pair
- 4.12.6 Hirshfeld surface analysis and fingerprint plot analysis on urea crystal
- 4.12.7 Two tricks to reduce computational time in ESP analysis on vdW surface
- 4.12.8 Quantitative analysis of orbital overlap distance function D(r) on thioformic acid molecular surface
- 4.13 Process grid data
- 4.13.1 Extract data points in a plane
- 4.13.2 Perform mathematical operation on grid data
- 4.13.3 Scaling numerical range of grid data
- 4.13.4 Screen isosurfaces in local regions
- 4.13.5 Acquire barycenter of a molecular orbital
- 4.13.6 Plot charge displacement curve
- 4.13.7 Evaluation of electron density overlap
- 4.14 Adaptive natural density partitioning (AdNDP) analysis
- 4.15 Fuzzy atomic space analysis
- 4.16 Charge decomposition analysis and plotting orbital interaction diagram
- 4.17 Basin analysis
- 4.17.1 AIM basin analysis for HCN
- 4.17.2 ELF basin analysis for acetylene
- 4.17.3 Electrostatic potential basin analysis for H2O
- 4.17.4 Basin analysis of electron density difference for H2O
- 4.17.5 Calculate source function in AIM basins
- 4.17.6 Local region basin analysis for polyyne
- 4.17.7 Evaluate atomic contribution to population of ELF basins
- 4.18 Electron excitation analysis
- 4.18.1 Analyze hole-electron distribution, transition density, transition dipole moment, charge-transfer and so on for N-phenylpyrrole
- 4.18.2 Plot transition density matrix of large-size conjugated molecule as color-filled map
- 4.18.3 Analyze charge-transfer during electron excitation based on electron density difference
- 4.18.4 Generate and analyze natural transition orbitals (NTOs)
- 4.18.5 Plot transition dipole moment vector contributed by molecular fragments as arrows
- 4.18.6 Calculate interfragment charge transfer during electronic excitation for 4-nitroaniline
- 4.100 Other functions, Part 1
- 4.100.1 Visual study of weak interaction by RDG (NCI) and DORI method
- 4.100.4 Calculate kinetic energy and nuclear attraction potential energy of phosgene by numerical integration
- 4.100.8 Perform simple energy decomposition by using combined fragment wavefunctions
- 4.100.13 Calculate HOMA and Bird aromaticity index for phenanthrene
- 4.100.14 Calculate LOLIPOP for phenanthrene
- 4.100.15 Calculate intermolecular orbital overlap integral of DB-TTF
- 4.100.18 Yoshizawa's electron transmission route analysis for phenanthrene
- 4.100.19 ELF analysis on the promolecular wavefunction combined from fragment wavefunctions
- 4.100.22 Analyze ( electron character of non-planar system: cycloheptatriene
- 4.200 Other functions, Part 2
- 4.200.1 Visually studying weak interaction in molecular dynamics simulation by aRDG method
- 4.200.4 Study iso-chemical shielding surface (ICSS) and magnetic shielding distribution for benzene
- 4.200.5 Plot radial distribution function of electron density
- 4.200.8 Calculate polarizability and hyperpolarizability for NH3 via sum-over-states (SOS) method
- 4.200.12 Calculate energy index (EI) and bond polarity index (BPI)
- 4.200.13 Localizing molecular orbital of 1,3-butadiene by Pipek-Mezey method
- 4.200.14 Integrate real space function within reduced density gradient (RDG) isosurfaces to study weak interaction
- 4.A Special topics and advanced tutorials
- 4.A.1 Study variation of electronic structure along IRC path
- 4.A.2 Calculate spin population
- 4.A.3 Study aromaticity
- 4.A.4 Predict reactive sites
- 4.A.5 Study weak interactions
- 4.A.6 Calculate odd electron density and local electron correlation function
- 4.A.7 Plot (hyper)polarizability density
- 4.A.8 Analyze higher level of wavefunction than CCSD
- 5 Skills
- Appendix
i
!!!!!!!!!! ALL USERS MUST READ !!!!!!!!!!
I know, most people, including myself, are unwilling to read lengthy manual. Since Multiwfn
is a heuristic and very user-friendly program, it is absolutely unnecessary to read through the
whole manual before using it. However, you should never skip reading following content!
1. The BEST way to get started quickly is first reading Chapter 1, Section
2.1~2.5 of Chapter 2, and then follow the tutorials in Chapter 4. After that if you want
to learn more about theoretical backgrounds and details of Multiwfn, then read
Section 2.6~2.8 of Chapter 2 and Chapter 3. Note that the tutorials and examples
given in Chapter 4 only cover the most important and frequently used functions rather
than all functions of Multiwfn. Some application skills are described in Chapter 5,
which may be useful for you.
2. Different functions of Multiwfn require different type of input file, please read
Section 2.5 for explanation.
3. If you do not know how to copy the output of Multiwfn from command-line
window to a plain text file, consult Section 5.4. If you do not know how to enlarge
screen buffer size of command-line window of Windows system, consult Section 5.5.
4. If the error “No executable for file l1.exe” appears in screen when Multiwfn is
invoking Gaussian, you should set up Gaussian environment variable first. For
Windows version, you can refer Appendix 1. (Note: Most functions in Multiwfn DO
NOT require Gaussian installed on your local machine)
5. The so-called ”current directory” in this manual is the path where you are
invoking Multiwfn. If you boot up Multiwfn by clicking the icon of executable file in
Windows, the “current directory” is the position of the executable file. For the case of
command-line mode, if you are in “D:\study\” directory when invoking Multiwfn,
then “D:\study\” is “current directory”.
6. Please often check Multiwfn website and update the program to the latest
version. Multiwfn is always in active development, useful functions are continuously
added, bugs are continuously fixed and efficiency is continuously improved.
7. Please feel free to ask questions about using Multiwfn by posting topics in
Multiwfn forum (http://sobereva.com/wfnbbs), you can also send me E-mail
(sobereva@sina.com), but please ensure that you have read this manual carefully to
find solution, and have updated your Multiwfn to the latest version. I would like to
provide as much help as I can for any Multiwfn user. \()/
ii
Linux and Mac OS USERS MUST READ
1. See Section 2.1.2 and 2.1.3 on how to install Linux and Mac OS versions of
Multiwfn, respectively.
2. When graphical user interface (GUI) appears, the graph cannot be shown
automatically, you have to do something to active the graph, e.g. clicking "up" button
or dragging a scale bar in the GUI.
3. Transparent style does not work when showing isosurfaces in GUI window.
But if you choose to save the picture, the transparent isosurfaces can be rendered
normally in the resulting graphical file.
iii
About the manual
This manual is organized as following sequence:
Chapter 1 Overview: Briefly describes what is Multiwfn and what Multiwfn
can do.
Chapter 2 General information: Introduces all aspects beyond specific
functions of Multiwfn, such as how to install, how to use, supported file types, etc.
Chapter 3 Functions: Describes all functions and related theories of Multiwfn
in detail.
Chapter 4 Tutorials and examples: Plenty of practical examples are provided
for helping users to use Multiwfn.
Chapter 5 Skills: Some useful skills in using Multiwfn.
Appendix
In general, italics font is used for input commands and journal name throughout
this manual. Very important contents are highlighted by red color.
You can directly jump to specific section by choosing corresponding entry in
bookmark window of your pdf reader.
The purpose of this manual is not only helping users to use Multiwfn, but also
introducing related theories. I hope any quantum chemist can benefit from this manual.
Albeit I have tried to write this manual as readable as possible for beginners,
some topics request the readers have basic knowledges of quantum chemistry. If the
readers have carefully read the book "Quantum Chemistry 7ed" written by Ira. Levine,
then they will never encounter any difficulty during reading through the whole
manual.
iv
Content
!!!!!!!!!! ALL USERS MUST READ !!!!!!!!!!......................................... i
Linux and Mac OS USERS MUST READ............................................ ii
About the manual.................................................................................... iii
1 Overview...............................................................................................1
2 General information............................................................................6
2.1 Install.......................................................................................................................................6
2.1.1 Windows version..............................................................................................................6
2.1.2 Linux version ...................................................................................................................6
2.1.3 Mac OS version................................................................................................................7
2.2 Using Multiwfn.......................................................................................................................7
2.3 The files of Multiwfn ..............................................................................................................8
2.4 Parallel implementation ..........................................................................................................8
2.5 Input files and wavefunction types..........................................................................................9
2.6 Real space functions..............................................................................................................13
2.7 User defined real space function...........................................................................................25
2.8 Graphic formats and image size............................................................................................33
3 Functions ............................................................................................34
3.2 Showing molecular structure and viewing orbitals / isosurfaces (0).....................................34
3.3 Outputting all properties at a point (1)..................................................................................36
3.4 Outputting and plotting specific property in a line (3)..........................................................36
3.5 Outputting and plotting specific property in a plane (4) .......................................................37
3.5.1 Graph types ....................................................................................................................38
3.5.2 Setting up grid, plane and plotting region......................................................................42
3.5.3 Options in post-process interface...................................................................................44
3.5.4 Setting up contour lines..................................................................................................45
3.5.5 Plot critical points, paths and interbasin paths on plane graph.......................................46
3.6 Outputting and plotting specific property within a spatial region (5) ...................................47
3.7 Custom operation, promolecular and deformation properties (subfunction 0, -1, -2 in main
function 3, 4, 5)...........................................................................................................................50
3.7.1 Custom operation for multiple wavefunctions (0) .........................................................50
3.7.2 Promolecular and deformation properties (-1, -2)..........................................................51
3.7.3 Generation of atomic wavefunctions..............................................................................51
3.7.4 Sphericalization of atom wavefunction..........................................................................52
3.8 Checking & Modifying wavefunction (6).............................................................................53
v
3.9 Population analysis and atomic charges (7) ..........................................................................55
3.9.1 Hirshfeld population (1).................................................................................................55
3.9.2 Voronoi deformation density (VDD) population (2)......................................................56
3.9.3 Mulliken atom & basis function population analysis (5) ...............................................57
3.9.4 Löwdin population (6)....................................................................................................58
3.9.5 Modified Mulliken population defined by Ros & Schuit (SCPA) (7)............................59
3.9.6 Modified Mulliken population defined by Stout & Politzer (8).....................................59
3.9.7 Modified Mulliken population defined by Bickelhaupt (9) ...........................................59
3.9.8 Becke atomic charge with atomic dipole moment correction (10).................................60
3.9.9 Atomic dipole moment corrected Hirshfeld charges (ADCH, 11) .................................60
3.9.10 CHELPG (Charges from electrostatic potentials using a grid based method, 12) .......61
3.9.11 Merz-Kollmann charge (13).........................................................................................62
3.9.12 AIM charge (14)...........................................................................................................63
3.9.13 Hirshfeld-I population (15) ..........................................................................................63
3.9.14 CM5 charge (16) ..........................................................................................................65
3.9.15 Electronegativity Equalization Method (EEM) (17)....................................................66
3.10 Orbital composition analysis (8).........................................................................................68
3.10.1 Output basis function, shell and atom composition in a specific orbital by Mulliken,
Stout-Politzer and SCPA approaches (1, 2, 3).........................................................................68
3.10.2 Define fragment 1 and 2 (-1, -2) ..................................................................................70
3.10.3 Output composition of fragment 1 and inter-fragment composition by Mulliken, Stout-
Politzer and SCPA approaches (4, 5, 6)...................................................................................70
3.10.4 Orbital composition analysis by natural atomic orbital approach (7) ..........................71
3.10.5 Calculate atom and fragment contributions by Hirshfeld or Hirshfeld-I method (8,10)
.................................................................................................................................................72
3.10.6 Calculate atom and fragment contributions by Becke method (9)...............................73
3.10.7 Evaluate oxidation state by LOBA method..................................................................73
3.11 Bond order analysis (9) .......................................................................................................74
3.11.1 Mayer bond order analysis (1)......................................................................................74
3.11.2 Multi-center bond order analysis (2, -2, -3) .................................................................75
3.11.3 Wiberg bond order analysis in Löwdin orthogonalized basis (3).................................78
3.11.4 Mulliken bond order analysis (4) and decomposition (5).............................................79
3.11.5 Orbital occupancy-perturbed Mayer bond order (6).....................................................79
3.11.6 Fuzzy bond order (7)....................................................................................................80
3.11.7 Laplacian bond order (8)..............................................................................................80
3.11.8 Decompose Wiberg bond order in NAO basis as atomic orbital pair contributions (9)81
3.12 Plotting total, partial, and overlap population density-of-states (10)..................................82
3.12.1 Theory..........................................................................................................................82
3.12.2 Input file.......................................................................................................................84
3.12.3 Options for plotting DOS.............................................................................................84
3.12.4 Local DOS....................................................................................................................86
3.13 Plotting IR/Raman/UV-Vis/ECD/VCD spectrum (11)........................................................86
3.13.1 Theory..........................................................................................................................86
3.13.2 Input file.......................................................................................................................88
vi
3.13.3 Usage and options........................................................................................................91
3.13.4 Plotting multiple files and weighted spectrum.............................................................93
3.14 Topology analysis (2)..........................................................................................................94
3.14.1 Theory..........................................................................................................................94
3.14.2 Search critical points....................................................................................................97
3.14.3 Generate paths..............................................................................................................99
3.14.4 Generate interbasin surfaces.........................................................................................99
3.14.5 Visualize, analyze, modify and export results............................................................100
3.14.6 Calculate the aromaticity indices based on topology properties of electron density..101
3.15 Quantitative analysis of molecular surface (12)................................................................102
3.15.1 Theory........................................................................................................................102
3.15.2 Numerical algorithm ..................................................................................................106
3.15.3 Parameters and options ..............................................................................................107
3.15.4 Options at post-process stage.....................................................................................109
3.15.5 Special topic: Hirshfeld and Becke surface analyses.................................................112
3.16 Process grid data (13)........................................................................................................116
3.16.0 Visualize isosurface of present grid data (-2).............................................................116
3.16.1 Output present grid data to Gaussian cube file (0).....................................................116
3.16.2 Output all data points with value and coordinate (1) .................................................116
3.16.3 Output data points in a XY/YZ/XZ plane (2, 3, 4).....................................................116
3.16.4 Output average data of XY/YZ/XZ planes in a range of Z/X/Y (5,6,7).....................116
3.16.5 Output data points in a plane defined three atom indices or three points (8,9)..........117
3.16.6 Output data points in specified value range (10)........................................................117
3.16.7 Grid data calculation (11)...........................................................................................117
3.16.8 Map values of a cube file to specified isosurface of present grid data (12) ...............118
3.16.9 Set value of the grid points that far away from / close to some atoms (13) ...............118
3.16.10 Set value of the grid points outside overlap region of two fragments (14) ..............119
3.16.11 If data value is within certain range, set it to a specified value (15) ........................119
3.16.12 Scale data range (16)................................................................................................119
3.16.13 Show statistic data of the points in specific spatial and value range (17) ................119
3.16.14 Calculate and plot integral curve in X/Y/Z direction (18) .......................................120
3.17 Adaptive natural density partitioning (AdNDP) analysis (14)..........................................121
3.17.1 Theory........................................................................................................................121
3.17.2 Input file.....................................................................................................................123
3.17.3 Options.......................................................................................................................124
3.18 Fuzzy atomic space analysis (15)......................................................................................126
3.18.0 Basic concepts............................................................................................................126
3.18.1 Integration of a real space function in fuzzy atomic spaces (1) .................................129
3.18.2 Integration of a real space function in overlap spaces (8)..........................................130
3.18.3 Calculate atomic multipole moments (2) ...................................................................130
3.18.4 Calculate atomic overlap matrix (3)...........................................................................132
3.18.5 Calculate localization and delocalization index (4)....................................................133
3.18.6 Calculate PDI (5)........................................................................................................135
3.18.7 Calculate FLU and FLU-π (6,7).................................................................................136
vii
3.18.8 Calculate condensed linear response kernel (9) .........................................................137
3.18.9 Calculate para linear response index (10) ..................................................................138
3.18.10 Calculate multi-center delocalization index (11)......................................................138
3.19 Charge decomposition analysis and plotting orbital interaction diagram (16)..................138
3.19.1 Theory........................................................................................................................138
3.19.2 Input file.....................................................................................................................142
3.19.3 Usage..........................................................................................................................143
3.20 Basin analysis (17)............................................................................................................146
3.20.1 Theory........................................................................................................................146
3.20.2 Numerical aspects ......................................................................................................147
3.20.3 Usage..........................................................................................................................150
3.21 Electron excitation analysis (18).......................................................................................155
3.21.1 Analyze and visualize hole-electron distribution, transition dipole moment and
transition density (1) .............................................................................................................155
3.21.1.1 Theory .................................................................................................................155
3.21.1.2 Input file..............................................................................................................160
3.21.1.3 Functions.............................................................................................................161
3.21.2 Plot transition density matrix as color-filled map (2).................................................164
3.21.3 Analyze charge-transfer based on density difference grid data (3) ............................166
3.21.4 Calculate r index to measure charge-transfer length (4)..........................................168
3.21.5 Calculate transition dipole moments between all excited states (5)...........................170
3.21.6 Generate natural transition orbitals (NTOs) (6) .........................................................170
3.21.7 Calculate ghost-hunter index (7)................................................................................172
3.21.8 Calculate interfragment charge transfer in electronic excitation (8)..........................173
3.100 Other functions part 1 (100)............................................................................................174
3.100.1 Draw scatter graph between two functions and generate their cube files ................175
3.100.2 Export .pdb, .xyz, .wfn, .wfx, .molden, .fch, NBO .47 or input file of mainstream
quantum chemistry codes......................................................................................................176
3.100.3 Calculate molecular van der Waals volume .............................................................176
3.100.4 Integrate a function in whole space..........................................................................177
3.100.5 Show overlap integral between alpha and beta orbitals ...........................................178
3.100.6 Monitor SCF convergence process of Gaussian.......................................................178
3.100.7 Generate Gaussian input file with initial guess from converged wavefunction .......179
3.100.8 Generate Gaussian input file with initial guess from fragment wavefunctions........180
3.100.9 Evaluate coordination number for all atoms ............................................................182
3.100.11 Calculate overlap and centroid distance between two orbitals...............................182
3.100.13 Calculate HOMA and Bird aromaticity index........................................................183
3.100.14 Calculate LOLIPOP (LOL Integrated Pi Over Plane)............................................184
3.100.15 Calculate intermolecular orbital overlap................................................................184
3.100.18 Yoshizawa's electron transport route analysis ........................................................185
3.100.19 Generate promolecular .wfn file from fragment wavefunctions ............................187
3.100.20 Calculate Hellmann-Feynman forces.....................................................................187
3.100.21 Calculate properties based on geometry information for specific atoms ...............188
3.100.22 Detect π orbitals and set occupation numbers........................................................189
viii
3.100.23 Fit function distribution to atomic value................................................................190
3.100.24 Obtain NICS_ZZ for non-planar system................................................................191
3.100.25 Calculate area and perimeter for a ring ..................................................................192
3.200 Other functions part 2 (200)............................................................................................193
3.200.1 Weak interaction analysis for fluctuation environment by RDG method.................193
3.200.2 Calculate atomic and bond dipole moments in Hilbert space ..................................194
3.200.3 Generate cube file for multiple orbital wavefunctions.............................................197
3.200.4 Generate iso-chemical shielding surfaces (ICSS) and related quantities .................197
3.200.5 Plot radial distribution function for a real space function........................................198
3.200.6 Analyze correspondence between orbitals in two wavefunctions ............................199
3.200.7 Parse output of (hyper)polarizability task of Gaussian ............................................201
3.200.8 Calculate (hyper)polarizability by sum-over-states (SOS) method..........................204
3.200.9 Calculate average bond length and average coordinate number ..............................208
3.200.10 Output various kinds of integral between orbitals..................................................209
3.200.11 Calculate center, the first and second moments of a real space function................209
3.200.12 Calculate energy index (EI) or bond polarity index (BPI) .....................................211
3.200.13 Pipek-Mezey orbital localization ...........................................................................211
3.200.14 Perform integration within isosurfaces of a real space function ............................213
3.200.15 Calculate electron correlation index.......................................................................214
3.200.16 Generate natural orbitals based on the density matrix in .fch/.fchk file.................214
4 Tutorials and Examples ..................................................................217
Prologue and generation of input files ......................................................................................217
4.0 View orbitals and structure..................................................................................................219
4.0.1 Viewing molecular orbitals of monofluoroethane........................................................219
4.0.2 Viewing natural bond orbitals (NBO) of ethanol .........................................................221
4.1 Calculate properties at a point.............................................................................................223
4.1.1 Show all properties of triplet water at a given point ....................................................223
4.1.2 Calculate ESP at nuclear positions to evaluate interaction strength of H2O···HF ........225
4.2 Topology analysis................................................................................................................227
4.2.1 Atoms in molecules (AIM) and aromaticity analysis for 2-pyridoxine 2-aminopyridine
...............................................................................................................................................227
4.2.2 LOL topology analysis for acetic acid..........................................................................232
4.2.3 Plot electron density ellipticity along bond path..........................................................234
4.3 Plot properties in a line .......................................................................................................235
4.3.1 Plot the spin density curve of triplet formamide along carbon and oxygen atoms.......235
4.3.2 Study Fermi hole and Coulomb hole of H2..................................................................236
4.3.3 Study interatomic interaction via PAEM-MO method.................................................239
4.4 Plot properties in a plane.....................................................................................................241
4.4.1 Color-filled map of electron density of hydrogen cyanide...........................................241
4.4.2 Shaded surface map with projection of localized orbital locator in a plane of
monofluoroethane .................................................................................................................242
4.4.3 Contour map of electron density Laplacian of uracil without contributions from some
atoms.....................................................................................................................................244
ix
4.4.4 Contour map of electrostatic potential of chlorine trifluoride......................................245
4.4.5 Contour map of two orbital wavefunctions..................................................................246
4.4.6 Gradient+contour map with topology paths of electron density of hydrogen peroxide
...............................................................................................................................................248
4.4.7 Deformation map of electron density of acetyl chloride..............................................251
4.5 Generate grid data and view isosurface...............................................................................253
4.5.1 Electron localization function of chlorine trifluoride...................................................253
4.5.2 Laplacian of electron density of 1,3-butadiene............................................................254
4.5.3 Calculate ELF-α and ELF-π to study aromaticity of benzene......................................255
4.5.4 Use Fukui function and dual descriptor to study favorable site for electrophilic attack of
phenol....................................................................................................................................258
4.5.5 Plot difference map of electron density to study electron transfer of imidazole
coordinated magnesium porphyrin........................................................................................262
4.5.6 Study electron delocalization range function EDR(r;d) of anionic water dimer..........265
4.5.7 Study orbital overlap distance function D(r) of thioformic acid..................................266
4.6 Modify wavefunction..........................................................................................................267
4.6.1 Delete certain Gauss functions.....................................................................................267
4.6.2 Remove contributions from certain orbitals to real space functions ............................268
4.6.3 Translate and duplicate graphene primitive cell wavefunction to periodic system......269
4.7 Population analysis and atomic charge calculation.............................................................271
4.7.1 Calculate Hirshfeld and CHELPG charges for chlorine trifluoride .............................271
4.7.2 Calculate and compare ADCH charges with Hirshfeld charges for acetamide............271
4.7.3 Calculate condensed Fukui function and condensed dual descriptor...........................273
4.7.4 Illustration of computing Hirshfeld-I charges..............................................................274
4.7.5 Calculating EEM charges for ethanol-water cluster.....................................................276
4.8 Molecular orbital composition analysis ..............................................................................278
4.8.1 Analyze acetamide by Mulliken method......................................................................278
4.8.2 Analysis on water by natural atomic orbital method....................................................281
4.8.3 Analyze acetamide by Hirshfeld and Becke method....................................................284
4.8.4 Calculate oxidation state by LOBA method.................................................................285
4.9 Bond order analysis.............................................................................................................287
4.9.1 Mayer bond order and fuzzy bond order analysis on acetamide..................................287
4.9.2 Three-center bond order analysis on Li6 cluster...........................................................289
4.9.3 Calculate Laplacian bond order (LBO)........................................................................291
4.9.4 Decomposition analysis of Wiberg bond order in NAO basis for formaldehyde.........292
4.10 Plot density of states (DOS)..............................................................................................294
4.10.1 Plot total, partial and overlap DOS for N-phenylpyrrole ...........................................294
4.10.2 Plot local DOS for butadiene .....................................................................................298
4.11 Plot spectrums ...................................................................................................................300
4.11.1 Plot infrared spectrum for NH3BF3............................................................................300
4.11.2 Plot UV-Vis spectrum and the contributions from individual transitions for acetic acid
...............................................................................................................................................301
4.11.3 Plot electronic circular dichroism spectrum for asparagine .......................................303
4.11.4 Plot conformational weighted spectrum for plumericin.............................................303
x
4.11.5 Plot Raman spectrum for 2-methyloxirane based on Raman intensity.......................307
4.11.6 Simultanously plot multiple systems..........................................................................308
4.12 Quantitative analysis of molecular surface .......................................................................309
4.12.1 Electrostatic potential analysis on phenol molecular surface.....................................309
4.12.2 Average local ionization energy analysis on phenol molecular surface .....................314
4.12.3 Local molecular surface analysis for acrolein............................................................316
4.12.4 Fukui function distribution on local molecular surface of phenol .............................318
4.12.5 Becke surface analysis on guanine-cytosine base pair...............................................319
4.12.6 Hirshfeld surface analysis and fingerprint plot analysis on urea crystal....................321
4.12.7 Two tricks to reduce computational time in ESP analysis on vdW surface................325
4.12.8 Quantitative analysis of orbital overlap distance function D(r) on thioformic acid
molecular surface..................................................................................................................327
4.13 Process grid data ...............................................................................................................328
4.13.1 Extract data points in a plane .....................................................................................328
4.13.2 Perform mathematical operation on grid data............................................................329
4.13.3 Scaling numerical range of grid data..........................................................................330
4.13.4 Screen isosurfaces in local regions.............................................................................330
4.13.4.1 Screen isosurfaces inside or outside a region......................................................330
4.13.4.2 Screen isosurfaces outside overlap region of two fragments ..............................331
4.13.5 Acquire barycenter of a molecular orbital..................................................................333
4.13.6 Plot charge displacement curve..................................................................................334
4.13.7 Evaluation of electron density overlap.......................................................................337
4.14 Adaptive natural density partitioning (AdNDP) analysis..................................................339
4.14.1 Analyze Li5+ cluster....................................................................................................339
4.14.2 Analyze B11- cluster....................................................................................................340
4.14.3 Analyze phenanthrene ................................................................................................343
4.15 Fuzzy atomic space analysis .............................................................................................346
4.15.1 Study delocalization index of benzene.......................................................................346
4.15.2 Study aromaticity of phenanthrene by PDI, FLU, FLU-π and PLR...........................347
4.16 Charge decomposition analysis and plotting orbital interaction diagram .........................348
4.16.1 Close-shell interaction case: COBH3.........................................................................349
4.16.2 Open-shell interaction case: CH3NH2........................................................................353
4.16.3 More than two-fragments case: Pt(NH3)2Cl2..............................................................355
4.17 Basin analysis....................................................................................................................356
4.17.1 AIM basin analysis for HCN......................................................................................357
4.17.2 ELF basin analysis for acetylene................................................................................361
4.17.3 Electrostatic potential basin analysis for H2O............................................................364
4.17.4 Basin analysis of electron density difference for H2O ...............................................368
4.17.5 Calculate source function in AIM basins ...................................................................370
4.17.6 Local region basin analysis for polyyne.....................................................................372
4.17.7 Evaluate atomic contribution to population of ELF basins........................................373
4.18 Electron excitation analysis...............................................................................................374
4.18.1 Analyze hole-electron distribution, transition density, transition dipole moment,
charge-transfer and so on for N-phenylpyrrole.....................................................................375
xi
4.18.2 Plot transition density matrix of large-size conjugated molecule as color-filled map386
4.18.3 Analyze charge-transfer during electron excitation based on electron density difference
...............................................................................................................................................389
4.18.4 Generate and analyze natural transition orbitals (NTOs)...........................................392
4.18.5 Plot transition dipole moment vector contributed by molecular fragments as arrows394
4.18.6 Calculate interfragment charge transfer during electronic excitation for 4-nitroaniline
...............................................................................................................................................397
4.100 Other functions, Part 1 ....................................................................................................399
4.100.1 Visual study of weak interaction by RDG (NCI) and DORI method.......................399
4.100.4 Calculate kinetic energy and nuclear attraction potential energy of phosgene by
numerical integration ............................................................................................................408
4.100.8 Perform simple energy decomposition by using combined fragment wavefunctions
...............................................................................................................................................409
4.100.13 Calculate HOMA and Bird aromaticity index for phenanthrene............................410
4.100.14 Calculate LOLIPOP for phenanthrene ...................................................................411
4.100.15 Calculate intermolecular orbital overlap integral of DB-TTF................................412
4.100.18 Yoshizawa's electron transmission route analysis for phenanthrene ......................413
4.100.19 ELF analysis on the promolecular wavefunction combined from fragment
wavefunctions .......................................................................................................................414
4.100.22 Analyze electron character of non-planar system: cycloheptatriene...................417
4.200 Other functions, Part 2 ....................................................................................................418
4.200.1 Visually studying weak interaction in molecular dynamics simulation by aRDG
method...................................................................................................................................418
4.200.4 Study iso-chemical shielding surface (ICSS) and magnetic shielding distribution for
benzene .................................................................................................................................423
4.200.5 Plot radial distribution function of electron density.................................................427
4.200.8 Calculate polarizability and hyperpolarizability for NH3 via sum-over-states (SOS)
method...................................................................................................................................431
4.200.12 Calculate energy index (EI) and bond polarity index (BPI)...................................434
4.200.13 Localizing molecular orbital of 1,3-butadiene by Pipek-Mezey method...............435
4.200.14 Integrate real space function within reduced density gradient (RDG) isosurfaces to
study weak interaction ..........................................................................................................436
4.A Special topics and advanced tutorials.................................................................................441
4.A.1 Study variation of electronic structure along IRC path ...............................................441
4.A.2 Calculate spin population............................................................................................446
4.A.3 Study aromaticity ........................................................................................................447
4.A.4 Predict reactive sites....................................................................................................450
4.A.5 Study weak interactions...............................................................................................452
4.A.6 Calculate odd electron density and local electron correlation function.......................455
4.A.7 Plot (hyper)polarizability density................................................................................458
4.A.8 Analyze higher level of wavefunction than CCSD......................................................458
5 Skills..................................................................................................461
5.1 Make Multiwfn support more quantum chemistry programs..............................................461
xii
5.2 Running Multiwfn in silent mode .......................................................................................461
5.3 Running Multiwfn in batch mode (for Windows)...............................................................463
5.4 Copy outputs from command-line window to clipboard.....................................................463
5.5 Make command-line window capable to record more outputs ...........................................464
5.6 Rapidly load a file into Multiwfn........................................................................................465
Appendix................................................................................................466
1 Setting up environment variable for Gaussian in Windows...................................................466
2 The routines for evaluating real space functions....................................................................466
3 Detail of built-in atomic densities..........................................................................................468
4 Details about supplying inner-core electron density for the wavefunctions involving
pseudopotential .........................................................................................................................469
5 Check sanity of wavefunction................................................................................................470
6 Special functions....................................................................................................................470

1 Overview
1
1 Overview
Multiwfn is an extremely powerful wavefunction analysis program, it supports almost all of
the most important wavefunction analysis methods. Multiwfn is free, open-source, high-efficient,
very user-friendly and flexible. 64 bit Windows, Linux and Mac OS platforms are supported.
Multiwfn can be downloaded at Multiwfn official website http://sobereva.com/multiwfn.
Input files supported by Multiwfn
Multiwfn accepts several kinds of files for loading wavefunction information: .wfn/.wfx
(Conventional / Extended PROAIM wavefunction file), .fch (Gaussian formatted check
file), .molden (Molden input file), .31~.40 (NBO plot files) and .gms (GAMESS-US output file).
Other type of files such as Gaussian output file, .cub file, DMol3 .grd file, .pdb file, .xyz file, .mol
file can be used for specific functions.
Special points of Multiwfn
(1) Comprehensive functions. Almost all of the most important wavefunction analysis
methods (except for NBO methods) are supported by Multiwfn.
(2) Very user-friendly. Multiwfn is designed as an interactive program, prompts shown on
screen in each step clearly tell users what should do next, Multiwfn also never prints obscure
messages, hence there is no barrier even for beginners. In addition, there are about 100 well-
written tutorials in the manual, which are very helpful for new users.
(3) High efficiency. The code of Multiwfn is substantially optimized. Most parts are
parallelized by OpenMP technology. For computationally intensive tasks, the efficiency of
Multiwfn exceeds analogous programs significantly.
(4) Results can be visualized directly. A high-level graphical library DISLIN is invoked
internally and automatically by Multiwfn for visualizing results, most plotting parameters are
controllable in interactive interface. This remarkably simplified wavefunction analysis, especially
for studying distribution of real space functions.
Primary functions of Multiwfn
1) Showing molecular structure and viewing orbitals (MO, NBO, natural orbital, etc.).
2) Outputting all supported real space functions as well as gradient and Hessian at a point.
Value can be decomposed to orbital contributions
3) Outputting real space function in a line and plot it as curve map.
4) Outputting real space function in a plane and plot it as graph. Supported graph types
include filled-color map, contour map, relief map (with/without projection), gradient
map, vector field map.
5) Outputting real space function in a spatial scope, data can be exported to Gaussian-type
grid file (.cub) and can be visualized as isosurface.
6) For the calculation of real space functions in one-, two- and three-dimensions, user can
define the operations between the data generated from multiple wavefunction files.
Therefore one can calculate and plot such as Fukui function, dual descriptor and density
1 Overview
2
difference very easily. Meanwhile promolecule and deformation properties for all real
space functions can be calculated directly.
7) Topology analysis for electron density (AIM analysis), Laplacian, ELF/LOL etc. Critical
points and gradient paths can be searched and visualized in terms of 3D or plane graph.
Interbasin surfaces can be drawn. Values of real space functions can be calculated at
critical points or along topology paths.
8) Checking and modifying wavefunction. For example print orbital and basis function
information, manually set orbital occupation number and type, translate and duplicate
system, discard wavefunction information from specified atoms.
9) Population analysis. Hirshfeld, Hirshfeld-I, VDD, Mulliken, Löwdin, Modified
Mulliken (including three methods: SCPA, Stout & Politzer, Bickelhaupt), Becke,
ADCH (Atomic dipole moment corrected Hirshfeld), CM5, CHELPG, Merz-Kollmann
and Electronegativity Equalization Method (EEM) are supported.
10) Orbital composition analysis. Mulliken, Stout & Politzer, SCPA, Hirshfeld, Hirshfeld-I,
Becke and natural atomic orbital (NAO) methods are supported to obtain orbital
composition.
11) Bond order analysis. Mayer bond order, multi-center bond order in AO or NAO basis
(up to 12-centers), Wiberg bond order in Löwdin orthogonalized basis and Mulliken
bond order are supported. Mayer and Mulliken bond order can be decomposed to orbital
contributions. Wiberg bond order can be decomposed to contribution from various
natural atomic orbital pairs.
12) Plotting Total/Partial/Overlap population density-of-states (TDOS, PDOS, OPDOS), up
to 10 fragments can be very flexibly and conveniently defined. Local DOS (LDOS) can
also be plotted for a point as curve map or for a line as color-filled map.
13) Plotting IR/Raman/UV-Vis/ECD/VCD spectrum. Abundant parameters (broadening
function, FWHM, etc.) can be determined by users, individual contribution from each
transition to the spectrum can be easily studied. Spectrum of multiple systems can be
conveniently plotted together. Plotting conformational weighted spectrum is well
supported.
14) Quantitative analysis of molecular surface. Surface properties such as surface area,
enclosed volume, average value and std. of mapped functions can be computed for
overall molecular surface or local surfaces; local minima and maxima of mapped
functions on the surface can be located. Becke and Hirshfeld surface analysis, as well as
fingerprint analysis are also supported.
15) Processing grid data (can be loaded from .cub/.grd or generated by Multiwfn). User can
perform mathematical operations on grid data, set value in certain range, extract data in
specified plane, plot integral curve, etc.
16) Adaptive natural density partitioning (AdNDP) analysis. The interface is interactive and
the AdNDP orbitals can be visualized directly.
17) Analyzing real space functions in fuzzy atomic spaces (defined by Becke, Hirshfeld or
Hirshfeld-I partitions). Integral of selected real space function in atomic spaces or in
overlap regions of atomic spaces, atomic multipole moments, atomic overlap matrix
(AOM), localization and delocalization index (DI), condensed linear response kernel,
multi-center DI, as well as four aromaticity indices, namely FLU, FLU-pi, PDI and PLR
1 Overview
3
can be computed.
18) Charge decomposition analysis (CDA) and extended CDA analysis. Orbital interaction
diagram can be plotted. Infinite number of fragments can be defined.
19) Basin analysis. Attractors can be located for any real space function, corresponding
basins can be generated and visualized at the same time. All real space functions can be
integrated in the generated basins. Electric multipole moments, orbital overlap matrix,
localization index and delocalization index can be calculated for the basins. Atomic
contribution to basin population can be obtained.
20) Electron excitation analysis, including: Visualizing and analyzing hole-electron
distribution, transition density, transition electric/magnetic dipole moment and charge
density difference; calculating Coulomb attractive energy between hole and electron;
Calculating atomic transition charges; decomposing transition dipole moment to MO
pair contribution or basis function/atom contribution; analyzing charge-transfer by the
method proposed in JCTC, 7, 2498; plotting transition density matrix or atom-atom
contribution matrix of transition dipole moment as colored matrix map; calculating r
index to reveal electron excitation mode; calculating transition dipole moments between
all excited states; generating natural transition orbitals (NTOs); calculating ghost-hunter
index proposed in JCC, 38, 2151.
21) Other useful functions or utilities involved in quantum chemistry studies: Weak
interaction analysis via RDG method (including fluctuation environment analysis);
plotting scatter map for two functions in specific spatial scope; integrating a real space
function over the whole space by Becke's multi-center method; evaluating overlap
integral between alpha and beta orbitals; evaluating overlap and centroid distance
between two orbitals; monitoring SCF convergence process; generating Gaussian input
file with initial guess from converged wavefunction or multiple fragment wavefunctions;
calculating van der Waals volume; calculating HOMA and Bird aromaticity indices;
calculating LOLIPOP index; calculating intermolecular orbital overlap; Yoshizawa's
electron transport route analysis; calculating atomic and bond dipole moment in Hilbert
space; plotting radial distribution function for real space functions; plotting iso-chemical
shielding surface (ICSS); calculating overlap integral between orbitals in two different
wavefunctions; parsing output of (hyper)polarizability task of Gaussian; calculating
polarizability and 1st/2nd/3rd hyperpolarizability by sum-over-states (SOS) method;
outputting various kinds of integrals between orbitals; calculating center; the first and
second moments and radius of gyration for a real space function; exporting
wavefunction to .wfn, .wfx, .molden, .fch, NBO .47 and yield input file for a batch of
known quantum chemistry codes; calculating bond polarity index (BPI); evaluating
oxidation state; Pipek-Mezey orbital localization; perform integration within isosurface
defined by a real space function; calculate electron correlation indices; automatically
detect orbitals and so on.
The real space functions supported by Multiwfn
Real space function analysis is one of the most powerful feature of Multiwfn, about 100 real
space functions are supported and listed below, detailed descriptions can be found in Section 2.6
and 2.7 of the manual:

1 Overview
4
• Electron density
• Gradient norm of electron density
• Laplacian of electron density
• Value of orbital wavefunction
• Electron spin density
• Hamiltonian kinetic K(r)
• Lagrangian kinetic G(r)
• Electrostatic potential from nuclear / atomic charges
• Electron localization function (ELF) defined by Becke and the one defined by Tsirelson
• Localized orbital locator (LOL) defined by Becke and the one defined by Tsirelson
• Local information entropy
• Electrostatic potential (ESP)
• Reduced density gradient (RDG) with/without promolecular approximation
• Sign(lambda2)*rho (The product of the sign of the second largest eigenvalue of electron
density Hessian matrix and electron density) with/without promolecular approximation
• Exchange-correlation density, correlation hole and correlation factor
• Average local ionization energy
• Source function
• Electron delocalization range function EDR(r;d) and orbital overlap distance function D(r)
(Related code was kindly contributed by Arshad Mehmood)
Others: Such as potential energy density, electron energy density, shape function, local
temperature, bond metallicity, linear response kernel, local electron
affinity/electronegativity/hardness, ellipticity of electron density, eta index, on-top pair density,
numerous DFT exchange-correlation potential, Weizsäcker potential, Fisher information entropy,
Ghosh/Shannon entropy density, integrand of Rényi entropy, steric energy/potential/charge, Pauli
potential/force/charge, quantum potential/force/charge, PAEM, density overlap regions indicator
(DORI), region of slow electrons (RoSE), PS-FID, single exponential decay detector (SEDD),
electron linear momentum density, electric/magnetic dipole moment density, local electron
correlation function.
Implementing a new real space function into Multiwfn is extremely easy, as illustrated in
Section 2.7 of the manual.
Citing Multiwfn
If Multiwfn is used in your research, this paper should be cited:
If quantitative molecular surface analysis module of Multiwfn is involved, citing below paper
is also highly welcomed, in which the algorithm was described in detail
If orbital composition analysis module of Multiwfn is involved, citing below paper is
recommended, in which different orbital composition calculation methods are detailedly discussed
Tian Lu, Feiwu Chen, Quantitative analysis of molecular surface based on
improved Marching Tetrahedra algorithm, J. Mol. Graph. Model., 38, 314-323 (2012)
Tian Lu, Feiwu Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J.
Comput. Chem. 33, 580-592 (2012)

1 Overview
5
If CDA module of Multiwfn is involved, citing below paper is recommended, in which the
generalized CDA method that implemented in Multiwfn is introduced
Citing Multiwfn website in your work is also highly welcomed, but please do not ONLY cite
the website, thanks!
Discussion zone
There are two Multiwfn official forums, with different languages. You can discuss anything
about Multiwfn and wavefunction analysis in either one.
Multiwfn English forum: http://sobereva.com/wfnbbs
Multiwfn Chinese forum: http://bbs.keinsci.com/forum.php?mod=forumdisplay&fid=112
Meng Xiao, Tian Lu, Generalized Charge Decomposition Analysis (GCDA)
Method, Journal of Advances in Physical Chemistry, 4, 111-124 (2015) (in Chinese)
http://dx.doi.org/10.12677/JAPC.2015.44013
Tian Lu, Feiwu Chen, Calculation of Molecular Orbital Composition, Acta Chim.
Sinica, 69, 2393-2406 (2011) (in Chinese)

2 General information
6
2 General information
2.1 Install
2.1.1 Windows version
What you need to do is just uncompressing the program package. You can place Multiwfn
anywhere, however the name of the path (including file name) should less than 80 characters,
otherwise some unexpected problems may occur. A few functions in Multiwfn rely on Gaussian,
you may need to setup environment variable for Gaussian manually, see Appendix 1.
Multiwfn is compatiable with 32 or 64bit version of Windows XP/Vista/7/8/10.
2.1.2 Linux version
1 Uncompress the program package to for example /sob/Multiwfn. Notice that the path
(including file name) should less than 80 characters.
2 Make sure that you have installed openmotif package, which provides libXm.so.4,
Multiwfn cannot boot up without this file. The openmotif is freely available at
http://motif.ics.com/motif/downloads. If you are a CentOS/RHEL user, download corresponding
rpm package (e.g. motif-2.3.4-1.x86_64_0.rpm); if you are a Ubuntu user, download
corresponding deb package (e.g. libmotif4_2.3.4-1_amd64.deb). Then install the package.
3 Add below sentense to your .bashrc file, e.g. /root/.bashrc, then reboot your shell
export KMP_STACKSIZE=64000000
KMP_STACKSIZE defines stacksize (in bytes) for each thread in parallel implementation,
see Section 2.4 for detail.
4 Run /sbin/sysctl -a|grep shmmax to check if the size of SysV shared memory segments is
large enough (unit is in bytes), if the value is too small, Multiwfn may crashes when analyzing big
wavefunction. In order to enlarge the size, for example you can add kernel.shmmax = 512000000
to /etc/sysctl.conf and reboot system, then the upper limit will be enlarged to about 512MB.
5 If you prefer to boot up Multiwfn from different folders, you'd better set Multiwfnpath
environment variable, so that Multiwfn can find settings.ini file properly (see Section 2.3 for more
detail about this file). For example, the executable file of Multiwfn is
/sob/Multiwfn_3.3.8_bin_Linux/Multiwfn, then Multiwfnpath should be set to /sob/
Multiwfn_3.3.8_bin_Linux.
Linux version of Multiwfn works well on Red Hat Enterprise Linux 6 & 7, CentOS 6 & 7
and Ubuntu 12. I can not guarantee that the program is completely compatible with all other Linux
distributions. If system prompts you that some dynamical link libraries (.so files) are missing
when booting up Multiwfn, try to find and install the packages which contain corresponding .so
files.
If you are using using Ubuntu and Multiwfn crashes when dealing with large systems, try adding "ulimit -s
unlimited" in your .bashrc file to set the available stacksize to be formally unlimited. Because Ubuntu is one of the
most foolish systems that I have ever used, its default stacksize is quite small (8MB in some versions)!
If you encounter difficulty when running/compiling Multiwfn due to missing or incompatibility of some

2 General information
7
graphical related library files, and in the meantime you don't need visualization functions in Multiwfn, you can
run/compile Multiwfn without GUI supported, all functions irrelevant to GUI and map plotting will still work
normally. Please check document of compilation method in source code package on how to compile this version,
the pre-compiled binary of this version can also be downloaded from Multiwfn website (termed as noGUI version).
2.1.3 Mac OS version
If you are using relatively old Mac OS version, e.g. OS X 10.8, please follow the instruction
given in this section. If you intend to install Multiwfn in relatively new Mac OS systems, such as
OS X 10.11 EI Capitan and macOS 10.12 Sierra, please follow steps in this page:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:multiwfn.
1 Uncompress the program package to for example /Users/sob/Multiwfn. Notice that the path
(including file name) should less than 80 characters.
2 Download .dmg file of Mac OS version of openmotif from http://www.ist-
inc.com/downloads/motif_download.html and then install it. The openmotif package I installed is
openmotif-compat-2.1.32_IST.macosx10.5.dmg.
If your system does not natively support X11 (i.e. OS X Mountain Lion), you should
download XQuartz from http://xquartz.macosforge.org/landing and install it.
3 Add below sentense to your .profile file (e.g. /Users/sob/.profile) to make them take effect
automatically, then reboot your terminal. If the .profile is unexisting, you should create it manually.
export KMP_STACKSIZE=64000000
KMP_STACKSIZE defines stacksize (in bytes) for each thread in parallel implementation,
see Section 2.4 for detail.
4 Run sysctl -a|grep shmmax to check if the size of SysV shared memory segments is large
enough (unit is in bytes), if the value is too small, Multiwfn may crashes when analyzing big
wavefunction. In order to enlarge the size, you should edit or create the file /etc/sysctl.conf, and
add kern.sysv.shmmax = 512000000 to it and reboot system, then the upper limit will be enlarged
to about 512MB.
5 Move libdislin_d.11.dylib in the Multiwfn package to /usr/local/lib folder.
6 Set Multiwfnpath environment variable if needed, see point 5 of Section 2.1.2.
Now enjoy!
2.2 Using Multiwfn
Using Multiwfn is very easy, simply read the prompts printed on screen, you will know what
should input next. If you are stuck, please read corresponding section carefully in Chapter 3 or
corresponding tutorials in Chapter 4.
The first thing to do after boot up Multiwfn is inputting the path of the input file, e.g.
E:\ltwd\bitboys.wfn. If the input file is in current directory, you can input file name without the
path of directory. If the input file is just the one that last time used, you can simply input the letter
o (The path of the input file successfully read at last time was recorded in settings.ini). If the input
file is in the same path as the one last time used, for convenience, the path can be replaced by
symbol ?. For example, last time you loaded c:\sob\wives\K-ON\Mio.wfn, this time you can
simply input ?Azusa.fch to load c:\sob\wives\K-ON\Azusa.fch. If you preferred to select file in
2 General information
8
GUI window, you can directly press ENTER button, then a GUI window will be shown used to
select input file.
You can press CTRL+C or click “×” button at right-top of command-line window any time to
exit Multiwfn. When graphical window is showing on screen, you can click “RETURN” button to
close the window, if there is no such button, click right mouse button on the graph to close it.
Another way (an elegant way) to exit Multiwfn is selecting option -10 (an hidden option) in main
function menu.
If you want to load another file into Multiwfn, you can reboot Multiwfn or start a new
Multiwfn task. Alternatively, in main function menu you can select option -11 (a hidden option) to
re-initialize Multiwfn and load a new file.
Multiwfn also supports silent mode, by which users needn’t to click any button during
running, it is useful for batch process or repeating similar tasks, please consult Chapter 5.
All involved theories and options in Multiwfn are introduced in Chapter 3. Numerous
tutorials, which cover most important functions of Multiwfn are provided in Chapter 4.
2.3 The files of Multiwfn
You will find following files after uncompressing Multiwfn package, only the bolded files are
indispensable for running Multiwfn:
Multiwfn.exe (Windows) or Multiwfn (Linux/Mac OS) : The executable file of Multiwfn.
libiomp5md.dll (Windows) : Intel OpenMP Runtime library.
settings.ini : All detail parameters for running Multiwfn are recorded here, most of them do
not need to be frequently modified. When booting up, Multiwfn will try to find and use this file in
current folder, if it is not presented in current folder, the file in the path defined by "Multiwfnpath"
environment variable will be used; if the file still cannot be found, default settings will be used
instead. The meanings of all parameters in settings.ini are not documented in this manual
systematically, since they have already been commented in detail, only those important will be
mentioned in this manual. I suggest you read through settings.ini and find out the ones useful for
you.
“examples” folder : Some useful files and the files involved in examples of Chapter 4.
2.4 Parallel implementation
Most time-consuming codes of Multiwfn have been parallelized by OpenMP. If your
computer is SMP architecture, you can greatly benefit from parallelization (For grid calculation,
the speed up ratio versus the number of CPU cores is nearly linear). To enable parallel mode, just
modify “nthreads” parameter in settings.ini to your situation. For example, your computer have a
12-cores CPU installed, then change “nthreads” to 12.
If Multiwfn crashes during parallel calculation, try to enlarge “ompstacksize” in settings.ini
(for Windows version) or enlarge the value of the environment variable KMP_STACKSIZE (for
Linux or Mac OS version).
2 General information
9
2.5 Input files and wavefunction types
Wavefunction types supported by Multiwfn include restricted/unrestricted single-determinant
wavefunction, restricted open-shell wavefunction and post-HF wavefunction (in natural orbital
formalism).
For basis function, Cartesian or spherical harmonic Gauss functions with angular moment up
to h are supported.
There is no upper limit of the number of atoms / basis functions / GTFs / orbitals in Multiwfn,
the actual upper limit is only decided by available memory on your computer.
Multiwfn determines the input file type by file extension. Notice that different function need
different types of information, you should choose proper type of input file, see the table below. For
example, the wavefunction represented by GTFs is enough for Hirshfeld population, so you can
use .fch/.molden/.gms/.31~.40/.wfn/.wfx file as input, but .pdb, .xyz, .mol, .chg, .cub and .grd files
do not carry any wavefunction information hence cannot be used. While generating grid data of
RDG function with promolecular approximation only requires atom coordinates, so all supported
file formats can be used (except for plain text file). The requirements of information types by each
function are described at the end of corresponding section in Chapter 3 by red text.
Contained information types
File Format
Basis functions GTFs Atom
coordinates Grid data
.fch/.fchk
.molden
.gms
.31~.40
.wfn
.wfx
.pdb .xyz .mol
.chg
.cub/.cube
DMol3 .grd
Plain text file
1 PROAIM wavefunction file (.wfn) : This format was first introduced by Bader’s AIMPAC
program, and currently supported by a lot of mainstream quantum chemistry softwares, such as
Gaussian, GAMESS-US/UK, Firefly, Q-Chem. The information of .wfn files include atomic
coordinates/types, orbital energies, occupation numbers, expansion coefficients of Cartesian Gauss
type functions (GTF). Supported angular momentum of GTF is up to f. The wfn file does not
contain any virtual orbital. The generation method of .wfn file is documented at the beginning of
2 General information
10
Chapter 4.
Note: Although GTFs with angular moment of g and h are not formally supported by original .wfn format, if g
and h-type GTFs are recorded in following manner, then Multiwfn is able to recognize them: 21~35 in "TYPE
ASSIGNMENT" correspond to YZZZ, XYYY, XXYY, XYZZ, YZZZ, XYYZ, XXXX, XXXY, XZZZ, XXYZ,
XXXZ, XXZZ, YYYY, YYYZ, ZZZZ, respectively. 36~56 correspond to ZZZZZ, YZZZZ, YYZZZ, YYYZZ,
YYYYZ, YYYYY, XZZZZ, XYZZZ, XYYZZ, XYYYZ, XYYYY, XXZZZ, XXYZZ, XXYYZ, XXYYY,
XXXZZ, XXXYZ, XXXYY, XXXXZ, XXXXY, XXXXX, respectively. The sequence shown here in fact is also
the sequence used in the .wfn outputted by Molden2AIM and Gaussian09 since B.01.
2 AIM extended wavefunction files (.wfx) : This is a newly introduced format as an
extension of .wfn, the file can be generated by Gaussian09 since B.01 revision. Relative to .wfn
format, .wfx supports higher data precision and infinite high angular moment of GTF. The most
special point is the newly added electron density function (EDF) field, that is using multiple GTFs
to represent inner core electron density of the wavefunction in which effective core potential (ECP)
is used. Thus, the results of electron density analysis of the wavefunction used ECP are nearly
identical to full electron wavefunction. Currently the real space functions supported EDFs in
Multiwfn include: electron density, its gradient and Laplacian, local information entropy, reduced
density graident as well as Sign(λ2(r)). Meanwhile topology analyses of electron density and its
Laplacian also take into account EDFs. Notice that EDF informations have neither effect on ESP
nor the real space functions that relied on wavefunction (e.g. kinetic energy density, ELF). If you
you want to analyze these properties for heavy elements, you should use full-electrons basis-sets,
at lease small-core ECP. Currently the only supported GTF type in EDF field is S-type (actually S-
type is enough for fitting inner density, since which is nearly spherical symmetry). Like .wfn,
Multiwfn does not allow virtual orbitals presented in .wfx file.
Notice that for certain version of Gaussian (e.g. G09 B.01), I found that the EDF field
recorded in .wfx for rare cases is problematic, namely the number of electrons represented by EDF
field is unequal to the actual number of core electrons exhibited by ECP. In order to verify if the
EDF field is correct, you can use subfunction 4 in main function 100 to obtain the integral of total
electron density over the whole space, if the result is approximately equal to the total number of
electrons (core+valence electrons), that means the EDF field is correct.
Multiwfn has a powerful built-in EDF library, as long as the input file contains GTF
information (e.g. .fch and .wfn ...), Multiwfn always automatically loads EDF information from
this library for the atoms using pseudopotential basis set. Only when you use .wfx file as input and
the .wfx itself already contains EDF field, the EDF information will be loaded from the .wfx file
rather than from EDF library. See Appendix 4 for more details.
3 Gaussian formatted checkpoint file (.fch/.fchk) : Checkpoint file of Gaussian program
(.chk) can be converted to formatted checkpoint file (.fch/.fchk) via formchk utility in Gaussian
package. There is no any difference between .fch and .fchk. "fch" ("fchk") is the default extension
generated by Windows (Linux) version of formchk.
.fch/.fchk contains richer information than .wfn/.wfx files, virtual orbital wavefunctions are
also recorded, and meanwhile it provides basis function information for Multiwfn. If you want to
use .fch/.fchk file as carrier for post-HF wavefunction, read the beginning of Chapter 4 carefully!
Notice that for single-determinant wavefunctions, before some calculations involving real
space function (e.g. main function 2, 4, 5), virtual orbitals higher than LUMO+10 will be deleted
automatically to speed up calculations, therefore you cannot analyze those orbitals after the
2 General information
11
calculation, unless you reboot Multiwfn. If you want to disable this treatment, set "idelvirorb" in
settings.ini to 0.
The .fch file generated by Q-Chem and PSI4 can also be used as input file of Multiwfn.
4 Molden input file (.molden or .molden.input) : Currently, a wide variety of quantum
chemistry packages, such as Molpro, Molcas, ORCA, Q-Chem, CFour, Turbomole, PSI, MRCC
and NWChem are able to produce input file of Molden visualization program. This type of file
records atomic coordinates, basis set definition, information of all occupied and virtual orbitals
(including expansion coefficient of basis functions, occupation number, spin, energy and
symmetry), meanwhile there is no information only specific for Molden. So in fact, Molden input
file can be regarded as a standard and general file format for exchanging wavefunction
information. For Multiwfn, this type of file can provide atomic coordinate, basis function
information and GTF information. .molden file supports basis functions up to g angular moment.
Beware that the Molden input files produced by a lot of program are quite non-standard,
currently Multiwfn only supports the Molden input file generated by Molpro, ORCA, MRCC
(only for spherical harmonic case), deMon2k and BDF. If the Molden input file you used is
generated by other programs, the analysis result may or may not be correct, you should first use
the methods described in Appendix 5 to check if the wavefunction has been correctly loaded.
Hint: Multiwfn fully supports the Molden input file standardized by molden2aim utility (see Section 5.1 for
detail), which is able to properly recognize Molden input files generated by many other quantum chemistry codes,
such as CFOUR and Molcas.
Although Molden input file also supports Slater type orbital (STO), Multiwfn can only utilize
the Molden input file recording Gauss type basis functions.
One drawback of Molden input file is that it does not explicitly record nuclear charges as
other formats such as wfn and fch, therefore the results relying on nuclear charges (e.g.
electrostatic potential) will be problematic when pseudo-potential is used. To address this problem,
Multiwfn loads atomic indices in the file (i.e. the third column in [Atoms] field) as nuclear charges,
thus if you manually change the atomic index as the number of atomic valence electrons that
explicitly represented in the quantum chemistry calculation, then the result will be correct. (Note
that Multiwfn determines element of each atom according to atomic name in .molden file,
therefore even after above modification, the elements can still be correctly identified)
A disadvantage of Molden input file as wavefunction carrier is that its format is not as
compact as .fch. Due to this fact, for the same wavefunction, the loading speed of .molden file is
much slower than .fch. Therefore, if you need to frequently analyze a .molden file, I suggest you
use subfunction 2 of main function 100 to convert it to .fch format.
In analogy to .fch file, Multiwfn may delete virtual orbitals higher than LUMO+10. To avoid
this, you should set "idelvirorb" in settings.ini to 0.
PS: Detailed description about .molden format can be found on Molden official site:
http://www.cmbi.ru.nl/molden/molden_format.html.
5 GAMESS-US output file (.gms): If you want to use GAMESS-US output file as input file,
you can change its suffix as .gms, then Multiwfn will properly recognize it. Currently, I can only
guarantee that output file of HF/DFT calculation with default NPRINT option can be normally
loaded by Multiwfn. The role of .gms is similar as .molden and .fch file, i.e. all of them provide
atomic coordinates, GTF and basis function informations.
2 General information
12
6 Plot files of NBO program (.31~.40) : The main purpose of supporting these file types is
for visualizing PNAO/NAO/PNHO/NHO/PNBO/NBO/PNLMO/NLMO/MO (their orbital
coefficients are recorded in .32~.40 respectively), .31 recorded basis function information. After
boot up Multiwfn, you should input the path of .31 file first, and then input the path of one
of .32~.40 files (for simplicity, you can only input the suffix when the filenames are identical).
Notice that among all types of the orbitals generated by NBO program, only using NBO or
NLMO to calculate real space functions is meaningful!
7 Protein data bank format (.pdb), .xyz format and MDL Molfile (.mol) format : These
are the most widely used formats for recording atom coordinates. They do not carry any
wavefunction information, but for the functions which only require atom coordinates, using these
kind of files as input is enough. A unique advantage of .mol with respect to .pdb and .xyz is that it
contains atomic connectivity table, which is need by a few functions of Multiwfn, e.g. Calculation
of EEM atomic charges.
Notice that the .mol file supported by Multiwfn is V2000 version, both the maximum number
of atoms and bonds that can be recorded are 999. More description about .mol format can be
found in https://en.wikipedia.org/wiki/Chemical_table_file.
8 Charge files (.chg) : This type of plain text file can be generated by some functions of
Multiwfn (e.g. population analysis functions), it contains element names (less than or equal to two
characters), atom coordinates (first three columns, in Angstrom) and charges (the fourth column),
users can modify them manually. The main use of this format is to visualize electrostatic potential
and analyze it on molecular surface based on atomic charges. An example of .chg file is given
below:
O 0.000000 0.000000 0.119308 -0.301956
H 0.000000 0.758953 -0.477232 0.150977
H 0.000000 -0.758953 -0.477232 0.150977
9 Gaussian-type cube file (.cub or .cube) : This is the most prevalent volumetric data
format, can be generated by vast computational chemistry softwares and can be recognized by the
majority of molecular graphics programs. Atom coordinates, a set of grid data of real space
function or multiple sets of grid data of molecular orbitals could be recorded in this file. Multiwfn
only supports cubic grid, that means the three translation vectors must be parallelized with
Cartesian axes. After cube file is loaded into Multiwfn, one can choose main function 0 to
visualize isosurfaces, or use main function 13 to process the grid data.
10 DMol3 grid file (.grd) : .grd file is the volumetric data format mainly used by DMol3
program. This file is very similar to .cub file, but atomic information is completely omitted.
11 Plain text file: This file type is only used for special functions, such as plotting DOS
graph, plotting spectrum, generating Gaussian input file with initial guess. See explanations in
corresponding sections. Gaussian output files also belong to this type.
2 General information
13
2.6 Real space functions
Real space function analysis is one of the most important functions of Multiwfn, the
supported real space functions are listed below. All wavefunctions are assumed to be real type, all
units are in atomic unit (a.u.).
Notice that for speeding up calculation, especially for big system, when evaluating a
exponential function (except for some real space functions, such as 12, 14 and 16), if the exponent
is more negative than -40, then this evaluation will be skipped. The default cutoff value is safe
enough and cannot cause detectable loss of precision even in quantitive analysis, you can also
disable this treatment or adjust cutoff, see “expcutoff” in settings.ini.
1 Electron density
il lili
iii C
2
.
2)()()( rrr
where
i is occupation number of orbital i,
is orbital wavefunction,
is basis function. C is
coefficient matrix, the element of ith row jth column corresponds to the expansion coefficient of
orbital j respect to basis function i. Atomic unit for electron density can be explicitly written as
|e|/Bohr3.
2 Gradient norm of electron density
2
2
2)()()(
)(
zyx
rrr
r
3 Laplacian of electron density
2
2
2
2
2
2
2)()()(
)( zyx
rrr
r
The positive and negative value of this function correspond to electron density is locally
depleted and locally concentrated respectively. The relationships between
2
and valence
shell electron pair repulsion (VSEPR) model, chemical bond type, electron localization and
chemical reactivity have been built by Bader and many other researchers.
If “laplfac” in settings.ini is set to other value rather than the default one 1.0, )(
2r
will
be multiplied with this value. Setting it to negative value is convenient for analysis of electron
density concentration.
4 Value of orbital wavefunction
llili C)()( ,rr
When you select this function, you will be prompted to input the index of orbital i.

2 General information
14
5 Electron spin density
Spin density is defined as the difference between alpha and beta density
)()()( rrr
s
If “ipolarpara” in settings.ini is set to 1, then spin polarization parameter function will be
returned instead of spin density
)()(
)()(
)( rr
rr
r
The absolute value of going from zero to unity corresponds to the local region going from
unpolarized case to completely polarized case.
6 Hamiltonian kinetic energy density K(r)
The kinetic energy density is not uniquely defined, since the expected value of kinetic energy
operator
|)2/1(| 2 can be recovered by integrating kinetic energy density from
alternative definitions. One of commonly used definition is
iiii
K)()(
2
1
)( 2* rrr
7 Lagrangian kinetic energy density G(r)
Relative to K(r), the local kinetic energy definition given below guarantee positiveness
everywhere, hence the physical meaning is clearer and more commonly used. G(r) is also known
as positive definite kinetic energy density.
i
iii
i
iii zyx
G
2
2
2
2)()()(
2
1
)(
2
1
)( rrr
rr
Since iiiiii
2)( 2, there is an equivalent form of G(r):
ii
ii
8
1.
K(r) and G(r) are directly related by Laplacian of electron density
)()(4/)(
2rrr KG
8 Electrostatic potential from nuclear / atomic charges
AA
A
Z
VRr
r)(
nuc
where RA and ZA denote position vector and nuclear charge of atom A, respectively. If pseudo-
potential is used, then Z is the number of explicitly expressed electrons. When .chg file is used as
input, Z will stand for the atomic charges recorded in the file (the fourth column), at this time Vnu
is useful for analyzing the difference between exact electrostatic potential and the electrostatic
potential reproduced by atomic charges.
2 General information
15
Notice that at nuclear positions, this function will be infinite and may cause some numerical
problems in program, hence at these cases this function always returns 1000 instead of infinity.
9 Electron localization function (ELF)
The larger the electron localization is in a region, the more likely the electron motion is
confined within it. If electrons are completely localized, then they can be distinguished from the
ones outside. Bader found that the regions which have large electron localization must have large
magnitudes of Fermi hole integration. However, the Fermi hole is a six-dimension function and
thus difficult to be studied visually. Becke and Edgecombe noted that spherically averaged like-
spin conditional pair probability has direct correlation with the Fermi hole and then suggested
electron localization function (ELF) in the paper J. Chem. Phys., 92, 5397. The ELF used in
Multiwfn is generalized for spin-polarized system, see Acta Phys. -Chim. Sin., 27, 2786
(http://www.whxb.pku.edu.cn/EN/abstract/abstract27788.shtml) for derivation. For a review, see
Chapter 5 of Theoretical Aspects of Chemical Reactivity (2007).
2
0)](/)([1
1
)ELF( rr
rDD
where
])()([6
10
3
)(
)(
)(
)(
)(
8
1
)(
2
1
)(
3/53/5
3/2
2
0
2
2
2
rrr
r
r
r
r
rr
D
D
iii
For close-shell system, since
)2/1(
, D and D0 terms can be simplified as
3/53/22
0
2
2
)()3)(10/3()(
)(
)(
8
1
)(
2
1
)(
rr
r
r
rr
D
D
iii
Savin et al. have reinterpreted ELF in the view of kinetic energy, see Angew. Chem. Int. Ed.
Engl., 31, 187, which makes ELF also meaningful for Kohn-Sham DFT wavefunction or even
post-HF wavefunction. They indicated that D(r) reveals the excess kinetic energy density caused
by Pauli repulsion, while D0(r) can be considered as Thomas-Fermi kinetic energy density. Since
D0(r) is introduced into ELF as reference, what the ELF reveals is actually a relative localization.
ELF is within the range of [0,1]. A large ELF value means that electrons are greatly localized,
indicating that there is a covalent bond, a lone pair or inner shells of the atom involved. ELF has
been widely used for a wide variety of systems, such as organic and inorganic small molecules,
atomic crystals, coordination compounds, clusters, and for different problems, such as the
revealing atomic shell structure, classification of chemical bonding, verification of charge-shift
bond, studying aromaticity.
Notice that there is a deficiency of ELF, sometimes with r going beyond from molecular
boundary, D(r) decreases faster than D0(r) and then ELF reaches 1 (completely localized). To

2 General information
16
overcome the problem, Multiwfn automatically adds a minimal value 10-5 to D(r), this treatment
almost does not affect the ELF value in interesting regions. You can also disable this treatment by
modifying “ELF_addminimal” in settings.ini to 0.
Tsirelson and Stash put forward an approximate version of ELF in Chem. Phys. Lett., 351,
142, in which the actual kinetic energy term in D(r) is replaced by Kirzhnits type second-order
gradient expansion, that is
)()6/1()(/)()72/1()()()2/1( 2
2
0
2rrrrr
D
iii
so that ELF is totally independent from wavefunction, and then can be used to analyze electron
density from X-ray diffraction data. Of course Tsirelson’s ELF can also be used to analyze
electron density from quantum chemistry calculation, but is not as good as the ELF defined by
Becke owing to the approximation introduced in kinetic energy term, however, qualitative
conclusions can still be recovered in general. If you want to use Tsirelson’s definition of ELF,
change “ELFLOL_type” in settings.ini from 0 to 1.
If “ELFLOL_type” is set to 2, another formalism will be used:
)(/)(1
1
0rr DD.
If the parameter "ELFLOL_cut" in settings.ini is set to x, then ELF will be zero where ELF is
less than x.
10 Localized orbital locator (LOL)
This is another function for locating high localization regions likewise ELF, defined by
Schmider and Becke in the paper J. Mol. Struct. (THEOCHEM), 527, 51.
)(1
)(
)LOL( r
r
r
where
iii
D
2
0
)()2/1(
)(
)( r
r
r
D0(r) for spin-polarized system and close-shell system are defined in the same way as in ELF.
LOL has similar expression compared to ELF. Actually, the chemically significant regions
that highlighted by LOL and ELF are generally qualitative comparable, while Jacobsen pointed
out that LOL conveys more decisive and clearer picture than ELF, see Can. J. Chem., 86, 695.
Obviously LOL can be interpreted in kinetic energy way as for ELF, however LOL can also be
interpreted in view of localized orbital. Small (large) LOL value usually appears in boundary
(inner) region of localized orbitals because the gradient of orbital wavefunction is large (small) in
this area. The value range of LOL is identical to ELF, namely [0,1].
Multiwfn also supports the approximate version of LOL defined by Tsirelson and Stash (Acta.
Cryst., B58, 780), namely the actual kinetic energy term in LOL is replaced by second-order
gradient expansion, as what they do for ELF. This Tsirelson’s version of LOL can be activated by
setting “ELFLOL_type” to 1.

2 General information
17
For special reason, if “ELFLOL_type” in settings.ini is changed from 0 to 2, another
formalism will be used: 2
)](/1[1
1
)LOL( r
r
.
If the parameter "ELFLOL_cut" in settings.ini is set to x, then LOL will be zero where LOL
is less than x.
11 Local information entropy
Information entropy is a quantification of information, this theory was proposed by Shannon
in his study of information transmission in noise channel, nowadays its application has been
largely widened to other areas, including theoretical chemistry. For example, Aslangul and
coworkers attempted to decompose diatomic and triatomic molecules into mutually exclusive
space by minimizing information entropy (Adv. Quantum Chem., 6, 93), Parr et al. discussed the
relationship between information entropy and atom partition as well as molecular similarity (J.
Phys. Chem. A, 109, 3957), Noorizadeh and Shakerzadeh suggested using information entropy to
study aromaticity (Phys. Chem. Chem. Phys., 12, 4742). The formula of Shannon’s information
entropy for normalized and continuous probability function is
dxxPxPS )(ln)(
For chemical system, if P(x) is replaced by N/)(r
, then the integrand may be called local
information entropy of electrons
NN
S)(
ln
)(
)( rr
r
where N is the total number of electrons in current system. Integrating this function over whole
space yields information entropy.
12 Total electrostatic potential (ESP)
'
'
)'(
)()()( elenucESP r
rr
r
Rr
rrr d
Z
VVV
AA
A
where ZA is nuclear charge. If pseudopotential is used, then ZA is the number of explicitly
expressed electrons
This function measures the electrostatic interaction between a unit point charge placed at r
and the system of interest. A positive (negative) value implies that current position is dominated
by nuclear (electronic) charges. Molecular electrostatic potential (ESP) has been widely used for
prediction of nucleophilic and electrophilic sites for a long time. It is also valuable in studying
hydrogen bonds, halogen bonds, molecular recognitions and the intermolecular interaction of
aromatics. Moreover, based on statistical analysis, Murray and coworkers found a set of functions
called GIPF, see J. Mol. Struct. (THEOCHEM), 307, 55, which connects ESP in molecular surface
and macroscopic properties. There are a lot of reviews on ESP, interested readers are suggested to
consult WIREs Comput. Mol. Sci., 1, 153 (2011), Theor. Chem. Acc., 108, 134 (2002), Chapter 17
of the book Chemical Reactivity Theory-A Density Functional View, the entry "Electrostatic
Potentials: Chemical Applications" (page 912) in the book Encyclopedia of Computational

2 General information
18
Chemistry and Chapter 7 of the book Reviews in Computational Chemistry vol.2.
Notice that evaluating ESP is much more time-consuming than evaluating other functions.
Also note that ESP in Multiwfn is evaluated exactly by nuclear attractive integrals rather than
using approximate methods (such as multipole expansion, numerical Poisson equation), hence you
may find the results generated by Multiwfn are somewhat different from those outputted by other
quantum chemistry codes.
In order to speed up ESP evaluation, Multiwfn ignores some integrals that have little
contributions. The threshold for ignoring is controlled by "espprecutoff" in settings.ini, enlarging
this parameter results in more accurate ESP value, but also brings more computational cost. The
ESP evaluated under default value is accurate enough in general cases.
By the way, if you only want to obtain the electrostatic potential contributed by electrons,
namely Vele(r), you can use the 14th user-defined function. If you want to omit contribution of
specific nucleus during evaluating VESP(r), use 39th user-defined function. See corresponding
entris in Section 2.7 for details.
13 Reduced density gradient (RDG)
RDG and Sign(-2)*
are a pair of very important functions for revealing weak interaction
region, see J. Am. Chem. Soc., 132, 6498 (2010) for detail. The basic applications are exemplified
in Sections 4.100.1 and 4.200.1. RDG is defined as
3/43/12 )(
)(
)3(2
1
)RDG( r
r
r
Notice that there is a parameter “RDG_maxrho” in settings.ini, if the value is set to x, then
RDG function will be set to an arbitrary big value (100.0) where the electron density is larger than
x. This mechanism allows uninteresting regions to be shielded when viewing isosurfaces of weak
interaction regions. By default x is 0.05, you can nullify this treatment by setting the parameter to
zero.
14 Reduced density gradient (RDG) with promolecular approximation
Weak interaction has significant influence on conformation of macromolecules, binding
mode of proteins and ligands; however reproduction of electron density by ab initio and grid data
calculation of RDG for such huge systems are always too time-consuming. Fortunately, it is found
that weak interaction analysis under promolecular density is still reasonable. Promolecular density
is simply constructed by superposing electron densities of free-state atoms and hence can be
evaluated extremely rapidly
AAA )()( free,fitpro Rrr
where )(
fitfree, r
A
is pre-fitted spherically averaged electron density of atom A. The atomic
densities for H~Lr are built-in data of Multiwfn, among which the data for H~Ar are taken from
supplemental material of J. Am. Chem. Soc., 132, 6498 (2010), while those for other elements are
evaluated according to the description in Appendix 3. For elements heavier than Lr the
promolecular approximation is not currently available.
For efficiency consideration, if contribution from H, C, N or O atom to the function value at a specific point is
less than 0.00001, then the contribution will not be calculated, for huge system this treatment improves efficiency

2 General information
19
several times and the result is almost unperturbed. You can also disable this treatment by setting “atomdenscut” in
settings.ini to 0.
The parameter “RDGprodens_maxrho” in settings.ini is the counterpart of “RDG_maxrho” in
the case of promolecular approximation.
15 Sign(lambda2)*rho
)())(()( 2rrr
-
Sign
where Sign(λ2(r)) means the sign of the second largest eigenvalue of electron density Hessian
matrix at position r.
16 Sign(lambda2)*rho with promolecular approximation
The real density used to determine Sign(λ2(r)) is approximated by promolecular electron
density, see the description in real space function 14.
17 Exchange-correlation density, correlation hole and correlation factor
These functions involve advanced topics, in order to clarify their physical meanings and to
avoid confusion of the symbols used in a wide variety of literatures, I think it is worth to use much
more texts to introduce theoretical background. For more detail discussions, please consult
Chapter 2 of A Chemist's Guide to Density Functional Theory 2ed and Chapter 5 of Methods of
molecular quantum mechanics (2ed, McWeeny).
======= Theoretical basis ======
Pair density is defined as
NN dddddNN xxxxxxrr ...)...,()1(),( 4321
2
2121
where Ψ is system wavefunction, r is space coordinate, σ is spin coordinate, x is space-spin
coordinate. Pair density denotes the probability that finding an electron at r1 and another electron
at r2, regardless of the spin type. If we perform double-integration for pair density over the whole
space, we will get N(N-1), reflecting the nature that there are N(N-1) electron pairs in present
system. Obviously, pair density can be decomposed to contributions from different spin types of
electron pairs
),(),(),(),(),( 2121212121 rrrrrrrrrr
If the electron motions are completely independent with each other, then the probability
density of finding two electrons with spin σ1 at r1 and with σ2 at r2 respectively should simply be
)()( 21 21 rr
. Of course, in real world electrons always interacting with each other, so their
motions are correlated. The pair density thereby should be corrected by exchange-correlation
density Г
),()()(),( 212121 212121 rrrrrr
XC
If we have already known that an electron with spin σ1 presents at r1, then the probability of
finding another electron with spin σ2 at r2 is known as conditional probability (This function is
also known as Lennard-Jones function)

2 General information
20
)(
),(
)(
)(
),(
),(
1
21
2
1
21
21 1
21
2
1
21
21 r
rr
r
r
rr
rr
XC
Correlation hole reveals the decrease of probability of finding another electron with spin σ2
at r2 when an electron with spin σ1 presents at r1 owing to electron correlation effect
)(
)(
),(
)(),(
)(
),(
),( 2
1
21
221
1
21
21 2
1
21
221
1
21
21 r
r
rr
rrr
r
rr
rr
XC
XC
h
Correlation factor is a function closely related to correlation hole
)()(
),(
)(
),(
),(
21
21
2
21
21 21
21
2
21
21 rr
rr
r
rr
rr
XCXC
XC
h
f
Collectively, one can write out
)],(1[)()(),()()()(),( 21212112121 21212112121 rrrrrrrrrrr
XCXC fh
ГXC can be decomposed to the sum of exchange correlation (also called as Fermi correlation)
part ГX and Coulomb correlation part ГC, therefore hXC can be straightforwardly decomposed to
exchange hole hX (also called as Fermi hole) and Coulomb hole hC as follows. Likewise, fXC can
be decomposed to fX and fC
),(),(),(
),(),(),(
),(),(),(
212121
212121
212121
212121
212121
212121
rrrrrr
rrrrrr
rrrrrr
CXXC
CXXC
CXXC
fff
hhh
Fermi correlation only presents between like-spin electrons; while Coulomb correlation
occurs between any two electrons. Fermi correlation is much more important than Coulomb
correlation, even at Hartree-Fock level, Fermi correlation is always well represented due to the
anti-symmetry requirement of Slater determinant, while Coulomb is completely ommited. Only
post-HF wavefunction is capable to simultaneously exhibit Fermi and Coulomb correlation effects.
Commonly we only focus on Fermi hole while neglecting Coulomb hole. One can easily show that
integration of hX over whole space is exactly equal to -1, hence Fermi correlation perfectly
avoided self-pairing problem, which may cause significant rise in system energy; while the
integration for hC is zero, this is mainly why Coulomb correlation has less influence on system
energy.
It is also rather straightforward to obtain the pair density and conditional probability when
only exchange correlation or Coulomb correlation is taken into account.
The total π, Ω, ГXC (or ГX, ГC) and hXC (or hX, hC) for an electron with spin σ, regardless the
spin of another electron can be defined as
),(),(),(
),(),(),(
),(),(),(
),(),(),(
212121
,
212121
,
212121
,
212121
,
rrrrrr
rrrrrr
rrrrrr
rrrrrr
XCXC
tot
XC
XCXC
tot
XC
tot
tot
hhh

2 General information
21
======= Technical aspects ======
For single-determinant wavefunctions, exchange-correlation density for an electron can be
explicitly written as
occ occ
212
*
1
*
2121
,)()()()(),(),(
ij ijjiXC
tot
XC rrrrrrrr
Note that 0),(),( 2121 rrrr
XCXC for this type of wavefunction. To obtain the
expression for β electron, just replace by β, similarly hereafterin.
For post-HF wavefunction, exact evaluation of pair density requires two-particle density
matrix (2PDM). Unfortunately 2PDM is very difficulty to be obtained, mainstream quantum
chemistry packages including Gaussian can't directly output it. In Multiwfn, exchange-correlation
density for post-HF wavefunction is approximately evaluated by natural orbital formalism. Note
that the approximate method is not unique, see J. Chem. Theory Comput., 6, 2736 for discussion.
The most popular form among them, which is firstly derived by Müller, is currently implemented
in Multiwfn as below. See Phys. Lett., 105A, 446, also see Mol. Phys., 100, 401 for extensive
discussion (especially equation 32).
ij ijjiji
tot
approxXC )()()()(),( 212
*
1
*
21
,,rrrrrr
Obviously, if occupation numbers of natural spin orbitals are integer (0 or 1), then tot
approxXC
,,
reduces to single-determinant form. so tot
approxXC
,,
can be regarded as a general form to evaluate
exchange-correlation density. Note that post-HF wavefunction has taken Coulomb correlation
between unlike-spin electrons into account, however there is no way to separate
approxXC,
and
approxXC,
from tot
approxXC
,,
.
The exchange-only part of Г for post-HF wavefunction can be approximately evaluated as
below (of course, there is no exchange correlation between β electron pair)
ij ijjijiapproxX
tot
approxX )()()()(),(),( 212
*
1
*
21,21
,
,rrrrrrrr
So Coulomb-only part of Г can be evaluated as (including both and β pair contributions)
ij ijjijiji
approxX
tot
approxXC
tot
approxC
)]()()()()[(
),(),(),(
212
*
1
*
21,21
,,21
,
,
rrrr
rrrrrr
Since we already have explicit expression to calculate ГXC term, other quantities introduced
eariler can be easily computed according to the relationships between them and ГXC. Recall that
iii
2
)()( rr .
Postscript: One can show that ),( 21
,,rr
tot
approxXC
also exactly holds the requirement that
2 General information
22
integration of r2 over the whole space is equal to )( 1
r
. However, in common, integrating r2
over the whole space for ),( 21
,
,rr
tot
approxX
and ),( 21
,
,rr
tot
approxC
deviate from )( 1
r
and
zero, respectively, which are basic properties of exact form of tot
X,
and tot
C,
.
======= Usage ======
In Multiwfn, r1 is seen as reference point and r2 is seen as variable, to define the coordinate
of reference point, just modifying “refxyz” in settings.ini before booting up.
“paircorrtype” parameter in settings.ini controls which type of correlation effect will be taken
into consideration in calculation of Г. Since correlation hole and correlation factor are calculated
based on Г, this setting also affects them. For single-determinant wavefunction, =1 and =3 are
equivalent and =2 is meaningless, because Coulomb correlation is completely ommited.
=1: Only consider exchange correlation
=2: Only consider Coulomb correlation
=3: Consider both exchange and Coulomb correlation
“pairfunctype” parameter in settings.ini controls which function and which spin will be
calculated by real space function 17, see below, those enclosed by parentheses are for single-
determinant wavefunction cases. Of course, for close-shell system, the results for spin are
exactly identical to those for β spin. Note that correlation factor for post-HF wavefunction case is
undefined.
=1: tot
h,
(
h) =2: tot
h,
(
h)
=4: Undefined (
f) =5: Undefined (
f)
=7: tot,
(
) =8: tot,
(
)
=10:
when paircorrtype =1 (
) =11:
when paircorrtype =1 (
)
=12: anyany,
( anyany,
)
For example, if paircorrtype=1 and pairfunctype=2, for post-HF wavefunction, what will be
calculated is ),( 21
,rr
tot
X
h
, which is equivalent to ),( 21 rr
X
h since β electron pairs have no
exchange correlation. This quantity can be interpreted as Fermi hole at r2 caused by a electron
present at r1.
18 Average local ionization energy
Average local ionization energy is written as (Can. J. Chem., 68, 1440)

2 General information
23
)(
||)(
)( r
r
r
iii
I
where )(r
i
and i
are the electron density function and orbital energy of the ith molecular
orbital, respectively. Hartree-Fock and typical DFT functionals such as B3LYP are both suitable
for computing )(rI. Lower value of )(rI indicates that the electrons at this point are more
weakly bounded. )(rI has widespread uses, for example revealing atomic shell structures,
measuring electronegativity, predicting pKa, quantifying local polarizability and hardness, but the
most important one may be predicting reactive site of electrophilic or radical attack. It is proved
that the minima of ALIE on vdW surface are good indicator to reveal which atoms are more likely
to be the preferential site of electrophilic or radical attack.. There are also many potential uses of
)(rI waiting for further investigation. Excellent reviews of )(rI have been given by Politzer
et al, see J. Mol. Model, 16, 1731 and Chapter 8 of the book Theoretical Aspects of Chemical
Reactivity (2007).
Since )(rI is dependent upon orbital energies, while orbital energy for post-HF
wavefunction is undefined, therefore when post-HF wavefunction is used, )(rI will be simply
outputted as zero everywhere.
If the parameter "iALIEdecomp" in settings.ini is set to 1, in main function 1, not only )(rI
will be outputted, the contribution from each occupied MOs will also be outputted, the
contribution due to MO i is defined as
)(
||)(
)( r
r
r
ii
i
I
19 Source function
Source function was proposed by Bader and Gatti, see Chem. Phys. Lett., 287, 233.
r'r
r'
r'r
4
)(
),( 2
SF
It can be shown that
'rr'rr
dSF ),()(
where r' ranges entire space. This equation suggests that ),( r'rSF represents the effect of
electronic Laplacian at r' on electron density at r. If at r' the electron is concentrated (namely
Laplacian is negative, also suggesting potential energy dominates kinetic energy), then r' will be a
source for the electron density at r; conversely, if at r' the electron is depleted, then r' diminish the

2 General information
24
electron density at r. If the range of integration in above formula is restricted to a local region
and we get a value S(r,), then S(r,)/ρ(r)*100% can be regarded as the contribution from region
to the electron density at r. Source function has many uses, when it is used to discuss bonding
problems, usually bond critical points are taken as r. A very comprehensive review of theoretical
background and applications of source function is given by Gatti in Struct. & Bond., 147, 193
(2010).
In Multiwfn, source function has two modes: (1) If "srcfuncmode" in settings.ini is set to 1,
then r' is regarded as variable, while r is regarded as fixed reference point, whose coordinate is
determined by “refxyz” in settings.ini. This is default mode, useful to study effect of electronic
Laplacian at everywhere on specific point (2) If "srcfuncmode" is set to 2, then r becomes variable
and r' becomes reference point, this is useful to study effect of electronic Laplacian at specific
point on everywhere.
When r=r', this function will return 001.0/)(
2r'
to avoid numerical problem.
20,21 Electron delocalization range function EDR(r;d) and orbital overlap
distance function D(r)
Content of this section and all analysis code of EDR(r;d) and D(r) was kindly contributed by Arshad
Mehmood and then slightly adapted by Tian Lu.
The electron delocalization range function EDR(r;d) (J. Chem. Phys., 141, 144104 (2014); J.
Chem. Theory Comput., 12, 3185 (2016); Angew. Chem. Int. Ed., 56, 6878 (2017)) quantifies the
extent to which electrons at point r in a wave function occupy orbital lobes of size d. EDR(r;d) is
built from the nonlocal one-particle reduced density matrix (1-RDM)
ii)'()()',( rrrr
as
2
2
2/1
4/3
2
|'|
exp)(
2
)',(
')',()',();EDR(
dd
g
dgd
d
d
rr
rrr
rrrrrr
Here
(r) is the electron density at point r. The prefactor ensures that the EDR is between -1 and
+1. The Multiwfn implementation evaluates the EDR on grids, for a single global input value of
distance d. Section 4.5.6 illustrates an example.
At each point, the orbital overlap distance function D(r)=argmaxdEDR(r;d) corresponds to
the distance d that maximizes EDR(r;d). Compact, chemically "hard" regions of small D(r) are
distinguished from diffuse, chemically "soft" regions of large D(r). Atomic averages of valence-
electron D(r) complement the information obtailed from atomic partial charges. Plots of D(r) on
density isosurfaces, and quantitative analysis of such surfaces, complements molecular
electrostatic potentials. The Multiwfn implementation evaluates EDR(r;di) on a grid of distances
di, then uses a three-point numerical fit to find the maximum. Sections 4.5.7 and 4.12.8 illustrate
example calculations.

2 General information
25
2.7 User defined real space function
In real space function selection menu you can find a term named "User defined real space
function", this function corresponds to “userfunc” routine in source file function.f90. By filling
codes by yourself, the functions of Multiwfn can be easily extended. For examples, after filling the
code userfunc=fgrad(x,y,z,'t')**2/8/fdens(x,y,z) and recompile Multiwfn, you will get the
integrand of Weizsäcker functional
r
r
rd
)(8
)(
][
2
w
. When you write code you can
consult Appendix 2 of this manual as well as the codes of other functions. If you would like to
define several custom functions, you can fill their codes in branch statement “if (iuserfunc==1)
then ... else if (iuserfunc==2) then ... end if”, where “iuserfunc” is an external parameter in
settings.ini file, by which you can select which custom function to be used.
In addition, in order to avoid lengthy list of real space functions, numerous uncommonly used
real space functions are not explicitly present in the list. However, if you want to use them, you
can set "iuserfunc" parameter in settings.ini to one of below values, then the user defined function
will point to corresponding function. For example, before running Multiwfn, if you set "iuserfunc"
to 2, then the user defined real space function will be equivalent to density of Beta electrons.
-2 Promolecular density calculated based on built-in sphericalized atomic densities, you can check
Appendix 3 on how these atomic densities are produced.
Please note that this promolecular density is slightly different to the promolecular density used in real space
functions 14 and 16, because in which the atomic densities from H to Ar are directly taken from the original paper
of RDG method rather than calculated according to the method described in Appendix 3.
-1 The function value evaluated by trilinear interpolation from grid data. The grid data can be
generated by main function 5, or loaded from .cub/.grd file when Multiwfn boot up.
1 Alpha density: 2/)]()([)( rrr s
2 Beta density: 2/)]()([)( rrr s
3 Integrand of electronic spatial extent <R**2>: )()( 222 zyx r
4 Weizsäcker potential: )(
)(
4
1
)(
)(
8
12
2
2
Wr
r
r
r
V
5 Integrand of Weizsäcker functional: )](8/[)( 2rr
, which is the exact kinetic energy
density of any one-orbital system (one or two electrons, or any number of bosons).
6 Radial distribution function of electron density: )()(4 222 zyx r
. Clearly,
spherical symmetry of electron density is assumed.
7 Local temperature, in kB-1 (PNAS, 81, 8028): )(
)(
3
2
)( r
r
r
G
T

2 General information
26
8 Average local electrostatic potential (J. Chem. Phys., 72, 3027): )(/)(
ESP rr
V
9 Shape function: N/)(r
, where N is the total number of electrons
10 Potential energy density (Virial field): )(2)()4/1()()()( 2rrrrr GGKV
11 Electron energy density: )()()()( rrrr KVGE
(Sometimes E is written as H)
12 Local nuclear attraction potential energy: )()( nuc rr V
13 Kinetic energy density per electron: )(/)( rr
G This quantity at bond critical point is useful
to discriminate covalent bonding and close-shell interaction
14 Electrostatic potential from electrons: )()()( nucESPele rrr VVV
15 Bond metallicity: )(/)()( 2rrr
J At bond critical point, J
>1 indicates metallic
interaction, see J. Phys.: Condens. Matter, 14, 10251.
16 Dimensionless bond metallicity: )(
)(
5
)π3(36
)( 2
3/53/22
mr
r
r
At bond critical point, larger
value corresponds to stronger metallicity of the bond, see Chem. Phys. Lett., 471, 174.
17 Energy density per electron: )(/)( rr
E, this value at BCP is called as bond degree
parameter (BD), see J. Chem. Phys., 117, 5529 (2002) for detail, in which the authors advocate
that for covalent bonds (viz. EBCP<0), the BD renders covalence degree, and the stronger the
interaction the greater the BD magnitude; while for closed-shell interactions (viz. EBCP>0), the BD
can be viewed as softening degree, and the weaker the interaction the larger the BD magnitude.
18 Region of Slow Electrons (RoSE), which is defined in Chem. Phys. Lett., 582, 144 (2013) and
has a pattern very similar to ELF, with value space of [-1,1]: )()(
)()(
0
0rr
rr
GD
GD
19 Single exponential decay detector (SEDD), which is highly analogous to ELF. Its updated
definition in J. Chem. Theory Comput., 10, 3745 (2014) is implemented:
2
2
)(
))(/)((
1ln)SEDD( r
rr
r
20 Density overlap regions indicator (DORI), which is defined in J. Chem. Theory Comput., 10,
3745 (2014). Its value range is [0,1]. The advantage of DORI is that it can simultaneously reveal
covalent and non-covalent interaction regions, and the pattern is similar to ELF+RDG. It is also
possible to map Sign(λ2(r)) on to its isosurfaces. The expression of DORI is:
)(1
)(
)DORI( r
r
r
, where 622 )](/)(/[]))(/)(([)( rrrrr
. (In fact, RDG is

2 General information
27
also able to reveal covalent and non-covalent interaction at the same time when "RDG_maxrho"
parameter is set to zero, but the graphical effect is not as good as DORI, because perfectly
exhibiting these two kinds of regions require somewhat different RDG isovalues)
21 Integrand of X component of electric dipole moment: )(r
x
22 Integrand of Y component of electric dipole moment: )(r
y
23 Integrand of Z component of electric dipole moment: )(r
z
24 Approximate form of DFT linear response kernel for close-shell (Phys. Chem. Chem. Phys., 14,
3960):
occ vir
22
*
11
*
21
)()()()(
4),(
ij ji
ijji
rrrr
rr
25 Magnitude of fluctuation of the electronic momentum: )(
)(
2
1
)(
~
r
r
r
P, which is useful to
discuss bonding and very similar to reduced density gradient, see Theor. Chim. Acc., 127, 393
26 Integrand of Thomas-Fermi functional: 3/53/22
TF )()3)(10/3()( rr
t, which is the exact
kinetic energy density of noninteracting, uniform electron gas
27 Local electron affinity:
vir
2
vir
2
L)(
)(
)(
ii
iii
EA r
r
r
, which is very similar to average local
ionization energy, but i cycles all unoccupied orbitals. See J. Mol. Model., 9, 342
28 Local Mulliken electronegativity: 2/)]()([)( LL rrr EAI
, see J. Mol. Model., 9, 342
29 Local hardness: 2/)]()([)( LL rrr EAI
, see J. Mol. Model., 9, 342
Note: In order to use EAL,
L and
L, the wavefunction must contain both occupied and
unoccupied orbitals, therefore such as .fch, .molden and .gms rather than .wfn/.wfx file must be
used. Meanwhile, "idelvirorb" in settings.ini must be set to 0. Besides, these quantities are
meaningful only when minimal basis-set is used.
30 Ellipticity of electron density:
1)(/)()( 21
rrr
-
-
, where
-
1 and
-
2 are the lowest and
the second lowest eigenvalues of Hessian matrix of
, respectively. At bond critical point,
-
1 and
-
2 are both negative and exhibit the curvature of electron density perpendicular to the bond.
31 eta index: )(/)()( 31 rrr
--
, where
-
1 and
-
3 are the lowest and the highest eigenvalues
of Hessian matrix of
, respectively. It was argued that the value of
at bond critical point is less
than unity for closed shell interactions and increases with increasing covalent character, see Angew.
Chem. Int. Ed., 53, 2766 (2014), as well as J. Phys. Chem. A, 114, 552 (2010) for discussions.
32 Modified eta index by Tian Lu: 1)(/)()(' 31 rrr
--
. Similar to
, but negative value

2 General information
28
of
' corresponds to closed shell interactions.
33 Potential acting on one electron in a molecule (PAEM), see J. Comput. Chem., 35, 965 (2014):
r'
r'r
r'r
rRr
rd
||
),(
)(
1
||
)(
PAEM
AA
A
Z
V, π is pair density. It can be further written as
r'
r'r
rrrr
r
rrrr d
||
)',()',(
)(
1
)()()()( tot,
XC
tot,
XC
ESPXCESPPAEM
VVVV , where
VESP is the total molecular electrostatic potential and VXC is exchange-correction potential. In
Multiwfn, the exchange-correlation density Γ is evaluated in terms of Müller approximation, see
part 17 of Section 2.6 for detail. It was shown in the original paper that PAEM may be useful to
distinguish covalent and noncovalent interactions. An example of application of PAEM can be
found in Section 4.3.3.
34 The same as 33, but now VXC directly corresponds to DFT exchange-correlation potential. Its
specific form can be chosen via "iDFTxcsel" parameter, see the end of this section for detail. This
form of PAEM is several times more computationally economical than 33 but only supports close-
shell wavefunction.
35 )(/|)(| rr GV . In J. Chem. Phys., 117, 5529 (2002) it was proposed that this quantity at BCP
can be used to discriminate interaction types. <1 corresponds to closed-shell interaction; >2
corresponds to covalent interaction; while >1 and < 2 corresponds to intermediate interaction.
36 On-top pair density, namely the two positions of the pair density are identical: (r,r). See such
as Int. J. Quantum Chem., 61, 197 (1995) for discussion. "paircorrtype" parameter in settings.ini
mentioned earlier affects the result.
38 The angle between the second eigenvector of Hessian of electron density and the vector
perpendicular to a given plane, which can be defined by option 4 of main function 1000; the unit
vector normal to the plane will be shown on screen, assume that you use three points A, B, C to
define the plane and you get vector u, but what you really want is -u, you can then input the points
again but in reverse sequence, i.e. C, B, A. In J. Phys. Chem. A, 115, 12512 (2011) this quantity
along bond paths was used to reveal π interaction.
39 Electrostatic potential without contribution of a specific nucleus:
'
'
)'(
)(
nr
rr
r
Rr
rd
Z
V
KA A
A
, where the nucleus K can be set by option 3 of main function
1000 (which is hidden in main interface but can be chosen). Vn is a useful quantity, for example if
K is chosen as index of a hydrogen, then the value correlates with its pKa, because in this case Vn
approximately reflects the interaction energy of a proton at the position of K and rest of the system;
In addition, J. Phys. Chem. A, 118, 1697 (2014) showed that Vn can be used to quantitatively
predict interaction energy of the weak interactions dominated by electrostatic effect (viz. H-bonds,
halogen-bonds, dihydrogen bonds), see Section 4.1.2 for introduction and example.
40 Steric energy density: )](8/[)( 2rr
, which is equivalent to integrand of Weizsäcker
functional.

2 General information
29
41 Steric potential:
)(
)(
4
1
])([
|)(|
8
1
)( 2
2
2
sr
r
r
r
r. The negative of this quantity is also
known as one-electron potential (OEP). Notice that the
is a very small term artifically introduced
to avoid the denominator converges to zero faster than nominator. The value of
can be
determined by "steric_addminimal" in settings.ini. If
is set to 0, then the original expression of
steric potential is recovered.
42 Steric charge: )4/()()( S
2
s
rrq.
43 The magnitude of steric force: |)(|)( SS rr
F.
Notice that the
term, which is mentioned above, also affects steric force and steric charge.
Discussions of steric energy/potential/force/charge can be found in J. Chem. Phys., 126, 244103.
44,45,46 Damped Steric potential, steric force based on damped steric potential, directly damped
Steric force: Documented privately
50 Shannon entropy density: )(ln)()(
srrr
s.
51 Fisher information density: )(/|)(|)( 2
Frrr
i. Note that this quantity is only different
from Weizsäcker functional by a constant factor of 1/8.
52 Second Fisher information density: )(ln)()( 2
Frrr
i. The relationship between
Shannon entropy and Fisher information can be found in J. Chem. Phys., 126, 191107. The
integration of this function over the whole space is exactly identical to that of Fisher information
density.
53 Ghosh entropy density (or Ghosh-Berkowitz-Parr entropy), in kB (PNAS, 81, 8028):
)]}(/)(ln[){()2/3()( TF rrrr tts
-
, where
3/4ln3/5 k
c
-
, ck is Thomas-Fermi
constant 2.871234)3)(10/3( 3/22
, Lagrangian kinetic energy density G(r) is chosen to be
the kinetic energy density term t(r).
54 The same as 53, but 8/)()( 2rr
G, which is the kinetic energy density exactly
corresponding to Eq. 22 of PNAS, 81, 8028, is employed as the t(r). In rare cases this definition of
kinetic energy density leads to a very small negative value, since at these points tTF(r) is also very
close to zero, in order to normally get result, )](/)(ln[ TF rr tt in this case is simply set to zero.
55 Integrand of quadratic form of Rényi entropy: )(
2r
56 Integrand of cubic form of Rényi entropy: )(
3r
60 Pauli potential: WXCESPθ
VVVV
, where VESP is total electrostatic potential (as shown in
Section 2.6), VXC is exchange-correlation potential (its specific form is determined by "iDFTxcsel"
2 General information
30
in settings.ini, see below), VW is Weizsäcker potential. This quantity corresponds to Eq. 17 of
Comput. Theor. Chem., 1006, 92-99 and is only applicable to close-shell cases.
61 The magnitude of Pauli force: |)(|)( θrr VF
.
62 Pauli charge: )4/()()( θ
2
θ
rr Vq .
63 Quantum potential: XCθqVVV
64 The magnitude of quantum force: |)(|)( qq rr VF
65 Quantum charge: )()()( XCθqrrr qqq
66 The magnitude of electrostatic force: |)(|)( ESPESP rr VF
67 Electrostatic charge: )4/()()( ESP
2
ESP
rr Vq
70 Phase-space-defined Fisher information density (PS-FID): )(
)(
2
9
)(
)(3
)( 2
B
fr
r
r
r
rGTk
i
,
where T(r) is local temperature as shown above. This function has very similar characters to ELF
and LOL, the spatial localization of electron pairs can be clearly revealed. See Chem. Phys., 435,
49 (2014) for introduction and illustrative applications.
71, 72, 73, 74 Electron linear momentum density (EMD) in 3D representation. The electron linear
momentum operator is i, for an orbital the expectation value of linear momentum in X is
i, so X component of EMD for a wavefunction can be defined as (the imaginary sign
is ignored)
i
i
iix x
p)(
)()( *r
rr
, similar for Y and Z components. The 71, 72, 73th
user-defined functions correspond to X, Y, Z component, respectively. The magnitude (74) of
EMD is defined as )()()()( 222
tot rrrr zyx pppp .
75, 76, 77, 78 Magnetic dipole moment density (MDMD). The operator for magnetic dipole
moment is the angular momentum operator (see Theoret. Chim. Acta, 6, 341)
x
y
y
x
z
x
x
z
y
z
z
yii kjir ˆ
ˆˆ
)(
where i, j, k are unity vectors in X, Y and Z directions, respectively. Therefore, X, Y and Z
component of MDMD may be defined as follows (the imaginary sign is ignored)
i
ii
iix y
z
z
ym )()(
)()( *rr
rr
2 General information
31
i
ii
iiy z
x
x
zm )()(
)()( *rr
rr
i
ii
iiz x
y
y
xm )()(
)()( *rr
rr
The 75, 76, 77th user-defined functions correspond to X, Y, Z component, respectively. The
magnitude (78) of MDMD is )()()()( 222
tot rrrr zyx mmmm .
79 Gradient norm of electron density: |)(| rE
80 Laplacian of electron density: )(
2rE
81, 82, 83 X, Y, Z component of Hamiltonian kinetic energy density, respectively
84, 85, 86 X, Y, Z component of Lagrangian kinetic energy density, respectively
87 Local total electron correlation function:
iiii
I22/1
4
1
T|)(|)]1([)( rr
. The i denotes
index of natural spin orbital, the
is corresponding occupation number. This and below two
functions are very useful for revealing electron correlation in different regions, see J. Chem.
Theory Comput., 13, 2705 (2017) for introduction, illustrative example can also be found in
Section 4.A.6. Note that in some cases,
may be marginally larger than 1.0 or negative, Multiwfn
automatically set it to 1.0 and 0.0 respectively to make the calculation feasible.
88 Local dynamic electron correlation function:
iiiiii
I22/1
4
1
D|)(|)}1(2)]1({[)( rr
89 Local nondynamic electron correlation function:
iiii
I2
2
1
ND |)(|)1()( rr
It is clear that )()()( NDDT rrr III
100 Disequilibrium (also known as semi-similarity): )()( 2
rrr
D. See Int. J. Quantum.
Chem., 113, 2589 (2013) for illustrative applications.
101 Positive part of ESP:
ESP
V. In the region where ESP
V is positive, ESPESP VV
; where ESP
is negative, 0
ESP
V.
102 Negative part of ESP:
ESP
V.
900, 901, 902 X, Y and Z coordinate variables, respectively: x, y, z.
1000 Integrand of DFT exchange-correlation functionals, which is also known as exchange-
correlation energy density.
1100 DFT exchange-correlation potential, i.e. )(
)]([
)( XC
XC r
r
r
E
V

2 General information
32
For user-defined function 1000 and 1100, "iDFTxcsel" in settings.ini is used to select XC
functional. 0~29 are X part only, 30~69 are C part only, 70~99 are whole XC. For example, if
iDFTxcsel=32, then iuserfunc=1000 corresponds to integrand of LYP, and iuserfunc=1100
corresponds to LYP potential.
Notice that both 1000 and 1100 are applicable for close-shell cases. But currently only 1000
can be applied to open-shell cases.
[See below for details]
Available options of "iDFTxcsel" parameter
Currently only LSDA and some GGA functionals are supported
0 LSDA exchange:
])()([)4/(3)2/3( 3/43/4
3/1 rr
. For close-shell cases the
equivalent form is 3/43/1 )()/3)(4/3( r
.
1 Becke 88 (B88) exchange, see Phys. Rev. A, 38, 3098-3100 (1988).
2 Perdew-Burke-Ernzerhof (PBE) exchange, see Phys. Rev. Lett., 77, 3865-3868 (1996).
3 Perdew-Wang 91 (PW91) exchange, see Electronic Structure of Solids '91; Ziesche, P., Eschig,
H., Eds.; Akademie Verlag: Berlin, 1991; p. 11.
30 Vosko-Wilk-Nusair V (VWN5) correlation, see Can. J. Phys., 58, 1200-1211 (1980).
31 Perdew 86 (P86) correlation, see Phys. Rev. B, 33, 8822-8824 (1986).
32 Lee-Yang-Parr (LYP) correlation, see Phys. Rev. B, 37, 785-789 (1988).
33 Perdew-Wang 91 (PW91) correlation, see the reference of its exchange counterpart.
34 Perdew-Burke-Ernzerhof (PBE) correlation, see the reference of its exchange counterpart.
70 Becke 97 (B97) exchange-correlation, see J. Chem. Phys., 107, 8554-8560 (1997).
71 Hamprecht-Cohen-Tozer-Handy with 407 training molecules (HCTH407) exchange-
correlation, see J. Chem. Phys., 114, 5497-5503 (2001).
80 SVWN5 exchange-correlation.
81 BP86 exchange-correlation.
82 BLYP exchange-correlation.
83 BPW91 exchange-correlation.
84 PBEPBE exchange-correlation.
85 PW91PW91 exchange-correlation.
2 General information
33
2.8 Graphic formats and image size
Benefiting from DISLIN graphical library, Multiwfn supports a lot of mainstream graphic
formats, including:
1 Postscript (ps)
2 Encapsulated postscript (eps)
3 Portable document format (pdf)
4 Windows metafile format (wmf)
5 Graphics interchange format (gif)
6 TIFF (tiff)
7 Portable network graphics (png)
8 Windows bitmap format (bmp)
The graphic format of the picture exported by Multiwfn is controlled by “graphformat”
parameter in settings.ini, you can set this parameter to the texts in the parentheses listed above, the
default format is “png”.
Tip: If the graph is mainly composed of lines, e.g. contour line map, the best format is pdf.
For curve maps, the height and weight of the image file are controlled by “graph1Dsize”
parameter in settings.ini. “graph2Dsize” is responsible for two-dimension data plotting (color-
filled map, contour map, relief map, etc.). “graph3Dsize“ is responsible for three-dimension data
plotting (isosurface graph, molecular structure graph).
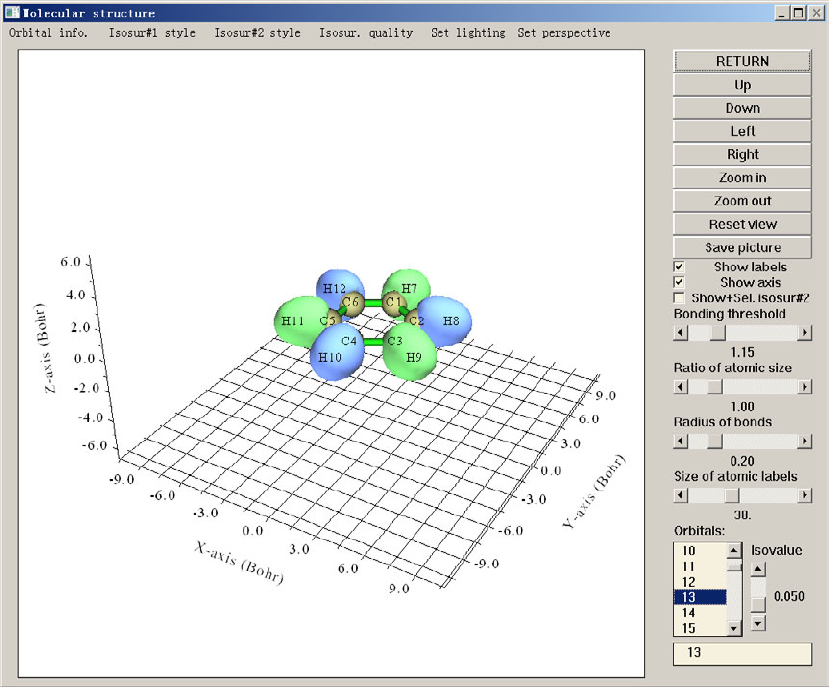
3 Functions
34
3 Functions
This chapter introduces all functions of Multiwfn in detail, the numbers in the parentheses of
secondary titles are indices of corresponding functions in main menu, the numbers in the
parentheses of tertiary titles are indices of corresponding options in corresponding submenus.
Different functions of Multiwfn require different types of input file, the information needed by
each function are shown in the final line of corresponding section. Please choose proper type of
input file according to the table in Section 2.5.
3.2 Showing molecular structure and viewing orbitals /
isosurfaces (0)
When function 0 is selected, all atom coordinates will be printed on text window, meanwhile
molecular structure will be shown in a GUI window. If the input file contains orbital information,
the orbitals can be viewed by selecting corresponding orbital index in the list at right-bottom
corner of the window, or by directly inputting orbital index in the text box, see below screenshot.
If the input file is .cub or .grd format, then one can view isosurface.
3 Functions
35
Since most widgets in this GUI are self-explained, I only mention some worthnoting points
here.
For unrestricted wavefunction, the alpha and beta orbitals are recorded separately. Assume
that there are N basis functions, then the first and latter N orbitals in the orbital selection list
correspond to alpha and beta orbitals, respectively. Whereas in the orbital selection box, negative
index corresponds to beta orbitals. For example, if you input -9, then the 9th beta orbital will be
shown, and the orbital selection list will be automatically switched to the N+9 term.
By clicking "Orbital info." and then selecting corresponding options, basic orbital
information can be printed on text window.
"Ratio of atomic size" is the ratio of one-fourth of atom radius shown on screen to its van
der Waals (vdW) radius, so if the slide bar is dragged to 4.0, then what to be shown is vdW surface.
Multiwfn determines if two atoms are bonded by empirical distance criteria, if the distance
between two atoms is short than 1.15 times of the sum of their CSD covalent radii, they will be
considered as bonded. You can adjust this criteria by dragging "Bonding threshold" slide bar.
All orbital indices are listed in the right-bottom box, default selection is “none” (no orbital is
shown). If you click an orbital index, Multiwfn will calculate grid data of wavefunction value for
corresponding orbital, and then the orbital isosurface appears immediately. Green and blue parts
correspond to positive and negative regions, respectively. The “Isovalue” slide bar controls the
isovalue of the isosurface. For efficiency consideration, the default quality of grid data is relatively
coarse, the number of grid points can be set by "Isosur. quality", the larger number leads to the
finer isosurface (Note that after you adjust the number, present isosurface will be deleted). You can
also set default number of grid points through changing “nprevorbgrid” in settings.ini.
Sometimes it is useful to display two orbitals simultaneously, for example, analysis of phase
overlapping of two NBOs. This can be realized by "Show+Sel. Isosur#2" (Sel.=Select) check
box. This check box is inactive by default, once you have chosen an orbital (corresponding
isosurface will be referred to as Isosurface #1), this check box will be actived. After you clicked
the check box, the isosurface of the orbital you newly selected (which will be referred to as
Isosurface #2) will be shown together with the orbital you previously selected, yellow-green and
purple parts correspond to positive and negative regions respectively. If the check box is
deselected, Isosurface #2 will disappear, then if you reselect the check box the same Isosurface #2
will be redrawn.
The representation styles of Isosurface #1 and #2 can be adjusted by suboptions in "Isosur.
#1" and "Isosur. #2" individually, available styles include solid face (default), mesh, points, solid
face+mesh and transparent face. (Notice that Multiwfn cannot plot only one isosurface as
transparent face). The colors for face and mesh/points can be set by corresponding suboptions too,
users will be prompted to input Red, Green, Blue components for positive and negative parts in
turn. The component values should between 0.0 and 1.0, for instance, 1.0,1.0,0.0 corresponds to
Yellow. Opacity for transparent face can also be customly set, valid range is from 0.0 (completely
transparent) to 1.0 (completely opaque).
The perspective can be adjusted by "Left", "Right", "Up", "Down", "Zoom in" and "Zoom
out". To exactly control the viewpoint, you can also directly input value of rotation angle by
selecting "Set rotation angle" option in "Set perspective" in the menu.
When orbital isosurfaces are portrayed as solid face, in rare cases you may see some ugly
3 Functions
36
dark polygons, or positive and negative regions are difficult to be distinguished, in these cases you
can try to adjust lighting setting by using "Set lighting" option in the GUI menu or rotate the
system to solve the problem.
Information needed: GTFs (only for viewing orbitals), atom coordinates, grid data (only for
viewing isosurface of grid data)
3.3 Outputting all properties at a point (1)
Input coordinate of a point or index of an atom, then the values of all real space functions
supported by Multiwfn at the point or corresponding nuclear position will be printed on screen, as
well as each component of gradient and Hessian matrix of specified function (default is electron
density). The function can be specified by f?, for example f9 select ELF, you can input allf to
check all available functions. The orbital whose wavefunction value will be outputted can be
selected by command o?, for example o4 choose the fourth orbital. If the input file merely
contains atom coordinates (such as pdb file), then only limited functions based on electron density
will be outputted, the electron density used is promolecular density constructed from fitted free
atom density, see the introduction of real space function 14 in Section 2.6.
If input d, value of a real space function at a given point can be decomposed into orbital
contributions. The contribution from orbital i is evaluated as follows: First set occupation number
of all orbitals to zero except for orbital i, and then calculate real space function as usual. Note that
sum of contribution of all orbitals may be different to the result when all orbitals are
simultaneously into account, since many real space functions contain non-linear operators, such as
ELF.
Electrostatic potential is the most expensive one among all of the real space functions
supported by Multiwfn. If you are not interested in it, you can set "ishowptESP" parameter in
"settings.ini" to 0 to skip calculation of electrostatic potential.
Information needed: GTFs (depends on the choice of real space function), atom coordinates
3.4 Outputting and plotting specific property in a line (3)
What you should do is just select a real space function and then define a line. There are two
ways to define the line: (1) By inputting indices of two atoms, the line will be automatically
extended by a small distance in each side, the extended distance can be adjusted by “aug1D” in
settings.ini or by the option “0 Set extension distance for mode 1”, default value is 1.5 Bohr. (2)
By inputting the coordinates of the two endpoints. Generally, the calculation only takes a few
seconds, and then curve map pops up immediately, like this
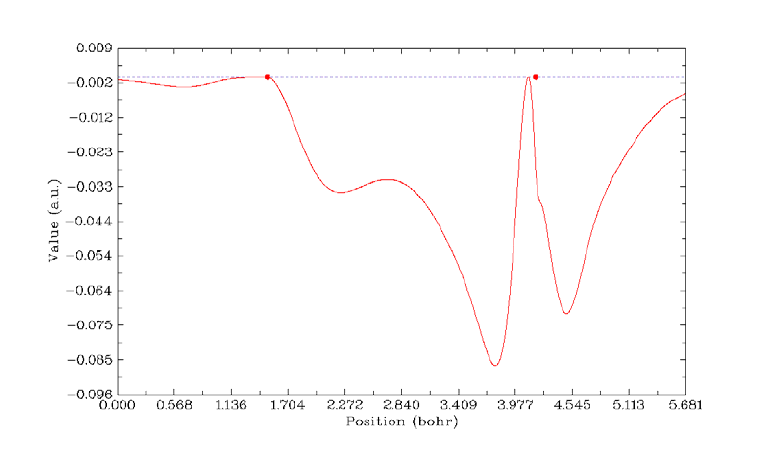
3 Functions
37
The gray dash line indicates the position of Y=0. If the line is defined by the second way, two
red circles with Y=0 will appear in the graph, they indicate the position of the two nuclei. Click
right button on the graph and then you can select what to do next, you can redefine the scale of Y-
axis, export the data to line.txt in current directory, save the graph to a file, locate minimal and
maximal positions and so on. Note that the process for searching stationary points and the position
where Y equals to specified value is based on the data you have calculated, that means the finer
the points, the more accurate X position you will get.
The data points are evenly distributed in the line, the number of points is 3000 by default,
which is fine enough for most cases. The number can also be adjusted by “num1Dpoints”
parameter in settings.ini. Of course, the more points the more time is needed for calculating data.
Notice that for ESP calculation, the number of points is decreased to one-sixth automatically,
because it is much more time-consuming than other task.
Information needed: GTFs (except for ESP from nuclear/atomic charges and promolecular
approximation version of RDG and sign(lambda2)*rho), atom coordinates
3.5 Outputting and plotting specific property in a plane (4)
The basic steps of using this function are listed below. Users can finish all operations by
simply following program prompts, there are only a few key points are needed to be described.
1. Select a real space function
2. Select a graph type
3. Set the number of grid points in both dimensions
4. Define a plane
5. View the graph
6. Post-processes (Adjust plotting parameters, save graph, export data to plain text file, etc.)
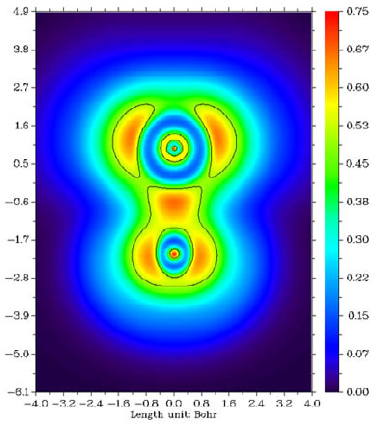
3 Functions
38
Worthnotingly, after you enter this function, you will see real space function selection menu; if you select
option 111 (a hidden option), then the real space function to be plotted will be Becke weight of an atom or Becke
overlap weight between two atoms. If you select option 112 (another hidden option), Hirshfeld weight of a given
atom or fragment will be plotted.
If the parameter "iplaneextdata" in settings.ini is set to 1, then the data in the plane will not be
calculated by Multiwfn internally but directly loaded from an external plain text file. The
coordinate of the points in the plane will be automatically outputted to current folder, you can use
third-party tools (e.g. cubegen utility of Gaussian) to calculate function value at these points. (If
you don't know how to use cubegen, you may consult Section 4.12.7)
3.5.1 Graph types
Currently Multiwfn supports seven graph types for exhibiting data in a plane.
1 Color-filled map. This type of map uses different colors to represent real space function
value in different region. By default, if the function value exceeds lower (upper) limit of color
scale, then the region will be filled by black (white); if you want to avoid this treatment, simply set
the parameter "inowhiteblack" in settings.ini to 1. If you want to reverse color scale as red-white-
blue, in post-process menu you can set the lower limit smaller than upper limit, e.g. inputting 1,-1.
By selecting “Enable showing contour lines“ in post-process menu, contour lines can be
plotted together on the graph:
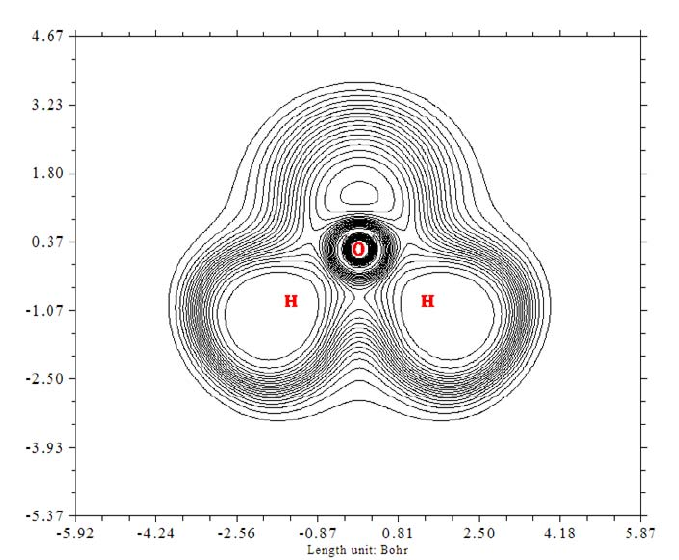
3 Functions
39
2 Contour line map. This map uses solid lines to represent positive regions, and dash lines to
exhibit negative regions.
The number of isovalue lines can be adjusted by user (see Section 3.5.4), you can also mark
the isovalues on the contour lines by using the option “2 Enable showing isovalue on contour
lines” in post-process step.
Only for contour line map, if the real space function you selected to be plotted is orbital
wavefunction, you can not only plot one orbital by inputting one orbital index, but also plot two
orbitals simultaneously by inputting two orbital indices (e.g. 3,5), see Section 4.4.5 for example.
Option 4 in post-process menu is used to toggle if showing atoms labels or reference point
(involved in some real space functions such as correlation hole and source function) in the graph.
The size and form (i.e. if showing atom index or element name) of the atom labels can be set by
"pleatmlabsize" and "iatmlabtype" parameters in settings.ini, respectively. The reference point is
represented as a blue asterisk on the graph. By default only when the distance between the atoms
and the plane is smaller than "disshowlabel" in settings.ini the corresponding atom labels will be
shown. To change this distance threshold, you can either adjust this value in setting.ini or choose
option 17 in post-process menu. If "iatom_on_contour_far" parameter in settings.ini is set to 1,
then even if the distance is larger than the threshold, the label will still be shown, but in thin text
rather than bold text.
Option 15 in post-process is used to plot a contour line corresponding to vdW surface
(electron density=0.001 a.u., which is defined by R. F. W Bader in J. Am. Chem. Soc., 109, 7968
(1987)). This is useful to analyze distribution of electrostatic potential on vdW surface. Such a
contour line can be plotted in gradient line and vector field map too by the same option. Color,
label size and line style of the contour line can be adjusted by Option 16.
Notice that the discussion in above two paragraphs also applies to color-filled map, gradient
lines map and vector field map (see below).
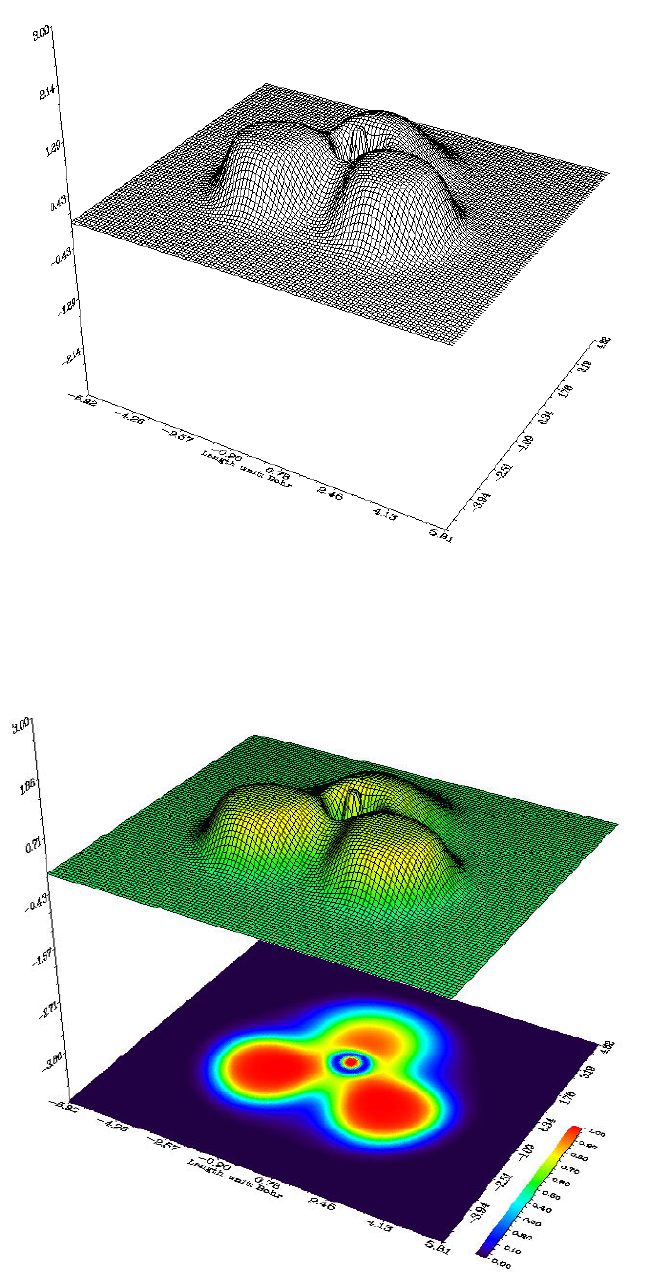
3 Functions
40
3 Relief map. Use height to represent value at every point. If values are too large they will be
truncated in the graph, you can choose to scale the data with a factor to avoid truncation. The
graph is shown on interactive interface, you can rotate, zoom in/out the graph.
4 Shaded surface map and 5 Shaded surface map with projection. The relief map is
shaded in these two types. The latter also plots color-filled map as projection. The meshs on the
surface can disabled at post-process stage.
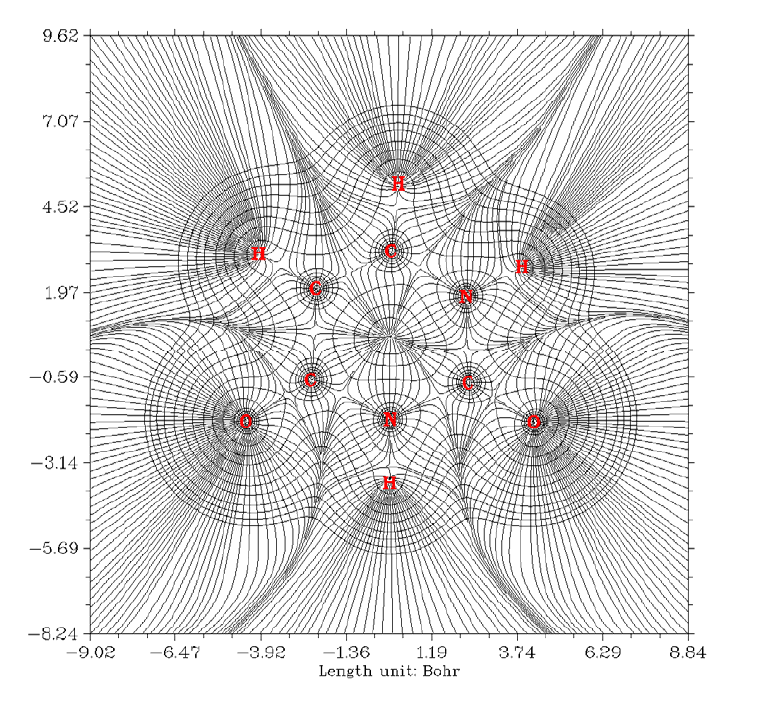
3 Functions
41
6 Gradient line map with/without contour lines. This graph type represents gradient
direction of real space function, you can determine if the contour lines also be shown on the graph.
Note that since gradients of real space function are needed to be evaluated, and graphical library
needs to take some time to generate gradient lines, the computational cost is evidently higher than
other graph type.
By option 11 at post-process stage you can control the integration step for gradient lines, the
smaller value you set the graph looks finer. By option 12 you can set interstice between gradient
lines, the smaller value you set the lines become denser. By option 13 you can set the criteria for
plotting new gradient line, try to play with it and you will know how the parameter affects the
graph.
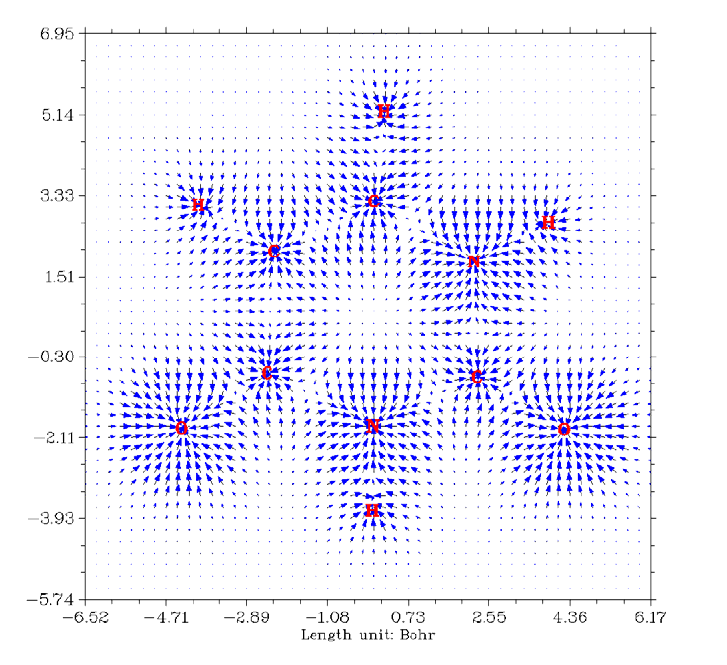
3 Functions
42
7 Vector field map with/without contour lines. This graph type is very similar to last graph
type, however the gradient lines are replaced by arrows, which distribute on grids evenly and
represent gradient vectors at corresponding point. You can set color of arrows, or map different
colors on arrows according to magnitude of function value, you can also invert the direction of
arrows. The option 10 is worth mentioning, if you set upper limit for scaling to x by this option,
then if the norm of a gradient vector exceeds this value, the vector will be scaled so that its norm
equals to x.
3.5.2 Setting up grid, plane and plotting region
When program asking you to input the number of grid points in both dimensions, you can
input such as 100,150, which means in dimensions 1 and 2 the number of grid points are 100 and
150, respectively, so total number is 100*150=15000, they are evenly distributed in the plotting
region. For “Relief map”, “Shaded surface map” and “Shaded surface map with projection”,
commonly I recommend 100,100; if this value is exceeded, the lines in the graph will look too
crowd. For other graph types I recommend 200,200. Of course the picture will become more
pretty and smoother if you set the value larger, but you have to wait more time for calculation.
Bear in mind that total ESP calculation is very time-consuming, you’d better use less grid points,
for previewing purpose I recommend 80,80 or less.
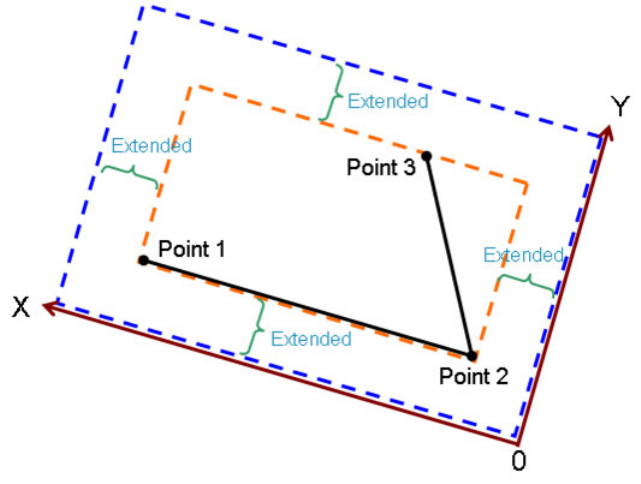
3 Functions
43
Multiwfn provides seven modes to define the plotting plane:
1. XY plane: User inputs Z value to define a XY plane uniquely.
2. XZ plane: User inputs Y value to define a XZ plane uniquely.
3. YZ plane: User inputs X value to define a YZ plane uniquely.
4. Define by three atoms: Input indices of three atoms to define a plane by their nuclear
coordinates.
5. Define by three points: Input coordinates of three points to define a plane.
6. Input origin and transitional vector: This way is only suitable for expert, the two
inputted translation vectors must be orthogonal.
7. Define a plane parallel to a bond and meantime normal to a plane defined by three atoms
For modes 1~5, the actual plotting region is a subregion of the plane you defined. Multiwfn
automatically sets the plotting region to tightly enclose the whole molecule (for modes 1, 2 and 3)
or cover the three nuclei / points you inputted (for modes 4 and 5), finally the plotting region is
extended by a small distance to avoid truncating the interesting region. The extension distance is
4.5 Bohr by default, if you find the region you interested in is still be truncated, simply enlarging
the value by option “0 Set extension distance for plane type 1~5”, you can also directly modify the
default value, which is controlled by “Aug2D” parameter in settings.ini.
Below illustrate how the actual plotting region is determined when you select mode 4 or 5 to
define the plane. The X and Y axes shown in the graph correspond to the actual X and Y axes you
will finally see. Evidently, the input sequence of the three points or atoms directly affects the
graph.
For mode 6, the plotting region is determined as follows, in which each black arrow denotes
translational vector 1, each brown arrow denotes translational vector 2, blue point denotes origin
point. The number of arrows is the number of grids set by users. Evidently, this mode enables
users to fully control the plotting plane setting.
3 Functions
44
Mode 7 is very useful when you want to define a plotting plane cutting a bond but there is no
proper reference atoms to use mode 4, below graph is such an instance, the purple rectangle is the
plane you want to plot:
To define this plane, you should select mode 7, and then input 3,5 to use these two atoms to define
the axis that the plotting will be parallel to, and then input 2,3,10 (or 2,5,10 etc.) to use them to
define a plane that the plotting plane will be normal to. After that you need to input the length of X
and Y axes, e.g. 10 Bohr and 7 Bohr, respectively.
3.5.3 Options in post-process interface
After plotting the graph, you will see a menu, in which there are a lot of options used to
adjust or improve the quality of the graph. Since many of them have already been introduced
above and some of them will be mentioned in next sections, and lots of them are self-explained,
only a few will be mentioned here.
-9 Only plot the data around certain atoms: Sometimes in the graph only a few regions are
interesting; if you want to screen other regions, you may find this option useful. After selecting
this option, assume that you input 2,4,8-10, then only the real space function around atoms
2,4,8,9,10 will be plotted (the data to be plotted then in fact is the original plane data multiplied by
the Hirshfeld weight of the fragment you inputted). Next time you select this option, the original
data will be recovered.
-7 Multiply data by a factor: This is mainly used to scale the range of the plane data.
-6 Export calculated plane data to plane.txt in current folder: After using this option to
export the plane data, you can very conveniently using third-part plotting softwares such as
Sigmaplot to redraw the data.
3 Functions
45
-2 Set stepsize in X,Y(,Z) axes: This option determines the spacing between the labels in the
coordinate axes. If axis labels are not shown, that means you need to decrease the stepsizes.
-1 Show the graph again: After adjusting plotting parameters, choose this option to replot
the graph to check the effect.
0 Save the graph to a file: Export the graph to a graphic file in current folder. See Section
2.8 on how to determine the graphic format and size.
3.5.4 Setting up contour lines
For graph types 1, 2, 6 and 7, the contour lines can be plotted (if not shown, select "2 Enable
showing contour lines" in the post-process menu). There is also an option “Change contour line
setting” in the post-process menu used to adjust the setting of contour lines. In this interface,
current isovalues are first listed and you can modify them by using below suboptions:
Option 1: Save current setting and return to upper menu. Then if you select “Show the graph
again”, the graph with new isovalue setting will appears.
Option 2: Input a new value to replace old isovalue of a contour line.
Option 3: Add a new contour line and input the isovalue for it.
Option 4: Delete a contour line. The indices of the contour lines behind it will move forward.
Option 5: Delete contour lines whose index is in a certain range.
Option 6: Export current isovalue setting to a plain text file, you can use this function to save
multiple sets of your favourite isovalue settings for different systems and real space functions.
Option 7: Load isovalue setting from external file, the format should be identical to the file
outputted by subfunction 6.
Option 8: Generate isovalues according to arithmetic sequence, user need to input initial
value, step size and total number. For plotting ELF/LOL, I suggest user input 0,0.05,21 to generate
isovalues in the range 0.0~1.0 with step size 0.05. You can choose if clean existed contour lines, if
you select "n", then new contour lines will be appended to old ones.
Option 9: Like function 8, but according to geometric series.
Option 10: Some contour lines can be bolded with this function, by default no line is bolded.
To bold some lines, select this function and input how many lines you want to bold, then input
indices of them in turn. If there are some lines already been bolded, selecting this function will
unbold all of them.
Option 11: Set color for positive contour lines, you need to input a color index.
Option 12: Set line style for positive contour lines, you need to input two integer number, the
first one denotes the length of line segment, the second one denotes the length of interstice
between line segment. For example 10,15 means positive contour lines are composed of line
segments with length of 10 and spaces with length of 15 alternatively.
Option 13, 14: Like option 11 and 12, but for negative part.
Option 15: If this option is selected, the positive and negative lines will be set to "crimson,
width=6, solid line" and "blue, width=6, long dash line", respectively. Then the saved picture will
be very suitable for publication; as you can see in the resulting graphical file, the two kinds of
lines are clear and can be distinguished easily.
3 Functions
46
3.5.5 Plot critical points, paths and interbasin paths on plane graph
CPs and paths can be plotted on plane graph type 2, 6 and 7. In order to do that, before
drawing a plane graph, you need to go into topology analysis module (main function 2), search
CPs and generate paths. After that, return to main menu and draw plane graph as usual, you will
find that the CPs and paths have appeared on the graph automatically, such as below (without deep
blue lines). Brown, blue, orange, green dots denote (3,-3), (3,-1), (3,+1), (3,+3) critical points
respectively. Bold dark-brown lines depict bond paths. Notice that if the distance between a CP
and the plane exceeds "disshowlabel" in settings.ini, the CP will not be shown.
In the option “Set marks of critical points and paths” at post-process stage, you can choose
which types of CPs are allowed to be shown, and you can set size of markers, thickness and color
of path lines.
Interbasin paths (deep blue lines in above graph) are derived from (3,-1) CPs, these paths
dissect the whole space into individual basins, within each of which a (3,-3) CP can be found. In
order to draw interbasin paths, you should confirm first that at least one (3,-1) CP has been found
in topology analysis module and it is close enough to current plane (less than "disshowlabel" in
settings.ini), then you can find a option "Generate and show interbasin paths" in post-process stage,
choose it, wait until the generation of interbasin paths is completed, then show the plane graph
again, you will find these interbasin paths have already presented.
If you expect the interbasin paths to be shorter or longer, choose option "Set stepsize and
maximal iteration for interbasin path generation" in post-process stage before generating
interbasin paths, you will be prompted to input two values, the length of interbasin paths equals to
the product of the two value. Note that if distance between a point in the path and the given plane
3 Functions
47
exceeds "disshowlabel" in settings.ini, corrsponding segment of the path will not be shown on the
plane graph.
Information needed: GTFs (depends on the choice of real space function), atom coordinates
3.6 Outputting and plotting specific property within a
spatial region (5)
The main purpose of this function is generating Gaussian-type grid file (.cub) for specific
property, the .cub file is supported by a lot of chemistry visualization softwares, such as VMD,
GaussView, ChemCraft, and Molekel. The isosurface of generated grid data can be viewed directly
in Multiwfn too. This function is also used to calculate function values for a set of points recorded
in external file.
The basic procedure of using this function is:
1. Select a real space function
2. Set up grid
3. Use post-process options to visualize isosurfaces, modify and export data
In the real space function selection menu, if you select option 111 (a hidden option), then the real space
function to be calculated will be Becke weight of an atom or Becke overlap weight between two atoms. If you
select option 112 (another hidden option), Hirshfeld weight of a given atom or fragment will be calculated.
Set up grid
Multiwfn provides seven modes for setting up grid point:
Mode 1: Low quality grid, about 125000 points in total (corresponding to 50*50*50 grid,
assuming the spatial region is cubic), this mode is recommended for previewing.
Mode 2: Medium quality grid, about 512000 points in total (corresponding to 80*80*80 grid,
assuming the spatial region is cubic). For small molecular, this quality is enough for most analysis.
Mode 3: High quality grid, about 1728000 points in total (corresponding to 120*120*120
grid, assuming the spatial region is cubic).
For modes 1, 2 and 3, the actual number of points in each direction is automatically
determined by Multiwfn so that grid spacings in each direction are nearly equal. The method of
determining spatial scope of grid data is illustrated below in two-dimension case.
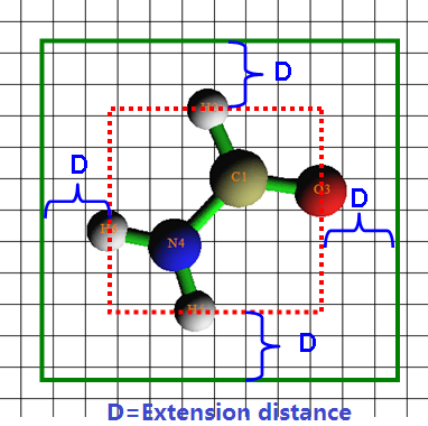
3 Functions
48
First, Multiwfn sets up a box (red dashed line) to just enclose the entire molecule, and then
the box is suitably extended in each dimension to avoid truncating boundary part of isosurfaces,
the green rectangle in below graph is the actual spatial scope of grid data. If the extension distance
is inappropriate, you can customly set the value by using option “-10 Set extension distance of
grid range", or directly set default value by modifying “Aug3D” in settings.ini.
The so-called “Low quality”, “Medium quality” and “High quality” are only relative to small
system, if spatial scope is large, then density of grid points of mode 3 is not high and should be
called “Medium quality”, mode 2 should be call “Low quality” at this time. While for very small
system, the mode 1 is enough for general purposes.
Mode 4: Specify the number of grid points or grid spacing in X, Y and Z directions by
yourself, the spatial scope is determined automatically as shown above.
Mode 5: Specify all details of grid setting by user, including the number of points in X, Y
and Z directions, initial point, translation vectors. This mode is useful for reproducing existed cube
files.
Mode 6: Specify the center coordinate, number of points and extension distance in X, Y and
Z directions. For example, the center coordinate you inputted is 2.3,1.0,5.5, the extension distance
in X, Y and Z is k,k,m, then the coordinates of two most distant endpoints are (2.3-k,1.0-k,5.5-m)
and (2.3+k,1.0+k,5.5+m). This mode is useful for analyzing local properties.
Mode 7: Like function 6, but input indices of two atoms instead of inputting center
coordinate, the midpoint between the two nuclei will be set as center. This mode is very useful for
weak interaction analysis by RDG function, for examples, we want to study the weak interaction
region between the dimer shown below, and we found C1 and C14 may enclose this region, so we
input 1,14. see Section 4.100.1 for example. If the two atom indices are identical, then the nuclear
coordinate will be set as center.
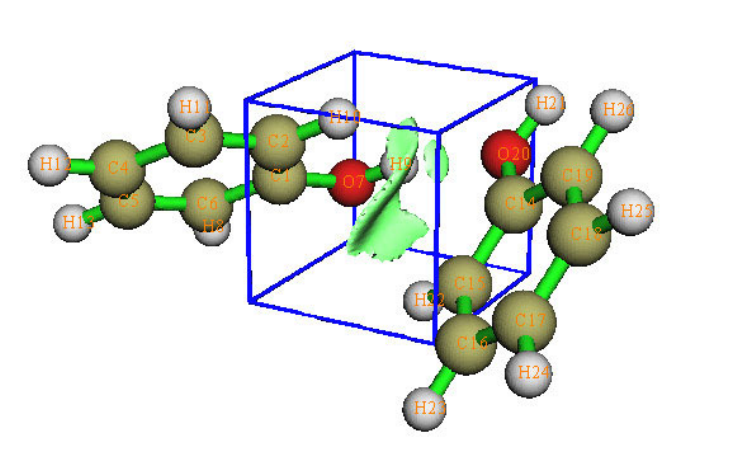
3 Functions
49
Mode 8 Use grid setting (origin, number of points and grid spacing) of another Gaussian-
type cube file. You will be prompted to input the file name. This mode is useful to generate
multiple cube file with exactly identical grid setting.
Notice that the more grid points you set, the finer the isosurface graph you will get, however
the more time is needed for calculating data and generating isosurface graph, and the size of
exported cube file will be bigger. Except for total ESP function, the increase of calculation time
with the number of points is nearly linear.
After setting grid points, the program starts to calculate grid data, once the calculation is
finished, the minimum/maximum and corresponding coordinate, the sum of all/positive/negative
data multiplied by differential element are printed on screen immediately. If what you calculated is
electron density, the molecular dipole moment evaluated based on grid data is also printed out.
Then you will see post-process menu.
Post-process options
In the post-process menu if the option “-1 Show isosurface graph” is selected, a GUI window
will pop up, which shows the isosurface of grid data, all widgets are self-explained, you can
change isosurface value by both dragging slide bar (upper and lower limit are -5 and +5
respectively) or inputting precise value in text box (then press “Enter” button in you keyboard); if
“Show data range” is selected, the spatial scope will be marked by a blue frame as the one in
above picture (if spatial scope exceeds the range of coordinate axis, the frame will no be
displayed). The isosurfaces with the same and reverse sign of current isovalue are in green and
blue respectively.
Option 1 can export isosurface graph to graphic file in current directory. Option 2 can export
grid data to .cub file in current directory. By selecting option 3 the grid data will be exported to
plain text file “output.txt” in current directory. Using option 4 you can set isovalue without
entering GUI window and dragging slide bar, it is useful for batch process and in command-line
3 Functions
50
environment. With options 5~8, you can perform addition, subtraction, multiplication and division
operations on the grid data, respectively.
Special note: Calculate data for a set of points
If you want to use Multiwfn to calculate real space function value for a set of points (may be
arbitrarily distributed), in the interface for setting up grid, you should choose "100 Load a set of
points from external file" and then input the path of the plain text file recording the points. In the
file the first line should be the number of points recorded, and followed by X/Y/Z coordinates of
all points. For example
1902
-3.3790050 -2.0484700 0.0274117
-3.3844930 -1.9472468 -0.2500274
-3.4064601 -1.9221635 -0.1287148
-3.4118258 -1.9232203 -0.0003350
-3.4059106 -1.9218280 0.1351179
....
The coordinates must be given in Bohr. The format is in free format, and can have more than four
columns of data, but the columns after the fourth one will be simply ignored.
Multiwfn will load coordinates of the points from this file, and then calculate function value
for them. Finally, the X/Y/Z coordinate and function value of all points will be outputted to a plain
text file, whose path is specified by users.
Information needed: GTFs (depends on the choice of real space function), atom coordinates
3.7 Custom operation, promolecular and deformation
properties (subfunction 0, -1, -2 in main function 3, 4, 5)
3.7.1 Custom operation for multiple wavefunctions (0)
In main function 3, 4 and 5, there is a subfunction allow you to set custom operation for
multiple wavefunctions. Supported operators include + (add), (minus), * (multiply), / (divide),
there is no upper limit of the number of wavefunctions involved in custom operation. For example,
if the first loaded wavefunction after booting up Multiwfn is a.wfn, then in the setting step of
custom operation you inputted 2 (viz. there are two wavefunctions will be put into “custom
operation list” and thus will be operated with a.wfn in turn), then you inputted -,b.wfn and *,c.wfn,
the property finally you get will be [(property of a.wfn) - (property of b.wfn)] * (property of
c.wfn). If you are confused, you can consult the example in Sections 4.5.4 and 4.5.5.
Sometimes the molecular structure in the first loaded file and that in the subsequently loaded
files are not identical, the grid points you set will be for the first loaded file, all of the other files
will share the same grid setting.
Avoid using custom operation in conjunction with main functions -4, -3 and 6, otherwise you
may get absurd result.
3 Functions
51
3.7.2 Promolecular and deformation properties (-1, -2)
If you selected subfunction -1 in main functions 3, 4 or 5 before choosing a property (viz. a
real space function), what you finally get will be promolecular property. Promolecular property is
the superposition property of atoms in their free-states
AAA
PP )()( freepro Rrr
If the property you chose is electron density, then the promolecular property is generally
referred to as promolecular density
AAA )()( freepro Rrr
This is an artificial density that corresponds to the state when molecule has formed but the density
has not relaxed.
Deformation property is the difference between actual property and promolecular property of
a molecule under the same geometry
)()()( promoldef rrr PPP
If the property is chosen as electron density, then the deformation property is generally called
deformation density or known as electronic bonding charge distributions (BCD), which is very
useful for analyzing charge transfer and bonding nature.
3.7.3 Generation of atomic wavefunctions
Evaluation of promolecular and deformation properties and some functions in Multiwfn
request atomic wavefunction files, such as calculating Hirshfeld, VDD and ADCH charges, fuzzy
atomic space analysis and orbital composition analysis based on Hirshfeld partition, etc. The
process of generating atomic .wfn files are exactly the same.
After you select subfunctions -1 or -2 to study promolecular and deformation properties,
Multiwfn checks whether .wfn files of all elements involved in present system have been
presented in “atomwfn” subdirectory of current directory, if not, Multiwfn automatically invokes
Gaussian to generate the missing element .wfn files and sphericalizes their densities. If the path of
Gaussian executable file (“gaupath” parameter in settings.ini) is incorrect or has not been defined,
Multiwfn will ask you to input the path of Gaussian executable file. The basis-set for generating
the element wavefunctions can be arbitrarily set by user, however it is suggested to use the same
basis-set as the molecular wavefunction.
The newly generated element wavefunction files or those taken from “atomwfn” directory are
stored in “wfntmp” subdirectory in current directory. They will be translated to actual position of
the atoms in present system, meanwhile atomic indices will be added to the .wfn filename (e.g.
"Cr 30.wfn"). These are the files will directly be used to calculate promolecular and deformation
properties.
Details and skills
If you want to avoid the step of generating element wavefunctions every time, you can move
the.wfn files that without number suffix (such as “C .wfn”) from “wfntmp” directory to
“atomwfn” directory (if “atomwfn” directory is non-existing, build it by yourself), next time if
Multiwfn detected that all needed element .wfn files have already been presented in“atomwfn”
3 Functions
52
folder, then Multiwfn will directly use them. Multiwfn only invokes Gaussian to calculate the
missing element .wfn files.
“atomwfn” subdirectory in “examples” directory contains element wavefunction files of all
first four rows, they were generated under 6-31G*, and they have been sphericalized. If you want
to use them, simply copy the "atomwfn" directory to current folder.
There is a quick way to generate all first four-rows element wavefunction files: the file
“examples\genatmwfn.pdb” contains all first four-rows atoms, load it into Multiwfn and generate promolecular
property, after the calculation of element wavefunctions is finished, copy the .wfn files that without suffix in
“wfntmp” directory to “atomwfn” directory.
If your system involves elements heavier than Kr, Multiwfn is unable to generate atom
wavefunction files by invoking Gaussian and sphericalize their density automatically; in that cases
you have to calculate and sphericalize atom wavefunctions manually, and then put them into
“atomwfn” directory, Multiwfn will directly use them.
The default theoretical method for generating wavefunction for main group elements in first
four-rows (index from 1 to 20 and 31 to 36) is ROHF, for the transition metals in the fourth row,
UB3LYP is used. In general, the promolecular and deformation properties are insensitive to
theoretical method. If you want to specify theoretical method by yourself, you can input
theoretical method and basis-set at the same time with slash as separator, for example BLYP/6-
311G*. Do not add “RO” or “U” prefix since they will be added automatically. If error occurs
during generation of atom wavefunctions, please check Gaussian input and output files in
“wfntmp” directory carefully.
Notice that the maximum character length of the path of .wfn file permitted by Gaussian is
only 60! The path will be truncated and cause error if the length exceeded this threshold. So do not
put Multiwfn in the directory with too long path!
3.7.4 Sphericalization of atom wavefunction
The main purpose of Multiwfn supporting promolecular and deformation property is for
generating promolecular and deformation density, however, electron density of most elements in
free and ground state is not in spherical symmetry, hence will lead to orientation dependence
problem. To tackle it, atomic electron density must be sphericalized. However, there is no unique
way to do this. In Multiwfn, atom electron density is sphericalized by modifying atom
wavefunction artificially, here I describe the detail. If you want to skip the sphericalization step,
simply set the “ispheratm” in settings.ini to 0.
For elements in IV A group, Multiwfn uses sp3 configuration to replace s2p2 ground state by
default. This treatment is reasonable, since in most molecules these atoms are in sp3 hybridization.
For VI A, VII A and Fe, Co, Ni, Multiwfn equalizes the occupation number of orbitals within the
same shell; for example, oxygen has two singly occupied 2p orbitals and one doubly occupied 2p
orbitals in ground state, the number of electrons in this shell is 4, so Multiwfn sets the occupation
number of all the three orbitals to 4/3. This method works because the shape of occupied orbitals
are always nearly identical, regardless of the original occupation number is one or two. However,
the difference between virtual orbital and occupied orbital is remarkable, thus Multiwfn uses
another method to sphericalize electron density of elements in III A group, as well as Sc, Ti and V.
In this method, the singly occupied orbitals are duplicated and rotated. Taking boron as example,
assume that the singly occupied 2p orbital is directing along Z-axis, Multiwfn replicates this
orbital twice and turn them toward X-axis and Y-axis respectively, finally the occupation numbers
3 Functions
53
of the three orbitals are set to 1/3. (Users needn’t to check the orientation of singly occupied
orbital by themselves). If you hope that Multiwfn sphericalizes atoms in IV A group in such
manner instead of using sp3 configuration, set “SpherIVgroup” in settings.ini to 1.
Notice that the sphericalization methods used in Multiwfn are closely related to wavefunction
type, the methods fail if unrestricted wavefunction is used for main group elements or restricted
open-shell wavefunction is used for transition metals. These methods also fail if Hartree-Fock
method is used for transition metals, because orbital order produced by HF is different from most
DFT cases (the HF’s order is wrong, 4s is higher than 3d).
3.8 Checking & Modifying wavefunction (6)
This function provides a lot of subfunctions for checking and modifying loaded wavefunction,
all subfunctions take effect immediately, so after modification you can print related information to
check if your operations are correct. Once you finished all modifications of wavefunction, you can
save current wavefunction to “new.wfn” file or return to main menu, all following tasks which
make use of wavefunction information will be affected. The title in this interface shows the
number of GTFs, orbitals, atoms and alpha/beta electrons of current wavefunction.
Below is explanation of each subfunction in this catagory.
Subfunction -1: Return to main menu.
Subfunction -3 and -4: Defining molecular fragment. In -3 you directly define fragment by
inputting atomic indices; while in -4 you should input the indices of the atoms to be excluded, the
remaining atoms will constitute the fragment. The GTFs whose centers do not belong to this
fragment will be discarded (can be imagined as corresponding GTF coefficients in all orbitals are
set to zero). This function affects all the following tasks which make use of GTF information, in
particular, the calculations involving real space functions.
When use these two functions? For large molecules, what you are interested in may be only a
small region, by discarding atoms in other region, the calculation speed of time-consuming task
such as generating grid data can be increased evidently. Besides, sometimes you may only want to
obtain real space function contributed by certain atoms, these two functions can fulfill your
purpose.
This function can be safely used together with main function 1~6. For other tasks, DO NOT
use this function if you do not understand what you are exactly doing, otherwise you may obtain
wrong or meaningless results. Notice that this function is irreversible, the discarded GTFs cannot
be recovered, unless you reboot the program and reload the wavefunction file.
Subfunction 0: Save current modified wavefunction to “new.wfn” file in current directory.
Multiwfn can be used as an .fch/.molden/.gmswfn format converter through this function.
Notice that the orbitals with zero occupation number and the atoms do not have GTFs will be
automatically discarded during saving.
Subfunction 1: Print information of all GTFs, including the centers they are belonging to,
GTF types and exponents.
Subfunction 2: Print information of all basis functions, including the shells/centers they
attributed to, types, and corresponding GTF index ranges.
Subfunction 3: Print basic information of all orbitals, including energies, occupation
3 Functions
54
numbers, orbital types (Alpha, beta or alpha+beta).
Subfunction 4: Print detail information of an orbital, including the expansion coefficients
with respect to GTFs (along with GTF information), note that the coefficients include GTF
normalization constants.
Subfunction 5: Print coefficient matrix in basis function (not the coefficients with respect to
GTFs), only available when the input file contains basis function information.
Subfunction 6: Print one-particle density matrix in basis functions, only available when the
input file contains basis function information.
Subfunction 7: Print various kinds of integral matrix between basis functions, such as
overlap integrals, electric/magnetic dipole moment integrals, kinetic energy integrals and velocity
integrals. For overlap matrix, eigenvalues are printed together, which are useful for checking
linear dependency. Only available when the input file contains basis function information.
Subfunction 11: Swap centers or types or exponents or orbital expansion coefficients of two
GTFs, or swap all information of two GTFs at once (identical to swap record order of two GTFs,
thus does not affect any analysis result)
Subfunction 21 to 24: Set the center, type, exponent and expansion coefficient of a specific
GTF in an orbital respectively.
Subfunction 25: Set the expansion coefficients of some GTFs that satisfied certain
conditions in some orbitals. The conditions you can set for GTFs include: Index range of GTFs,
index range of atoms, GTF types (you can input such as YZ, XXZ). The selected GTFs are
intersection of these conditions. When program is asking you for inputting range, you can input
such as 3,8 to select those from 3 to 8, input 6,6 to select only 6, especially, input 0,0 to select all.
If the input file also contains basis function information, by this option you can also set
expansion coefficients of basis functions.
Subfunction 26: Set occupation number of some orbitals. This function is very useful for
shielding the contributions from certain orbitals to real space functions, namely setting their
occupation numbers to zero before calculating real space functions.
Subfunction 27: Set orbital type of some orbitals, then wavefunction type will be
automatically updated, please check the prompts shown on the screen.
Subfunction 31: Translate the whole wavefunction and all atom coordinates of current
system by inputting translation vectors and their units.
Subfunction 32: Translate and duplicate the whole wavefunction and all atom coordinates of
current system, users need to input translation vectors, their units and how many times the system
will be translated and duplicated according to the translation vectors. This function is useful for
extending the primitive cell wavefunction outputted by Gaussian PBC function to supercell
wavefunction, of course you can calculate supercell wavefunction directly by Gaussian, but much
more computational time will be consumed. Notice that constructing wavefunction of supercell by
this way is only an approximation, because the mix between orbitals of neighbouring primitive
cell to new supercell orbitals is completely ignored.
Subfunction 33: Rotate wavefunction, namely XY, YZ, ZX
Subfunction 34: Set occupation number of all inner molecular orbitals in present system to
zero, namely only contribution from valence orbitals will be reserved for following studies. The
number of inner MOs is automatically determined, howver, the atoms using pseudopotential are
not taken into account.

3 Functions
55
Subfunction 35: This function is very useful if you want to discard contribution of orbitals
with certain irreducible representation (IRREP) in all kinds of analyses. After you enter this
subfunction, IRREP of all occupied orbitals will be shown, the "N_orb" denotes the number of
occupied orbitals belonging to the corresponding IRREP. If you want to discard contribution of
some IRREPs in the succeeding analyses, you can select option 1 and input the index of the
IRREPs, then the occupation number of corresponding orbitals will be set to zero and thus their
contributions are eliminated, and you will also see their status are changed from "Normal" to
"discarded". Then you can choose option 0 to save wavefunction and quit. You can also choose
option 2 to recover the original occupation number of all orbitals, or choose 3 to reverse the status
of every IRREP between "Normal" and "Discarded". Note that this subfunction only works
for .molden and .gms files, because only these files record orbital IRREPs (beware that the
IRREPs in the .molden file produced by many quantum chemistry programs are missing or
incorrect). Besides, only restricted and unrestricted SCF wavefunctions are supported.
Subfunction 36: Invert phase of some orbitals (i.e. replacing expansion coefficients of basis
functions and GTFs of these orbitals with their negative values).
Information needed: Basis function (only for subfunction 2, 5, 6, 7), GTFs, atom coordinates
3.9 Population analysis and atomic charges (7)
This module is used to calculate population number of basis functions, shells, atoms,
fragments, or atomic charges.
Regardless of which function you choose, if you want to study fragment charge (the sum of
charge of the atoms in a fragment), you should select option -1 first and input atom indices to
define the fragment. Then once the calculation of atomic charges is finished, fragment charge will
be printed together.
3.9.1 Hirshfeld population (1)
Hirshfeld is a very popular population method based on deformation density partition,
Hirshfeld charge is defined as (Theor. Chim. Acta (Berl.), 44, 129)
rrr dwq AA )()( def
Hirsh
where
)(
)(
)(
)()(
)()()(
pro
free
Hirsh
freepro
prodef
r
Rr
r
Rrr
rrr
AA
A
AAA
w
The advantages of Hirshfeld population are:
1. Result is qualitatively consistent with general chemical concepts such as electronegativity
rule.
3 Functions
56
2. The weighting function w for space partition has clear physical meaning.
3. Unlike the methods based on integrating electron density such as AIM charge, what the
Hirshfeld charge reflects is the amount of transfered electron density during molecule formation,
the density not transfered is not involved.
4. Insensitive to the quality of wavefunction.
5. Although calculating Hirshfeld charge needs integration in real space, due to the smooth
integrand, sophisticated density functional theory (DFT) grid-based integration schemes can be
directly used, so Hirshfeld population is high-efficient.
6. The wide application field. Deformation density data can also be obtained by X-ray
crystallography experiments. Moreover, the applicability of Hirshfeld population is not
constrainted by the type of wavefunction, the method can be directly applied to solid system,
where the wavefunction generally be described by plane-wave functions.
The disadvantages of Hirshfeld population are the charge is always too small and the poor
reproducibility of observable quantities, such as molecular dipole moment and ESP, the reason is
Hirshfeld population completely ignores atomic dipole moments.
When calculation is finished, along with Hirshfeld charges following contents are printed
1 Summing up all charges: The value of summing up all Hirshfeld charges, if the value is
very close to integer, means the quadrature is accurate; if not, that means the outputted Hirshfeld
charges are unreliable, you need to increase the density of integration points by setting “radpot”
and “sphpot” to larger value and calculate again. For balancing computational time and accuracy,
the default value of “radpot” and “sphpot” are 75 and 434, respectively, you can set them to 100
and 590 respectively for obtaining more accurate results.
2 Atomic dipole moments: They are the simplest representation of density anisotropy
around corresponding atom.
3 Total dipole moment from atomic charges: Molecular dipole moment evaluated from
Hirshfeld charges, following the components in X, Y and Z directions.
4 Total atomic dipole moment: The sum of all atomic dipole moments, following the
components in X, Y and Z directions.
Finally, you can choose to output Hirshfeld charges to [name of loaded file].chg file in
current directory, see Section 2.5 for detail about chg format.
An example is given in Section 4.7.1.
3.9.2 Voronoi deformation density (VDD) population (2)
The only difference between VDD and Hirshfeld population is the weighting function w. In
VDD population, the Voronoi cell-like partition is used, see J. Comput. Chem., 25, 189.
The results of VDD population are similar to Hirshfeld population in common, because the
magnitude of deformation density is always small, so there is no significant change in charges
when different weighting functions are used. The outputted terms are identical to Hirshfeld
population. Personally, I suggest you use Hirshfeld population instead of VDD.
Note that if the sum of VDD atomic charge deviates from molecular net charge evidently, that
means the numerical integration accuracy is not satisfactory, and hence you should enlarge

3 Functions
57
"sphpot" parameter in settings.ini to improve the result. "radpot" parameter also influences the
result, but not so significantly as "sphpot".
3.9.3 Mulliken atom & basis function population analysis (5)
Mulliken analysis is the oldest population method based on orbital wavefunction, supported
by almost all quantum chemistry packages.
Orthonormality condition of spin orbital wavefunction entails
rr d
2
)(1
, if we assume
that the orbital is real type and insert the linear combination equation
aaiai C)()( ,rr
into
it, we get
aaabbaibiaia
aaabbaibiaia
aaia SCCCSCCCC ,,,
2,,,,
2,
2
,2d)(1 rr
where
rrr d)()(
,baba
S
, the normality of basis functions are used in derivation. The first
term is “local term”, denotes the net population of each basis function in orbital i, the second term
is “cross term”, denotes the shared electrons between basis function pairs in orbital i. Certainly the
local terms should be completely attributed to corresponding basis functions, however for cross
terms the partition method is not unique. Mulliken defined the population of basis function a in
spin orbital i as
ab baibiaiaai SCCC ,,,
2,,
That is each cross term baibia SCC ,,,
2 is equally partitioned to corresponding two basis functions.
The population number of atom A is simply the sum of population numbers of all basis
functions attributed to atom A in all orbitals. Mulliken atomic charge is defined as
iAaaiiA
iAiAA ZnZq ,,
where
is orbital occupation number, ni,A is the contribution from orbital i.
In subfunction 1 (“Output Mulliken population/charges and decompose them to MO's
contribution”), not only atomic charges but also contributions of basis functions and shells to
population are outputted, the latter are the sum of contributions from basis functions within
corresponding shells. You can choose to decompose atom population number to orbitals’
contributions.
In subfunction 2 (“Output gross atomic population matrix and decompose it”), the gross
atom population matrix is printed, from which you can get local terms of each atom (diagonal
element) and cross terms between each atom pair (non-diagonal element multiplies 2). The matrix
is defined as
iAaBbbaibiai
i
iBABA SCC ,,,,,
3 Functions
58
Notice that the last row of outputted matrix is the sum of corresponding column elements,
that is the total population number of corresponding atom. You can also choose to decompose it to
orbital’s contribution (
AaBbbaibiai
iBA SCC ,,,,
), owing to the very large amount of
information, results will be outputted to “groatmdcp.txt” in current directory rather than printing
on screen.
By the way, the quantity 2* iBA,
is just the Mulliken bond order between atom A and B
contributed from orbital i, as we will see in Section 3.11.4.
In subfunction 3 (“Output gross basis function population matrix & decompose it”), the
gross basis function population matrix can be outputted for analyzing detail information further,
the matrix element is defined as
ibaibiai
i
ibaba SCC ,,,,,
Likewise in subfunction 2, the last row of outputted matrix is total population number of
corresponding basis function. You can also select to output orbital’s contribution
baibiai
iba SCC ,,,,
to “grobasdcp.txt” in current directory.
Mulliken analysis is deprecated for practical application due to the serious shortcomings: 1.
Poor reproducibility of observable properties 2. The “equal partition” of cross term have no strict
physical meaning 3. Very high basis-set dependence 4. Occasionally meaningless result occurs
(population number is negative).
3.9.4 Löwdin population (6)
The only difference between Löwdin and Mulliken population analysis is whether Löwdin
orthogonalization is performed first. In Löwdin orthogonalization, the linear transformation matrix
is
H
UUsX 5.0
where U is eigenvector matrix of overlap matrix, matrix s is diag(-1, -2...), here {-} is eigenvalue
set of overlap matrix. After Löwdin orthogonalization, the overlap matrix becomes identity matrix,
and new coefficient matrix is CX 1.
Ostensibly, Löwdin population avoids the partition for cross terms since they have become
zero, actually, the partition step is no more than hidden in the orthogonalization. Since Löwdin
orthogonalization still has no strong physical meaning, it cannot make conclusion that Löwdin
population is better than Mulliken. In view of practical results, one also found Löwdin charges
have no any evident advantages relative to Mulliken charges, though some people argued that
Löwdin charges have better basis-set stability and reproducibility of molecular dipole moment.
Besides, Mayer et. al. found Löwdin population has rotation dependence to some extent when
cartesian type Gauss basis functions are used, however the dependency can be safely ignored in
generally, for detail please see Chem. Phys. Lett., 393, 209 and Int. J. Quantum. Chem., 106, 2065.

3 Functions
59
3.9.5 Modified Mulliken population defined by Ros & Schuit (SCPA)
(7)
Some people had proposed several different partition methods of cross term to improve
Mulliken analysis, they are generally called as modified Mulliken population analysis (MMPA). In
the method proposed by Ros and Schuit (Theo. Chim. Acta, 4, 1), the composition of basis
function a in orbital i is defined as
bib
ia
ai C
C
2,
2,
,
only the square of coefficients are presented in the formula, so this method is also called C-
squared Population Analysis (SCPA). By inserting the identity
aaabbaibiaia SCCC ,,,
2,
1
into the right most of above formula, can be rewritten as
aabbaibia
bib
ia
iaai SCC
C
C
C,,,
2,
2,
2,,
It is clear that when calculating composition of basis function a in orbital i, what is partitioned is
not the cross terms between atom a and other atoms, but the total cross term of all atom pairs. The
SCPA atomic charges can be calculated in the same manner as Mulliken charges by using the
newly defined . Relative to Mulliken population, the advantage of SCPA is that negative value of
population number never occurs.
3.9.6 Modified Mulliken population defined by Stout & Politzer (8)
Stout and Politzer defined the as (Theo. Chim. Acta, 12, 379)
ab baibia
ibia
ia
iaai SCC
CC
C
C,,,
2,
2,
2,
2,, 2
That is cross terms are partitioned according to the ratio of the squares of corresponding
coefficients. Ostensibly, this definition has more consideration on the unbalanced nature of cross
term, however in practical applications the results are even worse than Mulliken, therefore this
method is rarely used now. Besides, Grabenstetter and Whitehead had pointed out that this MMPA
definition has unitary transformation dependence, so if the molecule is rotated the results changed
(the dependence is remarkable and cannot be ignored).
3.9.7 Modified Mulliken population defined by Bickelhaupt (9)
The total population number of a basis function defined in Organometallics, 15, 2923 is
ibaibiai
ab ba
iiaia SCCwC ,,,,
2,2
where the weight of basis function a for partitioning the total cross term between a and b in all
orbitals is

3 Functions
60
jjbj
iiai
kkak
ba CC
C
w2,
2,
2,
,
Essentially, it is equivalent to define as
ab baibiabaiaai SCCwC ,,,,
2,, 2
This method is similar to the MMPA defined by Stout and Politzer, the difference is in the
latter the weight wa,b is only related to local terms of basis functions a and b in current orbital,
while in present method the weight is related to total local terms of basis functions a and b.
3.9.8 Becke atomic charge with atomic dipole moment correction (10)
In the paper J. Chem. Phys., 88, 2547, Becke proposed a weighting function for converting
whole space integral to multiple single-center spherical integrals, although the weighting function
is not intend for population analysis, Multiwfn still makes an attempt to use this weighting
function as atomic space to obtain atomic charges. The Becke charge can be defined as
rrr dwZq AAA )()(
The radii used for evaluating the Becke weighting function (or say Becke atomic space) can be
controlled by uses, see corresponding options shown on screen. For details about Becke weighting
function please see J. Chem. Phys., 88, 2547 or Section 3.18.0. According to my experiences, by
using the default "modified CSD" radii, Becke charge is reasonable for typical organic systems,
but not very appropriate for ionic systems. For detail about "modified CSD" radii, see the end of
Section 3.18.0.
After the Becke charges are calculated, atomic dipole moment correction will be performed
automatically. The correction process is identical to the one used for correcting Hirshfeld charge
(see next section). After the correction the charges will have better electrostatic potential
reproducibility and can exactly reproduce molecular dipole moment.
3.9.9 Atomic dipole moment corrected Hirshfeld charges (ADCH, 11)
The main reason why Hirshfeld charges are too small and have poor reproducibility of
observable quantity is that atomic dipole moments are completely neglected. In ADCH method (J.
Theor. Comput. Chem., 11, 163 (2012)), Hirshfeld charges are corrected by expanding atomic
dipole moments to correction charges placed at neighbour atoms. ADCH atomic charges are very
reasonable in chemical sense, molecular dipole moment is exactly reproduced, the reproducibility
of ESP is close to the atomic charges from fitting ESP. Compared with another method that
corrected Hirshfeld charges, namely Hirshfeld-I, the computational cost of ADCH correction is
almost zero! Owing to its many advantages, ADCH is a highly recommended atomic charge model.
For an extensive comparison of atomic charge models, see Acta Phys. -Chim. Sin, 28, 1 (2012, in
Chinese, http://www.whxb.pku.edu.cn/EN/abstract/abstract27818.shtml)
Before doing ADCH correction, Hirshfeld charge will be calculated first. In the summary
field, “corrected” and “before” correspond to ADCH charge and Hirshfeld charge respectively. At
final stage, the “Error” means the the difference between molecular dipole moment produced by
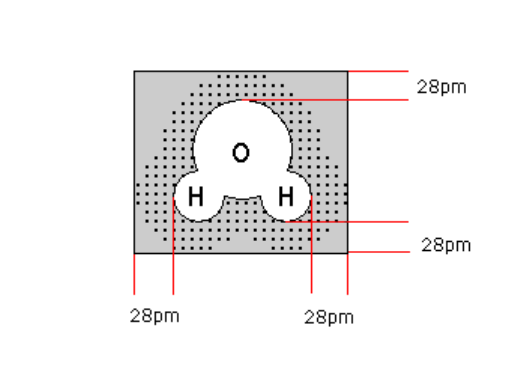
3 Functions
61
ADCH charges and the one produced by ab initio density, “Error” is always equals to or very close
to zero, because ADCH charge preservers molecular dipole moment.
If you would like to know the detail of charge transfer in the ADCH correction process, you
can set “ADCHtransfer” in settings.ini to 1.
An example is given in Section 4.7.2.
3.9.10 CHELPG (Charges from electrostatic potentials using a grid
based method, 12)
Theory
CHELPG (J. Comput. Chem., 11, 361) is one of the most widely used electrostatic potentials
(ESP) fitting charge model. Compared to CHELP and Merz-Kollman methods, CHELPG charges
have the best rotational invariance, mostly due to the fitting points are distributed in cubic grid
manner.
In CHELPG model, a box is defined first to enclose the whole molecule, extension distance
in each side is 28 pm, see the picture below
Fitting points are evenly scatter in the box, the default spacing is 0.3 angstrom. For any fitting
point, if the distance between the point and any nucleus is smaller than vdW radius of
corresponding atom, or the distances between the point and all nuclei are larger than 28pm, then
the fitting point will be discarded. The black dots shown above are final fitting points.
Like other ESP fitting methods, in CHELPG, the deviation function shown below is
minimized to make the ESP calculated by atomic charges (Vq) close to the ESP calculated by
quantum chemistry (V) as well as possible.
2
21 )()()...,(
iiiqN VVqqqF rr
where ri is the coordinates of fitting point i. q are fitted point charges, the position are called
fitting center. Notice that q does not necessarily mean atomic charge, the fitting center can be
defined beyond nucleus.
Usage
In Multiwfn, you can find the options used to set grid spacing of fitting points and box
extension. The coordinates of additional fitting centers, which are beyond atomic nuclei, can be
3 Functions
62
read from external file by option 4, the format of the file is
numdata
X Y Z For additional fitting center 1
X Y Z For additional fitting center 2
...
numdata denotes how many entries are there in this file. X, Y and Z are coordinates (in Bohr).
For flexibility consideration, coordinates of fitting points are allowed to be read from external
file to replace the CHELPG fitting points. The format of the file is
numdata
X Y Z [ESPval] For fitting point 1
X Y Z [ESPval] For fitting point 2
...
The ESPval is an optional term, which denotes precalculated ESP value at corresponding
point. If numdata is a negative value, then the ESP values used in charge fitting will be read from
the fourth column rather than calculated by Multiwfn internally.
When you choose selection 1, Multiwfn will start to calculate ESP value at each fitting point,
the process may take long time for big system, then fitted charges of all fitting centers will be
outputted on screen. The coordinates and ESP value calculated by quantum chemistry of all fitting
points can optionally be exported to ESPfitpt.txt in current folder.
RMSE and RRMSE are outputted automatically, they measure the quality of fitting, the
smaller value suggests that the fitted charges have better ESP reproducibility. RMSE and RRMSE
are defined as (where N is the number of fitting points)
N
VV
iiiq
2
)()(
RMSE
rr
ii
iiiq
V
VV
2
2
)(
)()(
RRMSE r
rr
Notice that only small part of vdW radii are predefined in original and related papers, if your
system contains other elements, Multiwfn will ask you to input vdW radius. If you do not have
proper data in hand, you can input a somewhat arbitrary value, 3.4 Bohr is recommended.
An example is given in Section 4.7.1.
3.9.11 Merz-Kollmann charge (13)
Merz-Kollmann (MK) charge is another well known charge model derived from ESP fitting,
see J. Comput. Chem., 11, 431. The only difference between MK and CHELPG is grid setting. In
MK, the fitting points are evenly distributed on the layers of 1.4, 1.6, 1.8 and 2.0 times the vdW
radii of each atoms, all fitting points enclosed by vdW surface are discarded.
In Multiwfn, the number of layers, the ratio of vdW radii used to define the layers, and the
density of points per square Ångstrom on the shells are controllable. For detail of selections and
outputs, see last section.

3 Functions
63
3.9.12 AIM charge (14)
AIM (Atoms in molecules) population is the number of electrons in AIM basin, and
accordingly, nuclear charge minusing AIM population yields AIM charge, which is also known as
Bader charge. AIM charges can be calculated in basin analysis module, please check the example
given in 4.17.1 on how to do this. Related theories and algorithms of basin analysis module are
introduced in Section 3.20.
3.9.13 Hirshfeld-I population (15)
Hirshfeld-I (HI) method was proposed in J. Chem. Phys., 126, 144111 (2007), it is an
important extension of Hirshfeld method. It is believed that the atomic space defined by Hirshfeld
is not quite ideal, because it does not respond actural molecular environment. In HI, atomic spaces
are gradually refined via an iterative scheme. After convergence, the final HI atomic spaces are
evidently more physically meaningful than the Hirshfeld ones.
There are some variants of HI method, including the Hirshfeld-E proposed in J. Chem.
Theory Comput., 9, 2221 (2013), the Hirshfeld-I- proposed in J. Comput. Chem., 32, 1561 (2011)
and the fractional occupation Hirshfeld-I (FOHI) proposed in J. Chem. Theory Comput., 7, 1328
(2011). Also, there is an iterative atomic space method name iterated stockholder atoms (ISA),
which is closely related to HI, see Chem. Commun., 2008, 5909. However, since in my personal
viewpoint these variants and ISA are not quite important, I do not intend to implement them in
Multiwfn.
Basic theory of HI method
In HI method, the weighting function of atom A at iteration n is defined as
)(
)(
)(
)(
)( )1(
pro
)1(
)1(
)1(
)(
r
Rr
Rr
Rr
Rr
nA
n
A
BB
n
B
A
n
A
A
n
A
w
where r and R denote spatial coordinate and position of atomic nucleus, respectively. The atomic
density involved in HI is obtained by linear interpolation between spherically averaged free-state
atomic density of adjacent charge states:
)()()()()( free
high,low
)1(free
,low
)1(
high
)( rqqrqqr A
n
AA
n
A
n
A
where qhigh and qlow are ceiling and floor integer of atomic charge of atom A at n-1 iteration, while
free
high,A
and free
,lowA
are spherically averaged atomic density of atom A at these two charge states,
respectively. For example, if atom A carries 0.2 charge at n-1 step, then its radial atomic density at
step n will be computed as
)(2.0)(8.0)( free 1,
free 0,
)( rrr qAqA
n
A
Before the HI iteration, radial density of all atoms are initialized to their neutral state.
Based on HI atomic weighting functions, HI atomic charges can be straightforwardly
obtained. The HI iteration continues until all atomic charges converged to a given criterion.
Note: It is clear that the HI atomic charges yielded at the first iteration are in principle identical to Hirshfeld
3 Functions
64
charges. However, this is not exactly true in Multiwfn, because currently the rule of generating spherically
averaged free-state atomic density involved in HI is not completely identical to that used in Hirshfeld, but the
difference is very small and can be ignored. It is never incorrect to directly take the atomic charges printed at the
first iteration of HI as Hirshfeld charges.
Usage
After you entered the HI analysis module, you can adjust convergence criterion and the
maximum number of cycles, also you can switch the algorithm for realizing HI iterations (see
below), as well as choose if printing atomic charges every iteration. If you select option 0,
Multiwfn will first try to yield atomic radial density file (.rad) for all elements in the systems by
invoking Gaussian, and then start the HI iteration. After convergence, HI atomic charges and
fragment charge (if you have defined fragment) are printed. Note that the printed HI atomic
charges have been properly normalized (i.e. making sum of HI population of all atoms equal to
total number of electrons) to eliminate noise of numerical integration. Finally, you can select if
outputting resulting atomic charges as .chg file.
Procedure of preparing atomic radial density files
Before igniting HI iteration, atomic radial density files (.rad files) must be first prepared. The
steps are detailed below:
(1) Generating atomic .wfn files in "atmrad" folder: Multiwfn generate Gaussian input
files (.gjf) in "atmrad" subdirectory of current folder and invokes Gaussian to run them to generate
atomic .wfn files for all elements involved in present system. The charge states range from -2 to
+2 are taken into account. Calculation of useless charge states are skipped. For example, its
meaningless to calculate -2 and +2 charge states for alkali elements, since in practical systems it is
impossible that an alkali atom has charge between -1 to -2, or between +1 to +2. The multiplicity
of each charge state of each element is set to ground state (this cannot be well guaranteed for all
cases, for example, ground state at different calculation level is even different. However, this is
never an important problem, so please do not concern it too much). The path of Gaussian
executable file should be set by "gaupath" in settings.ini file, if it is not properly set, you will be
prompted to input it in the Multiwfn interface. You also need to input the keywords of Gaussian
used to calculate the atomic .wfn files. After Gaussian calculation finished, the atomic .wfn files
are generated in "atmrad" folder, the file name directly corresponds to element name and charge
state. For example, the file corresponding to -1, 0, +1 and +2 charge states of Be will be generated
in "atmrad" folder as "Be-1.wfn", "Be_0.wfn", "Be+1.wfn" and "Be+2.wfn", respectively. If
corresponding file has already been found in "atmrad" folder, then the file will be retained and not
be recalculated. If you find Gaussian calculation is failed (mostly due to SCF unconvergence
problem), you should carefully check Gaussian output file and properly adjust the keyword used.
(2) Converting atomic .wfn files to .rad files: As mentioned earlier, HI calculation requires
spherically averaged atomic densities. However, the electron density corresponding to the
atomic .wfn files generated at last step often does not meet this requirement. For example, carbon
at its neutral ground state has s2p2 configuration, and thus "C_0.wfn" corresponds to elliptical
density distribution. To get spherically averaged representation of atomic densities, Multiwfn
automatically loads each atomic .wfn files in "atmrad" folder, calculates spherically averaged
radial density, and write the data as .rad file, whose name is identical to its parental .wfn file. i.e.
"C_0.wfn" will be converted to "C_0.rad". The .rad file is plain text file, the first line is the
number of data points, the first and second columns respectively correspond to radial distance with
3 Functions
65
respect to nucleus (in Bohr) and corresponding electron density. Note that if needed .rad file is
already presented in "atmrad" folder, then the conversion of .wfn.rad will be skipped.
It is suggested (but not compulsory) that the atomic .wfn files are generated at the same
calculation level as the molecule under study, so that the result has good physical meaning. You
should always make sure that the atomic .wfn and .rad files in "atmrad" folder were generated at
expected level. For example, in the "atmrad" folder if some .wfn/.rad files were generated at
B3LYP/cc-pVDZ level, and some were generated at M06-2X/def2-TZVP level, while the
molecular wavefunction file was obtained at PBE/6-311G** level, then the resulting HI charges
must be problematic. If you want to let Multiwfn regenerate all needed atomic .wfn/.rad files at
given level during HI analysis, simply cleaning up the "atmrad" folder before calculation.
Note: If you are using Windows version of Multiwfn, while Gaussian cannot be invoked properly, please read
Appendix 1 to set environment variable for Gaussian.
Two numerical algorithms of HI
Multiwfn provides below two algorithms to realize HI methods, the results are exactly the
same, they only differ by efficiency and memory requirement.
(1) Fast & large memory requirement (default): This algorithm computes as much as possible
data before starting iteration. Therefore, once initialization stage is done, the HI iteration can be
finished rapidly. The drawback of this algorithm is that large amount of memory is needed, the
memory consumed is at least 5natmnatmnradnang, where natm is the number of total atoms, nrad
and nang corresponds to the number of radial and angular integration grid per atom. Evidently, this
algorithm is unable to be applied for very large systems unless you have huge physical memory.
(2) Slow & low memory requirement: This algorithm utilizes very low amount of memory,
however, the data needed to be calculated in each iteration is much more than algorithm (1), thus
the total computational cost is much higher.
For both the two algorithms, the higher number the integration grid, the more accurate the
result. By default nrad and nang are properly set by Multiwfn. If the system only consists of first two
rows elements, then nradnsph will be 30*170=5100. If you want to manually set nrad and nsph, you
can set "iautointgrid" in settings.ini to 0 and change "radpot" and "sphpot" parameters.
An example of computing HI charges is given in Section 4.7.4.
3.9.14 CM5 charge (16)
CM5 charge was proposed by Truhlar et al. in J. Chem. Theory Comput., 8, 527 (2012). This
charge is somewhat akin to the ADCH charge proposed by me, both of them are defined as
applying additional correction to Hirshfeld charges. Unlike ADCH, which is free of empirical
parameters, CM5 method contains global parameters as well as parameters for individual elements.
The CM5 parameters are optimized for best reproduction of highly accurate experimental or
theoretical molecular dipole moment.
Worthnotingly, there is a remarkable difference between the basic feature of ADCH and CM5:
ADCH charges can exactly reproduce molecular dipole moment corresponding to present
calculation level, that means if the level used is very high (e.g. CCSD/aug-cc-pVTZ), then the
dipole moment calculated by the resulting ADCH charge must be very close to the molecular
dipole moment in real world; while if the used level is poor (e.g. HF/6-31G), then the ADCH

3 Functions
66
charges will be almost useless. In contrast, the CM5 charges do not attempt to reproduce
molecular dipole moment at present calculation level, but to reproduce real molecular dipole
moment, therefore even if low level such as B3LYP/6-31G* is used, which is certainly unable to
give good dipole moment result, the CM5 charges derived at this level commonly are still able to
yield molecular dipole moment at acceptable accuracy.
The expression of CM5 charge is
)](exp[
Hirsh5CM
jiijij
ij ijijii
RRrB
BTqq
where rij is distance between atom i and j, Bij may be regarded as their Pauling bond order, Ri and
Rj are their atomic covalent radii, which are defined as follows: For Z=1~96, the average between
CSD radii and Pyykkö radii are used, while for Z=97~118, the Pyykkö radii are employed. The
global parameter
equals to 2.474 Å-1. The Tij is defined as Dij if both i and j are attributed to H,
C, O, N, note that Dij=0 when i and j belong to the same element and Dij=-Dji. All the involved six
Dij parameters (H-C, H-N, H-O, C-N, C-O, N-O) are tabulated in the original paper. For other
cases, Tij is defined as Di - Dj, the optimized D parameters for all elements through out the whole
periodic table are provided in the supplemental material of CM5 original paper.
Like usual Hirshfeld and ADCH calculations, after you enter this function, I suggest you
select option 1 to use the build-in sphericalized atomic densities in free-states, since it is the most
convenient. Then Multiwfn starts calculation of Hirshfeld charges, and then print CM5 charges. If
you want to gain detailed information about the CM5 correction process during the calculation,
you can set ishowchgtrans parameter in settings.ini to 1.
3.9.15 Electronegativity Equalization Method (EEM) (17)
Theory
The EEM method is also known as Full Equalization of Orbital Electronegativity (FEOE), it
was firstly proposed in J. Am. Chem. Soc., 107, 829 (1985). The idea of EEM is very clear. The
electronegativity of atom i can be written as
ij ji
j
iiiiii r
q
q
.
00 )(2)(
where 0
i
and 0
i
are Sanderson electronegativity and Parr-Pearson hardness of corresponding
element, respectively, while i
and j
are fitted parameters. qi denotes atomic charge of
atom i, and ri,j is distance between atoms i and j. For convenience, above formula is commonly
expressed as
ij ji
j
iiii r
q
qBA
,
where
is global parameter, A and B are element parameters. It can be seen that, atomic
electronegativity in a chemical system is function of atomic charges.
EEM method assumes that in a chemical system, all atoms have equal electronegativity,

3 Functions
67
hence the EEM charges can be determined by solving linear equations according to below
conditions
ii
N
Qq
mol21 ...
where Q stands for net charge of the whole system,
mol is molecular electronegativity
It is easy to show that the working matrix equation for solving EEM charges can be written as
follows
Q
A
A
A
q
q
q
B
B
B
N
N
N
rr
rr
rr
NN
N
N
2
1
mol
2
1
2
1
0111
1
1
1
2,1,
,21,2
,12,1
Since EEM matrix element is very simple and the above matrix equation can be solved easily,
EEM charges could be evaluated rather rapidly even for very large systems.
Parameters
The result of EEM charges are directly dependent of EEM parameters
, {A} and {B}. There
is no unique way to determine the parameters, the most common way to obtain them is fitting, so
that the resulting EEM charges are close to quantum chemistry atomic charges (e.g. NPA,
CHELPG, Mulliken) as much as possible. Many papers presented EEM parameters fitted to
various kinds of atomic charges calculated at different levels. In Multiwfn, below EEM parameters
can be directly chosen:
Parameters fitted to Mulliken charges at HF/STO-3G, see Int. J. Mol. Sci., 8, 572-582 (2007).
Available for H, C, N, O, S
Parameters fitted to CHELPG charges at B3LYP/6-31G* and at HF/6-31G*, see J. Comput.
Chem., 30, 1174 (2009). Available for H, C, N, O, F, S, Cl, Br, Zn
Parameters fitted to NPA charges at B3LYP/6-311G*, they were extracted from SI of J.
Cheminform., 8, 57 (2016). Available for H, C, N, O, F, P, S, Cl, Br
Note that for some elements, their A and B parameters also depend on multiplicity, namely
the maximal formal bond order between this atom and its neighboring atoms, so that influence of
chemical environment can be taken into account.
With above mentioned parameters, EEM charges have good reproducibility of target atomic
charges for typical organic systems, but do not expect EEM method can work well for systems
with complicated electronic structure, since common training set of EEM parameters only include
organic systems with typical bonding.
Usage
Since formal bond order is involved in the EEM calculation, you must use MDL molfile
(.mol) as input file, because in all file types that supported by Multiwfn, only this file contains
connectivity information between atoms. The .mol file can be outputted by many programs, such
as GaussView and OpenBabel. OpenBabel is recommended to use, since the format of .mol file
outputted by OpenBabel is very standard. Do not use GaussView to generate .mol file if dashed

3 Functions
68
bond is presented (e.g. for benzene, each C-C bond is described by default as a single bond with a
dashed bond, the .mol file is unable to record such non-Lewis representation of bonding).
After you load a .mol file and then enter present function, you can directly choose option 0 to
calculate EEM charges, the molecular electronegativity will also be outputted together. The default
EEM parameters are those fitted for reproducing B3LYP/6-31G* CHELPG charges.
Before calculation, you can choose option "1 Choose EEM parameters", present EEM
parameters will be shown on screen, and then you can select a built-in parameter set that you want
to use. Alternatively, you can load parameters from external file using suboption 0, the format of
parameter file should mimic to this:
0.302000
H 1 2.38500 0.73700
C 1 2.48200 0.46400
C 2 2.46400 0.39200
N 1 2.59500 0.46800
N 2 2.55600 0.37700
O 1 2.82500 0.84400
O 2 2.78900 0.83400
The first line is
, after that, defining parameter for each element of each multiplicity. The second,
third and fourth columns are multiplicity, A and B, respectively. Free format is used. Using
corresponding option, the present parameters can also be exported to EEMparm.txt in current
folder.
If the system under study is an ionic system, do not forget to use option "2 Set net charge" to
set net charge to actual status before calculation!
An example of calculating EEM charges is given in Section 4.7.5.
Information needed: Basis functions (Mulliken, Löwdin, MMPA), GTFs (Hirshfeld,
Hirshfeld-I, VDD, Becke, ADCH, CHELPG, MK, AIM, CM5), atom coordinates (EEM)
3.10 Orbital composition analysis (8)
Notice that the word “orbital” here is not restricted to molecular orbital, for example, if the
input file carries natural bond orbitals (NBO), then what will be analyzed is NBOs. There is an
excellent paper compared various orbital composition analysis approaches, see Acta Chim. Sinica,
69, 2393 (in Chinese, http://sioc-journal.cn/Jwk_hxxb/CN/abstract/abstract340458.shtml).
3.10.1 Output basis function, shell and atom composition in a specific
orbital by Mulliken, Stout-Politzer and SCPA approaches (1, 2, 3)
Mulliken, SCPA and Stout-Politzer methods support decomposing orbital to basis function,
shell and atom compositions. Actually I have introduced the theories in Sections 3.9.5, 3.9.6 and
3.9.7, i,a*100% is just the composition of basis function a in orbital i, if we sum up all the
compositions of basis functions that within a shell we will get shell composition, and if we sum up
all the compositions of shells that attributed to the same atom we will get atom composition.
3 Functions
69
These approaches rely on basis expansion, in current Multiwfn version you must
use .fch, .molden and .gms as input file.
When you entered “Orbital composition analysis” submenu from main menu, select which
method you want to use for decomposition, and then input the index of orbital, the result will be
printed on screen immediately, you can also input -1 to print basic information of all orbitals to
find which one you are interested in. By default, only those terms with composition larger than
0.5% will be printed, this threshold can be adjusted by “compthres” in settings.ini.
If the basis functions stored in .fch/.molden file are spherical harmonic type, then the label of
basis functions printed will look like D+1, F-3 rather than XX, XYY. The labels of spherical
harmonic basis functions used in Multiwfn are completely identical to Gaussian program, the
conversion relationship is:
D 0=-0.5*XX-0.5*YY+ZZ
D+1=XZ
D-1=YZ
D+2=√3/2*(XX-YY)
D-2=XY
F 0=-3/2/√5*(XXZ+YYZ)+ZZZ
F+1=-√(3/8)*XXX-√(3/40)*XYY+√(6/5)*XZZ
F-1=-√(3/40)*XXY-√(3/8)*YYY+√(6/5)*YZZ
F+2=√3/2*(XXZ-YYZ)
F-2=XYZ
F+3=√(5/8)*XXX-3/√8*XYY
F-3=3/√8*XXY-√(5/8)*YYY
G 0=ZZZZ+3/8*(XXXX+YYYY)-3*√(3/35)*(XXZZ+YYZZ-1/4*XXYY)
G+1=2*√(5/14)*XZZZ-3/2*√(5/14)*XXXZ-3/2/√14*XYYZ
G-1=2*√(5/14)*YZZZ-3/2*√(5/14)*YYYZ-3/2/√14*XXYZ
G+2=3*√(3/28)*(XXZZ-YYZZ)-√5/4*(XXXX-YYYY)
G-2=3/√7*XYZZ-√(5/28)*(XXXY+XYYY)
G+3=√(5/8)*XXXZ-3/√8*XYYZ
G-3=-√(5/8)*YYYZ+3/√8*XXYZ
G+4=√35/8*(XXXX+YYYY)-3/4*√3*XXYY
G-4=√5/2*(XXXY-XYYY)
H 0=ZZZZZ-5/√21*(XXZZZ+YYZZZ)+5/8*(XXXXZ+YYYYZ)+√(15/7)/4*XXYYZ
H+1=√(5/3)*XZZZZ-3*√(5/28)*XXXZZ-3/√28*XYYZZ+√15/8*XXXXX+√(5/3)/8*XYYYY+√(5/7)/4*XXXYY
H-1=√(5/3)*YZZZZ-3*√(5/28)*YYYZZ-3/√28*XXYZZ+√15/8*YYYYY+√(5/3)/8*XXXXY+√(5/7)/4*XXYYY
H+2=√5/2*(XXZZZ-YYZZZ)-√(35/3)/4*(XXXXZ-YYYYZ)
H-2=√(5/3)*XYZZZ-√(5/12)*(XXXYZ+XYYYZ)
H+3=√(5/6)*XXXZZ-√(3/2)*XYYZZ-√(35/2)/8*(XXXXX-XYYYY)+√(5/6)/4*XXXYY
H-3=-√(5/6)*YYYZZ+√(3/2)*XXYZZ-√(35/2)/8*(XXXXY-YYYYY)-√(5/6)/4*XXYYY
H+4=√35/8*(XXXXZ+YYYYZ)-3/4*√3*XXYYZ
H-4=√5/2*(XXXYZ-XYYYZ)
3 Functions
70
H+5=3/8*√(7/2)*XXXXX+5/8*√(7/2)*XYYYY-5/4*√(3/2)*XXXYY
H-5=3/8*√(7/2)*YYYYY+5/8*√(7/2)*XXXXY-5/4*√(3/2)*XXYYY
An example is given in Section 4.8.1.
Information needed: Basis functions
3.10.2 Define fragment 1 and 2 (-1, -2)
Before doing composition analysis for fragments by Mulliken, Stout-Politzer and SCPA
approachs, you have to define fragment in advance. If what you are interested in is only
composition of one fragment rather than the composition between two fragments (cross term
composition), you only need to define fragment 1. The content of fragment can be chosen to basis
functions, shells, atoms or mixture of them, whatever you choose, only the indices of
corresponding basis functions are recorded eventually. Notice that the "fragment" I referred here
has no any relationship with the "fragment" involved in Section 3.1, the fragment defined here
does not disturb wavefunction at all.
All supported commands in the interface of defining fragment are self-explained, so I will not
reiterate them but only give an examples, that is define fragment as all P-shells of atom 3: First,
type command all, information of all basis functions are listed, find out the shells that attributed to
center 3 and contain X, Y and Z type of basis functions (viz. PX, PY and PZ). Assume that the
indices of such shells are 3, 6 and 7, then input s 3,6,7 to add them into fragment. If you want to
verify your operation, input all again and check if asterisks have appeared in the leftmost of
corresponding rows, the marked basis functions are those that have been included in the fragment.
Finally, input the letter q to save current fragment and return to last menu, the indices of basis
functions in the fragment will be printed at the same time.
By default, fragments do not have any content. Each time you enter the fragment definition
interface, the status of fragment is identical to that when you leave the interface last time. So, if
you have defined the fragment earlier and you want to completely redefine it, do not forget to use
“clean” command to empty the fragment first.
3.10.3 Output composition of fragment 1 and inter-fragment
composition by Mulliken, Stout-Politzer and SCPA approaches (4, 5, 6)
After you defined fragment 1, the fragment composition analysis based on Mulliken, Stout-
Politzer and SCPA approaches is available. The fragment composition is the sum of all basis
function compositions within the fragment, in this function the fragment compositions of all
orbitals are printed on screen at the same time. If the analysis method you chose is Mulliken
(subfunction 4) or Stout-Politzer (subfunction 5), below component terms are outputted together
with total composition:
c^2 term: The sum of square of coefficients of basis functions within fragment 1, namely
%100*
1
2,
fraga ia
C.
3 Functions
71
Int.cross: The sum of internal cross terms in fragment 1,
namely %100*
11 ,,,
fraga fragb baibia SCC .
Ext.cross: Fragment 1 part of the total cross term between fragment 1 and all other atoms,
namely
11 ,,,, %100*2
fraga fragb baibiaba SCCw .
It is clear that total composition of fragment 1 equals to c^2 term + Int.cross + Ext.cross.
If the fragment 2 is also defined (you must have already defined fragment 1), in subfunction 5
(Mulliken) or subfunction 5 (Stout-Politzer) the cross term between fragment 1 and fragment 2 in
each orbital, namely %100*2
12 ,,,
fraga fragb baibia SCC will be outputted too. “Frag1 part” and
“Frag2 part” correspond to the components of cross term attributed to fragment 1 and fragment 2
respectively, for Mulliken analysis the two terms are of course exactly equal due to the “equal
partition”.
3.10.4 Orbital composition analysis by natural atomic orbital
approach (7)
Theory
The first step of the famous natural bond orbital (NBO) analysis is converting original basis
functions to natural atomic orbitals (NAOs) by use of density matrix. Resulting NAOs can be
classified into three categories: (1) Core-type NAOs, describing inner core densities, their
occupation numbers are almost equal to integer (2) Valence-type NAOs, describing valence
densities, generally they have high occupation numbers (3) Rydberg-type NAOs, mainly
displaying characteristics of polarization and delocalization of electrons, the occupation numbers
of them are very low. Core and valence NAOs are collectively named as minimal-set, they have
strong physical meaning and have one-to-one relationship with "actual" atomic orbitals, so they
are what we should be most concerned. Occupied MOs are almost exclusively contributed by
minimal-set NAOs. Rydberg NAOs do not have clear physical interpretations, their contribution
can be ignored in occupied MOs, however they often have great contribution to virtual orbitals.
Since NAOs is an orthonormal set, if we have MO coefficient matrix in NAO basis, we can
get contribution from a NAO to specific MO by simply squaring corresponding expansion
coefficient and then multipy it by 100%. Composition of an atom can be calculated by summing
up composition of minimal-set NAOs in this center.
This NAO approach has great basis-set stability as Hirshfeld approach, especially suitable for
analyzing composition of occupied orbitals. However for virtual orbitals, contribution from
Rydberg NAOs is often large, the NAO approach is no longer works well.
Input file
The MO coefficient matrix in NAO basis cannot be generated by Multiwfn itself, you need to
provide a output file of NBO program containing this matrix as Multiwfn input file. By default
NBO program does not output this matrix, you need to manually add NAOMO keyword between
3 Functions
72
$NBO ... $END field in NBO input file. The NBO program we referred here may be stand-alone
NBO program (also known as GENNBO), or NBO module embedded in quantum chemistry
software such as L607 in Gaussian. The output from NBO3.1 and NBO5.0 are formally supported,
I estimate that no problem for other NBO versions.
Options
You will find following options in the interface:
-1 Define fragment: This option is used to define fragment, which is needed by fragment
contribution analysis (option 1). All commands are self-explained. You can also refer to Section
3.10.2, the difference is that shell information cannot be utilized here.
0 Show composition of an orbital: Print contribution from some or all NAOs to specific
MO. Since the numerical precision of expansion coefficients recorded in NBO output is not high,
if you choose to output all NAOs, the sum may be slightly deviate from 100%, it is unnecessary to
take care of this problem. If you choose to output core and valence NAOs only, the larger
deviation of the sum from 100% denotes the larger Rydberg composition is. The printed NAO
contributions are also summed up according to the atom center they attributed to, and then be
outputted as "Condensed above result to atoms".
1 Show fragment contribution in a range of orbitals: Contribution from the fragment you
defined to specified range of orbitals will be printed. The total contribution consists of
contribution from core, valence, Rydberg NAOs in the fragment.
2 Select output mode: This option controls which set of NAOs will be outputted by option 0,
there are three modes:
(1) Show all NAOs
(2) Only show core and valence NAOs: This is default mode, Rydberg NAOs will be
ignored.
(3) Show NAOs whose contribution is larger than specified criteria: Only the NAO (any
type) whose contribution to specific MO is larger than you specified criteria will be outputted.
3 Switch spin type: One can find this option only if the NBO output file is for open-shell
system. One can select which spin type of MOs to be analyzed.
An example is given in Section 4.8.2.
Information needed: MO coefficients in NAO basis
3.10.5 Calculate atom and fragment contributions by Hirshfeld or
Hirshfeld-I method (8,10)
Hirshfeld and Hirshfeld-I weighting function (see Sections 3.9.1 and 3.9.13, respectively) can
also be used for decomposing orbital to atom and fragment compositions, the composition of atom
A in orbital i is %100d)()(
2
rrr Ai w
. The composition of a fragment is simply the sum of
the compositions of the atoms that belongs to the fragment. These methods have great basis-set
stability and are always more reliable and reasonable than Mulliken and MMPA. In fact the
3 Functions
73
Hirshfeld partition is already good enough, the more sophisticated and computationally
demanding Hirshfeld-I partition is not necessary.
If you choose to use Hirshfeld partition, you will be prompted to select the way to generate
atomic densities for constructing Hirshfeld weighting function, I strongly suggest using the built-
in atomic densities rather than using atomic .wfn files, since the former is much more convenient.
If you choose to use Hirshfeld-I partition, regular HI iterations will be performed first to yield
converged atomic weighting functions (if you are confused by the operations, please consult the
example of computing HI charges in Section 4.7.4 and the implementation details of Hirshfeld-I
introduced in Section 3.9.13).
Before calculating orbital composition, data initialization is automatically carried out. Once it
is finished, you can input the orbital index that you are interested in. Because numerical
quadrature always introduces some errors, so the sum of all atom compositions is not exactly
equals to 100%, the deviation might be relatively significant in rare cases, so Multiwfn normalizes
results automatically and prints them under the title “After normalization”.
If you want to view composition of an atom in specific range of orbitals at the same time,
choose option -2, then input the atom index and the index range of orbitals.
If you wish to study contribution of a fragment to orbitals, use -9 to define a fragment first,
then when you input an orbital index, the contribution of the fragment will be outputted along with
the contributions of all atoms. Also, you can choose -3 to calculate the contribution from the
fragment you defined to a range of orbitals.
If selecting option -4, program will calculate composition of every atom in every orbitals and
then export all of them to orbcomp.txt in current folder.
An example is given in Section 4.8.3.
Information needed: Atom coordinates and GTFs
3.10.6 Calculate atom and fragment contributions by Becke method (9)
This function is very similar to the function introduced in Section 3.10.5, the only difference
is that Becke partition is used instead of Hirshfeld partition. For most cases, their results are in
qualitative agreement with each other. Using Becke partition instead of Hirshfeld partition has a
prominent advantage, namely the atomic wavefunction files are not needed, since the Becke
atomic space can be simply constructed based on atomic radius. For more detail about Becke
partition, see Section 3.18.0. An example is given in Section 4.8.3.
Information needed: Atom coordinates and GTFs
3.10.7 Evaluate oxidation state by LOBA method
This function is an implementation the LOBA method proposed in Phys. Chem. Chem. Phys.,
11, 11297-11304 (2009). LOBA (localized orbital bonding analysis) is a method used to evaluate
atomic oxidation state based on orbital composition of localized MOs (LMOs). The idea is very
simple: if an atom has N nuclear charges, and its composition in M occupied LMOs are larger than
3 Functions
74
a threshold (e.g. 50%. In this case the electrons in these LMOs can be approximately viewed as
completely attributed to the atom. If a LMO is doubly occupied, it should be counted twice), then
the oxidation state of the atom is N-M.
In my opinion, this idea can also be extended to define fragmental oxidation state, namely if
the sum of nuclear charge in a fragment is N, and the fragment contribution to M LMOs are larger
than a certain threshold, then the fragment oxidation state will be N-M.
To use this function, you should provide .fch or .molden file containing LMOs (or NBOs).
For example, if you are a Gaussian user, you can use the .fch file resulting from pop=saveNBO or
pop=saveNLMO task as input. Alternatively, you can directly use Multiwfn to carry out orbital
localization to generate .fch containing localized orbitals. An example is given in Section 4.8.4.
The result of LOBA method somewhat depends on the choice of orbital composition analysis
method. For simplicity in Multiwfn the SCPA method is used for LOBA analysis, therefore diffuse
function should not be used!
Information needed: Basis functions
3.11 Bond order analysis (9)
In bond order analysis module, you can directly select corresponding option to calculate bond
order by corresponding method. If you want to obtain total bond order between atoms in two
molecular fragments, you can manually sum up corresponding terms, however this work is tedious,
the better way is using option -1 to define fragment 1 and 2 first before bond order analysis, after
that the inter-fragment bond order will be outputted alongside two-center bond orders. This feature
is not available for multi-center bond order analysis and orbital occupancy-perturbed Mayer bond
order.
3.11.1 Mayer bond order analysis (1)
The Mayer bond order between atom A and B is defined as (Chem. Phys. Lett, 97, 270)
AaBbabbaabbaABABAB SPSPSPSPIII ])()()()[(2
where P
and P
are alpha and beta density matrix respectively, S is overlap matrix. Above
formula can be equivalently rewritten using total density matrix
P
P
P
and spin density
matrix
P
P
P
S
AaBbab
S
ba
S
abbaAB SPSPPSPSI ])()()()[(
For restricted close-shell circumstance, since spin density matrix is zero, the formula can be
simplified to
AaBbbaabAB PSPSI )()(
Generally, the value of Mayer bond order is in agreement with empirical bond order, for single,
double and triple bond the value is close to 1.0, 2.0 and 3.0 respectively. For unrestricted or
restricted open-shell wavefunction, alpha, beta and total Mayer bond orders will be outputted
3 Functions
75
separately. By default, only the bonds whose bond order exceed 0.05 will be printed on screen, the
threshold can be adjusted by “bndordthres” parameter in settings.ini, you can also select to export
full bond order matrix.
Moreover, Multiwfn outputs total and free valences, the former is defined as
AaAbbaab
Aa aa
APSPSPSV 2
The latter is defined as
ba
s
AaAbab
s
AB ABAA SPSPIVF )()(
where Ps is spin density matrix, namely P
minusing P
.
For restricted close-shell wavefunctions free valences are zero since Ps=0, thus total valence
of an atom is simply the sum of the related bond orders
AB ABA IV
Total valence (also known as atomic valence) measures atomic bonding capacity, while free
valence characterizes the remaining ability of forming new bonds by sharing electron pairs.
For unrestricted or restricted open-shell system, there is another way to calculate total bond
order rather than summing up alpha and beta bond orders, that is summing up alpha and beta
density matrices to form total density matrix first and then calculate Mayer bond order by using
restricted close-shell formula, this treatment is sometimes called “generalized Wiberg bond order“,
these total bond orders are printed following the title “Mayer bond order from mixed alpha&beta
density matrix”.
Similar to Mulliken population, Mayer bond order and the multi-center bond order described
below are sensitive to basis-set, so do not use the basis-sets having diffuse functions, otherwise the
bond order result will be unreliable.
Although Mayer bond order was originally defined for single-determinant wavefunctions, for
post-HF wavefunctions, Multiwfn calculates Mayer bond orders via exactly the same formulae as
shown above based on corresponding post-HF density matrix. The reasonableness of this
treatment has been validated in Chem. Phys. Lett., 544, 83 (2012).
Some applications of Mayer bond order can be seen in J. Chem. Soc., Dalton Trans., 2001,
2095.
Information needed: Basis functions
3.11.2 Multi-center bond order analysis (2, -2, -3)
In main function 9 there are three options (2, -2, -3) used to calculate multi-center bond order,
they are very similar. I first carefully introduce option 2, then discuss the difference between
options -2 and 2. Finally, -3 is briefly mentioned.
Option 2
The multi-center bond order, which is also known as multi-center index, was originally
proposed in Struct. Chem., 1, 423 (1990), in some sense it may be viewed as an extension of
Mayer bond order to multi-center cases. Multiwfn supports it up to 12 centers. Three/four/five/six-
3 Functions
76
center bond orders are defined respectively as
AaBbCccabcabABC PSPSPSI )()()(
AaBbCcDddacdbcabABCD PSPSPSPSI )()()()(
AaBbCcDdEeeadecdbcabABCDE PSPSPSPSPSI )()()()()(
AaBbCcDdEeFffaefdecdbcabABCDEF PSPSPSPSPSPSI )()()()()()(
Similarly, infinite-center bond order can be written as
AaBbKkkacdbcab
Cc
KABCDEF PSPSPSPSI )()()()(
For open-shell cases, there are two definitions of the multi-center bond order, the first one is
the sum of alpha part and beta parts:
AaBbKkkacdbcab
Cc
n
AaBbKkkacdbcab
Cc
n
KABCDEFKABCDEFKABCDEF
SPSPSPSP
SPSPSPSP
III
)()()()(2
)()()()(2
1
1
Another definition is using the mixed density matrix, this is not rigorous as above:
P
P
P
SPSPSPSPI
AaBbKkkacdbcab
Cc
KABCDEF
mixed
mixedmixedmixedmixed )()()()(
For unrestricted or restricted open-shell wavefunction, the output of multi-center bond order
analysis consists of four terms, which have been explained above: (1) The result from alpha
density matrix (2) The result from beta density matrix (3) The sum of the result of alpha and beta
parts (4) The result from mixed alpha&beta density matrix.
Notice that the multi-center bond orders for different number of centers are not directly
comparable, since the result is not in the same magnitude. However, in Phys. Chem. Chem. Phys.,
118, 11839 (2016), it was shown that the normalized multi-center bond order is comparable for
different ring size and can be simply calculated as MCI1/n, where n is the number of centers and
MCI it the multi-center bond order defined above. For example, at B3LYP/6-31G* level, the MCI
for H3+, benzene (6 centers) and naphthalene (12 centers) are 0.2963, 0.0863 and 0.0080,
respectively, while the normalized result are 0.667, 0.665 and 0.617, respectively. When MCI is
negative, the normalized value should be calculated as -|MCI|1/n.
Due to the ambiguity of definition and the use of non-orthogonal basis functions, the value of
multi-center bond order may relies on input direction if the atoms lack of symmetry. For example,
the result of ABCD can be different from DCBA (the opposite input direction of ABCD). The
reason is clear: The term in the summation in the case of ABCD is dacdbcab PSPSPSPS )()()()( ,
while if we invert the input direction, the term will become adbacbdc PSPSPSPS )()()()( .
Although both P and S are symmetry matrices, their product PS is not necessarily symmetry, so
3 Functions
77
the two terms are not equivalent. In my own viewpoint, in order to obtain reasonable result, for
example A-B-C-D-E-F, one should calculate ABCDEF and FEDCBA respectively and take their
average. While some people advocated that it is needed to take all possible permutations into
account to get a definitive result, see J. Phys. Org. Chem., 18, 706, that means the bond order of
BCADEF, CABDEF, DBCAFE and so on (6!=720 in total) are all required to be calculated and
then summed up. This treatment does not have clear physical meaning and is absolutely
unnecessary, it also elevates the computational cost significantly.
The computational cost for multi-center bond order increases exponentially with the number
of centers; for ring size larger than 12 centers the cost will be prohibitively high, so Multiwfn
doesn't support higher number of centers.
Automatical search of multi-center bonds: If you input -3 when Multiwfn asks you to input
atom combination, all three-center bond order will be calculated, only those larger than the
threshold you inputted will be printed. Similarly, four-, five- and six-center bonds can be searched
by inputting -4, -5 and -6 respectively. Due to efficiency consideration, the search may be not
exhaustive. Also note that the search is based on mixed alpha&beta density matrix for open-shell
cases.
Option -2
The most severe drawback of multi-center bond order is its high basis-set dependency. In
particular, if diffuse functions are involved, then multi-center bond order may be completely
wrong. In order to tackle this problem, I proposed an alternative way (to be published) to calculate
the multi-center bond order, and the idea is implemented as option -2.
Option -2 is very similar to option 2 (as introduced above), the only difference is that the
multi-center bond order is calculated based on natural atomic orbital (NAO) basis rather than
based on the basis functions originally defined by the basis-set. Since NAO is an orthonormal set
and thus overlap matrix S is an identity matrix, the formula can be simplified as (using closed-
shell form for example)
AaBbKkkacdbcab
Cc
KABCDEF PPPPI
The multi-center bond order calculated in this manner has very good stability with respect to
change of basis-set. Even when diffuse functions are presented the result is still highly reliable.
According to my experience, if no basis functions show diffuse character, the results given by
option 2 and -2 will be very similar, though not exactly identical.
Another advantage of employing NAO basis is that the ambiguity of multi-center bond order
due to the input direction of atom indices is completely eliminated, that means the result of ABCD
must be identical to DCBA. This is because the matrix involved in the summation (P) is symmetry.
In order to use option -2, the output file of NBO module embedded in Gaussian or standalone
NBO program should be used as input file, and DMNAO keyword must be used to make NBO
print density matrix in NAO basis. If you are a Gaussian user, for example, you can use the output
file of below instance as input file of Multiwfn.
#p PBE1PBE/6-311G** pop=nboread
opted
3 Functions
78
0 1
C 0.00000000 1.38886900 0.00000000
... [ignored]
H -2.14060700 1.23588000 0.00000000
$NBO DMNAO $END
In this function, if you only input indices of two atoms, then the result is just Wiberg bond
order under NAO basis, which is completely identical to that printed by bndidx keyword of NBO
program.
Option -3
There is a hidden option -3 in main function 9, it is used to calculate multi-center bond order
under Löwdin orthogonalized basis (see next section for more information). Since this method
should not have evident advantages over original mult-center bond order definition, this option is
invisible in the interface. However, if you have interesting, you can have a try.
Information needed: Basis functions (options 2, -3), NBO output file with DMNAO keyword
(option -2)
3.11.3 Wiberg bond order analysis in Löwdin orthogonalized basis (3)
Wiberg bond order is defined as follows, see footnote in Tetrahedron, 24, 1083 (1968)
AaBbabAB PI 2
The original definition of Wiberg bond order is only suitable for the wavefunction
represented by orthogonal basis functions such as most of semiempirical wavefunctions, and only
defined for restricted close-shell system. Actually, Mayer bond order can be seen as a
generalization of Wiberg bond order, for restricted close-shell system and orthonormal basis
functions (namely S matrix is identity matrix) cases their results are completely identical.
In this function, Multiwfn first orthogonalizes basis functions by Löwdin method and then
performs usual Mayer bond order analysis. The threshold for printing is controlled by
“bndordthres” in settings.ini too.
As shown in J. Mol. Struct. (THEOCHEM), 870, 1 (2008), the Wiberg bond order calculated
in this manner, say WL, has much less sensitivity to basis set than Mayer bond order (whereas for
small basis-sets, their results are closed to each other). One should be aware that WL tends to
overestimates bond order for polar bonds in comparison with Mayer bond order.
Commonly, if there is not special reason, using Mayer bond order is more preferred.
Notice that numerous literatures used NBO program to calculate Wiberg bond order, the
result must be somewhat different to that produced by present function, because in NBO program
the Wiberg bond orders are calculated in the basis of natural atomic orbitals (NAO), which are
generated by OWSO orthogonalization method. Multiwfn is also possible to calculate Wiberg
bond order under NAO basis, and furthermore, the result can be decomposed as atomic orbital pair
contributions, see Section 3.11.8 for details.
3 Functions
79
Information needed: Basis functions
3.11.4 Mulliken bond order analysis (4) and decomposition (5)
Mulliken bond order is the oldest bond order definition, it is defined as
AaBbbaba
iAaBbbaibiaiAB SPSCCI ,,,,, 22
Mulliken bond order has low agreement with empirical bond order, it is deprecated for
quantifying bonding strength, for which Mayer bond order always performs better. However,
Mulliken bond order is a good qualitative indicator for bonding (positive value) and antibonding
(negative value). The threshold for printing results is controlled by “bndordthres” parameter in
settings.ini.
Mulliken bond order is easy to be decomposed to orbital contributions, the contribution from
orbital i to bond order AB is
AaBbbaibiai
i
AB SCCI ,,,
2
From the decomposition, we can know which orbitals are favourite and unfavourite for
specific bonding.
Information needed: Basis functions
3.11.5 Orbital occupancy-perturbed Mayer bond order (6)
Orbital occupancy-perturbed Mayer bond order was firstly proposed in J. Chem. Theory
Comput., 8, 908. Put simply, by using this method one can obtain how large is the contribution
from specific orbital to Mayer bond order.
Orbital occupancy-perturbed Mayer bond order can be written as
AaBbabXbaXabXbaXABABBA SPSPSPSPIII ])()()()[(2
,,
,
The only difference between this definition and Mayer bond order shown in Section 3.11.1 is that
P
and
P
have been replaced by
X
P and
X
P respectively. X
P stands for the density
matrix generated when occupation number of a specific orbital is set to zero. The difference
between BA
I, and Mayer bond order can be regarded as a measure of contribution from the
orbital to Mayer bond order. Bear in mind, because Mayer bond order is not a linear function of
density matrix, the sum of BA
I, for all orbitals is not equal to Mayer bond order generally.
In Multiwfn, you only need to input indices of two atoms, then BA
I, for all occupied
orbitals and the difference between BA
I, and Mayer bond order will be outputted. The more
negative (positive) the difference, the more beneficial (harmful) to the bonding due to the

3 Functions
80
existence of the orbital.
You can also use another way to calculate BA
I,, that is using wavefunction modification
module (main function 6) to manually set occupation number of a specific orbital to zero, and then
calculate Mayer bond order as usual, but this manner may be tedious if you want to calculate
BA
I, for many orbitals.
Information needed: Basis functions
3.11.6 Fuzzy bond order (7)
Fuzzy bond order (FBO) was first proposed by Mayer in Chem. Phys. Lett., 383, 368
ij ji
B
ij
A
ji
B
ij
A
ABABAB SPSPSPSPBBB ])()()()[(2
where S is overlap matrix of basis functions in fuzzy atomic spaces. In Multiwfn, Becke's fuzzy
atomic space with sharpness parameter k=3 in conjunction with modified CSD radii is used for
calculating FBO. (See Section 3.18.0 for introduction of fuzzy atomic space)
rrrr dwS nmA
A
mn )()()(
Commonly the magnitude of FBO is close to Mayer bond order, especially for low-polar
bonds, but much more stable with respect to the change in basis-set. According to the comparison
between FBO and delocalization index (DI) given in J. Phys. Chem. A, 109, 9904, FBO is
essentially the DI calculated in fuzzy atomic space. See Section 3.18.5 for detail about DI.
Calculation of FBO requires performing Becke's DFT numerical integration, due to which the
computational cost is larger than evaluation of Mayer bond order. By default, 40 radial points and
230 angular points are used for numerical integration. This setting is able to yield accurate enough
results in general. If you want to further refine the result, you can set the number of radial and
angular points by "radpot" and "sphpot" in settings.ini manually, and ensure that "iautointgrid" has
been set to 0.
The threshold for printing results is controlled by “bndordthres” parameter in settings.ini.
Information needed: GTFs, atom coordinates
3.11.7 Laplacian bond order (8)
In J. Phys. Chem. A, 117, 3100 (2013) (http://pubs.acs.org/doi/abs/10.1021/jp4010345), I
proposed a novel definition of covalent bond order based on the Laplacian of electron density
2
in fuzzy overlap space, called Laplacian bond order (LBO). The LBO between atom A and
B can be simply written as
3 Functions
81
0
2
,
2
d)()()(10
rrrr BABA wwL
where w is a smoothly varying weighting function proposed by Becke and represents fuzzy atomic
space, hence wAwB corresponds to fuzzy overlap space between A and B. Note that the integration
is only restricted to negative part of
2
. The physical basis of LBO is that the larger magnitude
the integral of negative
2
in the fuzzy overlap space, the more intensive the electron density
is concentrated in the bonding region, and therefore, the stronger the covalent bonding.
The reasonableness and usefulness of LBO were demonstrated by applying it to a wide
variety of molecules and by comparing it with many existing bond order definitions. It is shown
that LBO has a direct correlation with the bond polarity, the bond dissociation energy and the bond
vibrational frequency. The computational cost of LBO is low, also LBO is insensitive to the
computational level used to generate electron density. In addition, since LBO is inherently
independent of wavefunction, one can in principle obtain LBO by making use of accurate electron
densities derived from X-ray diffraction data.
In Multiwfn, Becke's fuzzy atomic space with sharpness parameter k=3 in conjunction with
modified CSD radii is used for calculating LBO. (See Section 3.18.0 for detail about fuzzy atomic
space). The threshold for printing results is controlled by “bndordthres” parameter in settings.ini.
Note that in current implemention, LBO is particularly suitable for organic system, but not
for ionic bonds since in these cases a better definition of atomic space should be used to faithfully
exhibit actual atomic space. LBO is also not very appropriate for studying the bond between two
very heavy atoms (heavier than Ar), because these bonds are often accompanied by insignificant
charge concentration in the fuzzy overlap space, even though the bonding is doubtless covalent.
Information needed: GTFs, atom coordinates
3.11.8 Decompose Wiberg bond order in NAO basis as atomic orbital
pair contributions (9)
As mentioned in Section 3.11.3, Wiberg bond order is expressed as
AaBbabAB PI 2
The data is calculated for atom pair. Since the expression is simply a linear summation of square
of density matrix element, it is straightfoward to decompose Wiberg bond order as basis function
pair contribution (this idea is to be published). For example, Pab2 is simply the contribution from
interaction between basis functions a and b. Since one-to-one correspondence between basis
function and atomic orbital is lacking when extended basis set is used, in order to make the
decomposition method full of physical meaning, the decomposition is best to be carried out under
natural atomic orbitals (NAOs). Each non-Rydberg type of NAO uniquely corresponds to an
atomic orbital, thus, by above decomposition method, Wiberg bond order at the atomic orbital
scale can be obtained.

3 Functions
82
In addition, contribution from interaction between atomic orbital shells i and j can be
obtained as
iajbab
P
shell shell
2.
After you enter this function, simply input indices of two atoms, the non-neglectable
contribution from NAO pairs and NAO shell pairs together with total Wiberg bond will be printed.
This function currently is limited for closed-shell systems.
The input file of this function is completely identical to the option -2 described in Section
3.11.2, namely the output file of NBO program containing density matrix information (i.e.
DMNAO keyword is required).
By the way, it is also possible to decompose multi-center bond order as atomic orbital
contribution. For example, three-center bond order is expressed as
AaBbCccabcabABC PPPI
Clearly, cabcab PPP can be regarded as contribution from interacting between NAOs a, b and c.
However, decomposition of multi-center bond order under NAO basis has not been implemented.
An illustrative example of this decomposition analysis is given in Section 4.9.4.
3.12 Plotting total, partial, and overlap population
density-of-states (10)
3.12.1 Theory
Density-of-states (DOS) is an important concept of solid physics, which represents the
number of states in unit energy interval, since energy levels are contiguous, so DOS can be plotted
as curve map. In isolated system (such as molecule), the energy levels are discrete, the concept of
DOS is questionable and some people argued that DOS is completely valueless in this situation.
However, if the discrete energy levels are broadened to curve artifically, DOS graph can be used
as a valuable tool for analyzing the nature of electron structure.
The original total DOS (TDOS) of isolated system can be written as
ii
EE )()TDOS(
where {} is eigenvalue set of single-particle Hamilton, is Dirac delta function. If is replaced
by broadening function F(x), such as Gaussian, Lorentzian and pseudo-Voigt function, we get
broadened TDOS.
The normalized Gaussian function is defined as
2
2
2
2
1
)( c
x
e
c
xG
where 2ln22
FWHM
c
FWHM is acronym of “full width at half maximum”, it is an adjustable parameter in
Multiwfn, the larger FWHM the TDOS graph looks more smooth and analysis is easier to perform,

3 Functions
83
but more fine-structure is masked.
The normalized Lorentzian function is defined as
22 FWHM25.0
1
2
FWHM
)(
x
xL
Pseudo-Voigt function is weighted linear combination of Gaussian function and Lorentzian
function:
)()1()()( xLwxGwxP gaussgauss
Obviously, if G(x) and L(x) are normalized, normalization condition for P(x) always holds
regardless of the select of wgauss.
The curve map of broadened partial DOS (PDOS) and overlap DOS (OPDOS) are valuable
for visualizing orbital composition analysis, PDOS function of fragment A is defined as
iiAiA EFE )()(PDOS ,
where i,A is the composition of fragment A in orbital i. The OPDOS between fragment A and B is
defined as
ii
iBABA EFE )()(OPDOS ,,
where iBA,
is the composition of total cross term between fragment A and B in orbital i. I have
discussed how to calculate and in Section 3.10.3.
Let us see an example, from which we can know what new information can be revealed by
DOS map. This is a water molecule under HF/6-31G* wavefunction in ground state, the orbitals
are canonical MOs; fragment 1 is defined as P-shells of oxygen (correspond to 2p atomic orbitals),
fragment 2 is defined as two hydrogens, both original and broadened TDOS/PDOS/OPDOS are
shown in the graph below. Notice that the height is only meaningful for lines (original data) but
not for curves, left-axis and right-axis correspond to TDOS/PDOS and OPDOS respectively. The
vertical dashed line indicates the position of HOMO level. The original DOS graph is discrete
comb-like lines, from which we cannot obtain any additional information other than energy level
distribution, it is impossible to distinguish different type of lines and degenerate energy levels
owing to the overlapping. However if the discrete lines are broadened, from the height of black
curve (TDOS) we can clearly know how dense the energy levels are distributed everywhere.
Besides, the curves corresponding to TDOS, PDOS (red line for fragment 1, blue line for fragment
2) and OPDOS (green line) no longer overlap, we can clearly identify characters of each orbital by
observing these curves. For example, the red curve is high and nearly approachs black line in the
region of -0.9 a.u. to -0.3 a.u., so we can be concluded that 2p atomic orbitals of oxygen have
significant contribution to corresponding MOs. Since the green curve is greater than or less than
zero respectively denote corresponding MOs are favorable or unfavorable for forming chemical
bond between oxygen 2p orbitals and hydrogens, it is shown that the orbital pointed by the
leftmost arrow is very helpful for bonding, while the high-energy state orbitals (> 0.1 a.u.) are not
conducive for bonding (namely antibonding character), fortunately they haven’t been occupied,
otherwise the molecule must be broken. These conclusions can be confirmed further by observing
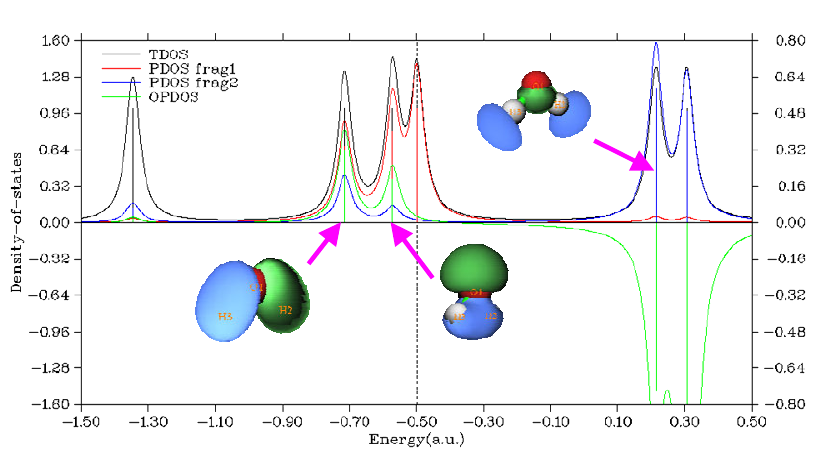
3 Functions
84
isosurfaces of corresponding MOs.
3.12.2 Input file
.fch/.molden/.gms files can be used as input. You can also use output file of single point task
of Gaussian program as input (“pop=full” keyword must be specified). For generality, Multiwfn
supports plain text file as input too, the format is
nmo inp
energy occ [strength] [FWHM] For orbital 1
energy occ [strength] [FWHM] For orbital 2
energy occ [strength] [FWHM] For orbital 3
...
energy occ [strength] [FWHM] For orbital nmo
where energy and occ denote orbital energy and occupation number. nmo is the number of orbitals
recorded in this file. inp is input type, if it is set to 1, only energies (in a.u.) and occupation
numbers will be loaded, strengths and FWHMs of all orbitals will be set to 1.0 and 0.25
respectively and automatically; if it is set to 2, you have to specify strength and FWHM for each
orbital. If the strength of an orbital is set to k, then the broadened curve from this orbital will be
normalized to k rather than 1 (default value). The format of this file is free, there is no upper limit
of the number of orbitals.
3.12.3 Options for plotting DOS
When you entered the interface of plotting DOS, you will see below options. The most
important ones among them may be option 0 and option -1.
-5 Customize energy levels, occupations, strengths and FWHMs for specific MOs: By
this option, you can manually set energies, occupations, strengths and FWHMs for specific
orbitals. For example, if you would like only to plot DOS for a few MOs, you can set strengths of
the other MOs to zero (by default, strengths for all MOs are 1.0).
3 Functions
85
-4 Show all orbital information: Print information of all orbitals on screen, also point out
Fermi energy (when occupation number informaiton is available).
-3 Export energy levels, strengths, FWHMs to plain text file: Export energy, strength and
FWHM of each orbital to “orginfo.txt” in current directory, this file complies the format
introduced in last section, so can be directly used as input file.
-1 Define fragments: You can define up to 10 fragments in this option. After you entered this
option, the information of present fragments are shown on screen. You can input x to define
fragment x, and input -x to unset fragment x, or input i,j to exchange the definition of fragment i
and j. To leave this interface, input 0. The PDOS will be plotted for all of the fragments defined in
this option. OPDOS will be drawn only when both fragments 1 and 2 have been defined.
DOS graph wll contain the line and curve of “PDOS frag 1” only when fragment 1 is defined.
0 Draw TDOS graph!: Draw DOS graph right now! If any fragment has been defined, the
texts in this option will become “TDOS+PDOS”; if both fragments 1 and 2 have been defined, the
texts will become “TDOS+PDOS+OPDOS”.
1 Select broadening function: Select which broadening function will be used, you can select
Lorentzian, Gaussian or Pseudo-Voigt function. Default is Gaussian.
2 Set energy range: This option is used to set the lower limit, upper limit and step between
labels of X-axis.
3 Set full width at half maximum (FWHM): As the title says.
4 Set scale ratio for DOS curve: If this option is set to k, then height of all curves will
multiply k (in full energy range).
5 Set Gaussian-weighting coefficient: This option sets wgauss, which is mentioned in last
section. This option only appears when Pseudo-Voigt function is chosen.
6 Switch spin: Appears only when the loaded wavefunction is unrestricted .fch/.molden/.gms
file. This option determines which set of energy levels (alpha or beta) will be used for analysis.
7 Switch method for calculating PDOS: Switch method of composition analysis between
SCPA and Mulliken.
8 Switch unit between a.u. and eV
Notice that option -1 and 7 only appear when the input file contains basis function
information, that is if you want to draw PDOS and OPDOS graph, you have to
use .fch/.molden/.gms file as input.
Once you choose option 0, Multiwfn starts to calculate data set and then DOS graph pops up,
after clicking right mouse button on the graph to close it, post-process menu will appear on the
screen, which has many options. They control the range and stepsize of Y-axis, if the lines or
curves corresponding to TDOS, PDOS and OPDOS will be shown on DOS graph, if a vertical
dashed line will be drawn to highlight HOMO level, the texts in the legends, etc. Worthnotingly,
there is an option named “Set scale factor of Y-axis for OPDOS”, if the value is set to k and the
range of left-axis (for TDOS/PDOS) is set to e.g. [-3.5, 2.0], then the range of right-axis (for
OPDOS) will become [-3.5*k, 2.0*k]. The reason why Multiwfn uses double axis is because the
magnitude of OPDOS is generally much smaller than TDOS and PDOS.
You can also choose to export the DOS map you have seen as graphical file in current folder,
or export X-Y data set of DOS to plain text files for replotting the graph by external softwares,
such as Origin. By choosing option 0 you can return to initial interface, the quality of DOS graph
3 Functions
86
can be gradually improved by repeating the adjustments until you are satisfied.
3.12.4 Local DOS
There is a special kind of DOS named local DOS (LDOS). LDOS curve for a given point r is
evaluated as follows:
iii EfE )()(),LDOS( 2
rr
To plot such a map, choose "10 Draw local DOS for a point", you will be prompted to input the
coordinate of the point r.
One can also plot LDOS for a set of points placed evenly in a line as color-filled map, the X-
axis correspond to energy, while the Y-axis corresponds to coordinate in the line relative to starting
point. To plot this kind of LDOS map, choose "11 Draw local DOS along a line", you will be
prompted to input the coordinate of starting point and end point defining the line, as well as the
number of points consisting of the line.
In the DOS module, the options controlling FWHM, energy unit, energy range and scale ratio
affect the resulting LDOS graphs.
An example relating to LDOS can be found in Section 4.10.2.
Note that fragment definition does not affect the result of LDOS, i.e. the LDOS always
corresponds to total DOS. However, if you want to separate angular moment contribution to
LDOS, you can use subfunction 25 of main function 6 to set coefficient of unwanted GTF in all
MOs to zero, then they will not contribute to LDOS.
Information needed: Basis functions and atom coordinates (only for PDOS, OPDOS and local
DOS), energy levels and occupation numbers (.fch/.molden/.gms file, Gaussian output file or the
plain text file recording them)
3.13 Plotting IR/Raman/UV-Vis/ECD/VCD spectrum (11)
Although spectrum plotting is beyond the scope of wavefunction analysis, due to this
function is very useful for theoretical spectrum research, the spectrum plotting function is also
included in Multiwfn. Multiwfn is able to plot IR (Infrared), regular Raman / Pre-resonance
Raman, UV-Vis (ultraviolet-visible), ECD (electronic circular dichroism) and VCD (vibrational
circular dichroism) spectra.
3.13.1 Theory
For comparing theoretical results with experimental spectrum, the discrete lines
corresponding to each transition mode have to be broadened to emulate the situation in real world,
the commonly used broadening function for IR, Raman and VCD spectra is Lorentzian function,
while for UV-Vis and ECD spectra Gaussian function is often used, see Section 3.12.1 for details.
Unlike DOS graph, in which the strengths for each energy level are always simply set to 1.0
(namely broadened curves from each energy level are normalized to 1.0), the strengths of
transitions are very important data for plotting spectrum.
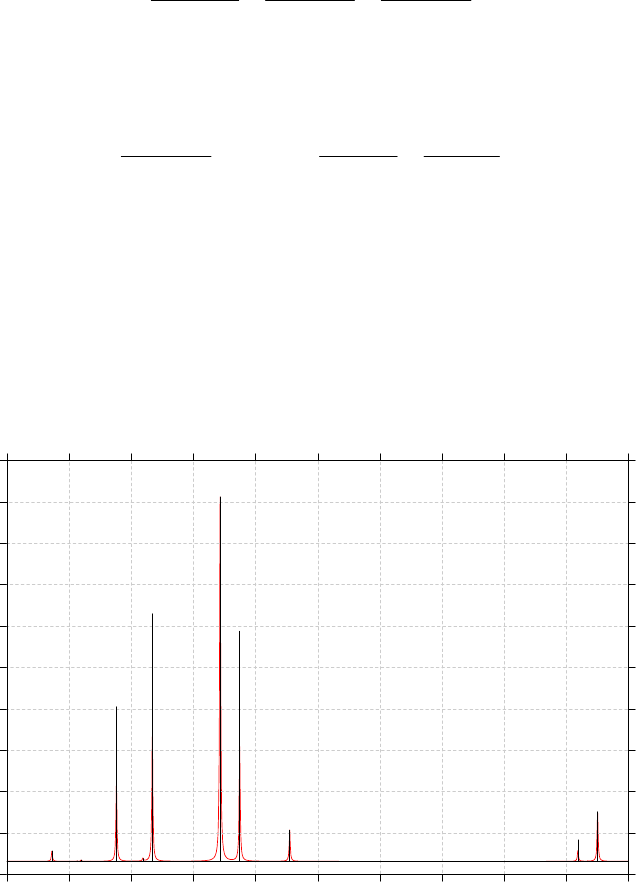
3 Functions
87
The unit of transition energy of IR, Raman and VCD spectra is cm-1 in common, for UV-Vis
and ECD spectra all of eV (1eV=8.0655*1000cm-1), nm and 1000cm-1 are common units. IR
intensity, Raman activity, oscillator strength and rotatory strength of each transition mode
outputted by quantum chemistry programs are proportional to the area under the broadened curve.
Below we discuss these five spectra respectively.
IR: The frequently used unit of molar absorptivity
, that is L/mol/cm can be rewritten as
mol
1000cm
c
m
*mol
1000cm
c
m
*mol
L23
Since IR intensity
d)( , where
is transition frequency, the unit of
should be
mol
0.01km
mol
1000cm
)(cm*
mol
1000cm 1
2
However km/mol is the more commonly used unit for IR intensity, therefore if IR intensity of a
vibrational mode is p km/mol, then the broadened curve from which should be normalized to
100*p (in the other words, the area under the curve is 100*p). Sometimes the unit esu2*cm2 is
used for IR intensity, the relationship with km/mol is 1 esu2*cm2 = 2.5066 km/mol.
Below is an example of IR spectrum plotted by Multiwfn. Notice that the left axis
corresponds to the curve (artificially broadened data), the right axis corresponds to the discrete
lines (original transition data).
0.00 401.37 802.74 1204.12 1605.49 2006.86 2408.23 2809.60 3210.98 3612.35 4013.72
F
r
e
q
u
e
n
cies
(
c
m
**-1
)
-249.34
523.61
1296.57
2069.52
2842.48
3615.43
4388.39
5161.34
5934.30
6707.25
7480.21
Molar absorption coefficient (L/mol/cm)
-15.79
33.15
82.09
131.03
179.96
228.90
277.84
326.78
375.72
424.65
473.59
IR intensities (km/Mol)
Raman (regular or pre-resonance): First beware that for a specific vibration mode i, its
Raman activity Si and Raman intensity Ii are two different quantities. Raman activity is a intrinsic
property of each molecular vibrational mode, while Raman intensity is directly related to
experimental Raman spectrum, and its value is dependent of the choice of wavenumber of incident
light
0 as well as temperature. The conversion relationship can be found in some literatures, e.g. J.
Mol. Struct., 702, 9-21 (2004):

3 Functions
88
kT
hc
B
B
SvC
Ii
i
ii
ii
i
exp1
)( 4
0
where C is a suitably chosen common normalization factor for all peak intensities,
i is vibrational
frequency. Only the Raman spectrum broadened based on Raman intensities can be strictly
comparable to the experimental one; however, as the peak position of Raman activity and intensity
are identical, and for a specific vibrational mode its intensity is proportional to its activity, the
Raman spectrum broadened from Raman activities is also useful enough.
Almost all quantum chemistry codes only output Raman activities, therefore by default,
Multiwfn emulates the Raman spectrum in terms of broadening Raman activities. However you
can also let Multiwfn to first convert the activities to intensities via option 19 (v0 and T are
provided by users) based on above formula, then the Raman spectrum will be obtained by
broadening Raman intensities. The normalization coefficient C is fixed to 10-12 in Multiwfn
(which is not important since what we are interested in is the shape rather than the absolute height
of Raman spectrum). The integral of the peak broadened by one unit of Raman activity or intensity
is equal to 1.
UV-Vis: In theoretical chemistry field, oscillator strength is always used for representing
transition strength in UV-Vis spectrum, however this is a dimensionless quantity and the precise
relationship with molar absorptivity haven’t been built. However, there is a well-known relation
between theoretical data and experimental spectra: If the unit 1000cm-1 and L/mol/cm are used for
X-axis and Y-axis respectively, then the area under the curve that broadened from per unit
oscillator strength should be 1/4.32*106. Equivalently, if eV is used as X-axis unit, the value
should be 1/4.32/8.0655*106=28700. By this relation, UV-Vis spectrum can be simulated by
theoretical data.
Fluorescence (or phosphorescence, as long as you can obtain oscillator strength by means of
spin-orbit coupling calculation) spectrum can also be plotted with exactly the same manner as UV-
Vis, the only difference is that according to Kasha's rule you should only take the first excited state
into account.
ECD:The significance of rotatory strengths in ECD spectrum is analogous to oscillator
strengths in UV-Vis spectrum, each electron transition mode corresponds to a rotatory strength. If
the rotatory strengths are broadened, after somewhat scaling and shifting, the resultant curve will
be comparable to experimental ECD spectrum. The integral of the peak broadened by one unit of
rotatory strength is equal to 1. In quantum chemistry programs, such as Gaussian, rotatory
strengths can be calculated in length representation or in velocity representation, in the former
case the strengths are origin-dependent, while in the latter case the strengths are origin-
independent. For complete basis-set situation, the results in the two repsentations converge to the
same values. Commonly velocity representation is recommended to be used.
VCD: VCD is akin to ECD, each vibrational mode has a rotatory strength. After broadening
them, the curve will be comparable to experimental VCD spectrum.
3.13.2 Input file
Currently below input files are supported:
1 Gaussian output file:
IR spectrum: Use the output file of “freq” task as input. If you use Gaussian 09 D.01 or later
3 Functions
89
revisions and meantime freq=anharm keyword was specified to carry out anharmonic analysis,
Multiwfn will prompt you to choose if load anharmonic frequencies and IR intensities instead of
the harmonic ones.
Raman spectrum: Use the output file of freq=raman task as input. If you would like to plot
pre-resonance Raman spectrum, you should at the same time use CPHF=rdfreq keyword and
write the frequencies of the incident lights after a blank line under the geometry specification, e.g.
300nm 400nm 500nm. If you hope to plot anharmonic Raman spectrum, use freq(raman,anharm)
keywords, then Multiwfn will prompt you to choose if load anharmonic frequencies and Raman
activities instead of the harmonic ones.
VCD spectrum: Use the output file of freq=VCD task as input. If you hope to plot
anharmonic Raman spectrum (supported by Gaussian since G16), use freq(VCD,anharm)
keywords, then Multiwfn will prompt you to choose if load anharmonic frequencies and rotatory
strengths instead of the harmonic ones.
UV-Vis or ECD spectrum: Use the output file of TDDFT, TDHF, CIS or ZINDO task as input,
no any additional keywords are required. The rotatory strengths in both length and velocity
representation (the data under "R(length)" and "R(velocity)", respectively) can be chosen to be
loaded by Multiwfn.
2 ORCA output file:
IR spectrum: Use freq keyword.
Raman spectrum: Use keywords like below
! b3lyp def2-SVP numfreq
%elprop Polar 1 end
UV-Vis or ECD spectrum: Use keywords like below (CIS, TDHF and ZINDO calculations
are also supported)
! b3lyp def2-SVP
%tddft
nroots 20
TDA false
end
Notice that for TDDFT calculation, ORCA by default uses Tamm-Dancoff Approximation
(TDA), in this case the oscillator strength and rotatory strengths are evidently not as good as that
produced by TDDFT, therefore in above example TDA false is used to make ORCA use standard
TDDFT formalism. Also it is worth noting that ORCA employs length representation for rotatory
strengths in ECD.
Output file of sTDA or sTD-DFT task of ORCA (see below for details) is also supported by
Multiwfn for plotting UV-Vis or ECD spectrum purpose. Below is example keywords:
! PBE0 def2-SVP def2/J RIJCOSX
%maxcore 6000
%pal nprocs 36 end
%tddft
Mode sTDDFT
Ethresh 10.0
maxcore 6000
3 Functions
90
end
VCD spectrum is currently not supported by ORCA.
3 Grimme's sTDA output file
The sTDA proposed by Grimme in J. Chem. Phys., 138, 244104 (2013) is a method
approximately solve the TDDFT equation and thus reduces the computational cost of the
electronic excitation part of TDDFT calculation by about two or three orders of magnitude. The
correpsonding sTDA program can be freely downloaded at
https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/stda/stda
Although the Grimme's sTDA code has already been implanted into ORCA program, the
stda.dat file outputted by standalone sTDA code can also be used as input file of Multiwfn for
plotting UV-Vis or ECD purpose.
When ECD is to be plotted, you can choose which representation of rotatory strength will be
used. The length and velocity representations have been mentioned above, while the mixed-form
of representation, which is recommended in the sTDA original paper, is defined as RM= RV fL / fV,
where fL and fV are length and velocity representations of oscillator, repespectively, and RV is the
velocity representation of rotatory strength.
4 Grimme's xtb output file
The xtb program written by Grimme is mainly used to carry out GFN-xtb calculation (J.
Chem. Theory Comput., 13, 1989 (2017)), which may be viewed as a semiempirical version of
DFT method. It is not only robust but also rather fast, it can be conveniently applied to systems
consisted of hundreds of atoms. Note that although the accuracy of xtb frequency has been
verified to be basically reasonable, the quality of IR intensities outputted by xtb is not good
(according to my experiences). xtb program can be freely obtained via https://www.chemie.uni-
bonn.de/pctc/mulliken-center/software/xtb/xtb.
By using following command, xtb will optimize the structure in test.xyz and then perform
frequency analysis: xtb test.xyz -ohess |tee test.out. Then the output file test.out will contain
harmonic frequencies and IR intensities, it can be used as input file of Multiwfn for plotting IR
spectrum purpose.
Note that xtb outputs 3N modes, where N is the number of atoms. When plotting spectrum,
Multiwfn will ask you how many lowest modes will be removed to discard the overall movement
modes, you should input 5 and 6 for linear and non-linear system, respectively.
5 Plain text file:
For generality, Multiwfn supports plain text file as input, you can extract transition data from
output files of quantum chemistry packages other than Gaussian/ORCA/sTDA, and then fill them
into a file according to the format shown below
numdata inptype
energy strength [FWHM] For transition 1
energy strength [FWHM] For transition 2
energy strength [FWHM] For transition 3
...
energy strength [FWHM] For transition numdata
3 Functions
91
where numdata denotes how many entries in this file. If inptype is set to 1, then only energy and
strength will be read, and FWHMs for all transitions will be automatically set. If inptype is set to 2,
then FWHMs will be read too. The transitions should be sorted according to the energies from low
to high. The unit of both energy and FWHM should be in cm-1 for IR, Raman and VCD spectra, in
eV for UV-Vis and ECD spectra. The unit of strength should be in km/mol, Å4/amu, cgs (10-40 erg-
esu-cm/Gauss), 10-44 esu2 cm2 for IR, Raman, ECD and VCD spectra, respectively (oscillator
strength of UV-Vis is dimensionless).
An example of the plain text file is shown below (for IR)
6 2
81.32920 0.72170 8.0
417.97970 3.58980 8.0
544.67320 21.06430 8.0
583.12940 41.33960 8.0
678.66900 91.47940 8.0
867.37410 2.94480 8.0
3.13.3 Usage and options
After boot up Multiwfn, first input path of Gaussian/ORCA/sTDA output file or the plain text
file containing transition data, then enter main function 11, and you will be prompted to select the
type of spectrum (for pre-resonance Raman then you also need to choose the interested frequency),
after that you will see below options. The meaning of some options may be different for various
types of spectra.
-2 Export transition data to plain text file: Output energies, intensities and FWHMs of all
transitions to “transinfo.txt” in current directory, this file fully complies with the format introduced
in last section, so it can be directly used as input file.
-1 Show transition data: Print energy and intensity data of all transitions on screen.
0 Plot spectrum: Plot spectrum right now!
1 Save graphical file of the spectrum in current folder: As the title says.
2 Export X-Y data set of lines and curves to plain text file: Export X-Y data set of lines
and broadened spectrum to "spectrum_line.txt" and "spectrum_curve.txt" in current directory,
respectively, you can replot the curve and discrete line graph directly by the two files via external
program, such as Origin.
3 Set lower and upper limit of X-axis: As the title says. The stepsize between ticks also
needs to be inputted. By default the range of X-axis is adjusted automatically according to
minimum and maximum transition energies.
4 Set left Y-axis: Set starting value, ending value and step size for left Y-axis. By default the
range of Y-axis is adjusted automatically according to the maximum peak.
5 Set right Y-axis: Like option 4, but for right Y-axis.
In many cases, after you adjusting setting for Y-axis at one side, the position of zero point of
this Y-axis deviates from that of Y-axis at another side, which makes the graph weird; To address
this problem, options 4 and 5 enable you to choose if correspondingly adjusting range of Y-axis at
another side. If you input y, then lower/upper limit and stepsize of Y-axis at another side will be
3 Functions
92
proportionally scaled to make zero point of left and right Y-axes are in the same horizontal line.
6 Select broadening function: Gaussian, Lorentzian and Pseudo-Voigt function can be
selected for broadening discrete lines as curves.
7 Set scale ratio for curve: If the value is set to k, then the height of curve will multiply k in
full range. For Raman, ECD and VCD spectra the default value is 1.0, for IR the value is 100, for
UV-Vis spectrum an empirical value 28700.0 is used when energy unit is eV or nm, when unit is
1000cm-1 the value 1/(4.32*10-6) is used.
8 Input full width at half maximum (FWHM): As the title says.
9 Toggle showing discrete lines: Choose if show the discrete lines corresponding to
transitions on the spectrum graph.
10 Switch the unit of infrared intensity / Set the unit of excitation energy: For IR
spectrum, switch the unit of IR intensities between km/mol (default) and esu2*cm2. For UV-Vis
and ECD spectra, choose the unit of energies between eV, nm and 1000cm-1.
11 Set Gaussian-weighting coefficient: Sets wgauss, which is mentioned in Section 3.12.1,
this option only appears when Pseudo-Voigt function is chosen.
12 Set shift value in X: If the value is set to k, then the final curve and discrete lines will be
shifted by k in X direction.
13 Set colors of curve and discrete lines: As the title says.
14 Multiply the transition energies (or vibrational frequenices) by a factor: The selected
transition energies (or vibrational frequencies) can be scaled by a given factor. This is option is
mainly used to apply frequency scaling factor onto the calculated harmonic frequencies.
15 Output contribution of individual transition to the spectrum: If select this option, user
will be prompted to input a criterion (e.g. k), then not only the total spectrum (as option 2), but
also the contributions from the individual transitions whose absolute value of strength larger than
k will be outputted to spectrum_curve.txt in current folder. This feature is particularly useful for
identifying the nature of total spectrum.
16 Find the positions of local minima and maxima: After you select this option, the
positions of the maxima and minima of the spectrum will be located.
17 Toggle showing dashed grid lines: Choose if plotting gray dashed grid lines on the
spectrum.
18 Toggle weighting spectrum of each system: See explanation in next section.
19 Convert Raman activities to intensities: As mentioned earlier, this option is used to
convert Raman activities to intensities. After that, the Raman spectrum plotted by option 0 will be
the one broadened based on Raman intensities rather than Raman activities. The wavenumber of
incident light and temperature are inputted by users.
20 Modify oscillator strengths/Raman activities/rotatory strengths: You can select some
transitions and change their oscillator strengths/Raman activities/rotatory strengths (depending on
spectrum type) to specific value. This option is very useful if you would like to plot fluorescence
spectrum, in this case you need to set oscillator strength of all transitions except for the lowest
excitation to zero (Kasha's rule).
Note that the actual number of points constituting the spectrum is controlled by
"num1Dpoints" parameter in settings.ini. The default value is commonly large enough and thus
need not to be adjusted.
3 Functions
93
3.13.4 Plotting multiple files and weighted spectrum
In Multiwfn, it is possible to simultaneously plot spectrum for multiple files, and meantime
taking weights into account. This feature is quite useful for obtaining actual spectrum of flexible
molecule with many thermally accessible conformations.
For example, there is a molecule containing four accessible conformations, their distribution
ratio have been determined according to Boltzmann's method based on calculated free energies. If
you want to plot its weighted spectrum and spectrum of each conformation, you should write a
plain text file named "multiple.txt" (other file name cannot be recognized by Multiwfn), the
content is:
boltz\Excit\a.out 0.6046
boltz\Excit\b.out 0.1950
boltz\Excit\c.out 0.1686
boltz\Excit\d.out 0.0317
where the first and second column correspond to path of input file and weight of each
conformation. Different type of input file can be presented together in this file. If you use this file
as input file, after you entered spectrum plotting module, Multiwfn will load data from these files
in turn. When plotting spectrum, spectrum of all the four conformations will be separately
calculated and drawn with different colors. In addition, the weighted spectrum is plotted on the
graph as thick red curve, it is simply evaluated as follows:
weighted spectrum = 0.6046*a + 0.1950*b + 0.1686*c + 0.0317*d
In the graph you can also observe many black discrete lines, these are collection of discrete lines
corresponding to different conformations. Notice that their heights have already been multiplied
by corresponding weights.
If before plotting spectrum you have chosen option 18 once, then the spectrum of various
conformations shown on graph are the weighted ones; in other words, these curves represent
contribution of each conformation to actual spectrum (thick red curve). In this case, the color of
weighted discrete lines are no longer all black but in accordance with color of curves, so that user
can easily recognize correspondence between curve and discrete among different systems.
If you simply want to simultaneously plot spectrum for multiple systems but do not want to
draw weighted spectrum, then the second column of multiple.txt should not be weights, but
customized legends, for example
boltz\Excit\a.out Molecular a
boltz\Excit\b.out Molecular b
boltz\Excit\c.out Molecular c
boltz\Excit\d.out Molecular d
Then plot spectrum as usual, curve of all the four systems will be shown together, and the legends
will be "Molecular a", "Molecular b", etc.
Note that the files included in multiple.txt may contain different number of transitions,
however, in this case the file containing the maximum number of transitions must be placed at the
beginning of multiple.txt.
3 Functions
94
Many examples of plotting various kinds of spectra are given in Section 4.11.
Information needed: Transition energies and strengths
3.14 Topology analysis (2)
3.14.1 Theory
Some real space functions in Multiwfn are available for topology analysis, such as electron
density, its Laplacian, orbital wavefunction, ELF, LOL etc. One can select real space functions by
selection -11. Notice that once this selection is chosen, all previous topology analysis results will
be clean.
The topology analysis technique proposed by Bader was firstly used for analyzing electron
density in "atoms in molecules" (AIM) theory, which is also known as "the quantum theory of
atoms in molecules" (QTAIM), this technique has also been extended to other real space functions,
e.g. the first topology analysis research of ELF for small molecules is given by Silvi and Savin,
see Nature, 371, 683. In topology analysis language, the points at where gradient norm of function
value is zero (except at infinity) are called as critical points (CPs), CPs can be classified into four
types according to how many eigenvalues of Hessian matrix of real space function are negative.
(3,-3): All three eigenvalues of Hessian matrix of function are negative, namely the local
maximum. For electron density analysis and for heavy atoms, the position of (3,-3) are nearly
identical to nuclear positions, hence (3,-3) is also called nuclear critical point (NCP). Generally the
number of (3,-3) is equal to the number of atoms, only in rarely cases the former can be more than
(e.g. Li2) or less than (e.g. KrH+) the latter.
(3,-1): Two eigenvalues of Hessian matrix of function are negative, namely the second-order
saddle point. For electron density analysis, (3,-1) generally appears between attractive atom pairs
and hence commonly called as bond critical point (BCP). The value of real space functions at BCP
have great significance, for example the value of
and the sign of
2
at BCP are closely
related to bonding strength and bonding type respectively in analogous bonding type (The
Quantum Theory of Atoms in Molecules-From Solid State to DNA and Drug Design, p11); the
potential energy density at BCP has been shown to be highly correlated with hydrogen bond
energies (Chem. Phys. Lett., 285, 170); local information entropy at BCP is a good indicator of
aromaticity (Phys. Chem. Chem. Phys., 12, 4742).
(3,+1): Only one eigenvalue of Hessian matrix of function is negative, namely first-order
saddle point (like transition state in potential energy surface). For electron density analysis, (3,+1)
generally appears in the center of ring system and displays steric effect, hence (3,+1) is often
named as ring critical point (RCP).
(3,+3): None of eigenvalues of Hessian matrix of function are negative, namely the local
minimum. For electron density analysis, (3,+3) generally appears in the center of cage system (e.g.
pyramid P4 molecule), hence is often referred to as cage critical point (CCP).
The positions of CPs are searched by Newton method, one need to assign an initial guess
point, then the Newton iteration always converge to the CP that is closest to the guess point. By
3 Functions
95
assigning different guesses and doing iteration for each of them, all CPs could be found. Once
searches of CPs are finished, one should use Poincaré-Hopf relationship to verify if all CPs may
have been found, the relationship states that (for isolated system)
n(3,-3) – n(3,-1) + n(3,+1) – n(3,+3) = 1
If the relationship is unsatisfied, then some of CPs must be missing, you may need to try to
search those CPs by different guesses. However even if the relationship is satisfied, it does not
necessarily mean that all CPs have been found. Notice that the function spaces of ELF/LOL and
Laplacian of
are much more complex than
, it is very difficult to locate all CPs for these
functions, especially for middle and large system, so, you can stop trying for searching CPs once
all CPs that you are interested in have been found.
The maximal gradient path linking BCP and associated two local maxima of density is
termed as “bond path”, which reveals atomic interaction path for all kinds of bonding. The
collection of bond paths is known as molecular graph, which provides an unambiguous definition
of molecular structure. Bond path can be straight line or curve, obviously for the latter case the
length of bond path is longer than the sum of the distances between BCP and associated two (3,-3)
CPs.
Let us see an example. In the complex shown below, the imidazole plane is vertical to
magnesium porphyrin plane, the nitrogen in imidazole coordinated to magnesium. Magenta,
orange and yellow spheres correspond to (3,-3), (3,-1) and (3,+1) critical points, brown lines
denote bond paths.
3 Functions
96
The topology paths for other real space functions can be generated too in Multiwfn, they are
very helpful to clarify intrinsic relationship between CPs.
About degenerate CP
Appearance of degenerate CPs in general system is very rare, so I mention it in the final of
this section. The so-called degenerate CP is the CP have one or two zero eigenvalues of Hessian
matrix. These CPs are very instable, slight perturbation of molecular geometry can break them
into other type CPs. However, degenerate CPs are commonly occur in axisymmetric system. For
example, in fluorine atom at groundstate, one of p orbital is singly occupied while other two are
doubly occupied, topology analysis on LOL gives below picture:

3 Functions
97
The two (3,-3) correspond to the two valves of the singly occupied p orbital, while the locally
maximum of electron localization arise from the other two p orbitals are represented by a circle of
CPs. Ostensibly, the CPs in the circle are either (3,-1) or (3,+1) type, but in fact they are the same
type degenerate CP, in which one eigenvalue is zero. Simply because the reasons of numerical
convergence of the eigenvalue, they are formally recorded as different CP types in Multiwfn.
3.14.2 Search critical points
In Multiwfn several modes used to assign initial guesses are provided for Newton method:
(1) Search CPs from a given starting point: If you already know the position of CPs or you
are able to guess where CPs may appear, this mode is suitable for you, the Newton iteration will
start from the coordinate you inputted. You can also input two atomic indices, then corresponding
midpoint will be taken as starting point for locating CP.
(2) Search CPs from nuclear positions: Use all nuclear positions in turn as starting points, this
mode is very suitable for searching all (3,-3) for
, and those (3,-3)s in innermost of atom for
ELF/LOL and Laplacian. For electron density analysis, if you found n CPs after you used this
mode, while there are more than n atoms in your system, it generally turns out that Newton
method missed some (3,-3) CPs.
(3) Search CPs from midpoint of atom pairs: Use midpoint of all atom pairs in turn as starting
points. This mode is very suitable for searching all (3,-1) for
.
(4) Search CPs from triangle center of three atoms: Likewise mode 3, but use triangle center
of all combinations of three atoms in your system. Suitable for searching all (3,+1).
(5) Search CPs from pyramid center of four atoms: Likewise mode 3, but use pyramid center
of all combinations of four atoms in your system. For electron density analysis, if you have tried
mode 2 and mode 3 but still cannot find certain (3,+3), this mode is worth to try. This mode is
more expensive than mode 3.
(6) Search CPs from a batch of points within a sphere: You need to set sphere center, radius
and the number of points first, then select option 0, the specified number (not the exact number
you have set) of points will randomly distributed in the sphere as starting points for Newton
method. The sphere center can be defined in very flexible way by option 2~6. If you choose option
-1, then the search starts and each atom center will be taken as sphere center in turn, assume that
there are n atoms and the number of points in sphere you set is m, then about n*m points will be
used as initial guesses. If you choose option -2, then you will be prompted to input indices of
3 Functions
98
atoms, the nuclei of these atoms will be used as sphere center in turn.
This mode is very appropriate for searching the CPs that are difficult to be located by other
modes. For ELF, LOL and Laplacian, it is highly recommended to use option -1 in this mode
to try to locate all possible CPs. Note that each time you carry out the search the positions of
starting points are different, if some expected CPs were not found in previous searches, try to
launch the search again and again to locate missing CPs.
Beware that the index of the CPs located by this searching mode may be different in each
time of execution!
The default searching parameters are appropriate for most systems, however in some cases
you have to adjust parameters manually to ensure expected CPs could be found. Those parameters
can be adjusted in the option "Set CP searching parameters".
(1) Set maximal iterations: If the number of Newton iteration exceeds this value before
converged to a CP or before Hessian matrix became singular (that is the iteration cannot continue),
then the Newton iteration will be terminated.
(2) Set scale factor for stepsize: The default value is 1.0, that is using original form of
Newton method. Sometimes reduce the stepsize is benefit for locate CPs. For example the
“Uracil.wfn” in example folder, by using mode 2 with default parameter the BCP linking N6 and
H12 cannot be found, if you reduce the stepsize to 0.5, then the problem solved.
(3)/(4) Criteria for gradient-norm/displacement convergence: If both gradient-norm in current
position and displacement in last step is smaller than the two values then the iteration stops and
current position will be regarded as a critical points. Notice that for the elements heavier than Ar,
during the search of their nuclear critical points, the convergence criteria are automatically
multiplied by 10000, because the cusps of electron density at these nuclear positions are very
sharp and hence hard to be located by default criteria.
(5) Minimal distance between CPs: If an iteration converged to a CP, however the distance
between this CP and any CP that has been found is smaller than this value, then the CP just found
will not be considered as a new CP, and hence discarded.
(6) Skip search if distance between atoms is longer than the sum of their vdW radius
multiplied by: In CP searching mode 3, 4 and 5, if the distance of any two atoms that involved in
the combination is longer than the sum of their vdW radii multiplied this value then current search
will be skipped. The purpose of this option is to reduce the number of searches and hence
computational cost of huge system. For example the imidazole--magnesium porphyrin complex
mentioned earlier, there are 49*48/2=1176 atom pairs, hence if this cutoff strategy is not employed
when you choose searching mode 2, Multiwfn will try as many as 1176 searches. While if this
strategy is used, since only closely related atom pairs will be considered, only 274 searches are
needed be performed, it can be found that their results are identical.
(7) If print details of CP searching procedure: This option is present only in serial mode. User
can select output level of details of CP searching procedure. This option is mainly used for
debugging.
(8) Criteria for determining if Hessian matrix is singular: If the absolute value of determinant
of Hessian matrix is lower than this value, then the Hessian matrix will be regarded as singular
and terminate search. Too large of this value may lead some CPs be ommitted, while too small of
this value may cause numerical instability and occurence of CPs in the regions far from system.
3 Functions
99
Default value is appropriate for most cases.
(9) Select rule for reserving CPs: By making use of this option, during the CP searching, only
the CP with value within user-defined range will be reserved, and thus unnecessary CPs could be
ignored. By default all CPs are reserved.
3.14.3 Generate paths
Once CPs are found, you can choose to generate paths. In fact, the so-called “path” is a bunch
of points evenly distributed in a curve.
(1) Generate the path connected (3,-3) and (3,-1): As the title says. Arithmetically, firstly
displace the coordinate of each (3,-1) forward and backward respectively along the eigenvector
that correspond to the positive eigenvalue of Hessian, and then go uphill following the gradient
vector until encounters a (3,-3), the resultant trajectories compose the bond paths.
(2) Generate the path connected (3,+1) and (3,+3): Likewise above, the difference is that the
starting points are (3,+1), and their coordinates are firstly moved forward and backward along the
eigenvector correspond to the negative eigenvalue of Hessian, and then go downhill following the
gradient vector.
In the option "Set path searching parameters", there are some suboptions used to adjust
parameters for generating paths.
(1) Maximal number of points of a path: In each generation of paths, if the number of steps is
reached this value before encounters a CP, then the trajectory will be discarded. For generating
very long path, default value may need to be enlarged.
(2) Stepsize: The space between neighbour points that composed the paths. For paths with
large curvature, sometimes they cannot be generated under default stepsize, you need to properly
decrease the stepsize and regenerate paths. If you set maximal number of points and stepsize of
paths as m and n respectively, then the maximal length of path is m*n.
(3) Stop generation if distance to any CP is smaller than: During the generation of paths, if
the distance between current position and a CP that has been found, then it will be regarded as that
the path has already reached the CP.
3.14.4 Generate interbasin surfaces
The interbasin surfaces (IBS) generated by Multiwfn actually consist of a bunch of paths
derived from (3,-1) CPs, these surfaces divide the whole space into respective region for each (3,-
3) CPs. By the function "Add or delete interbasin surfaces", you can generate, delete and check
interbasin surfaces. Notice that before generating IBS, generation of CPs should be completed first,
and at lease one (3,-1) must be found.
If you want to generate the IBS from the (3,-1) CP with index of 15, then simply input 15
(you will find it is useful to visualize CPs by function 0 first to get the CP index). To delete this
surface, input -15 (negative sign means "delete"). If there is no IBS presented and you hope to
generate all IBSs, input 0. To delete all already generated IBS, also input 0. A list of generated IBS
can be printed by inputting the letter l If you need to export the paths of a specific IBS (e.g.
corresponding to the (3,-1) CP with index of 4) to external file, input o 4, then the coordinates of
all paths derived from the 4th CP will be saved to surpath.txt in current folder. Input letter q can
3 Functions
100
return to upper level menu.
Parameters for generating IBSs can be adjusted by the option "Set interbasin surface
generating parameters". Enlarging number of paths in each IBS or lowering stepsize make IBSs
looks more smooth. The length of paths in IBSs, or say the area of IBSs, is proportional to product
of stepsize and number of points in each IBS path. Notice that once the parameters are changed,
all generated IBSs will be lost.
There are three ways to portray IBSs in Multiwfn, which can be controlled by "isurfstyle" in
settings.ini. Way 1 represents the IBS directly by the paths derived from corresponding (3,-1) CP;
By Way 2 IBSs are shown by solid surfaces, this is default style; Way 3 is uncommonly used, you
can try it by yourself.
3.14.5 Visualize, analyze, modify and export results
If you select the function “0 Print and visualize all generated CPs, paths and surfaces”, a
GUI will pop up, you can control if showing each type of CPs, paths, interbasin surfaces,
molecular structure, labels etc. Meanwhile, a summary of found CPs and paths are printed in the
command-line window. The satisfaction of Poincaré-Hopf relationship is also checked.
You can obtain values of all real space functions supported by Multiwfn (as well as gradient
and Hessian matrix of the selected real space function) at a given CP or at all CPs by function “7
Show real space function values at specific CP or all CPs”. Note that electrostatic potential is the
most expensive one among all of the real space functions, if you are not interested in it, you can
set "ishowptESP" parameter in "settings.ini" to 0 to skip calculation of electrostatic potential.
In this function, you can also decompose a selected real space function at a given CP as
contributions from a range of orbitals. The way of evaluating orbital contribution is mentioned in
Section 3.3.
In the option “-4 Modify or export CPs”, you can print, delete, add and export CPs. The
positions and types of all found CPs can be saved to a formatted text file “CPs.txt” in current
folder by choosing suboption 4, the information of CPs can also be loaded from an external
formatted text file by suboption 5 (the found CP at current session will be clean), notice that the
file format must be identical to the one outputted by suboption 4. All CPs can be exported as pdb
file by suboption 6, so that CPs can be conveniently visualized by external visualization softwares,
element C/N/O/F correspond to (3,-3)/(3,-1)/(3,+1)/(3,+3) respectively.
3 Functions
101
In the option “-5 Modify or print detail or export paths, or calculate property along a path”,
you can print summary of generated paths, print positions of all points in specified path or delete
some paths via suboption 1, 2 and 3 respectively. By suboption 4 you can export out the detail
information of all paths to “paths.txt” in current folder. By suboption 5 the paths can be imported
from an external file, the file format must be identical to the one outputted by suboption 4. By
suboption 6, all points in all paths can be exported to a pdb file in current folder, so that paths can
be conveniently visualized by external visualization softwares. For example, we use Multiwfn to
perform AIM analysis for serine, then export CPs and paths as pdb file, then load them into VMD
program, set the drawing method as "Points" and slightly adjust point size and color, we get below
graph. The yellow paths are bond paths, blue and cyan points correspond to (3,-3) and (3,-1) CPs.
By suboption 7, value of real space functions along selected topology paths can be outputted and
plotted as curve map. You can also take the data shown in "Dist." and "Value" column as X and Y
axes respectively to plot curve graph by third-part plotting tools.
Distance, angle and dihedral angle between atoms and CPs can be conveniently measured by
using the option "-9 Measure distances, angles and dihedral angles between CPs or atoms".
3.14.6 Calculate the aromaticity indices based on topology properties
of electron density
If the real space function you selected is electron density, option 20 and 21 will be visible,
they are utilities used to analyze aromaticity.
Shannon aromaticity index
Option 20 is used to calculate Shannon aromaticity (SA) index, see Phys. Chem. Chem. Phys.,
12, 4742 (2010) for detail. The formula can be briefly written as
N
iN
ii
i
iii pppNSA
)(
)(
)ln()ln(
BCP
BCP
r
r
In above formula, N is the total number of the BCPs in the ring you want to study aromaticity,

3 Functions
102
BCP
ris the position of BCP. In option 20, you need to input N and the index of these CPs in turn,
then Shannon aromaticity index will be printed immediately. The smaller the SA index, the more
aromatic is the molecule. The range of 0.003 < SA < 0.005 is chosen as the boundary of
aromaticity/antiaromaticity in original paper.
Curvature of electron density perpendicular to ring plane at RCP
In Can. J. Chem., 75, 1174 (1997), the authors showed that electron density at RCP is closely
related to aromaticity of corresponding ring. The larger the density, the stronger the aromaticity.
They also pointed out that the curvature of electron density perpendicular to the ring plane at the
RCP has more significant correlation with the ring aromaticity. The more negative the curvature,
the stronger the aromaticity. Assume that the ring is strictly perpendicular to a Cartesian axis, for
example, a ring perpendicular to Z axis (viz. the ring is in XY plane), then the curvature is just ZZ
component of Hessian matrix of electron density at the RCP, which can be directly obtained by
using option 7 to print out properties of a given RCP. However, if the ring is distorted, or is not
exactly perpendicular to any Cartesian axis, you should use option 21 to calculate the curvature. In
option 21, you need to input the index of the RCP (or directly input coordinate of a point), and
then input indices of three atoms, their nuclei position will be used to define the ring plane. Then,
the electron density, the gradient and the curvature of electron density perpendicular to the ring
plane at the RCP will be outputted on screen. In addition, unit normal vector, the coordinates of
the two points above and below 1 Angstrom of the RCP in normal direction will be outputted
together, which can be taken as the point used to calculate NICS(1).
Information needed: GTFs, atom coordinates
3.15 Quantitative analysis of molecular surface (12)
The theory and numerical algorithm involved in present module have been detailedly
described in J. Mol. Graph. Model., 38, 314 (2012). In the next two sections, these two aspects
will only be briefly introduced.
3.15.1 Theory
Electrostatic potential on vdW surface
Molecular electrostatic potential (ESP), )(rV, has been widely used for prediction of
nucleophilic and electrophilic sites, as well as molecular recognition mode for a long time, the
theoretical basis is that molecules always tend to approach each other in a complementary manner
of ESP. These analyses of ESP are common performed on molecular van der Waals (vdW) surface.
Although the definition of such a surface is arbitrary, most people prone to take the 0.001
isosurface of electron density as vdW surface, since this definition reflects specific electron
structure features of a molecule, such as lone pairs, π electrons etc., this is also what the definition
used in our analyses.
The analysis of ESP on vdW surface has been further quantified to extract more information.

3 Functions
103
It is shown that the strength and orientation of weak interaction, including such as hydrogen
bonding, dihydrogen bonding and halogen bonding, can be well predicted and explained by
analyzing the magnitude and positions of minima and maxima on the surface. Politzer and
coworkers (J. Mol. Struct. (THEOCHEM), 307, 55) have defined a set of molecular descriptors
based on ESP on vdW surface, which are taken as independent variables of general interaction
properties function (GIPF). GIPF successfully connects distribution of ESP on vdW surface and
many condensed phase properties, including density, boiling point, surface tension, heats of
vaporization and sublimation, LogP, impact sensitivity, diffusion constant, viscosity, solubility,
solvation energy and so on. Below I enumerate and brief these descriptors.
A+ and A- indicate the surface area in which the ESP has positive and negative value,
respectively. Total surface area A is the sum of them.
S
V and
S
V denote average of positive and negative ESP on vdW surface respectively
n
jj
S
m
ii
SVnVVmV
11
)()/1()()/1( rr
where i and j are indices of sampling points in positive and negative regions respectively. The S
subscript means "Surface". The average of ESP over the entire surface is
t
kk
SVtV
1
)()/1( r
is the average deviation over the surface, which is viewed as an indicator of internal
charge separation:
t
k
S
kVVt
1
)()/1( r
The total ESP variance can be written as the sum of positive and negative parts:
n
j
S
j
m
i
S
iVVnVVm
1
2
1
2222
tot ])([)/1(])([)/1( rr
The variance reflects the variability of ESP. The larger the 2
and 2
, the more tendency that
the molecule interacts with other molecules by positive and negative ESP regions respectively.
Degree of charge balance is defined as
22
tot
22
)(
When 2
equals to 2
,
attains its maximum value of 0.250. The closer the
is to 0.250, the
more possible that the molecule can interact to others through positive and negative region with
similar extent.
The product of 2
tot
and
is a very useful quantity too, a large value of 2
tot
is an
indicative of a molecule that has relatively strong tendencies to interact with others of its own kind

3 Functions
104
electrostatically.
Some practical applications of GIPF
A practical application of above GIPF descriptors is presented in J. Phys. Chem. A, 110, 1005
(2006). The authors showed that for a series of molecules containing C, H, N and O elements, the
heat of vaporization can be well evaluated as
cbAaH 2
totvap
with least-squares fit coefficients a = 2.130, b = 0.930 and c = -17.844. The heat of sublimation
can be predicted as
cbaAH 2
tot
2
sub
with a = 0.000267, b = 1.650087 and c = 2.966078. In above equations the surface area A is in Å2,
sub
H is in kcal/mol, 2
tot
is in (kcal/mol)2. Note that the coefficients are more or less
dependent on the calculation level used. The author used B3LYP/6-31G* to optimize geometry
and B3LYP/6-311++G(2df,2p) to calculate ESP.
Another typical application of statistical data of ESP on vdW surface is predicting crystal
density of organic molecules containing C, H, N and O elements. The crystal density is a crucial
property of energetic compounds. In J. Phys. Chem. A, 111, 10874 (2007), it was shown that the
density can be estimated by m
/VM
, where M is molecular mass and Vm is molecular vdW
volume defined by
=0.001 isosurface; for ionic crystal (e.g. ammonium azide), M and Vm
correspond the sum of mass and volume of the cation and anion comprising a formula unit of the
compound. Although the relationship is quite simple, it indeed works well for most neutral species,
but the error is evidently larger for ionic species. In order to improve the prediction accuracy for
neutral ones, in Mol. Phys., 107, 2095 (2009), the authors introduced GIPF descriptors into the
formula:
)( 2
tot
m
V
M
At B3PW91/6-31G** level, the fitted coefficients are
= 0.9183,
= 0.0028 and
= 0.0443. This
formula has proven to have improved accuracy, because intermolecular electrostatic interaction is
somewhat effectively taken into considered. In a succeeding paper Mol. Phys., 108, 1391 (2010),
the author showed that the crystal density of ionic compounds can be estimated much better than
m
/VM
if GIPF descriptors are introduced:
(anion)
(anion)
(cation)
(cation)
mA
V
A
V
V
MSS
with least-squares fit coefficients
= 1.0260,
= 0.0514,
= 0.0419 and
= 0.0227 at
B3PW91/6-31G** level. In the equation,
(cation)S
V and
(cation)
A denote the
S
V and
A of
the cation;
(anion)S
V and
(anion)
A denote the
S
V and
A of the anion. For 30 test cases, the
3 Functions
105
average absolute error is merely 0.033g/cm3.
Noticed that above relationships are only appropriate for small organic compounds
containing C, H, N, O elements, the error are significantly larger for other kinds of systems.
In J. Phys. Chem., 97, 9369 (1993), it is shown that boiling point can be predicted as
2
totbp AT
where
= 2.736,
= 33.31,
= -72.05 were fitted at HF/STO-5G*//HF/STO-3G* level. This
paper also showed equations for predicting critical temperature, volume and pressure.
In J. Phys. Chem. A, 103, 1853 (1999), the prediction equation for solvation free energy is
presented as (Vmin denotes the ESP value at its global minimum in the whole space):
827.46)/(2.9704051892.0
)(106412.217201.0(kJ/mol) 3
minS,maxS,
5
minsolv
SS VAVA
VVVG
In addition, the equations used to predict heat of fusion, surface tension and crystal/liquid
density can be found in J. Phys. Chem., 99, 12081 (1995), the equations used to predict lattice
energy for ionic crystal containing NH4+, K+ and Na+ are given in J. Phys. Chem. A, 102, 1018
(1998). More formulae used to predict physical properties of organic molecules based on GIPF
descriptors are summarized in Table 3 of J. Mol. Struct. (THEOCHEM), 425, 107 (1998). GIPF
also has many important uses in study of biochemical systems, see Int. J. Quantum Chem., 85, 676
for a review.
Average local ionization energy and local electron affinity on vdW surface
The value of average local ionization energy, )(rI, has attracted more and more attentions.
This function has many uses, for example reproducing atomic shell structure, measuring
electronegativity, quantifying local polarizability and hardness. However, the most important use
maybe the prediction of reactivity according to function value on vdW surface, )(r
S
I. Lower
value of )(r
S
I indicates that the electron at r are more weakly bounded, therefore more likely r
is the site of electrophilic or radical attack. Many studies have shown that the global minimum of
)(rI on vdW surface exactly locates the experimental reaction site, while relative magnitude of
)(rI at corresponding reaction site in homologues correlates well with relative reactivity. The
interested user is recommended to take a look at J. Mol. Model, 16, 1731 and Chapter 8 of the
book Theoretical Aspects of Chemical Reactivity (2007).
Local electron affinity EAL is a quantity very similar to )(rI, the only difference is that the
MOs under consideration is not all occupied ones, but all unoccupied ones. It was shown that EAL
on molecular surface is useful for analyzing nuclophilic attacking, for detail see J. Mol. Model., 9,
342.
In Multiwfn, above mentioned surface descriptors can be calculated not only on the whole

3 Functions
106
vdW surface, but also on the subregions corresponding to atoms or user-defined fragments. The
detail of the theory is to be published, and thus not documented here at the moment.
3.15.2 Numerical algorithm
In summary, in the quantitative analysis of molecular surface task, what we need to obtain are
minima and maxima of ESP or )(rI or EAL on vdW surface, as well as
S
V,
S
V, S
V,
,
2
, 2
, 2
tot
,
, and 2
tot
. Here I briefly describe how these properties are computed in
Multiwfn in accordance with the sequence of steps.
1. Grid data of electron density enclosed the entire molecular space is compute. The smaller
the grid spacing is used, the more accurate result you will get, however the more vertices will be
generated in next step and therefore you will wait longer time in step 3.
2. Marching Tetrahedra algorithm is performed by making use of the grid data generated
above, this step generally does not cost much computational time. The volume enclosed by the
isosurface is computed at the same time. This step generates vertices representing the isosurface,
along with their connectivity. Each neighbouring three vertices constitute a triangle (will be
referred to as facet below). Below example is a water molecule, vertices (red points) and
connectivity (black lines) are portrayed:
3. Since computing ESP is time consuming, in order too cut down computational time,
Multiwfn removes redundant points. Specifically, if the distance between two points is smaller
than a specific value, one of the points will be eliminated, and the other point will be moved to
their average position. In above graph, the aggregated points such as those inside blue circles will

3 Functions
107
be finally merged to one point.
4. Calculate mapped function (ESP, )(rI and so on) at each vertex on the isosurface. For
ESP, this is the most time consuming step, however for )(rI and EAL, this step can be finished
immediately.
5. Locate and then output minima and maxima of the mapped function on the surface by
making use of connectivity. If the mapped function value at a vertex is both lower (larger) than
that at its first-shell neighbours and second-shell neighbours, then this vertex will be regarded as
surface minimum (maximum).
6. Compute and output
S
V,
S
V, S
V,
, 2
, 2
, 2
tot
,
, and 2
tot
, as well as vdW
volume, area of total vdW surface, the area where the mapped function is positive and where is
negative. As an example, S
V is computed as
N
iii
SFAAV
1
tot )/1(
where N is the total number of facets, Atot is the sum of area of all facets, Ai is the area of facet i, Fi
is the ESP value of facet i, which is calculated as the average of ESP at the three vertices
composing the facet.
3.15.3 Parameters and options
You will see below options in the main interface of quantitative analysis of molecular surface.
0 Start analysis now!: When this option is selected, the analysis boots up. All steps described
in last section will be implemented sequentially.
1 The isovalue of electron density used to define molecular surface: Default value is 0.001,
corresponding to the most frequently used definition of vdW surface. In general it is not
recommended to adjust this value.
2 Select mapped function: The mapped function can be selected by this option. Currently
ESP, )(rI, EAL and user defined real space function (Section 2.7) are directly supported and can
be automatically computed by internal module of Multiwfn during the surface analysis.
Alternatively, if you choose "A function loaded from external file", then the value of mapped
functions at all surface vertices will be loaded from an external file, so that you can analyze other
mapped functions (e.g. Fukui function), see the description of option 5 below for detail about the
format of the external file.
Note that by default the ESP is evaluated based on wavefunction, this process may be quite
time-consuming for large systems. However, if you choose "Electrostatic potential from atomic
charge", then Multiwfn will evaluate ESP based on atomic charges, the computational time will be
reduced by several orders. The atomic charges will be loaded from a .chg file, you can use main
3 Functions
108
function 7 to produce the .chg file, or you can write the file manually, see corresponding part of
Section 2.5 on the .chg file format. Note that the analysis result will be reasonable only when the
the way to generate atomic charges can reproduce ESP well (e.g. CHELPG, MK and ADCH
methods).
3 Spacing of grid points for generating molecular surface: This setting defines the spacing
of electron density grid data, see step 1 introduced in the last section. The spacing directly
determines the accuracy and computational cost of the analysis. Default value is suitable for
general cases. Largening this value can reduce computational time evidently, however if this value
is not small enough, the vertices on the isosurface will be spare, this may cause missing or
erroneous locating of some extrema. In general, the results under the default spacing are accurate
and reliable. If you find some extrema were not located under default spacing, try to decrease
spacing and rerun the task.
4 Advanced options: Suboptions in this option is not needed to be frequently adjusted by
normal users.
(1) The ratio of vdW radius used to extend spatial region of grid data: The role of this
parameter is exactly identical to the parameter k introduced in Section 3.100.3. Enlarging this
value will lead larger spatial extension of grid data of electron density around molecule. If
isovalue of electron density is set to a lower value than default, or the system is negatively charged,
you may need to enlarge this parameter to ensure that the isosurface will not be truncated.
(2) If eliminate redundant vertices: If this option is switched to "No", then the elimination
of redundant vertices (step 3 described in last section) will be skipped, and you will waste vast
time to calculate mapped function at those meaningless vertices. If this option is switched to "Yes",
you will be prompted to input a distance criterion for merging adjacent vertices. Commonly,
0.4~0.5 times of grid spacing is recommended to be used as the criterion.
(3) Number of bisections before linear interpolation: Simply speaking, the larger the value,
the more exactly the isosurface (corresponding to vdW surface) can be generated. Enlarging this
value will bring additional cost in step 2. The generated isosurface under default value is exact
enough in general. You can descrease it to 2 even to 1 to save computational time, however
decrease it to 0 will frequently lead to false surface extrema.
5 If load mapped function values from external file
Via this option, during surface analysis, the value of mapped function at all surface vertices
can be loaded from external file rather than directly calculated by Multiwfn. This option has two
purposes: (1) Reduce overall analysis time (2) Analyze some special functions that cannot be
directly produced by Multiwfn, or those requiring mathematical operations and thus not directly
available in present module (e.g. dual descriptor). This option has four suboptions:
(0) Do not load mapped function but directly calculate by Multiwfn: This is default case.
(1) Load mapped function at all surface vertices from plain text file: If this option is
selected, then after generation of molecular surface, coordinate of all surface vertices (in Bohr)
will be automatically exported to surfptpos.txt in current folder. Then you can use your favourite
program to calculate mapped function value at these points, and write the values as the fourth
column in this file (in free format, unit is in a.u.). For example
3 Functions
109
1324 // The first line is the total number of points
-1.6652369 -0.5480503 -0.2554867 -0.0196978306
-1.6835983 -0.5563165 -0.1342924 -0.0242275610
-1.6977125 -0.5530614 -0.0099311 -0.0287667191
-1.7013207 -0.5536310 0.1194197 -0.0330361826
-1.6954099 -0.5523031 0.2547866 -0.0371580132
....
Then input the path of this file (the name can still be surfptpos.txt), Multiwfn will directly read the
values. An exemplificative application of this option is given in Section 4.12.4.
Hint: If you will analyze a system twice or more times, and want to avoid calculating mapped
function values every time for saving time, at the first time you analyze the system, you can select
option 7 at post-process interface to export coordinates and corresponding mapped function values
of surface vertices to vtx.txt in current folder. At next time you analyze the system, if you choose
this option, and input the path of the vtx.txt during the surface analysis, then mapped function
values will be directly loaded rather than re-calculated. (See Section 4.12.7 for example)
(2) Similar to 1, but specific for the case of using cubegen utility of Gaussian: A file
named cubegenpt.txt will be generated in current folder after generation of molecular surface. This
file is very similar to surfptpos.txt, the difference is that in this file the first line is not presented,
and coordinate unit is in Angstrom. Based on this file, you can make use of cubegen utility of
Gaussian to calculate mapped function at all surface vertices. After that, input the path of cubegen
output file, the data will be loaded by Multiwfn. The main use of this option is to reduce
computational cost in ESP analysis, see Section 4.12.7 for illustration.
(3) Interpolate mapped function from an external cube file: After generation of molecular
surface, a template cube file named template.cub will be generated in current folder. Then you will
be prompted to input the path of a cube file representating the mapped function you are interested
in, the grid setting of this cube file must be exactly identical to template.cub. The mapped function
values at surface vertices will be evaluated by interpolation from the cube file you provided.
3.15.4 Options at post-process stage
Once the all calculations of surface analysis are finished, a summary will be printed on screen.
Meanwhile below options will appear on screen used to check, adjust and export results.
-3 Visualize the surface: By this option you can directly visualize the isosurface analyzed.
-2 Export the grid data to surf.cub in current folder: The grid data used to generated
isosurface will be exported to the cube file surf.cub in current folder.
-1 Return to upper level menu
0 View molecular structure, surface minima and maxima: A GUI window will pop up if
this option is chosen. Red and blue spheres represent the position of maxima and minima. All
widgets are self-explained and hence not be referred here.
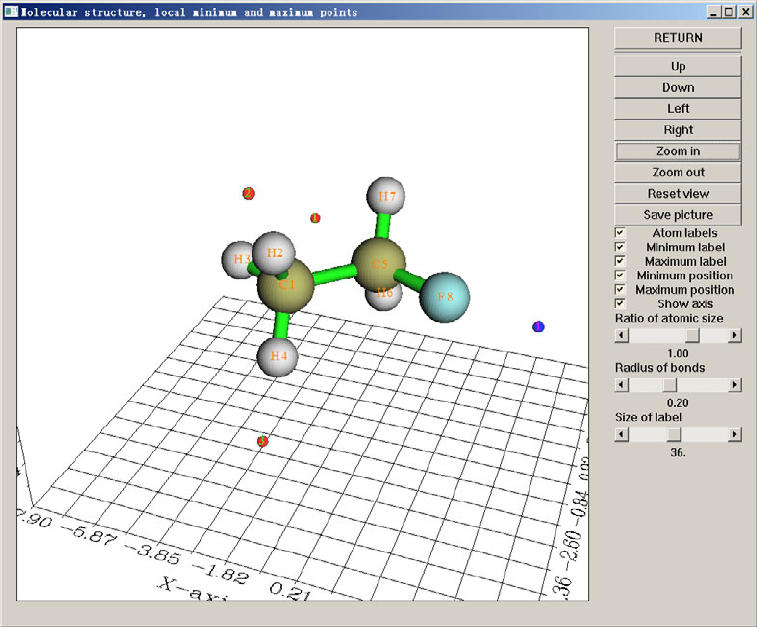
3 Functions
110
1 Export surface extrema as plain text file: This option exports value of mapped function
and X,Y,Z coordinates of surface extrema to surfanalysis.txt in current folder.
2 Export surface extrema as pdb file: This option outputs surface extrema to
surfanalysis.pdb in current folder. The B-factor column records mapped function value.
3 Discard surface minima in certain value range: If the mapped function value at a surface
minima is between the lower and upper limit inputted by user, then this minimum will be
discarded and cannot be recovered afterwards. This option is useful to screen the minima with too
large value.
4 Discard surface maxima in certain value range: If the mapped function value at a
surface maximum is between the lower and upper limit inputted by user, then this maximum will
be discarded and cannot be recovered afterwards. This option is useful to screen the maxima with
too small value.
5 Export present molecule as pdb format file: This option output structure of present
system to a specified pdb file. Since pdb is a widely supported format, in conjunction with the
output by option 2, surface extrema can be conveniently analyzed in external visualization
softwares such as VMD.
6 Export all surface vertices to vtx.pdb in current folder: This option outputs the surface
vertices to vtx.pdb file in current folder, the connectivity are written to CONECT field, mapped
function values are written to B-factor field. This option is mainly used to check validity of
isosurface polygonization and visualize distribution of mapped function on vdW surface.
7 Export all surface vertices to vtx.txt in current folder: Namely output all reserved
surface vertices to a plain text file named vtx.txt in current folder, including vertex X/Y/Z
coordinates in Bohr, mapped function values in a.u., eV and kcal/mol.
3 Functions
111
9 Output surface area in specific value range of mapped function
By this option, one can gain the knowledge of the distribution of molecular surface area in
various range of mapped function. First one needs to input the index range of the atoms in
consideration, then input overall range, interval and the unit. For example, one sequentially inputs
2,6-9, -45,50 and 10 and 3, the statistic then is applied on the local molecular surface
corresponding to atoms 2, 6, 7, 8 and 9, the output looks like below:
Begin End Center Area %
-50.0000 -40.0000 -45.0000 4.8764 1.5171
-40.0000 -30.0000 -35.0000 28.0413 8.7242
-30.0000 -20.0000 -25.0000 23.2699 7.2397
-20.0000 -10.0000 -15.0000 17.6022 5.4764
-10.0000 0.0000 -5.0000 61.4759 19.1263
0.0000 10.0000 5.0000 72.6197 22.5933
10.0000 20.0000 15.0000 55.2707 17.1957
20.0000 30.0000 25.0000 53.9060 16.7712
30.0000 40.0000 35.0000 2.8590 0.8895
40.0000 50.0000 45.0000 1.5000 0.4667
Sum: 321.4212 100.0000
where "begin" and "end" is the lower and upper limit of local value range, respectively. "Center" is
their average value. Area is in Å2, "%" denotes the proportion of the area in overall molecular
surface area.
10 Output the closest and farthest distance between the surface and a point
In this option, after defining a point (you can define a nuclear position or geometry center as
the point, you can also directly input the coordinate of the point), the closest and farthest distance
between the molecular surface and the point will be outputted. These two quantities have two
main uses:
(1) In atoms in molecules (AIM) theory, for systems in gas phase, the vdW isosurface is
defined as the ρ=0.001 a.u. isosurface. The closest distance between a nucleus and the surface can
be regarded as non-bonded atomic radius. For a non-covalently interacting atom pair AB, The
difference between the length of A-B and the sum of their non-bonded radii is termed as mutual
penetration distance. In general, the larger the distance is, the stronger the interaction will be.
(2) The farthest distance between molecular surface and geometry center can be viewed as a
definition of molecular radius. Of course, the concept of molecular radius is only meaningful for
sphere-like molecules.
If you input f, Multiwfn will output the farthest distance between all surface points. This can
be regarded as a definition of molecular diameter.
11 Output the surface properties of each atom
By default, the surface properties, such as average of ESP, are calculated on the whole
molecular surface. By using this function, the whole surface will be first decomposed to local
surfaces corresponding to individual atoms, and then the surface properties will be calculated on
these atomic surfaces. This function is very helpful to study atomic properties.
After outputting the surface properties, the user can select if output the surface facets to
locsurf.pdb in current folder. If choose "y", then in the outputted pdb file, each atom corresponds
to a surface facet, and the B-factor field records the attribution of the surface facets, e.g. a facet

3 Functions
112
having B-factor of 11.00 means the facet belongs to the local surface of atom 11. If you load the
pdb file into VMD and set "Coloring Method" as "Beta", then you can directly visualize how the
whole molecular surface is decomposed to atomic surfaces.
12 Output the surface properties of specific fragment
Similar to function 11, but user can define a fragment, the surface properties will only be
calculated on the local surface corresponding to this fragment, so that one can study fragment
properties according to the local surface descriptors. Also, you can choose to output the surface
facets to locsurf.pdb in current folder, in which the atom having B-factor of 1 and 0 means
corresponding surface facet belongs to and does not belong to the local surface of the fragment
you defined, respectively.
3.15.5 Special topic: Hirshfeld and Becke surface analyses
The quantitative molecular surface analysis module is also able to carry out Hirshfeld and
Becke surface analysis, present section is devoted to introduce this point.
Theory of Hirshfeld and Becke surface analyses
Hirshfeld surface analysis was first proposed in Chem. Phys. Lett., 267, 215 (1997) and
comprehensively reviewed in CrystEngComm, 11, 19 (2009). This method focus on analyzing the
so-called Hirshfeld surface to reveal weak interactions between monomers in complex or in
molecular crystal.
Hirshfeld surface in fact is a kind of inter-fragment (or inter-monomer) surface, which is
defined based on the concept of Hirshfeld weight. Probably Hirshfeld surface is the most
reasonable way to define inter-fragment surface.
Atomic Hirshfeld weighting function of an atom is expressed as
BB
A
A
w)(
)(
)( 0
0
Hirsh
r
r
r
where 0
A
denotes the density of atom A in free-state. Summing up weight of all atoms in a
fragment yields Hirshfeld weight of this fragment
PA AP ww )()( HirshHirsh rr
Hirshfeld surface of fragment P is just the isosurface of 5.0
Hirsh
P
w.
Motivated by Hirshfeld surface, I proposed Becke surface, which replaces Hirshfeld weight
with Becke weight (see Section 3.18.0 for introduction of Becke weight), only geometry and
atomic radii are required to construct Becke surface. Generally the shape of Becke surface and
Hirshfeld surface are comparable, but I prefer to use Becke surface, mostly because Becke surface
does not rely on atomic density and thus somewhat easier to be constructed.
To intuitively illustrate Hirshfeld/Becke surface, acetic acid dimer in 2D case is taken as
example here

3 Functions
113
Becke weighting function of the monomer at left side of the graph is represented by color, going
from red to purple corresponds to the weight varying from 1.0 to 0.0. The black line, which is the
contour line of 0.5, is just its Becke surface. Evidently, Becke surface very elegantly partitioned
the whole space into two monomer regions, the difference of atomic size is properly and
automatically taken into account. The Becke surface in this case is an open surface, the surface
extends to infinity; while if the monomer is completely buried, such as in molecular crystal or
metal-organic framework environment, then its Becke surface will be a close surface and encloses
all of its nuclei, just like common molecular surface.
If we map specific real space functions on Becke/Hirshfeld surface and study their
distributions, just like quantitative analysis on molecular surface, we can gain many important
information about intermolecular interaction. There are three real space functions very useful for
this purpose
(1) Normalized contact distance vdW
e
vdW
ee
vdW
i
vdW
ii
norm r
rd
r
rd
d
, where di (de) is the
distance from a point on the surface to the nearest nucleus inside (outside) the surface, vdW
i
r and
vdW
e
r denote vdW radius of the corresponding two atoms. Small value of dnorm indicates close
intermolecular contact and implies evident interaction.
(2) Electron density. If electron density is large in some local region of Becke/Hirshfeld
surface, obviously the intermolecular interactions crossing these regions must be strong. The
usefulness of electron density is similar to dnorm, but the former is more physically meaningful.
While dnorm also has its own advantage, namely only geometry and vdW radii information are
needed.
(3) Sign(λ2(r)), see corresponding part Section 2.6 for detailed explanation. This function can
not only exhibit interaction strength but also reveal interaction type.
Below is urea crystal, the mesh represents Becke surface of the central urea, and dnorm is the
mapped function. Blue part corresponds to small dnorm and thus exhibits close contact, which
mainly originates from H-bond interaction.
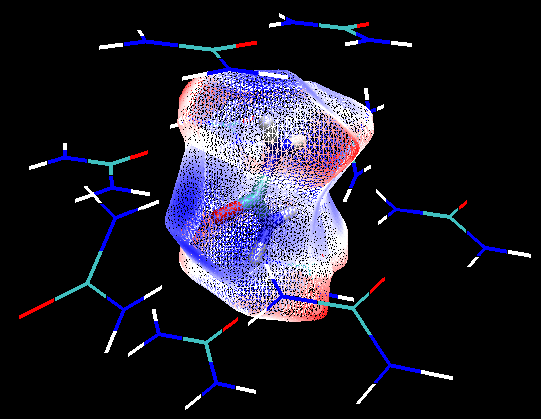
3 Functions
114
Fingerprint plot
The so-called "fingerprint plot" defined in the framework of Hirshfeld surface analysis is
very useful for investigating the non-covalent interactions in molecular crystals. X and Y axes in
this plot correspond to di and de, respectively. The plot is created by binning (di, de) pairs in certain
intervals and colouring each bin of the resulting 2D histogram as a function of the number of
surface points in that bin, ranging from purple (few points) through green to red (many points).
Black region means there are not surface points. If you are confused, see the fingerprint plot in
Section 4.12.6 for example. The usefulness of fingerprint plot is demonstrated in page 24 and 25
of CrystEngComm, 11, 19 (2009). Although in Multiwfn fingerprint plot can also be drawn in
Becke surface analysis, the plot in this case is not as useful as that in Hirshfeld surface analysis.
The Hirshfeld surface in fact can be viewed as the contact surface between the atoms in the
Hirshfeld fragment you defined and all of the other atoms. The remarkable flexibility of Multiwfn
allows the overall contact surface be decomposed to many local contact surfaces and draw the
corresponding fingerprint plots. For example, in Multiwfn one can draw fingerprint plot for the
local contact surface between the nitrogen in the central urea and the hydrogens in specific
peripheral ureas. In this case, all surface points in the contact surface satisfy two conditions: (1) In
the Hirshfeld fragment (viz. the central urea), the atom closest to the surface point is the nitrogen
(2) Among all of the atoms that do not belong to the Hirshfeld fragment, the atom closest to the
surface point is one of hydrogen in specific peripheral ureas. Undoubtedly, fingerprint plot of local
contact surface greatly facilitates one to study the non-covalent interaction in local region due to
the contact between specific atoms.
Usage
The procedure to perform Becke/Hirshfeld surface analysis is similar to normal quantitative
molecular surface analysis. After you entered main function 12, choose option 1 and select Becke
or Hirshfeld surface, then input the index of the atoms in the fragment (referred to as Hirshfeld
fragment below), and use option 2 to select mapped function. After that choose 0 to start
calculation. Quantitative data on the surface such as average value and standard deviation will be
outputted, and surface extrema will be located. Then via corresponding options you can visualize
3 Functions
115
surface minima/maxima, export result and so on, all of the options in post-process menu (except
one, see below) have already been introduced in Section 3.15.4 and thus are not described again
here. If you use option 6 to export the surface vertices to pdb file, based on which you can also
plot color-mapped Hirshfeld/Becke surface by means of VMD program, the drawing method
should be set to "Points" and coloring method should be set to "Beta" (viz. B-factor in the pdb file,
which records mapped function value).
Becke surface analysis and Hirshfeld surface analysis commonly work equally well.
Current Multiwfn does not support .cif file. So if you would like to use Multiwfn to perform
Hirshfeld/Becke surface analysis to study intermolecular interaction in molecular crystals, you
may need to use some third-part softwares such as Material Studio to open the corresponding .cif
file and then properly dig out a cluster of molecules.
In order to draw fingerprint plot, the mapped function must be set to dnorm, which is default.
Then after the Hirshfeld/Becke surface analysis is finished, in the post-process menu you will see
an option titled "20 Fingerprint plot analysis", after enter it you will see a menu. If you select
option 0, the fingerprint analysis will start. By default the fingerprint analysis is performed for the
overall Hirshfeld surface. If you intend to study fingerprint plot in local contact region, you should
use options 1 and 2 to properly define the "inside atoms" set and "outside atoms" set, only the
contact surface between these two sets will be taken into account in the fingerprint plot analysis.
The "inside atoms" set must be a subset of Hirshfeld fragment, while the atoms in "outside atoms"
set must not belong to the Hirshfeld fragment. In options 1 and 2 you will be asked to input two
filter conditions, their intersection defines the set. Condition 1 corresponds to the atom index
range, the condition 2 corresponds to the type of element. For example, you inputted 1,3-6 and Cl,
then among atoms 1, 3, 4, 5, 6 if there are Cl atoms they will be defined as the set. If you directly
press ENTER button when inputting condition 1, for "inside atoms" set and "outside atoms" set
the condition will be defaulted to all atoms in Hirshfeld fragment and all atoms external to
Hirshfeld fragment, respectively. If directly pressing ENTER for condition 2, the condition will be
defaulted to all elements. For example, when you define "inside atoms" set, if you want to only
select nitrogens in the Hirshfeld fragment, simply press ENTER button for condition 1 and input N
for condition 2. Another example, if you want atoms 1~4, 7, 8 to be presented in the set regardless
of their elements, you should input 1-4,7,8 for condition 1 and then directly press ENTER button
for condition 2
After the fingerprint analysis is carried out, in post-process menu, by option 1~3 you can
draw the fingerprint plot, save the plot, and export the original data of the plot (namely the number
of surface points in each bin) to plain text file. By option 3 and 4 you can adjust color scale and
the range of X/Y axes, respectively. By option 5 you can export the surface points corresponding
to the current fingerprint plot to finger.pdb in current folder. In addition, by option 10 and 11, you
can draw scatter map for the surface points between di and de , and export di and de values of all
surface points to plain text file.
An example of Becke surface analysis is given in Section 4.12.5. An example of Hirshfeld
analysis and drawing fingerprint plot is given in Section 4.12.6.
Information needed: GTFs, atom coordinates. (For local electron affinity, virtual MOs must
3 Functions
116
be presented, hence such as .fch, .molden and .gms should be used)
3.16 Process grid data (13)
If Gaussian-type cube file (.cub) or DMol3 grid file (.grd) was loaded, or grid data has been
generated by main function 5 or other functions, a set of grid data will present in memory (which
will be referred to as "present grid data" below), then this module will be available. If grid data
has not been presented in memory but you choose this main function, you can also directly load
grid data from an external file.
In this module, you can visualize present grid data, extract data in a specified plane, perform
mathmetical algorithm, set value in specified range by corresponding options and so on. These
options will be described below.
3.16.0 Visualize isosurface of present grid data (-2)
Visualize isosurface of present grid data in a GUI window, this is useful to check validity of
the grid data updated by some functions (e.g. function 11)
3.16.1 Output present grid data to Gaussian cube file (0)
If you choose this function, present grid data (may be has updated by using function 11, 13,
14, 15) along with atom information will be outputted to a cube file.
3.16.2 Output all data points with value and coordinate (1)
By this function, all present grid data will be outputted to output.txt in current folder, the first
three columns correspond to X,Y,Z value (in angstrom), the last column is data value.
3.16.3 Output data points in a XY/YZ/XZ plane (2, 3, 4)
By these functions, the grid data in the XY/YZ/XZ plane with specified Z/X/Y value will be
outputted to output.txt in current folder, which is a plain text file, you can load it to visualization
softwares such as sigmaplot and then plot plane graphs. Since grid data is discretely distributed,
the actual outputted plane is the one nearest to your input Z/X/Y value.
Please read program prompts for the meaning of each column in output file.
3.16.4 Output average data of XY/YZ/XZ planes in a range of Z/X/Y
(5,6,7)
By these functions, the average grid data in some XY/YZ/XZ planes whose Z/X/Y coordinate
are in specified range will be outputted to output.txt in current folder. The column 1/2/3/4
correspond to X,Y,Z,value respectively, unit is angstrom.
3 Functions
117
3.16.5 Output data points in a plane defined three atom indices or
three points (8,9)
By these two functions, the data in an arbitrary plane can be outputted to plain text file.
However if the plane you are interested in is XY/YZ/XZ plane, you should use function 2,3,4
instead respectively. You can define the plane by inputting three atom indices or by inputting three
points.
You need to input tolerance distance, the data points whose distance to the plane are short
than this value will be outputted. In general it is recommended to input 0 to use default value.
Then if you want to project the data points to XY plane so that you can load them into some
visualization softwares and then plot them as plane graph, you can input 1 to tell program to do
that. You will find Z values of all points in the output file are zero.
3.16.6 Output data points in specified value range (10)
Like function 2, but only the data points whose value are in specified range will be outputted.
If you input both lower and upper limit of value as k, then the data between k-abs(k)*0.03 and
k+abs(k)*0.03 will be outputted.
3.16.7 Grid data calculation (11)
In this function, you can perform algorithm for present grid data by corresponding options,
then the grid data will be updated, and then you can use such as function -2 to visualize the
updated grid data, use function 0 to output the updated grid data as cube file or extract data in a
plane by function 2~9, etc.
Supported operations are shown below, where A means value of present grid data, B means
value at corresponding point in the cube file that will be loaded. C means the updated value at
corresponding point.
1 Add a constant e.g. A+0.1=C
2 Add a grid file i.e. A+B=C
3 Subtract a constant e.g. A-0.1=C
4 Subtract a grid file i.e. A-B=C
5 Multiplied by a constant e.g. A*0.1=C
6 Multiplied by a grid file i.e. A*B=C
7 Divided by a constant e.g. A/5.2=C
8 Divided by a grid file i.e. A/B=C
9 Exponentiation e.g. A^1.3=C
10 Square sum with a grid file i.e. A^2+B^2=C
11 Square subtract with a grid file i.e. A^2-B^2=C
12 Get average with a grid file i.e. (A+B)/2=C
13 Get absolute value i.e. |A|=C
14 Get exponential value with base 10 i.e. 10^A=C
15 Get logarithm with base 10 i.e. log10(A)=C
16 Get natural exponential value i.e. e^A=C
17 Get natural logarithm i.e. ln(A)=C
3 Functions
118
18 Add a grid file multiplied by a value i.e. A+0.4*B=C
19 The same as 6, but multiplied by a weighting function at the same time. The weighting
function is defined as min(|A|,|B|)/max(|A|,|B|). So, at any point, the more the magnitude of the
data in A deviates from the counterpart in B, the severely the result will be punished.
20 Multiplied by a coordinate variable: This option multiplies all grid data by one of selected
coordinate variables X, Y and Z.
21 Get minimal value with another function i.e. min(A,B)
22 Get min(|A|,|B|)
If the operation you selected involves a constant, you will be prompted to input its value; If
involves another cube or Dmol3 .grd file, you will be prompted to input its filename, of which the
origin point, translation vectors and data points in each dimensions must be identical to the grid
data presented in memory.
3.16.8 Map values of a cube file to specified isosurface of present grid
data (12)
The function is especially useful if you have a electron density cube file and corresponding
ESP cube file, you can obtain ESP values of the points laying on the vdW surface, which may be
defined as the isosurface with electron density isovalue of 0.001. (Note that main function 12 can
realize the same goal, meanwhile the accuracy is higher)
You need to input a isovalue to define the isosurface of present grid data, assume that you
input p, and then input deviation in percentage, referred to as k here, then the data points whose
values are between p+abs(p)*0.01*k and p-abs(p)*0.01*k will be regarded as isosurface points.
Subsequently, you need to input the filename of another cube file (should has identical grid setting
as present grid data), the value in this cube file of those isosurface points will be exported to
output.txt in current folder, along with X/Y/Z coordinates.
3.16.9 Set value of the grid points that far away from / close to some
atoms (13)
By this function, the value of grid points beyond or within scaled vdW region of a molecular
fragment can be set to a specific value. This is very useful for screening uninteresting region when
showing isosurface, namely setting value of this region to a very large value (very positive or very
negative, according to the character of the grid data).
You need to input a scale factor for vdW radius, then input expected value. After that, you
need to specify fragment, you can either directly input atomic indices (e.g. 3,5,1-15,20), or input
filename of a plain text file, in which a molecular fragment is defined as atomic list, below is an
example of the file:
3
1 3 4
where 3 means there are three atoms in this fragment, 1, 3, 4 are corresponding atom indices.
Then all grid points that beyond the region occupied by scaled vdW spheres of the fragment
atoms will be set to specific value.
If the scale factor of vdW sphere is set to a negative value, e.g. -1.3, then all grid points that
3 Functions
119
within the scaled vdW surface of the fragment will be set to the specific value.
An example of using this function is given in Section 4.13.4.1.
3.16.10 Set value of the grid points outside overlap region of two
fragments (14)
This function is similar to function 13, but only the grid points outside superposition region
of scaled vdW regions of two fragments will be set to a specified value. You can either directly
input atomic indices of the two fragments, or prepare two files containing atom lists for the two
fragments, the format is the same as function 13.
This function is very useful if you are only interested in studying isosurfaces between two
fragments, all isosurfaces outside this region can be screened by setting grid data value to very
large. An illustrative example is given in Section 4.13.4.2.
3.16.11 If data value is within certain range, set it to a specified value
(15)
You need to input lower and upper limit value and a expected value, if any value in present
grid data is within the range you inputted, its value will be set to the expected value.
3.16.12 Scale data range (16)
By this function, the value of present grid data can be linearly scaled to certain range. You
need to input original data range, assumed that you inputted 0.5,1.7, and you inputted -10,10 as
new data range, then all the value of present grid data that higher than 1.7 will be set to 1.7, all the
value lower than 0.5 will be set to 0.5. After that, the value between 0.5 and 1.7 will be linearly
scaled to -10,10. It may be more clear if the algorithm is expressed as pseudo-code:
where (value>0.5) value=0.5
where (value<1.7) value=1.7
all value = all value - 0.5
ratiofac = [10 - (-10)] / (1.7 - 0.5) = 20/1.2
all value = all value * ratiofac
all value = all value + (-10)
3.16.13 Show statistic data of the points in specific spatial and value
range (17)
This function can output statistic data of the points in specific spatial and value range. If user
do not want to impose any constraint (namely the statistic data is for all data points), input 1. If
constraint is needed to be imposed, user should input 2, and then input lower and upper limit of
X,Y,Z coordinates and value in turn.
The minimum and maximum value, average, root mean square, standard deviation, volume,
sum, integral and barycenter position of the data points satisfied the constraints will be outputted.
The positive, negative and total barycenter are computed respectively as
3 Functions
120
all
kk
all
kkktot
jj
jjj
ii
iii
ff
ff
ff
)(/)(
)(/)(
)(/)(
rrrR
rrrR
rrrR
where f is the data value, r denotes coordinate vector, the indices i, j and k run over positive,
negative and all grid points respectively.
3.16.14 Calculate and plot integral curve in X/Y/Z direction (18)
Integral curve is defined as below (e.g. in Z direction)
'),,()'( z
zini
dzdydxzyxpzI
Local integral curve may be defined as (e.g. in Z direction)
dydxzyxpzIL),,()(
Evidently
')()'( z
z
L
ini
dzzIzI
In Multiwfn, I and IL curves are evaluated based on cubic numerical integration of grid data.
User first needs to choose which direction will be integrated, and then input the lower and upper
limit of the coordinate in this direction. Then integral curve and local integral curve will be
calculated within this range. After that, by corresponding options, the graph of the curves can be
plotted or saved, the curve data can be exported to current folder as plain text file.
Assume that user has chosen Z direction, and the lower and upper limit were set to -5 and 10,
respectively, then the spatial range of the curve generated by Multiwfn will be z=[-5,10], and the
zini in above formula will be -5. If user input the letter a (denotes "all"), then the minimal and
maximal value of Z coordinate of current grid data will regarded as lower and upper limit,
respectively.
Worthnotingly, if the integrand is chosen as electron density difference, then the integral
curve sometimes is known as "charge displacement curve" and useful in discussion of charge
transfer, see J. Am. Chem. Soc., 130, 1048 for example. If you want to obtain such a curve, before
entering present function, you should calculate grid data of electron density difference, or directly
load the grid data from external file (e.g. cube file). A practical example is given in Section 4.13.6.
Information needed: Grid data, atom coordinates
3 Functions
121
3.17 Adaptive natural density partitioning (AdNDP)
analysis (14)
3.17.1 Theory
Famous NBO analysis developed by Weinhold and coworkers is able to recover up to 3-
centers 2-electrons (3c-2e) orbitals from density matrix (e.g. by using "3cbond" keyword in NBO
program). Adaptive natural density partitioning (AdNDP), which was proposed by Zubarev and
Boldyrev in year 2008 (Phys. Chem. Chem. Phys., 10, 5207), may be viewed as a natural
extension of NBO analysis aiming for locating N>3 centers orbitals. AdNDP has been extensively
used to study electronic structure characteristic of widespread of cluster systems, by googling
"AdNDP" you can find many related literatures.
Canonical molecular orbitals (CMOs) are generally highly delocalized, often lacking of
chemical significances; While 2c or 3c NBOs are substantially localized, for highly conjugated
system resonant description is often needed (otherwise large non-Lewis composition will occur,
that means current system is inappropriate to be portrayed by single set of NBOs), this somewhat
conflicts with modern quantum chemistry concepts and obscures delocalization natural of
electrons in conjugated system. AdNDP orbitals seamlessly bridged CMOs and NBOs, AdNDP
bonding patterns avoid resonant description and are always consistent with the point symmetry of
the molecule.
The basic idea of AdNDP to generate multi-center orbitals is very similar to NBO analysis,
that is constructing proper sub-block of density matrix in natural atomic orbital (NAO) basis and
then diagonalize it, the eigenvalues and eigenvectors correspond to occupation number and orbital
wavefunction respectively. For example, we want to generate all possible 4-centers orbitals for
atom A,B,C,D, we first pick out corresponding sub-blocks and then combine them to together:
DDCDBDAD
DCCCBCAC
DBCBBBAB
DACABAAA
DCBA
PPPP
PPPP
PPPP
PPPP
P
,,,,
,,,,
,,,,
,,,,
),,,(
After diagonalization of P(A,B,C,D), if one or more eigenvalues exceeded the predefined threshold,
which is commonly set to close to 2.0 (e.g. 1.7), then corresponding orbitals will be regarded as
candidate 4c-2e bonds. Completely identical strategy can be used to generate orbitals with higher
number of centers.
Indeed, the orbital generating process of AdNDP is quite easy once atom combination is
determined, however the searching process of final Nc-2e orbitals in entire system is complicated,
manual inspections and operations are necessary. AdNDP approach has large ambiguity, it is
possible that the searching process carried out by different peoples finally results in different
AdNDP pattern, I think this is the most serious limitation of current AdNDP approach. So, AdNDP
is never a black box, before using it users must have preliminary understanding of the searching
process of the AdNDP implemented in Multiwfn.
Before the search, densities from core-type NAOs are automatically eliminated from the
density matrix, since they have no any contribution to bonding. After that, 1-center orbitals (lone
3 Functions
122
pair), 2-centers orbitals, 3-centers orbitals, 4-centers orbitals ... will be searched in turn, until
residual density (trace of density matrix) is close to zero. The search could be exhaustive, that
means when searching N-centers orbitals, Multiwfn will construct and diagonalize M!/(M-N)!/N!
sub-blocks of density matrix, where M is the total number of atoms. All of the orbitals whose
occupation numbers are larger than the threshold will be added to candidate orbital list. For large
system, the searching process may be very time-consuming or even forbidden, for example,
exhaustive search of 10-centers orbitals in the system with 30 atoms needs to construct and
diagonalize 30045015 sub-blocks of density matrix! This is very difficult to be finished in
personal computer, for such case, user-directed searching is necessary. In Multiwfn you can
customly define a search list, then the exhaustive search will only apply to the atoms in the search
list, so that the amount of computation would be greatly reduced. You can also directly let
Multiwfn construct and diagonalize sub-block of density matrix for specified atom combination.
Note that user-directed searching has relatively high requirements of skill and experience on users.
Once the search of N-centers orbitals is finished, we will get a list containing candidate N-
centers orbitals. We need to pick some of them out as final N-centers AdNDP orbitals. Commonly,
one or more orbitals with the highest occupation numbers will be picked out. Notice that, since
some densities are simultaneously shared by multiple candidate orbitals, if we directly pick out
several candidate orbitals with the largest occupation at one time, the electrons may be
overcounted. To avoid this problem, assume that K orbitals with the highest occupation numbers
obviously overlap with some other candidate orbitals meanwhile there is no evident overlapping
between the K orbitals, we should first pick out K orbitals as final AdNDP orbitals, then Multiwfn
will automatically deplete their density from the density matrix and then reconstruct and
diagonalize the corresponding sub-blocks of density matrix for remained candidate orbitals to
update their shapes and occupation numbers. If there are still some candidate orbitals with
occupation numbers close to 2.0, you may consider picking them out, then remained orbitals will
be updated again. Such process may be repeated several times until there is no orbitals have high
occupation numbers. After that, you can start to search N+1 centers orbitals.
The general requirements of AdNDP analysis are that: The final residual density (corresponds
to non-Lewis composition in NBO analysis) should as low as possible; the occupation numbers of
each AdNDP orbital should as close to 2.0 as possible; the number of centers of AdNDP orbitals
should as less as possible; the resulting orbitals must be consistent with molecular symmetry.
However, there is no unique rule on how to search orbitals and pick out candidate orbitals as
AdNDP orbitals. For example, one can first search 5-centers orbitals before completing search of
3-centers orbitals, and one can also directly search 6-centers orbitals after the search of 2-centers
orbitals has finished. The sequence of picking out candidate orbitals is also not necessarily always
in accordance to magnitude of occupation numbers. The final AdNDP pattern obtained by different
operations may be different, how to do AdNDP analysis is largely dependent on users themselves.
Actually some molecules may have two or even more equally reasonable AdNDP patterns,
sometimes it is difficult to discriminate which pattern is the best. I have confidence to say that
some AdNDP patterns presented in publicated papers are not the optimal ones. The experience of
using AdNDP approach can be gradually accumulated in practices and during reading related
literatures.
AdNDP is very insensitive to basis-set quality as NBO analysis, 6-31G* is enough to produce
accurate results for main group elements in the first few rows. Over enhancing basis-set quality
3 Functions
123
will not improve AdNDP analysis results but only lead to increase of the computational burden in
diagonalization step, since the size of sub-block of density matrix is directly determined by size of
basis set.
Multiwfn offers capacity of evaluating AdNDP orbital energies. You need to provide a file
containing Fock (or Kohn-Sham) matrix in original basis functions. The Fock matrix can be
obtained from output of Gaussian or other programs. The energy of AdNDP orbital is
corresponding diagonal term of Fock matrix in AdNDP orbital representation. Specifically,
Multiwfn performs below representation transform:
cXCCFCF AONAOAO
T
AdNDP
where FAO is the Fock matrix in original basis function that loaded from user-provided file, C(r,i)
corresponds to coefficient of basis function r in AdNDP orbital i. c(s,i) corresponds to coefficient
of NAO s in AdNDP orbital i. XAONAO is transformation matrix between original basis function
and NAO, i.e. X(t,s) is coefficient of basis function t in NAO s. Energy of AdNDP orbital j is
simply FAdNDP(j,j), which is expectation value of Fock operator of AdNDP orbital wavefunction.
3.17.2 Input file
The output file of NBO program containing density matrix in NAO basis (DMNAO) can be
used as input file for AdNDP analysis. If you also need to visualize AdNDP orbitals or export
orbitals as cube files, .fch file must be provided, meanwhile transformation matrix between NAO
and original basis functions (AONAO) must be presented in the NBO output file.
Assume that you are a Gaussian user, in order to obtain an Gaussian output file containing all
of the information needed by Multiwfn to do the AdNDP analysis and visualization, you should
write an Gaussian input file for single point task with pop=nboread keyword in route section, and
write $NBO AONAO DMNAO $END after molecular geometry section with a blank line as
separator. Then run the input file by Gaussian and then convert checkpoint file to .fch format by
formchk utility.
The Gaussian output file should be used as the initial input file when Multiwfn boots up.
Once you entered AdNDP module, Multiwfn will load NAO information and DMNAO matrix
from this file. If you choose corresponding options to visualize or export orbitals, AONAO matrix
will be loaded and the program will prompt you to input the path of the .fch file (if .fch is in the
same folder and has identical name as the Gaussian output file, then the .fch will be directly
loaded).
Multiwfn is also compatible with the output files of stand-alone NBO program (GENNBO),
of course you have to add DMNAO keywords in $NBO section in .47 file. In this case it is
impossible to visualize AdNDP orbitals.
Formally, AdNDP approach is also applicable to open-shell systems; of course, the
occupation threshold should be divided by 2. When you enter AdNDP module, Multiwfn will ask
you which density matrix should be used, the so-called total density matrix is the sum of alpha and
beta density matrix.
Notice that if after you entered AdNDP module Multiwfn suddenly crashes, and the basis set
you used contains diffuse functions, you can try to use another basis set without diffuse functions.
This problem is caused by the bug in NBO 3.1 module, namely in rarely cases the DMNAO output
3 Functions
124
may be slightly problematic if diffuse functions present. Since AdNDP analysis is quite insensitive
to diffuse functions, they can be safely removed without any loss of accuracy.
If you want to obtain AdNDP orbital energies, Fock matrix corresponding to present system
at the same calculation level must be provided in lower-triangular sequence in a plain text file,
namely: F(1,1) F(2,1) F(2,2) F(3,1) F(3,2) F(3,3) ... F(nbasis,nbasis), where nbasis is the total
number of basis functions. The format is free. If you are a Gaussian user, you can add archive
file=XXX keyword between $NBO ... $END, then in the resulting XXX.47 file, search $FOCK
and copy all data between $FOCK ... $END to a plain text file, then this file can be directly used
to provide Fock matrix to Multiwfn.
3.17.3 Options
All of the options involved in AdNDP module are introduced below, some options are
invisible in certain cases. If current candidate orbital list is not empty, then all candidate orbitals
will always be printed on screen in front of the menu (except when you select option 5 or 13), the
candidate orbital indices are determined according to occupation numbers. The number of residual
valence electrons of all atoms in the search list is always printed at the upper of the menu, this
value decreases with gradually picking out candidate orbitals as final AdNDP orbitals. If this value
is very low (e.g. lower than 1.4), it is suggested that new Nc-2e AdNDP orbitals will be impossible
to be found between the atoms in the search list.
AdNDP analysis is more complex than other functions in Multiwfn, if you are confused,
please do the exercises in Section 4.14, you will learn the basic steps of AdNDP analysis.
-10 Return to main menu: Once you choose this option, you will return to main menu,
meantime all results of AdNDP analysis will be lost. Hence the status of AdNDP module can be
reseted by choosing this option and then re-entering the module.
-2 Switch if output detail of exhaustive searching process: If this option is switched to
"Yes", then details of exhaustive searching process will be printed during searching
-1 Define exhaustive search list: In this option, one can customly define search list,
exhaustive search (option 2) will only apply to the atoms in the search list. All commands in this
defining interface are self-explained. Notice that default search list includes all atoms of the
molecule.
0 Pick out some candidate orbitals and update occupations of others: Users need to input
two numbers, e.g. i,j, then all candidate orbitals from i to j will be picked out and saved as final
AdNDP orbitals. If user only input one number, e.g. k, then k candidate orbitals with the largest
occupation numbers will be picked out. After that, the eigenvectors (orbital shape) and eigenvalues
(occupation numbers) of remained candidate orbitals will be updated as mentioned earlier.
1 Perform orbitals search for a specific atom combination: Users need to input indices of
some atoms, e.g. 3,4,5,8,9, then sub-block of density matrix for atom 3,4,5,8,9 will be constructed
and diagonalized, all resultant eigenvectors will be added to candidate orbitals list, meantime all
previous candidate orbitals will be removed. There is no limit on the number of inputted atoms.
2 Perform exhaustive search of N-centers orbitals within the search list: N atoms will be
selected out from the search list in an exhaustive manner, assume that the search list contains M
atoms, then totally M!/(M-N)!/N! atom combinations will be formed. For each combination,
corresponding sub-block of density matrix will be constructed and diagonalized, all eigenvectors
3 Functions
125
with eigenvalues larger than user-defined threshold will be add to candidate orbital list. Old
candidate orbital list will be cleaned.
3 Set the number of centers in the next exhaustive search: Namely set the value N in
option 2. Once exhaustive search of N-centers orbitals is finished, N will be automatically
increased by one.
4 Set occupation threshold in the next exhaustive search: Namely set the threshold used in
option 2.
5 Show information of all AdNDP orbitals: Print occupation numbers and involved atoms
of all saved AdNDP orbitals.
6 Delete some AdNDP orbitals: Input two numbers, e.g. i, j, then saved AdNDP orbitals
from i to j will be removed.
7 Visualize AdNDP orbitals and molecular geometry: The path of corresponding .fch file
will be prompted to be inputted, after loading some necessary information from the file, a GUI
window will pop up and molecular geometry will be shown. Isosurfaces of AdNDP orbitals can be
plotted by clicking corresponding numbers in the right-bottom list
8 Visualize candidate orbitals and molecular geometry: Analogous to option 7, but used to
visualize isosurfaces of candidate orbitals. It is useful to visualize the isosurfaces before picking
out some candidate orbitals as final AdNDP orbitals.
9 Export some AdNDP orbitals to Gaussian-type cube files: User need to input two
numbers, e.g. 2,6, then wavefunction value of AdNDP orbitals from 2 to 5 will be respectively
exported to AdNDPorb0002.cub, AdNDPorb0003.cub, AdNDPorb0004.cub and
AdNDPorb0005.cub in current folder, they are Gaussian-type cube files and can be visualized by
many softwares such as VMD. The total number of grid points is controlled by "nprevorbgrid" in
settings.ini. The length left in each direction is controlled by "Aug3D" in settings.ini.
10 Export some candidate orbitals to Gaussian-type cube files: Analogous to option 9, but
used to export cube files for candidate orbitals.
11/12 Save/Load current density matrix and AdNDP orbital list: Option 11 is used to save
current density matrix and AdNDP orbital list in memory temporarily, when density matrix and
AdNDP orbital list is changed, you can choose option 12 to recover previous state.
13 Show residual density distributions on the atoms in the search list: After choosing this
option, population number of each atom in the search list will be calculated according to present
density matrix and then printed out. If some neighboring atoms have large population number, it is
suggested that multi-center orbitals with high occupation number may appear on these atoms;
while the atoms with low population number often can be ignored in the following searching
process. Thus this option is very helpful for setting up user-directed searching.
14 Output all AdNDP orbitals as .molden file: The path of corresponding .fch file will be
prompted to be inputted, after that all saved AdNDP orbitals will be outputted as AdNDP.molden
in current folder (see Section 2.5 for introduction of .molden format). By using this file as input
file, you can conveniently analyze composition of AdNDP orbitals by main function 8. Note that if
there are N basis functions and M AdNDP orbitals have been picked out, then the first M orbitals
in the AdNDP.molden will correspond to the M AdNDP orbitals, while the other N-M orbitals in
this file are meaningless and can be simply ignored.
16 Output energy of picked AdNDP orbital: This function is used to evaluate energy of
AdNDP orbitals that have already been picked out. Multiwfn will prompt you to input the path of
3 Functions
126
the file containing Fock matrix in original basis functions, the elements of the matrix should be
recorded in lower-triangular sequence. Then after a simple transformation, orbital energies are
immediately outputted.
Some examples of AdNDP analysis are given in Section 4.14.
Information needed: NBO output file (with AONAO DMNAO keywords), .fch file (only
needed when visualizing and exporting cube file for AdNDP orbitals, or exporting AdNDP orbitals
as .molden file), plain text file (containing Fock matrix. Only needed if you want to gain orbital
energies)
3.18 Fuzzy atomic space analysis (15)
3.18.0 Basic concepts
Before introducing each individual function, here I first introduce some basic concepts of
fuzzy atomic space.
Atomic space is the local space attributed to specific atom in the whole three-dimension
molecular space. Below we will express atomic space as weighing function w. The methods used
to partition the whole space into atomic spaces can be classified to two categories:
1 Discrete partition methods: The two representative methods are Bader's partition (also
known as AIM partition) and Voronoi partition. They partition molecular space discretely, so any
point can be attributed to only one atom, in other words,
A
A
if0)(
if1)(
rr
rr
A
A
w
w
where ΩA is atomic space of atom A.
2 Fuzzy partition methods: The representative methods include Hirshfeld, Becke,
Hirshfeld-I and ISA. They partition molecular space contiguously, atomic spaces overlap with
each other, any point may simultaneously attributed to many atoms to different extent, and the
weights are normalized to unity. In other words, below two conditions hold for all atoms and any
point
1)(
1)(0
BB
A
w
Aw
r
r
The most significant advantage of fuzzy partition may be that the integration of real space
function in fuzzy atomic space is much easier than in discrete atomic space. By using Becke's
numerical DFT integration scheme (J. Chem. Phys., 88, 2547), high accuracy of integration in
fuzzy atomic space can be achieved for most real space functions at the expense of relatively low
computation effort. In the fuzzy atomic space analysis module of Multiwfn, all integrations are
realized by this scheme. The more integration points are used, the higher integration accuracy can
be reached, one can adjust the number of points by "radpot" and "sphpot" parameter in settings.ini.

3 Functions
127
In fuzzy atomic space analysis module of Multiwfn, one can obtain many properties that
based on fuzzy atomic spaces. Currently, the most widely used definitions of fuzzy atomic spaces,
namely Hirshfeld, Hirshfeld-I and Becke are supported, they are introduced below. One can
choose which fuzzy atomic spaces will be used by option -1.
Hirshfeld atomic space: In Theor. Chim. Acta (Berl.), 44, 129, Hirshfeld defined the atomic
space as
BAB
AA
A
w)(
)(
)( free
free
Hirsh
Rr
Rr
r
where R is coordinate of nucleus, ρfree denotes spherically averaged atomic electron density in
free-state.
In option -1, you will found two options "Hirshfeld" and "Hirshfeld*". The former uses
atomic .wfn files to calculate the weights, they must be provided by yourself or let Multiwfn
automatically invoke Gaussian to generate them, see Secion 3.7.3 for detail. The latter evaluates
the weights directly based on built-in radial atomic densities and thus is more convenient, detail
can be found in Appendix 3. I strongly suggest using "Hirshfeld*" instead of "Hirshfeld".
Hirshfeld-I (HI) atomic space: This is a well-known extension of Hirshfeld method, it was
proposed in J. Chem. Phys., 126, 144111 (2007). Commonly the atomic space defined by HI is
more physically meaningful than that of Hirshfeld, since it can respond actual molecular
environment. Unfortunately, HI is much more expensive than Hirshfeld due to its iterative nature.
Details of Hirshfeld-I and its implementation in Multiwfn have been introduced in Section 3.9.13
and thus will not be repeated here. When you choose HI in option -1, Multiwfn will first perform
regular HI iterations (If you are confused by the operations, please consult the example of
computing HI charges in Section 4.7.4). After HI atomic spaces have converged, you can do
subsequent analyses.
Becke atomic space: First, consider a function p
3
)2/1()2/3()( dddp
which can be iterated many times
...
)]}([{)(
)]([)(
)()(
3
2
1
dpppdf
dppdf
dpdf
Then define a function s
)](1)[2/1()( tfts kk
The plot of sk versus to t is
3 Functions
128
-1.0 -0.8 -0.6 -0.4 -0.2 0.0 0.2 0.4 0.6 0.8 1.0
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
sk(t)
t
k=1
k=2
k=3
k=4
k=5
From above graph it can be seen that sk gradually reduces from 1 to 0 with t varying from -1
to 1. The larger the k is, the sharper the curve becomes. The weighting function of Becke atomic
space is based on simple transformation of sk, for details please consult original paper J. Chem.
Phys., 88, 2547.
BB
A
AP
P
w)(
)(
)(
Becke
r
r
r
BBAABAAB
AB
BA
AB
ABAB
ABAB
B
A
AB
AB
AB
AB
AB
AB
AB
ABABABAB
AB ABkA
rrR
R
rr
aa
aa
R
R
u
u
u
a
asP
RrRrRRr
rrrrr
)(
5.0if5.0
5.0if5.0
1
1
1
))(1()()())(()(
cov
cov
2
2
where R stands for coordinates of nucleus. Rcov denotes covalent radius.
The number of iterations, namely k value, can be set by option -3. The default value (3) is
appropriate for most cases. The definition of the covalent radius used to generate Becke atomic
space can be chosen by option -2. Through corresponding suboptions, one can directly select a set
of built-in radii (CSD radii, modified CSD radii, Pyykkö radii, Suresh radii, Hugo radii), load radii
information from external plain text file (the format required is described in the program prompts),
or modify current radii by manual input.
The origin paper of CSD radii is Dalton Trans., 2008, 2832, these radii were deduced from
statistic of Cambridge Structural Database (CSD) for the elements with atomic numbers up to 96.
Pyykkö radii was defined in Chem. Eur. J., 15, 186, which covers the entire periodic table, Groups
1–18, Z=1–118. Suresh radii was proposed in J. Phys. Chem. A, 105, 5940, which is based on
theoretically calculated geometries of H3C-EHn, the defined radii cover most of main group and
transition elements in periodic table. Hugo radii was proposed in Chem. Phys. Lett., 480, 127,
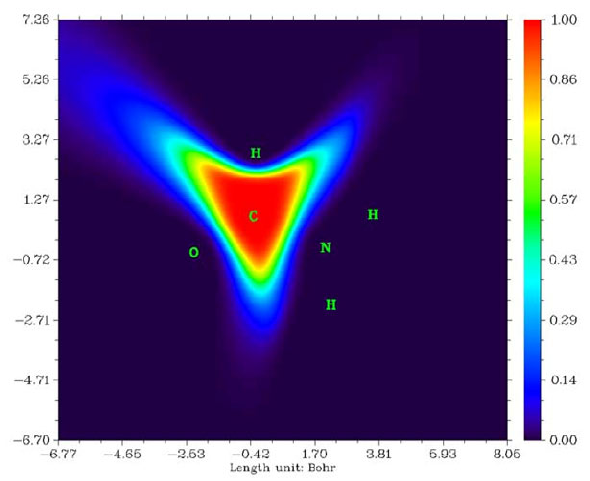
3 Functions
129
which has clear physical meaning and is based on atomic ionization energy. Notice that Hugo radii
for hydrogen is rather large (even larger than Kr by 0.01 Bohr).
I found it is inappropriate to directly use any covalent radii definition shown above to define
Becke's atomic space. The covalent radii of metal elements in IA and IIA groups are always large,
e.g. CSD radius of lithium is 1.28 Angstrom. While covalent radii of elements in such as VIIA
group are always small, e.g. CSD radius of fluorine is only 0.58 Angstrom. For main groups, the
elements with small (large) covalent radius generally have large (small) electronegativity. So, in
molecule environment, the atoms with small (large) covalent radius prefer to withdraw (donate)
electrons to expand (shrink) their effective size, this behavior makes actual radii of main group
elements in each row equalized. In order to faithfully reflect this behavior, I defined the so-called
"modified CSD radii", namely the CSD radii of all main group elements (except for the first row)
are replaced by CSD radii of the IVA group element in corresponding row, while transition
elements still use their original CSD radii. The modified CSD radii are the default radii definition
for Becke's atomic space.
The Becke atomic space of carbon in acetamide constructed by default parameters is
illustrated below
3.18.1 Integration of a real space function in fuzzy atomic spaces (1)
This function is used to integrate real space function P in atomic spaces
rrr dPwI AAA
)()(
For example, if P is chosen as electron density, then IA will be the electron population
number of atom A.
P may be also chosen as the real space functions involving coordinates of two electrons, such
as exchange-correlation density and source function. For this case, the coordinate of reference
point can be set by option -10 (this is equivalent to set "refxyz" in settings.ini). If you have carried
out topology analysis, you can also use -11 to set a critical point as reference point, this is

3 Functions
130
especially convenient for studying source function (for which bond critical point is usually set as
reference point).
The "% of sum" and "% of sum abs" in output is defined as %100
BB
A
I
I and
%100
BB
A
I
I respectively.
By default, all atomic spaces will be integrated. If you only need integral value of certain
atoms, you can use option -5 to define the atom list.
Special note: This option uses single-center integration grid to integrate each atom, commonly this is no
problem. However, if you choose to use Hirshfeld or Hirshfeld-I partition, and the real space function to be
integrated varies very fast around nuclei (e.g. Laplacian of electron density), then this option is unable to give
accurate result. You should use option 101 (invisible in the interface) instead, which employs molecular integration
grid to integrate every Hirshfeld atoms, the result is always very accurate.
3.18.2 Integration of a real space function in overlap spaces (8)
This function is used to integrate specified real space function P in overlap spaces between
atom pairs
rrrr dPwwI ABAAB
)()()(
For example, if P is chosen as electron density, then IAB will be the number of electrons
shared by atom A and B. P may be also chosen as the real space functions involving coordinates of
two electrons.
Integrations of positive and negative parts of P are outputted separately. Meanwhile, sum of
diagonal elements
AAA
I, sum of non-diagonal elements
AABAB
I and sum of all elements
AB AB
I for positve and negative parts are also outputted together.
Currently only the fuzzy atom space defined by Becke can be used together with this function.
3.18.3 Calculate atomic multipole moments (2)
This function is used to evaluate atomic monopole, dipole, quadrupole moments and octopole
moments. All units in the output are in a.u.
In below formulae, superscript A means an atom named A. x, y and z are the components of
electron coordinate r relative to nuclear coordinate R.
A
zz
A
yy
A
xx RrzRryRrx
and 2222 zyxr .
Atomic monopole moment due to electrons is just negative of electron population number

3 Functions
131
AAA dwp rrr )()(
Atomic charges are outputted together, namely AAA Zpq
, where Z denotes nuclear charge.
Atomic dipole moment is useful to measure polarization of electron distribution around the
atom, which is defined as
AA
A
z
A
y
A
x
Adw
z
y
x
rrrμ)()(
Its magnitude, or say its norm is
222 )()()( A
z
A
y
A
x
A
μ
Multiwfn also outputs the contribution of present atom to total molecular dipole moment,
which is evaluated as A
A
qμR.
Cartesian form of atomic quadrupole moment tensor is defined as (see Section 1.8.7 of the
book The Quantum Theory of Atoms in Molecules-From Solid State to DNA and Drug Design).
AA
A
zz
A
zy
A
zx
A
yz
A
yy
A
yx
A
xz
A
xy
A
xx
Adw
rzzyzx
yzryyx
xzxyrx
rrrΘ)()(
333
333
333
)2/1(
22
22
22
The its magnitude can be calculated as
])()()[()3/2( 222 A
zz
A
yy
A
xx
AΘ
Atomic quadrupole moments in Cartesian form can be used to exhibit the deviation of the
distribution from spherical symmetry. For example, 0A
xx ( 0A
xx ) indicates the electron
density of atom A elongated (contracted) along X axis. If the atomic electron density has spherical
symmetry, then zzyyxx . Noticeably, the Cartesian quadruple moment tensor Θ given
here is in traceless form, that means the condition 0 zzyyxx always holds.
The atomic quadrupole and octopole moments in spherical harmonic form are also outputted.
The general expression of multipole moments in spherical harmonic form is
AA
A
ml
A
ml dwRQ rrrr )()()(
,,
All of the five components of quadrupole moment in spherical harmonic form correspond to
3 Functions
132
))(2/3(3
33
)3)(2/1(
22
2,22,2
1,21,2
22
0,2
yxRxyR
xzRyzR
rzR
All of the seven components of octopole moment in spherical harmonic form correspond to
xyxRyyxR
zyxRxyzR
xrzRyrzR
zrzR
)3(8/5)3(8/5
))(2/15(15
)5(8/3)5(8/3
)35)(2/1(
22
3,3
22
3,3
22
2,32,3
22
1,3
22
1,3
22
0,3
The magnitude of multipole moments in spherical harmonic form is calculated as
m
A
ml
A
lQQ 2
,)(
At the end of the output, the total number of electrons, molecular dipole moment and its
magnitude are outputted. Molecular dipole moment is calculated as the sum of the contribution
from atomic dipole moments and atomic charges (i.e. the sum of all "Contribution to molecular
dipole moment" terms)
A
AA
A
q)(
mol μRμ
By default, atomic multipole moment for all atoms are evaluated. If you only need some of
them, you can use option -5 to define the atom list.
3.18.4 Calculate atomic overlap matrix (3)
This function is used to calculate atomic overlap matrix (AOM) for molecular orbitals or
natural orbitals in atomic spaces, the AOM will be outputted to AOM.txt in current folder. The
element of AOM is defined as
Ajiij dAS rrr )()()(
where i and j are orbital indices. Notice that the highest virtual orbitals will not be taken into
account. For example, present system has 10 orbitals in total, 7,8,9,10 are not occupied, and user
has set the occupation number of orbital 3 to zero by option 26 in main function 6, then the
dimension of each AOM outputted by Multiwfn will be (6,6), corresponding to the overlap
integral between the first 6 orbitals in each atomic space.
Since orbitals are orthonormal in whole space, in principle, summing up AOMs for all atoms
(corresponding to integrating in whole space) should yield an identity matrix
ISSUM
)(A
A
Of course, this condition does not strictly hold, because the integration is performed numerically
as mentioned earlier. The deviation of SUM to identity matrix is a good measure of numerical
integration accuracy

3 Functions
133
Atom
ij jiji
N
,,
SUM
ERROR
I
Multiwfn automatically calculates and outputs the ERROR value. If ERROR is not small
enough, e.g. >0.001, you may want to improve the integration accuracy by increasing "radpot" and
"sphpot" in settings.ini.
For unrestricted HF/DFT or unrestricted post-HF wavefunction, AOM for and β orbitals
will be outputted respectively.
3.18.5 Calculate localization and delocalization index (4)
Delocalization index (DI) is a quantitative measure of the number of electron pairs
delocalized (or say shared) between two atomic spaces, while localization index λ (LI)
quantitatively measures how many electron are localized in an atomic space. (Only the expression
for electrons is given below. For β electrons, just replace by β, similarly hereinafter)
2/),(),()(
),(2),(
2121
,
2121
,
AAddA
ddBA
AA
tot
XC
AB
tot
XC
-
rrrr
rrrr
where ГXC is exchange-correlation density, if you are not familiar with it, please consult the
discussion in part 17 of Section 2.6. Using the approximate expression of ГXC, DI and LI can be
explicitly written as
-
iijij
jji
iijij
jji
ASASA
BSASBA
)()()(
)()(2),(
The relationship between LI, DI and the population number of electrons in atomic space is
-
A
AA
tot
XC
AB
NdddBAA
rrrrrr )(),(2/),()( 2121
,
Total DI and LI are the summation of part and β part
)()()(
),(),(),(
AAA
BABABA
---
For close-shell cases, since ),(),( BABA
, one can evaluate total DI as
mn mnmnnm
mmnmn
n
nm BSASBSASBABA )()(2)()(
22
2*2),(2),(
where m and n denote close-shell natural orbitals. Similarly, the total LI for close-shell cases is
mn mnmnnm ASASA )()()(
-
If single-determinant wavefunction, because of integer occupation number of orbitals, LI and
DI can be simplified as
3 Functions
134
occ
m
occ
nmnmn
occ
i
occ
jijij
occ
m
occ
nmnmn
occ
i
occ
jijij
ASASA
ASASA
BSASBA
BSASBA
)()(2)(
)()()(
)()(4),(
)()(2),(
-
-
Conventionally, LI and DI are calculated in AIM atomic space (also called as AIM basin),
while in fuzzy atomic space analysis module of Multiwfn, they are calculated in fuzzy atomic
space, the physical nature is the same.
According to the discussion presented in J. Phys. Chem. A, 109, 9904 (compare Eq.13 and Eq.
18), the DI calculated in fuzzy atomic space is just the so-called fuzzy bond order, which was
defined by Mayer in Chem. Phys. Lett., 383, 368.
For close-shell system, atomic valence can be calculated as the sum of its fuzzy bond orders
AB
BAAV ),()(
In Multiwfn, before calculating LI and DI, AOM is calculated first automatically, this is the
most time-consuming step. For open-shell systems, the LI and DI for and β electrons, as well as
for all electrons are outputted respectively. Notice that the diagonal terms of DI matrix are
calculated as the sum of corresponding off-diagonal row (or column) elements. For close-shell
system, as stated above, they correspond to atomic valence.
For strictly planar molecules, because overlap integral of σ orbital and π orbital is exactly
zero in atomic space, the contributions from σ and π electrons to DI can be exactly decomposed as
DI-σ and DI-π
ij ijijji
ij ijijji
BSASBA
BSASBA
BABABA
)()(2),(
)()(2),(
),(),(),(
Similarly, LI can be decomposed as LI-σ and LI-π. Summing up corresponding off-diagonal
elements in DI-σ and DI-π matrix gives σ-atomic valence and π-atomic valence, respectively. If
you want to compute DI/LI-σ (DI/LI-π), before the DI/LI calculation, you should set the
occupation numbers of all π orbitals (σ orbitals) to zero by subfunction 26 of main function 6.
By the way, in some literatures, especially the ones written by Bernard Silvi, the variance of
electronic fluctuation in atomic space σ2(A) and the covariance of fluctuation of electron pair
between two atomic spaces cov(A,B) are discussed. They are not directly outputted by Multiwfn,

3 Functions
135
because there is a very simple relationship correlates σ2(A), cov(A,B) and DI(A,B), thus you can
calculate them quite easily, see Chem. Rev., 105, 3911 for derivation
2/),(),cov()()(
2
/
),(),cov(
2
ABAB
ABABAANA
B
A
B
A
-
where NA is the electron population number in A. As mentioned above, the diagonal terms of the
DI matrix outputted by Multiwfn are calculated as the sum of off-diagonal elements in the
corresponding row (or column), hence you can simply obtain σ2 by dividing corresponding
diagonal term of DI matrix by two.
A quantity closely related to σ2 is the relative fluctuation parameter introduced by Bader,
which indicates the electronic fluctuations for a given atomic space relative to its electron
population, you can calculate it manually if you want
AF NAA /)()( 2
-
Alternatively, you can calculate below value to measure the proportion of the electrons localized
in the atomic space
A
NAAl /)()(
-
3.18.6 Calculate PDI (5)
Para-delocalization index (PDI) is a quantity used to measure aromaticity of six-membered
rings. PDI was first proposed in Chem. Eur. J., 9, 400, also see Chem. Rev., 105, 3911 for more
discussion. PDI is essentially the averaged para-delocalization index (para-DI) in six-membered
rings.
3
)6,3()5,2()4,1(
PDI
The basic idea behind PDI is that Bader and coworkers reported that DI in benzene is greater
for para-related than for meta-related carbon atoms. Obviously, the larger the PDI, the larger the
delocalization, and the stronger the aromaticity. The main limitation of the definition of PDI is that
it can only be used to study aromaticity of six-membered rings, and it was shown that PDI is
inappropriate for the cases when the ring plane has an out-plane distortion.
In Multiwfn, before calculating PDI, AOM and DI are first calculated automatically. Then
you will be prompted to input the indices of the atoms in the ring that you are interested in, the
input order must be consistent with atom connectivity.
PDI currently is only available for close-shell systems, although theoretically it may be
possible to be extended to open-shell cases.
Note that for completely planar systems, since DI can be decomposed to and π parts, PDI
can also be separated as PDI- and PDI-π to individually study aromaticity and π aromaticity. In
order to calculate PDI- (PDI-π), before enter present module, you should first manually set
occupation number of all MOs except for π () MOs to zero (or you can utilize option 22 in main
function 100 to do this step, which will be much more convenient).

3 Functions
136
3.18.7 Calculate FLU and FLU-π (6,7)
Aromatic fluctuation index (FLU) was proposed in J. Chem. Phys., 122, 014109, also see
Chem. Rev., 105, 3911 for more discussion. Like PDI, FLU is an aromaticity index based on DI,
but can be used to study rings with any number of atoms. The FLU index was constructed by
following the HOMA philosophy (see Section 3.100.13), i.e. measuring divergences (DI
differences for each single pair bonded) from aromatic molecules chosen as a reference. FLU is
defined as below
RING 2
ref
ref
),(
),(),(
)(
)(1
FLU
BA BA
BABA
AV
BV
n
where the summation runs over all adjacent pairs of atoms around the ring, n is equal to the
number of atoms in the ring,
ref is the reference DI value, which is precalculated parameter. is
used to ensure the ratio of atomic valences is greater than one
)()(1
)()(1
AVBV
AVBV
The first factor in the formula of FLU penalizes those with highly localized electrons, while
the second factor measures the relative divergence with respect to a typical aromatic system.
Obviously, lower FLU corresponds to stronger aromaticity.
The dependence on reference value is one of main weakness of FLU. The default ref in
Multiwfn for C-C, C-N, B-N are 1.468, 1.566 and 1.260 respectively, they are obtained from
calculation of benzene, pyridine and borazine respectively under HF/6-31G* (geometry is
optimized at the same level. Becke's atomic space with modified CSD radii and with sharpness
parameter k=3 is used to derive
ref). Users can modify or add ref through option -4.
The original paper of FLU also defined FLU-π, which is based on DI-π and π-atomic valence
RING 2
Avg
Avg
),(
)(
)(
1
FLU
BA
BA
AV
BV
n
where
π is the average value of the DI-π for the bonded atom pairs in the ring, and the other
symbols denote the aforementioned quantities calculated using π-orbitals only. The advantage of
FLU-π over FLU is that FLU-π does not rely on predefined reference DI value, while the
disadvantage is that FLU-π can only be exactly calculated for planar molecules.
Akin to FLU, the lower the FLU-π, the stronger aromatic the ring. If FLU-π is equal to zero,
that means DI-π is completely equalized in the ring. The reasonableness to measure aromaticity by
FLU-π is that aromaticity for most aromatic molecules are almost purely contributed by π
electrons, rather than σ electrons.
In fuzzy atomic space analysis module of Multiwfn, PDI, FLU and FLU-π are calculated in
fuzzy atomic spaces. In J. Phys. Chem. A, 110, 5108, the authors showed that the correlation
between the PDI, FLU and FLU-π calculated in fuzzy atomic space and the ones calculated in
AIM atomic space is excellent.

3 Functions
137
In Multiwfn, before calculating FLU and FLU-π, AOM will be calculated automatically. If
you are calculating FLU-π, you will be prompted to input the indices of π orbitals, you can find
out their indices by checking isosurface of all orbitals by main function 0. Then DI or DI-π matrix
will be generated. Next, you should input the indices of the atoms in the ring, the input order must
be consistent with atom connectivity. Besides FLU or FLU-π value, the contributions from each
bonded atom pair are outputted too.
FLU and FLU-π are only available for close-shell system in Multiwfn. It is not well known
whether FLU and FLU-π are also applicable for open-shell systems.
3.18.8 Calculate condensed linear response kernel (9)
Linear response kernel (LRK) is an important concept defined in DFT framework, which can
be written as
NN
E
)(
)(
)()(
),(
2
1
21
2
21 r
r
rr
rr
This quantity reflects the impact of the perturbation of external potential at r2 on the electron
density at r1, which may also be regarded as the magnitude coupling between electron at r1 and r2.
In Multiwfn, LRK is evaluated by an approximation form based on second-order perturbation
theory (see Eq.3 of Phys. Chem. Chem. Phys., 14, 3960)
occ vir
22
*
11
*
21
)()()()(
4),(
ij ji
ijji
rrrr
rr
where φ is molecular orbital, ε stands for MO energy. Note that this approximation form is only
applicable to HF/DFT close-shell systems, therefore present function only works for HF/DFT
close-shell systems.
Condensed linear response kernel (CLRK) is calculated as
occ vir
2121,
)()(
4),(
ij ji
jiij
AB
BA
BSAS
dd
rrrr
where A and S(A) denote fuzzy atomic space and atomic overlap matrix for atom A, similar for
atom B. In Phys. Chem. Chem. Phys., 15, 2882 (2013), it was shown that CLRK is useful for
investigation of aromaticity and anti-aromaticity.
Present function is used to calculate CLRK between all atom pairs in current system, and the
result will be ouputted as a matrix. Due to evaluation of LRK requires virtual MO information, in
current version .fch/.molden/.gms file must be used as input file.
Note that CLRK can be decomposed to orbital contribution, e.g. for MO i
vir
)( ,
)()(
4
jji
jiij
iBA
BSAS
For instances, assume that you want to evaluate the contribution from MO 3,4,7, then before
calculating CLRK, you should enter main function 6 and use option 26 to set occupation number
of all MOs except for 3,4,7 to zero. (Note that the virtual MOs used to calculate LRK will
automatically still be the original virtual MOs, rather than the ones after modification of MO
occupation numbers.)

3 Functions
138
3.18.9 Calculate para linear response index (10)
The definition of para linear response index (PLR) has an analogy to PDI, the only difference
is that DI is replaced by CLRK
3
),( 6,35,24,1
BAPLR
In Phys. Chem. Chem. Phys., 14, 3960 (2012), the authors argued that PLR is as useful as
PDI in quantitatively measuring aromaticity, and it is found that the linear relationship between
PLR and PDI is as high as R2=0.96.
Present function is used to calculate PLR. Multiwfn will first calculate CLRK, and then you
should input the indices of the atoms consituting the ring in quesiton, e.g. 3,5,6,7,9,2. The input
order must be consistent with atom connectivity. Then PLR will be immediately outputted on
screen. PLR is only applicable to HF/DFT close-shell systems, and currently .fch/.molden/.gms
must be used as input file.
Note that for completely planar systems, PLR can be exactly separated as PLR- and PLR-π
to individually study aromaticity and π aromaticity. In order to calculate PLR- (PLR-π), before
enter present module, you should first manually set occupation number of all MOs except for π ()
MOs to zero (or you can utilize option 22 in main function 100 to do this step, which will be much
more convenient).
3.18.10 Calculate multi-center delocalization index (11)
n-center multi-center DI is calculated as
ijk q qikljkij
nHSCSBSASHCBA )()()()(2)...,,( 1
where i, j, k... only cycle occupied orbitals. The normalized form of multi-center DI is defined as
1/n, and may be compared between rings with different number of members.
Currently this function is only available for single-determinant close-shell wavefunctions,
and supports up to 10 centers. Note that for relatively large size of systems, calculating multi-
center DI for more than 6 centers may be quite time-consuming.
Information needed: GTFs, atom coordinates, basis functions (only for calculating condensed
linear response kernel and PLR)
3.19 Charge decomposition analysis and plotting orbital
interaction diagram (16)
3.19.1 Theory
The charge decomposition analysis (CDA) proposed by Dapprich and Frenking (J. Phys.
Chem., 99, 9352) is used to provide deep insight on how charges are transferred between
fragments in a complex to achieve charge equilibrium. The idea of CDA is based on fragment
3 Functions
139
orbital (FO), which denotes the molecular orbital (MO) of fragment in its isolated state. Besides,
once the compositions of FOs in MOs of complex are obtained, the orbital interaction diagram can
be directly plotted, which allows one visually and directly understand how orbitals of fragments
are mixed to form orbitals of complex.
For simplicity, in this section we assume that the complex consists of only two fragments.
However, the CDA can be straightforwardly used for more than two fragments cases.
Fragment orbital
Consider we are studying a complex AB, NA basis functions are located in the atoms of
fragment A, NB basis functions in fragment B, then each MO of complex will be linearly
expanded by NA+NB basis functions, and meanwhile, the complex has NA+NB MOs. By using the
same basis-set, and maintaining the same geometry as in complex, if we calculate the two
fragments respectively, we can obtain NA MOs of fragment A, and NB MOs of fragment B, they
are collectively called as fragment orbital (FO). We can take these FOs as basis functions to
linearly expand the MOs of complex. Since the dimension (the number of basis functions) is still
NA+NB, the expansion is exact. In other words, we equivalently transformed the basis.
Charge decomposition analysis
In the original paper of CDA, the authors defined three terms:
occ occ
,,,
vir occ
,,,
occ vir
,,,
AmBnnminimii
AmBnnminimii
AmBnnminimii
SCCr
SCCb
SCCd
where i and η are index and occupation number of MO of complex, respectively.
rrr dS nmnm )()(
,
is overlap integral between FO m and FO n. Note that though the NA
and NB FOs are respectively orthonormalization sets, the NA set are in common not normal to the
NB set, so S is not an identity matrix. Cm,i denotes the coefficient of FO m in MO i of complex.
The superscript "vir" and "occ" mean virtual (viz. unoccupied) and occupied, respectively.
The term di denotes the amount of electron donated from fragment A to B via MO i of
complex; similarly, the term bi denotes the electron back donated from B to A. In fact,
nminimi SCC ,,,
can be regarded as the half of overlap population between FO m and n in MO i.
Hence, the difference between term d and b is that which fragment provides its electrons from its
occupied FOs to virtual FOs of another fragment. The term r reveals close-shell interaction
between two occupied FOs in different fragments; positive value of ri means that owing to MO i,
the electrons of the two fragments are accumulated in their overlap region and shows bonding
character, while negative value indicates that the electrons are depleted from the overlap region
and thus reflecting electron repulsive effect. The sum of all ri terms is in general negative, because
overall interaction between filled orbitals are generally repulsive. r is also known as "repulsive
polarization" term

3 Functions
140
Beware that although the CDA formulae given in original paper are correct, by carefully
inspecting the data, I found the d, b and r terms in the examples presented in the original paper are
erroneous (the data should be divided by two).
Generalizing CDA
The original definition of CDA has two drawbacks. First, it is only applicable to close-shell
cases (namely, complex and each fragment must be close-shell) and hence unable to be used when
the two fragments are bound by covalent bonding. Second, in post-HF calculations, though the
MOs of complex can be replaced by natural orbitals (NOs), the FOs can only be produced by HF
or DFT calculation, because occupation numbers of FOs are not explicitly considered in the
original CDA formulae.
To address the limitations of the original definition, in J. Adv. Phys. Chem., 4, 111-124 (2015)
(http://dx.doi.org/10.12677/JAPC.2015.44013) I proposed a generalized form of CDA, which is
the form used in CDA module of Multiwfn:
AmBnnminimi
nm
i
AmBnnminim
nm
ii
SCCr
SCCt
,,,
ref
FOFO
,,,
ref
FOFO
),min(
2
In the generalized CDA, orbitals of complex and fragments can be produced either by HF/DFT or
by post-HF method, corresponding to MOs and NOs, respectively. FO
m
stands for occupation
number of FO m. For open-shell cases, ηref is 1.0, CDA will be performed for alpha spin and beta
spin separately; for the former, i denotes alpha orbital of complex, m and n run over all alpha FOs;
for the latter, i denotes beta orbital of complex, m and n run over all beta FOs. For close-shell
cases, ηref is 2.0, m and n run over space orbitals. min() is the function used to extract minimum
from two values. During calculation of t, if the values are only accumulated for the cases
FOFO nm
, then the resulting t is d; if only for the cases FOFO nm
, then t will be b.
For the situations when the original CDA is applicable, the b and d calculated by the
generalized form are exactly identical to the ones obtained via original definition; while r will be
exactly twice of the one produced via original definition. The reason why the factor 2 is
introduced into the generalized form of r is because after doing so, r has more clear physical
meaning, namely it equals to overlap population (also known as Mulliken bond order) between the
occupied FOs in the two fragments.
Because the CDA has been generalized, below, FO will stand for MO or NO of fragment,
"complex orbital" will denote MO or NO of complex. The orbitals can either be spin-space orbital
(for open-shell) or space orbital (for close-shell).
It is clear that the d, b and r terms can be decomposed into FO pair contributions, this kind of
decomposition is supported by Multiwfn and greatly faciliates analysis of the nature of FO
interaction.
Composition of FO in complex orbital and orbital interaction diagram
By using the methods discussed in Section 3.10, the composition of FO in complex orbital
3 Functions
141
can be calculated. In common, Mulliken method is the best choice for this purpose, the
composition of FO m in complex orbital i is calculated as
%100
,,,
2,,
mn nminimimim SCCC
Although using SCPA method to calculate composition is more convenient (since overlap matrix
is not involved), if i is a high-lying virtual orbital, the calculated composition is not very
reasonable. Note that due to a well-known drawback of Mulliken method, sometimes negative
contributions occur, since the values are often not large, you can simply ignored them.
From Θ, we can clearly understand how each complex orbital is formed by mixing FOs of the
two fragments. Furthermore, one can plot orbital interaction diagram to visually and intuitively
study the relationship between complex orbitals and FOs, namely plot a bar for each complex
orbital and FO according to its energy, and then check each Θ to determine how to link the bars,
e.g. if the value of Θm,i is larger than 5%, then the two bars corresponding to FO m and complex
orbital i will be linked. Consequently, from the graph we will directly know that FO m has
important contribution to complex orbital i.
Extended charge decomposition analysis
The difference between the total number of donation and back donation electrons, that is d - b,
may be regarded as the net transferred electrons. However, in J. Am. Chem. Soc., 128, 278, the
authors argued that this viewpoint is not correct, because b and d terms not only represent charge
transfer effect (CT), but also electron polarization effect (PL); the latter describes the adjustment
of electron distribution within the fragment, which is caused by mixing virtual and occupied FOs
of the same fragment during formation of the complex, and should be excluded in the calculation
of the amount of net transferred electrons. In this paper they proposed extended charge
decomposition analysis (ECDA) method, by which they argued that the number of net transferred
electrons can be calculated more reasonably.
In ECDA viewpoint, four terms can be defined as follows
1. PL(A) + CT(A→B) = The sum of compositions of occupied FOs of fragment A in all
virtual orbitals of complex, multiplied by Occ
2. PL(A) + CT(B→A) = The sum of compositions of virtual FOs of fragment A in all
occupied orbitals of complex, multiplied by Occ
3. PL(B) + CT(B→A) = The sum of compositions of occupied FOs of fragment B in all
virtual orbitals of complex, multiplied by Occ
4. PL(B) + CT(A→B) = The sum of compositions of virtual FOs of fragment B in all
occupied orbitals of complex, multiplied by Occ
where Occ is 1.0 and 2.0 for open-shell and close-shell cases, respectively.
After the four terms are calculated, the number of net transferred electrons from A to B can
be directly obtained as
CT(A→B) - CT(B→A) = [ PL(A) + CT(A→B) ] - [ PL(A) + CT(B→A) ]
The composition of complex orbitals can be calculated by various methods, leading to
different ECDA result. The method used in Multiwfn is identical to the one in ECDA original
paper, namely Mulliken method.
Note that ECDA can neither be applied to post-HF calculation nor the system consisting more
3 Functions
142
than two fragments.
According to the name, ECDA is as if an extension of CDA, however in my personal opinion,
ECDA is irrelevant to CDA, their basic ideas are quite different, and thus the amount of net
transferred electron calculated by ECDA is not comparable with the d - b produced by CDA at all.
In addition, though ECDA is realized in Multiwfn, I do not think this is a useful method. The most
remarkable feature of CDA is that the electron transfer can be decomposed to contribution of
complex orbitals, however ECDA is incapable to do this; ECDA can only reveal how many
electrons is transferred between two fragments, but this quantity actually can be obtained by a
more straightforward approach, namely calculating the fragment charge by summing up all atomic
charges in the fragment, and then subtracting it by the net charge of the fragment in its isolated
state.
3.19.2 Input file
There are several points you should note:
In Multiwfn, infinite number of fragments can defined; however, if more than two fragments
are defined, ECDA analysis will be unavailable.
If the complex or any one fragment is an open-shell system, then CDA will be performed
separately for alpha and beta electrons.
If in the calculation of the complex or any one fragment post-HF method is employed to
produce natural orbitals, then ECDA analysis cannot be performed, and orbital interaction diagram
cannot be drawn (since orbital energy of natural orbitals is not well-undefined).
For Gaussian users
Below files are required as input files of CDA module:
(1) Gaussian output file of single point task of complex. The keywords nosymm pop=full
IOp(3/33=1) must be specified in route section; in which 3/33=1 makes Gaussian output overlap
matrix between basis functions.
(2) Gaussian output file of single point task of each fragment. The keywords nosymm
pop=full must be specified in route section.
Notice that the atomic coordinates in fragment calculations must be exactly in accordance
with that in complex calculation, therefore do not optimize geometry for each fragment, you only
need to directly extract fragment coordinates from the optimized complex coordinate. The atomic
sequence in fragments and complex must be identical, that means the atomic sequence in the
complex can be retrieved by successively combining the atoms in fragment 1, 2, 3 ... n. Molecular
geometry must be given in Cartesian coordinate. The basis-set used in the complex and fragment
calculations must be completely the same. Notice that if you intent to use mixed basis-set, and in
particular when Pople type basis-set is involved (such as 6-31G*), you'd better specify "5d 7f"
keywords in the fragment calculations to force Gaussian to use spherical-harmonic type basis
functions.
By default Gaussian automatically eliminates linearly dependant basis functions, hence in
some cases the number of basis functions will not be equal to the number of orbitals and thus CDA
cannot be performed, in this case IOp(3/32=2) should be specified, which avoids Gaussian
eliminating linearly dependant basis functions. The common reason of this problem comes from
the use of diffuse basis functions. According to my experiences, when diffusion basis functions are
presented, the CDA results are often unreasonable or even completely meaningless. So, DO NOT
3 Functions
143
use diffuse functions in CDA analysis!
The theoretical method used in the calculations can be HF/DFT or post-HF. Closed-shell and
unrestricted open-shell wavefunctions are supported (In fact ROHF/ROKS is also supported and
closed-shell form of CDA will be employed, however the result is often not very useful). For post-
HF calculation, in order to output coefficient and occupation number for natural orbitals, do not
use "pop=full" but use "density pop=NO" and "density pop=NOAB" for close-shell and open-shell
cases, respectively.
It is also completely OK to use the corresponding .fch as input file of CDA module instead of
Gaussian output file for HF/DFT, and in this case IOp(3/33=1) and pop=full are not needed.
However for post-HF case, you need to follow the steps given in the beginning of Chapter 4 to
save natural orbitals into .fch file, this is somewhat cumbersome and not as straightforward as
using Gaussian output file.
For other ab-initio program users
You can also use CDA module as long as your favourite ab-initio program is able to produce
Molden input file (.molden), such as ORCA and Molpro. Note that not the .molden outputted by
all of quantum chemistry codes can be properly recognized by Multiwfn, see part 4 of Section 2.3
for explanation. In addition, .gms file (GAMESS-US output file) may also be used as input file.
Similar to the case of Gaussian, you need to use your ab-initio program generate .molden
or .gms file for complex and all fragments. All of the points mentioned above must be fulfilled,
namely the avoidance of elimination of linearly dependant basis functions, the consistency of the
atomic coordinates and the correspondence of atomic sequence in complex and fragments .molden
files. An example is given in "examples\CDA\COBH3_ORCA" folder, the .molden files were
generated by ORCA 3.0.1.
3.19.3 Usage
After booting up Multiwfn, first you should input the path of the file (i.e. Gaussian output file
or .fch or .molden or .gms) for complex, and then enter the CDA module. Next, you should set the
number of fragments, and then input the path of the file for each fragment in turn, the orbital
information recorded in which will be loaded into memory.
For the open-shell fragments, you will be prompted to select if flip its spin. If select "y", then
orbital information of its alpha and beta orbitals will be exchanged. The reason for introduction of
this step is obvious, for example, we want to use CDA to decompose electron transfer between
fragment CH3 and NH2 in CH3NH2; CH3NH2 has 9 alpha and 9 beta electrons, while in the
calculations of quantum chemistry codes, both CH3 and NH2 will be regarded as having 5 alpha
and 4 beta electrons. In order to carry out CDA, we have to flip electron spin of either CH3 or NH2,
otherwise the total numbers of alpha and beta electrons in the two fragments, namely 5+5 and 4+4
respectively, will be unequal to the ones of complex, namely 9 and 9, respectively.
After the loading is finished, Multiwfn will calculate some data. If only two fragments are
defined, CDA and ECDA result will be directly shown. Then you will see a menu:
-2 Switch output destination (for options 0 and 1): By default the options 0 and 1 output
results on screen; if you select this option once, then their results will be outputted to CDA.txt in
current folder.
0 Print CDA result and ECDA result: Input the index of two fragments, then the CDA and
ECDA analysis result between them will be outputted.
3 Functions
144
1 Print full CDA result: If you select this option, the CDA result for all complex orbitals
will be outputted. By default, Multiwfn does not output CDA result for the complex orbitals lying
higher than LUMO+5, because the number of such orbitals is too large, whereas their
contributions to d, b and r terms are often completely negligible due to their occupation numbers
are often quite small. (For HF/DFT wavefunctions, the occupation numbers of the orbitals lying
higher than HOMO are exactly zero, and thus have no contribution to d, b and r terms at all. So for
this case this option is meaningless)
2 Show fragment orbital contributions to specific complex orbital: If you input x, then the
composition of complex orbital x will be outputted (for open-shell cases, the xth alpha and the xth
beta complex orbital will be outputted respectively). By default only the FOs having contribution
1% will be shown, but this threshold can be altered by "compthresCDA" parameter in settings.ini.
If you want to obtain composition of a fragment orbital in all complex orbitals, you can input
for example 1,6, which means orbital 6 of fragment 1 is selected.
3 Export coefficient matrix of complex orbitals in fragment orbital basis: The coefficient
matrix corresponding to all FOs in all complex orbitals will be outputted to "coFO.txt" in current
folder.
4 Export overlap matrix between fragment orbitals: The overlap matrix between all FOs
will be outputted to "ovlpint.txt" in current folder.
6 Decompose complex orbital contribution to CDA: You need to input index of a complex
orbital and set threshold for printing, if contribution of a pair of fragmental orbitals to any of d, b
and r term of this complex orbital is larger than the threshold then the contribution value will be
shown. This greatly faciliates analysis of interaction between fragment orbitals.
5 Plot orbital interaction diagram: This option is only available for HF/DFT wavefunctions.
If you select this option, you will enter a new menu, in which by corresponding options you can
plot and save orbital interaction diagram and adjust plotting parameters, such as size of labels,
energy range (namely Y-axis range) and the criterion for linking bars. The orbital interaction
diagram plotted under default settings looks like this:
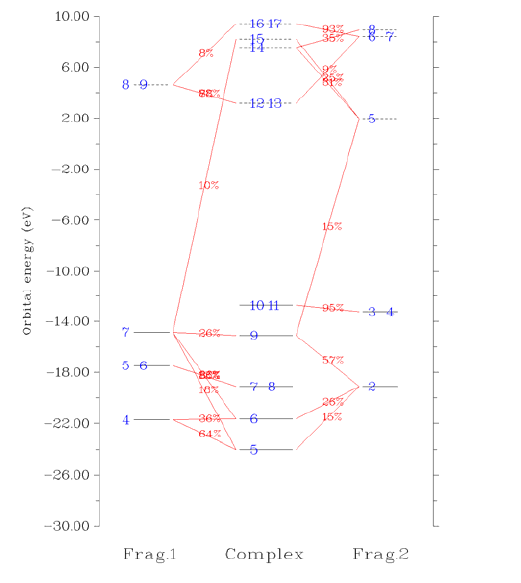
3 Functions
145
In above graph, occupied and virtual orbitals are represented as solid and dashed bars,
respectively, the vertical positions are determined by their energies. The bars at left and right sides
correspond to the FOs of the two fragments you selected; the bars in the middle correspond to
complex orbitals. Orbital indices are labelled by blue texts. If two or more labels occur in the same
bar, that means these orbitals are degenerate in energy. If composition of a FO in a complex orbital
is larger than specific criterion, then the corresponding two bars will be connected by red line, so
that simply by viewing the diagram one can directly understand the complex orbitals are
constructed by mainly mixing which FOs. The compositions are labelled in the center of the lines.
By default, all FOs and complex MOs are plotted, and if the contribution of a FO of fragment
A or B to a complex MO is larger than 10% then they will be connected. For large systems,
usually there are too many bars and linking lines in the diagram, and it is hence difficult to identify
the orbital interaction mode based on the diagram. In these cases, you should properly use the
option "4 Set the rule for connecting and drawing orbital bars" to manually set up the rule for
connecting and plotting the orbital bars. See the prompt shown on the screen on how to use this
option.
Sometimes the difference between orbital energies of the two fragments in the orbital
interaction diagram is too large and thus hinders one to analyze the diagram, so you may want to
equalize their energies. In this case, you can use the option "12 Set orbital energy shifting value"
to set the value used to shifting orbital energies of the complex or the two fragments presented at
the left and right side of the diagram; their orbital energies will be agumented by the given value.
Some examples of CDA are given in Section 4.16.
Information needed: Gaussian output files of complex and fragments
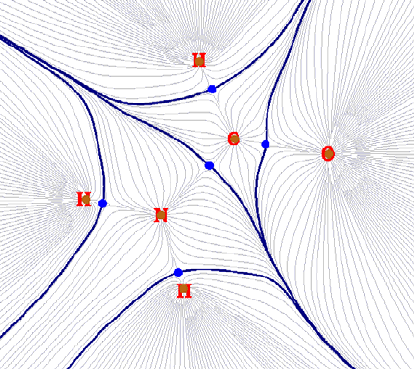
3 Functions
146
3.20 Basin analysis (17)
3.20.1 Theory
The concept of basin was first introduced by Bader in his atom in molecular (AIM) theory,
after that, this concept was transplant to the analysis of ELF by Savin and Silvi. In fact, basin can
be defined for any real space function, such as molecular orbital, electron density difference,
electrostatic potential and even Fukui function.
A real space function in general has one or more maxima, which are referred to as attractors
or (3,-3) critical points. Each basin is a subspace of the whole space, and uniquely contains an
attractor. The basins are separated with each other by interbasin surfaces, which are essentially the
zero-flux surface of the real space functions; mathmatically, such surfaces consist of all of the
points r satisfying 0)()( rnrf, where n(r) stands for the unit normal vector of the surface
at position r.
Below figure illustrates the basins of total electron density of NH2COH, such figure is often
involved in AIM analysis. Brown points are attractors; in this case they correspond to maxima of
total electron density and thus are very close to nuclei. Blue bolded lines correspond to interbasin
surfaces, they dissect the whole molecular space into basins, which in present case are also known
as AIM atomic space or AIM basin. Grey lines are gradient paths of total electron density, they are
emanated from attractors.
Multiwfn is able to generate basins for any supported real space functions, such as electron
density, ELF, LOL, electrostatic potential. Alternatively, one can let Multiwfn load the grid file
generated by third-part programs (e.g. cube file or .grd file) and then generate basins for the real
space function recorded in the grid data.
After the basins were generated, some analyses based on the basins can be conducted to
extract information of chemical interest. The three most useful types of basin analyses are
supported by Multiwfn and are briefed below. All of them require performing integration in the
basin.
(1) Study integral of a real space function in the basins. For example, one can first use
electron density to define the basins, and then integrate electron density in the basins to acquire
3 Functions
147
electron population numbers in the basins; this quantity is known as AIM atomic population
number. Another example, one can first partition the space into basins according to ELF function,
and then calculate integral of spin density in the basins.
(2) Study electric multipole moments in the basins. In Multiwfn electric monopole, dipole
and quadrupole moments can be calculated in the basins. This is very useful to gain a deep and
quantitative insight on how the electrons are distributed in different regions of a system. Based on
these data, one can clearly understand such as how lone pair electrons contribute to molecular
dipole moment (see J. Comput. Chem., 29, 1440 for example, in which ELF basins are used), how
the electron density around an atom is polarized as another molecule approaching.
(3) Study localization index and delocalization index in the basins. The former one measures
how many electrons are localized in a basin in average, while the latter one is a quantitative
measure of the number of electrons delocalized (or say shared) between two basins. They have
been very detailedly introduced in Section 3.18.5 and hence will not be reintroduced here. The
only difference relative to Section 3.18.5 is that the range of integration in our current
consideration is basins rather than fuzzy atom spaces.
3.20.2 Numerical aspects
This section I will talk about many numerical aspects involved in basin analysis, so that you
can understand how the basin analysis module of Multiwfn works.
Algorithms for generating basins
The algorithms used to generate/integrate basins can be classified into three categories:
(1) Analytical methods. Due to the popularity and importance of AIM theory, and the
complex shape of AIM basins, since long time ago numerous methods have been proposed to
attempt to speed up integration efficiency and increase integration accuracy for AIM basins, e.g. J.
Comput. Chem., 21, 1040 and J. Phys. Chem. A, 115, 13169. All of these methods are analytical,
and they are employed by almost all old or classical AIM programs, such as AIMPAC, AIM2000,
Morphy and AIMAll. This class of methods suffers many serious disadvantages: 1. The algorithm
is very complicated 2. High computational cost 3. Only applicable to the analysis of total electron
density 4. Before generating basins, (3,-3) and (3,-1) critical points must be first located in some
ways. The only advantage of these methods is that the integration accuracy is very satisfactory.
(2) Grid-based methods. This class of methods relies on cubic (or rectangle) grid data. Since
the publication of TopMoD program, which aims to analyze ELF basin and for the first time uses a
grid-based methods, grid-based methods continue to be proposed and incurred more and more
attention. Grid-based methods solved all of the drawbacks in analytical methods; they are easy to
be coded, the computational cost is relative low, and more important, they are suitable for any type
of real space function. Unfortunately these methods are not free of shortcomings, the central one is
that the integration accuracy is highly dependent on the quality of grid data; to obtain a high
accuracy of integral value the grid spacing must be small enough.
(3) Mixed analytical and grid-based method. The only instance in this class of method is
described in J. Comp. Chem., 30, 1082, in which Becke's multicenter integration scheme is used to
integrate basins. This method is faster than analytical method, and more accurate than grid-based
method, but it is only suitable to analyze total electron density, thus the application range is
seriously limited. Since the basin analysis module of Multiwfn focuses on universality, this
3 Functions
148
method is not currently implemented.
Currently the best grid-based method is near-grid method (J. Phys.: Condens. Matter, 21,
084204), which is employed in Multiwfn as default method to generate basins. Multiwfn also
supports on-grid method (Comput .Mat. Sci., 36, 354), which is the predecessor of near-grid
method.
Basic steps of generating basins and locating attractors in Multiwfn
In Multiwfn, generating basin and locating attractor are carried out simultaneously; the basic
process can be summarized as follows: Given a grid data, all grids (except for the grids at box
boundary) are cycled in turn. From each grid, a trajectory is evolved continuously in the direction
of maximal gradient. Each step of movement is restricted to its neighbour grid, and the gradient in
each grid is evaluated via one direction finite difference by using the function values of it and its
neighbour grids. There are four circumstances to terminate the evolvement of present trajectory
and then cycle the next grid (a) The trajectory reached a grid, in which the gradients in all
directions is equal or less than zero; such a grid will be regarded as an attractor, meanwhile all
grids contained in the trajectory will be assigned to this attractor. (b) The trajectory reached a grid
that has already been assigned; all of the grids contained in the trajectory will be assigned to the
same attractor. This treatment greatly reduced computational expense. (c) The upper limit of step
number is reached (d) The trajectory reached the grids at box boundary; all of the grids in the
trajectory will be marked as "travelled to boundary" status.
After all grids have been cycled, we obtained position of all attractors covered by the spatial
scope of the grid data. Each set of grids that assigned to a same attractor collectively constitutes
the basin corresponding to the attractor. Interbasin grids will then be detected, according to the
criterion that if any neighbour grid belongs to different attractor. Note that sometimes after
finished above processes, some grids may remain unassigned, and some grids may have the status
"travelled to boundary". Such grids are often far away from atoms and thus unimportant, in
general you can safely ignore them.
The only difference between on-grid method and near-grid method is that in the latter one,
the so-called "correction step" is introduced to continuously calibrate the evolvement direction of
the trajectory, which greatly eliminates the artificiality problem of interbasin surfaces due to on-
grid method, and in turn makes the basin integration more close to actual values. Near-grid
method can be supplemented by a refinement step for interbasin surfaces at the final stage, so that
the partition of basin can be even more accurate, this additional step is not very time-consuming.
For ELF (and may be other real space functions), if sphere- or ring-shape attractors exist in
the system, in corresponding regions a large number of attractors having basically the same value
will be found. Below two examples illustrated the existence of the ring-shape ELF attractor
encircling N-C bond of HCN and the sphere-shape ELF attractor encompassing the Ar atom.
Based on nearest neighbour algorithm, Multiwfn automatically checks the distances and the
relative value differences between all pairs of located attractors, and then clusters some attractors

3 Functions
149
together. The resulting attractors thus have multiple member attractors, and will be referred to as
"degenerate attractors" later. For example, the left graph and right graph given below displayed the
attractor indices before and after clustering, respectively. As you can see, after clustering, all of the
attractors constituting the ring-shape ELF attractor now have the same index, suggesting that the
corresponding basins have been merged together as basin #2.
For certain cases, in the regions far beyond the systems, some artifical or physically
meaningless attractors are located. These attractors have very low function value and thus are
called as "insignificant" attractors; in constrast, other attractors can be called as "significant"
attractors. The presence of insignificant attractors is because in corresponding regions the function
values are rather small, hence the function behavior is not very definitive, even a very slight
fluctuation of function value or trivial numerical perturbation is enough to result in new attractors.
When insignificant attractors are detected, Multiwfn will prompt you to select how to deal with
them, there are three options: (1) Do nothing, namely do not remove these attractors (2) Remove
these attractors meanwhile set corresponding grids as unassigned grids (3) Remove these attractors
meanwhile assign corresponding grids to the nearest significant attractors. The third option is
generally recommended.
If the real space function simultaneously possesses positive and negative parts, e.g.
electrostatic potential, Multiwfn will automatically invert the sign of negative part of the grid data
and then locate attractors and generate basins as usual, after that the sign will be retrieved.
Therefore, for negative parts, the "attractors" located by Multiwfn actually are "repulsors".
Integration of basins
Once the basins have been generated by grid-based method, the integral of a real space
function f in a basin P can be readily evaluated as
Pi idVfF )(r, where i is grid index, dV
is volume differential element. Evidently, the finer the grid data (smaller grid spacing) is used, the
more accurate the integral values will be, and correspondingly, the more computational effort must
be paid.
Since the arrangement of grids in general is not in coincident with system symmetry, one
should not expect that the integral values always satisfy system symmetry well, unless very fine
grid is used.
Note that different functions have different requirement on the quality of grid data. For the
same grid spacing, the faster the function varies, the lower the integration accuracy will be. Due to
Laplacian of electron density, source function and kinetic density function etc. fluctuate violently
near nuclei, it is impossible to directly integrate these functions in AIM basins solely by grid-
based method at satisfactory accuracy (since only uniform grids are used, which is incapable to
represent nuclear region well enough). In order to tackle this difficulty, an integration method
based on mixed atomic-center and uniform grids is supported by Multiwfn, in which the regions
3 Functions
150
close to nuclei are integrated by atomic-center grids, while the other regions are integrated by
uniform grids. This method is able to integrate AIM basin for any real space function, including
the ones having complicated behavior at generally acceptable accuracy without evident additional
computational cost with respect to grid-based method. In order to further improve the integration
accuracy for AIM basins, Multiwfn also enables one to exactly refine the assignment of the grids
at basin boundary. An exact steepest ascent trajectory is emitted from each boundary grid, and
terminates when reaches an attractor. Since there are often very large number of boundary grids
and each steepest ascent step requires evaluating gradient of electron density once, this process is
time-consuming. In Multiwfn these gradients can also be approximately evaluated by trilinear
interpolation based on pre-calculated grid data of gradient, 1/3~1/2 of overall time cost of the AIM
basin integration can be saved. Note that if the mixed type of atomic-center and uniform grids is
employed, and especially when the exact refinement process of boundary basin is enabled at the
same time, then the requirement on quality grid will be markedly lowered, usually accurate result
can be obtained at "Medium-quality grid" level (grid spacing=0.1 Bohr).
It is worth noting that even though basin analysis module of Multiwfn can be used to acquire
position of attractors, the accuracy is directly limited by the quality of grid data, since the
attractors will be located on a grid point. Moreover, this module is unable to be used to search
other types of critical points (attractor corresponds to (3,-3) type critical point); So if you want to
obtain accurate coordinate and value for all types of critical points, you should make use of main
function 2, namely topology analysis function.
3.20.3 Usage
The basin analysis module in Multiwfn is very powerful, fast and flexible. Basins can be
generated and visualized for any real space function, meanwhile any real space function can be
integrated in the generated basins. Electric multipole moments and localization index in the basins
and delocalization index between basins can be calculated.
Basic steps
To perform basins analysis in Multiwfn, there are five basic steps you need to do
(1) Load input file into Multiwfn and then enter main function 17.
(2) Select option 1 to generate basins and locate attractors. Before doing this, you can change
the method used to generate basins via option -1, or adjust the parameters for clustering attractors
via option -6.
(3) Visualize attractors and basins by option 0. This step is optional.
(4) Perform the analyses you want. Integral of a real space function in generated basins,
electric multipole moments in the basins and localization/delocalization index of the basins can be
calculated by option 2 (or 7), 3 (or 8) and 4, respectively.
You can export the generated basins as cube files by option -5, export attractors as .pdb file
by option -4, check the coordinate of the located attractors by option -3, measure the distances,
angles and dihedrals angles between attractors or atoms by option -2. Also you can use suboption
3 in option -6 to manually merge specified basins as a single one. If you want to regenerate basins
and locate attractors for other real space functions or under new settings, you can select option 1
again.
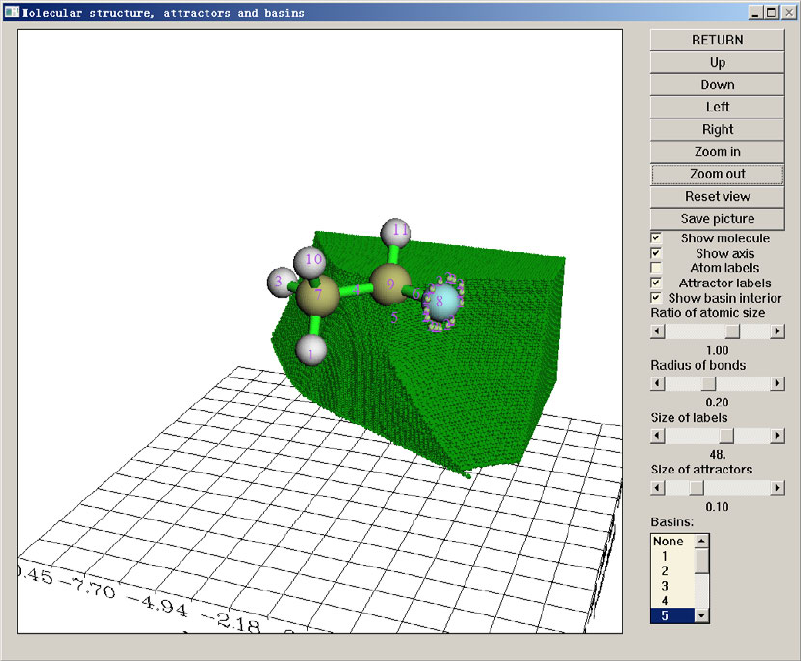
3 Functions
151
About input file and grid data
Grid data must be obtained first before generating basins. In option 1 of basin analysis
module, you can let Multiwfn calculate the grid data. However, if a grid data has already been
stored in memory, you can directly choose to use it. There are two circumstances in which grid
data will be stored in memory: (1) The input file contains grid data, e.g. .cub and .grd file (2) You
have used main function 5 or 13 to calculate grid data before entering main function 17. This
design makes Multiwfn rather flexible: you can use Multiwfn to generate basins for a real space
function recorded in a .cub or .grd file, which may be outputted by a third-part program; and you
can also first use main function 5 or 17 to generate grid data for electron density difference, Fukui
function, dual descriptor and so on, and then generate basins for them.
In the function of basin integration, namely option 2, the value of integrand at each grid must
be available so that the integral can be evaluated. These values can come from three ways, you can
choose any one: (1) Let Multiwfn directly calculate them (2) Load and use the grid data in
a .cub/.grd file, note that this operation will not overwrite the grid data already stored in memory
(3) Use the grid data already stored in memory. Beware that the grid setting of the grid data stored
in memory or the grid data recorded in a .cub/.grd must be exactly in coincidence with that of the
grid data used to generate basin, otherwise the integral is meaningless.
Note that if you have made Multiwfn calculate grid data for a real space function, then this
grid data will be stored in memory and hence you can directly use it in the basin integration step.
Visualization
In option 0, you can visualize attractors and basins, for example
3 Functions
152
Most of buttons are self-explained, please feel free to play with them. You can plot basin by
choosing corresponding term in the basin list at right-bottom corner. By default, only the grids at
basin boundary are shown. If you want the entire basin to be portrayed, "Show basin interior"
check box should be selected. At the end of the list, the "Unas" term means unassigned grid during
basin generation, while "Boun" term means the grid travelled to box boundary, you can select
them to plot the corresponding grids. Some basins are very small and very close to nucleus, such
as core-type basin of ELF, they are often screened by molecular structure; if you want to inspect
these basins you should deselect "Show molecule" check box.
Light green spheres denote attractors, and corresponding basins are colored as green. If the
real space function simultaneously has positive and negative parts, the "attractors" in negative
regions (in fact they are repulsors) will be shown as light blue spheres, and corresponding basin
will be portrayed as blue color.
If a set of attractors have been clustered as a single one, although all of them will be
displayed in the GUI, the index labels shown above them will be the same, which is the index of
corresponding degenerate attractor.
After using option 1 to locate the attractors, if you visualize isosurface by the GUI of main
function 5 or 13, you can also see the attractors and their labels. This design faciliates comparative
study of attractors and isosurfaces.
Detail of all options
All of the options involved in basin analysis module are described below; some options have
been partially discussed above.
-6 This option controls the parameter used in attractor clustering. If the parameters in
suboption 1 and 2 are set as A and B, respectively, that means for any two attractors, if between
them the relative value difference is smaller than A, meanwhile their interval is less than
B*sqrt(dx^2+dy^2+dz^2), where dx,dy,dz are grid spacings in X,Y,Z, then they will be clustered
together. If you want to nullify the automatic clustering step after generating basins, simply set the
parameter in suboption 2 to 0.
After basins have been generated, you can also use suboption 3 to manually cluster specified
attractors.
-5 Export basins as cube file. The basins in the specified index range will be successively
outputted to basinXXXX.cub in current folder, where XXXX is the index of the basin. In the cube
file, the value 1 and 0 denote the corresponding grid belongs and not belongs to the basin,
respectively. Therefore you can plot isosurface with isovalue=0.5 to visualize the basins in your
favourite visualization software. For example, below graph is plotted by VMD, the grey isosurface
corresponds to AIM basin of fluorine atom
3 Functions
153
Note that when Multiwfn asking you "If output internal region of the basin?", if you input "n"
rather than "y", then in the exported cube file, only boundary grids of the basin will have value of
1, and the other grids will have value 0. Therefore only interbasin surface will be shown when you
visualizing isosurface.
You can also choose 0,0, then basin.cub will be outputted, in which grid value corresponds to
basin index. This is important if you would like to
-10 Return to main menu.
-4 Export attractors as pdb file. The coordinate of all attractors will be outputted to
attractors.pdb in current folder. In this file, the atom indices correspond to the attractor indices
before clustering, while the residue indices indicate the attractor indices after clustering.
-3 Show information of attractors. The coordinate and value of all attractors will be outputted
on screen. For degenerate attractors, the shown coordinates and values are the average ones of
their member attractors, the coordinate and the value of all of the member attractors will also be
individually shown on screen.
-2 Measure distances, angles and dihedral angles between attractors or atoms. As the title
says. Please follow the prompts shown on the screen.
-1 Select the method for generating basins. Three methods are available now: (1) On-grid
method (2) near-grid method (3) near-grid method with boundary refinement step. Note that the
near-grid method used in Multiwfn has been adapted by me, and thus became more robost. In
general I recommend method 3, and this is also the default method.
0 Visualize attractors and basins. This option has already been introduced above.
1 Generate basins and locate attractors. Choose a real space function, and select a grid setting,
then Multiwfn will calculate grid data, and then generate basins meanwhile locate attractors. After
that, as mentioned earlier, if there are some attractors having similar value and closely placed then
they will be automatically clustered. If a grid data has been stored in memory, you can directly
choose to use this grid data to avoid calculating new grid data. You can use this option to
regenerate basins again and again.
Multiwfn provided a lot of ways to define the grid setting. If you want to study the basins in
the whole system, in commonly "medium quality grid" is recommended for qualitative analysis
purposes; while if you want to obtain higher integration accuracy, "high quality grid" is in general
recommended. If you only need to study the basins in a local region of the whole system, you can
make the spatial scope of the grid data only cover this region; for this purpose, I suggest you to
use the option "Input center coordinate, grid spacing and box length", by which you can easily
define the spatial scope of the grid data.
2 Integrate real space functions in the basins. Select a real space function, or select the grid
data stored in memory, or choose to use external .cub/.grd file, then the real space function you
3 Functions
154
selected or the real space function recorded in the grid data will be integrated in the basins that
have been generated by option 1, the integral in each basin and basin volumes will be outputted. If
there are some unassigned grids or the grids travelled to box boundary, their integrals will also be
shown.
If the basins you analyzed are AIM basins, it is highly recommended to use option 7 instead
to gain much better integration accuracy.
3 Calculate electric multipole moments in the basins. Please consult Section 3.18.3. The
differences relative to Section 3.18.3 are that the ranges of integration in our current consideration
are basins rather than fuzzy atom spaces, and nuclear positions should be replaced by attractor
positions. The multipole moments are outputted up to quadrupole, while octopole and higher
orders are not supported, because based on grid integration they are difficult be evaluated
accurately.
If the basins you analyzed are AIM basins, it is highly recommended to use option 8 instead
to gain much better integration accuracy.
4 Calculate localization index and delocalization index for the basins. Please consult Section
3.18.5. The only difference relative to Section 3.18.5 is that the range of integration in our current
consideration is basins rather than fuzzy atom spaces.
5 Calculate and output orbital overlap matrix in all basins to BOM.txt in current folder. All
virtual orbitals are ignored.
Below options are available only when the real space function used to define the basins is
chosen as electron density
7 Integrate real space functions in AIM basins with mixed type of grids. This option is
specific for integrating AIM basins; there are three different ways to realize it:
Hint: Accuracy: (2)≥(3)>>(1). Time spent: (2)>(3)>>(1). Memory requirement: (3)>(2)=(1)
(1) Integrate a specific function with atomic-center + uniform grids: Atomic-center grids are
mainly used to integrate the real space function near nuclei, while uniform grids are mainly used
for other regions. The accuracy is much better than solely using uniform grids (namely option 2 in
basin analysis module).
(2) The same as (1), but with exact refinement of basin boundary: Compared to option (2),
when integrating the grids at basin boundary, the assignment of these grids will be exactly refined
by steepest ascent scheme, hence the result will be more accurate than using option (1),
unfortunately the refinement step is time consuming.
(3) The same as (2), but with approximate refinement of basin boundary: This is an
approximate version of option (2). The gradient of electron density used in refinement step will
not be evaluated exactly, but obtained by trilinear interpolation of pre-calculated grid data of
gradient. Although evaluating the grid data of gradient is also time consuming, the overall time
cost is lower than option (2), and the loss of accuracy is trival.
After you used option (2) or (3) once, the assignment of the boundary grids will be updated
permanently, that means then if you use option (1), the result will be identical to (2) or (3).
Not only the basin volumes are outputted along with the integrals, the basin volumes with
electron density > 0.001 are also outputted, which can be regarded as atomic sizes.
8 Calculate electric multipole moments in AIM basins with mixed type of grids. Similar to
option 3, but use mixed atomic-center and uniform grids to calculate electric multipole moments
to gain better accuracy without bringing evident additional computational cost. This option is only
applicable to AIM basins.
3 Functions
155
9 Obtain atomic contribution to population of external basins. The external basins means the
basin defined by a cube file named basin.cub in current folder, in which the grid value corresponds
to basin index. This option aims to obtain atomic contribution to population of ELF bond basins
(or other type of basins) based on AIM partition. Please check Section 4.17.7 for example.
Notice that if you use option 7 and 8, when you generating AIM basin, the spatial range of
the grid data must cover the whole system. If effective core potential (ECP) is used for an atom,
then many attractors will occur at valence region of the atom; before entering option 7 and 8, you
have to manually cluster these attractors as single one by suboption 3 in option -6, otherwise the
program does not know which attractors correspond to this atom.
For option 3, 4, 5, 7 and 8, if the input file you used does not contain GTF information
(e.g. .cub file), then Multiwfn will prompt you to input a new file, which should contain GTF
information of present system, you can use for example .wfn/.wfx/.fch/.molden/.gms file as input.
Information needed: GTFs or grid data, atom coordinates
3.21 Electron excitation analysis (18)
3.21.1 Analyze and visualize hole-electron distribution, transition
dipole moment and transition density (1)
This very powerful module is used to analyze and visualize hole-electron distribution,
transition density, transition dipole moment density and charge difference density. Moreover,
transition density matrix can be generated, and transition dipole moment can be decomposed to
MO pair contributions, hole and electron can be decomposed to MO contributions.
3.21.1.1 Theory
This module involves many theories, which will be described below in turn.
Theory 1: Hole and electron
In single-electron excitation process, an electron leaves A and goes to B; where A and B are
real space functions, and they will be respectively named as "hole" and "electron" in the following
texts. If the excitation can be perfectly described as HOMOLUMO transition, then A and B are
just HOMO and LUMO, respectively. However, in most practical cases, this single-orbital pair
model is not suitable, and the excitations have to be represented as the transition of multiple MO
pairs with proper weighting coefficients. The most straightforward way to deal with electron
excitation problem is CIS, the CIS excited state wavefunction is written as
li
l
i
l
i
w
exc
where i and l respectively run over all occupied and all virtual MOs, similarly hereafterin. l
i
is
the configuration state wavefunction corresponding to moving the electron from originally
occupied MO i to virtual MO l. w is configuration coefficient.
3 Functions
156
I and my collaborator Cheng Zhong have shown (to be published) that the density
distribution of hole and electron can be gracefully defined as
lilij ji
l
j
l
i
li ii
l
iwww )()()()()()()()( 2hole
(cross)
hole
(loc)
hole rrrrrrr
lilmi ml
m
i
l
i
li ll
l
iwww )()()()()()()()( 2ele
(cross)
ele
(loc)
ele rrrrrrr
where
denotes MO. "loc" and "cross" stand for the contribution of local term and cross term to
the hole/electron distribution. Note that what we are discussing is distribution rather than
wavefunction of hole and electron, so
hole and
ele do not have phase.
Due to the orthonormality of MOs, and the fact that the sum of the square of all configuration
coefficients is 1, it is clear that
1)(1)( elehole rrrr dd
This is an important expected property of the definition of hole and electron distribution.
The overlap between hole and electron distribution is defined as )](),(min[ elehole rr
,
namely taking the minimal value of
hole and
ele everywhere.
The charge density difference between excited state and ground state can be exactly
evaluated as
)()()( holeele rrr
Beware that if you are a Gaussian user, the calculated in this way is obviously different to the produced
by minusing ground state density from excited state density unless you specified the keyword "density=rhoci"
when generating excited state wavefunction, because by default the excited state density outputted by Gaussian is
the relaxed one, rather the unrelaxed one (directly constructed by CIS excited state wavefunction)
After generalization, above definitions can also be applied to TDHF and TDDFT cases,
where de-excitations occur. The generalized local terms are
li l
l
i
li l
l
i
li i
l
i
li i
l
i
ww
ww
22ele
(loc)
22hole
(loc)
)()(
)()(
The generalized cross terms are
lilmi ml
m
i
l
i
lilmi ml
m
i
l
i
lilij ji
lj
l
i
lilij ji
lj
l
i
wwww
wwww
ele
(cross)
hole
(cross)
In order to investigate which MOs have significant contribution to hole and electron, I
defined the contribution of occupied MO to hole and virtual MO to electron as follows
li
l
i
li
l
il
li
l
i
li
l
ii wwww 22ele22hole )()()()(
The normalization conditions are held evidently
11 elehole
ll
ii
Theory 2: Quantitative representation of hole and electron distribution
3 Functions
157
The distribution of hole and electron can be quantitatively represented in following ways.
rrr dS
)](),(min[ elehole
is used to characterize the overlapping extent of hole and
electron.
Centroid of hole and electron can be calculated. For example, X coordinate of centroid of
electron is
rr dxX )(
ele
ele
where x is X component of r.
The distance between the two centroids measures the CT length
holeeleCT, XXD x holeeleCT, YYD y holeeleCT, ZZD z
2
CT,
2
CT,
2
CT,CT )()()( zyx DDDD
It is noteworthy that the variations of dipole moment of excited state with respect to ground
state in X, Y and Z can be simply calculated as (not true if relaxed density of excited state is used)
)()()( holeeleholeeleholeele ZZYYXX zyx
The RMSDs of hole and electron are used to characterize their distribution breadths. For
example, Y component of RMSD of hole
rr dYy
y)()( hole2
holehole,
The difference between RMSD of hole and electron is defined as follows
|| holeeleholeele σσ
S
There are often many nodes or fluctuations in hole and electron distributions. In order to
visually study them more easily, Chole and Cele functions are defined, whose structures are similar
to Gauss function, and the value asymptotically approaches zero.
2
hole,
2
hole
2
hole,
2
hole
2hole,
2
hole
holehole
2
ele,
2
ele
2
ele,
2
ele
2
ele,
2
ele
eleele
2
)(
2
)(
2
)(
exp)(
2
)(
2
)(
2
)(
exp)(
zy
zyx
ZzYyXx
AC
ZzYyXx
AC
r
r
The factor A is introduced so that Chole and Cele are normalized.
H and t indices are defined as
---
---
HDt
H
CT,
hole,ele, 2/)(
where
-
corresponds to the direction in which CT occurred. t may be regarded as the separation
degree of hole and electron. If t<0, an evident overlap between hole and electron is expected.
Clear separation of hole and electron distributions must correspond to a larger positive value of t.
Theory 3: Transition density matrix and transition density

3 Functions
158
(One-electron, spinless) transition density matrix between excited state and ground state of an
N-electron system in real space representation is defined as follows (I assume that all
wavefunctions are real type, so complex conjugation sign is omitted)
NNN dddTT xxxxxxxxxrrrr d),,'(),,()';()';( 32121
exc
21
0
11
where 0 is the Slater-determinant of ground state wavefunction. x is spin-space coordinate,
stands for spin coordinate.
For CIS/TDHF/TDDFT excited state wavefunction, after we expanded exc and applied
Slater-Condon rule, it can be easily shown that T can be explicity written as
)'()()';( rrrr
il li
l
i
wT
If we only take the diagonal terms of the transition density matrix, then we obtain transition
density
)()()( rrr
il li
l
i
wT
T(r) can be studied as a normal real space function, for example, visualized in terms of isosurface.
Note that due to the orthonormality of MOs, integration of T(r) over the whole space is
exactly zero. If the excited state and ground state correspond to different spin states, due to the
orthonormality of spin coordinate, T(r;r') must be a zero matrix, and T(r) is zero everwhere.
In basis function representation, transition density matrix can be written as
il li
l
iCCwP
tran
where C
i denotes the expansion coefficient of basis function
in MO i.
Transition density matrix in real space and in basis function representations are correlated as
)'()()';( tran rrrr PT
Notice that transition density matrix in general is not a symmetric matrix (though the
deviation is often very small), however it can be symmetrized as follows (the case
=
is also
included)
il lili
l
iCCCCw
PP
P)(
2
1
2
)( trantran
tran
Theory 4: Transition dipole moment and oscillator strength
X, Y and Z components of transition dipole moment density can be defined as are the
negative value of product of X, Y and Z coordinate variables and transition density
)()()()()()( rrrrrr zTTyTTxTT zyx
Integrating transition dipole moment density over the whole space yields transition dipole
moment D
rrrrrr dTDdTDdTD zzyyxx )()()(
Obviously, one can conveniently study the contribution to transition dipole moment from different
molecular regions by visualizing transition dipole moment density.
3 Functions
159
Alternatively, transition dipole moment can be calculated based on dipole moment integral
between occupied and virtual MOs
il li
l
iz
il li
l
iy
il li
l
ix zwDywDxwD
The contribution from each MO pair to transition dipole moment can be straightforwardly
evaluated (namely the term in the summation notation).
Oscillator strength of a transition mode directly relates to the integral area of the
corresponding absorption peak. The relationship between oscillator strength f and transition dipole
moment D is (in atomic unit)
)(
3
22
z
2
y
2
xDDDEf
where E denotes the transition energy between the two states.
Theory 5: Transition magnetic dipole moment and the corresponding density
The transition dipole moments involved in all of above discussions are transition electric
dipole moment, while the other kind of transition dipole moment, namely transition magnetic
dipole moment, is also an important property for some special systems.
The operator for magnetic dipole moment due to movement of electrons is the angular
momentum operator L (see e.g. Theoret. Chim. Acta, 6, 341)
x
y
y
x
z
x
x
z
y
z
z
yi
LLLi zyx
kji
kjirL
ˆ
ˆˆ
ˆ
ˆˆ
)(
where i, j, k are unity vectors in X, Y and Z directions, respectively. Therefore, the X component
of transition magnetic dipole moment is defined as below. Noticed that in order to provide a real
value I ignored the imaginary and negative signs simultaneously; the symbol "←" denotes de-
excitation MO pairs in TDHF/TDDFT formalism.
mj mj
m
j
li li
l
ix y
z
z
yw
y
z
z
yw
y
z
z
yM
exc0
Clearly, it is straightfoward to define the X component of transition magnetic dipole moment
density mx(r) as follows to satisfy the condition rr dmM xx
)( , so that the distribution of
transition magnetic dipole moment can be visualized as isosurface or plane map
mj
mm
j
m
j
li
ll
i
l
ix y
z
z
yw
y
z
z
ywm )()()()()()()( rrrrrrr
Y and Z components are defined similarly.
Theory 6: Coulomb attraction between hole and electron
The "electron" of course carries negative charge, while "hole" can be regarded as carrying
positive charge, therefore formally there is Coulomb attractive energy between them, which can be
calculated as simple Coulomb formula:

3 Functions
160
21
21
2
ele
1
hole
Cdd
||
)()( rr
rr
rr
E
In Multiwfn, above integral is directly calculated based on evenly distributed grid data of
hole and electron. Notice that although the code has been substantially optimized and parallelized,
the computational cost is still high, so you need to wait patiently during calculation. Thc cost is
formally proportionally to square of the number of grids; therefore, the cost of medium quality
grid will be higher than low quality grid by one order of magnitude.
3.21.1.2 Input file
This module requests two types of files as input.
(1) A file containing molecular orbitals of ground states. .fch/.molden/.gms file produced
by excited state calculation (CIS, TDHF or TDDFT method) can be used. This file should be
loaded when Multiwfn boots up. Multiwfn will utilize the molecular orbitals and basis function
information recorded in it during the electron excitation analysis.
(2) A file containing configuration coefficients of excited states. The path of this kind of
file should be inputted when you enter present module. There are three cases, as shown below:
(a) Gaussian user: Output file of CIS, TDHF, TDDFT and TDA-DFT tasks can be used. Since
by default Gaussian only outputs the configuration coefficients larger than 0.1, in order to gain
acceptable results, you must add IOp(9/40=4) keyword in the route section so that all
configuration coefficients whose magnitude larger than 0.0001 will be printed. Using IOp(9/40=5)
instead will result in marginally better accuracy, however the Gaussian output file will become
larger and computational cost of present module will be higher.
Note: DO NOT use the Gaussian output file of excited state optimization or frequency analysis task as input
file! Multiwfn cannot properly parse this kind of output file!
(b) ORCA user: Output file of CIS, TDHF and TDA-DFT tasks can be used. Beware that
TPrint keyword should be used within %cis or %tddft, otherwise only very small amount of
configuration coefficients will be printed. TPrint x means outputting configurations whose
contribution to excited state larger than x*100%. Typically, I suggest using TPrint 1E-8. Since
contribution is calculated as square of configuration coefficient, TPrint 1E-8 simply corresponds
to outputting configurations who have absolute value of coefficients larger than 1E-4, its effect is
identical to IOp(9/40=4) in Gaussian. Below is an example input:
! PBE0 def2-SVP nopop
%tddft
nroots 8
tprint 1E-8
end
Note: It is also possible to use ORCA TDDFT/TDHF output file, but the analysis result may be reliable!!!
Because in TD task, ORCA only print configuration contributions but does not print configuration coefficients, so
Multiwfn automatically generate the latter by computing square root of the former. This treatment looks reasonable,
however when de-excitation is significant, the configuration coefficients yielded in this manner must be nonsense,
because in TD task output file, de-excitation contribution and excitation contribution of an orbital pair are summed
up and outputted as a single term.
(c) If you are neither a Gaussian user nor an ORCA user, you can also use plain text file as
the input file, the format of transition information should be completely identical to Gaussian
output, for instance:
1 11.4194
3 Functions
161
3 -> 10 -0.00361
5 -> 7 0.69644
5 -> 8 0.07291
5 -> 12 0.09814
5 -> 18 -0.00375
where the 1 and 11.4194 in the first line are spin multiplicity of the excited state and transition
energy (eV), respectively. (For de-excitation transitions, should be written as ).
Both close-shell and open-shell calculations are fully supported.
3.21.1.3 Functions
Present module has many functions, they will be described below in turn
Function 1: Visualize and analyze hole, electron and transition density and so on
After you enter this function, you are requested to select a way to define grid data, then grid
data will be calculated for hole distribution, electron distribution, overlap of hole and electron
distribution, transition density, transition electric/magnetic dipole moment density, charge density
difference and Cele/Chole functions. Then these grid data can be directly visualized as isosurface, or
exported as cube file in current folder by corresponding options. In the post-process menu, you
can also choose to calculate Coulomb attractive energy between hole and electron distribution,
notice that this calculation is expensive even if you are using low quality grid.
After the calculation of the grid data have been finished, some statistic data will be shown.
The ideal value of the integral of hole or electron distribution is 1, while for transition density the
ideal value is 0. The transition electric/magnetic dipole moment is calculated by integrating the
grid data of transition dipole moment density, the value should be very close to the one directly
outputted by quantum chemistry program. RMSDs of hole and electron exhibit their distribution
breadth in each direction. Integral of overlap of hole-electron distribution can be used to identify if
a transition mode is local excitation, and the distance between centroid of hole and electron is a
good indicative of charge-transfer length of present electron transition mode. t index reveals if
hole and electron distributions are separated clearly.
When you choose to visualize/export hole and electron distribution, you can visualize/export
their local term, cross term or total distribution (local term + cross term) separately. The hole and
electron distributions involved in other options corresponds to their total distributions.
By default the transition magnetic dipole moment density is not evaluated because it is less
important than the transition electric dipole moment density. If you want to calculate it, select
option -1 before using this function. An example of analyzing transition magnetic dipole moment
density can be found in Section 4.18.1.
Function 2: Show contribution of MO pairs to transition dipole moment
The transition dipole moment in X/Y/Z can be decomposed into MO pair contributions (in
other words, configuration contribution) by this function. Since there may be very large number of
MO pairs recorded in the input file, you need to input the threshold for printing the result. For very
large system, calculating contributions from all MO pairs is quite expensive, therefore Multiwfn
enables the user to set a threshold, if absolute value of coefficient of a configuration is lower than
3 Functions
162
this threshold, then contribution to transition dipole moment from the corresponding MO pair will
not be computed but simply regarded as zero. Evidently, the lower the threshold, the higher the
computational cost. If you set threshold to 0, then all configurations will be evaluated.
You can also choose to print the contributions from all MO pairs to transdip.txt in current
folder. This function is very useful for figuring out which MO pairs have large contribution to
transition dipole moment and thus oscillator strength.
Finally, the norm of transition dipole moment and the corresponding oscillator strength are
also outputted (The threshold you set for considering MO pairs evidently affects there values).
Function 3: Show contribution of each MO to hole and electron distribution
You only need to input printing threshold, then contribution of MO to hole and electron
distribution will be shown. This function is very useful to identify which MOs significantly
constitute the hole and electron.
Function 4: Generate and export transition density matrix
According to MO expansion coefficients and configuration coefficients, transition density
matrix in basis function representation can be constructed by this function. You can choose if
symmetrizing the matrix according to the formula shown above. The generated matrix will be
outputted to tdmat.txt in current folder, which can be plotted as color-filled map by function 2 of
main function 18, see Section 3.21.2 for detail.
Note that when ground state and excited state have different spin multiplicities, due to the
orthonormality of spin coordinate, although in principle the transition density matrix should be
zero, the outputted matrix is not, because Multiwfn only takes space part of the MOs into account
during constructing the matrix.
Function 5: Decompose transition dipole moment to basis function and atom
contributions
This function is used to decompose the total transition electric or magnetic dipole moment
into contributions from each basis function and atom. As there is no unique way to derive
population number, there are also many possible ways to realize the decomposition. In this
function Mulliken partition is employed. For example, the contribution from basis function μ to Z
component of transition electric dipole moment is evaluated as follows
2/][ trantrantran)( zPzPzPDz
and the contribution from basis function μ to Z component of transition magnetic dipole moment
2/][ trantran
tran)(
x
y
y
xP
x
y
y
xP
x
y
y
xPMz
Then the contribution from an atom is simply the sum of the contribution from the basis functions
belonging to it.
The result is unreliable if diffuse functions are presented in your calculation. In this case, the
best way to study the contribution from atoms is visualizing the aforementioned transition dipole

3 Functions
163
moment density.
You can select decomposing which type of transition dipole moment when enter this function.
Notice that in order to decompose transition electric (magnetic) dipole moment, before booting up
Multiwfn, you must set "igenDbas" ("igenMagbas") parameter in settings.ini to 1, so that electric
(magnetic) dipole moment integral matrix, which is required in present function, can be generated
when loading input file.
This function also asks you if outputting atom-atom contribution matrix of transition dipole
moment, if you choose y, then the matrix will be exported to AAtrdip.txt in current folder. This
matrix is defined as below (I take atom-atom contribution matrix of transition electric dipole
moment as example, the matrix for transition magnetic dipole moment is defined similarly and
thus not explicitly shown here)
zyxiiD
DDDD
AB
iBA
BABABABA
,,
)()()(
,
2Z,
2Y
,
2X
,,
For example, the term xBA
D, corresponds to contribution of A-B atom pair to X component of
transition dipole moment, and DA,B measures magnitude of total contribution. The content of
AAtrdip.txt then can be directly plotted as colored matrix map by subfunction 2 of main function
18 (see Section 3.21.2).
Function 6: Calculate Mulliken atomic transition charges
This function is used to calculate atomic transition charges, which is useful for studying
Coulomb coupling between ground state and excited state of two molecules (see e.g. J. Phys.
Chem. B, 110, 17268).
Transition population of a basis function μ derived by Mulliken method is
2/)( trantrantrantran SPPP
So, the Mulliken atomic transition charge of atom A should be
A
tran . The sum of all atomic
transition charges must be equal to zero.
The result will be outputted to .chg file in current folder, the format of this kind of file has
been introduced in Section 2.5. You can use your text editor to open it, the last column is what you
need.
Function 7: Decompose transition magnetic dipole moment as basis function and atom
contributions
Very similar to function 5, but the transition dipole moment to be decomposed is the
magnetic one rather than the electric one. You must set "igenMagbas" in settings.ini to 1.
Function 10: Modify or check excitation coefficients
This function allows one to modify or check coefficient of MO pairs (or say configuration
coefficient). If you have modified the coefficients, then during the calculation of hole-electron
distribution, transition dipole moment density, oscillator strength and so on, the modified
3 Functions
164
coefficients will be used. Obviously, if you set the coefficient of some MO pairs to zero, then their
contributions to the quantities you calculated will be ignored; while if you clean all coefficients
but for a specific MO pair (this can be directly realized via suboption 3), then the resultant
quantities will only characterize this MO transition.
An very detailed example of this hole-electron module is given in Section 4.18.1.
Information needed: GTF and basis function (for all MOs, so use .fch/.molden/.gms),
Gaussian output file or plain text file which describes electron transition information
3.21.2 Plot transition density matrix as color-filled map (2)
Theory
Transition density matrix (TDM) between electronic state K and state L is denoted by KL
P
,
during excited state calculation in many quantum chemistry programs this matrix can be outputted
in the form of expansion by atomic-center basis functions. We can further contract such matrix by
following equation to make it represented by atom centers:
AB
KLKL
BA PP
2
,
~
where
and
denote the basis functions centered at atom A and on B respectively.
Diagonal terms, e.g. KL
AA
P,
~
, represents the magnitude of induced charge on atom A when the
system undergoes electron transition from state K to L. While off-diagonal terms, e.g. KL
BA
P,
~
,
displays the strength of hole-electron coherence between atom A and B when electron transits. If
this matrix is plotted as a color-filled map, then the primary atoms involved in specific electron
transition mode, and the spatial span of the electron transition can be clearly and visually studied,
this is especially useful for analyzing large-size and conjugated molecules. Commonly hydrogens
can be omitted when plotting.
Input file
This function requires two files as input. The first one is the .fch/.molden/.gms file
corresponding to current system. This file can be obtained by any type of calculation, since only
the elements and the correspondence between basis functions and the atoms will be loaded from
this file.
The second one must be an ASCII type file containing TDM. There are two circumstances:
(1) If you are a Gaussian user, you can directly let Gaussian to write TDM in the output file.
However, by default, TDM is not printed in output file, thus you have to specify
density=transition=X IOp(6/8=3) in route section of Gaussian input file, so that TDM between
ground state and excited state X can be written in Gaussian output file by Link 601 module.
Note that in fact, TDM is not exactly symmetrical, but commonly very close to a symmetry matrix. In
Gaussian, the outputted TDM is artificially symmetrized; that is the elements of the outputted TDM (referred to as
P') are generated as P'=P'=(P+P)/2, including both cases = and . If you want to plot original TDM,
you can use option 4 in subfunction 1 of main function 18 to generate the TDM and use resulting tdmat.txt as input
file.
(2) If you are not a Gaussian user but the program you used can output .molden or .gms file,
3 Functions
165
you can make use of option 4 in subfunction 1 of main function 18 to generate the tdmat.txt file,
which contains TDM and can be directly used as input file for present function, see corresponding
section of the manual for detail. Alternatively, you can try to use proper keywords in your
quantum chemistry program to let it output TDM, and then write a small program by yourself to
make the format of the TDM completely consistent with examples\tdmat.txt file, then the file
could be used as input file.
Usage
After you boot up Multiwfn, first you should input the path of .fch/.molden/.gms file
corresponding to current system, and then choose main function 18 and subfunction 2 to enter
TDM plotting module, then input the path of the Gaussian output file or the plain text file
containing TDM. After that you will see several options, you can choose 0 to show KL
P
~
graph
on screen immediately, or choose 1 to save the TDM plot to graphical file in current folder with
DISLIN prefix. Labels in abscissa and ordinate of the plot correspond to indices of atom (notice
that only if hydrogens are taken into account, then the indices in the plot will be consistent with
actual atom indices in present system). By option 3 the data point can be exported to external file,
so that the KL
P
~
can be conveniently replotted by some third-party plotting tools such as Origin
and Sigmaplot. By option 4 you can choose if hydrogens will be taken into account in the KL
P
~
graph. Upper and lower range of color scale can be changed by option 5, by default these two
values are set automatically to maximal and minimal values of KL
P
~
. Through option 6 you can
change the number of interpolation steps between grid data, if you want to make the graph looks
more smooth then set it to a larger value, if the value is set to 1 then interpolation will not be
performed. Steps between labels in abscissa and ordinate can be set by option 7. Option 8
determine if performing normalization for KL
P
~
, if perform, then the sum of all elements of the
normalized KL
P
~
will be equal to unity.
Please note that, if the basis set you used contains diffuse basis functions, in rare cases, the
transition density outputted by Gaussian may be incorrect, and thus the TDM map will be useless.
Hint 1: It is also possible to use present function to plot density matrix (DM) for a given state,
then how the atoms are correlated to each other can be clearly seen, since the off-diagonal
elements can be approximately regarded as the bond orders between the corresponding atoms. The
steps of plotting DM in Multiwfn is completely identical to plotting TDM. The only difference
comes from Gaussian input files. If you intend to plot DM for ground state, simply use the
keyword IOp(6/8=3) in the ground state calculation, then the DM will be printed in the Gaussian
output file. If you wish to plot DM for the ith excited state, then you should specify the keyword
density IOp(6/8=3), and meantime set the root keyword in CIS/ZINDO/TD to i. For example #P
cis(root=5, nstates=10)/6-31g(d) density iop(6/8=3).
Hint 2: It is also possible to use present function to plot the atom-atom contribution matrix of
transition electric/magnetic dipole moment generated by hole-electron analysis module (see
description of function 5 in Section 3.21.1.3). After you boot up Multiwfn, first load .fch file, then
enter present function, input the path of the AAtrdip.txt file (the filename should not be changed to
others), then the atom-atom contribution matrix in this file will be loaded and can be plotted as
colored matrix.
3 Functions
166
An example of plotting TDM is given in Section 4.18.2.
Information needed: Basis functions, Gaussian output file or plain text file containing TDM
3.21.3 Analyze charge-transfer based on density difference grid data
(3)
Theory
In the paper J. Chem. Theory Comput., 7, 2498 (2011), the authors proposed a method for
analyzing charge-transfer (CT) during electron transition. It is also probable that this method can
be used to study CT in other processes, such as formation of complex. In the original paper, the
author only discussed the cases when charge-transfer is in one-dimension, while in Multiwfn this
scheme is generalized in three-dimension cases.
The electron density variation between excited state (EX) and ground state (GS) is
)()()( GSEX rrr
Notice that the geometry used in calculating )(
EX r
and )(
GS r
must be identical, otherwise
the resulting )(r
is meaningless. )(r
can be divided into positive and negative parts,
namely )(r
and )(r
. Of course, the integral of )(r
and )(r
over the whole
space should be equal, if evident unequality is observed, that means the error in numerical integral
is unneglectable, and denser grid is required. Even though what you analyzed is single-electron
excitation, the magnitude of )(r
and )(r
as well as their integrals can also be larger than
1.0 theoretically, this is because the excitation of an electron leads to reorganization of distribution
of the rest of electrons, which also make contribution to )(r
.
The transferred charge CT
qis the magnitude of the integral of )(r
or )(r
. It is
important to correctly recognize the physical meaning of this quantity. CT
q only corresponds to
the total amount of charge whose distribution is perturbed during electron transition, it does not
corresponds to net charge transfer from one fragment to another fragment (e.g. from donor group
to acceptor group)
The barycenters of positive and negative parts can be computed as
rrrrrR
rrrrrR
dd
dd
)(/)(
)(/)(
The component coordinates of R+ will be referred to as ,Z,YX , of R- will be referred to as
Z,Y,X .
3 Functions
167
The distance between the two barycenters measures the CT length
XXD XCT, , YYD YCT, , ZZD ZCT,
The dipole moment variation caused by CT is evaluated as
CTCT, )( qXX
X
, CTCT, )( qYY
Y
, CTCT, )( qZZ
Z
Notice that the Eq. 7 in the original paper is ||μCT||=DCT*qCT = |R+ - R-|*qCT, this relationship
is not rigorously and evidently only holds for one-dimension transfer cases (namely only one of
DCT,X, DCT,Y, DCT,Z is not zero). Only the equations shown above, which are used by Multiwfn, are
correct for all cases! So DO NOT suspect whether Multiwfn is reliable or buggy due to the results
often seemingly violates Eq. 7 of the original paper!
The RMSDs of the distribution of )(r
and )(r
in each direction are defined as
rr
rr
d
d
a
aa
a)(
)')(( 2
,
--
-
where a={+,-},
-
’={x,y,z},
-
={X, Y, Z}. x, y and z are components of integral variable r. For
example
rr
rr
d
dYy
y)(
))(( 2
,
)(r
C and )(r
C functions are defined aiming for visualizing CT more clearly than
)(r
, their structure are similar to Gauss function, the value asymptotically approaches zero.
2,
2
2,
2
2,
2
2,
2
2,
2
2,
2
2
)(
2
)(
2
)(
exp)(
2
)(
2
)(
2
)(
exp)(
zyx
zyx
ZzYyXx
AC
ZzYyXx
AC
r
r
The normalization factor A are introduced so that the integrals of )(r
C and )(r
C are
equal to the integrals of )(r
and )(r
, respectively.
H and t indices are defined as
---
---
HDt
H
CT,
,, 2/)(
where
-
corresponds to the direction in which CT occurred. t may be regarded as the separation
degree of )(r
and )(r
. If t<0, an overlap between the distribution of )(r
and
3 Functions
168
)(r
is expected. If t is evidently less than 0, then the excitation must not be a charge-transfer
excitation.
I defined another quantity to measure overlapping extent between )(r
C and )(r
C
rrr dACACS /)(/)(
If the value equals to 1, that means the two functions are completely superposed, else if the value
equals to zero, it indicates that the distribution of them are completely separated. This index is
dimensionless.
DCT index is exactly zero for centrosymmetric systems, therefore, it is useless for discussing
CT problem of this kind of system. In DOI: 10.1021/acs.jpca.7b07080, the author proposed
another index
||
CT
σσ
This index measures difference between RMSD of positive and negative parts, and thus can
somewhat reveal charge transfer character of centrosymmetric systems.
Implementation
Because all numerical integrals mentioned above are computed based on cubic grid data, user
needs to generate grid data for )(r
by using custom operation, see Section 3.7.1. After that,
return to main menu, and go into subfunction 3 in main function 18. The results will be shown up
immediately, user can choose to visualize )(r
C and )(r
C, or export the grid data of the two
functions to Gaussian cube file in current folder.
The outputs are self-explained. The “Overlap integral between C+ and C-“ term is the S+-
defined above.
An example is given in Section 4.18.3.
Information needed: GTFs, atom coordinates
3.21.4 Calculate r index to measure charge-transfer length (4)
Theory
In the paper J. Chem. Theory Comput., 9, 3118 (2013), r index was proposed to measure
charge-transfer length during electron excitation. However, I found this argument is wrong. One
only can say that the smaller the r is, the more likely the transition is local excitation (LE) rather
than charge-transfer excitation (CT) or Rydberg excitation.
The definition of r is

3 Functions
169
li
l
i
li iill
l
i
K
K
r
,
2
,
2
)(
)(
rr
where index i and l run over all occupied and virtual MOs, respectively.
is orbital wavefunction.
Assume that the method you used to calculate electron excitation is CIS or the TDDFT under
Tamm-Dancoff approximation, then l
i
K is simply the configuration coefficient corresponding to
the excitation il. If the method you used is TDHF or full TDDFT, then l
i
l
i
l
iYXK , where
l
i
X and l
i
Y denote the configuration coefficient corresponding to the excitation il and de-
excitation il. These cofficients are directly outputted by commonly used quantum chemistry
program such as Gaussian.
r is especially useful for diagnosing when conventional DFT functional is failure for
TDDFT purpose, that is when r is large, such as B3LYP, BPW91 and PBE1PBE will not work
well, and long-range corrected functionals should be employed, for instance, CAM-B3LYP, LC-
PBE and ωB97X.
Usage
The input files needed by this function are completely identical to that requested by hole-
electron analysis (Section 3.21.1). Two files are needed to calculate r, the first one is
the .fch/.molden/.gms file produced by ground state calculation and should be loaded when
Multiwfn boots up. Multiwfn will utilize the orbital wavefunctions (
) recorded in this file. The
second one is the Gaussian or ORCA output file of excited state calculation (also you can use the
plain text file containing electron transition information), see Section 3.21.1.2 for detail. The path
of the second file should be inputted when you enter present function.
After the r is calculated, Multiwfn will ask you to choose if decompose r into orbital pair
contributions. If you input for example 0.01, then below term will be outputted for all i-l orbital
pairs with l
i
K larger than 0.01
li
l
i
iill
l
iK
r
,
2
)(
rr
Therefore, from the output, you can easily identify which orbital pairs markedly participated the
electron transfer.
The example in Section 4.18.1 involves present function.
Information needed: GTF (for all MOs, so use .fch/.molden/.gms), Gaussian/ORCA output
file or plain text containing electron transition information
3 Functions
170
3.21.5 Calculate transition dipole moments between all excited states
(5)
This function is used to calculate transition dipole moment between all excited states.
The requirement on input file of this function is exactly identical that of hole-electron
analysis (Section 3.21.1), see Section 3.21.1.2 for detail. It is worth noting that for present
function, I strongly suggest you use IOp(9/40=5) keyword of Gaussian or TPrint 1E-10 keyword
of ORCA to make program print as more configurations as possible, so that accurate transition
dipole moment can be obtained by Multiwfn.
This function first prints summary of all excited states. "Multi." denotes multiplicity of the
excited state; "N_pairs" is the number of configurations involved in the state, which is directly
associated to N. "Sum coeff.^2" should as closed to expected value as possible (0.5 and 1.0 for
close- and open-shell cases, respectively), evident deviation implies that the result will be
inaccurate and N must be set larger. Multiwfn then let you select the destination of the output (you
can also choose to generate input file of SOS module of Multiwfn, as introduced in Section
3.200.8), and calculates transition dipole moments between all excited states. Finally the X, Y, Z
components of transition dipole moments, energy differences and corresponding oscillator
strengths of each pair of excited states will be printed. Note that in the case that the index of the
two excited states are identical, the transition dipole moment simply corresponds to the electric
dipole moment of this excited state.
Fortunately, if you are not a Gaussian or ORCA user, it is also possible to use this function.
You can use a file containing basis functions and ground state orbitals information as the first
input file, and use a plain text file containing electronic excitation information as the second input
file. The format of the plain text file should be consistent with below example file (free format is
allowed):
Excited State 1 1 5.7945 // index, multiplicity and excitation energy(eV)
5 -> 6 0.70642 // MO pairs and transition coefficients
// Use a blank line to separate each excited state
Excited State 2 1 7.8943
5 -> 7 0.63860
5 -> 8 0.30006
Excited State 3 1 7.8943
5 -> 7 -0.30006
5 -> 8 0.63860
3.21.6 Generate natural transition orbitals (NTOs) (6)
This function is used to generate natural transition orbitals (NTOs) based on excited state task
of quantum chemistry packages. NTO was proposed in J. Chem. Phys., 118, 4775 (2003), it is a
very popular and useful way to analyze the electronic excitation result of CIS or TDDFT
calculation.
3 Functions
171
Transition of electronic state is often not predominated by only one pair of MO transition, in
most cases many different MO transitions simultaneously have non-negligible contributions,
which can be evaluated as square of corresponding configuration coefficient. This fact brings great
hindrance of analyzing transition character by means of visualizing related MOs. The NTO
method aims to relieve this difficulty, it separately performs unitary transformation for occupied
MOs and virtual MOs, so that only one or very few number of orbital pairs have dominant
contributions, which makes orbital inspection much easier.
The basic procedure of yielding NTOs are outlined below:
(1) Generating transition density matrix in MO basis (T). Assume that the system has nocc
occupied MOs and nvir virtual MOs, then T has dimension of (nocc, nvir), its (i,l) element is simply
calculated as
li
l
ili wT ,
where w stands for configuration coefficient outputted by CIS/TDDFT calculation. Note that for
TD formalism, there may be some de-excitations, their corresponding configuration coefficients
are simply ignored in the summation.
(2) Generating temporary matrix for occupied and unoccupied orbitals, respectively
TTTTTT T
vir
T
occ
Evidently, both Tocc and Tvir are square matrices, their dimension are nocc and nvir, respectively.
(3) Diagonalizing Tocc and Tvir to obtain eigenvalues and eigenvectors
virvirvir
1
viroccoccocc
1
occ ΛUTUΛUTU
(4) The diagonal terms of occ and vir are eigenvalues of occupied and virtual NTOs,
respectively. For the former, the eigenvalues are commonly sorted from low to high, while for the
latter, the eigenvalues are commonly sorted from high to low. A NTO pair consists of an occupied
NTO and a virtual NTO sharing the same eigenvalue. Eigenvalue of a NTO pair multiplied by 100
is just its percentage contribution to the electronic excitation.
(5) MOs are transformed to NTOs according to unitary transformation matrix U
vir
MO
vir
NTO
virocc
MO
occ
NTO
occ UCCUCC
where MO
occ
C and MO
vir
C are coefficient matrix of occupied MOs and virtual MOs in original
basis functions, respectively; their columns correspond to different MOs. The counterpart matrices
with NTO superscript denote coefficient matrix of occupied and virtual NTOs, by utilizing which
the NTOs can be visualized or subject to further analysis.
The input files needed for generating NTOs are exactly the same as the ones requested by
hole-analysis module (Section 3.21.1), namely a file containing basis function information (such
as .fch and .molden file, loaded when Multiwfn boots up), and a file containing electronic
transition information. See Section 3.21.1.2 for detail.
After you enter present function, you should select the index of the electronic excitation to be
studied, then Multiwfn will load corresponding configuration coefficients and generate NTOs
according to the equations shown above, and then output eigenvalues of occupied and virtual
NTOs. At the meantime, the MOs stored in memory are transformed to NTOs, and the orbital

3 Functions
172
energies are filled by corresponding NTO eigenvalues. Next, you can choose if output the NTOs
to .fch or .molden file, if you choose to output, then you can use Multiwfn to load the newly
generated .fch or .molden file to visualize the NTOs, analyze NTO orbital composition, and so on.
Present function works for both restricted and unrestricted wavefunction as reference state,
for the latter, the result of Alpha part and Beta part are printed separately, you only need to pay
attention to the NTO pairs having largest eigenvalues (e.g. the largest eigenvalue of Alpha part is
0.03, while the largest eigenvalue of Beta part of 0.95, that means this electronic excitation is
dominated by transition of that Beta NTO pair)
According to my experiences, NTO analysis often works equally well as the hole-electron
analysis introduced in Section 3.21.1, namely both of them are able to avoid inspecting many
orbitals when discussing electronic excitation, and an additional advantage of NTO analysis is that
the orbital phase character is reserved; however, in some cases NTO analysis completely fails, that
is even after transformation to NTO representation, there is still no dominant pair of orbital
transition can be found, and you have to resort to hole-electron analysis.
An example of generating and analyzing NTOs is provided in Section 4.18.4.
Information needed: Basis function, Gaussian/ORCA output file or plain text file which
describes electron transition information
3.21.7 Calculate ghost-hunter index (7)
In J. Comput. Chem., 38, 2151 (2017), Adamo et al. proposed an index used to diagnose if an
excited state yielded by TDDFT calculation is a ghost state. The ghost states are artificial low-
lying CT states resulting from evidently incorrect asymptotic behavior of exchange potential of
pure DFT functionals or the hybrid functionals with low Hartree-Fock exchange composition.
Since the ghost states are untrue states, they should be ignored when discussing electronic
excitation problems; if there many ghost states which significantly polluted electronic spectrum,
then DFT functional with higher HF exchange composition (e.g. M06-2X) or long-range corrected
functional (e.g. B97X) must be used to get rid of them. The ghost-hunter index (MAC) aims to
present a quantitative criterion to judge if a excited state should be regarded as a ghost state.
The ghost-hunter index in its original paper is defined as
ai
ai
a
i
ai
a
iDC
C
M
,CT
,
AC 1)(
where i and a denote occupied and virtual MOs, respectively. The summation loops all TDDFT
configurations, the C is configuration coefficient.
stands for MO energy. DCT is charge-transfer
index (see below for more details). MAC is acronym of Mulliken averaged configuration,
essentially it is an approximate estimation of lower limit of CT excitation energy.
In my opinion, above definition of MAC is somewhat peculiar, since it employs
ai
a
i
a
iCC
,
/
as weight of ia excitation rather than
ai
a
i
a
iCC
,
22 )(/)( as expected. In addition, it does not
consider excitation and de-excitation separately (i.e. the summation simply loops all

3 Functions
173
configurations irrespective of excitation and de-excitation). Taking these problems into account,
here I defined an another form of MAC:
CT
2
2
AC 1
)(
)()(
DC
C
M
ai
ai
a
i
ai
a
i
In which all de-excitations are ignored in the summation.
In the original paper, it is argued that if calculated excitation energy is lower than MAC, then
the excited state should be regarded as ghost state, and the result should be dealt with caution.
However, according to my personal experience, this criterion is somewhat too strong.
In Multiwfn, the MAC is not calculated in subfunction 7 of main function 18. To calculate it,
you should perform usual hole-electron analysis (see introduction in Section 3.21.1 and example
in Section 4.18.1). Once calculation of grid data of the hole and electron is finished, Multiwfn
automatically prints the MAC index as well as its two terms (their difference corresponds to the
MAC index). The MAC index is calculated and given as two forms, the definition 1 corresponds to
the formula in original paper, while the definition 2 corresponds to the formula defined by me,
both of them have been explicitly shown above.
Beware that in Multiwfn, the DCT used in the MAC expression is evaluated as distance
between centroid of electron and hole distributions, it is more or less different to the DCT used in
MAC original paper (referred to as DCT' below), which is calculated as centroid distance between
positive and negative parts of density difference between relaxed excited state density and ground
state density. The DCT used by Multiwfn is not only reasonable enough, but also much cheaper
than DCT' (since evaluating TDDFT relaxed density for large system is fairly expensive). However,
if you really want to calculate MAC index based on DCT', you should obtain the first term of MAC
via electron-hole module, and then calculate the second term (i.e. DCT') via subfunction 3 of main
function 18 (see the example given in Section 4.18.3), and then manually get their difference.
It is worth to mention that the MAC index is only applicable to one-dimension CT problem, if
the CT takes place in multiple directions, then this index is incapable and must be properly
generalized.
A very brief illustration of MAC is presented in Part 7 of Section 4.18.1.
Information needed: Identical to hole-electron analysis (see Section 3.21.1.2)
3.21.8 Calculate interfragment charge transfer in electronic excitation
(8)
Interfragment charge transfer is a very important phenomenon in electronic excitation process.
I devised a very simple but useful way of evaluating amount of interfragment charge transfer
between any two fragment, the method is described below (To be published publicly).
This method contains three steps:
(1) Calculating atomic contribution to all molecular orbitals.
(2) Constructing interatomic charge transfer matrix Q. Its (A,B) element corresponds to the
electron transfer from atom A to atom B during the excitation, and can be expressed as
3 Functions
174
ij jBiA
ij
ji jBiA
j
iBA wwQ ,,
2
,,
2
,)()(
where A,i denotes contribution of atom A in MO i, w is configurational coefficient, the first and
the second summations cycle all MO transition of excitation and de-excitation types, respectively
(the latter is only involved in TDHF and TDDFT). Above formula is very easy to comprehend, it
essentially assumes that electron transfer from A to B is proportional to both composition A in
origin MO and composition B in target MO. The diagonal terms of Q, e.g. QA,A, may be regarded
as amount of electron involved in the electronic excitation within atom A.
(3) Evaluating charge transfer between two molecular fragments based on interatomic charge
transfer matrix. For example, electron transfer from fragments r to s:
rAsBBAsr QQ
frag frag ,frag,frag
There are two additional useful quantities:
Electron net transferred from fragments r to s: rssrsr QQp frag,fragfrag,fragfragfrag
Variation of electron population of fragment r:
ssr
srsr QQp
frag frag,frag
frag frag,fragfrag
The use of present function is quite easy, the input files are completely identical to the hole-
electron analysis (see Section 3.21.1.2). After steps (1) and (2) are done, you will be prompted to
input atom list of fragments 1 and 2, then amount of electron transfer from fragment 1 to 2, that
from fragment 2 to 1, net transfer, as well as variation of electron population of fragments 1 and 2
will be evaluated according to above formulae.
By default, SCPA method is automatically employed to calculate orbital composition, since it
is very fast and commonly reasonable (diffuse functions must not be used in this case, otherwise
SCPA result will be meaningless. See Section 3.10 for more information). If you prefer to use the
composition values computed by Hirshfeld, Hirshfeld-I or Becke method, you should first enter
corresponding subfunction of main function 8, and select "-4: Export composition of every atom
in every orbital to orbcomp.txt", then return to main menu and perform interfragment charge
transfer analysis as usual. If orbcomp.txt is found by Multiwfn in current folder, Multiwfn will
automatically load composition from this file and then use these data to evaluate charger transfer
between user-defined fragments.
An example of present function is given in Section 4.18.6.
3.100 Other functions part 1 (100)
Since Multiwfn has too many functions, some of the functions are relatively "small"
compared to main functions, and some functions are not closely related to wavefunctions analysis,
these functions are classified as "other functions". Because the number of subfunctions in "other
functions" are huge, "other functions" are splitted as part1 (main function 100) and part 2 (main
function 200). Part 1 will be described below, and part 2 will be intorduced in Section 3.200.
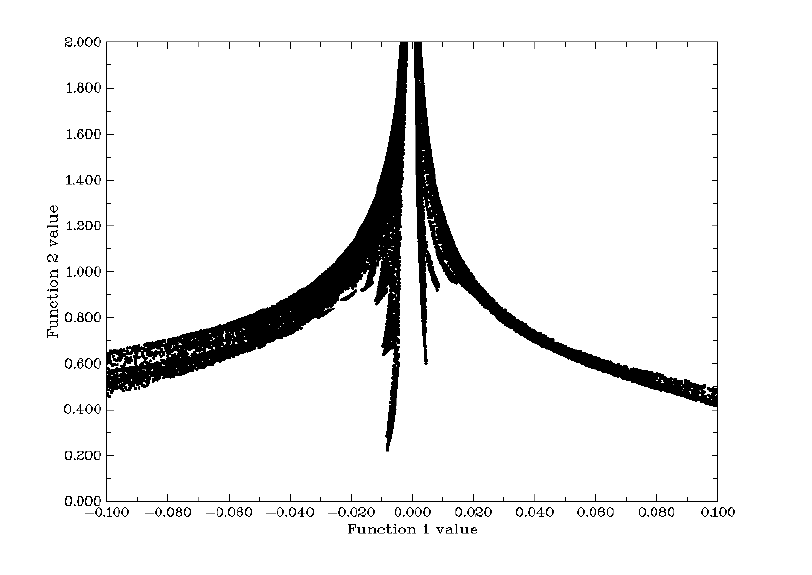
3 Functions
175
3.100.1 Draw scatter graph between two functions and generate their
cube files
This function allows grid data of two functions to be generated at the same time with sharing
grid setting, you can choose to export their cube files, view their isosurfaces and plot scatter graph
between them. It is extremely useful for correlation analysis of two functions in specific spatial
scope and visual research of noncovalent interaction (also known as NCI analysis, see J. Am.
Chem. Soc., 132, 6498 for details).
After you entered this function, select two real space functions that you are interested in, for
example you want to analyze real space function 16 and 14, you should input 16,14 (the first and
the second function will be referred to as functions 1 and 2 respectively below). Then select a
mode to set up grid points. After that Multiwfn starts the calculation of grid data for them
(computing time is identical to calculate grid data for the two real space functions in turn by using
main function 5, except special case, see below), once the calculation is finished, Pearson
correlation coefficient of the two functions in all grid points is printed and a menu appears on
screen, all options are self-explained. If you choose -1 to draw scatter graph, a graph like this will
pop up immediately:
Each scatter point corresponds to each grid point, the position in X-axis and Y-axis
corresponds to the value of function 1 and function 2 at this point respectively. Multiwfn
determines the range of axes automatically according to the minimum and maximum value,
sometimes you have to use option 4 and 5 to reset the range by yourself, otherwise barely points
can be seen in the graph. The size of points can be adjusted by “symbolsize” in settings.ini. The
graph can be saved to current directory by option 1. The X-Y data set of the points can be exported
to output.txt in current directory by option 2.
Option -2 and -3 set the value of function 2 where the value of function 1 is within or without
3 Functions
176
of a specific range respectively. Notice that the data once modified cannot be retrieved again, for
example you set the value of function 2 to 0.0 where function 1 is in the range of 1.4 to 3.5, then
you reuse option -2 to set the value of function 2 to 0.1 where function 1 is in the range of 2.5 to
3.5, now the value of function 2 is 0.0 rather than original data where function 1 is within 1.4 to
2.5.
Since the combination of real space function 15 and 13 (as well as 16 and 14 for promolecule
approximation) is frequently used in weak interaction analysis, for improving calculation speed, a
special routine will be invoked to evaluate grid data for them simultaneously, hence the
computational cost is obviously lower than evaluating the two real space functions separately.
Special usage: If you already have cube files of the two functions to be studied (referred to
as func1.cub and func2.cub, respectively) and you want to directly use the functions in post-
process menu (e.g. plotting scatter map, modifying values), you should follow these steps: Input
the path of func1.cub after booting up Multiwfn, then enter main function 100 and select
subfunction 1, then input 0,0 when selecting real space functions, then input the path of func2.cub,
after that the grid data of the two cube files will be directly taken as function 1 and function 2.
Notice that, of course, the grid setting of func1.cub and func2.cub must be exactly identical.
3.100.2 Export .pdb, .xyz, .wfn, .wfx, .molden, .fch, NBO .47 or input
file of mainstream quantum chemistry codes
This function can be used to output current structure to .pdb and .xyz files. Wavefunction
information can be exported as .wfn or .wfx file when GTF information is available, and can be
exported as .molden, .fch or GENNBO input file (.47) when basis function information is
presented. By this function Multiwfn can be used as file format converter,
e.g. .wfn/.wfx/.fch/.molden/.gms ... .pdb/.xyz/.gjf/.wfn/.wfx/.molden/.fch/.47 ...
For convenience, this function is also able to yield basic input file for a batch of known
quantum chemistry codes based on current structure, net charge and multiplicity, including
Gaussian, GAMESS-US, ORCA, MOPAC, Dalton, MRCC, Molpro, NWChem, PSI, CFOUR,
Molcas. The task type is single point except for MOPAC. For GAMESS-US input file, if basis
function information is presented, you can select if writing the orbital coefficients as $VEC field
so that they can be used as initial guess.
Information needed: Atom coordinates, GTFs (for exporting .wfn/.wfx), basis functions (for
exporting .fch/.molden/.47)
3.100.3 Calculate molecular van der Waals volume
In this function Monte Carlo method is used for evaluating van der Waals (vdW) volume of
present system, two definitions of vdW region are provided: (1) The superposition of vdW sphere
of atoms. This definition is not very accurate, because electron effect is not taken into
consideration, but the speed of evaluation is very fast and wavefunction information is not
required. (2) The region encompassed by certain isosurface of electron density, the isovalue of
0.001 is suitable for isolated system, while 0.002 is more suitable for molecules in condensed
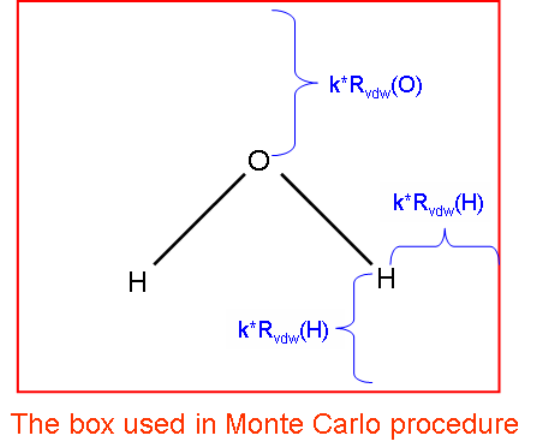
3 Functions
177
phase. One can choose the definition by "MCvommethod" in settings.ini.
The principle of the Monte Carlo procedure is very simple: If we define a box (volume is L)
which is able to hold the entire system, and let N particles randomly distributed in the box, if n
particles are presented in the vdW region, then the vdW volume of present system is n/N*L. Of
course, the result improves with the increase of N. In Multiwfn, you need to define N by input a
number i, the relationship is N=100*2i, for small molecular when i=9 the accuracy is generally
acceptable, for large system you may need to increase i gradually until the result variation between
i and i+1 is small enough to be acceptable as converged. For definition 2 of vdW region, you also
need to input the isovalue of density, and the factor k used to define the box, see below illustration,
where Rvdw is vdW radius. If k is too small, then the vdW region may be truncated, however if k is
too large, more points are needed to maintain enough accuracy. For isovalue of 0.001, k=1.7 is
recommended.
Information needed: atom coordinates (for definition 1), GTFs (for definition 2)
3.100.4 Integrate a function in whole space
This is a very useful and powerful function for integrating selected real space function in the
whole space. The numerical integration method used here is based on the one proposed by Becke
in the paper J. Chem. Phys., 88, 2547 for integrating DFT functional, which is also suitable for any
real space function, but notice that the function must be smooth and converges to zero at infinite
asymptotically. The accuracy is determined by the number of integration points, you can adjust the
number of radial and angular integration points by “radpot” and “sphpot” parameters in
settings.ini, respectively. The integrand can be selected from built-in functions, and you can also
write new function by yourself as user-defined function, see Sections 2.6 and 2.7.
Information needed: Atom coordinates, GTFs.

3 Functions
178
3.100.5 Show overlap integral between alpha and beta orbitals
For unrestricted wavefunctions, orthonormalization condition does not in general hold
between alpha and beta orbitals. This function computes the overlap matrix between alpha and
beta orbitals
rrr dS jiji )()(
,
The diagonal elements are useful for evaluating the matching degree of corresponding spin orbital
pairs, evident deviation to 1 indicates that spin polarization is remarkable.
In present function, there are two options, option 1 calculates the full overlap matrix, the
diagonal elements will be printed on screen and the whole overlap matrix can be selected to output
to ovlpmat.txt in current folder; in addition, the maximum pairing between Alpha and Beta orbitals
are shown. This calculation may be time-consuming for large system. Option 2 only calculates and
prints the diagonal elements, this is always fast.
Since the expectation of S2 operator for single determinant (SD) wavefunction can be easily
derived from the overlap matrix, if option 1 is selected, Multiwfn also outputs this quantity:
N
i
N
jji
SNSS 2
,
Exact
2
SD
2
where N
and N
are the number of alpha and beta electrons. Exact
S 2 is the exact value of
square of total spin angular momentum
1
22
)1(
Exact
2
NNNN
SSS
Information needed: GTFs
3.100.6 Monitor SCF convergence process of Gaussian
Difficulty in SCF convergence is an annoying problem that always encountered in daily work,
monitoring the convergence is important for finding solutions. Multiwfn can monitor SCF process
by using the output file of Gaussian as input, notice that “#P” has to be specified in the route
section, otherwise no intermediate information of SCF process will be recorded in output file.
When you entered this function, all information of previous steps and the thresholds of
convergence are printed on screen, such as
Step# RMSDP Conv? MaxDP Conv? DE Conv?
8 3.51D-06 NO 5.15D-05 NO -8.43D-08 YES
9 1.37D-06 NO 9.11D-06 NO -2.17D-09 YES
10 3.03D-07 NO 2.91D-06 NO -3.75D-10 YES
11 3.12D-08 NO 4.76D-07 YES -1.07D-11 YES
12 7.69D-09 YES 5.72D-08 YES -1.56D-13 YES
Goal 1.00D-08 1.00D-06 1.00D-06
SCF done!
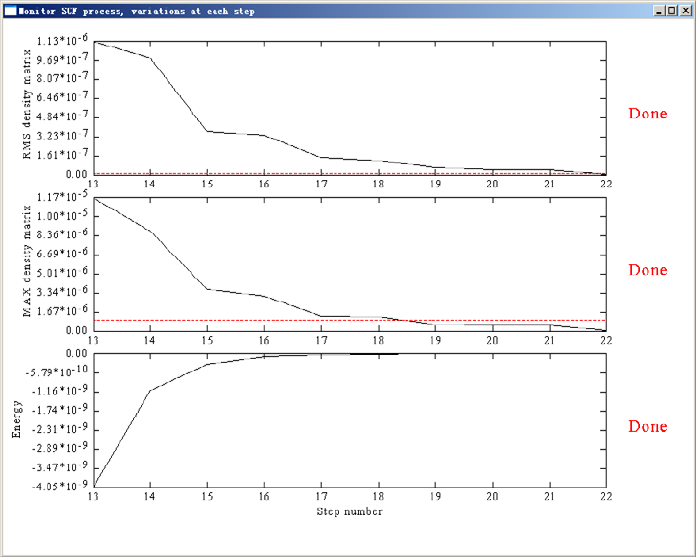
3 Functions
179
Meanwhile a window pops up, which contains curves that corresponding to convergence process
of energy, maximum value and RMS variation of density matrix. After you close the window, you
can print the information and draw the curve graphs again in specific step range by choosing
corresponding options, the Y-axis is adjusted automatically according to the data range.
If the SCF task is work in progress, that is output file is updated constantly, every time you
choose to print and draw the convergence process, the Gaussian output file will be reloaded, so
what you see is always the newest information. For monitoring a time-consuming SCF process, I
suggest you keep the interface on until the SCF task is finished, during this period you choose
option 2 every so often to show the latest 5 steps and analyze convergence trend.
In the graph, gray dash line shows the zero position of Y-axis, the red dash line shows the
threshold of convergence. The picture below shows the last 10 SCF steps of a system. If “Done”
appears in the rightmost, that means corresponding property has already converged, here all three
terms are marked by “Done”, so the entire SCF process has finished.
This function is also compatible with keyword “SCF=QC” and “SCF=XQC”, but not with
“SCF=DM”.
3.100.7 Generate Gaussian input file with initial guess from converged
wavefunction
In Gaussian, the keyword “guess=read” tells the program to read guess wavefunction from
checkpoint file, unfortunately sometimes the checkpoint file is missing. If you still have the output
file of last task and in which “pop=full” keyword is used, you can load that file into Multiwfn, and
then select this function, a new input file named “new.gjf” will be generated in current directory,
in which the converged wavefunction is presented. If the keyword “guess=card” is specified in

3 Functions
180
route section, these wavefunction information will be used as initial guess.
3.100.8 Generate Gaussian input file with initial guess from fragment
wavefunctions
This function is used to combine several fragment wavefunctions to an initial guess
wavefunction, there are three main uses:
1 Generate high quality initial guess wavefunction for complex: If you already have
converged wavefunctions for each fragment, and the interaction between fragments is not very
strong, by using the combined wavefunction as initial guess the SCF process of complex will
converge faster.
2 Perform simple energy decomposition: The total energy variation of forming a complex
can be decomposed as
polarstericorbexels
fragcomplex
tot EEEEEEEE
ii
where Eels is electrostatic interaction term, normally negative if the two fragments are neutural;
EEx is exchange repulsion term, which comes from the Pauli repulsion effect and is invariably
positive. For convenience, it is customary to combine these two terms as steric term (Esteric).
Eorb in above formula is orbital interaction term, and sometimes also known as induction term
or polarization term. Eorb arises from the mix of occupied MOs and virtual MOs. If the combined
wavefunction is used as initial guess for complex, then Eorb can be evaluated by subtracting the the
first SCF iteration energy from the last SCF iteration energy.
st1SCF,lastSCF,orb EEE
Note that complex
SCF,last EE , obviously we can write out below relationship
ii
EEEEEEE frag
stSCF,1orbtotexelssteric
By the way, if the complex you studied concerns evident dispersion interaction (vdW
interaction), there are two possible ways to evaluate the dispersion energy component:
(1) Use Hartree-Fock to calculate interaction energy first ( HF
tot
E), then use MP2 (or better post-
HF method) to calculate interaction energy again ( 2MP
tot
E), then HF
tot
2MP
totdisp EEE .
This relationship comes from the fact that dispersion energy is completely missing in HF energy.
(2) Use HF or the DFT functionals that completely failed to represent dispersion energy to
calculate interaction energy (e.g. B3LYP and BLYP), then use Grimme's DFT-D3 program
(http://www.thch.uni-bonn.de/tc/index.php?section=downloads&) with corresponding parameter
to evaluate DFT-D3 dispersion correlation to interaction energy, which can be simply regarded as
the dispersion component in total interaction energy. If you do not know how to do this and you
can read Chinese, you may consult the post in my blog: http://sobereva.com/210

3 Functions
181
3 Modelling antiferromagnetic coupling system: I exemplify this concept and show you
how to use the function by a representative antiferromagnetic coupling system -- Mn2O2(NH3)8,
The ground state is singlet, while the two Mn atoms have opposite spin and each Mn atom has
high spin. Obviously, restricted close-shell calculation is not suitable for this system, unrestricted
calculation is required, however, the default initial guess is non symmetry-broken state, therefore
the converged unrestricted wavefunction returns to restricted close-shell wavefunction. In order to
make the wavefunction converges to expected state, we have to compute wavefunction for four
fragments separately and then combine them by Multiwfn to construct a proper symmetry-broken
initial guess. The four fragments should be defined as
Fragment 1: Mn(NH3)4 at left side. Charge=+2, sextet.
Fragment 2: Mn(NH3)4 at right side. Charge=+2, sextet.
Fragment 3: One of bridge oxygen atoms. Charge=-2, singlet.
Fragment 4: Another bridge oxygen atom. Charge=-2, singlet.
Notice that “nosymm” and “pop=full” keywords must be specified in the calculation of each
fragment. Assuming the output files are “frag1.out”, “frag2.out”, “frag3.out” and “frag4.out”
respectively, let Multiwfn load “frag1.out” first after boot up, then select function 100 and
subfunction 8 to enter present function, input 4 to tell Multiwfn there are four fragments in total;
since “frag1.out” has already been loaded, you only need to input the path (including filename)
of ”frag2.out”, “frag3.out” and “frag4.out” in turn. After that a Gaussian input file named
“new.gjf” will be outputted in current directory. Notice that everytime you input a fragment,
Multiwfn asks you if flip its spin, only for fragment 2 you should choose “y”, that is make the spin
direction of unpaired electrons down (by default the spin is in up direction) to exactly counteract
the opposite spin in fragment 1, so that multiplicity of complex is 1.
From the comment of “new.gjf” (the texts behind exclamation mark), you can know clearly
how the MOs of complex are combined from MOs of fragments. For example, a two-fragment
system, one of complex MOs in “new.gjf” is
! Alpha orbital: 12 Occ: 1.000000 from fragment 2
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00
0.00000E+00 0.00000E+00 0.00000E+00 0.18850E-01 -0.53690E-01
-0.74180E-01 0.48861E+00 0.16080E+00 -0.12897E+00 -0.12897E+00
0.47150E-01 -0.25269E+00 0.39361E+00 -0.48811E+00 0.36123E+00
We already know there are 8 basis functions in fragment 1 and 12 basis functions in fragment 2,
and this complex MO comes from fragment 2, so the first 8 data (highlighted) are zero and only
the last 12 data have values (the same as corresponding MO coefficients in Gaussian output file of
fragment 2).
If you used diffuse functions and encounter problem at Link401 when running .new by

3 Functions
182
Gaussian, you can add IOp(3/32=2) keyword and retry.
3.100.9 Evaluate coordination number for all atoms
The method come from the original paper of DFT-D3 (J. Chem. Phys.,132,154104). The
coordination number of atom A can be approximately expressed as
AB BA
Ar]1/)RR)(3/4[(16exp1
1
CN
where R is covalent radius from Chem. Eur. J.,15,186.
Although the formula is very simple, however the result is surprisingly good, for example,
the Multiwfn output of formamide in equilibrium structure:
1 N Coordination number 3.0268
2 H Coordination number 1.0039
3 H Coordination number 1.0049
4 C Coordination number 3.0027
5 H Coordination number 0.9973
6 O Coordination number 1.0315
We can see that the result is very close to empirical coordination number, which is integer. By
using this function, atoms in different chemical environment could be readily distinguished.
The so-called “Coordination matrix” is also outputted. The A,B element is the coordination
number between atom A and atom B. The sum of row or column A is CNA value.
Information needed: atom coordinates
3.100.11 Calculate overlap and centroid distance between two orbitals
This function is used to calculate overlap and centroid distance between two orbitals, this is
useful for many purposes, e.g. analyzing charge transfer during electronic excitation. You need to
input index of two orbitals, then X, Y, Z of centroid of the orbitals will be calculated as follows
rrrrrr zdZydYxdX iiiiii 222 |)(||)(||)(|
then the centroid distance between orbital i and j is calculated as
222 )()()( jijijiij ZZYYXXD
Present function also calculates overlap degree of the two orbitals, below two quantities are
calculated respectively (while directly calculating overlap integral of two orbital wavefunctions is
clearly meaningless, since it must be zero due to orthonormalization condition):
rrrrrr dd jiji 22 |)(||)(||)(||)(|
The integrals shown above are not calculated analytically but numerically via Becke's grid-
based integration approach. The integration grid can be set by "radpot" and "sphpot" in settings.ini,
the default values are high enough, and you may want to somewhat decrease them to reduced

3 Functions
183
computational cost for large system, especially when you want to study many orbital pairs.
When the calculation is finished, Multiwfn will ask you whether or not add the two centroids
as two additional dummy atoms (the symbol is Bq). If you choose y, then you can go to main
function 0 to visualize corresponding orbital isosurfaces by transparent or mesh style to examine
correspondence between centroid position and orbital shape.
Information needed: GTFs, atom coordinates
3.100.13 Calculate HOMA and Bird aromaticity index
HOMA is one of the most popular indexes for measuring aromaticity. This quantity was
originally proposed in Tetrahedron Lett., 13, 3839, and then the generalized form was given in J.
Chem. Inf. Comput. Sci., 33, 70. The generalized HOMA can be written as (notice that the HOMA
formula has been incorrectly cited by numerous literatures)
iji
ji
N
2
,Ref
,)R(R1HOMA
where N is the total number of the atoms considered, j denotes the atom next to atom i, and RRef
are pre-calculated constants given in original paper for each type of atom pair. If HOMA equals to
1, that means length of each bond is identical to optimal value RRef and thus the ring is fully
aromatic. While if HOMA equals to 0, that means the ring is completely nonaromatic. If HOMA is
significant negative value, then the ring shows anti-aromaticity characteristic.
HOMA can be calculated by subfunction 13 in main function 100. The built-in and RRef
parameters are directly taken from Chem. Inf. Comput. Sci., 33, 70, they can be adjusted customly
by option 1. When you choose option 0, Multiwfn will prompt you to input the indices of the
atoms in the local system, for example, 2,3,4,5,6,7 (assume that there are six atoms in the ring.
The input order must be consistent with atom connectivity), then HOMA value and contributions
from each atom pair will be immediately outputted on the screen. For example, thiophene
optimized under MP2/6-311+G**, the output is
Atom pair Contribution Bond length(Angstrom)
1(C ) -- 2(C ): -0.001852 1.382006
2(C ) -- 3(C ): -0.056708 1.421170
3(C ) -- 4(C ): -0.001852 1.382006
4(C ) -- 5(S ): -0.023886 1.712627
5(S ) -- 1(C ): -0.023886 1.712627
HOMA value is 0.891817
Since 0.891817 is close to 1, the HOMA analysis suggests that thiophene has relatively
strong aromaticity.
Bird index (Tetrahedron, 41, 1409) is another geometry-based quantity aimed at measuring
aromaticity, and can be calculated by option 2 of subfunction 13 in main function 100. The
formula is
)]/(1[100 K
VVI

3 Functions
184
where
b
R
a
N
n
NN
N
V
ji
ji
iji
,
.
2
.)(
100
In the formula, i cycles all of the bonds in the ring, j denotes the atom next to atom i. n is the
total number of the bonds considered. N denotes Gordy bond order, N is the average value of
the N values. Ri,j is bond length. a and b are predefined parameters respectively for each type of
bonds. VK is pre-determined reference V, for five and six-membered rings the value is 35 and 33.2,
respectively. The more the Bird index close to 100, the stronger the aromaticity is.
Available a and b include C-C, C-N, C-O, C-S, N-O and N-N; for other type of bonds user
should set corresponding parameter by option 3. By option 4 user can adjust or add VK parameter.
Information needed: Atom coordinates
3.100.14 Calculate LOLIPOP (LOL Integrated Pi Over Plane)
In the paper Chem. Commun., 48, 9239, the authors proposed a quantity named LOLIPOP
(Localized Orbital Locator Integrated Pi Over Plane) to measure π-stacking ability of aromatic
systems, they argued that a ring with smaller LOLIPOP value has stronger π-depletion (namely
lower π-delocalization), and hence shows stronger π-stacking ability.
LOLIPOP is defined as definite integral of LOL-π (the LOL purely contributed by π-orbitals)
from a distance of 0.5Å away from the molecular plane. Only points with LOL-π>0.55 are taken
into account. The integration is made in a cylindrical region perpendicular to the molecular plane,
with a radius of 1.94Å corresponding to the average between the C and H ring radii in benzene.
In Multiwfn, function 14 in main function 100 is designed for calculating LOLIPOP, the
default value 0.5Å and 1.94Å mentioned above can be changed by option 4 and 3 respectively.
Before starting the calculation, you have to choose which orbitals are π orbitals by option 3, you
can find out π orbitals by visualizing orbital isosurfaces via main function 0. The calculation can
be triggered by option 0, you need to input the indices of the atoms in the ring in accordance with
the atom connectivity, then grid data of LOL around the ring will be evaluated, then the LOLIPOP
value is computed by numerical integration. Of course, smaller grid spacing gives rise to higher
integration accuracy, but brings severer computational requirement on evaluating LOL. The
default spacing of grid data is 0.08 Bohr, this value is fine enough in general.
Information needed: GTFs, atom coordinates
3.100.15 Calculate intermolecular orbital overlap
This function is used to calculate orbital overlap integral between two molecules, namely
rrr dS Monomer
l
Monomer
ili
)()( 21molInt
,

3 Functions
185
where i and l are molecular orbital indices of monomer 1 and monomer 2, respectively. This
integral is useful in discussions of intermolecular charge transfer, e.g. J. Phys. Chem. B, 106, 2093.
Three files are required for evaluating the integral:
(1) Gaussian output file of dimer, "iop(3/33=1) nosymm guess(only)" should be specified in
route section. Multiwfn will read overlap matrix from this file.
(2) Gaussian output file of monomer 1, "nosymm pop=full" should be specified in route
section. Multiwfn will read orbital coefficients of monomer 1 from this file.
(3) Gaussian output file of monomer 2, "nosymm pop=full" should be specified in route
section. Multiwfn will read orbital coefficients of monomer 2 from this file.
Notice that, the atomic coordinates in file (2) and (3) must be in accordance with the one in
file (1). The basis-set used should be the same for the three calculations. The atomic sequence
should be identical. Molecular geometry must be given in Cartesian coordinate.
To calculate the intermolecular orbital overlap integral, after booting up Multiwfn, the file (1)
should be loaded first. After entering present module, the paths of file (2) and (3) should be
inputted in turn. Then one can input such as 8,15 to obtain Intmol
15,8
S. If user input the letter o, then
the entire SIntmol matrix will be outputted to "ovlpint.txt" in current folder.
Information needed: Gaussian output files
3.100.18 Yoshizawa's electron transport route analysis
Theory
This function is used to analyze electron transport route and is mainly based on Yoshizawa's
formula (Acc. Chem. Res., 45, 1612), At the Fermi energy, the matrix elements of the zeroth
Green's function, R/A)0(
rs
G, which describes the propagation of a tunneling electron from site r to
site s through the orbitals in a molecular part, can be written as follows:
kk
skrk
rs iE
CC
EG
F
*
F
R/A)0( )(
where Crk is the kth MO coefficient at site r, asterisk on the MO coefficient indicates a complex
conjugate, εk is the kth MO energy, and η is an infinitesimal number determined by a relationship
between the local density of states and the imaginary part of Green's function. By this formula, if
two electrodes are connected to site r and s, by this formula we can readily predict the transmittion
probability between the two sites. From the expression of the denoiminator, it can be seen that
HOMO and LUMO have the largest contribution to G. If only HOMO and LUMO are taken into
account, the formula can be explicitly written as
iE
CC
iE
CC
EG srsr
rs
LUMOF
*LUMOLUMO
HOMOF
*HOMOHOMO
F
R/A)0( )(
This formula allows one to visually examine the possibility of electron transmission between site r
and s by means of observing molecular orbital diagram. If both site r and s have large C in
magnitude, and their relative phase in HOMO and in LUMO is different, then the magnitude of G

3 Functions
186
will be large, indicating that transmission between r and s will be favourable. For examples, see
Acc. Chem. Res., 45, 1612. Note that G may be positive and negative, but only absolute value of G
is meaningful for discussing transmission.
In Multiwfn, iη term in G is always ignored, since this is an infinitesimal number. The
coefficient C comes from the output of "NAOMO" keyword in NBO program. In almost all
organic conductors, σ orbitals have little contribution to conductance, therefore present function
only takes π orbitals into account, and the molecular plane must be parallel in XY or YZ or XZ
plane.
Input file
Gaussian output file is required as input file. In the route section, pop=nboread must be
specified, and "$NBO NAOMO $END" must be written at the last line, for example:
Usage
After you enter this function, you need to select which plane is the one your molecular plane
parallel to. Then program will load Gaussian output file and find out the atoms having expected π
atomic orbital (restrictly speaking, the "Val"-type p natural atomic orbitals that perpenticular to the
chosen plane). The coefficient of these atomic orbitals will be used to compute G.
Then you will see a menu, the options are explained below:
-4 Set distance criterion: Input lower and upper limits. Then in option 2 and 3, the route
whose distance exceeds this criterion will not be shown.
-3 Set value criterion: In option 1, the MO whose contribution to G is less than this criterion
will not be shown. In option 2 and 3, the route whose |G| is smaller than this criterion will not be
shown.
-2 Set Fermi energy level: Namely set EF in the Yoshizawa's formula.
-1 Select the range of MOs to be considered: Namely set the MO range of the summation
in the Yoshizawa's formula.
0 View molecular structure: As the title says.
1 Output detail of electron transport probability between two atoms: You need to input
index for two atoms, they will be regarded as site r and s, then Grs (the value behind "Total value")
will be outputted; meanwhile program also outputs the contribution from each MO, the distance
between the two atoms, and the calculated Grs for the case when only HOMO and LUMO are
taken into the summation.
2 Output and rank all electron transport routes in the system: All routes in current
system will be tested, if the route simultaneously fulfills the G and distance criteria set by -3 and -
#P b3lyp/6-31g* pop=nboread
b3lyp/6-31g* opted
0 1
[Molecular geometry field]
$NBO NAOMO $END
3 Functions
187
4, then the involved atoms, G and distance of the route will be printed. The routes are ranked by
aboslute value of G.
3 Output and rank all electron transport routes for an atom: Similar to option 2, but only
consider the routes involving specific atom.
Information needed: Gaussian output files containing NAOMO information
3.100.19 Generate promolecular .wfn file from fragment
wavefunctions
This function is used to generate promolecular wavefunction in .wfn format based on
fragment wavefunctions. In the promolecular state, the electron distribution simply comes from
the superposition of the electron distribution of the related fragments; in other words, in this state
the electron transfer and polarization between the fragments have not started. Each promolecular
orbital directly corresponds to one of fragment orbitals.
The input file can be in any wavefunction format, such as .wfn, .wfx, .fch, .molden and .gms,
any kind of wavefunction is supported. Infinite number of fragments are supported.
Assume that the promolecular wavefunction consists of N fragments, after boot up Multiwfn,
you should make Multiwfn load the first fragment wavefunction file, and then go to this function,
input the total number of fragments (N), then input the path of the wavefunction files
corresponding to the other fragments in turn. The promolecule .wfn file will be generated in
current folder as "promol.wfn".
For SCF wavefunctions, the MOs are sorted according to orbital energies from low to high,
virtual MOs are not recorded. For post-HF wavefunctions, the natural orbitals are sorted according
to orbital occupation from high to low.
If any fragment is unrestricted open-shell, then the promolecular wavefunction will be
regarded as unrestricted open-shell type, namely the alpha and beta orbitals will separately occur
in the resultant .wfn file. In this case, for each unrestricted open-shell fragment Multiwfn will ask
you if flipping the spin of its orbitals; if you choose yes, then the energies and occupations of all
alpha and all beta orbitals will be exchanged; this treatment is particularly important if you want to
get the promolecular wavefunction combined from free-radical fragments.
Please always carefully check the resultant .wfn file to examine its reasonableness before
using it.
Some examples are given in Section 4.100.19.
Information needed: GTFs, atom coordinates
3.100.20 Calculate Hellmann-Feynman forces
The Hellmann-Feynman (H-F) force is the actual force acting on nuclei in a quantum system,
which is exerted by electron density and other nuclei:
3 Functions
188
AB BA
BAB
A
A
A
AAA
A
AZ
ZdZ
H
33
nucele
||
)(
||
))((
ˆ
RR
RR
r
rR
rRr
FF
R
F
Present function calculates and prints total H-F force as well as the contribution from electron
density and other nuclei respectively.
In practice, notice that the H-F forces calculated as above based on the electronic
wavefunction and nuclear information recorded in the wavefunction file are generally not
equivalent to the forces computed by quantum chemistry program at current calculation level
(FQC), which may be expressed as:
H
HE
AAA
Aˆ
2
ˆ
QC
RRR
F
The partial derivative of wavefunction with respect to nuclear coordinate involves partial
derivative of orbital coefficients, configuration state coefficients and basis functions with respect
to RA. Therefore, only for the fully variational wavefunctions such as HF, DFT and MCSCF with
basis functions independent of nuclear coordinates (e.g. plane wave), the second term on the r.h.s.
of above equation is vanishing, and then the H-F forces just equals to the force at current
calculation level.
Information needed: GTFs, atom coordinates
3.100.21 Calculate properties based on geometry information for
specific atoms
Input index range of some atoms (or input all to select the whole system), then many
properties based on geometry information will be calculated for them, including
(1) Mass
(2) Geometry center, center of mass, center of nuclear charges
(3) Radius of gyration
(4) Sum of nuclear charges and dipole moments from nuclear charges
(5) The atom having minimum/maximum coordinate in X/Y/Z
(6) Minimum and maximum distance
(7) Moments of inertia tensor, principal axes and principal moments of inertia
(8) Rotational constant
(9) Electrostatic interaction energy between nuclear charges
Note: If the input file is .chg, then "nuclear charges" mentioned above will stand for atomic
charges.
Radius of gyration is computed as
jj
icii
m
m2
)( rr
, where r is the coordinate of nucleus,
rc is mass center, m is atomic mass.

3 Functions
189
The moments of inertia tensor, which is a symmetry matrix, is calculated as
iiii
iiii
iiii
iiii
iiii
iiii
iiii
iiii
iiii
ZZZYZX
YZYYYX
XZXYXX
yxmyzmxzm
zymzxmxym
zxmyxmzym
III
III
III
)(
)(
)(
22
22
22
I
In the output, "The moments of inertia relative to X,Y,Z axes" correspond to the three diagonal
terms of I.
The three eigenvectors of I are known as principal axes, they are outputted as the three
columns of the matrix with the title "***** Principal axes (each column vector) *****". The
corresponding three eigenvalues of I are the moments of inertia relative to principal axes.
If the moments of inertia are given in amu*Å2, then the rotational constants in GHz can be
directly evaluated; for example, the rotational constant relative to Z axis is 11
210
8
ZZ
I
h, where
h is Planck constant, and
=1.66053878*10-27 is a factor used to convert amu to kg.
Information needed: Atom coordinates
3.100.22 Detect π orbitals and set occupation numbers
Sometimes one wants to analyze π properties of a conjugated system, e.g. calculating ELF-π,
hence one must first find out which ones are π orbitals by visualizing orbital isosurfaces, and then
set occupation number of all the other orbitals to zero. Unfortunately, for large system this work is
very tedious and time-consuming. To make your life easier, this function is developed to
automatically identify π orbitals, and then set their occupation numbers. There are two cases:
(1) The input file contains non-localized orbitals (e.g. canonical orbital, natural orbital, etc.):
In this case, present function is only applicable to exactly planar system, namely in the input file
all atoms are exactly in the same Cartesian plane XY, YZ or XZ. You can use options 1, 2 and 3 to
choose Cartesian plane according to actual situation, or you can directly choose 0 to let program
automatically determine the plane. Then π orbitals will be detected automatically.
(2) The input file contains localized molecular orbitals (LMOs): In this case, π orbitals are
identified using following method (to be published): First, Multiwfn calculates orbital composition
of present orbital (SCPA method is used in present function), and finds out the atom having the
largest contribution and the one having the second largest contribution (they will be referred to as
atom A and B, respectively). If contribution of A is larger than a given threshold (default is 85%),
then the orbital will be regarded as single-center orbital and thus be skipped. If the orbital is not
singly centered, occupation of this orbital will be temporarily set to 2.0 and electron density due to
this orbital at midpoint of A and B will be calculated. If the result is smaller than a given density
threshold (default is 0.02 a.u.), the orbital will be finally regarded as π orbital. The reason of
introduction of the density threshold is easy to understand: if a standard π orbital forms between
two atoms, because π orbital must have a nodal plane along the bond, the electron density at their
midpoint should be exactly zero. However, when the two atoms are not in a exactly planar local
3 Functions
190
region, since and orbitals are not strictly separable due to unavoidable mixing, the density at
midpoint must not be exactly zero, therefore, a threshold should be employed to tolerate this
circumstance.
The case (2) corresponding to option -1, after you select it, you will enter an interface, in
which you can manually set the two above-mentioned thresholds. Also, in the interface you can set
constraint of atom range by inputting atom indices. For example, if you inputted 2,4-7,9, then only
the orbitals in which the two atoms with largest contributions are both in the range of 2,4,5,6,7,9
may be finally identified as π orbitals. Clearly, you can use this feature to identify all π type of
LMOs lying at an interesting region, e.g. conjugated ring.
During identification process, indices, occupation numbers and energies of identified π
orbitals are shown on screen. Then you can choose option 1 to set the occupation numbers of these
π orbitals to zero, or choose option 2 to set the occupation number of all other orbitals to zero.
Option 3 is akin to option 1, but only valence π orbitals are taken into account. Option 4 is used to
clean occupation number for all orbitals except for valence π orbitals.
The use of this function is illustrated in Section 4.100.22. Section 4.5.3 also involves this
function.
Information needed: GTFs (case 1), basis functions (case 2), atom coordinates
3.100.23 Fit function distribution to atomic value
This function is very similar to the function used to fit ESP charge (see Section 3.9.10 and
3.9.11), but the real space function to be fitted is not limited to ESP, for example you can fit
average local ionization energy or even Fukui function distributed on molecular surface to atomic
values.
After select option 1, and then select a real space function, the function value will be
calculated on the fitting points and then fit to atomic value by least-squares method, namely
minimizing below error function
2
21 )]()([)...,(
iiiN VVpppF rr
where i denotes the index of fitting points, p is atomic value, V is the value of real space function,
while V' is the function value evaluated by atomic value, which is defined as
AiA
A
ir
p
V
,
)(r
where A denotes atom index, rA,i corresponds to the distance between nucleus of atom A and the
fitting point i.
The error of fitting are measured by RMSE and RRMSE
N
VV
iii
2
)()(
RMSE
rr
ii
iii
V
VV
2
2
)(
)()(
RRMSE r
rr
3 Functions
191
where N denotes the number of fitting points.
By default all fitting centers are placed at nuclei, you can also load additional fitting centers
from external file by option -2, see Section 3.9.10 for the format.
The default fitting points are exactly the ones used by Merz-Kollman method (see Section
3.9.11). You can use option 3 to customize the number of layers, use option 2 to adjust the density
of the fitting points distributed on the surface, and use option 4 to set the scale factor of the vdW
radii used for constructing each layer. (e.g. If you set two layers, and their scale factors are set to
1.0 and 1.2 respectively, then the first and the second layer will be constructed by superposing the
vdW radii of all atoms multiplied by 1.0 and 1.2, respectively)
No constraint on the total value (viz.
ii
p) is applied by default. However, you can use
option 5 to set a constraint on the total value. Evidently, if the constraint is set to the net charge of
your system, and you choose ESP as fitting function, then the result will be identical to MK
charges.
The fitting points can be directly defined via external plain text file by option -1 (and thus
will not be constructed by superposing vdW spheres), see Section 3.9.10 for the file format. If the
file contains calculated function values of all fitting points and meanwhile the first line of this file
(the number of points) is set as negative value, then the real space function at each fitting point
will not be evaluated by Multiwfn but loaded from this file directly.
Information needed: GTFs, atom coordinates
3.100.24 Obtain NICS_ZZ for non-planar system
NICS is a very popular index used to measure aromaticity. In many literatures, such as Org.
Lett., 8, 863, It was shown that NICS(0)ZZ or NICS(1)ZZ is a better index than the original
definition of NICS, which is current known as NICS(0).
For exactly planar systems, if the system plane is parallel to XY plane, then NICS(0)ZZ means
the ZZ component of magnetic shielding tensor at ring center. The only different from NICS(1)ZZ
to NICS(0)ZZ is that the calculated point is not ring center, but the point above (or below) 1Ǻ of
the plane from ring center. Note that the definition of ring center is highly arbitrary, the original
definition uses geometry center, while some people use center of mass, and some researchers
recommend using ring critical point (RCP) of AIM theory as ring center, for example WIREs
Comput. Mol. Sci., 3, 105. (Personally, I think using RCP is the best choice)
If the ring of interest is skewed or not exactly planar, calculation of NICSZZ is somewhat
cumbersome, because one cannot directly acquire the component of magnetic shielding tensor
perpendicular to the plane from output file of quantum chemistry programs. Moreover, for
NICS(1)ZZ, it is difficult to properly set the position to be calculated. Present function is designed
to solve these difficulties.
For example, you want to calculate NICS(1)ZZ for a non-planar system, you can follow below
steps:
(1) Use Multiwfn to open a file containing atomic coordinates of your system
(e.g. .xyz/.pdb/.mol/.wfn/.wfx/.fch/.molden/.gms...)
(2) Find out ring center. You can use topology analysis module (main function 2) to locate
3 Functions
192
RCP, or use subfunction 21 in main function 100 to obtain geometry center or center of mass.
Using which method to define the ring center depends on yourself.
(3) Enter subfunction 24 of main function 100 (namely the function I am describing), input
the ring center you just obtained, and input index of three atoms to define the ring plane. Then the
coordinate of the points above and below 1Ǻ of the ring plane from the ring center will be
outputted. You can use any one of these two points in quantum chemistry program to calculate
magnetic shielding tensor at this position.
Hint: The unit normal vector perpendicular to the ring plane is also outputted by Multiwfn, by which you can
easily derive the position used to calculate such as NICS(2), NICS(3.5)...
(4) Input all components of the magnetic shielding tensor in Multiwfn according to the output
of your quantum chemistry program. Then the negative value of "The shielding value normal to
the plane" outputted by Multiwfn is just NICS(1)ZZ.
For calculating NICS(0)ZZ, the process is more simple:
(1) Identical to the step 1 shown above
(2) Identical to the step 2 shown above
(3) Use the ring center you just obtained in your quantum chemistry program to calculate the
magnetic shielding tensor at this position.
(4) Enter subfunction 24 of main function 100, input ring center, and input index of three
atoms to define the ring plane. Then input all components of the magnetic shielding tensor
according to the output of your quantum chemistry program. Then the negative value of "The
shielding value normal to the plane" outputted by Multiwfn is just NICS(0)ZZ.
Information needed: Atom coordinates
3.100.25 Calculate area and perimeter for a ring
This is a utility used to calculate ring area (as well as perimeter), since ring area is sometimes
involved in wavefunction analysis. For example, in J. Org. Chem., 72, 9163 (2007), it is proposed
that the aromaticity of an entire polycyclic system can be evaluated as ΣNICS(1)ZZ/area2.
In this function, you need to input the index of the atoms in the ring in clockwise manner, for
example, the phenanthrene,
If you would like to calculate the area of the middle ring, you can input for example 3,4,8,9,10,7.
During the calculation, the ring will be partitioned into multiple triangles, whose areas will be
calculated separately and then summed up.
The ring can contain arbitrary number of atoms, and the ring may be non-planar; however
you should make sure that the ring is convex, otherwise the result could be meaningless. So for a
large ring with complex shape (e.g. porphyrin), you'd better to calculate the area of its each part
respectively and then sum up the results.

3 Functions
193
The ring perimeter is outputted along with ring area.
Information needed: Atom coordinates
3.200 Other functions part 2 (200)
3.200.1 Weak interaction analysis for fluctuation environment by
RDG method
Theory
Reduced density gradient (RDG) method is a very powerful way to analyze weak interaction,
if you are not familiar with it, please first check Section 4.100.1 for a brief introduction. In J.
Chem. Theory Comput., 9, 2226, RDG method is extended to analyze fluctuation environment (e.g.
molecular dynamics trajectory), resulting in averaged RDG (aRDG) method. Present function
aims at realizing aRDG analysis.
The only different between aRDG and the original RDG method is that in the former, the
electron density
and its gradient norm |
| are not calculated for only one geometry, but for
multiple frames of a dynamics trajectory and then get average (namely
and
). Therefore,
the isosurface of averaged reduced density gradient
3/4
3/12 )(
|)(|
)3(2
1
)aRDG( r
r
r
can be directly used to reveal the averaged weak interaction regions in the dynamics process.
Similarly, in order to exhibit averaged weak interaction type, in aRDG method, the λ2 term in
Sign(λ2)
function is obtained as the second largest eigenvalue of the averaged electron density
Hessian matrix computed through out the dynamical trajectory.
aRDG method also defines a new quantity named thermal fluctuation index (TFI) to reveal
the stability of weak interaction
)(
)]([
)TFI( r
r
r
std
Whose numerator is standard deviation of electron density in the dynamical trajectory, which can
be calculated as
n
Std ii
2
])()([
))((
rr
r
where n is the number of frames in consideration,
i is the density calculated based on the
geometry of frame i. After mapping TFI on the isosurface of aRDG, the stability of each weak
interaction region can be clearly identified by visually examining the color.
Evidently, the quality of aRDG graph directly depends on how many frames are taken into
3 Functions
194
account. Small number of frames, for example 50 frames, only leads to very inaccurate and very
unsmooth isosurface graph. In general, at least 500 frames are recommended to be used to
generate aRDG graph.
Usage
First note that since calculating electron density based on wavefunction for large number of
geometries is very expensive, promolecular approximation is forced to be used in the aRDG
analysis function of Multiwfn. This approximation is highly reasonable and always works well.
The trajectory stored in .xyz file is allowed as input file. You can use such as VMD program
to convert other format of trajectory files to .xyz trajectory file.
PS: The structure of a multiple frame .xyz file looks like below
[The number of atoms in frame 1]
[Element, x, y and z of atom 1 in frame 1]
[Element, x, y and z of atom 2 in frame 1]
...
[Element, x, y and z of atom n in frame 1]
[The number of atoms in frame 2]
[Element, x, y and z of atom 1 in frame 2]
[Element, x, y and z of atom 2 in frame 2]
...
[Element, x, y and z of atom n in frame 2]
[The number of atoms in frame 3]
...
In all of the frames, the coordinate of the interesting molecule should be fixed. For example,
if you want to study the weak interaction between solvents and a benzene molecule, then the
position of the benzene must be fixed through out the whole trajectory.
After you enter present function, you will be prompted to input the frame range to be
analyzed, for example inputting 140,450 means the frame from 140 to 450 will be used in the
aRDG analysis. Then you need to set up grid, the spatial range of the box of course should
properly enclose the molecule of interest. After that, averaged electron density, averaged density
gradient and averaged density Hessian will be calculated for each frame, you should wait patiently.
Once the calculation is finished, you can use corresponding options to draw scatter graph between
averaged RDG and averaged Sign(λ2)
, output scatter points, export their cube files, etc. Thermal
fluctuation index can also be calculated and export to cube file.
An example is given in Section 4.200.1.
Information needed: Multiple frames of atom coordinates
3.200.2 Calculate atomic and bond dipole moments in Hilbert space
This function is used to calculate atomic and bond dipole moments directly based on basis
functions (viz. in Hilbert space). You can also consult Section 12.3.2 of the book Ideas of
Quantum Chemistry (L. Piela, 2007).
Theory
In the formalism of basis functions, the system dipole moment can be expressed as follows
ij jiji
AAA PZ
||
,
elenuc rRμμμ
3 Functions
195
where Z and R are charge and coordinate of nuclei. P is density matrix,
ji
|| r is dipole
moment integral between basis function i and j.
The system dipole moment can be decomposed as the sum of single-atom terms and atom
pair terms
AABABABAA
AA
AABAB
AA)()( dippopdippopnuctottot μμμμμμμμ
The expression and physical meaning of the five terms are
nuc
A
μ: Dipole moment due to nuclear charge
AAA ZRμ
nuc
pop
A
μ: Dipole moment due to the electron population number localized on single atom
(Notice that this is different to the electron population number calculated by Mulliken or similar
methods, because the overlap population numbers have not been absorbed into respective atoms)
AiAjjijiAAAA Ppp
|
,
loclocpop Rμ
dip
A
μ
: Atomic dipole moment, which reflects the electron dipole moment around an atom. rA
is the coordinate variable with respect to nucleus A
pop
,
,
dip
||
where||
A
AiAjjiji
AA
AiAjjAijiA
P
P
μr
Rrrrμ
pop
AB
μ: Dipole moment due to the overlap population between atom A and B
2/)(|2 ,
pop BAAB
AiBjjijiABABABAB Ppp RRRRμ
dip
AB
μ
: Bond dipole moment, which somewhat reflects the electron dipole moment around
geometry center of corresponding two atoms. Of course, if A and B are not close to each other,
then this term will be very small, and thus inappropriate to be called as bond dipole moment.
pop
,
,
dip
||2
where||2
AB
AiBjjiji
ABAB
AiBjjABijiAB
P
P
μr
Rrrrμ
By means of Mulliken-type partition, the bond dipole moments can be incorporated into
atomic dipole moments, so that the system dipole moment can be written as the sum of single
center terms
)( dippopnuc AA
AAμμμμ
where pop
A
μ is the dipole moment due to the Mulliken population number of atom A
3 Functions
196
BBiBjjijiAAAA Ppp
|
,
MulMulpop Rμ
and dip
A
μ is the atomic overall dipole moment of atom A
Mul
,,
dip |||| A
BBiBjjiji
BBiBjjAijiA PP μrrμ
Note that the B index in above formulae runs over all atoms.
Usage
The input file must contain basis function information (e.g. .fch, .molden and .gms).
After you enter present function, you can choose option 1 to output information of a specific
atom, including: Atomic local population number, loc
A
p; atomic dipole moment, dip
A
μ;
contribution to system dipole moment due to nuclear charge, nuc
A
μ; contribution to system dipole
moment due to electron, dip
A
μ+pop
A
μ; contribution to system dipole moment, nuc
A
μ+dip
A
μ+pop
A
μ.
You can also choose option 2 to output information between specific atom pair, including:
bond population number, pop
AB
μ; bond dipole moment, dip
AB
μ
; contribution to system dipole
moment, pop
AB
μ+dip
AB
μ
.
If choose 3, atomic overall dipole moment and related information of selected atoms will be
outputted, including: Atomic Mulliken population number, Mul
A
p; atomic overall dipole moment,
dip
A
μ; contribution to system dipole moment due to nuclear charge, nuc
A
μ; contribution to system
dipole moment due to electron, dip
A
μ+pop
A
μ; contribution to system dipole moment,
nuc
A
μ+dip
A
μ+pop
A
μ.
If you choose option 10, then X/Y/Z components of electron dipole moment matrix will be
outputted to dipmatx.txt, dipmaty.txt and dipmatz.txt in current folder, respectively. For example,
the (i, j) element of Z component of electron dipole moment matrix corresponds to
ij jiji zP
||
,
Information needed: Atom coordinates, basis functions
3 Functions
197
3.200.3 Generate cube file for multiple orbital wavefunctions
By this function, grid data of multiple orbital wavefunctions can be calculated and then
exported to a single cube file or separate cube files at the same time.
After you entered this function, you need to first define the orbitals you are interested in (e.g.
3,5,9-17), and then define grid setting, after that choose the scheme to export the grid data. If you
select scheme 1, then grid data of all orbitals you selected will be outputted to orbital.cub in
current folder. Lots of visualization programs, including VMD and Multiwfn, support the cube file
containing multiple sets of grid data. If you select scheme 2, then the grid data will be exported as
separate files, for example orb000003.cub, orb000005.cub, orb000009.cub, etc. The number in the
filename corresponds to orbital index.
Information needed: Atom coordinates, GTFs
3.200.4 Generate iso-chemical shielding surfaces (ICSS) and related
quantities
Theory
Nuclear independent chemical shielding (NICS) is commonly studied at some special points
(e.g. ring center), and in some papers NICS is investigated by scanning its value in a line (1D) or
in a plane (2D). The so-called iso-chemical shielding surface (ICSS) actually is the isosurface of
NICS, which clearly exhibits the distribution of NICS in 3D space, and thus presents a very
intuitive picture on aromaticity.
Present function is used to generate grid data and visualize isotropic ICSS, anisotropic ICSS,
ICSSXX, ICSSYY and ICSSZZ, they correspond to the isosurface of NICS, NICSani, NICSXX,
NICSYY and NICSZZ, respectively. At a given point, NICSani is defined as 3 - (1 + 2)/2, where
denotes the eigenvalue of magnetic shielding tensor ranked from small to large (viz. 3 is the
largest one).
The original paper of ICSS is J. Chem. Soc. Perkin Trans. 2, 2001, 1893. While ICSSani,
ICSSXX, ICSSYY and ICSSZZ are proposed by me. I believe for planar systems, the component
form of ICSS must be more meaningful and useful than ICSS, just like NICSZZ has conspicuous
advantage over NICS. ICSSani is useful to reveal the anisotropic character of NICS in different
regions.
Usage
Multiwfn itself is incapable of calculating magnetic shielding tensor and thus requires
Gaussian to do that. The general steps is shown below
(1) Prepare an input file of Gaussian single point task for the system under study, %chk have
to be explicitly specified. For example, see "examples\ICSS\anthracene.gjf". This file will be
taken as template to automatically build Gaussian input file of NMR task
(2) After boot up Multiwfn, load the file containing the atomic coordinate of your system
(e.g. .pdb/.xyz/.wfn/.fch ...), then enter subfunction 4 of main function 200. Beware that the atomic
coordinates loaded must exactly accord with the ones in the file prepared in step 1.
3 Functions
198
(3) Set up grid by following the prompt. Beware that even using medium quality grid may be
fairly time-consuming. Hence low quality grid is in general recommended for medium-size system.
(4) Input n, namely do not skip step 5 and 6.
(5) Input the path of the Gaussian input file you prepared in step 1.
(6) Many input files of Gaussian NMR task are generated in current folder, they are named as
NICS0001.gjf, NICS0002.gjf ...
In these files, each Bq atom corresponds to a grid point. In the NMR task Gaussian will output magnetic
shielding tensor at each Bq along with that at each nuclei. By default 8000 atoms (the real ones + Bq) are presented
in each input file, but this can be altered via "NICSnptlim" parameter in settings.ini. The reason why separate files
rather than a single file are generated is because Gaussian cannot run properly if the number of Bq atoms is too
large due to over-consume of memory, also there is upper limit on the total number of atoms in each Gaussian run.
You can try to set NICSnptlim to a larger value if you have large physical memory, this will reduce overall cost of
ICSS analysis.
Note that for G09 D.01, due to a bug in memory allocation when using the default Harris initial guess, you
should always add "guess=huckel" to route section, otherwise the NICSnptlim has to be set to a very small value
(e.g. 1000) to make Gaussian work; in this case the overall cost of ICSS calculations is often quite high.
(7) Feed all of the input files generated in last step to Gaussian to yield output files. If
possible, please keep Multiwfn running (If you have terminated it, reboot Multiwfn and repeat
step 2, 3 with the same setting and input y at step 4).
Hint: You can make use of the script "examples\runall.sh" (for Linux) or "examples\runall.bat" (for Windows),
which invokes Gaussian to run all .gjf files in current folder to yield output files with the same name but with .out
suffix.
(8) Input the path of the folder containing Gaussian output files yielded in the last step. Then
Multiwfn will load the magnetic shielding tensors from the NICS0001.out, NICS0002.out ... in
this folder.
(9) Select the property you are interested in.
(10) Visualize isosurface or export the grid data to cube file by corresponding option. For
example, in step 9 you selected "ZZ component", then the isosurface and the grid data will
correspond to ICSSZZ. You can also select "-1 Load other property" to load other property.
Notice that if this is not the first time you analyze your system and you already have
Gaussian output files of NMR task of present system in hand, you can start from step 2 and select
y in step 4 to bypass the step 5, 6 and 7. Of course, the grid setting in step 3 must be exactly
accord with the one used in generating the Gaussian output files of NMR task.
An example is given in Section 4.200.4.
Information needed: Atom coordinates, input file of Gaussian single point task, output file of
Gaussian NMR task.
3.200.5 Plot radial distribution function for a real space function
This function is used to plot radial distribution function (RDF) for a real space function
drrfrRDF 2
),()(
where r is radial distance from sphere center, and denotes angular coordinate in a sphere layer.
The integration curve of RDF can also be plotted
'2
'
lowlow ),()()'( r
r
r
rdrdrrfdrrRDFrI

3 Functions
199
Clearly, if rlow is set to 0 (viz. sphere center), then I() will be the integral of f over the whole
space.
In present function, one can choose the real space function to be studied, set the position of
sphere center, set the lower and upper limit to be calculated and plotted, set the number of points
in radial and angular parts. The larger the number of points, the more accurate the integration
curve.
After the parameters are set, select option 0 to start the calculation, and then you will see a
new menu, in which you can plot RDF and its integration curve, save the graph or export the
corresponding original data.
An example is given in Section 4.200.5.
Information needed: Atom coordinates, GTFs
3.200.6 Analyze correspondence between orbitals in two
wavefunctions
Theory
This function is used to analyze correspondence between the orbitals in two wavefunctions.
The two sets of orbitals can be produced under different basis-sets, by different theoretical
methods, at different external environments, in different electronic states, or at slightly different
geometries. The two sets of orbitals can also be different types, for example the first set of orbitals
are canical MOs produced by Hartree-Fock calculation, while the second set of orbitals are natural
orbitals produced by post-HF calculation.
The orbitals {i} in present wavefunction (the wavefunction loaded when Multiwfn boots up)
can be represented as linear combination of the orbitals {j} in another wavefunction (the
wavefunction you specified after entering present module), i.e.
jji jCi , where jiC ji
,
Once we have the overlap integral, we immediately know how j is associated to i. The
contribution from orbital j to orbital i is simply the square of overlap integral, namely <i|j>2100%.
Usage
After you enter this function, first you need to input the orbital range to be considered for
present wavefunction (istart1~iend1), and then input the path of the second wavefunction and the
orbital range to be considered (istart2~iend2). After that the overlap matrix between istart1~iend1
and istart2~iend2 will be calculated by Becke's multi-center numerical integration scheme. Then
you will see the five largest contributions from istart2~iend2 to each orbital in istart1~iend1. If
you want to obtain all coefficients (as well as the corresponding contributions) of istart2~iend2 in
a given orbital among istart1~iend1, you can then directly input the index of the orbital. If you
need all overlap integrals between istart1~iend1 and istart2~iend2, input -1, then they will be
outputted to convmat.txt in current folder.
If an orbital (i) in present wavefunction can be exactly expanded as linear combination of

3 Functions
200
istart2~iend2, then the normalization condition must be satisifed:
%100%100
2iend
2istart
2
j
ji
From the Multiwfn output you can find the maximum deviation to normalization condition. If the
value is zero, that means all orbitals in istart1~iend1 can be exactly represented by the orbitals in
istart2~iend2.
Note that the atomic coordinate of present wavefunction and that of the second wavefunction
are not necessarily identical, the two wavefunctions can even correspond to different molecules.
However if the difference of the distribution scope of the atomic coordinates in the two
wavefunctions is large, the integration accuracy must be low and the result is not reliable.
Commonly the default integration grid is fine enough, i.e. 50 radial points and 230 angular
points. If you wish to improve the accuracy, you should set "iautointgrid" in settings.ini file to 0,
then the number of radial and angular integration grids will be directly determined by "radpot" and
"sphpot" in settings.ini; set them to a large value will result in good integration accuracy.
The computational cost of this function directly depends on the number of orbitals in
consideration; so if your system contains very large number of orbitals, do not choose all orbitals
at once.
Example
As an example, we use present function to study the conversion relationship between HF/6-
31+G* MOs and MP2/6-31+G* natural orbitals (NO) for CH3NH2.
After boot up Multiwfn we input
C:\CH3NH2_MP2.wfn // MP2/6-31+G* wavefunction file, there are 48 NOs
200
6
[Press ENTER button directly to choose all orbitals]
C:\CH3NH2_HF.wfn // HF/6-31+G* wavefunction file, there are 9 MOs
[Press ENTER button directly to choose all orbitals]
Then you will see
1: 2( 94.63%) 1( 5.36%) 4( 0.01%) 3( 0.00%) 6( 0.00%)
2: 1( 94.64%) 2( 5.36%) 3( 0.00%) 9( 0.00%) 6( 0.00%)
3: 3( 85.21%) 4( 9.87%) 7( 3.24%) 9( 0.88%) 6( 0.79%)
4: 4( 86.88%) 3( 10.66%) 6( 1.94%) 9( 0.48%) 7( 0.02%)
5: 6( 54.88%) 7( 41.11%) 9( 3.20%) 4( 0.45%) 3( 0.34%)
6: 8( 57.50%) 5( 42.47%) 7( 0.00%) 6( 0.00%) 4( 0.00%)
7: 5( 57.50%) 8( 42.48%) 7( 0.00%) 4( 0.00%) 6( 0.00%)
8: 9( 86.62%) 6( 10.30%) 7( 1.63%) 4( 0.89%) 3( 0.50%)
9: 7( 53.98%) 6( 32.07%) 9( 8.76%) 3( 3.28%) 4( 1.89%)
10: 9( 0.00%) 7( 0.00%) 6( 0.00%) 4( 0.00%) 2( 0.00%)
11: 5( 0.00%) 8( 0.00%) 3( 0.00%) 7( 0.00%) 4( 0.00%)
... (ignored)
47: 6( 0.01%) 7( 0.00%) 9( 0.00%) 3( 0.00%) 4( 0.00%)
48: 9( 0.04%) 7( 0.00%) 6( 0.00%) 4( 0.00%) 3( 0.00%)

3 Functions
201
The first column denotes the index of the MP2 NOs, the largest five contributions from the
Hartree-Fock MOs to them are shown at right side. As can be seen, the first (second) NO is nearly
equivalent to the second (first) MO. While the 9th NO cannot be solely represented by any MO, it
mainly arises from the severe mix of the 7th (53.98%) and 6th MOs (32.07%), the 9th MO also
has non-neglectable contribution (8.76%).
If you want to get all coefficients and compositions of an orbital of present wavefunction (e.g.
the 5th NO), then simply input 5, you will see
1 Contribution: 0.000 % Coefficient: 0.001509
2 Contribution: 0.000 % Coefficient: -0.000042
3 Contribution: 0.339 % Coefficient: -0.058201
4 Contribution: 0.447 % Coefficient: 0.066869
5 Contribution: 0.000 % Coefficient: 0.000000
6 Contribution: 54.882 % Coefficient: 0.740826
7 Contribution: 41.113 % Coefficient: -0.641194
8 Contribution: 0.000 % Coefficient: 0.000000
9 Contribution: 3.199 % Coefficient: -0.178856
Total: 99.980 %
this output suggests 9MO1788.07MO6412.06MO7408.05NO The
99.98% at the last line indicates that the 5th NO can be perfectly represented by linear
combination of these nine MOs.
Information needed: Atom coordinates, GTFs
3.200.7 Parse output of (hyper)polarizability task of Gaussian
The output of (hyper)polarizability task of Gaussian (polar keyword) is difficult to
understand, at least for beginners. This function is used to parse these outputs and then print them
in a more readable format, and at the same time some quantities relating to (hyper)polarizability
analysis will be outputted. Currently this function is formally compatible with Gaussian 09 and 16.
Basic concepts
Energy of a system can be written as Taylor expansion with respect to uniform external
electric field F
65432
0
4
0
4
4
3
0
3
3
2
0
2
2
0
720
1
120
1
24
1
6
1
2
1
)(
24
1
6
1
2
1
)()(
εFδFγFβFαFFμ0
F
F
F
F
F
F
F
F
0F
FFF
F
E
EEEE
EE
0
4
4
0
3
3
0
2
2
0
0
FFF
FF
γ
F
β
F
α
F
μEEEE
where 0 is permanent dipole moment, which is a vector; is polarizability, which is a matrix
(second rank tensor); is first hyperpolarizability, which is a third rank tensor and known as

3 Functions
202
second-order nonlinear optical response (NLO) coefficient; is second hyperpolarizability, which
is a fourth rank tensor and known as third-order NLO coefficient. The higher terms such as and
are very unimportant and thus rarely discussed. The (hyper)polarizability tensors are directly
correlated to the frequency of external field F. If F has zero-frequency (static electric field), then
the (hyper)polarizabilities are known as static or frequency-independent ones. The dynamic or
frequency-dependent (hyper)polarizabilities correspond to those at external electromagnetic fields
with non-zero frequency.
Dipole moment of a system in uniform electric field can be written as
32
1
32
0)6/1()2/1(
μμ
μ
γFβFαFμ
F
μE
The linear response of dipole moment with respect to F, namely the 1 term, can be explicitly
written as below
z
y
x
zzzyzx
yzyyyx
xzxyxx
z
y
x
F
F
F
Fαμ1
The polarizability is a symmetric matrix rather than a scalar, implying the difference of
polarizability in different directions. In order to facilitate comparison of overall polarizability
between various systems, it is convenient to define the isotropic average polarizability
3/)(3/)Tr( zzyyxx
α
Anisotropy of polarizability can be defined in various ways:
Definition1 see Chem. Phys., 410, 90 for example
2/)](6)()()[( 222222 yzxzxyzzyyzzxxyyxx
Definition 2 This definition is the most commonly use one, see J. Chem. Phys., 98, 3022
(1993) for example
2/])()()[( 222 zzyyzzxxyyxx
Definition 3 {
} stand for eigenvalues of ranking from small to large
2/)( 213
Hyperpolarizability is a third rank tensor that can be described by a 3*3*3 matrix. For
dynamic , Gaussian is capable of calculating its dc-Pockels form
i,j,k(-;,0) and SHG form
i,j,k(-2;,). For the former, the i and j index can be freely exchanged, while for the later the j
and k index can be freely exchanged, therefore the 3*3*3=27 components can be reduced to 18
unique ones. For static case, viz.
i,j,k(0;0,0), since all of the three indices are exchangeable
(known as Kleinman's symmetry, e.g.
xyy=
yxy=
yyx,
zyy=
yzy=
yyz …), only 10 components are
unique. The Kleinman's symmetry is only approximately applied to dyanmic at low-frequency
external field.
The value in one of the three Cartesian axes can be calculated by the general equation

3 Functions
203
},,{,)()3/1( zyxji
jjijjjiijji
The magnitude of is defined as
222
tot zyx
prj (also known as
vec), which is the projection of on dipole moment vector , can be
sampled experimentally (electric field induced second harmonic generation (EFISH) experiment).
|| is the component in the direction of
i
ii
||
prj
prj|| )5/3(
Some people prefer to discuss the perpendicular and parallel components of with respect to
Z axis, they are defined respectively as
jjjzjzjzjjZ )232()5/1(
)(
zZ
)5/3(
)(||
For static case, we can explicitly write out in x, y and z directions as
zzzzyyzxxz
yzzyyyyxxy
xzzxyyxxxx
and zZ
)5/1(
)(
.
Usage
The polar keyword in Gaussian is specific for calculating and based on analytic
derivatives (by means of coupled-perturbed SCF equation) or numerical derivatives (by means of
finite field treatment).
After you enter this function of Multiwfn, you should select which calculation combination is
used, so that Multiwfn can properly parse the output. In Gaussian 09/16 there are several
circumstances:
(1) polar keyword + the methods supporting analytic 3-order derivatives (HF/DFT/Semi-
empirical methods)
(2) polar keyword + the methods supporting analytic 2-order derivatives (e.g. MP2)
(3) polar=Cubic keyword + the methods supporting analytic 2-order derivatives
(4) polar keyword + the methods supporting analytic 1-order derivatives (CISD, QCISD,
CCSD, MP3, MP4(SDQ), etc.)
(5) polar=DoubleNumer (equivalent to Polar=EnOnly) keyword + the methods supporting
analytic 1-order derivatives
(6) polar keyword + the methods only supporting energy calculation (CCSD(T), QCISD(T),
MP4(SDTQ), MP5, etc.)
Only (1), (3) and (5) produce hyperpolarizability, other combinations only produce
polarizability. Notice that in the Gaussian input file you must specify #P!
Only for (1), if CPHF=RdFreq is also specified along with polar, or you used
polar=DCSHG, and meantime the external field frequencies (e.g. 0.05 0.07 0.1) are written after

3 Functions
204
molecular geometry with a blank line in front of it, Gaussian will calculate and output frequency-
dependent (hyper)polarizabilities along with static (hyper)polarizability. CPHF=RdFreq polar
cases only evaluate
(-;,0) values, while polar=DCSHG cases evaluate both
(-;,0) and
(-
2;,) values. By default Multiwfn only parses the static (hyper)polarizability. If you wish to
parse the frequency-dependent ones instead of the static one, before selecting option 1 you should
select -1 first. The user then can choose the result at which frequency will be parsed. Also, one can
choose parsing the
(-;,0) one or the
(-2;,) one, the latter can be chosen only for the case
of polar=DCSHG.
Worthnotingly, it is well known that the sign of all hyperpolarizability components outputted
by Gaussian are wrong and should be multiplied by -1, Multiwfn automatically accounts for this
problem. This problem exists at least in G09 D.01.
In this function, Multiwfn outputs all unique components of dipole moment, polarizability
and hyperpolarizability (if available) with explicit labels, as well as isotropic polarizability,
polarizability anisotropy (in definitions 1 and 2), hyperpolarizability in three axes (
x,
y,
z),
magnitude of hyperpolarizability (
tot) and so on. All of them have been introduced above.
By using option -3, you can choose the unit in the output. Atomic unit, SI unit and esu unit
can be chosen. The conversion factors are
SI esu
1 a.u. 8.4783510-30 C m 2.54175 10-18 esu
1 a.u. 1.648810-41 C2m2J-1 1.481910-25 esu
1 a.u. 3.2063610-53 C3m3J-2 8.6392210-33 esu
1 a.u. 6.2353810-65 C4m4J-3 5.0367010-40 esu
In "example" folder, DFT_polar_static.out and DFT_polar_freq.out are example files of
static and frequency-dependent calculations of case (1), respectively.
Information needed: Output file of "polar" task of Gaussian
3.200.8 Calculate (hyper)polarizability by sum-over-states (SOS)
method
This function is used to calculate polarizability, first, second, and third hyperpolarizabilities
based on sum-over-states method.
A brief survey of the theories for evaluating (hyper)polarizability
Some basic concepts of (hyper)polarizability are introduced in Section 3.200.7. There are a
few different ways to calculate (hyper)polarizability, including derivative method, sum-over-states
(SOS) and response method
(1) Derivative method: This is the most straightforward and commonly used one. The
derivatives needed by static (hyper)polarizability can be evaluated analytically by means of
coupled-perturbed SCF (CPSCF) equation; specifically, CPHF for HF and CPKS for KS-DFT.
These derivatives can also be evaluated numerically by means of finite difference technique,
which is also known as finite field (FF) method. Evidently FF is much slower and not as accurate
3 Functions
205
as CPSCF, however it is still useful, because high-order of analytic derivatives, especially the ones
at sophisticated post-HF levels, are not widely supported by many quantum chemistry programs
due to the difficulties in coding. When all requested derivatives are available analytically,
derivative method will be very efficient. The frequency-dependent variant of CPSCF equation
enables the derivative method to evaluate dynamic (hyper)polarizability, but there is no way to
evaluate dynamic (hyper)polarizability in terms of FF treatment. The polar keyword in Gaussian,
as discussed carefully in Section 3.200.7, corresponds to this derivative method.
(2) SOS method: This method for evaluating static and dynamic (hyper)polarizability is
relatively inefficient, because in principle it involves a sum over all excited states (in practical
applications, taking 60~120 lowest states into account is often enough), while determination of a
large number of excited states is usually quite time comsuming in ab initio cases (e.g. CIS and
TDDFT), especially for large system (e.g. >40 atoms). Due to the high computational cost, SOS is
generally not recommended for evaluation of (hyper)polarizability when derivative method can be
carried out analytically. The only advantages of SOS may be that the contribution from different
states can be separated and discussed respectively, and when transition dipole moments between
different excited states are available in hand, the (hyper)polarizability at different frequencies can
be evaluated rather rapidly. Worthnotingly, the SOS based on the cheap semi-empirical ZINDO
calculation (SOS/ZINDO) is very popular for evaluating (hyper)polarizability of large system.
(3) Response method: This method is specific for dynamic (hyper)polarizability and also
known as propagator method. TDHF and TDDFT are its two practical realizations. This method is
not prevalently supported by mainstream quantum chemistry codes.
(4) Correction vector method: Proposed by Zhigang Shuai, not popular currently.
Working equations of SOS method
The explicit SOS equations for evaluating polarizability and 1st/2nd/3rd hyperpolarizability
can be found in J. Chem. Phys., 99, 3738 (1993), the idea was originally proposed by Orr and
Ward in Mol. Phys., 20, 512 (1971).
The equations for polarizability
and first hyperpolarizability
are (all units are in a.u.)
0
00
0
0000 )](),([
ˆ
);(
ii
B
i
A
i
ii
A
i
B
i
i
B
i
A
i
AB BAP
00 2
00
2121 ))((
)](),(),([
ˆ
),;(
ij ji
C
j
B
ij
A
i
ABC CBAP
where
ji AA
ij
ˆ
ij
AA
ij
A
ij
00
ii
A,B,C... denote one of directions {x,y,z};
is energy of external fields,
=0 corresponds to static
electric field; i stands for excitation energy of state i with respect to ground state 0.
P
ˆ is
permutation operator, for
and
evidently there are 2!=2 and 3!=6 permutations, respectively.
A
ij
is A component of transition dipole moment between state i and j; when i=j the term simply
corresponds to electric dipole moment of state i.
ˆ is dipole moment operator, e.g. x
x
ˆ.

3 Functions
206
The SOS equation for second hyperpolarizability
is
00 31
0000
II
000 332
00
I
III
321321
))()((
))()((
))]((),(),(),([
ˆ
),,;(
ij jii
D
j
Cj
B
i
A
i
ijk kji
D
k
C
jk
B
ij
A
i
ABCD DCBAP
The Z components of
is defined as
AzzAAzAzAzAAzz )()15/1(
Similarly for X and Y components. The total magnitude of
may be measured as
222
tot zyx
. There are two common definitions of average value of
:
])[5/1(:2def
:1def
zzyyzzxxyyxxyyzzxxzzxxyyzzzzyyyyxxxx
zyx
The SOS equation for third hyperpolarizability
is
))((
1
))((
1
))((
)2/1(
1111
))((
)2/1(
))()()((
))]((),(),(),(),([
ˆ
),,,;(
322443
)0( ,, 1
0000
III
32431
)0( ,, 42
0000
II
)0( ,,, 4431
00
I
IIIIII
43214321
kjkj
kji ii
E
k
D
jk
Cj
B
i
A
i
kjii
kji kj
E
k
D
jk
Cj
B
i
A
i
lkjl lkji
E
l
D
kl
C
jk
B
ij
A
i
ABCDE EDCBAP
Input file
Two kinds of input files may be used:
(1) Plain text file containing excitation energies and transition dipole moments for all
involved states. Polarizability, first, second and third hyperpolarizabilities can be calculated in this
case. Below format should be satisfied (assume a very simple case, only 2 excited states).
2 // The number of excited states
1 1.1 // Excited state 1, its index and excitation energy (eV)
2 3.2
0 0 0.845 0.2 0.4 // Electric dipole moment of ground in X,Y,Z (a.u.)
0 1 0.231 0.3 0.7 // Transition dipole moment between ground state and excited state 1
0 2 0.112 0.564 0.21
1 1 0.021 0.465 0.0 // Electric dipole moment of excited state 1
3 Functions
207
1 2 0.001 0.3 0.11 // Transition dipole moment between excited states 1 and 2
2 2 0.432 0.14 0.42
Important hint: You can directly utilize the function introduced in Section 3.21.5 to generate such a plain text
file based on the Gaussian or ORCA output file of electron excitation task.
If merely polarizability is interesting, only the content before the line "1 1" is needed to be
provided, all other contents can be ommited; in this case, the number of excited states should be
written as a negative number (-2 in above case) to tell Multiwfn do not to load them.
(2) Gaussian output file of common CIS, TDHF, TDDFT or ZINDO task. Since Gaussian
does not output all transition dipole moments needed by SOS hyperpolarizability calculation, only
polarizability will be calculated by Multiwfn in this case. In order to obtain accurate polarizability,
the number of calculated states should be large enough. If nstates keyword is specified to a very
large value, e.g. 1000000, then all states will be calculated. #P is suggested to be used, since the
excitation energy will then be printed in a higher precision format.
Usage
After you entered this function you will see a menu, there are three kinds of functions:
(1) Option 1~4: Used to calculate , , and at a given frequency, respectively. User needs
to input frequency of each external field. Since calculation of and are often time-consuming, in
these cases users will be prompted to input the number of states in consideration, small number is
evidently cheaper, but may give rise to lower accurate result.
(2) Option 5~7: Used to study the variation of , and with respect to the number of states
in consideration. User needs to input frequency of each external field. For and , the number of
states taken into account ranges from 1 to all states loaded, the stepsize is 1. While for , since the
computational cost may be quite high, users are allowed to customly defined the ending value and
stepsize. The result will be outputted to plain text file "alpha_n.txt" or "beta_n.txt" or
"gamma_n.txt" in current folder, the meaning of each column can be seen in command-line
window. One can directly drag these plain text files into window of Origin program to plot the
variations as curve maps.
(3) Option 15~17: Used to study the variation of the , and with respect to frequency of
external fields. For , users need to input initial value, ending value and stepsize of external field
frequencies. For and , users should write a plain text file, each row corresponds to a pair of
frequency (in a.u.) to be calculated. Multiwfn will prompt users to input the path of the file. Below
is an example file used to study how (-0;0,,-) varies as goes from 0 to 0.2 a.u. with stepsize
of 0.02
0.0 0.0 0.0
0.0 0.02 -0.02
0.0 0.04 -0.04
...[ignored]
0.0 0.2 -0.2
Since the computational cost for evaluating may be quite high, in this case users are
allowed to set the number of states in consideration. The result will be outputted to plain text file
"alpha_w.txt" or "beta_w.txt" or "gamma_w.txt" in current folder, the meaning of each column can
be seen in command-line window. One can directly drag these plain text files into window of
Origin program to plot the variations as curve maps.
3 Functions
208
Multiwfn not only outputs the tensor of (hyper)polarizability, but also outputs many related
quantities, such as anisotropy, magnitude and the component along Z axis. The quantities
involving and are discussed in Section 3.200.7, the ones involving have been introduced
above.
An example is given in Section 4.200.8.
3.200.9 Calculate average bond length and average coordinate
number
This function is used to calculate average bond length between two elements and average
coordinate number. This function is particularly useful for analyzing structure character of atom
clusters, for example the Ge12Au cluster shown below (the structure file is provided as
examples\Ge12Au.pdb). By using this function, we can immediately obtain the average Ge-Ge
bond length and average Au-Ge bond length, as well as average coordinate number of Ge due to
Ge-Au or Ge-Ge bonds, or of Au due to Ge-Au bonds. A nice application of this kind of analysis
on Al clusters can be found in J. Chem. Phys., 111, 1890 (1999).
The average bond length is defined as follows
ji ij
b
R
n
R1
where Rij is the distance between atom i and j, only the terms smaller than or equal to a given
distance cutoff (e.g. 2.2Å) will be regarded as bonds and thus be taken into the summation. nb is
the total number of bonds.
The average coordinate number is calculated as follows
ii
N
n
CN 1
where Ni is the number of bonds surrounding the atom i, n is the total number of atoms.
3 Functions
209
After you entered this function, you need to input two elements, for example Ge,Au, and
input a distance cutoff, for example 3.2, then the Ge-Au contacts 3.2Å will be regarded as Ge-
Au bonds and the average bond length will be calculated, the minimum and maximum bond
lengths will also be outputted. After that, if you select y, the average coordinate number of Ge due
to Ge-Au bonds will be shown.
Information needed: Atom coordinates
3.200.10 Output various kinds of integral between orbitals
This function is used to calculate electric/magnetic dipole moment integral, velocity integral,
kinetic energy integral and overlap integral between orbitals, advanced users may recognize the
significance of these data. In the case of a range of orbitals, the results are exported to orbint.txt in
current folder, the first and second columns correspond to the index of the two orbitals; In the case
of a pair of orbitals, the result is directly printed on screen.
The electric dipole moment integral vector between two orbitals is defined as
jijiij
|| rμμ
The magnetic dipole moment integral vector between two orbitals is calculated as (more
detail can be found in Section 3.21.1.1. The negative sign is ignored)
jiij i
|| rM
The velocity integral vector between two orbitals is evaluated as (the negative sign is ignored)
jiij i
||v
Worthnotingly, due to the Hermitian of the operators, we have
jijiijii
jijiijii
vvvv
MMMM
0
0
Note that the imaginary sign is not explicitly shown in the output.
The kinetic energy and overlap integrals between two orbitals are respectively evaluated as
jiijjiij SK
|||)2/1( 2
Information needed: Atom coordinates, GTFs
3.200.11 Calculate center, the first and second moments of a real space
function
This function is used to calculate center, integral value, the first and second moments of a
specific real space function for present system.

3 Functions
210
Theory
The center of a real space function f is defined as
rr
rrr
rdf
df
)(
)(
c
where the denominator is the integral of the function over the whole space.
The first moment is a vector and is evaluated as
rrμdf
z
y
x
z
y
x
)(
The second moment is a matrix and defined as
rrΘdf
zzyzx
yzyyx
xzxyx
zzzyzx
yzyyyx
xzxyxx
)(
2
2
2
where x, y, z are the coordinate components relative to rc.
If its eigenvalues {
} are sorted from low to high, then the anisotropy of can be calculated
as 2/)( 213
. The radius of gyration can be calculated as
rr df )(
321
.
Usage
This function employs Becke's multicenter integration method for evaluating above
mentioned quantities. The accuracy is determined by radial points and angular points, which can
be set by "radpot" and "sphpot" in settings.ini, respectively.
The option 1 calculates and outputs the integral, the first and second moments (relative to rc),
and the corresponding anisotropy and radius of gyration of the real space function selected by
option 3. The center (rc) should be properly first set by option 4. Of course, commonly rc is
initially unknown, the default value is (0,0,0), you may use option 2 to evaluate the actual center
of a real space function and take it as the center for the succeeding calculations triggered by option
1.
For example, to evaluate the first and second moments of spin density (relative to the center
of spin density), after you entered this function you should input
3 // Select real space function
5 // Spin density
2 // Calculate center of spin density
y // Take the resultant center as the one for evaluating the first and second moments
1 // Evaluate the first and second moments
When using option 1, if the function to be studied is chosen as electron density, then the
nuclear quadrupole and molecular quadrupole moment tensors will also be outputted, the latter can
be straightforwardly obtained by substracting the former by the second moment of electron density.
Information needed: Atom coordinates, GTFs

3 Functions
211
3.200.12 Calculate energy index (EI) or bond polarity index (BPI)
This function is used to calculate energy index (EI) or bond polarity index (BPI), which were
defined in J. Phys. Chem., 94, 5602 (1990).
The EI for atom A in a molecule is defined as follows
val
iAii
val
iAiii
A
,
,
EI
where i,A denotes composition of atom A in MO i.
i and
i are occupation and energy of MO i,
respectively. The summation runs over valence MOs. In fact, the denominator is simply the
number of valence electrons of atom A, and the numerator corresponds to total energy of its
valence electrons. Therefore, EIA can be regarded as average energy per valence electron of atom
A. In the original paper of EI, Mulliken method was used to compute the atomic contribution to
MOs, thus this method is also employed in present implementation of EI, though other methods
such as Hirshfeld partition should work equally well or even better. (Note that since Mulliken
method is used, which is incompatible with diffuse functions, the use of diffuse basis functions
must be avoided!)
The BPI between atoms A and B in a molecule is defined as
)EIEI()EIEI(BPI refref BBAAAB
where EIref is reference EI value derived from calculation of homonuclear species. For example,
you study BPICN for H3C-NH2, then ref
C
EI is computed as EIC in ethane, and ref
N
EI is computed
as EIN in H2N-NH2. The larger value of BPIAB implies higher bond polarity of the A-B bond.
Group electronegativity is evaluated as negative of EIX for corresponding radical, X is the
attaching atom. For example, to obtain group electronegativity for -CH3 group, you should
calculate -EIC for CH3 radical.
This function of Multiwfn is used to calculate EI for specific atom in present system, all the
R, RO and U types of HF/DFT wavefunction are supported. Multiwfn automatically detects the
number of inner-core electrons and determines which MOs are the valence ones and thus should
be taken into account.
An example is given in Section 4.200.12.
Information needed: Atom coordinates, basis functions
3.200.13 Pipek-Mezey orbital localization
Canonical molecular orbital often shows strong delocalization character and thus does have
direct correlation with bonding. There are many ways to localize MOs, the most popular ones are
Boys localization, Edmiston–Ruedenberg localization and Pipek–Mezey (PM) localizaiton. PM
3 Functions
212
localization is preferred over the other two because it is relatively cheap and easy to be
implmented. The essence of PM localization is to maximize below quantity:
iA
i
A
pP 2
)(
where pAi denotes Mulliken population of atom A in MO i. For details, see its origin paper J. Chem.
Phys., 90, 4916 (1989), the working equation can be found in J. Comput. Chem., 14, 736 (1993).
Present function was developed for realizing PM localization. The input file must contain
basis function information, thus you can use e.g. .fch, .molden and .gms as input file. This
function only works for restricted and unrestricted SCF wavefunction.
PM localization is an iterative process, thus you should set criterion of convergence and
maximum number of cycles. The default values are commonly appropriate and need not to be
changed. You can choose to localize occupied MOs only, or localize both occupied and
unoccupied MOs (the two set of orbitals are localized separately, i.e. no mixure between occupied
and unoccupied orbitals will occur). For unrestricted wavefunction, the alpha and beta parts are
dealt with separately.
By default, once the localization is converged, the localized wavefunction will be exported to
new.fch in current folder, and then Multiwfn automatically load it, after that you can analyze the
localized orbitals in various ways, for example, plotting them as isosurfaces by main function 0. If
you don't want to let Multiwfn automatically load the newly generated new.fch, you can choose
option -3 once.
If you want to obtain energy of the localized orbitals, you need to choose option -4, and input
path of a file containing Fock (or Kohn-Sham) matrix in original basis functions. The matrix
elements should be provided in lower-triangular form, namely in this sequence: F(1,1) F(2,1)
F(2,2) F(3,1) F(3,2) F(3,3) ... F(nbasis,nbasis), where nbasis is the total number of basis functions.
The format is free. The Fock matrix can be obtained from output of some quantum chemistry
codes. The energy of localized orbital is corresponding diagonal term of Fock matrix in localized
orbital representation. Specifically, Multiwfn performs below representation transform:
CFCF AO
T
LMO
where FAO is the Fock matrix in original basis function that loaded from external file, C(r,i)
corresponds to coefficient of basis function s in localized orbital i. Energy of localized orbital j is
simply FLMO(j,j).
Although PM localization is fast for small systems, for large systems it becomes
computationally expensive. If you really want to apply it to large systems, the basis set used
should not be too large. In addition, PM localization should not be used when diffuse functions are
used, because this method is essentially based on Mulliken population, which is not compatible
with diffuse functions.
Hint: If you do not have special reasons, you only need to localize occupied orbitals.
Localization of unoccupied orbitals is much more time-consuming than that of occupied orbitals,
since the number of unoccupied orbitals is often very higher when extended basis set is used.
Moreover, only occupied orbitals are commonly chemically interesting.
An example is provided in Section 4.200.13.
3 Functions
213
Information needed: Atom coordinates, basis functions
3.200.14 Perform integration within isosurfaces of a real space
function
This function is used to integrate specific real space function in domains, which denote
individual spatial regions enclosed by isosurfaces of a given real space function. For example, you
can integrate electron density within various domains defined by isosurfaces of reduced density
gradient (RDG) to study strength of weak interaction.
Below is basic procedure of using this module:
(1) Use option 2 and 3 to set the way to define the domains. For example, you selected RDG by
option 2 and input <0.5 in option 3, then the region where RDG is less than 0.5 will be integrated.
(2) Choose option 1 and properly define grid, then Multiwfn starts to calculate the grid data for the
real space function you selected and identifies domains that statisfied the criterion you set. (If you
already have grid data in memory, you may also choose option -1 to directly use it rather than
calculate new grid data)
(3) Once calculation in last step is finished, Multiwfn prints the number of grids in each domain.
In very simple case, from these information you may directly infer which domain is the one you
want to study, while for common case, you need to use option "3 Visualize domains" to visualize
domains in a GUI, in which you can select domain at the right-bottom list and check its profile,
each green point on the graph corresponds to a grid in the domain. Once you found the domain
you are interested in, close GUI and choose "1 Perform integration for a domain", the real space
function (can be selected by option 4, the default one is electron density) will be integrated in the
domain, the integral value, domain volume and average/maximum/minimum value of the
integrand in the domain are outputted. You can also select "2 Perform integration for all domains"
to obtain integral values for all domains. In addition, some regions you are interested in may be
identified as separate domains by Multiwfn, to study the property of the regions more conveniently,
you can choose "-1 Merge specific domains" to merge selected domains are a single domain, so
that you do not need to manually sum up their integral values.
By the way, in the menu there is an option "5 Calculate q_bind index for a domain", this is
used to calculate the qbind index defined in J. Phys. Chem. A, 115, 12983 (2011), in which it was
demonstrated that for hydrogen-bond dimer, the scan curve of qbind index well mimics to actual
potential energy curve. This index for a domain is defined as:
)(
effectrepulsived)(
effectattractived)(
repattbind
0)(
rep
0)(
att
2
2
qqq
q
q
n
n
r
r
rr
rr
-
-
where
-
2(r) is the second largest eigenvalue of electron density Hessian matrix at r, its sign can be
utilized to discriminate interaction type. Since the paper showed that n=4/3 gives best correlation
between qbind and actual potential curve, in Multiwfn the n parameter is chosen as 4/3. Note that
the paper used isosurface of RDG=0.6 when calculating this index. More negative of qbind may
imply more stablized interaction.

3 Functions
214
The method used to integrate domains is even-grid integration method. In other words, the
integration value of a real space function for a domain is simply the sum of the real space function
value of the grids constituting the domain multiplied by grid volume. Therefore, the accuracy of
integration result is directly affected by the quality of grid you set.
An illustrative example of present module is given in Section 4.200.14.
Information needed: Atom coordinates, GTF information
3.200.15 Calculate electron correlation index
The total, dynamic and nondynamic electron correlation indices proposed by Matito et al. in
Phys. Chem. Chem. Phys., 18, 24015 (2016) are useful indicator of measuring magnitude of
electron correlation in present system.
Dynamic and nondynamic electron correlation indices (ID and IND) are defined as
iii
iiiii
I
I
)1(
)}1(2)]1({[
2
1
ND
2/1
4
1
D
Where i denotes index of natural spin orbital,
is corresponding occupation number. Note that in
some cases,
may be marginally larger than 1.0 or negative, Multiwfn automatically set it to 1.0
and 0.0 respectively to make the calculation feasible.
Total electron correlation index defined is
iiii
III 22/1
4
1
NDDT |)(|)]1([ r
Present function is used to calculate all the three electron correlation indices. Any
wavefunction file carrying occupation number of natural orbitals may be used as input file,
e.g. .wfn, .wfx and .molden files. An example is given in Section 4.A.6.
Note that Matito et al. also proposed local version of the three functions to characterize
electron correlation in local regions, Multiwfn is also able to study them, see Section 4.A.6 for
example.
3.200.16 Generate natural orbitals based on the density matrix
in .fch/.fchk file
In .fch (or .fchk) file, density matrix is always recorded. For example, if you carried out a
MP2 task for an open-shell system with keyword "# MP2/cc-pVTZ density", then the
resulting .fch file will have below four fields recording corresponding type of density matrix:
Total SCF Density, Spin SCF Density, Total MP2 Density, Spin MP2 Density
While for a closed-shell system, if the keyword used is "# TD PBE1PBE/6-311G* density", then
the resulting .fch file will contain below type of density matrix:
Total SCF Density, Total SCF Density, Total CI Rho(1) Density, Total CI Density
If you don't know which kinds of density matrix are recorded in the .fch file, simply search
3 Functions
215
"Density" in the file.
Various kinds of natural orbitals can be obtained via diagonalization of proper type of density
matrix:
Natural orbitals (NOs): Diagonalizing total density matrix. The occupation is from 0.0 to
2.0. This type of NOs is also known as spatial NOs, and specifically, unrestricted natural orbital
(UNO) for unrestricted wavefunctions
Alpha and beta natural orbitals (collectively known as natural spin orbitals, NSOs):
Diagonalizing alpha and beta density matrix, respectively. The occupation is from 0.0 to 1.0.
Spin natural orbitals (SNOs): Diagonalizing spin density matrix (i.e. Difference between
alpha and beta density matrix). The occupation is from -1.0 to 1.0. SNO with positive (negative)
occupation represent distribution of unpaired alpha (beta) electrons.
Using present function, you can obtain any set of above mentioned types of NOs. For
example, you want to obtain SNOs of triplet water at CCSD/cc-pVDZ level, you can run below
Gaussian input file:
%chk=C:\CCSD_water_m3.chk
#p CCSD/cc-pVDZ density
test
0 3
O 0.00000000 0.00000000 0.11930801
H 0.00000000 0.75895306 -0.47723204
H 0.00000000 -0.75895306 -0.47723204
Convert the .chk file to .fch, then boot up Multiwfn and input
C:\CCSD_water_m3.fch
200
16
CC // Meaning we want to analyze coupled-cluster density matrix. You can also input SCF
here to analyze Hartree-Fock density matrix
3 // Generate SNOs (if the system is closed-shell, this selection will not occur, since only
NOs can be generated in this case)
Now the basis function information in memory has been updated to SNOs. If then you want
to visualize SNOs, or to perform real space function analysis (e.g. analyzing orbital composition
of SNOs via Hirshfeld partition), you should choose y to export wavefunction information to
new.molden file in current folder, and then program will automatically load it. After that, all
following analysis will correspond to SNOs.
Note: Once .molden file containing SNOs is loaded into Multiwfn, the system will be
regarded as open-shell and there will be the same number of alpha and beta orbitals, only the
former correspond to SNOs, while the latter are completely meaningless and you should simply
ignore them.
3 Functions
216
This function works well for .fch/.fchk files produced by Gaussian, but I am not pretty sure
whether the ones produced by Q-Chem and PSI4 are also fully compatible.
Information needed: .fch/.fchk file
4 Tutorials and Examples
217
4 Tutorials and Examples
Prologue and generation of input files
Welcome to use Multiwfn! If you have not read "ALL USERS MUST READ" at page 2 of
this manual, please read it first.
Different functions in Multiwfn require different type of input file, see Section 2.5 for
explanation. .wfn/.wfx/.fch/.molden/.gms files can be used as input file for most functions of
Multiwfn, before getting start I would like to first show you how to generate them. A few
functions (e.g. AdNDP analysis) in Multiwfn rely on some special files, the requirements on the
input files in these cases are clearly indicated in corresponding section in Chapter 3.
Generating .wfn and .wfx files
In Gaussian, write out=wfn in route section, leave a blank line after molecular coordinate
section and write the destination path of .wfn file, e.g. C:\otoboku\H2O.wfn (you can consult
H2O.gjf in “examples” folder), then run this file. If the task terminates normally, H2O.wfn will
appear in C:\otoboku folder.
If you use MCSCF in Gaussian, in order to generate and export natural orbitals to .wfn, you
should also use pop=no keyword. If you are using Gaussian older than G09 C.01, please carefully
read below information:
If the theoretical method is post-HF type, you have to also add “density” keyword in route section to use
current density, otherwise what outputted to .wfn file will still be HF orbitals. If you are using TDDFT or CIS and
you want to export natural orbitals corresponding to excited state wavefunction, you also need to specify "density"
keyword.
For CCD/CCSD, QCISD or MP2/3, MP4SDQ tasks based on unrestricted HF reference state, only when
“pop=NOAB” keyword is also specified then natural spin orbitals rather than spatial natural orbitals will be saved
to the .wfn file. TD, CI and MCSCF tasks of Gaussian can not produce natural spin orbitals.
If the Gaussian you are using is older than G09 B.01, be aware that there is a serious bug, if your task is
restricted open-shell (ROHF and RODFT), the occupation numbers of singly occupied orbitals in .wfn file will
erroneously be 2.0, you have to open the file by text editor, locate the last entry "OCC NO =", and then manually
change the value behind it to 1. 0000000.
In GAMESS-US, add AIMPAC=.TRUE. in $CONTRL section. After the task is finished, the
generated .dat file in the folder defined by $SCR environment variable (see rungms script) will
contain wavefunction information with the same format as .wfn file, extract the content between "-
---- TOP OF INPUT FILE FOR BADER'S AIMPAC PROGRAM -----" and "----- END OF
INPUT FILE FOR BADER'S AIMPAC PROGRAM -----" and save them to a new file with “.wfn”
prefix.
In ORCA, .wfn file can be generated simply using aim keyword in the input file, or using the
command orca_2aim XXX to convert XXX.gbw to XXX.wfn. However, the .wfn file generated by
ORCA are usually non-standard and cannot be properly recognized by Multiwfn. Therefore,
using .molden file as input file of Multiwfn instead is highly recommended, see below.
As regards the method of outputting .wfn files in other quantum chemistry packages, please
consult corresponding manuals.
If you would like to generate .wfx file in Gaussian09 (since revision B.01), simply write
4 Tutorials and Examples
218
out=wfx instead of out=wfn in route section.
Generating .fch file
Some functions of Multiwfn require basis function information, you have to use formatted
checkpoint file of Gaussian (.fch) or Molden input file (.molden) as input. Since .fch/molden file
contain richer information than .wfn/wfx file, for all of the functions that require .wfn/wfx file as
input, you can also use .fch/molden instead. See Section 2.5 for more details.
In Gaussian, you can run command such as formchk h2o2.chk to convert binary checkpoint
file h2o2.chk to h2o2.fch. The .fchk files produced by Q-Chem and PSI4 programs are also
compatible with Multiwfn. Please check corresponding manual on how to generate it.
Note: There is no any difference between .fch and .fchk formats. The former and the latter are the default
extensions of formatted checkpoint file of Windows and Linux version of Gaussian, respectively. You can use
either of them as input file of Multiwfn.
When post-HF task is performed, the orbitals and occupations recorded in Gaussian .fch file
by default are the HF ones, hence the Multiwfn analysis results are identical to HF. Similarly,
under default case, analysis results based on .fch file produced by TDDFT task are identical to
ground state DFT wavefunction. To analyze wavefunction for post-HF wavefunction or TDDFT
excited state wavefunction, analysis should be done using natural orbitals (NOs) at corresponding
level, there are two ways to yield them:
(1) Make Multiwfn generate natural orbitals (or spin natural orbitals, natural spin orbitals) by
using subfunction 16 of main function 200. See Section 3.200.16 for detail. This way is
recommended since it is very convenient.
(2) Make Gaussian write natural orbitals into .fch file. You should first perform post-HF or
TDDFT task with “density” keyword, and then rerun the task only with "guess
(save,only,naturalorbitals) chkbasis" in route section. Note that Gaussian fills orbital occupation
numbers into orbital energy field in .fch file, hence you should write “saveNO” in the first line
of .fch file to let Multiwfn know this behavior. Beware that if what you performed is open-shell
post-HF calculation, even above process is unable to correctly store natural spin orbitals into .fch
file. Generally, I strongly recommend using .wfn file to view natural orbitals and analyze real
space functions for post-HF wavefunctions.
Generating .molden file
In ORCA, use the command orca_2mkl XX -molden to convert XX.gbw to Molden input file.
You don't need to then manually change the suffix from .molden.input to .molden, since the
former can also be recognized by Multiwfn.
In Molpro, write such as put,molden,ltwd.molden at the last line of your input file, the
Molden input file ltwd.molden will be produced.
Regarding the method of outputting Molden input files in other quantum chemistry packages,
please consult corresponding manuals.
When pseudo-potential is used and you need to do some analyses relating to nuclear charges,
do not forget to manually change atomic indices in the .molden file as nuclear charges, see Section
2.5 for details.
Note: Currently, only the Molden input file generated by Molpro, ORCA (up to angular moment of f), MRCC,
deMon2k and BDF program are formally supported. If the file is generated by other programs, the result may or
may not be correct, because the files produced by numerous programs are non-standard or problematic. Fortunately,
molden2aim utility is able to deal with the Molden input files produced by wider scope of programs and can output

4 Tutorials and Examples
219
standardized Molden input files, which is then able to be used as Multiwfn input file. See Section 5.1 for detail.
Generating .gms file
GAMESS-US output file can also be used as Multiwfn input file, you need to change its
suffix as .gms so that Multiwfn can recognize it. Currently, I can only guarantee that output file of
HF/DFT calculation with default NPRINT option can be normally loaded by Multiwfn. A sample
of input and output files of GAMESS-US are provided as GAMESS_US.inp and UKS_cc-
pVDZ.gms in examples folder, respectively.
Now let’s start! Note that the examples in 4.x section are relevant to main function x,
therefore you can quickly find the examples you needed. Section 4.A includes special topics and
advanced tutorials, in which more than one functions and some advanced skills may be involved,
such as studying aromaticity and weak interactions. You can find almost all of the files involved in
these examples in “examples” folder. All the texts behind // are comments and should not be
inputted as command. Tutorials in this chapter only cover basic applications of Multiwfn, if you
want to learn the usage of more functions and more options, please read corresponding sections in
Chapter 3 and play with the options that not mentioned in the examples.
PS1: If you can read Chinese, reading these two articles is highly helpful: "Tips for getting
start with Multiwfn" (http://sobereva.com/167), "The significance, functions and uses of
multifunctional wavefunction analysis program Multiwfn" (http://sobereva.com/184).
PS2: If you would like to analyze wavefunction higher than CCSD level, reading Section
4.A.8 is suggested, you will need PSI4 or MRCC program.
4.0 View orbitals and structure
In Multiwfn, you can use main function 5 to generate cube file of an orbital wavefunction, or
you can use subfunction 3 in main function 200 to generate single or multiple cube files for a
batch of orbitals, then you can load them to your favourite visualization programs (e.g. VMD) to
visualize corresponding orbitals. However, the simplest way to view orbitals is using main
function 0 of Multiwfn, as described below.
4.0.1 Viewing molecular orbitals of monofluoroethane
First, run a single point task for monofluoroethane to get its wavefunction file, which has
already been provided as examples\C2H5F.wfn. Boot up Multiwfn, input this path, then select
main function 0, a GUI window will pop up, meanwhile all atom coordinates are printed on
Multiwfn console window.
4 Tutorials and Examples
220
You can rotate molecule, zoom in/out, adjust bonding threshold, save graph and so on via
corresponding widgets. The numbers in right-bottom list are orbital indices, you can view orbital
isosurface by selecting corresponding number, green and blue isosurfaces correspond to positive
and negative regions, respectively. The isovalue can be adjusted by dragging slide bar. Isosurface
style and colors and be altered by corresponding suboptions in "Isosur#1 style". The quality of the
isosurface can be set by the option in "Isosur. quality", the isosurface will be finer/coarser if you
input a larger/smaller value than default. See Section 3.2 for detail. In Section 4.0.2, you will learn
how to plot two orbitals simultaneously in this window. By selecting "Orbital info."-"Show all",
energy, occupation number and type of all orbitals will be shown in Multiwfn console window. If
you do not want too many high-lying virtual MOs are shown, you can choose "Show up to
LUMO+10". If irreducible reprenstations are recorded in the loaded .molden/.gms file, then they
will be shown as the last column.
The color of bonds, atomic labels and atom spheres can be set by parameters "bondRGB",
"atmlabRGB" and "atmcolorfile" in settings.ini, respectively. See corresponding comments for
detail. After adjusting these parameters, you need to reboot Multiwfn to make them take effect.
To close the window, click “RETURN” button.
Note: Visualizing isosurface of Rydberg orbitals by main function 0 of Multiwfn is also possible, however,
since they show very diffuse character, in order to avoid truncating of isosurfaces, you should enlarge "aug3D" in
settings.ini. An example of visualizing Rydberg orbitals is given in Part 2 of Section 4.200.5.
4 Tutorials and Examples
221
4.0.2 Viewing natural bond orbitals (NBO) of ethanol
There are two ways to view NBOs, if you are a Gaussian user, way 2 may be more
convenient, however if you also need to view natural hybrid orbital (NHO) or natural atomic
orbital (NAO) or some other types of orbitals generated by NBO program, you have to use way 1.
Way 1: Use NBO plot files
The common way is to generate NBO plot files (.31~.40) and load them into Multiwfn. To
generate these files by Gaussian, you should add “pop=nboread” in route section, that means the
keywords of NBO at the end of input file will be passed to NBO module (Link 607 in Gaussian),
then add e.g. “$NBO plot file=c:\NH2COH $END” at the end of the input file (leave a blank line
before), you can refer to NH2COH_NBO.gjf in “example” directory. Run the input file by
Gaussian, you will find NH2COH.31, NH2COH.32 ... NH2COH.41 are generated in c:\. Now
boot up Multiwfn and input following commands
c:\NH2COH.31 // .31 file contains necessary basis function information for plotting
c:\NH2COH.37 // .37 file contains NBO information. .32~.40 files correspond to
PNAO/NAO/PNHO/NHO/PNBO/NBO/PNLMO/NLMO/MO respectively. Hint: You can only
input 37, because in present example the .37 and the .31 file share the same name
0 // Enter the GUI
You can choose corresponding NBO orbital from right-bottom list to view the isosurface.
Multiwfn is also capable to plot two orbitals simultaneously, for instance, here we will plot NBO
12 and NBO 56, which correspond to occupied lone pair of nitrogen atom and unoccupied anti-π
bond between carbon and oxygen atoms respectively. Firstly, we choose 12 from the orbital list to
plot NBO 12, and then click "Show+Sel. isosur#2", after that we click 56 in the list, you will see
both of NBO 12 and NBO 56 are shown. The yellow-green and purple parts of NBO 56
(isosurface#2) correspond to positive and negative parts, respectively.
4 Tutorials and Examples
222
It is somewhat difficult to study overlapping extent between the two orbitals from the solid
face graph, so we choose "Use mesh" in "Isosur#1 style" and the counterpart in "Isosur#2 style" to
make the two isosurfaces represented as mesh, see below. (Please also try "transparent face" style)
Now the overlapping extent become distinct, it is quite clear that NBO 12 substantially overlapped
with NBO 56, the resulting strong delocalization is one of the main reasons why the second-order
perturbation energy between them is very large (~60kcal/mol). In Section 4.4.5, you will learn
how to obtain contour map for the two orbitals.
4 Tutorials and Examples
223
Notice that for unrestricted calculations, .32 and .33 files outputted by NBO 3.1 module in
Gaussian are incorrect -- the title parts are missing, which will lead to strange result, you should
fix them by imitating other plot files such as .34, it is very easy.
As regards the ways to pass the keywords for generating plot files to NBO module in other
quantum chemistry packages, please consult corresponding manual. You can also use stand-alone
version of NBO program (GENNBO) to generate plot files, an input file (.47) is needed to be
prepared first. In Gaussian, run a single point task with “$NBO archive file=C:\NH2COH $end” at
the end of input file, then add “plot file=C:\NH2COH” between “$NBO” and “$END” in the
resultant ethanol.47, after that feed this file into GENNBO you will get the NBO plot files.
Way 2: Use .fch as NBO/NLMO information carrier
Gaussian provides keywords “pop=saveNBO” and “pop=saveNLMO”, if you specified one
of them in your input file, NBOs or NLMOs will be saved to checkpoint file instead of MOs when
the task is finished. You can use corresponding .fch file as Multiwfn input file to view NBOs or
NLMOs. If theoretical level of the task is HF or DFT, you should add “saveNBOene” in the first
line of .fch file; if post-HF is used and “density” keyword is also specified, you should add
“saveNBOocc” in the first line of .fch file, Multiwfn will do some special treatments internally,
however, if your aim is just viewing NBOs and NLMOs in function 0, you can ignore this step.
Beware that when Gaussian storing the NBOs/NLMOs to checkpoint file, they may be
automatically reordered. For example, you may see the information like below in the Gaussian
output file:
Reordering of NBOs for storage: 7 8 3 1 2 4 6 5 9 38 ...
That means the 1st, 2nd, 3rd, 4th ... orbitals in the .chk/.fch file correspond to the 7th, 8th, 3rd,
1st ... NBOs generated by the NBO module, respectively.
4.1 Calculate properties at a point
4.1.1 Show all properties of triplet water at a given point
In this example we calculate a wide variety of real space functions at a given point for triplet
water. Boot up Multiwfn and input below commands
examples\h2o-m3ub3lyp.wfn
1 // Function 1, show properties at a point
0.2,2.1,2 // X, Y, Z coordinate of the point
1 // The unit of inputted coordinate is Bohr
Now all real space functions supported by Multiwfn at this point are printed along with
components of electron density gradient/Laplacian, Hessian matrix and its
eigenvalues/eigenvectors. If you are unable to fully understand the output, please read Sections 2.6
and 2.7 carefully, all terms are very detailed described.
Density of all electrons: 0.4598301528E-02
Density of Alpha electrons: 0.2861566387E-02
Density of Beta electrons: 0.1736735141E-02
Spin density of electrons: 0.1124831246E-02
4 Tutorials and Examples
224
Lagrangian kinetic energy G(r): 0.3365319167E-02
Hamiltonian kinetic energy K(r): 0.1088761528E-03
Potential energy density V(r): -0.3474195320E-02
Energy density: -0.1088761528E-03
Laplacian of electron density: 0.1302577206E-01
Electron localization function (ELF): 0.1998328717E+00
Localized orbital locator (LOL): 0.1008002781E+00
Local information entropy: 0.3533635333E-02
Reduced density gradient (RDG): 0.2033111359E+01
Reduced density gradient with promolecular approximation: 0.2294831921E+01
Sign(lambda2)*rho: -0.4598301528E-02
Sign(lambda2)*rho with promolecular approximation: -0.3918852312E-02
Corr. hole for alpha, ref.: 0.00000 0.00000 0.00000 : -0.1251859403E-03
Source function, ref.: 0.00000 0.00000 0.00000 : -0.3565867942E-03
Wavefunction value for orbital 1 : 0.1536978161E-03
Average local ionization energy: 0.4664637535E+00
User defined real space function: 0.1000000000E+01
ESP from nuclear charges: 0.3453377860E+01
ESP from electrons: -0.3439063818E+01
Total ESP: 0.1431404144E-01 a.u. ( 0.3895049E+00 J/C, 0.8981488E+01 kcal/mol)
Note: Below information are for electron density
Components of gradient in x/y/z are:
-0.7919856828E-03 -0.6903543769E-02 -0.6651181972E-02
Norm of gradient is: 0.9618959378E-02
Components of Laplacian in x/y/z are:
-0.3809549089E-02 0.1052804857E-01 0.6307272576E-02
Total: 0.1302577206E-01
Hessian matrix:
-0.3809549089E-02 0.1394394193E-02 0.1197923973E-02
0.1394394193E-02 0.1052804857E-01 0.1008387143E-01
0.1197923973E-02 0.1008387143E-01 0.6307272576E-02
Eigenvalues of Hessian: -0.3959672207E-02 0.1886890004E-01 -0.1883455778E-02
Eigenvectors(columns) of Hessian:
0.9964397434E+00 0.8076452238E-01 0.2418531975E-01
-0.4735415689E-01 0.7734993430E+00 -0.6320255930E+00
-0.6975257409E-01 0.6286301443E+00 0.7745700228E+00
Determinant of Hessian: 0.1407217564D-06
Ellipticity of electron density: 1.102344
All data are expressed in scientific notation, the value behind E is exponent, e.g.
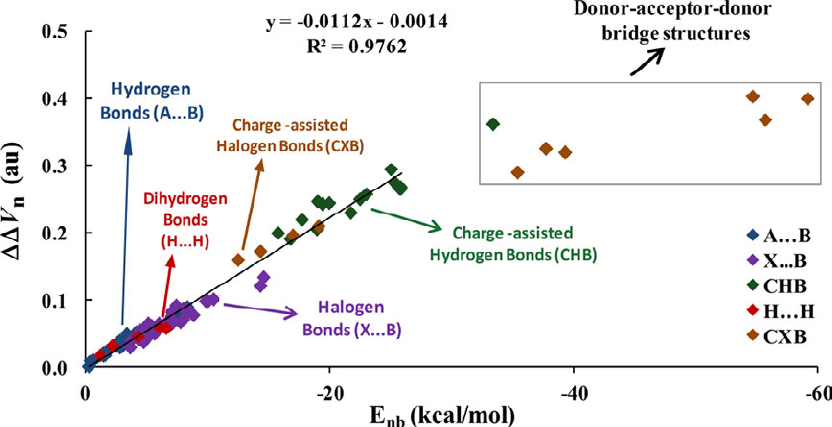
4 Tutorials and Examples
225
0.6307272576E-02 corresponds to 0.006307272576.
In the line of Corr. hole (correlation hole) and source function, the so-called "ref" is the
position of reference point, which is determined by "refxyz" in settings.ini.
By default the wavefunction value outputted is for orbital 1, you can input such as "o6" to
choose orbital 6.
By default, the components of gradient and Laplacian as well as Hessian and its
eigenvalue/eigenvectors are for electron density. You can input such as f10 to choose the real
space function with index of 10 (namely ELF), after that all these quantities will be for ELF. If
you want to inquire indices of all real space functions, input allf.
You can continue to input other coordinates, when you want to return to upper level menu,
input q; If you want to exit the program, press “CTRL+C” or close commond-line window.
4.1.2 Calculate ESP at nuclear positions to evaluate interaction
strength of H2O···HF
This is an advanced example, if you are not interested in weak interactions you may skip this section.
In J. Phys. Chem. A, 118, 1697 (2014), Mohan and Suresh studied a batch of electrostatic
dominated interacting systems, including hydrogen, halogen and dihydrogen bonds, all of them
belong to electron donor-acceptor interactions, where donor stands for electron-rich moiety (Lewis
base), while acceptor is electron-deficient moiety (Lewis acid). They fitted a surpringly good
linear equation to correlate Vn index with interaction energy (Enb) for all kinds of interactions,
the R2 is as high as 0.9762. Their results can be summarized as following graph
For an electrostatic dominated complex, assume that we can obtain Vn, then according to
the equation shown in above graph, we can easily predict the interaction energies as
125.02857.89E nnb
V
The Vn is defined based on ESP at nuclear positions
4 Tutorials and Examples
226
)()( AnA'nDnD'nAnDnn
VVVVVVV
where Vn-D' is the ESP at nuclear position of donor atom in complex environment, but the
contribution due to nucleus of this donor atom is ignored. The only difference between Vn-D and
Vn-D' is that the former is calculated in monomer state, therefore Vn-D = V
n-D' - V
n-D can be
regarded as the change in ESP at nuclear position of donor atom due to presence of another
molecule, which directly reflects strength of intermolecular interaction. The definition of Vn-A' and
Vn-A are identical to Vn-D' and Vn-D, respectively, but they are calculated for acceptor atom.
In this example, we calculate Vn for H2O···HF and check if the interaction energy
predicted based on Vn is really closed to the accurately calculated interaction energy. In this
complex the oxygen of H2O is electron donor atom and hydrogen of HF is electron acceptor atom.
Because the equation presented by Mohan and Suresh was fitted for specific calculation level, in
order to properly use their equation, the calculation level we employed here is identical to them.
The .wfn files used below were produced at MP4(SDQ)/aug-cc-pVTZ level at MP2/6-311++G**
optimized geometries, these .wfn files and the corresponding Gaussian input files can be found in
"examples\Vn" folder.
Note that because we employed post-HF method, "density" keyword is indispensable, otherwise the density in
the resultant .wfn file may be Hartree-Fock density. Besides, in Gaussian09, the density cannot be produced at
MP4 level, so we use MP4(SDQ) keyword instead (MP4 keyword is default to MP4(SDTQ), which is more
accurate and but much expensive than MP4(SDQ)).
First we calculate Vn-A' and Vn-D'. Set "iuserfunc" parameter in settings.ini to 39 to enable the
39th user-defined function, which is used to calculate ESP without contribution of a specific
nucleus (see Section 2.7 for more details), then boot up Multiwfn and input
examples\Vn\H2O-HF.wfn
1000 // A hidden interface
3 // Set which nucleus will be ignored in the calculation of ESP
1 // Oxygen is atom 1
1 // Calculate properties at a point
a1 // Nuclear position of atom 1
From the output you can see
User defined real space function: -0.2228775074E+02
That means Vn-D' is -22.2877 a.u. Then input
q // Return to main menu
1000
3
5 // Hydrogen of HF is atom 5
1
a5
You can find Vn-A' is -0.9608 a.u.
Next we calculate Vn-D. Reboot up Multiwfn and input below commands
examples\Vn\H2O.wfn
1000
3
1 // In H2O.wfn oxygen is atom 1
1
a1
4 Tutorials and Examples
227
We find Vn-D is -22.3339 a.u. Then we calculate Vn-A. Reboot Multiwfn and input
examples\Vn\HF.wfn
1000
3
2 // In HF.wfn hydrogen is atom 2
1
a2
The Vn-A is -0.9136 a.u.
The Vn is thus -22.2877-(-22.3339) - [-0.9608-(-0.9136)] = 0.0462 + 0.0472 = 0.0933 a.u.
Using the equation mentioned earlier, the interaction energy can be approximately predicted
as -89.2857*0.0933-0.125 = -8.45 kcal/mol, this value is quite close to the accurate interaction
energies (-8.31 kcal/mol) obtained by Mohan and Suresh at MP4/aug-cc-pVTZ level with
Counterpoise correction.
Generating wavefunction at MP4(SDQ)/aug-cc-pVTZ is quite time consuming even for small complex such
as the system we studied here, thus it is important to find a calculation level that significantly saves computational
time but without too much sacrifice in accuracy. For present system, based on the MP2/6-311++G** geometry, I
tried using several levels to evaluate the Vn:
B3LYP/6-311+G**: 0.1021 a.u.
MP2/cc-pVTZ: 0.1052 a.u.
MP2/aug-cc-pVTZ: 0.0955 a.u.
B3LYP/aug-cc-pVTZ: 0.0985 a.u.
MP2/aug-cc-pVDZ: 0.0939 a.u.
B3LYP/aug-cc-pVDZ: 0.0980 a.u.
The Vn produced at MP2/aug-cc-pVDZ (0.0939) is very close to the value we obtained above at
MP4(SDQ)/aug-cc-pVTZ (0.0933), while the computational cost is reduced by factors of two. So, in practical
studies, using MP2/aug-cc-pVDZ level to evaluate Vn is a very ideal choice.
4.2 Topology analysis
Multiwfn is able to perform topology analysis for various kinds of real space functions, such
as electron density, its Laplacian function, ELF, LOL, orbital wavefunctions, as well as user-
defined functions. Four kinds of critical points (CPs) can be located and real space function values
at these points can be easily obtained; topology paths linking CPs and interbasin surfaces can be
generated. There are also many additional capacities, see Section 3.14 for details. Below I will
present some practical applications to illustrate how to use this powerful module.
4.2.1 Atoms in molecules (AIM) and aromaticity analysis for 2-
pyridoxine 2-aminopyridine
Topology analysis of electron density is a main ingredient of Bader's atoms in molecules
(AIM) theory. In this example we will perform this kind of analysis for 2-pyridoxine 2-
aminopyridine complex.
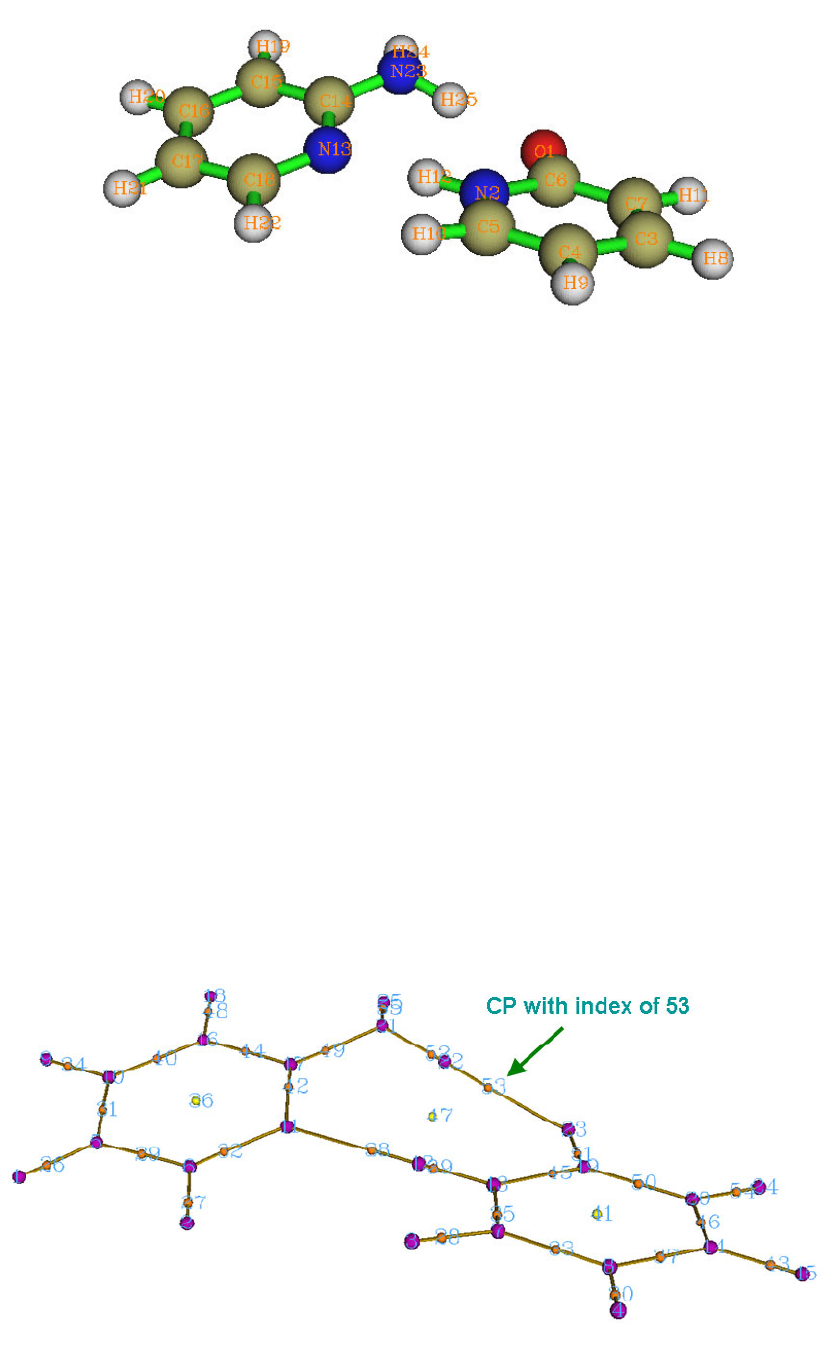
4 Tutorials and Examples
228
Boot up Multiwfn and input following commands
examples\2-pyridoxine_2-aminopyridine.wfn // Assume that the input file is in a subdirectory
of current directory, we can only input relative path rather than entire absolute path
2 // Topology analysis
Then we search all critical points (CPs) by inputting:
2 // Use nuclear positions as initial guesses, generally used to search (3,-3) CPs
3 // Use midpoint of each atom pair in turn as initial guesses, generally all (3,-1) CPs could be
found, some (3,+1) or (3,+3) may be found at the same time
The search of CPs is very fast. After that input 0, the positions and types of all found CPs will
be printed in the command-line window, at the end of the output the number of each type of CPs is
shown:
(3,-3): 25, (3,-1): 27, (3,+1): 3, (3,+3): 0
25 - 27 + 3 - 0 = 1
These two lines show that Poincaré-Hopf relationship is satisfied, that means all CPs may have
been found. If this relationship is unsatisfied, then some CPs must be missing. From the GUI that
popped up, we can see all expected CPs are presented, hence we can confirm that all CPs have
been found.
Click "RETURN" button in the GUI window and input 8 to generate bond paths, select
function 0 again to view CPs and paths, after slightly adjust of plot settings, the graph looks like
below (Click "CP labels" at the right side of the GUI if index of the CPs are not shown):
4 Tutorials and Examples
229
Magenta, orange and yellow spheres correspond to (3,-3), (3,-1) and (3,+1) critical points,
brown lines denote bond paths. The indices of CPs are labelled by cyan numbers. It can be seen
that index 53 and 38 corresponds to the bond critical point (BCP) of N-H----O and N-H----N
hydrogen bond, respectively.
Now close the GUI window. As an exercise, let's measure the distance between CP30 and the
nucleus of H25. Select option -9, and input c30 a25, the result is 1.268379 Bohr. Then we measure
the angle between C14-N13-H12, namely input a14 a13 a12, the result is 120.297432 degree.
Now, we input q to return.
In Chem. Phys. Lett., 285, 170, the authors stated that for the hydrogen bond [X-H----O
(X=C,N,O)], the relationship between bond energy EHB and potential energy density V(r) at
corresponding BCP can be approximately described as
EHB=V(rbcp)/2
Let’s evaluate the energy of N-H----O hydrogen bond in our system by this formula. Choose
function 7 and then input the index of corresponding BCP, namely 53, you will see value of all
real space functions at this point
CP Position: 0.44887255865472 3.56434324597741 -0.10652884364257
CP type: (3,-1)
Density of all electrons: 0.3129478049E-01
Density of Alpha electrons: 0.1564739024E-01
Density of Beta electrons: 0.1564739024E-01
Spin density of electrons: 0.0000000000E+00
Lagrangian kinetic energy G(r): 0.2530207716E-01
Hamiltonian kinetic energy K(r): 0.8463666362E-03
Potential energy density V(r): -0.2614844379E-01
Energy density: -0.8463666362E-03
Laplacian of electron density: 0.9782284209E-01
Electron localization function (ELF): 0.1105388527E+00
... (Ignored)
The output indicates that the V(r) at this BCP is -0.026148, therefore the hydrogen bond energy
could be evaluated as EHB=-0.026148/2*2625.5= -34.3 KJ/mol.
Here we use information entropy method to examine if the aminopyridine (the monomer at
the left side of above graph) in the dimer can be regarded as an aromatic molecule. This method
was proposed in Phys. Chem. Chem. Phys., 12, 4742 and is based on electron density at BCPs of a
ring, see Section 3.14.6 for detail. First, we select option 20, and then input indices of the BCPs in
the ring, namely 44,42,32,29,31,40, the outputted Shannon aromaticity index (SA) is 0.000812.
The smaller the SA index, the more aromatic is the ring. In origin paper, 0.003 < SA < 0.005 is
chosen as the boundary of aromaticity/antiaromaticity. Since our result is much smaller than 0.003,
we can conclude that aminopyridine is an aromatic molecule. The SA for 2-pyridoxine (the
monomer at the right side of above graph) is 0.000865, hence shows slightly weaker aromaticity
than aminopyridine.
Next, we calculate the curvature of electron density perpendicular to ring plane at RCP. In
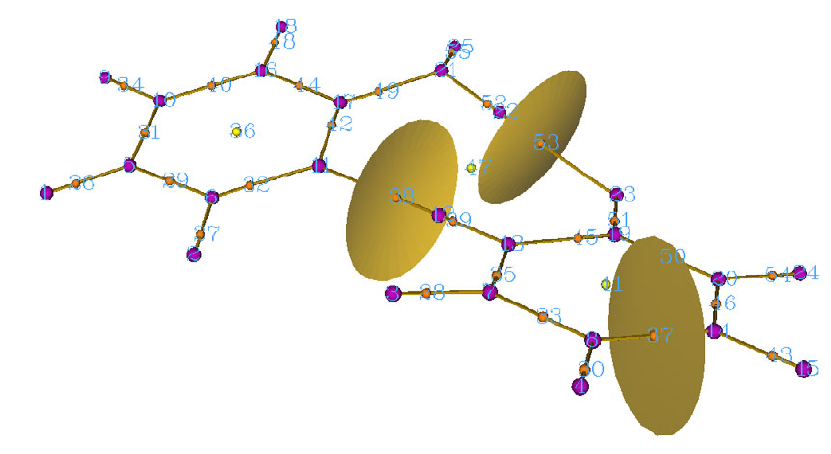
4 Tutorials and Examples
230
Can. J. Chem., 75, 1174, it was shown that more negative curvature implies stronger aromaticity.
We first calculate the curvature for aminopyridine. Select option 21, input the index of the RCP
(namely 36), and then input three atoms to define the ring plane, here we input 15,13,17 (also, you
can input such as 14,16,18 and 13,15,18, because all of them correspond to the same plane). From
the output we find the curvature is -0.0187. Then we calculate the curvature for 2-pyridoxine,
namely input 41 and 2,7,4, the result is -0.0164. Comparison between the two curvatures again
shows that aminopyridine has stronger aromaticity. In Multiwfn, aromaticity can also be measured
in many other schemes, such as HOMA, FLU, PDI, ELF-π and multicenter bond order, they are
collectively discussed in Section 4.A.3.
Interbasin surfaces (IBS) dissect the whole molecular space into individual basins, each IBS
actually is a bunch of gradient paths derived from a (3,-1) CP. Now we generate IBS
corresponding to the (3,-1) with index of 53, 38 and 37. Choose function 10, and input
53 // Generate the IBS corresponding to the (3,-1) CP with index of 33, the same as below.
You may need to wait a few seconds for each generation of IBS
38
37
q // Return
Visualize the results by choose function 0, the graph will be shown as below. The three
surfaces are IBS.
There are two important points regarding AIM topology analysis I would like to mention here,
though they are not related to present example.
Tip 1: What should I do if some CPs of electron density are missing?
For small systems, commonly we can check whether all CPs have been located by simply
enter the GUI and visualize the distributions of the CPs. There is also an useful equation named
Poincaré-Hopf relationship. For isolate system, the relationship is
1
CCPRCPBCPNCP
nnnn

4 Tutorials and Examples
231
If all CPs have been found, this relationship must be satisfied, but the satisfication of this
relationship does not necessarily mean all CPs have been found. If the Poincaré-Hopf relationship
is unsatisfied, then some CPs must be missing.
Sometimes, you may find some expected CPs are not successfully located after searches.
There are two reasons may cause this problem: (1) The position of initial guesses are not close
enough to the CPs (2) The default CP searching parameters are not well-suited for present case.
There are some commonly used ways to solve this problem. More detailed descriptions may be
found in Section 3.14.2.
a) If you have tried options 2~5 and some CPs are not located, try to use suboption -1 of
option 6. This searching mode is powerful but expensive, which by default places 1000 guessing
points within in a spherical region around every atom. If after repeating this mode several times
the missing CPs are still unable to be located, it is highly possible that the reason is due to the
inappropriate searching parameters rather than the positions of guessing points.
b) If some BCPs are unable to be located, you can enter option -1, set the scale factor of
stepsize to 0.5, and then try again
c) NCPs of very heavy atoms are difficult to be located, because the peak of electron density
at nucleus in these cases are very sharp, thus under default parameters the searching algorithm is
difficult to capture the NCPs. In order to locate them, you can enter option -1, loose the criteria for
gradient-norm and displacement convergences by several factors, and then try to use option to 2
search the NCPs again. If the NCPs are then successfully found, do not forget to recover the
convergence criteria. In fact, since NCP of heavy atoms are almost exactly located at nuelcus
position, you can directly enter option -4 and choose suboption 3 to add NCPs artificially at the
corresponding nuclear positions.
d) If some missing CPs are far away from atoms, for example, the CCP at the center of a very
large cage or tube system, try to enter option -1 and decrease the criterion for determining
singularity of Hessian matrix via option 8 by several factor, and then search the CPs again.
Tip 2: Describing electron density of very heavy atoms
Very heavy atoms (heavier than Kr) bring much more computational burden than light atoms,
and relativistic effect is non-neglectable. There are several different ways to describe them.
(1) Using pseudo-potential (PS): If you decide to use PS, you must use small core PS! If large
core PS is used, the electron structure in valence regions will be far from truth, and thus the
positions and properties of related CPs will be highly artificial. Small core PS means at least sub-
valence electrons are explicitly taken into consideration. Commonly used PS are listed below, note
that for main group elements only cc-pVnZ-PP series are small core.
Lanl1 Lanl2, Lan2TZ/08 SDD cc-pVnZ-PP SBKJC
Main groups Large Large Large Small Large
Transition metals Large Small L/S (optional) Small Small
Since when PS is used the inner-core electron density is missing, evidently it is impossible to
find out (3,-3) CP at nuclear position, and accordingly, the bond paths emitted from BCP will be
unable to connect to the nucleus. Instead, you may find (3,+3) at nucleus position due to the
vacancy of inner-core density, and a lot of CPs in different types will occur around the nucleus,
this is because the electron density no longer decreases exponentially from nucleus, so the
topology structure of electron density becomes quite complicated. However, you can simply

4 Tutorials and Examples
232
ignore those irrelvant CPs but only focus on the BCPs that you are really interested in.
(2) Using pseudo-potential but with EDF (electron density functions) information supplied:
As mentioned in Section 2.5, if PS is employed but the .wfx file produced by Gaussian is used as
input file, the EDF field in the .wfx file will be loaded into Multiwfn, which represents the inner-
core electron density. In this case, all CPs of electron density can be properly located and artifical
CPs will never occur, the bond paths emitting from BCPs can connect to NCPs normally, all CP
properties that solely based on electron density will be reasonable. Although large core PS can be
employed without problems in this situation, I still recommend using small core PS, because the
accuracy of resultant CP positions and properties must be better than using large core PS. Note
that currently only the .wfx produced by Gaussian contains EDF field, which does not exist in
the .wfx file produced by other programs such as Firefly.
For other type of input files, such as .wfn, .fch, .molden and .gms, by default Multiwfn
automatically loads proper EDF information from built-in EDF library. Alternatively, you can let
Multiwfn to load EDF information from atomic .wfx file produced by Gaussian. The behavior to
load EDF information can be changed by "isupplyEDF" parameter in settings.ini, please check
Appendix 4 for details
(3) Using all-electron basis-set with relativistic Hamiltonian: Clearly, this is the perfect
solution for representing electron structure of heavy atoms, but the most expensive. In this case,
the position and all properties of CPs are the most accurate. The lowest level of consideration of
relativistic effect, namely scalar relativistic, is totally enough. DKH2 Hamiltonian is a very good
choice (in Gaussian, simply using "int=DKH2" to employ it, beware that basis set optimized for
DKH calculation must be used in combination, e.g. cc-pVDZ-DK).
For more discussions, please consult my post "Some explaination of performing
wavefunction analysis under pseudo-potentials" (in Chineses, http://sobereva.com/156)
4.2.2 LOL topology analysis for acetic acid
A brief of localized orbital locator (LOL) has been given in Section 2.6, and its graphical
interpretation will be illustrated in later examples. In this example, we will locate CPs and
generate topology paths of LOL for acetic acid.
Boot up Multiwfn and input following commands
examples\acetic_acid.wfn
2 // Enter topology analysis module
-11 // Select real space function
10 // Localized orbital locator (LOL)
Notice that the surfaces of LOL is much more complex than electron density, so it is very
diffcult to locate all CPs. Fortunately, in general only a small subset of CPs is what we are
interested in, the search of CPs can be terminated once all expected CPs have been found.
We first use option "2 Search CPs from nuclear positions" to locate the CPs that very close to
nuclei. However the positions of CPs in other regions are somewhat unpredictable, hence a lot of
initial guess points have to be randomly scattered around each atom to try to locate those CPs.
6 // In this searching mode, initial guessing points will randomly scattered in a sphere, the
sphere center, radius, number of points and so on can be defined by users, this time we leave the
default value unchanged
4 Tutorials and Examples
233
-1 // Use each nucleus as sphere center in turn to search CPs. Since there are 8 atoms, and
guessing points in each sphere is 1000, Multiwfn will try to search CPs from 8*1000 guessing
points. Of course, the more the guessing points you set, the larger probability all CPs could be
found in this search
-9 // Return to upper menu
0 // Visualize the searching result
It is clear that the number of CPs in LOL function space is very large. Actually there are still
some CPs were not been found in the search, if you repeat the search one time or several times,
some missing CPs could be found. Since all interesting CPs have been found, repeat the search is
unneccessary. From the graph, it can be seen that the three (3,-3) type CP, namely CP20, 29 and 52
correspond to the locally maximal electron localization in covalent bond regions. Note that the
three CPs very close to hydrogens have no strong physical meaning, in my own viewpoint they are
the consequence of failure of definition of LOL. CP12, 22, 16 and 56 correspond to lone pairs of
oxygens.
Now choose option 8 to generate the topology paths linking (3,-1) and (3,-3) CPs, then
choose option 0 to visualize the result again. The paths clarify the intrinsic relationship between
CPs. You may find there are too many objects in the graph and they confused you visually. To
relieve your visual burden, some uninteresting object can be screened by properly adjusting GUI
widgets, as shown below.
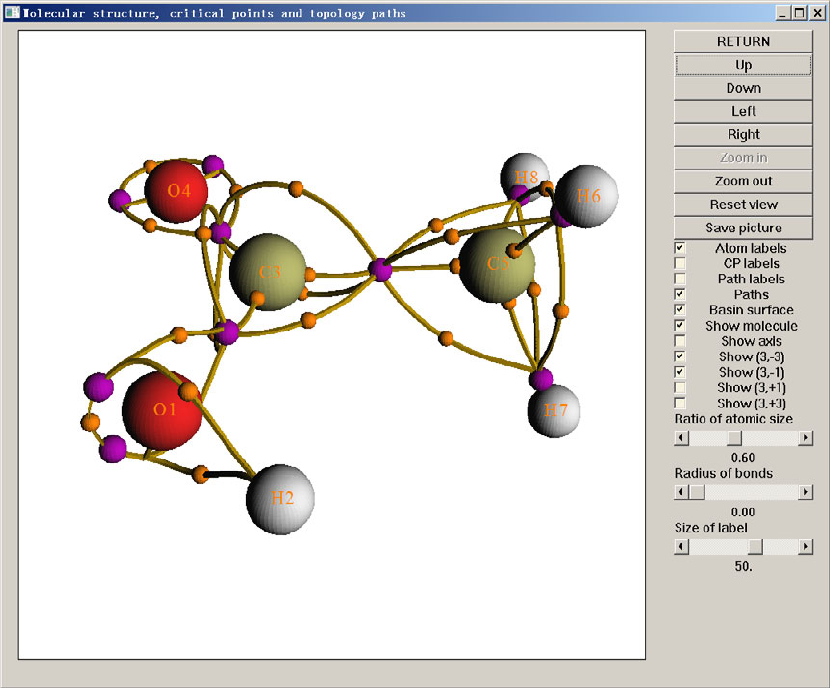
4 Tutorials and Examples
234
With completely identical procedure shown in this example, you can also analyze topology
structure for electron localization function (ELF) as well as Laplacian of electron density.
4.2.3 Plot electron density ellipticity along bond path
In this example we plot ellipticity of electron density along bond path of boundary C-C bond
of butadiene.
First open settings.ini file and change "iuserfunc" parameter to 30, because the 30th user-
defined function corresponds to electron density ellipticity, see Section 2.7 for detail.
Then boot up Multiwfn and input below commands:
examples\butadiene.fch
2 // Topology analysis
2 // Search nuclear critical points from nuclear positions
3 // Search bond critical points from midpoint of atom pairs
8 // Generate bond path
0 // Enter GUI window to visualize result
In the GUI window, with the help of "Atom labels" and "Path labels" widgets at right side,
we find paths 5 and 6 collectively constitute the bond path of boundary C-C bond. Clicking
"RETURN" to close the window and input
-5
7 // Calculate specific real space funtion along a path

4 Tutorials and Examples
235
5,6 // The index of the paths
100 // User-defined function, which corresponds to ellipticity of electron density currently
The curve of electron density ellipticity along the boundary C-C bond path immediately
shows on the screen, the dash line denotes the position of bond critical point. At the same time, the
raw data of the curve are shown on the command-line window and you can copy them out, so that
the map can be further analyzed or reploted in third-part plotting tools such as Origin.
From the graph it is clear that the electron density ellipticity is positive in the middle region
of the bond path, exhibiting the double-bond character of the C-C bond.
You can also plot other real space functions such as ELF and kinetic energy density along
bond paths, please have a try.
4.3 Plot properties in a line
4.3.1 Plot the spin density curve of triplet formamide along carbon
and oxygen atoms
Boot up Multiwfn and input following commands
examples\formamide-m3.wfn // Assuming this input file is in current directory, so the path of
directory is not needed to input
3 // Function 3, plot property in the line
5 // Spin density function
1 // Defining the line by nuclear coordinates of two atoms
1,6 // The indices of the two atoms, carbon and oxygen atoms correspond to 1 and 6 in
present example
The graph shows up immediately:
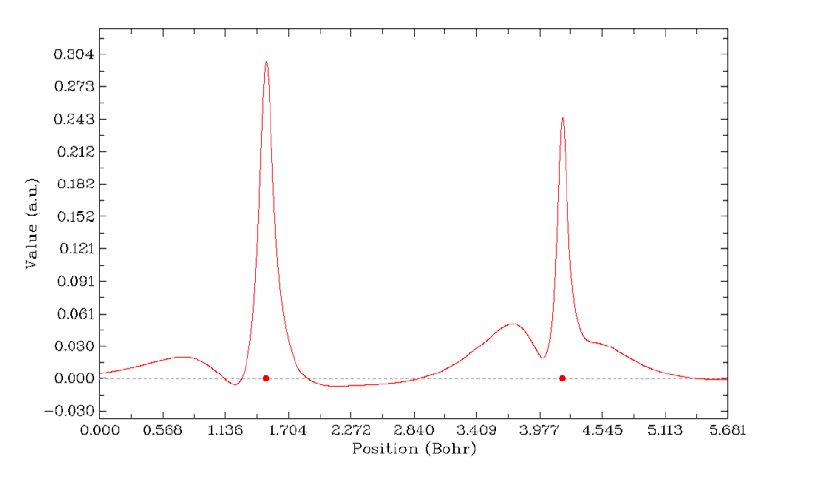
4 Tutorials and Examples
236
The X-axis corresponds to the position in the line you defined, the dash line corresponds to
the position of Y=0, two red circles denote the position of the two atom nuclei. After you click
right mouse button on the graph to close it, a new menu appears on command-line interface, you
can export the graph, adjust the range of Y-axis, export X-Y data set and replot the graph and so on
by corresponding options. By selecting option 6, minimum and maximum positions can be located:
Local maximum X: 0.753677 Value: 0.20104903D-01
Local minimum X: 1.219518 Value: -0.55161276D-02
Local maximum X: 1.503567 Value: 0.29655008D+00
Local minimum X: 2.145518 Value: -0.70202704D-02
Local maximum X: 3.736194 Value: 0.51047629D-01
Local minimum X: 4.006988 Value: 0.18918295D-01
Local maximum X: 4.184992 Value: 0.24448996D+00
Totally found 3 local minimum, 4 local maximum
4.3.2 Study Fermi hole and Coulomb hole of H2
This is a relatively advanced example, you can skipped this section if you are a newbie of quantum chemistry.
In this example we will plot correlation hole (Fermi hole and Coulomb hole) along the axis of
H2. This is an advanced topic, if you are not familiar with the concept of correlation hole, please
consult the discussion in part 17 of Section 2.6.
Hartree-Fock wavefunction is capable to exhibit Fermi correlation, but Coulomb correlation
is completely ommitted. In this case exact Fermi hole can be calculated and plotted by Multiwfn.
If Coulomb hole is needed to be analyzed, then post-HF wavefunction must be employed. In
current version, Multiwfn is able to evaluate and plot approximate Fermi hole and Coulomb hole
for post-HF wavefunctions by Müller approximation, which makes use of natural orbitals to
mimic exact pair density. Although the approximation is introduced, the results are generally at
least qualitative correct. In the future version, I might try to make Multiwfn able to evaluate
correlation hole for post-HF wavefunction exactly, but this is a nontrivial task, mainly because
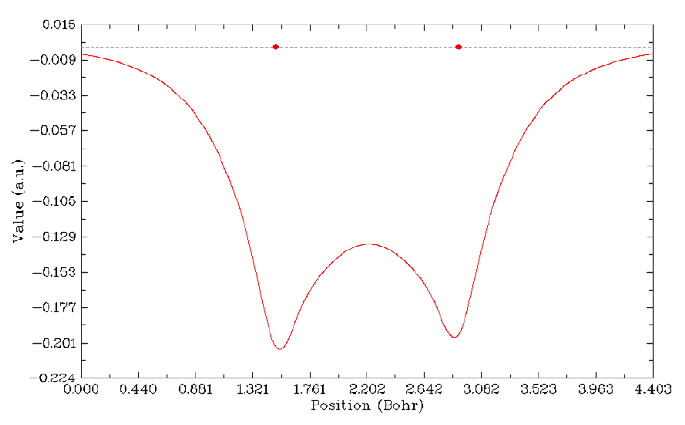
4 Tutorials and Examples
237
two-particle density matrix (2PDM) has to be acquired in some ways.
First, we optimize and generate .wfn file for H2 under CCSD/cc-pVTZ level. CCSD may be
the highest level of wavefunction that can be generated by current Gaussian program. The file has
been provided in "examples" folder as H2_CCSD.wfn. The coordinate of H1 is 0.0, 0.0,
0.70160240 Bohr, the coordinate of H2 is 0.0, 0.0, -0.70160240 Bohr.
Correlation hole involves coordinates of two electrons, to study it visually we must determine
coordinate of a reference electron. In this example, we set reference point at 0.0,0.0,-0.3 Bohr. So
we open settings.ini, change "refxyz" parameter to 0.0,0.0,-0.3.
The correlation hole we first analyzed is Fermi hole (also known as exchange hole), so we
change "paircorrtype" in settings.ini to 1. Since this is close-shell system, the results for or β
electron are exactly the same, while for open-shell system, you should use "pairfunctype" in
settings.ini to select which type of spin electrons will be studied, you can also choose to study
exchange-correlation density or correlation factor by adjusting this parameter.
Now boot up Multiwfn, input following commands
examples\H2_CCSD.wfn
3
17
1
2,1 // Draw the line graph along H2 and H1
You will get below graph
This graph suggests that if we place an electron at 0.0,0.0,-0.3, then the probability of
finding another electron around the two nuclei will be significantly decreased by almost
identical extent due to Pauli repulsion between like-spin electrons. In the bonding region, the
probability decreased obviously too. According to Bader's statement "An elecron can go where its
hole goes and, if the Fermi hole is localized, then so is the electron" (p251 in Atoms in molecules -
A quantum theory), we can say that if an electron can present at 0.0,0.0,-0.3, then it must be able
to easily delocalize over the whole molecular space of H2.
Now we study Coulomb hole. Close Multiwfn, change "paircorrtype" to 2, reboot Multiwfn
and then replot the line graph by using the same procedure, you will see
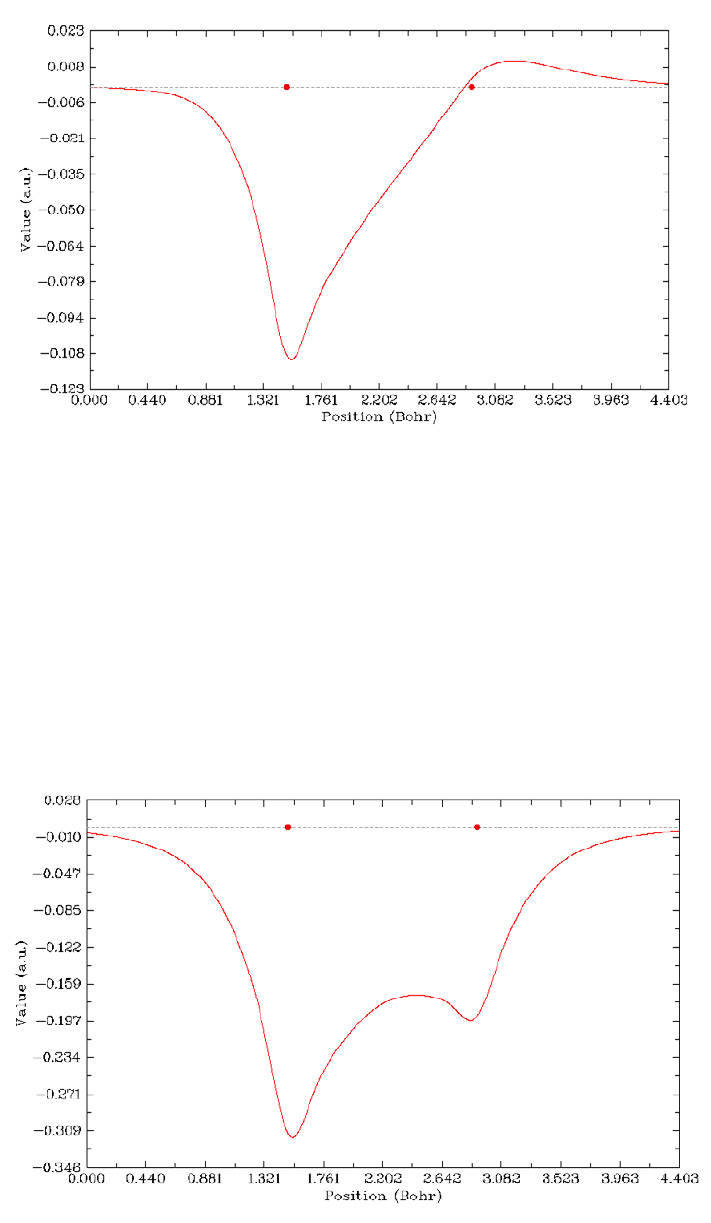
4 Tutorials and Examples
238
How can I infer the coordinate of the reference point on the graph? From the promption "Set
extension distance for mode 1, current: 1.500000 Bohr" we know that the plot range is extended
by 1.5 Bohr to both sides relative to Z coordinates of H2 and H1, and we have already known that
Z coordinate of reference point is larger than H2 by about 0.4016 Bohr, so the reference point on
above graph is 1.5+0.4016=1.9016. The graph reveals that owing to Coulomb repulsion, the
probability of finding another electron ( or β) around the hydrogen closest to reference electron,
namely H2, is largely decreased. While as a compensation, the probability is increased at backside
of H1.
Finally, we study the collective effect of Fermi correlation and Coulomb correlation. Change
"paircorrtype" to 3, and plot the line graph again, you will see
This graph is actually the sum of the first two graphs. From this graph it is clear that the
probability decrease of finding an electron ( or β) around the hydrogen closest to reference
electron is more severe than around another hydrogen.

4 Tutorials and Examples
239
4.3.3 Study interatomic interaction via PAEM-MO method
This is a relatively advanced example, you can skipped this section if you are a newbie of quantum chemistry.
In J. Comput. Chem., 35, 965 (2014), the authors proposed a method named PAEM-MO to
reveal the nature of interaction between two atoms (covalently or non-covalently bounded). In this
example I will briefly introduce this method and show how to realize PAEM-MO analysis in
Multiwfn.
PAEM (potential acting on one electron in a molecule) refers to the total potential acting on
an electron at point r, and can be written as )()()( XCESPPAEM rrr VVV
; where ESP
V is
molecular electrostatic potential and has been introduced in part 12 of Section 2.6. -VESP can be
regarded as the classical potential acting on an electron in the system, while the exchange-
correlation (XC) potential VXC represents the important correction to the classical potential due to
quantum effect. VXC has two components, namely correlation potential (VC) and exchange
potential (VXC); in fact only the latter is important, that means even the potential obtained at
Hartree-Fock level is in general a good approximation to exact VXC.
In wavefunction theory, the exchange-correlation potential can be explicitly written as
r'
r'r
rr
r
rd
||
)',(
)(
1
)( XC
XC
V, where Γ is known as exchange-correlation density, see part 17
of Section 2.6 for detail. In DFT theory, the XC potential directly comes from the variation of
exchange-correlation functional with respect to electron density, i.e. )(
)]([
)( XC
XC r
r
r
E
V.
The VXC can be used in Multiwfn in terms of user-defined function. If parameter "iuserfunc" is set
to 33, then VXC will be calculated based on Γ; if it is set to 34, VXC will be evaluated in terms of
DFT XC potential, in this case the computational cost is several times lower than 33. For more
information please check corresponding description in Section 2.7.
The core of HF and KS-DFT theories is the one-electron eigenvalue equation
)()(
ˆrr
h where )()2/1(
ˆPAEM
2rVh
Solving the equation results in a set of MOs {
}, their eigenvalues correspond to the energy of the
electrons running in the orbitals.
According to the viewpoint of PAEM-MO, if the energy of an occupied MO is higher than
the barrier of VPAEM between a pair of atoms, then the electrons in this MO will be able to freely
delocalize over the two atoms, and thus have direct contribution to covalent bonding.
Below I present two very simple examples of using PAEM-MO method to judge the type of
interatomic interaction. More examples and discussions can be found in J. Comput. Chem., 35,
965.
H-H interaction in hydrogen molecule
First set "iuserfunc" in settings.ini to 33, then user-defined function will be equivalent to the
VXC evaluated based on Γ. Boot up Multiwfn and input below commands
examples\H2.fch // Produced at HF/6-311++G** level
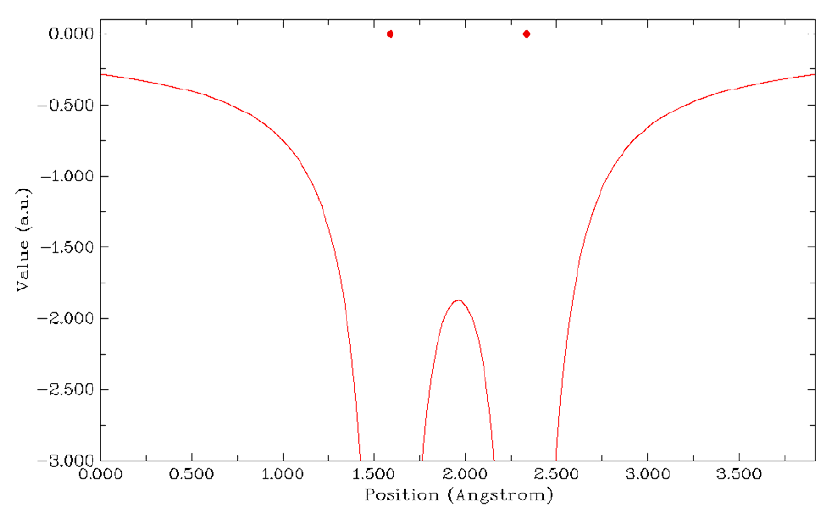
4 Tutorials and Examples
240
3 // Plot real space function in a line
100 // User-defined function
0 // Adjust extension size in the plot
3 // 3 Bohr, which is larger than the default value
1 // Use two nuclei to define the line
1,2
Close the graph, then adjust some plotting parameters to make the graph better
11 // Change length unit of the graph to Angstrom
3 // Change range of Y axis
-3,0.1 // From -3.0 a.u. to 0.1 a.u.
10 // Set stepsize of X and Y axes
0.5,0.5
-1 // Replot
You will see below graph, which exhibits the PAEM curve along the H2 axis
As you can see, there is a barrier of PAEM around the midpoint of H-H bond. In order to
locate the exact value of the barrier, we close the graph and select 6. From the output we find the
maximum of the curve is -1.873 a.u. (-50.96 eV). Present system only has one doubly occupied
MOs, whose energy (-16.15eV) significantly exceeded the PAEM barrier, implying that the
electron is not confined in any hydrogen atom but substantially contributes to the H-H binding, so
the H-H bond must be covalent.
He-He interaction in He2
Please plot PAEM curve along the He-He axis in He2 with the same steps as above. The
wavefunction file used here is examples\He2.fch. The resultant graph should look like below
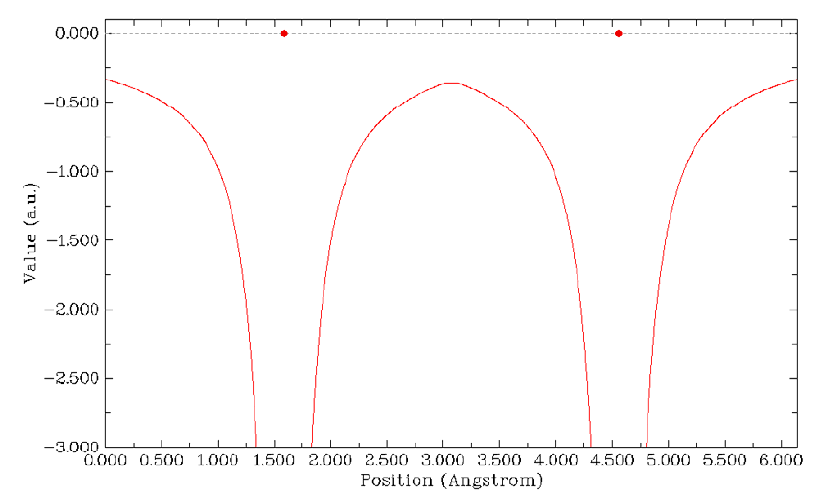
4 Tutorials and Examples
241
Obviously, the PAEM barrier (-9.78 eV) is higher than that in the case of H2. The energy of
the two doubly occupied MOs are -25.03 and -24.91 eV respectively, both of them are lower than
the barrier, therefore the electrons in each He atom are difficult (but not completely impossible
due to tunnel effect) to overcome the barrier to freely delocalize to another He. The He-He
interaction thus should be regarded as non-covalent interaction.
Note that in the original paper of PAEM-MO the PAEM is evaluated based on the expensive
CISD wavefunction, while we merely use HF wavefunction. However, our results are in good
agreement with that at CISD level, showing that correlation potential can be safely neglected in
the study of PAEM.
The interested users are suggested to replot the PAEM with iuserfunc=34 to employ DFT XC
potential in PAEM, you will find the results are very similar to those we obtained earlier.
Worthnotingly, although the PAEM-MO analysis method has clear physical meaning, its
many limitations severely hinders it to be a universal method to distinguish covalent and non-
covalent interactions like ELF or LOL: (1) PAEM-MO analysis does not always present
reasonable conclusion in all cases. For example, PAEM-MO erroneously indicates that the H-bond
in water dimer is covalent interaction. (2) PAEM-MO is difficult to be applied to polyatomic
molecules, since there are often too many occupied orbitals with complex shape. (3) If the two
atoms are placed too close to each other, then PAEM-MO almost always indicates that the
interaction is covalent.
4.4 Plot properties in a plane
4.4.1 Color-filled map of electron density of hydrogen cyanide
In this example we plot slice map for electron density of hydrogen cyanide. Boot up
Multiwfn and input following commands
examples\HCN.wfn
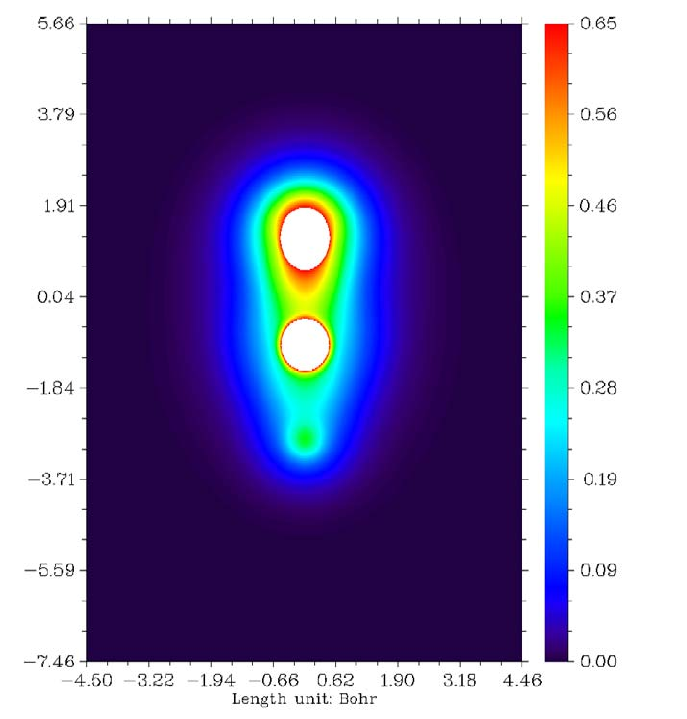
4 Tutorials and Examples
242
4 // Plot graph in a plane
1 // Electron density function
1 // Select color-filled map as graph type
Press ENTER button to use the recommended grid setting, namely 200,200. If you increase
the number of grid points, graph will become finer, but you have to wait longer time for
calculating data and plotting
2 // Select XZ plane (in hcn.wfn, Z-axis is molecular axis)
0 // The number of XZ planes is infinite, here we choose the only one with Y=0 Bohr
After a few seconds the graph pops up
The central regions of carbon and nitrogen are white, suggesting that electron density exceeds
the upper limit of color scale (0.65). Close the graph, then a menu appears, you can choose
corresponding options to adjust plotting parameters and then use -1 to replot again, or export X-Y
data set to plain text file for replotting the graph by external data visualization software (sigmaplot,
matlab, etc.), or save the picture in current directory (the graphical format can be controlled by
"graphformat" in settings.ini) and so on.
4.4.2 Shaded surface map with projection of localized orbital locator
in a plane of monofluoroethane
Boot up Multiwfn and input following commands
examples\C2H5F.wfn
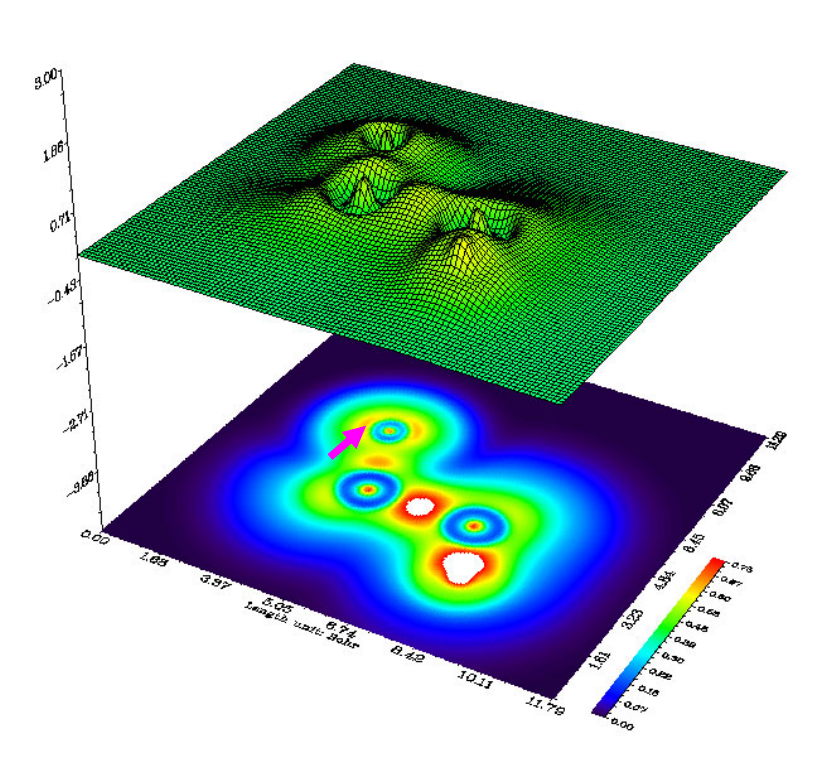
4 Tutorials and Examples
243
0 // Let’s view the molecular structure first to find the plane we are interested in, suppose that
the C-C-F plane is what we want, remember the indices of the three atoms: 1, 5, 8, and then press
RETURN button
4 // Plot graph in a plane
10 // Localized orbital locator (LOL)
5 // Shaded surface map with projection
Press ENTER button to use recommended grid setting, namely 100,100
4 // Define the plane by three atoms. If you want to enlarge plotting region, select 0 first and
input a larger value than the default one (4.5 Bohr)
1,5,8 // The indices of the three atoms
The graph immediately pops up:
We can see that covalent regions have high LOL value, the electron depletion regions
between valence shell and inner shell are shown by the blue circles around nuclei. A lone pair of
fluorine atom is pointed out by purple arrow.
The graph you have seen in the GUI can be saved to graph file by option 0 at post-process
interface, if you found the exported picture is truncated at edge, select option -1 to reenter the GUI
window, zoom out the graph and then export the picture again.
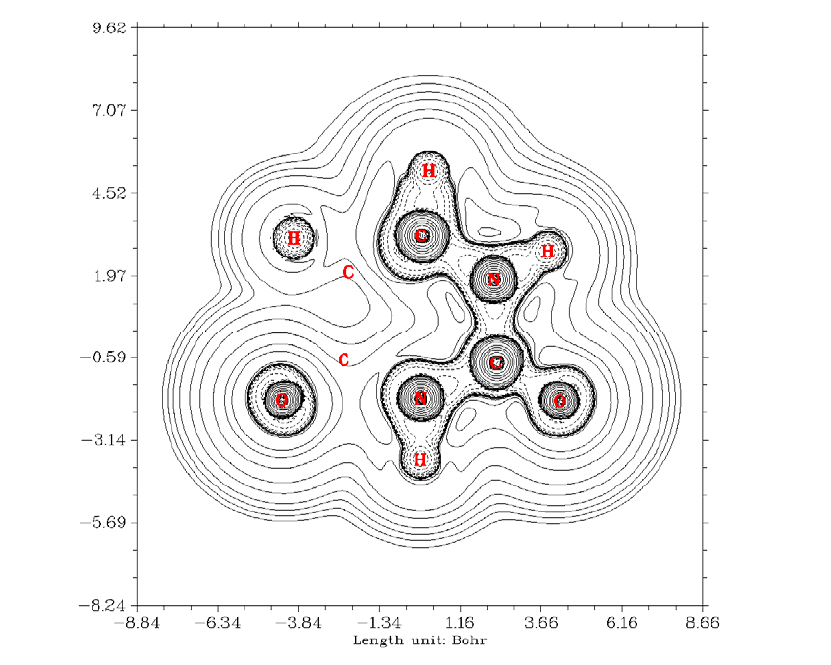
4 Tutorials and Examples
244
4.4.3 Contour map of electron density Laplacian of uracil without
contributions from some atoms
Boot up Multiwfn and input following commands
examples\Uracil.wfn
6 // Modify wavefunction
-4 // Discard contribution of some atoms
3,4 // All GTFs in atom 3 and 4 will be discarded. In other words, atom 3 and 4 will be
removed from current wavefunction
-1 // Return to main menu
4 // Plot graph in a plane
3 // Laplacian function
2 // Contour line map
Press ENTER button to use default grid setting
1 // XY plane will be plotted
0 // The Z-position of the XY plane is zero, that is molecular plane
Below is the resultant graph, solid and dash line correspond to positive and negative regions
respectively.
From the graph you can see the contribution from the two carbons have been discarded as
expected. By using the options shown on the command-line screen, you can save, export, redraw
the picture, adjust plotting parameters, etc. If option 2 is chosen, the isovalues will be marked on
corresponding contour lines. Once option 3 is chosen, you will enter an interface for setting up
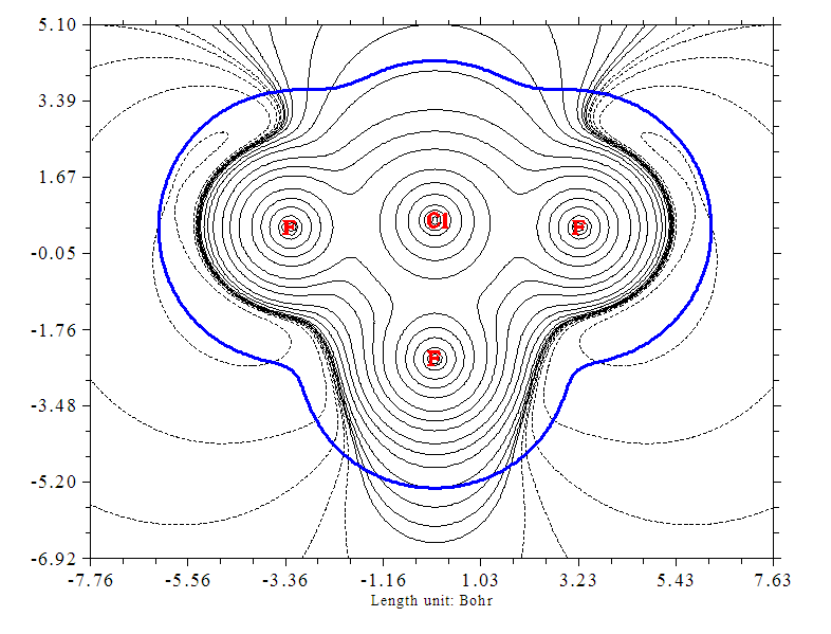
4 Tutorials and Examples
245
contour lines, please consult Section 3.5.4. For more about molecular fragment setting please
consult Section 3.1.
4.4.4 Contour map of electrostatic potential of chlorine trifluoride
This example we plot electrostatic potential (ESP) for chlorine trifluoride as contour map.
Boot up Multiwfn and input following commands
examples\ClF3.wfn // ClF3.wfn was generated at B3LYP/6-31G* level
4 // Plot graph in a plane
12 // Total electrostatic potential
2 // Draw contour line map
120,120
3 // YZ plane
0 // Set x coordinate of the YZ plane to 0
Because evaluation of ESP is evidently more time-consuming than other real space functions,
you need to wait for a while.
PS: For very large system, the cost of plotting plane map for ESP may be prohibitively high. However, this
task is still feasible if you make use the cubegen utility in Gaussian to generate ESP value at the plotting points,
since cubegen calculates ESP much faster than Multiwfn for the case of large systems or high-quality basis-sets.
See Part 2 of Section 4.12.7 on how to do this.
After the calculation is finished, ESP map will pop up. This map is inconvenient to be
visually analyzed, since what we are interested in is often the ESP distributed on molecular vdW
surface, so it is better to plot the vdW surface on this map simultaneously. In order to do this, we
close the graph by clicking right mouse button, choose option 15, and then choose option -1 to
replot the graph, you will see such a picture
4 Tutorials and Examples
246
The bold blue line corresponds to vdW surface (isosurface of electron density=0.001 a.u., as
defined by R. F. W. Bader). From the graph it is clear that chlorine atom is positively charged,
because the local vdW surface closed to chlorine atom largely intersected solid contour lines
(correspond to positive ESP). For the same reason, we can see that the equatorial fluorine atom
possesses less electrons than the two axial fluorine atoms, this point can be further verified when
we calculate Hirshfeld atomic charges for this molecule in section 4.7.1.
Plane map of the ESP derived from atomic charges can be directly plotted by Multiwfn too.
First, you need to prepare a plain text file with .chg extension, the first column corresponds to
element name, the 2th, 3th and 4th columns correspond to X,Y and Z cooredinates in Angstrom
respectively, the last column is atomic charge. For example:
Cl 0.000000 0.000000 0.359408 0.529971
F 0.000000 1.726507 0.294501 -0.228394
F 0.000000 0.000000 -1.267884 -0.073185
F 0.000000 -1.726507 0.294501 -0.228394
Boot up Multiwfn as usual, and then use the .chg file as input. The plotting procedure is
completely identical to the one given above, except that when the program prompts you to select
real space function, you should select 8 (ESP from atomic charges) instead of 12.
4.4.5 Contour map of two orbital wavefunctions
Multiwfn is capable to plot contour map for two orbitals simultaneously, in this section, we
will draw contour map for NBO 12 and NBO 56 of NH2COH (recall Section 4.0.2). The plane we
selected is perpendicular to molecular plane and passed through both carbon and nitrogen atoms.
Boot up Multiwfn and input:
examples\NH2COH.31
37 // Will load NH2COH.37
0 // This step prints all atom coordinates in Multiwfn console window, which will be used
later. This step is not compulsory
4 // Plot plane graph
4 // Orbital wavefunction
12,56 // The two orbital indices. If you only input one index, then only one orbital will be
plotted
Press ENTER to use default grid setting
5 // The plane we want to plot is neither a XY/YZ/XZ plane nor a plane that can be defined
by three atoms, the best way to define the plane is to input three points
0.000000 0.794089 0.000000 // The coordinate of the first point, this is just the
coordinate of carbon atom, which has printed on screen when you selected main function 0
-1.778942 -1.064235 0.000000 // The coordinate of the second point, this is just the
coordinate of nitrogen atom
-1.778942 -1.064235 1.000000 // The coordinate of the third point, X and Y coordinates
are identical to the ones of nitrogen atoms, but Z value is suitably moved in Z-direction (you can
use trial&error method to find the most suitable movement distance)
Immediately a graph pops up. We close it by clicking right mouse button, choose option 2
and input 25 to enable showing isovalue on contour lines, then choose -1 to redraw the graph, we
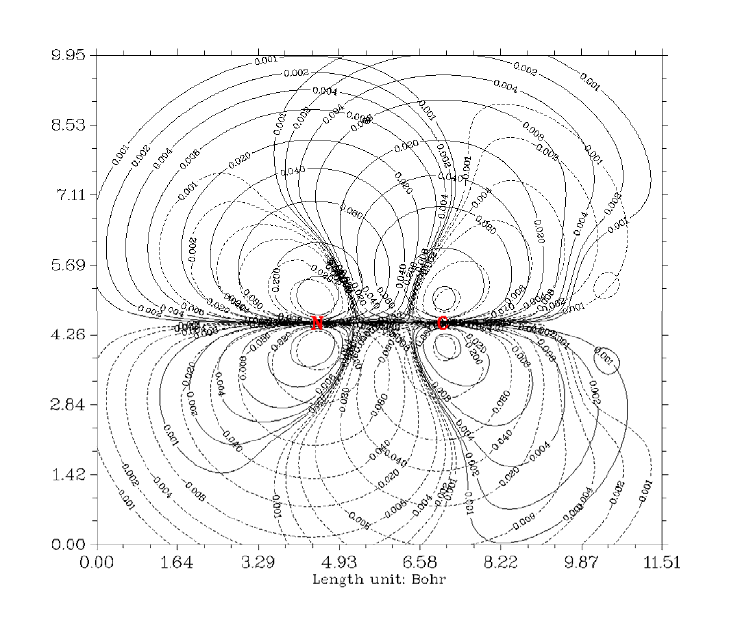
4 Tutorials and Examples
247
will see:
This contour map is not ideal, there are too many contour lines interwined together and
confused us. The culprits are the contour lines with too small isovalue (i.e. magnitude smaller than
0.01), since they are not important, we can delete them to make the graph clearer. So, next we
input
3 // Change contour line setting
5 // Delete a range of contour lines
1,4 // Delete the four contour lines: 0.001, 0.002, 0.004, 0.008
5 // Delete a range of contour lines
28,31 // Delete the four contour lines: -0.001, -0.002, -0.004, -0.008. For convenience, you
can choose option 6 to export current contour line setting to an external file, when you use
Multiwfn next time you can load present setting directly by choose option 7 in current interface
1 // Return to the upper menu
-1 // Replot the contour map
Now the graph become informative, the overlapping regions of identical phases are quite
distinct. Notice that only the labels of the atoms whose vertical distance to the plane are smaller
than "disshowlabel" in settings.ini will be shown.
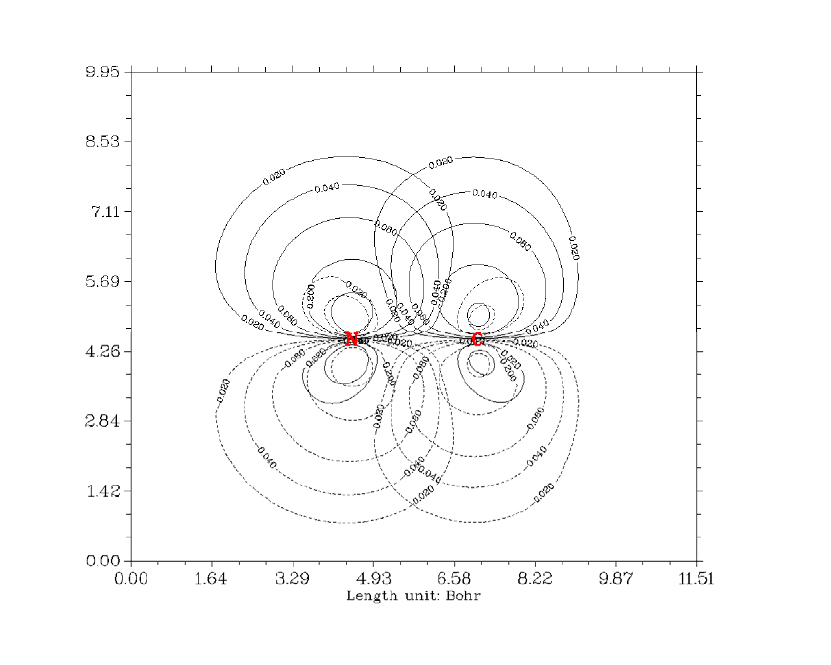
4 Tutorials and Examples
248
4.4.6 Gradient+contour map with topology paths of electron density
of hydrogen peroxide
As introduced in Section 3.5.5, critical points, bond paths and interbasin surfaces can also be
plotted on plane map, here I give a very simple example.
Boot up Multiwfn and input following commands
vb1510s\kabat\h2o2.fch // Of course, you can also use .wfn file as input
4
1 // Electron density
6 // Gradient line with/without contour line map
Press ENTER to use default grid setting
4
2,1,3 // Define the plane by nuclear coordinates of atom 1, 2 and 3
Generating data and plotting gradient map take more computational time relative to other
graph type, however since present system is small and basis-set is only 6-31G*, resultant graph
shows up immediately:
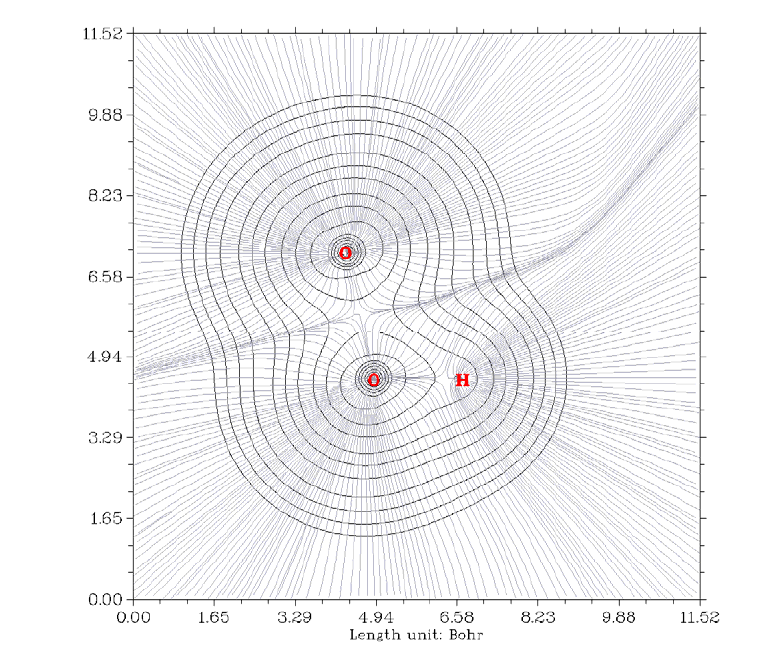
4 Tutorials and Examples
249
This type of graph is very useful in Bader’s AIM analysis. You can also plot gradient+contour
map for any other real space functions supported by Multiwfn.
If you want critical points and paths also to be portrayed on the graph, you need to do
topology analysis as described in Section 4.2.1, then return to main menu, and then draw contour
or gradient map as usual. The resultant graph looks like below. Brown, blue, and orange circles
denote (3,-3), (3,-1) and (3,+1) critical points, respectively, bold dark-brown lines depict bond
paths.
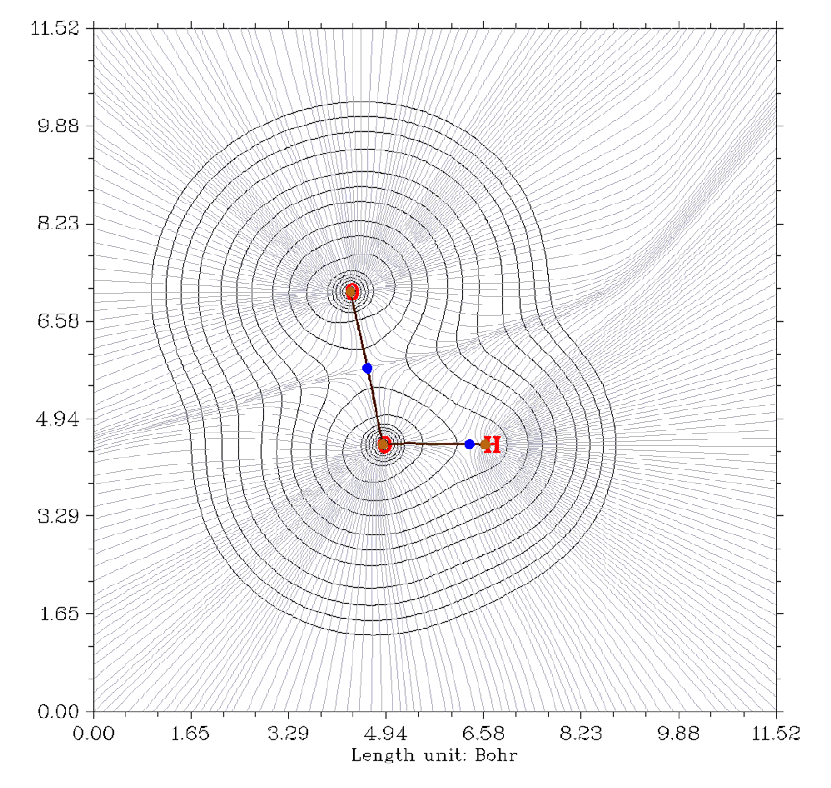
4 Tutorials and Examples
250
Interbasin paths can also be drawn on the graph. If you have finished the search of CPs in
topology analysis module, after you draw contour/gradient/vector field map, you could find a
option named "Generate and show interbasin paths" in post-process stage, select it, and show the
graph again, the interbasin paths will be drawn on the graph by bold deep blue lines:
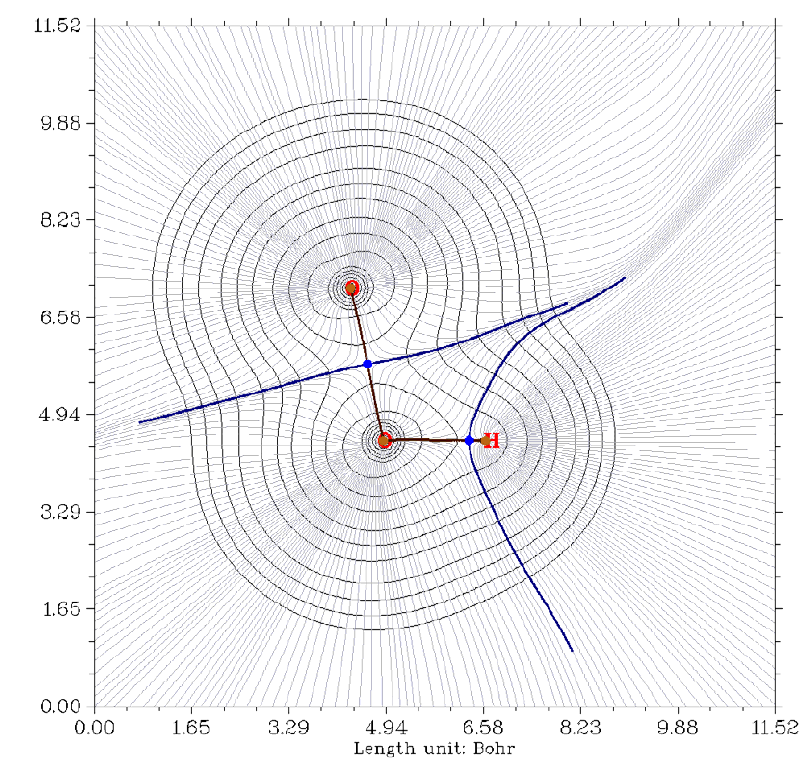
4 Tutorials and Examples
251
4.4.7 Deformation map of electron density of acetyl chloride
Deformation map of electron density clearly shows you the electron density variation during
formation of molecule, which is actually molecular electron density minus electron densities of
each atom in free-state. It is a labor work to draw such a graph. However, with Multiwfn this task
is very easy. Boot up Multiwfn and input following commands
examples\CH3COCl.wfn
4
-2 // Tell Multiwfn you want to draw deformation map, then Multiwfn prepares free-state
atom wavefunctions
6-31G* // The basis-set used to generate atom wavefunctions by Gaussian. Because the basis-
set used for CH3COCl.wfn is 6-31G*, here you'd better use 6-31G* too
d:\study\g09w\g09.exe // The path of executable file of Gaussian (you can also use other
Gaussian version). If you already set correct path in “gaupath” parameter in settings.ini, then
Multiwfn will not ask you to input the path every time
Now Multiwfn starts to invoke Gaussian to calculate atom wavefunctions, then Multiwfn
translates and sphericalizes them internally. These temporary wavefunction files are stored in
“wfntmp” folder in current directory, after you get the expected graph you can delete the folder.
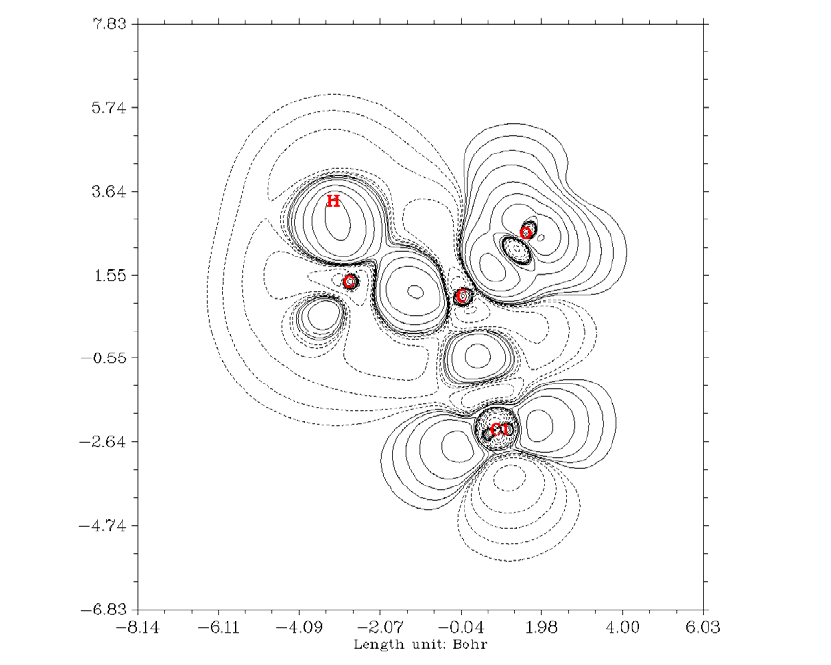
4 Tutorials and Examples
252
Let’s continue to input the remain commands.
1 // Electron density function
2 // Contour map
Press ENTER button to use default grid setting
1
0 // The XY plane with Z=0 is the plane of acyl chloride
Then the deformation map pops up:
As we expected, electron density concentrates towards bonding regions, we also find the
density distribution around chlorine atom is largely desphericalized, satisfied with hybrid orbital
theory, chlorine atom forms somewhat sp3 hybrid state.
You can also plot deformation maps for other functions by choosing corresponding real space
function, however not all of them are meaningful.
If you want to avoid recalculating atom wavefunction files next time, you can copy the .wfn
files without number suffix (such as “C .wfn“) from “wfntmp” folder to “atomwfn“ folder in
current directory, if Multiwfn finds all needed atom wavefunctions have already existed in
“atomwfn” folder, then Multiwfn will not invoke Gaussian to calculate them again.
Hint: You can also use “genatmwfn.pdb” in “examples” directory to generate all atom wavefunctions under
specific basis-set in a single run, please consult Section 3.7.3.
The “atomwfn” folder in “examples” directory contains atom wavefunctions (by 6-31G*) for
all first-four row elements, you can directly copy this folder to current directory, after that you will
not need Gaussian again during plotting deformation map.
If your system involves some elements heavier than Kr, you have to manually calculate the
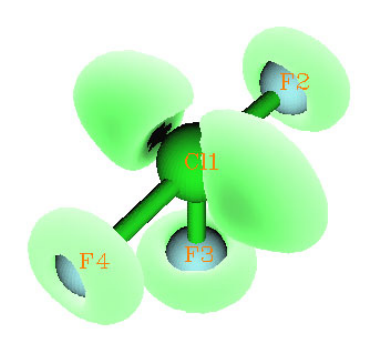
4 Tutorials and Examples
253
corresponding atomic .wfn files and put them into "atomwfn" folder".
4.5 Generate grid data and view isosurface
This section contains examples for main function 5 of Multiwfn, all of them need to calculate
grid data. Once the grid data is generated, it can be visualized as isosurface, or be exported to .cub
file so that it can be rendered by third-part tool such as VMD or be further utilized by other
analysis codes.
4.5.1 Electron localization function of chlorine trifluoride
Boot up Multiwfn and input following commands
examples\ClF3.wfn // Chlorine trifluoride at B3LYP/6-31G*
5 // Generate grid data and view isosurface
9 // Electron localization function (ELF)
2 // Medium quality grid, about 512000 points will be evaluated, this setting is fine enough
for small system. Please consult Section 3.6 for more about grid setting information.
Now Multiwfn starts to calculate grid data, this is a time-consuming task, you have to wait
for a while. Notice that if your computer have multiple CPU cores (SMP parallel architecture), I
strongly suggest you enable the parallel mode, that is set “nthreads” parameter in settings.ini to
the number of CPU cores, you will find calculation speed improved significantly! (By default, the
parallel implementation is enabled for four cores)
When the calculation is finished, Multiwfn outputs some statistical information, in the new
menu you can draw the isosurface by option -1, then a GUI window pops up, input isovalue of
0.85 in the text box and press “Enter” button on your keyboard, the isosurface would looks like
this
The ELF isosurface clearly points out the lone electron pair regions of fluorine and chlorine
atoms. After click “Return” button to close GUI window, you can use option 1 to save the graph in
current directory (the effect is the same as clicking the button “save pic” in GUI), or use 2 and 3 to
export grid data to Gaussian cube file and to plain text file in current directory respectively.
If you want to use different colors to shade different isosurfaces, you can download a mini
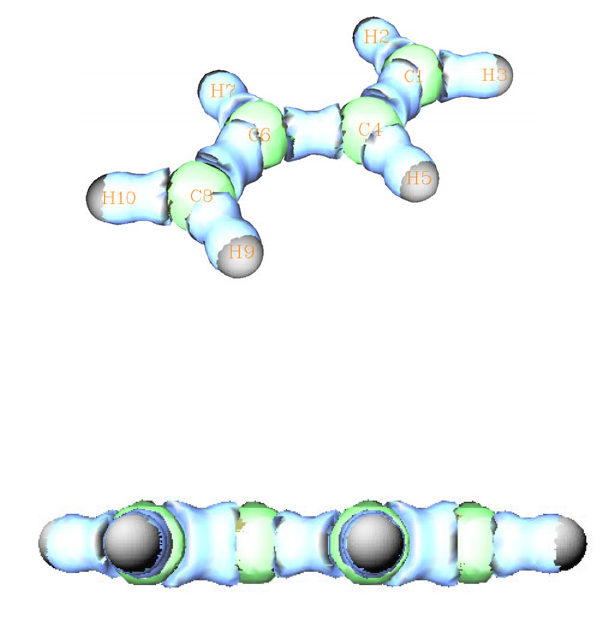
4 Tutorials and Examples
254
tutorial named "Drawing ELF isosurfaces with different colors for different domains" from
"Related resources and posts" section of Multiwfn website and then follow its steps.
4.5.2 Laplacian of electron density of 1,3-butadiene
Electron density Laplacian is another localization indicator as ELF and LOL but with longer
history. Laplacian is not as good as ELF and LOL for highlighting localization region, its
distinguishability is weak, for example, the shell structures of atoms heavier than krypton cannot
be fully illustrated by Laplacian, and if you attempt to use Laplacian to analyze chlorine trifluoride,
you will find the lone pair regions of fluorine atoms (circular isosurfaces) are hard to identify.
Moreover, the value range of Laplacian is too large, which brings difficulties on analysis.
However for most system Laplacian still works fine and now I illustrate its usefulness by an
example. Boot up Multiwfn and input following commands
examples\butadiene.fch // Yielded under B3LYP/6-31G** level
5 // Generate grid data and view isosurface
3 // Electron density Laplacian
2 // Medium quality grid
-1 // View isosurface
In the newly occurred window, change isosurface value from default value to 0.3, then the
green and blue isosurfaces will correspond to isovalue of 0.3 and -0.3 respectively. The presence
of blue isosurfaces between C-C and C-H suggests that valence-shell electrons are strongly
concentrated on these regions, these are typical pattern of covalent bonding.
If you inspect the isosurfaces between carbon atoms carefully, you will find that the
isosurface between C6-C8 or C1-C4 is wider than the isosurface between C4-C6, this
phenomenon reflects that the two boundary C-C covalent bonds are stronger than the central one.
This conclusion can also be verified by other wavefunction analysis schemes, for example, Mayer
bond order (bond order between C6-C8 is 1.863, while the bond order between C4-C6 is only
1.136).
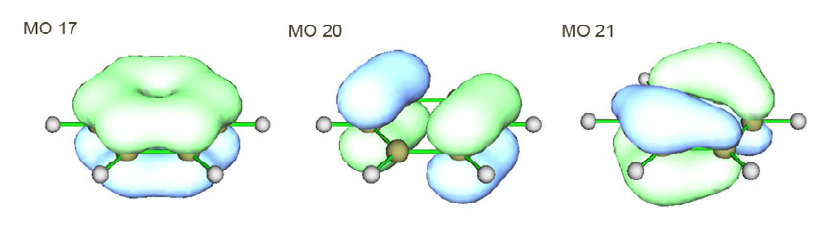
4 Tutorials and Examples
255
4.5.3 Calculate ELF-α and ELF-π to study aromaticity of benzene
ELF-α and ELF-π indices are commonly used α and π aromaticity indices, they are defined as
the ELF value at bifurcation point (i.e. (3,-1) CP) of ELF domain that solely contributed from α
orbitals and π orbitals, respectively, see J. Chem. Phys., 120, 1670 (2004) and J. Chem. Theory
Comput., 1, 83 (2005) for detail. The theoretical basis of these indices is that the ELF value at
bifurcation point measures interaction between adjointing ELF domains, the larger value means
electrons have better delocalization between these domains, which is commonly recognized as the
nature of aromaticity. It is argued that if ELF-π is larger than 0.70, then the molecule has π
aromaticity. While if the average of ELF-π and ELF-α is larger than 0.70, one can say that the
molecule is global aromatic. In present example, we will calculate ELF-α and ELF-π for benzene.
In order to separate α and π orbitals, we need to know which orbitals are π orbitals first. Boot
up Multiwfn and input following commands
examples\benzene.wfn // Optimized at B3LYP/6-311G* level, the same level used in Chem.
Phys. Lett, 443, 439
0 // View molecular orbitals (MOs)
Now check orbital shape of each MO in turn, we found 17th, 20th and 21th MOs are π
orbitals, as shown below. All other MOs are recognized as α orbitals.
We first calculate ELF-π. The contribution to ELF from α orbitals should be ommited; this
can be realized by setting occupation number of all orbitals to zero.
6 // Enter "Modify & Check wavefunction" interface
26 // Set occupation number for some orbitals
0 // 0 means selecting all orbitals
0 // Set occupation number of all orbitals to zero
17,20,21 // Select MO 17, 20 and 21
2 // Set occupation numbers of MO 17, 20 and 21 to 2.0, since they are close-shell system. If
you want to check if occupation numbers have been correctly set, choose option 3. You will find
occupation number of all α orbitals have become zero, which means they will have no any
contribution when we calculate any real space functions
q // Return to last menu
-1 // Return to main menu
Note: There is a much more convenience way to set occupation number of π orbitals to zero.
By this way you do not need to visually and manually find out the π orbitals, which will be rather
laborious for large systems. The procedure is: Enter subfunction 22 in main function 100, select 1
to choose actual molecular plane (in this example the plane is XY), then choose 1 to set
occupation number of all orbitals except for the identified π orbitals to zero (or may be 3, if
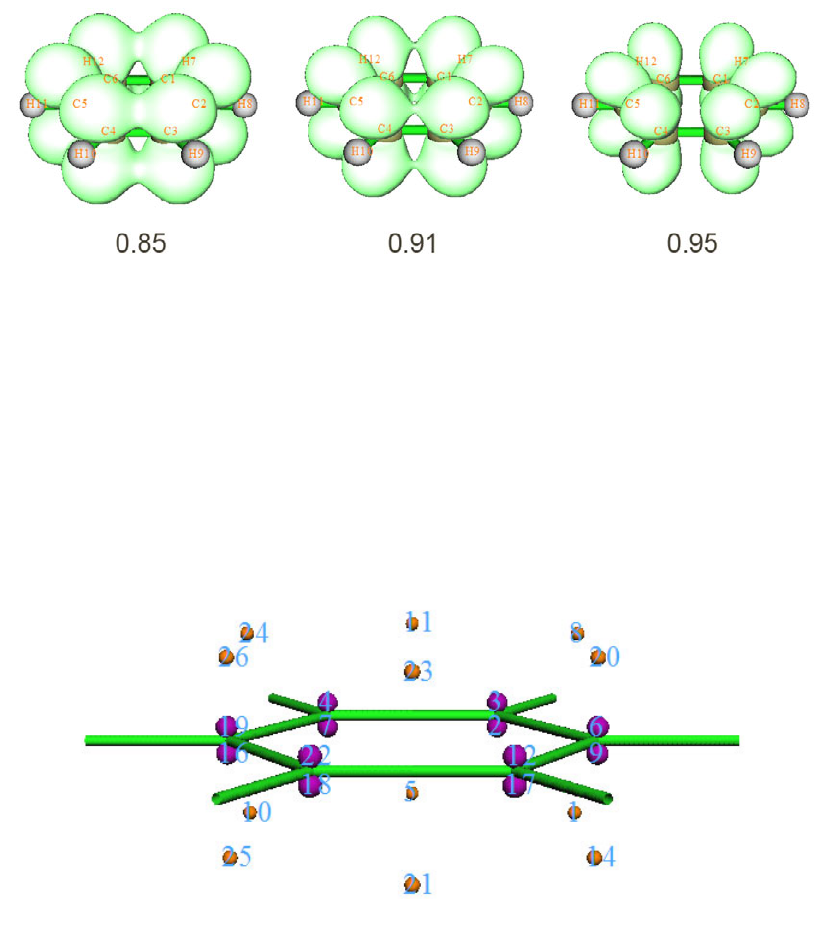
4 Tutorials and Examples
256
heavier elements are involved such as silicon), and finally choose 0 to return to main menu.
There are two ways to study ELF-π, way 1 is to examine ELF isosurface directly, while way
2 is performing topology analysis. Way 1 is more intuitive but less accurate than way 2. We use
way 1 first. Generate and view isosurface for ELF by main function 5 as usual (like Section 4.5.1.
High quality grid is recommended). This time the ELF isosurface only reflects π electron
localization. By gradually increasing isovalue, you will find that the two circle-shape ELF
domains are bifurcated to twelve sphercial-like domains at about the isovalue of 0.91 (see below
graph), which implies ELF-π index of benzene is about 0.91.
Let us use way 2 to calculate ELF-π index again, in principle this way is more rigorous than
way 1. Choose 0 to return to main menu.
2 // Topology analysis
-11 // Select real space function
9 // Select ELF
6 // This searching mode is the most appropriate one for locating ELF CPs
-1 // Start the search. The guessing points will be scattered around each atom in turn.
-9 // Return to upper menu
0 // Visualize results. The resultant graph are shown below, two (3,+1) CPs are not shown
Compare this graph with ELF isosurface map, it clear that the (3,-1) CPs (orange) are
bifurcation position of ELF domains, while (3,-3) CPs (purple) correspond to the maximal points
of the twelves ELF domains. Now we check ELF value at a (3,-1) CPs, we can choose any one,
since they are all equivalent.
7 // Show all properties at a CP
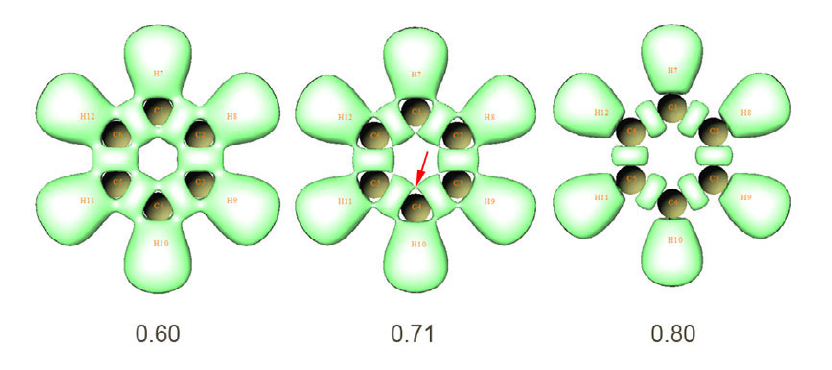
4 Tutorials and Examples
257
23 // CP23
From the output, we find the ELF value at CP 23, namely ELF-π index of benzene is 0.91247,
this result is in very good agreement with the value 0.913 given in Chem. Phys. Lett., 443, 439.
Evidently, this value exceeds the criteria (0.70) of π aromaticity, which implies that benzene has
strong π aromaticity.
Now we calculate ELF-α for benzene. Reboot Multiwfn and load benzene.wfn, set
occupation number of MO 17, 20 and 21 to zero (it is more convenient to use subfunction 22 in
main function 100 to do this). Then generate isosurface for ELF as usual, gradually adjust isovalue,
try to find out at which isovalue the domains corresponding to the α bonds between carbon atoms
are bifurcated. One can finally find that at the isovalue equals to 0.71 the domain are bifurcated,
suggesting that ELF-α index is about 0.71. The bifurcation point is pointed by red arrow in below
graphs:
Enter topology analysis module and search ELF CPs, like what we did in way 2 of ELF-π
analysis. You will obtain below graph. For clarity, (3,+1) and (3,+3) CPs are hidden.
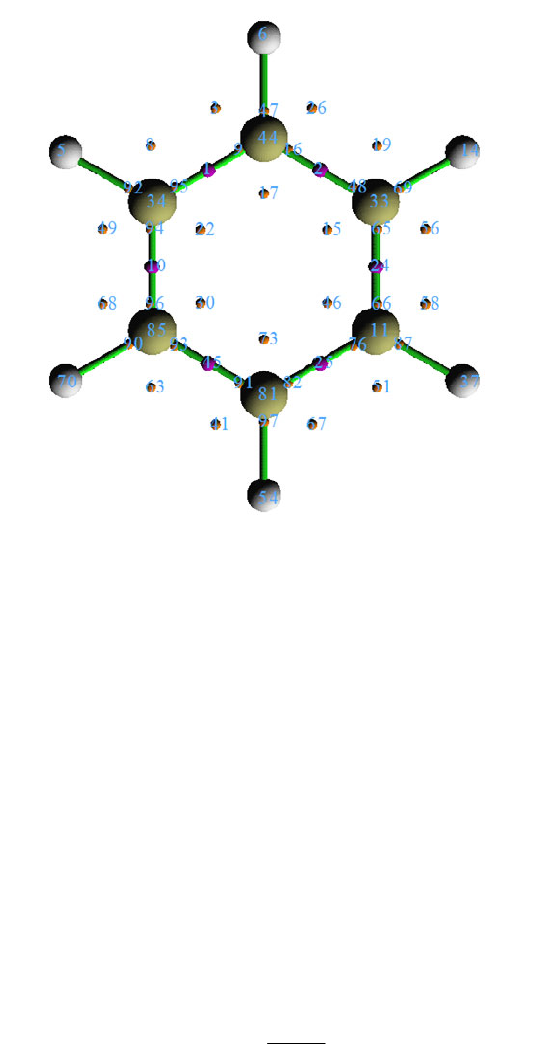
4 Tutorials and Examples
258
Compare positions of CPs with ELF isosurface map, it is clear that the (3,-1) CPs such as CP
73 correspond to bifurcation points of the α bond domains between the carbon atoms. Check ELF
value at CP 73, we get 0.70907, which is the accurate ELF-α value. Our result agrees well with the
value 0.717 from Chem. Phys. Lett., 443, 439.
The average of ELF-α and ELF-π is (0.70907+0.91247)/2=0.81077, which is larger than the
criteria of global aromaticity, so benzene possesses global aromatic character.
4.5.4 Use Fukui function and dual descriptor to study favorable site
for electrophilic attack of phenol
Fukui function
Fukui function is an important concept in conceptual density functional theory, it has been
widely used in prediction of reactive site. Fukui function is defined as (J. Am. Chem. Soc., 106,
4049)
N
f)(
)( r
r
where N is number of electrons in present system, the constant term
in the partial derivative is
external potential. Generally the external potential only comes from nuclear charges, so
can be
seen as nuclear coordinates for isolated chemical system. It is argued that reactive sites have larger
value of Fukui function than other regions. We cannot directly evaluate the partial derivative due
to the discontinuity when N is integer. In the finite difference approximation, Fukui function can
be calculated unambiguously for three situations:
Nucleophilic attack: )()()()( LUMO
1rrrr
NN
f
Electrophilic attack: )()()()( HOMO
1rrrr
NN
f

4 Tutorials and Examples
259
Radical attack: 2
)()(
2
)()(
2
)()(
)( LUMOHOMO
11
0rr
rr
rr
r
NN
ff
f
In this example, we first attempt to find out the reactive sites for electrophilic attack of
phenol by means of Fukui function given above. The approximate form of Fukui function based
on frontier orbitals will not be used here.
First of all, use quantum chemistry program to optimize structure and generate .wfn file for
neutral state phenol, and then generate another .wfn file for phenol with charge of +1. Notice that
at the second step you only need to change the charge and multiplicity to 1 and 2 respectively
from 0 and 1, do not reoptimize molecule structure for +1 state phenol, because
(nuclear
coordinates in this context) is defined as constant in the partial derivative of Fukui function. I
assume that the two .wfn files are named as phenol.wfn and phenol+1.wfn, you can find them in
“examples” directory.
For studying the isosurface of
f, you can generate cube files for the two .wfn files
separately by main function 5 of Multiwfn and then calculate the difference cube file by main
function 13, and then visualize the cube file. However this work is more convenient to be achieved
via “custom operation” function in Multiwfn (see Section 3.7.1 for detail), just boot up Multiwfn
and input following commands:
examples\phenol.wfn //Calculated at HF/6-31G* level
5
0 // Set custom operation
1 // Only 1 file will be operated with the file has been loaded (namely phenol.wfn)
-, examples\phenol+1.wfn // “-“ is minus operator, that means the property of phenol.wfn
will minus corresponding property of phenol+1.wfn, which is the wavefunction of the phenol with
+1 net charge (corresponds to N-1 electron state)
1 // Electron density
2 // Medium quality grid
Now Multiwfn starts to calculate electron density grid data for phenol.wfn, and then calculate
for phenol+1.wfn, finally the grid data of phenol.wfn, namely N
, will minus the grid data of
phenol+1.wfn, namely 1N
, the result is
f. Let’s choose option -1 to check the isosurface,
after adjusting the isovalue to a proper value (0.007), the graph will be
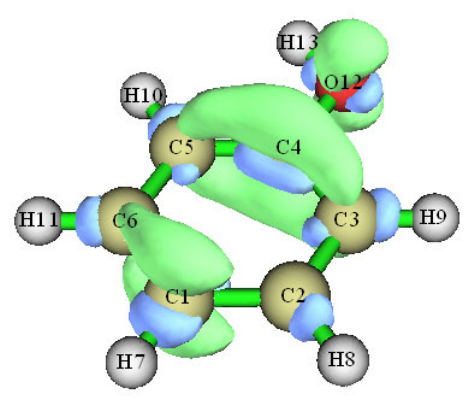
4 Tutorials and Examples
260
Clearly, most positive part of
f function are localized in O12, C1, C3, C4 and C5, that
means para and ortho positions of hydroxyl are favourite reactive sites for electrophilic attack,
this conclusion is in agreement with empirical rule, that is hydroxyl is an ortho-para- director.
Dual descriptor
Dual descriptor is another useful function used to reveal reactive sites, see J. Phys. Chem. A,
109, 205 for detail. Formally, the definition of the dual descriptor f
has close relationship with
Fukui function:
)()(2)()()()()(
)()()(
1111 rrrrrrr
rrr
NNNNNNN
fff
Worthnotingly, dual descriptor can also be evaluated in terms of spin density s
. Since
NN
1 and 1
NN
can be approximated as s
N1
and s
N1
respectively, it is clear
that )()()( 11 rrr s
N
s
N
f
. Commonly, there is no evident qualitative difference between
the dual descriptor evaluated based on electron density of three states (N+1, N, N-1) and the one
based on spin density of two states (N+1, N-1).
Unlike Fukui function, via f both types of reactive sites can be revealed simultaneously. It is
argued that if f > 0, then the site is favorable for a nucleophilic attack, whereas if f < 0, then the
site is favorable for an electrophilic attack. However, according to my experience, if your aim is to
figure out which ones are more favorable among many potential sites, you do not need to concern
the sign of f, you only need to study which sites have more positive or more negative of f. If the
distribution of f around a site A is more positive than another site B, then one can say A is a more
favorable site for nucleophilic attack than B, and meantime B is a more preferential site for
electrophilic attack than A.
Here we calculate dual descriptor for phenol based on spin density of N+1 and N-1 states.
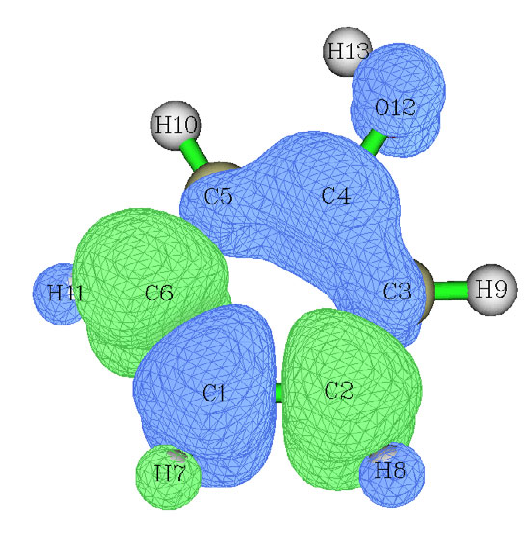
4 Tutorials and Examples
261
Since we have calculated phenol+1.wfn earlier, now we only need to calculate phenol-1.wfn (this
file has been provided in "example" folder). After that boot up Multiwfn and input:
examples\phenol-1.wfn // Corresponds to N+1 electron system
5
0 // Set custom operation
1 // Only one file will be operated with the file that has been loaded
-,examples\phenol+1.wfn // Corresponds to N-1 electron system
5 // Electron spin density
2 // Medium quality grid
4 // Change the isovalue
0.005
-1 // Visualize isosurface of dual descriptor
Change isosurface style to "solid face+mesh" from menu of the GUI, then you will see below
graph. The region covered by negative isosurfaces (blue) suggests that only para- and ortho-
carbons were activated for electrophilic attack by hydroxyl, this conclusion is in agreement with
Fukui function.
If you would like to evaluate f in its exact form (based on of three states), you can follow below steps:
examples\phenol-1.wfn // N+1 electron system
5
0 // Set custom operation
3 // Three files will be operated with the file that has been loaded
-,examples\phenol.wfn // N electron system
-,examples\phenol.wfn // N electron system
+,examples\phenol+1.wfn // N-1 electron system
1 // Electron density
The remaining steps are identical as above. If you visualize the isosurface, you will find this time the ortho-
carbons do not have negative value of f, they are only very slightly more negative than the para- carbons, that
means this time f does not have good ability to discriminate preferential sites. So, using exact form to evaluate f
does not necessarily give rise to better result than using spin density to approximately evaluate f!
Above we used visualization manner to examine Fukui function and dual descriptor and
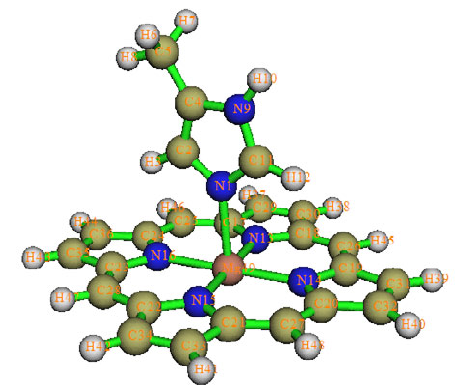
4 Tutorials and Examples
262
obtained the conclusion what we expected. However, visual analysis is somewhat ambiguous and
the discussion is inconvenient to be given in literature. Therefore sometimes we hope that the
discussions of Fukui function and dual descriptor can be quantified, namely using a value for each
atom to indicate the probability that it can be acted as reactive site. To do so, one should calculate
"condensed" version of Fukui function and dual descriptor based on population analysis
techniques. Since population analysis is exemplified in Section 4.7, the method for calculating
condensed Fukui function and condensed dual descriptor will be deferred to be introduced as
Section 4.7.3. Another scheme to study Fukui function and dual descriptor is to first partition the
whole molecular surface to local surface corresponding to each atom, and then examine the their
average values on these local surfaces. Because this scheme relies on quantitative molecular
surface analysis technique, it will be deferred to be illustrated in Section 4.12.4.
4.5.5 Plot difference map of electron density to study electron transfer
of imidazole coordinated magnesium porphyrin
In this example, I will show you how to do fragmental electron density difference in
Multiwfn. It can be imagined that during the course of imidazole coordinating to magnesium
porphyrin, electron density transfer occurs, the variation can be made clear by subtracting electron
density of imidazole (referred to as NN below) and magnesium porphyrin (referred to as MN
below) in standalone state from the whole system (referred to as MN-NN below). The geometry of
MN-NN is shown below:
MN-NN.gjf in “examples” folder is Gaussian input file of MN-NN system (geometry has
been optimized), run it by Gaussian after modifying the wfn output path at the last line, then MN-
NN.wfn will be yielded. Next, respectively delete MN and NN parts from MN-NN.gjf and
properly modify wfn output path and then save it as MN.gjf and NN.gjf (which have already been
provided in "example" folder). Then run them by Gaussian to produce MN.wfn and NN.wfn. It
should be paid attention that by default, Gaussian always puts input orientation to standard
orientation, which will make the coordinates in MN.wfn and NN.wfn inconsistent with MN-
NN.wfn, and thus the density difference will meaningless. So “nosymm” keyword must be
specified in route section to avoid the automate adjustment of coordinates.
Now we generate grid data of fragmental electron density difference by Multiwfn. Boot up
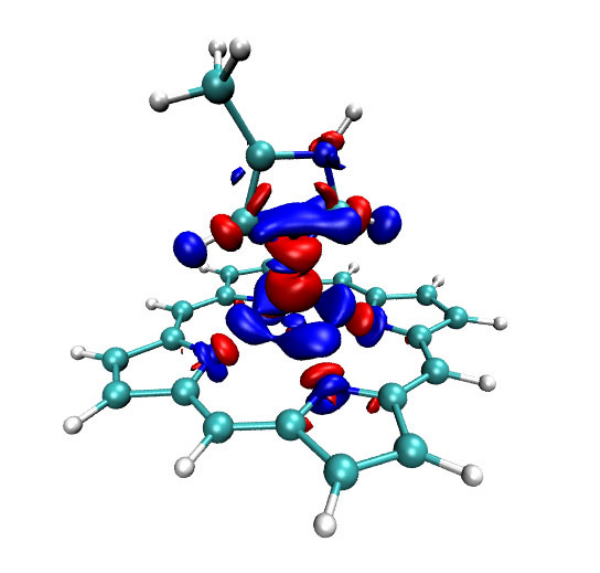
4 Tutorials and Examples
263
Multiwfn and input following commands
MN-NN.wfn
5
0 // Set custom operation
2 // Two files will be operated with MN-NN.wfn
-,MN.wfn // Subtract a property of MN.wfn from that of MN-NN.wfn
-,NN.wfn // Subtract a property of NN.wfn from that of MN-NN.wfn
1 // The property is selected as electron density
3 // Since present system is relative huge, we need more grid points than normal cases
After the calculation is finished, you can choose option -1 and then set isovalue to about
0.001 to visualize the isosurface of the grid data. However Multiwfn is not very professional at
visualization of grid data, for large size of grid data the visualization speed is relatively slow; you
can choose option 2 to export the grid data to cube file and then visualize it by external tools, such
as VMD, ChemCraft, Molekel and GaussView. Below is the graph generated by VMD
(http://www.ks.uiuc.edu/Research/vmd/), which is my favourite tool.
The red and blue isosurfaces (+0.0012 and -0.0012 a.u., respectively) represent the region in
which electron density is increased and decreased after NN coordinated to MN, respectively. It is
obvious that electron density is shifted from backside of nitrogen in NN toward magnesium atom
to strengthen the coordination bond. Besides, the appearance of NN didn't perturbe electron
density distribution of porphyrin remarkably, only slight polarization effect occurs in the four
coordination nitrogens of MN (by lowering isovalue you may obtain richer information, but they
can be ignored due to the small magnitude).
The detail step of drawing above graph in VMD: First drag the cube file density.cub into VMD main window.
Select Graphics-Representations, create a new representation by clicking "Create Rep" button, change the
"drawing method" to "isosurface", set "Draw" to "solid surface", set "Show" to "Isosurface", change the isovalue to
0.0012, set "coloring method" to "ColorID" and choose red. Now the isosurface of positive part of density
difference has been displayed. Then click "Create Rep" button again to create another representation, select blue in
4 Tutorials and Examples
264
"ColorID" and change the isovalue to -0.0012. If you would like to use white background instead of the default
black background, select Graphics-Colors-Display-Background-8 white.
Next, let's generate contour map of fragmental electron density difference in the plane
defined by atoms 16, 14, 9. Input following commands:
0 // Return to main menu
4 // Draw plane graph
0
2
-,MN.wfn
-,NN.wfn
1
2 // Contour line map
Press ENTER to use default setting
4 // Define the plane by three atoms
16,14,9
Immediately the contour map pops up. The solid and dashed contour lines exhibit where
electron density is increased and decreased, respectively. The contour lines in the graph are a bit
sparse; let's adjust contour line setting to make the graph look denser. Click right mouse button on
the window to close it, and input
3 // Change contour line setting
9 // Generate contour value by geometric series
0.0001,2,30 // Start value, step size and the number of steps, respectively
y // Clean existed contour lines
9
-0.0001,2,30 // Set negative contour lines
n // Append the contour lines to existed ones
1 // Save setting and return
-1 // Redraw the graph
Below is the final graph you will see, quite pretty!
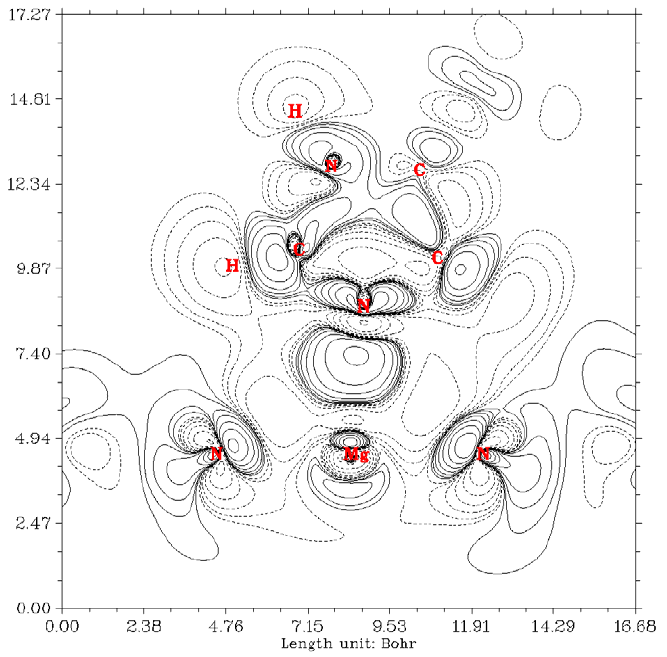
4 Tutorials and Examples
265
Hint: After finished setting contour lines, you can choose option 6 to save the setting to
external plain text file. Next time you can directly load the setting by option 7.
4.5.6 Study electron delocalization range function EDR(r;d) of anionic
water dimer
Content of this section was contributed by Arshad Mehmood and slightly adapted by Tian Lu.
This example shows how to calculate electron delocalization range function EDR(r;d) at
user-defined length scale d for anionic water cluster (H2O)2 (cf. Phys. Chem. Chem. Phys., 17,
18305 (2015)). Using EDR(r;d) we can vividly inspect distribution of solvated electron.
Boot up Multiwfn and input following commands:
examples\solvatedelectron.wfn // Anionic water dimer optimized at B3LYP/6-
311++G(2d,2p) level
5 // Calculate grid data
20 // EDR(r;d)
11.22 // Input length scale d (Bohr). Here we consider the relatively delocalized solvated
electron at d=11.22 Bohr. Further details are given in J. Chem. Phys., 141, 144104 (2014).
2 // Medium quality grid
-1 // Show isosurface graph
Now a GUI window pop up. Input isovalue of 0.74 in the “Isosurface value” box and press
ENTER button. The following isosurface will appear.
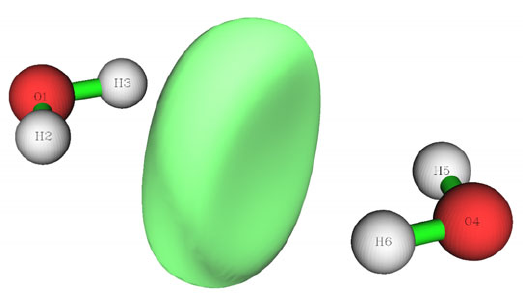
4 Tutorials and Examples
266
This figure shows that at length scale of d=11.22 Bohr the solvated electron is between the
two H2O molecules.
4.5.7 Study orbital overlap distance function D(r) of thioformic acid
Content of this section was contributed by Arshad Mehmood and slightly adapted by Tian Lu.
This example will show the calculation procedure of orbital overlap distance function D(r) of
thioformic acid and map it on molecular electron density surface. If you are not familiar with D(r),
you may check entry 21 of Section 2.6 or J. Chem. Theory Comput., 12, 3185−3194 (2016).
Boot up Multiwfn and input following commands:
examples\ThioformicAcid.wfn // Thioformic acid optimized at B3LYP/6-311++G(2d,2p)
5 // Calculate grid data
21 // Orbital overlap length function D(r), which maximizes EDR(r;d) with respect to d
Now we need to set input total number, start and increment of EDR exponents αi=1/di2, since
the overlap distance is fit using an even-tempered grid of exponents. The start value is the largest
exponent (α1), subsequent exponents are yielded by αi+1/αi = 1/αinc, where αinc is increment. The
default setting (i.e. n=20, α1=2.50, αinc=1.50) suffices for common systems. After selecting the
manual input (option 1) or default setting (option 2), a list of exponents will be appeared, which
will be used in evaluation of D(r)
2 // Medium quality grid
At this stage Multiwfn starts calculation. Wait until calculation is finished, then choose option
2 to export grid data of D(r) as EDRDmax.cub in current folder. The next step is to generate
molecular density isosurface.
0 // Return to main menu
5 // Calculate grid data
1 // Electron density
2 // Medium quality grid. The grid should be same as for D(r) calculation
Then export grid data of electron density in current folder as density.cub by selecting option 2.
Based on EDRDmax.cub and density.cub, then the D(r) grid data can be mapped on
molecular density isosurface by many visualization programs, such as VMD and GaussView.
Below is the D(r) mapped electron density isosurface (
=0.001 a.u.) plotted by GaussView.
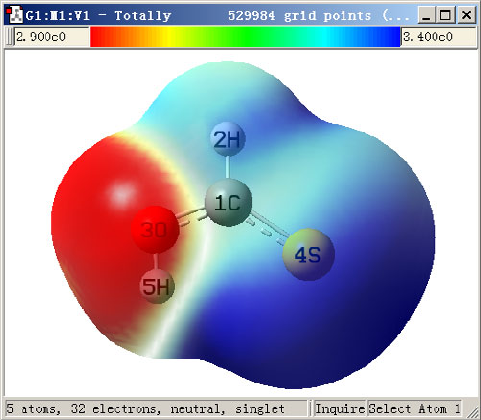
4 Tutorials and Examples
267
As can be seen from the graph, D(r) plotted between 2.9 Bohr (red) to 3.4 Bohr (blue) clearly
distinguishes the chemically hard oxygen lone pair (red) from the softer sulfur lone pair (blue).
This system will be further studied in Section 4.12.8 by means of quantitative molecular
surface analysis module.
4.6 Modify wavefunction
4.6.1 Delete certain Gauss functions
In subfunction 25 of main function 6, you can set orbital expansion coefficients of Gauss type
functions (GTFs) which satisfied certain conditions. If the coefficients are set to zero, that means
the information of these GTFs are deleted. In this example, we delete all Z-type GTFs of atom 2,3
and 4 from orbital 23 of phenol and then plot isosurface for this molecular orbital. Boot up
Multiwfn and input following commands
examples\phenol.wfn
6 // Modify wavefunction
25 // Set the coefficients of some GTFs that satisfied certain conditions
0,0 // Set the index range of GTFs, only the GTFs satisfied this condition will be reservered
to next step. 0,0 tell Multiwfn the range is “ALL”
2,4 // Only the GTFs attributed to atom 2, 3, 4 will be reserved to next step
Z // Only reserve Z-type GTFs to next step
23,23 // Set lower and upper limit of orbital, if they are identical, then only one orbital is
selected
0 // Set coefficients of selected GTFs in orbital 23 to zero, that is delete their information
0 // Save current wavefunction to new.wfn in current directory
You can choose option 4 and input 23 to check expansion coefficient of orbital 23 to verify if
your operation is correct. Let’s compare the isosurfaces of orbital 23 before and after modification.
In order to plot the modified orbital 23, you can close Multiwfn and load new.wfn, or directly
select option -1 to return main menu, and then enter main function 0 to plot the isosurface of
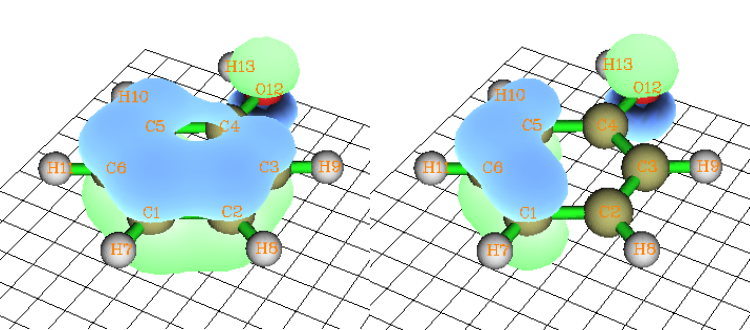
4 Tutorials and Examples
268
orbital 23.
Left side is unmodified state, the molecular plane is parallel to XY plane, so if Z-type GTFs
in some atoms are deleted, the corresponding part of isosurface should disappear, this is what we
have seen at right side (modified state).
4.6.2 Remove contributions from certain orbitals to real space
functions
In Multiwfn, contributions from certain orbitals to real space functions can be removed. From
formulae in Section 2.6 it is clear that if occupation numbers of certain orbitals are set to zero,
they will have no contribution, as if they were not existed. Actually in Section 4.5.3 we have
already used this trick to separate ELF as ELF-α and ELF-π. Notice that some real space functions
are not linear, such as ELF and LOL, so they cannot be computed as the sum of contributions from
each occupied orbitals. In contrast, some real space functions are linear, such as electron density
and kinetic energy density.
In this example, we will remove contributions from the MOs consist of inner-core atomic
orbitals to electron density for hydrogen cyanide, so that we can obtained valence electron density
map.
The principle is very sample. Inner-core atomic orbitals always have very low energies, so
they can only compose MOs with the lowest energies. Hydrogen has no inner-core atomic orbital,
both carbon and nitrogen have one inner-core atomic orbital, hence what we need to do is to set
occupations numbers of the first two MOs to zero (assume that this is close-shell wavefunction).
Now boot up Multiwfn, and input following commands
examples\HCN.wfn
6 //Modifying wavefunction
26 // Set occupation numbers
1,2 // Select MO 1 and 2
0 // Set their occupation numbers to zero
q // Return to last menu
-1 // Return to main manu
Then, if we redo the example in Section 4.4.1, we will get below graph

4 Tutorials and Examples
269
From the picture we find that the white circles in carbon and nitrogen center are largely
contracted, this is because the contributions from their 1s atomic orbitals are removed. Electron
structures are exhibited more clearly in this picture than in Secton 4.4.1.
For convenience consideration, Multiwfn provides function 34 in main function 6, one can
directly choose it to set occupation numbers of the MOs that consist of inner-core atomic orbitals
to zero.
4.6.3 Translate and duplicate graphene primitive cell wavefunction to
periodic system
The .fch or .wfn file generated by periodic boundary condition (PBC) calculation of Gaussian
only contains wavefunction of primitive cell, so the analysis results do not show any periodic
character, of course you can enlarge your inputted system to multiple cells before PBC calculation,
but you have to spend much more time for computation. Multiwfn provides a way to convert
primitive cell wavefunction to a large supercell wavefunction, so that in the region you are
interested the real space functions show periodic character.
Note: Beware that constructing supercell wavefunction in this manner is only a crude approximation! Since
the orbital mix between neighbouring primitive cells is ignored, therefore the orbital wavefunctions of supercell
cannot be faithfully reproduced.
In this section I use graphene as example. First, generate .fch (or .wfn) file of graphene
primitive cell. The content of “molecular specification” field in the Gaussian input file is
C 0.000000 0.000000 0.000000
C 0.000000 1.429118 0.000000
TV 2.475315 0.000000 0.000000
TV -1.219952 2.133447 0.000000
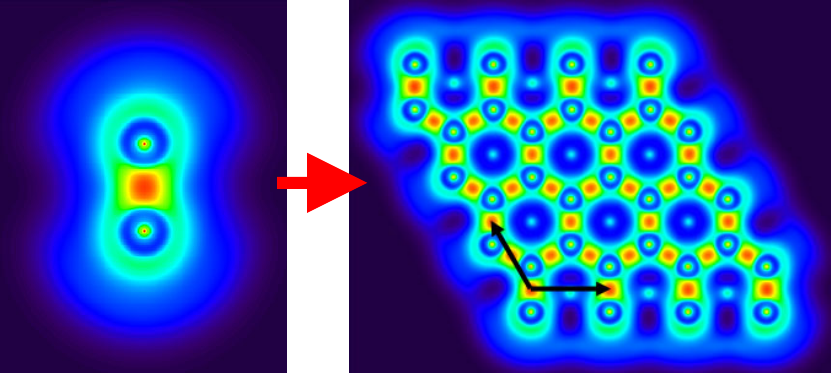
4 Tutorials and Examples
270
In route section, fill “#P PBEPBE/3-21g/Auto SCF=Tight”. Use Gaussian to run this input
file and then use formchk to convert the binary checkpoint file to graphene.fch. Then boot up
Multiwfn and input:
examples\graphene.fch
6
32 // Translate and duplicate primitive cell wavefunction
2.475315 0.000000 0.000000 // Translation vector 1
2 // Unit is Angstrom
3 // Translate and duplicate present system three times in this direction
32 // Notice that current system already have four primitive cells, this time we will translate
and duplicate current system in another direction three times, so the final system will contain 16
primitive cells
-1.219952 2.133447 0.000000 // Translation vector 2
2 // Unit is Angstrom
3 // Translate and duplicate present system three times in this direction
The left part of the picture below is LOL function of primitive cell. After above manipulation,
we recalculate LOL function and then the right graph is obtained (black arrows denote translation
vectors). Apparently, the central region of the extended system shows correct periodic character,
however the behavior of boundary region is still incorrect, you can extend the system further to
enlarge “correct” region.
Notice that if “nosymm” keyword is not specified in PBC calculation, Gaussian may
automatically put the system into standard orientiation, at this time you should not use the
translation vectors in Gaussian input file as the translation vectors for translating and duplicating
system in Multiwfn, but should use the content in “Translation vectors” field of .fch file or “PBC
vector” segment in Gaussian output file.
4 Tutorials and Examples
271
4.7 Population analysis and atomic charge calculation
4.7.1 Calculate Hirshfeld and CHELPG charges for chlorine
trifluoride
I have introduced the theory of Hirshfeld population in Section 3.9.1, to calculate Hirshfeld
charges for ClF3, input below commands in Multiwfn
examples\ClF3.wfn
7 // Population analysis
1 // Hirshfeld population
Hirshfeld population analysis requires electron density of atoms in their free-states, you need
to choose a method to calculate atomic densities. Selecting 1 to use built-in atomic densities is
very convenient, see Appendix 3 for detail; alternatively, you can select 2 to evaluate atomic
densities based on atomic .wfn files, see Secion 3.7.3 for detail. Here we choose option 1.
From the result we find the charges of the three fluorine atoms are unequal, the equatorial one
is -0.075 while the axial ones have more electrons, are -0.224.
Finally Multiwfn asks you if exporting the result, if you select ‘y’, the element names, atom
coordinates and atomic charges will be outputted to a plain text file with .chg extension. You can
use this file as Multiwfn input and select “Electrostatic potential from atomic charges” in main
function 3, 4 or 5 to study the electrostatic potential distribution from Hirshfeld charges.
Next, we calculate CHELPG charge. CHELPG charge has been introduced in Section 3.9.10.
First select option 12 in the population analysis module, you will see a new menu, in general you
do not need to modify the default options, and you can directly select option 1 to start the
calculation. Since calculation of ESP is time-consuming, for large system you may need to wait
for a while. The result is 0.5772 for Cl, -0.2496 for axial F and -0.0779 for equatorial F. The
conclusion of CHELPG charge is the same as Hirshfeld charge, namly axial F are more negatively
charged than the equatorial one.
Fragment charge is defined as the sum of charge of atoms constituting a fragment, it is useful
to study net charge of local regions, such as a group. You can manually sum up atomic charges to
derive fragment charge; however, for large systems this process may be laborious. In Multiwfn it
is possible to directly calculate fragment charge, for doing this you should first enter main
function 7, select option "-1 Define fragment" and then input atomic indices. After that, once
atomic charges are calculated by a chosen method, the fragment charge will be shown together.
4.7.2 Calculate and compare ADCH charges with Hirshfeld charges
for acetamide
The ADCH (atomic dipole moment corrected Hirshfeld population) charge proposed by me is
an improved version of Hirshfeld charge, which resolved many inherent drawbacks of Hirshfeld
charge, such as poor dipole moment reproducibility, see Section 3.9.9 for brief introduction and J.
Theor. Comput. Chem., 11, 163 (2012) for discussion and comparison. I highly recommend using

4 Tutorials and Examples
272
ADCH charge to discuss charge distribution. The calculation process of ADCH charges is exactly
identical to the one described in last section, the only difference is that you should select option 11
rather than option 1 in population analysis interface. For example, we calculate ADCH charge for
CH3CONH2. Boot up Multiwfn and input
examples\CH3CONH2.fch
7
11
1
Multiwfn will calculate Hirshfeld charge first, and then perform atomic dipole moment
correction for them to yield ADCH charges. The result is shown below
======= Summary of atomic dipole moment corrected (ADC) charges =======
Atom: 1C Corrected charge: -0.265810 Before: -0.090370
Atom: 2H Corrected charge: 0.096194 Before: 0.037254
Atom: 3H Corrected charge: 0.105928 Before: 0.043058
Atom: 4H Corrected charge: 0.117916 Before: 0.048339
Atom: 5C Corrected charge: 0.271667 Before: 0.170596
Atom: 6O Corrected charge: -0.364284 Before: -0.308866
Atom: 7N Corrected charge: -0.676238 Before: -0.159120
Atom: 8H Corrected charge: 0.355141 Before: 0.131920
Atom: 9H Corrected charge: 0.359404 Before: 0.127108
Note: The values shown after "Corrected charge" are ADCH charges, the ones afte
r "Before" are Hirshfeld charges
Total dipole from ADC charge(a.u.) 1.4367898 Error: 0.0001153
X/Y/Z of dipole moment from the charge(a.u.) 0.0432323 -1.4253551 0.1756673
It is obvious that for all atoms, the magnitude of ADCH charge are evidently larger than
Hirshfeld charges, the former are well in line with common chemical senses, while the latter turns
out to be too small.
A remarkable feature of ADCH charges is that the molecular dipole moment can be exactly
reproduced by ADCH charges! The dipole moment derived from ADCH charges is 1.4368 a.u. (as
shown above), which is exactly identical to the actual dipole moment, namely the one derived
from present electron density distribution. (The error 0.0001153 comes from numerical accuracy
aspects and is totally negligible).
If you scroll up the command-line window, you will find following information
Total dipole from atomic charges: 1.073849 a.u.
This is the dipole moment derived from Hirshfeld charges, which deviates to actual dipole
moment (1.4368) apparently. In fact, for almost all small molecules, Hirshfeld charge always
severally underestimates molecular dipole moments.
4 Tutorials and Examples
273
4.7.3 Calculate condensed Fukui function and condensed dual
descriptor
In Section 4.5.4, I have introduced how to calculate and visualize Fukui function and dual
descriptor. In this section, we will calculate "condensed" version of these two functions, so that the
discussion of the possibility that an atom could act as a reactive site can be upgraded to
quantitative level. Phenol will still be used as example case.
Before calculating phenol, we first derive the expression of condensed Fukui function and
condensed dual descriptor. In the condensed version, atomic population number is used to
represent the amount of electron density distribution around an atom. Recall the definition of
Fukui function f +:
)()()( 1rrr NN
f
The definition of condensed Fukui function for an atom, say A, can be written as
AA 1A NN ppf
where pA is the electron population number of atom A.
Since atomic charge is defined as AA pZqA , where Z is the charge of atomic nuclear,
the f + can be expresssed as the difference of atomic charges in two states (note that the two Z
terms are cancelled)
A1
A
A
NN qqf
By analogous treatment, one can easily formulate other types of condensed Fukui function
2/)( :attack Radical
:attack licElectrophi
:attack icNucleophil
A1
A1
0
A
AA 1A
A1
A
A
NN
NN
NN
qqf
qqf
qqf
Similarly, condensed dual descriptor can be written as
A1
A1
AAA 1
A1
A
AAA 2)()(
NNNNNNN qqqqqqqfff
There are numerous ways to calculate atomic charge, although currently there is no
consensus that which method is the most suitable to calculate condensed Fukui function and dual
descriptor, in my opinion, Hirshfeld charge and NPA charge are the ones most worth to be
recommended for this purpose. For example, J. Phys. Chem. A, 106, 3885 illustrated how
successfully is Hirshfeld charge used to study reactive site by means of condensed Fukui function.
According to the method introduced in Section 4.5.4, we calculate Hirshfeld charges for all
carbons in phenol in its N, N+1 and N-1 electrons states, respectively. The atomic charges are
listed in below table as column 2, 3 and 4. The molecular wavefunction files used here are the

4 Tutorials and Examples
274
same with the ones used in Section 4.5.4. By the formulae shown above, the condensed f - and f +
and dual descriptor can be readily calculated, and they are listed below as the last three columns.
N N-1 N+1 f f + Δf
C1 -0.0596 0.0725 -0.0992 0.1321 0.0396 -0.0925
C2 -0.0249 0.0297 -0.1620 0.0546 0.1371 0.0825
C3 -0.0597 0.0375 -0.2043 0.0973 0.1446 0.0473
C4 0.1017 0.2526 0.0619 0.1510 0.0397 -0.1112
C5 -0.0740 0.0153 -0.2112 0.0893 0.1372 0.0479
C6 -0.0276 0.0416 -0.1649 0.0691 0.1373 0.0682
Note: The Hirshfeld charges reported above were estimated based on build-in sphericalized atomic densities.
For f -, the smallest two values occur at C2 and C6, therefore meta atoms are unfavorable sites
for electrophilic attack.
For dual descriptor, the most positive values occur at C2 and C6, suggesting that they are the
most unfavorable sites for electrophilic attack. C4 has a large negative value and hence favored by
electrophilic reactant. Although the two ortho carbons (C3 and C5) have positive value, its
magnitude is not as large as meta carbons, so dual descriptor indicates that ortho carbons are more
possible than meta carbons to be reactive site for electrophilic attack. Our conclusion is
completely in line with that of Section 4.5.4, in which we obtained the conclusion by visual
inspecting isosurface of Fukui function and dual descriptor.
PS: In Section 4.5.4, when we calculate dual descriptor, we used spin density as
approximation for electron density difference between two states. However, it seems that this
approximation is not necessary for calculating condensed dual descriptor.
4.7.4 Illustration of computing Hirshfeld-I charges
Hirshfeld-I (HI) is a more advanced technique to define atomic spaces than its predecessor
(Hirshfeld). In this section I will illustrate how to compute HI charges using two systems as
examples. Before reading this section please read Section 3.9.13 to gain basic knowledge of HI
method and its implementation in Multiwfn.
(1) CH3COCl
Here we calculate HI charges for CH3COCl. Before calculation, you should properly set
"gaupath" in settings.ini file to actual Gaussian executable file. Boot up Multiwfn and input
examples\CH3COCl.wfn // Generated at B3LYP/6-31G* level
7 // Population analysis
15 // Hirshfeld-I method
1 // Start calculation with default settings
B3LYP/6-31G* // The keyword of Gaussian used to calculate atomic .wfn files
From the prompts shown on screen, you can find that Multiwfn invokes Gaussian to calculate
atomic .wfn files for all elements involved in present molecule at various charge states. Then
Multiwfn converts atomic .wfn files to .rad files, which record spherically averaged atomic radial
density. The automatically generated Gaussian input file (.gjf), the resulting Gaussian output file
(.out or .log) and the .rad files are all produced in "atmrad" subdirectory of current folder, you can
manually inspect them if you have interesting.
Once all .rad files have been generated, Multiwfn initializes some data, and then starts to
carry out HI iteration, the convergence status can be seen on the screen:
4 Tutorials and Examples
275
Cycle 1
Cycle 2 Maximum change: 0.215441
Cycle 3 Maximum change: 0.154451
Cycle 4 Maximum change: 0.105326
Cycle 5 Maximum change: 0.080011
...
The "maximum change" denotes the maximum change of HI atomic charges, the iteration
continues until "maximum change" is smaller than the given criterion. After convergence,
Multiwfn prints final HI atomic charges:
Atom 1(C ): -0.667920
Atom 2(H ): 0.194766
Atom 3(H ): 0.188545
Atom 4(H ): 0.194766
Atom 5(C ): 0.755439
Atom 6(O ): -0.414041
Atom 7(Cl): -0.251555
Then you can choose if outputting these charges to .chg file in current folder. I suggest you
compare above result with Hirshfeld charges, you will find the magnitude of HI charges is much
higher than Hirshfeld charges. This phenomenon is expected, because HI atomic spaces properly
contract or expand with respect to that of neutral state according to actual chemical environment,
hence the difference of diffuse extent of atomic space between various atoms is greatly increased.
If you do not delete the "atmrad" folder or clean it up, then when you recalculate HI charges
for CH3COCl, or calculate a molecule only consisting of C, H, O and Cl elements (or some of
them), Multiwfn will directly perform HI calculation based on existing .rad files in "atmrad"
folder rather than invokes Gaussian to calculate any new file.
(2) Pt(NH3)2Cl2
The Pt(NH3)2Cl2.wfn in "examples" folder was calculated by B3LYP functional, Lanl2DZ
pseudopotential basis set was used to Pt, while 6-31G* was applied to other atoms. To calculate
HI charges for this system, two steps are needed since we are unable to specify calculation level
using a single set of keywords. In the first step, we arbitrarily use a file solely containing Pt atom
as input file, and specify B3LYP/Lanl2DZ keyword during HI charge calculation, so that .rad files
of Pt can be generated at this level. In the second step, we use Pt(NH3)2Cl2.wfn as input file to
calculate HI charges as usual, in the meantime we specify B3LYP/6-31G* keyword to
generate .rad files for all remaining elements. The .rad files of Pt will not be calculated in this step
at B3LYP/6-31G* level because they have existed in "atmrad" folder.
Notice that "atmrad" folder should be deleted if it has existed in current folder, otherwise
Multiwfn may employs old files from it. Now let's start.
Firstly, we build a .xyz file containing only one Pt atom, namely editing a plain text file
named "Pt.xyz" and fill below content into it:
1
test
Pt 0. 0. 0.
Now boot up Multiwfn and input
4 Tutorials and Examples
276
Pt.xyz
7
15
1
B3LYP/lanl2DZ // The level used to generate .wfn files for Pt
After generation of .rad files is finished, Multiwfn suddenly crashes, because the input file
does not contain wavefunction information, and thus the HI charge cannot be computed. Then
boot up Multiwfn again and input below commands:
examples\Pt(NH3)2Cl2.wfn
7
15
1
B3LYP/6-31G*
From the prompts on screen you can find the files corresponding to Pt are not calculated
since they have already existed. The final HI charges are
Atom 1(Pt): 0.410827
Atom 2(Cl): -0.414569
Atom 3(Cl): -0.414549
Atom 4(N ): -0.928921
Atom 5(H ): 0.382603
Atom 6(H ): 0.382600
Atom 7(N ): -0.928945
Atom 8(H ): 0.382606
Atom 9(H ): 0.382603
Atom 10(H ): 0.372874
Atom 11(H ): 0.372872
The result is in good agreement with our common chemical intuition.
Worthnotingly, the support of Hirshfeld-I in Multiwfn is never limited to population analysis,
this partition manner can also be used to calculate orbital composition (main function 8), and be
applied in fuzzy analysis module (main function 15).
4.7.5 Calculating EEM charges for ethanol-water cluster
Please first read Section 3.9.15 to understand basic features of Electronegativity Equalization
Method (EEM) charges before following this example. Here we calculate EEM charges for
ethanol-water cluster, which contains as many as 492 atoms:
4 Tutorials and Examples
277
Evidently, calculating atomic charges by quantum chemistry method for such a large system
is too expensive; however, as you will see, evaluation of EEM charges even for a system
composed by hundreds of atoms is rather easy.
Note that in order to calculate EEM charges in Multiwfn, currently you have to use MDL
molfile (.mol) as input file, because only this file provides atomic connectivity information, which
is needed in the calculation of EEM charges.
Boot up Multiwfn and input below commands
examples\ethanol_water.mol // This is a snapshot of molecular dynamics simulation
7 // Population and atomic charge analysis
17 // EEM charge
0 // Start calculation
You will immediately see
EEM charge of atom 1(O ): -0.658886
EEM charge of atom 2(H ): 0.322520
EEM charge of atom 3(H ): 0.270187
...
EEM charge of atom 488(C ): -0.071564
EEM charge of atom 489(H ): 0.145191
EEM charge of atom 490(H ): 0.125555
EEM charge of atom 491(O ): -0.616013
EEM charge of atom 492(H ): 0.310970
Electronegativity: 2.454144
The default EEM parameters were fitted by some researchers for reproducing B3LYP/6-31G*
CHELPG charges, therefore, the above EEM charges should be close to CHELPG charges
evaluated at B3LYP/6-31G* level (In fact, for present system, even if calculation of CHELPG
charges is feasible, the result should be much worse than the EEM charges we just obtained.
Because it is well-known that the quality of electrostatic fitting charges is very low for the atoms
far from van der Waals surface, while in present system there are numerous heavily buried atoms).
Note that there are also many other built-in EEM parameters, you can choose them via option
1 before calculation.

4 Tutorials and Examples
278
4.8 Molecular orbital composition analysis
In this section, I will show how to use Mulliken, NAO and Hirshfeld/Becke methods to
analyze molecular orbital composition.
These methods are also applicable to other type of orbitals, e.g. natural orbitals and localized
MO. The details about orbital composition analysis can be found in Section 3.10. The pros and
cons of these methods are very detailedly discussed in my paper Acta Chim. Sinica, 69, 2393 (in
Chinese, http://sioc-journal.cn/Jwk_hxxb/CN/abstract/abstract340458.shtml). Also you can
consult my post http://sobereva.com/131 (in Chinese).
Simply speaking, if your aim is merely obtaining atom composition in orbitals,
Hirshfeld/Becke method may be the most robust and convenient way, see Section 4.8.3; if you
also would like to obtain atomic orbital composition, then the NAO method exemplified in
Section 4.8.2 is the best choice. The Mulliken method illustrated in Section 4.8.1 also generally
works well but diffuse functions must not be used.
4.8.1 Analyze acetamide by Mulliken method
In this example we employ Mulliken method to first analyze the composition of the 6th
molecular orbital of acetamide, and then analyze which orbitals have main contribution to the
bonding between formamide part and methyl group. Beware that Mulliken method is incompatible
with diffuse functions, if they are involved, you should either choose other orbital composition
methods (e.g. NAO, Hirshfeld...) or remove them from your basis-set.
Boot up Multiwfn and input following commands
examples\CH3CONH2.fch // You have to use .fch/.molden/.gms file as input for this type of
analysis
8 // Orbital composition analysis
1 // Use Mulliken partition
6 // The orbital index is 6
The composition of basis functions, shells and atoms are printed immediately, see below.
Threshold of absolute value: > 0.500000% // Only the basis functions with composition
larger than 0.5% will be printed, you can change the threshold by “compthres” parameter in
settings.ini.
Orbital: 6 Energy(a.u.): -0.90528995 Occ: 2.00000000 Type: Alpha&Beta
Basis Type Atom Shell Local Cross term Total
23 S 5(C ) 14 0.44902% 0.67507% 1.12409%
24 X 5(C ) 15 0.31240% 0.50522% 0.81762%
25 Y 5(C ) 15 4.25271% 5.88221% 10.13493%
29 Y 5(C ) 17 0.00777% -0.61063% -0.60286%
38 S 6(O ) 20 3.50037% 2.65507% 6.15544%
42 S 6(O ) 22 3.29488% 1.71316% 5.00803%
53 S 7(N ) 26 15.20411% 15.32688% 30.53098%

4 Tutorials and Examples
279
57 S 7(N ) 28 16.89006% 17.40040% 34.29046%
61 XX 7(N ) 30 0.00774% 0.58279% 0.59053%
63 ZZ 7(N ) 30 0.02793% -0.98090% -0.95297%
67 S 8(H ) 31 1.27855% 3.03091% 4.30946%
69 S 9(H ) 33 1.52931% 3.60949% 5.13880%
Sum up listed above: 46.75484% 49.78967% 96.54451%
Sum up all basis functions: 51.95605% 48.04395% 100.00000%
Composition of each shell, threshold of absolute value: > 0.500000%
Shell 14 Type: S in atom 5(C ) : 1.12409%
Shell 15 Type: P in atom 5(C ) : 10.95268%
Shell 17 Type: P in atom 5(C ) : -0.97156%
Shell 20 Type: S in atom 6(O ) : 6.15544%
Shell 22 Type: S in atom 6(O ) : 5.00803%
Shell 26 Type: S in atom 7(N ) : 30.53098%
Shell 28 Type: S in atom 7(N ) : 34.29046%
Shell 31 Type: S in atom 8(H ) : 4.30946%
Shell 33 Type: S in atom 9(H ) : 5.13880%
Composition of each atom:
Atom 1(C ) : 1.172494%
Atom 2(H ) : 0.054446%
Atom 3(H ) : 0.032119%
Atom 4(H ) : 0.008171%
Atom 5(C ) : 11.812452%
Atom 6(O ) : 11.632739%
Atom 7(N ) : 65.500850%
Atom 8(H ) : 4.470224%
Atom 9(H ) : 5.316506%
The result indicates that nitrogen has primary contribution (65.5%) to orbital 6, and the
contribution consists of two S-shells (30.5% and 34.3%). P-shells of neighbour carbon and S-
shells of oxygen have slight contribution too (both are about 12%). We can check if the result is
reasonable by viewing isosurface (isovalue is set to 0.1 here):
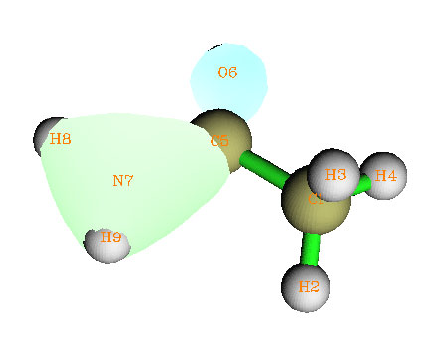
4 Tutorials and Examples
280
From the graph, the region where the value of orbital wavefunction is large is mainly
localized around nitrogen, and there is no nodal plane, so the orbital wavefunction in this region
should be constructed from s-type orbitals. The isosurface also somewhat intrudes into the region
of atom C5 and O6, so they should have small contribution to MO 6, moreover, because there is a
nodal plane in C5, the atomic orbitals of C5 used to form MO 6 should be p-type. Obviously, these
conclusions are in fairly agreement with composition analysis. The advantage of composition
analysis is that the result can be quantified, while by visual study we can only draw qualitative
conclusion, for some complex system we cannot draw even qualitative conclusion.
Now let’s find which molecular orbitals have main contribution to the bonding between
formamide part and methyl group.
examples\CH3CONH2.fch
8 // Orbital composition analysis
-1 // Define fragment 1
a 1-4 // Add all basis functions in atom 1, 2, 3, 4 (methyl group) into fragment1
q // Save fragment and return to upper menu
-2 // Define fragment 2
a 5-9 // Add all basis functions in atom 5, 6, 7, 8, 9 (formamide moiety) into fragment 2
q
4 // Print composition of fragment 1 and the cross term between fragment 1 and 2 in all
orbitals by Mulliken analysis. If you only defined fragment 1, then only composition of fragment
1 will be printed
Amount of the information printed is huge, so I only extract cross term composition in all
occupied orbitals:
Cross term between fragment 1 and 2 and individual parts:
Orb# Type Energy Occ Frag1 part Frag2 part Total
1 AB -19.104 2.000 -0.0013% -0.0013% -0.0026%
2 AB -14.349 2.000 -0.0001% -0.0001% -0.0003%
3 AB -10.282 2.000 0.0606% 0.0606% 0.1211%
4 AB -10.184 2.000 0.0604% 0.0604% 0.1209%
5 AB -1.038 2.000 0.3535% 0.3535% 0.7070%
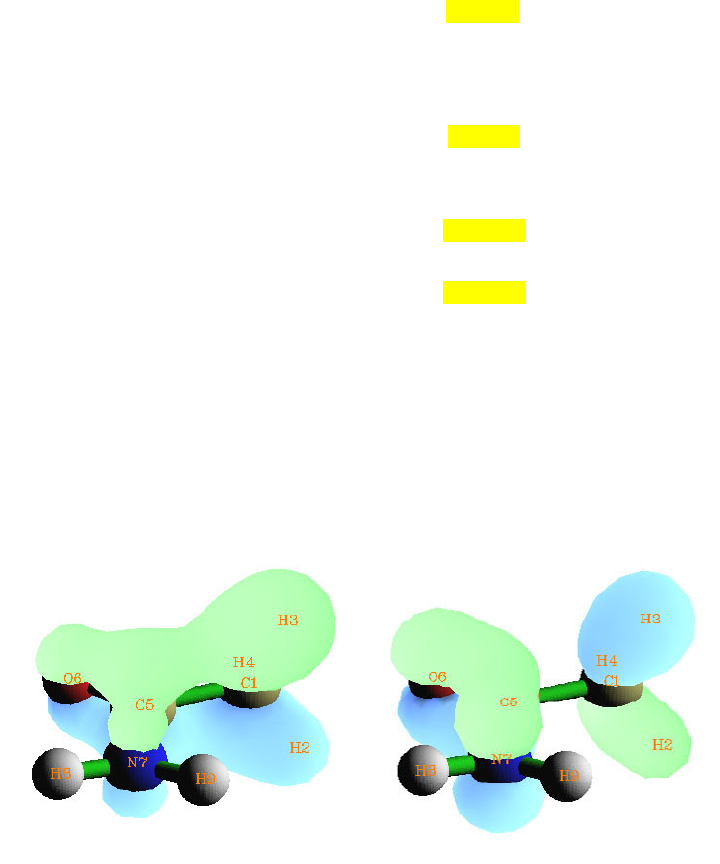
4 Tutorials and Examples
281
6 AB -0.905 2.000 0.7295% 0.7295% 1.4590%
7 AB -0.739 2.000 7.9504% 7.9504% 15.9008%
8 AB -0.588 2.000 -1.8755% -1.8755% -3.7510%
9 AB -0.541 2.000 -0.7506% -0.7506% -1.5011%
10 AB -0.466 2.000 3.8098% 3.8098% 7.6197%
11 AB -0.447 2.000 5.5270% 5.5270% 11.0539%
12 AB -0.402 2.000 -0.3983% -0.3983% -0.7965%
13 AB -0.396 2.000 -0.4274% -0.4274% -0.8549%
14 AB -0.367 2.000 -5.8826% -5.8826% -11.7653%
15 AB -0.266 2.000 0.1192% 0.1192% 0.2383%
16 AB -0.244 2.000 -6.0931% -6.0931% -12.1863%
The product of the cross term composition between fragment 1 and 2 in orbital i and
corresponding orbital occupation number is the total Mulliken bond order between them
contributed from orbital i. From above information we can see MO 7 and 11 are helpful for
bonding, because the composition are relative large, while MO 14 and 16 are not conducive for
bonding. The isosurfaces of MO 11 (left side) and 14 (right side) are shown below, it is clear that
the result of composition analysis is reasonable.
As you have seen, using Mulliken method to analyze orbital composition is very convenient.
However, the result of Mulliken method is sensitive to basis-set, and is not as robust as NAO
method and Hirshfeld method discussed below. Especially, do not use Mulliken method when
diffuse functions are involved in your calculation, otherwise the result will be meaningless!
4.8.2 Analysis on water by natural atomic orbital method
In this example we analyze molecular orbital composition of water by the natural atomic
orbital (NAO) method discussed in Section 3.10.4. NAO method has much better basis-set
stability (i.e. insensitive to the choice of basis-set) and stronger theoretical basis than Mulliken or
Mulliken-like methods (such as SCPA and Stout-Politzer).
Performing NAO method requires MO coefficient matrix in NAO basis, this matrix cannot be
generated by Multiwfn itself, but Multiwfn can utilize the output information containg this matrix
by stand-alone NBO program or NBO module embedded in quantum chemistry softwares. The
NBO 3.1 module embedded in Gaussian program is L607. Below is a Gaussian input file for water,
4 Tutorials and Examples
282
which will output the matrix we needed. Notice that the Gaussian task should be single point task,
do not perform geometry optimization together!
# HF/6-31g* pop=nboread
Title Card Required
0 1
O 0.00000000 0.00000000 0.11472000
H 0.00000000 0.75403100 -0.45888100
H 0.00000000 -0.75403100 -0.45888100
$NBO NAOMO $END
[space line]
[space line]
where pop=nboread keyword indicates that the texts enclosed by $NBO and $END, namely
NAOMO, will be passed to NBO module. NAOMO keyword tells NBO module to output MO
coefficient matrix in NAO basis.
Assume that the Gaussian output file is named as H2O_NAOMO.out (can be found in
"example" folder), we start Multiwfn and input:
examples/H2O_NAOMO.out // Note that DO NOT use .fch as input file!
8 // Enter orbital composition analysis module
7 // Enter NAO analysis function
You will find the default output mode is "Only show core and valence NAOs". Core and
valence NAOs have one-to-one relationship with actual atomic orbitals, if the MO to be analyzed
is occupied, in general we only need to concern these NAOs, while Rydberg NAOs can be ignored.
Assume that we want to analyze MO 4, we input
0 // Show orbital composition of specific MO
4 // Analyze MO 4
Below information will appear on screen
NAO# Center Label Type Composition
1 1(O ) S Cor(1S) 0.031329%
2 1(O ) S Val(2S) 8.573184%
5 1(O ) px Val(2p) 0.000000%
7 1(O ) py Val(2p) 0.000000%
9 1(O ) pz Val(2p) 84.088900%
16 2(H ) S Val(1S) 3.541924%
18 3(H ) S Val(1S) 3.541924%
Summing up the compositions listed above: 99.777261%
Rydberg composition: 0.222739%
Condensed above result to atoms:
Center Composition
1(O ) 92.693413%
2(H ) 3.541924%
4 Tutorials and Examples
283
3(H ) 3.541924%
According to the result, we can say for example, 2pz atomic orbital of oxygen has 84.09%
contribution to MO 4 in current geometry. The contribution from the NAOs listed above (Rydberg
composition is not included in present example) are also summed up to atom contribution
according to which center they are attributed to.
Note that the sum of non-Rydberg compositions, as shown above, is not 100% rather than
99.777%. To make the physical meaning more clear, I personally recommend to manually perform
renormalization process for the result, for example, the composition of 2pz should be
84.089%/0.99777=84.277%. Since before and after the renormalization the difference is only
0.188%, the renormalization is not necessary for current case. Only when the non-Rydberg
composition is unnegligible (e.g. larger than 2%), the renormalization is indispensable.
You can further analyze specific orbital composition by inputting corresponding MO number,
but here we input 0 to return to last menu. We will analyze contribution from the NAOs centered
on the two hydrogens to MO 1~10.
Input -1 to enter the interface for defining fragment, and then input all to check all NAOs, we
will see:
NAO# Atom Label Type Occupancy Energy
14 O 1 dx2y2 Ryd( 3d) 0.00073 2.47969
... [ignored]
15 O 1 dz2 Ryd( 3d) 0.00254 2.02361
16 H 2 S Val( 1S) 0.52321 0.33308
17 H 2 S Ryd( 2S) 0.00086 0.70497
18 H 3 S Val( 1S) 0.52321 0.33308
19 H 3 S Ryd( 2S) 0.00086 0.70497
We input a 2,3, that means all NAOs attributed to atom 2 and 3 will be added to current
fragment. Then input q to save and quit. From the prompt printed on screen you will know NAO
16, 17, 18 and 19 have presented in this fragment.
Then select option 1 and input 1,8, the contribution from the four NAOs to MO 1~8 will be
shown as below
Orb.# Core Valence Rydberg Total
1 0.000000% 0.119072% 0.001568% 0.120640%
2 0.000000% 18.556232% 0.054450% 18.610682%
3 0.000000% 26.557472% 0.018050% 26.575522%
4 0.000000% 7.083848% 0.012482% 7.096330%
5 0.000000% 0.000000% 0.000000% 0.000000%
6 0.000000% 35.481888% 46.831842% 82.313730%
7 0.000000% 27.557888% 61.538418% 89.096306%
8 0.000000% 32.433458% 29.568050% 62.001508%
Since none of the four NAOs in the fragment is core-type, the Core term is 0% in all MOs.
Valence and Rydberg terms correspond to the contribution from NAO 16, 18 and NAO 17, 19
respectively. The first five MOs are doubly occupied in present system. It is clear that Rydberg
NAOs have very low contribution to occupied MOs, while their contribution to virtual MOs are
significant and no longer can be ignored. NAO 16 and 18 directly correspond to 1s atomic orbital
4 Tutorials and Examples
284
of H2 and H3, so we can say the two hydrogens collectively contribute 26.56% to MO 3.
The physical meaning of Rydberg NAOs is difficult to be interpreted, and these NAOs do not
directly reflect atomic orbital characteristics. It is questionable to say the two hydrogens
contributed either 32.43% or 62.00% to MO 8. Although seemingly one can employ
renormalization process to "annihilate" the Rydberg composition, however when Rydberg
composition is too large, for example larger than 10%, this treatment will make the result lack of
reliability. So it is not generally recommended to use NAO method to analyze atomic
contributions to virtual MOs; for this case, the Hirshfeld or Becke method introduced in Section
3.10.5 and exemplified in next section may be the best choice.
4.8.3 Analyze acetamide by Hirshfeld and Becke method
In this section, we will first use Hirshfeld method and then Becke method to analyze the MO
composition of acetamide and compare the result with the one obtained by Mulliken method in
Section 4.8.1. Note that Hirshfeld and Becke methods are only capable of analyzing composition
of atom or fragment in orbitals, while the composition of atomic orbitals are impossible to be
obtained by these approaches.
Boot up Multiwfn and input
examples\CH3CONH2.fch // You can also use such as .wfn and .wfx file as input. But .wfn
and .wfx files do not contain virtual orbital information!
8 // Orbital composition analysis
8 // Use Hirshfeld partition
Hirshfeld analysis requires electron density of atoms in their free-states, you need to choose a
method to calculate atomic densities. Selecting 1 to use built-in atomic densities is very
convenient, see Appendix 3 for detail; alternatively, you can select 2 to evaluate atomic densities
based on atomic .wfn files, see Secion 3.7.3 for detail. Here we choose option 1.
Then Multiwfn initializes the data, for large system you may need to wait for a while.
Assume that you want to analyze MO 6, then simply input 6, the result will be printed on screen,
as shown below. (Because the integrals are evaluated numerically, the sum of all terms will be
slightly deviated to 100%, so Multiwfn automatically normalizes the result.)
Atom 1(C ) : 1.553970%
Atom 2(H ) : 0.248499%
Atom 3(H ) : 0.154527%
Atom 4(H ) : 0.037207%
Atom 5(C ) : 14.924962%
Atom 6(O ) : 12.109412%
Atom 7(N ) : 56.338603%
Atom 8(H ) : 6.687609%
Atom 9(H ) : 7.945211%
The composition of C5, O6 and N7 are 14.92%, 12.11% and 56.34%, respectively. This result
is close to the one obtained by Mulliken method (Section 4.8.1), namely 11.81%, 11.63% and
65.50%, respectively. In fact, for occupied MOs, if diffuse basis functions are not employed, in
general Mulliken, NAO and Hirshfeld methods give similar results.
Now let us check the composition of 7N in MO from 14 to 19. We input
-2
4 Tutorials and Examples
285
7 // Atomic index
14,19 // Orbital range
You will see:
Orb# Type Ene(a.u.) Occ Composition Population
14 Alpha&Beta -0.3674 2.000 16.075% 0.321499
15 Alpha&Beta -0.2661 2.000 48.508% 0.970170
16 Alpha&Beta -0.2438 2.000 6.794% 0.135870
17 Alpha&Beta 0.0410 0.000 12.390% 0.000000
18 Alpha&Beta 0.0762 0.000 21.757% 0.000000
19 Alpha&Beta 0.1252 0.000 14.516% 0.000000
Population of this atom in these orbitals: 1.427539
where 1.427539 (namely 0.321499+0.970170+0.135870) is the total population number of N7 in
MO 14~19.
PS: If the orbital range you specified is 1~16, namely all occupied MO, then the outputted value 7.1586 will
be the atomic population number of N7, and its Hirshfeld atomic charge is therefore 7.0-7.1586=-0.1586.
The steps of analyzing orbital composition by Becke method are completely identical to that
of Hirshfeld method. Here we calculate the composition of MO 6. Boot up Multiwfn and input
examples\CH3CONH2.fch
8 // Orbital composition analysis
9 // Use Becke partition
6 // The 6th orbital
The result is
Atom 1(C ) : 1.229610%
Atom 2(H ) : 0.085144%
Atom 3(H ) : 0.048572%
Atom 4(H ) : 0.002414%
Atom 5(C ) : 14.901723%
Atom 6(O ) : 12.069731%
Atom 7(N ) : 60.741513%
Atom 8(H ) : 4.929374%
Atom 9(H ) : 5.991918%
As you can see, the result is highly close to that produced by Hirshfeld method.
In Multiwfn it is also possible to use Hirshfeld-I partition to calculate orbital composition,
however this is not commonly employed, because generating Hirshfeld-I atomic space requires
additional computational cost, while the result is not greatly improved (the orbital composition
computed by Hirshfeld method is already reliable and meaningful enough).
4.8.4 Calculate oxidation state by LOBA method
Please read Section 3.10.7 first to comprehend basic idea of LOBA method. This is a simple
and useful method to evaluate oxidation state (OS). In this section I will use two examples to
illustrate this function. Notice that the implementation of LOBA in Multiwfn is incompatible with
diffuse functions, if basis set containing diffuse functions is used, the result may be meaningful.
(1) Fe(CN)63-
First, we use Gaussian to perform regular calculation of this system, the input file is
4 Tutorials and Examples
286
example\Fe(CN)6_3-.gjf, please run it by yourself to get Fe(CN)6_3-.fch file. LOBA analysis
needs localized MO (LMO), thus we use Multiwfn to carry out Pipek-Mezey orbital localization.
Boot up Multiwfn and input following commands:
Fe(CN)6_3-.fch
200
13 // Pipek-Mezey orbital localization
1 // Only localize occupied orbitals, this is enough for LOBA analysis
Now the orbitals recorded in memory has been updated to localized orbitals
0 // Return to main interface
8 // Orbital composition analysis
100 // LOBA analysis
50 // Percentage threshold for performing LOBA
Oxidation state of atom 1(Fe) : 3
Oxidation state of atom 2(C ) : 2
Oxidation state of atom 3(C ) : 2
Oxidation state of atom 4(C ) : 2
Oxidation state of atom 5(C ) : 2
Oxidation state of atom 6(C ) : 2
Oxidation state of atom 7(C ) : 2
Oxidation state of atom 8(N ) : -3
Oxidation state of atom 9(N ) : -3
Oxidation state of atom 10(N ) : -3
Oxidation state of atom 11(N ) : -3
Oxidation state of atom 12(N ) : -3
Oxidation state of atom 13(N ) : -3
The sum of oxidation states: -3
The result looks reasonable and in good agreement with chemical intuition. The sum of all
oxidation states just corresponds to the total net charge of -3. However, the LOBA is not free of
ambiguity, the choice of the threshold is highly arbitrary. If we input 60 instead of 50, we will see
oxidation state of carbon and oxygen become 4 and -1, respectively, and the sum of oxidation
states become 21. Fortunately, the OS of transition metal is never so sensitive to the choice of
threshold, the iron always keeps +3 oxidation state in present case as long as the threshold is not
set to very small or very large. (In my viewpoint, the most appropriate threshold for evaluating OS
of transition metal is 50~60%)
(2) Ferrocene
For this system, we will not only check OS of iron, but also check OS of C5H5 fragment. The
corresponding regular Gaussian input file is example\Ferrocene.gjf, run it by yourself to obtain
corresponding .fch file, then load it into Multiwfn and perform orbital localization first as shown
above, after that enter LOBA analysis interface and input below commands:
-1 // Define fragment
1-5,7-11 // Index of the atoms constituting the C5H5 fragment
50 // Percentage threshold for performing LOBA
The result is
Oxidation state of atom 1(C ) : 2
4 Tutorials and Examples
287
Oxidation state of atom 2(C ) : 2
Oxidation state of atom 3(C ) : 2
Oxidation state of atom 4(H ) : 1
Oxidation state of atom 5(H ) : 1
Oxidation state of atom 6(Fe) : 2
Oxidation state of atom 7(C ) : 2
Oxidation state of atom 8(C ) : 2
...[ignored]
The sum of oxidation state: 32
Oxidation state of the fragment: -1
In this system the OS of Fe is +2, which is again reasonable. From the output it is seen that
the OS of individual carbons are not useful, however, the OS of the whole C5H5 fragment is a
meaningful value -1.
Above two examples exhibit usefulness of LOBA method. We should always focus on OS of
transition metal or OS of whole ligands, while the OS of individual atom in ligand often does not
make sense.
4.9 Bond order analysis
4.9.1 Mayer bond order and fuzzy bond order analysis on acetamide
In this instance we will calculate Mayer bond order and fuzzy bond order for acetamide.
Related theories have been introduced in Section 3.11.1 and 3.11.6, respectively.
We first calculate Mayer bond order. Note that calculating Mayer bond order requires basis
function information, thus currently .fch/.molden/.gms file must be used as input file.
Boot up Multiwfn and input:
examples\ CH3CONH2.fch
9 // Bond order analysis
1 // Calculate Mayer bond order
Immediately you get below output:
The total bond order > 0.100000
# 1: 1(C ) 2(H ) 0.93802674
# 2: 1(C ) 3(H ) 0.93473972
# 3: 1(C ) 4(H ) 0.94494566
# 4: 1(C ) 5(C ) 0.96585484
# 5: 5(C ) 6(O ) 1.90392771
# 6: 5(C ) 7(N ) 1.11849509
# 7: 7(N ) 8(H ) 0.83250273
# 8: 7(N ) 9(H ) 0.83869874
Total valences and free valences defined by Mayer:
Atom 1(C ) : 3.77555991 0.00000000

4 Tutorials and Examples
288
Atom 2(H ) : 0.93147308 0.00000000
Atom 3(H ) : 0.92778456 0.00000000
Atom 4(H ) : 0.93657474 0.00000000
Atom 5(C ) : 3.97788022 0.00000000
Atom 6(O ) : 2.05925868 0.00000000
Atom 7(N ) : 2.85041375 0.00000000
Atom 8(H ) : 0.86522064 0.00000000
Atom 9(H ) : 0.85875080 0.00000000
By default, only the bond order terms larger than specific criteria will be outputted, the
criteria can be adjusted in "bndordthres" in settings.ini. Mayer bond order often coincide with
empirical bond order well. In this example, bond order between C5 and O6 is 1.9, which is very
close to ideal value 2.0 (double bonds).
Total valence of an atom is the sum of Mayer bond orders that it formed. Free valence of a
atom measures its remained capacity to form new bonds by sharing electron pairs, for close-shell
this quantity is always zero.
Then if you choose "y", entire bond order matrix will be outputted to bndmat.txt in current
folder.
Next, we want to try to find which orbitals have main contributions to Mayer bond order
between C5 and O6, calculating the so-called "Orbital occupancy-perturbed Mayer bond order" is
useful for realizing this goal. Hence, we select option 6 in bond order analysis module, and then
input 5,6. Below information will be outputted:
Mayer bond order before orbital occupancy-perturbation: 1.903928
Orbital Occ Energy Bond order Variance
1 2.00000 -19.10356 1.906089 0.002162
2 2.00000 -14.34920 1.903934 0.000006
3 2.00000 -10.28192 1.905514 0.001586
4 2.00000 -10.18447 1.903939 0.000011
5 2.00000 -1.03758 1.606912 -0.297016
6 2.00000 -0.90529 1.825661 -0.078267
7 2.00000 -0.73868 1.872011 -0.031917
8 2.00000 -0.58838 1.896333 -0.007594
9 2.00000 -0.54103 1.868127 -0.035801
10 2.00000 -0.46630 1.799351 -0.104576
11 2.00000 -0.44722 1.512533 -0.391394
12 2.00000 -0.40158 1.830827 -0.073101
13 2.00000 -0.39610 1.659075 -0.244853
14 2.00000 -0.36742 1.393122 -0.510805
15 2.00000 -0.26611 1.743383 -0.160545
16 2.00000 -0.24383 1.796157 -0.107770
Summing up occupancy perturbation from all orbitals: -2.03987
4 Tutorials and Examples
289
From the output we can know that, for example, if the two electrons are removed from orbital
15, then Mayer bond order between C5 and O6 will decreased from 1.903928 to 1.743383, we can
also say that the contribution from orbital 15 is 0.160545. The sum of contributions from all
occupied MOs is 2.03987, the reason that this value is not equal to 1.903928 is that Mayer bond
order is not a linear function of density matrix, we needn't to concern this.
Orbital 14 has the largest negative value of orbital occupancy-perturbed Mayer bond order,
therefore this orbital must be greatly beneficial to the bonding. This conclusion can be further
testified by visual inspection of the orbital isosurface, see the graph given at the end of Section
4.8.1. As expected, this orbital shows strong character of π-bonding between C5 and O6.
Now we calculate fuzzy bond order. Unlike Mayer bond order, fuzzy bond order does not
rely on basis function, therefore you can also use such as .wfn/.wfx as input file. Calculating fuzzy
bond order is more time consuming than Mayer bond order, its advantage over Mayer bond order
is that the basis-set sensitivity is greatly reduced, and using diffuse basis functions will never
deteriorate result.
In the bond order analysis menu, we select "7 Fuzzy bond order analysis", the result will be
printed, as shown below
The total bond order >= 0.050000
# 1: 1(C ) 2(H ) 0.89666213
# 2: 1(C ) 3(H ) 0.89075146
# 3: 1(C ) 4(H ) 0.88888051
# 4: 1(C ) 5(C ) 1.08050669
# 5: 1(C ) 6(O ) 0.13600686
# 6: 1(C ) 7(N ) 0.11096284
# 7: 3(H ) 5(C ) 0.05357850
# 8: 5(C ) 6(O ) 2.00411901
# 9: 5(C ) 7(N ) 1.40339002
# 10: 6(O ) 7(N ) 0.24523041
# 11: 7(N ) 8(H ) 0.87233783
# 12: 7(N ) 9(H ) 0.88243512
Comparing the result with that of Mayer bond order, you will find the results of both types of
bond orders are very similar, in fact this is the common case. However, for highly polar bonds
their results may deviate with each other relatively evidently.
4.9.2 Three-center bond order analysis on Li6 cluster
The electron structure character of complex system, such as cluster is hard to predict by
simple empirical rules, we have to resort to wavefunction analysis methods. In this section we use
three-center bond order to study which type of three-membered ring in Li6 cluster is the most
stable. We will calculate the three-member ring consisting of Li1, Li4 and Li3 first.
Notice that multi-center bond order analysis requires basis function information, therefore in
current Multiwfn version, you have to use .fch/.molden/.gms file as input file.
Boot up Multiwfn and input following commands
examples\Li6.fch
9 // Bond order analysis
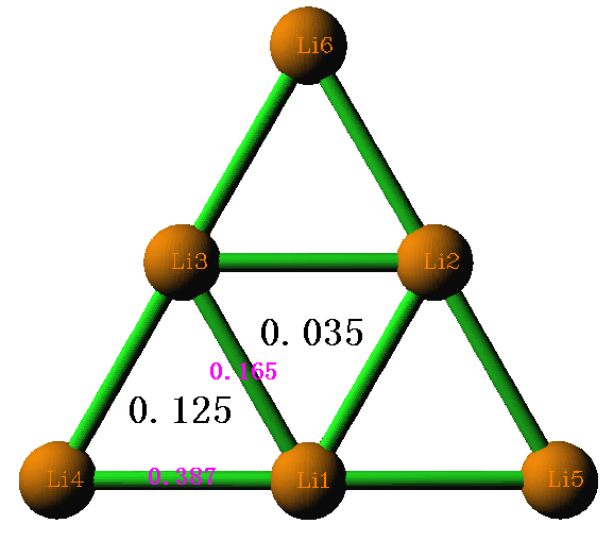
4 Tutorials and Examples
290
2 // Multi-center bond order analysis
1,4,3 // Input the indices of the atoms constituted the three-member ring
The result is 0.12478846. Then repeat above procedure to calculate three-center bond order
of central three-member ring, the result is 0.03517822. I marked the results in the graph below.
The pink texts denote two-center Mayer bond orders, you can calculate them by subfunction 1.
Evidently, the outer-side three-member rings are more stable than the central one, even with
two-center bond order this conclusion can be drawn too. We can further demonstrate this
viewpoint by LOL graph in molecular plane
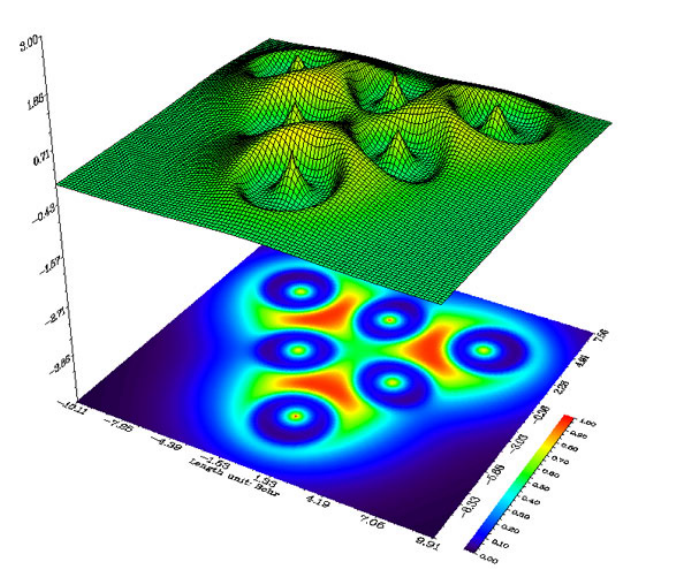
4 Tutorials and Examples
291
It is clearly that electrons tend to localized in the outer-side three-member rings to stabilize
them, the conclusion of real space function analysis is in fairly agreement with bond order analysis.
By checking Laplacian map, ELF map and electron density deformation map, you will draw the
same conclusion.
The Li6.fch used in this example was produced at B3LYP/6-31G* level. Sometimes diffuse
functions must be employed for properly describing a system (in particular, anions), in this case
you should evaluate the multi-center bond order based on natural atomic orbitals (NAO) rather
than based on original basis functions as illustrated above, otherwise the result may be even
completely useless, see Section 3.11.2 for detail.
4.9.3 Calculate Laplacian bond order (LBO)
Laplacian bond order (LBO) was proposed by me in J. Phys. Chem. A, 117, 3100, see Section
3.11.7 for detail. LBO is very suitable for organic system and has close correlation with bonding
strength. Let's calculate LBO for C-C bond of ethane, ethene and acetylene.
Boot up Multiwfn and input following commands
examples\ethane.wfn // Optimized and produced at B3LYP/6-31G**
9 // Bond order analysis
8 // Laplacian bond order
You will see the result:
The bond order >= 0.050000
# 1: 1(C ) 2(H ): 0.887111
# 2: 1(C ) 3(H ): 0.889492
# 3: 1(C ) 4(H ): 0.889492
# 4: 1(C ) 5(C ): 1.059879
4 Tutorials and Examples
292
# 5: 5(C ) 6(H ): 0.887111
# 6: 5(C ) 7(H ): 0.889492
# 7: 5(C ) 8(H ): 0.889492
As you can see, LBO is very close to formal bond order (1.0) for C-C and C-H. LBO only
reflects covalent bonding character, due to C-H is a weakly polar bond, the value is slightly
smaller than 1.0.
Then use "examples\ethene.wfn" to calculate LBO for ethene
# 1: 1(C ) 2(H ): 0.919443
# 2: 1(C ) 3(H ): 0.919443
# 3: 1(C ) 4(C ): 2.022583
# 4: 4(C ) 5(H ): 0.919443
# 5: 4(C ) 6(H ): 0.919443
Then calculate LBO for acetylene by using "examples\C2H2.wfn"
# 1: 1(C ) 2(H ): 0.958393
# 2: 1(C ) 3(C ): 2.767449
# 3: 3(C ) 4(H ): 0.958393
The LBO of the C-C bonds in the three systems are 1.060, 2.022 and 2.767, the ratio is
1:1.907:2.61. It is known that the ratio of the bond dissociation energy (BDE) of the three bonds is
1:1.85:2.61. Clearly, LBO has surprisingly good correlation with BDE, in other words, LBO
exhibits bonding strength fairly well (no other bond order definitions have so close relationship
with BDE in comparison with LBO)
Moreover, LBO predicts that the sequence of the C-H bonding strength in the three systems
is acetylene (0.958) > ethene (0.919) > ethane (0.889), this is completely in agreement with the
experimental BDE sequence! (Other bond order definitions, such as Mayer bond order, fail to
reproduce this sequence)
Finally, calculate LBO for O-H bond in water by using "examples\H2O.fch", the result is
0.585. This value is significantly smaller than the C-H bond order, reflecting that O-H bond is
much more polar than C-H bond.
4.9.4 Decomposition analysis of Wiberg bond order in NAO basis for
formaldehyde
This example briefly illustrates a unique feature of bond order analysis module of Multiwfn,
namely decomposing Wiberg bond order to atomic orbital pair and atomic shell pair contributions.
A very simple molecule formaldehyde will be used as example, of course you can extend the
analysis to much more complicated systems. Please read Section 3.11.8 first to understand basic
idea of this analysis method.
This analysis requires natural atomic orbital (NAO) information and density matrix in NAO
basis outputted by Weinhold's NBO program. For Gaussian user, you can run
examples\H2CO_DMNAO.gjf and use the output file (examples\H2CO_DMNAO.out) as input file
for this analysis. The orientation of the H2CO molecule in Cartesian system is shown in below
graph.
4 Tutorials and Examples
293
Boot up Multiwfn and input below command:
examples\H2CO_DMNAO.out
9 // Bond order analysis
9 // Decompose Wiberg bond order in NAO basis
Then you can input two atom indices to obtain their Wiberg bond order calculated under
NAO basis, and meantime obtain major components (the threshold for printing components is
controlled by "bndordthres" parameter in settings.ini). For example, we input 1,4, below result is
immediately shown on screen:
Contribution from NAO pairs that larger than printing threshold:
Contri. NAO Center NAO type NAO Center NAO type
0.0823 2 1(C ) Val(2S) S --- 21 4(O ) Val(2S) S
0.1907 2 1(C ) Val(2S) S --- 28 4(O ) Val(2p) pz
0.9145 5 1(C ) Val(2p) px --- 24 4(O ) Val(2p) px
0.0658 7 1(C ) Val(2p) py --- 26 4(O ) Val(2p) py
0.2482 9 1(C ) Val(2p) pz --- 21 4(O ) Val(2S) S
0.3700 9 1(C ) Val(2p) pz --- 28 4(O ) Val(2p) pz
Contribution from NAO shell pairs that larger than printing threshold:
Contri. Shell Center Type Shell Center Type
0.0823 2 1(C ) 2S --- 2 4(O ) 2S
0.1907 2 1(C ) 2S --- 5 4(O ) 2p
0.2482 5 1(C ) 2p --- 2 4(O ) 2S
1.3504 5 1(C ) 2p --- 5 4(O ) 2p
Total Wiberg bond order: 1.9161
From above information, the detail of total Wiberg bond order of 1.9161 becomes quite clear.
According to the molecular graph shown earlier, the px type of NAO corresponds to the 2p atomic
orbital perpendicular to molecular plane, thus the px-px mixing results in bond, its contribution to
the total bond order (0.9145) is close to unity, which is in line with chemical intuition. The 2s-2s
interaction only has weak contribution to the C=O bond, since the value 0.0823 is almost
negligible; the reason should be attributed to the fact that the orbital overlap is insufficient. In
addition, the 2py-2py interaction also plays insignificant role, the contribution is merely 0.0658.
The interaction between 2s(C)-2pz(O), 2pz(C)-2pz(O) and 2pz(C)-s(O) have remarkable
4 Tutorials and Examples
294
contribution to total bond order, which are 0.1907, 0.3700 and 0.2482, respectively, and the sum
reaches as high as 0.8089. The large contributions must mainly stem from good orbital
overlapping.
In order to facilitate discussion, the program also outputs contribution to Wiberg bond order
from various atomic shell pairs. For example, as you can see from above information, interaction
between all 2p orbitals of carbon and all 2p orbitals of oxygen totally contributes 1.3504 of bond
order.
4.10 Plot density of states (DOS)
4.10.1 Plot total, partial and overlap DOS for N-phenylpyrrole
In this example, we will plot total, partial and overlap density-of-states (TDOS, PDOS and
OPDOS) for N-phenylpyrrole. Please read Section 3.12.1 first if you are not familiar with DOS.
Because basis function information is required in plotting PDOS and OPDOS, we use .fch as
input file in this example; .molden and .gms files are also OK, but .wfn/.wfx are not supported,
since which do not contain information of basis function and virtual MOs. If you only need to
obtain TDOS, you can also simply use a plain text file recording MO energy levels or the
Gaussian output file with pop=full keyword as input file, see Section 3.12.1 for file format.
Worthnotingly, if you intend to plot PDOS and OPDOS, employing diffuse basis functions in the basis-set is
highly deprecated, because they lack of chemical meaning and thus always worsen the reliability of the results.
The wavefunction of present system was generated at B3LYP/6-31G* level.
Boot up Multiwfn and input below commands
examples\N-phenylpyrrole_6-31Gx.fch
10
0 // Plot DOS
Since currently no fragment is defined, only TDOS is plotted. The TDOS map pops up
immediately, see below
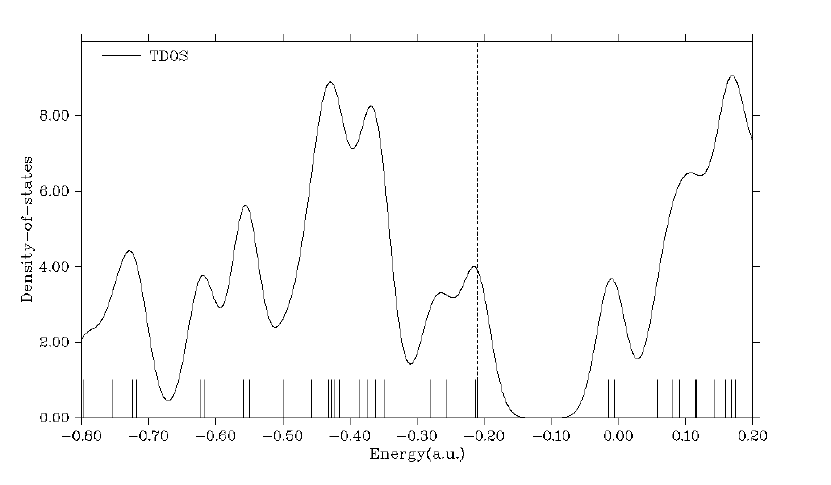
4 Tutorials and Examples
295
In the TDOS map, each discrete vertical line correspond to a molecular orbital (MO), the
dashed line highlights the position of HOMO. The curve is the TDOS simulated based on the
distribution of MO energy levels. In the negative part, the region around -0.40 a.u. has obviously
larger state density than other regions.
Clicking mouse right button on the graph to close it, and select option 0 to return to last menu.
Next, we define the heavy atoms of pyrrole moiety as fragment 1 and that of the phenyl
moiety as fragment 2 to check their PDOS and OPDOS. In addition, we define all hydrogens as
fragment 3.
-1 // Enter the interface for defining fragments. You can define up to 10 fragments. PDOS
will be plotted for all of them but OPDOS will only be drawn between fragment 1 and 2
1 // Define fragment 1
a 1-5 // Add carbons and nitrogen of pyrrole moiety (atoms 1~5) to the fragment
q // Save fragment 1
2 // Define fragment 2
a 10-13,15,17 // Add phenyl moiety (atoms 10~13, 15 and 17) to the fragment
q // Save fragment 2
3 // Define fragment 3
a 6-9,14,16,18-20 // Add all hydrogens to the fragment
q // Save fragment 3
0 // Return to last menu
2 // Set X-axis
-1.1,-0.1,0.1 // Set the range of X-axis to -1.2 ~ -0.1 a.u., so that all valence MOs can be
shown in the graph. The step between labels is set to 0.1 a.u..
0 // Draw TDOS+PDOS+OPDOS
Current graph is not very ideal. Close the graph, you can see many options used to customize
the graph, such as setting curve colors, setting legend texts. Try to play with them and if you are
confused you can consult Section 3.12.3. Here we select option 4 and input -2,9,1 to set lower,
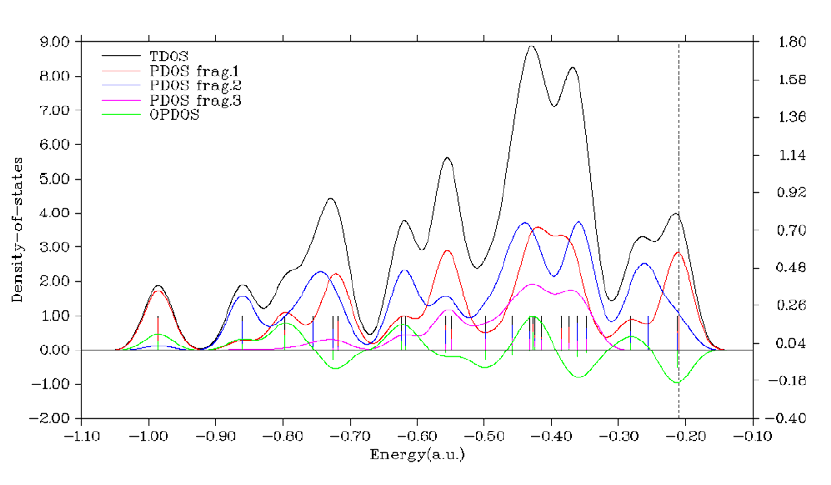
4 Tutorials and Examples
296
upper limits and stepsize of Y-axis as -2.0, 9.0 and 1.0, respectively. Select 14 and input the scale
factor 0.2, then the range of the Y-axis corresponding to OPDOS are set to -0.4, 1.8 (because -
2.0*0.2=-0.4 and 9.0*0.2=1.8). Shrinking the range of the Y-axis at right side is equivalent to
enhancing the amplitude of OPDOS curve, which makes the variation of OPDOS in the map more
clear. Then select 1 to replot the DOS map, you will see
The axis at left side corresponds to TDOS and PDOS, while the one at right side corresponds
to OPDOS. The red, blue and magenta curves and discrete lines represent PDOS of fragment 1, 2
and 3, respectively. It can be seen that in most valence MOs, the fragments 1 and 2 have
comparable amount of contribution. The fragment 3 (hydrogens) mainly contributes to the MOs
between -0.60~-0.35 a.u. Green curve is the OPDOS between fragments 1 and 2, its positive part
implies that the MOs in corresponding energy range show bonding character between the two
fragments (e.g. the one at -0.8 a.u., which corresponds to MO14); there are also regions where
OPDOS is negative, e.g. the HOMO-1 (-0.213 a.u.) behave as antibonding orbitals between the
two fragments.
Current molecule is in YZ plane, let's check the PDOS of px atomic orbital of the nitrogen
atom. Select 0 to return to last menu and then input
-1 // Define fragments
-2 // Fragment 2 is not needed, so we input corresponding negative value to unset it
-3 // Unset fragment 3
1 // Redefine fragment 1
clean // Clean the content of the fragment
all // Print out information of all basis functions
The information corresponding to nitrogen atom is extracted and shown below
Basis: 61 Shell: 25 Center: 5(N ) Type: S
Basis: 62 Shell: 26 Center: 5(N ) Type: S
Basis: 63 Shell: 27 Center: 5(N ) Type: X
Basis: 64 Shell: 27 Center: 5(N ) Type: Y
4 Tutorials and Examples
297
Basis: 65 Shell: 27 Center: 5(N ) Type: Z
Basis: 66 Shell: 28 Center: 5(N ) Type: S
Basis: 67 Shell: 29 Center: 5(N ) Type: X
Basis: 68 Shell: 29 Center: 5(N ) Type: Y
Basis: 69 Shell: 29 Center: 5(N ) Type: Z
Basis: 70 Shell: 30 Center: 5(N ) Type: XX
Basis: 71 Shell: 30 Center: 5(N ) Type: YY
Basis: 72 Shell: 30 Center: 5(N ) Type: ZZ
Basis: 73 Shell: 30 Center: 5(N ) Type: XY
Basis: 74 Shell: 30 Center: 5(N ) Type: XZ
Basis: 75 Shell: 30 Center: 5(N ) Type: YZ
Current system is calculated under 6-31G* basis set, according to the basis-set definition,
each valence atomic orbital is represented by two basis functions of corresponding type. Therefore,
what we should do is to put basis functions 63 and 67 into the fragment, they collectively
represent the px orbital of nitrogen. Input below commands
b 63,67 // Then you can input command all again, the basis functions added to present
fragment are marked by asterisks
q // Save fragment
0 // Return
0 // Plot TDOS and PDOS
Please analyze the resulting graph by yourself.
This molecule is in YZ plane, assume that we only intend to study PDOS/OPDOS of π
orbitals of pyrrole and phenyl moieties and want to get rid of effect of all other MOs, although in
the fragment definition interface we can choose each PX basis function in turn, because there are
too many atoms, this process will take you a lot of time and is very boring. A much better way is
to use the condition selection command. Select 0 to return to last menu and then input
-1 // Define fragments
1 // Redefine fragment 1
clean // Clean the content of the fragment
cond // Use conditions to select basis functions. You will be prompted to input three
conditions, the basis functions simultaneously satisfying the three conditions will be added to
current fragment
1-5 // The first condition is that the basis functions must belong to the heavy atoms in
pyrrole moiety (atoms 1~5)
a // The second condition is the index range of basis functions. Inputting a means any basis
function is OK (in other words, do not employ this condition)
X // The third condition is that the type of basis function should be PX
q // Save fragment 1
2 // Define fragment 2
cond
10-13,15,17 // Atom index of the carbons in phenyl moiety
a
X
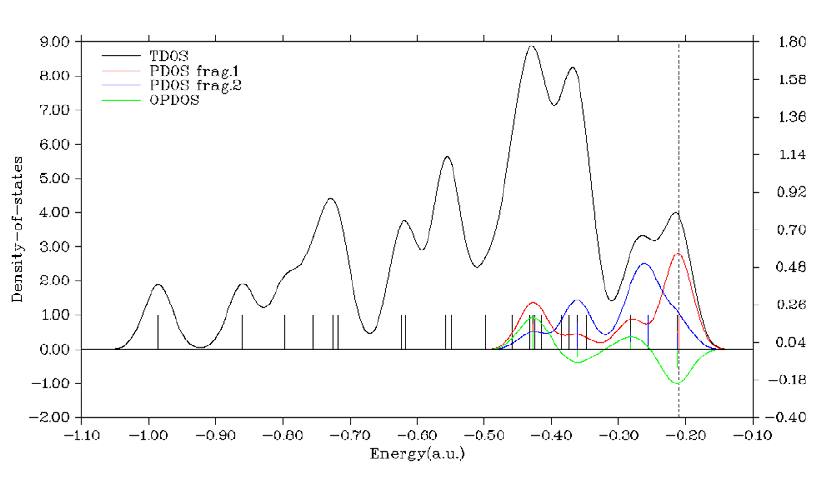
4 Tutorials and Examples
298
q // Save fragment 2
0 // Return to last menu
0 // Plot DOS
This time the PDOS curves only cover high-energy regions, implying that most π MOs in
present system have higher energy than MOs. Please use main function 0 of Multiwfn to
visualize corresponding MO isosurfaces.
PS: If you only need to obtain TDOS, you can simply use a plain text file recording MO energy levels or
Gaussian output file with pop=full keyword as input file, see Section 3.12.1 for file format.
4.10.2 Plot local DOS for butadiene
If you don't know what is local DOS (LDOS), please check Section 3.12.4 first. Briefly
speaking, TDOS represents DOS curve for the whole system, PDOS describes DOS curve for an
atom (or fragment), while LDOS exhibits DOS curve for a point (i.e. space-resolved). In addition,
we can plot LDOS for a set of point constituting a line as color-filled map, the X-axis corresponds
to energy while the Y-axis shows position in the line. LDOS is useful when interpreting the data
from an scanning tunneling microscope (STM), you can find relating experimental data in e.g. J.
Phys. Chem. Lett., 5, 3701 (2014).
In the current example, we plot LDOS for butadiene at selected points. First, we plot LDOS
for the point over 1.5 Bohr of terminal carbon of butadiene. Boot up Multiwfn and input following
commands:
examples\butadiene.fch
0 // From output in command-line we can find the expected point should be 1.137 3.308
1.5 (1.5 Bohr above C1)
10 // DOS plotting module
10 // Draw local DOS for a point
1.137 3.308 1.5
Then you will see (you can compare it with TDOS map)
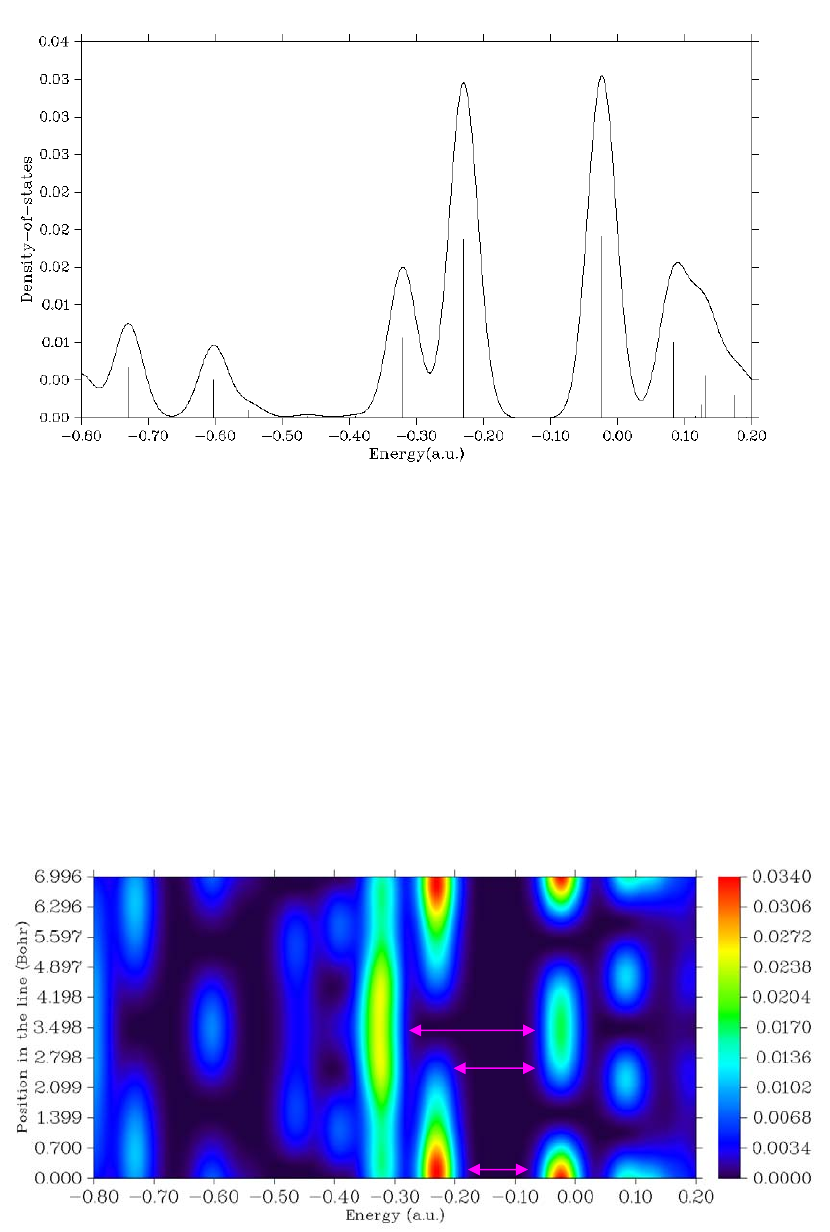
4 Tutorials and Examples
299
Close the graph and select 0 to return to the last menu.
Next, we plot color-filled map along the line connecting the two points above 1.5 Bohr of the
two terminal carbons (C1 and C8):
1.137 3.308 1.5
-1.137 -3.308 1.5
200 // Evenly taking 200 points along line
Then close the graph that pops up and input
4 // Modify the ratio between Y and X axes
0.5 // The length of Y-axis will be half of X-axis
1 // Replot
Then you can see
The lowermost part of the graph (viz. Y=0, standing for the point 1.5 Bohr above C1)
corresponds to the LDOS curve map we have obtained. The pink arrows highlight the gaps at
three different positions in the line.
4 Tutorials and Examples
300
4.11 Plot spectrums
Multiwfn has a very powerful spectrum plotting module. The basic principles, supported
input files and all options of this module have been detailedly introduced in Section 3.13, below
sections will briefly exemplify the usage of this module.
4.11.1 Plot infrared spectrum for NH3BF3
This example plots infrared (IR) spectrum for NH3BF3. Multiwfn can read in frequencies and
intensities from output file of Gaussian or ORCA vibration analysis task (“freq” keywords). Boot
up Multiwfn and input following commands
examples\spectra\NH3BF3_freq.out // The output file of optimization and vibrational analysis
task of Gaussian at B3LYP/6-31G* level
11 // Plot spectrum
1 // The type of the spectrum is IR
0 // Plot spectrum right now
You will get below graph
4000.0 3600.0 3200.0 2800.0 2400.0 2000.0 1600.0 1200.0 800.0 400.0 0.0
W
a
v
e
n
u
m
b
e
r
(
c
m
^-1
)
-200.46
420.97
1042.40
1663.83
2285.27
2906.70
3528.13
4149.56
4771.00
5392.43
6013.86
Molar absorption coefficient (L/mol/cm)
-12.60
26.46
65.51
104.57
143.62
182.68
221.73
260.79
299.84
338.90
377.95
IR intensities (km/mol)
The left axis corresponds to curve (broadened data), the right axis corresponds to discrete
lines (original transition data). Plotting parameters such as full width at half maximum (FWHM),
broadening function, unit and range of the axes can be adjusted by corresponding options in the
interface. The graph and X-Y data set of discrete lines/curve can be exported by option 1 and 2,
respectively.
It is well known that the frequencies produced under harmonic approximation deviate to
experimental vibrational frequencies systematically. In order to correct this problem, fundamental
frequency scale factor should be applied, this can be done easily in Multiwfn. We close the
spectrum and then choose "14 Multiply the vibrational frequencies by a factor", then input all to
choose all vibrational modes, then input the scale factor fitted for B3LYP/6-31G* level, namely
0.9614, which can be found in Table 1 of J. Phys. Chem., 100, 16502 (1996). After that, if you plot
4 Tutorials and Examples
301
the spectrum again, the resulting spectrum will be the scaled corrected one.
Many experimental spectra use different convention to the spectrum we obtained above,
namely the Y-axis corresponds to transmition rather than absorption, therefore the peaks point
downtowards. To plot such a spectrum, you can select "4 Set left Y-axis" and then input e.g. 6000,-
200,-400 to set lower limit, upper limit and stepsize to 6000, 200 and -400, respectively. Since
currently lower limit is larger than upper limit, the Y-axis is inverted.
The procedure of plotting Raman, UV-Vis, electronic/vibrational circular dichroism
(ECD/VCD) spectra are very similar with plotting IR spectrum. If the quantum chemistry program
you used for spectrum calculation is not Gaussian, ORCA or sTDA, you can manually extract data
from corresponding output file and then write them into a plain text file according to the format
shown in Section 3.13.2, then the file can be used as input file of Multiwfn for plotting spectrum.
4.11.2 Plot UV-Vis spectrum and the contributions from individual
transitions for acetic acid
The spectrum plotting module of Multiwfn is quite flexible, not only the total spectrum but
also the contribution from individual transitions can be exported. This feature is particularly useful
when you want to identify nature of spectrum. In this section I will show how to realize this
analysis, UV-Vis spectrum of acetic acid is taken as example.
Boot up Multiwfn and input
examples\spectra\acetic_acid_TDDFT.out // Calculated at TD-B3LYP/cc-pVDZ level by
Gaussian
11 // Plot spectrum
3 // The type of the spectrum is UV-Vis
15 // Output the spectrum including the contributions from certain individual transitions
0.01 // The criterion of selecting transitions is oscillator strength > 0.01
The curve of the UV-Vis spectrum together with the contributions from the transitions whose
absolute value of strength are larger than 0.01 have been outputted to "spectrum_curve.txt" in
current folder. The first two columns correspond to energies and molar absorption coefficients, the
correspondence between the other columns and transition modes are clearly indicated on screen:
Column# Transition#
3 2 //i.e. transition S0S2
4 3 //i.e. transition S0S3
5 5 //i.e. transition S0S5
6 11 //i.e. transition S0S11
7 13 //i.e. transition S0S13
The discrete line data are outputted to "spectrum_line.txt" in current folder.
Now you can plot the data in the two files as curves in a single graph by your favourite
program (if you use Origin to plot, you can directly drag these two files into Origin window to
import them). In the two files, the first column should be taken as X-axis data, while the other
columns should be taken as Y-axis data. The spectrum plotted by Origin is shown below, if you are
confused about the procedure, you can consult "acetic_acid_TDDFT.opj" provided in
"examples\spectra" folder, which is the corresponding .opj file of Origin 8.
4 Tutorials and Examples
302
80 100 120 140 160 180 200
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
Molar absorption coefficient (L/mol/cm)
Wavelength (nm)
Total
S0S2
S0S3
S0S5
S0S11
S0S13
Oscillator strength
0.00
0.02
0.04
0.06
0.08
0.10
0.12
0.14
0.16
0.18
0.20
0.22
0.24
From the graph the underlying character of the total UV-Vis spectrum (black curve) is now
very clear. Although the S0S3 transition (146.28nm) does not has very small oscillator strength
(0.036), no absorption peak directly corresponds to this transition, since its absorption curve (blue
curve) has been completely merged into the neighboring large absorption peak due to S0S5
transition (cyan curve).
Multiwfn is able to locate minima and maxima of spectrum curve. Select option 16, then you
will see their positions and values. This feature is quite useful for pointing out the exact position
of the peaks
Local maximum X: 113.1515 Value: 5680.8733
Local maximum X: 122.6050 Value: 8239.3520
Local maximum X: 138.1754 Value: 4667.8074
Local maximum X: 159.8627 Value: 2123.3503
Local maximum X: 213.9266 Value: 48.5312
Local minimum X: 116.9205 Value: 4222.4896
Local minimum X: 130.5755 Value: 1866.1290
Local minimum X: 152.0775 Value: 1515.6418
Local minimum X: 187.9759 Value: 1.5107
Totally found 4 local minimum, 5 local maximum
Based on above outputs, we can calculate the contributions from different transitions to a
peak. For example, we want to study the composition of the peak at 138.1754 nm. In
spectrum_line.txt, move to the line correpsonding to 138.17536 nm, you can find the total value is
4667.80738, while the values in column 4 and 5 are 310.33658 and 4272.69585, respectively.
Therefore, the contribution from S0S3 and S0S5 can be respectively calculated as
310.33658/4667.80738*100%=6.65% and 4272.69585/4667.80738*100%=91.53%.
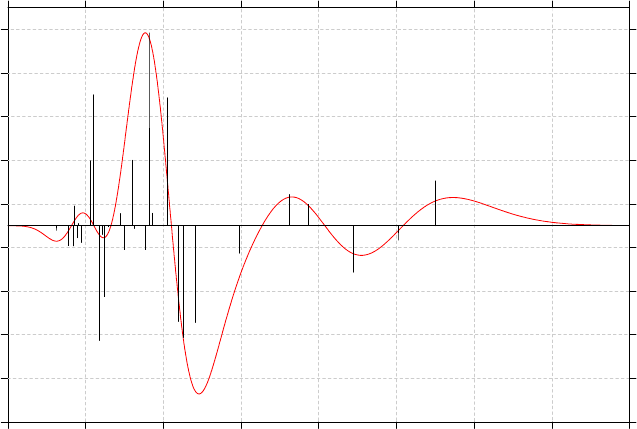
4 Tutorials and Examples
303
4.11.3 Plot electronic circular dichroism spectrum for asparagine
In this example we plot electronic circular dichroism (ECD) spectrum for asparagine. Boot
up Multiwfn and input
examples\spectra\Asn_TDDFT.out // Gaussian TDDFT task at PBE1PBE/6-311G* level, 30
lowest states were calculated
11
4 // ECD
2 // Use the rotatory oscillator in velocity representation
0 // Plot spectrum
From the resulting spectrum, you will find the labels of X-axis and Y-axis are decimal. In
order to make the graph more beautiful, it is suggested to modify the scale so that label of each
tick is integer. Therefore, we close current graph and input below commands:
3 // Set X-axis
120,280,20 // Lower and upper limits, as well as spacing between ticks of X-axis
4 // Set left Y-axis
-90,100,20 // Lower and upper limits, as well as spacing between ticks of left Y-axis
y // Let program properly adjust right Y-axis to guarantee that zero point of left and right
axes are in the same horizontal line
0 // Plot spectrum
Then you will see below graph
120.0 140.0 160.0 180.0 200.0 220.0 240.0 260.0 280.0
Wavelength (nm)
-90.000
-70.000
-50.000
-30.000
-10.000
10.000
30.000
50.000
70.000
90.000
Delta molar absorption coefficient (L/mol/cm)
-56.90
-44.26
-31.61
-18.97
-6.32
6.32
18.97
31.61
44.26
56.90
Rotatory strength (cgs)
Note that you can use exactly the same way as that illustrated in Section 4.11.2 to decompose
the total ECD spectrum to individual contribution from each transition.
4.11.4 Plot conformational weighted spectrum for plumericin
For a flexible system with many thermally accessible conformation (or configurations), when
plotting its spectrum, it is crucial to take weighting average of various conformations into account,
otherwise the resulting spectrum is impossible to be compared well with experimental spectrum.
4 Tutorials and Examples
304
Fortunately, weighted spectrum can be very conveniently plotted by Multiwfn, I will show how to
do this in present section. Plotting conformationally weighted UV-Vis and ECD spectra of
plumericin are taken as instances.
(1) Preparation
Before calculating conformationally weighted spectrum, we need to evaluate population of
these conformations, commonly Boltzmann's weight is used. We assume that plumericin has four
accessible conformations, and properly construct their initial geometries, then optimize them and
perform frequency analysis at B3LYP/6-31G* level with zero-point energy scale factor of 0.9806.
Based on optimized geometries, high-accuracy single point energies at M06-2X/def2-TZVP level
were calculated. Finally, we add the Gibbs thermal corrections produced by frequency analysis to
the single point energies to yield relatively accurate Gibbs energy of various conformations. After
that, according to Boltzmann's formula and relative Gibbs energy among these conformations, we
calculate their weights at 298.15K. Then, using TD-PBE0/TZVP level we calculate the lowest 20
excited states for these conformations. The output file of the TDDFT tasks have been provided in
"examples\spectra\weighted" folder as a.out, b.out, c.out and d.out (the names are arbitrary, you
can also use other file names).
Now we write a plain text file named "multiple.txt" with below content (the name
"multiple.txt" should not be changed, otherwise Multiwfn will unable to properly recognize it):
examples\spectra\weighted\a.out 0.6046
examples\spectra\weighted\b.out 0.1950
examples\spectra\weighted\c.out 0.1686
examples\spectra\weightedt\d.out 0.0317
The first column records path of Multiwfn input file for various conformations, the second
column is the Boltzmann weights we calculated above. Below the four conformations will be
called as a, b, c and d, respectively.
(2) Plot conformationally weighted UV-Vis spectrum
Boot up Multiwfn and input
examples\spectra\weighted\multiple.txt // The file mentioned in last section
11
3 // Plot UV-Vis
0
The resulting graph is shown below
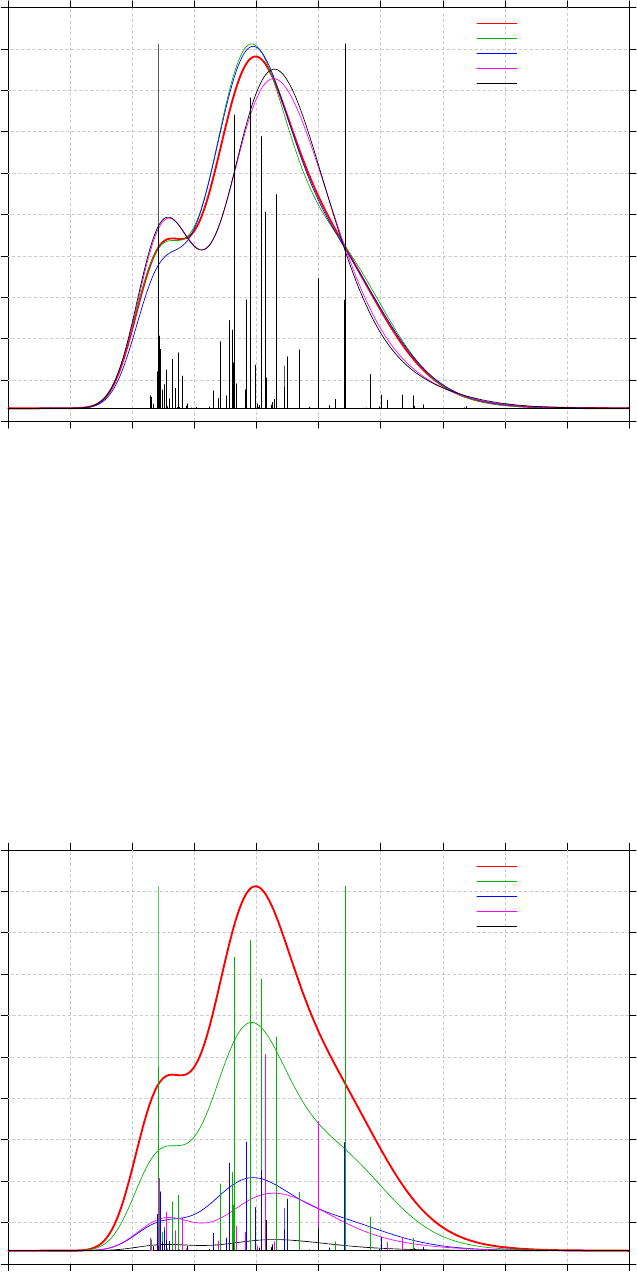
4 Tutorials and Examples
305
137.1 154.5 172.0 189.5 206.9 224.4 241.8 259.3 276.8 294.2 311.7
Wavelength (nm)
-880.08
1848.16
4576.40
7304.64
10032.88
12761.12
15489.36
18217.59
20945.83
23674.07
26402.31
Molar absorption coefficient (L/mol/cm)
Weighted
1 ( 60.5%)
2 ( 19.5%)
3 ( 16.9%)
4 ( 3.2%)
-0.004
0.008
0.021
0.033
0.046
0.058
0.070
0.083
0.095
0.107
0.120
Oscillator strength
The thick red curve corresponds to conformationally weighted UV-Vis spectrum, while the
green, blue, purple and black curves correspond to UV-Vis spectrum of conformation a, b, c and d,
respectively. The weight of each conformation is also shown in the legend. From this graph the we
can very conveniently compare the character of weighted spectrum and spectra of individual
conformations.
The black discrete lines on the graph represent all transition data of the four conformations,
their heights have already been scaled by conformational weight. Hence, the thick red curve can
be regarded as broadened by all discrete lines shown on the graph.
Multiwfn provides another mode to plot spectrum of individual conformations. We close
above graph and choose "18 Toggle weighting spectrum of each system" once, then choose option
0 to view the spectrum again, we will see
137.1 154.5 172.0 189.5 206.9 224.4 241.8 259.3 276.8 294.2 311.7
Wavelength (nm)
-849.54
1784.04
4417.62
7051.20
9684.78
12318.37
14951.95
17585.53
20219.11
22852.69
25486.27
Molar absorption coefficient (L/mol/cm)
Weighted
1 ( 60.5%)
2 ( 19.5%)
3 ( 16.9%)
4 ( 3.2%)
-0.004
0.008
0.021
0.033
0.046
0.058
0.070
0.083
0.095
0.107
0.120
Oscillator strength
The spectrum curve of each conformation shown on this graph has already been multiplied by
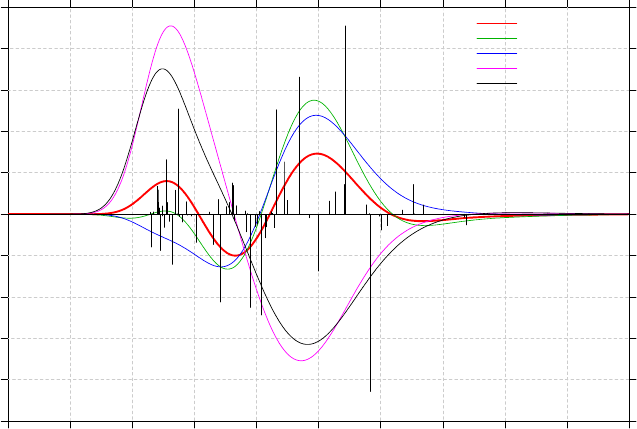
4 Tutorials and Examples
306
corresponding weight. Obviously, what this graph represents is contribution of each conformation
to the conformationally weighted spectrum. In other words, the height of thick red curve is simply
the sum of height of all other curves. It can be seen that conformation a (green line) has major
contribution to the conformationally weighted spectrum, their profiles are rather similar, this is
because a has as high as 60.5% population.
The discrete lines in above graph now have different colors, the color correspond to legend
shown at right-top side. For each conformation, since both discrete lines and curve currently have
identical color, we can say for example, green curve can be directly yielded by broadening the
green discrete lines.
(3) Plot conformationally weighted ECD spectrum
Using the same procedure illustrated in the last section, we plot conformationally weighted
ECD spectrum and ECD spectrum for all the four conformations.
Boot up Multiwfn and input
examples\spectra\weighted\multiple.txt
11
4 // Plot ECD
2 // Read rotatory strength in velocity representation from the 1st file in multiple.txt
2 // ibid, but for the 2nd file
2 // ibid, but for the 3rd file
2 // ibid, but for the 4th file
0 // Plot spectrum
You will see
137.1 154.5 172.0 189.5 206.9 224.4 241.8 259.3 276.8 294.2 311.7
Wavelength (nm)
-153.883
-123.106
-92.330
-61.553
-30.777
0.000
30.777
61.553
92.330
123.106
153.883
Delta molar absorption coefficient (L/mol/cm)
Weighted
1 ( 60.5%)
2 ( 19.5%)
3 ( 16.9%)
4 ( 3.2%)
-33.49
-26.79
-20.09
-13.40
-6.70
0.00
6.70
13.40
20.09
26.79
33.49
Rotatory strength (cgs)
From this graph you can see conformationally weighted ECD spectrum (thick red curve) as
well as ECD spectrum of individual conformations (other curves).
Then choose "18 Toggle weighting spectrum of each system" option once and plot spectrum
again, you will see
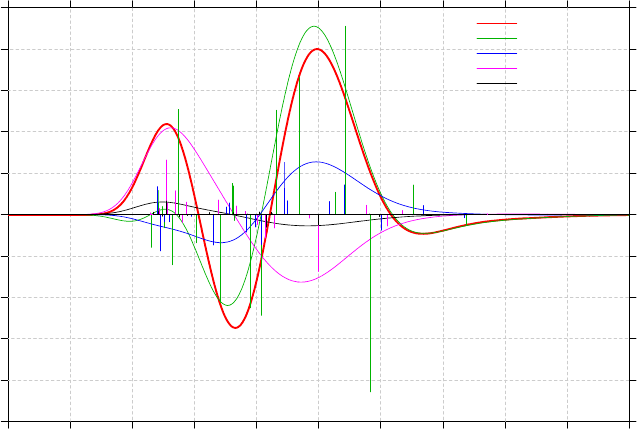
4 Tutorials and Examples
307
137.1 154.5 172.0 189.5 206.9 224.4 241.8 259.3 276.8 294.2 311.7
Wavelength (nm)
-56.295
-45.036
-33.777
-22.518
-11.259
0.000
11.259
22.518
33.777
45.036
56.295
Delta molar absorption coefficient (L/mol/cm)
Weighted
1 ( 60.5%)
2 ( 19.5%)
3 ( 16.9%)
4 ( 3.2%)
-33.49
-26.79
-20.09
-13.40
-6.70
0.00
6.70
13.40
20.09
26.79
33.49
Rotatory strength (cgs)
This graph decomposes the final weighted ECD spectrum to contribution of individual
conformation. Again, since conformation a (green) has very high population and thus dominates
the final weighted curve, most characters of these two curves are similar. However, influence from
other conformations cannot be simply ignored. From the graph it is easy to find that if
conformation c (purple) is missing, then there will not be an evident ECD peak at approximately
180 nm, since only ECD of c at this wavelength has significant signal.
4.11.5 Plot Raman spectrum for 2-methyloxirane based on Raman
intensity
The procedure of plotting Raman spectrum is very similar with plotting IR spectrum, the only
additional step you would better do is to convert the Raman activities directly outputted by Raman
task of quantum chemistry codes to Raman intensities before plotting the spectrum, so that the
resulting spectrum can be comparable with the experimental one. The Raman intensities are
dependent of wavelength of excitation light source and ambient temperature, while Raman
activities are not. This point has been emphasized in Section 3.13.1. In this section, I illustrate
how to properly plot Raman spectrum using (2S)-2-methyloxirane as example.
Boot up Multiwfn and input
examples\spectra\2-methyloxirane_Raman.out // Output file of Raman task calculated at
B3LYP/6-31G* level by Gaussian09
11
2 // Raman spectrum
14 // Apply frequency scale factor
all
0.9614 // Scale factor suitable for fundamental frequencies at B3LYP/6-31G* level
19 // Convert Raman activities to intensities
15000 // Wavenumber (cm-1) of excitation light source. This value should be consistent
with actual experimental condition, the value we inputted here is arbitrarily chosen
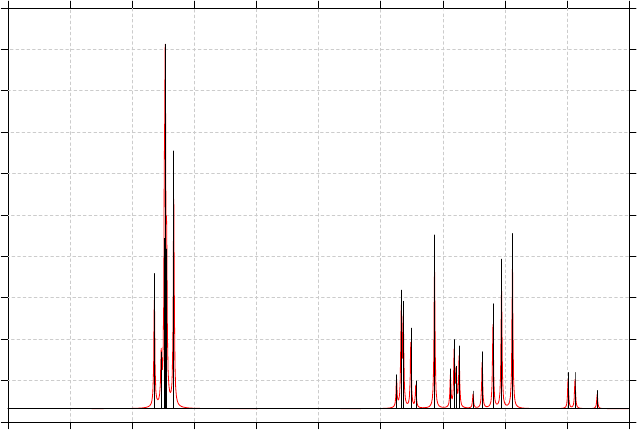
4 Tutorials and Examples
308
298.15 // Assume that experimental temperature is 298.15K
Then input 0 to plot spectrum, you will see below Raman spectrum
4000.0 3600.0 3200.0 2800.0 2400.0 2000.0 1600.0 1200.0 800.0 400.0 0.0
Wavenumber (cm^-1)
-4.10
8.60
21.30
34.00
46.69
59.39
72.09
84.79
97.48
110.18
122.88
Relative Raman intensity
-41.49
87.13
215.75
344.37
472.99
601.61
730.23
858.84
987.46
1116.08
1244.70
Raman scattering intensities
Multiwfn can also plot pre-resonance Raman spectrum. An example output file of pre-
resonance Raman task of Gaussian is "examples\spectra\2-methyloxirane_Raman.out", the
corresponding input file (.gjf) is also given. This task calculates Raman activity at excitation
wavelength of 150nm and 140nm, which are close to S0S1 and S0S2 TDDFT excitation
energies at the same calculation level (147.36nm and 138.81nm at TD-B3LYP/6-31G* level,
respectively). You can load this output file into Multiwfn and plot Raman spectrum as usual. The
only difference is that, before entering spectum plotting interface, Multiwfn asks you to choose the
excitation frequency for which the Raman activities will be loaded. If you choose 2 or 3, the
spectrum you finally obtained will be pre-resonance Raman at corresponding frequency; if you
choose " 1: 0.00000000", namely the static limit case, the resulting spectrum will be exactly
identical to the one we obtained earlier.
4.11.6 Simultanously plot multiple systems
In Multiwfn, it is very easy to plot spectrum for multiple systems simultaneously, these
systems may correspond to different conformations, different configurations, different molecules
or different calculation conditions. In examples\spectra\indigo folder, you can find Gaussian
output file of electronic excited state task carried out at different levels. In this example, we plot
them together so that their results can be conveniently compared.
What we need to do first is to prepare a file named multiple.txt including path of various
systems with their legends, such a file is already provided as examples\spectra\indigo\multiple.txt:
examples\spectra\indigo\ZINDO.out ZINDO
examples\spectra\indigo\TD-PBE0.out TD-PBE0/6-31G*
examples\spectra\indigo\TD-PBE0_TZVP.out TD-PBE0/def-TZVP
Note that the legends must not simply be a digital, otherwise it will be interpreted as weight
of corresponding system (see Section 4.11.4).
Boot up Multiwfn, load multiple.txt and then plot UV-Vis spectrum as usual, you will see
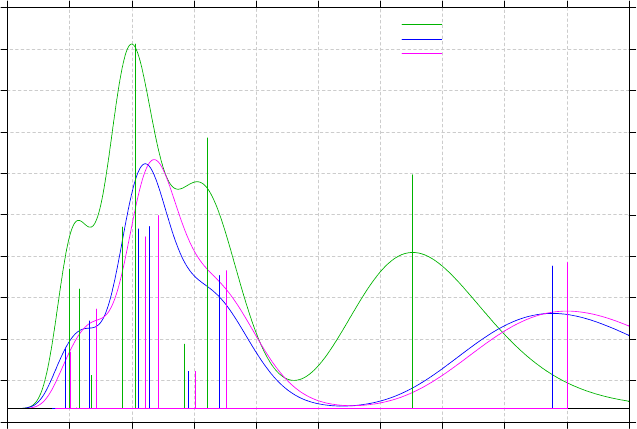
4 Tutorials and Examples
309
below graph
171.0 211.0 251.1 291.1 331.1 371.2 411.2 451.3 491.3 531.3 571.4
Wavelength (nm)
-1610.82
3382.72
8376.26
13369.79
18363.33
23356.87
28350.41
33343.94
38337.48
43331.02
48324.55
Molar absorption coefficient (L/mol/cm)
1 ZINDO
2 TD-PBE0/6-31G*
3 TD-PBE0/def-TZVP
-0.027
0.056
0.138
0.221
0.303
0.385
0.468
0.550
0.633
0.715
0.798
Oscillator strength
From the graph it is clear that basis set only has small influence on the resulting spectrum,
while the spectrum profile of ZINDO differs from that of TD-PBE0 significantly. The curve of all
systems may be exported via option 2 as curveall.txt and then replotted via third-part program
such as Origin.
In examples\spectra\indigo folder you can also find ZINDO_30.out, it corresponds to a
ZINDO calculation with 30 excited states produced. You can also include it into multiple.txt,
however, notice that since it contains more states than other files, it must be added as the first
entry in multiple.txt. (It is compulsory that the file with maximum number of transitions must
present at the beginning of the list)
4.12 Quantitative analysis of molecular surface
4.12.1 Electrostatic potential analysis on phenol molecular surface
Below I will introduce quantitative analysis of molecular surface by case study of phenol.
The theoretical basis has been documented in Section 3.15.1 and thus will not be repeated here. In
this section we only analyze electrostatic potential (ESP) on phenol vdW surface, in next section
we will then analyze average local ionization energy on the phenol surface.
Boot up Multiwfn and input following commands
examples\phenol_DFT.wfn // phenol wavefunction produced at B3PW91/6-31G** level. For
most systems this level can give satisfactory result. Hartree-Fock wavefunction is not
recommended to use, since HF completely ignored electron correlation and hence lead to
unreliable ESP distribution
12 // Quantitative analysis of molecular surface
0 // Start the analysis under default settings. By default the mapped function is ESP
Now the calculation starts. Since computing ESP is time consuming, you need to wait for a
while. During the calculation some intermediate information are printed, ordinary users do not
4 Tutorials and Examples
310
need to concern them. Below results will be printed on screen once the calculation has been finally
finished:
Global surface minimum: -0.041203 a.u. at 1.455097 3.343708 -0.007902 Ang.
Global surface maximum: 0.085761 a.u. at -1.936645 3.093464 0.021360 Ang.
Number of surface minima: 3
# a.u. eV kcal/mol X/Y/Z coordinate(Angstrom)
1 -0.03046066 -0.828877 -19.112843 0.150202 -1.011077 -1.882004
2 -0.03045989 -0.828856 -19.112362 0.192185 -0.985412 1.877656
* 3 -0.04120321 -1.121196 -25.853368 1.455097 3.343708 -0.007902
Number of surface maxima: 5
# a.u. eV kcal/mol X/Y/Z coordinate(Angstrom)
1 0.02275520 0.619200 14.277975 -3.344441 -2.281045 0.047286
* 2 0.08576096 2.333674 53.811572 -1.936645 3.093464 0.021360
3 0.01935782 0.526753 12.146259 0.066223 -4.286661 0.040555
4 0.01980285 0.538863 12.425498 3.340574 -2.325727 0.021485
5 0.01583741 0.430958 9.937340 3.419218 1.225375 -0.019326
================= Summary of surface analysis =================
Volume: 835.71041 Bohr^3 ( 123.83953 Angstrom^3)
Overall surface area: 476.05682 Bohr^2 ( 133.30951 Angstrom^2)
Positive surface area: 231.09186 Bohr^2 ( 64.71232 Angstrom^2)
Negative surface area: 244.96497 Bohr^2 ( 68.59719 Angstrom^2)
Overall average value: -0.00020233 a.u. ( -0.12695332 kcal/mol)
Positive average value: 0.01877643 a.u. ( 11.78145591 kcal/mol)
Negative average value: -0.01810626 a.u. ( -11.36095315 kcal/mol)
Overall variance (sigma^2_tot): 0.00041488 a.u.^2 ( 163.34165024 (kcal/mol)^2)
Positive variance: 0.00031106 a.u.^2 ( 122.46642148 (kcal/mol)^2)
Negative variance: 0.00010382 a.u.^2 ( 40.87522876 (kcal/mol)^2)
Balance of charges (miu): 0.18762182
Product of sigma^2_tot and miu: 0.00007784 a.u.^2 ( 30.6464578 (kcal/mol)^2)
Internal charge separation (Pi): 0.01842642 a.u. ( 11.56183883 kcal/mol)
Above information includes all quantities that involving ESP mentioned in Section 3.15.1. In
Multiwfn, the vdW volume can also be computed by Monte Carlo method through subfunction 3
of main function 100, see Section 3.100.3, the results match fairly well. Now select option 0 in the
post-process interface to view molecular structure and surface extrema (red and blue spheres
correspond to maxima and minima, respectively):
4 Tutorials and Examples
311
In side view:
Minimum 3 (-25.85kcal/mol) is global minimum on the surface, its large negative value is
owing to the lone pair of oxygen. Maximum 2 (53.81kcal/mol) is global maximum arising from
the positively charged H13, the ESP at this point is much larger than that at other maxima (where
the ESP ranges from 10 to 15kcal/mol). This is because the presence of oxygen, which attracted a
great deal of electrons from H13. In complex, assume that only electrostatic interaction exists,
4 Tutorials and Examples
312
monomers always contact each other in maximally ESP complementary manner. So we can
expected that in phenol dimer, H13 and maximum 2 in a monomer, and O12 and minimum 3 in
neighbour monomer will be in a straight line (resulting hydrogen bonding), this is the exactly
situation in actual geometry of phenol dimer, see below graph. Notice that in the dimer, maximum
2 and minimum 3 shown above have cancelled each other out.
Minimum 1 and 2 (both are -19.11kcal/mol) are local minimum on the surface, mainly arise
from the abundant π electrons above and below the ring. It is well know that electrophiles always
prefer to attack the atom which has very low ESP around it, so C1 should be an ideal reaction site
for electrophilic reaction. This conclusion is partially consistent with the general knowledge that
hydroxyl is an ortho-para directing group. However, although the global minimum is closest to
O12, O12 is not the electrophilic reaction site; this contradiction reveals the inherent limitation of
ESP analysis method.
Note: Since the molecule has Cs symmetry, in principle, minimum 1 and 2 should have identical X and Y
coordinates. However, this cannot be exactly fulfilled in numerical process, because the points scattered on
molecular surface do not have the molecular symmetry, see Section 3.15.1 for detail. So X and Y coordinates of
minimum 1 and 2 are slightly deviated to each other. If you want to refine the result, choose option 3 "Spacing of
grid data for generating molecular surface" and input a smaller value than default value. Smaller spacing of grid
points yields more accurate result, but bring higher computational burden.
The non-bonded radius defined in the framework of atoms in molecule (AIM) theory is the
shortest distance between a nucleus and ρ=0.001 isosurface. Let's calculate the non-bonded radius
for O12 and H13. Select option 10 in the post-process interface and input 12, we can see that the
non-bonded radius of O12 is 1.701 Angstrom. Select 10 and input 13, the non-bonded radius of
H13 is 1.172 Angstrom. In the phenol dimer, the H---O of the H-bond is 1.937 Angstrom,
therefore the so-called mutual peneration distance is 1.701+1.172-1.937=0.936 Angstrom. This is
a nontrivial value, indicating the H-bond is strong.
As the final part of ESP analysis, we examine the molecular surface area in each ESP range,
this is useful to quantitatively discuss ESP distribution on the whole molecular surface. We choose
option 9 in the post-process interface, and then input:
all // All atoms are taken into the statistics (alternatively, if you input for example 2-4, then
only the local surfaces corresponding to atom 2, 3 and 4 will be taken into account, see Section
4.12.3 for illustration of the concept of local molecular surface)
-30,55 // The ESP range you are interested in. Since we have already known that the
minimum and the maximum ESP on the surface are -25.85 and 53.81 kcal/mol respectively, here
we input a slightly larger range to enclose them
4 Tutorials and Examples
313
15 // The number of intervals
3 // Both the inputted and outputted units are in kcal/mol
Then you will see surface area (in Å2) and corresponding percentage in the whole surface
area in each successive ESP range.
Begin End Center Area %
-30.0000 -24.3333 -27.1667 1.8192 1.3647
-24.3333 -18.6667 -21.5000 6.0284 4.5221
-18.6667 -13.0000 -15.8333 20.9732 15.7327
-13.0000 -7.3333 -10.1667 19.0390 14.2818
...
43.6667 49.3333 46.5000 1.2690 0.9519
49.3333 55.0000 52.1667 1.0457 0.7844
Sum: 133.3095 100.0000
By using these data you can use your favourite program to draw a histogram graph. For
example, we choose "center" column as X-axis and "Area" column as Y-axis to plot below graph
-30 -20 -10 0 10 20 30 40 50
0
4
8
12
16
20
24
28
Surface area (Å2)
Electros tatic po tential (k cal/mol)
From the graph it can be seen that there is a large portion of molecular surface having small
ESP value, namely from -20 to 20 kcal/mol. Among these areas, the negative part mainly
corresponds to the surface above and below the six-membered ring and shows the effect of the
abundant π-electron cloud; the positive part mainly arises from the positive charged C-H
hydrogens; the near-neutral part represents the border area between the negative and positive parts.
There are also small areas having remarkable positive and negative ESP value, corresponding to
the regions closed to the global ESP minimum and maximum, respectively.
With the help of VMD program, one can plot very nice color-filled molecular surface map
with surface extrema for various real space functions based on the output of Multiwfn. Below is
such a plot for ESP, which was presented in my study of benzoapyrene diol epoxide, see Struct.
Chem., 25, 1521 (2014). In which blue, white and red correspond to ESP varying from -30 to 35
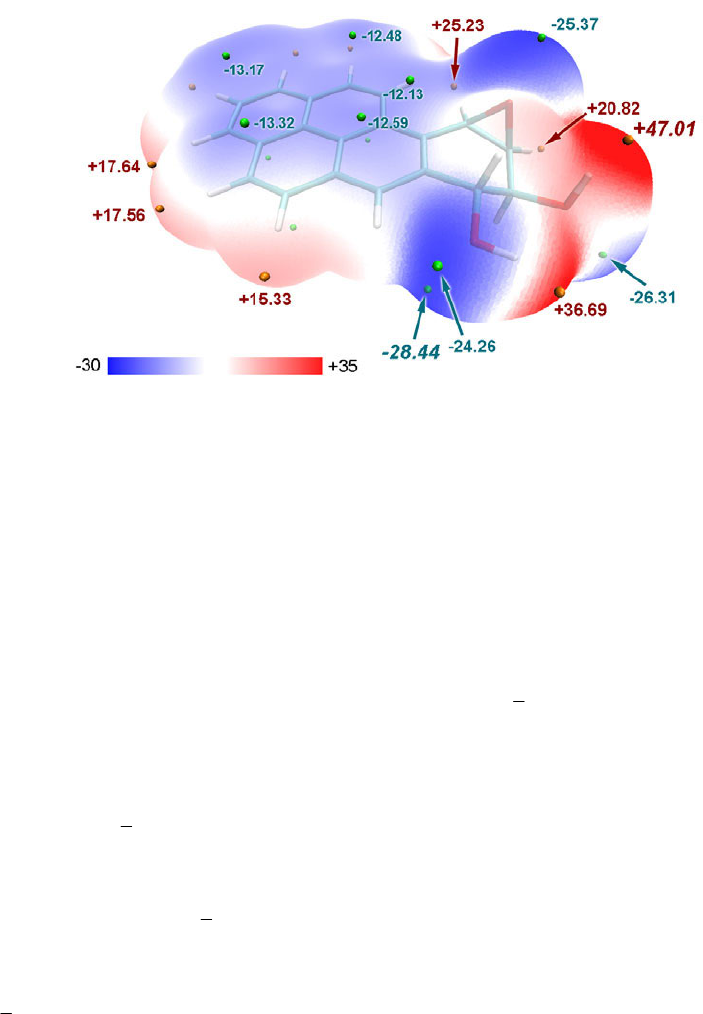
4 Tutorials and Examples
314
kcal/mol, the green and orange spheres correspond to ESP surface minima and maxima,
respectively
If you would like to plot similar graphs, please download and follow the tutorial "Plotting
electrostatic potential colored molecular surface map with ESP surface extrema via Multiwfn and
VMD" in "Related resources and posts" section of Multiwfn website.
4.12.2 Average local ionization energy analysis on phenol molecular
surface
This example is a continuation of the last example, please finish the last example first if you
haven't. Below we will analyze average local ionization energy
I
on phenol vdW surface.
-1 // Return to the parameter setting interface from post-process stage
2 // Reselect mapped function
2 // Choose
I
as mapped function
0 // Start the surface analysis.
Since calculation of
I
is much simple than ESP, the calculation will be finished soon.
Unlike surface analysis for ESP, at this time only vdW volume, surface area, average and variance
of
I
on vdW surface are outputted alongside extrema information.
Hint: If you only want to use Multiwfn to obtain molecular volume and surface area, you can simply perform
quantitative molecular surface analysis for average local ionization energy. As you have seen, this task can be
finished rather quickly.
Choose 0 to visualize extrema, in order to make the correspondence between extrema and
atoms clearer, we can drag the "Ratio of atomic size" scale bar to 4.0, which correspond to vdW
surface, we will see:
4 Tutorials and Examples
315
In side view (For clarity, only minima are shown)
Low value of
I
suggests the electron at this position is not tightly bounded, the site with
lowest
I
on vdW surface is usually recognized as the most vulnerable site to electrophilic or to
free radical attack. The regions easy to be polarized such as π electron and lone pair generally
have corresponding surface minima of
I
. In present instance, minimum 8 and 9 correspond to
lone pair of O12, both the
I
value are 10.59eV. Minimum 4,5,11, and 3,7,10 correspond to π
electrons, all of them the
I
values are about 8.9eV and can be viewed as degenerate global
minima. Worthnotingly, the minima above and below the conjugated ring only present at ortho-
and para-carbon. These observations perfectly explained the effect of hydroxyl as an ortho-para
4 Tutorials and Examples
316
directing group. Since
I
at minimum 8 and 9 are obviously larger than the
I
at the minima
surrounding the carbon ring, oxygen is not a vulnerable site for electrophilic reaction.
4.12.3 Local molecular surface analysis for acrolein
It is well known that acrolein (see below) tends to undergo nucleophilic attrack at carbonyl
carbon and carbon; in particular, the former is the primary site for hard nucleophilic reagent. The
so-called hard means the electron cloud of the nucleophilic reagent is difficult to be polarized; the
selectivity of reactive site for this case is usually dominated by ESP.
In this example, we will try to interpret the site-selectivity of acrolein by analyzing ESP on its
vdW surface. Note that average local ionization energy is only useful for studying electrophilic
attack, but completely useless for analyzing nucleophilic attrack.
Boot up Multiwfn and input:
examples\acrolein.wfn // Optimized and produced at B3LYP/6-31G** level
12 // Quantitative analysis of molecular surface
0 // Start the analysis for ESP
After the calculation is finished, choose 0 to visualize surface extrema:
As you can see, there is a surface minimum of ESP at the boundary of carbon and it is very
close to carbon. This observation indirectly reveals that nuclear charge of carbon is more
heavily screened by electron cloud, and hence is less probable to be the site of nucleophilic attack.
4 Tutorials and Examples
317
However, quantitative analysis of ESP on the whole acrolein surface does not provide a direct and
definitive interpretation on the preference of reactive sites, because no surface maxima are found
on carbonyl and carbons, hence we are unable to directly investigate the characteristic of
carbonyl and carbon.
In Multiwfn, the quantitative analysis can not only be applied to the whole molecular surface,
but is also applicable to local molecular surface to reveal characteristic of atom or fragment. Here
we select option 11 in post-process interface to calculate and output properties of the local
surfaces corresponding to each atom. Some of the results are shown below
Note: Average and variance below are in kcal/mol and (kcal/mol)^2 respectively
Atom# All/Positive/Negative average All/Positive/Negative variance
1 -24.35251 NaN -24.35251 NaN NaN 72.72766
2 4.65672 5.74594 -1.45401 9.79575 9.01495 0.78080
3 1.30965 2.36405 -0.88391 2.70896 2.45972 0.24925
4 8.37174 10.35813 -6.00120 36.74187 17.22299 19.51888
5 7.07040 8.67973 -6.35468 49.99108 25.33899 24.65209
6 2.21578 3.02322 -0.73880 5.15593 4.95305 0.20288
7 15.34251 15.34251 NaN NaN 22.85377 NaN
8 14.68486 14.68486 NaN NaN 25.92230 NaN
As you can see, the average ESP values on the local surface of carbonyl carbon (atom 2),
carbon and carbon are 4.657, 1.310 and 2.216 kcal/mol, respectively. This result clearly
explained the site-selectivity; the carbonyl carbon is the most favorable site because the average
ESP on its local surface is the most positive, and hence nucleophilic reagents (especially the hard
ones) tend to be attracted to this site. In contrast, on the local surface of carbon the average of
ESP is the smallest compared to the other two carbons, and thus carbon has less capacity to
attract nucleophilic reagents.
Note that some of the outputted data are NaN (Not a Number), these are not bug but
understandable. For example, the average of positive part of ESP of atom 1 is NaN, this is because
oxygen has large electronegativity, and thus on the local surface of atom 1 the ESP is completely
negative, so the average of positive ESP is unable to be computed.
If you are confused about what is "local surface of atoms" or you want to visualize them,
after you choose option 11 you can select "y" to output the surface facets to locsurf.pdb file in
current folder. Each atom in this file corresponds to a surface facet, the B-factor value corresponds
to its attribution. By this file you can visualize how the whole molecular is partitioned, the method
is: boot up VMD program and drag the pdb file into the VMD main window, in "Graphics"-
"Representation" set the "Drawing method" as "Points", set the point size to 4, and set "Coloring
Method" as "Beta". In VMD main window select "Display"-"Orthographic" and deselect
"Display"-"Depth Cueing". Then load the molecular structure file of acrolein into VMD and
render it as CPK mode, you will see below graph

4 Tutorials and Examples
318
In the graph, each point represents a surface facet; different colors represent different local surface
regions, and each one corresponds to an atom.
Beware that the "imolsurparmode" parameter in settings.ini directly affect the result of local
surface analysis, currently we are using imolsurparmode=1.
4.12.4 Fukui function distribution on local molecular surface of
phenol
I have exemplified how to study Fukui function by visualizing its isosurface (Section 4.5.4)
and by condensing it to atomic value via population analysis (Section 4.7.3). In this section, I will
introduce another way to study this function, namely examine its average value on the local
molecular surface corresponding to each atom. The advantage of this scheme over visualizing
isosurface is that the relative magnitude of Fukui function can be obtained clearly and
quantitatively. Meanwhile, unlike condensed Fukui function, this scheme is free of ambiquity of
selection of population methods. I will still use phenol as example.
Boot up Multiwfn (referred to as Multiwfn A) and input following commands
examples\phenol.wfn
12
2 // Select the mapped real space function on the molecular surface
0 // The function value will be loaded from an external file
1 // Set the way to define the surface
1 // Use electron density isosurface as molecular surface
0.01 // Because Fukui function on default isosurface
=0.001 is often too small, enlarging the
isovalue to 0.01 makes the discussion easier
0 // Start the surface analysis
Multiwfn will generate grid data of electron density and then generate the surface vertices.
4 Tutorials and Examples
319
After the coordinate of these vertices are automatically outputted to surfptpos.txt in current folder,
Multiwfn A pauses. Do not terminate Multiwfn A, we boot up another Multiwfn now (referred to
as Multiwfn B), and then input below commands in Multiwfn B
examples\phenol.wfn
5 // We use this module to generate Fukui function on the points recorded in surfptpos.txt
0 // Set custom operation
1
-,examples\phenol+1.wfn // Subtract the properties from phenol+1.wfn from phenol.wfn
1 // Electron density
100 // Load the coordinate of the points to be calculated from an external file
surfptpos.txt
t.txt // Output the coordinate and calculated function values (Fukui function) of the points
(surface vertices) to this file
Now we terminate Multiwfn B, and return to Multiwfn A, then input
t.txt // Load the Fukui function values at the surface vertices from this file
11 // Output the quantitative data of Fukui function distributed on the local vdW surface
corresponding to each atom
You can find below content from the output
Atom# All/Positive/Negative average
1 1.93967E-03 1.93967E-03 NaN
2 8.13794E-04 8.13794E-04 NaN
3 1.41595E-03 1.41595E-03 NaN
4 2.01898E-03 2.01898E-03 NaN
5 1.25625E-03 1.25625E-03 NaN
6 9.39694E-04 9.39694E-04 NaN
... [ignored]
NaN means there is not negative value of Fukui function on the local molecular surfaces. From the
result it is clear that the averages of the Fukui function on the local molecular surface
corresponding to ortho and para carbons are larger value than that of meta carbons, thus correctly
reflecting the fact that hydroxyl is an ortho-para- director.
4.12.5 Becke surface analysis on guanine-cytosine base pair
The concept of Hirshfeld and Becke surface analysis have been detailedly introduced in
Section 3.15.5, please read them first. In this section I will exemplify how to perform Becke
surface analysis on guanine-cytosine (GC) base pair to analyze the weak interaction between the
two monomers.
Boot up Multiwfn and input
examples\GC.wfn // Generated at M06-2X/6-31+G** level, optimized at PM7 level
12
1 // Change the definition of surface
6 // Use Becke surface. You can also select 5 to use Hirshfeld surface
1-13 // The index range of the atoms you are interested in (cytosine in present case)
2 // Change mapped function
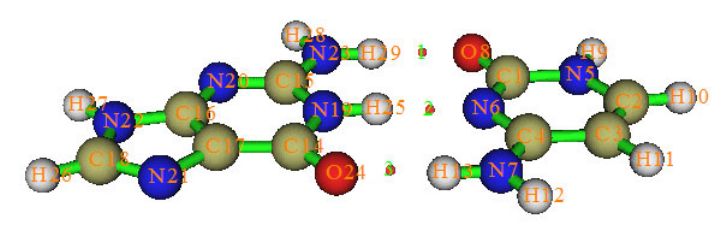
4 Tutorials and Examples
320
11 // Electron density
0 // Start calculation
Multiwfn found numerous surface minima, which are meaningless in this case, and at the
same time three surface maxima are found
Number of surface maxima: 3
# Value X/Y/Z coordinate(Angstrom)
1 0.042331 -0.721650 2.605906 0.043754
2 0.049281 0.767524 0.959671 -0.013820
* 3 0.053205 1.628343 -1.269364 0.030387
You can choose 0 to visualize them, see below
Since the sequence of electron density at these maxima is 32>1, one can expect that the
sequence of H-bond strength is O24-H13 H25-N6 H29-O8. This conclusion is identical to the
analysis of AIM bond critical point analysis.
If you want to visualize the shape of Becke surface, simply choose option -3. If you want to
plot the Becke surface colored by mapped function value, you need to make use of VMD, as
described below. Select option 6 and input 100 to export all surface vertices to vtx.pdb in current
folder and in the meantime multiply the data by 100 (since electron density in the Becke surface is
small, while the B-factor in pdb format only has two decimal places). Each atom in vtx.pdb now
corresponds to a surface vertex, and its B-factor stands for electron density at corresponding
position.
Drag "examples\GC.pdb" into main window of VMD program, this file contains geometry of
present system. Select "Graphics"-"Representation", change the drawing method to "Licorice" and
decrease bond radius to 0.2. Then drag the vtx.pdb into VMD, select "Graphics"-"Representation",
change the drawing method from "Lines" to "Points", set coloring method to "Beta", enlarge the
size to 6. Run the command color scale method BWR in VMD console window. Then you will see
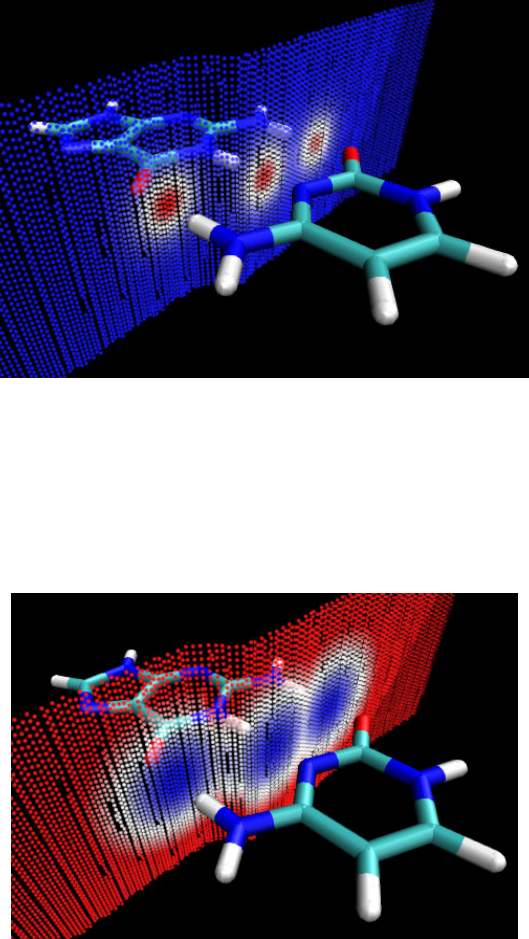
4 Tutorials and Examples
321
Becke surface is represented by points, and the three red zones correspond to high electron
density region, which stem from H-bonds. This example demonstrated that Becke surface analysis
is useful to reveal the region where intermolecular interaction is evident.
Repeat above analysis but with dnorm as mapped function, and replot the Becke surface with
the same procedure. Then in the graphical representation window, select "Trajectory" tab, input -
0.5 and 2.0 in the "Color scale data range", you will see below graph
As you can see, using dnorm as mapped function is also capable of revealing weak interactions;
the blue regions corresponds to close contact between the fragment you are interested in (cytosine)
and other fragments (guanine only). The advantage of using dnorm over electron density is that the
former does not rely on wavefunction information, so the input file you used can only contain
geometry information, such as .pdb and .xyz are completely acceptable in this case. However the
physical meaning and robustness of dnorm is not as good as electron density.
4.12.6 Hirshfeld surface analysis and fingerprint plot analysis on urea
crystal
This time we perform Hirshfeld surface analysis for urea crystal. .cif is the most popular
crystal structure format, however currently Multiwfn does not support it. So I dug out a cluster of
4 Tutorials and Examples
322
ureas from its crystal structure; the file "examples\Urea_crystal.pdb" contains 11 ureas, the central
one will be defined as the fragment in our Hirshfeld surface analysis.
Notice that Hirshfeld surface analysis requires electron density of atoms in their free-states,
in Multiwfn there are to ways to generate them: 1. Using built-in atomic densities, this is very
convenient, see Appendix 3 for detail; 2. Evaluating atomic densities based on atomic .wfn files,
see Secion 3.7.3 for detail. In this example we will use way 2 (way 1 works equally well). What
we need to do is simply moving the "atomwfn" folder in "examples" folder to current folder. Then
during generating Hirshfeld surface, Multiwfn will automatically use the atomic wavefunction
files in this folder.
Boot up Multiwfn and input
examples\Urea_crystal.pdb
12
1 // Change surface type
5 // Use Hirshfeld surface
16,36,58,2,77,55,34,13 // The index of the atoms in the central urea
0 // Start calculation. Note that the default mapped function dnorm is used here
2 // Evaluating atomic densities based on atomic .wfn files
After the calculation is finished, select option 6 to export the surface vertices with dnorm value
to vtx.pdb, and then plot them in VMD by using the method shown in the last section, you will see
a graph very similar to the second figure in Section 3.15.5.
Next, we draw fingerprint plot. In the post-process menu select 20 and choose option 0, then
choose option 0 again, you will see below graph
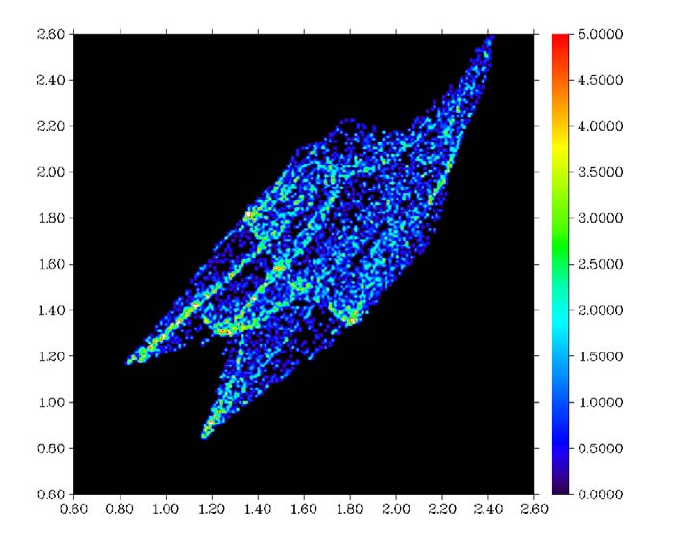
4 Tutorials and Examples
323
In this figure, X and Y axes correspond to di and de, respectively. It can be seen that there is a pair
of spikes at the bottom left of the plot (i.e. short di and de), this observation suggests that urea
behaves as both H-bond acceptor (the lower spike, di > de) and H-bond donor (the upper spike, di
< de).
In Multiwfn, the fingerprint plot can be drawn not only for overall Hirshfeld surface, but also
for local contact surface (see section 3.15.5 for detail). Let's check the fingerprint plot of the local
contact surface between the four hydrogens in central urea and all of the atoms in peripheral ureas.
After closing the window showing fingerprint plot, select -1 to return, then input 20 to enter the
interface of fingerprint plot analysis again. We need to first define "inside atoms" set and "outside
atoms" set, because only the points on the contact surface between the two sets will be taken into
account in the fingerprint plot analysis. Choose option 1 to define "inside atoms" set, then press
ENTER button directly to use default atom range (i.e. all atoms in the central urea) and then input
H. Now all hydrogens in the central urea are defined as the "inside atoms" set. Since the default
"outside atoms" set is just all of the atoms in peripheral ureas, we do not need to modify it. Select
option 0 to start the fingerprint plot analysis, then choose 0, you will see
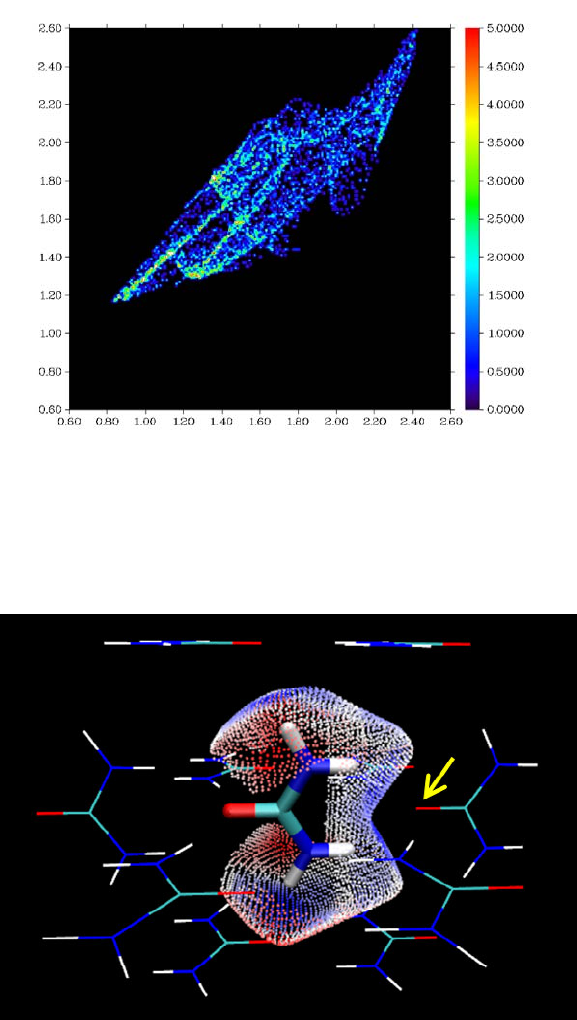
4 Tutorials and Examples
324
As you can see, since this time we only considered the hydrogens in the central urea, the urea
purely behaves as hydrogen donor, so only on spike at bottom left of the plot is observed
It is interesting to check the shape of the local contact surface, so after closing the window
we choose option 5 to export all of the points on the surface to finger.pdb in current folder. Plot
them in VMD by using the method shown in the last section, you will see
Clearly, the surface very well portrays the contact between the hydrogens in central urea and the
atoms in peripheral ureas. The color corresponds to dnorm value, more blue imples more close
contact.
Next, we check the fingerprint plot between the hydrogens in central urea and the oxygen
marked by yellow arrow in above figure. Input below commands
-1 // Return
20 // Fingerplot analysis
1 // Set inside atoms set
[Press ENTER directly]
H
2 // Set outside atoms set
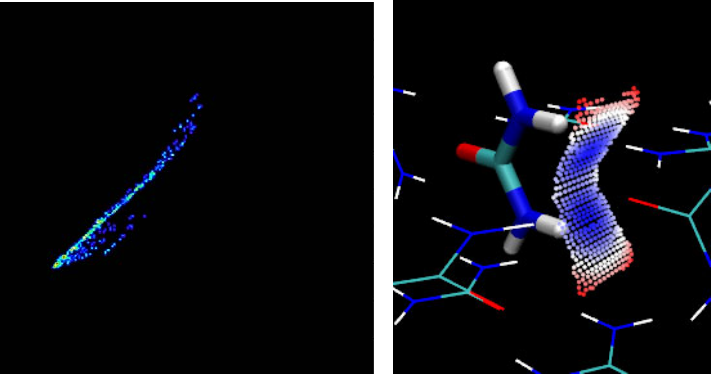
4 Tutorials and Examples
325
76 // The index of the oxygen marked by yellow arrow
[Press ENTER directly] // Namely do not use element type as filter condition
0 // Start fingerprint analysis
3 // Set color scale. Because the default color scale in this case is different to above
fingerprints, the plots are not directly comparable
0,5
0 // Show fingerprint graph on screen
The fingerprint plot and the corresponding surface points are shown below
In the fingerprint plot you can see that the distribution scope of surface points is narrow, and
the spike is quite evident, showing strong H-bond character due to the contact of H and O.
Fingerprint is especially useful for comparison of the intermolecular interactions in different
crystals, see CrystEngComm, 11, 19 (2009) for discussions.
4.12.7 Two tricks to reduce computational time in ESP analysis on
vdW surface
Evaluation of ESP on vdW surface is time-consuming, especially for large system with high-
quality basis-set. Here I introduce two tricks to reduce computational time in ESP analysis on vdW
surface.
Part 1 Reuse ESP data from previous calculations
If you have performed ESP analysis on a system, and which will be analyzed again later, you
can export the ESP data to a plain text file, so that next time when you analyze the same system
you can directly make use of the data.
Let's see an example. We first perform ESP analysis on vdW surface as usual
examples\N-phenylpyrrole.fch
12
0
Once the calculation is finished, select option 7 to export the surface vertices with ESP values
to a plain text file named vtx.txt in current folder. After that select -1 to return to last menu.
Assume that we want to perform the analysis again. This time we will directly use the ESP
data recorded in the plain text file rather than let Multiwfn calculate them. Input below commands
4 Tutorials and Examples
326
5 // Load mapped function values from external file
1 // Load mapped function at all surface vertices from plain text file
0 // Start the analysis. After the molecular surface is constructed, Multiwfn will prompt you
to input the path of the plain text file recording mapped function values at the surface vertices.
vtx.txt
Since the ESP values are not calculated this time but readed from vtx.txt directly, the analysis
results immediately show up on the screen, and they are exactly identical to the ones we obtained
at the first time.
Part2 Using cubegen to significantly reduce calculation cost of ESP
Frankly speaking, the calculation speed of ESP in Multiwfn is not as fast as the cubegen
utility of Gaussian. For very large system, such as carbon nanotube, if you directly use Multiwfn
to calculate the ESP value at all surface points, you will find the computational cost is
prohibitively high. In this circumstance, one can make use of cubegen to calculate the ESP values
to significantly reduce the overall time-consuming of quantitative molecular surface analysis. This
section will illustrate how to do this. Note that even if you are not a Gaussian user, as long as the
program you used can produce .molden file (e.g. ORCA), or are using GAMESS-US, you can also
benefits from cubegen, because by using subfunction 2 of mainfunction 100 Multiwfn can convert
loaded .molden/.gms file to .fch file.
We take N-phenylpyrrole as example. cubegen can be found in the Gaussian installation
directory.
Boot up Multiwfn and input following commands
examples\N-phenylpyrrole.fch
12
5 // Load data of mapped function (viz. ESP in this example) from external file rather than
directly calculate them via Multiwfn during the surface analysis
2 // This option is specific for cubegen
0 // Start analysis
Multiwfn will calculate electron density and generate surface vertices as usual, then the
coordinate (in Angstrom) of all surface vertices will be outputted to cubegenpt.txt in current folder.
Now we invoke cubegen to calculate ESP at these points. Run the command like below in
MS-DOS/Linux/Mac OS command-line window. (Beware that the N-phenylpyrrole.fch provided
herein may or may not be incompatible with your cubegen version)
cubegen 4 potential N-phenylpyrrole.fch result.cub -5 h < cubegenpt.txt
where the argument 4 means using 4 threads for parallel calculation; potential means calculating
ESP; -5 means the points to be calculated are inputted by users manually or redirected in from an
external file (cubegenpt.txt in this case); h means the output file, namely result.cub, will be a
formatted plain text file. For more detail about cubegen utility please consult Gaussian manual.
Return to the Multiwfn window and input the path of the cubegen output file result.cub,
Multiwfn will load the calculated ESP data from it and performs subsequent analysis as usual. You
will find that the result is almost exactly identical to that based on the ESP directly evaluated by
Multiwfn.
As mentioned in Section 4.4.4, by making use of the cubegen, the total time cost of plotting
4 Tutorials and Examples
327
plane map for ESP can also be significantly reduced. We still take N-phenylpyrrole as example,
we will plot ESP for its YZ plane of X=0.
First set parameter "iplaneextdata" in settings.ini to 1, then boot up Multiwfn and input
examples\N-phenylpyrrole.fch
4 // Plot plane map
12 // ESP
2 // Contour map
[Press ENTER to use default grid setting]
0 // Adjust extension distance
10 // 10 Bohr
2 // XZ plane
0 // Y=0
Now cubegenpt.txt has been generated in current folder, which contains coordinate of all
points in the plotting plane. Run below command to invoke cubegen to generate their ESP values
cubegen 4 potential N-phenylpyrrole.fch result.cub -5 h < cubegenpt.txt
In the Multiwfn window, input the path of the result.cub, Multiwfn will load the ESP data
from this file and then immediately presents the ESP contour map on screen.
4.12.8 Quantitative analysis of orbital overlap distance function D(r)
on thioformic acid molecular surface
Content of this section was contributed by Arshad Mehmood and slightly adapted by Tian Lu.
This example is a continuation of Section 4.5.7. Here I illustrate the quantitative analysis of
orbital overlap length function D(r) on molecular electron density isosurface of thioformic acid.
Boot up Multiwfn and input following commands:
examples\ThioformicAcid.wfn // Thioformic acid optimized at B3LYP/6-311++G(2d,2p)
12 // Quantitative analysis of molecular surface
2 // Select mapped function
6 // Orbital overlap distance function D(r), which maximizes EDR(r;d) with respect to d
2 // Use default value of total number, start and increment of EDR exponents. Please consult
Section 4.5.7 for more information.
0 // Start analysis now!
Now the analysis starts. This step will take some time. Once calculation is finished, following
results will be printed on screen along with other information:
Global surface minimum: 2.789918 a.u. at 1.983402 -0.346198 1.757884 Ang
Global surface maximum: 3.541349 a.u. at -2.861073 -1.074395 -0.095237 Ang
The number of surface minima: 4
# Value X/Y/Z coordinate(Angstrom)
1 3.296958 -1.622302 2.055665 0.423383
2 3.218284 0.950838 2.841231 0.010991
* 3 2.789918 1.983402 -0.346198 1.757884
4 2.790103 2.078805 -0.344424 -1.731277
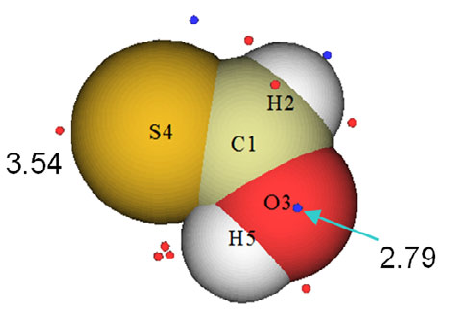
4 Tutorials and Examples
328
The number of surface maxima: 10
# Value X/Y/Z coordinate(Angstrom)
* 1 3.541349 -2.861073 -1.074395 -0.095237
2 3.401958 -0.539716 2.324441 0.014652
3 3.502485 0.041422 -2.239222 -0.308278
4 3.502696 0.089030 -2.257271 0.004859
5 3.494004 0.207205 -2.075594 -0.673828
6 3.496480 0.164501 -2.070255 0.707373
7 3.359381 0.542328 1.465019 -1.650518
8 3.358980 0.496994 1.456262 1.657761
9 3.311711 2.030429 1.904600 0.023877
10 2.918240 2.847314 -1.370280 0.021275
Now select 0 to view surface minima and maxima:
This graph shows molecular structure and surface extrema (red and blue spheres correspond
to surface maxima and minima, respectively). It can be seen that surface minima is present on
oxygen atom due to compact lone pair and surface maxima is located on sulfur atom due to its
more diffuse and weakly bound lone pair.
4.13 Process grid data
Main function 13 includes a bunch of subfunctions, by using them you can process the grid
data loaded from Gaussian-type cube file (.cub) or DMol3 grid file (.grd) or the grid data directly
generated by such as main function 5 of Multiwfn. In this section I present several simple
applications, please play with other subfunctions by yourself.
4.13.1 Extract data points in a plane
In this example we extract average XY-plane data between Z=28 and Z=32 angstrom to a
plain text file.
dens.cub // A cube file generated by Multiwfn or by some external programs, since cube file
is generally large, it is not provided in "example" folder. You can also use the grid data generated
internally by Multiwfn instead, that is use main function 5 to calculate grid data first and then
4 Tutorials and Examples
329
choose 0 to return to main menu (the just generated grid data is present in memory)
13 // Process grid data
5 // Extract average plane data
28,32 // Range of Z (in Angstrom)
Now the data points are exported to output.txt in current folder, including X,Y coordinates
and value. You can import this file to plotting software such as sigmaplot to draw plane graph.
Another example, we extract data point on the plane defined by atom 4,6,2.
dens.cub
13 // Process grid data
8 // Output data in a plane by specifying three atom indices. This function is commonly used
to extract tilted plane, if the plane is parallel to XY, YZ or XZ, you should use function 1,2 or 3
instead respectively
0 // Use automatically determined tolerance distance. If vertical distance between any point
and the plane you defined is smaller than tolerance distance, then the point will be outputted.
1 // Project the data points in the plane you defined to XY plane, so that you can directly
import the outputted file to plotting software to draw plane graphs
Now the data value along with coordinates is exported to output.txt in current folder.
Notice that Multiwfn does not do interpolation during plane data extraction, hence if the
quality of grid data is not fine enough (namely spacing between points is large), then the extracted
plane data will be sparse (especially severe for the plane not parallel to XY, YZ or XZ plane).
4.13.2 Perform mathematical operation on grid data
Example 1
Assume that we have two cube files A.cub and B.cub, in this example we obtain their
difference cube file (viz. A.cub minus B.cub).
Boot up Multiwfn and input following commands
A.cub // Load the first cube file into memory
13 // Process grid data
11 // Grid data calculation
4 // Subtract the grid data in memory by another grid data
B.cub // The cube file containing another grid data. Notice that this cube file must have
identical grid setting as the first cube file
Now the grid data in the memory has been updated, choose 0 to export it as a new cube file,
which is what we need.
Example 2
Assume that we have two cube files MO1.cub and MO2.cub, each of them records
wavefunction value of an orbital. In this example we will generate a cube file containing total
electron density deriving from these two orbitals. According to Born's probability interpretation,
square of an orbital wavefunction value is simply its density probability, therefore what we need is
the sum of square of the two grid data.
4 Tutorials and Examples
330
Boot up Multiwfn and input following commands
MO1.cub
13 // Process grid data
11 // Grid data calculation
10 // Perform A^2+B^2=C operation, where A is present grid data (MO1.cub), B is another
cube file (MO2.cub), C is the new grid data
MO2.cub // Load another cube file
After calculation, the grid data in memory has been updated to C.
0 // Output the updated grid data
totdes.cub // Filename of the new cube file, which contains total electron density of the two
orbitals
4.13.3 Scaling numerical range of grid data
The numerical range of ELF function is [0,1], in this example, we scale its numerical range to
[0,65535] (which is value range of unsigned 16bit integer). We first compute ELF grid data in
Multiwfn as described in Section 4.5.1, and then input
0 // Return to main menu from post-process interface of grid data calculation
13 // Process grid data
16 // Scale data range
0,1 // Original data range
0,65535 // The range after scaling. Please read Section 3.16.12 for the detail of scaling
algorithm.
Now the grid data has been scaled. You can choose function 0 to export the updated grid data
to Gaussian cube file, or extract plane data to plain text file by corresponding functions.
4.13.4 Screen isosurfaces in local regions
Sometimes we do not want all isosurfaces in the whole space are shown, because too many
isosurfaces will confuse our eyes. This section I will show how to screen the isosurfaces of not
interest
4.13.4.1 Screen isosurfaces inside or outside a region
This section I take electron density of phenol dimer as example. First we generate the grid
data as follows (you can also directly load a .cub/.grd file and then enter main function 13)
examples\phenoldimer.wfn
5
1
2
-1 // Visualize isosurface
As you can see, the isosurfaces appear on both phenol molecules.
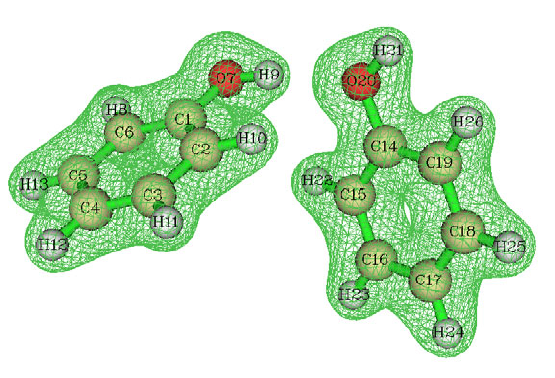
4 Tutorials and Examples
331
Assume that we only want the isosurface around the right phenol will be shown, we need to set the
value of the grid points that close to the left phenol to a very small value, for example, zero.
Close the Multiwfn GUI window and input
0 // Return to main menu
13 // Process grid data
13 // Set value of the grid points that far away from / close to some atoms
-0.7 // That means we will set the value of the grid points inside 0.7 times of vdW radius of
the atoms. If input 0.7, then the value of the grid points outside 0.7 times of the vdW radius will be
set
0 // Set the value to 0
2 // Defining mode. 2 means inputting atomic indices by hand (if choose 1, external file
containing atomic index list will be used to define fragment, see Section 3.16.9 for the format or
the next example)
1-13 // Range of atomic indices of the left phenol
Now the grid data has been updated, let's choose option -2 to visualize the isosurface of current
grid data. As you can see, the isosurface of the left phenol has disappeared.
4.13.4.2 Screen isosurfaces outside overlap region of two fragments
During analysis of inter-molecular interaction by reduced density gradient method (Section
4.100.1), what we want to study is only the isosurfaces in inter-molecular regions. In order to
screen isosurfaces in other regions, we can set the value of grid points outside superposition region
of scaled vdW regions of two molecules to a very large value (at least larger than maximum value
in current grid data). In this section I give you a practical example.
The so-called "scaled vdW regions" is the superposition region of scaled vdW spheres of all
atoms in the fragment. While the "scaled vdW sphere" denotes the sphere corresponding to the
scaled vdW radii.
Below is a segment of dimeric protein plotted by VMD program (you will know how to draw
a similar picture after reading Section 4.100.1), red and blue representing backbone structure of
the two chains respectively. Isosurfaces of reduced density gradient exhibit weak interaction
region. However, these isosurfaces include both intermolecular and intramolecular parts, they are
interwinded and result in difficulty in visual study of weak interaction between the two chains.
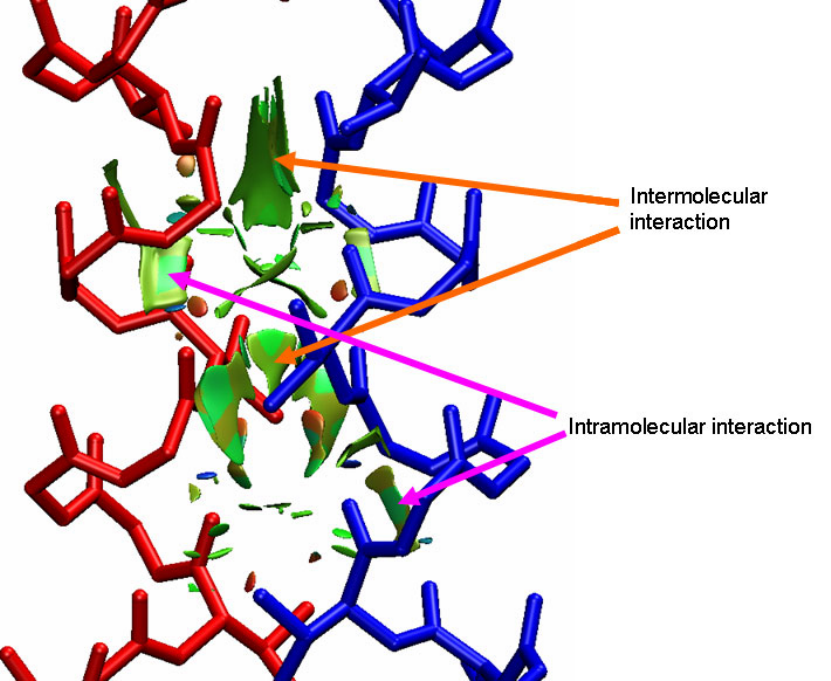
4 Tutorials and Examples
332
In order to screen those intramolecular isosurfaces, we will use subfunction 14 in main
function 13 of Multiwfn. First, we prepare two atom list files for the two chains (each chain
corresponds to a fragment). atmlist1.txt includes atom indices of chain 1, the head and tail of the
file are:
159 <--- Total number of atoms in chain 1
1 <--- Atom index of the first atom in chain 1
2 <--- Atom index of the second atom in chain 1
...
159 <--- Atom index of the last atom in chain 1
Similarly, atmlist2.txt defines atom list for chain 2, its head and tail parts are:
159 <--- Chain 2 has 159 atoms too
160 <--- Atom index of the first atom in chain 2
161 <--- Atom index of the second atom in chain 2
...
318 <--- Atom index of the last atom in chain 2
Then boot up Multiwfn and input:
RDG.cub // The cube file of reduced density gradient corresponding to above graph
13 // Process grid data
14 // Set value of the grid points outside overlap region of the scaled vdW regions of the two
fragments
1.8 // The value for scaling vdW radius. In your practical studies, you may need to try this
value many times to find a proper value
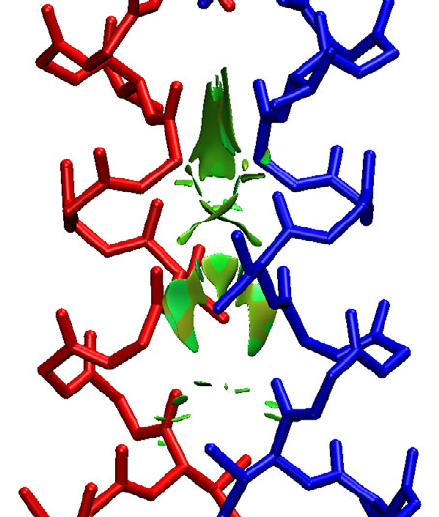
4 Tutorials and Examples
333
1000 // Set value of those grid points to 1000, this value is large enough
1 // Defining mode, 1 means using external file to define the fragment
atmlist1.txt // The name of the atom list file for chain 1
atmlist2.txt // The name of the atom list file for chain 2
Wait for a while, the grid data will be updated. Then choose function 0 to export it as cube
file. Using this new cube file to redraw above picture, we find all of intramolecular isosurfaces
have disappeared, the graph becomes very clear.
In fact, when the case is not complicated (as present example), preparing atomic list files are
not needed, you can choose defining mode as 2 and then directly input atomic indices (i.e. 1-159
for chain 1 and 160-318 for chain 2).
4.13.5 Acquire barycenter of a molecular orbital
In this example, we will calculate barycenter of a molecular orbital. You can also obtain
barycenter of other real space functions by similar manner. The definition of barycenter is given in
Section 3.16.13. Below is the isosurface of the 10th MO of phenol.
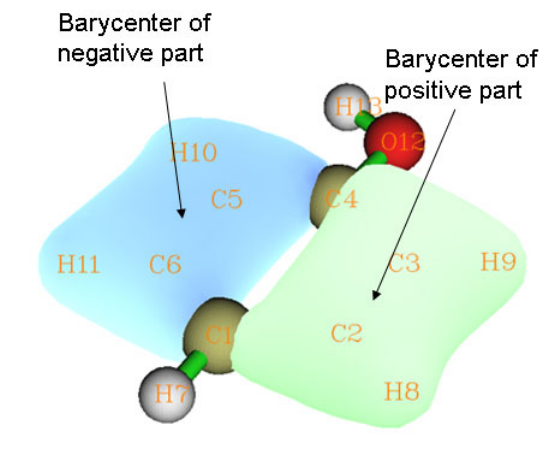
4 Tutorials and Examples
334
Before calculate the barycenter of the MO, we need to obtain the grid data of the MO. We
can do this in Multiwfn, namely boot up Multiwfn and input following commands:
examples/phenol.wfn
5 // Calculate grid data
4 // Choose orbital wavefunction
10 // The 10th orbital
2 // Medium quality grid. Finer quality of grid will give rise to more accurate barycenter
position
0 // Return back to main menu
Now the grid data has been stored in memory, we will analyze it now
13 // Process grid data
17 // Show statistic data
1 // Select all points
From the output, we can find that the X, Y, Z components of barycenter of the positive part of
the MO are (in Bohr) 2.612, -0.524, 0.000 respectively, while that of the negative part are -2.586, -
0.710, 0.000. The total barycenter is meaningless currently, since total integral value is zero for
this MO. However, total barycenter of absolute value of the MO is useful, especially for
macromolecules, from this we can understand where the MO is mainly located. In order to do this,
we input:
11 // Grid data calculation
13 // Get absolute value
17 // Show statistic data
1 // Select all points
We find X, Y, Z of total barycenter of the MO are -0.015, -0.618, 0.000. Since there is no
negative region now, barycenter of negative part is shown as NaN (Not a Number).
4.13.6 Plot charge displacement curve
Multiwfn is able to calculate and plot integral curve for grid data, see the introduction in
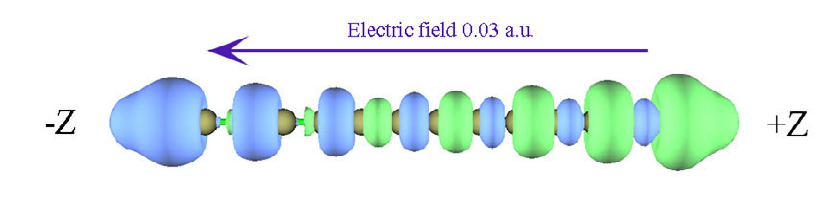
4 Tutorials and Examples
335
Section 3.16.14. If the grid data is selected as electron density difference, then the integral curve is
commonly known as charge displacement curve (CDC), by which the charge transfer can be
studied visually and quantitatively, extremely suitable for linear systems. In this example, by
means of CDC, we will investigate the intermolecular charge transfer in polyyne (n=7) due to the
externally applied electric field of 0.03 a.u. along the molecular axis.
The polyyne.wfn and polyyne_field.wfn files in "example" folder correspond to the polyyne
in its isolated state and in the case that external electric field of 0.03 a.u. is applied, respectively.
B3LYP/6-31G* is used in the calculations, and the geometry optimized in isolated state is used for
both cases. In Gaussian program, the field can be activated via keyword "field=z+300".
Before plotting the CDC, we must calculate the grid data of electron density difference
between these two files first. Boot up Multiwfn and input following commands:
examples\polyyne_field.wfn
5 // Calculate grid data
0 // Custom operation
1
-,examples\polyyne.wfn //Subtract the propery of polyyne.wfn from polyyne_field.wfn
1 // Electron density
2 // Medium quality grid
We first visualize the isosurface of the electron density difference. After select -1 and set the
isovalue to 0.004, we will see the graph like below
The green and blue parts represent the regions where electron density is increased and decreased
after the external electric field is applied, respectively. It can be seen that although green and blue
parts interlace with each other, the total trend is that electron transferred to positive side of Z-axis
(namely toward the source of the electric field). Next we will plot CDC, which is able to
characterize the electron transfer in different regions quantitatively.
Click "Return" button in the GUI and then input
0 // Return to main menu
13 // Process grid data
18 // Calculate and plot integral curve
Z // The curve will be plotted in Z direction
a // Select the entire range
In the menu, we first choose 2 to plot local integral curve of the grid data of the electron
density difference. You will see
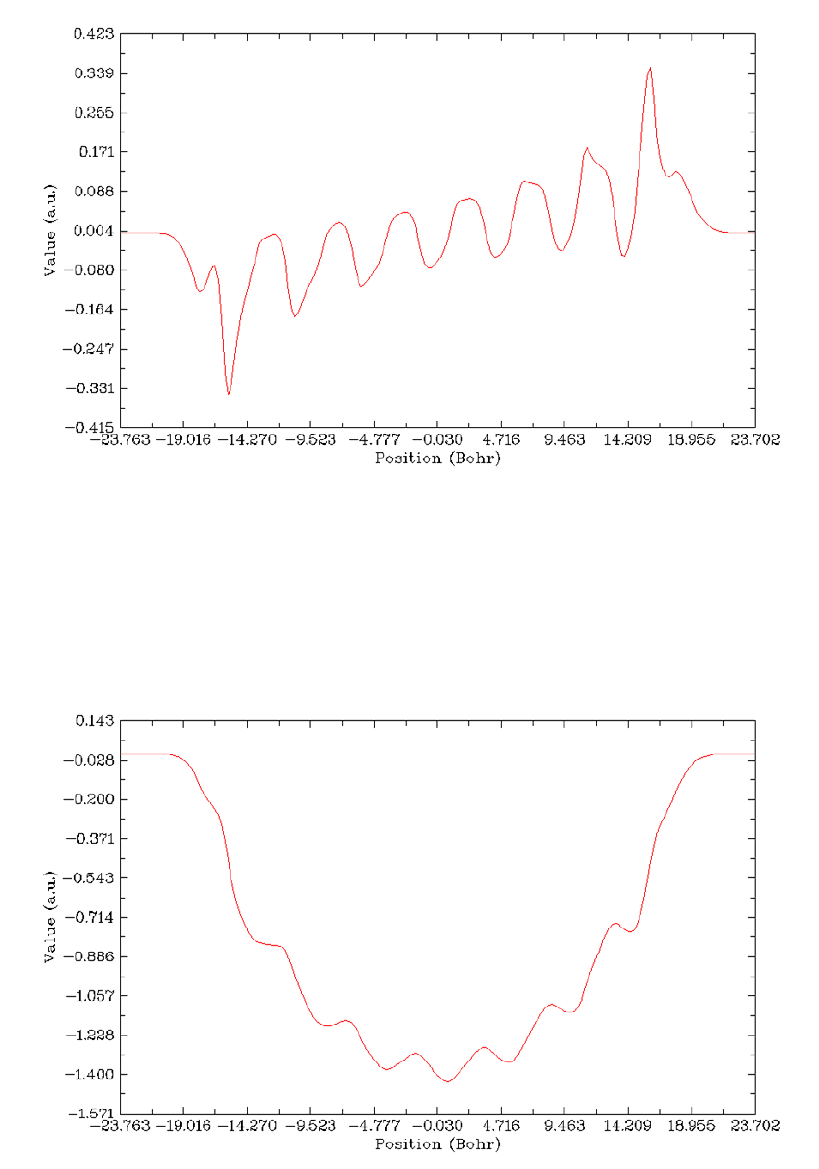
4 Tutorials and Examples
336
From the graph we can examine the integral of electron density difference in the XY planes
corresponding to different Z coordinates. The Z coordinate and the value correspond to X and Y
axes of the graph. You can directly compare this curve with the isosurface graph shown above, the
peaks lower and higher than zero (dashed line) correspond to the blue and green isosurfaces.
Clicking right mouse button on the graph to close it, and then select option 1, the CDC will
be shown immediately
This graph is yielded by integrating the curve shown in the last graph along the molecular axis. In
its left part, although there are some fluctuations, the CDC gradually becomes more and more
negative and reaches minimum value of 1.4 in the midpoint of the X-axis (corresponding to the
center of the polyyne), that means due to the external electric field, the number of lost electrons in
the left part of polyyne is 1.4. In the right part of the graph, the CDC increases gradually from -1.4
and finally reaches zero, suggesting that 1.4 electrons are transferred to right part of the polyyne,
4 Tutorials and Examples
337
and due to the amount of increase and decrease of electron are cancelled with each other exactly in
the whole molecular space, there is no variation of the total number of electrons (in other words,
integral of the electron density difference in the whole molecular space is exactly zero).
4.13.7 Evaluation of electron density overlap
In this example we take methane dimer as example to evaluate where electron density of the
two monomers overlap with each other evidently. The structure of the methane dimer is
We first obtain grid data for an arbitrary real space function for the dimer. Boot up Multiwfn
and input:
examples\rho_overlap\dimer.pdb
5
100 // User define function, by default this function doesn't take any computational time
-10 // Set grid extension distance
2 // Decrease the distance to 2 Bohr to avoid waste of grid at system boundray
2 // Medium quality grid
2 // Export grid data as userfunc.cub
Now we calculate wavefunction file by Gaussian for the two monomers, the input files are
monomer1.gjf and monomer2.gjf in examples\rho_overlap folder. Finally we obtained
monomer1.wfn and monomer2.wfn. Beware that the nosymm keyword must be used in Gaussian
calculation to avoid the automatic reorientation and translation.
Now we calculate electron density grid for monomer 1 over the whole space
monomer1.wfn
5
1 //Electron density
8
userfunc.cub // Use this cube file to define the grid, which correpsonds to the whole space
2 // Export grid data
Then rename the resulting density.cub to density1.cub. Repeat above steps for monomer2 to obtain
density2.cub.
Now we calculate grid data of min(rho(1),rho(2)), namely take the minimal value of the two
sets of electron density everywhere. Boot up Multiwfn and input:
density1.cub
13
11
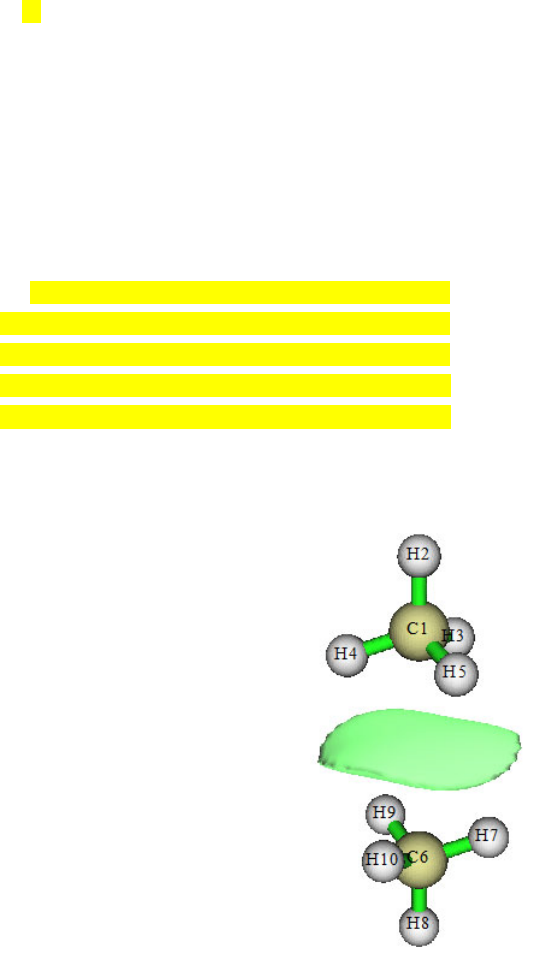
4 Tutorials and Examples
338
21 // Take min(rho(1),rho(2))
density2.cub
0 //Export resulting grid data
overlap.cub
we open the overlap.cub and density2.cub by text editor, copy atomic coordinates from the
latter to the former, and meantime change the number of atoms. Then the head of the overlap.cub
should look like below (the highlighted texts are modified parts)
Generated by Multiwfn
Totally 531846 grid points
10 -3.693194 -3.955866 -7.444301
63 0.119334 0.000000 0.000000
67 0.000000 0.119334 0.000000
126 0.000000 0.000000 0.119334
6 6.000000 0.000000 0.000000 3.371271
1 1.000000 0.000000 0.000000 5.444301
1 1.000000 0.000000 1.955867 2.677742
1 1.000000 -1.693195 -0.976988 2.677742
1 1.000000 1.693195 -0.976988 2.677742
6 6.000000 0.000000 0.000000 -3.371271
1 1.000000 1.693195 0.976988 -2.677742
1 1.000000 0.000000 0.000000 -5.444301
1 1.000000 -1.693195 0.976988 -2.677742
1 1.000000 0.000000 -1.955867 -2.677742
Boot up Multiwfn and load the overlap.cub, enter main function 0, change the isovalue to a
small one such as 0.0005, you will clearly see the density overlap region:
4 Tutorials and Examples
339
4.14 Adaptive natural density partitioning (AdNDP)
analysis
Theory basis of AdNDP analysis has been introduced in Section 3.17.1, please read it first.
Below I will show you how to use AdNDP approach to study multi-centers orbitals of several
practical molecules.
NOTICE: Using diffuse functions in AdNDP analysis is strongly deprecated, because they often cause
numerical problems (which sometimes leads to crash when Multiwfn loading input file) and never improve
AdNDP results at all!
4.14.1 Analyze Li5+ cluster
In Chem. Eur. J., 6, 2982, the authors showed that Li5+ cluster has two 4-centers 2-electrons
(4c-2e) bonds by examining ELF isosurfaces. In present example, we will use AdNDP approach to
study this cluster to verify their statement. We first optimize Li5+ cluster under B3LYP/6-311G*
level and then compile an input file of single point task for Gaussian. pop=nboread keyword must
be specified in route section, and $NBO AONAO DMNAO $END must be added to the end of the
input file. Run this file by Gaussian, and then convert check point file to .fch format. The input file,
output file and .fch file have been given in "examples\AdNDP" folder.
Boot up Multiwfn and input examples\AdNDP\Li5+.out, and then choose main function 14.
After Multiwfn loaded some necessary information, a menu appears. Since this cluster is small,
we can directly use exhaustive manner to search all possible 1c-2e, 2c-2e, 3c-2e, 4c-2e and 5c-2e
orbitals in turn. We first choose option 2 to search 1c-2e orbitals (namely lone pairs), however,
because occupation numbers of all tried 1c orbitals are lower than default threshold (which is a
value close to 2.0 and can be adjusted by option 4), the candidate orbitals list shown in front of the
menu is still empty. We then choose option 2 twice to search 2c-2e and 3c-2e orbitals in turn, we
still can't find any orbital with high occupation numbers. Next we select option 2 again to search
4c-2e orbitals, this time the candidate orbital list is no longer empty, there are two orbitals in it:
# 2 Occ: 1.9966 Atom: 1Li 2Li 3Li 4Li
# 1 Occ: 1.9966 Atom: 1Li 2Li 3Li 5Li
Due to their high occupation number, it clear that they are ideal 4c-2e orbitals, therefore we decide
to choose option 0 and input 2 to pick them out from candidate list and save as AdNDP orbitals.
Whereafter the list of AdNDP orbitals can be printed by option 5.
You may have noticed that the number of residual valence electrons (shown at the top of the
menu) has been updated to 0.020027, which is already very close to zero, it is suggested it is
meaningless to continue to search 5c-2e orbitals because they would be impossible to be found.
Now you can choose option 7 to visualize the two 4c-2e AdNDP orbitals. In order to
calculate orbital wavefunction, Multiwfn needs to load basis-set information from
corresponding .fch file first. Since Li5+.fch is in the same folder and has identical name as
Li5+.out, the .fch file will be directly loaded. When loading is finished, a GUI pops up, which is
completely identical to the one of main function 0. AdNDP orbitals can be plotted by selecting
corresponding numbers in the right-bottom list. The 0.05 isosurfaces of the two orbitals are shown
below.
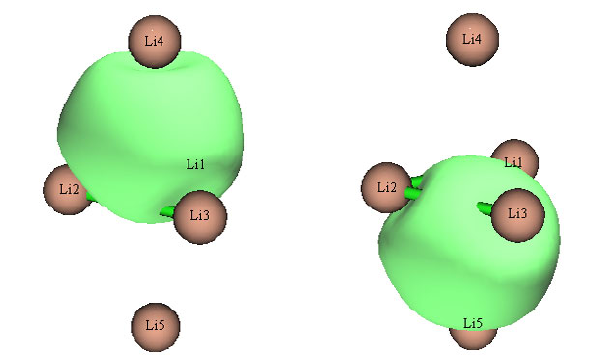
4 Tutorials and Examples
340
Grid data of AdNDP orbitals can be exported as Gaussian cube files by option 9, so that you
can draw them by some third-part visualization programs such as VMD. You need to input orbital
index range, assume that we want to output the two 4c-2e AdNDP orbitals we just found, we
should input 1,2, then they will be exported as AdNDPorb0001.cub and AdNDPorb0002.cub in
current folder.
By option 3, you can set the number of centers of multi-centers orbitals in the next exhaustive
search. So, assume that you have already known that there are two 4c-2e orbitals in present system,
you can directly choose option 3, input 4 and then select option 2 to start the exhaustive search of
4c-2e orbitals, the exhaustive searchs of 1c-2e, 2c-2e and 3c-2e orbitals will be skipped.
It is also possible to obtain energies of the AdNDP orbitals that have been picked out. To
realize this, you need to provide additional plain text file containing Fock matrix of present system
in lower-triangular sequence, so that orbital energies can be yielded after some transformations of
this matrix. The most straightforward procedure is as follows: Copy examples\Li5+.gjf as
examples\Li5+_47.gjf, change content between $NBO ... $END to archive file=C:\Li5+. Then
after running this file, C:\Li5+.47 will be yielded, which is input file of GENNBO program and
contains the Fock matrix that we need. Open this file by text editor, search $FOCK, and then copy
all data between $FOCK ... $END to a plain text file named Li5+_FOCK.txt. Then choose " 16
Output energy of picked AdNDP orbital" in the AdNDP analysis interface, input the path of
Li5+_FOCK.txt, Multiwfn will load it and immediately print out AdNDP orbital energies, as
shown below:
Energy of picked AdNDP orbitals:
Orbital: 1 Energy (a.u./eV): -0.325776 -8.8648
Orbital: 2 Energy (a.u./eV): -0.325776 -8.8648
As expected, the two orbitals are degenerate in energy, since they have exactly equivalent shape.
4.14.2 Analyze B11- cluster
This time, we will try to reproduce the AdNDP analysis result of B11- cluster that given in
AdNDP original paper (Phys. Chem. Chem. Phys., 10, 5207).
The files needed by this instance, namely B11-.out and B11-.fch can be found in
"examples\AdNDP" folder. The geometry was optimized under B3LYP/6-311+G*, while the
wavefunction was generated under HF/STO-3G level. You may wonder whether the result is
meaningful under such low level of basis-set, actually, AdNDP analysis is rather insensitive to
4 Tutorials and Examples
341
basis-set quality, even STO-3G is able to produce at least qualitative resonable result. In addition,
using larger basis set will bring additional cost at AdNDP analysis stage.
Boot up Multiwfn and input examples\AdNDP\B11-.out, then choose 14 to enter AdNDP
module. As usual, we select 2 to search 1c-2e orbitals first, but we find nothing (this is common
case). Then select 2 again to exhaustively search 2c-2e orbitals from the 11 atoms, Multiwfn will
totally try 11!/(11-2)!/2!=55 combinations, finally there are nine 2c orbitals present in candidate
list (sorted according to occupation number from large to small):
# 9 Occ: 1.9727 Atom: 6B 10B
# 8 Occ: 1.9727 Atom: 5B 11B
# 7 Occ: 1.9742 Atom: 7B 9B
# 6 Occ: 1.9742 Atom: 7B 8B
# 5 Occ: 1.9869 Atom: 2B 6B
# 4 Occ: 1.9869 Atom: 3B 5B
# 3 Occ: 1.9871 Atom: 9B 11B
# 2 Occ: 1.9871 Atom: 8B 10B
# 1 Occ: 1.9942 Atom: 2B 3B
All of them have occupation number close to 2.0, ostensibly one can directly pick all of them out
as AdNDP orbitals, however, it is not recommended to do so, because neighboring orbitals may
share the same densities. For example, the 1th and the 4th candidate orbitals share the some
densities, since both of them related to atom 3. In order to avoid overcount of electrons, firstly you
should pick out the first three orbitals by choosing option 0 and input 3, then the density of the
first three orbitals will be depleted from density matrix, after that wavefunction and occupation
number of remained candidate orbitals will be updated automatically. After that the candidate list
becomes
# 6 Occ: 1.9538 Atom: 6B 10B
# 5 Occ: 1.9538 Atom: 5B 11B
# 4 Occ: 1.9556 Atom: 7B 8B
# 3 Occ: 1.9556 Atom: 7B 9B
# 2 Occ: 1.9750 Atom: 2B 6B
# 1 Occ: 1.9750 Atom: 3B 5B
Since some densities have been depleted, occupation number of remained six candidate orbitals
slightly decreased. Now, we pick out the first four candidate orbitals by choosing option 0 and
input 4. Although both of 3th and 4th orbitals related to atom 7, here we have to ignore the slight
overcount of electrons, otherwise their degeneration will be broken and thus the final AdNDP
pattern will not be consistent with molecular symmetry anymore (you can choose option 8 to
carefully inspect candidate orbitals before you decide to pick them out). Finally, we pick out the
last two orbitals (6-10 and 5-11). Currently the number of residual valence electrons is 16.307, it
reveals that it is probable to find several higher number of centers orbitals with nearly two
electrons occupied.
Now we select option 2 to start the search of 3c-2e orbitals, the resulting candidate orbital list
is
# 9 Occ: 1.7399 Atom: 1B 6B 10B
# 8 Occ: 1.7399 Atom: 4B 5B 11B
# 7 Occ: 1.7502 Atom: 1B 3B 4B
4 Tutorials and Examples
342
# 6 Occ: 1.7502 Atom: 1B 2B 4B
# 5 Occ: 1.8504 Atom: 1B 2B 6B
# 4 Occ: 1.8504 Atom: 3B 4B 5B
# 3 Occ: 1.8603 Atom: 1B 4B 7B
# 2 Occ: 1.8673 Atom: 4B 9B 11B
# 1 Occ: 1.8673 Atom: 1B 8B 10B
After we pick out two orbitals (1-8-10 and 4-9-11), one orbital (1-4-7) and two orbitals (3-4-5
and 1-2-6) as AdNDP orbitals in turn, the highest occupation number of remained candidate
orbitals is 1.41, which is obviously too low to be recognized as 3c-2e orbital, so they will not be
concerned. Currently the number of residual valence electrons is 7.03.
Then you can start to search higher number of centers orbitals, however this is never a trivial
task, and there is no absolute rule on how to pick out candidate orbitals, different picking manners
result in diverse AdNDP patterns. You may have to try many times before obtaining an optimal
AdNDP pattern. It is recommended to use option 11 to save present density matrix and AdNDP
orbital list into memory, so that you needn't to worry about improperly picking out candidate
orbitals, since present state can be recovered anytime by choosing option 12.
Assumed that you didn't pick out any 4c orbital and have performed exhaustive search of 5c-
2e orbitals, you will find many 5c candidate orbitals whose occupation numbers are about 1.9.
Indeed they have qualifications to be picked out as AdNDP orbitals since their occupation number
is high, however it does not mean that picking them out is the best choice, since it is possible that
one can find higher nunber of centers orbitals with occupation numbers more closed to 2.0.
Canonical molecular orbitals (CMOs) sometimes are useful guidances on the search of multi-
centers orbitals. From CMO graph of B11- (see Fig. 6 in AdNDP original paper) we find there are
three globally delocalized π-orbitals, they may mixed with each other in some way to form 11c-2e
AdNDP orbitals. Therefore we choose option 3, input 11 and then choose option 2 to directly
search 11c orbitals. As expected, three orbitals present in candidate orbitals list with ideal double
occupation. After picking them out as AdNDP orbitals, the entire analysis process is finished. The
number of residual valence electrons is 1.03 currently, this value reflects the electrons that cannot
be fully represented by present AdNDP pattern (analogous to non-Lewis composition in NBO
language). By choosing option 5, information of all AdNDP orbitals can be printed out:
# 1 Occ: 1.9942 Atom: 2B 3B
# 2 Occ: 1.9871 Atom: 8B 10B
# 3 Occ: 1.9871 Atom: 9B 11B
# 4 Occ: 1.9750 Atom: 2B 6B
# 5 Occ: 1.9750 Atom: 3B 5B
# 6 Occ: 1.9556 Atom: 7B 9B
# 7 Occ: 1.9556 Atom: 7B 8B
# 8 Occ: 1.9337 Atom: 5B 11B
# 9 Occ: 1.9337 Atom: 6B 10B
# 10 Occ: 1.8673 Atom: 1B 8B 10B
# 11 Occ: 1.8673 Atom: 4B 9B 11B
# 12 Occ: 1.8533 Atom: 1B 4B 7B
# 13 Occ: 1.8451 Atom: 3B 4B 5B
# 14 Occ: 1.8451 Atom: 1B 2B 6B
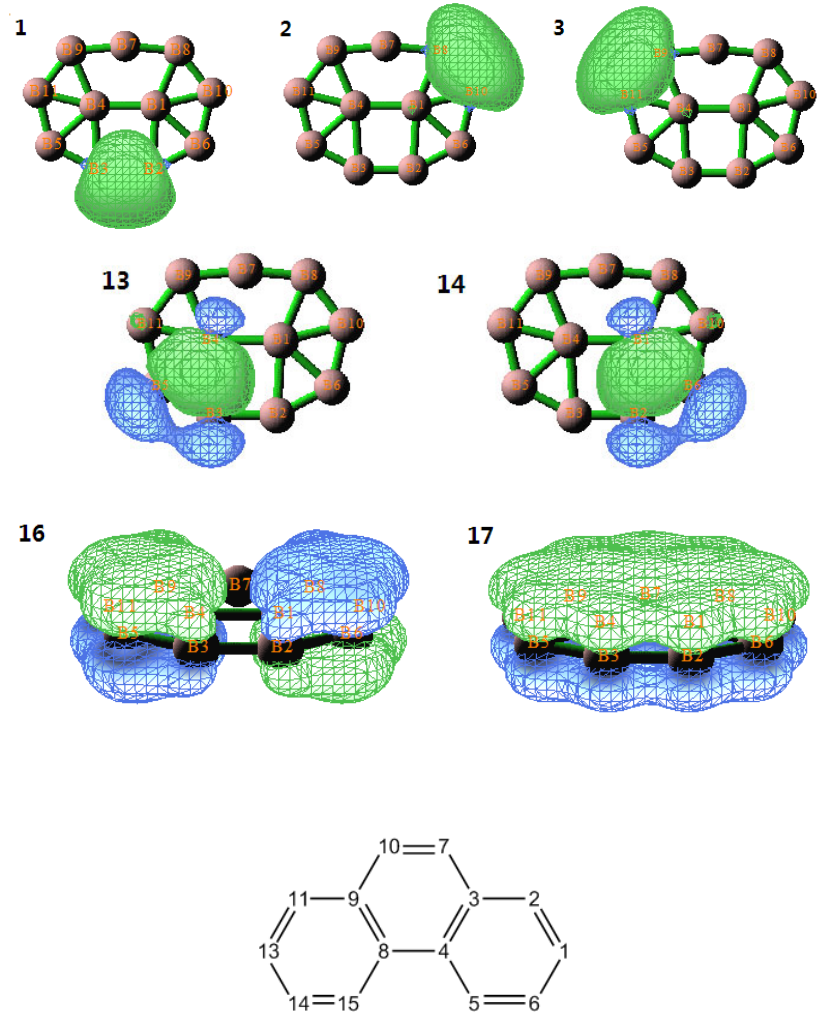
4 Tutorials and Examples
343
# 15 Occ: 2.0001 Atom: 1B 2B 3B 4B 5B 6B 7B 8B 9B
10B 11B
# 16 Occ: 2.0000 Atom: 1B 2B 3B 4B 5B 6B 7B 8B 9B
10B 11B
# 17 Occ: 1.9999 Atom: 1B 2B 3B 4B 5B 6B 7B 8B 9B
10B 11B
Total occupation number in above orbitals 32.9754
Isosurface of several selected 2c-2e, 3c-2e and 11c-2e AdNDP orbitals are shown below
(plotted by option 7), isovalue is set to 0.03.
4.14.3 Analyze phenanthrene
AdNDP analysis of phenanthrene (C14H10, see above) has been given in J. Org. Chem., 73,
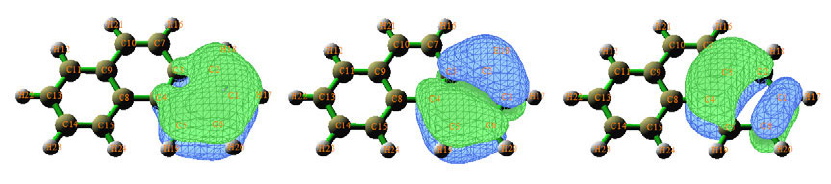
4 Tutorials and Examples
344
9251, in this section we will repeat their result, you will learn how to use user-directed search.
Files used in this example can be found in examples\AdNDP folder with phenanthrene prefix.
First we load examples\AdNDP\phenanthrene.out and enter main function 14. Consistent
with the previous examples, we select option 2 twice to search 1c orbitals and then search 2c
orbitals. No 1c-2e orbitals can be found, while there are 31 candidate 2c orbitals present in the list.
Ten of them correspond to C-H σ-bonds and have no overlapping with each other, so we can pick
them out first, namely choosing option 0, input 8,15, then choose option 0 again and input 9,10.
Next, we successively pick out sixteen 2c candidate orbitals that corresponding to C-C σ-bonds
(the most careful input is 0 2 0 1 0 2 0 1 0 2 0 2 0 2 0 2 0 2, where space denotes pressing ENTER
key). Then there are only five orbitals remain, the first orbital with occupation number of 1.80
corresponds to the π-bond between C7 and C10, it seems worth to be picked out. The occupation
numbers of the four remained orbitals are about 1.72, thus they are not ideal 2c-2e bonds, we do
not concern these five orbitals at the moment.
Although we can use option 2 to exhaustively search 3c, 4c, 5c ... orbitals as usual, however
this may be not a good idea for present system, user-directed search is often more effective. We
first choose option 13 to check population of residual electrons on each atom, see below, this
information is usually helpful for guiding users to properly set up exhaustive search list. (Note:
The exhaustive search triggered by option 2 is only applied to the atoms in exhaustive search list,
which contains all atoms in present system by default)
1C : 1.0250 2C : 1.0370 3C : 1.0280 4C : 1.0414
5C : 1.0339 6C : 1.0262 7C : 0.1322 8C : 1.0414
9C : 1.0280 10C : 0.1322 11C : 1.0370 12H : 0.0117
13C : 1.0250 14C : 1.0262 15C : 1.0339 16H : 0.0121
17H : 0.0113 18H : 0.0117 19H : 0.0126 20H : 0.0111
21H : 0.0121 22H : 0.0113 23H : 0.0111 24H : 0.0126
From above data it is clear that hydrogens have almost zero population numbers, hence they
could be safely removed from the exhaustive search list. Due to the same reason C7 and C10 can
be removed too. The other atoms, whose occupation numbers are about 1.03, are the carbons
composing the two 6-member rings in both sides of the molecule. It can be expected that the two
rings may be analogous to benzene ring and hence representing local aromaticity in phenanthrene.
Based on this consideration, we choose option -1 to enter the interface for defining exhaustive
search list, input clean to clean up the default content first, then input a 1-6 to add atom 1,2,3,4,5,6
into the list, and then input x to save and exit. Now the search list only contains carbon atoms in a
single ring. Select option 3 and input 6, then choose option 2 to search 6-centers orbitals in the
ring, three candidate orbitals will be found, whose occupation numbers are 2.000, 1.985 and 1.821
respectively, they are appropriate to be picked out as 6c-2e AdNDP orbitals, so we pick them out
now. Their 0.03 isosurfaces are shown below, which look like π molecular orbitals of benzene.
Next, with the same method, we define exhaustive search list as atoms 8,9,11,13,14,15 and
4 Tutorials and Examples
345
then search out the corresponding three 6c-2e orbitals, then finally pick them out. Now all AdNDP
orbitals (26*2c-2e, 6*6c-2e) have been found, the AdNDP analysis is finished.
With similar procedure, we evaluate AdNDP orbital energies like Section 4.14.1. The plain
text file containing Fock matrix of current molecule is directly provided as examples\
phenanthrene_FOCK.txt, which was yielded by examples\ phenanthrene_47.gjf. We choose option
16 and input the path of this file, Multiwfn immediately outputs the orbital energies:
...(ignored)
Orbital: 23 Energy (a.u./eV): -0.697578 -18.9821
Orbital: 24 Energy (a.u./eV): -0.697578 -18.9821
Orbital: 25 Energy (a.u./eV): -0.685803 -18.6616
Orbital: 26 Energy (a.u./eV): -0.685803 -18.6616
Orbital: 27 Energy (a.u./eV): -0.348201 -9.4750
Orbital: 28 Energy (a.u./eV): -0.255535 -6.9535
Orbital: 29 Energy (a.u./eV): -0.264372 -7.1939
Orbital: 30 Energy (a.u./eV): -0.348201 -9.4750
Orbital: 31 Energy (a.u./eV): -0.255535 -6.9535
Orbital: 32 Energy (a.u./eV): -0.264372 -7.1939
As you can see, the last six, which correspond to orbitals, have energy much higher than
orbitals. The three orbitals in left six-membered ring is symmetric to the counterpart three
orbitals in right six-membered ring. In each set, the highest two are nearly degenerate and
evidently higher than the lowest one, this situation is very similar to occupied orbitals of isolated
benzene.
Sometimes composition of AdNDP orbitals are interesting. In order to perform the analysis,
we select option 14 to output all of the 26+6=32 AdNDP orbitals as AdNDP.molden in current
folder, note that this step requests .fch file of present system. Our system has 146 basis functions,
so there are 146 orbitals in the .molden file, but only the first 32 orbitals correspond to the AdNDP
orbitals that we have found, the other orbitals are meaningless and should be simply ignored.
By using the AdNDP.molden as input file, you can use main function 8 to analyze the
composition of AdNDP orbitals. Some examples of orbital composition analysis can be found in
Section 4.8, related theoretical introductions can be found in Section 3.10. All orbital composition
analysis methods except for NAO method can be applied to AdNDP orbitals. For example, here
we analyze the composition of the 27th AdNDP orbital, namely the orbital at left side of above
graph. Boot up a new Multiwfn and input below command:
AdNDP.molden
8
1 // Mulliken analysis
27
Contribution of the six carbons in the ring are shown below, please compare the data with the
corresponding AdNDP orbital isosurface.
Atom 1(C ) : 33.144079%
Atom 2(C ) : 13.320911%
Atom 3(C ) : 1.585369%
4 Tutorials and Examples
346
Atom 4(C ) : 1.925742%
Atom 5(C ) : 15.297803%
Atom 6(C ) : 34.805871%
4.15 Fuzzy atomic space analysis
Delocalization index, PDI, FLU and FLU-π were originally proposed for AIM atomic space,
it has been shown that, if they are calculated in fuzzy atomic space, the computational cost would
be significantly reduced, while the results are still reasonable. The introduction of basic concepts
of fuzzy atomic space has been given in Section 3.18.0. In this section, we will calculate these
quantities in the fuzzy atomic space defined by Becke. Multiwfn also supports Hirshfeld and
Hirshfeld-I methods to defined atomic space, however, the Becke's definition has the advantage
that the calculation is independent on reference atomic densities, so we do not need to concern the
preparation of .wfn files for atoms in their free-states, and therefore the calculation procedure is
somewhat simpler.
4.15.1 Study delocalization index of benzene
The definition of delocalization index (DI) has been detailedly introduced in Section 3.18.5.
In present instance we will calculate DI in Becke's fuzzy atomic space to study the extent of
electron delocalization between different atom pairs in benzene. Notice that the original DI is
defined in Bader's AIM atomic space, so the DIs calculated in this example may somewhat differ
to the ones in some literatures.
Boot up Multiwfn, and input following commands
examples\benzene.wfn // Generated under B3LYP/6-311G*
15 // Fuzzy atomic space analysis
4 // Calculate localization index (LI) and DI. Multiwfn first makes use of DFT numerical
quadrature scheme to calculate atomic overlap matrix (AOM) in each fuzzy atom space, and then
convert AOM to DI and LI.
n // Do not output LI and DI to plain text file
Multiwfn automatically checks and output the error of AOM, for present calculation the error
is less than 0.001, which is completely negligible. If the error is too larger to be accepted, you can
set "iautointgrid" in settings.ini to 0, and set "radpot" and "sphpot" to a large value. When
"iautointgrid" is equal to 1, Multiwfn uses (40,230) grid points to calculate AOM, accuracy of
which directly affect the accuracy of LI, DI, as well as of PDI and FLU.
From the DI matrix outputted on the screen, we can see that DI between adjacent two carbon
atoms and adjacent C-H atoms are large (1.467 and 0.877, respectively), that means electron
delocalization between bonded atoms is strong, this is mainly due to the shared electron of σ bond.
In contrast, the DI between non-bonded carbon atoms is very small, about 0.1, nevertheless
evidently not zero, reflecting the high-degree delocalization nature of π electrons.
The DI calculated in fuzzy atomic space is essentially the fuzzy bond order proposed by
Mayer. According the DI data, we can say that the bond order between C-C bond and C-H bond in
benzene is 1.467 and 0.877 respectively, the former corresponds to single σ bond + "semi" π bond,

4 Tutorials and Examples
347
while the latter corresponds to typical single σ bond.
Since benzene is an exactly planar molecule, we can decompose DI to DI-σ and DI-π. Here
we calculate the latter. Input 0 to return to main menu, and then following commands
6 //Modify wavefunction
26 //Modify occupation number
0 // Select all orbitals
0 // Make occupation number of all orbitals to zero
17,20,21 // MO 17,20,21 correspond to π orbitals.
2 // Set their occupation numbers to 2 (close-shell orbitals)
q // Return to upper level of menu
-1 //Return to main menu
Now recalculate DI as before, since the occupation numbers of all orbitals except π orbitals
have been set to zero, the result will be DI-π.
The DI-π between C1-C6, C1-C5 and C1-C4 are 0.438, 0.055 and 0.093 respectively, it is
obvious that π electron delocalization is larger for para-related than for meta-related carbon atoms.
4.15.2 Study aromaticity of phenanthrene by PDI, FLU, FLU-π and
PLR
PDI, FLU, FLU-π and PLR are very useful aromaticity indices, their definitions have been
introduced in Section 3.18.6, 3.18.7 and 3.18.9. In present instance, we will calculate them in
Becke's fuzzy atom space to study aromaticity of different rings of phenanthrene.
We first calculate PDI. Boot up Multiwfn, and input following commands:
examples\phenanthrene.wfn // Optimized at B3LYP/6-31G* level
15 // Fuzzy atomic space analysis
5 // Calculate PDI
Then Multiwfn starts to calculate atomic overlap matrix (AOM), this is a computationally
intensive work. After that AOM will be converted to delocalization index (DI), then DI matrix will
be outputted on screen. Finally, you will be prompted to input atom indices of the ring you are
interested in, the input order should be in consistency with atomic connectivity. We first calculate
PDI of the central ring, namely input 4,8,9,10,7,3, the result is
4 Tutorials and Examples
348
Delocalization index of 4(C ) -- 10(C ): 0.053069
Delocalization index of 8(C ) -- 7(C ): 0.053069
Delocalization index of 9(C ) -- 3(C ): 0.036350
PDI value is 0.047496
PDI value is just the average of the DIs between C4-C10, C8-C7 and C9-C3. Now we input
8,9,11,13,14,15 to calculate PDI of the boundary ring, the result is 0.0817. From this result it is
evident that the electron delocalization in the boundary rings is stronger than in the central ring, so
boundary rings possess larger aromaticity. Next, we use FLU and FLU-π to study the aromaticity,
and check if we can draw the same conclusion.
Input q to return to upper level of menu, and input 6 to calculate FLU, then input 4,8,9,10,7,3
and 8,9,11,13,14,15 in turn. The FLU of central ring and of boundary rings are 0.025311 and
0.007537 respectively, this result suggests that the boundary rings is more like to typical aromatic
system (benzene), and hence possesses larger aromaticity than the central ring. Note that since the
AOM has already been calculated during calculating PDI, so this time the calculation process of
AOM is automatically skipped.
Next, input q to return to upper level of menu, and input 7 to calculate FLU-π. First you need
to input the indices of π orbitals. By visually checking isosurface of all orbitals (or utilizing option
22 in main function 100), we know that 36, 40, 43, 44, 45, 46, and 47 are π orbitals, so here we
input 36,40,43,44,45,46,47, then DI of π electrons will be outputted. After that you will be
prompted to input the atom indices in the ring, we input 4,8,9,10,7,3 and 8,9,11,13,14,15 in turn.
The FLU-π of central ring and boundary rings are 0.149288 and 0.035037, respectively. Obviously,
FLU-π analysis also confirms that boundary ring is more aromatic.
Finally, let's calculate para linear response index (PLR). PLR is based on linear response
kernel, which relies on virtual MOs information; however .wfn file only contains occupied MOs,
therefore we must use .fch/.molden/.gms file as input. Reboot Multiwfn and input following
commands
examples\phenanthrene.fch // Obtained at the same level as phenanthrene.wfn
15
10 // Calculate PLR
Multiwfn will calculate condensed linear response kernel (CLRK) matrix, after that input
4,8,9,10,7,3 and 8,9,11,13,14,15 in turn, the result is 0.247848 and 0.489434, respectively. Since
the former is much smaller than the latter, PLR also validates the conclusion that boundary rings
have larger aromaticity than central ring.
Note that both PDI and PLR can be separated as and π parts to respectively investigate
and π aromaticity, see Section 3.18.6 and 3.18.9 for detail.
4.16 Charge decomposition analysis and plotting orbital
interaction diagram
The theoretical background of charge decomposition analysis (CDA, J. Phys. Chem., 99,
9352), extended CDA (J. Am. Chem. Soc., 128, 278), and general CDA (GCDA, J. Adv. Phys.
Chem., 4, 111-124 (2015)), as well as usage of CDA module of Multiwfn have been detailedly
introduced in Section 3.19. In this section I present several practical examples.

4 Tutorials and Examples
349
The CDA module of Multiwfn supports Gaussian output file, .fch file, Molden input file
(.molden) and GAMESS-US output file (.gms) as input. If the calculation conditions are identical,
they will give rise to the same CDA result. In the next severals sections only Gaussian .fch files
will be used to exemplify the usage of the CDA module.
4.16.1 Close-shell interaction case: COBH3
In COBH3, CO makes use of its lone pair to form coordinate bond with BH3, which is an
electron-deficient system (Lewis acid). Therefore, electrons will transfer from CO to BH3 during
the formation of the complex. In this example we will employ CDA scheme to provide a deeper
insight on the electron transfer.
First we generate Gaussian output file for CO (fragment 1), BH3 (fragment 2) and COBH3
(complex). The .fch files and corresponding input files have been provided in
"examples\CDA\COBH3" folder. The calculations were performed at HF/6-31G* level. On how to
prepare the input files for CDA, see Section 3.19.2 for detail
Now boot up Multiwfn, and input following contents:
examples\CDA\COBH3\COBH3.fch // Gaussian .fch file of the complex
16 // Enter CDA module
2 // We define two fragments
examples\CDA\COBH3\CO.fch // Gaussian .fch file of fragment 1
examples\CDA\COBH3\BH3.fch // Gaussian .fch file of fragment 2
Immediately, below CDA result will be outputted on screen
Orb. Occ. d b d - b r
1 2.000000 -0.000004 -0.000000 -0.000004 -0.000001
2 2.000000 0.001119 -0.000023 0.001141 0.000326
3 2.000000 -0.000002 -0.000471 0.000469 0.000313
4 2.000000 -0.013250 -0.000704 -0.012546 -0.005676
5 2.000000 0.041648 -0.003309 0.044957 0.232262
6 2.000000 0.037385 -0.020136 0.057521 0.212422
7 2.000000 -0.000543 0.000647 -0.001190 0.022166
8 2.000000 -0.000543 0.000647 -0.001190 0.022166
9 2.000000 0.171353 0.026952 0.144401 -0.741381
10 2.000000 -0.000569 0.043713 -0.044281 -0.038916
11 2.000000 -0.000569 0.043713 -0.044282 -0.038916
12 0.000000 0.000000 0.000000 0.000000 0.000000
13 0.000000 0.000000 0.000000 0.000000 0.000000
14 0.000000 0.000000 0.000000 0.000000 0.000000
15 0.000000 0.000000 0.000000 0.000000 0.000000
......
-------------------------------------------------------------------
Sum: 22.000000 0.236023 0.091027 0.144996 -0.335233
"Orb." denotes the indices of the orbitals of the complex; "occ." is corresponding occupation
number. "d(i)" stands for the amount of donated electrons from fragment 1 to 2 via corresponding
complex orbital, "b(i)" stands for the amount of electrons back donated from fragment 2 to 1 via
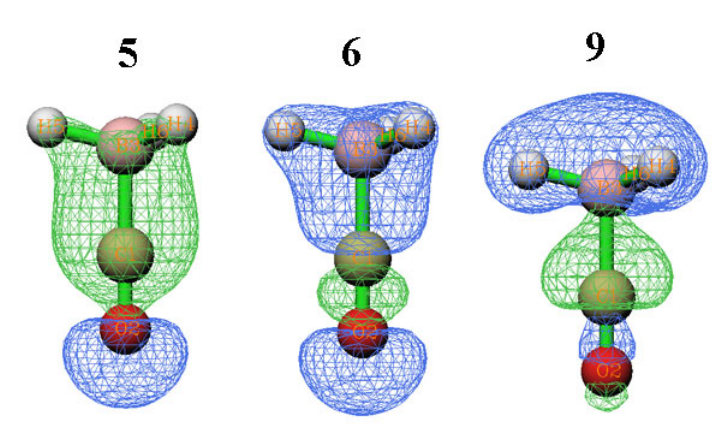
4 Tutorials and Examples
350
corresponding complex orbital. "r(i)" corresponds to the overlap population between the occupied
fragment orbitals (FOs) of the two fragments in corresponding complex orbital; its positive and
negative signs imply that in this complex orbital, the electrons of occupied FOs are accumulated to
and depleted (mainly due to Pauli repulsion) from the overlap region between the two fragments,
respectively. The sum of r(i), namely -0.335, reveals that repulsive effect dominates the overall
interaction between occupied FOs, which results in corresponding electrons moved away towards
nonoverlapping regions from overlap regions.
The difference between d(i) and b(i), to some extent can be viewed as the number of net
transferred electrons from fragment 1 to 2 due to formation of corresponding complex orbital. But
bear in mind, electron polarization effect is also included into this value.
From the data, it can be seen that the first three complex orbitals have almost zero b, d and r
values, this is because they are core orbitals of O, C and B, respectively, and hence it can be
expected that they are not involved in bond formation. The virtual complex orbitals have exactly
zero b, d and r terms, since their occupation numbers are exactly zero. Orbital 9 leads 0.171
electrons donate from CO to BH3, which is the primary source of the donor-acceptor bonding, and
causes as high as 0.741 electrons removed from overlap region between CO and BH3, which
stabilized the complex by diminishing electron repulsion. Orbital 5 and 6 have small contributions
to electron donation, meanwhile lead evident accumulation of electrons from respective occupied
FOs to the overlap region, which must be beneficial to the bonding between the two fragments.
Orbital 10 and 11 are π orbitals and degenerate in energy, they exhibit π-back donation
characteristics.
Isosurfaces of orbital 9, 5 and 6 are shown below. As you can see, a node occurs in the
overlap region between CO and BH3 in orbital 9, while the isosurfaces of orbital 5 and 6
uniformly cover the overlap region. These observations largely explained why r(9) is a large
negative value, and r(5) and r(6) are obvious positive values.
Notice that the definition of CDA used in Multiwfn is a generalized version proposed by me,
so that CDA is also applicable to post-HF and open-shell circumstances, see corresponding part of
Section 3.19.1 for detail. For the cases when original CDA is applicable (namely MO for FO, MO
or natural orbital for complex orbital), the d and b terms produced by generalized CDA are exactly
4 Tutorials and Examples
351
identical to the ones produced by original definition, while the r term is exactly twice of the one
produced by original definiton.
Note: The COBH3 example was also given in original paper of CDA, in which, althought the formulae of d, b
and r are correct, the data in their examples are incorrectly: all of the data should be divided by two. I also found
that all of the results of the CDA program written by Dapprich and Frenking (http://www.uni-marburg.de/fb15/ag-
frenking/cda), and the results of AOMix program (http://www.sg-chem.net) should be divided by two. So, if you
want to compare the CDA results calculated by Multiwfn with theirs, the d and b terms should be multiplied by
two first. But do not do this for r term, since the r term computed by Multiwfn has already been doubled with
respect to its original definition.
The amount of net electron transfer between the two fragments can be characterized by b-d
term, however it was argued that ECDA is a more reasonably method to calculate the amount of
net electron transfer, since the contribution of electron polarization effect (PL) is completely
excluded. ECDA result is outputted after CDA result:
========== Extended Charge decomposition analysis (ECDA) ==========
Contribution to all occupied complex orbital:
Occupied, virtual orbitals of fragment 1: 680.4194% 8.0593%
Occupied, virtual orbitals of fragment 2: 390.3988% 21.1226%
Contribution to all virtual complex orbital:
Occupied, virtual orbitals of fragment 1: 19.5806% 2291.9407%
Occupied, virtual orbitals of fragment 2: 9.6012% 1678.8774%
PL( 1) + CT( 1-> 2) = 0.3916 PL( 1) + CT( 2-> 1) = 0.1612
PL( 2) + CT( 1-> 2) = 0.4225 PL( 2) + CT( 2-> 1) = 0.1920
The net electrons obtained by frag. 2 = CT( 1-> 2) - CT( 2-> 1) = 0.2304
Commonly, you only need to pay attention to the last line. The data shows that the net
number of electrons transferred from fragment 1 to 2 is 0.2304.
In the menu that appears on screen, by using option 2, composition of FOs in a specific
complex orbital can be outputted. Here we select this option and input 9, the composition of
complex orbital 9 are shown below
Occupation number of orbital 9 of the complex: 2.00000000
Orbital 7 of fragment 1, Occ: 2.00000 Contribution: 25.8560%
Orbital 13 of fragment 1, Occ: 0.00000 Contribution: 1.0798%
Orbital 2 of fragment 2, Occ: 2.00000 Contribution: 57.2921%
Orbital 5 of fragment 2, Occ: 0.00000 Contribution: 14.5640%
Only the FOs with contribution 1% to the complex orbital are shown (the threshold can be
altered by "compthresCDA" in settings.ini). As already mentioned, the electron transfer from CO
to BH3 is mainly due to the complex orbital 9, therefore from above data we can infer that the
nature of the CO→BH3 electron transfer can be largely interpreted as the mix between FO 7 of CO
(an occupied orbital) and FO 5 of BH3 (a virtual orbital). This viewpoint can also be manifested by
comparing the shape of the two FOs (see below) with the shape of complex orbital 9 given above.
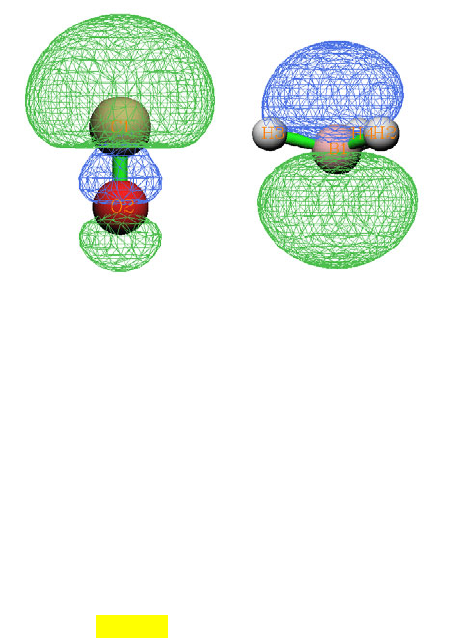
4 Tutorials and Examples
352
Note: Sometimes a few contributions of FOs may be negative, this is a well-known drawback of Mulliken
analysis, which is the method employed in CDA module to calculate the complex orbital composition. Since the
magnitudes of the negative values are often small, you can simply ignore them.
We can also directly decompose d, b, r terms of a complex orbital to FO pair contributions,
let's do this for complex orbital 9. Now input 0 to return to the last menu, select option 6 and input
9, then input a threshold e.g. 0.005, then all FO pairs whose contribution to any of d, b, r term
larger than 0.005 are printed:
FragA Orb(Occ.) FragB Orb(Occ.) d b d - b r
4( 2.0000) 2( 2.0000) 0.000000 0.000000 0.000000 -0.009969
7( 2.0000) 1( 2.0000) 0.000000 0.000000 0.000000 -0.005759
7( 2.0000) 2( 2.0000) 0.000000 0.000000 0.000000 -0.723845
7( 2.0000) 5( 0.0000) 0.176503 0.000000 0.176503 0.000000
7( 2.0000) 8( 0.0000) 0.006221 0.000000 0.006221 0.000000
7( 2.0000) 11( 0.0000) 0.005846 0.000000 0.005846 0.000000
7( 2.0000) 12( 0.0000) -0.023941 0.000000 -0.023941 0.000000
13( 0.0000) 2( 2.0000) 0.000000 0.021958 -0.021958 0.000000
From the output it is clear that the mix between FO 7 of CO and FO 5 of BH3 contributes most of
the d term of complex orbital 9.
Finally, we plot orbital interaction diagram. Input 0 to return to the last menu, and then select
5 to enter the menu for plotting orbital interaction diagram. Choose option 3 and input -30,10 to
set lower and upper energy limits of the plot to -30eV and 10eV, respectively. Then select option 1
to plot the diagram under default settings, a graph will pop up on screen:
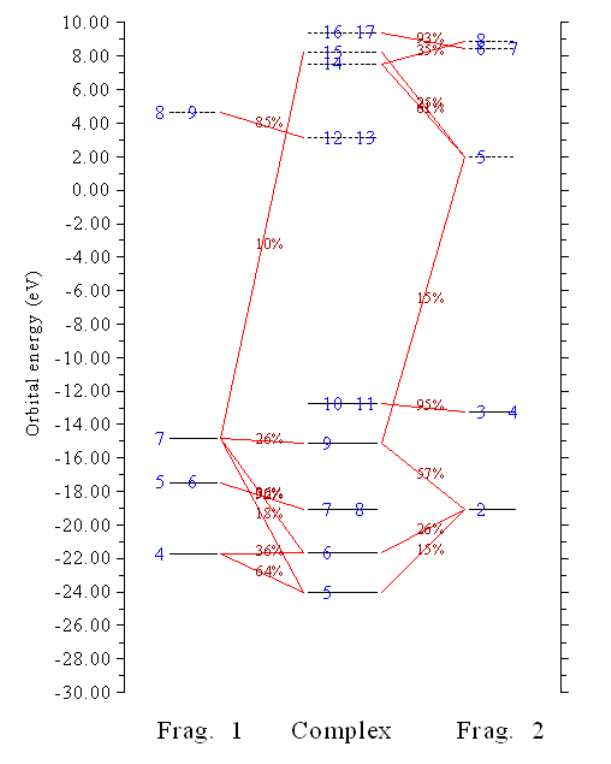
4 Tutorials and Examples
353
In above graph, occupied and virtual orbitals are represented as solid and dashed bars,
respectively. Orbital indices are labelled by blue texts. If two or more labels occur in the same bar,
e.g. 7 and 8, that means these orbitals are degenerate in energy. If composition of a FO in a
complex orbital is larger than 10%, then the corresponding two bars will be linked by red line, and
the composition will be labelled on the lines. By simply viewing the diagram we can directly
understand how the MOs of COBH3 are constructed by FOs of CO and BH3. For example,
complex orbital 7 and 8 only link to FO 5 and 6 of CO in this diagram, hence we immediately
know that these two orbitals basically remain unperturbed during formation of the complex. In
fact they are π orbitals of CO, certainly they cannot participate to the σ type donor-acceptor
interaction between CO and BH3.
There are many options used to adjust plotting parameters (such as label size, the rule for
drawing and linking bars, position of composition labels, energy range), please play with them,
and replot the graph to check their effects.
4.16.2 Open-shell interaction case: CH3NH2
In this example, I use CH3NH2 to illustrate how to perform CDA for the complex in which
the two fragments interact with each other covalently (open-shell interaction).
First we need to generate Gaussian output file for CH3 (fragment 1), NH2 (fragment 2) and
CH3NH2 (complex). For fragment 1 and 2, in present example we use unrestricted B3LYP method;
4 Tutorials and Examples
354
while for the complex, since this is a close-shell system, we use restricted B3LYP method
(unrestricted B3LYP can also be used, the CDA result will be the same). The .fch files and
corresponding input files can be found in "examples\CDA\CH3NH2" folder, the geometry was
pre-optimized under B3LYP/6-31G** level.
Note that both CH3 and NH2 have 5 alpha and 4 beta electrons, while CH3NH2 has 9 alpha
and 9 beta electrons. Evidently, the total numbers of alpha and beta electrons in the two fragments,
namely 5+5 and 4+4, does not match the ones of the complex. So, we must flip electron spin of
one fragment (either CH3 or NH2). In this example, we will flip electron spin of NH2, i.e.
exchanging all information of its alpha and beta electrons.
Boot up Multiwfn and input following contents:
examples\CDA\CH3NH2\CH3NH2.fch // Gaussian output file of the complex
16 // Enter CDA module
2 // We define two fragments
examples\CDA\CH3NH2\CH3.fch // Gaussian output file of fragment 1
examples\CDA\CH3NH2\NH2.fch // Gaussian output file of fragment 2
n // Do not flip electron spin of fragment 1
y // Flip electron spin of fragment 2, then NH2 will have 4 alpha and 5 beta electrons.
CDA and ECDA results will be calculated and printed on screen for alpha electrons and beta
electrons separately. As you can see, for alpha (beta) part, both d - b and CT(1->2) - CT(2->1)
terms are positive (negative), showing that alpha (beta) electrons are tranferred from CH3 to NH2
(from NH2 to CH3). This is mainly because CH3 has more alpha electrons (5) than beta electrons
(4), while after flipping electron spin, NH2 has more beta electrons (5) than alpha electrons (4),
hence when they combine together to form CH3NH2, CH3 prefer to donate alpha electrons to NH2
and accept beta electrons from NH2.
Result of total electrons, namely the sum of alpha and beta results are also outputted. Below
is total result of CDA and ECDA, respectively
d= 0.044335 b= 0.145181 d - b = -0.100847 r= -0.172318
CT( 1-> 2) - CT( 2-> 1) for all electrons: 0.1252
It is obvious that electron should transfer from CH3 to NH2, because nitrogen has evidently
larger electronegativity. The total ECDA result is in line with our expectation, it shows that the
amount of transferred electrons from CH3 to NH2 is 0.1249. However, the d - b term conflicts with
our expectation, the transfer direction is totally inverted. This example illustrates that d - b term is
not as reliable as ECDA to reveal total amount of net electron transfer for open-shell interaction,
although d and b terms are still quite useful for decomposing electron tranfer into orbital
contributions.
If you select to flip electron spin for CH3 rather than for NH2 when loading their Gaussian
output files, you will see the alpha and beta results of CDA and ECDA are exchanged, but the
result for total electrons remains unchanged.
Now select 2 and input 6, you will see both the composition of the 6th alpha orbital and the
6th beta orbital of the complex are printed on screen. Though the complex is a close-shell system
and thus the two orbitals are essentially the same, owing to the alpha and beta FOs in the two
fragments are not equivalent, the printed compositions have slight difference. Then input 0 to
return.
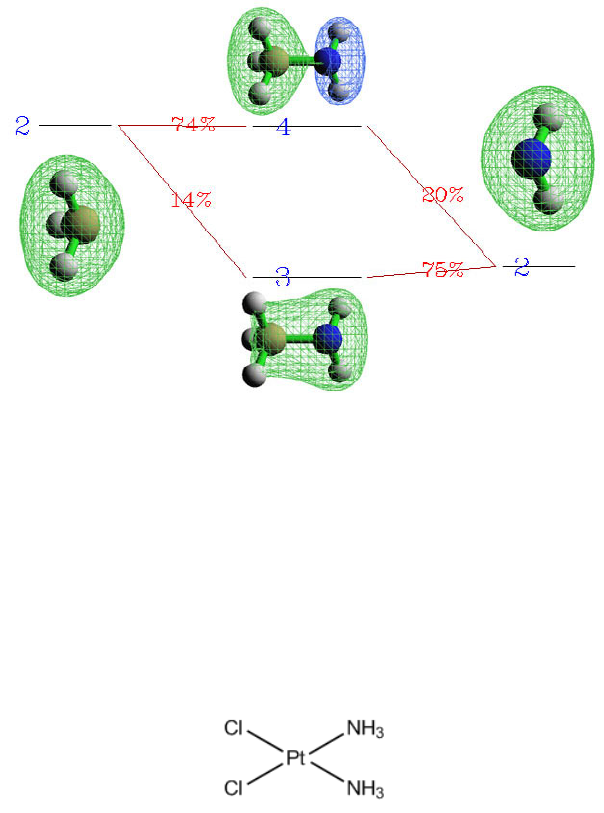
4 Tutorials and Examples
355
Select option 5 to enter the menu for plotting orbital interaction diagram. By option 5 in the
menu, you can control for which set of spin-space orbitals the diagram will be plotted. We select it
once to switch the status to "Beta". Then select option 1 to plot the orbital interaction diagram.
From the graph it is very clear that, beta orbital 3 and 4 of CH3NH2 are formed by mixing beta FO
2 in CH3 and beta FO 2 in NH2. To illustrate this point more intuitively, corresponding part is
extracted from the whole diagram, and the orbital isosurfaces are attached on it, see below
It can be seen that, beta complex orbital 3 shows bonding character (this is why r(3) is a
positive value, namely 0.103), which is constructed by slightly mixing beta FO 2 of CH3 into beta
FO 2 of NH2 with the same wavefunction phase. Beta complex orbital 4 is an anti-bonding orbital
(this explained why r(4) is a negative value, namely -0.056), formation of which is due to the
mixture of beta FO 2 of NH2 into beta FO 2 of CH3 in terms of different phase.
4.16.3 More than two-fragments case: Pt(NH3)2Cl2
In this section I use cisplatin (see below) as instance to show how to perform CDA analysis
on the system consisting of more than two fragments.
We will define Pt2+ cation, (Cl2)2- anion and (NH3)2 as fragment 1, 2 and 3 respectively. This
definition of fragments is the best choice for present system. Note that the Pt2+ cation is in 3d8
low-spin configuration, so that all fragments are in closed-shell status and thus we will not need to
analyze alpha and beta spins separately.
The related Gaussian input files and resulting .fch files have been provided in
examples\CDA\Pt(NH3)2Cl2 folder. Lanl2DZ pseudo-potential basis set was used for Pt, cc-
pVDZ was used for other atoms. B3LYP functional was chosen as the theoretical method. The
geometry of the complex has already been optimized. In the input file of Pt2+, "scf=xqc" keyword
was used to solve the unconvergence problem, but this is not needed in general.
Note 1: For certain types of basis-sets, such as Pople series of basis-sets (e.g. 6-31G*), by default Gaussian
employs Cartesian type basis functions rather than spherical-harmonic basis functions, which may results in
inconsistency problem of basis set between complex and fragment calculations. If you are not very familiar with
Gaussian, I highly recommend you always add "5d 7f" keyword in all Gaussian input files when mixed basis set is
used in the calculation of the complex.

4 Tutorials and Examples
356
Note 2: The sequence of the fragments is crucial. Because in the input file of complex, the atomic sequence is
Pt--Cl2--(NH3)2, we should not for example define Pt2+, (NH3)2 and (Cl2)2- as fragment 1, 2 and 3, respectively.
Now boot up Multiwfn and input:
examples\CDA\Pt(NH3)2Cl2\Pt(NH3)2Cl2.fch // Complex
16 // Enter CDA module
3 // We define three fragments
examples\CDA\Pt(NH3)2Cl2\Pt.fch // Fragment 1
examples\CDA\Pt(NH3)2Cl2\Cl2.fch // Fragment 2
examples\CDA\Pt(NH3)2Cl2\(NH3)2.fch // Fragment 3
Then choose option 0 and input 1,2 to output CDA analysis result for fragment pair 1-2.
Similarly, we get the CDA result for fragment pair 1-3 and 2-3. We cannot obtain ECDA result for
present system because ECDA is only applicable to two-fragment cases. The total CDA results are
summarized below.
1-2 1-3 2-3
d 0.0017 0.0538 0.0538
b 0.5156 0.0071 0.0071
d-b -0.5139 -0.0467 0.0467
r 0.0581 -0.1415 -0.1415
The table shows that there are 0.5156 and 0.0071 net electrons transferred from (Cl2)2- and
(NH3)2 to Pt2+, respectively. Basically no electrons are donated from Pt2+ to its ligands. This result
is in line with our chemical intuition because according to classical theory, the electrons of
coordinate bonds are purely contributed from ligands. The charge transferation between (Cl2)2- and
(NH3)2 is trivial, mainly due to there is no direct chemical interaction between them. Note that the
r term between fragment 2 and 3 is a small but non-negligible negative value, exhibiting that there
is detectable electron repulsion effect between the ligands.
Deeper analyses on this system are left for you. You can discuss orbital contribution to charge
transferation based on the detail output of CDA analysis, use option 2 to study the composition of
complex orbital in fragment orbital basis, and use option 5 to plot orbital interaction diagram.
4.17 Basin analysis
Below I will show how to use basin analysis module of Multiwfn to perform basin analysis
for several molecules and for various real space functions. Related theory, numerical algorithms
and the usage of this module have been detailedly introduced in Section 3.20. If you are not
familiar with the concept of basin, please consult Section 3.20.1 first. While if you want to know
more detail about basin analysis, please concult Sections 3.20.2 and 3.20.3.
You should know that Multiwfn uses a grid-based method (in particular, near-grid method) to
locate attractors, generate and integrate basins; in other words, most tasks realized in the basin
analysis module rely on grid data. This is why in below sections "grid data" is frequently
mentioned.
4 Tutorials and Examples
357
4.17.1 AIM basin analysis for HCN
In this example we will analyze the basins of total electron density (also known as AIM
basins) for HCN molecule. After you finished it you will understand most of the basic operations
of the basin analysis module in Multiwfn.
Generate basins and locate attractors
Boot up Multiwfn and input following commands
examples\HCN.wfn
17 // Basin analysis
1 // Generate basins and locate attractors
1 // The grid data to be calculated and thus analyzed is for electron density
2 // Medium quality grid. This is enough for most cases, if you want to obtain a better result,
you can choose "High quality grid", but much more computational time will be spent
Multiwfn now starts to calculate grid data for electron density, and then generates basins and
locates attractors based on the grid data; soon you will see attractor information, as shown below
(notice that the attractor sequence may be different to your actual case if parallel mode is enabled,
similarly hereinafter):
Attractor X,Y,Z coordinate (Angstrom) Value
1 -0.02645886 -0.02645886 -1.52058663 0.33959944
2 0.02645886 0.02645886 -0.51514986 49.48609717
3 -0.02645886 -0.02645886 0.64904009 76.55832377
From now on you can check the information of the located attractors anytime by option -3.
Visualization of basins and attractors
Now choose 0 to visualize the basins and attractors. The purple labels indicate the index of
the located attractors. Since attractors of electron density are very close to nuclei, if you want to
see them, you should deselect "Show molecule" check box first. Here we select 1 from the basin
list at the right-bottom corner, the basin corresponding to attractor 1 will be immedately shown.
By default only interbasin part of the basin is shown, if you want to inspect the whole basin you
should select "Show basin interior" checkbox. After we select it, the GUI will look like below:
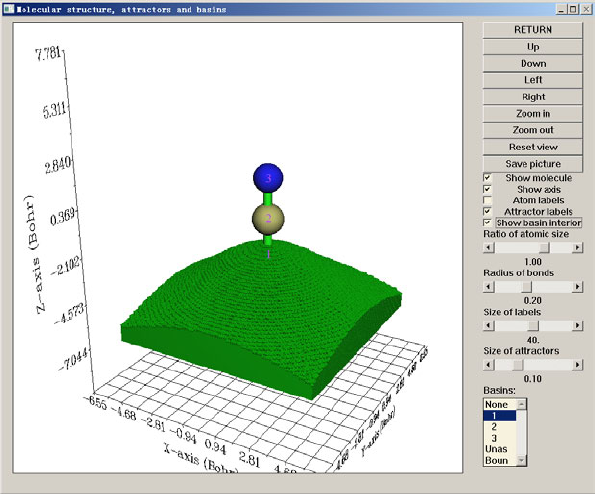
4 Tutorials and Examples
358
Now click "RETURN" button to close the GUI.
Hint: If you are not satisfied with the graph shown in the Multiwfn GUI, you can choose function -4 to export
the attractors as .pdb file, and choose option -5 to export the basins as cube file, then you can easily plot them in
your favourite visualization software such as VMD. The isosurface representing the basin can be visualized by
plotting an isosurface with isovalue of 0.5. Note that When Multiwfn asking you "If output internal region of the
basin?", if you input "n" rather than "y", only interbasin surface will be shown when you plotting the isosurface.
You may have noticed below statements in command-line window
The number of unassigned grids: 0
The number of grids travelled to box boundary: 0
Commonly the number of these two types of grid should be zero, only in rare cases they are not
zero; in such cases, you can visualize them by respectively selecting "Unas" and "Boun" in the
basin list of the GUI. These grids do not belong to any basin, and generally they lack of physical
meaning; to understand when and why they occur please consult Section 3.20.2.
Integrating basins
Next, we calculate the integral of electron density (electron population number) in these
basins. Select function 2, then you will see many options. Each option with the serial >= 1
corresponds to a real space function; if you select one of them, corresponding real space function
will be integrated in the generated basins. In present example we can select option 1, which
corresponds to electron density. However, since we have already calculated grid data for electron
density, and the grid data of electron density thus have been stored in memory, we can directly use
it rather than recompute it again to reduce computational time, so here we select option 0 to use
"The values of the grid data stored in memory".
Since electron density at the grids is not needed to be re-evaluated, the integrals are outputted
immediately:
#Basin Integral(a.u.) Volume(a.u.^3)
1 0.7356142812 441.70000000
2 5.3511723358 566.84900000
3 7.9020047534 829.72600000
4 Tutorials and Examples
359
Sum of above values: 13.98879137
There should be totally 1+6+7=14 electrons in present system; unfortunately the sum of the
integrals of electron density is 13.98879, which evidently deviates from the ideal value!
Because the basin we are studying is AIM basin, the best choice to obtain the basin integral is
using function 7 rather than function 2. In function 7, mixed atomic-center and uniform grid is
used, while function 2 only employs uniform grid to integrate. We input:
7 // Integrate real space functions in AIM basins with mixed type of grids
1 // Integrate a specific function with atomic-center + uniform grids
1 // Select electron density as the integrand
The result is
#Basin Integral(a.u.) Vol(Bohr^3) Vol(rho>0.001)
1 0.7356461193 441.700 34.884
2 5.3552283604 566.849 102.832
3 7.9086490986 829.726 134.228
Sum of above integrals: 13.99952358
Sum of basin volumes (rho>0.001): 271.944 Bohr^3
As you can see, the sum of the integrals of electron density (13.9995) is almost exactly
identical to the expected value 14.0, obviously the result is much better than using function 2. The
basin volumes are also outputted. The terms "vol(Bohr^2)" do not have clear physical meaning,
since they are directly affected by the spatial range of grid setting. However, the terms
"vol(rho>0.001)" are useful, they exhibit the volume of the basin enclosed by the isosurface of
electron density > 0.001 (Bader's vdW surface) and thus can be regarded as atomic sizes.
The atomic charge (AIM charge) of these atoms and their volumes are also outputted
1 (C ) Charge: 0.644589 Volume: 102.832 Bohr^3
2 (N ) Charge: -0.908918 Volume: 134.228 Bohr^3
3 (H ) Charge: 0.264329 Volume: 34.884 Bohr^3
Note that above AIM charges are inaccurate! To obtain more accurate integrals in AIM basins,
you should select 2 or 3 in function 7, compared to 1, they will refine the assignment of basin
boundary to improve the integration result, but additional computational cost must be afforded.
Here we try it, select option 2 in function 7, then input 1, the result is
1 (C ) Charge: 0.748979 Volume: 100.160 Bohr^3
2 (N ) Charge: -1.003917 Volume: 136.304 Bohr^3
3 (H ) Charge: 0.254938 Volume: 35.480 Bohr^3
Although the sum of the integral of electron density is still 13.9995, the charge of the atoms
are somewhat varied (more accurate than before).
To further improve the integration accuracy, when generating basins one should select a grid
setting better than "medium quality grid", e.g. "High quality grid" or even "Lunatic quality grid".
But bear in mind that for large systems, "high quality grid" (or a better one) may consumes very
large amount of computational time and memory.
Although as we have seen the integration accuracy of function 7 is much better than function
2, the former is only applicable to AIM basins, while the latter can be used for any type of basin
(e.g. ELF basin).
Note: If you used option 2 or 3 in function 7, during the bounary grid refinement process, the assignment of
basin boundary will be updated permanently, that means the result of later analysis (e.g. calculating LI/DI, electric
multipole moment) will become more accurate.
4 Tutorials and Examples
360
Hint: In summary, the general steps for obtaining reliable AIM charges after you entered
basin analysis module is
1 // Generate basin
1 // Electron density
2 // Medium quality grid. Select high quality grid if you wish to get more accurate result
7 // Integrate real space functions in AIM basins with mixed type of grids
2 // Integrate and meanwhile refine basin boundary
1 // Electron density
Calculate electric multipole moments in basins
Enter function 8 to calculate electric multipole moments in the AIM basins (you can also use
3 to do this, but the accuracy is much lower). Only the result for carbon is pasted below
Result of atom 1 (C )
Basin electric monopole moment: -5.250849
Basin electric dipole moment:
X= 0.000003 Y= 0.000003 Z= 1.095846 Magnitude= 1.095846
Basin electron contribution to molecular dipole moment:
X= 0.000003 Y= 0.000003 Z= 6.026238 Magnitude= 6.026238
Basin electric quadrupole moment (Cartesian form):
QXX= -0.759571 QXY= 0.000000 QXZ= -0.000002
QYX= 0.000000 QYY= -0.759571 QYZ= -0.000002
QZX= -0.000002 QZY= -0.000002 QZZ= 1.519142
The magnitude of electric quadrupole moment (Cartesian form): 1.519142
Electric quadrupole moments (Spherical harmonic form):
Q_2,0 = 1.519142 Q_2,-1= -0.000002 Q_2,1= -0.000002
Q_2,-2= 0.000000 Q_2,2 = 0.000000
Magnitude: |Q_2|= 1.519142
The formulae used to evaluate these terms are basically identical to the ones given in Section
3.18.3, the only differences are that in that formulae the nuclear positions should be replaced by
attractor positions, and the ranges of integration should be basins rather than fuzzy atomic spaces.
The electric monopole moment (-5.251) is just the negative value of electron population
number in the basin. Z-component of electric dipole moment of the basin is a positive value
(1.096), suggesting that in basin 2, most of electrons are distributed in the regions where Z-
coordinate is more negative than attractor 2. The ZZ-component of basin electric quadrupole
moment is positive (1.519), while the other diagonal components are negative, indicating that
relative to attractor 2, electron cloud in this basin contracts in Z-direction but elongates in other
directions.
Calculate localization index and delocalization index in basins
Delocalization index (DI) is a quantitative measure of the number of electrons delocalized (or
say shared) between two regions, while localization index (LI) quantitatively measures how many
electron are localized in a region. For details about LI and DI please see Section 3.18.5. The only
difference relative to the statements in that section is that here the LI and DI will be calculated
4 Tutorials and Examples
361
based on basins rather than based on fuzzy atomic spaces.
Enter function 4, Multiwfn will start to calculate LI and DI, then you will see:
************ Total delocalization index matrix ************
1 2 3
1 0.97290584 0.90037928 0.07252656
2 0.90037928 3.49303345 2.59265416
3 0.07252656 2.59265416 2.66518072
Total localization index:
1: 0.259 2: 3.496 3: 6.658
Since present molecule is a close shell system, only total LI and DI are outputted, the LI and
DI for and electrons are not outputted separately. As you can see, between basin 2 and 3,
which correspond to AIM atomic space of C and N respectively, the DI is 2.593, exhibiting that in
average there are 2.593 electrons shared by the two atoms. To some extent DI can be regarded as
covalent bond order, the DI value 2.593 is indeed comparable with the formal bond order (3.0)
between C and N in HCN. The diagonal terms are the sums of the elements in corresponding
row/column, for close-shell cases they can be somewhat considered as atomic valency. So we can
say in HCN the nitrogen atom has atomic valency of 2.665.
The LI of basin 1 is only 0.259 which conspicuously deviates from the basin electron
population number. This observation reflects that in HCN, the electron in the AIM atomic space of
hydrogen can easily delocalize out.
4.17.2 ELF basin analysis for acetylene
This time we analyze ELF basin for acetylene. Boot up Multiwfn and input
examples\C2H2.wfn
17
1 // Generate basins and locate attractors
9 // ELF
2 // Medium quality grid
0 // Visualize attractors and basins
In the GUI, as the graph shown below, you can see there are lots of closely placed attractors
encircling the C-C bond. In fact, they have very similar ELF values, and collectively represent the
ring-type ELF attractor. These attractors have been clustered together by Multiwfn automatically,
therefore all of them have identical attractor index, namely 2; in another word, attractor 2 is a
"degenerate" attractor, which has many member attractors. Correspondingly, basin 2 is composed
by the member basins. The interested user is recommended to visualize basin 2 in the GUI.

4 Tutorials and Examples
362
The presence of attractor 2 signifies the π electrons shared by the two carbons. According to
the well-known ELF symbolic method, basin 2 should be identified as V(C1,C3), which means this
basin is comprised by the valence electrons of C1 and C3.
Attractor 3 and 4 correspond to core-type ELF attractors, their basins should be identified as
C(C3) and C(C1), respectively, where the letter C out of parentheses stands for "Core". If you
deselect the "Show molecule" check box and select corresponding terms in the basin list then you
can visualize the basins. The graph shown below portrays C(C3).
Although basin 1 and 5 cover the whole hydrogen spaces, they should be identified as
V(C3,H4) and V(C1,H2), rather than C(H4) and C(H2), respectively. This is because hydrogen does
not have core electrons.
Now close the GUI window by clicking "RETURN" button, and then input
2 // Integrate a real space functions in the basins
1 // Electron density
Soon, we get the integrals, namely the average electron population number in each basin:
#Basin Integral(a.u.) Volume(a.u.^3)
1 2.2159821115 768.39800000
2 5.3670485473 972.79700000
4 Tutorials and Examples
363
3 2.0949016050 0.83200000
4 2.0949016050 0.83200000
5 2.2159824751 768.55500000
Sum of above values: 13.98881634
Both C(C1) and C(C3) in average contain 2.095 electrons, which is in line with the fact that
carbon has two electrons in its core. Also, the average population number in V(C3,H4) and
V(C1,H2) are close to two, approximately reflecting that in average there is a pair of electron
shared between C and H.
According to classical chemical bond theory there are three electron pairs and hence six
electrons are shared by the two carbons, however in the V(C1,C3) basin the integral is only 5.37.
Although the deviation is relatively large, this is a normal situation. It is senseless to require that
the result of ELF basin analysis must be able to reproduce classical Lewis picture, and actually,
ELF analysis is more advanced and more close to real physical picture.
Next, enter function 3 to calculate electric multipole moments. We want the result for all
basins to be outputted, so we input -1. The result of C(C1) is pasted below
Basin 4
Basin electric monopole moment: -2.094902
Basin electric dipole moment:
X= -0.104745 Y= -0.104745 Z= 0.020728 Magnitude= 0.149575
Basin electron contribution to molecular dipole moment:
X= 0.000000 Y= 0.000000 Z= -2.388409 Magnitude= 2.388409
Basin electric quadrupole moment (Cartesian form):
QXX= -0.003034 QXY= -0.007856 QXZ= 0.001555
QYX= -0.007856 QYY= -0.003034 QYZ= 0.001555
QZX= 0.001555 QZY= 0.001555 QZZ= 0.006067
The magnitude of electric quadrupole moment (Cartesian form): 0.006067
Electric quadrupole moments (Spherical harmonic form):
Q_2,0 = 0.006067 Q_2,-1= 0.001795 Q_2,1= 0.001795
Q_2,-2= -0.009071 Q_2,2 = 0.000000
Magnitude: |Q_2|= 0.011205
First you should note that although in present case, due to the symmetry, the X and Y
components of the basin electric dipole moment should vanish, the actual values are not so close
to zero, rendering that the integration accuracy is not very high. This is why "high quality grid" is
often necessary when electric multipole moment analysis is involved. However, present result is
still useful on the qualitative level. The magnitude of electric quadrupole moment in the basin
measures how evidently does the electron distribution in the basin deviate from spherical
symmetry. This value for C(C1) is very small (0.0061), showing that the distribution of core
electron of the carbon basically remains unperturbed during the formation of the molecule.
Note: If the basins you are interested in are only valence basins, "medium quality grid" is enough for electric
multipole moment analysis, since valency density is not as high as core density, and hence does not need high
accuracy of integration.
Input 0 to return. Finally, let's choose option 4 to study LI and DI. The result is shown below
************ Total delocalization index matrix ************
1 2 3 4 5
4 Tutorials and Examples
364
1 1.31231709 1.03496561 0.16085935 0.02291204 0.09358009
2 1.03496561 2.71090548 0.32048710 0.32048709 1.03496568
3 0.16085935 0.32048710 0.51131492 0.00705643 0.02291205
4 0.02291204 0.32048709 0.00705643 0.51131492 0.16085937
5 0.09358009 1.03496568 0.02291205 0.16085937 1.31231719
Total localization index:
1: 1.560 2: 4.011 3: 1.834 4: 1.834 5: 1.560
Between C(C1) and C(C3), namely DI(3,4), the value is trivial, reflecting the general rule that
the electron delocalization between atomic cores is rather difficult. DI(1,3) and DI(2,3) are very
small values but not close to zero, representing that the electrons in C(C3) have a few probability
to exchange with the ones in V(C3,H4) and V(C1,C3), which are the only two basins adjacent to
C(C3).
DI(2,1) and DI(2,5) are about 1.0, such a large value indicates that the electron delocalization
between C-C bonding region and C-H bonding region is easy. Though the average electron
population number in C(C1) and C(C3) are 2.095, their LI values are as high as 1.834, implying
that the core electrons of carbon highly prefer to stay in the core region rather than delocalize out.
In constrast, for V(C,H) and V(C,H), their LI values are less than their average electron population
numbers distinctly, revealing that the electrons in these basins do not express very strong
localization character.
In the ELF basin analyses, some researchers prefer to use the concept of variance (σ2) and
covariance (Cov) rather than LI and DI to discuss problems. Covariance of electron pair
fluctuation is simply the half of the negative value of DI, for example, Cov(2,5) = -DI(2,5)/2 = -
1.035/2 = -0.518. The variance of electronic fluctuation can be calculated as the half of the
corresponding diagonal term of the DI matrix outputted by Multiwfn, for instance, σ2(2) =
DI(2,2)/2 = 2.710/2 = 1.355 (note that as mentioned earlier, the diagonal terms of the DI matrix
outputted by Multiwfn are the sums of the elements in corresponding row/column).
4.17.3 Electrostatic potential basin analysis for H2O
In literatures, basin analysis technique is rarely applied on electrostatic potential (ESP). To
illustrate the universality of basin analysis module of Multiwfn, in this example we will generate
ESP basins for H2O, and then evaluate electron population numbers in them. In the first part of
this section, we will let Multiwfn directly calculate ESP and electron density, while in the second
part we will make use of the cube files produced by third-part program to do the same things.
It is noteworthy that unlike electron density and ELF, which we have analyzed earlier, ESP
has positive part and negative part simultaneously. For such real space functions, Multiwfn will
automatically locate attractors (maxima) for positive part and locate "repulsors" (minima) for
negative part, but in Multiwfn all of them are collectively recorded as "attractors". You can easily
discriminate them by inspecting their colors in the GUI, as illustrated below.
Part 1
Boot up Multiwfn and input following commands:
examples\H2O.fch // Optimized and produced at HF/6-31G* level. Of course you can also
use .wfn/.wfx file
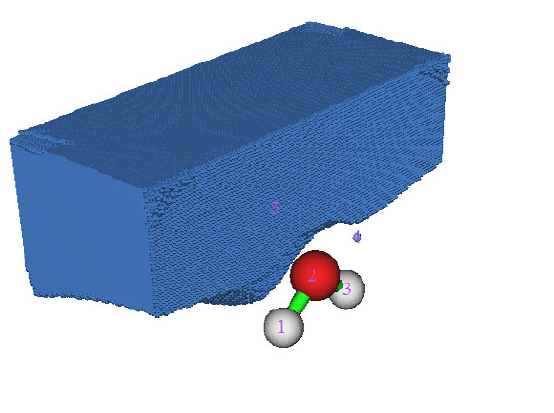
4 Tutorials and Examples
365
17
1
12 // ESP
2 // Medium quality grid. Note that calculation of ESP is rather time-consuming, so do not
use too high quality of grid, especially for large systems
After the calculation of ESP grid data and the basin generation are finished, five attractors are
founded. Notice that this time the number of grids travelled to box boundary is not zero again
(about 1627 grids).
Choose option 0 to open GUI, you can see that attractor 1, 2 and 3 correspond to ESP
maxima due to nuclear charges. It is well known that the lone pairs of oxygen make the ESP at
corresponding region negative, clearly attractor 4 and 5 reflected this effect. Attractor 4 and 5 are
colored by light blue because they are lying in negative region, in fact they are not attractors but
"repulsors" (minima) of ESP. By clicking term 5 in the basin list and checking "show basin
interior" box, you will see below graph, which exhibits the basin corresponding to attractor 5.
If you want to visualize which grids have travelled to box boundary during basin generation,
you can select "Boun" in the basin list, see below graph. Evidently, these grids lack of physical
meaning and hence can be simply ignored. They only present at the regions far from atoms.

4 Tutorials and Examples
366
Now click "RETURN" button to close the GUI.
Sometimes one needs to obtain geometry information between attractors and nuclei. As an
instance, we enter function -2, and input a1 c4, the distance between nucleus of atom 1 (namely
oxygen) and attractor 4 will be shown on the screen, the value is 2.237 Bohr. Next, input c4 a1 c5,
then the angle of "attractor 2 -- atom 1 -- attractor 3" will be outputted, the value is 80.84 degree,
which in some sense can be regarded as the angle between the two lone pairs.
Input q to exit the geometry measurement interface.
Assume that we want to cluster attractor 4 and 5 together as a degenerate attractor, we can
input
-6 // Set parameter for attractor clustering or manually perform clustering
3 // Cluster specified attractors
4,5 // attractor 2 and 3 will be clustered as a single one
0 // Return
Select option 0 to open GUI, as shown below, you can find that the index of all attractors
have changed, and the two attractors corresponding to the oxygen lone pairs now sharing the same
index, namely 4.
Close the GUI by clicking "RETURN" button, choose option 2 and then select 1 to integrate
electron density in the ESP basins, the result is
#Basin Integral(a.u.) Volume(a.u.^3)
1 0.8647179457 391.74200000
2 7.5147940814 25.01400000
4 Tutorials and Examples
367
3 0.8647179450 391.65000000
4 0.7405385242 703.11200000
Sum of above values: 9.98476850
Integral of the grids travelled to box boundary: 0.00000002
Since currently basin 4 is just the whole negative ESP region, the result shows that in average
there are 0.740 electrons in the negative ESP region. Indeed this value is not large (one may
expects that there should be about four electrons due to the two lone pairs), this is because most
parts of the molecular space are dominated by nuclear charges and hence having positive ESP.
Part 2
Now we redo some analyses in part 1 but using the grid data comes from external file. Since
external grid data is supported, one can use third-part programs to generate the grid data, and then
use basins analysis module of Multiwfn to study the basins of the real space functions recorded in
the grid data. The real space function to be analyzed may be the one cannot be directly calculated
by Multiwfn, or the one requires large amount of computational time, e.g. ESP (compared to some
ab initio programs, using current Multiwfn to calculate ESP grid data is a bit slow).
Here we use cubegen utility in Gaussian package to yield grid data of ESP and electron
density for the H2O.fch file. Run below commands in MS-DOS/Linux/Mac OS console to
produce density.cub and ESP.cub. cubegen utility is assumed to be placed in current path
cubegen 0 fdensity H2O.fch density.cub 0 h
cubegen 0 potential H2O.fch ESP.cub 0 h
Then boot up Multiwfn and input
ESP.cub // This file contains ESP grid data. After loading it, the grid data will be stored in
memory
17
1
2 // Generate the basins by using the grid data stored in memory
Now visualize the attractors in function 0
Exit GUI, after that input following commands
2 // Integrate real space functions in the basins
-1 // Use the grid data stored in external file as integrand
density.cub // This file contains electron density grid data
The result is very close to the one we obtained in Part 1 of present section. For example, the
electron population number in negative ESP region we get here is 0.367*2=0.734, while the
counterpart one we obtained in Part 1 is 0.740.
4 Tutorials and Examples
368
At last, we select function 3 to calculate electric multipole moments for the basins. Because
cube file does not contain GTF (Gauss type function) information, you will be prompted to input
the path of a file containing GTF information of present system, so that electric multipole
moments can be calculated. We input the path of the H2O.fch file, and then input -1, the electric
multipole moments of all basins will be immediately outputted on screen.
4.17.4 Basin analysis of electron density difference for H2O
In this example we analyze basins of electron density difference for H2O to quantitatively
study the electron density deformation during formation of the molecule.
Before doing the basin analysis, we need to generate grid data of electron density difference
first by main function 5, wavefunction file of all related elements must be available. Here we
directly use the set of atomic wavefunction files provided in Multiwfn package, namely copying
"atomwfn" subfolder in "example" folder to current folder, then during generating grid data of
electron density difference Multiwfn will automatically use them. There are several different ways
to prepare atomic wavefunction files, please recall Section 4.4.7 and consult Section 3.7.3.
After that, boot up Multiwfn and input:
examples\H2O.fch
5 // Calculate grid data
-2 // Obtain deformation property
1 // Electron density
3 // High quality grid. Because the variation of electron density difference is complicated,
using relatively high quality of grid is compulsory. Note that the "high quality grid" we selected
here only defines the total number of grids, and hence has different meaning to the one involved in
function 1 of basin analysis module
0 // After the calculation is finished, return to main menu
17 // Basin analysis module
1 // Generate basins and locate attractors
2 // Generate the basins by using the grid data stored in memory (namely the grid data we
just calculated by main function 5)
Enter function 0 to visualize the result, you will see the left graph shown below. After
deselect "Show molecule", the graph will look like the right one
Positive (negative) part of electron density difference corresponds to the region where
electron density is increased (decreased) after formation of the molecule. Light green spheres
denote the maxima of the positive part, while light blue ones denote the minima of the negative
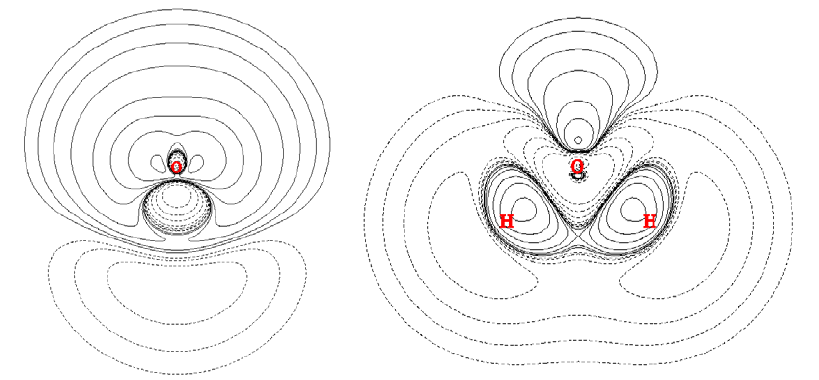
4 Tutorials and Examples
369
part.
If you feel difficult to imagine why the maxima and minima distribute like this, I suggest you
to plot plane maps for electron density difference. The left graph shown below is the electron
density difference map vertical to the molecular plane, while the right graph is the map in the
molecular plane.
By comparing the attractors with plane maps, it is evident that attractor 3 and 4 are the
maxima of the region where electron density is enhanced due to the formation of the O-H bonds.
While the presence of attractor 5 and 6 mainly arise from the electron aggregation due to the
formation of the lone pairs.
Note: In this example there are missing and misplaced attractors in negative regions (in fact they are
repulsors). As you can see, attractor 8 does not have its counterpart in another side of molecular symmetry plane.
Besides, attractor 7 deviates from its ideal position. The reason of these problems is that the grid quality is still not
high enough relative to the complicated characteristic of electron density difference. However, since these
attractors are not of chemical interested, these problems can be simply ignored.
It is interesting to examine how many electrons are aggregated between C and H due to the
bond formation. There can be many ways to measure this quantity; the most reasonable one for
present case is to integrate the electron density difference in basin 3 or in basin 4. Let's do this now.
Choose function 2, and then select option 0 to take the grid data of electron density difference as
integrand. From the output we can find that the integral is about 0.09e.
If you would like to compare the attractors with the isosurface of electron density difference,
you can simply choose -10 to return to main menu of Multiwfn, and then choose suboption -2 in
main function 13 to plot the isosurface of the grid data stored in memory, the attractors we located
will be shown together, as shown below (isovalue=0.05), where green and blue parts correspond to
positive and negative regions, respectively.

4 Tutorials and Examples
370
4.17.5 Calculate source function in AIM basins
Source function has been briefed in part 19 of Section 2.6. Commonly, bond critical point
(BCP) is taken as the reference point of source function when bonding problem is discussed. In
this example we calculate source function in AIM basins for ethane; in particular, based on source
function we will get the contribution from methyl group to the electron density at the BCP of its
C-H bond. Before calculating source function we should perform topology analysis first to find
out the position of the BCP.
Boot up Multiwfn and input:
examples\ethane.wfn // Optimized and produced at B3LYP/6-31G*
2 // Topology analysis
2 // Search nuclear critical points
3 // Search BCPs
0 // Visualize result, see below
Critical point 11 will be selected as the reference point of the source function. Of course,
selecting which BCP is completely arbitrary. Now close the GUI of topology analysis module
You'd better choose option 7 and then input 11 to check the electron density at this CP,
4 Tutorials and Examples
371
because theoretically the integral of source function in the whole space should equal to the
electron density at its reference point, therefore this value is important to examine if the
integration of source function is accurate enough. The electron density at CP11 is 0.276277.
From the information shown in the command-line window you can find the coordinate of
CP11 is (0.0,-1.199262548,-1.909104063), copy it from the window to clipboard (if you do not
know how to do this please consult Section 5.4). Next, we will set CP11 as the reference point of
the source function. Although you can define reference point by "refxyz" parameters in settings.ini,
there is a trick can do the same thing, by which you needn't to close Multiwfn and then reboot it to
make the parameters take effect!
Input below commands
-10 // Return to main menu from topology analysis module
1000 // Secret menu
1 // Set reference point
Paste the coordinate of CP11 to the window and then press ENTER button.
17 // Basin analysis
1 // Generate basins and locate attractors
1 // Electron density
2 // Medium quality grid
Enter GUI by choosing function 0, you will see
Now we integrate source function in the AIM basins. Input following commands
7 // Integrate real space functions in AIM basins with mixed type of grids
1 // Integrate a specific function with atomic-center + uniform grids
19 // Source function
The result is
Atom Basin Integral(a.u.) Vol(Bohr^3) Vol(rho>0.001)
1 (C ) 5 0.00361772 149.307 70.392
2 (H ) 8 0.00289355 468.732 50.058
3 (H ) 6 0.00280041 443.982 50.097
4 (H ) 7 0.00280276 418.343 50.095
5 (C ) 2 0.12224052 150.514 70.396
6 (H ) 1 0.12040142 475.383 50.054
7 (H ) 4 0.01051821 424.105 50.095
8 (H ) 3 0.01051742 450.072 50.097
Sum of above integrals: 0.27579202
4 Tutorials and Examples
372
Sum of basin volumes (rho>0.001): 441.284 Bohr^3
The sum of the integrals is very close to the electron density at CP13 (0.276277). The sum of
the integral in basin of 1, 2, 3 and 4 is 0.1204+0.1222+0.0105*2=0.2636, which represents the
integral in the space of methyl group and accounts for 0.2636/0.2758*100%=95.6% of the total
integral value, exhibiting that methyl group is the main source of the electron density of the BCP
of its C-H bonds.
4.17.6 Local region basin analysis for polyyne
Sometimes, the geometry of the system we studied is rather extended, for instance, polyyne
C14H2, which can be formally illustrated as
H1−C2≡C3−C4≡C5−C6≡C7−C8≡C9−C10≡C11−C12≡C13−C14≡C15−H16
If we are only interested in the electronic structure characteristic of local region in this system, by
properly setting up grid, basin analysis can be conducted only for the interesting region rather than
for the whole system to save computational time. As an example, in this section we will try to
acquire electron population number in the ELF basin of V(C7,C8) and V(C8,C9) with minimum
computational cost.
Boot up Multiwfn and input following commands:
examples\polyyne.wfn // Optimized and produced under B3LYP/6-31G*
17 // Basin analysis
1 // Generate basins and locate attractors
9 // ELF
8 // Set the grid by inputting center coordinate, grid spacing and box length
a8 // Take the position of atom 8 as box center
0.08 // Grid spacing (Bohr)
10,10,8 // Box length in X, Y and Z directions (Bohr). Note that current
molecule is aligned in Z-axis. Obvisouly, the larger the box, the longer the
computational time must be spent. While the box should not be too small, otherwise the
basins of interest may be truncated. Choosing appropriate box size highly relies on
users' experience
After the calculation is finished, enter GUI by selecting option 0, you will see the
graph shown at the right side. Clearly, only several attractors near C8 are located. Basin
5 and basin 21 correspond to V(C7,C8) and V(C8,C9), respectively. Notice that although
attractor 1 and 6 are also located, due to their corresponding basins are not only large
but also close to box boundary, it can be expected basin 1 and 6 are severely truncated
and hence studying them are meaningless.
When you use above manner to study local region, you will always find there are
many grids travelled to box boundary. In present example, as shown in command-line
window, the number of such type of grids is 60668. You can visualize them by
choosing "Boun" in basin list of GUI, see the graph below
4 Tutorials and Examples
373
Now close GUI, select option 2 and then select 1, the result shows that the integral of
electron density in V(C7,C8) and V(C8,C9) are 2.78 and 5.02, respectively. Evidently, the bonding
between C8-C9 is much stronger than C7-C8, this is why the bond length of the former (1.236Ǻ)
is shorter than the latter (1.338Ǻ). Note that the electron population number in V(C,C) of
acetylene is 5.37 (see Section 4.17.2), therefore it can be expected that C8-C9 is weaker than
typical C-C triple bond, mostly due to the electron global conjugation in polyyne.
The interested users can redo the basin analysis for the whole system with using the same
grid spacing (0.08 Bohr), the computational amount will be much larger than current example. For
V(C7,C8) and V(C8,C9), you will find the result does not differ from the one we obtained above
detectably.
4.17.7 Evaluate atomic contribution to population of ELF basins
In this section, I will use CH3NH2 as example to show how to obtain contribution of C and N
to population of V(C,N) ELF bond basin based on AIM partition of atomic space, this is useful to
examine bond polarity. You can also use the similar way to obtain atomic contribution to
population of any other kind of basins (e.g. LOL basin, ESP basin).
First, we need to generate a cube file named basin.cub, whose grid value corresponds to
index of ELF basins. Boot up Multiwfn and input
examples\CH3NH2.wfn
17
1
9 // ELF
2 // Medium quality grid
Now enter option 0 to examine the basin index

4 Tutorials and Examples
374
Evidently basin 5 corresponds to V(N,C), which is the one we will study. Then close the GUI
and input
-5 // Export basin as cube file
0,0 // Export basin.cub in current folder, whose grid value directly defines ELF basin
Next, we generate AIM basins as usual, the grid setting must be exactly identical to basin.cub
1 // Regenerate basins
1 // Select real space function
1 // Electron density
9 // Use grid setting of another cube file, this is the safest way to ensure the grid data to be
generated has the same grid setting as basin.cub
basin.cub
0 // Check attractors
It is clear that the attractor index corresponding to N and C are 2 and 4, respectively. Then we
evaluate atomic contribution to population of the basins defined in basin.cub
9 // Then program loads basin.cub in current folder
2 // The index of the attractor corresponding to N
5 // The 5th ELF basin, i.e. V(N,C) basin
The result is 1.15866, namely N contributes 1.159 electrons to V(N,C) basin. Then input
4 // The index of the attractor corresponding to C
5
From the result we know C contributes 0.463 electrons to the V(N,C) basin.
Since N contributes much more electrons than C to their ELF bond basin, it may thus be
concluded that C-N is a bond with significant polarity.
4.18 Electron excitation analysis
Main function 18 of Multiwfn is very powerful, which is a collection of electron excitation
analysis tools and able to provide very deep insight into electron transition problems.
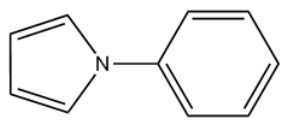
4 Tutorials and Examples
375
4.18.1 Analyze hole-electron distribution, transition density, transition
dipole moment, charge-transfer and so on for N-phenylpyrrole
In this example we will study distribution of hole and electron, transition density, transition
dipole moment, charge density difference, charge-transfer length and so on for different electronic
excitations of N-phenylpyrrole (PP). All of the related theories in this example have been detailed
in Sections 3.21.1, 3.21.4 and 3.21.7, please read them first. The structure of PP is shown below
All calculations were finished by Gaussian 09. Note that the geometry PP is not in this
minimum geometry, but in planar transition state geometry, so that electronic excitation analyses
could be illustrated easier. At this geometry, the excited state (TDDFT) calculation was performed
at CAM-B3LYP/6-31+G* level. The five lowest excited states were taken into account. Note that
in the excited state calculation, IOp(9/40=4) is used so that all configuration coefficients >0.0001
could be printed out (otherwise only the ones >0.1 will be printed and will result in inaccurate
analysis results). In summary, both the .fch file and .out file used below came from the calculation
via #p cam-b3lyp/6-31+g(d) td(nstates=5) IOp(9/40=4).
In single-electron excitation process, hole and electron distributions respectively denote the
region where an electron leaves and goes to. According to the characteristic of hole and electron,
there are three well-known types of excitations:
(1) Local excitation (LE): The hole and electron significantly share the same spatial range.
Note that even though the hole and electron distributions cover the whole system, the excitation is also
identified as local excitation.
(2) Charge-transfer excitation (CT): The spatial separation of hole and electron is large,
leading to evident movement of charge density from one place to another place.
(3) Rydberg excitation (R): Electron mainly consists of high-lying MOs, therefore the overlap
between electron and hole is small. Note that Rydberg type of excitation in general does not lead
to prominent long-range movement of charge density; in other words, the interval between the
centroid of hole and electron is small.
Present example consists of many parts, it is not necessary to read through all of them, some
parts that you are not interested in may be skipped. However, you should read at least Part 2.
Although in this section .fch file along with Gaussian excited state output file are used as input files, the
functions involved in this section are never only limited to Gaussian users. For example, you can also use .molden
file in combination with output file of CIS or TD/TDA-DFT task produced by ORCA as input files, see Section
3.21.1.2 for detail.
Part1: Calculating r index
The r index proposed in J. Chem. Theory Comput., 9, 3118 (2013) is a quantitative indicator
of electron excitation mode. The smaller the r index is, the more likely the excitation is a LE
mode (the original paper also argued that r index is a measure of CT length, but this is often not
true!).
First we examine r index of the five transition modes. Boot up Multiwfn and input
examples\N-phenylpyrrole.fch // The .fch file from excited state calculation (you can also

4 Tutorials and Examples
376
use the .fch file from ground state calculation at exactly the same geometry and identical level)
18 // Electron excitation analysis
4 // Calculate r index
examples\N-phenylpyrrole_ext.out // The output file of excited state calculation
1 // Select the first transition mode
You will see the r index is 0.793 Å. If you wish to examine the contribution of MO pair to
this quantity, you can then input y and input a threshold for printing result. However, here we
input n to skip this step.
Next, examine the r index for the second transition mode, namely select option 4 again and
input 2 (the file N-phenylpyrrole_ext.out will be loaded automatically, its path is not needed to be
input this time). The result is 1.846 Å. Repeat this operation to obtain r index for the other three
transition modes. The results, as well as excitation energies (E) and oscillator strengths (f) are
summarized below.
Excited states
1 2 3 4 5
ΔE (eV) 5.0615 5.0739 5.2451 5.9365 5.9669
f 0.3935 0.0139 0.0214 0.0000 0.1674
Δr (Å) 0.793 1.846 2.456 3.106 3.752
It is highly possible that modes 3, 4 and 5 possess strong CT character or Rydberg character
since they have large r, while modes 1 and 2 may be regarded as LE mode due to their r indices
are smaller than 2.0 (this threshold value was proposed in the original paper of r). Bear in mind,
the final conclusion can only be drawn after we have visualized the hole and electron distributions.
In below text we will focus on analyzing transition modes 1 and 5.
Part 2: Visualizing and analyzing hole, electron, their overlap and charge density
difference
Now we perform another type of analysis. Boot up Multiwfn and input
examples\N-phenylpyrrole.fch
18 // Electron excitation analysis
1 // Analyze and visualize hole-electron distribution, transition dipole moment and
transition density
examples\N-phenylpyrrole_ext.out // The output file of excited state calculation
1 // Select the first transition mode
1 // Visualize and analyze hole, electron and transition density and so on
2 // Medium quality grid
Multiwfn will calculate grid data for hole, electron, transition density and so on at medium
quality grid. Once the calculation is finished, many statistic data are shown
Integral of hole: 0.999384
Integral of electron: 0.990516
Integral of transition density: -0.000453
Transition dipole moment in X/Y/Z: -0.000021 -0.000045 1.767332 a.u.
Integral of overlap of hole-electron distribution: 0.5296733
Centroid of hole in X/Y/Z: 0.000020 0.000000 0.294862 Angstrom
Centroid of electron in X/Y/Z: 0.000277 0.000110 -0.152844 Angstrom
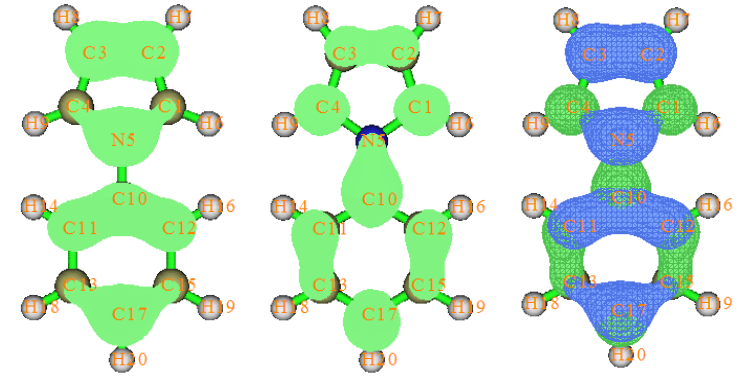
4 Tutorials and Examples
377
Distance between centroid of hole and electron in X/Y/Z:
0.000257 0.000110 0.447706 Angstrom Norm: 0.447706 Angstrom
Variation of dipole moment with respect to ground state in X/Y/Z:
-0.000484 -0.000207 0.841769 a.u. Norm: 0.841769 a.u.
RMSD of electron in x,y,z: 0.992 1.291 2.263 Total: 2.788 Angstrom
RMSD of hole in x,y,z: 0.764 0.817 2.289 Total: 2.547 Angstrom
Difference between RMSD of hole and electron: 0.527 Angstrom
H index in x,y,z: 0.878 1.054 2.276 Norm: 2.657 Angstrom
t index in x,y,z: -0.878 -1.054 -1.828 Norm: 2.286 Angstrom
...[ignored]
The ideal result of integral of hole and electron is 1.0, while for transition density the ideal
value is 0. Our results are close to corresponding ideal values, reflecting that "medium-quality
grid" is fine enough for present case. Transition dipole moment is calculated by integrating
transition dipole moment density at uniform grids, the result is very close to the one outputted by
Gaussian (namely 0.0, 0.0, 1.7813). The integral of overlap of hole-electron distribution is a
measure of spatial separation of hole and electron. The distance between centroid of hole and
electron is a measure of CT length; the larger the value, the longer length the charge transfers. As
you can see, the variation of dipole moment with respect to ground state is also outputted, which is
directly evaluated based on the position of centroid of hole and electron. RMSD of hole or
electron quantitatively characterizes their distribution breadth, for example, the RMSD of electron
in X and in Z is 0.992 and 2.263, respectively, indicating the electron distribution is much broader
in Z than in X direction. t index is another measure of the separation of hole-electron. t>0 means
the separation is clear. In present case t is evident negative in all directions, reflecting that hole
and electron overlap with each other severely.
In the new menu choose 1 and then select 1 to visualize hole distribution, and then choose 2
and then select 1 to visualize electron distribution. You can also choose option 3 to visualize hole
and electron simultaneously, the hole and electron distributions will be represented as blue and
green isosurfaces, respectively. The three graphs are shown below at left, middle and right sides,
respectively (at default isovalue 0.002).
As you can see, there is no evident spatial separation between hole and electron, exhibiting
that this transition mode is not a CT or Rydberg excitation.
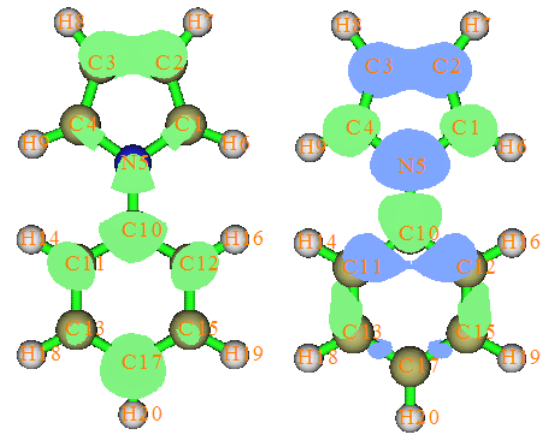
4 Tutorials and Examples
378
Overlap between hole and distributions is defined as min(hole,electron), you can select option
4 to visualize it (see left graph below). The charge density difference is calculated by minusing
hole from electron distribution, to visualize it you can choosing option 7 (see right graph below,
green and blue parts correspond to the region where electron density is increased and decreased
after electron excitation, respectively)
Clearly, the overlap between hole and electron is significant; the charge density difference
map does not show overall charge transfer or spatial separation, again reflecting that this is a LE
mode.
Now we study the 5th transition mode. Input below commands
0 // Return
0 // Return to the interface of main function 18
1 // Enter function 1 of main function 18 again
5 // Select the 5th transition mode
1 // Visualize and analyze hole, electron and transition density and so on
2 // Medium quality grid
From the output we can see that the integral of overlap of hole-electron distribution is 0.0883,
which is much smaller than that of transition mode 1 (0.5297); while the distance between
centroid of hole and electron now is 3.6433 Å, which is much larger than that of transition mode 1
(0.4477 Å). These quantitative data show that transition mode 5 has conspicuously stronger CT
character than mode 1.
Then choose option 3 to visualize isosurface of hole and electron distribution simultaneously
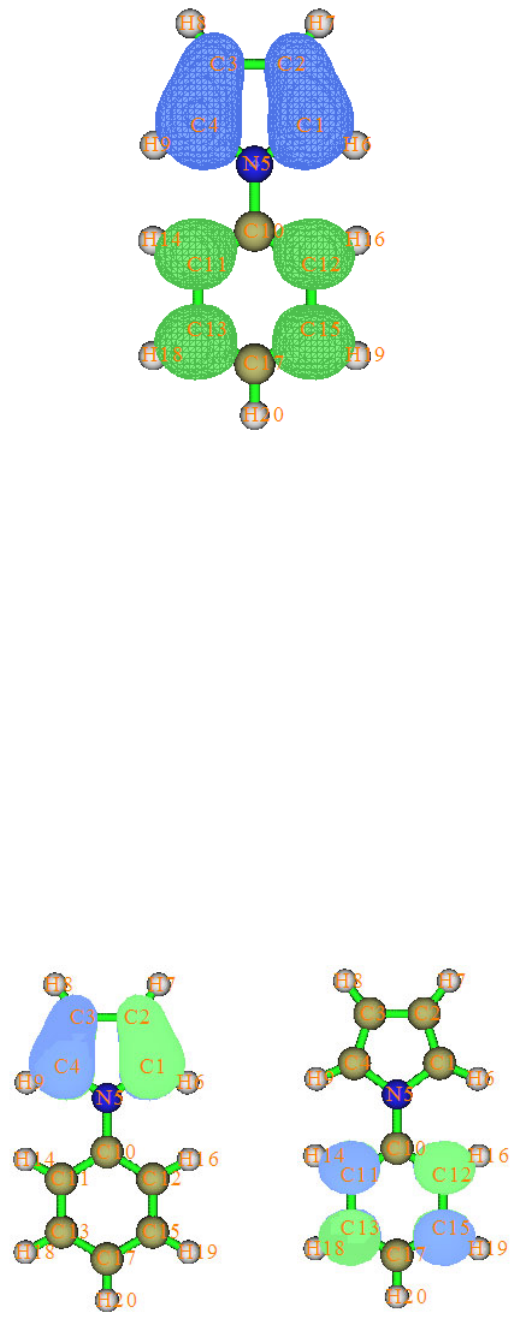
4 Tutorials and Examples
379
Undoubtedly this is a typical CT transition mode, corresponding to charge transfer from
pyrrole to phenyl region. If you visualize the overlap between hole and electron, at default
isosurface (0.002), nothing is shown, suggesting that the spatial overlap between hole and electron
is trivial.
Choose 0 to return to upper level of menu, then select option 3 and input 0.001 to show MO
contribution to hole and electron, you will see
MO 35, Occ: 2.00000 Hole: 0.00132 Electron: 0.00000
MO 37, Occ: 2.00000 Hole: 0.95980 Electron: 0.00000
MO 38, Occ: 2.00000 Hole: 0.03589 Electron: 0.00000
MO 39, Occ: 0.00000 Hole: 0.00000 Electron: 0.03551
MO 40, Occ: 0.00000 Hole: 0.00000 Electron: 0.95461
MO 52, Occ: 0.00000 Hole: 0.00000 Electron: 0.00522
Sum of hole: 1.00000 Sum of electron: 1.00000
Since MO37 and MO 40 dominate hole and electron respectively, it is evident that the 5th
transition mode can be approximately symbolized as MO37MO40. The graph of MO 37 and 40
are shown at left and right side below, respectively.
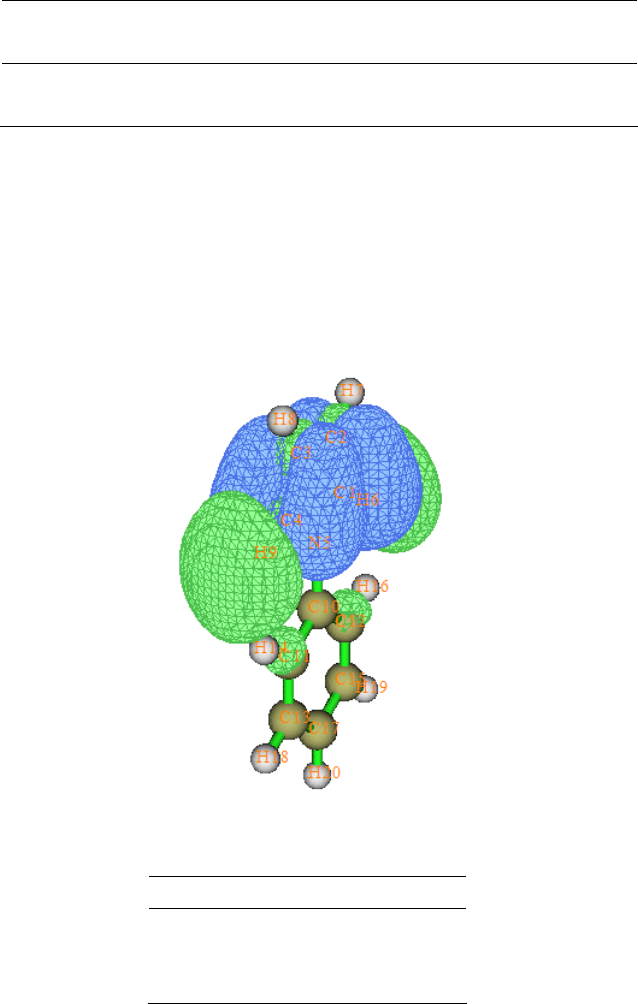
4 Tutorials and Examples
380
Repeat above steps to investigate hole, electron and related quantities for other transition
modes. The integral of overlap of hole-electron (S) and the distance between centroid of hole and
electron (D) are collected below
Excited state
1 2 3 4 5
S 0.530 0.650 0.364 0.132 0.088
D (Å) 0.448 0.705 1.946 0.308 3.643
According to D values, we can conclude that both mode 3 and 5 belong to CT type, since
their D are large; while modes 1 and 2 should be attributed to LE type.
If you carefully study transition mode 4, although its S value is small, you will find this is not
a CT mode, since both hole and electron are mainly localized in pyrrole region. The hole (blue)
and electron (green) distributions are shown below (isovalue=0.001). The reason why S is small is
mainly because the hole exhibits character, while electron primarily shows character with
some portion of Rydberg component, therefore their overlap is impossible to be very large.
Personally, I recommend using below criterion to identify the type of electron excitation
D S
LE Small Large
CT Large Small
Rydberg Small Small
I found the definition r has a drawback and thus should be used with caution. LE mode
should have small r, but in rare cases the value may be large!
Worthnotingly, after the grid data was calculated, you can find an option "8 Show isosurface
of Cele and Chole functions simultaneously". Cele (Chole) is a Gauss type function transformed
from electron (hole) distribution. For excitation mode 1 and 5, if we select this option you will see
left and right graph below, respectively (isoval=0.002)
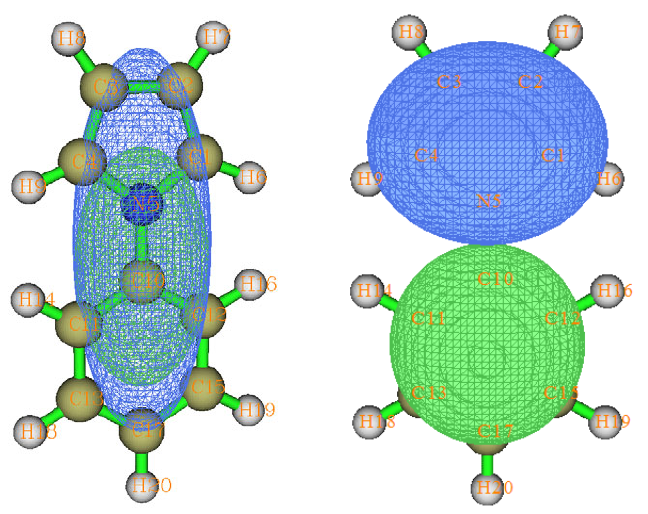
4 Tutorials and Examples
381
Please compare the Cele and Chole functions with the electron and hole distributions shown
earlier. Evidently, Cele (Chole) has the similar spatial scope and exactly the same centroid as
electron (hole) distribution, but is free of node and fluctuation characters. Therefore Cele (Chole)
can be regarded as an abstract and meantime much more clear representation of electron (hole)
distribution.
Part 3: Analyzing transition density and transition dipole moment
In order to gain a deeper insight into transition dipole moment, we can decompose it to MO
pair contributions. Let's do this for transition mode 1.
Return to the interface of main function 18, then choose 1 and input 1 to select the first
transition mode. Next, select option 2 and input 0.02, and then input 0, immediately the orbital
pairs whose contribution to transition dipole moment larger than 0.02 are shown, see below (Note:
For very large system, e.g. more than 100 atoms, if contribution of all orbital pairs are calculated,
the cost will be forbiddingly high. In this case, the 0 you input above should be replaced with such
as 0.002, so that only the orbital pair with absolute value of coefficient larger than 0.002 will be
computed.)
#Pair Coefficient Transition dipole X/Y/Z (au)
1213 35 -> 46 0.040230 0.000000 0.000000 0.037709
1214 35 -> 50 -0.047670 0.000000 0.000000 0.040152
1239 36 -> 40 -0.101270 0.000000 0.000000 -0.280355
1259 37 -> 40 -0.127550 0.000000 0.000000 -0.148489
1260 37 -> 52 0.069960 0.000000 0.000000 -0.122222
1262 37 -> 58 -0.036060 0.000000 0.000000 -0.025065
1278 38 -> 39 0.672690 0.000000 0.000000 2.796678
1280 38 -> 50 0.052570 0.000000 0.000000 0.046724
2489 36 <- 40 -0.014330 0.000000 0.000000 -0.039671
2506 37 <- 52 0.015140 0.000000 0.000000 -0.026450
4 Tutorials and Examples
382
2522 38 <- 39 -0.027240 0.000000 0.000000 -0.113249
Sum (including the ones not shown): 0.000000 0.000000 1.781438
Norm of transition dipole moment: 1.7814377 a.u.
Oscillator strength: 0.3935307
From the output, we can figure out which MO pairs have primary contribution to transition
dipole moment. As you can see, the configuration corresponding to MO38MO39 is the main
source (2.797 a.u.) of Z component of transition dipole moment (1.7814 a.u.). X and Y
components of transition dipole moment are exactly zero, this is because no MO pair has
contribution to them.
Oscillator strength directly relates to norm of transition dipole moment, therefore it can be
expected that if the configuration coefficient corresponding to MO38MO39 is set to zero,
namely ignore its contribution, then oscillator strength will be lowered evidently. Let's check this
point. Input following commands
n // Do not output all results to transdip.txt
10 // Modify or check excitation coefficients
1 // Set coefficient of an orbital pair
38,39 // The MO indices in the orbital pair
1 // Excitation, namely MO38MO39 (if input 2, then what we selected is MO38MO39)
0 // Set the configuration coefficient to zero
0 // Return
2
0.02
Now the oscillator strenght is only 0.1278, which is less than 1/3 of its original value.
Note that since the coefficient of MO38MO39 is as large as 0.6727, the sum of the square of remaining
coefficients is less than 0.1, which is far from the ideal value 0.5 (not 1.0 since this is a close-shell calculation).
Next, we visualize transition density and transition dipole moment density. Before doing this
we should retrieve the original configuration coefficients. Input below commands
n // Do not output all result to transdip.txt
10 // Modify or check excitation coefficients
-1 // Reset coefficient of all orbital pairs
0 // Return
1 // Visualize and analyze hole, electron and transition density and so on
2 // Medium quality grid
5 // Show isosurface of transition density
You will see left graph below, which exhibits the transition density in real space
representation. If the transition density is multiplied by negative value of Z coordinate variable,
then we obtain Z component of transition dipole moment density. To visualize it, choose "6 Show
isosurface of transition dipole moment density" and then select "3: Z component", you will see
right graph below
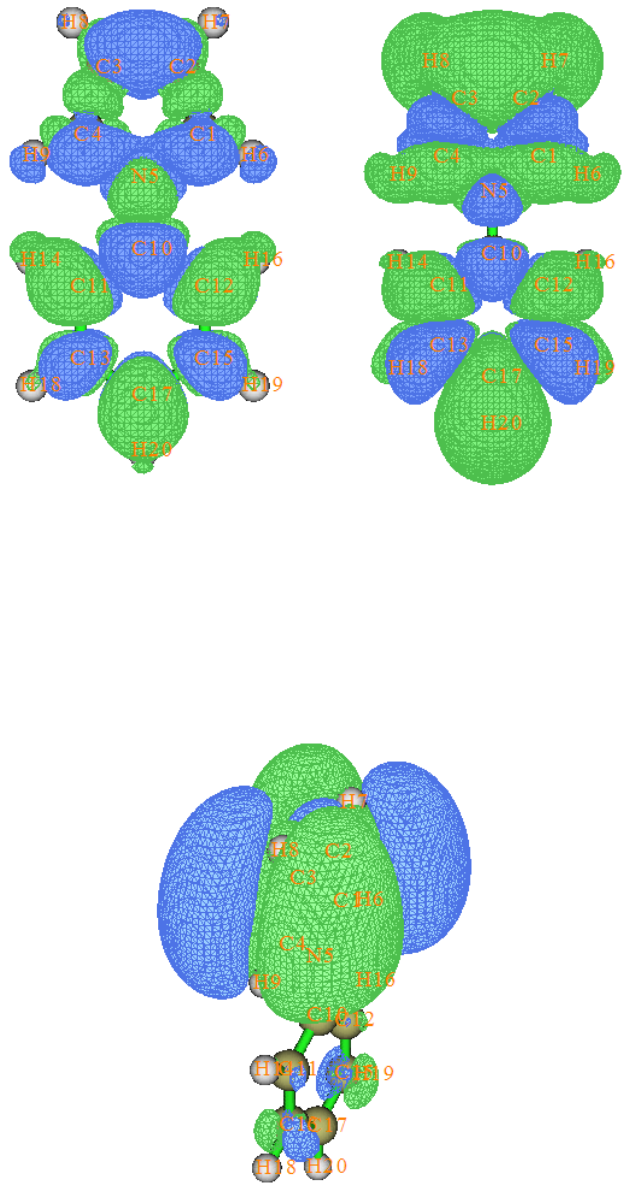
4 Tutorials and Examples
383
The integral of Z component of transition dipole moment density over the whole space is just
Z component of transition dipole moment (Dz). From right graph above one can see that the
positive (green) part is obviously larger than negative (blue) part. Since the former (latter)
contribute positive (negative) value to Dz, Dz must be an evident positive value (1.7814 a.u.).
Now draw the isosurface of Z component of transition dipole moment density for transition
mode 4 by yourself (see graph below)
The green and blue isosurfaces occupy the same amount of space, indicating that positive and
negative contributions to Dz are exactly the same, this is why Dz of present transition mode is zero.
Note that the transition dipole moment density almost only distributes in the pyrrole region, this is
because this transition mode corresponds to the local excitation on pyrrole moiety (as we have
shown earlier).
4 Tutorials and Examples
384
You may have felt that visual study of transition dipole moment density is interesting and
useful, indeed, by which you can clearly identify the contribution of transition dipole moment
from different molecular regions.
Part 4: Visualizing transition magnetic dipole moment density
The transition dipole moment we discussed above is transition electric dipole moment. There
are also other kinds of transition dipole moments, such as transition velocity dipole moment and
transition magnetic dipole moment. Multiwfn is also capable of calculating transition magnetic
dipole moment and showing the corresponding density, the definitions can be found in "Theory 5"
of Section 3.21.1. Since this quantity is less important than transition electric dipole moment, I
will not discuss it deeply, but only give a simple example:
examples\N-phenylpyrrole.fch
18 // Electron excitation analysis
1
examples\N-phenylpyrrole_ext.out // The output file of excited state calculation
2 // Select the second transition mode
-1 // By default, transition magnetic dipole moment density is not calculated by option 1 for
saving time, we select this option to make option 1 also calculate magnetic dipole moment density
1
2 // Medium quality grid
After the calculation is finished, from screen you can find the transition magnetic dipole
moment evaluated based on the grid data:
Transition magnetic dipole moment in X/Y/Z: -0.503315 0.000548 -0.000758 a.u.
Then select option 9 and select the component, you will see the isosurface of transition
magnetic dipole moment density. You can also export the grid data as cube file in current folder by
option 17.
Part 5: Calculating Coulomb attractive energy between hole and electron
The Coulomb attractive energy (Ec) has been introduced as theory 6 in Section 3.21.1.1. Here
I show how to calculate it. Boot up Multiwfn and input
examples\N-phenylpyrrole.fch
18
1
examples\N-phenylpyrrole_ext.out
1 // The first transition mode
1 // Calculate hole and electron
1 // Low quality grid
18 // Calculate hole-electron Coulomb attractive energy
Even if low quality grid is used, the cost of Ec is still high, you need to wait very patientialy.
The cost is proportional to square of the number of grids, therefore if you use medium quality grid
instead, the cost will be excessively expensive. Once the calculation is finished, you will find Ec
on screen, the value of the 1st transition is -0.211870 a.u. (If you use medium quality grid, the
result will be -0.212691. Clearly, low quality grid is adequate for producing reliable Ec). Similarly,
we calculate Ec for all other transitions, the results are
4 Tutorials and Examples
385
S0S1: -0.211870 a.u.
S0S2: -0.229754 a.u.
S0S3: -0.199335 a.u.
S0S4: -0.182067 a.u.
S0S5: -0.144489 a.u.
You can find Ec closely relates with the S and D index that we calculated earlier, the
underlying reason is easy to understand. For example, S0S2 has large S and small D, implying
the hole and electron distribution are essentially the same, evidently their Coulomb attraction must
very strong, this explains why the Ec (-0.229754 a.u.) is quite negative. In contrast, S0S5 has
very small S and very large D, which imply very low degree of similarity between hole and
electron distributions, this is the reason why the corresponding Ec (-0.144489 a.u.) is not so
negative as S0S2.
Part 6: Calculating contribution of each atom to hole and electron
It is possible to calculate contribution of each atom to hole or electron distribution in
Multiwfn. To do this, it is best to make use of fuzzy analysis module (you may also use basin
analysis module to realize AIM partition of hole or electron distribution). Here I illustrate how to
decompose hole distribution of S0S5 transition to atomic contributions.
Boot up Multiwfn and input
examples\N-phenylpyrrole.fch
18
1
examples\N-phenylpyrrole_ext.out
5 // The 5th transition mode
1 // Calculate hole and electron
2 // Medium quality grid
10 // Export hole distribution as cube file hole.cub in current folder
1 // Total
Now quite Multiwfn. Set "iuserfunc" in settings.ini to -1, so that the user-defined function
corresponds to interpolated function based on grid data (see Section 2.7 for detail). Then boot up
Multiwfn and input
hole.cub
15 // Fuzzy analysis module
1 // Integrate a real space function over each atomic space
100 // User-defined function
The result corresponding to pyrrole moiety is shown below
Atomic space Value % of sum % of sum abs
1(C ) 0.31123048 31.155665 31.155665
2(C ) 0.13948638 13.963256 13.963256
3(C ) 0.13953801 13.968425 13.968425
4(C ) 0.31123654 31.156272 31.156272
5(N ) 0.04320178 4.324706 4.324706
6(H ) 0.00738105 0.738879 0.738879
7(H ) 0.00309722 0.310047 0.310047
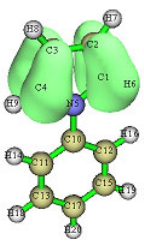
4 Tutorials and Examples
386
8(H ) 0.00309738 0.310062 0.310062
9(H ) 0.00737876 0.738649 0.738649
From above data we can find, for example, C4 contributes 31.16% to the hole. Please
compare the data with the isosurface map of hole shown below, it is clear that the quantitative data
well describes the actual hole distribution.
Part 7: About the ghost-hunter index
The ghost-hunter index (MAC) is used to judge if an excited state should be regarded as a
ghost state, which is physically meaningless and results from inappropriate choice of DFT
functional in the TDDFT calculation, please check Section 3.21.7 for introduction. In the hole-
analysis module, the MAC is printed automatically once calculation of grid data of hole and
electron is finished. For example, we calculate hole and electron distribution for the fifth excited
state, you will find below output
...
H index in x,y,z: 0.920 1.274 1.621 Norm: 2.257 Angstrom
t index in x,y,z: -0.920 -1.274 0.325 Norm: 1.605 Angstrom
Ghost-hunter index (defin. 1): 0.495 eV, 1st/2nd terms: 7.895 7.399 eV
Ghost-hunter index (defin. 2): -0.250 eV, 1st/2nd terms: 7.149 7.399 eV
Excitation energy of this state: 5.245 eV
The MAC is given as two definitions, the first is the one proposed in its original paper, while
the second one is a modified version proposed by me (see Section 3.21.7). Personally I think the
latter definition is better. Since the TDDFT excitation energy (5.245 eV) is higher than MAC (-
0.250 eV), it can be safely believed that this is not an artificial ghost state.
4.18.2 Plot transition density matrix of large-size conjugated molecule
as color-filled map
Plotting transition density matrix (TDM) as color-filled map is especially useful for visually
studying spatial span and primary sites of electron transitions, the basic principle has given in
Section 3.21.2. Here we use this approach to study below molecule:
4 Tutorials and Examples
387
This molecule contains four fragments: anthracene, biphenyl, 1,3,5-Hexatriene and thiophene.
Since this system is relatively large, in order to reduce computational cost, we use semi-empirical
method ZINDO (strictly speaking what we will use should be called as ZINDO/S, also known as
INDO/S) to calculate electron transition. You can also use other methods, such as CIS, TDHF,
TDDFT, etc.
First, run tdmat.gjf provided in "examples" folder by Gaussian to produce tdmat.out. The
keyword "density=transition=1" in route section means the TDM between S0 (ground state) and
S1 (the first singlet excited state) will be passed to L601 module, while IOp(6/8=3) tell L601 to
write the received TDM to output file. Then we use formchk to convert tdmat.chk to tdmat.fch.
Boot up Multiwfn and input following commands
xxx\tdmat.fch // The path of .fch file
18 // Electron excitation analysis
2 // The function used to plot TDM
xxx\tdmat.out // The path of .out file
1 // Show graph on screen
You will see the color-filled map shown below. Labels in abscissa and ordinate correspond to
indices of heavy atoms, for clarity, the correspondence between labels and atoms is marked on the
plot. Hydrogens are ignored by default, since usually they have little contribution to the transitions
we are interested in.
From this graph we can understand which atoms are mainly affected by the electron
transition and which atom pairs are strongly coherent when electron transits. A large value in
diagonal term corresponds to large charge variance of corresponding atom. While a large value in
non-diagonal term denotes that strong hole-electron coherence presents between corresponding
two atoms. From the graph corresponding to S0→S1 transition we can clearly see that the
transition only involves 1,3,5-Hexatriene and thiophene parts (spanned by red arrow in the graph,
the length is denoted by Ld), while anthracene and biphenyl almost didn't participated in. We can
also find that most heavy atoms in 1,3,5-Hexatriene and thiophene are evidently coherent with
surrounding atoms, the spatial span is indicated by pink two-way arrow with length of Lc in the
graph.
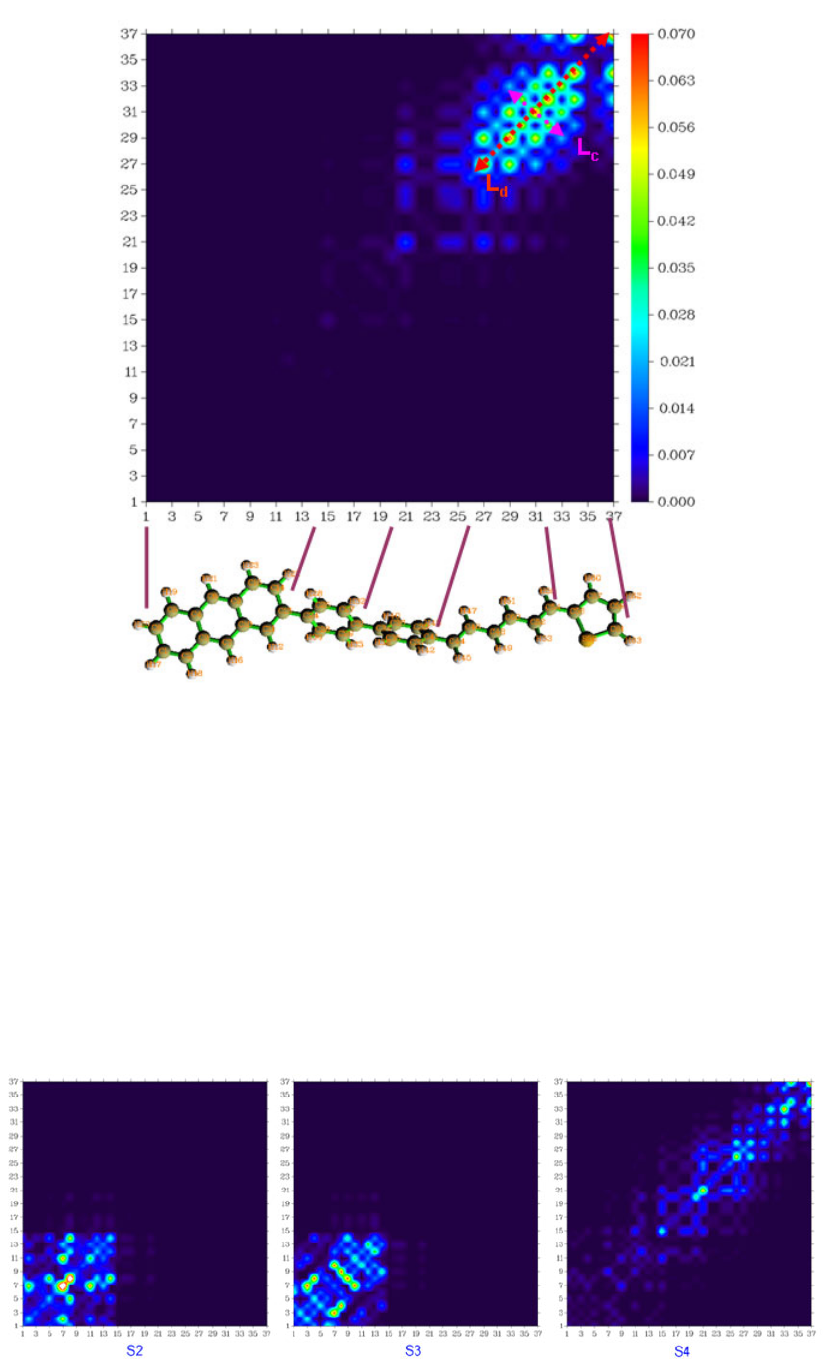
4 Tutorials and Examples
388
TDM map between S0 and S1, S2 ... S10 are shown below. They can be easily obtained by
repeating above procedure, only if X in the keyword "density=transition=X" is changed to
corresponding state. (while .fch file is unnecessary to be regenerated, the utilized information
in .fch file are identical to all states) Obviously, the electron transitions from S0 to S2, to S3 and to
S8 of present system essentially reflect the local transitions within anthracene. Since anthracene is
a high delocalization system, relatively widespread coherence span can be observed. S0 to S5 and
to S6 correspond to the local transitions occurred within the respective two benzene rings, the
coherence between atoms in each benzene ring is very strong, however the coherence between the
two benzene is much weaker. S0 to S4, to S7 and to S10 are the transition modes involving large
spatial range.
4 Tutorials and Examples
389
4.18.3 Analyze charge-transfer during electron excitation based on
electron density difference
In this instance we will analyze charge-transfer (CT) between the first singlet excited state
and ground state of the molecule shown below in ethanol solvent, which will be referred to as P2.
The related theory has been introduced in Section 3.21.3. The discussions in this example are
somewhat related to the ones involved in Section 4.18.1, however the methods employed in this
section are purely based on electron density difference.
Since the .wfn files corresponding to the excited and ground state are huge, they are not
provided. Instead, the input files of Gaussian for generating the two .wfn files are provided in
“example” folder (extP2.gjf and basP2.gjf). I assume that the corresponding .wfn files are
produced at "CT" subfolder in current folder. I would like to remind you once again, the
geometries in the wavefuncition files of the two states must be exactly identical, otherwise the
result will be meaningless!
First, we calculate grid data of electron density variation
. Boot up Multiwfn and input:
CT\extP2.wfn // Excited state wavefunction file
5 // Generate grid data
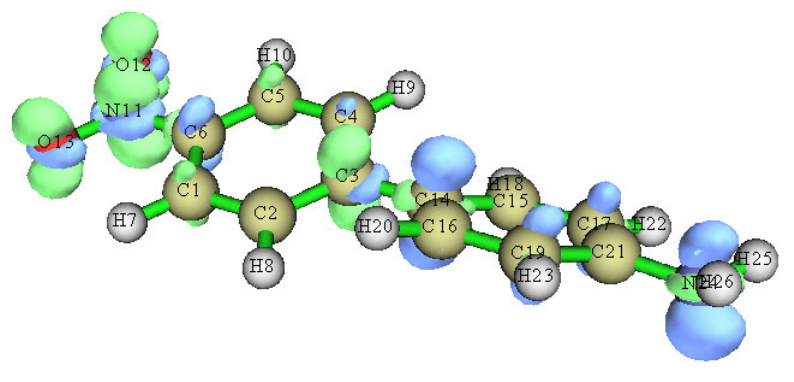
4 Tutorials and Examples
390
0 // Set custom operation
1 // Only one file will be dealt with
-,CT\basP2.wfn // Ground state wavefunction file. Corresponding density will be subtracted
from the excited one to generate
1 // Electron density
2 // If the system is much larger than present one, more grid points is required.
Once the calculation is normally terminated, you can choose option -1 to view the electron
density variation before and after excitation (Default value is too large, 0.005 is recommended as
isovalue). Green and blue regions correspond to positive and negative regions, respectively, and
thus represent increase and decrease in electron density due to the excitation.
However this difference graph is not intuitive, positive and negative parts interwined together,
we will see that C+ and C- functions make the picture much clearer.
0 // Return to main menu
18 // Electron excitation analysis
3 // The routine for analyzing CT
The following information are displayed immediately. Note that if positive and negative parts
of transferred charge are obvious unequal, that means the grid setting used in generating
is too
coarse, and you need to calculate again with finer grid setting.
Transferred charge (positive and negative parts): 0.844 -0.844
Barycenter of positive part in x,y,z (Angstrom): -2.659 -0.001 -0.000
Barycenter of negative part in x,y,z (Angstrom): 2.294 -0.009 -0.029
Distance of CT in x,y,z (Angstrom): 4.953 0.009 0.029 Norm: 4.953
Dipole moment variation (a.u.) : 7.896 -0.014 -0.046 Norm: 7.896
Dipole moment variation (Debye): 20.070 -0.035 -0.117 Norm: 20.070
RMSD of positive part in x,y,z (Angstrom): 2.993 1.250 0.821 Tot: 3.346
RMSD of negative part in x,y,z (Angstrom): 3.290 1.144 0.881 Tot: 3.593
Difference between RMSD of positive and negative parts (Angstrom): 0.321
H index in x,y,z (Angstrom): 3.141 1.197 0.851 Norm: 3.468
t index in x,y,z (Angstrom): 1.811 -1.188 -0.822 Norm: 2.317
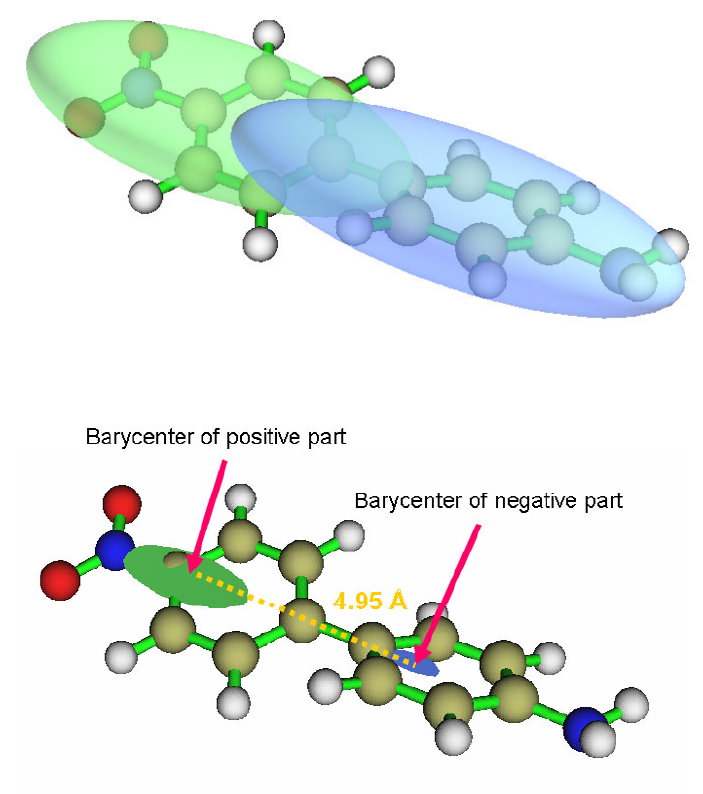
4 Tutorials and Examples
391
Overlap integral between C+ and C-: 0.742365
These information are self-explained, if you are confused, recall Section 3.21.3.
By selecting option 1, C+ (green) and C- (blue) functions can be shown up. The isovalue of
the graph shown below is 0.0015.
If the isovalue is increased to 0.0024, the positions of barycenters can be approximately
located.
From the graph it is evident that the direction of electron-transfer is from amino group side
(electron donor) to nitryl group side (electron acceptor). However the barycenters are not located
at the two substituents exactly, and especially the displacement at amino group side is non-
negligible, it suggests that electron depletion zone is markedly shifted to nearby phenyl, also the
actual electron donor is not amino group but phenyl. This finding parallels that phenyl is a weak
electron donor.
Hint: If you would like to get better display effect of the C+ and C- isosurfaces, you can use VMD program
(freely available at http://www.ks.uiuc.edu/Research/vmd/) to display them, the procedure is: Boot up VMD first,
drag Cpos.cub into VMD main window, and then drag Cneg.cub into it. Select "Graphics"-"Representations",
choose the first term in "Selected Molecule", click "Create Rep" button to create a new representation (the existing
representation is used to show molecular structure), change the "drawing method" to "isosurface", set "Draw" to
"solid surface", change the isovalue to 0.0015, set "coloring method" to "ColorID" and choose "7 green". Now the
isosurface of Cpos has been properly displayed. Next, choose the second term in "Selected Molecule", use the
similar methods to set each options, but select "0 blue" in "ColorID", and use isovalue of -0.0015. Finally, the
graph will look like the one shown above. You can also set "Material" to "transparent" so that the overlap region of
C+ and C- can be clearly distinguished.
4 Tutorials and Examples
392
4.18.4 Generate and analyze natural transition orbitals (NTOs)
In this section I illustrate how to use Multiwfn to perform the very popular natural transition
orbital (NTO) analysis with uracil as example. Please first read Section 3.21.6 to acquire basic
knowledge of NTO. Although in this example the files outputted by Gaussian were used as input
file, in fact the files outputted by ORCA are also fully supported, see Section 3.21.1.2 for detailed
requirement about the input file.
Before showing how to perform NTO analysis, I would like to let you apprehend why NTO
analysis is meaningful. As an instance, we use Gaussian to perform TDDFT calculation at
PBE0/6-31G* level for singlet excited states of uracil, you will find below information
Excited State 3: Singlet-A" 6.0180 eV 206.02 nm f=0.0000 <S**2>=0.000
26 -> 30 0.54135
26 -> 31 -0.20634
28 -> 30 -0.15424
28 -> 31 0.36715
Clearly, in excitation of S0S3, there is no dominant MO transition, the largest contribution of a
single MO pair is merely 0.541^2*2*100%=58.5%, therefore it is impossible to identify the nature
of this excitation by viewing only one MO pair. In such difficult cases, NTO analysis is often
useful, because after transforming MOs to NTOs, commonly you will be able to find only one pair
of NTO having eigenvalue very close to 1, transition between the two NTOs in this pair faithfully
represents the real character of the electronic excitation.
The input files needed for NTO analysis are the same as those needed for hole-electron
analysis exemplified in Section 4.18.1. Assume that you are a Gaussian user and you want to study
electronic excitation from ground state to the lowest three singlet excited states for uracil at TD-
PBE0/6-31G* level, what you need to do is carrying out a normal TDDFT calculation with these
keywords: # PBE1PBE/6-31G* TD IOp(9/40=4), also you need to make Gaussian generate
corresponding .fch file. The input file, output file and.fch file have already been provided in
"examples\NTO" folder. The keyword IOp(9/40=4) is very important, without it the NTO result
will be evidently inaccurate, the meaning of this IOp has been mentioned in Section 4.18.1.
Now we start to carry out NTO analysis. Boot up Multiwfn and input
examples\NTO\uracil.fch
18 // Electronic excitation analysis
6 // Generate NTOs
examples\NTO\uracil.out // Gaussian calculated three lowest excited states, you can
analyze any one of them
3 // Study transition from ground state (S0) to the 3rd excited state (S3)
Now Multiwfn loads transition information of S0S3 from the Gaussian output file and
generate NTOs, the eigenvalues of occupied and virtual NTOs are shown below
The highest 10 eigenvalues of occupied NTOs:
0.000006 0.000007 0.000015 0.000016 0.000024
0.000063 0.000121 0.000582 0.134025 0.865529
The highest 10 eigenvalues of virtual NTOs:
0.865529 0.134025 0.000582 0.000121 0.000063
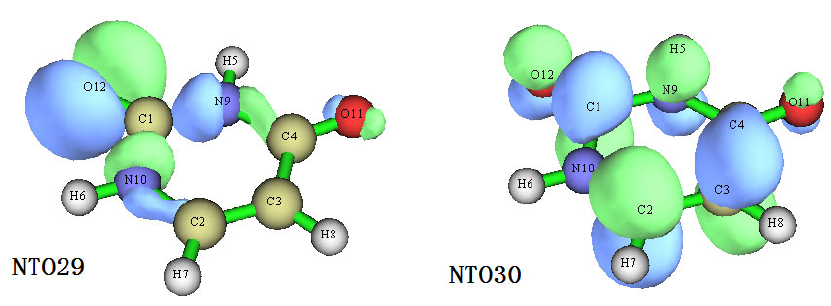
4 Tutorials and Examples
393
0.000024 0.000016 0.000015 0.000007 0.000006
It can be seen that, the eigenvalues of occupied and virtual NTOs have one-to-one correspondence,
the largest eigenvalue is 0.8655, that means that NTO pair contributes as high as 86.55% of the
S0S3 transition. So, if we would like to characterize the nature of this transition, we can only
study the occupied NTO and virtual NTO in this NTO pair.
Now you can select if outputting .fch or .molden file containing the NTOs. We choose "2
Output NTO orbitals to .fch file" and input the path to output, such as C:\S3.fch. After the .fch has
been successfully generated, you can reboot Multiwfn and load the S3.fch, in main function 0 you
can visualize the NTOs, the orbital energies now correspond to NTO eigenvalue. To plot the two
NTOs in the NTO pair with 86.55% contribution, in the GUI of main function 0 you can select
"orbital info." - "Show up to LUMO+10" in the menu, in the text window you will find output like
below
Orb: 27 Ene(au/eV): 0.000582 0.0158 Occ: 2.000000 Type: A+B
Orb: 28 Ene(au/eV): 0.134025 3.6470 Occ: 2.000000 Type: A+B
Orb: 29 Ene(au/eV): 0.865529 23.5522 Occ: 2.000000 Type: A+B
Orb: 30 Ene(au/eV): 0.865529 23.5522 Occ: 0.000000 Type: A+B
Orb: 31 Ene(au/eV): 0.134025 3.6470 Occ: 0.000000 Type: A+B
Orb: 32 Ene(au/eV): 0.000582 0.0158 Occ: 0.000000 Type: A+B
We can see that the occupied NTO with index of 29 and the virtual NTO with index of 30
constitute the NTO pair with eigenvalue of 0.8655, there we select corresponding index in the
GUI to visualize them, the isosurfaces are shown below
Undoubtedly, this S0S3 excitation can be regarded as transition from lone pair of O12 to anti-
bonding orbital of the uracil ring, at least we have 86.55% confidence to say that. From NTO
eigenvalues we notice that NTO28NTO31 transition also has small contribution (13.40%) to the
excitation, please plot corresponding orbitals and discuss their characteristic.
Note that the NTOs can also be subjected to quantitative analyses. For example, you can
enter main function 8 and use suitable options to analyze their orbital composition at quantitative
level, or you can use subfunction 11 of main function 100 to evaluate overlap extent and centroid
distance between selected two NTOs.
Sometimes we want to perform NTO analysis for a batch of excitations, for example, we
want to generate a batch of .fch files that respectively contain NTOs of S0S1, S0S2 and
S0S3 transitions, although you can manually do this in the interactive interface of Multiwfn, a
more efficient and clever way is employing shell script. If you are a Linux user, we can run below
shell script to yield S1.fch, S2.fch and S3.fch, which contain NTOs corresponding to S0S1,
4 Tutorials and Examples
394
S0S3 and S0S3. This script is very easy to understand as long as if you have basic level of
knowledge about shell programming.
#!/bin/bash
cat << EOF > allNTO.txt
18
6
examples/NTO/uracil.out
EOF
for ((i=1;i<=3;i=i+1))
do
cat << EOF >> allNTO.txt
$i
2
S$i.fch
6
EOF
done
./Multiwfn examples/NTO/uracil.fch < allNTO.txt
rm ./allNTO.txt
This script is also provided as "examples\NTO\allNTO.sh". If you do not make any modification
to the script, this script should be copied to the Multiwfn folder and run as "./allNTO.sh" in
Multiwfn folder, then S1.fch, S2.fch and S3.fch will be yielded at the same folder. In practical
studies, you should properly modify the script according to actual situation, the range of the
excitations to be studied is determined by "i=1;i<=3".
Note that NTO analysis has both advantage and disadvantage with respect to the hole-
electron analysis, this point has been mentioned at the end of Section 3.21.6. For many systems
and excitations, even if NTO transformation has been applied, there are still no NTO pair with
predominant contribution, in this case you have to use hole-electron analysis to facilitate
discussion of excitation characteristic. The drawback of hole-electron analysis is that it is unable
to present orbital phase information like NTO analysis, and it takes more computational cost.
4.18.5 Plot transition dipole moment vector contributed by molecular
fragments as arrows
In Section 4.18.1, I have shown how to plot transition dipole moment density, which is
extremely useful for studying contribution of different regions in three-dimension space. In the
hole-electron analysis module of Multiwfn, via Mulliken partition, the transition dipole moment
contributed by basis functions and atoms can also be calculated and exported, and if using a
special plotting script of VMD (http://www.ks.uiuc.edu/Research/vmd/) provided below, transition
dipole moments contributed by molecular fragments can be easily drawn as arrows, which greatly
facilitates discussion of composition of total transition dipole moment.
Here, azobenzene is taken as example. The input file of TDDFT task of Gaussian for
azobenzene is provided as example\Azobenzene.gjf. Note that IOp(9/40=4) is used and .chk file is
4 Tutorials and Examples
395
saved after calculation. Run it by Gaussian, and then convert azobenzene.chk to azobenzene.fch.
Change igenDbas parameter in settings.ini to 1, then boot up Multiwfn, load the
azobenzene.fch, then input
18 // Electronic excitation analysis
1 // hole-electron analysis
Azobenzene.out // The Gaussian output file obtained by running Azobenzene.gjf
2 // Assume that we want to study transition between ground state and the second excited
state
5 // Decompose transition dipole moment
1 // The type of transition dipole moment to be decomposed is electric
Now trdipcontri.txt is outputted to current folder, which contains transition dipole moment
contributed by each basis function and each atom. Move this file to VMD folder.
Enter subfunction 2 of main function 100, export current molecular geometry to
azobenzene.pdb.
Copy examples\loadip.tcl to VMD folder, this is a VMD script written by me, it can load data
from trdipcontri.txt. It also defines custom commands "dip" and "dipatm" used to draw transition
dipole moment contributed by specific molecular fragment as arrow.
Boot up VMD, drag azobenzene.pdb file into VMD main window to load it, then run source
loaddip.tcl in VMD console window to execute the script. Assume that we want to divide the
molecule as three parts to separately investigate their contributions to transition dipole moment,
namely the first phenyl group (atom 1~11), N2 part (atom 12 and 13) and the second phenyl group
(atom 14~24), we should run below commands in VMD console window in turn
draw color red
dip "serial 1 to 11"
dip "serial 12 13"
dip "serial 14 to 24"
Now you will see three red arrows in the VMD graphical window. The length of cylindrical part of
the arrows correspond to magnitude of fragmental transition dipole moments, the center of the
arrows correspond to geometric center of the fragments. Note that when we use "dip" command,
the fragment geometry center and quantitative contribution to transition dipole moment by the
selected fragment are also shown in VMD console window.
In order to improve the graphical quality, we input color Display Background white in
console window to set white as background color, enter Graphics - Representation and set
Drawing method to CPK, and then choose Display - Orthographic in VMD main window. The
final graph will look like below.
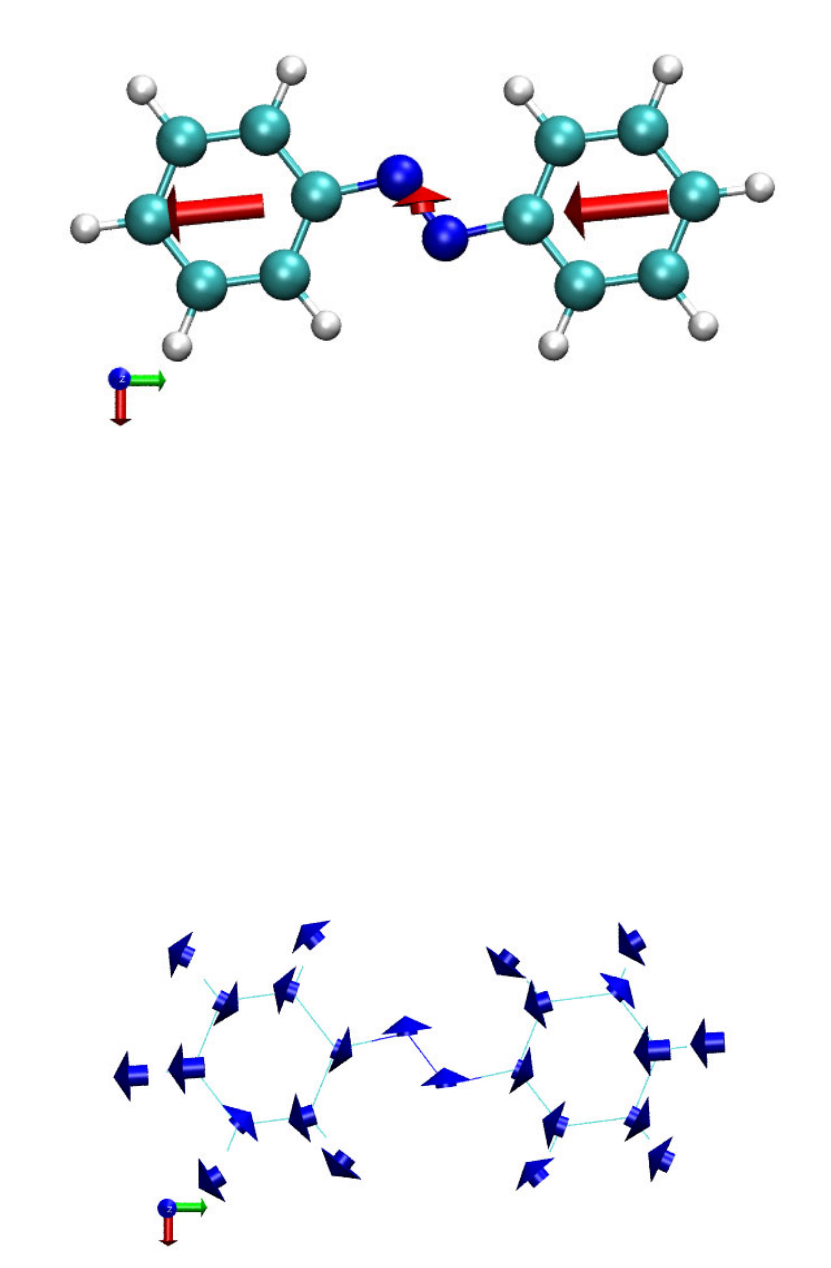
4 Tutorials and Examples
396
As you can see, both the two phenyl groups have significant contribution to Y component of
total transition dipole moment (the red, green and blue of the axis shown at left-bottom part of the
graph correspond to X, Y and Z directions, respectively). For quantitative comparison purpose,
total transition dipole moment vector and its compositions are also listed below
Total: 0.1155 -2.8868 0.0
Phenyl group 1:0.14262 -1.43288 0.0
N2: -0.16948 -0.02138 0.0
Phenyl group 2:0.14262 -1.43288 0.0
If you also want to plot total transition dipole moment as green arrow on the graph, you can
input draw color green and then input dip all.
It is also possible to plot transition dipole moment contributed by each atom. To do that, we
input draw delete all to remove all existing arrows, and then input dipatm, you will immediately
see
There is a very important point that should be paid attention to when using above method to
decompose transition dipole moment, namely contribution of a fragment is often dependent of
choice of origin, because transition charge of a fragment is often non-zero. For example, if we use
4 Tutorials and Examples
397
subfunction 6 of hole-electron analysis module to export atomic transition charges and then sum
them as fragment transition charges, you will find the value of the first phenyl group is 0.2116.
Since it is non-zero, it can be proved that if overall coordinate of the azobenzene is translated, the
transition dipole moment corresponding to this fragment must be varied; in other words, the result
is not definite. Therefore, one should carefully discuss fragmental transiton dipole moment in
papers.
Another very important point is that since the transition dipole moment is decomposed via
Mulliken method, the analysis method shown above will be meaningless when diffuse functions
are presented in the electronic excitation calculation.
4.18.6 Calculate interfragment charge transfer during electronic
excitation for 4-nitroaniline
Multiwfn has a special function to study interfragment charge transfer (CT) during electronic
excitation, please read Section 3.21.8 first before following this example. In this example, I will
illustrate how to use this function to study CT between fragments of 4-nitroaniline during its
electronic excitation. The two fragments can be defined in any manner.
The Gaussian input file of TDDFT task at PBE0/6-311G* level for 4-nitroaniline has been
provided as examples\4-nitroaniline.gjf. Note that IOp(9/40=4) is used so that Gaussian can print
enough configurational coefficients. Run it by Gaussian to obtain 4-Nitroaniline.chk and output
file, then convert the .chk file to .fch file.
Boot up Multiwfn and input below commands
4-Nitroaniline.fch
18
8 // Calculate interfragment charge transfer in electronic excitation
4-Nitroaniline.out
2 // We first analyze transition from ground state (S0) to the second excited state (S2)
Now we input atom list of fragment 1 and that of fragment 2. For example, we want to check
amount of electron transferred between the amino group and benzene moiety, we input 11-13 and
then 1-10, you will see
Electron transferred from fragment 1 to 2: 0.13129
Electron transferred from fragment 2 to 1: 0.03024
Electron net transferred from fragment 1 to 2: 0.10106
Variation of electron population of fragment 1: -0.32169
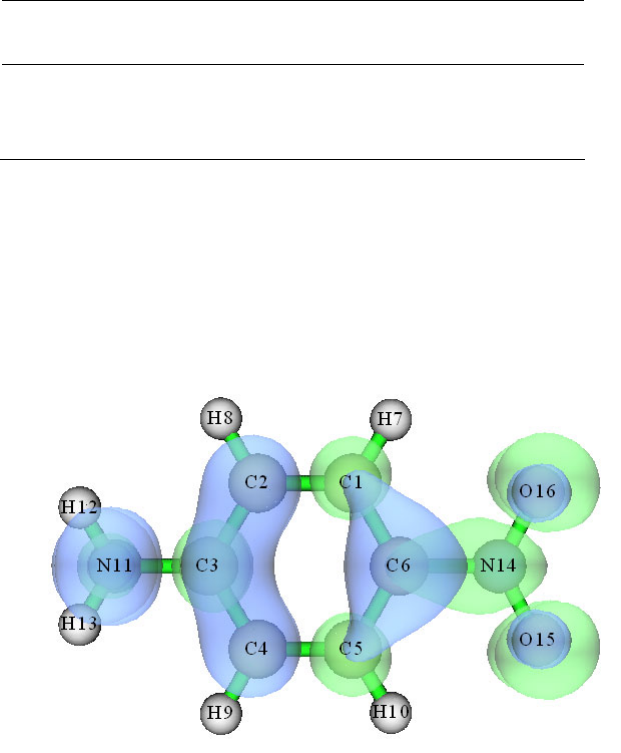
4 Tutorials and Examples
398
Variation of electron population of fragment 2: -0.19760
All the five terms are very easy to understand, if you are confused, please check corresponding
formulae in Section 3.21.8.
Then assume that we want to examine the amount of intrafragment CT within the nitro group
during the electronic excitation, we define both the two fragments as 14-16, you will see
Electron transferred from fragment 1 to 2: 0.03558
Electron transferred from fragment 2 to 1: 0.03558
Electron net transferred from fragment 1 to 2: 0.00000
Variation of electron population of fragment 1: 0.51929
Variation of electron population of fragment 2: 0.51929
The data shows that in the nitro group, 0.035 electrons are involved in the S0S2 excitation, and
the excitation leads to increase in fragment electron population by 0.519.
For facilitating discussion, I calculated all kinds of CT among the amino group, benzene
moiety and nitro group, and summarized the result in below table
Acceptor
Donor amino group benzene nitro group
amino group 0.021 0.131 0.224
benzene 0.030 0.208 0.323
nitro group 0.004 0.024 0.036
Summation of all terms exactly equals to 1.0, since what we studied is single-electron
excitation. As you can see from the table, there are three prominent interfragment CT terms (sorted
according to magnitude): benzenenitro, aminonitro, aminobenzene, all of them direct from
amino group towards nitro group. Also note that intrafragment CT within the benzene moiety is
remarkable.
For intuitively understanding above data, we plot hole-electron distribution map using the
method described in Section 4.18.1:
In the graph, hole and electron distribution correspond to blue and green, respectively. As you can
see, hole mainly distributes on the amino group and benzene moiety, while electron mainly locates
at the benzene moiety and nitro group, clearly the overall CT direction is from amino group to
nitro group, this is completely in line with our observation from quantitative interfragment CT
analysis.

4 Tutorials and Examples
399
Notice that Multiwfn by default use SCPA method to calculate atomic contributions to all
orbitals, which are needed by interfragment CT analysis. In Multiwfn, it is also possible to employ
Hirshfeld, Hirshfeld-I or Becke orbital composition to evaluate interfragment CT quantities. For
example, next we will redo above analysis based on orbital composition obtained by Hirshfeld
partition. Boot up Multiwfn and then input below commands
4-Nitroaniline.fch
8 // Orbital composition analysis
8 // Hirshfeld method
1 // Use built-in free-atom densities
-4 // Calculate and export composition of all orbitals to orbcomp.txt in current folder
0 // Return to last menu
-10 // Return to main menu
18
8 // Calculate interfragment charge transfer in electronic excitation (Since this time the
orbcomp.txt file can be found in current folder by Multiwfn, orbital composition will be directly
loaded from this file rather than automatically calculated by SCPA method)
4-Nitroaniline.out
2 // Analyze S0S2
We input 11-13 and then 1-10 to examine CT between amino group to benzene moiety, from
the printed information you can find:
Electron transferred from fragment 1 to 2: 0.10010
It is in qualitatively agreement with the result calculated based on SCPA orbital composition
(0.131).
Commonly I suggest using the default SCPA orbital composition to study interfragment CT
problem, since no additional procedure is needed and the cost of SCPA calculation is negligible.
However, if due to some special reasons diffuse functions must be employed (e.g. anion systems),
you should employ such as Hirshfeld orbital composition instead as illustrated above, because in
this case SCPA data is completely physically meaningless.
4.100 Other functions, Part 1
4.100.1 Visual study of weak interaction by RDG (NCI) and DORI
method
The RDG method, which is also known as NCI (non-covalent interaction) method is a very
popular method for studying weak interaction, and realizing this analysis is a very important
application of Multiwfn. The theory of RDG/NCI method has been detailed in J. Am. Chem. Soc.,
132, 6498 (2010) and my blog article "Visual research of weak interaction by Multiwfn" (in
Chinese, see http://sobereva.com/68). Some additional discussions and ways to improve plotting
quality can be found in "Some key points and common problems of carrying out RDG analysis via
Multiwfn+VMD" (in Chinese, see http://sobereva.com/291).
4 Tutorials and Examples
400
Use isosurface to represent weak interaction regions
The first thing is to find a way to distinguish weak interaction region from other regions.
From the table below we can know if only the regions where the value of reduced density gradient
(RDG) function is in the range of 0 to medium are reserved, then “around nuclei” and “edge of
molecule” regions will be shielded. The RDG function is defined as
3/43/12 )(
)(
)3(2
1
)RDG( r
r
r
Around nuclei Around chemical
bond
Weak interaction
region Edge of molecule
|(r)| Large 0~Minor 0~Small Very small~Small
(r) Large Medium Small 0~Small
RDG(r) Medium 0~Minor 0~ Medium Medium ~Very large
Then from remained regions, if we only extract the region where (r) is small rather than
middle, the region “around chemical bond” will be shielded and only weak interaction region is
eventually remained. Now I use phenol dimer to exemplify this analysis method. Boot up
Multiwfn and input following commands
examples\PhenolDimer.wfn
5 // Generate grid data
13 // RDG function
7 // Use middle point of two atoms as center of grid data, this way to define spatial scope is
very suitable for weak interaction analysis
1,14 // The indices of the two atoms are set to 1 and 14, because from molecular structure
(see below graph) we can estimate that the weak interaction region is between C1 and C14
40,40,40 // The weak interaction region is small, so 40*40*40=64000 grid is fine enough
3,3,3 // Extension distance in all directions are 3 Bohr, so the volume of spatial scope is
(2*3)3=216 Bohr3. This extension value is generally too small, but enough for present study.
4 // After Multiwfn finished the calculation of grid data, set isovalue for viewing RDG
isosurface
0.5 // Set isovalue to 0.5, this is recommended value for most cases, if too small, then
isosurface is too small, if too big, then unwanted “Around nuclei” and “Around chemical bond”
region will appear
-1 // Show the isosurface
You will get below graph:
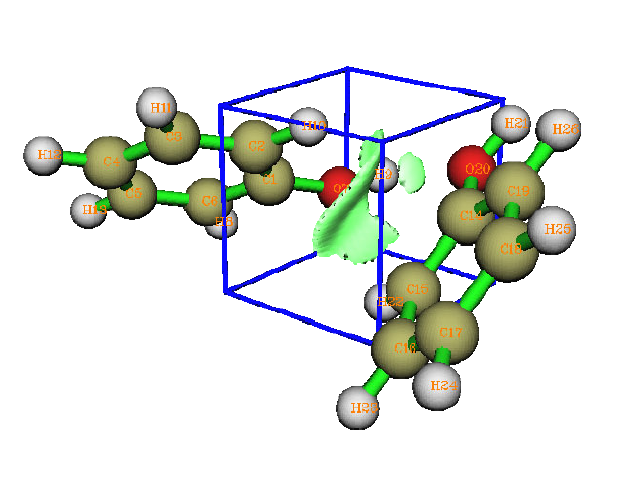
4 Tutorials and Examples
401
The isosurface represents the weak interaction region between phenol dimer very clearly.
Notice that by default, RDG function is set to an arbitrary large value (100.0) where electron
density is larger than or equal to 0.05, so that the isosurfaces in the regions “around chemical
bond” will be shielded. The threshold is determined by “RDG_maxrho” parameter in settings.ini,
0.05 is suitable for most cases.
The cubic blue frame shows spatial scope of grid data, only appears when “Show data range”
is selected in GUI window. Because the extension distance from center of grid data is set to 3.0
Bohr, so the side length is 2*3=6 Bohr.
Discriminate weak interaction types by filling color to RDG isosurface
In Bader’s AIM theory, the (3,-1) type critical point indicates electron density is aggregated at
this point, appears in chemical bond path or between the atoms which have attractive interaction;
while (3,+1) type critical point indicates electron density is depleted at this point and displays
steric effect (also called nonbond overlap), generally appears in the center of ring system. The
criterion for distinguishing (3,-1) and (3,+1) is the second largest eigenvalue of Hessian matrix of
electron density (called -2 here), if -2 exceed zero, then (3,+1), else (3,-1). Besides, the strength of
weak interaction has positive correlation with electron density in corresponding region, van der
Waals interaction regions always have very small , while the regions correspond to strong steric
effect and hydrogen bond always have relative large . So we can define a real space function
sign(-2(r))(r), that is the sign of -2 multiples . If we use different colors to represent this
function value as below and fill them to RDG isosurfaces, we can not only know where weak
interaction region is, but also know the interaction type.
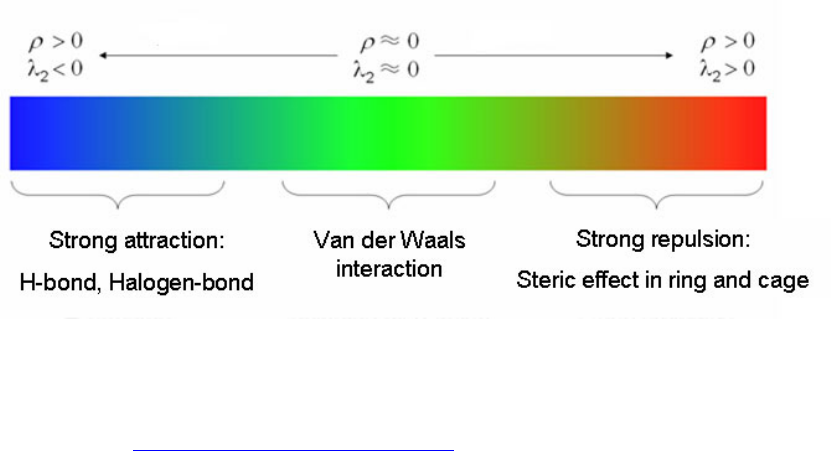
4 Tutorials and Examples
402
Unfortunately, current Multiwfn does not support plotting color-filled isosurface graph, I
recommend you to generate grid data for sign(-2) and RDG simultaneously by subfunction 1 of
function 100 of Multiwfn, and then plot the graph by VMD, which is a free software and can be
downloaded at http://www.ks.uiuc.edu/Research/vmd. I again use phenol dimer as example, this
time I do not only show you the characteristic of weak interaction region, but also ring center
region, so the spatial scope of grid data should be set to cover entire dimer.
Boot up Multiwfn and input following commands
examples\PhenolDimer.wfn
100 // Other functions
1 // Generate grid data for two real space functions in same spatial scope
15,13 // Define sign(-2) as function 1 and RDG as function 2
-10 // Set extension distance in all directions
0 // Because weak interaction regions only appear in internal region of present system, we do
not need to leave a buffer region at system boundary, so we set the extension distance to 0 Bohr
here
2 // Medium quality grid (totally about 512000 points). Because the spatial scope is larger
than last example, we need more grid points, otherwise the the RDG isosurface may look discrete
I first show you the characteristics of different kinds of regions via scatter graph, I think it
will be helpful to understand the underlying mechanism. Select option -1, a scatter graph pops up
(you can also select option 1 to export this graph as file). The X-axis and Y-axis are sign(-2) and
RDG functions respectively, each point in the graph corresponds to each grid point. There are four
spikes, and the points in their peaks are just the critical points in AIM theory. If you draw a
horizontal line, then the segments crossing the spikes just correspond to the RDG isosurfaces. So
RDG analysis method can be seen as an extension of AIM theory for visual study. The spikes can
be classified into three types, I marked them by blue, green and red circle, see below.
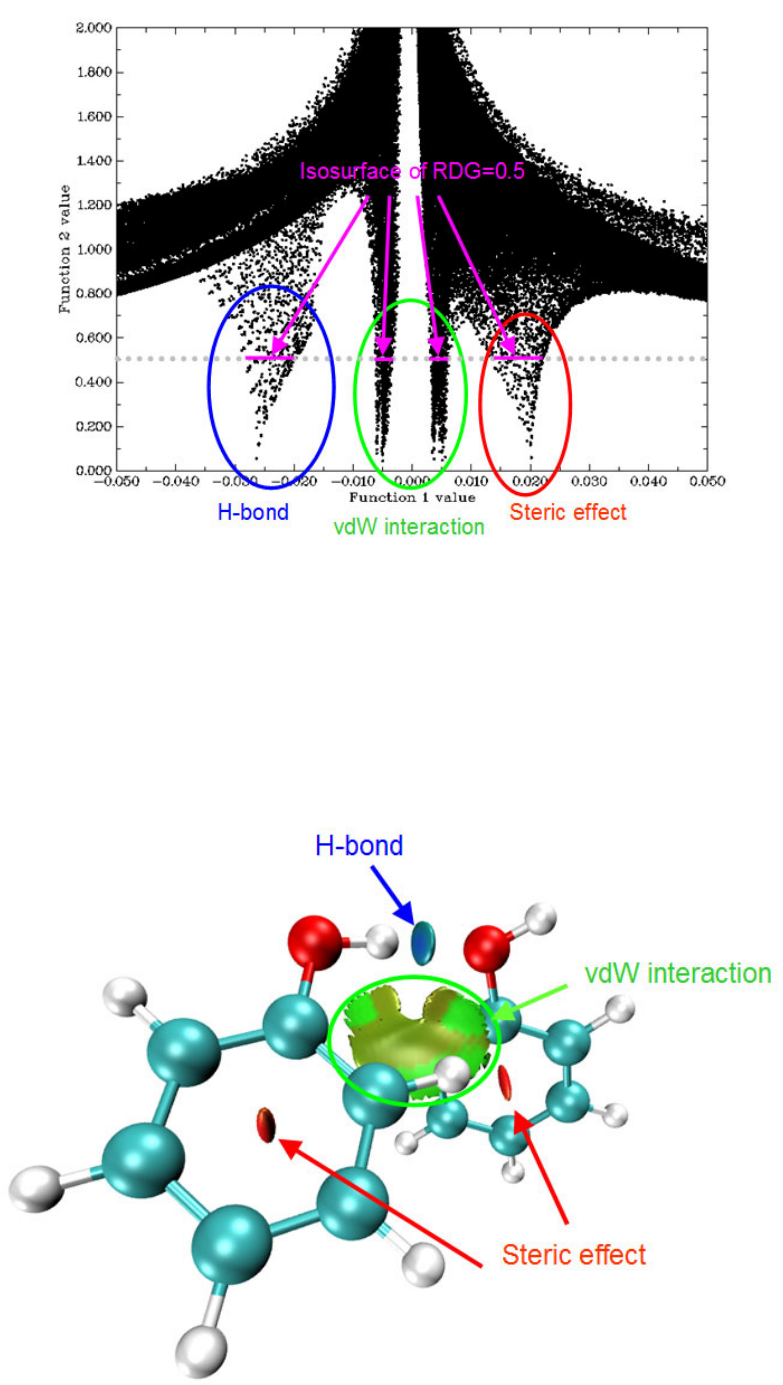
4 Tutorials and Examples
403
Now, select option 3 to export grid data of sign(-2) and RDG to func1.cub and func2.cub in
current directory, then copy them and the RDGfill.vmd file in “examples” folder to VMD install
directory. The RDGfill.vmd is a plotting script of VMD. Then boot up VMD (here I use version
1.9.2), select “file”-“Load state”, choose “RDGfill.vmd”, you will see the graph below in OpenGL
window. The default RDG isosurface is 0.5, and color range is -0.035 to 0.02, you can manually
edit the RDGfill.vmd to change the default values, current values are suitable for general cases.
(for present example, I suggest enabling "Display"-"Light 3", otherwise some parts of the
isosurfaces will be in shadow and the color cannot be faithfully exhibited)
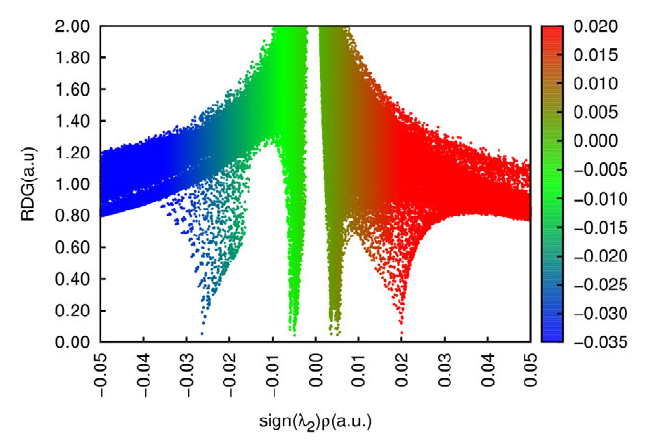
4 Tutorials and Examples
404
From the color-filled RDG isosurface, we can identify different type regions by color. Recall
the color scale bar I showed you, the more blue means the stronger interactive interaction, the
elliptical slab between oxygen and hydrogen shows light blue color, so we can conclude that there
is a hydrogen bond, but not strong. The interaction region marked by green circle can be identified
as vdW interaction region, because the filled-color is green or light brown, that means the density
electron in this region is low. Obviously, the regions in the center of rings show strong steric effect,
since they are filled by red.
It is also possible to map color to scatter map to facilitate identification of correspondence
between spikes and RDG isosurfaces. A plotting script of gnuplot program
(http://www.gnuplot.info) is provided as examples\RDGmap.gnu, which can realize this. First,
select "2 Output scatter points to output.txt", then delete first three columns of data from this file
(you can use text editor with column mode such as Ultraedit or notepad++ to do this, or simmply
use this command under Linux: cut -c 34-66 output.txt > t.txt;mv t.txt output.txt -f). Then move the
output.txt and RDGmap.gnu into the folder containing gnuplot executable file, run this command:
gnuplot RDGmap.gnu. Soon, you will obtain RDGmap.ps in present folder, this is a graphic file of
postscript format, you can open it using such as Acrobat or photoshop. The graph looks like this:
Notice that the default color range in this plotting script is from -0.035 to 0.02, if you would like
to compare this map with RDG color-filled map, you should make sure that the color scale of
RDGmap.gnu and RDGfill.vmd are completely identical.
Promolecular approximation
Calculation of wavefunction and grid data for macrosystem is very time-consuming, however,
the electron density can be approximately constructed by superposing electron densities of free-
stated atoms (so-called “Promolecular approximation”), at this time the results of RDG analysis
are shown to be still reasonable, the B3LYP/6-31G* densities of free-stated atoms (for first three
rows) are built-in data of Multiwfn. To active promolecular approximation, simply use function 14
instead of function 13 and use function 16 instead function 15 when you selecting real space
function. Since only atom coordinate information is required when promolecular approximation is
used, you can use .pdb file as input. As an example, let’s do RDG analysis for a DNA molecule
4 Tutorials and Examples
405
with 10 base-pairs, what we are interested in is only the region in the box, see below.
Boot up Multiwfn and input:
examples\DNA.pdb
100
1
16,14 // sign(-2) and RDG function with promolecular approximation
7
84,565 // Use middle point of atom 84 and 565 as center. You can view molecule structure in
main function 0 in advance to find two proper atoms used to define center
120,120,120 // Because the spatial scope of grid data is large, we need more grid points
9,9,9 // Set the extension distances in all directions to 9 Bohr
When calculation is finished, export func1.cub and func2.cub and then plot the graph by
VMD as the procedure described in last section. From the graph you will see the default isovalue
0.5 is not suitable for plotting RDG isosurface when promolecular approximation is used, so you
need to adjust it manually, choose “Graphics”-“Representation”, select the representation whose
style is “Isosurface”, then reset isovalue by inputting expected value in text box or dragging scale
bar, for present system I recommend 0.25. For better visualization, you’d better adjust “cue mode”
and “Cue Start/End” in “Display”-“Display settings...”. Finally, you will get the graph below
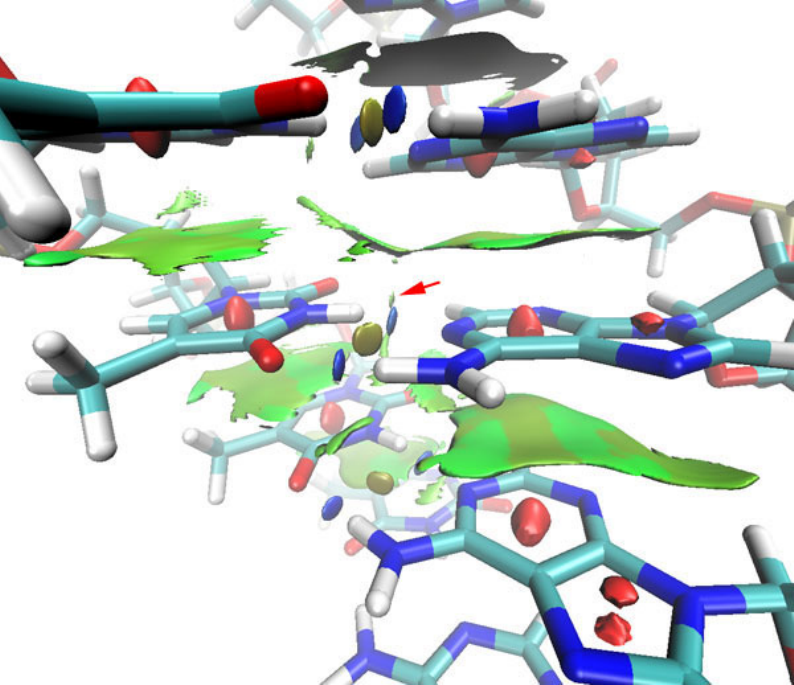
4 Tutorials and Examples
406
It is clear that there are - stacking interactions between neighbour base pairs (big pieces),
and there are two strong hydrogen bonds within each base-pairs. The region pointed by red arrow
seems to be hydrogen bond because it connects hydrogen and oxygen, however since the filled-
color is green, we can conclude that this is only vdW interaction.
Notice that, by default RDG value will be set to 100.0 where is larger than 0.1 if
promolecular approximation is used, this value may not be suitable for certain circumstance, you
can set the default threshold by “RDGprodens_maxrho” in settings.ini.
Interactively set RDG value where sign(-2) is in specific range
Multiwfn allows you to interactively set RDG value where sign(
-
2)
is in specified range.
Here I use phenol dimer under promolecular approximation as example. Firstly, set
“RDGprodens_maxrho” to 0.0 to disable automatic truncation, then generate grid data of RDG
and sign(
-
2)
for present system, after the calculation is finished, if you set X-axis range from -0.5
to 0.5 and then plot scatter graph, you will see (blue box and dash line are added by external
plotting tools)
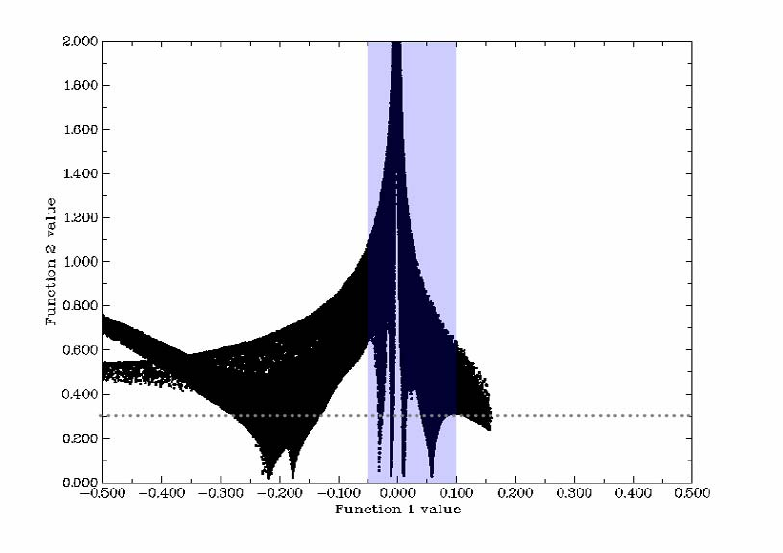
4 Tutorials and Examples
407
In above scatter plot, the blue box corresponds to weak interaction regions. Assume that you
want to plot the RDG=0.3 isosurfaces only for weak interaction regions, you should first screen
the region outside the blue box, otherwise the dashed line will intersect with the spikes around
sign(
-
2)
=-0.2 (corresponding to chemical bond regions) and the small tail at rightmost the graph,
resulting in unnecessary isosurfaces. So we choose option -3, input -0.05,0.1 and 100 in turn, then
draw scatter graph again, you will find only the region where sign(
-
2)
is within -0.05~0.1 is
preserved, and then if you plot the RDG=0.3 isosurface, only weak interaction region will be
revealed.
Simultaneously reveal covalent and non-covalent interactions
Sometimes ELF and RDG are used in combination to simultaneously investigate covalent
and non-covalent interactions, see J. Chem. Theory Comput., 8, 3993 (2012) for example. Is it
possible to study both kinds of interactions by single real space function? The answer is yes. In J.
Chem. Theory Comput., 10, 3745 (2014) the authors proposed a function named density overlap
regions indicator (DORI), it is found that when properly choosing an isosurface, both covalent and
non-covalent interaction regions can be well exhibited, and sign(
-
2)
can also be mapped on to
DORI isosurfaces to faciliate analysis of the nature of interactions. Here I use phenol dimer as
instance to show how to do this, most steps are identical to RDG analysis.
DORI is the 20th user-defined function, so before booting up Multiwfn, you should set
"iuserfunc" in settings.ini to 20. Then boot up Multiwfn and input
examples\PhenolDimer.wfn
100
1
15,100 // As seen here, user-defined function is chosen as "function 2", which corresponds to
DORI currently
-10
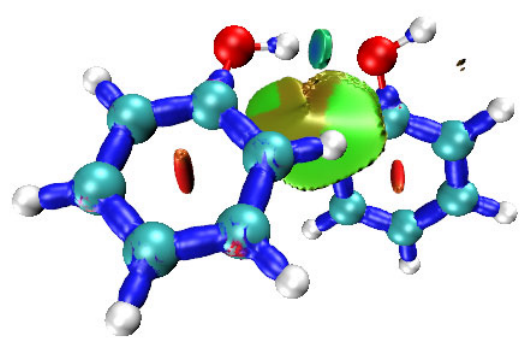
4 Tutorials and Examples
408
0 // Remove extension distance
2 // Medium quality grid
3 // Export cube file
Move func1.cub, func2.cub and examples\DORIfill.vmd to VMD folder. Then boot up VMD
and input source DORIfill.vmd in console window, you will immediately see
The graphic effect is clearly satisfactory. The weakly interaction regions are exhibited almost the
same as RDG, while the strong chemical bonding regions are nicely portrayed as blue isosurfaces.
Note that the most suited isovalue of DORI must be different for different systems, the default
isovalue is 0.95, you can modify it in the .vmd script file, or manually adjust it in Graphics -
Representations panel of VMD.
Finally, please note that Multiwfn is capable of integrating any real space function within
isosurface defined by any real space function, therefore you can study such as volume and the
number of electrons within isosurfaces of RDG or DORI to study weak interactions at quantitative
level. Illustrative examples are given in Section 4.200.14.
4.100.4 Calculate kinetic energy and nuclear attraction potential
energy of phosgene by numerical integration
I suggest you read Section 3.100.4 first, the aim of this example is to show you the usefulness
and universality of numerical integration. In quantum chemistry program, kinetic energy and
nuclear attraction potential energy integration are evaluated analytically, analytical method has
advantage in both speed and accuracy. In Multiwfn you can evaluate them by general numerical
integration function. Local kinetic energy (or called “kinetic energy density”) is a built-in function,
we first integrate this function in whole space to get total kinetic energy. Boot up Multiwfn and
input:
examples\COCl2.wfn // HF/6-31G* wavefunction
100
4 // Integrate a function in whole space
6 // Hamiltonian kinetic density K(r)
The result is 1031.1092, which is very close to the Gaussian outputted value 1031.1107.
4 Tutorials and Examples
409
Because I do not want the list of real space function becomes lengthy, so rarely used
functions such as local nuclear attraction potential energy are not chosen as built-in function,
however you can still easily make these functions available by hacking source code, please consult
Appendix 2. First, search “function userfunc” in function.f90, change the default content, namely
userfunc=1.0D0, to userfunc = -nucesp(x,y,z)*fdens(x,y,z), then recompile Multiwfn, redo above
procedure but select function 100 as integrand, you will get nuclear attraction potential energy -
2839.1668, the value outputted by Gaussian is -2839.1629, evidently they are rather close. If you
want to obtain nuclear attraction potential energy contributed from a specific orbital, use
subfunction 26 of main function 6 to set occupation number of other orbitals to zero, and then do
the integration as before.
To further illustrate the flexibility of numerical integration function in Multiwfn, assume that
you want to calculate expectation of r2 operator, you can modify the content of “userfunc” routine
to userfunc = (x*x+y*y+z*z)*fdens(x,y,z), then recompile Multiwfn and redo the integration, you
will get 444.6523, which is in excellent agreement with the Gaussian outputted value 444.6524
(behind “Electronic spatial extent (au): <R**2>”).
Tip: You may have already noticed that the two lines of the codes colored by blue above have presented in
"userfunc" routine, and they correspond to iuserfunc==12 and iuserfunc==3 respectively. So actually you needn't
to modify and recompile the source code of Multiwfn, by simply changing "iuserfunc" parameter in settings.ini
from the default value 0 to 12 and 3 respectively, the user defined real space function will be equivalent to the two
functions. For more about the built-in real space functions in "userfunc" routine, see Section 2.7.
4.100.8 Perform simple energy decomposition by using combined
fragment wavefunctions
The principle of the simple energy decomposition has been introduced in Section 3.100.8,
please read it first. Here we try to use this method to analyze components of interaction energy
between NH3 and BH3 in the adduct NH3BH3 at HF/6-31G* level. The Gaussian input and output
files involved in this section can be found in "EDA" subdirectory in "example" folder. The
Gaussian used here is G09 E.01.
(1) Perform structure optimization task for NH3BH3, and then create a new input file with the
optimized coordinate, named NH3BH3.gjf.
(2) Duplicate NH3BH3.gjf as NH3.gjf and BH3.gjf, then remove BH3 fragment in NH3.gjf,
and remove NH3 fragment in BH3.gjf. Add "pop=full nosymm" keywords in both NH3.gjf and
BH3.gjf.
(3) Run the input file of the two fragments by Gaussian respectively to generate NH3.out and
BH3.out.
(4) Boot up Multiwfn, input following commands
NH3.out //Fragment 1
100
8
2 // There are two fragments in total
BH3.out //Fragment 2
Multiwfn generates new.gjf in current folder, this is the Gaussian input file for NH3BH3 with
fragment-combined wavefunction as initial guess.
4 Tutorials and Examples
410
(5) Make sure "nosymm" keyword is presented in new.gjf. In order to output SCF energy in
each iteration, change "#" to "#P". "pop=full" keyword can be deleted.
(6) Run new.gjf by Gaussian to generate new.out.
From NH3.out, BH3.out and new.out, following information can be found
E(NH3) = -56.184295 a.u.
E(BH3) = -26.368199 a.u.
E(NH3BH3) = E_SCF_last = -82.611817 a.u.
E_SCF_1st = -82.535276 a.u.
PS: If you don't know where to find E_SCF_1st, search below information from new.out:
Cycle 1 Pass 1 IDiag 1:
E= -82.5352762791642
DIIS: error= 5.16D-02 at cycle 1 NSaved= 1.
The E_SCF_1st is the SCF energy in the first cycle of SCF process.
According to the equations shown in Section 3.100.8, we can calculate each energy term:
namely the total interaction energy between NH3 and BH3 is -155.75 KJ/mol, the orbital
interaction energy -200.96 KJ/mol stablized the adduct, while the steric energy, which is the sum
of electrostatic and exchange repulsion energy, destablized the adduct by 45.20 KJ/mol.
In present system, compared to other energy components the dispersion interaction can be
safely neglected, so we did not discuss it. However if the system you studied is the complex
bounded by weak interaction, you must evaluate the dispersion component in total interaction
energy, see the discussion in Section 3.100.8 on how to do this.
4.100.13 Calculate HOMA and Bird aromaticity index for
phenanthrene
HOMA is the most prevalently used aromaticity index based on geometry equalization, see
Section 3.100.13 for detail. Here we use HOMA to study which ring of phenanthrene has stronger
aromaticity.
Since calculation of HOMA only requires molecular coordinate, you can simply use such
as .pdb and .xyz as input file. Of course, other files containing molecular coordinate, such as .wfn
and .fch files are acceptable too. The geometry in present instance is optimized under B3LYP/6-
31G* level.
Etot = E(NH3BH3) - E(NH3) - E(BH3)= -0.059323 a.u.= -155.75 KJ/mol
Eorb = E_SCF_last - E_SCF_1st = -0.076541 a.u.= -200.96 KJ/mol
Esteric = Eels+Eex = Etot - Eorb = 0.017218 a.u.= 45.20 KJ/mol
4 Tutorials and Examples
411
Boot up Multiwfn and input following commands
examples/phenanthrene.pdb
100
13
0 // Start the calculation
You will see the default parameters are printed, they are taken from J. Chem. Inf. Comput.
Sci., 33, 70, you can also change these parameters by yourself via option 1 before the calculation.
Now we input the atom indices in the ring that we are interested in, we calculate HOMA for
the central ring first, so input 3,4,8,9,10,7, the input order must be consistent with atom
connectivity. You will immediately obtain the result shown below
Atom pair Contribution Bond length(Angstrom)
3(C ) -- 4(C ): -0.065698 1.427111
4(C ) -- 8(C ): -0.210455 1.458000
8(C ) -- 9(C ): -0.065698 1.427111
9(C ) -- 10(C ): -0.096016 1.435282
10(C ) -- 7(C ): -0.033673 1.360000
7(C ) -- 3(C ): -0.096016 1.435282
HOMA value is 0.432442
Obviously, C4-C8 deviates to ideal bond length 1.388 most significantly, giving rise to large
negative contribution to HOMA, in other words, significantly breaked aromaticity. The HOMA
value is calculated as 1 plus the contributions from all bonds in the ring.
Then input 8,15,14,13,11,9 to calculate HOMA for the boundary ring, the result is 0.855126.
Since this value is much closer to 1 than the one for central ring, HOMA suggests that the two
boundary rings have stronger aromaticity.
Bird index is another quantity used to measure degree of aromaticity, see Section 3.100.13
for a brief description. Now choose option 2 to calculate Bird index for the two rings, you will
find the value for boundary ring is more close to 100 than the central ring. Likewise HOMA, Bird
index also indicates that the two boundary rings have stronger aromaticity.
4.100.14 Calculate LOLIPOP for phenanthrene
In this instance, we use LOLIPOP (Localized Orbital Locator Integrated Pi Over Plane) index
to evaluate which ring of phenanthrene has stronger π-stacking ability. For detail about LOLIPOP,
see Section 3.100.14 and the paper Chem. Commun., 48, 9239.
Boot up Multiwfn and input following commands
examples/phenanthrene.wfn
100
4 Tutorials and Examples
412
14
1 // Specify π orbitals
36,40,43,44,45,46,47 //These orbitals are π orbitals. You can find out π orbitals by
visualizing orbital isosurfaces via main function 0 or by function 22 of main function 100
0 // Start the calculation
8,9,11,13,14,15 // The indices of the atoms in the ring you are interested in. This ring is
boundary ring
Wait for a while, from screen we can see that the LOLIPOP value is 8.233.
0 // Start the calculation again
7,3,4,8,9,10 // Central ring
The LOLIPOP value is 6.183
Since smaller LOLIPOP value corresponds to stronger π-stacking ability, we can expect that
the tendency of forming π-stacking structure for central ring is stronger than for boundary ring.
4.100.15 Calculate intermolecular orbital overlap integral of DB-TTF
Intermolecular orbital overlap integral is important in discussions of intermolecular charge
transfer, see Section 3.100.15 for introduction. In this example, we calculate HOMO-HOMO and
LUMO-LUMO overlap integrals between the two DB-TTF (Dibenzotetrathiafulvalene) monomers
in below dimer. The dimer structure was extracted from CSD (Cambridge Structural Database).
The wavefunction level we used is PW91PW91/6-31G*, MO78 and MO79 correspond to HOMO
and LUMO, respectively.
First, we construct a Gaussian input file for dimer according to the structure. iop(3/33=1)
nosymm guess(only) should be present in route section. IOp(3/33=1) tells Gaussian to output
overlap matrix in original basis; nosymm instructs Gaussian to do not adjust the coordinate to
standard orientation; guess(only) is specified because we do not require converged wavefunction
of the dimer. The input file is provided as examples\intermol\DB-TTFdimer.gjf. Run it by Gaussian,
and then we obtain DB-TTFdimer.out.
Next, we extract the first and the second monomer coordinates in turn from the dimer input
file to construct two Gaussian input files for the two monomers, named as DB-TTF1.gjf and DB-
TTF2.gjf, the two files can also be found in examples\intermol folder. nosymm and pop=full
should be specified in route section. Use Gaussian to run the two files to yield DB-TTF1.out and
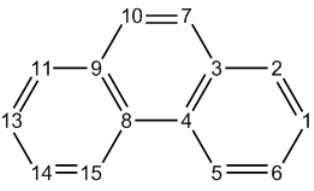
4 Tutorials and Examples
413
DB-TTF2.out.
After that, boot up Multiwfn, and input below commands:
DB-TTFdimer.out
100
15 // Then Multiwfn will read overlap matrix (in original basis) from DB-TTFdimer.out
DB-TTF1.out // Multiwfn will read MO coefficients of monomer 1 from the file
DB-TTF2.out // Multiwfn will read MO coefficients of monomer 2 from the file
Now, input such as i,j then the intermolecular orbital overlap integral between MO i in
monomer 1 and MO j in monomer 2 will be printed. To obtain the integral between HOMO-
HOMO, input 78,78, we immediately get -0.01389242; Then input 79,79, we will find the integral
between LUMO-LUMO is 0.00906935.
4.100.18 Yoshizawa's electron transmission route analysis for
phenanthrene
In this example, we will use Yoshizawa's formula (Acc. Chem. Res., 45, 1612) to analyze
favourable electron transimission routes for phenanthrene. Related theory, requirement of input
file and program options have been introduced in Section 3.100.18. The numbering scheme of the
carbons is shown below.
Boot up Multiwfn and input following commands:
examples\phenanthrene_NAOMO.out //The Gaussian output file containing "NAOMO"
information
2 // Select YZ plane, which is the molecular plane
Then program will detect which atom has expected pz atomic orbitals, and load their
expansion coefficients in all MOs.
Now we select 1, and input 2,11 to check the the transmission probability between 2 and 11.
From the output we can know that the transmission probability is 0.855879. The contributions
from each MO are also shown. From the output we also know that the probability will be
2.144432 if only HOMO and LUMO are considered. Although Yoshizawa's paper said that in
common one only need to taken HOMO and LUMO into account, it seems that this approximation
is not true in quantitative level. The distance route 5.674656 Angstrom is the distance between
atom 2 and 11.
Next, we examine which transport routes are the most favourable. Suppose that this time we
only want to consider HOMO and LUMO, so we choose option -1 and input 47,48. Then choose
option 2, you will see
Note: The routes whose absolute value < 0.010000 will not be shown
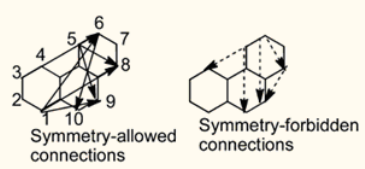
4 Tutorials and Examples
414
Note: The routes whose distance < 0.0000 or > 9999.0000 Angstrom will not be shown
Atom 7 -- Atom 10 Value and distance: 3.743670 1.359562
Atom 6 -- Atom 10 Value and distance: 3.098919 5.081382
Atom 7 -- Atom 14 Value and distance: 3.098919 5.081382
Atom 7 -- Atom 11 Value and distance: -2.831680 3.720990
Atom 2 -- Atom 10 Value and distance: -2.831680 3.720990
Atom 6 -- Atom 14 Value and distance: 2.565337 5.765892
...
Atom 6 -- Atom 9 Value and distance: -0.016585 4.927289
Atom 3 -- Atom 14 Value and distance: -0.016585 4.927289
Atom 2 -- Atom 4 Value and distance: -0.014931 2.456189
Atom 8 -- Atom 11 Value and distance: -0.014931 2.456189
The routes are ranked by transmission probability (absolute value). If we ignore the atoms
linking three carbons and the duplicated routes due to symmetry, the most favourable four routes
are 7-10, 6-10, 7-11, 6-14. This conclusion is completely in line with below graph in Yoshizawa's
paper!
Note that Yoshizawa stated that connection 9-10 (corresponding to 7-10 in our numbering
scheme) is predicted to be the best route from the rule, but it is too close to construct a metal-
molecule-metal junction for connection, so the route was not marked on the his graph.
Now we check the feasible routes started from atom 2. Choose option 3, and input 2, you will
see
To atom 10 Value and distance (Angstrom): -2.831680 3.720990
To atom 14 Value and distance (Angstrom): -2.344569 6.206600
To atom 11 Value and distance (Angstrom): 2.144432 5.674656
To atom 5 Value and distance (Angstrom): -1.571512 2.787501
...
Evidently, 2-10 is the most favourable route.
4.100.19 ELF analysis on the promolecular wavefunction combined
from fragment wavefunctions
Before reading this section please read Section 3.100.19 first.
It is usually interesting to analyze the characteristic of promolecular wavefunction, which
corresponds to the state without any electron transfer and polarization due to the interaction
between the fragments constituting the system. Commonly, we can use "custom operation" in
main function 3, 4 and 5 to realize this purpose, see Section 3.7 for introduction of custom
operation and some illustrative applications in Sections 4.5.4 and 4.5.5. For example, we want to
4 Tutorials and Examples
415
study electron density distribution of promolecular state of a complex AB, by using custom
operation, we can very conveniently instruct Multiwfn to calculate electron density of A and that
of B respectively, and then sum them up as electron density of the promolecule state. However,
this process is not applicable to non-linear real space functions such as ELF; that is to say, ELF of
promolecular state of AB is not equal to the sum of ELF of A and ELF of B, the result is
completely meaningless. For such cases, we should combine fragment wavefunctions first as
promolecular wavefunction, and then calculate ELF for it to obtain the ELF distribution in
promolecular state.
Below I will show how to use Multiwfn to produce promolecular wavefunction for COBH3
based on fragment wavefunctions of CO and BH3, and then discuss the corresponding ELF
character. The .wfn files used below and the corresponding Gaussian .gjf files can be found in
"examples\genpromol" folder.
Boot up Multiwfn and then input
examples\genpromol\COBH3\CO.wfn // The path of wavefunction file of fragment 1
100
19 // Generate promolecular .wfn file from fragment wavefunctions
2 // Two fragments in total
examples\genpromol\COBH3\BH3.wfn // The path of wavefunction file of fragment 2
Now the promolecular wavefunction file of COBH3 has been outputted to promol.wfn in
current folder.
Let's plot ELF for this promolecular wavefunction. Reboot Multiwfn and input
promol.wfn
4 // Draw plane map
9 // ELF
1 // Color-filled map
[Press ENTER button]
2 // XZ plane
0 // Y=0
Interestingly, even in the promolecular state, from the resultant graph it looks as if the carbon
and boron have been bonded to each other. In order to make clear how the relaxation of electron
distribution affects the ELF character of COBH3, we decide to draw difference map of ELF
between the actual state and promolecular state.
Reboot Multiwfn and input
examples\genpromol\COBH3\COBH3.wfn // Wavefunction file of actual state of COBH3
4 // Draw plane map
0 // Custom operation
1 // Deal with only one file
-,promol.wfn // Subtracting property of COBH3.wfn by that of promol.wfn
9 // ELF
1 // Color-filled map
[Press ENTER button]
2 // XZ plane
0 // Y=0
Close the graph and then input
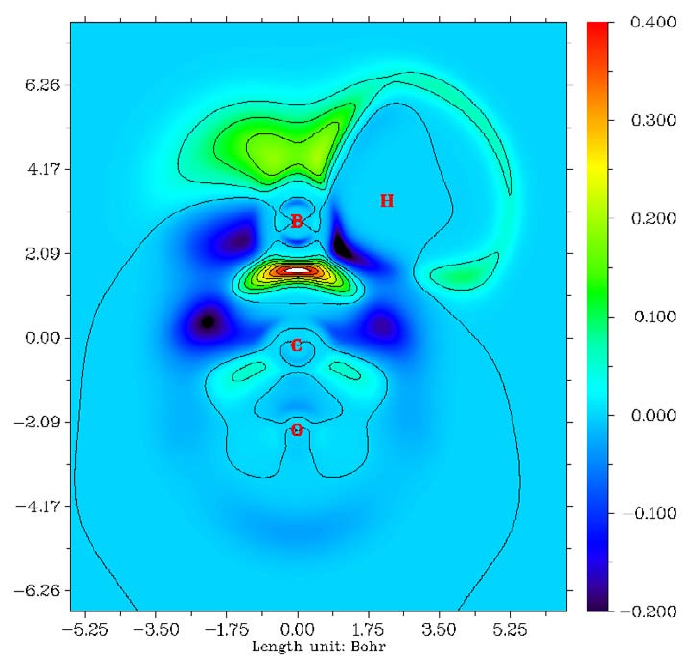
4 Tutorials and Examples
416
1
-0.2,0.4 // Set the color scale from -0.2 to 0.4, since as you can see from the command-line
window, in this plane the data range is from -0.248 to 0.436
2 // Enable showing contour lines
-1 // Show the graph again
From this difference map of ELF, it is very clear that after electron relaxation, the electron
localization character between the C-B bond enhanced evidently.
Next I will show how to create promolecular wavefunction when open-shell fragments are
involved. CH3NH2 is taken as example, the two fragments are CH3 and NH2 free-radicals. Boot up
Multiwfn and input
examples\genpromol\CH3NH2\CH3.wfn
100
19
2
examples\genpromol\CH3NH2\NH2.wfn
n // Do not flip spin of orbitals of CH3
y // Flip spin of orbitals of NH2. If you do not understand why the spin should be flipped,
you can consult the corresponding CDA example in Section 4.16.2.
Now you have promolecular wavefunction of CH3NH2 in current folder. Try to plot ELF for
it and compare the result with actual state (i.e. examples\genpromol\CH3NH2\CH3NH2.wfn)
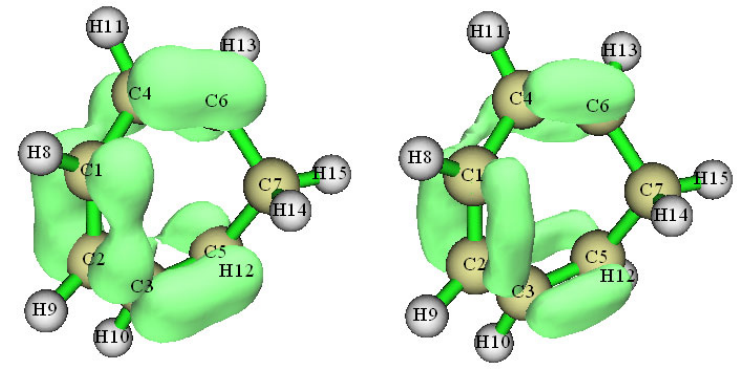
4 Tutorials and Examples
417
4.100.22 Analyze electron character of non-planar system:
cycloheptatriene
Before reading this section please read Sections 3.100.22 and 4.5.3 first. In Section 4.5.3, I
have mentioned how to let Multiwfn automatically detect orbitals for a exactly planar system
and then separately study and electron characters by means of ELF- and ELF-. In this
section, I will show that it is also possible to make Multiwfn automatically identify type of
localized molecular orbitals for non-planar system, so that individually studying and electrons
can be easily carried out. We will use a simple non-planar molecule cycloheptatriene as example.
For non-planar system, to separate and electrons, the molecular orbitals must be firstly
transformed to localized molecular orbitals (LMOs). Boot up Multiwfn and input:
examples\ cycloheptatriene.fch
200
13 // Orbital localization
1 // Localize occupied orbitals
0 // Return
100
22 // Detect orbitals
-1 // This mode is specific for LMOs
0 // Detect LMOs under default settings
There are three LMOs identified, assume that we will study electron character, so we
choose 2 to set occupation number of all other orbitals to zero. Then we can carry out any kind of
analysis, the result will be only contributed by electrons. For example, we plot electron density
isosurface map (isovalue=0.03 a.u.) and LOL isosurface map (isovalue=0.5) using main function 5,
they are shown below as left and right graphs, respectively.
From both the graphs, it is easy to recognize that C4-C6, C1-C2 and C3-C5 must be stronger than
C1-C4 and C2-C3, since electrons are delocalized much more substantially among the
corresponding two atoms in the formers
The function illustrated in this section is quite powerful, and can also be applied to large
systems. For example, below left graph is LOL- isosurface map (isovalue=0.55) of helicene
plotted using above procedure. Moreover, using option "5 Set constraint of atom range", one can
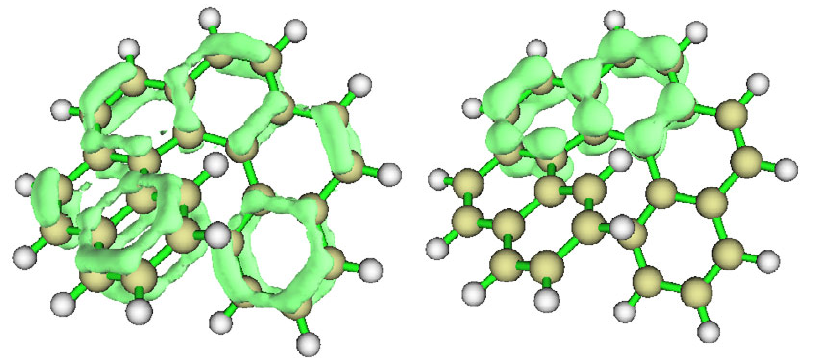
4 Tutorials and Examples
418
define constraint of the region for identifying LMOs. For example, below right graph shows the
electron density of helicene contributed by five LMOs located at the central two six-membered
rings.
4.200 Other functions, Part 2
4.200.1 Visually studying weak interaction in molecular dynamics
simulation by aRDG method
If you are not familiar with RDG analysis method, you should first read the introduction
given in Section 4.100.1. The theory exemplified in this section is a generalization of RDG
analysis method (known as aRDG method), so that the weak interaction can also be revealed in
fluctuation environment, e.g. molecular dynamics (MD) or Monte Carlo simulation. The basic
principle of aRDG is proposed in J. Chem. Theory Comput., 9, 2226, and I have also briefed it in
Section 3.200.1.
In this example I will show how to use Multiwfn to visually study the weak interaction
between waters in the MD simulation of bulk water system. You can use any program to perform
the MD, as long as you know how to convert the trajectory to .xyz trajectory. Here I assume that
you are a GROMACS 4.5 user. The detailed steps of the MD process are given below, all of the
related files can be found in "examples\aRDG" folder.
Generating MD trajectory by GROMACS
First, build a file named "emptybox.gro", which records a blank box, and the side length in
each direction is 2.5nm. Then run below command to fill the box with waters.
genbox -cp emptybox.gro -cs spc216.gro -o water.gro
Run below command and select "GROMOS96 53a6 force field" to obtain the top file of the
bulk water system. SPC/E water model is employed.
pdb2gmx -f water.gro -o water.gro -p water.top -water spce

4 Tutorials and Examples
419
Then carry out NPT MD by 100ps to equilibrate the bulk water at 298.15K, 1atm
environment.
grompp -f pr.mdp -c water.gro -p water.top -o water-pr.tpr
mdrun -v -deffnm water-pr
Using VMD program to load water-pr.gro, select a water close to the center of the box. We
select the water with resid index of 101, which is highlighted in below graph. Note that the two
hydrogens in this water have index of 302 and 303, and the index of the oxygen is 301.
This water will be freezed in the following MD simulation. In order to do so, we generate
index file, namely inputting below commands
make_ndx -f water-pr.gro
ri 101
q
Run following command to do 1ns equilibrium MD simulation at 298.15K, the trajectory will
be saved every 1ps, and finally we will obtain 1000 frames. The water with resid index of 101 is
freezed via the keyword "freezegrps = r_101". Note that NVT ensemble instead of NPT is used,
because NPT process will scale the coordinate of the atoms, which somewhat destorys the effect
of freezing.
grompp -f md.mdp -c water-pr.gro -p water.top -o water-md.tpr -n index.ndx
mdrun -v -deffnm water-md
Load "water-pr.gro" and "water-md.xtc" into VMD in turn, select "File"-"Save Coordinate..."
option and set the file type as xyz, then set "Selected atoms" as "all", input 1 and 1000 in the
"First" and "Last" window respectively, then click "Save" button to convert the GROMACS
trajectory to wat.xyz.
Generating grid data by Multiwfn
Boot up Multiwfn and input following commands
wat.xyz
200 // Main function 200
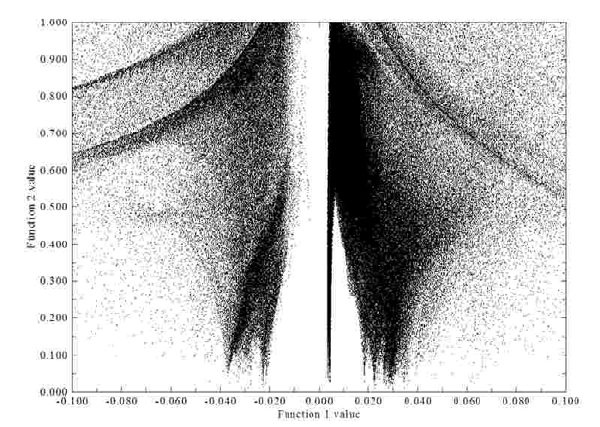
4 Tutorials and Examples
420
1 // aRDG analysis
1,1000 // The range of the frames to be analyzed
7
301,301 // Using atom 301 (the oxygen of the freezed water) as the box center of the grid
data
80,80,80 // The number of grid points in each side
4.5,4.5,4.5 // Extend 4.5 Bohr in each side
Now Multiwfn starts to calculate electron density, its gradient and Hessian of each frame,
then their average quantities will be obtained, and finally Multiwfn calculates average RDG and
average sign(lambda2)rho. The whole process is time-consuming; at a common Intel 4-cores
computer about half an hour will be consumed. (Note that the electron density I referred here is
produced by promolecular approximation, which is constructed by simply superposing the density
of the atoms in their free-state)
After the calculation is finished, you can select option 1 to check the scatter plot between
average RDG (X-axis) and average sign(lambda2)rho (Y-axis), see below, there is also option used
to export the corresponding data points to plain text file.
Select 6 to export the grid data of average RDG and average sign(lambda2)rho as
avgRDG.cub and avgsl2r.cub in current folder, respectively.
Since we wish to check the stability of weak interaction, we also select 7 to export thermal
fluctuation index to thermflu.cub in current folder. Note that this process requires recomputing
electron density of each frame, and thus is time-consuming.
Analysis
Copy avgRDG.cub, avgsl2r.cub, thermflu.cub as well as avgRDG.vmd and
avgRDG_TFI.vmd in "examples\aRDG" folder to the directory of VMD program.
Simply boot up VMD and input source avgRDG.vmd in its console window, the average RDG
isosurface will be shown up with isovalue of 0.25, meantime the average sign(lambda2)rho is
mapped on the isosurface by various color. In order to make the graph clearer, one should screen
unrelated atoms, that is enter "Graphics-Representation", then select the entry whose "style" is

4 Tutorials and Examples
421
"CPK", and input serial 301 302 303 in the "Selected Atoms" box and then press ENTER button.
Now only the water with resid index of 101 presents in the graph. After proper rotation and
translation of view, you will see
Unfortunately, around the water of interest, there are large amount noisy isosurfaces, which
somewhat messed up the graph, thus it is better to shield them. This aim can be achieved by main
function 13 of Multiwfn, the steps are described below.
Write a plain text file named index.txt, whose content is
3 // The number of atoms
301 302 303 // The index of the atoms
Then boot up Multiwfn and input
avgRDG.cub
13 // Process grid data
13 // Set the value of the grid points far away from specific atoms
1.5 // If the distance between a grid point and any atom recorded in index.txt is longer than
1.5 times of vdW radius of corresponding atom, then the value of the grid point will be set as
given value
100 // The given value is 100, which is arbitrary, as long as larger than the isovalue of the
RDG isosurfaces (0.25)
index.txt // Which specifies the atoms of interest
0 // Export the updated grid data to a new cube file
avgRDG.cub // The name of the new cube file
Copy the newly generated avgRDG.cub to the folder of VMD program to overlay the old one,
then use the script avgRDG.vmd again to plot the graph, after some adjustments you will see (for
clarity, the view of two sides are shown at the same time)

4 Tutorials and Examples
422
The graph we obtained this time is very clear. The color scale is from -0.25 to 0.25,
corresponding to the color variation of Blue-Green-Red. More blue denotes electrostatic
interaction or H-bond effect in corresponding region is stronger, and more red suggests more
intensive steric effect. Green region implies low electron density, corresponding to vdW
interaction. From the graph one can see that there are two blue ellipses near the two hydrogens,
rendering that in the MD process, strong H-bonds are formed due to the O-H group. The slender
green isosurface exhibits in which direction this water prefers to interact with other waters by vdW
interaction. There is a big lump of isosurface above the oxygen, on which the red color appears in
the middle part, while blue color occurs at the two ends; the latter reflects that the two lone pairs
of the oxygen act as H-bond acceptors during the simulation, while the former reveals the
repulsive interaction zone between waters. Note that if we set the isosurface of RDG smaller (e.g.
0.18), then this isosurface will be dissected as two, which perhaps correspond to the two
coordination shells of the water.
Next, we study the stability of the weak interactions. First disable present isosurfaces, and
then input the command source avgRDG_TFI.vmd in the console window, after some adjustments
you will see
The color scale is 0~1.5, still corresponding to the color transition of Blue-Green-Red. More
blue (red) means the thermal fluctuation index (TFI) is smaller (larger), and hence the weak
4 Tutorials and Examples
423
interaction in corresponding region is more stable (unstable). The graph shows that it is stable that
the water behaves as H-bond donor, while the stability of the water acting as H-bond acceptor is
slightly weaker; the vdW interaction region is totally red, rendering that vdW interaction is
evidently unstable compared to hydrogen bonding.
4.200.4 Study iso-chemical shielding surface (ICSS) and magnetic
shielding distribution for benzene
Iso-chemical shielding surface (ICSS) denotes isosurface of magnetic shielding value, which
presents intuitive picture on aromaticity. If you are familiar with NICS, you can also simply view
ICSS as the isosurface of NICS with inverted sign. Please see Section 3.200.4 for more
information. In this example we will study benzene, since this is a planar system, we will plot
ICSSZZ instead of ICSS, namely only the component of magnetic shielding tensor perpendicular to
molecular planar will be taken into account. ICSSZZ must be more physically meaningful than
ICSS, just like NICSZZ is a better aromaticity index than NICS (proved in Org. Lett., 8, 863).
Meanwhile I will also show how to plot magnetic shielding value in a line and in a plane.
Note that Multiwfn itself is incapable of calculating magnetic shielding tensor and requires
Gaussian to do that.
Before running Multiwfn, you should prepare a Gaussian input file of standard single point
task for present system, which later will be taken as template. This file has already been provided
as "examples\ICSS\benzene.gjf". Meantime, you should prepare a file containing the structure of
corresponding system, for benzene this file is provided as "examples\ICSS\benzene.pdb"
Boot up Multiwfn and input below commands
examples\ICSS\benzene.pdb // Note that molecular plane is in XY plane
200 // Other functions (Part2)
4 // Generate grid data of ICSS or related quantities
-10 // Change extension distance, because the default value is somewhat too small for this
molecule
12 // 12 Bohr of extension distance
1 // Low quality grid, magnetic shielding tensor at 130910 points will be calculated by
Gaussian later. Since present system is not very small, using medium or better quality grid will be
expensive
n // Do not skip the step of generating Gaussian input file, because this is the first time we
carry out analysis and thus currently we do not have Gaussian input/output files in hand
examples\ICSS\benzene.gjf // The path of template input file
Now Multiwfn generates a lot of Gaussian input files of NMR task in currenet folder based
on the template file. The files are named as NICS0001.gjf, NICS0002.gjf ... NICS0017.gjf. Run
these files by Gaussian.
Note: If these files cannot be runned by your Gaussian normally, please check the tail of the output file, there
are two common reasons:
(1) The %mem is too small to finish the task, you need to set %mem in the template .gjf file to a large value
and retry.
(2) The "NICSnptlim" in settings.ini is too large, you should properly reduce it and try again. The reason is
that in Gaussian there is a limit on the number of Bq atoms, and it is somewhat dependant of the version of
Gaussian and your computer. Beware that for G09 D.01 and may be some later versions, you should always add
"guess=huckel" keyword, otherwise due to memory allocation bug the NICSnptlim has to be reduced to a very
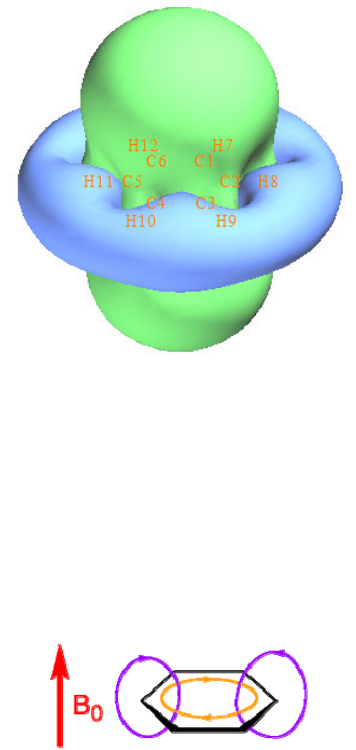
4 Tutorials and Examples
424
small value to make Gaussian run normally; in this case the overall computational cost will be quite high.
Hint: You can make use of the script "examples\runall.sh" (for Linux) or "examples\runall.bat" (for Windows),
which invokes Gaussian to run all .gjf files in current folder to yield output files with the same name but with .out
suffix.
Assume that the output files (NICS0001.out, NICS0002.out...) have been placed in
"C:\benzene" folder, in the window of Multiwfn input C:\benzene\NICS and then input 5 to select
ZZ component, Multiwfn will load these output files and convert magnetic shielding tensors to
grid data of ICSSZZ. After that you can see a new menu, you can directly visualize isosurface of
the grid data by option 1, export it as cube file by option 2 or re-select the property you are
interested in, for example ICSS or ICSSXX. The isosurface of ICSSZZ=2.0 is shown below
As you can see, the green isosurface (positive Z-component shielding value), completely
covers the region above and below the benzene ring, suggesting that due to the induced ring
current originated from the globally delocalized π-electrons, the Z-direction external magnetic
field is largely shielded in these regions, this observation implies the strong aromaticity of
benzene. From below scheme we can understand the ICSSZZ more deeply; in the cylindrical
region perpendicular to and through the benzene, the direction of induced magnetic field (purple
arrows) is exactly opposite to external magnetic field (B0), this is why in this region Z-component
of magnetic shielding value is large.
You can also see, blue isosurface (negative Z-component shielding value) presents in the
outlier region of benzene, exhibiting de-shielding effect. This is mostly because the induced
magnetic field is parallel to B0 and thus enhances B0 in this region.
If you properly rotate viewpoint, you will clearly find the C-H bond is also completely
covered by the green surface. The reason is that the σ-electrons involved in the C-H bonding form
conspicuous local induced ring current, so the external magnetic field is also strongly shielded
around the C-H bond.
Now close the GUI window, and select 2 to export the grid data to ICSSZZ.cub in current
folder.
Digression: Assume that you have obtained the Gaussian output files, and the Multiwfn instance has been
terminated due to some reasons, but now you would like to re-analyze ICSS for this system, you should exactly
repeat the steps what you have done before, the grid must be set in the same manner, then when Multiwfn asks you
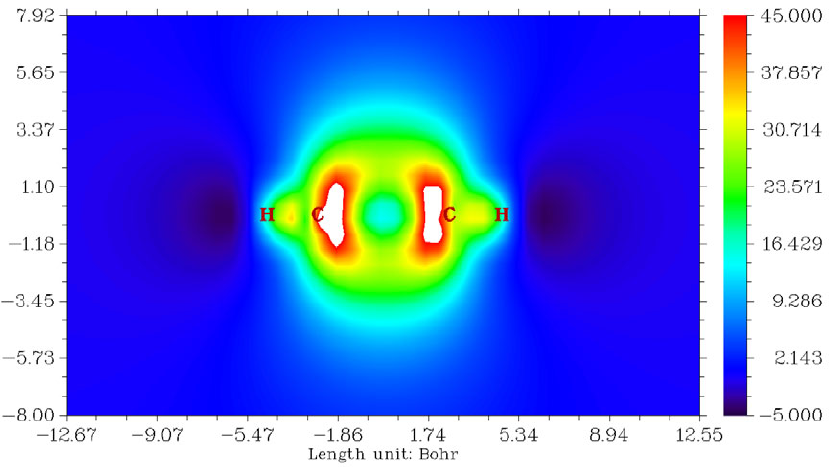
4 Tutorials and Examples
425
"If skip generating Gaussian input file of NMR task?", you should input "y", then the Gaussian input files will not
be re-generated, and you can directly feed the Gaussian output files you have obtained into Multiwfn.
Next I will show how to plot magnetic shielding value in a line and in a plane. Since we
already have grid data of ICSSZZ in hand, magnetic shielding value at any point in a line/plane can
be easily obtained by means of linear interpolation technique based on the grid data.
We first plot color-filled map for ICSSZZ in the YZ plane with X=0. This plane is normal to
benzene and crosses C4-H10 and C1-H7. Set "iuserfunc" in settings.ini to -1, and then boot up a
new Multiwfn instance and input below commands
ICSSZZ.cub
4 // Plot plane map
100 //User-defined function, which now corresponds to the function interpolated by the
grid data of ICSSZZ.cub
1 // Color-filled map
[Press Enter]
0 // Set extension distance of the plot
8
3 // YZ plane
0 // X=0
Now the graph pops up, close it and then input
4 // Show atom labels
11 // Crimson text
1 // Change lower and upper limit
-5,45
-1 // Replot the map
Now you can see below map
From the graph one can find that although Z-component of magnetic shielding in the center
of benzene is an evident positive value, the magnitude is by far less than in the region above and
below the ring plane. The reason is clear, that is benzene only has π-aromaticity, while its σ-
electrons are not globally delocalized to form σ-aromaticity, so the shielding effect is relatively
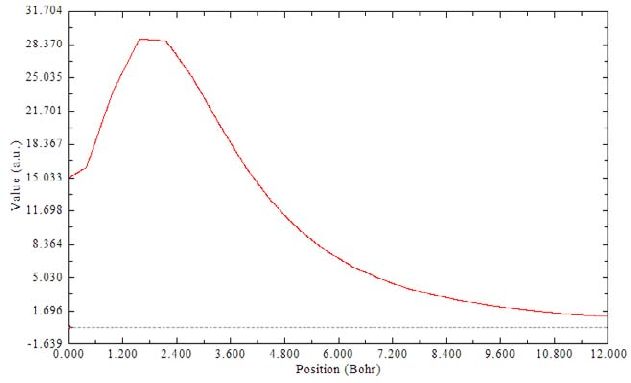
4 Tutorials and Examples
426
weak in the plane due to lack of contribution of σ-ring current.
Next, we plot curve map to study the variation of magnetic shielding in the line perpendicular
to ring plane and starting from ring center. Choose -5 to return to main menu and input
3 // Plot curve map
100
2 // Input coordinate of two points to define a line
0,0,0,0,0,12 // The line starts from ring center (0,0,0) and ends at 12 Bohr above the ring
plane
You will immediately see
It can be seen that the maximum of Z-component of magnetic shielding value occurs about
1.8 Bohr above the ring plane.
Probably you have noticed that in some regions the curve map and plane map are not smooth
enough, this is because the grid of ICSSZZ.cub is relative coarse (the grid spacing is large). If we
use denser grid when calculating ICSSZZ, the graphs will be improved. Also beware that since the
extension distance used in the calculation of grid data of ICSSZZ is only 12 Bohr, when we plot
curve or plane map based on the interpolated data of ICSSZZ, the spatial range involved in the map
should not be too large. For example, we cannot plot the curve map from (0,0,0) to (0,0,20).
ICSS is very useful for discussing aromaticity and anti-aromaticity, many instances can be
found in the original paper of ICSS (J. Chem. Soc. Perkin Trans. 2, 2001, 1893), and in some
applicative papers, such as J. Phys. Chem. A, 116, 5674 (2012). AFAIK, ICSSZZ is first proposed
by me in this manual and has not been discussed in any literature yet.
I strongly recommend the users do some more practices about plotting and analyzing
ICSS/ICSSZZ, I provided some ideal exercise systems in "examples\ICSS" folder, including
azulene, cyclobutadiene, cycloheptatriene, porphyrin, propane and pyracylene; among them
cyclobutadiene is the most simple one. Below is the ICSS=0.5 isosurface of cyclobutadiene
showing in two representations; from the graph it is clear that this system shows strong anti-
aromaticity character, the 4n π-electrons cause evident de-shielding effect in the cylindrical region
perpendicular to and through the ring, this situation is in complete contrast to benzene.
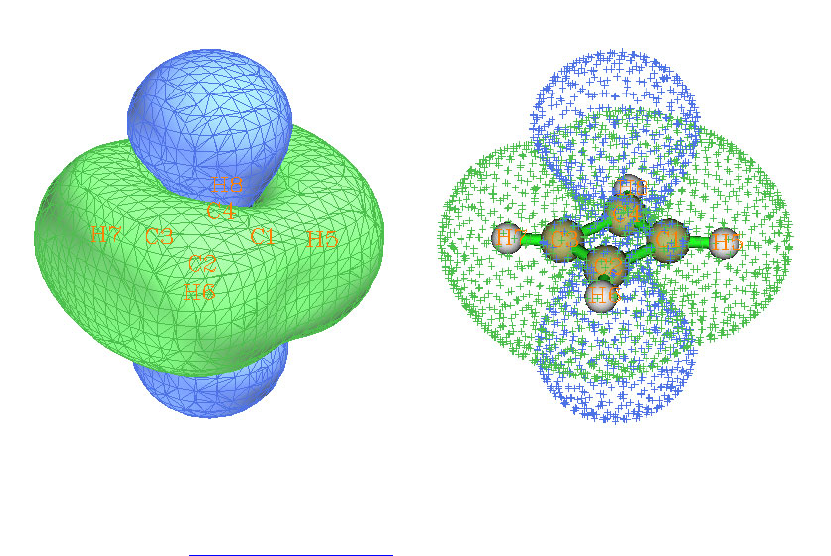
4 Tutorials and Examples
427
I wrote a very detailed post to discuss ICSS, in which all systems in "examples\ICSS" folder
are involved, see "Using Multiwfn to study aromaticity by drawing iso-chemical shielding
surfaces" (in Chinese, http://sobereva.com/216).
4.200.5 Plot radial distribution function of electron density
Multiwfn is capable of plotting radial distribution function (RDF) for any real space function,
see Section 3.200.5 for detail. This function is particularly useful for studying electronic structure
character of sphere-like system.
This section consists of two parts. In part 1, we will plot RDF for electron density of
fullerene (C60); while in part 2, I will show how to plot RDF of electron density for a Rydberg
orbital to characterize it quantatively.
Part 1: RDF of electron density for fullerene
Since .wfn file of fullerene at B3LYP/6-31G* level is large, I only provide the corresponding
Gaussian input file for you (C60.gjf in example folder), please properly modify and run it by
Gaussian to produce C60.wfn.
Boot up Multiwfn and input:
C60.wfn
200 // Other functions (Part 2)
5 // Plot RDF for a real space function
3
1,6 // Set the lower and upper limit of RDF to 1.0 and 6.0 Angstrom, respectively
0 // Calculate RDF and its integration curve
After the calculation is finished, select option 0, below RDF map will be shown on the screen,
the X-axis corresponds to radial distance
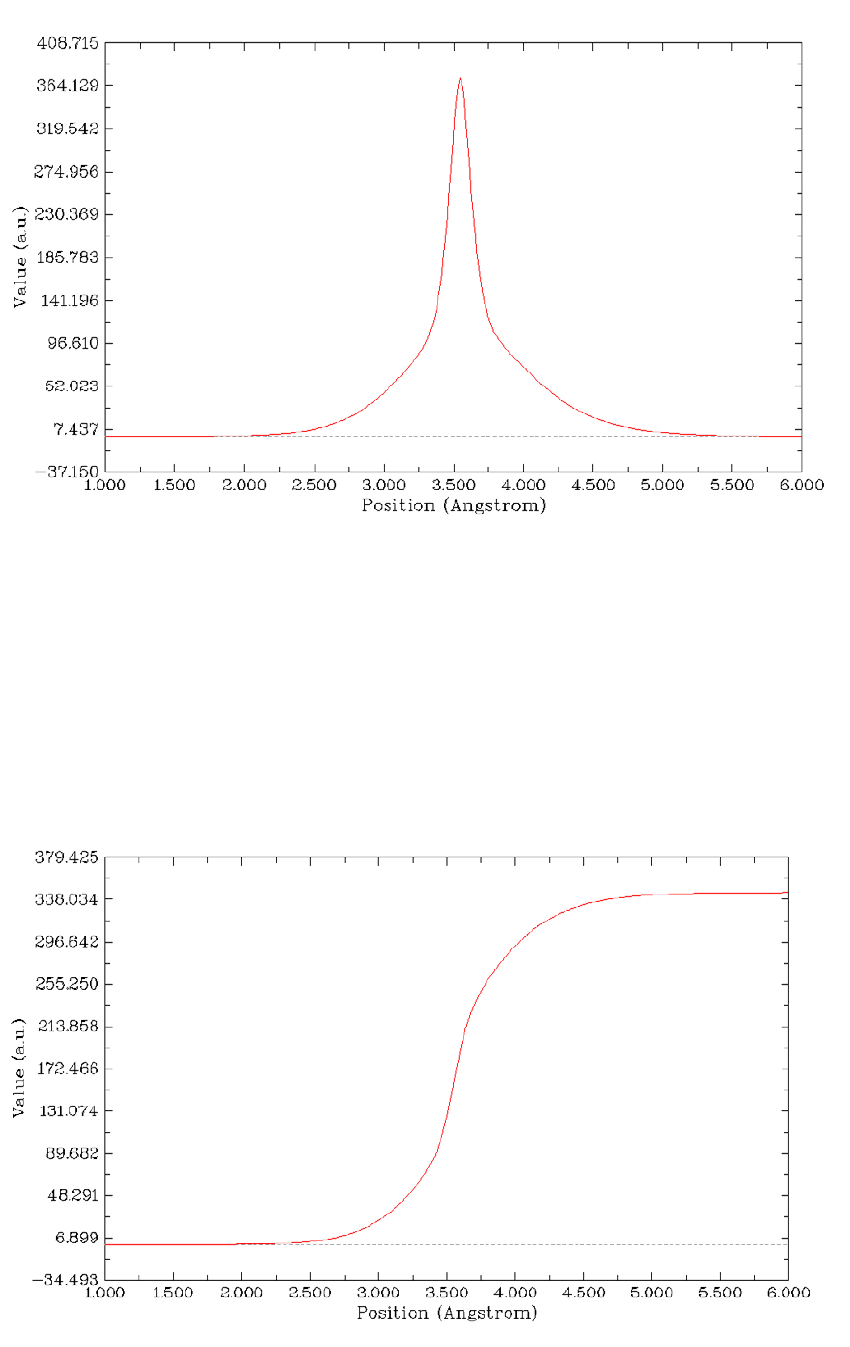
4 Tutorials and Examples
428
As you can see, the peak of RDF is about 3.5 Å, this is because the distance between nucleus
of carbons and the sphere center is 3.545 Å. It is known that electron density has maximum at
nuclear position for any atom except for hydrogen.
If you carefully examine the RDF curve, you will find that the curve on the right side of the
peak is slightly higher than that on the left sight. The reason is that the amount of electrons at
outer side of fullerene is richer than inner side. You can also draw and analyze ELF isosurface
map to confirm this point.
You can also choose option 2 to plot integration curve of RDF, as shown below

4 Tutorials and Examples
429
Probably you have noticed that after the calculation there is a prompt on screen:
Integrating the RDF in the specified range is 344.9321931513
which means integrating the RDF from r=1.0 to r=6.0 Å yields 344.932, it also corresponds to the
value of integration curve at r=6.0. This value deviates evidently from our expectation, namely the
number of electrons in current system (360). One reason is that the default number of integration
points is not large enough (500 and 2030 for radial and angular parts, respectively. You can
manually increase them), while another reason is more important, that is the size of current system
is too large, using single-center integration method is too difficult to yield very accurate result, at
least for integrating electron density.
Part 2: Using RDF of electron density to quantitatively characterize Rydberg orbital for
acetone
Rydberg orbitals denote the spatially very diffuse MOs, their orbital shapes are akin to atomic
orbitals, since electrons in Rydberg orbitals can be regarded as weakly bounded by a small cation
core, which behaves as an atomic nucleus. In order to faithfully represent the diffuse character of
Rydberg orbitals, basis set with substantial diffuse functions must be employed, e.g. aug-cc-pVTZ.
The example file we used below is formaldehyde calculated at B3LYP/aug-cc-pVTZ level by
Gaussian. We will first visualize Rydberg orbitals as isosurfaces, and then calculate RDF of
electron density corresponding to these orbitals to characterize them quantitatively.
Since Rydberg orbitals are very diffuse, in order to avoid truncating their isosurfaces when
viewing them by main function 0, we should enlarge "aug3D" in settings.ini first, here we set it to
12. After that, boot up Multiwfn, input examples\H2CO_aVTZ.fch, then enter main function 0,
change isovalue to a much smaller value than default, e.g. 0.01, and then randomly examine some
virtual MOs. You will find a lot of virtual MOs show very diffuse character, for example, MO10
and MO11:
The main distribution region of both of them are far from the molecule. MO10 is almost
spherically symmetric, thus is can be denoted as s type of Rydberg orbital. While MO11 has two
phases, they equally distribute at the two sides, the overall shape is very close to atomic p orbitals,
therefore MO11 can be identified as p type of Rydberg orbital.
How to quantitatively demonstrate that the main distribution region of these Rydberg orbitals
is far from the molecular center? One of the best way is plotting RDF of electron density
corresponding to these orbitals. Here we plot this kind of RDF map for MO11. We close the GUI
of main function 0, and then input below commands:
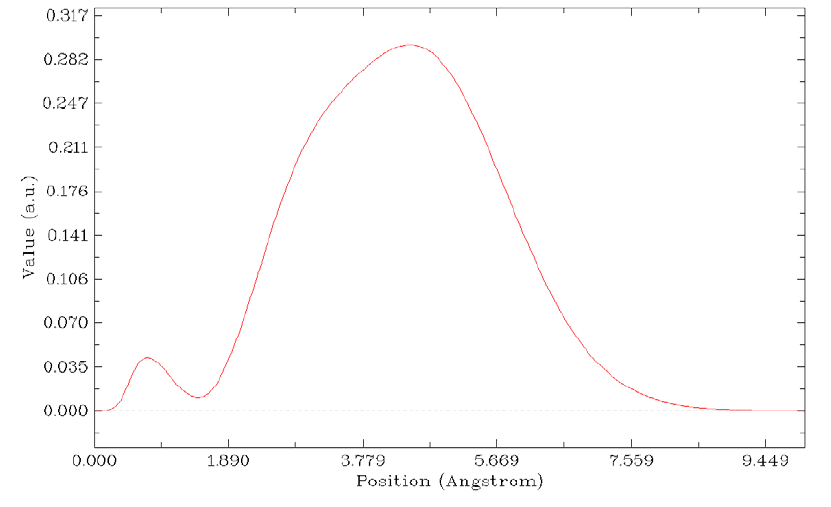
4 Tutorials and Examples
430
6 // Modify wavefunction
26 // Modify orbital occupation number
0 // Select all orbitals
0 // Select occupation number of all orbitals to zero
11 // Select orbital 11
2 // Set occupation number of orbital 11 to 2.0 (assume it is doubly occupied)
q // Return
-1 // Return to main menu
200
5 // Plot RDF
3 // Set lower and upper limit of radial plotting
0,10 // From 0 to 10 Å
4 // Set angular number of integration points. The default value is unnecessarily high for
present purpose, therefore we set it to a smaller value to reduce computational time
302 // 302 angular points
0 // Calculate RDF for electron density (which is the default real space function)
1 // Plot the RDF map
From the map it can be seen that the global maximum peak is at about 4.6Å, indicating that
the major distribution region of this orbital wavefunction is very far from origin (in present .fch
file, Cartesian origin corresponds to molecular center), and thus MO11 can be unambiguously
identified as a Rydberg orbital.
Please also plot such a RDF map for a regular valence virtual MO, e.g. MO9, which is pi*
orbital. Where is its peak position?
4 Tutorials and Examples
431
4.200.8 Calculate polarizability and hyperpolarizability for NH3 via
sum-over-states (SOS) method
In this example I will show how to use Multiwfn to calculate polarizability and
hyperpolarizability based on sum-over-states (SOS) method for HF molecule. Please make sure
that you have read Section 3.200.8.
As introduced in Section 3.200.8, SOS calculation requires information of a large amount of
electronic states, including electric dipole moments, excitation energies, and transition dipole
moments between these states. Commonly these information can be obtained by ZINDO, CIS,
TDHF and TDDFT calculations. In this example we use the very popular CIS method. According
to my experiences, the more expensive methods TDHF and TDDFT, which can produce more
accurate excitation energies, do not necessarily give rise to better (hyper)polarizability than CIS
when used in combination with SOS technique.
In this example we use Gaussian program to carry out the CIS calculation. However,
Gaussian itself cannot output enough information for SOS calculation. Though for CIS (and
ZINDO) there is a keyword alltransitiondensities, which makes Gaussian output transition density
moment between each pair of excited states, however electric dipole moment of all states still
cannot be obtained in a single run. Fortunately, we can use the very powerful electron excitation
analysis module of Multiwfn to generate all information needed by SOS based on the output file
of CIS/TDHF/TDDFT task of Gaussian or ORCA program.
First, run "examples\NH3_SOS.gjf" to produce output file of Gaussian CIS task
(NH3_SOS.out), and use formchk utility to convert the checkpoint file to NH3_SOS.fch.
Since the SOS results converge often slow with respect to the number of excited states taken into account, we
produce as high as 150 excited states in this example to substantially avoid truncation error. Of course, employing
higher number of excited states needs more computational time in both of the CIS calculation and the subsequent
SOS calculation in Multiwfn. In most practical studies, 100 states is generally large enough, and even 70 is often
enough to provide usable results. Calculation of hyperpolarizability, especially the high-order ones, has very
stringent requirements on the quality of basis-set, abundant diffuse functions are absolutely indispensable. In this
example we employ def2-TZVPPD (J. Chem. Phys., 133, 134105), which is a high-quality basis-set optimized for
calculation of molecular response properties. Since this is not a built-in basis-set in current version of Gaussian, it
was picked from EMSL website (https://bse.pnl.gov/bse/portal). The keyword IOp(9/40=5) is important, because
in the ZINDO/CIS/TDHF/TDDFT task by default Gaussian only outputs the transition coefficients whose absolute
values are larger than 0.1, while IOp(9/40=5) lowers the criterion to 0.00001, so that much more coefficients can
be outputted, and thereby we can obtain accurate transition dipole moments by Multiwfn at next step.
Worthnotingly, you can also use TDHF or TDDFT instead of CIS, for example you can write #P TD(nstates=150)
CAM-B3LYP/gen IOp(9/40=5).
Boot up Multiwfn and input below commands
C:\gtest\NH3_SOS.fch
18 // Electron excitation analysis module
5 // Calculate transition dipole moments between all excited states
C:\gtest\NH3_SOS.out
3
The file SOS.txt generated in current folder contains all information needed by SOS
(hyper)polarizability calculation. This file can be directly used by SOS module of Multiwfn.
Reboot Multiwfn and input
SOS.txt
200 // Other function (Part 2)
7 // Calculate (hyper)polarizability by sum-over-states (SOS) method
4 Tutorials and Examples
432
Note that all units used in the SOS module are atomic units.
Select 1 and input 0 to calculate static polarizability (0;0) first, the result is
Polarizability tensor:
1 2 3
1 14.610682 0.000000 0.000000
2 0.000000 14.610682 0.000000
3 0.000000 0.000000 14.552483
Isotropic polarizability: 14.591283
Polarizability anisotropy (definition 1): 0.058199
Eigenvalues: 14.552483 14.610682 14.610682
Polarizability anisotropy (definition 2): 0.029100
As can be seen, not only the polarizability tensor, but also some related quantities are
outputted. Their definitions can be found in Section 3.100.20. The isotropic average polarizability
we obtained here is 14.59, which is in perfect agreement with the experimentally determined value
14.56 ! (Mol. Phys., 33, 1155)
Then we calculate dynamic polarizability (-;) and assume the frequency of external field
to be 0.0719 a.u. Select option 1 again, input 0.0719, from the output we can see the dynamic
isotropic polarizability at =0.0719 is 14.86, which is slightly larger than the static counterpart.
Next, we calculate first hyperpolarizability and consider the static case (0;0,0). Select option
2 and input 0,0. Only the component along the dipole moment direction, namely ||, is what we
are particularly interested in, since only this quantity can be determined experimentally. From the
output we find ||(0;0,0) is -38.98. The corresponding experimental value is not available, however
this value is close to the highly accurate value calculated by CCSD(T) method (-34.3, see J. Chem.
Phys., 98, 3022).
Now we calculate (-2;,) at =0.0656 a.u. Select option 2 again and input 0.0656,
0.0656 to set the frequency of both two external fields as 0.0656 a.u. This time the || value is -
49.69, which is again in excellent agreement with the experimentally determined value -48.91.2
(see A. Hernández-Laguna et al. (eds.), Quantum Systems in Chemistry and Physics, Vol. 1, p111)
Note: Although in this example the agreement between our SOS/CIS calculations and the reference values is
suprisingly good, this is not always hold for other systems. The SOS/CIS method sometimes severely
overestimates value!
Finally, we tentatively calculate second hyperpolarizability . Select 3 and input 0,0,0 to
assume static electric fields. Since calculation of is evidently more time-consuming than ,
Multiwfn does not automatically use all states but allow you to set the number of states to be taken
into account. Larger value in principle gives rise to better result, but of course more time will be
consumed in the calculation. Here, we input 150 to use all states. After a while, the result is shown
on screen, the average of is 928.74. Beware that this value may be inaccurate (reference value is
not available, so I am not sure if this is a good result), one of the main reasons is that the basis-set
we used in the electron excitation calculation is not large enough. Accurate calculation of usually
requests a basis-set like d-aug-cc-pVTZ (or a even better one), which has an additional shell of
diffuse functions compared to the commonly used aug-cc-pVTZ.
Multiwfn is also capable of calculating third hyperpolarizability (-;1,2,3,4) where
=1+2+3+4, but we do not do this in present example, because this quantity is fairly
unimportant, and the calculation is terribly expensive when the number of states in consideration
is large; moreoever, a sky-high quality of basis-set must be employed in the calculation...
4 Tutorials and Examples
433
A very important point in SOS calculation is that the number of states used must be high
enough; in other words, if n states are involved in your SOS studies, the variation of the
(hyper)polarizability with respect to the number of states have to be converged before n, otherwise
n must be enlarged. By using Multiwfn we can readily examine if the convergence condition is
satisfied. Here we check the convergence of static . Select option 6 and input 0,0, after a while,
the result is exported to "beta_n.txt" in current folder, the meaning of each column is clearly
indicated on screen. Use your favourite tool to plot the data in "beta_n.txt". If you are an Origin
user, you can directly drag this file into Origin window and plot the data as curve maps. You can
also similarly use option 5 and 7 to study the convergence of and . Below graphs show the
variation of static || as well as static isotropic average polarizability <> with respect to the
number of states.
0 20 40 60 80 100 120 140
0
2
4
6
8
10
12
14
16
Number of states
<>
0 20406080100120140
-70
-60
-50
-40
-30
-20
||
Number of states
It is clear that both of the two quantities have basically converged at n=100. Since we employed
150 states in our calculations, the error due to the truncation of states can be safely ignored. From
the graph one can also see that if the number of states is truncated at 70, the results are still
qualitatively correct.
In the SOS module of Multiwfn one can also easily study the variation of dynamic
(hyper)polarizability with respect to the frequency of external fields. For example, we investigate
the variation of (-1;1,0) as 1 varies from 0 to 0.5 a.u. with stepsize of 0.01. Write a plain text
file, each row corresponds to a pair of 1, 2 (2 is fixed at zero in this example), for example
0.00 0
0.01 0
0.02 0
...
0.5 0
Tips: For convenience, you can utilize Microsoft Excel program to generate frequency list, and save the table
as .txt file (you can select such as "Text (tab delimited)", but do not choose "Unicode text").
Then choose option 16, input the path of the plain text file, the will be calculated at each pair of
frequencies, the result will be outputted to "beta_w.txt" in current folder; the meaning of each
column of the data is clearly indicated on screen. The data can be directly plotted as curve map by
Origin, like below:
4 Tutorials and Examples
434
0.00.10.20.30.40.5
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
100000
110000
Magnitude of 1;1,0
Frequency of external field 1
4.200.12 Calculate energy index (EI) and bond polarity index (BPI)
In this section I will illustrate how to calculate EI and BPI indices, which were defined in J.
Phys. Chem., 94, 5602 (1990). If you are not familiar with these two quantities, please read
Section 3.200.12 first. The geometry and wavefunction involved in this example were produced at
HF/6-31G* level, which is the one used in above mentioned paper.
We will calculate BPI for C-N bond of CH3NH2, before this we first need to calculate
reference EI value for C and N atoms, which correspond to EI of C in ethane and N in H2N-NH2,
respectively. Boot up Multiwfn and input
examples\EI_BPI\ethane.fch
200
12
1 // C1 atom
You will see the EI value for C in reference molecule ethane is -0.667639 a.u. Reboot Multiwfn
and input
examples\EI_BPI\N2H4.fch
200
12
1 // N1 atom
You can see the EI value for N in reference molecule H2N-NH2 is -0.718126 a.u.
Next we calculate EI for C and N in CH3NH2. Reboot Multiwfn and input
examples\EI_BPI\CH3NH2.fch
200
12
1 // C1, the result is -0.693374 a.u.
5 // N5, the result is -0.698092 a.u.
The BPICN in CH3NH2.is computed as
4 Tutorials and Examples
435
046.0
0.7181260.6980920.6676390.693374
)EI(EI)EI(EIBPI ref
NN
ref
CCCN
As a comparison, use examples\EI_BPI\F2.fch to calculate reference value for F, the result
should be -0.992542 a.u., and use examples\EI_BPI\CH3F.fch to calculate EI for C and F in CH3F
molecule, the result should be -0.750302 and -0.885961, respectively. Then compute the BPICF
value as -0.750302+0.667639+0.885961-0.992542= -0.189. Since BPICF in CH3F is evidently
more negative than BPICN in CH3NH2, it can be concluded that C-F bond in CH3F is more polar
than C-N bond in CH3NH2.
Via EI index we can also evaluate the so-called group electronegativity, which is often more
useful than atomic electronegativity. Here we calculate electronegativity for -CH3 group, which is
simply the negative of EIC for CH3 radical. Boot up Multiwfn and input
examples\EI_BPI\CH3.fch // Optimized and produced at UHF/6-31G*
200
12
1 // Carbon atom
The result is -0.630656 a.u., corresponding to electronegativity of CH3 group of 0.631. Then
we use examples\EI_BPI\F.fch to calculate group electronegativity for -F, the result is 0.957. It is
clear that -F group has much higher electronegativity, and thus has stronger capacity to attract
electrons than -CH3 group due to its lower average energy per valence electron.
4.200.13 Localizing molecular orbital of 1,3-butadiene by Pipek-
Mezey method
This section illustrates the use of Pipek-Mezey (PM) localization function of Multiwfn with
trans-1,3-butadiene as example. Before reading this section please read Section 3.200.13 first to
gain some basic knowledges.
The input file is examples\butadiene.fch, which was yielded at B3LYP/6-31G** level. You
can first visualize its MOs via main function 0, you will found all MOs except for inner-core ones
are highly delocalized, none of them have direct correlation with classical concept of chemical
bond theory. Now we perform orbital localization to transform them to more chemically
meaningful orbitals. Boot up Multiwfn and input
examples\butadiene.fch
200
13 // Pipek-Mezey orbital localization
1 // Perform localization for both occupied and unoccupied MOs
Since this system is small, convergence of localization iteration promptly achieved. After that
Multiwfn automatically exports the localized orbitals as new.fch in current folder and then load it.
Now, the orbital coefficients in memory have been completely updated to localized orbitals. You
may use different ways to characterize them, for example, we enter main function 0 to visualize
these orbitals, you will find all orbitals show strong localization character, in particular the
4 Tutorials and Examples
436
occupied ones. Below are screenshot of three localized orbital involving C6-C8, the first two are
occupied, and they correspond to bond and bond, respectively; the third one is unoccupied, it
can be ambiguously identified as anti- bond orbital.
It is also possible to obtain energy for the localized MOs, you should provide Fock matrix
(strictly speaking, Kohn-Sham matrix in current case). To realize this for present system, we enter
main function 100 and choose subfunction 2, and then select option 10 to write current molecular
geometry as a Gaussian input file. We properly modify it to make Gaussian output NBO .47 file,
which contains Fock matrix, and we need to ensure that the calculation level is identical to the .fch
we used (i.e. B3LYP/6-31G**). The .gjf file after modification is provided as butadiene_47.gjf in
"examples" folder. Run it by Gaussian, you will find BUTADIENE.47 at C:\, search $FOCK in this
file, and extract all content between $FOCK and the $END next to it into a plain text file named
butadiene_FOCK.txt (this file is also provided in "examples" folder).
We have finished preparation. Now reboot Multiwfn and input
examples\butadiene.fch
200
13
-4 // Allow Multiwfn to generate and print energy for localized orbitals
examples\butadiene_FOCK.txt
2
After convergence finished, Multiwfn evaluates energy of the localized MOs and sort orbitals
according to their energies from low to high. The information of the highest occupied localized
orbitals and lowest unoccupied localized orbitals are shown below
14 Energy (a.u.): -0.27507273 Type: A+B Occ: 2.0
15 Energy (a.u.): -0.27507273 Type: A+B Occ: 2.0
16 Energy (a.u.): 0.21859103 Type: A+B Occ: 0.0
17 Energy (a.u.): 0.21859121 Type: A+B Occ: 0.0
Please plot them in main function 0 to try to identify their characters.
4.200.14 Integrate real space function within reduced density gradient
(RDG) isosurfaces to study weak interaction
Before reading this, please read Section 4.100.1 to understand how to use reduced density
gradient (RDG) to reveal weak interaction regions. In this section, I show the possibility of
characterizing weak interaction by integrating domains enclosed by RDG isosurfaces.
System 1: Phenol dimer
First, we use phenol dimer as example. Boot up Multiwfn and input
examples\phenoldimer.wfn
4 Tutorials and Examples
437
200 // Main function 200
14 // Integrate real space functions within isosurfaces of a real space function
Here we want to study RDG domains defined as regions enclosed by isosurface of RDG=0.5;
in other words, these domains composed of grid points where RDG<0.5. Therefore, we select
option 2 and choose "13 Reduced density gradient", and then select option 3 and input criterion,
namely <0.5 (In fact, RDG<0.5 is the default setting and you do not need to manually do these
steps). Next, input below commands:
1 // Start calculation grid data and generate domains
-10 // Adjust extension distance
0 // Set extension distance to zero to avoid wasting of grid points at boundary area, where
RDG isosurfaces commonly do not occur
2 // Medium quality grid (i.e. grid spacing=0.1 Bohr), generally this is accurate enough
Now Multiwfn starts calculation of grid data for the selected real space function (i.e. RDG),
and then identifies individual RDG domains according to the criterion of RDG<0.5. Finally, four
domains are found, the number of grid points constituting the domains are shown as the last
column:
Domain: 1 Grids: 208
Domain: 2 Grids: 290
Domain: 3 Grids: 200
Domain: 4 Grids: 2597
To visualize them, select "3 Visualize domains". In the GUI, you can select domain index at
right-bottom list. The 2nd and 4th domains are shown below:
If you have read Section 4.100.1, you must know these domains correspond to H-bond and van
der waals (vdW) interactions between the two phenols, respectively. We can study properties of
these domains in terms of integrating specific real space functions in them. The real space function
to be integrated can be selected by option 4, it is default to electron density, which is just the one
we want to integrate in the domains. So we directly select option 1 and input 2, then integral of
electron density in domain 2 is shown on the screen:
Integration result: 0.6932973049E-02 a.u.
Volume: 0.290000 Bohr^3 ( 0.042974 Angstrom^3 )
Average: 0.2390680362E-01
Maximum: 0.2766231164E-01 Minimum: 0.1994457517E-01
Similarly, we do this for domain 4:
Integration result: 0.1181667175E-01 a.u.
Volume: 2.597000 Bohr^3 ( 0.384836 Angstrom^3 )
Average: 0.4550123895E-02
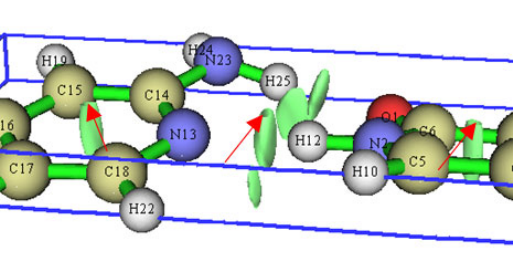
4 Tutorials and Examples
438
Maximum: 0.6217203920E-02 Minimum: 0.3102088666E-02
From the output we know the number of electrons involved in the domains corresponding to
H-bond and vdW interactions are 0.006933 and 0.011817, respectively. They can be interpreted as
overlapping electrons and are closely related to strength of same type of interactions (see
discussion in Section 5.2 of DORI original paper J. Chem. Theory Comput., 10, 3745 (2014)).
However, since these two domains correspond to different type of weak interactions, the
magnitude of overlapping electrons is not positively correlated to their strengths, namely we are
unable thus to say that the vdW interaction between the two phenols is stronger than the
intermolecular H-bond. The "Volume" in the output denotes volume of the domain, we can find
that vdW interaction involves much wider spatial region than H-bond. "Average" correspond to
average value of real space function in the domain, from this quantity one can easily infer that the
strength of interaction per contact region of H-bond must be significantly higher than that of vdW
interaction, since as shown above, their average values are 0.0239 and 0.0045, respectively, the
former is much larger than the latter.
System 2: 2-pyridoxine 2-aminopyridine
Intermolecular H-bonds of 2-pyridoxine 2-aminopyridine (PP) has been investigated in
Section 4.2.1 by means of AIM analysis, while this time we will analyze them by means of qint
index. This index was proposed in J. Phys. Chem. A, 115, 12983 (2011) for judging interaction of
H-bond at various intermolcular distance, please check Section 3.200.14 for its definition.
Commonly, the more negative of the qint index, the more stable the interaction.
qint index is defined based on integrating domains enclosed by RDG=0.6 isosurfaces,
therefore we need to first calculate RDG grid data and generate corresponding domains. Note that
it is not always appropriate to set extension distance of RDG grid data to zero. For present system,
if you calculate RDG grid data by main function 5 with extension distance of zero, you will see
some RDG isosurfaces are truncated by box boundary, as shown below and highlighted by red
arrows. In this case domain integrating module of Multiwfn does not work.
Therefore, when we calculate RDG grid data for this case, extension distance should be set
somewhat larger than zero, 3 Bohr is safe enough for avoiding unexpected truncation. Extension
distance should also never be set to a too large value, otherwise the number of grid points to be
calculated will be very high and thus very time-consuming.
Boot up Multiwfn and input below commands:
examples\2-pyridoxine_2-aminopyridine.wfn
200
14
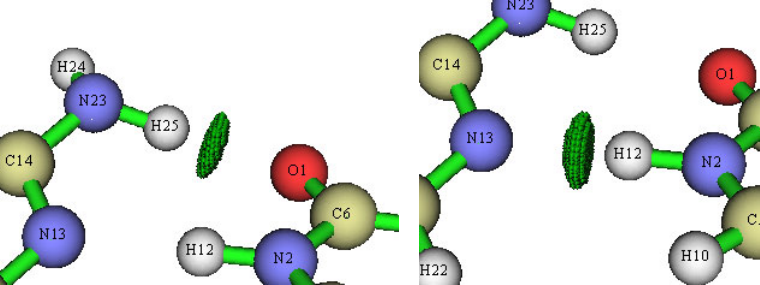
4 Tutorials and Examples
439
3 // Change the default criterion of defining domain
<0.6
1 // Start calculation of grid data
-10 // Change extension distance
3 // 3 Bohr of extension distance
2 // Medium quality grid
Now visualize resulting domains. Domain 2 and 4 are shown below, clearly they correspond
to H-bond of N23-H25O1 and N2-H12N13, respectively.
Now select "5 Calculate q_bind index for a domain" and input 2, the resulting qint and related
details of the domain are shown below
q_att: 0.00490957 a.u.
q_rep: 0.00005590 a.u.
q_bind: -0.00485367 a.u.
Volume (lambda2<0): 0.599000 Bohr^3
Volume (lambda2>0): 0.010000 Bohr^3
Volume (Total): 0.609000 Bohr^3
Similarly, we obtain results for domain 4
q_att: 0.00805204 a.u.
q_rep: 0.00037346 a.u.
q_bind: -0.00767858 a.u.
Volume (lambda2<0): 0.745000 Bohr^3
Volume (lambda2>0): 0.052000 Bohr^3
Volume (Total): 0.797000 Bohr^3
Since the qbind corresponding to N2-H12N13 (-0.007678) is much more negative than that
of N23-H25O1 (-0.004854), the former should be stronger than the latter.
Since both the interactions are H-bond, it is also possible to simply compare the number of
electrons contained in the domains to estimate their relative strength. We choose "2 Perform
integration for all domains" to print out integral of electron density (the default real space function)
in all domains:
Domain Integral (a.u.) Volume (Bohr^3) Average
1 0.1212147834E-03 0.111000 0.1092025076E-02
2 0.1647945811E-01 0.609000 0.2705986553E-01
3 0.1714432107E-02 0.319000 0.5374395319E-02
4 0.2618188584E-01 0.797000 0.3285054685E-01
4 Tutorials and Examples
440
5 0.8932587581E-02 0.412000 0.2168103782E-01
6 0.7764521413E-02 0.394000 0.1970690714E-01
Integration result of all domains: 0.6119409984E-01 a.u.
Volume of all domains: 2.642000 Bohr^3 0.391504 Angstrom^3
Not only the integration value of domain 2 (0.01648) is evidently smaller than domain 4
(0.02618), but also the average value of domain 2 (0.02706) is smaller than domain 4 (0.03285),
therefore we have strong evidence to say N2-H12N13 is stronger than N23-H25O1.
With similar steps illustrated in this section, you can also integrate other real space functions
such as potential energy density and spin density, in the domains enclosed by isosurfaces of other
real space functions, e.g. DORI and ELF.
Note that the accuracy of integration in the domains is directly determined by grid setting,
higher quality of grid leads to better accuracy. For example, when visualizing domains, if you
found a domain only consists of very few grid points, and its profile is very coarse, then
integration accuracy of this domain must be very low.
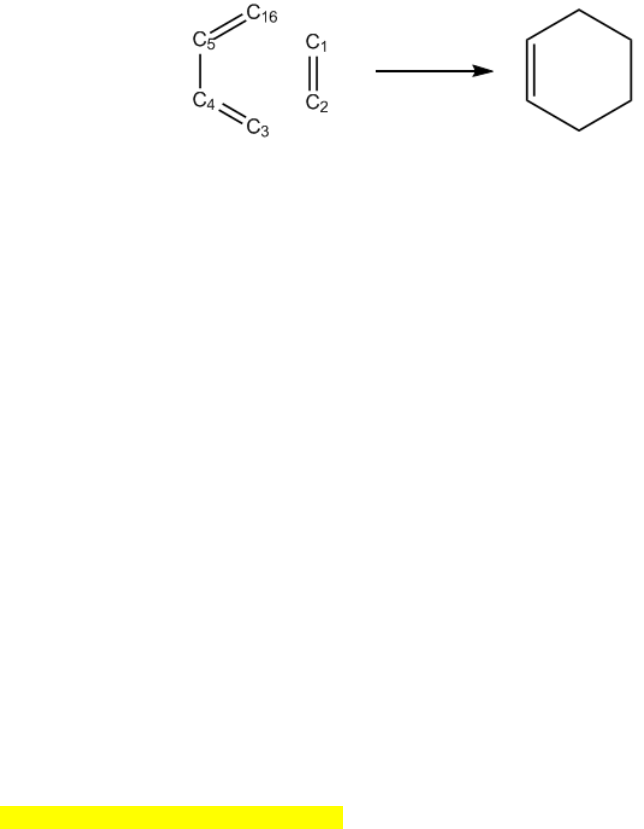
4 Tutorials and Examples
441
4.A Special topics and advanced tutorials
The contents in this Section involve more than one main functions of Multiwfn.
4.A.1 Study variation of electronic structure along IRC path
In this tutorial, I will briefly show you how to use Multiwfn to study variation of electronic
structure along the IRC path of Diels-Alder adduction. We will study the variation of Mayer bond
order, and will animate the deformation of ELF isosurface. With the similar fashion you can also
easily investigate variation of other properties, such as atomic charges, electron density,
aromaticity and so on.
Gaussian 09 A.02 was used throughout this tutorial. Unless otherwise specified, all
calculations will be performed under Windows 7 64bit system. In this tutorial the files marked by
crimson can be found in "examples\IRC" or "examples" folder.
Before starting this tutorial, you should setup running environment for Gaussian first,
otherwise Gaussian cannot be properly invoked in Windows environment. The setup method is:
Enter “control panel”-“System properties”-“Advanced”, click “Environment variables” button,
then click “New” button in “User variables” frame, input GAUSS_EXEDIR as variable name,
input the install directory of Gaussian as variable value (e.g. d:\study\g09w\, assuming that
g09.exe is in this folder). After that modify "PATH" environment variable to add the install
directory of Gaussian into it.
1 Perform IRC calculation
Run DA_IRC.gjf by Gaussian to produce DA_IRC.out. We will find this IRC path actually
contains 18 and 13 points in the two directions, respectively. B3LYP/6-31+G* is used in this
calculation.
2 Generate wavefunction file for each point of IRC
Write an input file of single point task of Gaussian (DA_SP.gjf), which will be used as
"template" later. The geometry in fact can be arbitrarily filled.
DO NOT write anything here (e.g. %chk)
#p B3LYP/6-31G* nosymm
DA adduction
0 1

4 Tutorials and Examples
442
C -0.26156800 1.56679300 0.69509600
C -0.26156800 1.56679300 -0.69509600
C 0.50031400 -0.43279300 -1.43864500
C -0.26156800 -1.32826500 -0.70392000
C -0.26156800 -1.32826500 0.70392000
H -1.19341600 1.44689700 -1.23752300
H -1.19341600 1.44689700 1.23752300
H 0.52507600 2.08588200 1.23621300
H 0.38154400 -0.37781200 2.51847500
H 0.38154400 -0.37781200 -2.51847500
H 1.46467600 -0.09643600 -1.07409700
H -1.04094400 -1.89294000 -1.21418700
H -1.04094400 -1.89294000 1.21418700
H 1.46467600 -0.09643600 1.07409700
H 0.52507600 2.08588200 -1.23621300
C 0.50031400 -0.43279300 1.43864500
blank line
blank line
Notice that the basis-set we used here (6-31G*) is different to the one used in IRC task (6-
31+G*), because Mayer bond order does not work well when diffuse functions are presented. By
the way, ignoring diffuse functions will not lead to detectable change of ELF isosurface. Also note
that the "nosymm" keyword is specified, because if we do not do this Gaussian will automatically
translate and rotate the molecule to put it to standard orientation, which may leads to discontinuity
problem in the animation of ELF (You will see molecule suddenly jumps in certain frames of the
animation).
IRCsplit.exe is a tool used to produce .wfn/.chk file for each point of IRC and SCAN tasks of
Gaussian 09, IRCsplit.f90 is the corresponding source code, by which you can compile Linux
version of IRCsplit. Boot up IRCsplit.exe by double click its icon and then input
DA_IRC.out //The file of the output file of the IRC task
DA_SP.gjf //The template file used to generate single point input files
2 //Only yield .chk files
c:\DA_IRCchk\DA //The path and prefix of the finally generated .chk files
18,13 // The program detected that in DA_IRC.out there are 18 and 13 points in the
two directions of IRC, respectively. Here we extract all of them, together with the TS point
Now you can find DA_SP0001.gjf, DA_SP0002.gjf ... DA_SP0032.gjf in current folder.
Please manually check one of them to verify the reasonableness of these input files. Note that
DA_SP0014.gjf corresponds to the TS geometry.
Build a new folder "c:\DA_IRCchk" and copy the .gjf files as well as the script runall.bat into
it. Double clicking the icon of runall.bat, which will invoke Gaussian 09 to run all of the .gjf files.
Now you have DA0001.chk, DA0002.chk ... DA0032.chk in "c:\DA_IRCchk" folder. Copy
chk2fch.bat to this folder and run it, then the formchk utility in Gaussian package will be
automatically invoked to convert all .chk files to .fch files.
4 Tutorials and Examples
443
3 Calculate Mayer bond orders for all IRC points
Mayer bond order of C1-C16 is the one we are particularly interested in, whose formation is
the key process of the DA adduction. Since by default Multiwfn only outputs Mayer bond orders
with value > 0.05, while C1-C16 must be very weak at the initial stage of DA adduction, we need
to set "bndordthres" parameter in the settings.ini file in Multiwfn folder to 0.0, so that all of the
bond orders larger than 0.0 can be outputted.
Write a plain text file (MBObatch.txt) and put it into Multiwfn folder, the content is
9 // Enter bond order analysis module
1 // Calculate Mayer bond order
Note: If you are confused why this file is written in such manner, please read Section 5.2 to study how to run
Multiwfn in silent mode.
Then write a plain text file with .bat suffix (MBObatchrun.bat) and put it into Multiwfn
folder, the content should be
for /f %%i in ('dir c:\DA_IRCchk\*.fch /b') do Multiwfn c:\DA_IRCchk\%%i <
MBObatch.txt > c:\DA_IRCchk\%%~ni.txt
batchrun.bat in fact is a Windows batch script. Double clicking its icon to run it, the .fch files
in "c:\DA_IRCchk\" folder will be sequentially loaded into Multiwfn, and the calculated Mayer
bond orders will be exported to .txt files in the same folder.
4 Plot Mayer bond order
Now what we should do next is to extract the bond order of C1-C16 from the DA0001.txt,
DA0002.txt ... DA0032.txt. The most convenient way is to utilize "grep" command in Linux. So
we copy all of these .txt files to a folder in Linux system, then in this folder we run
grep "1(C ) 16(C )" * > out.txt
The out.txt file now contains C1-C16 bond order of all points in the IRC:
DA0001.txt:# 9: 1(C ) 16(C ) 0.05929972
DA0002.txt:# 7: 1(C ) 16(C ) 0.06877306
DA0003.txt:# 7: 1(C ) 16(C ) 0.07926829
DA0004.txt:# 7: 1(C ) 16(C ) 0.09089774
DA0005.txt:# 7: 1(C ) 16(C ) 0.10380144
DA0006.txt:# 7: 1(C ) 16(C ) 0.11815120
DA0007.txt:# 7: 1(C ) 16(C ) 0.13417828
DA0008.txt:# 7: 1(C ) 16(C ) 0.15218555
...
The last column is the values of Mayer bond order of C1-C16, you can plot them by your
favorite program now, you will see
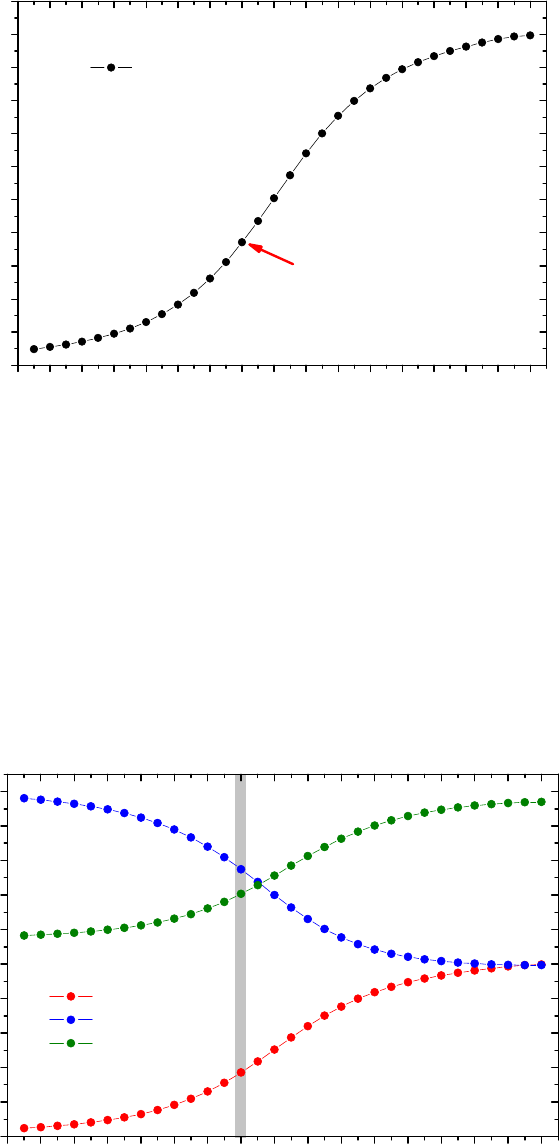
4 Tutorials and Examples
444
02468101214161820222426283032
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
Mayer bond order
IRC point
C1-C16
TS
Clearly, C1-C16 become stronger and stronger as the reaction proceeds, its Mayer bond order
gradually increases to 1.0 (typical single bond).
With the same method, we also calculate the Mayer bond order of C1-C2 and C4-C5, namely
run below commands
grep "1(C ) 2(C )" * > out2.txt
grep "4(C ) 5(C )" * > out3.txt
Plot the data in out.txt, out2.txt and out3.txt together, you will see
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
Mayer bond order
IRC point
C1-C16
C1-C2
C4-C5
TS
This graph vividly shows that the C1-C2 smoothly becomes to a single bond from a double
bond during the DA adduction, and the reaction increases the double-bond character of C4-C5
significantly.

4 Tutorials and Examples
445
5 Make animation of ELF isosurface
Next we make animation to study how the ELF isosurface varies during the DA adduction.
Create a plain text file ELFbatch.txt in Multiwfn folder with below content
5 // Generate grid data
9 // ELF
2 // Medium quality grid
2 // Export the grid data to ELF.cub in current folder
Create a script file named ELFbatchrun.bat, whose content is
for /f %%i in ('dir c:\DA_IRCchk\*.fch /b') do (
Multiwfn c:\DA_IRCchk\%%i < ELFbatch.txt
rename ELF.cub %%~ni.cub
)
Run ELFbatchrun.bat, Multiwfn will sequentially load the .fch files in "c:\DA_IRCchk" and
export the corresponding ELF grid data to DA0001.cub, DA0002.cub ... DA0032.cub in current
folder.
We use VMD 1.9.1 program (freely available at http://www.ks.uiuc.edu/Research/vmd/) to
render isosurface for these cube files. Move all of the cube files to VMD folder, and create a plain
text file named isoall.tcl in the VMD folder, the content is
set isoval 0.88
axes location Off
color Display Background white
for {set i 1} {$i<=32} {incr i} {
set name DA[format %04d $i]
puts "Processing $name.cub..."
mol default style CPK
mol new $name.cub
#translate by -0.100000 0.20000 0.000000
#scale to 0.30
rotate y by 50
rotate z by 90
rotate x by -30
rotate y by -20
mol addrep top
mol modstyle 1 top Isosurface $isoval 0 0 0 1 1
mol modcolor 1 top ColorID 3
render snapshot $name.bmp
mol delete top
}
This file essentially is a VMD script, in which the command set isoval 0.88 means the isosurface
of 0.88 will be plotted, the default view point is adjusted by scale, rotate and translate commands.
for {set i 1} {$i<=32} {incr i} means the file from DA0001.cub to DA0032.cub will be processed.
Now boot up VMD, and input the command source isoall.tcl in its command line window,
4 Tutorials and Examples
446
then you will have DA0001.bmp, DA0002.bmp ... DA0032.bmp.
There are numerous programs that can convert single-frame graphic files to animation, such
as Atani, Premiere, Vegas, Ulead Video Studio, Videomach, etc. Here we use ImageMagick tool in
Linux to do this, and we choose gif as the animation format, since gif animation can be directly
embedded into webpages.
Copy all of the .bmp files to Linux system, and run below command in the corresponding
folder:
convert -delay 12 -colors 100 -monitor *.bmp ELF_IRC.gif
in which -delay controls the time inverval between each frame in the animation, and -colors
determines the number of colors used, the larger the value, the more smoothly the color changes,
but the larger the animation file. You can run convert --help to study more arguments of this tool
If the the resultant ELF_IRC.gif cannot be properly displayed on your system, use your
webpage explorer or advanced image explorers (e.g. IrfanView) to open it. The deformation of
ELF isosurface in this animation very intuitively exhibits how the new bonds are formed and how
the characteristic of existing bonds changed.
4.A.2 Calculate spin population
As there are many ways to calculate atomic charges (see Section 3.9 for introduction and 4.7
for examples), there are various ways to calculate spin population. Spin population is defined as
the population number of alpha electrons minusing that of beta electrons. Spin population is a key
quantity for characterizing electronic structure of open-shell systems, i.e. radicals and
antiferromagnetic systems. From spin population we can clearly know where the spin electrons are
mainly distributed. Moreoever, we can discuss contribution from different regions (atomic orbitals,
atoms or fragments) to the total magnetic dipole moment m due to electron spin. If spin
population of a region is x, then its contribution to m will be x*μB, where the Bohr magneton
μB=e*ћ/(2me) (e: electron charge, me: mass of electron) represents the magnetic moment produced
by a single electron. Note that in chemical systems the movement of electron in orbitals and
nuclear spins also have contributions to m, but the magnitude is evidently weaker and thus can
often be neglected.
In Multiwfn, the spin population defined in many different ways can be calculated by three
modules, they are briefly discussed below.
(1) Population analysis module (main function 7). In this module, if you select Mulliken
population analysis, alpha, beta and spin population of each basis function, shell and angular
moment orbitals will be outputted. If you select Löwdin and modified Mulliken population
analysis, only the alpha/beta/spin population of each atom will be shown. Do not use these
methods when diffuse basis functions are presented in your basis-set, otherwise the result may or
may not be reliable.
(2) Fuzzy atomic spaces analysis module (main function 15). After you entered this
module, select option 1 and choose electron spin density, the spin population of each atom will be
shown. They are calculated by integrating electron spin density in fuzzy space of each atom. By
default the fuzzy atomic space defined by Becke is employed, so the result can be called Becke
spin population. If before calculation you selected option -1 to switch to Hirshfeld or Hirshfeld-I
fuzzy atomic space, then the result will correspond to Hirshfeld or Hirshfeld-I spin population. All

4 Tutorials and Examples
447
the Becke, Hirshfeld and Hirshfeld-I methods are reliable in all cases. For more detail you can
consult Section 3.18.
(3) Basin analysis module (main function 17). In this module, you can use AIM method to
calculate spin population. Please consult Section 4.17.1 on how to perform integration of real
space function in AIM atomic basins. If electron spin density is chosen to be the integrand, then
the result will correspond to AIM spin population. In general I do not suggest using this method,
because the computational cost is evidently higher than using population analysis module and
fuzzy atomic spaces analysis module.
Overall, if you only need to calculate atomic spin population, using fuzzy atomic spaces
analysis module is recommended. However, if more detailed information are requested, such as
spin population in different angular moment orbitals, please use Mulliken population analysis.
4.A.3 Study aromaticity
Aromaticity is a fundamental concept in organic chemistry and wavefunction analysis realm.
Previously I wrote a post to thoroughly discuss the methods for studying aromaticity, see "The
methods for measuring aromaticity and their calculations in Multiwfn" (in Chinese,
http://sobereva.com/176). Multiwfn support a very large number of methods for investigating
aromaticity, they are summarized in below table and will be briefly introduced in turn. There are
also many other methods, such as induced ring current, ARCS, magnetic susceptibility exaltation,
aromatic stabilization energy (ASE), CiLC; they will not be mentioned since they are not directly
related to the capacity of Multiwfn.
Method Principle Year Pop. Reliab. Univ. Ref. Anti-arom. Sep. σ/π Cost Value
1 Molecular orbital Hückel 1951 ++ 0 0 N Y Y 0 +
2 AdNDP Hückel 2008 + 0 + N Y Y 0 +
3 NICS Magnet. 1996 +++ ++ ++ N Y Y + +++
4 ICSS Magnet. 2001 0 ++ ++ N Y Y +++ +
5 HOMA Geom. 1972 + + 0 Y Y N
+
6 Bird Geom. 1985 0 Y ? N
7 Multi-center BO Delocal. 1990 + +++ ++ N N Y 0
+++
8 ELF-σ/π Delocal. 2004 + 0 N Y Y 0 +
9 PDI Delocal. 2003 0 + 0 N N Y 0 +
10 ATI Delocal. 2005 + 0 N N Y 0
11 PLR Delocal. 2012 + 0 N N Y 0 0
12 ΔDI Delocal. 2003 N N Y 0
13 FLU, FLU-π Delocal. 2005 0 + 0 Y/N N Y 0 +
14 RCP properties
1997 0 0 N N ? 0
15 Shannon aromaticity
2010 N Y N
16 EL index
2012 Y Y N
In the table, "+++", "++", "+", "0", "-" and "--" correspond to very high, high, relatively high,
normal, relatively low and low, respectively. "Y" and "N" stand for "Yes" and "No", respectively.
The meaning of each column are given below.
Principle: The principle behind the method. "Hückel" = Hückel rule; "Magnet." = Magnetic
4 Tutorials and Examples
448
properties; "Geom." = Molecular geometry; "Delocal." = Electron delocalization character; "
" =
Electron density distribution.
Year: The year that the method was first time proposed.
Pop.: Popularity in recent years.
Reliab.: Reliability, measuring if the method is able to faithfully reveal aromaticity.
Univ.: Universality. A method with high universality must be able to be applied to a wide variety
of kinds of systems and situations, such as the rings containing heteroatoms and transition metals,
non-equilibrium geometry (e.g. transition state of Diels-Alder adduction), excited state, etc.
Ref.: If the method relies on reference systems. A universal method must avoid this feature.
Anti-arom.: If the method is also able to measure anti-aromaticity.
Sep. σ/π: If the method can be used to separately discuss σ and π aromaticity.
Cost: The computational cost to apply the method.
Value: The overall value. This is the most important descriptor.
Next, the methods presented in above table will be briefed sequentially, and how to realize
them in Multiwfn will also be mentioned.
1. Molecular orbital (MO): The famous Hückel 4n+2 and 4n rule for determining
aromaticity character was first explicltly presented in J. Am. Chem. Soc., 73, 876 (1951). For a
molecule, if there are totally 4n+2 electrons in π () MOs, and this set of MOs share the similar
delocalization pattern, then the ring involved in these MOs will show π () aromaticity. If there
are 4n electrons, then the ring should possess anti-aromaticity. Note that for Möbius type of
molecule, the 4n+2 and 4n rule are inverted.
In order to use the Hückel rule to determine aromaticity, one should first pick out proper
MOs by visualizing MO isosurfaces, you can use main function 0 for this purpose. If the system is
exactly planar, you can directly make use the function introduced in Section 3.100.22 to find out
the indices of all π MOs.
2. AdNDP (Adaptive natural density partitioning): The MO method shown above
commonly is only applicable to the molecule containing only one ring. When there are multiple
rings, such as phenanthrene, the MOs are useless, since MOs in general delocalize over the whole
molecule and thus cannot be used to study local aromaticity of different rings. The AdNDP
method, which was proposed in Phys. Chem. Chem. Phys., 10, 5207 (2008), is able to overcome
this difficulty. AdNDP has been carefully introduced in Section 3.17, and many examples are
given in Section 4.14.
3. NICS (Nucleus-independent chemical shift): NICS uses the negative value of magnetic
shielding value at ring center to measure its aromaticity. This is the most popular aromaticity
index nowadays, it was originally proposed in J. Am. Chem. Soc., 118, 6317 (1996) and reviewed
in Chem. Rev., 105, 3842-3888. There are also a few variants, among them the best one is
NICS(1)ZZ, see Org. Lett, 8, 863 (2006). For non-planar system, it is often difficult to calculate
NICS(1)ZZ, in this case you will find the function introduced in Section 3.100.24 quite useful.
4. ICSS (Iso-chemical shielding surface): The original paper of ICSS is J. Chem. Soc.,
Perkin Trans., 2, 1893 (2001). This method analyzes aromaticity by visualizing isosurface of
magnetic shielding value around the molecule. See Section 3.200.4 for introduction and Section
4.200.4 for example. The main drawback of this method is that calculating grid data of magnetic
4 Tutorials and Examples
449
shielding values is fairly time-consuming.
5. HOMA (Harmonic oscillator measure of aromaticity): HOMA measures aromaticity
based on bond lengths in the ring of interest. See Section 3.100.13 for introduction and Section
4.100.13 for example.
6. Bird index: The same as above.
7. Multi-center bond order (MCBO): MCBO is an indicator of electron delocalization
ability over a ring and is the aromaticity index I most strongly recommended. Larger MCBO value
corresponds to stronger aromaticity. See Section 3.11.2 for introduction. Some applications of
MCBO in aromaticity studies can be found in J. Phys. Org. Chem., 26, 473 (2013), Phys. Chem.
Chem. Phys., 2, 3381 (2000) and J. Phys. Chem. A, 109, 6606 (2005). It is straightforward to
discuss π and σ aromaticities separately by MCBO, that is before calculating MCBO value, first
set occupation number of all σ and π MOs to zero respectively by subfunction 22 of main function
100.
Note that the definition of MCBO in many literatures differ with that in Multiwfn by a
constant coefficient. The calculation cost of MCBO for six-membered ring can be ignored,
however the cost increases exponentially with the number of atoms in the ring.
8. ELF-σ/π: The ELF calculated solely based on π orbitals and all other orbitals are referred
to as ELF-π and ELF-σ, respectively. It was argued that the value of bifurcation point of ELF-π
(ELF-σ) is an indicator of π (σ) aromaticity, some applications can be found in J. Chem. Phys.,
120, 1670 (2004), J. Chem. Theory Comput., 1, 83 (2005) and Chem. Rev., 105, 3911 (2005). An
example of calculating ELF-σ/π is given in Section 4.5.3. I do not think ELF-σ/π is a very ideal
method for measuring aromaticity, mostly because this method often suffers from ambiguity (you
will recognize this point if you have used this method to study many practical systems). Also note
that the bifurcation values of ELF-σ/π in a lot of literatures are incorrect; if you try, you will find it
is impossible to reproduce their results at all. (So do not always believe literatures but believe in
yourself!)
9. PDI (Para-delocalization index): This aromaticity index is only applicable to six-
membered rings. PDI was first proposed in Chem. Eur. J., 9, 400 (2003) and reviewed in Chem.
Rev., 105, 3911 (2005). Please check Section 3.18.6 for introduction of PDI and Section 4.15.2 for
example of using PDI.
10. ATI (Average two-center indices): ATI was first proposed in J. Phys. Org. Chem., 18,
706 (2005). In fact ATI does not contain any new idea, it simply replaces the delocalization indices
involved in PDI formula with corresponding Mayer bond orders, and according to the discussions
in J. Phys. Chem. A, 109, 9904 (2005), there is no essential difference between Mayer bond order
and delocalization index in physical nature. If you would like to use ATI, you can directly
calculate Mayer bond order by Multiwfn and then manually calculate ATI according to its formula.
11. PLR (Para linear response index): As ATI, PLR is also very akin to PDI. The only
difference between PLR and PDI is that the delocalization indices in PDI are replaced with
corresponding condensed linear response kernels. Original paper of PLR is Phys. Chem. Chem.
Phys., 14, 3960 (2012). You can check Section 3.18.9 for introduction of PLR and Section 4.15.2
for example of using PLR.
12. DI: This method was proposed in Chem. Eur. J., 9, 400 (2003) for measuring
aromaticity of 5-membered systems. Consider below case

4 Tutorials and Examples
450
The DI is simply defined as the difference of delocalization index (DI) between the formal C=C
bond and the C-C bond. The DI can be either calculated by fuzzy atomic space analysis module or
by basin analysis module (though the definition of atomic spaces are different in these two module,
the results are similar in common). In fact, you can also use Mayer bond order instead of DI. I do
not believe DI is reliable, since aromaticity is an overall property of a system, while the
delocalization over C-X bond is completely ignored in DI.
13. FLU and FLU-π (Aromatic fluctuation index): They were proposed in J. Chem. Phys.,
122, 014109 (2005). See Section 3.18.7 for introduction and Section 4.15.2 for example.
14. RCP properties: In Can. J. Chem.,75 , 1174 (1997) it was shown that the density and the
curvature of density perpendicular to the ring plane at ring critical point (RCP) closely relate to
aromaticity of the ring. The larger the density, or the more negative the curvature, the larger the
aromaticity. You can use topology analysis module of Multiwfn to apply this method. Detail
introduction can be found in Section 3.14.6, an example is given in Section 4.2.1.
15. Shannon aromaticity: This method was proposed in Phys. Chem. Chem. Phys., 12, 4742
(2010), which measures aromaticity based on electron density at bond critical points (BCP) in the
ring. See Section 3.14.6 for introduction and the example given in Section 4.2.1.
16. EL index: The idea of EL index is quite similar to HOMA, the most prominent difference
is that the bond lengths in HOMA formula are replaced with electron density ellipticity at BCPs in
the ring. For more detail see the original paper Struct. Chem., 23, 1173 (2012). Electron density
ellipticity at BCPs can be directly calculated by topology analysis module of Multiwfn. Since the
ellipticity at BCP is usually unclear for strongly polar bonds, EL index may be unreliable for the
ring containing heteroatoms. In addition, EL index shares the same drawback of HOMA, that is
reference system is need. If reference system cannot be obtained, such as the case of metal clusters,
this method does not work.
4.A.4 Predict reactive sites
There are numerous methods able to predict reactive site of electrophilic, nuelcophilic and
radical reactions, and almost all of them are supported by Multiwfn. In this section, I will
summary and briefly introduce the methods available in Multiwfn. The interested reader is highly
recommended to take a look at Acta Phys.-Chim. Sinica, 30, 628 (2014) (in Chinese,
http://www.whxb.pku.edu.cn/EN/abstract/abstract28694.shtml), in which various methods for
predicting electrophilic sites are carefully introduced and thoroughly compared. You may also find
the slideshow "Predicting reactive sites" in "Related resources and posts" Section of Multiwfn
website useful.
1 Electrostatic potential (ESP). If you are not familiar with ESP, please consult
corresponding introduction in Section 2.6. Since electrophile (nucleophile) locally carries negative
(positive) charge, and thus tends to be attracted to the region where ESP is negative (positive), the
position and value of minima (maxima) of ESP on molecular vdW surface is often used to reveal
favorable site of electrophilic (nucleophilic) attack. ESP analysis can be realized via quantitative
4 Tutorials and Examples
451
molecular surface analysis module, see Section 4.12 for detailed introduction and Section 4.12.1
for example. There are also alternative ways to study ESP; as illustrated in Section 4.12.3, the
average of ESP on local vdW surface corresponding to each atom is also very useful, and this
approach is more reliable and robust than analyzing ESP extrema on vdW surface. For planar
system, one can also calculate and compare the ESP value above 1.6Å (approximately equal to
vdW radius of carbon) of molecular plane from different atoms to examine their reactivities; to do
this, you need to use main function 1, which directly outputs various real space function values at
given points.
However, as shown in Acta Phys.-Chim. Sinica, 30, 628 (2014), ESP is usually not a reliable
property for predicting reactive sites.
2 Average local ionization energy (ALIE). If you are not familiar with ALIE, please consult
corresponding introduction in Section 2.6. ALIE can be studied in analogous ways to ESP. The
most common way to predict reactive sites in terms of ALIE is analyzing minima of ALIE on vdW
surface, see Section 4.12.2 for example. Also, you can study average of ALIE on local vdW
surface or evaluate ALIE above 1.6Å of molecular plane for planar system.
Note that ALIE analysis is applicable to electrophilic and radical attacks, but it is useless for
nucleophilic attack. However, another similar real space function named local electron affinity
(LEA) may be useful for this purpose, see J. Mol. Model., 9, 342 (2003). LEA can be studied in
Multiwfn via user-defined function, see Section 2.7 for detail. According to my experience, LEA
is not well defined and useually does not work well.
3 Atomic charges. It is easy to understand that favorable electrophilic and nucleophilic
reactive sites should carry negative and positive atomic charges respectively, so that they can
attract electrophile and nucleophile to attack them. Multiwfn supports a lot of methods to calculate
atomic charges, see Section 3.9 for introduction and Section 4.7 for some instances. Among the
available atomic charges, the best one for predicting reactive sites purpose may be Hirshfeld,
interested readers are suggested to consult J. Phys. Chem. A, 118, 3698 (2014). Do not use
Mulliken charges, which may be the worst one, though it is the most popular charge model.
4 Frontier molecular orbital (FMO) theory. Atom with larger contribution to HOMO
(LUMO) is more likely to be the preferential site of electrophilic (nucleophilic) attack. Multiwfn
supports many kinds of methods to calculate molecular orbital composition, see Section 3.10 for
introduction and Section 4.8 for examples. Commonly I suggest using Becke or Hirshfeld method.
Mulliken method works equally well if no diffuse functions are presented. NAO method is also a
good choice, but not suitable for analyzing virtual MOs. Besides, you can also directly visualize
the isosurface of MOs by main function 0 to discuss their compositions.
5 Fukui function and condensed Fukui function. The Fukui function proposed in J. Am.
Chem. Soc., 106, 4049 (1984) by Parr is the most prevalently used method for predicting reactive
sites nowadays. Please consult Section 4.5.4 for introduction and illustration. Fukui function is a
real space function, which is commonly studied by means of visualization of isosurface. In order
to faciliate quantitative comparison between difference sites, one can calculate condensed Fukui
function based on atomic charges, please consult Section 4.7.3. In addition, as demonstrated in
Section 4.12.4, the Fukui function can also be investigated in combination with local quantitative
molecular surface analysis technique.
6 Dual descriptor and condensed dual descriptor. As demonstrated in Acta Phys.-Chim.
Sinica, 30, 628, the dual descriptor proposed in J. Phys. Chem. A, 109, 205 (2005) may be the

4 Tutorials and Examples
452
most robust method for predicting reactive sites, at least for electrophilic reaction. Like Fukui
function, dual descriptor also has condensed version. Dual descriptor and the condensed version
are introduced in Section 4.5.4 and 4.7.3, respectively.
4.A.5 Study weak interactions
There are a lots of ways to characterize weak interactions, and most of them are supported by
Multiwfn, here I give you a brief summary. If you can read Chinese, I suggest reading my post
"An overview of the weak interaction analysis methods supported by Multiwfn"
(http://sobereva.com/252), in which this topic is discussed more deeply and extensively.
(1) AIM topology analysis is a very popular method for studying both strong and weak
interactions. Its use in weak interaction analysis is partially illustrated in Section 4.2.1.
(2) RDG analysis proposed in 2010 may be viewed as an extension of AIM analysis, this
method rapidly became quite popular after it was proposed. The example of using RDG analysis is
given in Section 4.100.1. RDG analysis is also able to be employed to study weak interaction in
dynamic environment such as molecular dynamic simulation, see the introduction in Section
3.200.1 and the accompanied example in Section 4.200.1. Integrating domain of RDG is a useful
way to discuss weak interactions quantitatively, examples are provided in Section 4.200.14.
(3) Electrostatic potential (ESP) analysis. ESP has been introduced in Section 2.6, this is a
extremely important real space function for studying electrostatic dominated weak interactions.
There are many different ways to carry out ESP analysis:
a) Visually studying ESP color-mapped molecular vdW surface, this analysis can be used to
quickly figure out potential electrostatic interaction sites and qualitatively study interaction
strength. See the end of Section 4.12.1 and J. Mol. Model., 13, 291 (2007) for example.
b) Studying ESP minima and maxima on molecular vdW surface. This can done by quantitative
molecular surface analysis module, see Section 4.12.1 for example and Section 3.15 for more
details. The value of these ESP extrema on vdW surface strongly correlate with electrostatic
interaction energies, and you can find many papers have used this method, for example Phys.
Chem. Chem. Phys., 15, 14377 (2013), J. Mol. Model., 13, 305 (2007), Int. J. Quantum. Chem.,
107, 3046 (2007), Phys. Chem. Chem. Phys., 12, 7748 (2010), J. Mol. Model., 14, 659 (2008), J.
Mol. Model., 18, 541 (2012), J. Mol. Model., 15, 723 (2009), Chapter 6 of book Practical Aspects
of Computational Chemistry (2009).
c) Superposition analysis of ESP contour map. This method was proposed by Tian Lu in J. Mol.
Model., 19, 5387 (2013), it is quite vivid, easy-to-use and powerful. It was demonstrated that
stability of complex configurations can be fairly well predicted by this method. Section 4.4.4
showed how to plot ESP contour map.
d) In J. Phys. Chem. A, 118, 1697 (2014), the authors showed that by making use of ESP at
nuclear positions the electrostatic dominated intermolecular interaction energies can be very
accurately predicted. See Section 4.1.2 for introduction and example.
(4) Atomic charge analysis. Atomic charge is a very simple and intuitive model for describing
charge distribution and can be used to analyze the strength of electrostatic interaction between
different sites. The functions for calculating atomic charges are introduced in Section 3.9, and
some practical examples are given in Section 3.7.
(5) Bond order and delocalization index (DI) analysis. Commonly weak interactions are
4 Tutorials and Examples
453
dominated by electrostatic and/or vdW interactions, so bond order and DI analysis, which mainly
reflect covalent character are often not useful in these cases. However, for "strong" weak
interactions, such as low-barrier hydrogen bonds (LBHB) and charge-assisted halogen bonds,
covalent contribution may be not negligible, and thus bond order and DI analysis can be applied.
Bond order calculations are illustrated in Section 4.9. In Multiwfn, DI can be calculated based on
fuzzy atomic space or AIM basin, the former is equivalent to fuzzy bond order, while the latter can
be evaluated in basin analysis module, see example in Section 4.17.1.
(6) ELF analysis. In Theor. Chem. Acc., 104, 13 (2000), Fuster and Silvi defined CVB index
based on ELF to classify strength of H-bonds. J. Phys. Chem. A, 115, 10078 (2011) employed this
method to study a large amount of resonance-assisted hydrogen bonds and find this index is in
good correlation with other H-bond strength indices. CVB index can easily calculated in Multiwfn
by plotting ELF curve between the two interacting atoms via main function 3. There are also other
papers using ELF to study H-bonds, e.g. Chem. Rev., 111, 2597 (2011).
(7) Charge variation analysis. Weak interactions often accompanied by charge transfer and
polarization, therefore studying how the electrons are transfered between or within molecules, as
well as how the electron density is polarized due to the presence another molecule are important.
There are many available ways to investigate these points:
a) Plotting difference map of electron density between complex and monomers. This is the most
straightforward and intuitive way to study variation of electron density. The procedure is
illustrated in Section 4.5.5.
b) Plotting charge displacement curve. After generating grid data of density difference, in order
to quantitatively study the charge variation in a direction, you can plot charge displacement curve,
see Section 3.16.14 for introduction and Section 4.13.6 for example.
c) Variation of atomic charges of monomers in their isolated states and in complex state can
quantitatively and clearly show how the electrons are transfered between different
atoms/fragments due to the interaction.
d) After generating grid data of electron density difference between complex and monomers,
you can use basin analysis module to integrate basin of density difference to study amount of
electron variation in various characteristic regions (e.g. the region corresponding to σ-hole). You
can consult the example in Section 4.17.4.
e) Charge decomposition analysis (CDA). CDA is used to reveal underlying details of charge
transfer, the amount of donation and back-donation of electrons between two fragments due to
various complex MOs can be studied. In addition, the CDA module of Multiwfn can tell you how
the fragment MOs are mixed and hence yield complex MOs. CDA is commonly applied to strong
interaction, but it may be also useful for exploring weak interactions. The theory of CDA is
introduced in Section 3.19, practical examples are given in Section 4.16.
f) Multiwfn has a function dedicated to analyze charge transfer in electron excitation based on
electron density difference, many important quantities characterizing the transfer can be obtained,
see Section 3.21.3 for introduction and 4.18.3 for example. Based on the grid data of electron
density difference between complex and monomers, this function may be also useful for studying
charge transfer due to weak interaction.
(8) Hirshfeld and Becke surface analysis. This kind of analysis is extremelly useful for
revealing weak interaction in molecular crystals, see the example in Sections 4.12.5 and 4.12.6 as
well as theory introduction in Section 3.15.5.
4 Tutorials and Examples
454
(9) LOLIPOP index is useful for measuring π-π stacking ability, see the introduction in
Section 3.100.14 and the example in Section 4.100.14.
(10) Energy decomposition analysis is a kind of important approachs for characterizing the
nature of weak interactions, physical components of total interaction energy can be separately
obtained. Multiwfn is capable of performing very simple energy decomposition analysis, see
Section 4.100.8 for example.
(11) Source function analysis is defined in the framework of AIM theory. Gatti et al.
suggested using source function to study both strong and weak interactions. Introduction of source
function can be found in Section 2.6, and tutorial of performing source function analysis is given
in Section 4.17.5. A thorough review is Struct. & Bond., 147, 193 (2010), in which H-bond
analysis is involved.
(12) Mutual penetration distance of vdW surfaces. For the same kind of weak interaction,
generally the larger the penetration of vdW surface, the stronger the interaction strength. For a
non-covalently interacting atom pair AB, the difference between the distance of A-B and the sum
of their non-bonded radii is termed as mutual penetration distance. The non-bonded atomic radius
is the closest distance between a nucleus and the molecular vdW surface, and can be obtained by
option 10 in post-process interface of quantitative molecular surface analysis module of Multiwfn.
(13) Atomic multipole moment analysis. The definition of atomic multipole moment can be
found in Section 3.18.3. Atomic multipole moment measures the anisotropy distribution of
electron density around an atom, which has important impact on interatomic electrostatic
interactions. See Section 7.4.3 of the Bader's book Atoms in molecules-A quantum theory for
illustrative examples. In Multiwfn, atomic multipole moment can be calculated by both fuzzy
space analysis module and basin analysis module, for the latter case see Section 4.17.1 for
example.
(14) Orbital overlap. For weak interactions involving orbital interaction, you can use
Multiwfn to study orbital overlap, which is closely related to orbital interaction strength. The
example Section in 4.100.15 illustrated how to calculate intermolecular orbital overlap integral.
Section 4.0.2 exemplified how to visualize overlap degree of two NBO orbitals, high (low)
overlap degree commonly implies large (small) second-order perturbation energy E(2) between
the two NBOs.
(15) As demonstrated in J. Mol. Model., 19, 2035 (2013), interaction energy of halogen-bond
complexes is well correlated with the properies of (3,-1) critcial point of Laplacian of electron
density at σ-hole location. The topology analysis of Laplacian of electron density can be
conveniently realized in main function 2. Section 4.2.2 showed how to perform topology analysis
for LOL, however you can use the same method to analyze Laplacian of electron density.
There are also other possibly ways to study weak interactions, but they are not directly
relevant to Multiwfn. These methods include: NBO E(2) and NBO deletion analyses (see the
tutorials in NBO official website), rehybridization analysis (specific for H-bond, based on natural
population analysis), variation of bond length and vibrational frequency, Mayer energy
decomposition analysis (Phys. Chem. Chem. Phys., 8, 4630 (2006)), magnetically induced current
(Phys. Chem. Chem. Phys., 13, 20500 (2011)), interacting quantum atoms (IQA, supported by
AIMALL, see J. Phys. Chem. A, 117, 8969 (2013) for example), SAPT analysis (supported by
Molpro, PSI4 etc. see WIREs Comput. Mol. Sci., 2, 254 (2012)), ETS-NOCV (supported by ADF,
4 Tutorials and Examples
455
see J. Chem. Theory Comput., 5, 962 (2009)).
4.A.6 Calculate odd electron density and local electron correlation
function
Part 1: Odd electron density
Some papers calculate the so-called odd electron density (OED), its was originally defined in
Chem. Phys. Lett., 372, 508 (2003), and employed in many papers, e.g. Theor. Chem. Acc., 130,
711 (2011) and J. Phys. Chem. C, 116, 19729 (2012). Here I introduce how to plot it by using
Multiwfn in combination with .wfn file produced by Gaussian.
Spatial natural orbitals are yielded by diagonalizing total density matrix and have occupation
number within 0 and 2.0. The OED of the kth natural orbital is defined as
)(),2min()(
odd rr kkkk nn
where )(r
k
and nk are its electron density and occupation number, respectively. Thus for nk1,
the prefactor corresponds to occupation number, while for nk1, the prefactor corresponds to the
complement to achieve a closed shell. In other words, the min(2-nk, nk) term can be regarded as
the probability of the electron to be unpaired in this orbital.
The total OED is defined as the summation of OED for all natural orbitals:
kk)()( oddodd rr
Now we calculate OED for a closed-shell system OC-BH3 at CCSD level (while at HF/DFT
level, this quantity is obviously zero everywhere). The Gaussian input file can be found in
examples\COBH3_CCSD.gjf, note that density out=wfn keywords are used. The resulting file
examples\COBH3_CCSD.wfn contains all CCSD natural orbitals.
We first calculate total OED. Boot up Multiwfn and input
examples\COBH3_CCSD.wfn
6
26 // Modify occupation number
0 // Select all orbitals
odd // Take min(2-nk, nk) as occupation number for all orbitals
q // Return
-1
Then we plot isosurface map of electron density as usual
5
1
2
-1
Then we set isovalue to 0.005, you will see the total OED, as shown below. Although the use
of OED in above mentioned papers aims to study biradical character, in my personal viewpoint,
this function is also useful to reveal where electron correlation is significant. As you can see in the
below graph, electron correlation is very strong in the multiple-bonds region of CO.

4 Tutorials and Examples
456
Next, we plot OED for natural orbital 11. What we need to do first is cleaning the occupation
number for all other orbitals. Close the GUI and input
0
6
26
1-10
0 // Clean the occupation number for orbitals 1 to 10
12-57
0 // Clean the occupation number for orbitals 12 to 57
Then return to main menu and plot electron density as usual. That's all.
Below we plot total OED for a typical biradical system C4H8 at M06-2X level. In this case,
unrestricted open-shell calculation is needed and guess=mix keyword should be used to achieve
symmetry-broken state. In addition, pop=no out=wfn must be specified so that spatial natural
orbital will be generated by mixing alpha and beta density matrix, diagonalization and then be
outputted to .wfn file. The natural orbitals obtained by such a UHF/UDFT calculation are
sometimes referred to as unrestricted natural orbitals (UNO). The Gaussian input file for
producing the .wfn file is examples\C4H8-UNO.gjf, and the resulting .wfn file is examples\C4H8-
UNO.wfn. Please use this file to plot total OED like above example, the isosurface map with
isovalue of 0.02 should look like below (its character is quite similar with spin density map)

4 Tutorials and Examples
457
Part 2: Local electron correlation functions
The local electron correlation functions proposed in J. Chem. Theory Comput., 13, 2705
(2017) are very useful real space functions to reveal total, dynamic and nondynamic electron
correlation in various molecular regions. The definition of these function can be found in entry 87,
88 and 89 of Section 2.7. As you can see, their forms are closely related to OED. Now let us plot
local total electron correlation functions IT for OC-BH3.
Set "iuserfunc" in settings.ini to 87, then boot up Multiwfn and input
examples\COBH3_CCSD.wfn
5
100 // User-defined function, now it corresponds to IT
2 // Medium quality grid
-1 // Visualize isosurface
Set isovalue to 0.013, then you will see
This graph is rather similar with the isosurface map of OED. Since IT is a real space function
specific for revealing electron correlation, our observation clearly demonstrates that OED is also
capable of exhibit electron correlation.
Local electron correlation function has another two forms, namely ID and IND, which aim for
representing dynamic and nondynamic electron correlation, respectively. They can be plotted with
the same way as shown above, but you need to set "iuserfunc" to 88 and 89, respectively.
Plotting individual contribution to local electron correlation functions is also possible, you
can screen uninteresting natural orbitals by setting their occupation numbers to zero via suboption
26 of main function 6.
Using subfunction 4 of main function 100 you can integrate local electron correlation
functions over the whole space, the result indicates the magnitude of electron correlation for the
whole system. For example, we return to main menu and input
100
4 // Integrate a real space function over the whole space
100 // User-defined function
The result, which is referred to as total electron correlation index, is 1.576. Repeat this
calculation for dynamic and nondynamic electron correlation functions, you will find the resulting
indices are 1.267 and 0.309, respectively. Evidently, dynamic correlation governs the total electron
correlation effect for present system.
In fact, the total, dynamic and nondynamic electron correlation indices can also be calculated
by subfunction 15 of main function 200, which is much faster and more convenient, see Section
3.200.15 for introduction. Now we have a try. Return to main menu and input 200 then 15, you

4 Tutorials and Examples
458
will immediately see
Nondynamic correlation index: 0.30880061
Dynamic correlation index: 1.26746042
Total correlation index: 1.57626103
4.A.7 Plot (hyper)polarizability density
By means of custom operation of main function 4 and 5, (hyper)polarizability density can be
easily plotted by Multiwfn as plane map and isosurface map. This is quite useful for discussing
nature of (hyper)polarizability of a given molecule. For details, please check my blog article
http://sobereva.com/305 (in Chinese). Illustrative applications can be found in e.g. J. Comput.
Chem., 38, 1574 (2017) and Phys. Chem. Chem. Phys., 19, 23951 (2017).
4.A.8 Analyze higher level of wavefunction than CCSD
In the most commonly used program Gaussian, the highest level of wavefunction is CCSD.
Although CCSD wavefunction is absolutely sufficient for almost all cases, due to some special
reasons, one may want to study wavefunction produced at higher level. Below I describe how to
make Multiwfn able to analyze CCSD(T) wavefunction generated by PSI4 program
(www.psicode.org), and arbitrary order of coupled cluster and CI wavefunction (including Full CI)
yielded by Kallay's MRCC program (www.mrcc.hu).
(1) PSI4
The version of PSI4 I currently use is 1.1. Below is an example of input file, which calculate
hydrogen fluoride at CCSD(T)/cc-pVTZ level, and produce HF_CCSDpT.fchk in current folder.
molecule HF {
H 0.0 0.0 -0.831975
F 0.0 0.0 0.092442
}
set basis cc-pVTZ
grad, wfn = gradient('CCSD(T)', return_wfn=True)
fchk_writer = psi4.FCHKWriter(wfn)
fchk_writer.write('HF_CCSDpT.fchk')
The resulting HF_CCSDpT.fchk records Hartree-Fock MOs and CCSD(T) density matrix. If
you directly feed this file into Multiwfn, because Multiwfn never utilizes density matrix but only
load orbitals from the file, the result of following analyses will correspond to Hartree-Fock level.
In order to make Multiwfn analyze CCSD(T) wavefunction, you should do below steps:
1. Boot up Multiwfn and load HF_CCSDpT.fchk as usual
2. Enter main function 1000 and select subfunction 98. This function is used to convert
density matrix in the .fch/.fchk file into natural orbitals. Then you will immediately see occupation
number of natural orbitals yielded by diagonalization of CCSD(T) density matrix.
3. Enter main function 100 and select subfunction 2, choose to export .molden file
4. Reboot Multiwfn, load the newly generated .molden file.
4 Tutorials and Examples
459
Now both the basis function information and GTF information in memory correspond to
CCSD(T) wavefunction, therefore all the following analyses will be carried out at CCSD(T) level.
Note that if this is an open-shell system, Multiwfn will ask you if generate UNO orbitals. If
you choose n, alpha and beta natural orbitals will be generated separately; while if you choose y,
only spatial natural orbitals will be yielded.
(2) MRCC
The version of PSI4 I currently use is Sept 25, 2017. Below is an example of input file, which
calculate hydrogen fluoride at CCSDT/cc-pVTZ level.
basis=cc-pvtz
calc=CCSDT
mem=2500MB
dens=1
geom=xyz
2
H 0.0 0.0 -0.831975
F 0.0 0.0 0.092442
After run it by MRCC, you will find a file named MOLDEN in current folder, which is a
Molden input file and records Hartree-Fock MOs. In current folder you can also find a file named
CCDENSITIES, which records the 2nd and 1st reduced density matrix (2RDM and 1RDM). In
order to make Multiwfn analyze CCSDT wavefunction, we must convert the 1RDM into natural
orbitals and save them to .molden file.
Change the name of MOLDEN to e.g. mrcc.molden, then boot up Multiwfn and load it. Enter
main function 1000 and select subfunction 97, input path of the CCDENSITIES file. Then input
the number of frozen core orbitals. By default, MRCC freezes core MOs in electron correlation
calculation. Current system has two core electrons (in the output file it can be seen that " Number
of core electrons: 2"), and this is a closed-shell system, each occupied MO has two electrons,
therefore only one core MO is frozen, so we input 1. Soon, generation of natural orbitals by
diagonalizing CCSDT density matrix is finished and occupation numbers are printed on screen.
We use subfunction 2 of main function 100 to export a .molden file. then reboot Multiwfn and
load it, now both the basis function information and GTF information in memory correspond to
CCSDT wavefunction, therefore all the following analyses will be carried out at CCSDT level.
The procedure of analyzing CI wavefunction produced by MRCC is exactly the same as
those shown above. Below is an example input file of calculating elongated LiH at FCI/aug-cc-
pVDZ level without frozen core treatment.
basis=aug-cc-pvdz
calc=fci
mem=2500MB
dens=1
core=0
geom=xyz
4 Tutorials and Examples
460
2
H 0.0 0.0 0.0
Li 0.0 0.0 3.0

5 Skills
461
5 Skills
5.1 Make Multiwfn support more quantum chemistry
programs
Although currently Multiwfn is able to directly accept Molden input file (.molden) as input
file, only the file generated by a few programs is formally supported (see the related description in
Section 2.5). If the Molden input file is generated by other programs then the analysis result may
be incorrect. For these cases, you can use Molden2aim program written by Wenli Zou
(https://github.com/zorkzou/Molden2AIM) to produce standardized Molden input file.
Using Molden2aim is easy. First move the Molden input file (e.g. ltwd.molden) into the
directory where molden2aim.exe is placed, then properly modify its setting file m2a.ini, then boot
up Molden2aim and follow its prompts to input commands, finally you will get ltwd_new.molden
(standardized Molden input file) and may be other files (.wfn, .wfx, etc.).
Since Molden2aim v2.0.5, orbital spin-types are explicitly written at the end of the converted
wfn file ($MOSPIN $END field), this information is automatically loaded by Multiwfn.
Molden2aim can output GTFs with angular moment up to g. Although g GTFs is not
originally defined in wfn format, these g GTFs can also be correctly identified and loaded into
Multiwfn.
The "charge" field of the wfn file outputted by Molden2aim is the serial number of the
element in periodic table rather than the effective nuclear charges, even if effective core potential
(ECP) is used. This treatment is inconsistent with the wfn file outtputted by Gaussian, in which
"charge" is effective core charges when ECP is used (e.g. the "charge" of Au under Lanl2DZ is
19.0). So, if ECP is used and you want to calculate electrostatic potential, do not forget to modify
"charge" field in the wfn file outputted by Molden2aim to effective nuclear charges.
5.2 Running Multiwfn in silent mode
Multiwfn aims for ease of use, so it is designed as an interactive program. Nevertheless
Multiwfn can also run in silent mode, by which you do not need to press any keys during
Multiwfn running. For example, you want to obtain the graph in example 4.4.1 silently, you need
to write an inputstream file first, the content is (red texts are comments):
4
1
1
200,200
2
5 Skills
462
0
0 Option 0: save graph to current directory
I suppose that the inputstream file is named as “4.4.1.txt”, I have already provided this file in
“examples” directory. Now change “isilent” parameter in "settings.ini" from 0 to 1, this step tells
Multiwfn to forbid any graph or GUI popping up automatically during running (otherwise you
have to close the window by clicking mouse button). Then run this command in MS-DOS (to
enter MS-DOS from Windows, click “Start”-“run” and type “cmd”): Multiwfn hcn.wfn < 4.4.1.txt
> medinfo.txt, here I assume that Multiwfn.exe, 4.4.1.txt and hcn.wfn are in current directory.
After a few seconds, you will find the expected graphic file appears in current directory, from
medinfo.txt you can find all intermediate information outputted by Multiwfn (the same as in
interactive mode).
What does the content in inputstream file mean? The answer is: the texts in each line of
inputstream file are just what you need to input in interactive mode, you can redo example 4.4.1 to
ensure it is true. It is easy to write a new inputstream file by following the prompts in interactive
mode. The symbol “<” and “>” are known as redirection operator, they respectively tell Multiwfn
that the contents in 4.4.1.txt are inputstream, while the outputstream should be stored into
medinfo.txt. This redirection mechanism is not provided by Multiwfn but provided by operation
system. Notice that the name of input file is missing in inputstream file, because it appears as an
argument.
You may have noted that when the task is finished, some errors like below appear. They are
not really errors, and hence you can safely ignore them.
forrtl: severe (24): end-of-file during read, unit -4, file CONIN$
Image PC Routine Line Source
Multiwfn.exe 00588F1A Unknown Unknown Unknown
Multiwfn.exe 00586438 Unknown Unknown Unknown
Multiwfn.exe 00530B3A Unknown Unknown Unknown
......
Another example, assume that you want to save detail compositions of orbital 1 to 3 of
COCl2.fch, just create an inputstream file dubbed “orbana_1_3.in” with below content:
8 Orbital composition analysis
1 Mulliken method
1 Orbital 1
2 Orbital 2
3 Orbital 3
Then run the command: Multiwfn COCl2.fch < orbana_1_3.in > orbana_1_3.txt.
If you are a Linux or Mac OS user, you can also make use of "echo" command to avoid
writting an inputstream file to run Multiwfn silently. The goal of the last example can be
equivalently realized by running this command:
echo -e "8\n1\n1\n2\n3" | Multiwfn COCl2.fch > orbana_1_3.txt
Each "\n" means pressing ENTER button once.
Alternatively, you can add below lines into your script file:
Multiwfn COCl2.fch > orbana_1_3.txt << EOF
5 Skills
463
8
1
1
2
3
EOF
5.3 Running Multiwfn in batch mode (for Windows)
If you are familiar with writing shell-scripts and you have read last section, you must have
already know how to use Multiwfn to process a batch of files, it is indeed very easy. Assume that
you want to generate cube files of ELF for these files: ultravox.wfn, chinaski.fch,
strawberry_egg.wfn, you should compile a plain text file named “batchrun.bat” with below
content:
Multiwfn ultravox.wfn < genELFcub.txt > null
move ELF.cub ultravox.cub
Multiwfn chinaski.fch < genELFcub.txt > null
move ELF.cub chinaski.cub
Multiwfn strawberry_egg.wfn < genELFcub.txt > null
move ELF.cub strawberry_egg.cub
del null
where "genELFcub.txt" is inputstream file for generating ELF cube file, its content is
5
9
2
2 Option 2: Exporting cube file in current directory
If you cannot understand the meaning, read last section and consult example 4.5.1.
Now, double click the icon of "batchrun.bat" or input the command batchrun in MS-DOS, the
work will start and then the three ELF cube files will be generated in current folder sequentially.
5.4 Copy outputs from command-line window to
clipboard
Sometimes the outputs of Multiwfn on command-line window are needed to be stored
permanently or transported to third-part softwares via plain text file. Here I describe how to copy
these outputs to Windows clipboard, assuming that you want to copy Hessian matrix of electron
density.
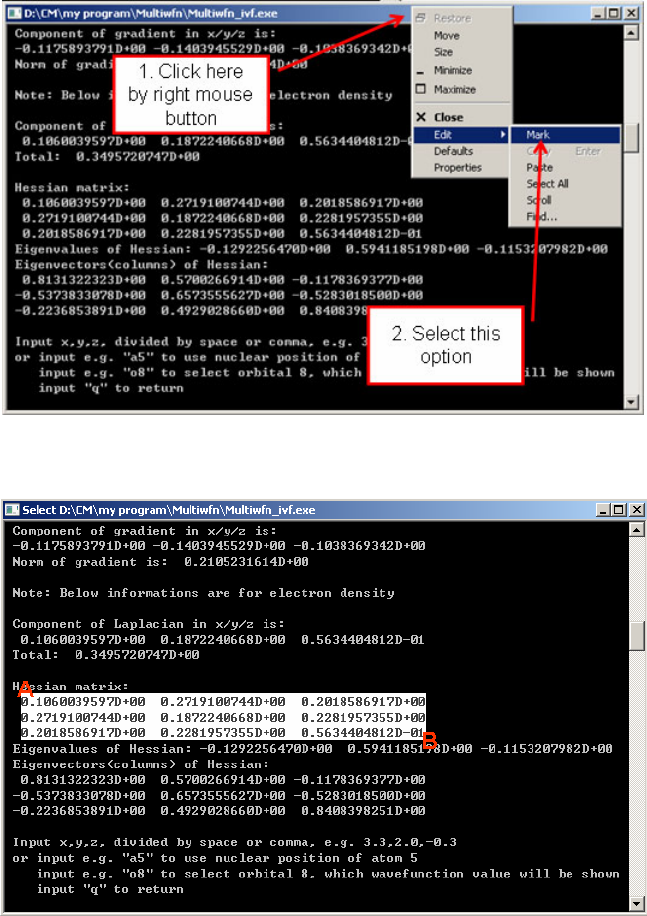
5 Skills
464
After you select "Mark", drag left mouse button from point A to point B
Then press ENTER button, the information highlighted by white rectangle will be stored to
clipboard, you can paste them to anywhere, such as plain text file.
For Mac OS or Linux system running in graphical environment, you can also copy the output
of Multiwfn from console to plain text file by similar manner.
5.5 Make command-line window capable to record more
outputs
Occasionally you may find command-line window cannot record entire outputs of Multiwfn.
For example, you select option 6 in wavefunction modification module to get density matrix for a
relative big wavefunction, however only the last part of the matrix can be found in the command-
line window. The solution of the problem is to enlarge buffer size of the window, please follow
below steps.
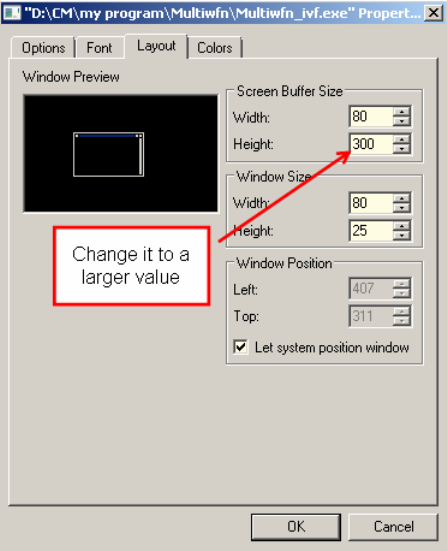
5 Skills
465
Boot up Multiwfn, click title of the window by right mouse button, click "Properties", select
"Layout" page, you will find the default buffer size of the window is 300 (see the screenshot
below), that means only up to 300 lines can be recorded in the window, which is obviously too
small. Change the value to a larger value, for example 9999, and then click OK button. After that
you will find the window capable to record much more outputs (If the complete output still cannot
be recorded, enlarge buffer size again).
The buffer size setting is saved permanently in system, you needn't to set this value again at
next time you boot up Multiwfn.
For Linux and Mac OS, you can also find similar option used to set buffer size of terminal.
5.6 Rapidly load a file into Multiwfn
Probably sometimes you feel inputting the path of input file is cumbersome, especially when
the path is very long. Below I provide you some tricks, which make this step much more easier.
If you want to rapidly load a file into Multiwfn without inputting its path, you can boot up
Multiwfn and then directly drag the icon of the file into the Multiwfn command-line window.
In Windows platform, an even more simple method is directly dragging the file onto the icon
of "Multiwfn.exe", then the file will be automatically loaded into Multiwfn. Notice that in this
situation, the "current folder" is the position of the input file.
If directly inputting letter o, the file last time loaded will be loaded again, whose path is
recorded as lastfile variable in settings.ini file.
Assume that the file you last time loaded is C:\sob\lover\K-ON\Mio.wfn, and this time you
want to load C:\sob\lover\K-ON\Azusa.wfn, you can simply input ?azusa.wfn, namely the path of
the folder last time involved can be replace with a question mark.
Appendix
466
Appendix
1 Setting up environment variable for Gaussian in
Windows
If the error “No executable for file l1.exe” occurs when Multiwfn is invoking Gaussian, that
means the environment variable “GAUSS_EXEDIR“ has not been set properly, therefore
Gaussian does not know where to find l1.exe. Here I show you how to set it.
(1) Windows XP users: Enter “control panel”-“System properties”-“Advanced”
(2) Windows 7 users: Enter “control panel”-“System”-“Advanced system setting”-
"Advanced"
Then click “Environment variables” button, then click “New” button (in “User variables”
frame), input GAUSS_EXEDIR in variable name, input the install directory of Gaussian in variable
value (e.g. d:\study\g09w\, assuming that g09.exe is in this folder). Afterwards when Gaussian is
invoking, Gaussian will search executable files of each link (such as l1.exe) in this folder.
2 The routines for evaluating real space functions
Below are the routines in function.f90 file. You can make use of them to construct new real
space function by yourself. For more details please check the comments in the code of
corresponding routine.
Calculate real space functions:
function calcfuncall: A warpper for calculating any supported real space function at a given
point
function userfunc: User defined real space function
function linintp3d: Function value obtained by trilinear interpolation from grid data in
memory
function fmo: Orbital wavefunction value
function fdens: Electron density
function fspindens: Spin or Alpha or Beta electron density
function fgrad: Gradient (x,y,z components or its norm) of density, or reduced density
gradient (RDG)
function flapl: Laplacian of electron density (xx or yy or zz part or total)
function Lagkin: Lagrangian kinetic G(r), or its components
function Hamkin: Hamiltonian kinetic K(r), or its components
function calcprodens: Promolecular density
function signlambda2rho: Sign(lambda2(r))*rho(r)
subroutine signlambda2rho_RDG: Calculate Sign(lambda2(r))*rho(r) and RDG at the same
Appendix
467
time
function signlambda2rho_prodens: Sign(lambda2(r))*rho(r) with promolecular
approximation
function RDGprodens: RDG with promolecular approximation
subroutine signlambda2rho_RDG_prodens: Calculate Sign(lambda2(r))*rho(r) and RDG at
the same time with promolecular approximation
function ELF_LOL: ELF and LOL
function avglocion: Average local ionization energy
function loceleaff: Local electron affinity
function edr: Electron delocalization range EDR(r;d)
function edrdmax: Orbital overlap distance function D(r)
function linrespkernel: Approximate form of DFT linear response kernel for close-shell
function pairfunc: Exchange-correlation density, correlation hole and correlation factor, on-
top pair density
function srcfunc: Source function
function infoentro: Shannon information entropy function or Shannon entropy density
function totesp: Total ESP
function nucesp: ESP from nuclear or atomic charges
function eleesp: ESP from electrons
function totespskip: ESP without contribution of nuclues defined by iskipnuc parameter
subroutine planeesp: Calculate ESP in a plane
subroutine espcub: Calculate grid data of ESP from electrons
function twoorbnorm: Product of norm of two orbitals
function beckewei: Generate Becke weighting function
function densellip: Ellipticity of electron density and
index
function xLSDA: Integrand of LSDA exchange functional
function xBecke88: Integrand of Becke88 exchange functional
function cLYP: Integrand of LYP corelation functional
function DFTxcfunc: Various kinds of integrand of DFT exchange-correlation functionals
function DFTxcpot: Various kinds of DFT exchange-correlation potentials
function weizsacker: Integrand of Weizsacker functional (steric energy)
function stericpot: Steric potential, which negative value is one-electron potential
function stericcharge: Steric charge
function stericforce: Magnitude of steric force
funciton paulipot: Pauli potential
function pauliforce: Magnitude of Pauli force
function paulicharge: Pauli charge
function Fisherinfo: Fisher information density
function calcatmdens: Promolecular density calculated based on Lagrange interpolation of
built-in atomic radial density
function PAEM: Potential acting on one electron in a molecule
function SEDD: Single exponential decay detector (SEDD)
function DORI: Density Overlap Regions Indicator (DORI)
function localcorr: Local electron correlation function
Appendix
468
function elemomdens: Electron linear momentum density
function magmomdens: magnetic dipole moment density
function energydens_grdn: Gradient norm of energy density
function energydens_lapl: Laplacian of energy density
Calculate derivatives of real space functions:
subroutine gencalchessmat: A general routine used to calculate value, gradient and Hessian
matrix at a given point for some real space functions
subroutine orbderv: Calculate wavefunction value of a range of orbitals and their derivatives
at given point, up to third-order
subroutine EDFrho: Calculate contribution from EDFs to density and corresponding
derivatives (up to third-order)
subroutine calchessmat_dens: Calculate electron density, its gradient and Hessian matrix
subroutine calchessmat_prodens: Calculate electron density, its gradient and Hessian matrix
with promolecular approximation
subroutine gendensgradab: Generate electron density and gradient norm for alpha and beta
electrons at the same time
subroutine calchessmat_lapl: Calculate Laplacian of electron density, its gradient and Hessian
matrix (Hessian is currently not available)
subroutine calchessmat_ELF_LOL: Calculate ELF/LOL, its gradient and Hessian matrix
(Hessian is currently not available)
subroutine calchessmat_mo: Calculate gradient and Hessian matrix for an orbital
wavefunction
subroutine stericderv: Calculate the first-order derivative of steric potential
3 Detail of built-in atomic densities
Some analyses, such as Hirshfeld/ADCH population analyses and Hirshfeld orbital
composition analysis request atomic densities. Though, as shown in Section 3.7.3, the atomic
densities can be evaluated based on atomic .wfn files, the process is slightly complicated, namely
the element .wfn files needed must be prepared and sphericalized first. In order to simplify these
analysis tasks, a set of built-in atomic densities (available from H to Lr) was provided in Multiwfn
and one can directly choose to use it.
These built-in atomic densities were evaluated at highly accurate computational level at atom
ground-states, and have been sphericalized (density distribution of many atoms in their ground
states are not spherically symmetric). Main group elements with index <=18 were calculated at
B3LYP/cc-pVQZ level, those >18 were calculated at B3LYP/ANO-RCC level (except for Ca,
UGBS is used since the ANO-RCC of Ca in EMSL website is wrong). Transition metals were
calculated at HF/UGBS level. Lanthanides and Actinides were calculated at B3LYP/SARC-DKH
level (except for U and Np, for which ROHF was used instead of B3LYP because DFT cannot
reproduce their correct ground state configurations). For all elements heavier than Ar, DKH2
method was employed to take scalar relativistic effect into account. Unless otherwise specified,
open-shell systems was treated by unrestricted open-shell formalism.
The atomic densities are recorded as radial points in "atmraddens.f90", the second kind of

Appendix
469
Gauss-Chebyshev method was used to generate the position of radial points, and the point
distribution is identical for all elements. The atomic density at any point is evaluated in terms of
Lagrange interpolation method based on the points.
If you want to replace built-in atomic density of an element with that calculated by yourself,
after booting up Multiwfn and loading corresponding atom wavefunction file, select main function
98 ( a hidden function), then Multiwfn will calculate radial electron density and output the result
to "sphavgval.txt" in current folder. You can directly copy the Fortran codes in this file into
corrsponding field of atmraddens.f90.
4 Details about supplying inner-core electron density for
the wavefunctions involving pseudopotential
In Section 2.5, the characteristic and the meaning of electron density function (EDF) have
been introduced. EDF information is used to represent the inner-core density replaced by
pseudopotential, so that for the wavefunctions involving pseudopotential, the result of the
wavefunction analyses that purely based on electron density can be almost exactly identical to
full-electron wavefunction.
When the input file you used contains GTF information, and meantime some atoms utilized
pseudopotential, Multiwfn automatically finds proper GTF information from built-in EDF library
for these atoms. The built-in EDF library was developed by Wenli Zou and coworkers, it was
originally released as a part of Molden2aim (https://github.com/zorkzou/Molden2AIM). The
quality of this EDF library is quite good, and is better than the EDF field contained in the .wfx file
produced by Gaussian program. This EDF library covers the entire periodic table, up to index of
120 currently. For most elements, it contains both EDF information for large and small core
pseudopotentials. Some descriptions about this library posted by its developer can be found in
http://bbs.keinsci.com/forum.php?mod=viewthread&tid=5354. If you do not want Multiwfn to
read EDF information from this library automatically, set "isupplyEDF" in settings.ini to 0.
As mentioned in Section 2.5, the .wfx file produced by Gaussian directly carries EDF field
when pseudopotential is used. When this kind of file is used as input, Multiwfn by default reads
EDF information from EDF field of this .wfx file rather than from the built-in EDF library. If you
do not want Multiwfn read EDF information from this file but from the built-in EDF library, you
can change "readEDF" in settings.ini from 1 to 0.
Worhnotingly, Multiwfn also allows reading EDF information from atomic .wfx file
produced by Gaussian rather than from the built-in EDF library of Multiwfn (This feature is rarely
useful, since as mentioned above, the quality of the built-in EDF library in Multiwfn is better than
the EDF library embedded in Gaussian). An example is provided as below:
"examples\Pt(NH3)2Cl2.wfn" is a file corresponding to Pt(NH3)2Cl2, Lanl2 pseudopotential
accompanied by Lanl2DZ basis-set is used for Pt and Cl, while 6-31G* is used for other atoms.
"examples\Pt_lanl2.wfx" and "examples\Cl_lanl2.wfx" are the Pt and Cl atomic .wfx files
produced by G09, in which Lanl2 is also used, therefore their EDF fields represent the inner-core
electron density of Pt and Cl replaced by Lanl2.
In order to borrow EDF information from the atomic .wfx files in the analysis of
Appendix
470
Pt(NH3)2Cl2.wfn, first we need to set "isupplyEDF" parameter in settings.ini file to 1. Then boot
up Multiwfn and input following commands
examples\Pt(NH3)2Cl2.wfn
Pt // Load EDF information for element Pt
examples\Pt_lanl2.wfx // Take EDF information of Pt from this file
Cl // Load EDF information for element Cl
examples\Cl_lanl2.wfx // Take EDF information of Cl from this file
q // We have finished, exit
Now we can perform wavefunction analysis as usual. But it is better to first carry out some
tests to check if inner-core electron density has been properly represented, for example, we
integrate electron density over the whole space
100 // 100 Other functions (Part1)
4 // Integrate a function in whole space
1 // Electron density
The result is 132.00, which is the expected total number of electron of Pt(NH3)2Cl2. Assume
that we didn't load the EDF information, then the result will be 52.00, which is just the number of
valence electrons of Pt(NH3)2Cl2.
Note that you can also directly input atomic indices instead of element name, for example,
inputting 4,8-10,11 means selecting atoms 4,8,9,10,11 in present system. Of course, the atoms you
selected each time must corresponds to the same element and the same pseudopotential.
It is users' responsibility to prepare the atomic .wfx files. Since there are too many kinds of
pseudopotentials and elements, evidently I am uncapable of providing all of them for you.
5 Check sanity of wavefunction
The input files of Multiwfn generated by various quantum chemistry codes are not always
standard. For example, .molden file generated by many programs are problematic in content or
format. After you feeding them to Multiwfn and you want to make sure if the wavefunction has
been correctly loaded, there are two useful ways to check sanity:
(1) Enter main function 100 and select subfunction 4, then choose electron density. If the
integral of electron density over the whole space is very close to the actual number of electrons,
then the wavefunction is ready for use.
(2) Enter main function 1000 (a hidden function) and select subfunction 100. This function
will check satisfaction of normalization condition of all orbitals, and show you the maximum
deviation to unity. If the maximum deviation is evidently larger than zero, then there must be some
problems in the input file.
6 Special functions
There are some special functions in Multiwfn, they are mainly used for debugging, and some
of them are requested by some Multiwfn users. Here a few of them are mentioned.
(1) Calculate nuclear attractive energy between a fragment and an orbital
You can use this function by entering subfunction 90 of main function 1000 (hidden in main

Appendix
471
menu). This function calculates attractive energy between all nuclei in a user-defined fragment and
an orbital, namely:
r
Rr
r
Rr d
ZZ
E
AA
A
ii
AA
A
ii
frag
2
frag
fragMO ||
|)(|
||
During the calculation, the atomic contributions to the result are outputted in turn, for
example, below output
Processing center 2(H ) / 3
Accumulated value: -8.3269642826 Current center: -0.0629848533
means
06298.0
||
|)(|)(
frag
2
H2
H2 fragMO
r
Rr
rr d
Z
wE
AA
A
ii
where w2H(r) is atomic weighting function of 2H atom defined by Becke's partition.
The integral is evaluated by Becke's multi-center integration method, therefore the radpot
and sphpot in settings.ini affect integral accuracy. Commonly the default value is accurate enough.
Note that, as shown in above formula, the occupation number of orbital is not taken into account
in the calculation.
Information needed: GTFs, atom coordinates
