ROOTUsers Guide A4
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 642 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Preface
- Introduction
- Getting Started
- Histograms
- The Histogram Classes
- Creating Histograms
- Bin Numbering
- Filling Histograms
- Random Numbers and Histograms
- Adding, Dividing, and Multiplying
- Projections
- Drawing Histograms
- Making a Copy of an Histogram
- Normalizing Histograms
- Saving/Reading Histograms to/from a File
- Miscellaneous Operations
- Alphanumeric Bin Labels
- Histogram Stacks
- TH2Poly
- Profile Histograms
- Iso Surfaces
- 3D Implicit Functions
- TPie
- The User Interface for Histograms
- Graphs
- Fitting Histograms
- A Little C++
- The C++ Interpreter Cling
- Object Ownership
- Graphics and the Graphical User Interface
- Folders and Tasks
- Input/Output
- Trees
- Why Should You Use a Tree?
- A Simple TTree
- Show an Entry with TTree::Show
- Print the Tree Structure with TTree::Print
- Scan a Variable the Tree with TTree::Scan
- The Tree Viewer
- Creating and Saving Trees
- Branches
- Adding a Branch to Hold a List of Variables
- Adding a TBranch to Hold an Object
- Adding a Branch with a Folder
- Adding a Branch with a Collection
- Examples for Writing and Reading Trees
- Example 1: A Tree with Simple Variables
- Example 2: A Tree with a C Structure
- Example 3: Adding Friends to Trees
- Example 4: A Tree with an Event Class
- Example 5: Import an ASCII File into a TTree
- Trees in Analysis
- Simple Analysis Using TTree::Draw
- Using Selection with TTree:Draw
- Using TCut Objects in TTree::Draw
- Accessing the Histogram in Batch Mode
- Using Draw Options in TTree::Draw
- Superimposing Two Histograms
- Setting the Range in TTree::Draw
- TTree::Draw Examples
- Multiple variables visualisation
- Using TTree::Scan
- TEventList and TEntryList
- Filling a Histogram
- Using TTree::MakeClass
- Using TTree::MakeSelector
- Impact of Compression on I/O
- Chains
- Math Libraries in ROOT
- MathCore Library
- MathMore Library
- TMath
- Random Numbers
- Mathematical Functions
- Numerical Algorithms
- ROOT::Math Function interfaces
- Numerical Integration
- Function Derivation
- Numerical Minimization
- ROOT Finder Algorithms
- Generic Vectors for 2, 3 and 4 Dimensions (GenVector)
- Linear Algebra: SMatrix Package
- ROOT Statistics Classes
- Linear Algebra in ROOT
- Adding a Class
- Collection Classes
- Physics Vectors
- The Geometry Package
- Python and Ruby Interfaces
- The Tutorials and Tests
- Example Analysis
- Networking
- Threads
- PROOF: Parallel Processing
- Writing a Graphical User Interface
- ROOT/Qt Integration Interfaces
- Automatic HTML Documentation
- Appendix A: Install and Build ROOT

User’s Guide
May 2014
2
Contents
Preface 21
1 Introduction 23
1.1 TheROOTMailingLists ........................................... 23
1.2 ContactInformation .............................................. 23
1.3 ConventionsUsedinThisBook........................................ 24
1.4 TheFramework................................................. 24
1.4.1 WhatIsaFramework?......................................... 24
1.4.2 WhyObject-Oriented?......................................... 25
1.5 InstallingROOT ................................................ 25
1.6 The Organization of the ROOT Framework . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.6.1 $ROOTSYS/bin ............................................ 26
1.6.2 $ROOTSYS/lib............................................. 26
1.6.3 $ROOTSYS/tutorials ......................................... 30
1.6.4 $ROOTSYS/test............................................ 31
1.6.5 $ROOTSYS/include .......................................... 31
1.6.6 $ROOTSYS/<library> ........................................ 31
1.7 HowtoFindMoreInformation ........................................ 31
1.7.1 ClassReferenceGuide......................................... 31
2 Getting Started 33
2.1 Setting the Environment Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.2 StartandQuitaROOTSession ....................................... 34
2.3 UsingtheGUI ................................................. 35
2.3.1 MainMenusandToolbar ....................................... 35
2.3.2 TheEditorFrame ........................................... 40
2.3.3 Classes, Methods and Constructors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
2.3.4 UserInteraction ............................................ 42
2.3.5 BuildingaMulti-padCanvas ..................................... 42
2.3.6 SavingtheCanvas ........................................... 44
2.3.7 PrintingtheCanvas .......................................... 44
2.4 TheROOTCommandLine .......................................... 45
2.4.1 Multi-lineCommands ......................................... 45
2.4.2 ClingExtensions ............................................ 46
2.4.3 Helpful Hints for Command Line Typing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
3
4CONTENTS
2.4.4 RegularExpression........................................... 46
2.5 Conventions................................................... 47
2.5.1 CodingConventions .......................................... 47
2.5.2 MachineIndependentTypes...................................... 48
2.5.3 TObject................................................. 48
2.6 GlobalVariables ................................................ 48
2.6.1 gROOT ................................................. 49
2.6.2 gFile................................................... 49
2.6.3 gDirectory................................................ 49
2.6.4 gPad................................................... 49
2.6.5 gRandom ................................................ 49
2.6.6 gEnv................................................... 50
2.7 EnvironmentSetup............................................... 50
2.7.1 LogonandLogoffScripts ....................................... 51
2.7.2 HistoryFile............................................... 51
2.7.3 TrackingMemoryLeaks........................................ 51
2.7.4 MemoryChecker............................................ 51
2.8 ConvertingfromPAWtoROOT ....................................... 52
2.8.1 Converting HBOOK/PAW Files . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
3 Histograms 53
3.1 TheHistogramClasses............................................. 53
3.2 CreatingHistograms .............................................. 53
3.2.1 Constant or Variable Bin Width . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
3.3 BinNumbering................................................. 55
3.3.1 Convention ............................................... 55
3.3.2 Re-binning ............................................... 55
3.4 FillingHistograms ............................................... 55
3.4.1 Automatic Re-binning Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
3.5 RandomNumbersandHistograms ...................................... 56
3.6 Adding, Dividing, and Multiplying . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
3.7 Projections ................................................... 57
3.8 DrawingHistograms .............................................. 58
3.8.1 SettingtheStyle ............................................ 58
3.8.2 DrawOptions.............................................. 58
3.8.3 Drawing a Sub-range of a 2-D Histogram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
3.8.4 Superimposing Histograms with Different Scales . . . . . . . . . . . . . . . . . . . . . . . . . . 75
3.8.5 StatisticsDisplay............................................ 77
3.8.6 Setting Line, Fill, Marker, and Text Attributes . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
3.8.7 Setting Tick Marks on the Axis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
3.8.8 Giving Titles to the X, Y and Z Axis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
3.9 MakingaCopyofanHistogram ....................................... 78
3.10NormalizingHistograms ............................................ 79
CONTENTS 5
3.11 Saving/Reading Histograms to/from a File . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
3.12MiscellaneousOperations ........................................... 79
3.13AlphanumericBinLabels ........................................... 80
3.13.1 Option1:SetBinLabel......................................... 80
3.13.2 Option2:Fill.............................................. 81
3.13.3 Option3:TTree::Draw ........................................ 81
3.13.4 SortOptions .............................................. 81
3.14HistogramStacks................................................ 82
3.15TH2Poly..................................................... 83
3.16ProfileHistograms ............................................... 83
3.16.1 BuildOptions.............................................. 84
3.16.2 Drawing a Profile without Error Bars . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
3.16.3 Create a Profile from a 2D Histogram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
3.16.4 Create a Histogram from a Profile . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
3.16.5 Generating a Profile from a TTree . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
3.16.6 2DProfiles ............................................... 87
3.17IsoSurfaces ................................................... 88
3.183DImplicitFunctions ............................................. 88
3.19TPie....................................................... 88
3.20 The User Interface for Histograms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
3.20.1 TH1Editor ............................................... 91
3.20.2 TH2Editor ............................................... 93
4 Graphs 97
4.1 TGraph ..................................................... 97
4.1.1 GraphDrawOptions.......................................... 97
4.2 SuperimposingTwoGraphs .......................................... 101
4.3 GraphswithErrorBars ............................................ 102
4.4 Graphs with Asymmetric Error Bars . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
4.5 Graphs with Asymmetric Bent Errors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
4.6 TGraphPolar .................................................. 105
4.7 TGraphExclusionZone ............................................ 107
4.8 TGraphQQ ................................................... 108
4.8.1 TwoDatasets.............................................. 108
4.8.2 OneDataset .............................................. 109
4.9 TMultiGraph .................................................. 109
4.10TGraph2D ................................................... 110
4.11TGraph2DErrors................................................ 112
4.12FittingaGraph................................................. 112
4.13SettingtheGraph’sAxisTitle ........................................ 114
4.14ZoomingaGraph................................................ 114
4.15TheUserInterfaceforGraphs......................................... 115
6CONTENTS
5 Fitting Histograms 117
5.1 TheFitMethod ................................................ 117
5.1.1 TheTH1::FitMethod ......................................... 117
5.1.2 TheTGraph::FitMethod ....................................... 118
5.2 The TF1 functionclass............................................. 118
5.2.1 Fit with a Predefined Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
5.2.2 Creating User-Defined Functions (TF1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
5.3 ConfiguringtheFit............................................... 121
5.3.1 Fixing and Setting Parameters’ Bounds . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
5.3.2 FittingSubRanges........................................... 122
5.3.3 FittingMultipleSubRanges ..................................... 122
5.3.4 AddingFunctionstotheList ..................................... 123
5.4 Example of fit: Combining Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
5.5 Resultofthefit................................................. 124
5.5.1 AssociatedFunction .......................................... 124
5.5.2 Access to the Fit Parameters and Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125
5.5.3 AssociatedErrors............................................ 125
5.5.4 FitStatistics .............................................. 126
5.6 TheFitPanel.................................................. 126
5.6.1 Function Choice and Settings . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126
5.6.2 FitterSettings ............................................. 126
5.6.3 DrawOptions.............................................. 128
5.6.4 AdvancesOptions ........................................... 128
5.6.5 PrintOptions.............................................. 128
5.6.6 CommandButtons........................................... 128
5.6.7 MinimizationOptions ......................................... 129
5.7 NewROOT::Fitclasses ............................................ 129
5.7.1 Creatingtheinputfitdata ...................................... 129
5.7.2 CreatingtheFitmodel ........................................ 131
5.7.3 FitConfiguration............................................ 132
5.7.4 Minimizer Libraries and Algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 132
5.7.5 PerformingtheFit........................................... 134
5.7.6 FitResult................................................ 135
5.7.7 TFitResult ............................................... 135
5.8 TheMinimizationpackages .......................................... 135
5.9 MINUIT(OldTMInuitVersion) ....................................... 135
5.9.1 BasicConceptsofMinuit ....................................... 136
5.9.2 The Transformation of Limited Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136
5.9.3 How to Get the Right Answer from Minuit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
5.9.4 Reliability of Minuit Error Estimates . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138
5.10Minuit2Package ................................................ 139
5.11FUMILIMinimizationPackage ........................................ 139
5.12NeuralNetworks ................................................ 140
CONTENTS 7
5.12.1 Introduction .............................................. 140
5.12.2 TheMLP ................................................ 140
5.12.3 LearningMethods ........................................... 140
5.12.4 UsingtheNetwork........................................... 142
5.12.5 Examples ................................................ 143
6 A Little C++ 147
6.1 Classes, Methods and Constructors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147
6.2 Inheritance and Data Encapsulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
6.2.1 MethodOverriding........................................... 148
6.2.2 DataEncapsulation .......................................... 148
6.3 Creating Objects on the Stack and Heap . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149
7 The C++ Interpreter Cling 153
7.1 TheROOTPrompt .............................................. 153
7.2 Feeding Sources Files To ROOT: C++ Scripts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
7.2.1 Executing a Script From a Script . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
7.2.2 Executing a Script From the Invocation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
7.3 C++ Extensions To Ease Scripting . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
7.4 ACLiC: Compiling Scripts Into Libraries . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157
7.4.1 Usage .................................................. 157
7.4.2 SettingtheIncludePath........................................ 158
7.4.3 DictionaryGeneration......................................... 159
7.4.4 Intermediate Steps and Files . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159
7.4.5 Moving between Interpreter and Compiler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 160
7.5 ClassesDefinedByScripts........................................... 161
7.6 InspectingObjects ............................................... 162
8 Object Ownership 165
8.1 Ownership by Current Directory (gDirectory) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165
8.2 Ownership by the Master TROOT Object (gROOT) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166
8.2.1 TheCollectionofSpecials....................................... 166
8.2.2 Access to the Collection Contents . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166
8.3 OwnershipbyOtherObjects ......................................... 167
8.4 OwnershipbytheUser............................................. 167
8.4.1 ThekCanDeleteBit .......................................... 167
8.4.2 ThekMustCleanupBit ........................................ 168
9 Graphics and the Graphical User Interface 169
9.1 DrawingObjects ................................................ 169
9.2 Interacting with Graphical Objects . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 169
9.2.1 Moving, Resizing and Modifying Objects . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170
9.2.2 SelectingObjects............................................ 171
9.2.3 Context Menus: the Right Mouse Button . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171
8CONTENTS
9.2.4 Executing Events when a Cursor Passes on Top of an Object . . . . . . . . . . . . . . . . . . . 173
9.3 Graphical Containers: Canvas and Pad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174
9.3.1 TheGlobalPad:gPad......................................... 176
9.3.2 The Coordinate Systems of a Pad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177
9.3.3 Converting between Coordinate Systems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178
9.3.4 Dividing a Pad into Sub-pads . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178
9.3.5 UpdatingthePad ........................................... 180
9.3.6 MakingaPadTransparent ...................................... 180
9.3.7 SettingtheLogScale ......................................... 180
9.3.8 WaitPrimitivemethod......................................... 181
9.3.9 LockingthePad ............................................ 181
9.4 GraphicalObjects ............................................... 181
9.4.1 Lines, Arrows and Polylines . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 181
9.4.2 CirclesandEllipses........................................... 183
9.4.3 Rectangles ............................................... 184
9.4.4 Markers................................................. 184
9.4.5 Curly and Wavy Lines for Feynman Diagrams . . . . . . . . . . . . . . . . . . . . . . . . . . . . 186
9.4.6 Text and Latex Mathematical Expressions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 187
9.4.7 GreekLetters.............................................. 188
9.4.8 MathematicalSymbols......................................... 188
9.4.9 TextinaPad.............................................. 193
9.4.10 The TeX Processor TMathText . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 194
9.5 Axis ....................................................... 194
9.5.1 AxisTitle................................................ 196
9.5.2 Axis Options and Characteristics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 196
9.5.3 Setting the Number of Divisions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 197
9.5.4 ZoomingtheAxis ........................................... 197
9.5.5 Drawing Axis Independently of Graphs or Histograms . . . . . . . . . . . . . . . . . . . . . . . 197
9.5.6 Orientation of Tick Marks on Axis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 198
9.5.7 Labels.................................................. 198
9.5.8 AxiswithTimeUnits ......................................... 200
9.5.9 AxisExamples ............................................. 204
9.6 GraphicalObjectsAttributes ......................................... 208
9.6.1 TextAttributes............................................. 208
9.6.2 LineAttributes............................................. 211
9.6.3 FillAttributes ............................................. 212
9.6.4 ColorandColorPalettes........................................ 212
9.7 TheGraphicsEditor.............................................. 215
9.7.1 TAxisEditor............................................... 215
9.7.2 TPadEditor............................................... 216
9.8 CopyandPaste................................................. 216
9.8.1 UsingtheGUI ............................................. 216
9.8.2 Programmatically ........................................... 218
CONTENTS 9
9.9 Legends ..................................................... 218
9.10ThePostScriptInterface............................................ 219
9.10.1 SpecialCharacters ........................................... 222
9.10.2 Writing Several Canvases to the Same PostScript File . . . . . . . . . . . . . . . . . . . . . . . 222
9.10.3 TheColorModels ........................................... 224
9.11ThePDFInterface............................................... 224
9.12CreateorModifyaStyle............................................ 225
9.133DViewers ................................................... 227
9.13.1 Invokinga3Dviewer.......................................... 227
9.13.2 TheGLViewer............................................. 228
9.13.3 TheX3DViewer ............................................ 235
9.13.4 Common 3D Viewer Architecture . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 235
10 Folders and Tasks 243
10.1Folders...................................................... 243
10.2WhyUseFolders? ............................................... 243
10.3HowtoUseFolders............................................... 243
10.3.1 CreatingaFolderHierarchy...................................... 243
10.3.2 Posting Data to a Folder (Producer) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 245
10.3.3 Reading Data from a Folder (Consumer) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 245
10.4Tasks ...................................................... 247
10.5ExecuteandDebugTasks ........................................... 250
11 Input/Output 251
11.1 The Physical Layout of ROOT Files . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 251
11.1.1 TheFileHeader ............................................ 252
11.1.2 The Top Directory Description . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 253
11.1.3 TheHistogramRecords ........................................ 253
11.1.4 The Class Description List (StreamerInfo List) . . . . . . . . . . . . . . . . . . . . . . . . . . . 254
11.1.5 The List of Keys and the List of Free Blocks . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255
11.1.6 FileRecovery.............................................. 255
11.2 The Logical ROOT File: TFile and TKey . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255
11.2.1 Viewing the Logical File Contents . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 256
11.2.2 TheCurrentDirectory......................................... 258
11.2.3 Objects in Memory and Objects on Disk . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 259
11.2.4 SavingHistogramstoDisk ...................................... 261
11.2.5 Histograms and the Current Directory . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 262
11.2.6 SavingObjectstoDisk......................................... 263
11.2.7 SavingCollectionstoDisk....................................... 263
11.2.8 A TFile Object Going Out of Scope . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264
11.2.9 Retrieving Objects from Disk . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264
11.2.10 Subdirectories and Navigation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264
11.3Streamers .................................................... 266
10 CONTENTS
11.3.1 Automatically Generated Streamers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 267
11.3.2 Transient Data Members (//!) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 267
11.3.3 The Pointer to Objects (//->) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 268
11.3.4 VariableLengthArray......................................... 268
11.3.5 Double32_t............................................... 268
11.3.6 PreventSplitting(//||) ........................................ 268
11.3.7 Streamers with Special Additions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270
11.3.8 WritingObjects ............................................ 270
11.3.9 IgnoreObjectStreamers........................................ 271
11.3.10StreamingaTClonesArray ...................................... 271
11.4 Pointers and References in Persistency . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 271
11.4.1 StreamingC++Pointers ....................................... 272
11.4.2 Motivation for the TRef Class . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 272
11.4.3 UsingTRef ............................................... 272
11.4.4 HowDoesItWork? .......................................... 273
11.4.5 ActiononDemand........................................... 274
11.4.6 ArrayofTRef.............................................. 275
11.5SchemaEvolution ............................................... 275
11.5.1 TheTStreamerInfoClass ....................................... 276
11.5.2 The TStreamerElement Class . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 277
11.5.3 Example:TH1StreamerInfo ..................................... 277
11.5.4 OptimizedStreamerInfo........................................ 278
11.5.5 Automatic Schema Evolution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 278
11.5.6 Manual Data Model Evolution Capabilities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 278
11.5.7 ManualSchemaEvolution....................................... 281
11.5.8 Building Class Definitions with the StreamerInfo . . . . . . . . . . . . . . . . . . . . . . . . . . 281
11.5.9 Example:MakeProject......................................... 281
11.6MigratingtoROOT3 ............................................. 284
11.7CompressionandPerformance ........................................ 284
11.8 Remotely Access to ROOT Files via a rootd . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 285
11.8.1 TNetFileURL ............................................. 285
11.8.2 RemoteAuthentication ........................................ 285
11.8.3 ASimpleSession............................................ 285
11.8.4 TherootdDaemon........................................... 286
11.8.5 Startingrootdviainetd ........................................ 286
11.8.6 Command Line Arguments for rootd . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 286
11.9 Reading ROOT Files via Apache Web Server . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 287
11.9.1 Using the General Open Function of TFile . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 287
11.10XMLInterface ................................................. 288
CONTENTS 11
12 Trees 289
12.1WhyShouldYouUseaTree? ......................................... 289
12.2ASimpleTTree................................................. 289
12.3ShowanEntrywithTTree::Show....................................... 290
12.4 Print the Tree Structure with TTree::Print . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 291
12.5 Scan a Variable the Tree with TTree::Scan . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 291
12.6TheTreeViewer ................................................ 291
12.7CreatingandSavingTrees........................................... 293
12.7.1 Creating a Tree from a Folder Hierarchy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 293
12.7.2 TreeandTRefObjects......................................... 295
12.7.3 Autosave ................................................ 295
12.7.4 TreeswithCircularBuffers ...................................... 295
12.7.5 SizeofTTreeintheFile........................................ 295
12.7.6 User Info Attached to a TTree Object . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 296
12.7.7 IndexingaTree............................................. 296
12.8Branches..................................................... 296
12.9 Adding a Branch to Hold a List of Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 297
12.10Adding a TBranch to Hold an Object . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 298
12.10.1SettingtheSplit-level ......................................... 298
12.10.2 Exempt a Data Member from Splitting . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 300
12.10.3 Adding a Branch to Hold a TClonesArray . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 300
12.10.4IdenticalBranchNames ........................................ 300
12.11AddingaBranchwithaFolder ........................................ 300
12.12Adding a Branch with a Collection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 301
12.13Examples for Writing and Reading Trees . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 301
12.14Example 1: A Tree with Simple Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 301
12.14.1WritingtheTree ............................................ 302
12.14.2ViewingtheTree............................................ 302
12.14.3ReadingtheTree............................................ 304
12.15Example 2: A Tree with a C Structure . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 305
12.15.1WritingtheTree ............................................ 307
12.15.2Analysis................................................. 308
12.16Example 3: Adding Friends to Trees . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 310
12.16.1 Adding a Branch to an Existing Tree . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 310
12.16.2TTree::AddFriend ........................................... 310
12.17Example 4: A Tree with an Event Class . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 313
12.17.1TheEventClass ............................................ 313
12.17.2TheEventHeaderClass ........................................ 313
12.17.3TheTrackClass ............................................ 314
12.17.4WritingtheTree ............................................ 314
12.17.5ReadingtheTree............................................ 315
12.18Example 5: Import an ASCII File into a TTree . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 317
12.19TreesinAnalysis ................................................ 317
12 CONTENTS
12.20Simple Analysis Using TTree::Draw . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 318
12.20.1 Using Selection with TTree:Draw . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 319
12.20.2 Using TCut Objects in TTree::Draw . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 319
12.20.3 Accessing the Histogram in Batch Mode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 320
12.20.4 Using Draw Options in TTree::Draw . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 320
12.20.5 Superimposing Two Histograms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 321
12.20.6 Setting the Range in TTree::Draw . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 321
12.20.7TTree::DrawExamples......................................... 321
12.20.8 Multiple variables visualisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 329
12.20.9UsingTTree::Scan ........................................... 337
12.20.10TEventList and TEntryList . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 338
12.20.11FillingaHistogram........................................... 341
12.21UsingTTree::MakeClass............................................ 343
12.21.1 Creating a Class with MakeClass . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 343
12.21.2MyClass.h................................................ 344
12.21.3MyClass.C ............................................... 345
12.21.4ModifyingMyClass::Loop ....................................... 345
12.21.5LoadingMyClass............................................ 346
12.22UsingTTree::MakeSelector .......................................... 347
12.22.1PerformanceBenchmarks ....................................... 348
12.23ImpactofCompressiononI/O ........................................ 348
12.24Chains...................................................... 349
12.24.1TChain::AddFriend........................................... 350
13 Math Libraries in ROOT 351
13.1MathCoreLibrary ............................................... 351
13.2MathMoreLibrary ............................................... 352
13.3TMath...................................................... 353
13.3.1 NumericalConstants.......................................... 353
13.3.2 ElementaryFunctions ......................................... 354
13.3.3 Statistic Functions Operating on Arrays. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 354
13.3.4 Special and Statistical Functions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 354
13.4RandomNumbers ............................................... 355
13.4.1 TRandom................................................ 355
13.4.2 TRandom1 ............................................... 355
13.4.3 TRandom2 ............................................... 355
13.4.4 TRandom3 ............................................... 355
13.4.5 SeedingtheGenerators ........................................ 356
13.4.6 Examples of Using the Generators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 356
13.4.7 Random Number Distributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 356
13.4.8 UNURAN................................................ 357
13.4.9 Performances of Random Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 358
13.5MathematicalFunctions ............................................ 358
CONTENTS 13
13.5.1 Special Functions in MathCore . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 358
13.5.2 Special Functions in MathMore . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 359
13.5.3 Probability Density Functions (PDF) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 360
13.5.4 Cumulative Distribution Functions (CDF) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 361
13.6NumericalAlgorithms ............................................. 362
13.7 ROOT::Math Function interfaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 362
13.7.1 One-dimensional Function Interfaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 362
13.7.2 Multi-dimensional Function Interfaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 363
13.7.3 Parametric Function Interfaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 365
13.7.4 WrapperFunctions........................................... 366
13.8NumericalIntegration ............................................. 369
13.8.1 Integration of One-dimensional Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 370
13.8.2 One-dimensional Integration Algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 371
13.8.3 Multi-dimensional Integration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 373
13.9FunctionDerivation .............................................. 374
13.10NumericalMinimization ............................................ 374
13.10.1 One-Dimensional Minimization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 375
13.10.2 Multi-Dimensional Minimization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 376
13.11ROOTFinderAlgorithms ........................................... 376
13.12Generic Vectors for 2, 3 and 4 Dimensions (GenVector) . . . . . . . . . . . . . . . . . . . . . . . . . . . 376
13.12.1MainCharacteristics.......................................... 376
13.12.2 Example: 3D Vector Classes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 379
13.12.3Example:3DPointClasses ...................................... 381
13.12.4 Example: LorentzVector Classes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 382
13.12.5 Example: Vector Transformations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 385
13.12.6 Example with External Packages . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 387
13.13Linear Algebra: SMatrix Package . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 388
13.13.1 Example: Vector Class (SVector) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 388
13.13.2 Example: Matrix Class (SMatrix) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 389
13.13.3 Example: Matrix and Vector Functions and Operators . . . . . . . . . . . . . . . . . . . . . . . 392
13.13.4 Matrix and Vector Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 393
13.14ROOTStatisticsClasses............................................ 394
13.14.1 Classes for Computing Limits and Confidence Levels . . . . . . . . . . . . . . . . . . . . . . . . 394
13.14.2 Specialized Classes for Fitting . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 394
13.14.3 Multi-variate Analysis Classes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 394
14 Linear Algebra in ROOT 395
14.1OverviewofMatrixClasses .......................................... 395
14.2MatrixProperties................................................ 397
14.2.1 AccessingProperties.......................................... 397
14.2.2 SettingProperties ........................................... 397
14.3CreatingandFillingaMatrix......................................... 398
14.4MatrixOperatorsandMethods........................................ 399
14 CONTENTS
14.4.1 Arithmetic Operations between Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 400
14.4.2 Arithmetic Operations between Matrices and Real Numbers . . . . . . . . . . . . . . . . . . . . 400
14.4.3 Comparisons and Boolean Operations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 400
14.4.4 MatrixNorms.............................................. 400
14.4.5 MiscellaneousOperators........................................ 401
14.5MatrixViews .................................................. 401
14.5.1 ViewOperators............................................. 402
14.5.2 ViewExamples............................................. 403
14.6MatrixDecompositions............................................. 403
14.6.1 TolerancesandScaling......................................... 405
14.6.2 Conditionnumber ........................................... 405
14.6.3 LU.................................................... 406
14.6.4 Bunch-Kaufman ............................................ 406
14.6.5 Cholesky ................................................ 407
14.6.6 QRH................................................... 407
14.6.7 SVD................................................... 407
14.7MatrixEigenAnalysis ............................................. 408
14.8SpeedComparisons............................................... 408
15 Adding a Class 411
15.1TheRoleofTObject.............................................. 411
15.1.1 Introspection, Reflection and Run Time Type Identification . . . . . . . . . . . . . . . . . . . . 411
15.1.2 Collections ............................................... 411
15.1.3 Input/Output.............................................. 412
15.1.4 Paint/Draw............................................... 412
15.1.5 Clone/DrawClone ........................................... 412
15.1.6 Browse ................................................. 412
15.1.7 SavePrimitive.............................................. 412
15.1.8 GetObjectInfo ............................................. 412
15.1.9 IsFolder ................................................. 412
15.1.10BitMasksandUniqueID ....................................... 412
15.2Motivation ................................................... 413
15.2.1 TemplateSupport ........................................... 414
15.3TheDefaultConstructor............................................ 415
15.4 rootcling: The Cling Dictionary Generator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 415
15.4.1 DictionariesforSTL.......................................... 418
15.5 Adding a Class with a Shared Library . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 418
15.5.1 TheLinkDef.hFile........................................... 419
15.6 genreflex: A Comfortable Interface to rootcling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 425
15.6.1 The ROOT::Meta::Selection namespace .............................. 425
15.7AddingaClasswithACLiC.......................................... 425
CONTENTS 15
16 Collection Classes 427
16.1UnderstandingCollections........................................... 427
16.1.1 GeneralCharacteristics ........................................ 427
16.1.2 Determining the Class of Contained Objects . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 428
16.1.3 TypesofCollections .......................................... 428
16.1.4 Ordered Collections (Sequences) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 428
16.2 Iterators: Processing a Collection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 429
16.3FoundationClasses............................................... 429
16.4ACollectableClass............................................... 430
16.5TheTIterGenericIterator........................................... 431
16.6TheTListCollection.............................................. 432
16.6.1 IteratingOveraTList......................................... 432
16.7TheTObjArrayCollection........................................... 433
16.8 TClonesArray An Array of Identical Objects . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 434
16.8.1 The Idea Behind TClonesArray . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 434
16.9TemplateContainersandSTL......................................... 435
17 Physics Vectors 437
17.1ThePhysicsVectorClasses .......................................... 437
17.2TVector3 .................................................... 437
17.2.1 Declaration / Access to the Components . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 438
17.2.2 OtherCoordinates ........................................... 438
17.2.3 Arithmetic/Comparison ....................................... 439
17.2.4 RelatedVectors............................................. 439
17.2.5 Scalar and Vector Products . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 439
17.2.6 AnglebetweenTwoVectors...................................... 439
17.2.7 RotationaroundAxes ......................................... 439
17.2.8 RotationaroundaVector ....................................... 439
17.2.9 Rotation by TRotation Class . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 440
17.2.10 Transformation from Rotated Frame . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 440
17.3TRotation.................................................... 440
17.3.1 Declaration, Access, Comparisons . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 440
17.3.2 RotationaroundAxes ......................................... 440
17.3.3 Rotation around Arbitrary Axis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 441
17.3.4 RotationofLocalAxes ........................................ 441
17.3.5 InverseRotation ............................................ 441
17.3.6 CompoundRotations ......................................... 441
17.3.7 RotationofTVector3 ......................................... 441
17.4TLorentzVector................................................. 442
17.4.1 Declaration ............................................... 442
17.4.2 AccesstoComponents......................................... 442
17.4.3 Vector Components in Non-Cartesian Coordinates . . . . . . . . . . . . . . . . . . . . . . . . . 443
17.4.4 Arithmetic and Comparison Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 443
16 CONTENTS
17.4.5 Magnitude/Invariant mass, beta, gamma, scalar product . . . . . . . . . . . . . . . . . . . . . . 443
17.4.6 LorentzBoost.............................................. 444
17.4.7 Rotations ................................................ 444
17.4.8 Miscellaneous.............................................. 444
17.5TLorentzRotation ............................................... 445
17.5.1 Declaration ............................................... 445
17.5.2 Access to the Matrix Components/Comparisons . . . . . . . . . . . . . . . . . . . . . . . . . . 445
17.5.3 Transformations of a Lorentz Rotation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 445
17.5.4 Transformation of a TLorentzVector . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 446
17.5.5 PhysicsVectorExample........................................ 446
18 The Geometry Package 447
18.1 Quick Start: Creating the “world” . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 447
18.1.1 Example 1: Creating the World . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 447
18.1.2 Example 2: A Geometrical Hierarchy Look and Feel . . . . . . . . . . . . . . . . . . . . . . . . 448
18.2MaterialsandTrackingMedia......................................... 450
18.2.1 Elements, Materials and Mixtures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 450
18.2.2 Radionuclides.............................................. 452
18.2.3 TrackingMedia............................................. 455
18.2.4 User Interface for Handling Materials and Media . . . . . . . . . . . . . . . . . . . . . . . . . . 455
18.3Shapes...................................................... 455
18.3.1 Units .................................................. 456
18.3.2 PrimitiveShapes............................................ 456
18.3.3 CompositeShapes ........................................... 469
18.3.4 Navigation Methods Performed By Shapes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 473
18.3.5 CreatingShapes ............................................ 474
18.3.6 DividingShapes ............................................ 475
18.3.7 ParametricShapes........................................... 475
18.4GeometryCreation............................................... 475
18.4.1 TheVolumeHierarchy......................................... 476
18.4.2 Creating and Positioning Volumes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 478
18.4.3 Geometrical Transformations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 484
18.4.4 Ownership of Geometry Objects . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 487
18.5NavigationandTracking............................................ 488
18.5.1 TGeoNavigatorClass ......................................... 488
18.5.2 Initializing the Starting Point . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 488
18.5.3 InitializingtheDirection........................................ 489
18.5.4 InitializingtheState.......................................... 489
18.5.5 CheckingtheCurrentState...................................... 489
18.5.6 Saving and Restoring the Current State . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 491
18.5.7 NavigationQueries........................................... 491
18.5.8 Creating and Visualizing Tracks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 494
18.6CheckingtheGeometry ............................................ 495
CONTENTS 17
18.6.1 TheOverlapChecker.......................................... 496
18.6.2 Graphical Checking Methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 498
18.7TheDrawingPackage ............................................. 501
18.7.1 Drawing Volumes and Hierarchies of Volumes . . . . . . . . . . . . . . . . . . . . . . . . . . . . 501
18.7.2 Visualization Settings and Attributes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 502
18.7.3 RayTracing............................................... 503
18.8 Representing Misalignments of the Ideal Geometry . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 504
18.8.1 PhysicalNodes............................................. 504
18.9GeometryI/O.................................................. 506
18.9.1 GDML.................................................. 507
18.10NavigationAlgorithms............................................. 507
18.10.1 Finding the State Corresponding to a Location (x,y,z) . . . . . . . . . . . . . . . . . . . . . . . 507
18.10.2 Finding the Distance to Next Crossed Boundary . . . . . . . . . . . . . . . . . . . . . . . . . . 508
18.11Geometry Graphical User Interface . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 512
18.11.1EditingaGeometry .......................................... 512
18.11.2 The Geometry Manager Editor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 515
18.11.3EditingExistingObjects........................................ 516
18.11.4CreationofNewObjects........................................ 519
18.11.5EditingVolumes ............................................ 519
18.11.6 How to Create a Valid Geometry with Geometry Editors . . . . . . . . . . . . . . . . . . . . . 523
19 Python and Ruby Interfaces 525
19.1PyROOTOverview............................................... 525
19.1.1 Glue-ingApplications ......................................... 525
19.1.2 Access to ROOT from Python . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 526
19.1.3 Access to Python from ROOT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 526
19.1.4 Installation ............................................... 527
19.1.5 UsingPyROOT ............................................ 527
19.1.6 MemoryHandling ........................................... 531
19.1.7 Performance .............................................. 532
19.1.8 UseofPythonFunctions........................................ 532
19.1.9 WorkingwithTrees .......................................... 534
19.1.10UsingYourOwnClasses........................................ 535
19.2HowtoUseROOTwithRuby ........................................ 536
19.2.1 Building and Installing the Ruby Module . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 537
20 The Tutorials and Tests 539
20.1$ROOTSYS/tutorials ............................................. 539
20.2$ROOTSYS/test ................................................ 539
20.2.1 Event - An Example of a ROOT Application . . . . . . . . . . . . . . . . . . . . . . . . . . . . 540
20.2.2 stress-TestandBenchmark ..................................... 544
20.2.3 guitest - A Graphical User Interface . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 546
18 CONTENTS
21 Example Analysis 547
21.1Explanation................................................... 547
21.2Script ...................................................... 550
22 Networking 555
22.1Setting-upaConnection............................................ 555
22.2 Sending Objects over the Network . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 555
22.3ClosingtheConnection ............................................ 556
22.4AServerwithMultipleSockets ........................................ 556
23 Threads 559
23.1ThreadsandProcesses............................................. 559
23.1.1 ProcessProperties ........................................... 559
23.1.2 ThreadProperties ........................................... 559
23.1.3 TheInitialThread........................................... 560
23.2 Implementation of Threads in ROOT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 560
23.2.1 Installation ............................................... 560
23.2.2 Classes ................................................. 560
23.2.3 TThreadforPedestrians........................................ 560
23.2.4 TThreadinMoreDetails ....................................... 561
23.3 Advanced TThread: Launching a Method in a Thread . . . . . . . . . . . . . . . . . . . . . . . . . . . 564
23.3.1 KnownProblems............................................ 565
23.4TheSignalsofROOT ............................................. 565
23.5Glossary..................................................... 566
24 PROOF: Parallel Processing 569
25 Writing a Graphical User Interface 571
25.1TheROOTGUIClasses............................................ 571
25.2WidgetsandFrames .............................................. 571
25.3TVirtualX.................................................... 572
25.4ASimpleExample ............................................... 572
25.4.1 AStandaloneVersion ......................................... 576
25.5WidgetsOverview ............................................... 578
25.5.1 TGObject................................................ 578
25.5.2 TGWidget ............................................... 578
25.5.3 TGWindow............................................... 579
25.5.4 Frames ................................................. 580
25.6LayoutManagement .............................................. 582
25.7 Event Processing: Signals and Slots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 584
25.8WidgetsinDetail................................................ 589
25.8.1 Buttons ................................................. 589
25.8.2 TextEntries............................................... 592
25.8.3 NumberEntries............................................. 593
CONTENTS 19
25.8.4 Menus.................................................. 595
25.8.5 Toolbar ................................................. 596
25.8.6 ListBoxes................................................ 598
25.8.7 ComboBoxes.............................................. 599
25.8.8 Sliders.................................................. 600
25.8.9 TripleSlider............................................... 601
25.8.10ProgressBars.............................................. 601
25.8.11StaticWidgets ............................................. 602
25.8.12StatusBar ............................................... 602
25.8.13Splitters................................................. 603
25.8.14 TGCanvas, ViewPort and Container . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 605
25.8.15EmbeddedCanvas ........................................... 605
25.9 The ROOT Graphics Editor (GED) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 606
25.9.1 ObjectEditors ............................................. 606
25.9.2 EditorDesignElements ........................................ 607
25.10DragandDrop ................................................. 608
25.10.1DragandDropDataClass ...................................... 609
25.10.2 Handling Drag and Drop Events . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 609
26 ROOT/Qt Integration Interfaces 611
26.1 Qt-ROOT Implementation of TVirtualX Interface (BNL) . . . . . . . . . . . . . . . . . . . . . . . . . 611
26.1.1 Installation ............................................... 611
26.1.2 Applications .............................................. 612
26.1.3 TQtWidget Class, Qt Signals / Slots and TCanvas Interface . . . . . . . . . . . . . . . . . . . . 619
26.2GSIQtROOT.................................................. 621
26.2.1 Create a New Project in the Designer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 623
26.2.2 main().................................................. 623
27 Automatic HTML Documentation 625
27.1ReferenceGuide ................................................ 625
27.1.1 Product and Module Documentation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 626
27.2 Converting Sources (and Other Files) to HTML . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 626
27.3 Special Documentation Elements: Directives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 626
27.3.1 LatexDirective............................................. 627
27.3.2 MacroDirective ............................................ 627
27.4CustomizingHTML .............................................. 628
27.4.1 Referencing Documentation for other Libraries . . . . . . . . . . . . . . . . . . . . . . . . . . . 628
27.4.2 SearchEngine.............................................. 628
27.4.3 ViewCVS ................................................ 628
27.4.4 WikiPages ............................................... 628
27.5Tutorial ..................................................... 628
20 CONTENTS
28 Appendix A: Install and Build ROOT 629
28.1License...................................................... 629
28.2InstallingROOT ................................................ 629
28.3ChoosingaVersion............................................... 629
28.4 Installing Precompiled Binaries . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 629
28.5InstallingtheSource .............................................. 630
28.5.1 Installing and Building the Source from a Compressed File . . . . . . . . . . . . . . . . . . . . 630
28.5.2 MoreBuildOptions .......................................... 630
28.6Filesystem.rootrc ............................................... 631
28.6.1 TCanvasSpecificSettings....................................... 633
28.6.2 THtmlSpecificSettings ........................................ 634
28.6.3 GUISpecificSettings ......................................... 635
28.6.4 TBrowserSettings ........................................... 636
28.6.5 TRintSpecificSettings ........................................ 636
28.6.6 ACLiCSpecificSettings........................................ 637
28.6.7 PROOFRelatedVariables....................................... 637
28.7DocumentationtoDownload ......................................... 641
Preface
In late 1994, we decided to learn and investigate Object Oriented programming and C++ to better judge the suitability
of these relatively new techniques for scientific programming. We knew that there is no better way to learn a new
programming environment than to use it to write a program that can solve a real problem. After a few weeks, we
had our first histogramming package in C++. A few weeks later we had a rewrite of the same package using the,
at that time, very new template features of C++. Again, a few weeks later we had another rewrite of the package
without templates since we could only compile the version with templates on one single platform using a specific
compiler. Finally, after about four months we had a histogramming package that was faster and more efficient than the
well-known FORTRAN based HBOOK histogramming package. This gave us enough confidence in the new technologies
to decide to continue the development. Thus was born ROOT. Since its first public release at the end of 1995, ROOT
has enjoyed an ever-increasing popularity. Currently it is being used in all major High Energy and Nuclear Physics
laboratories around the world to monitor, to store and to analyse data. In the other sciences as well as the medical and
financial industries, many people are using ROOT. We estimate the current user base to be around several thousand
people. In 1997, Eric Raymond analysed in his paper “The Cathedral and the Bazaar” the development method that
makes Linux such a success. The essence of that method is: “release early, release often and listen to your customers”.
This is precisely how ROOT is being developed. Over the last five years, many of our “customers” became co-developers.
Here we would like to thank our main co-developers and contributors:
Masaharu Goto
wrote the C++ interpreter CINT that was an essential part of ROOT before ROOT 6. Despite
being 8 time zones ahead of us, we have the feeling he has been sitting in the room next door since 1995.
Andrei
and
Mihaela Gheata
(Alice collaboration) are co-authors of the ROOT geometry classes and Virtual
Monte-Carlo. They have been working with the ROOT team since 2000.
Olivier Couet
, who after a successful development and maintenance of PAW, has joined the ROOT team in 2000 and
has been working on the graphics sub-system.
Ilka Antcheva
has been working on the Graphical User Interface classes. She is also responsible for this latest edition
of the Users Guide with a better style, improved index and several new chapters (since 2002).
Bertrand Bellenot
has been developing and maintaining the Win32GDK version of ROOT. Bertrand has also many
other contributions like the nice RootShower example (since 2001).
Valeriy Onoutchin
has been working on several ROOT packages, in particular the graphics sub-system for Windows
and the GUI Builder (since 2000).
Gerri Ganis
has been working on the authentication procedures to be used by the root daemons and the PROOF
system (since 2002).
Maarten Ballintijn (MIT) is one of the main developers of the PROOF sub-system (since 1995).
Valeri Fine
(now at BNL) ported ROOT to Windows and contributed largely to the 3-D graphics. He is currently
working on the Qt layer of ROOT (since 1995).
Victor Perevoztchikov
(BNL) worked on key elements of the I/O system, in particular the improved support for
STL collections (1997-2001).
Nenad Buncic
developed the HTML documentation generation system and integrated the X3D viewer inside ROOT
(1995-1997).
Suzanne Panacek
was the author of the first version of this User’s Guide and very active in preparing tutorials and
giving lectures about ROOT (1999-2002).
Axel Naumann
has been developing further the HTML Reference Guide and helps in porting ROOT under Windows
(cygwin/gcc implementation) (since 2000).
Anna Kreshuk
has developed the Linear Fitter and Robust Fitter classes as well as many functions in TMath, TF1,
TGraph (since 2005).
Richard Maunder has contributed to the GL viewer classes (since 2004).
21
22 CONTENTS
Timur Pocheptsov has contributed to the GL viewer classes and GL in pad classes (since 2004).
Sergei Linev has developed the XML driver and the TSQLFile classes (since 2003).
Stefan Roiser has been contributing to the reflex and cintex packages (since 2005).
Lorenzo Moneta has been contributing the MathCore, MathMore, Smatrix & Minuit2 packages (since 2005).
Wim Lavrijsen is the author of the PyRoot package (since 2004).
Further we would like to thank all the people mentioned in the
$ROOTSYS/README/CREDITS
file for their contributions,
and finally, everybody who gave comments, reported bugs and provided fixes.
Happy ROOTing!
Rene Brun & Fons Rademakers
Geneva, July 2007
Chapter 1
Introduction
In the mid 1990’s, René Brun and Fons Rademakers had many years of experience developing interactive tools and
simulation packages. They had lead successful projects such as PAW, PIAF, and GEANT, and they knew PAW the
twenty-year-old FORTRAN libraries had reached their limits. Although still very popular, these tools could not scale
up to the challenges offered by the Large Hadron Collider, where the data is a few orders of magnitude larger than
anything seen before.
At the same time, computer science had made leaps of progress especially in the area of Object Oriented Design, and
René and Fons were ready to take advantage of it.
ROOT was developed in the context of the NA49 experiment at CERN. NA49 has generated an impressive amount of
data, around 10 Terabytes per run. This rate provided the ideal environment to develop and test the next generation
data analysis.
ROOT was, and still is, developed in the “Bazaar style”, a term from the book “The Cathedral and the Bazaar” by
Eric S. Raymond. It means a liberal, informal development style that heavily relies on the diverse and deep talent of
the user community. The result is that physicists developed ROOT for themselves; this made it specific, appropriate,
useful, and over time refined and very powerful. The development of ROOT is a continuous conversation between users
and developers with the line between the two blurring at times and the users becoming co-developers.
When it comes to storing and mining large amount of data, physics plows the way with its Terabytes, but other fields
and industry follow close behind as they acquiring more and more data over time. They are ready to use the true and
tested technologies physics has invented. In this way, other fields and industries have found ROOT useful and they
have started to use it also.
In the bazaar view, software is released early and frequently to expose it to thousands of eager co-developers to pound
on, report bugs, and contribute possible fixes. More users find more bugs, because they stress the program in different
ways. By now, after ten years, the age of ROOT is quite mature. Most likely, you will find the features you are looking
for, and if you have found a hole, you are encouraged to participate in the dialog and post your suggestion or even
implementation on roottalk, the ROOT mailing list.
1.1 The ROOT Mailing Lists
The
roottalk
was the very first active ROOT mailing list. mailing list People can subscribe to it by registering at the
ROOT web site: http://root.cern.ch/root/Registration.phtml. The
RootTalk
Forum http://root.cern.ch/phpBB3/ has
been gradually replaced this mailing list since September 2003. The
RootTalk
Forum is a web-based news group with
about 10 discussion sub-units.
If you have a question, it is likely that it has been asked, answered, and stored in the
roottalk
or
RootTalk
Forum
archives. Please use the search engine to see if your question has already been answered before sending a mail to the
roottalk list or post a topic in the Forum.
You can browse the
roottalk
archives at: http://root.cern.ch/root/roottalk/AboutRootTalk.html. You can send your
question without subscribing to: roottalk@cern.ch
1.2 Contact Information
Several authors wrote this book and you may see a “change of voice” from one chapter to the next. We felt we could
accept this in order to have the expert explain what they know best. If you would like to contribute a chapter or
23
24 CHAPTER 1. INTRODUCTION
add to a section, please contact rootdoc@cern.ch. We count on you to send us suggestions on additional topics or on
the topics that need more documentation. Please send your comments, corrections, questions, and suggestions to the
rootdoc list: rootdoc@cern.ch
We attempt to give the user insight into the many capabilities of ROOT. The book begins with the elementary
functionality and progresses in complexity reaching the specialized topics at the end. The experienced user looking for
special topics may find these chapters useful: see “Networking”, “Writing a Graphical User Interface”, “Threads”, and
“PROOF: Parallel Processing”.
1.3 Conventions Used in This Book
We tried to follow a style convention for the sake of clarity. The styles in used are described below.
To show source code in scripts or source files:
{
cout << " Hello" << endl;
float x=3.;
float y=5.;
int i=101;
cout <<"x="<<x<<"y="<<y<<"i="<<i<< endl;
}
To show the ROOT command line, we show the ROOT prompt without numbers. In the interactive system, the ROOT
prompt has a line number (root[12]); for the sake of simplicity, the line numbers are left off.
root[] TLine l
root[] l.Print()
TLine X1=0.000000 Y1=0.000000 X2=0.000000 Y2=0.000000
Italic bold monotype font indicates a global variable, for example gDirectory .
When a variable term is used, it is shown between angled brackets. In the example below the variable term <library>
can be replaced with any library in the $ROOTSYS directory: $ROOTSYS/<library>/inc.
1.4 The Framework
ROOT is an object-oriented framework aimed at solving the data analysis challenges of high-energy physics. There are
two key words in this definition, object oriented and framework. First, we explain what we mean by a framework and
then why it is an object-oriented framework.
1.4.1 What Is a Framework?
Programming inside a framework is a little like living in a city. Plumbing, electricity, telephone, and transportation are
services provided by the city. In your house, you have interfaces to the services such as light switches, electrical outlets,
and telephones. The details, for example, the routing algorithm of the phone switching system, are transparent to you
as the user. You do not care; you are only interested in using the phone to communicate with your collaborators to
solve your domain specific problems.
Programming outside of a framework may be compared to living in the country. In order to have transportation and
water, you will have to build a road and dig a well. To have services like telephone and electricity you will need to
route the wires to your home. In addition, you cannot build some things yourself. For example, you cannot build a
commercial airport on your patch of land. From a global perspective, it would make no sense for everyone to build
their own airport. You see you will be very busy building the infrastructure (or framework) before you can use the
phone to communicate with your collaborators and have a drink of water at the same time. In software engineering,
it is much the same way. In a framework, the basic utilities and services, such as I/O and graphics, are provided.
In addition, ROOT being a HEP analysis framework, it provides a large selection of HEP specific utilities such as
histograms and fitting. The drawback of a framework is that you are constrained to it, as you are constraint to use the
routing algorithm provided by your telephone service. You also have to learn the framework interfaces, which in this
analogy is the same as learning how to use a telephone.
1.5. INSTALLING ROOT 25
If you are interested in doing physics, a good HEP framework will save you much work. Next is a list of the more
commonly used components of ROOT: Command Line Interpreter, Histograms and Fitting, Writing a Graphical User
Interface, 2D Graphics, Input/Output , Collection Classes, Script Processor.
There are also less commonly used components, as: 3D Graphics, Parallel Processing (PROOF), Run Time Type
Identification (RTTI), Socket and Network Communication, Threads.
1.4.1.1 Advantages of Frameworks
The benefits of frameworks can be summarized as follows:
•
Less code to write - the programmer should be able to use and reuse the majority of the existing code. Basic
functionality, such as fitting and histogramming are implemented and ready to use and customize.
•
More reliable and robust code - the code inherited from a framework has already been tested and integrated with
the rest of the framework.
•
More consistent and modular code - the code reuse provides consistency and common capabilities between
programs, no matter who writes them. Frameworks make it easier to break programs into smaller pieces.
•
More focus on areas of expertise - users can concentrate on their particular problem domain. They do not have to
be experts at writing user interfaces, graphics, or networking to use the frameworks that provide those services.
1.4.2 Why Object-Oriented?
Object-Oriented Programming offers considerable benefits compared to Procedure-Oriented Programming:
•Encapsulation enforces data abstraction and increases opportunity for reuse.
•Sub classing and inheritance make it possible to extend and modify objects.
•
Class hierarchies and containment containment hierarchies provide a flexible mechanism for modeling real-world
objects and the relationships among them.
•
Complexity is reduced because there is little growth of the global state, the state is contained within each object,
rather than scattered through the program in the form of global variables.
•
Objects may come and go, but the basic structure of the program remains relatively static, increases opportunity
for reuse of design.
1.5 Installing ROOT
To install ROOT you will need to go to the ROOT website at: http://root.cern.ch/root/Availability.html. You have
a choice to download the binaries or the source. The source is quicker to transfer since it is only ~22 MB, but you
will need to compile and link it. The binaries compiled with no degug information range from ~35 MB to ~45 MB
depending on the target platform.
The installation and building of ROOT is described in Appendix A: Install and Build ROOT. You can download the
binaries, or the source. The GNU g++ compiler on most UNIX platforms can compile ROOT.
Before downloading a binary version make sure your machine contains the right run-time environment. In most cases it
is not possible to run a version compiled with, e.g., gcc4.0 on a platform where only gcc 3.2 is installed. In such cases
you’ll have to install ROOT from source.
ROOT is currently running on the following platforms: supported platforms
•GNU/Linux x86-32 (IA32) and x86-64 (AMD64)(GCC,Intel/icc, Portland/PGCC,KAI/KCC)
•Intel Itanium (IA64) GNU/Linux (GCC, Intel/ecc, SGI/CC)
•FreeBSD and OpenBSD (GCC)
•GNU/Hurd (GCC)
•HP HP-UX 10.x (IA32) and 11 (IA64) (HP CC, aCC, GCC)
26 CHAPTER 1. INTRODUCTION
•IBM AIX 4.1 (xlC compiler, GCC)
•Sun Solaris for SPARC (SUN C++ compiler, GCC)
•Sun Solaris for x86 (SUN C++ compiler, KAI/KCC)
•Compaq Alpha (GCC, KAI/KCC, DEC/CXX)
•SGI Irix 32 and 64 bits (GCC, KAI/KCC, SGI C++ compiler)
•Windows >= 95 (Microsoft Visual C++ compiler, Cygwin/GCC)
•MacOS X PPC, x86-32, x86-64 (GCC, Intel/ICC, IBM/xl)
•PowerPC with GNU/Linux and GCC, Debian v2
•PowerPC64 with GNU/Linux and GCC
•ARM with GNU/Linux and GCC
•LynxOS
1.6 The Organization of the ROOT Framework
Now after we know in abstract terms what the ROOT framework is, let us look at the physical directories and files
that come with the ROOT installation. You may work on a platform where your system administrator has already
installed ROOT. You will need to follow the specific development environment for your setup and you may not have
write access to the directories. In any case, you will need an environment variable called
ROOTSYS
, which holds the
path of the top ROOT directory.
> echo $ROOTSYS
/opt/root
In the
ROOTSYS
directory are examples, executables, tutorials, header tutorials files, and, if you opted to download
it, the source is here. The directories of special interest to us are
bin
,
tutorials
,
lib
,
test
, and
include
. The next
figure shows the contents of these directories.
1.6.1 $ROOTSYS/bin
The bin directory contains several executables.
root shows the ROOT splash screen and calls root.exe
root.exe the executable that root calls, if you use a debugger such as gdb, you will need to run
root.exe directly
rootcling is the utility ROOT uses to create a class dictionary for Cling
rmkdepend a modified version of makedepend that is used by the ROOT build system
root-config a script returning the needed compile flags and libraries for projects that compile and
link with ROOT
proofd a small daemon used to authenticate a user of ROOT parallel processing capability
(PROOF)
proofserv the actual PROOF process, which is started by proofd after a user, has successfully
been authenticated
rootd is the daemon for remote ROOT file access (see the TNetFile)
1.6.2 $ROOTSYS/lib
There are several ways to use ROOT, one way is to run the executable by typing
root
at the system prompt another
way is to link with the ROOT libraries and make the ROOT classes available in your own program.
Here is a short description of the most relevant libraries, the ones marked with a * are only installed when the options
specified them.
•libAsImage is the image manipulation library
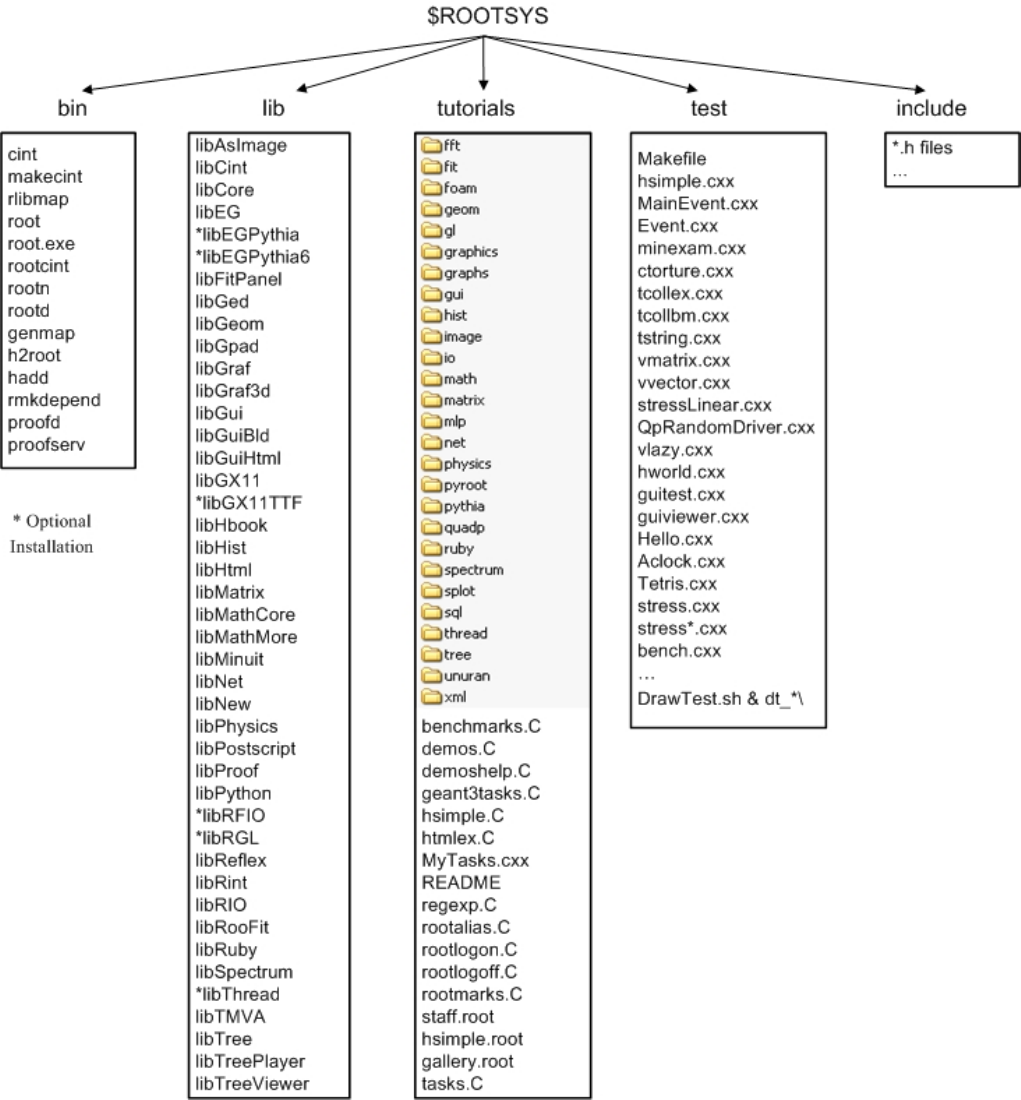
1.6. THE ORGANIZATION OF THE ROOT FRAMEWORK 27
Figure 1.1: ROOT framework directories
28 CHAPTER 1. INTRODUCTION
•libCling is the C++ interpreter (Cling)
•libCore is the Base classes
•libEG is the abstract event generator interface classes
•*libEGPythia is the Pythia5 event generator interface
•*libEGPythia6 is the Pythia6 event generator interface
•libFitPanel contains the GUI used for fitting
•libGed contains the GUI used for editing the properties of histograms, graphs, etc.
•libGeom is the geometry package (with builder and painter)
•libGpad is the pad and canvas classes which depend on low level graphics
•libGraf is the 2D graphics primitives (can be used independent of libGpad)
•libGraf3d is the 3D graphics primitives
•libGui is the GUI classes (depend on low level graphics)
•libGuiBld is the GUI designer
•libGuiHtml contains the embedded HTML browser
•libGX11 is the low level graphics interface to the X11 system
•*libGX11TTF is an add-on library to libGX11 providing TrueType fonts
•libHbook is for interface ROOT - HBOOK
•libHist is the histogram classes (with accompanying painter library)
•libHtml is the HTML documentation generation system
•libMatrix is the matrix and vector manipulation
•libMathCore contains the core mathematics and physics vector classes
•libMathMore contains additional functions, interfacing the GSL math library
•libMinuit is the MINUIT fitter
•libNet contains functionality related to network transfer
•libNew
is the special global new/delete, provides extra memory checking and interface for shared memory
(optional)
•libPhysics contains the legacy physics classes (TLorentzVector, etc.)
•libPostscript is the PostScript interface
•libProof is the parallel ROOT Facility classes
•libPython provides the interface to Python
•*libRFIO is the interface to CERN RFIO remote I/O system.
•*libRGL is the interface to OpenGL.
•libReflex is the runtime type database library used by Cling
•libRint is the interactive interface to ROOT (provides command prompt)
•libRIO provides the functionality to write and read objects to and from ROOT files
•libRooFit is the RooFit fitting framework
•libRuby is the interface to Ruby
•libSpectrum provides functionality for spectral analysis
•*libThread is the interface to TThread classes
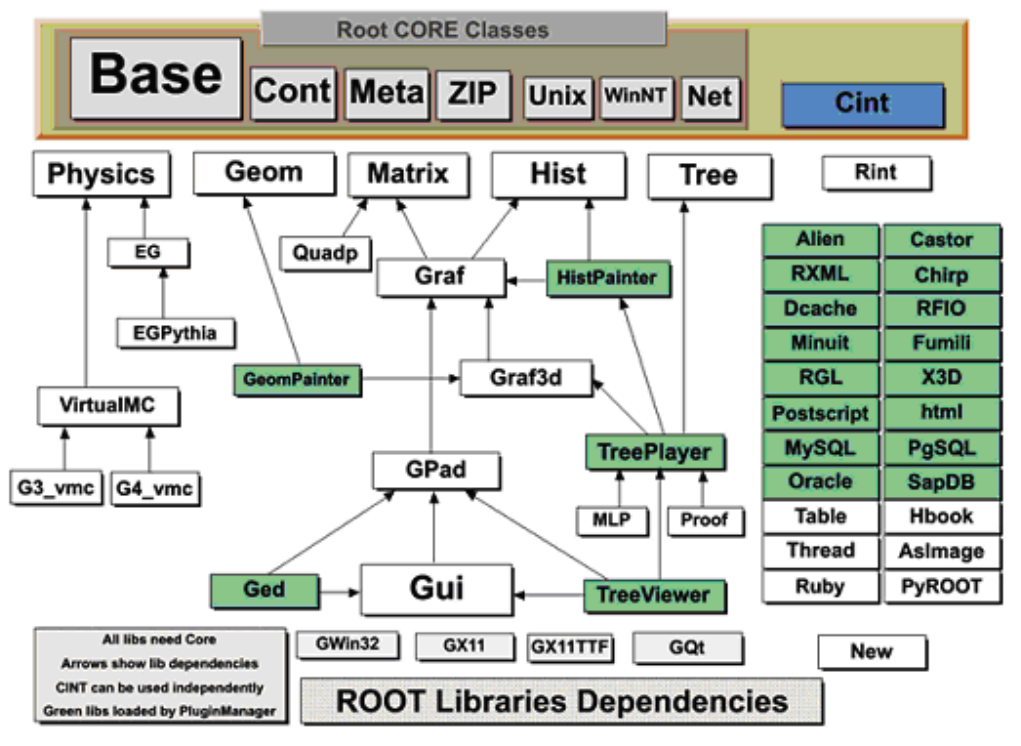
1.6. THE ORGANIZATION OF THE ROOT FRAMEWORK 29
•libTMVA contains the multivariate analysis toolkit
•libTree is the TTree object container system
•libTreePlayer is the TTree drawing classes
•libTreeViewer is the graphical TTree query interface
1.6.2.1 Library Dependencies
Figure 1.2: ROOT libraries dependencies
The libraries are designed and organized to minimize dependencies, such that you can load just enough code for the
task at hand rather than having to load all libraries or one monolithic chunk. The core library (
libCore.so
) contains
the essentials; it is a part of all ROOT applications. In the Figure 1-2 you see that libCore.so is made up of base
classes, container classes, meta information classes, operating system specific classes, and the ZIP algorithm used for
compression of the ROOT files.
The Cling library (
libCling.so
) is also needed in all ROOT applications, and even by
libCore
. A program referencing
only
TObject
only needs
libCore
;
libCling
will be opened automatically. To add the ability to read and write ROOT
objects one also has to load libRIO. As one would expect, none of that depends on graphics or the GUI.
Library dependencies have different consequences; depending on whether you try to build a binary, or you just try to
access a class that is defined in a library.
1.6.2.2 Linktime Library Dependencies
When building your own executable you will have to link against the libraries that contain the classes you use. The
ROOT reference guide states the library a class is reference guide defined in. Almost all relevant classes can be found
in libraries returned by
root-config -glibs
; the graphics libraries are retuned by
root-config --libs
. These
commands are commonly used in
Makefiles
. Using
root-config
instead of enumerating the libraries by hand allows
30 CHAPTER 1. INTRODUCTION
you to link them in a platform independent way. Also, if ROOT library names change you will not need to change your
Makefile.
A batch program that does not have a graphic display, which creates, fills, and saves histograms and trees, only needs
to link the core libraries (
libCore
,
libRIO
),
libHist
and
libTree
. If ROOT needs access to other libraries, it loads
them dynamically. For example, if the
TreeViewer
is used,
libTreePlayer
and all libraries
libTreePlayer
depends
on are loaded also. The dependent libraries are shown in the ROOT reference guide’s library dependency graph. The
difference between reference guide
libHist
and
libHistPainter
is that the former needs to be explicitly linked and
the latter will be loaded automatically at runtime when ROOT needs it, by means of the Plugin Manager. plugin
manager
In the Figure 1-2, the libraries represented by green boxes outside of the core are loaded via the plugin manager plugin
manager or equivalent techniques, while the white ones are not. Of course, if one wants to access a plugin library
directly, it has to be explicitly linked. An example of a plugin library is
libMinuit
. To create and fill histograms you
need to link
libHist.so
. If the code has a call to fit the histogram, the “fitter” will dynamically load libMinuit if it is
not yet loaded.
1.6.2.3 Plugins: Runtime Library Dependencies for Linking
plugin manager The Plugin Manager
TPluginManager
allows postponing library dependencies to runtime: a plu-
gin library will only be loaded when it is needed. Non-plugins will need to be linked, and are thus loaded at
start-up. Plugins are defined by a base class (e.g.
TFile
) that will be implemented in a plugin, a tag used to
identify the plugin (e.g.
ˆrfio:
as part of the protocol string), the plugin class of which an object will be created
(e.g.
TRFIOFile
), the library to be loaded (in short
libRFIO.so
to RFIO), and the constructor to be called (e.g.
“
TRFIOFile()
”). This can be specified in the
.rootrc
which already contains many plugin definitions, or by calls to
gROOT->GetPluginManager()->AddHandler().
1.6.2.4 Library Autoloading
When using a class in Cling, e.g. in an interpreted source file, ROOT will automatically load the library that defines
this class. On start-up, ROOT parses all files ending on
.rootmap
rootmap that are in one of the
$LD_LIBRARY_PATH
(or
$DYLD_LIBRARY_PATH
for
MacOS
, or
$PATH
for
Windows
). They contain class names and the library names that the
class depends on. After reading them, ROOT knows which classes are available, and which libraries to load for them.
When
TSystem::Load("ALib")
is called, ROOT uses this information to determine which libraries
libALib.so
depends
on. It will load these libraries first. Otherwise, loading the requested library could cause a system (dynamic loader)
error due to unresolved symbols.
1.6.3 $ROOTSYS/tutorials
tutorials The tutorials directory contains many example example scripts. They assume some basic knowledge of
ROOT, and for the new user we recommend reading the chapters: “Histograms” and “Input/Output” before trying the
examples. The more experienced user can jump to chapter “The Tutorials and Tests” to find more explicit and specific
information about how to build and run the examples.
The $ROOTSYS/tutorials/ directory include the following sub-directories:
fft
: Fast Fourier Transform with the fftw package
fit
: Several examples illustrating minimization/fitting
foam
:
Random generator in multidimensional space
geom
: Examples of use of the geometry package (
TGeo
classes)
gl
:
Visualisation with OpenGL
graphics
: Basic graphics
graphs
: Use of
TGraph
,
TGraphErrors
, etc.
gui
: Scripts to
create Graphical User Interface
hist
: Histograming
image
: Image Processing
io
: Input/Output
math
: Maths and
Statistics functions
matrix
: Matrices (
TMatrix
) examples
mlp
: Neural networks with
TMultiLayerPerceptron net
:
Network classes (client/server examples)
physics
: LorentzVectors, phase space
pyroot
: Python tutorials
pythia
:
Example with
pythia6 quadp
: Quadratic Programming
ruby
: ruby tutorials
smatrix
: Matrices with a templated
package
spectrum
: Peak finder, background, deconvolutions
splot
: Example of the
TSplot
class (signal/background
estimator)
sql
: Interfaces to SQL (mysql, oracle, etc)
thread
: Using Threads
tmva
: Examples of the MultiVariate
Analysis classes
tree
: Creating Trees, Playing with Trees
unuran
: Interface with the unuram random generator library
xml: Writing/Reading xml files
You can execute the scripts in
$ROOTSYS/tutorials
(or sub-directories) by setting your current directory in the script
directory or from any user directory with write access. Several tutorials create new files. If you have write access to the
tutorials directory, the new files will be created in the tutorials directory, otherwise they will be created in the user
directory.

1.7. HOW TO FIND MORE INFORMATION 31
1.6.4 $ROOTSYS/test
The test directory contains a set of examples example that represent all areas of the framework. When a new release is
cut, the examples in this directory are compiled and run to test the new release’s backward compatibility. The list of
source files is described in chapter “The Tutorials and Tests”.
The
$ROOTSYS/test
directory is a gold mine of ROOT-wisdom nuggets, and we encourage you to explore and exploit
it. We recommend the new users to read the chapter “Getting Started”. The chapter “The Tutorials and Tests” has
instructions on how to build all the programs and it goes over the examples Event and stress.
1.6.5 $ROOTSYS/include
The
include
directory contains all header files. It is especially important because the header files contain the class
definitions.
1.6.6 $ROOTSYS/<library>
The directories we explored above are available when downloading the binaries. When downloading the source you also
get a directory for each library with the corresponding header and source files, located in the
inc
and
src
subdirectories.
To see what classes are in a library, you can check the
<library>/inc
directory for the list of class definitions. For
example, the physics library libPhysics.so contains these class definitions:
> ls -m $ROOTSYS/math/physics/inc/
LinkDef.h, TFeldmanCousins.h, TGenPhaseSpace.h, TLorentzRotation.h,
TLorentzVector.h, TQuaternion.h, TRobustEstimator.h, TRolke.h,
TRotation.h, TVector2.h, TVector3.h
1.7 How to Find More Information
website The ROOT web site has up to date documentation. The ROOT source code automatically generates this
documentation, so each class is explicitly documented on its own web page, which is always up to date with the latest
official release of ROOT.
The ROOT Reference Guide web pages can be found at class index reference guide http://root.cern.ch/root/html/
ClassIndex.html. Each page contains a class description, and an explanation of each method. It shows the class
inheritance tree and lets you jump to the parent class page by clicking on the class name. If you want more details,
you can even see the source. There is a help page available in the little box on the upper right hand side of each class
documentation page. You can see on the next page what a typical class documentation web page looks like. The ROOT
web site also contains in addition to this Reference Guide, “How To’s”, a list of publications and example applications.
1.7.1 Class Reference Guide
The top of any class reference page lets you jump to different parts of the documentation. The first line links to the
class index and the index for the current module (a group of classes, often a library). The second line links to the
ROOT homepage and the class overviews. The third line links the source information - a HTML version of the source
and header file as well as the CVS (the source management system used for the ROOT development) information of
the files. The last line links the different parts of the current pages.
32 CHAPTER 1. INTRODUCTION
Figure 1.3: Example of function documentation, with automatically generated LaTeX-like graphics
Figure 1.4: Inheritance tree, showing what the current class derives from, and which classes inherit from it
Figure 1.5: HTML version of the source file linking all types and most functions
Chapter 2
Getting Started
We begin by showing you how to use ROOT interactively. There are two examples to click through and learn how to
use the GUI. We continue by using the command line, and explaining the coding conventions, global variables and the
environment setup. If you have not installed ROOT, you can do so by following the instructions in the appendix, or on
the ROOT web site: http://root.cern.ch/root/Availability.html
2.1 Setting the Environment Variables
Before you can run ROOT you need to set the environment variable
ROOTSYS
and change your path to include
root/bin
and library path variables to include root/lib. Please note: the syntax is for bash, if you are running tcsh you will
have to use setenv instead of export.
1. Define the variable $ROOTSYS to the directory where you unpacked the ROOT:
$ export ROOTSYS=$HOME/root
2. Add ROOTSYS/bin to your PATH:
$ export PATH=$PATH:$ROOTSYS/bin
3. Setting the Library Path
On HP-UX, before executing the interactive module, you must set the library path:
$ export SHLIB_PATH=$SHLIB_PATH:$ROOTSYS/lib
On AIX, before executing the interactive module, you must set the library path:
$ [ -z "$LIBPATH" ] && export LIBPATH=/lib:/usr/lib
$ export LIBPATH=$LIBPATH:$ROOTSYS/lib
On Linux, Solaris, Alpha OSF and SGI, before executing the interactive module, you must set the library path:
$ export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$ROOTSYS/lib
On Solaris, in case your LD_LIBRARY_PATH is empty, you should set it:
$ export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$ROOTSYS/lib:/usr/dt/lib
If you use the afs version you should set (vers = version number, arch = architecture):
$ export ROOTSYS=/afs/cern.ch/sw/lcg/external/root/vers/arch/root
If ROOT was installed in $HOME/myroot directory on a local machine, one can do:
cd $HOME/myroot
. bin/thisroot.sh // or source bin/thisroot.sh
The new
$ROOTSYS/bin/thisroot.[c]sh
scripts will set correctly the
ROOTSYS
,
LD_LIBRARY_PATH
or other paths
depending on the platform and the MANPATH. To run the program just type: root.
33
34 CHAPTER 2. GETTING STARTED
2.2 Start and Quit a ROOT Session
$ root
------------------------------------------------------------
| Welcome to ROOT 6.00/00 http://root.cern.ch |
| (c) 1995-2014, The ROOT Team |
| Built for linuxx8664gcc |
| From tag v6-00-00, 30 May 2014 |
| Try '.help','.demo','.license','.credits','.quit'/'.q'|
------------------------------------------------------------
root [0]
To start ROOT you can type
root
at the system prompt. This starts up Cling, the ROOT command line C/C++
interpreter, and it gives you the ROOT prompt (root[0]).
It is possible to launch ROOT with some command line options, as shown below:
% root -?
Usage: root [-l] [-b] [-n] [-q] [dir] [[file:]data.root]
[file1.C ... fileN.C]
Options:
-b : run in batch mode without graphics
-n : do not execute logon and logoff macros as specified in .rootrc
-q : exit after processing command line macro files
-l : do not show splash screen
-x : exit on exception
dir : if dir is a valid directory cd to it before executing
-? : print usage
-h : print usage
--help : print usage
-config : print ./configure options
-memstat : run with memory usage monitoring
•
-b ROOT session runs in batch mode, without graphics display. This mode is useful in case one does not want to
set the DISPLAY or cannot do it for some reason.
•
-n usually, launching a ROOT session will execute a logon script and quitting will execute a logoff script. This
option prevents the execution of these two scripts.
•
it is also possible to execute a script without entering a ROOT session. One simply adds the name of the script(s)
after the ROOT command. Be warned: after finishing the execution of the script, ROOT will normally enter a
new session.
•-q process command line script files and exit.
For example if you would like to run a script
myMacro.C
in the background, redirect the output into a file
myMacro.log
,
and exit after the script execution, use the following syntax:
root -b -q myMacro.C > myMacro.log
If you need to pass a parameter to the script use:
root -b -q 'myMacro.C(3)'> myMacro.log
Be mindful of the quotes, i.e. if you need to pass a string as a parameter, the syntax is:
root -b -q 'myMacro.C("text")'> myMacro.log
You can build a shared library with ACLiC and then use this shared library on the command line for a quicker execution
(i.e. the compiled speed rather than the interpreted speed). See also “Cling the C++ Interpreter”.
2.3. USING THE GUI 35
root -b -q myMacro.so > myMacro.log
ROOT has a powerful C/C++ interpreter giving you access to all available ROOT classes, global variables, and
functions via the command line. By typing C++ statements at the prompt, you can create objects, call functions,
execute scripts, etc. For example:
root[] 1+sqrt(9)
(const double)4.00000000000000000e+00
root[] for (int i=0; i<4; i++) cout << "Hello" << i << endl
Hello 0
Hello 1
Hello 2
Hello 3
root[] .q
To exit the ROOT session, type .q.
root[] .q
2.3 Using the GUI
The basic whiteboard on which an object is drawn in ROOT is called a canvas (defined by the class
TCanvas
). Every
object in the canvas is a graphical object in the sense that you can grab it, resize it, and change some characteristics
using the mouse. The canvas area can be divided in several sub areas, so-called pads (the class
TPad
). A pad is a
canvas sub area that can contain other pads or graphical objects. At any one time, just one pad is the so-called active
pad. Any object at the moment of drawing will be drawn in the active pad. The obvious question is: what is the
relation between a canvas and a pad? In fact, a canvas is a pad that spans through an entire window. This is nothing
else than the notion of inheritance. The
TPad
class is the parent of the
TCanvas
class. In ROOT, most objects derive
from a base class
TObject
. This class has a virtual method
Draw()
such as all objects are supposed to be able to be
“drawn”. If several canvases are defined, there is only one active at a time. One draws an object in the active canvas by
using the statement:
object.Draw()
This instructs the object “
object
” to draw itself. If no canvas is opened, a default one (named “
c1
”) is created. In the
next example, the first statement defines a function and the second one draws it. A default canvas is created since
there was no opened one. You should see the picture as shown in the next figure.
root[] TF1 f1("func1","sin(x)/x",0,10)
root[] f1.Draw()
<TCanvas::MakeDefCanvas>: created default TCanvas with name c1
The following components comprise the canvas window:
•Menu bar - contains main menus for global operations with files, print, clear canvas, inspect, etc.
•Tool bar - has buttons for global and drawing operations; such as arrow, ellipse, latex, pad, etc.
•Canvas - an area to draw objects.
•Status bar - displays descriptive messages about the selected object.
•
Editor frame - responds dynamically and presents the user interface according to the selected object in the canvas.
2.3.1 Main Menus and Toolbar
At the top of the canvas window are File, Edit, View, Options, Inspect, Classes and Help menus.
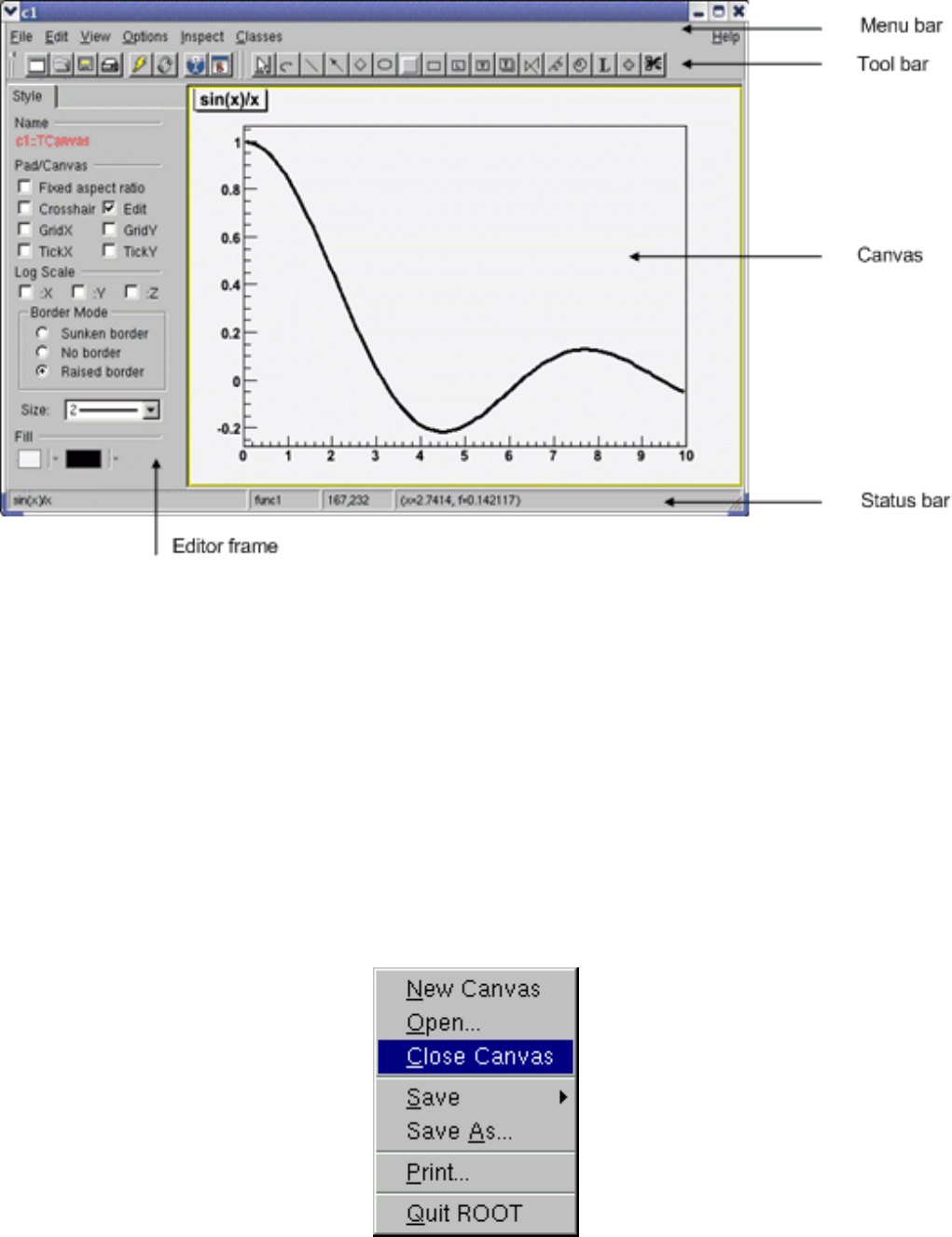
36 CHAPTER 2. GETTING STARTED
Figure 2.1: A canvas with drawing
2.3.1.1 File Menu
•New Canvas: creates a new canvas window in the current ROOT session.
•Open. . . : popup a dialog to open a file.
•Close Canvas: close the canvas window.
•
Save: save the drawing of the current canvas in a format selectable from the submenu. The current canvas name
is used as a file name for various formats such as PostScript, GIF, JPEG, C macro file, root file.
•Save As. . . : popup a dialog for saving the current canvas drawing in a new filename.
•Print: popup a dialog to print the current canvas drawing
•Quit ROOT: exit the ROOT session
2.3.1.2 Edit Menu
There is only one active menu entry in the Edit menu. The others menu entries will be implemented and will become
active in the near future.
•Clear: delete all objects in the canvas or in the selected pad according to the selected entry in the submenu.
2.3. USING THE GUI 37
2.3.1.3 View Menu
•
Editor: toggles the view of the editor. If it is selected activates and shows up the editor on the left side of the
canvas window. According to the selected object, the editor loads the corresponding user interface for easy change
of the object’s attributes.
•
Toolbar: toggles the view of the toolbar. If it is selected activates and shows up the toolbar. It contains buttons
for easy and fast access to most frequently used commands and for graphics primitive drawing. Tool tips are
provided for helping users.
•
Status Bar: toggles the view of the status bar. If it is selected, the status bar below the canvas window shows
up. There the identification of the objects is displayed when moving the mouse (such as the object’s name, the
object’s type, its coordinates, etc.).
•Colors: creates a new canvas showing the color palette.
•Markers: creates a new canvas showing the various marker styles.
•Iconify: create the canvas window icon, does not close the canvas
•
View With. . . : If the last selected pad contains a 3-d structure, a new canvas is created with a 3-D picture
according to the selection made from the cascaded menu: X3D or OpenGL. The 3-D image can be interactively
rotated, zoomed in wire-frame, solid, hidden line or stereo mode.
2.3.1.4 Options Menu
•Auto Resize Canvas: turns auto-resize of the canvas on/off :
–on - the canvas fits to the window when changing the window size;
–off - the canvas stays fixed when changing the window size.
•Resize Canvas: resizes and fits the canvas to the window size.
•
Move Opaque: if selected, graphics objects are moved in opaque mode; otherwise, only the outline of objects
is drawn when moving them. The option opaque produces the best effect but it requires a reasonably fast
workstation or response time.
•
Resize Opaque: if selected, graphics objects are resized in opaque mode; otherwise, only the outline of objects is
drawn when resizing them.
•Interrupt: interrupts the current drawing process.
•Refresh: redraws the canvas contents.
•Pad Auto Exec: executes the list of TExecs in the current pad.
•Statistics: toggles the display of the histogram statistics box.
•Histogram Title: toggles the display of the histogram title.
•Fit Parameters: toggles the display of the histogram or graph fit parameters.
•Can Edit Histogram: enables/disables the possibility to edit histogram bin contents.
38 CHAPTER 2. GETTING STARTED
2.3.1.5 Inspect Menu
•ROOT : inspects the top-level gROOT object (in a new canvas).
•Start Browser: starts a new object browser (in a separate window).
•GUI Builder: starts the GUI builder application (in a separate window).
2.3.1.6 Help Menu
•Canvas: help on canvas as a whiteboard area for drawing.
•Menus: help on canvas menus.
•Graphics Editor: help on primitives’ drawing and objects’ editor.
•Browser: help on the ROOT objects’ and files’ browser.
•Objects: help on DrawClass, Inspect and Dump context menu items.
•PostScript: help on how to print a canvas to a PostScript file format.
•About ROOT: pops up the ROOT Logo with the version number.

2.3. USING THE GUI 39
2.3.1.7 Classes Menu
•Classes: starts the ClassTree viewer that draws inheritance tree for a list of classes.
2.3.1.8 Toolbar
The following menu shortcuts and utilities are available from the toolbar:
Create a new canvas window.
Popup the Open File dialog.
Popup the Save As. . . dialog.
Popup the Print dialog.
Interrupts the current drawing process.
Redraw the canvas.
Inspect the gROOT object.
Create a new objects’ browser.
You can create the following graphical objects using the toolbar buttons for primitive drawing. Tool tips are provided
for helping your choice.
An Arc or circle
: Click on the center of the arc, and then move the mouse. A rubber band circle is shown. Click
again with the left button to freeze the arc.
A Line
: Click with the left button at the point where you want to start the line, then move the mouse and click
again with the left button to freeze the line.
An Arrow:
Click with the left button at the point where you want to start the arrow, then move the mouse and
click again with the left button to freeze the arrow.
A Diamond
: Click with the left button and freeze again with the left button. The editor draws a rubber band
box to suggest the outline of the diamond.
An Ellipse
: Proceed like for an arc. You can grow/shrink the ellipse by pointing to the sensitive points. They
are highlighted. You can move the ellipse by clicking on the ellipse, but not on the sensitive points. If, with the ellipse
context menu, you have selected a fill area color, you can move a filled-ellipse by pointing inside the ellipse and dragging
it to its new position.
A Pad
: Click with the left button and freeze again with the left button. The editor draws a rubber band box to
suggest the outline of the pad.
A PaveLabel
: Proceed like for a pad. Type the text of label and finish with a carriage return. The text will
appear in the box.
A Pave Text
: Proceed like for a pad. You can then click on the
TPaveText
object with the right mouse button
and select the option InsertText.
Paves Text: Proceed like for a TPaveText.
A Poly Line
: Click with the left button for the first point, move the moose, click again with the left button for a
new point. Close the poly-line with a double click. To edit one vertex point, pick it with the left button and drag to
the new point position.
A Curly Line
: Proceed as for the arrow or line. Once done, click with the third button to change the characteristics
of the curly line, like transform it to wave, change the wavelength, etc.

40 CHAPTER 2. GETTING STARTED
A Curly Arc
: Proceed like for an ellipse. The first click is located at the position of the center, the second click
at the position of the arc beginning. Once done, one obtains a curly ellipse, for which one can click with the third
button to change the characteristics, like transform it to wavy, change the wavelength, set the minimum and maximum
angle to make an arc that is not closed, etc.
A Text/Latex string
: Click with the left button where you want to draw the text and then type in the text
terminated by carriage return. All
TLatex
expressions are valid. To move the text or formula, point on it keeping the
left mouse button pressed and drag the text to its new position. You can grow/shrink the text if you position the
mouse to the first top-third part of the string, then move the mouse up or down to grow or shrink the text respectively.
If you position the mouse near the bottom-end of the text, you can rotate it.
A Marker
: Click with the left button where to place the marker. The marker can be modified by using the
method SetMarkerStyle() of TSystem.
A Graphical Cut
: Click with the left button on each point of a polygon delimiting the selected area. Close the
cut by double clicking on the last point. A
TCutG
object is created. It can be used as a selection for a
TTree::Draw
.
You can get a pointer to this object with:
TCutG cut = (TCutG*)gPad->GetPrimitive("CUTG")
Once you are happy with your picture, you can select the
Save as canvas.C
item in the canvas File menu. This will
automatically generate a script with the C++ statements corresponding to the picture. This facility also works if you
have other objects not drawn with the graphics editor (histograms for example).
2.3.2 The Editor Frame
The ROOT graphics editor loads the corresponding object editor
objEditor
according to the selected object
obj
in
the canvas respecting the class inheritance. An object in the canvas is selected after the left mouse click on it. For
example, if the selected object is
TAxis
, the
TAxisEditor
will shows up in the editor frame giving the possibility for
changing different axis attributes. The graphics editor can be:
Embedded - connected only with the canvas in the application window that appears on the left of the canvas window
after been activated via View menu / Editor. It appears on the left side if the canvas window allowing users to edit the
attributes of the selected object via provided user interface. The name of the selected object is displayed on the top of
the editor frame in red color. If the user interface needs more space then the height of the canvas window, a vertical
scroll bar appears for easer navigation.
Global - has own application window and can be connected to any created canvas in a ROOT session. It can be
activated via the context menu entries for setting line, fill, text and marker attributes for backward compatibility, but
there will be a unique entry in the near future.
The user interface for the following classes is available since ROOT v.4.04:
TAttLine
,
TAttFill
,
TAttMarker
,
TAttText
,
TArrow
,
TAxis
,
TCurlyArc
,
TCurlyLine
,
TFrame
,
TH1
,
TH2
,
TGraph
,
TPad
,
TCanvas
,
TPaveStats
. For more details,
see “The Graphics Editor”, “The User Interface for Histograms”, “The User Interface for Graphs”.
2.3.3 Classes, Methods and Constructors
Object oriented programming introduces objects, which have data members and methods. The next line creates an
object named
f1
of the class
TF1
that is a one-dimensional function. The type of an object is called a class. The object
itself is called an instance of a class. When a method builds an object, it is called a constructor.
TF1 f1("func1","sin(x)/x",0,10)
In our constructor the function sin(x)/x is defined for use, and 0 and 10 are the limits. The first parameter,
func1
is
the name of the object
f1
. Most objects in ROOT have a name. ROOT maintains a list of objects that can be searched
to find any object by its given name (in our example func1).
The syntax to call an object’s method, or if one prefers, to make an object to do something is:
object.method_name(parameters)
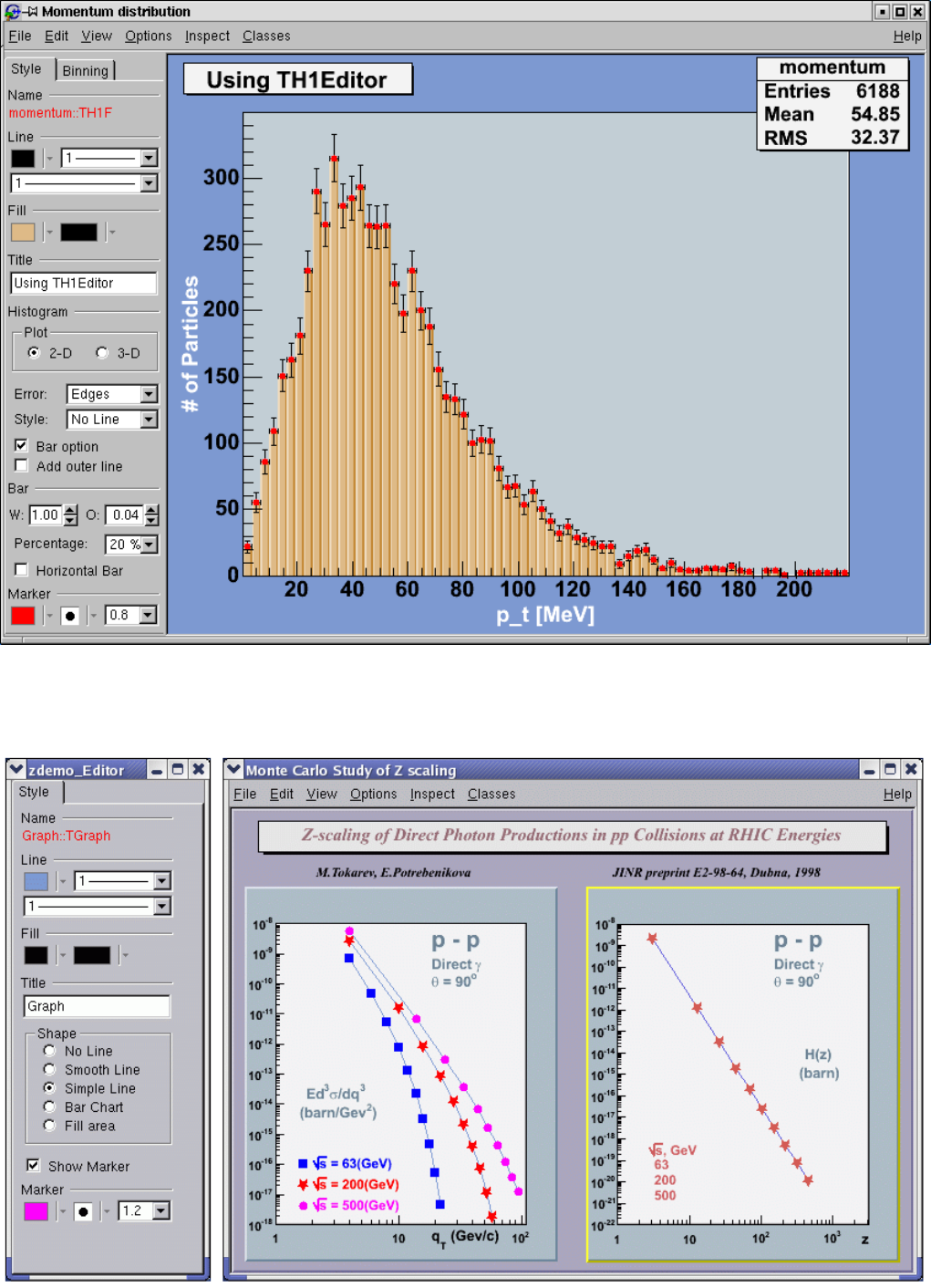
2.3. USING THE GUI 41
42 CHAPTER 2. GETTING STARTED
The dot can be replaced by “
->
” if
object
is a pointer. In compiled code, the dot MUST be replaced by a “
->
” if
object is a pointer.
object_ptr->method_name(parameters)
So now, we understand the two lines of code that allowed us to draw our function.
f1.Draw()
stands for “call the
method
Draw()
associated with the object
f1
of the class
TF1
”. Other methods can be applied to the object
f1
of the
class
TF1
. For example, the evaluating and calculating the derivative and the integral are what one would expect from
a function.
root[] f1.Eval(3)
(Double_t)4.70400026866224020e-02
root[] f1.Derivative(3)
(Double_t)(-3.45675056671992330e-01)
root[] f1.Integral(0,3)
(Double_t)1.84865252799946810e+00
root[] f1.Draw()
By default the method
TF1::Paint()
, that draws the function, computes 100 equidistant points to draw it. The
number of points can be set to a higher value with:
root[] f1.SetNpx(2000);
Note that while the ROOT framework is an object-oriented framework, this does not prevent the user from calling
plain functions.
2.3.4 User Interaction
Now we will look at some interactive capabilities. Try to draw the function
sin(x)/x
again. Every object in a window
(which is called a canvas) is, in fact, a graphical object in the sense that you can grab it, resize it, and change its
characteristics with a mouse click. For example, bring the cursor over the x-axis. The cursor changes to a hand with a
pointing finger when it is over the axis. Now, left click and drag the mouse along the axis to the right. You have a very
simple zoom.
When you move the mouse over any object, you can get access to selected methods by pressing the right mouse button
and obtaining a context menu. If you try this on the function
TF1
, you will get a menu showing available methods. The
other objects on this canvas are the title, a
TPaveText
object
;
the x and y-axis,
TAxis
objects, the frame, a
TFrame
object, and the canvas a TCanvas object. Try clicking on these and observe the context menu with their methods.
For example try selecting the
SetRange()
method and putting
-10
,
10
in the dialog box fields. This is equivalent to
executing
f1.SetRange(-10,10)
from the command line, followed by
f1.Draw()
. Here are some other options you
can try.
Once the picture suits your wishes, you may want to see the code you should put in a script to obtain the same result.
To do that, choose Save /
canvas.C
entry of the File menu. This will generate a script showing the options set in
the current canvas. Notice that you can also save the picture into various file formats such as PostScript, GIF, etc.
Another interesting possibility is to save your canvas into the native ROOT format (
.root
file). This will enable you to
open it again and to change whatever you like. All objects associated to the canvas (histograms, graphs) are saved at
the same time.
2.3.5 Building a Multi-pad Canvas
Let us now try to build a canvas with several pads.
root[] TCanvas *MyC = new TCanvas("MyC","Test canvas",1)
root[] MyC->Divide(2,2)
Once again, we call the constructor of a class, this time the class
TCanvas
. The difference between this and the previous
constructor call (
TF1
) is that here we are creating a pointer to an object. Next, we call the method
Divide()
of the
TCanvas
class (that is
TCanvas::Divide())
, which divides the canvas into four zones and sets up a pad in each of
them. We set the first pad as the active one and than draw the functionf1there.
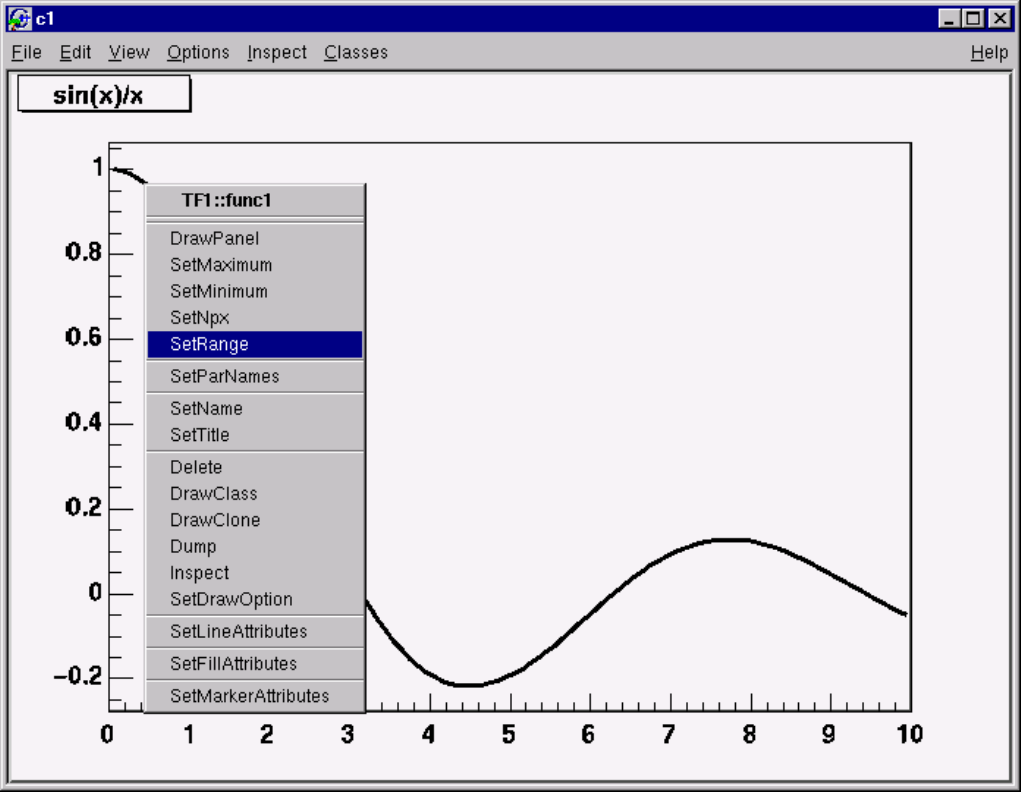
2.3. USING THE GUI 43
Figure 2.2: A context menu
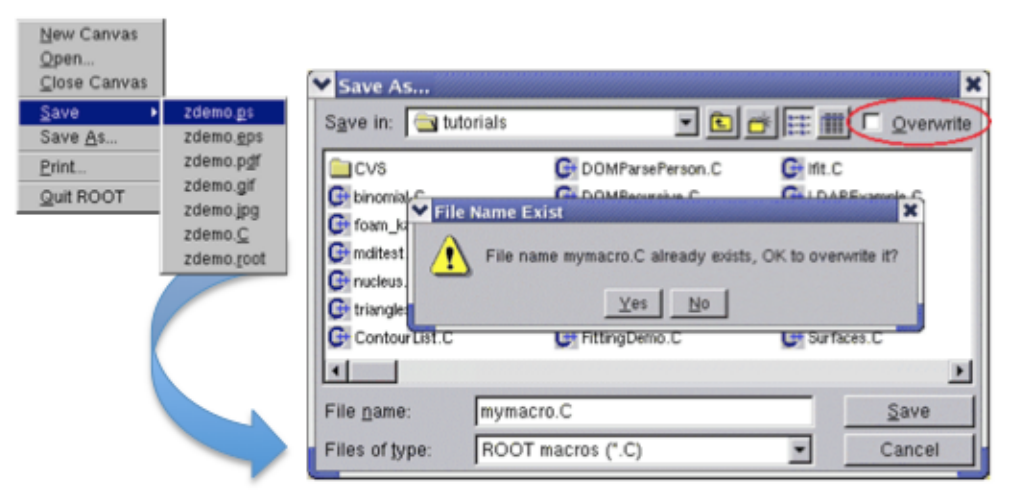
44 CHAPTER 2. GETTING STARTED
root[] MyC->cd(1)
root[] f1->Draw()
All objects will be drawn in that pad because it is the active one. The ways for changing the active pad are:
•Click the middle mouse button on a pad will set this pad as the active one.
•Use the method TCanvas::cd() with the pad number, as was done in the example above:
root[] MyC->cd(3)
Pads are numbered from left to right and from top to bottom. Each new pad created by
TCanvas::Divide()
has a
name, which is the name of the canvas followed by _1, _2, etc. To apply the method
cd()
to the third pad, you would
write:
root[] MyC_3->cd()
•
Third pad will be selected since you called
TPad::cd()
for the object
MyC_3
. ROOT will find the pad that was
namedMyC_3when you typed it on the command line (see ROOT/Cling Extensions to C++).
2.3.6 Saving the Canvas
Figure 2.3: The SaveAs. . . dialog
Using the File menu / Save cascade menu users can save the canvas as one of the files from the list. Please note that
saving the canvas this way will overwrite the file with the same name without a warning.
All supported file types can be saved via File menu / SaveAs. . . This dialog gives a choice to show or suppress the
confirmation message for overwriting an existing file.
If the Ovewrite check box is not selected, a message dialog appears asking the user to overwrite the file (Yes/No). The
user choice is saved for the next time the Save As. . . dialog shows up.
2.3.7 Printing the Canvas
The Print command in the canvas File menu pops-up a print dialog where the user can specify a preferred print
command and the printer name.
Both print parameters can be set via the new Print.Command and Print.Printer rootrc resources as follows:
2.4. THE ROOT COMMAND LINE 45
# Printer settings.
WinNT.*.Print.Command: AcroRd32.exe
Unix.*.Print.Command: xprint -P%p %f
Print.Printer: 32-rb205-hp
Print.Directory: .
If the
%p
and
%f
are specified as a part of the print command, they will be replaced by the specified printer name and
the file name. All other parameters will be kept as they are written. A print button is available in the canvas toolbar
(activated via View menu/Toolbar).
2.4 The ROOT Command Line
We have briefly touched on how to use the command line. There are different types of commands.
1. Cling commands start with “.”
root[] .? //this command will list all the Cling commands
root[] .L <filename> //load [filename]
root[] .x <filename> //load and execute [filename]
2. SHELL commands start with “.!” for example:
root[] .! ls
3. C++ commands follow C++ syntax (almost)
root[] TBrowser *b = new TBrowser()
2.4.1 Multi-line Commands
You can use the command line to execute multi-line commands. To begin a multi-line command you must type a single
left curly bracket {, and to end it you must type a single right curly bracket }. For example:
root[] {
end with '}'> Int_t j = 0;
end with '}'>for (Int_t i = 0;i<3; i++)
end with '}'> {
end with '}'>j=j+i;
end with '}'> cout << "i="<<i<<",j="<< j << endl;
end with '}'> }
end with '}'> }
i=0,j=0
i=1,j=1
i=2,j=3
It is more convenient to edit a script than the command line, and if your multi line commands are getting unmanageable,
you may want to start with a script instead.
46 CHAPTER 2. GETTING STARTED
2.4.2 Cling Extensions
We should say that some things are not standard C++. The Cling interpreter has several extensions. See “ROOT/Cling
Extensions to C++”.
2.4.3 Helpful Hints for Command Line Typing
The interpreter knows all the classes, functions, variables, and user defined types. This enables ROOT to help users to
complete the command line. For example, if we do not know anything about the
TLine
class, the Tab feature helps us
to get a list of all classes starting with TL(where <TAB> means type the Tab key).
root[] l = new TLi<TAB>
TList
TListIter
TLink
TLine
TLimitDataSource
TLimit
To list the different constructors and parameters for TLine use the <TAB> key as follows:
root[] l = new TLine(<TAB>
TLine TLine()
TLine TLine(Double_t x1,Double_t y1,Double_t x2,Double_t y2)
TLine TLine(const TLine& line)
2.4.4 Regular Expression
The meta-characters below can be used in a regular expression:
•‘ˆ’ start-of-line anchor
•‘$’ end-of-line anchor
•‘.’ matches any character
•‘[’ start a character class
•’]’end a character class
•’ˆ’negates character class if first character
•‘*’Kleene closure (matches 0 or more)
•’+’Positive closure (1 or more)
•‘?’ Optional closure (0 or 1)
When using wildcards the regular expression is assumed to be preceded by a ‘
ˆ
’ (BOL) and terminated by ‘
$
’ (EOL).
All ‘
*
’ (closures) are assumed to be preceded by a ‘
.
’, i.e. any character, except slash _
/_
. Its special treatment allows
the easy matching of pathnames. For example, _*.root_ will match _aap.root_, but not _pipo/aap.root_.
The escape characters are:
•\backslash
•bbackspace
•fform feed
•nnew line
•rcarriage return
•sspace
2.5. CONVENTIONS 47
•ttab
•eASCII ESC character (‘033’)
•DDD number formed of 1-3 octal digits
•xDD number formed of 1-2 hex digits
•ˆC C = any letter. Control code
The class
TRegexp
can be used to create a regular expression from an input string. If
wildcard
is true then the input
string contains a wildcard expression.
TRegexp(const char *re, Bool_t wildcard)
Regular expression and wildcards can be easily used in methods like:
Ssiz_t Index(const TString& string,Ssiz_t* len,Ssiz_t i) const
The method finds the first occurrence of the regular expression in the string and returns its position.
2.5 Conventions
In this paragraph, we will explain some of the conventions used in ROOT source and examples.
2.5.1 Coding Conventions
From the first days of ROOT development, it was decided to use a set of coding conventions. This allows a consistency
throughout the source code. Learning these will help you identify what type of information you are dealing with and
enable you to understand the code better and quicker. Of course, you can use whatever convention you want but if you
are going to submit some code for inclusion into the ROOT sources, you will need to use these.
These are the coding conventions:
•Classes begin with T:TLine,TTree
•Non-class types end with _t:Int_t
•Data members begin with f:fTree
•Member functions begin with a capital: Loop()
•Constants begin with k:kInitialSize,kRed
•Global variables begin with g:gEnv
•Static data members begin with fg:fgTokenClient
•Enumeration types begin with E:EColorLevel
•Locals and parameters begin with a lower case: nbytes
•Getters and setters begin with Get and Set:SetLast(), GetFirst()
48 CHAPTER 2. GETTING STARTED
2.5.2 Machine Independent Types
Different machines may have different lengths for the same type. The most famous example is the
int
type. It may
be 16 bits on some old machines and 32 bits on some newer ones. To ensure the size of your variables, use these pre
defined types in ROOT:
•Char_t Signed Character 1 byte
•UChar_t Unsigned Character 1 byte
•Short_t Signed Short integer 2 bytes
•UShort_t Unsigned Short integer 2 bytes
•Int_t Signed integer 4 bytes
•UInt_tUnsigned integer 4 bytes
•Long64_t Portable signed long integer 8 bytes
•ULong64_t Portable unsigned long integer 8 bytes
•Float_t Float 4 bytes
•Double_t Float 8 bytes
•Double32_t Double 8 bytes in memory, written as a Float 4 bytes
•Bool_t Boolean (0=false, 1=true)
If you do not want to save a variable on disk, you can use
int
or
Int_t
, the result will be the same and the interpreter
or the compiler will treat them in exactly the same way.
2.5.3 TObject
In ROOT, almost all classes inherit from a common base class called
TObject
. This kind of architecture is also used in
the Java language. The
TObject
class provides default behavior and protocol for all objects in the ROOT system. The
main advantage of this approach is that it enforces the common behavior of the derived classes and consequently it
ensures the consistency of the whole system. See “The Role of TObject”.
TObject provides protocol, i.e. (abstract) member functions, for:
•Object I/O (Read(),Write())
•Error handling (Warning(),Error(),SysError(),Fatal())
•Sorting (IsSortable(),Compare(),IsEqual(),Hash())
•Inspection (Dump(),Inspect())
•Printing (Print())
•Drawing (Draw(),Paint(),ExecuteEvent())
•Bit handling (SetBit(),TestBit())
•Memory allocation (operatornew and delete,IsOnHeap())
•Access to meta information (IsA(),InheritsFrom())
•Object browsing (Browse(),IsFolder())
2.6 Global Variables
ROOT has a set of global variables that apply to the session. For example,
gDirectory
always holds the current
directory, and gStyle holds the current style.
All global variables begin with “g” followed by a capital letter.
2.6. GLOBAL VARIABLES 49
2.6.1 gROOT
The single instance of
TROOT
is accessible via the global
gROOT
and holds information relative to the current session.
By using the
gROOT
pointer, you get the access to every object created in a ROOT program. The
TROOT
object has
several lists pointing to the main ROOT objects. During a ROOT session, the
gROOT
keeps a series of collections to
manage objects. They can be accessed via gROOT ::GetListOf... methods.
gROOT->GetListOfClasses()
gROOT->GetListOfColors()
gROOT->GetListOfTypes()
gROOT->GetListOfGlobals()
gROOT->GetListOfGlobalFunctions()
gROOT->GetListOfFiles()
gROOT->GetListOfMappedFiles()
gROOT->GetListOfSockets()
gROOT->GetListOfCanvases()
gROOT->GetListOfStyles()
gROOT->GetListOfFunctions()
gROOT->GetListOfSpecials()
gROOT->GetListOfGeometries()
gROOT->GetListOfBrowsers()
gROOT->GetListOfMessageHandlers()
These methods return a
TSeqCollection
, meaning a collection of objects, and they can be used to do list operations
such as finding an object, or traversing the list and calling a method for each of the members. See the
TCollection
class description for the full set of methods supported for a collection. For example, to find a canvas called
c1
you can
do:
root[] gROOT->GetListOfCanvases()->FindObject("c1")
This returns a pointer to a TObject, and before you can use it as a canvas you need to cast it to a TCanvas*.
2.6.2 gFile
gFile is the pointer to the current opened file in the ROOT session.
2.6.3 gDirectory
gDirectory
is a pointer to the current directory. The concept and role of a directory is explained in the chapter
“Input/Output”.
2.6.4 gPad
A graphic object is always drawn on the active pad. It is convenient to access the active pad, no matter what it is. For
that, we have
gPad
that is always pointing to the active pad. For example, if you want to change the fill color of the
active pad to blue, but you do not know its name, you can use gPad .
root[] gPad->SetFillColor(38)
To get the list of colors, if you have an open canvas, click in the “View” menu, selecting the “Colors” entry.
2.6.5 gRandom
gRandom
is a pointer to the current random number generator. By default, it points to a
TRandom3
object,
based on the “Mersenne-Twister” generator. This generator is very fast and has very good random proprieties
(a very long period of 10
600
). Setting the seed to 0 implies that the seed will be uniquely generated using
the
TUUID
. Any other value will be used as a constant. The following basic random distributions are provided:
Rndm()
or
Uniform(min,max)
,
Gaus(mean,sigma)
,
Exp(tau)
,
BreitWigner(mean,sigma)
,
Landau(mean,sigma)
,
Poisson(mean)
,
Binomial(ntot,prob)
. You can customize your ROOT session by replacing the random number
generator. You can delete gRandom and recreate it with your own. For example:
50 CHAPTER 2. GETTING STARTED
root[] delete gRandom;
root[] gRandom = new TRandom2(0); //seed=0
TRandom2 is another generator, which is also very fast and uses only three words for its state.
2.6.6 gEnv
gEnv
is the global variable (of type
TEnv
) with all the environment settings for the current session. This variable is set
by reading the contents of a
.rootrc
file (or
$ROOTSYS/etc/system.rootrc
) at the beginning of the root session. See
Environment Setup below for more information.
2.7 Environment Setup
The behavior of a ROOT session can be tailored with the options in the .
rootrc
file. At start-up, ROOT looks for a
.rootrc file in the following order:
•./.rootrc //local directory
•$HOME/.rootrc //user directory
•$ROOTSYS/etc/system.rootrc //global ROOT directory
If more than one
.rootrc
files are found in the search paths above, the options are merged, with precedence local,
user, global. While in a session, to see current settings, you can do:
root[] gEnv->Print()
The rootrc file typically looks like:
# Path used by dynamic loader to find shared libraries
Unix.*.Root.DynamicPath: .:~/rootlibs:$(ROOTSYS)/lib
Unix.*.Root.MacroPath: .:~/rootmacros:$(ROOTSYS)/macros
# Path where to look for TrueType fonts
Unix.*.Root.UseTTFonts: true
Unix.*.Root.TTFontPath:
...
# Activate memory statistics
Rint.Root.MemStat: 1
Rint.Load: rootalias.C
Rint.Logon: rootlogon.C
Rint.Logoff: rootlogoff.C
...
Rint.Canvas.MoveOpaque: false
Rint.Canvas.HighLightColor: 5
The various options are explained in
$ROOTSYS/etc/system.rootrc
. The
.rootrc
file contents are combined. For
example, if the flag to use true type fonts is set to true in the
system.rootrc
file, you have to set explicitly it false in
your local
.rootrc
file if you do not want to use true type fonts. Removing the
UseTTFonts
statement in the local
.rootrc
file will not disable true fonts. The value of the environment variable
ROOTDEBUG
overrides the value in the
.rootrc file at startup. Its value is used to set gDebug and helps for quick turn on debug mode in TROOT startup.
ROOT looks for scripts in the path specified in the
.rootrc
file in the
Root.Macro.Path
variable. You can expand
this path to hold your own directories.
2.7. ENVIRONMENT SETUP 51
2.7.1 Logon and Logoff Scripts
The
rootlogon.C
and
rootlogoff.C
files are scripts loaded and executed at start-up and shutdown. The
rootalias.C
file is loaded but not executed. It typically contains small utility functions. For example, the
rootalias.C
script
that comes with the ROOT distributions (located in
$ROOTSYS/tutorials)
defines the function
edit(char *file)
.
This allows the user to call the editor from the command line. This particular function will start the VI editor if the
environment variable EDITOR is not set.
root[0] edit("c1.C")
For more details, see $ROOTSYS/tutorials/rootalias.C.
2.7.2 History File
You can use the up and down arrow at the command line, to access the previous and next command. The commands
are recorded in the history file
$HOME/.root_hist
. It is a text file, and you can edit, cut, and paste from it. You
can specify the history file in the
system.rootrc
file, by setting the
Rint.History
option. You can also turn off the
command logging in the system.rootrc file with the option: Rint.History: -
The number of history lines to be kept can be set also in .rootrc by:
Rint.HistSize: 500
Rint.HistSave: 400
The first value defines the maximum of lines kept; once it is reached all, the last
HistSave
lines will be removed.
One can set
HistSize
to 0 to disable history line management. There is also implemented an environment variable
called
ROOT_HIST
. By setting
ROOT_HIST=300:200
the above values can be overriden - the first value corresponds to
HistSize, the (optional) second one to HistSave. You can set ROOT_HIST=0 to disable the history.
2.7.3 Tracking Memory Leaks
You can track memory usage and detect leaks by monitoring the number of objects that are created and deleted (see
TObjectTable
). To use this facility, edit the file
$ROOTSYS/etc/system.rootrc
or
.rootrc
if you have this file and
add the two following lines:
Root.MemStat: 1
Root.ObjectStat: 1
In your code or on the command line you can type the line:
gObjectTable->Print();
This line will print the list of all active classes and the number of instances for each class. By comparing consecutive
print outs, you can see objects that you forgot to delete. Note that this method cannot show leaks coming from the
allocation of non-objects or classes unknown to ROOT.
2.7.4 Memory Checker
A memory checking system was developed by D.Bertini and M.Ivanov and added in ROOT version 3.02.07. To activate
the memory checker you can set the resource
Root.MemCheck
to 1 (e.g.:
Root.MemCheck: 1
in the
.rootrc
file). You
also have to link with
libNew.so
(e.g. use
root-config --new --libs
) or to use
rootn.exe
. When these settings
are in place, you will find a file “
memcheck.out
” in the directory where you started your ROOT program after the
completion of the program execution. You can also set the resource
Root.MemCheckFile
to the name of a file. The
memory information will be written to that file. The contents of this
memcheck.out
can be analyzed and transformed
into printable text via the memprobe program (in $ROOTSYS/bin).
52 CHAPTER 2. GETTING STARTED
2.8 Converting from PAW to ROOT
The web page at: http://root.cern.ch/root/HowtoConvertFromPAW.html#TABLE gives the “translation” table
of some commonly used PAW commands into ROOT. If you move the mouse cursor over the picture at: http:
//root.cern.ch/root/HowtoConvertFromPAW.html#SET, you will get the corresponding ROOT commands as tooltips.
2.8.1 Converting HBOOK/PAW Files
ROOT has a utility called
h2root
that you can use to convert your HBOOK/PAW histograms or ntuple files into
ROOT files. To use this program, you type the shell script command:
h2root <hbookfile> <rootfile>
If you do not specify the second parameter, a file name is automatically generated for you. If
hbookfile
is of the
form
file.hbook
, then the ROOT file will be called
file.root
. This utility converts HBOOK histograms into ROOT
histograms of the class
TH1F
. HBOOK profile histograms are converted into ROOT profile histograms (see class
TProfile
). HBOOK row-wise and column-wise ntuples are automatically converted to ROOT Trees. See “Trees”.
Some HBOOK column-wise ntuples may not be fully converted if the columns are an array of fixed dimension (e.g.
var[6]) or if they are a multi-dimensional array.
HBOOK integer identifiers are converted into ROOT named objects by prefixing the integer identifier with the letter “
h
”
if the identifier is a positive integer and by
"h_"
if it is a negative integer identifier. In case of row-wise or column-wise
ntuples, each column is converted to a branch of a tree. Note that
h2root
is able to convert HBOOK files containing
several levels of sub-directories. Once you have converted your file, you can look at it and draw histograms or process
ntuples using the ROOT command line. An example of session is shown below:
// this connects the file hbookconverted.root
root[] TFile f("hbookconverted.root");
// display histogram named h10 (was HBBOK id 10)
root[] h10.Draw();
// display column "var" from ntuple h30
root[] h30.Draw("var");
You can also use the ROOT browser (see TBrowser) to inspect this file.
The chapter on trees explains how to read a tree. ROOT includes a function
TTree::MakeClass
to generate
automatically the code for a skeleton analysis function. See “Example Analysis”.
In case one of the ntuple columns has a variable length (e.g.
px(ntrack)
),
h.Draw("px")
will histogram the
px
column
for all tracks in the same histogram. Use the script quoted above to generate the skeleton function and create/fill the
relevant histogram yourself.
Chapter 3
Histograms
This chapter covers the functionality of the histogram classes. We begin with an overview of the histogram classes,
after which we provide instructions and examples on the histogram features.
We have put this chapter ahead of the graphics chapter so that you can begin working with histograms as soon as
possible. Some of the examples have graphics commands that may look unfamiliar to you. These are covered in the
chapter “Input/Output”.
3.1 The Histogram Classes
ROOT supports histograms up to three dimensions. Separate concrete classes are provided for one-dimensional,
two-dimensional and three-dimensional classes. The histogram classes are split into further categories, depending on
the set of possible bin values:
•TH1C, TH2C and TH3C contain one byte per bin (maximum bin content = 255)
•TH1S, TH2S and TH3S contain one short per bin (maximum bin content = 65 535).
•TH1I, TH2I and TH3I contain one integer per bin (maximum bin content = 2 147 483 647).
•TH1F, TH2F and TH3F contain one float per bin (maximum precision = 7 digits).
•TH1D, TH2D and TH3D contain one double per bin (maximum precision = 14 digits).
ROOT also supports profile histograms, which constitute an elegant replacement of two-dimensional histograms in
many cases. The inter-relation of two measured quantities X and Y can always be visualized with a two-dimensional
histogram or scatter-plot. Profile histograms, on the other hand, are used to display the mean value of Y and its RMS
for each bin in X. If Y is an unknown but single-valued approximate function of X, it will have greater precision in a
profile histogram than in a scatter plot.
•TProfile : one dimensional profiles
•TProfile2D : two dimensional profiles
All ROOT histogram classes are derived from the base class
TH1
(see figure above). This means that two-dimensional
and three-dimensional histograms are seen as a type of a one-dimensional histogram, in the same way in which
multidimensional C arrays are just an abstraction of a one-dimensional contiguous block of memory.
3.2 Creating Histograms
There are several ways in which you can create a histogram object in ROOT. The straightforward method is to use
one of the several constructors provided for each concrete class in the histogram hierarchy. For more details on the
constructor parameters, see the subsection “Constant or Variable Bin Width” below. Histograms may also be created
by:
•Calling the Clone() method of an existing histogram
53
54 CHAPTER 3. HISTOGRAMS
Figure 3.1: The class hierarchy of histogram classes
•Making a projection from a 2-D or 3-D histogram
•Reading a histogram from a file (see Input/Output chapter)
// using various constructors
TH1* h1 = new TH1I("h1","h1 title",100,0.0,4.0);
TH2* h2 = new TH2F("h2","h2 title",40,0.0,2.0,30, -1.5,3.5);
TH3* h3 = new TH3D("h3","h3 title",80,0.0,1.0,100, -2.0,2.0,
50,0.0,3.0);
// cloning a histogram
TH1* hc = (TH1*)h1->Clone();
// projecting histograms
// the projections always contain double values !
TH1* hx = h2->ProjectionX(); // ! TH1D, not TH1F
TH1* hy = h2->ProjectionY(); // ! TH1D, not TH1F
3.2.1 Constant or Variable Bin Width
The histogram classes provide a variety of ways to construct a histogram, but the most common way is to provide the
name and title of histogram and for each dimension: the number of bins, the minimum x (lower edge of the first bin)
and the maximum x (upper edge of the last bin).
TH2* h = new TH2D(
/* name */ "h2",
/* title */ "Hist with constant bin width",
/* X-dimension */ 100,0.0,4.0,
/* Y-dimension */ 200, -3.0,1.5);
When employing this constructor, you will create a histogram with constant (fixed) bin width on each axis. For the
example above, the interval
[0.0, 4.0]
is divided into 100 bins of the same width
w X = 4.0 - 0.0 100 = 0.04
for
the X axis (dimension). Likewise, for the Y axis (dimension), we have bins of equal width
w Y = 1.5 - (-3.0) 200 =
0.0225.
If you want to create histograms with variable bin widths, ROOT provides another constructor suited for this purpose.
Instead of passing the data interval and the number of bins, you have to pass an array (single or double precision) of
bin edges. When the histogram has
n
bins, then there are
n+1
distinct edges, so the array you pass must be of size
n+1
.
const Int_t NBINS = 5;
Double_t edges[NBINS + 1]={0.0,0.2,0.3,0.6,0.8,1.0};
// Bin 1 corresponds to range [0.0, 0.2]
// Bin 2 corresponds to range [0.2, 0.3] etc...
TH1* h = new TH1D(
/* name */ "h1",
3.3. BIN NUMBERING 55
/* title */ "Hist with variable bin width",
/* number of bins */ NBINS,
/* edge array */ edges
);
Each histogram object contains three
TAxis
objects:
fXaxis
,
fYaxis,
and
fZaxis
, but for one-dimensional histograms
only the X-axis is relevant, while for two-dimensional histograms the X-axis and Y-axis are relevant. See the class
TAxis for a description of all the access methods. The bin edges are always stored internally in double precision.
You can examine the actual edges / limits of the histogram bins by accessing the axis parameters, like in the example
below:
const Int_t XBINS = 5;const Int_t YBINS = 5;
Double_t xEdges[XBINS + 1]={0.0,0.2,0.3,0.6,0.8,1.0};
Double_t yEdges[YBINS + 1] = {-1.0, -0.4, -0.2,0.5,0.7,1.0};
TH2* h = new TH2D("h2","h2", XBINS, xEdges, YBINS, yEdges);
TAxis* xAxis = h->GetXaxis(); TAxis* yAxis = h->GetYaxis();
cout << "Third bin on Y-dimension: " << endl; // corresponds to
// [-0.2, 0.5]
cout << "\tLower edge: " << yAxis->GetBinLowEdge(3) << endl;
cout << "\tCenter: " << yAxis->GetBinCenter(3) << endl;
cout << "\tUpper edge: " << yAxis->GetBinUpEdge(3) << endl;
3.3 Bin Numbering
All histogram types support fixed or variable bin sizes. 2-D histograms may have fixed size bins along X and variable
size bins along Y or vice-versa. The functions to fill, manipulate, draw, or access histograms are identical in both cases.
3.3.1 Convention
For all histogram types: nbins ,xlow ,xup
Bin# 0 contains the underflow.
Bin# 1 contains the first bin with low-edge ( xlow INCLUDED).
The second to last bin (bin# nbins) contains the upper-edge (xup EXCLUDED).
The Last bin (bin# nbins+1) contains the overflow.
In case of 2-D or 3-D histograms, a “global bin” number is defined. For example, assuming a 3-D histogram
h
with
binx,biny,binz, the function returns a global/linear bin number.
Int_t bin = h->GetBin(binx, biny, binz);
This global bin is useful to access the bin information independently of the dimension.
3.3.2 Re-binning
At any time, a histogram can be re-binned via the
TH1::Rebin()
method. It returns a new histogram with the
re-binned contents. If bin errors were stored, they are recomputed during the re-binning.
3.4 Filling Histograms
A histogram is typically filled with statements like:
56 CHAPTER 3. HISTOGRAMS
h1->Fill(x);
h1->Fill(x,w); // with weight
h2->Fill(x,y);
h2->Fill(x,y,w);
h3->Fill(x,y,z);
h3->Fill(x,y,z,w);
The
Fill
method computes the bin number corresponding to the given x, y or z argument and increments this bin by
the given weight. The
Fill()
method returns the bin number for 1-D histograms or global bin number for 2-D and
3-D histograms. If
TH1::Sumw2()
has been called before filling, the sum of squares is also stored. One can increment a
bin number directly by calling
TH1::AddBinContent()
, replace the existing content via
TH1::SetBinContent()
, and
access the bin content of a given bin via TH1::GetBinContent() .
Double_t binContent = h->GetBinContent(bin);
3.4.1 Automatic Re-binning Option
By default, the number of bins is computed using the range of the axis. You can change this to re-bin automatically by
setting the automatic re-binning option:
h->SetBit(TH1::kCanRebin);
Once this is set, the
Fill()
method will automatically extend the axis range to accommodate the new value specified
in the
Fill()
argument. The used method is to double the bin size until the new value fits in the range, merging bins
two by two. The
TTree::Draw()
method extensively uses this automatic binning option when drawing histograms of
variables in
TTree
with an unknown range. The automatic binning option is supported for 1-D, 2-D and 3-D histograms.
During filling, some statistics parameters are incremented to compute the mean value and root mean square with the
maximum precision. In case of histograms of type
TH1C
,
TH1S
,
TH2C
,
TH2S
,
TH3C
,
TH3S
a check is made that the bin
contents do not exceed the maximum positive capacity (127 or 65 535). Histograms of all types may have positive
or/and negative bin contents.
3.5 Random Numbers and Histograms
TH1::FillRandom()
can be used to randomly fill a histogram using the contents of an existing
TF1
function or another
TH1
histogram (for all dimensions). For example, the following two statements create and fill a histogram 10 000 times
with a default Gaussian distribution of mean 0 and sigma 1 :
root[] TH1F h1("h1","Histo from a Gaussian",100,-3,3);
root[] h1.FillRandom("gaus",10000);
TH1::GetRandom()
can be used to get a random number distributed according the contents of a histogram. To fill a
histogram following the distribution in an existing histogram you can use the second signature of
TH1::FillRandom()
.
Next code snipped assumes that his an existing histogram (TH1 ).
root[] TH1F h2("h2","Histo from existing histo",100,-3,3);
root[] h2.FillRandom(&h1, 1000);
The distribution contained in the histogram
h1
(
TH1
) is integrated over the channel contents. It is normalized to one.
The second parameter (1000) indicates how many random numbers are generated.
Getting 1 random number implies:
•Generating a random number between 0 and 1 (say r1 )
•Find the bin in the normalized integral for r1
•Fill histogram channel
You can see below an example of the
TH1::GetRandom()
method which can be used to get a random number distributed
according the contents of a histogram.
3.6. ADDING, DIVIDING, AND MULTIPLYING 57
void getrandomh() {
TH1F *source = new TH1F("source","source hist",100,-3,3);
source->FillRandom("gaus",1000);
TH1F *final =new TH1F("final","final hist",100,-3,3);
// continued...
for (Int_t i=0;i<10000;i++) {
final->Fill(source->GetRandom());
}
TCanvas *c1 = new TCanvas("c1","c1",800,1000);
c1->Divide(1,2);
c1->cd(1);
source->Draw();
c1->cd(2);
final->Draw();
c1->cd();
}
3.6 Adding, Dividing, and Multiplying
Many types of operations are supported on histograms or between histograms:
•Addition of a histogram to the current histogram
•Additions of two histograms with coefficients and storage into the current histogram
•Multiplications and divisions are supported in the same way as additions.
•The Add ,Divide and Multiply methods also exist to add, divide or multiply a histogram by a function.
Histograms objects (not pointers) TH1F h1 can be multiplied by a constant using:
h1.Scale(const)
A new histogram can be created without changing the original one by doing:
TH1F h3 = 8*h1;
To multiply two histogram objects and put the result in a 3rd one do:
TH1F h3 = h1*h2;
The same operations can be done with histogram pointers TH1F *h1,*h2 following way:
h1->Scale(const) TH1F h3 = 8*(*h1); TH1F h3 = (*h1)*(*h2);
Of course, the TH1 methods Add ,Multiply and Divide can be used instead of these operators.
If a histogram has associated error bars (
TH1::Sumw2()
has been called), the resulting error bars are also computed
assuming independent histograms. In case of divisions, binomial errors are also supported.
3.7 Projections
One can make:
•
a 1-D projection of a 2-D histogram or profile. See
TH2::ProfileX
,
TH2::ProfileY,TProfile::ProjectionX
,
TProfile2D::ProjectionXY,TH2::ProjectionX,TH2::ProjectionY .
•a 1-D, 2-D or profile out of a 3-D histogram see TH3::ProjectionZ,TH3::Project3D.
These projections can be fit via: TH2::FitSlicesX,TH2::FitSlicesY,TH3::FitSlicesZ.
58 CHAPTER 3. HISTOGRAMS
3.8 Drawing Histograms
When you call the
Draw
method of a histogram (
TH1::Draw
) for the first time, it creates a
THistPainter
object and
saves a pointer to painter as a data member of the histogram. The
THistPainter
class specializes in the drawing of
histograms. It allows logarithmic axes (x, y, z) when the CONT drawing option is using. The
THistPainter
class is
separated from the histogram so that one can have histograms without the graphics overhead, for example in a batch
program. The choice to give each histogram has its own painter rather than a central singleton painter, allows two
histograms to be drawn in two threads without overwriting the painter’s values. When a displayed histogram is filled
again, you do not have to call the
Draw
method again. The image is refreshed the next time the pad is updated. A pad
is updated after one of these three actions:
•A carriage control on the ROOT command line
•A click inside the pad
•A call to TPad::Update()
By default, the
TH1::Draw
clears the pad before drawing the new image of the histogram. You can use the
"SAME"
option to leave thevprevious display in tact and superimpose the new histogram. The same histogram can be drawn
with different graphics options in different pads. When a displayed histogram is deleted, its image is automatically
removed from the pad. To create a copy of the histogram when drawing it, you can use
TH1::DrawClone()
. This will
clone the histogram and allow you to change and delete the original one without affecting the clone. You can use
TH1::DrawNormalized() to draw a normalized copy of a histogram.
TH1 *TH1::DrawNormalized(Option_t *option,Double_t norm) const
A clone of this histogram is normalized to norm and drawn with option. A pointer to the normalized histogram is
returned. The contents of the histogram copy are scaled such that the new sum of weights (excluding under and
overflow) is equal to norm .
Note that the returned normalized histogram is not added to the list of histograms in the current directory in memory.
It is the user’s responsibility to delete this histogram. The
kCanDelete
bit is set for the returned object. If a pad
containing this copy is cleared, the histogram will be automatically deleted. See “Draw Options” for the list of options.
3.8.1 Setting the Style
Histograms use the current style
gStyle
, which is the global object of class
TStyle
. To change the current style for
histograms, the
TStyle
class provides a multitude of methods ranging from setting the fill color to the axis tick marks.
Here are a few examples:
void SetHistFillColor(Color_t color = 1)
void SetHistFillStyle(Style_t styl = 0)
void SetHistLineColor(Color_t color = 1)
void SetHistLineStyle(Style_t styl = 0)
void SetHistLineWidth(Width_t width = 1)
When you change the current style and would like to propagate the change to a previously created histogram you can
call
TH1::UseCurrentStyle()
. You will need to call
UseCurrentStyle()
on each histogram. When reading many
histograms from a file and you wish to update them to the current style, you can use
gROOT ::ForceStyle
and all
histograms read after this call will be updated to use the current style. See “Graphics and the Graphical User Interface”.
When a histogram is automatically created as a result of a
TTree::Draw
, the style of the histogram is inherited from
the tree attributes and the current style is ignored. The tree attributes are the ones set in the current
TStyle
at the time
the tree was created. You can change the existing tree to use the current style, by calling
TTree::UseCurrentStyle()
.
3.8.2 Draw Options
The following draw options are supported on all histogram classes:
•“AXIS”: Draw only the axis.
3.8. DRAWING HISTOGRAMS 59
•
“
HIST
”: When a histogram has errors, it is visualized by default with error bars. To visualize it without errors
use HIST together with the required option (e.g. “HIST SAME C”).
•“SAME”: Superimpose on previous picture in the same pad.
•“CYL”: Use cylindrical coordinates.
•“POL”: Use polar coordinates.
•“SPH”: Use spherical coordinates.
•“PSR”: Use pseudo-rapidity/phi coordinates.
•“LEGO”: Draw a lego plot with hidden line removal.
•“LEGO1”: Draw a lego plot with hidden surface removal.
•“LEGO2”: Draw a lego plot using colors to show the cell contents.
•“SURF”: Draw a surface plot with hidden line removal.
•“SURF1”: Draw a surface plot with hidden surface removal.
•“SURF2”: Draw a surface plot using colors to show the cell contents.
•“SURF3”: Same as SURF with a contour view on the top.
•“SURF4”: Draw a surface plot using Gouraud shading.
•“SURF5”: Same as SURF3 but only the colored contour is drawn. Used with option CYL ,SPH or PSR it allows to
draw colored contours on a sphere, a cylinder or in a pseudo rapidly space. In Cartesian or polar coordinates,
option SURF3 is used.
The following options are supported for 1-D histogram classes:
•“AH”: Draw the histogram, but not the axis labels and tick marks
•“B”: Draw a bar chart
•“C”: Draw a smooth curve through the histogram bins
•“E”: Draw the error bars
•“E0”: Draw the error bars including bins with 0 contents
•“E1”: Draw the error bars with perpendicular lines at the edges
•“E2”: Draw the error bars with rectangles
•“E3”: Draw a fill area through the end points of the vertical error bars
•“E4”: Draw a smoothed filled area through the end points of the error bars
•“L”: Draw a line through the bin contents
•“P”: Draw a (poly)marker at each bin using the histogram’s current marker style
•“P0”: Draw current marker at each bin including empty bins
•“PIE”: Draw a Pie Chart
•“*H”: Draw histogram with a * at each bin
•
“
LF2
”: Draw histogram as with option “
L
” but with a fill area. Note that “
L
” also draws a fill area if the histogram
fill color is set but the fill area corresponds to the histogram contour.
•
“
9
”: Force histogram to be drawn in high resolution mode. By default, the histogram is drawn in low resolution
in case the number of bins is greater than the number of pixels in the current pad
•
“
][
”: Draw histogram without the vertical lines for the first and the last bin. Use it when superposing many
histograms on the same picture.
The following options are supported for 2-D histogram classes:
60 CHAPTER 3. HISTOGRAMS
•“ARR”: Arrow mode. Shows gradient between adjacent cells
•“BOX”: Draw a box for each cell with surface proportional to contents
•“BOX1”: A sunken button is drawn for negative values, a raised one for positive values
•“COL”: Draw a box for each cell with a color scale varying with contents
•“COLZ”: Same as “COL” with a drawn color palette
•“CONT”: Draw a contour plot (same as CONT0 )
•“CONTZ”: Same as “CONT” with a drawn color palette
•“CONT0”: Draw a contour plot using surface colors to distinguish contours
•“CONT1”: Draw a contour plot using line styles to distinguish contours
•“CONT2”: Draw a contour plot using the same line style for all contours
•“CONT3”: Draw a contour plot using fill area colors
•“CONT4”: Draw a contour plot using surface colors (SURF2 option at theta = 0)
•"CONT5": Use Delaunay triangles to compute the contours
•“LIST”: Generate a list of TGraph objects for each contour
•“FB”: To be used with LEGO or SURFACE , suppress the Front-Box
•“BB”: To be used with LEGO or SURFACE , suppress the Back-Box
•“A”: To be used with LEGO or SURFACE , suppress the axis
•“SCAT”: Draw a scatter-plot (default)
•“SPEC”: Use TSpectrum2Painter tool for drawing
•“TEXT”: Draw bin contents as text (format set via gStyle->SetPaintTextFormat) .
•“TEXTnn”: Draw bin contents as text at angle nn (0<nn<90 ).
•“[cutg]”: Draw only the sub-range selected by the TCutG name “cutg”.
•
“
Z
”: The “
Z
” option can be specified with the options:
BOX
,
COL
,
CONT
,
SURF
, and
LEGO
to display the color palette
with an axis indicating the value of the corresponding color on the right side ofthe picture.
The following options are supported for 3-D histogram classes:
•" " : Draw a 3D scatter plot.
•“BOX”: Draw a box for each cell with volume proportional to contents
•“LEGO”: Same as “BOX”
•“ISO”: Draw an iso surface
•“FB”: Suppress the Front-Box
•“BB”: Suppress the Back-Box
•“A”: Suppress the axis
Most options can be concatenated without spaces or commas, for example, if his a histogram pointer:
h->Draw("E1SAME");
h->Draw("e1same");
The options are not case sensitive. The options
BOX
,
COL
and
COLZ
use the color palette defined in the current style
(see
TStyle::SetPalette
). The options
CONT
,
SURF
, and
LEGO
have by default 20 equidistant contour levels, you can
change the number of levels with
TH1::SetContour
. You can also set the default drawing option with
TH1::SetOption
. To see the current option use TH1::GetOption . For example:
h->SetOption("lego");
h->Draw(); // will use the lego option
h->Draw("scat")// will use the scatter plot option
3.8. DRAWING HISTOGRAMS 61
3.8.2.1 The SCATter Plot Option
By default, 2D histograms are drawn as scatter plots. For each cell
(i,j)
a number of points proportional to the cell
content are drawn. A maximum of 500 points per cell are drawn. If the maximum is above 500 contents are normalized
to 500.
3.8.2.2 The ARRow Option
The
ARR
option shows the gradient between adjacent cells. For each cell
(i,j)
an arrow is drawn. The orientation of
the arrow follows the cell gradient.
3.8.2.3 The BOX Option
For each cell
(i,j)
a box is drawn with surface proportional to contents. The size of the box is proportional to the
absolute value of the cell contents. The cells with negative contents are drawn with an X on top of the boxes. With
option
BOX1
a button is drawn for each cell with surface proportional to contents’ absolute value. A sunken button is
drawn for negative values, a raised one for positive values.
3.8.2.4 The ERRor Bars Options
•"E" Default. Draw only error bars, without markers
•"E0" Draw also bins with 0 contents (turn off the symbols clipping).
•"E1" Draw small lines at the end of error bars
•"E2" Draw error rectangles
•"E3" Draw a fill area through the end points of vertical error bars
•"E4" Draw a smoothed filled area through the end points of error bars
Note that for all options, the line and fill attributes of the histogram are used for the errors or errors contours. Use
gStyle->SetErrorX(dx)
to control the size of the error along x. The parameter
dx
is a percentage of bin width for
errors along X. Set dx=0 to suppress the error along X. Use gStyle->SetEndErrorSize(np) to control the size of the
lines at the end of the error bars (when option 1 is used). By default np=1 (np represents the number of pixels).
3.8.2.5 The Color Option
For each cell
(i,j)
a box is drawn with a color proportional to the cell content. The color table used is defined in the
current style (gStyle ). The color palette in TStyle can be modified with TStyle::SetPalette .
3.8.2.6 The TEXT Option
For each cell (i,j) the cell content is printed. The text attributes are:
•Text font = current font set by TStyle
•Text size= 0.02 * pad-height * marker-size
•Text color= marker color
62 CHAPTER 3. HISTOGRAMS
Figure 3.2: The “E1” bars’ option
3.8.2.7 The CONTour Options
The following contour options are supported:
•"CONT": Draw a contour plot (same as CONT0)
•"CONT0": Draw a contour plot using surface colors to distinguish contours
•"CONT1": Draw a contour plot using line styles to distinguish contours
•"CONT2": Draw a contour plot using the same line style for all contours
•"CONT3": Draw a contour plot using fill area colors
•"CONT4":
Draw a contour plot using surface colors (SURF2 option at theta = 0); see also options “
AITOFF
”,
“MERCATOR”, etc. below
•"CONT5": Use Delaunay triangles to compute the contours
The default number of contour levels is 20 equidistant levels. It can be changed with
TH1::SetContour
. When option
“
LIST
” is specified together with option “
CONT
”, all points used for contour drawing, are saved in the
TGraph
object
and are accessible in the following way:
TObjArray *contours =
gROOT->GetListOfSpecials()->FindObject("contours");
Int_t ncontours = contours->GetSize(); TList *list =
(TList*)contours->At(i);
Where “
i
” is a contour number and list contains a list of
TGraph
objects. For one given contour, more than one disjoint
poly-line may be generated. The
TGraph
numbers per contour are given by
list->GetSize()
. Here we show how to
access the first graph in the list.
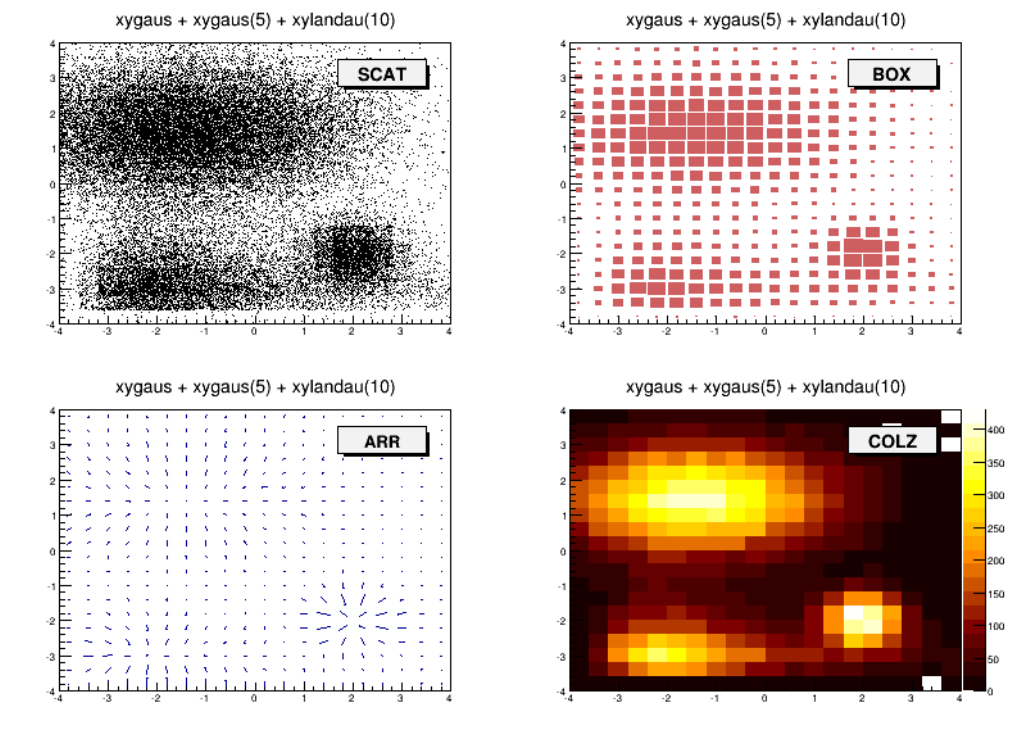
3.8. DRAWING HISTOGRAMS 63
Figure 3.3: Different draw options

64 CHAPTER 3. HISTOGRAMS
Figure 3.4: The TEXT option
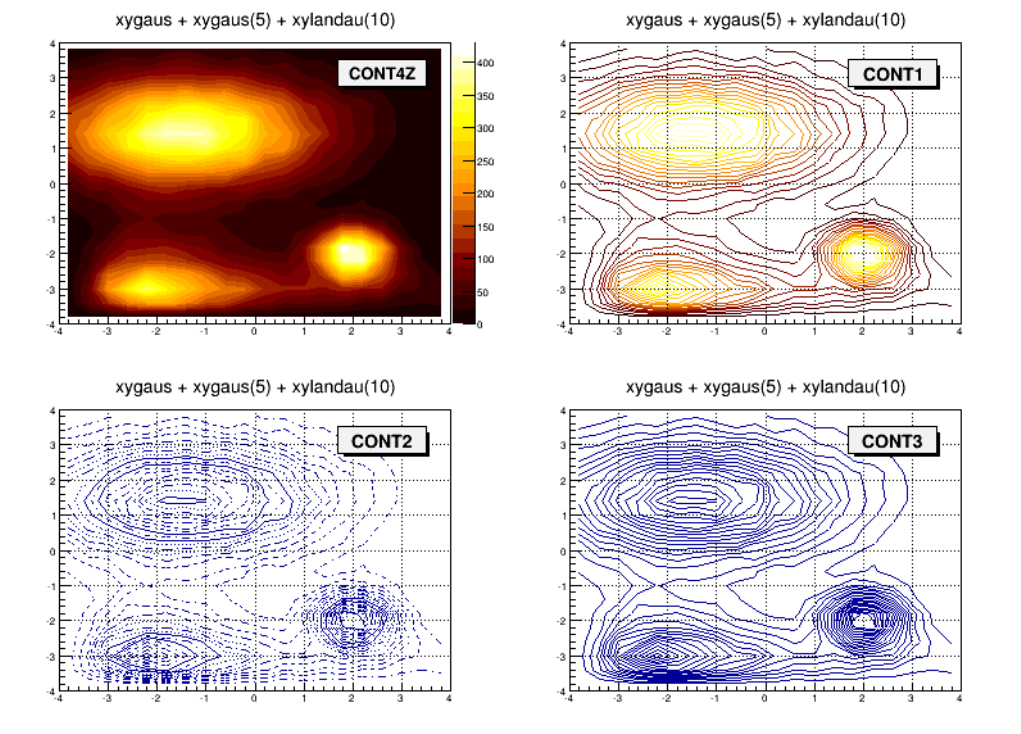
3.8. DRAWING HISTOGRAMS 65
Figure 3.5: Different contour options
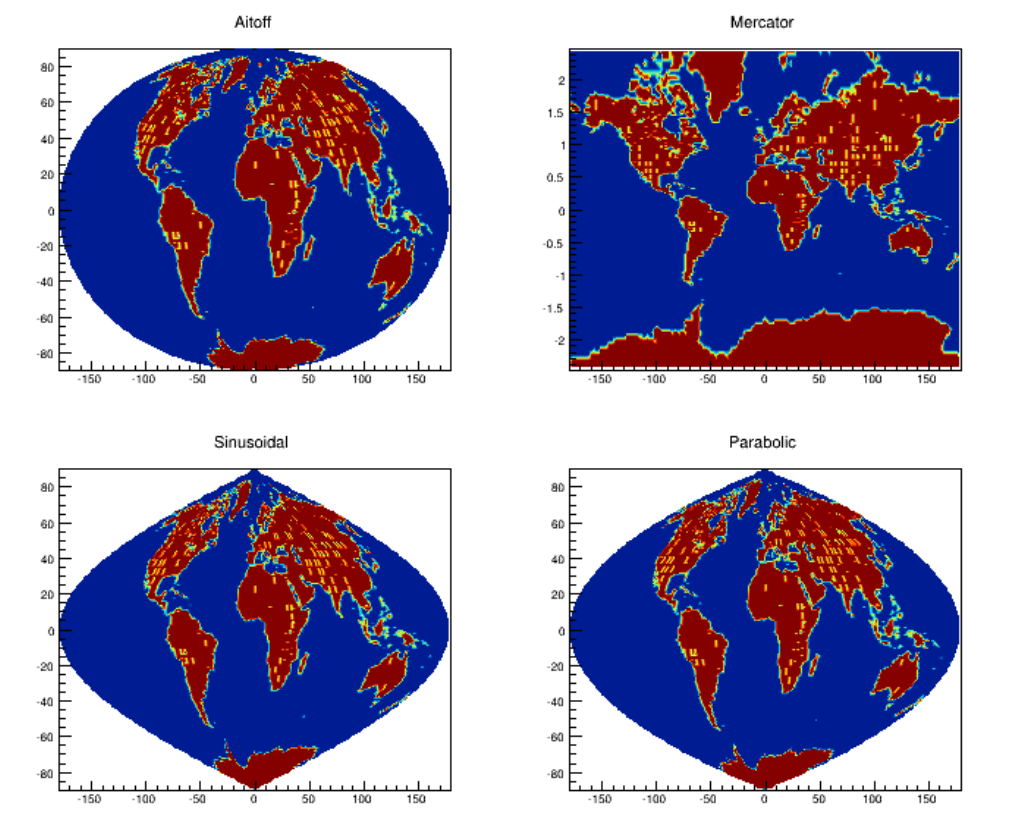
66 CHAPTER 3. HISTOGRAMS
TGraph *gr1 = (TGraph*)list->First();
•“AITOFF”: Draw a contour via an AITOFF projection
•“MERCATOR”: Draw a contour via a Mercator projection
•“SINUSOIDAL”: Draw a contour via a Sinusoidal projection
•“PARABOLIC”: Draw a contour via a Parabolic projection
The tutorial macro earth.C uses these four options and produces the following picture:
Figure 3.6: The earth.C macro output
3.8.2.8 The LEGO Options
In a lego plot, the cell contents are drawn as 3D boxes, with the height of the box proportional to the cell content.
•“LEGO”: Draw a lego plot with hidden line removal
•“LEGO1”: Draw a lego plot with hidden surface removal
•“LEGO2”: Draw a lego plot using colors to show the cell contents
A lego plot can be represented in several coordinate systems; the default system is Cartesian coordinates. Other
possible coordinate systems are CYL ,POL ,SPH , and PSR .
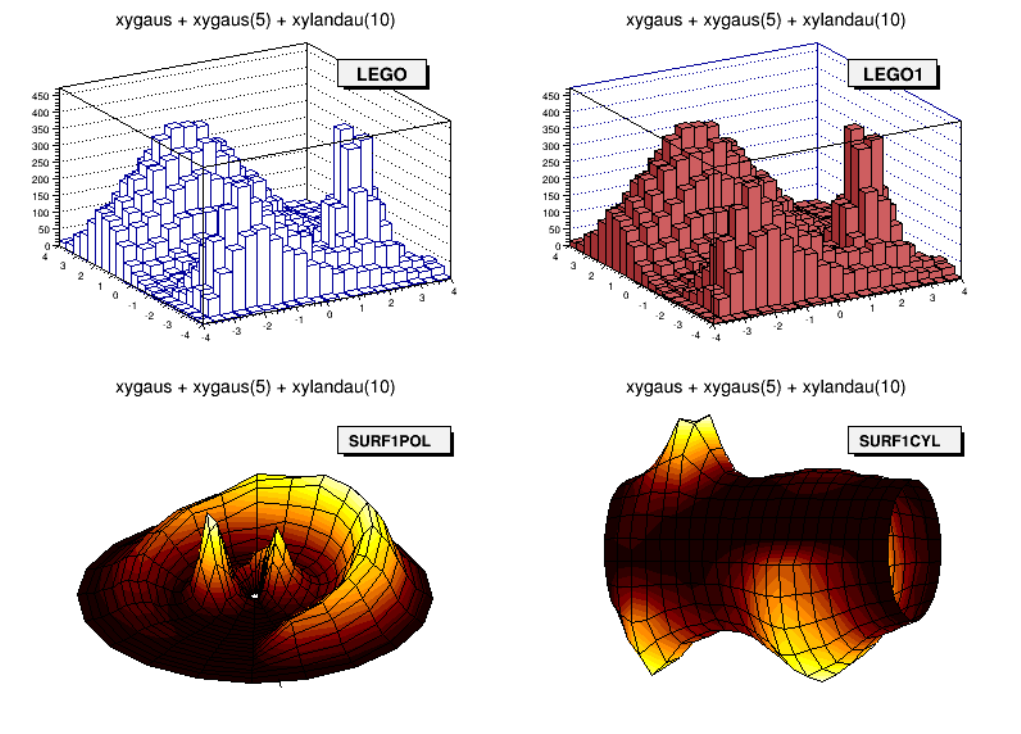
3.8. DRAWING HISTOGRAMS 67
Figure 3.7: “LEGO” and “SURF” options
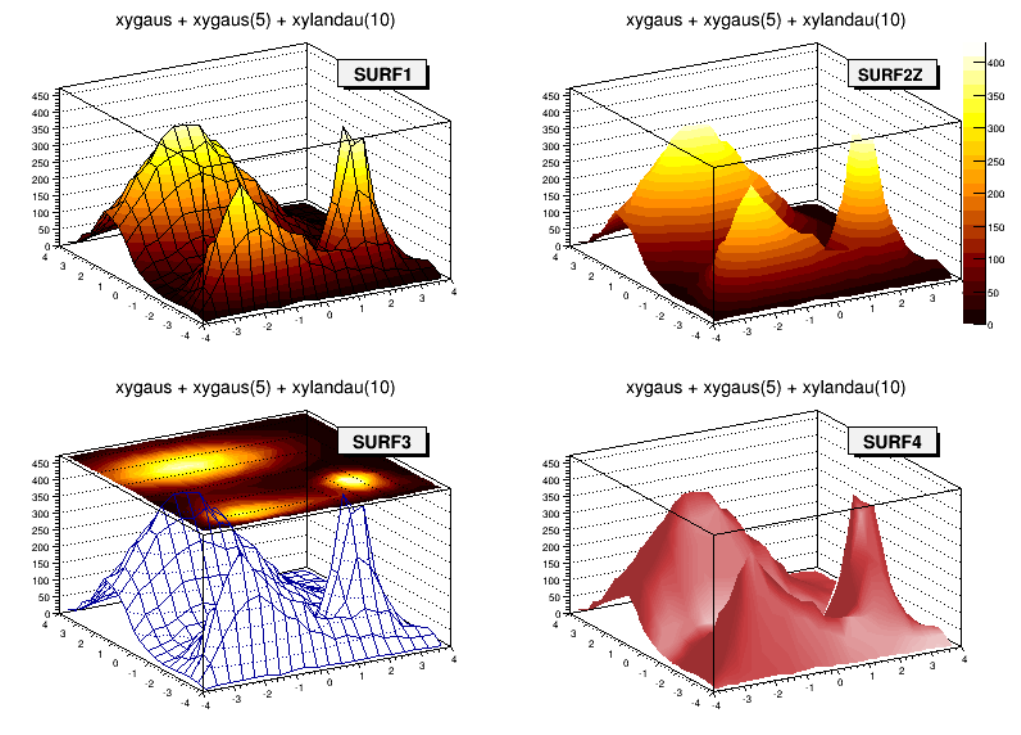
68 CHAPTER 3. HISTOGRAMS
•“CYL”: Cylindrical coordinates: x-coordinate is mapped on the angle; y-coordinate - on the cylinder length.
•“POL”: Polar coordinates: x-coordinate is mapped on the angle; y-coordinate - on the radius.
•“SPH”: Spherical coordinates: x-coordinate is mapped on the latitude; y-coordinate - on the longitude.
•“PSR”: PseudoRapidity/Phi coordinates: x-coordinate is mapped on Phi.
With TStyle::SetPalette the color palette can be changed. We suggest you use palette 1 with the call:
gStyle->SetPalette(1);
3.8.2.9 The SURFace Options
In a surface plot, cell contents are represented as a mesh. The height of the mesh is proportional to the cell content. A
surface plot can be represented in several coordinate systems. The default is Cartesian coordinates, and the other
possible systems are
CYL
,
POL
,
SPH
, and
PSR
. The following picture uses
SURF1
. With
TStyle::SetPalette
the color
palette can be changed. We suggest you use palette 1 with the call:
gStyle->SetPalette(1);
Figure 3.8: Different surface options
•“SURF”: Draw a surface plot with hidden line removal
•“SURF1”: Draw a surface plot with hidden surface removal
•“SURF2”: Draw a surface plot using colors to show the cell contents
•“SURF3”: Same as SURF with a contour view on the top
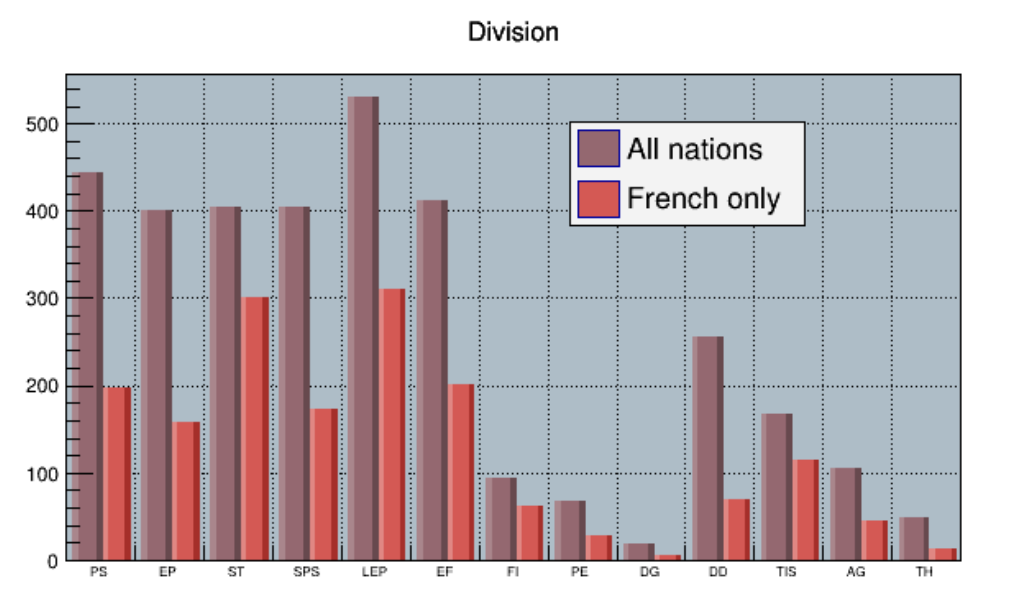
3.8. DRAWING HISTOGRAMS 69
•“SURF4”: Draw a surface plot using Gouraud shading
•
“
SURF5
”: Same as
SURF3
but only the colored contour is drawn. Used with options
CYL
,
SPH
or
PSR
it allows to
draw colored contours on a sphere, a cylinder or in a pseudo rapidly space. In Cartesian or polar coordinates,
option SURF3 is used.
3.8.2.10 The BAR Options
When the option “bar” or “hbar” is specified, a bar chart is drawn.
The options for vertical bar chart are “bar”, “bar0”, “bar1”, “bar2”, “bar3”, “bar4”.
Figure 3.9: Vertical bar charts
•The bar is filled with the histogram fill color.
•The left side of the bar is drawn with a light fill color.
•The right side of the bar is drawn with a dark fill color.
•The percentage of the bar drawn with either the light or dark color is:
–0 per cent for option "bar" or "bar0"
–10 per cent for option "bar1"
–20 per cent for option "bar2"
–30 per cent for option "bar3"
–40 per cent for option "bar4"
Use
TH1::SetBarWidth()
to control the bar width (default is the bin width). Use
TH1::SetBarOffset
to control the
bar offset (default is 0). See the example $ROOTSYS/tutorials/hist/hbars.C
The options for the horizontal bar chart are “hbar”, “hbar0”, “hbar1”, “hbar2”, “hbar3”, and “hbar4”.
•A horizontal bar is drawn for each bin.
•The bar is filled with the histogram fill color.
•The bottom side of the bar is drawn with a light fill color.
•The top side of the bar is drawn with a dark fill color.
•The percentage of the bar drawn with either the light or dark color is:
–0 per cent for option “hbar” or “hbar0”
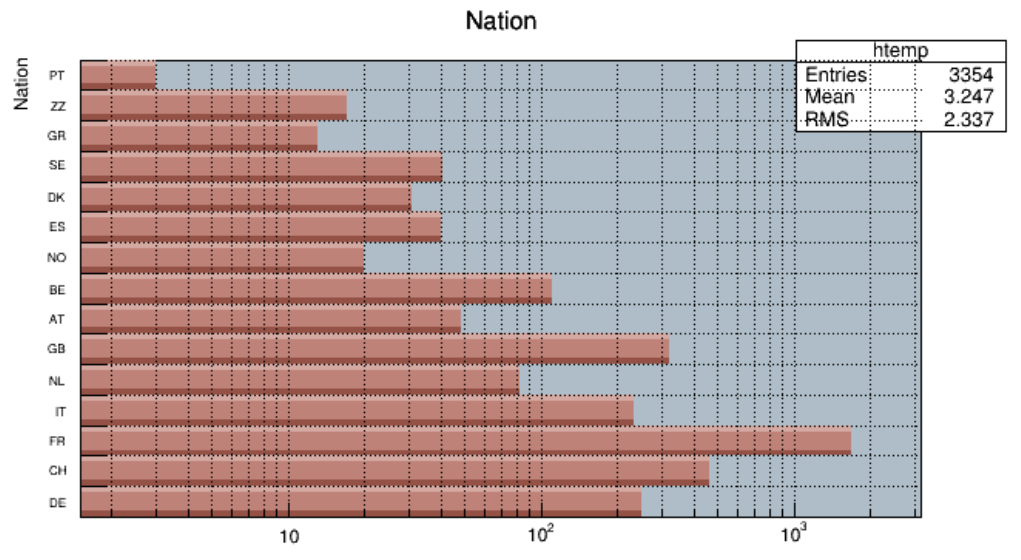
70 CHAPTER 3. HISTOGRAMS
–10 per cent for option “hbar1”
–20 per cent for option “hbar2”
–30 per cent for option “hbar3”
–40 per cent for option “hbar4”
Use
TH1::SetBarWidth
to control the bar width (default is the bin width). Use
TH1::SetBarOffset
to control the
bar offset (default is 0). See the example $ROOTSYS/tutorials/hist/hbars.C
Figure 3.10: Horizontal bar charts
3.8.2.11 The Z Option: Display the Color Palette on the Pad
The “
Z
” option can be specified with the options:
COL
,
CONT
,
SURF
, and
LEGO
to display the color palette with an axis
indicating the value of the corresponding color on the right side of the picture. If there is not enough space on the right
side, you can increase the size of the right margin by calling
TPad::SetRightMargin()
. The attributes used to display
the palette axis values are taken from the Z axis of the object. For example, you can set the labels size on the palette
axis with:
hist->GetZaxis()->SetLabelSize();
3.8.2.12 Setting the Color Palette
You can set the color palette with TStyle::SetPalette , e.g.
gStyle->SetPalette(ncolors,colors);
For example, the option
COL
draws a 2-D histogram with cells represented by a box filled with a color index, which is a
function of the cell content. If the cell content is N, the color index used will be the color number in
colors[N]
. If
the maximum cell content is greater than ncolors , all cell contents are scaled to ncolors. If ncolors<=0, a default
palette of 50 colors is defined. This palette is recommended for pads, labels. It defines:
•Index 0 to 9: shades of gray
•Index 10 to 19:shades of brown
•Index 20 to 29:shades of blue
•Index 30 to 39: shades of red
3.8. DRAWING HISTOGRAMS 71
•Index 40 to 49:basic colors
The color numbers specified in this palette can be viewed by selecting the menu entry Colors in the View menu of the
canvas menu bar. The color’s red, green, and blue values can be changed via TColor::SetRGB.
If
ncolors == 1 && colors == 0
, then a Pretty Palette with a spectrum violet to red is created with 50 colors.
That’s the default rain bow palette.
Other prefined palettes with 255 colors are available when
colors == 0
. The following value of
ncolors
(with
colors
= 0) give access to:
•ncolors = 51 : Deep Sea palette.
•ncolors = 52 : Grey Scale palette.
•ncolors = 53 : Dark Body Radiator palette.
•ncolors = 54 : Two-color hue palette palette. (dark blue through neutral gray to bright yellow)
•ncolors = 55 : Rain Bow palette.
•ncolors = 56 : Inverted Dark Body Radiator palette.
The color numbers specified in the palette can be viewed by selecting the item “colors” in the “VIEW” menu of the
canvas toolbar. The color parameters can be changed via TColor::SetRGB.
Note that when drawing a 2D histogram
h2
with the option “
COL
” or “
COLZ
” or with any “
CONT
” options using the
color map, the number of colors used is defined by the number of contours nspecified with: h2->SetContour(n)
3.8.2.13 TPaletteAxis
ATPaletteAxisobject is used to display the color palette when drawing 2D histograms. The object is automatically
created when drawing a 2D histogram when the option “z” is specified. It is added to the histogram list of functions.
It can be retrieved and its attributes can be changed with:
TPaletteAxis *palette=(TPaletteAxis*)h->FindObject("palette");
The palette can be interactively moved and resized. The context menu can be used to set the axis attributes. It is
possible to select a range on the axis, to set the min/max in z.
3.8.2.14 The SPEC Option
The “SPEC” option offers a large set of options/attributes to visualize 2D histograms thanks to “operators” following
the “SPEC” keyword. For example, to draw the 2-D histogram
h2
using all default attributes except the viewing angles,
one can do:
h2->Draw("SPEC a(30,30,0)");
The operators’ names are case unsensitive (i.e. one can use “a” or “A”) and their parameters are seperated by coma “,”.
Operators can be put in any order in the option and must be separated by a space " “. No space characters should be
put in an operator. All the available operators are described below.
The way how a 2D histogram will be painted is controled by two parameters: the “Display modes groups” and the
“Display Modes”. “Display modes groups” can take the following values:
•0 = Simple - simple display modes using one color only
•1 = Light - the shading is carried out according to the position of the fictive light source
•2 = Height - the shading is carried out according to the channel contents
•
3 = LightHeight - combination of two previous shading algorithms (one can control the weight between both
algorithms).
“Display modes” can take the following values:
•1 = Points
•2 = Grid
72 CHAPTER 3. HISTOGRAMS
•3 = Contours
•4 = Bars
•5 = LinesX
•6 = LinesY
•7 = BarsX
•8 = BarsY
•9 = Needles
•10 = Surface
•11 = Triangles
These parameters can be set by using the “dm” operator in the option.
h2->Draw("SPEC dm(1,2)");
The above example draws the histogram using the “Light Display mode group” and the “Grid Display mode”. The
following tables summarize all the possible combinations of both groups:
Points Grid Contours Bars LinesX LinesY
Simple x x x x x x
Light x x • • x x
Height x x x x x x
LightHeight x x • • x x
BarsX BarsY Needles Surface Triangles
Simple x x x •x
Light • • • x x
Height x x •x x
LightHeight • • • x x
The “Pen Attributes” can be changed using
pa(color,style,width)
. Next example sets line color to 2, line type to 1
and line width to 2. Note that if pa() is not specified, the histogram line attributes are used:
h2->Draw("SPEC dm(1,2) pa(2,1,2)");
The number of “Nodes” can be changed with n(nodesx,nodesy). Example:
h2->Draw("SPEC n(40,40)");
Sometimes the displayed region is rather large. When displaying all channels the pictures become very dense and
complicated. It is very difficult to understand the overall shape of data. “
n(nx,ny)
” allows to change the density of
displayed channels. Only the channels coinciding with given nodes are displayed.
The visualization “Angles” can be changed with “
a(alpha,beta,view)
”: “
alpha
” is the angle between the bottom
horizontal screen line and the displayed space on the right side of the picture and “
beta
” on the left side, respectively.
One can rotate the 3-d space around the vertical axis using the “view” parameter. Allowed values are 0, 90, 180 and
270 degrees.
h2->Draw("SPEC n(40,40) dm(0,1) a(30,30,0)");
The operator “zs(scale)” changes the scale of the Z-axis. The possible values are:
•0 = Linear (default),
•1 = Log,
•2 = Sqrt.
If
gPad->SetLogz()
has been set, the log scale on Z-axis is set automatically, i.e. there is no need for using the
zs()
operator. Note that the X and Y axis are always linear.
3.8. DRAWING HISTOGRAMS 73
The operator “
ci(r,g,b
)” defines the colors increments (
r
,
g
and
b
are floats). For sophisticated shading (Light, Height
and LightHeight Display Modes Groups) the color palette starts from the basic pen color (see
pa()
function). There is
a predefined number of color levels (256). Color in every level is calculated by adding the increments of the
r
,
g
,
b
components to the previous level. Using this function one can change the color increments between two neighboring
color levels. The function does not apply on the Simple Display Modes Group. The default values are: (1,1,1).
The operator “
ca(color_algorithm)
” allows to choose the Color Algorithm. To define the colors one can use one of
the following color algorithms (RGB, CMY, CIE, YIQ, HVS models). When the level of a component reaches the limit
value one can choose either smooth transition (by decreasing the limit value) or a sharp modulo transition (continuing
with 0 value). This allows various visual effects. One can choose from the following set of the algorithms:
•0 = RGB Smooth,
•1 = RGB Modulo,
•2 = CMY Smooth,
•3 = CMY Modulo,
•4 = CIE Smooth
•5 = CIE Modulo,
•6 = YIQ Smooth,
•7 = YIQ Modulo,
•8 = HVS Smooth,
•9 = HVS Modulo
This function does not apply on Simple display modes group. Default value is 0. Example choosing CMY Modulo to
paint the 2D histogram:
h2->Draw("SPEC c1(3) dm(0,1) a(30,30,0)");
The operator “
lp(x,y,z)
” sets the light position. In Light and LightHeight display modes groups the color palette is
calculated according to the fictive light source position in 3-d space. Using this function one can change the source’s
position and thus achieve various graphical effects. This function does not apply for Simple and Height display modes
groups. Default is: lp(1000,1000,100) .
The operator “
s(shading,shadow)
” allows to set the shading. The surface picture is composed of triangles. The edges
of the neighboring triangles can be smoothed (shaded). The shadow can be painted as well. The function does not
apply on Simple display modes group. The possible values for shading are:
•0 = Not Shaded,
•1 = Shaded.
The possible values for shadow are:
•0 = Shadows are not painted,
•1 = Shadows are painted.
Default values: s(1,0) .
The operator “
b(bezier)
” sets the Bezier smoothing. For Simple display modes group and for Grid, LinesX and
LinesY display modes one can smooth data using Bezier smoothing algorithm. The function does not apply on other
display modes groups and display modes. Possible values are: 0 = No bezier smoothing, 1 = Bezier smoothing. Default
value is: b(0).
The operator “
cw(width)
” sets the contour width. This function applies only on for the Contours display mode. One
can change the width between horizontal slices and thus their density. Default value: cw(50) .
The operator “
lhw(weight)
” sets the light height weight. For LightHeight display modes group one can change the
weight between both shading algorithms. The function does not apply on other display modes groups. Default value is
lhw(0.5) .
The operator “
cm(enable,color,width,height,style)
” allows to draw a marker on each node. In addition to the
surface drawn using any above given algorithm one can display channel marks. One can control the color as well as the
width, height (in pixels) and the style of the marks. The parameter
enable
can be set to 0 = Channel marks are not
drawn or 1 = Channel marks drawn. The possible styles are:
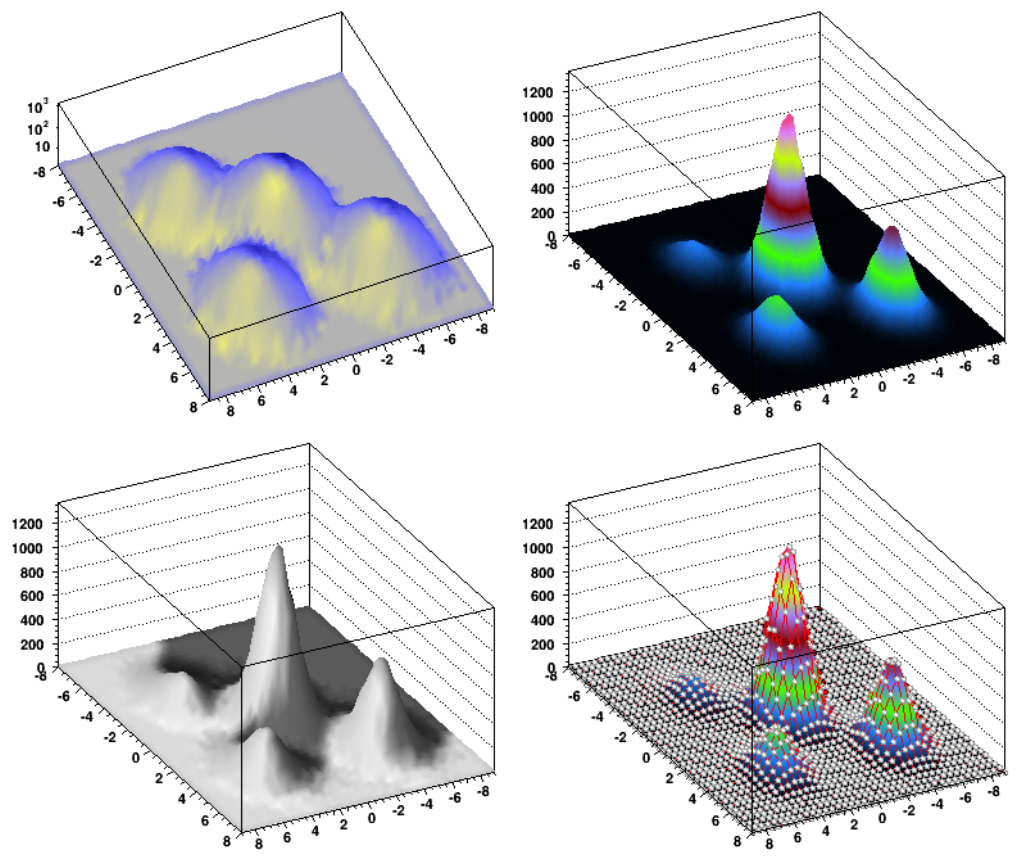
74 CHAPTER 3. HISTOGRAMS
•1 = Dot,
•2 = Cross,
•3 = Star,
•4 = Rectangle,
•5 = X,
•6 = Diamond,
•7 = Triangle.
The operator “
cg(enable,color)
” channel grid. In addition to the surface drawn using any above given algorithm
one can display grid using the color parameter. The parameter enable can be set to:
•0 = Grid not drawn,
•1 = Grid drawn.
See the example in $ROOTSYS/tutorials/spectrum/spectrumpainter.C .
Figure 3.11: The picture produced by spectrumpainter.C macro
3.8.2.15 3-D Histograms
By default a 3D scatter plot is drawn. If the “BOX” option is specified, a 3D box with a volume proportional to the
cell content is drawn.
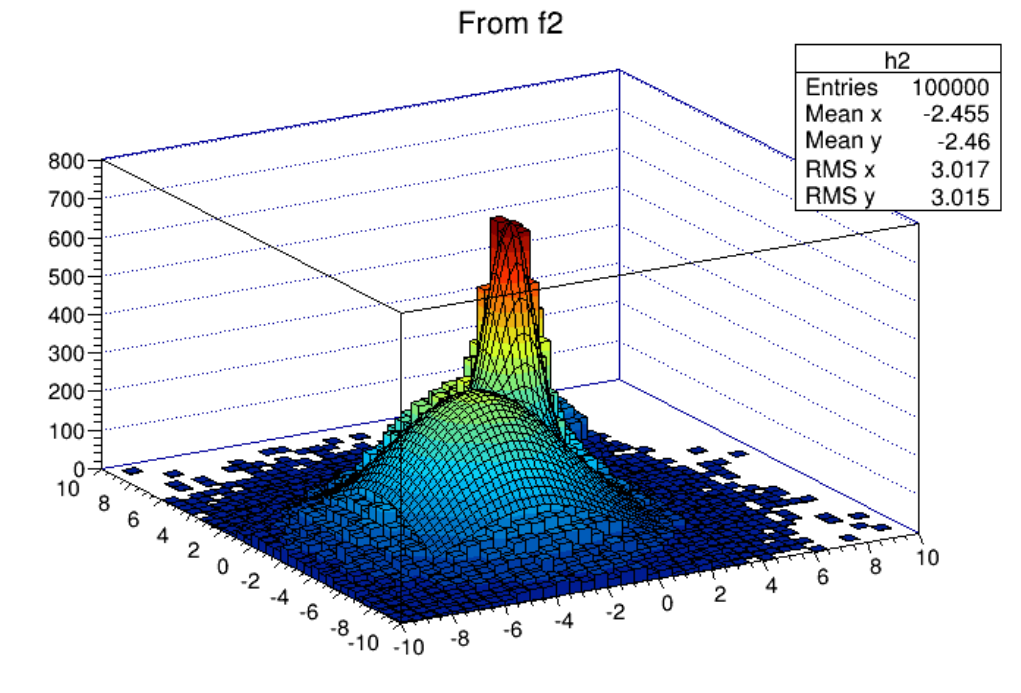
3.8. DRAWING HISTOGRAMS 75
Figure 3.12: The picture produced by fit2a.C macro
3.8.3 Drawing a Sub-range of a 2-D Histogram
Using a
TCutG
object, it is possible to draw a 2D histogram sub-range. One must create a graphical cut (mouse or
C++) and specify the name of the cut between “[” and “]” in the Draw option.
For example, with a TCutGnamed “cutg”, one can call:
myhist->Draw("surf1 [cutg]");
Or, assuming two graphical cuts with name “cut1” and “cut2”, one can do:
h1.Draw("lego");
h2.Draw("[cut1,-cut2],surf,same");
The second Draw will superimpose on top of the first lego plot a subset of h2using the “surf” option with:
•all the bins inside cut1
•all the bins outside cut2
Up to 16 cuts may be specified in the cut string delimited by
"[..]"
. Currently only the following drawing options are
sensitive to the cuts option:
col
,
box
,
scat
,
hist
,
lego
,
surf
and
cartesian
coordinates only. See a complete
example in the tutorial $ROOTSYS/tutorials/fit/fit2a.C .
3.8.4 Superimposing Histograms with Different Scales
The following script creates two histograms; the second histogram is the bins integral of the first one. It shows a
procedure to draw the two histograms in the same pad and it draws the scale of the second histogram using a new
vertical axis on the right side.
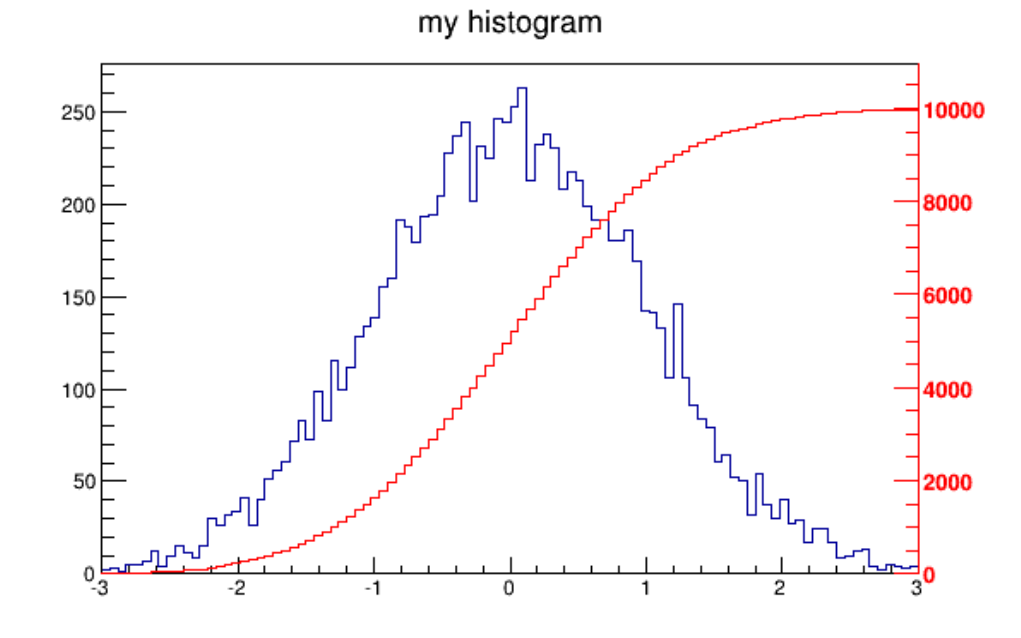
76 CHAPTER 3. HISTOGRAMS
Figure 3.13: Superimposed histograms with different scales
void twoscales() {
TCanvas *c1 = new TCanvas("c1","different scales hists",600,400);
//create, fill and draw h1
gStyle->SetOptStat(kFALSE);
TH1F *h1 = new TH1F("h1","my histogram",100,-3,3);
for (Int_t i=0;i<10000;i++) h1->Fill(gRandom->Gaus(0,1));
h1->Draw();
c1->Update();
//create hint1 filled with the bins integral of h1
TH1F *hint1 = new TH1F("hint1","h1 bins integral",100,-3,3);
Float_t sum = 0;
for (Int_t i=1;i<=100;i++) {
sum += h1->GetBinContent(i);
hint1->SetBinContent(i,sum);
}
//scale hint1 to the pad coordinates
Float_t rightmax = 1.1*hint1->GetMaximum();
Float_t scale = gPad->GetUymax()/rightmax;
hint1->SetLineColor(kRed);
hint1->Scale(scale);
hint1->Draw("same");
//draw an axis on the right side
TGaxis*axis = new TGaxis(gPad->GetUxmax(),gPad->GetUymin(),
gPad->GetUxmax(),gPad->GetUymax(),
0,rightmax,510,"+L");
axis->SetLineColor(kRed);
axis->SetLabelColor(kRed);
axis->Draw();
}
3.8. DRAWING HISTOGRAMS 77
3.8.5 Statistics Display
By default, a histogram drawing includes the statistics box. Use
TH1::SetStats(kFALSE)
to eliminate the statistics
box. If the statistics box is drawn,
gStyle->SetOptStat(mode)
allow you to select the type of displayed information
.
The parameter mode has up to nine digits that can be set OFF (0) or ON as follows:
mode = ksiourmen (default =000001111)
•n= 1 the name of histogram is printed
•e= 1 the number of entries
•m= 1 the mean value
•m= 2 the mean and mean error values
•r= 1 the root mean square (RMS)
•r= 2 the RMS and RMS error
•u= 1 the number of underflows
•o= 1 the number of overflows
•i= 1 the integral of bins
•s= 1 the skewness
•s= 2 the skewness and the skewness error
•k= 1 the kurtosis
•k= 2 the kurtosis and the kurtosis error
Never call SetOptStat(0001111) , but SetOptStat(1111) , because 0001111 will be taken as an octal number.
The method
TStyle::SetOptStat(Option_t*option)
can also be called with a character string as a parameter. The
parameter option can contain:
•nfor printing the name of histogram
•ethe number of entries
•mthe mean value
•Mthe mean and mean error values
•rthe root mean square (RMS)
•Rthe RMS and RMS error
•uthe number of underflows
•othe number of overflows
•ithe integral of bins
•sthe skewness
•Sthe skewness and the skewness error
•kthe kurtosis
•Kthe kurtosis and the kurtosis error
gStyle->SetOptStat("ne"); // prints the histogram name and number
// of entries
gStyle->SetOptStat("n"); // prints the histogram name
gStyle->SetOptStat("nemr"); // the default value
With the option
"same"
, the statistic box is not redrawn. With the option
"sames"
, it is re-drawn. If it hides the
previous statistics box, you can change its position with the next lines (where his the histogram pointer):
root[] TPaveStats *s =
(TPaveStats*)h->GetListOfFunctions()->FindObject("stats");
root[] s->SetX1NDC (newx1); // new x start position
root[] s->SetX2NDC (newx2); // new x end position
3.8.6 Setting Line, Fill, Marker, and Text Attributes
The histogram classes inherit from the attribute classes:
TAttLine
,
TAttFill
,
TAttMarker
and
TAttText
. See the
description of these classes for the list of options.
78 CHAPTER 3. HISTOGRAMS
3.8.7 Setting Tick Marks on the Axis
The
TPad::SetTicks()
method specifies the type of tick marks on the axis. Let
tx=gPad->GetTickx()
and
ty=gPad->GetTicky().
•tx = 1; tick marks on top side are drawn (inside)
•tx = 2; tick marks and labels on top side are drawn
•ty = 1; tick marks on right side are drawn (inside)
•ty = 2; tick marks and labels on right side are drawn
•tx=ty=0 by default only the left Y axis and X bottom axis are drawn
Use
TPad::SetTicks(tx,ty)
to set these options. See also the methods of
TAxis
that set specific axis attributes. If
multiple color-filled histograms are drawn on the same pad, the fill area may hide the axis tick marks. One can force
the axis redrawing over all the histograms by calling:
gPad->RedrawAxis();
3.8.8 Giving Titles to the X, Y and Z Axis
Because the axis title is an attribute of the axis, you have to get the axis first and then call TAxis::SetTitle.
h->GetXaxis()->SetTitle("X axis title");
h->GetYaxis()->SetTitle("Y axis title");
h->GetZaxis()->SetTitle("Z axis title");
The histogram title and the axis titles can be any
TLatex
string. The titles are part of the persistent histogram. For
example if you wanted to write E with a subscript (T) you could use this:
h->GetXaxis()->SetTitle("E_{T}");
For a complete explanation of the Latex mathematical expressions, see “Graphics and the Graphical User Interface”. It
is also possible to specify the histogram title and the axis titles at creation time. These titles can be given in the “title”
parameter. They must be separated by “;”:
TH1F* h=new TH1F("h","Histogram title;X Axis;Y Axis;Z Axis",
100,0,1);
Any title can be omitted:
TH1F* h=new TH1F("h","Histogram title;;Y Axis",100,0,1);
TH1F* h=new TH1F("h",";;Y Axis",100,0,1);
The method SetTitle has the same syntax:
h->SetTitle("Histogram title;An other X title Axis");
3.9 Making a Copy of an Histogram
Like for any other ROOT object derived from
TObject
, the
Clone
method can be used. This makes an identical copy
of the original histogram including all associated errors and functions:
TH1F *hnew = (TH1F*)h->Clone(); // renaming is recommended,
hnew->SetName("hnew"); // because otherwise you will have
// two histograms with the same
// name
3.10. NORMALIZING HISTOGRAMS 79
3.10 Normalizing Histograms
You can scale a histogram ( TH1 *h ) such that the bins integral is equal to the normalization parameter norm:
Double_t scale = norm/h->Integral();
h->Scale(scale);
3.11 Saving/Reading Histograms to/from a File
The following statements create a ROOT file and store a histogram on the file. Because
TH1
derives from
TNamed
, the
key identifier on the file is the histogram name:
TFile f("histos.root","new");
TH1F h1("hgaus","histo from a gaussian",100,-3,3);
h1.FillRandom("gaus",10000);
h1->Write();
To read this histogram in another ROOT session, do:
TFile f("histos.root");
TH1F *h = (TH1F*)f.Get("hgaus");
One can save all histograms in memory to the file by:
file->Write();
For a more detailed explanation, see “Input/Output”.
3.12 Miscellaneous Operations
•TH1::KolmogorovTest( TH1* h2,Option_t *option)
is statistical test of compatibility in shape between two
histograms. The parameter option is a character string that specifies:
•“U” include Underflows in test (also for 2-dim)
•“O” include Overflows (also valid for 2-dim)
•“N” include comparison of normalizations
•“D” put out a line of “Debug” printout
•“M” return the maximum Kolmogorov distance instead of prob
•
“
X
” run the pseudo experiments post-processor with the following procedure: it makes pseudo experiments based
on random values from the parent distribution and compare the KS distance of the pseudo experiment to the
parent distribution. Bin the KS distances in a histogram, and then take the integral of all the KS values above the
value obtained from the original data to Monte Carlo distribution. The number of pseudo-experiments NEXPT
is currently fixed at 1000. The function returns the integral. Note that this option “X” is much slower.
•TH1::Smooth - smoothes the bin contents of a 1D histogram.
•TH1::Integral(Option_t *opt)-
returns the integral of bin contents in a given bin range. If the option “
width
”
is specified, the integral is the sum of the bin contents multiplied by the bin width in x.
•TH1::GetMean(int axis) - returns the mean value along axis.
•TH1::GetRMS(int axis) - returns the Root Mean Square along axis.
•TH1::GetEntries() - returns the number of entries.
•TH1::GetAsymmetry(TH1 *h2,Double_t c2,Double_tdc2)
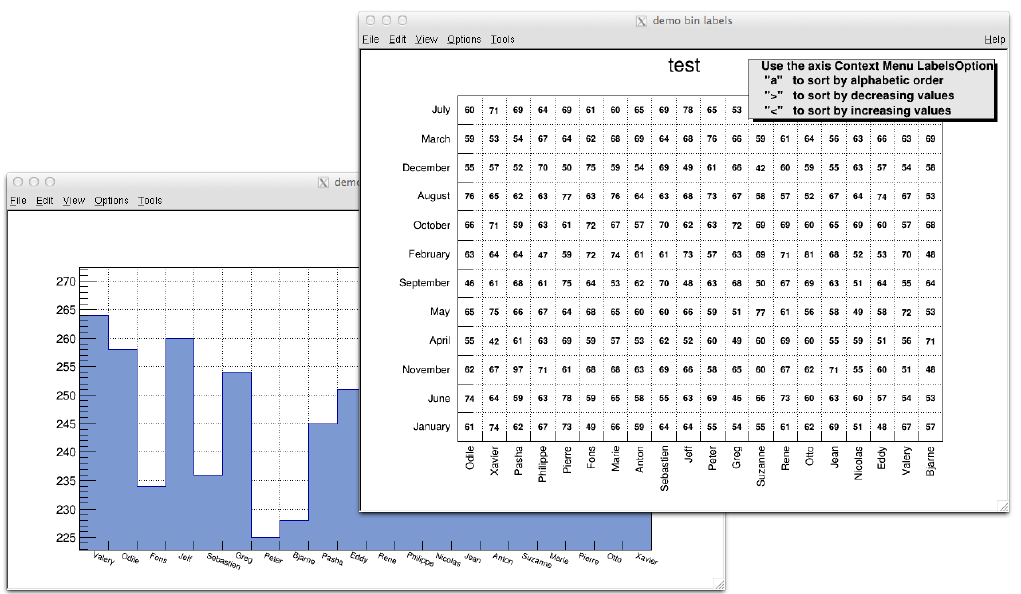
80 CHAPTER 3. HISTOGRAMS
–
returns an histogram containing the asymmetry of this histogram with
h2
, where the asymmetry is defined
as:
Asymmetry = (h1 - h2)/(h1 + h2); //where h1 = this
•
It works for
1D
,
2D
, etc. histograms. The parameter
c2
is an optional argument that gives a relative weight
between the two histograms, and
dc 2
is the error on this weight. This is useful, for example, when forming an
asymmetry between two histograms from two different data sets that need to be normalized to each other in
some way. The function calculates the errors assuming Poisson statistics on
h1
and
h2
(that is,
dh=sqrt(h)
). In
the next example we assume that h1 and h2 are already filled:
h3 = h1->GetAsymmetry(h2);
•Then h3 is created and filled with the asymmetry between h1 and h2 ;h1 and h2 are left intact.
•Note that the user’s responsibility is to manage the created histograms.
•TH1::Reset() - resets the bin contents and errors of a histogram
3.13 Alphanumeric Bin Labels
By default, a histogram axis is drawn with its numeric bin labels. One can specify alphanumeric labels instead.
3.13.1 Option 1: SetBinLabel
To set an alphanumeric bin label call:
TAxis::SetBinLabel(bin,label);
This can always be done before or after filling. Bin labels will be automatically drawn with the histogram.
Figure 3.14: Histograms with alphanumeric bin labels
See example in $ROOTSYS/tutorials/hist/hlabels1.C ,hlabels2.C
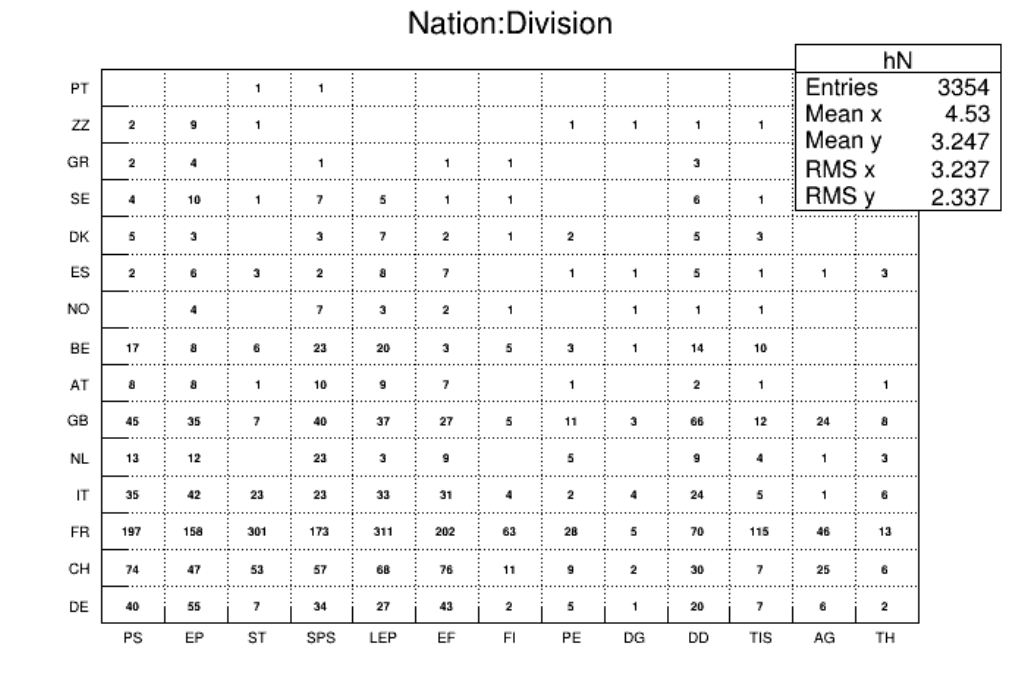
3.13. ALPHANUMERIC BIN LABELS 81
3.13.2 Option 2: Fill
You can also call a Fill() function with one of the arguments being a string:
hist1->Fill(somename,weigth);
hist2->Fill(x,somename,weight);
hist2->Fill(somename,y,weight);
hist2->Fill(somenamex,somenamey,weight);
3.13.3 Option 3: TTree::Draw
You can use a char* variable type to histogram strings with TTree::Draw().
// here "Nation" and "Division" are two char* branches of a Tree
tree.Draw("Nation::Division","","text");
Figure 3.15: Using a *char variable type in TTree::Draw
There is an example in $ROOTSYS/tutorials/tree/cernstaff.C.
If a variable is defined as
char*
it is drawn as a string by default. You change that and draw the value of
char[0]
as
an integer by adding an arithmetic operation to the expression as shown below.
// draw the integer value of MyChar[0] where "MyChar" is char[5]
tree.Draw("MyChar + 0");
3.13.4 Sort Options
When using the options 2 or 3 above, the labels are automatically added to the list (THashList) of labels for a given
axis. By default, an axis is drawn with the order of bins corresponding to the filling sequence. It is possible to reorder
the axis alphabetically or by increasing or decreasing values. The reordering can be triggered via the
TAxis
context
menu by selecting the menu item “LabelsOption” or by calling directly.
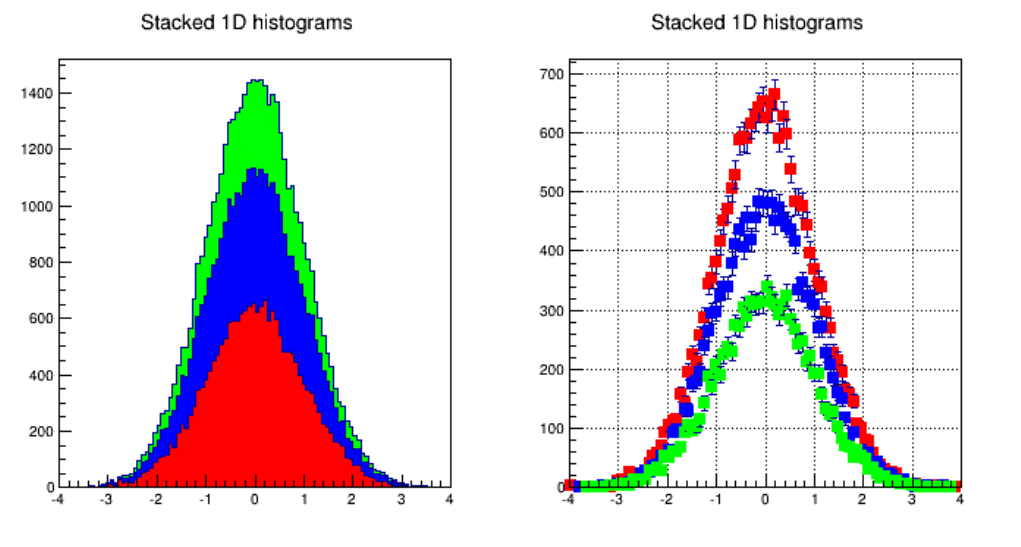
82 CHAPTER 3. HISTOGRAMS
TH1::LabelsOption(option,axis);
Here axis may be X, Y, or Z. The parameter option may be:
•“a” sort by alphabetic order
•“>” sort by decreasing values
•“<” sort by increasing values
•“h” draw labels horizontal
•“v” draw labels vertical
•“u” draw labels up (end of label right adjusted)
•“d” draw labels down (start of label left adjusted)
When using the option second above, new labels are added by doubling the current number of bins in case one label
does not exist yet. When the filling is terminated, it is possible to trim the number of bins to match the number of
active labels by calling:
TH1::LabelsDeflate(axis);
Here
axis
may be X, Y, or Z. This operation is automatic when using
TTree::Draw
. Once bin labels have been created,
they become persistent if the histogram is written to a file or when generating the C++ code via SavePrimitive .
3.14 Histogram Stacks
A
THStack
is a collection of
TH1
(or derived) objects. Use
THStack::Add( TH1 *h)
to add a histogram to the stack.
The THStack does not own the objects in the list.
Figure 3.16: Stacked histograms
By default,
THStack::Draw
draws the histograms stacked as shown in the left pad in the picture above. If the option
"nostack"
is used, the histograms are superimposed as if they were drawn one at a time using the
"same"
draw option
.The right pad in this picture illustrates the THStack drawn with the "nostack" option.
hs->Draw("nostack");
Next is a simple example, for a more complex one see $ROOTSYS/tutorials/hist/hstack.C.
3.15. TH2POLY 83
{
THStack hs("hs","test stacked histograms");
TH1F *h1 = new TH1F("h1","test hstack",100,-4,4);
h1->FillRandom("gaus",20000);
h1->SetFillColor(kRed);
hs.Add(h1);
TH1F *h2 = new TH1F("h2","test hstack",100,-4,4);
h2->FillRandom("gaus",15000);
h2->SetFillColor(kBlue);
hs.Add(h2);
TH1F *h3 = new TH1F("h3","test hstack",100,-4,4);
h3->FillRandom("gaus",10000);
h3->SetFillColor(kGreen);
hs.Add(h3);
TCanvas c1("c1","stacked hists",10,10,700,900);
c1.Divide (1,2);
c1.cd(1);
hs.Draw();
c1.cd(2);
hs->Draw("nostack");
}
3.15 TH2Poly
TH2Poly is a 2D Histogram class allowing to define polygonal bins of arbitary shape.
Each bin in the
TH2Poly
histogram is a
TH2PolyBin
object.
TH2PolyBin
is a very simple class containing the vertices
and contents of the polygonal bin as well as several related functions.
Bins are defined using one of the AddBin() methods. The bin definition should be done before filling.
The following very simple macro shows how to build and fill a TH2Poly:
{
TH2Poly *h2p = new TH2Poly();
Double_t x1[] = {0,5,5};
Double_t y1[] = {0,0,5};
Double_t x2[] = {0, -1, -1,0};
Double_t y2[] = {0,0, -1, -1};
Double_t x3[] = {4,3,0,1,2.4};
Double_t y3[] = {4,3.7,1,4.7,3.5};
h2p->AddBin(3, x1, y1);
h2p->AddBin(3, x2, y2);
h2p->AddBin(3, x3, y3);
h2p->Fill( 3,1,3); // fill bin 1
h2p->Fill(-0.5, -0.5,7); // fill bin 2
h2p->Fill(-0.7, -0.5,1); // fill bin 2
h2p->Fill( 1,3,5); // fill bin 3
}
More examples can bin found in $ROOTSYS/tutorials/hist/th2poly*.C
3.16 Profile Histograms
Profile histograms are in many cases an elegant replacement of two-dimensional histograms. The relationship of
two quantities X and Y can be visualized by a two-dimensional histogram or a scatter-plot; its representation is not
particularly satisfactory, except for sparse data. If Y is an unknown [but single-valued] function of X, it can be displayed
by a profile histogram with much better precision than by a scatter-plot. Profile histograms display the mean value
of Y and its RMS for each bin in X. The following shows the contents [capital letters] and the values shown in the
graphics [small letters] of the elements for bin j. When you fill a profile histogram with TProfile.Fill(x,y) :
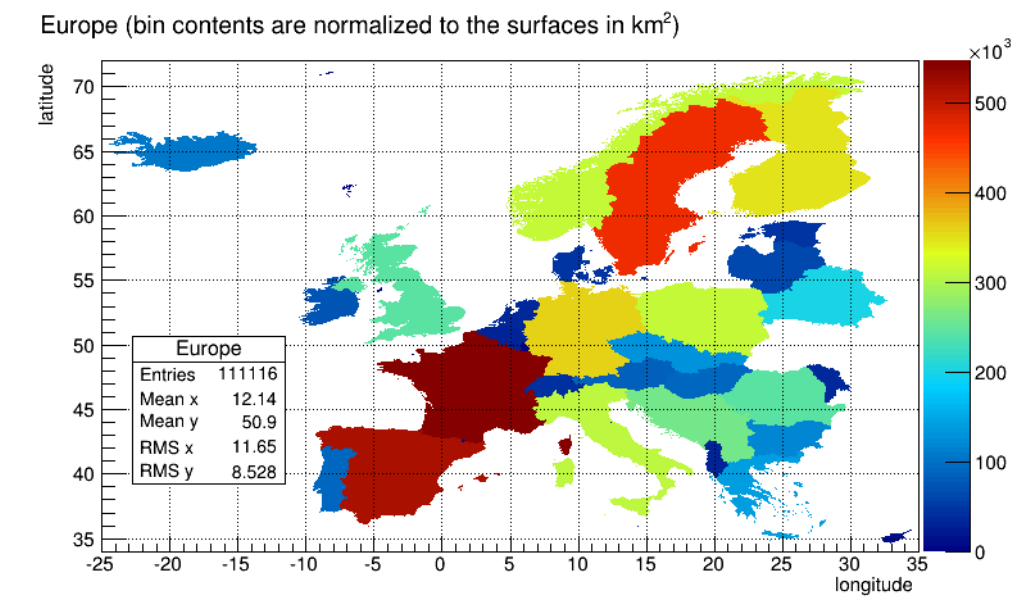
84 CHAPTER 3. HISTOGRAMS
Figure 3.17: A TH2Poly histogram example
•H[j] will contain for each bin jthe sum of the y values for this bin
•L[j] contains the number of entries in the bin j
•e[j] or s[j] will be the resulting error depending on the selected option. See “Build Options”.
E[j] = sum Y**2
L[j] = number of entries in bin J
H[j] = sum Y
h[j] = H[j] / L[j]
s[j] = sqrt[E[j] / L[j] - h[j]**2]
e[j] = s[j] / sqrt[L[j]]
In the special case where
s[j]
is zero, when there is only one entry per bin,
e[j]
is computed from the average of the
s[j]
for all bins. This approximation is used to keep the bin during a fit operation. The
TProfile
constructor takes
up to eight arguments. The first five parameters are similar to TH1D constructor.
TProfile(const char *name,const char *title,Int_t nbinsx,
Double_t xlow, Double_t xup, Double_t ylow, Double_t yup,
Option_t *option)
All values of
y
are accepted at filling time. To fill a profile histogram, you must use
TProfile::Fill
function. Note
that when filling the profile histogram the method
TProfile::Fill
checks if the variable
y
is between
fYmin
and
fYmax
. If a minimum or maximum value is set for the Y scale before filling, then all values below
ylow
or above
yup
will be discarded. Setting the minimum or maximum value for the Y scale before filling has the same effect as calling
the special TProfile constructor above where ylow and yup are specified.
3.16.1 Build Options
The last parameter is the build option. If a bin has N data points all with the same value Y, which is the case when
dealing with integers, the spread in Y for that bin is zero, and the uncertainty assigned is also zero, and the bin is
ignored in making subsequent fits. If
SQRT(Y)
was the correct error in the case above, then
SQRT(Y)/SQRT(N)
would
be the correct error here. In fact, any bin with non-zero number of entries N but with zero spread (
spread = s[j]
)
3.16. PROFILE HISTOGRAMS 85
should have an uncertainty
SQRT(Y)/SQRT(N)
. Now, is
SQRT(Y)/SQRT(N)
really the correct uncertainty ? That it is
only in the case where the Y variable is some sort of counting statistics, following a Poisson distribution. This is
the default case. However, Y can be any variable from an original
NTUPLE
, and does not necessarily follow a Poisson
distribution. The computation of errors is based on Y = values of data points; N = number of data points.
•’ ’ - the default is blank, the errors are:
•spread/SQRT(N) for a non-zero spread
•SQRT(Y)/SQRT(N) for a spread of zero and some data points
•0for no data points
•‘s’ - errors are:
•spread for a non-zero spread
•SQRT(Y) for a Spread of zero and some data points
•0for no data points
•‘i’ - errors are:
•spread/SQRT(N) for a non-zero spread
•1/SQRT(12*N) for a Spread of zero and some data points
•0for no data points
•‘G’ - errors are:
•spread/SQRT(N) for a non-zero spread
•sigma/SQRT(N) for a spread of zero and some data points
•0for no data points
The option ‘
i
’ is used for integer Y values with the uncertainty of
±
0
.
5, assuming the probability that Y takes any
value between Y-0.5 and Y+0.5 is uniform (the same argument for Y uniformly distributed between Y and Y+1).
An example is an ADC measurement. The ‘
G
’ option is useful, if all Y variables are distributed according to some
known Gaussian of standard deviation Sigma. For example when all Y’s are experimental quantities measured with the
same instrument with precision Sigma. The next figure shows the graphic output of this simple example of a profile
histogram.
{
// Create a canvas giving the coordinates and the size
TCanvas *c1 = new TCanvas("c1","Profile example",200,10,700,500);
// Create a profile with the name, title, the number of bins,
// the low and high limit of the x-axis and the low and high
// limit of the y-axis.
// No option is given so the default is used.
hprof = new TProfile("hprof",
"Profile of pz versus px",100,-4,4,0,20);
// Fill the profile 25000 times with random numbers
Float_t px, py, pz;
for ( Int_t i=0; i<25000; i++) {
// Use the random number generator to get two numbers following
// a gaussian distribution with mean=0 and sigma=1
gRandom->Rannor(px,py);
pz = px*px + py*py;
hprof->Fill(px,pz,1);
}
hprof->Draw();
}
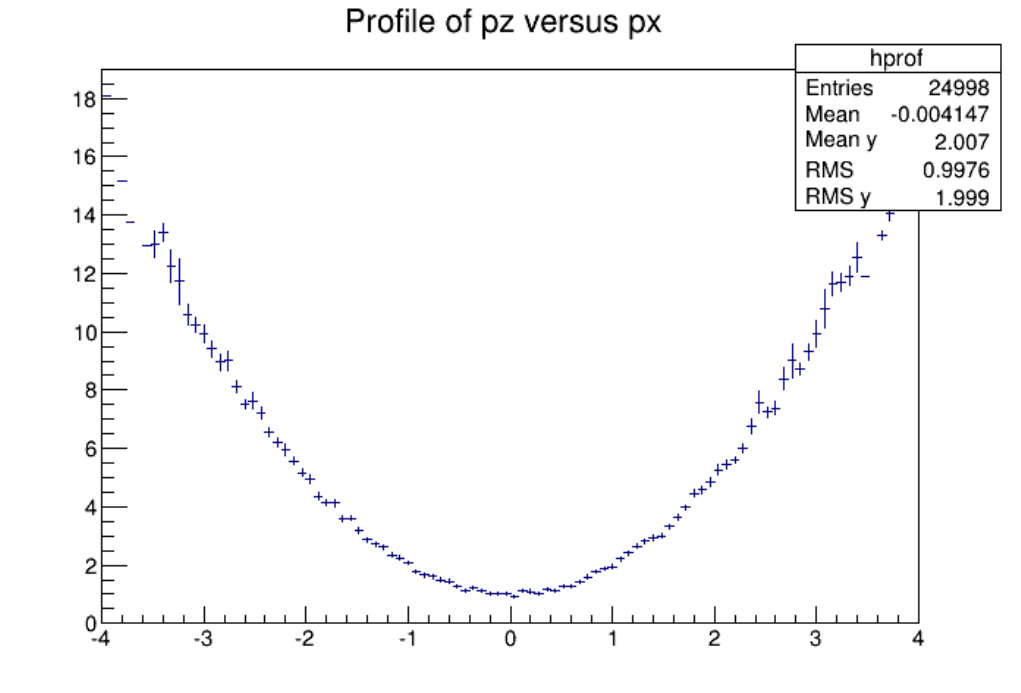
86 CHAPTER 3. HISTOGRAMS
Figure 3.18: A profile histogram example
3.16.2 Drawing a Profile without Error Bars
To draw a profile histogram and not show the error bars use the “
HIST
” option in the
TProfile::Draw
method. This
will draw the outline of the TProfile.
3.16.3 Create a Profile from a 2D Histogram
You can make a profile from a histogram using the methods TH2::ProfileX and TH2::ProfileY.
3.16.4 Create a Histogram from a Profile
To create a regular histogram from a profile histogram, use the method
TProfile::ProjectionX
.This example
instantiates a TH1D object by copying the TH1D piece of TProfile.
TH1D *sum = myProfile.ProjectionX();
You can do the same with a 2D profile using the method TProfile2D::ProjectionXY .
3.16.5 Generating a Profile from a TTree
The
’prof’
and
’profs’
options in the
TTree::Draw
method generate a profile histogram (
TProfile
), given a two
dimensional expression in the tree, or a
TProfile2D
given a three dimensional expression. See “Trees”. Note that you
can specify
’prof’
or
’profs’
:
’prof’
generates a
TProfile
with error on the mean,
’profs’
generates a
TProfile
with error on the spread.
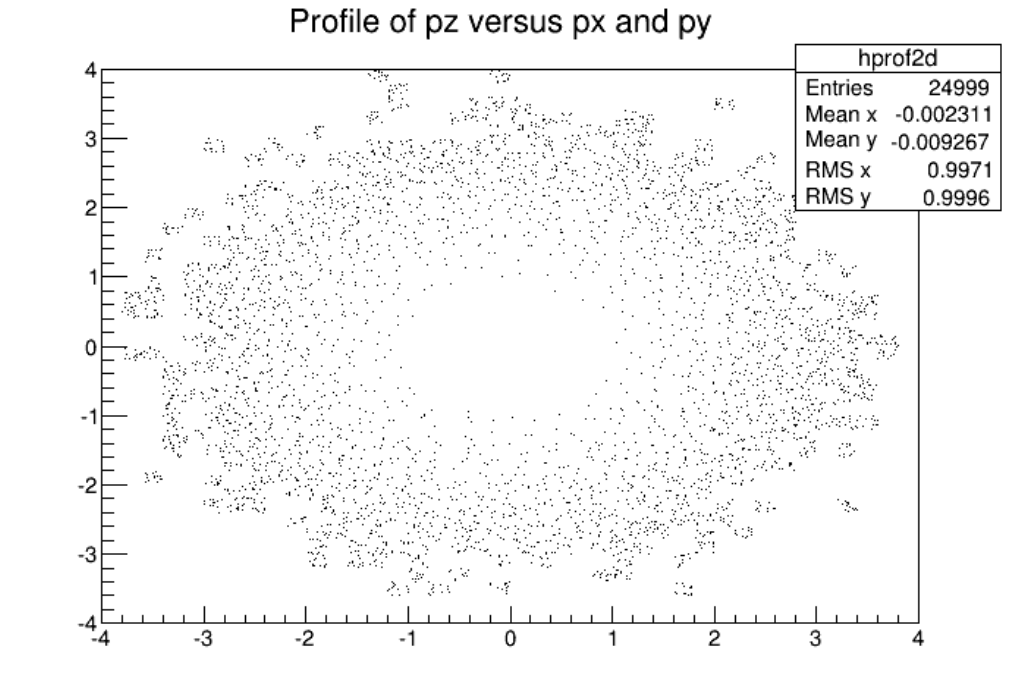
3.16. PROFILE HISTOGRAMS 87
3.16.6 2D Profiles
The class for a 2D Profile is called
TProfile2D
. It is in many cases an elegant replacement of a three-dimensional
histogram. The relationship of three measured quantities X, Y and Z can be visualized by a three-dimensional histogram
or scatter-plot; its representation is not particularly satisfactory, except for sparse data. If Z is an unknown (but
single-valued) function of (X,Y), it can be displayed with a
TProfile2D
with better precision than by a scatter-plot.
A
TProfile2D
displays the mean value of Z and its RMS for each cell in X, Y. The following shows the cumulated
contents (capital letters) and the values displayed (small letters) of the elements for cell i,j.
When you fill a profile histogram with TProfile2D.Fill(x,y,z):
•E[i,j] contains for each bin i,j the sum of the z values for this bin
•L[i,j] contains the number of entries in the bin j
•e[j] or s[j] will be the resulting error depending on the selected option. See “Build Options”.
E[i,j] = sum z
L[i,j] = sum l
h[i,j] = H[i,j ] / L[i,j]
s[i,j] = sqrt[E[i,j] / L[i,j]- h[i,j]**2]
e[i,j] = s[i,j] / sqrt[L[i,j]]
In the special case where
s[i,j]
is zero, when there is only one entry per cell,
e[i,j]
is computed from the average of
the s[i,j] for all cells. This approximation is used to keep the cell during a fit operation.
Figure 3.19: A TProfile2D histogram example
{
// Creating a Canvas and a TProfile2D
TCanvas *c1 = new TCanvas("c1",
"Profile histogram example",
200,10,700,500);
88 CHAPTER 3. HISTOGRAMS
hprof2d = new TProfile2D("hprof2d",
"Profile of pz versus px and py",
40,-4,4,40,-4,4,0,20);
// Filling the TProfile2D with 25000 points
Float_t px, py, pz;
for (Int_t i=0; i<25000; i++) {
gRandom->Rannor(px,py);
pz = px*px + py*py;
hprof2d->Fill(px,py,pz,1);
}
hprof2d->Draw();
}
3.17 Iso Surfaces
Paint one Gouraud shaded 3d iso surface though a 3d histogram at the value computed as follow:
SumOfWeights/(NbinsX*NbinsY*NbinsZ)
.
void hist3d() {
TH3D *h3 = new TH3D("h3","h3",20, -2,2,20, -2,2,20,0,4);
Double_t x,y,z;
for (Int_t i=0; i<10000; i++) {
gRandom->
Rannor(x,y);
z=x*x+y*y;
h3->Fill(x,y,z);
}
h3->Draw("iso");
}
3.18 3D Implicit Functions
TF3 *fun3 = new TF3("fun3","sin(x*x+y*y+z*z-36)",-2,2,-2,2,-2,2);
fun3->Draw();
3.19 TPie
The
TPie
class allows to create a Pie Chart representation of a one dimensional data set. The data can come from an
array of Double_t (or Float_t ) or from a 1D-histogram. The possible options to draw a TPie are:
•“R” Paint the labels along the central “R”adius of slices.
•“T” Paint the labels in a direction “T”angent to circle that describes the TPie.
•“3D” Draw the pie-chart with a pseudo 3D effect.
•“NOL” No OutLine: do not draw the slices’ outlines; any property over the slices’ line is ignored.
The method
SetLabelFormat()
is used to customize the label format. The format string must contain one of these
modifiers:
•–%txt : to print the text label associated with the slice
•–%val : to print the numeric value of the slice
•–%frac : to print the relative fraction of this slice
•–%perc : to print the % of this slice
mypie->SetLabelFormat("%txt (%frac)");
See the macro $ROOTSYS/tutorials/graphics/piechart.C .
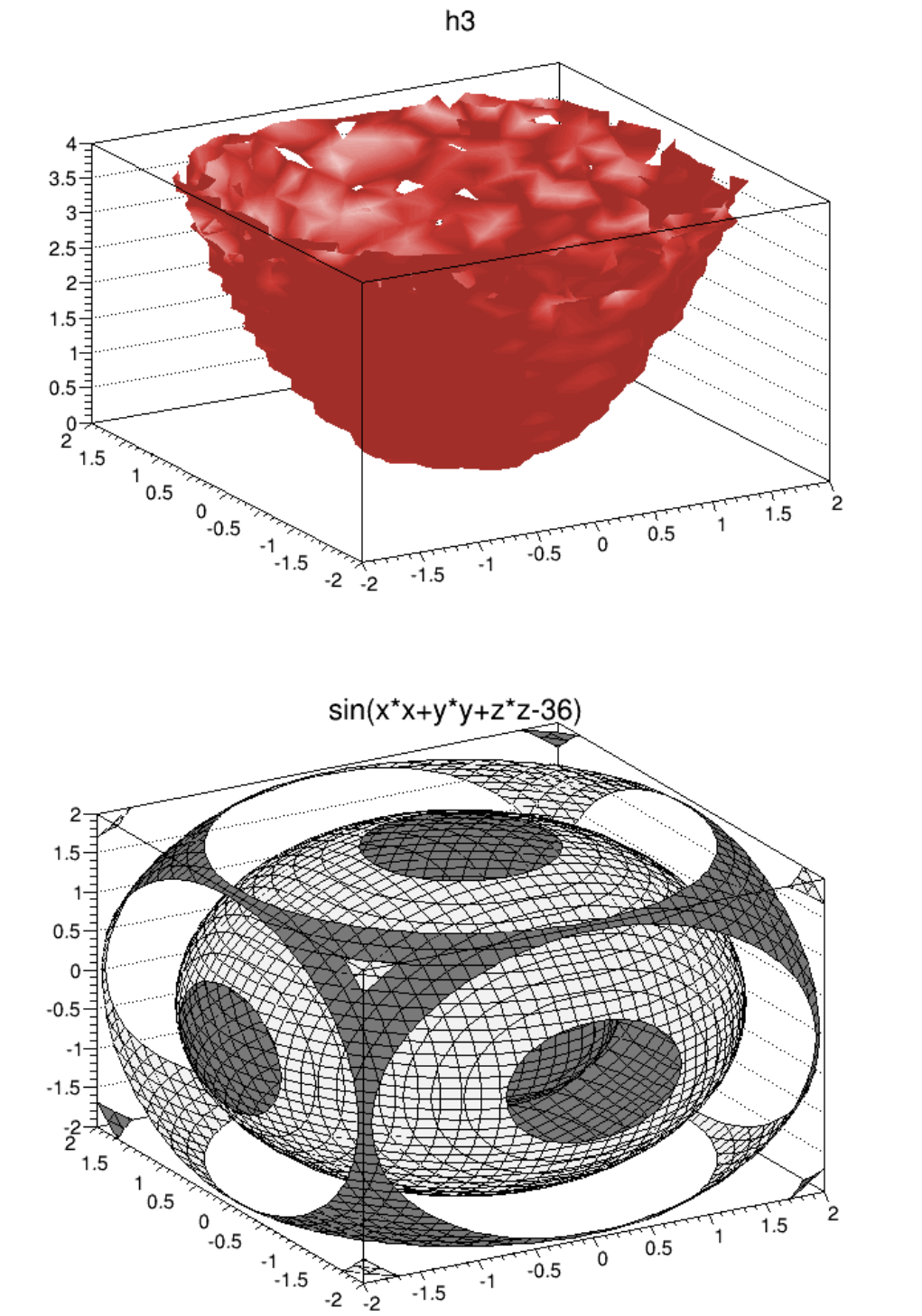
3.19. TPIE 89
Figure 3.20: Iso surfaces
Figure 3.21: 3D implicit function
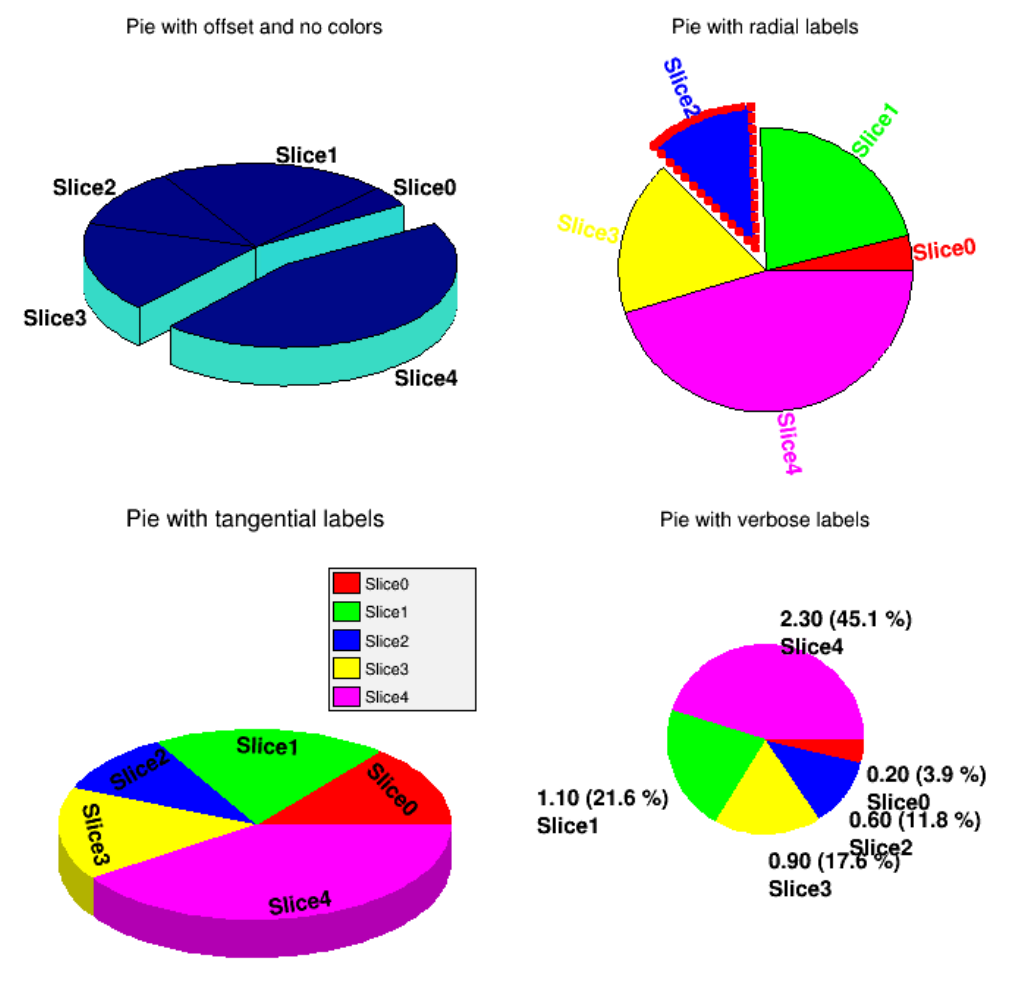
90 CHAPTER 3. HISTOGRAMS
Figure 3.22: The picture generated by tutorial macro piechart.C
3.20. THE USER INTERFACE FOR HISTOGRAMS 91
3.20 The User Interface for Histograms
The classes
T H1 Editor
and
T H2 Editor
provides the user interface for setting histogram’s attributes and rebinning
interactively.
3.20.1 TH1Editor
3.20.1.1 The Style Tab
3.20.1.1.1 Title sets the title of the histogram.
3.20.1.1.2 Plot draw a 2D or 3D plot; according to the dimension, different drawing possibilities can be set.
3.20.1.1.3 Error add different error bars to the histogram (no errors, simple, etc.).
3.20.1.1.4 Add further things which can be added to the histogram (None, simple/smooth line, fill area, etc.)
3.20.1.2 2-D Plot
3.20.1.2.1 Simple Drawing
draw a simple histogram without errors (= “HIST” draw option). In combination
with some other draw options an outer line is drawn on top of the histogram
3.20.1.2.2 Show markers draw a marker on to of each bin (=“P” draw option).
3.20.1.2.3 Draw bar chart draw a bar chart (=“B” draw option).
92 CHAPTER 3. HISTOGRAMS
3.20.1.2.4 Bar option
draw a bar chart (=“BAR” draw option); if selected, it will show an additional interface
elements for bars: width, offset, percentage and the possibility to draw horizontal bars.
3.20.1.3 3-D Plot
3.20.1.3.1 Add set histogram type Lego-Plot or Surface draw (Lego, Lego1.2, Surf, Surf1. . . 5).
3.20.1.3.2 Coords set the coordinate system (Cartesian, Spheric, etc.).
3.20.1.3.3 Error same as for 2D plot.
3.20.1.3.4 Bar set the bar attributes: width and offset.
3.20.1.3.5 Horizontal Bar draw a horizontal bar chart.
3.20.1.4 The Binning tab
The binning tab has two different layouts. One is for a histogram, which is not drawn from an ntuple. The other one
is available for a histogram, which is drawn from an ntuple. In this case, the rebin algorithm can create a rebinned
histogram from the original data i.e. the ntuple.
To see the differences do:
TFile f("hsimple.root");
hpx->Draw("BAR1"); // non ntuple histogram
ntuple->Draw("px");// ntuple histogram
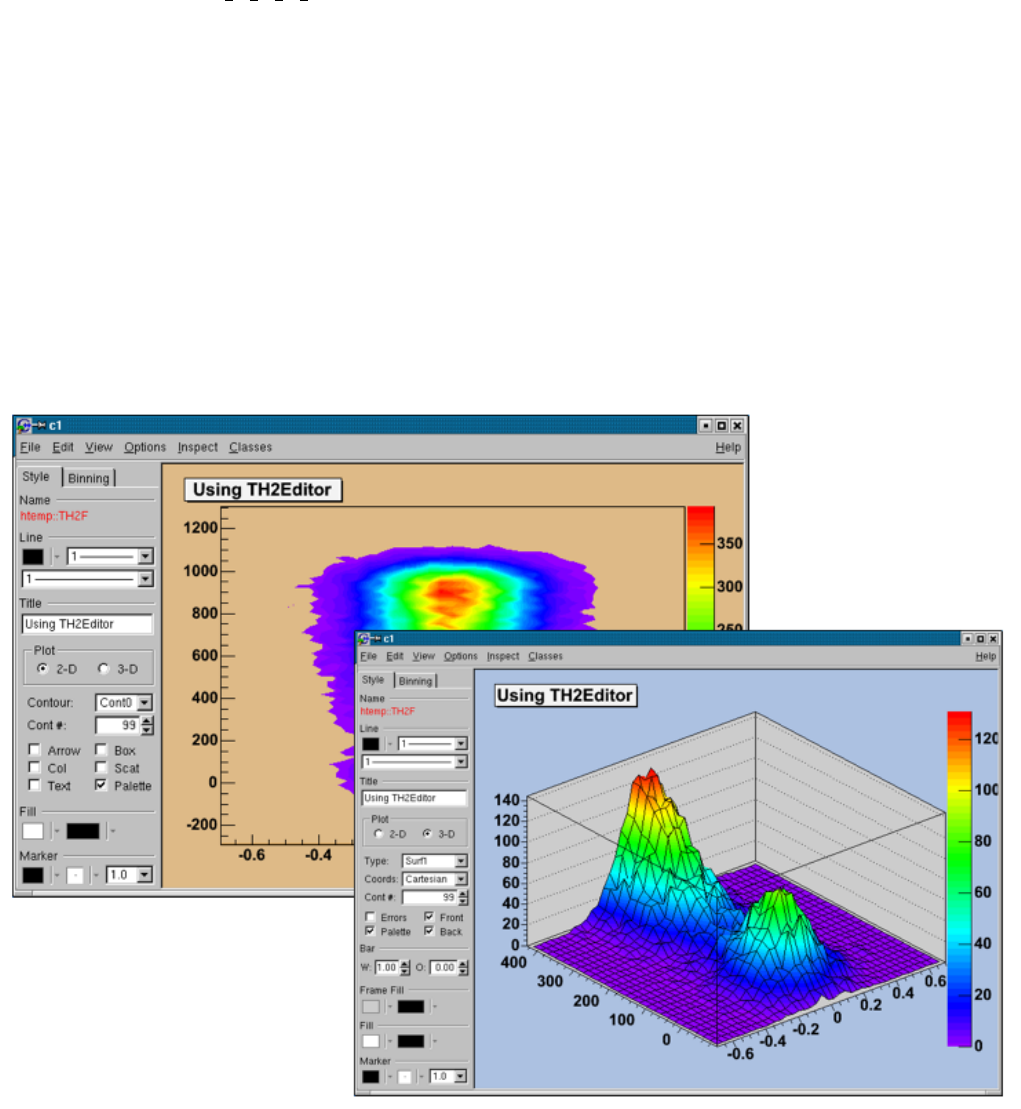
3.20. THE USER INTERFACE FOR HISTOGRAMS 93
3.20.1.5 Non ntuple histogram
Rebin with a slider and the number of bins (shown in the field below the slider). The number of bins can be changed
to any number, which divides the number of bins of the original histogram. A click on the Apply button will delete the
origin histogram and will replace it by the rebinned one on the screen. A click on the Ignore button will restore the
origin histogram.
3.20.1.6 Histogram drawn from an ntuple
3.20.1.6.1 Rebin
with the slider, the number of bins can be enlarged by a factor of 2, 3, 4, 5 (moving to the right)
or reduced by a factor of 1
2,1
3,1
4,1
5.
3.20.1.6.2 BinOffset with a BinOffset slider
the origin of the histogram can be changed within one binwidth.
Using this slider the effect of binning the data into bins can be made visible (statistical fluctuations).
3.20.1.6.3 Axis Range
with a double slider it is possible to zoom into the specified axis range. It is also possible
to set the upper and lower limit in fields below the slider.
3.20.1.6.4 Delayed drawing
all the Binning sliders can set to delay draw mode. Then the changes on the
histogram are only updated, when the Slider is released. This should be activated if the redrawing of the histogram is
time consuming.
3.20.2 TH2Editor
3.20.2.1 Style Tab:
3.20.2.1.1 Title set the title of the histogram
94 CHAPTER 3. HISTOGRAMS
3.20.2.1.2 Histogram change the draw options of the histogram.
3.20.2.1.3 Plot
draw a 2D or 3D plot of the histogram; according to the dimension, the drawing possibilities are
different.
3.20.2.2 2-D Plot
3.20.2.2.1 Contour draw a contour plot (None, Cont0. . . 5)
3.20.2.2.2 Cont # set the number of Contours;
3.20.2.2.3 Arrow set the arrow mode and shows the gradient between adjacent cells;
3.20.2.2.4 Col a box is drawn for each cell with a color scale varying with contents;
3.20.2.2.5 Text draw bin contents as text;
3.20.2.2.6 Box a box is drawn for each cell with surface proportional to contents;
3.20.2.2.7 Scat draw a scatter-plot (default);
3.20.2.2.8 Palette the color palette is drawn.
3.20.2.3 3-D Plot
3.20.2.3.1 Type set histogram type to Lego or surface plot; draw (Lego, Lego1.2, Surf, Surf1. . . 5)
3.20.2.3.2 Coords set the coordinate system (Cartesian, Spheric, etc.);
3.20.2.3.3 Cont # set the number of Contours (for e.g. Lego2 draw option);
3.20.2.3.4 Errors draw errors in a Cartesian lego plot;
3.20.2.3.5 Palette draw the color palette;
3.20.2.3.6 Front draw the front box of a Cartesian lego plot;
3.20.2.3.7 Back draw the back box of a Cartesian lego plot;
3.20.2.3.8 Bar change the bar attributes: the width and offset.
3.20.2.4 Rebinning Tab
The Rebinning tab has two different layouts. One is for a histogram that is not drawn from an ntuple; the other one
is available for a histogram, which is drawn from an ntuple. In this case, the rebin algorithm can create a rebinned
histogram from the original data i.e. the ntuple. To see the differences do for example:
TFile f ("hsimple.root");
hpxpy->Draw("Lego2"); // non ntuple histogram
ntuple->Draw("px:py","","Lego2"); // ntuple histogram
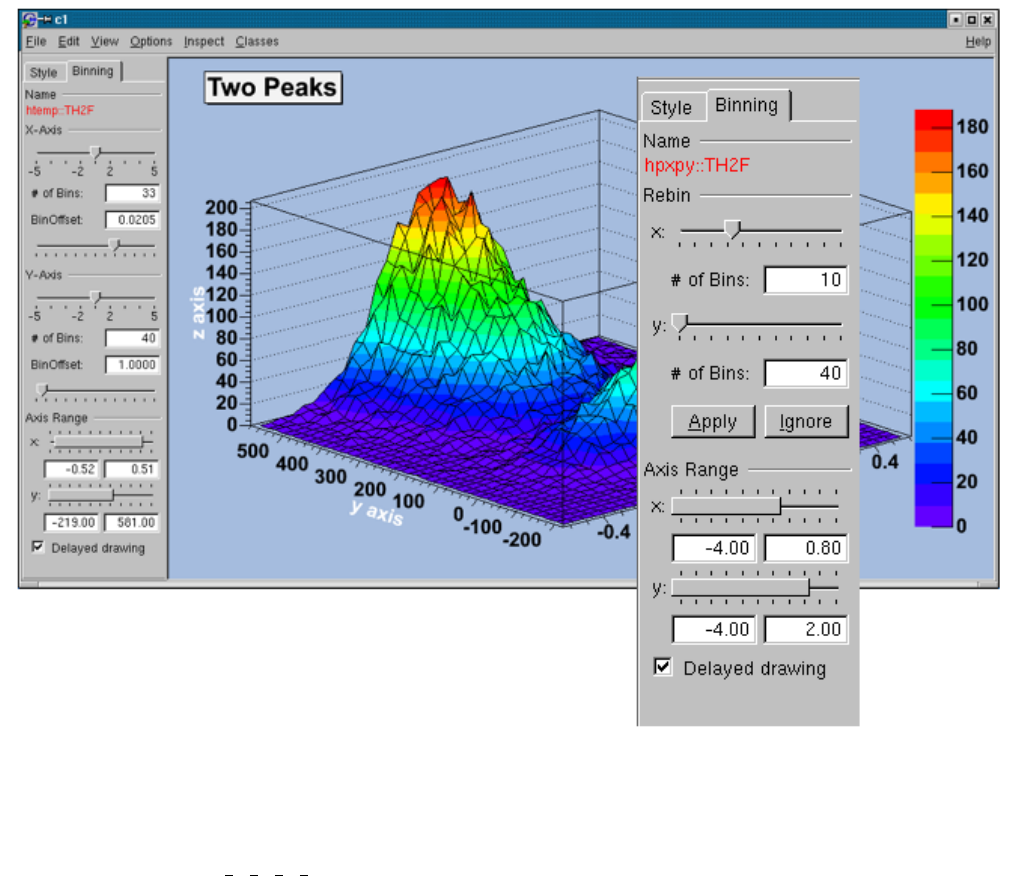
3.20. THE USER INTERFACE FOR HISTOGRAMS 95
3.20.2.5 Non-ntuple histogram:
Rebin with sliders (one for the x, one for the y-axis) and the number of bins (shown in the field below them can
be changed to any number, which divides the number of bins of the original histogram. Selecting the Apply button
will delete the origin histogram and will replace it by the rebinned one on the screen. Selecting the Ignore the origin
histogram will be restored.
3.20.2.6 Histogram drawn from an ntuple
3.20.2.6.1 Rebin
with the sliders the number of bins can be enlarged by a factor of 2,3,4,5 (moving to the right)
or reduced by a factor of 1
2,1
3,1
4,1
5.
3.20.2.6.2 BinOffset
with the BinOffset slider the origin of the histogram can be changed within one binwidth.
Using this slider the effect of binning the data into bins can be made visible (=> statistical fluctuations).
3.20.2.6.3 Axis Range
with a double slider that gives the possibility for zooming. It is also possible to set the
upper and lower limit in fields below the slider.
3.20.2.6.4 Delayed drawing
all the binning sliders can be set to delay draw mode. Then the changes on the
histogram are only updated, when the Slider is released. This should be activated if the redrawing of the histogram is
too time consuming.
96 CHAPTER 3. HISTOGRAMS
Chapter 4
Graphs
A graph is a graphics object made of two arrays X and Y, holding the x,y coordinates of
n
points. There are several
graph classes; they are TGraph,TGraphErrors,TGraphAsymmErrors, and TMultiGraph.
4.1 TGraph
The
TGraph
class supports the general case with non-equidistant points, and the special case with equidistant points.
Graphs are created with the
TGraph
constructor. First, we define the arrays of coordinates and then create the graph.
The coordinates can be arrays of doubles or floats.
Int_t n = 20;
Double_t x[n], y[n];
for (Int_t i=0; i<n; i++) {
x[i] = i*0.1;
y[i] = 10*sin(x[i]+0.2);
}
TGraph *gr1 = new TGraph (n, x, y);
An alternative constructor takes only the number of points n. It is expected that the coordinates will be set later.
TGraph *gr2 = new TGraph(n);
The default constructor can also be used. Further calls to SetPoint() will extend the internal vectors.
TGraph *gr3 = new TGraph();
4.1.1 Graph Draw Options
The various drawing options for a graph are explained in TGraph::PaintGraph. They are:
•“L” A simple poly-line between every points is drawn
•“F” A fill area is drawn
•“F1” Idem as “F” but fill area is no more repartee around X=0 or Y=0
•“F2” draw a fill area poly line connecting the center of bins
•“A” Axis are drawn around the graph
•“C” A smooth curve is drawn
•“*” A star is plotted at each point
•“P” The current marker of the graph is plotted at each point
•“B” A bar chart is drawn at each point
97
98 CHAPTER 4. GRAPHS
•
“
[]
” Only the end vertical/horizontal lines of the error bars are drawn. This option only applies to the
TGraphAsymmErrors.
•“1”ylow = rwymin
The options are not case sensitive and they can be concatenated in most cases. Let us look at some examples.
4.1.1.1 Continuous Line, Axis and Stars (AC*)
Figure 4.1: A graph drawn with axis, * markers and continuous line (option AC*)
{
Int_t n = 20;
Double_t x[n], y[n];
for (Int_t i=0;i<n;i++) {
x[i] = i*0.1;
y[i] = 10*sin(x[i]+0.2);
}
// create graph
TGraph *gr = new TGraph(n,x,y);
TCanvas *c1 = new TCanvas("c1","Graph Draw Options",
200,10,600,400);
// draw the graph with axis, continuous line, and put
// a * at each point
gr->Draw("AC*");
}
4.1.1.2 Bar Graphs (AB)
root[] TGraph *gr1 = new TGraph(n,x,y);
root[] gr1->SetFillColor(40);
root[] gr1->Draw("AB");
4.1. TGRAPH 99
Figure 4.2: A graph drawn with axis and bar (option AB)
This code will only work if n, x, and y is defined. The previous example defines these. You need to set the fill color,
because by default the fill color is white and will not be visible on a white canvas. You also need to give it an axis, or
the bar chart will not be displayed properly.
4.1.1.3 Filled Graphs (AF)
root[] TGraph *gr3 = new TGraph(n,x,y);
root[] gr3->SetFillColor(45);
root[] gr3->Draw("AF")
This code will only work if
n
,
x
,
y
are defined. The first example defines them. You need to set the fill color, because by
default the fill color is white and will not be visible on a white canvas. You also need to give it an axis, or the filled
polygon will not be displayed properly.
4.1.1.4 Marker Options
{
Int_t n = 20;
Double_t x[n], y[n];
// build the arrays with the coordinate of points
for (Int_t i=0; i<n; i++) {
x[i] = i*0.1;
y[i] = 10*sin(x[i]+0.2);
}
// create graphs
TGraph *gr3 = new TGraph(n,x,y);
TCanvas *c1 = new TCanvas ("c1","Graph Draw Options",
200,10,600,400);
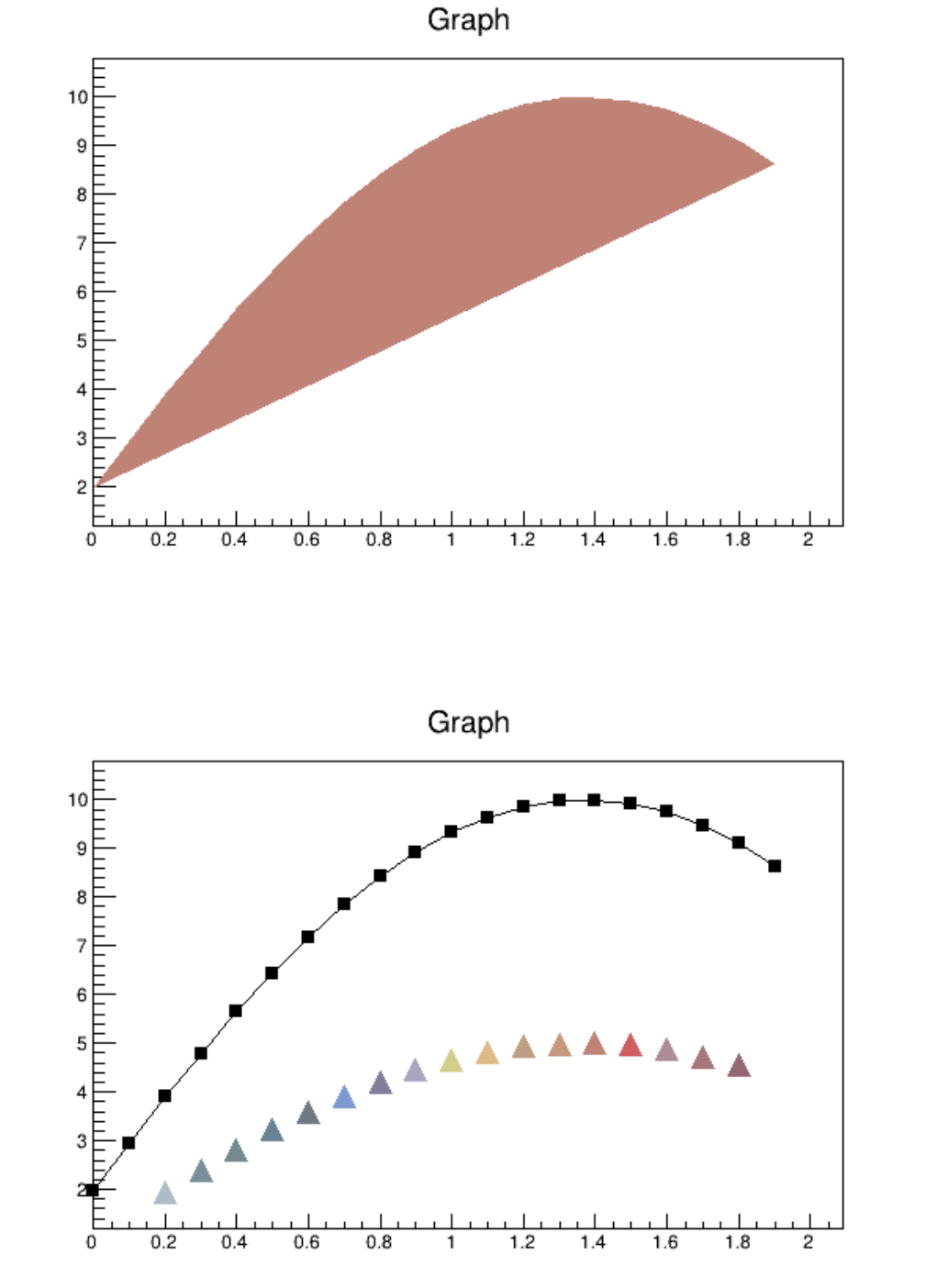
100 CHAPTER 4. GRAPHS
Figure 4.3: A graph drawn with axis and fill (option AF)
Figure 4.4: Graph markers created in different ways
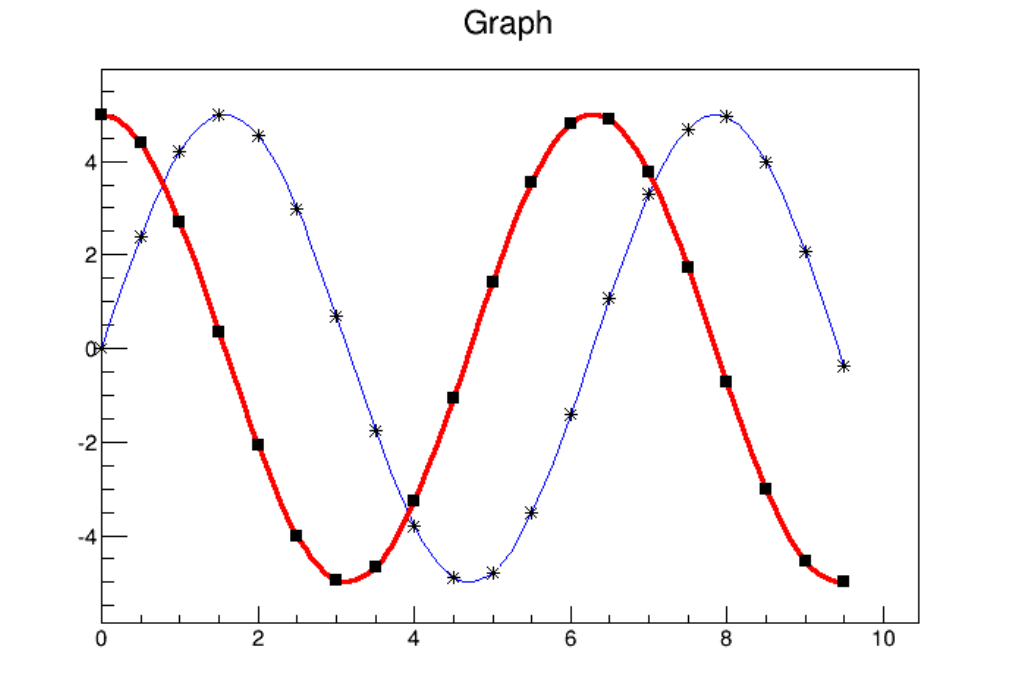
4.2. SUPERIMPOSING TWO GRAPHS 101
// draw the graph with the axis,contineous line, and put
// a marker using the graph's marker style at each point
gr3->SetMarkerStyle(21);
c1->cd(4);
gr3->Draw("APL");
// get the points in the graph and put them into an array
Double_t *nx = gr3->GetX();
Double_t *ny = gr3->GetY();
// create markers of different colors
for (Int_t j=2; j<n-1; j++) {
TMarker *m = new TMarker(nx[j], 0.5*ny[j], 22);
m->SetMarkerSize(2);
m->SetMarkerColor(31+j);
m->Draw();
}
}
4.2 Superimposing Two Graphs
To super impose two graphs you need to draw the axis only once, and leave out the “A” in the draw options for the
second graph. Next is an example:
Figure 4.5: Superimposing two graphs
{
Int_t n = 20;
Double_t x[n], y[n], x1[n], y1[n];
// create a blue graph with a cos function
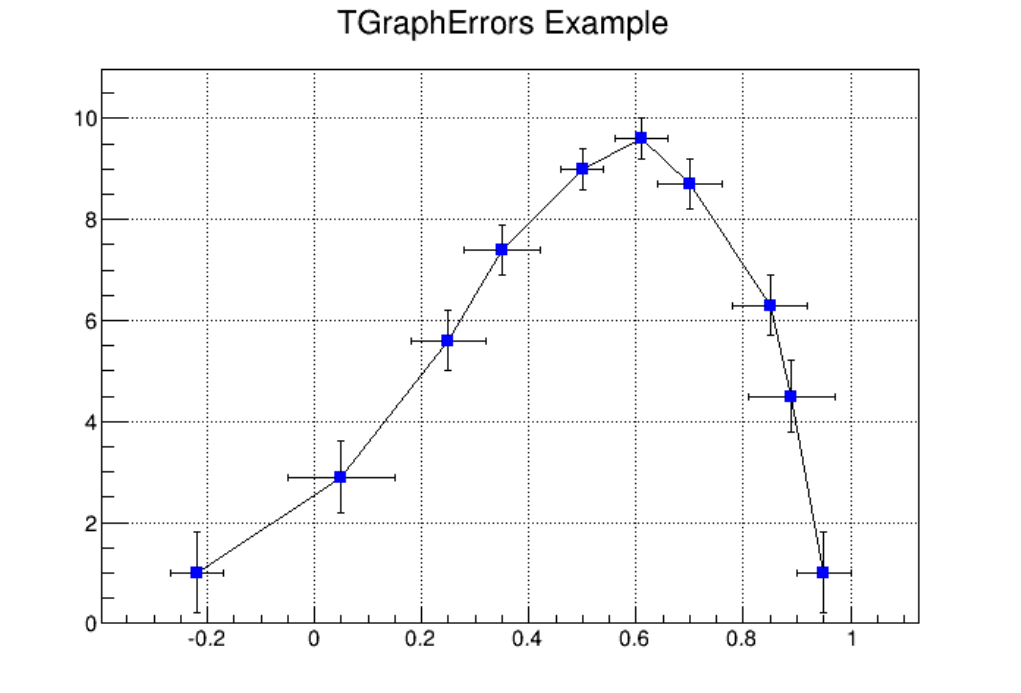
102 CHAPTER 4. GRAPHS
gr1->SetLineColor(4);
gr1->Draw("AC*");
// superimpose the second graph by leaving out the axis option "A"
gr2->SetLineWidth(3);
gr2->SetMarkerStyle(21);
gr2->SetLineColor(2);
gr2->Draw("CP");
}
4.3 Graphs with Error Bars
A
TGraphErrors
is a
TGraph
with error bars. The various draw format options of
TGraphErrors::Paint()
are derived
from TGraph.
void TGraphErrors::Paint(Option_t *option)
Figure 4.6: Graphs with different draw options of error bars
In addition, it can be drawn with the “
Z
” option to leave off the small lines at the end of the error bars. If option
contains “
>
”, an arrow is drawn at the end of the error bars. If option contains “
|>
”, a full arrow is drawn at the end
of the error bars. The size of the arrow is set to 2/3 of the marker size.
The option “
[]
” is interesting to superimpose systematic errors on top of the graph with the statistical errors. When it
is specified, only the end vertical/horizontal lines of the error bars are drawn.
To control the size of the lines at the end of the error bars (when option 1 is chosen) use
SetEndErrorSize(np)
. By
default np=1;np represents the number of pixels.
gStyle->SetEndErrorSize(np);
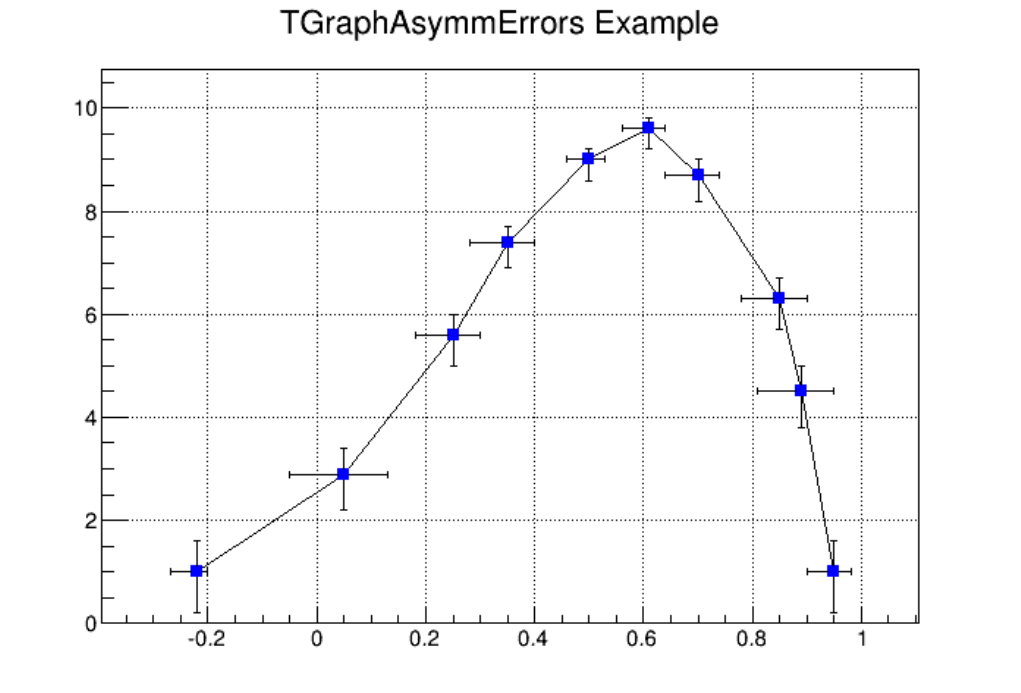
4.4. GRAPHS WITH ASYMMETRIC ERROR BARS 103
The four parameters of
TGraphErrors
are:
X, Y
(as in
TGraph
),
X
-errors, and
Y
-errors - the size of the errors in the
x
and ydirection. Next example is $ROOTSYS/tutorials/graphs/gerrors.C.
{
c1 = new TCanvas("c1","A Simple Graph with error bars",200,10,700,500);
c1->SetGrid();
// create the coordinate arrays
Int_t n = 10;
Float_t x[n] = {-.22,.05,.25,.35,.5,.61,.7,.85,.89,.95};
Float_t y[n] = {1,2.9,5.6,7.4,9,9.6,8.7,6.3,4.5,1};
// create the error arrays
Float_t ex[n] = {.05,.1,.07,.07,.04,.05,.06,.07,.08,.05};
Float_t ey[n] = {.8,.7,.6,.5,.4,.4,.5,.6,.7,.8};
// create the TGraphErrors and draw it
gr = new TGraphErrors(n,x,y,ex,ey);
gr->SetTitle("TGraphErrors Example");
gr->SetMarkerColor(4);
gr->SetMarkerStyle(21);
gr->Draw("ALP");
c1->Update();
}
4.4 Graphs with Asymmetric Error Bars
Figure 4.7: A graph with asymmetric error bars
A
TGraphAsymmErrors
is a
TGraph
with asymmetric error bars. It inherits the various draw format options from
TGraph
. Its method
Paint(Option_t *option)
paints the
TGraphAsymmErrors
with the current attributes. You can
set the following additional options for drawing:

104 CHAPTER 4. GRAPHS
•“z” or “Z”the horizontal and vertical small lines are not drawn at the end of error bars
•“>”an arrow is drawn at the end of the error bars
•“|>”a full arrow is drawn at the end of the error bar; its size is 2
3of the marker size
•
“
[]
”only the end vertical/horizontal lines of the error bars are drawn; this option is interesting to superimpose
systematic errors on top of a graph with statistical errors.
The constructor has six arrays as parameters: X and Y as
TGraph
and low X-errors and high X-errors, low Y-errors
and high Y-errors. The low value is the length of the error bar to the left and down, the high value is the length of the
error bar to the right and up.
{
c1 = new TCanvas("c1","A Simple Graph with error bars",
200,10,700,500);
c1->SetGrid();
// create the arrays for the points
Int_t n = 10;
Double_t x[n] = {-.22,.05,.25,.35,.5, .61,.7,.85,.89,.95};
Double_t y[n] = {1,2.9,5.6,7.4,9,9.6,8.7,6.3,4.5,1};
// create the arrays with high and low errors
Double_t exl[n] = {.05,.1,.07,.07,.04,.05,.06,.07,.08,.05};
Double_t eyl[n] = {.8,.7,.6,.5,.4,.4,.5,.6,.7,.8};
Double_t exh[n] = {.02,.08,.05,.05,.03,.03,.04,.05,.06,.03};
Double_t eyh[n] = {.6,.5,.4,.3,.2,.2,.3,.4,.5,.6};
// create TGraphAsymmErrors with the arrays
gr = new TGraphAsymmErrors(n,x,y,exl,exh,eyl,eyh);
gr->SetTitle("TGraphAsymmErrors Example");
gr->SetMarkerColor(4);
gr->SetMarkerStyle(21);
gr->Draw("ALP");
}
4.5 Graphs with Asymmetric Bent Errors
A
TGraphBentErrors
is a
TGraph
with bent, asymmetric error bars. The various format options to draw a
TGraphBentErrors
are explained in
TGraphBentErrors::Paint method. The TGraphBentErrors
is drawn by
default with error bars and small horizontal and vertical lines at the end of the error bars. If option “
z
” or “
Z
” is
specified, these small lines are not drawn. If the option “
X
” is specified, the errors are not drawn (the
TGraph::Paint
method equivalent).
•if option contains “>”, an arrow is drawn at the end of the error bars
•if option contains “|>”, a full arrow is drawn at the end of the error bars
•the size of the arrow is set to 2/3 of the marker size
•
if option “
[]
” is specified, only the end vertical/horizontal lines of the error bars are drawn. This option is
interesting to superimpose systematic errors on top of a graph with statistical errors.
This figure has been generated by the following macro:
{
Int_t n = 10;
Double_t x[n] = {-0.22,0.05,0.25,0.35,0.5,0.61,0.7,0.85,0.89,0.95};
Double_t y[n] = {1,2.9,5.6,7.4,9,9.6,8.7,6.3,4.5,1};
Double_t exl[n] = {.05,.1,.07,.07,.04,.05,.06,.07,.08,.05};
Double_t eyl[n] = {.8,.7,.6,.5,.4,.4,.5,.6,.7,.8};
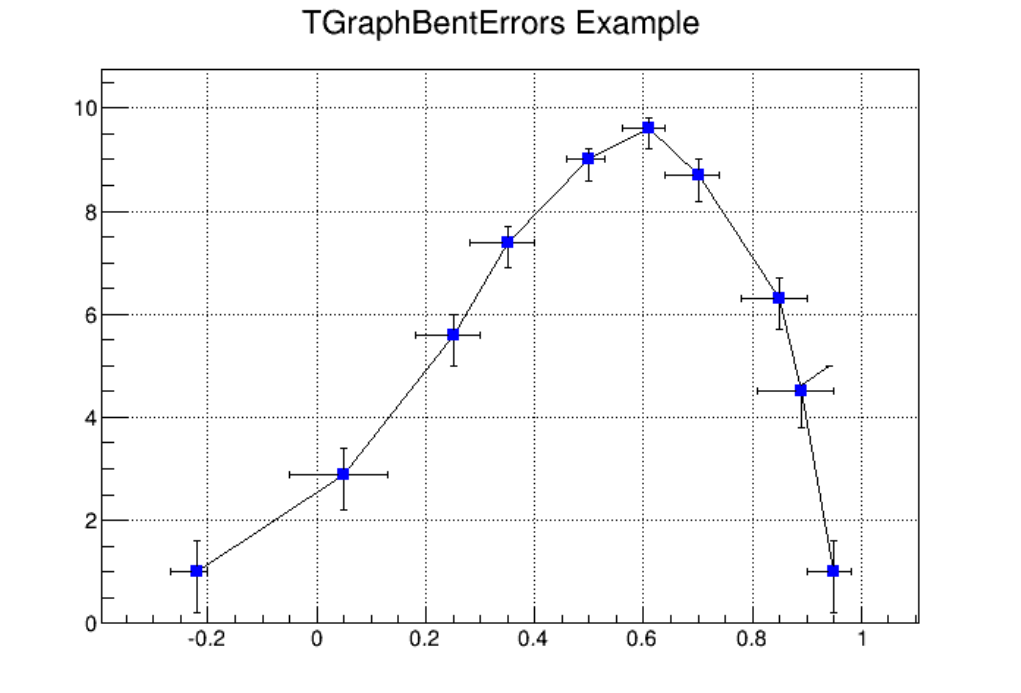
4.6. TGRAPHPOLAR 105
Figure 4.8: A graph with asymmetric bent error bars
Double_t exh[n] = {.02,.08,.05,.05,.03,.03,.04,.05,.06,.03};
Double_t eyh[n] = {.6,.5,.4,.3,.2,.2,.3,.4,.5,.6};
Double_t exld[n] = {.0,.0,.0,.0,.0,.0,.0,.0,.0,.0};
Double_t eyld[n] = {.0,.0,.0,.0,.0,.0,.0,.0,.0,.0};
Double_t exhd[n] = {.0,.0,.0,.0,.0,.0,.0,.0,.0,.0};
Double_t eyhd[n] = {.0,.0,.0,.0,.0,.0,.0,.0,.05,.0};
gr = new TGraphBentErrors(n,x,y,
exl,exh,eyl,eyh,exld,exhd,eyld,eyhd);
gr->SetTitle("TGraphBentErrors Example");
gr->SetMarkerColor(4);
gr->SetMarkerStyle(21);
gr->Draw("ALP");
}
4.6 TGraphPolar
The
TGraphPolar
class creates a polar graph (including error bars). A
TGraphPolar
is a
TGraphErrors
represented in
polar coordinates. It uses the class TGraphPolargram to draw the polar axis.
{
TCanvas *CPol = new TCanvas("CPol","TGraphPolar Examples",700,700);
Double_t rmin=0;
Double_t rmax=TMath::Pi()*2;
Double_t r[1000];
Double_t theta[1000];
TF1 * fp1 = new TF1("fplot","cos(x)",rmin,rmax);
for (Int_t ipt = 0;ipt<1000; ipt++) {
r[ipt] = ipt*(rmax-rmin)/1000+rmin;
theta[ipt] = fp1->Eval(r[ipt]);
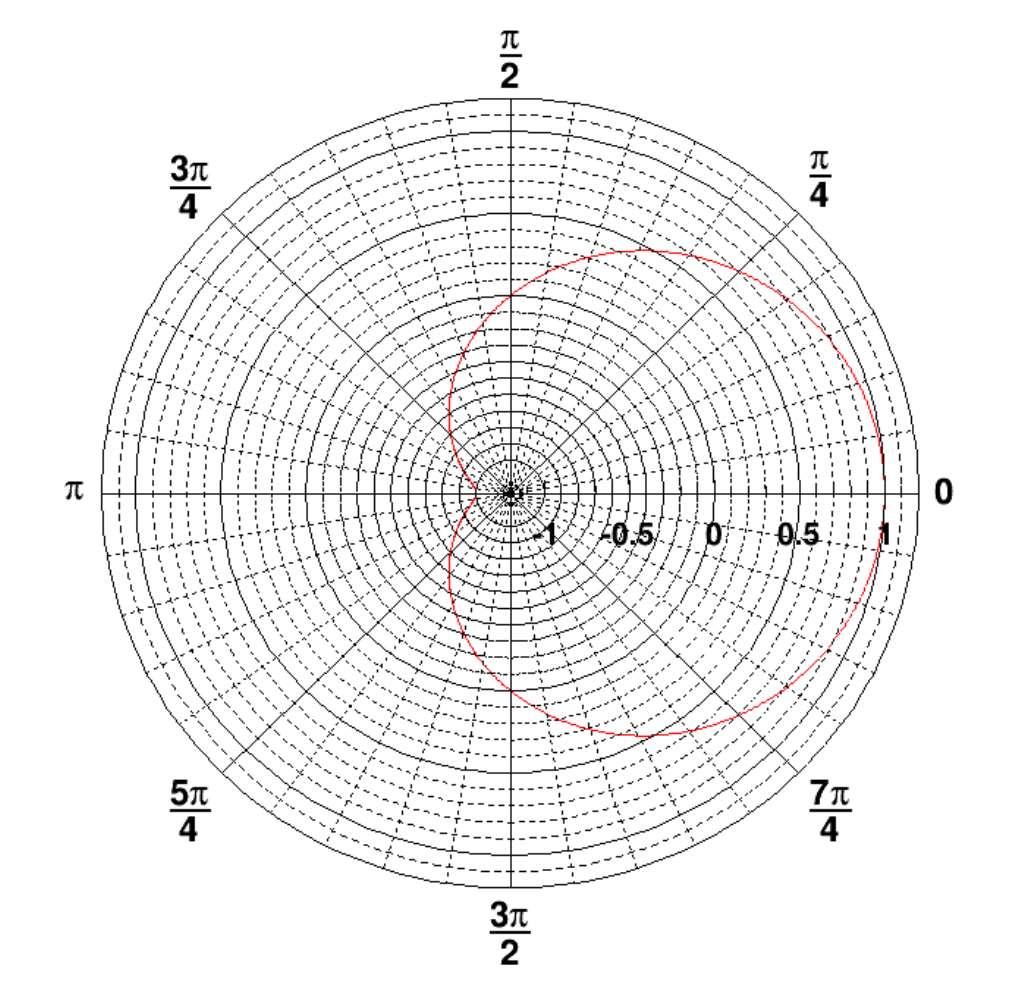
106 CHAPTER 4. GRAPHS
}
TGraphPolar * grP1 = new TGraphPolar(1000,r,theta);
grP1->SetLineColor(2);
grP1->Draw("AOL");
}
The TGraphPolar drawing options are:
“O” Polar labels are paint orthogonally to the polargram radius.
“P” Polymarker are paint at each point position.
“E” Paint error bars.
“F” Paint fill area (closed polygon).
“A”Force axis redrawing even if a polagram already exists.
Figure 4.9: A polar graph
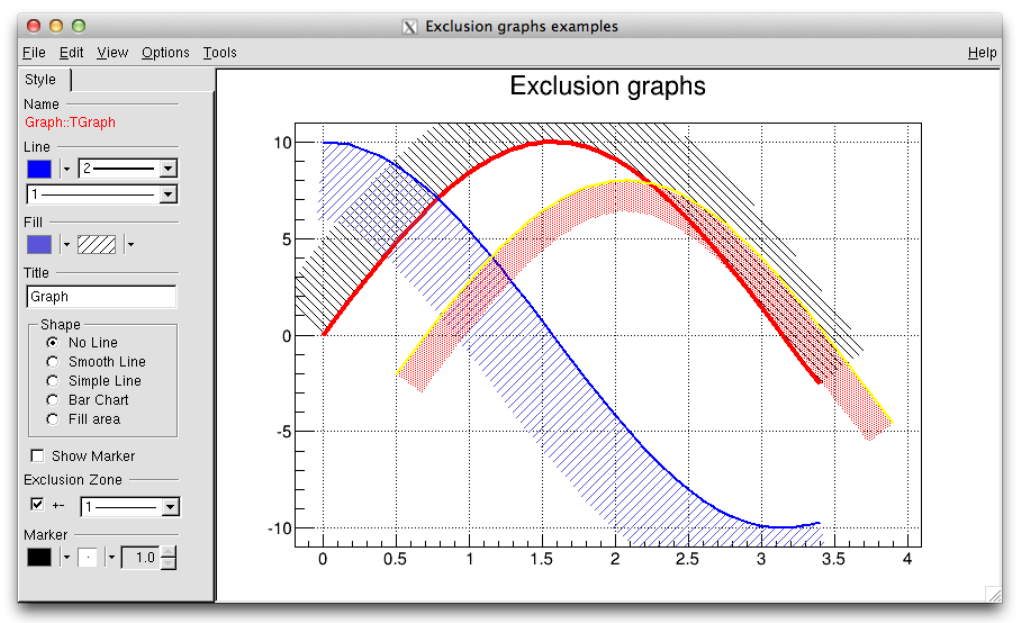
4.7. TGRAPH EXCLUSION ZONE 107
4.7 TGraph Exclusion Zone
When a graph is painted with the option “
C
” or “
L
”, it is possible to draw a filled area on one side of the line. This is
useful to show exclusion zones. This drawing mode is activated when the absolute value of the graph line width (set
thanks to
SetLineWidth
) is greater than 99. In that case the line width number is interpreted as
100*ff+ll = ffll
.
The two-digit numbers “
ll
” represent the normal line width whereas “
ff
” is the filled area width. The sign of “
ffll
”
allows flipping the filled area from one side of the line to the other. The current fill area attributes are used to draw
the hatched zone.
Figure 4.10: Graphs with exclusion zones
{
c1 = new TCanvas("c1","Exclusion graphs examples",200,10,700,500);
c1->SetGrid();
// create the multigraph
TMultiGraph *mg = new TMultiGraph();
mg->SetTitle("Exclusion graphs");
// create the graphs points
const Int_t n = 35;
Double_t x1[n], x2[n], x3[n], y1[n], y2[n], y3[n];
for (Int_t i=0;i<n;i++) {
x1[i] = i*0.1; y1[i] = 10*sin(x1[i]);
x2[i] = x1[i]; y2[i] = 10*cos(x1[i]);
x3[i] = x1[i]+.5; y3[i] = 10*sin(x1[i])-2;
}
// create the 1st TGraph
gr1 = new TGraph(n,x1,y1);
gr1->SetLineColor(2);
gr1->SetLineWidth(1504);
gr1->SetFillStyle(3005);
// create the 2nd TGraph
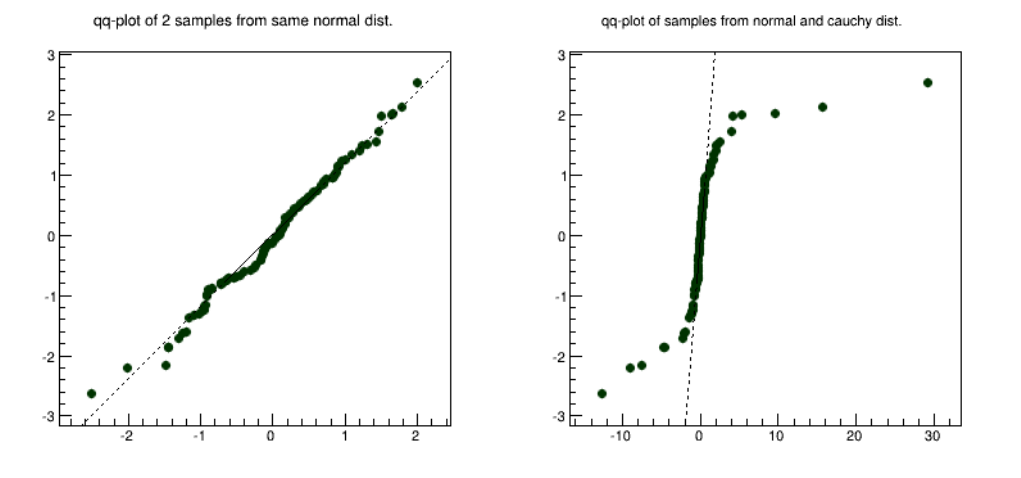
108 CHAPTER 4. GRAPHS
gr2 = new TGraph(n,x2,y2);
gr2->SetLineColor(4);
gr2->SetLineWidth(-2002);
gr2->SetFillStyle(3004);
gr2->SetFillColor(9);
// create the 3rd TGraph
gr3 = new TGraph(n,x3,y3);
gr3->SetLineColor(5);
gr3->SetLineWidth(-802);
gr3->SetFillStyle(3002);
gr3->SetFillColor(2);
// put the graphs in the multigraph
mg->Add(gr1);
mg->Add(gr2);
mg->Add(gr3);
// draw the multigraph
mg->Draw("AC");
}
4.8 TGraphQQ
A
TGraphQQ
allows drawing quantile-quantile plots. Such plots can be drawn for two datasets, or for one dataset and a
theoretical distribution function.
4.8.1 Two Datasets
Figure 4.11: Examples of qq-plots of 2 datasets
Quantile-quantile plots are used to determine whether two samples come from the same distribution. A qq-plot draws
the quantiles of one dataset against the quantile of the other. The quantiles of the dataset with fewer entries are on
Y-axis, with more entries - on X-axis. A straight line, going through 0.25 and 0.75 quantiles is also plotted for reference.
It represents a robust linear fit, not sensitive to the extremes of the datasets. If the datasets come from the same
distribution, points of the plot should fall approximately on the 45 degrees line. If they have the same distribution
function, but different parameters of location or scale, they should still fall on the straight line, but not the 45 degrees
one.
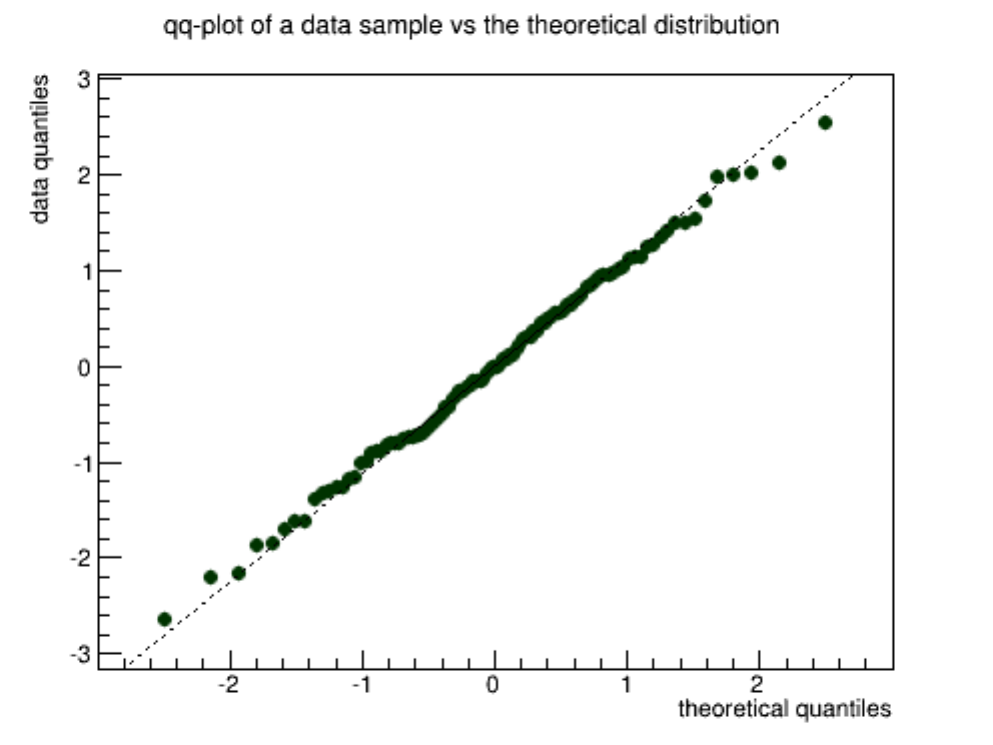
4.9. TMULTIGRAPH 109
The greater their departure from the straight line, the more evidence there is that the datasets come from different
distributions. The advantage of qq-plot is that it not only shows that the underlying distributions are different,
but, unlike the analytical methods, it also gives information on the nature of this difference: heavier tails, different
location/scale, different shape, etc.
4.8.2 One Dataset
Figure 4.12: Examples of qq-plots of 1 dataset
Quantile-quantile plots are used to determine if the dataset comes from the specified theoretical distribution, such as
normal. A qq-plot draws quantiles of the dataset against quantiles of the specified theoretical distribution. Note, that
density, not CDF should be specified a straight line, going through 0.25 and 0.75 quantiles could also be plotted for
reference. It represents a robust linear fit, not sensitive to the extremes of the dataset. As in the two datasets case,
departures from straight line indicate departures from the specified distribution. Next picture shows an example of a
qq-plot of a dataset from N(3, 2) distribution and TMath::Gaus(0, 1) theoretical function. Fitting parameters are
estimates of the distribution mean and sigma.
4.9 TMultiGraph
A
TMultiGraph
is a collection of
TGraph
(or derived) objects. Use
TMultiGraph::Add
to add a new graph to the list.
The TMultiGraph owns the objects in the list. The drawing and fitting options are the same as for TGraph.
{
// create the points
Int_t n = 10;
Double_t x[n] = {-.22,.05,.25,.35,.5,.61,.7,.85,.89,.95};
Double_t y[n] = {1,2.9,5.6,7.4,9,9.6,8.7,6.3,4.5,1};
Double_t x2[n] = {-.12,.15,.35,.45,.6,.71,.8,.95,.99,1.05};
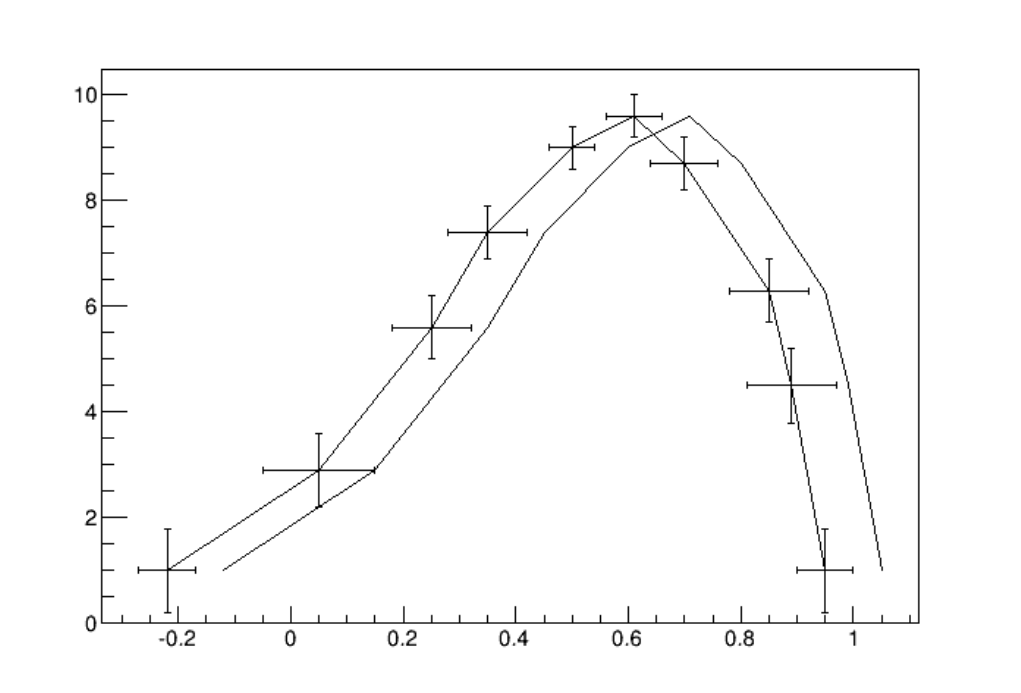
110 CHAPTER 4. GRAPHS
Figure 4.13: A multigraph example
Double_t y2[n] = {1,2.9,5.6,7.4,9,9.6,8.7,6.3,4.5,1};
// create the width of errors in x and y direction
Double_t ex[n] = {.05,.1,.07,.07,.04,.05,.06,.07,.08,.05};
Double_t ey[n] = {.8,.7,.6,.5,.4,.4,.5,.6,.7,.8};
// create two graphs
TGraph *gr1 = new TGraph(n,x2,y2);
TGraphErrors *gr2 = new TGraphErrors(n,x,y,ex,ey);
// create a multigraph and draw it
TMultiGraph *mg = new TMultiGraph();
mg->Add(gr1);
mg->Add(gr2);
mg->Draw("ALP");
}
4.10 TGraph2D
This class is a set of
N
points
x[i]
,
y[i]
,
z[i]
in a non-uniform grid. Several visualization techniques are implemented,
including Delaunay triangulation. Delaunay triangulation is defined as follow: ‘for a set
S
of points in the Euclidean
plane, the unique triangulation
DT(S)
of
S
such that no point in
S
is inside the circum-circle of any triangle in
DT(S)
.
DT(S)
is the dual of the Voronoi diagram of
S
. If n is the number of points in
S
, the Voronoi diagram of S is the
partitioning of the plane containing
S
points into n convex polygons such that each polygon contains exactly one point
and every point in a given polygon is closer to its central point than to any other. A Voronoi diagram is sometimes
also known as a Dirichlet tessellation.
The TGraph2D class has the following constructors:
•With an arrays’ dimension nand three arrays x,y, and z(can be arrays of doubles, floats, or integers):
4.10. TGRAPH2D 111
Figure 4.14: Delaunay triangles and Voronoi diagram
TGraph2D *g = new TGraph2D(n,x,y,z);
•With an array dimension only:
TGraph2D *g = new TGraph2D(n);
•Internal arrays are filled with the method SetPoint at the position “i” with the values x,y,z:
g->SetPoint(i,x,y,z);
•Without parameters; the method SetPoint must be used to fill the internal arrays.
TGraph2D *g = new TGraph2D();
•From a file:
TGraph2D *g = new TGraph2D("graph.dat");
The arrays are read from the ASCII file “
graph.dat
” according to a specified format. The format’s default value is
“
%lg %lg %lg
”. Note that in any of last three cases, the
SetPoint
method can be used to change a data point or to add
a new one. If the data point index (
i
) is greater than the size of the internal arrays, they are automatically extended.
Specific drawing options can be used to paint a TGraph2D:
•
“
TRI
” the Delaunay triangles are drawn using filled area. A hidden surface drawing technique is used. The surface
is painted with the current fill area color. The edges of the triangles are painted with the current line color;
•“TRIW”the Delaunay triangles are drawn as wire frame;
•
“
TRI1
” the Delaunay triangles are painted with color levels. The edges of the triangles are painted with the
current line color;
•“TRI2” the Delaunay triangles are painted with color levels;
•“P”draws a marker at each vertex;
•“P0” draws a circle at each vertex. Each circle background is white.
A
TGraph2D
can be also drawn with ANY options valid for 2D histogram drawing. In this case, an intermediate 2D
histogram is filled using the Delaunay triangles technique to interpolate the data set.
TGraph2D
linearly interpolate a
Z
value for any
(X,Y)
point given some existing
(X,Y,Z)
points. The existing
(X,Y,Z)
points can be randomly scattered.
The algorithm works by joining the existing points to make Delaunay triangles in
(X,Y)
. These are then used to define
flat planes in
(X,Y,Z)
over which to interpolate. The interpolated surface thus takes the form of tessellating triangles
at various angles. Output can take the form of a 2D histogram or a vector. The triangles found can be drawn in 3D.
This software cannot be guaranteed to work under all circumstances. It was originally written to work with a few
hundred points in anXY space with similar Xand Yranges.
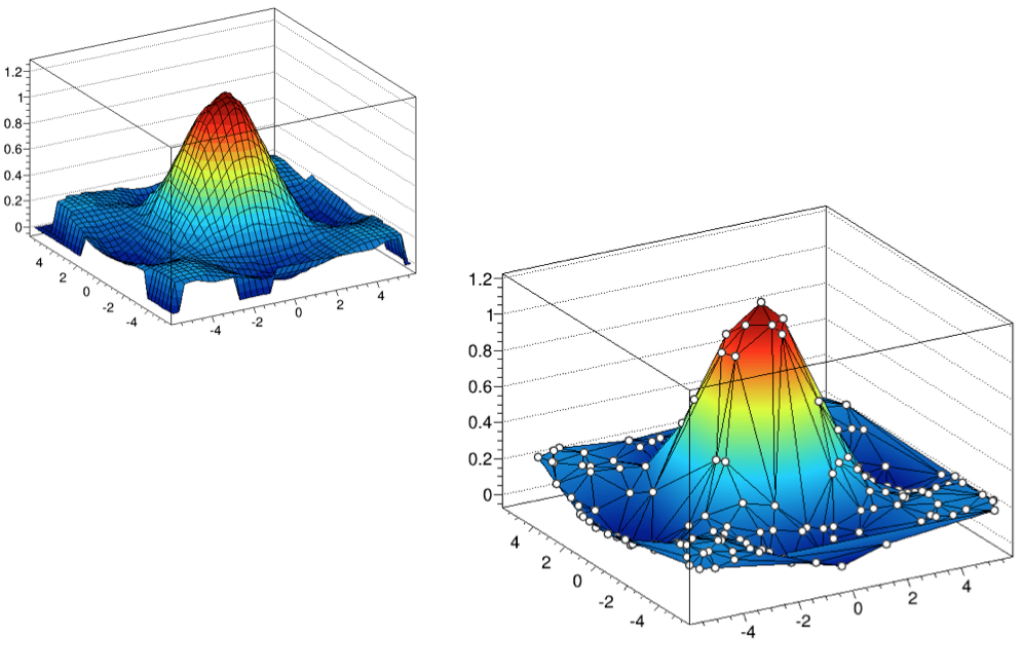
112 CHAPTER 4. GRAPHS
Figure 4.15: Graph2D drawn with option “surf1” and “tri1 p0”
{
TCanvas *c = new TCanvas("c","Graph2D example",0,0,700,600);
Double_t x, y, z, P = 6.;
Int_t np = 200;
TGraph2D *dt = new TGraph2D();
TRandom *r = new TRandom();
for (Int_t N=0; N<np; N++) {
x=2*P*(r->Rndm(N))-P;
y=2*P*(r->Rndm(N))-P;
z = (sin(x)/x)*(sin(y)/y)+0.2;
dt->SetPoint(N,x,y,z);
}
gStyle->SetPalette(55);
dt->Draw("surf1"); // use "surf1" to generate the left picture
}// use "tri1 p0" to generate the right one
A more complete example is $ROOTSYS/tutorials/fit/graph2dfit.C that produces the next figure.
4.11 TGraph2DErrors
A
TGraph2DErrors
is a
TGraph2D
with errors. It is useful to perform fits with errors on a 2D graph. An example is
the macro $ROOTSYS/tutorials/graphs/graph2derrorsfit.C.
4.12 Fitting a Graph
The graph Fit method in general works the same way as the TH1::Fit. See “Fitting Histograms”.
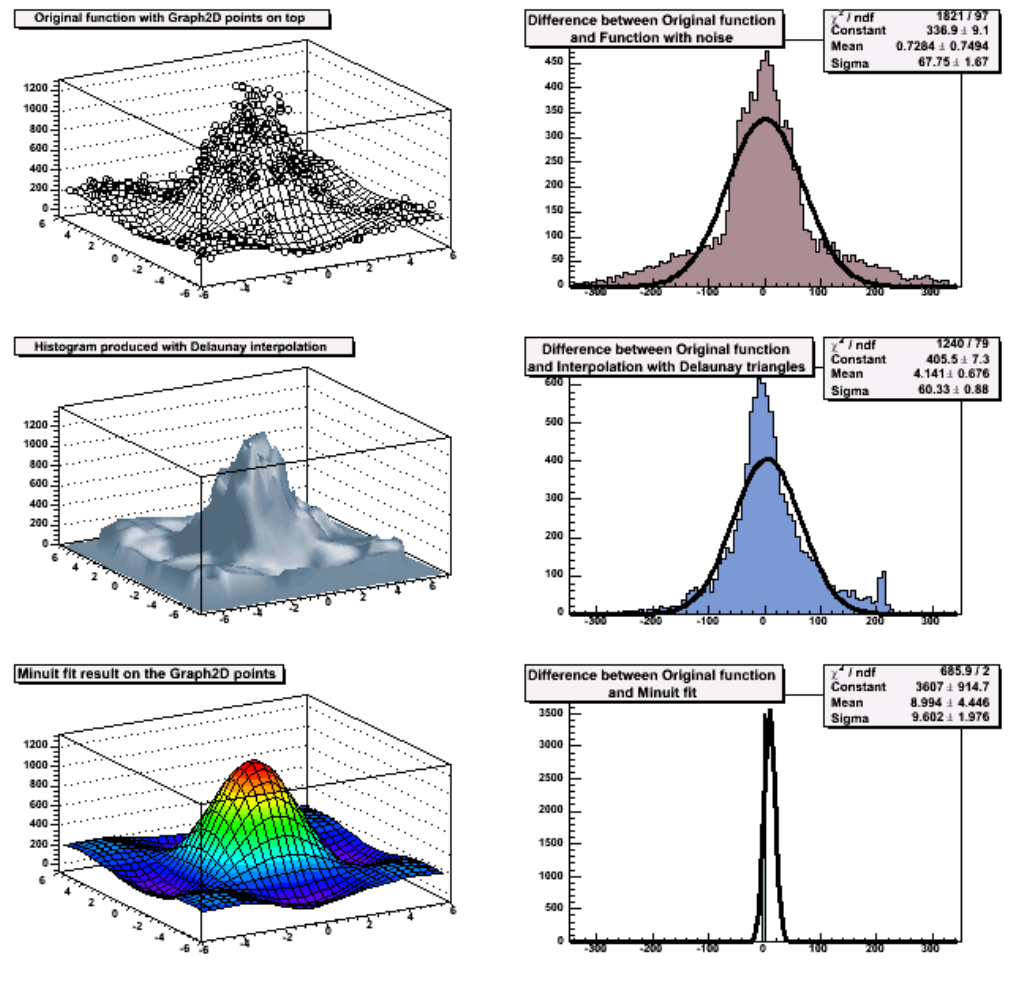
4.12. FITTING A GRAPH 113
Figure 4.16: Output of macro graph2dfit.C
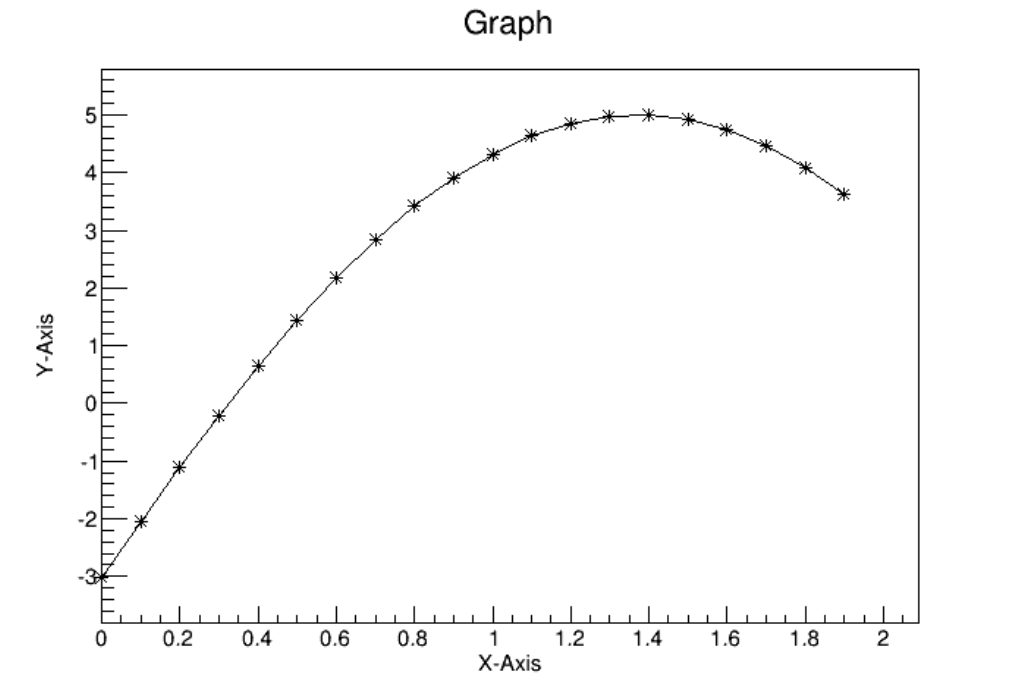
114 CHAPTER 4. GRAPHS
4.13 Setting the Graph’s Axis Title
To give the axis of a graph a title you need to draw the graph first, only then does it actually have an axis object.
Once drawn, you set the title by getting the axis and calling the
TAxis::SetTitle
method, and if you want to center
it, you can call the TAxis::CenterTitle method.
Assuming that n, x, and yare defined. Next code sets the titles of the xand yaxes.
root[] gr5 = new TGraph(n,x,y)
root[] gr5->Draw()
<TCanvas::MakeDefCanvas>: created default TCanvas with name c1
root[] gr5->Draw("ALP")
root[] gr5->GetXaxis()->SetTitle("X-Axis")
root[] gr5->GetYaxis()->SetTitle("Y-Axis")
root[] gr5->GetXaxis()->CenterTitle()
root[] gr5->GetYaxis()->CenterTitle()
root[] gr5->Draw("ALP")
For more graph examples see the scripts:
$ROOTSYS/tutorials
directory
graph.C
,
gerrors.C
,
zdemo.C
, and
gerrors2.C.
Figure 4.17: A graph with axis titles
4.14 Zooming a Graph
To zoom a graph you can create a histogram with the desired axis range first. Draw the empty histogram and then
draw the graph using the existing axis from the histogram.
{
c1 = new TCanvas("c1","A Zoomed Graph",200,10,700,500);
hpx = new TH2F("hpx","Zoomed Graph Example",10,0,0.5,10,1.0,8.0);
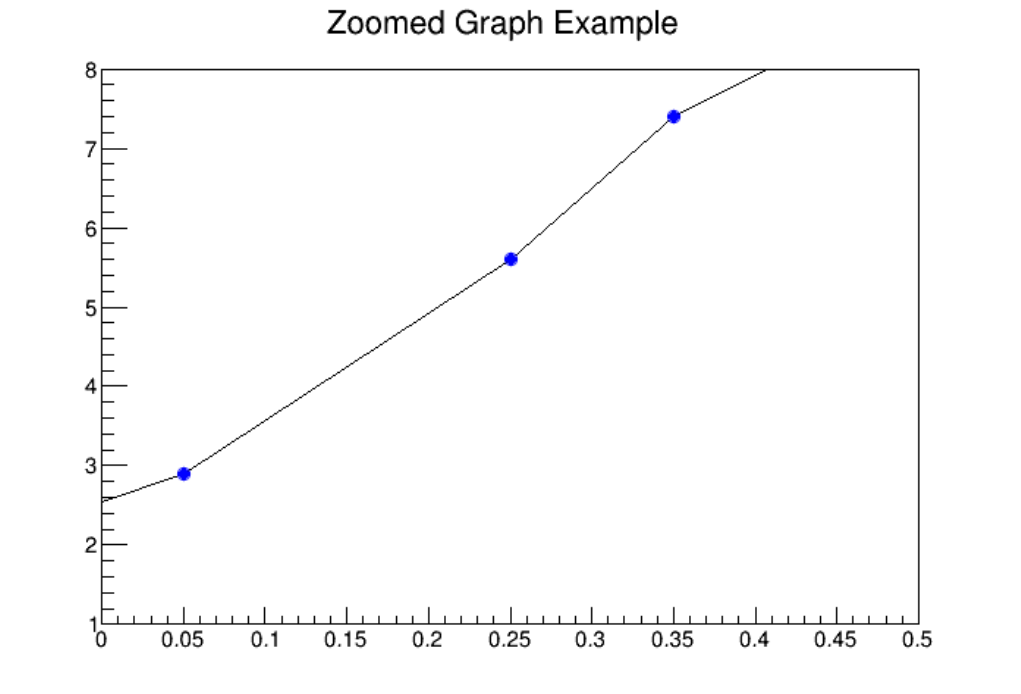
4.15. THE USER INTERFACE FOR GRAPHS 115
hpx->SetStats(kFALSE); // no statistics
hpx->Draw();
Int_t n = 10;
Double_t x[n] = {-.22,.05,.25,.35,.5,.61,.7,.85,.89,.95};
Double_t y[n] = {1,2.9,5.6,7.4,9,9.6,8.7,6.3,4.5,1};
gr = new TGraph(n,x,y);
gr->SetMarkerColor(4);
gr->SetMarkerStyle(20);
gr->Draw("LP");// and draw it without an axis
}
The next example is the same graph as above with a zoom in the x and y directions.
Figure 4.18: A zoomed graph
4.15 The User Interface for Graphs
The class TGraphEditor provides the user interface for setting the following graph attributes interactively:
•Title text entry field . . . sets the title of the graph.
•Shape radio button group - sets the graph shapes:
–No Line: draw unconnected points;
–Smooth Line: a smooth curve;
–Simple Line: a simple poly-line;
–Bart Chart: a bar chart at each point.
–Fill Area: a fill area is drawn.
•Show Marker - sets markers as visible or invisible.
•Exclusion Zone - specifies the exclusion zone parameters :
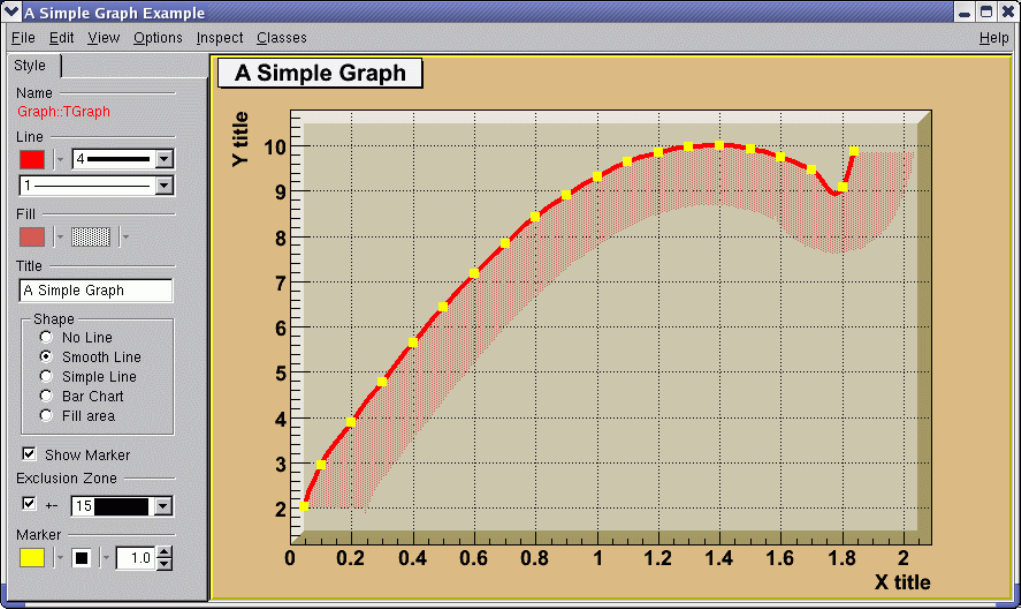
116 CHAPTER 4. GRAPHS
–’+-‘ check button: sets on which side of the line the exclusion zone will be drawn;
–Width combo box: defines the width of the zone.
Chapter 5
Fitting Histograms
To fit a histogram you can use the Fit Panel on a visible histogram via the context menu, or you can use the
TH1::Fit
method. The Fit Panel, which is limited, is best for prototyping. The histogram needs to be drawn in a pad before the
Fit Panel is invoked. The method TH1::Fit is more powerful and is used in scripts and programs.
5.1 The Fit Method
The Fit method is implemented in ROOT for the histogram classes
TH1
, the sparce histogram classes,
THnSparse
, the
graph classes, TGraph,TGraph2D and TMultiGraph for fitting a collection of Graphs with the same function.
5.1.1 The TH1::Fit Method
To fit a histogram programmatically, you can use the
TH1::Fit
method. Here is the signatures of
TH1::Fit
and an
explanation of the parameters:
TFitResultPtr Fit(TF1 *function, Option_t *option, Option_t *goption,
Axis_t xxmin, Axis_t xxmax)
•function
a pointer to the fitted function (the fit model) object. One can also use the function name. This name
may be one of ROOT pre-defined function names or a user-defined function. See the next paragraph for the list
of pre-defined functions.
•*option: The second parameter is the fitting option. Here is the list of fitting options:
–“W” Set all weights to 1 for non empty bins; ignore error bars
–“WW” Set all weights to 1 including empty bins; ignore error bars
–“I” Use integral of function in bin instead of value at bin center
–
“
L
” Use log likelihood method (default is chi-square method). To be used when the histogram represents
counts
–
“
WL
” Weighted log likelihood method. To be used when the histogram has been filled with weights different
than 1.
–
“
P
” Use Pearson chi-square method, using expected errors instead of the observed one given by
TH1::GetBinError
(default case). The expected error is instead estimated from the the square-root of the
bin function value.
–“Q” Quiet mode (minimum printing)
–“V” Verbose mode (default is between Q and V)
–“S” The result of the fit is returned in the TFitResultPtr.
–“E” Perform better errors estimation using the Minos technique
–“M” Improve fit results, by using the IMPROVE algorithm of TMinuit.
–“R” Use the range specified in the function range
–“N” Do not store the graphics function, do not draw
117
118 CHAPTER 5. FITTING HISTOGRAMS
–
“
0
” Do not plot the result of the fit. By default the fitted function is drawn unless the option “
N
” above is
specified.
–
“
+
” Add this new fitted function to the list of fitted functions (by default, the previous function is deleted
and only the last one is kept)
–
“
B
”Use this option when you want to fix one or more parameters and the fitting function is a predefined one,
like
polN
,
expo
,
landau
,
gaus
. Note that in case of pre-defined functions some default initial values and
limits are set.
–“C”In case of linear fitting, don’t calculate the chisquare (saves time).
–
“
F
”If fitting a linear function (e.g.
polN
), switch to use the default minimizer (e.g.
Minuit
). By default,
polN functions are fitted by the linear fitter.
•*goption:
The third parameter is the graphics option that is the same as in the
TH1::Draw
(see the chapter
Draw Options).
•xxmin,xxmax:Thee fourth and fifth parameters specify the range over which to apply the fit.
By default, the fitted function object is added to the histogram and is drawn in the current pad.
5.1.2 The TGraph::Fit Method
The signature for fitting a TGraph is exactly the same as for the
TH1
. Only some options apply only for fitting
histograms, these are the options “
L
”, “
WL
” and “
I
”. These options apply instead only for
TGraph::Fit
, the rest of
options (appart from “L”, “WL” and “I” are the same)
•TGraph specific options
–
“
EX0
” When fitting a
TGraphErrors
or a
TgraphAsymErrors
the errors on the coordinates are not used in
the fit
–
“
ROB
” in case of linear fitting use the Robust fitting. Compute the LTS regression coefficients (robust
(resistant) regression), using the default fraction of good points.
–“ROB=0.x” as above, but compute the LTS regression coefficients, using 0.x as a fraction of good points.
5.2 The TF1 function class
Here we will show how to create the TF1 class that is used for fitting histograms and graphs.
5.2.1 Fit with a Predefined Function
To fit a histogram with a predefined function, simply pass the name of the function in the first parameter of
TH1::Fit
.
For example, this line fits histogram object hist with a Gaussian.
root[] hist.Fit("gaus");
The initial parameter values (and eventual limits) for pre-defined functions are set automatically. For overriding the
default limits values use the fit option B.
The list of pre-defined functions that can be used with the Fit method is the following:
•“gaus” Gaussian function with 3 parameters: f(x) = p0*exp(-0.5*((x-p1)/p2)ˆ2)
•“expo”An Exponential with 2 parameters: f(x) = exp(p0+p1*x)
•“polN” A polynomial of degree N, where N is a number between 0 and 9: f(x) = p0 + p1*x + p2*x2 +...
•
“
chebyshevN
” A Chebyshev polynomial of degree N, where N is a number between 0 and 9:
f(x) = p0 + p1*x
+ p2*(2*x2-1) +...
•
“
landau
” Landau function with mean and sigma. This function has been adapted from the
CERNLIB
routine
G110 denlan (see TMath::Landau).
•
“
gausn
Normalized form of the gaussian function with 3 parameters
f(x) = p0*exp(-0.5*((x-p1)/p2)ˆ2)/(p2
*sqrt(2PI))
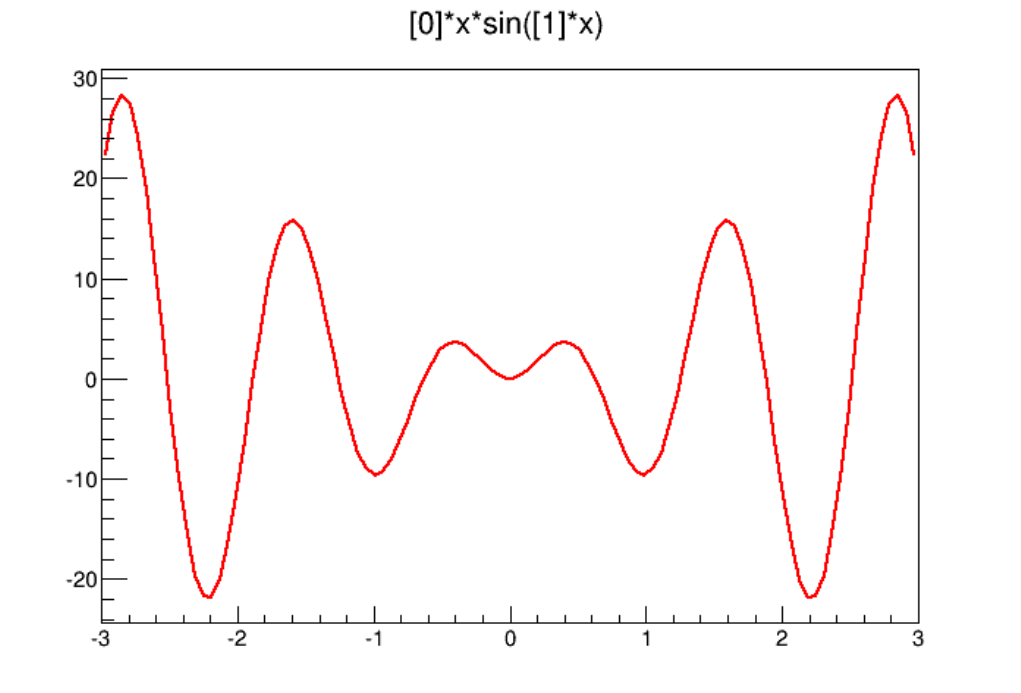
5.2. THE TF1 FUNCTION CLASS 119
5.2.2 Creating User-Defined Functions (TF1)
You can create a
TF1
object and use it in the call the
TH1::Fit
. The parameter in to the
Fit
method is the NAME of
the TF1 object. There are three ways to create a TF1.
•Using C++ expression using x with a fixed set of operators and functions defined in TFormula.
•Same as first one, with parameters
•
Using a function that you have defined. This can be a free function or a functor object or a particular member
function of a class.
5.2.2.1 Creating a TF1 with a Formula
Let’s look at the first case. Here we call the TF1 constructor by giving it the formula: sin(x)/x.
root[] TF1 *f1 = new TF1("f1","sin(x)/x",0,10)
You can also use a TF1 object in the constructor of another TF1.
root[] TF1 *f2 = new TF1("f2","f1*2",0,10)
5.2.2.2 Creating a TF1 with Parameters
The second way to construct a TF1 is to add parameters to the expression. Here we use two parameters:
root[] TF1 *f1 = new TF1("f1","[0]*x*sin([1]*x)",-3,3);
Figure 5.1: The function x*sin(x)
The parameter index is enclosed in square brackets. To set the initial parameters explicitly you can use:
120 CHAPTER 5. FITTING HISTOGRAMS
root[] f1->SetParameter(0,10);
This sets parameter 0 to 10. You can also use SetParameters to set multiple parameters at once.
root[] f1->SetParameters(10,5);
This sets parameter 0 to 10 and parameter 1 to 5. We can now draw the TF1:
root[] f1->Draw()
5.2.2.3 Creating a TF1 with a User Function
The third way to build a
TF1
is to define a function yourself and then pass the function pointer to the constructor. A
function for a TF1 constructor needs to have this exact signature:
Double_t fitf(Double_t *x,Double_t *par)
The two parameters are:
•x
a pointer to the dimension array. Each element contains a dimension. For a 1D histogram only
x[0]
is used, for
a 2D histogram
x[0]
and
x[1]
is used, and for a 3D histogram
x[0]
,
x[1]
, and
x[2]
are used. For histograms,
only 3 dimensions apply, but this method is also used to fit other objects, for example an ntuple could have 10
dimensions.
•par
a pointer to the parameters array. This array contains the current values of parameters when it is called by
the fitting function.
The following script
$ROOTSYS/tutorials/fit/myfit.C
illustrates how to fit a 1D histogram with a user-defined
function. First we declare the function.
// define a function with 3 parameters
Double_t fitf(Double_t *x,Double_t *par) {
Double_t arg = 0;
if (par[2]!=0) arg = (x[0] - par[1])/par[2];
Double_t fitval = par[0]*TMath::Exp(-0.5*arg*arg);
return fitval;
}
Now we use the function:
// this function used fitf to fit a histogram
void fitexample() {
// open a file and get a histogram
TFile *f = new TFile("hsimple.root");
TH1F *hpx = (TH1F*)f->Get("hpx");
// Create a TF1 object using the function defined above.
// The last three parameters specify the number of parameters
// for the function.
TF1 *func = new TF1("fit",fitf,-3,3,3);
// set the parameters to the mean and RMS of the histogram
func->SetParameters(500,hpx->GetMean(),hpx->GetRMS());
// give the parameters meaningful names
func->SetParNames ("Constant","Mean_value","Sigma");
// call TH1::Fit with the name of the TF1 object
hpx->Fit("fit");
}
5.3. CONFIGURING THE FIT 121
You can create a TF1 also from a C++ function object (functor) with parameters A TF1 can be created from any
C++ class implementing this member function:
double operator()(double *x, double *p)
The advantage of the function object is that it can have a state and reference therefore what-ever other object the user
needs, without using globals. This is an example to define first the function object
class MyFunctionObject {
public:
// use constructor to customize your function object
MyFunctionObject(......) { ......}
double operator() (double *x, double *p) {
// function implementation using class data members
}
};
and then use it to create the TF1:
MyFunctionObject fobj(....); // create the function object
TF1 * f = new TF1("f",fobj,xmin,xmax,npar); // create TF1 class with n-parameters and range [xmin,xmax]
If using C++11, one can create a TF1 also from a C++ lambda function:
// create TF1 class with 2 parameters and range [xmin,xmax] using a lambda
TF1 * f = new TF1("f",[](double*x,double*p){return p[0] + p[1]*x[0];},xmin,xmax,2);
5.3 Configuring the Fit
We will show here some configuration actions that can or must be done when fitting histogram or graph using the
Fit
method.
5.3.1 Fixing and Setting Parameters’ Bounds
Parameters must be initialized before invoking the
Fit
method. The setting of the parameter initial values is automatic
for the predefined functions:
poln
,
exp
,
gaus
, and
landau
. You can fix one or more parameters by specifying the “B”
option when calling the
Fit
method. When a function is not predefined, the fit parameters must be initialized to some
value as close as possible to the expected values before calling the fit function.
To set bounds for one parameter, use TF1::SetParLimits:
func->SetParLimits(0,-1,1);
When the lower and upper limits are equal, the parameter is fixed. Next two statements fix parameter 4 at 10.
func->SetParameter(4,10);
func->SetParLimits(4,10,10);
However, to fix a parameter to 0, one must call the FixParameter function:
func->SetParameter(4,0);
func->FixParameter(4,0);
Note that you are not forced to set the limits for all parameters. For example, if you fit a function with 6 parameters,
you can:
func->SetParameters(0,3.1,1.e-6,-1.5,0,100);
func->SetParLimits(3,-10,4);
func->FixParameter(4,0);
With this setup, parameters 0
->
2 can vary freely, parameter 3 has boundaries [-10, 4] with initial value -1.5, and
parameter 4 is fixed to 0.
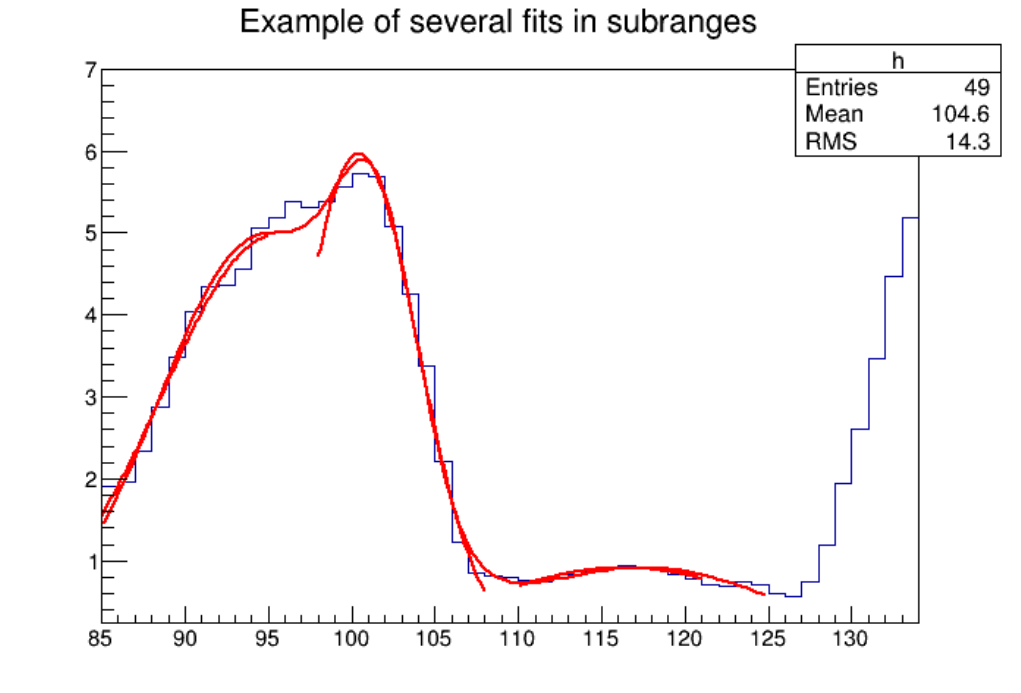
122 CHAPTER 5. FITTING HISTOGRAMS
5.3.2 Fitting Sub Ranges
By default,
TH1::Fit
will fit the function on the defined histogram range. You can specify the option “
R
” in the second
parameter of
TH1::Fit
to restrict the fit to the range specified in the
TF1
constructor. In this example, the fit will be
limited to -3 to 3, the range specified in the TF1 constructor.
root[] TF1 *f1 = new TF1("f1","[0]*x*sin([1]*x)",-3,3);
root[] hist->Fit("f1","R");
You can also specify a range in the call to TH1::Fit:
root[] hist->Fit("f1","","",-2,2)
See macros $ROOTSYS/tutorials/fit/myfit.C and multifit.C as more completed examples.
5.3.3 Fitting Multiple Sub Ranges
The script for this example is
$ROOTSYS/tutorials/fit/multifit.C
. It shows how to use several Gaussian functions
with different parameters on separate sub ranges of the same histogram. To use a Gaussian, or any other ROOT built
in function, on a sub range you need to define a new TF1. Each is ‘derived’ from the canned function gaus.
Figure 5.2: Fitting a histogram with several Gaussian functions
First, four TF1 objects are created - one for each sub-range:
g1 = new TF1("m1","gaus",85,95);
g2 = new TF1("m2","gaus",98,108);
g3 = new TF1("m3","gaus",110,121);
// The total is the sum of the three, each has 3 parameters
total = new TF1("mstotal","gaus(0)+gaus(3)+gaus(6)",85,125);
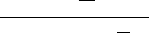
5.4. EXAMPLE OF FIT: COMBINING FUNCTIONS 123
Next, we fill a histogram with bins defined in the array x.
// Create a histogram and set it's contents
h = new TH1F("g1","Example of several fits in subranges",
np,85,134);
h->SetMaximum(7);
for (int i=0; i<np; i++) {
h->SetBinContent(i+1,x[i]);
}
// Define the parameter array for the total function
Double_t par[9];
When fitting simple functions, such as a Gaussian, the initial values of the parameters are automatically computed by
ROOT. In the more complicated case of the sum of 3 Gaussian functions, the initial values of parameters must be set.
In this particular case, the initial values are taken from the result of the individual fits. The use of the “+” sign is
explained below:
// Fit each function and add it to the list of functions
h->Fit(g1,"R");
h->Fit(g2,"R+");
h->Fit(g3,"R+");
// Get the parameters from the fit
g1->GetParameters(&par[0]);
g2->GetParameters(&par[3]);
g3->GetParameters(&par[6]);
// Use the parameters on the sum
total->SetParameters(par);
h->Fit(total,"R+");
5.3.4 Adding Functions to the List
The example
$ROOTSYS/tutorials/fit/multifit.C
also illustrates how to fit several functions on the same histogram.
By default a Fit command deletes the previously fitted function in the histogram object. You can specify the option
“+” in the second parameter to add the newly fitted function to the existing list of functions for the histogram.
root[] hist->Fit("f1","+","",-2,2)
Note that the fitted function(s) are saved with the histogram when it is written to a ROOT file.
5.4 Example of fit: Combining Functions
You can combine functions to fit a histogram with their sum as it is illustrated in the macro
FitDemo.C
(
$ROOTSYS/tutorials/fit/FittingDemo.C)
. We have a function that is the combination of a background and
Lorentzian peak. Each function contributes 3 parameters:
y(E) = a1+a2E+a3E2+Ap(G
2p)
(E−m)2+ (G
2)2
BackgroundLorentzian Peak
par[0] =a1par[0] =Ap
par[1] =a2par[1] =G
par[2] =a3par[2] =m
The combination function (fitFunction) has six parameters:
fitFunction = background(x,par) + LorentzianPeak(x,&par[3])
124 CHAPTER 5. FITTING HISTOGRAMS
par[0]=a1par[1]=a2par[2]=a3par[3]=Appar[4]=Gpar[5]=m
This script creates a histogram and fits it with the combination of two functions. First we define the two functions and
the combination function:
// Quadratic background function
Double_t background(Double_t *x, Double_t *par) {
return par[0] + par[1]*x[0] + par[2]*x[0]*x[0];
}
// Lorentzian Peak function
Double_t lorentzianPeak(Double_t *x, Double_t *par) {
return (0.5*par[0]*par[1]/TMath::Pi()) / TMath::Max(1.e-10,
(x[0]-par[2])*(x[0]-par[2])+ .25*par[1]*par[1]);
}
// Sum of background and peak function
Double_t fitFunction(Double_t *x, Double_t *par) {
return background(x,par) + lorentzianPeak(x,&par[3]);
}
void FittingDemo() {
// bevington exercise by P. Malzacher, modified by R. Brun
const int nBins = 60;
Stat_t data[nBins] = { 6,1,10,12,6,13,23,22,15,21,
23,26,36,25,27,35,40,44,66,81,
75,57,48,45,46,41,35,36,53,32,
40,37,38,31,36,44,42,37,32,32,
43,44,35,33,33,39,29,41,32,44,
26,39,29,35,32,21,21,15,25,15};
TH1F *histo = new TH1F("example_9_1",
"Lorentzian Peak on Quadratic Background",60,0,3);
for(int i=0; i < nBins; i++) {
// we use these methods to explicitly set the content
// and error instead of using the fill method.
histo->SetBinContent(i+1,data[i]);
histo->SetBinError(i+1,TMath::Sqrt(data[i]));
}
// create a TF1 with the range from 0 to 3 and 6 parameters
TF1 *fitFcn = new TF1("fitFcn",fitFunction,0,3,6);
// first try without starting values for the parameters
// this defaults to 1 for each param.
histo->Fit("fitFcn");
// this results in an ok fit for the polynomial function however
// the non-linear part (Lorentzian
5.5 Result of the fit
Here we will show how to obtain the result of the fit (fitted function, parameter values, errors and eventually the
covariance and correlation matrix).
5.5.1 Associated Function
One or more objects (typically a
TF1
*) can be added to the list of functions (
fFunctions
) associated to each histogram.
A call to
TH1::Fit
adds the fitted function to this list. Given a histogram
h
, one can retrieve the associated function
with:
TF1 *myfunc = h->GetFunction("myfunc");
5.5. RESULT OF THE FIT 125
Figure 5.3: The output of the FittingDemo() example
5.5.2 Access to the Fit Parameters and Results
If the histogram (or graph) is made persistent, the list of associated functions is also persistent. Retrieve a pointer to the
function with the
TH1
::GetFunction()
method. Then you can retrieve the fit parameters from the function
(**TF1‘**) with calls such as:
root[] TF1 *fit = hist->GetFunction(function_name);
root[] Double_t chi2 = fit->GetChisquare();
// value of the first parameter
root[] Double_t p1 = fit->GetParameter(0);
// error of the first parameter
root[] Double_t e1 = fit->GetParError(0);
Using the fit option
S
one can access the full result of the fit including the covariance and correlation matrix. See later
the paragraph TFitResult.
5.5.3 Associated Errors
By default, for each bin, the sum of weights is computed at fill time. One can also call
TH1::Sumw2
to force the storage
and computation of the sum of the square of weights per bin. If Sumw2 has been called, the error per bin is computed
as the
sqrt(sum of squares of weights)
; otherwise, the error is set equal to the
sqrt(bin content)
. To return
the error for a given bin number, do:
Double_t error = h->GetBinError(bin);
Empty bins are excluded in the fit when using the Chi-square fit method. When fitting an histogram representing
counts (i.e with Poisson statistics) it is recommended to use the Log-Likelihood method (option ‘
L
’ or “
WL
”), particularly
in case of low statistics. When the histogram has been filled with weights different than one, a weighted likelihood
method can be used and the errors retrieved from the fit are corrected following a procedure described in paragraph
8.5.2 of the book, F. James, Statistical Methods in Experimental Physics, 2nd Edition.
126 CHAPTER 5. FITTING HISTOGRAMS
5.5.4 Fit Statistics
You can change the statistics box to display the fit parameters with the
TStyle::SetOptFit(mode)
method. This
parameter has four digits: mode = pcev (default = 0111)
•p= 1 print probability
•c= 1 print Chi-square/number of degrees of freedom
•e= 1 print errors (if e=1,vmust be 1)
•v= 1 print name/values of parameters
For example, to print the fit probability, parameter names/values, and errors, use:
gStyle->SetOptFit(1011);
5.6 The Fit Panel
To display the Fit Panel right click on a histogram to pop up the context menu, and then select the menu entry Fit
Panel.
The new Fit Panel GUI is available in ROOT v5.14. Its goal is to replace the old Fit Panel and to provide more user
friendly way for performing, exploring and comparing fits.
By design, this user interface is planned to contain two tabs: “General” and “Minimization”. Currently, the “General”
tab provides user interface elements for setting the fit function, fit method and different fit, draw, print options. The
“Minimization tab” provides the option to set the Minimizer to use in the fit and its specific options.
The new fit panel is a modeless dialog, i.e. when opened, it does not prevent users from interacting with other windows.
Its first prototype is a singleton application. When the Fit Panel is activated, users can select an object for fitting in
the usual way, i.e. by left-mouse click on it. If the selected object is suitable for fitting, the fit panel is connected with
this object and users can perform fits by setting different parameters and options.
5.6.1 Function Choice and Settings
‘Predefined’ combo box - contains a list of predefined functions in ROOT. You have a choice of several polynomials, a
Gaussian, a Landau, and an Exponential function. The default one is Gaussian.
‘Operation’ radio button group defines the selected operational mode between functions:
Nop - no operation (default);
Add - addition;
Conv - convolution (will be implemented in the future).
Users can enter the function expression into the text entry field below the ‘Predefined’ combo box. The entered string
is checked after the Enter key was pressed and an error message shows up, if the function string is not accepted.
‘Set Parameters’ button opens a dialog for parameters settings, which will be explaned later.
5.6.2 Fitter Settings
‘Method’ combo box currently provides only two fit model choices: Chi-square and Binned Likelihood. The default one
is Chi-square. The Binned Likelihood is recomended for bins with low statistics.
‘Linear Fit’ check button sets the use of Linear fitter when is selected. Otherwise the minimization is done by Minuit,
i.e. fit option “
F
” is applied. The Linear fitter can be selected only for functions linears in parameters (for example -
polN).
‘Robust’ number entry sets the robust value when fitting graphs.
‘No Chi-square’ check button switch On/Off the fit option “C” - do not calculate Chi-square (for Linear fitter).
‘Integral’ check button switch On/Off the option “I” - use integral of function instead of value in bin center.
‘Best Errors’ sets On/Off the option “E” - better errors estimation by using Minos technique.
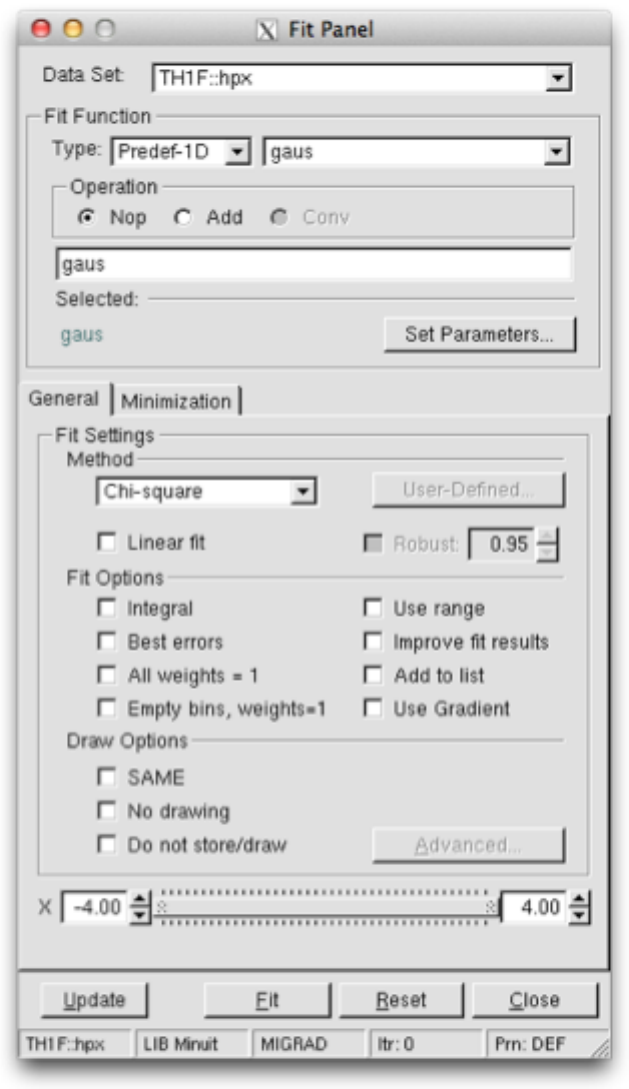
5.6. THE FIT PANEL 127
Figure 5.4: The Fit Panel
128 CHAPTER 5. FITTING HISTOGRAMS
‘All weights = 1’ sets On/Off the option “W”- all weights set to 1 excluding empty bins; error bars ignored.
‘Empty bins, weights=1’ sets On/Off the option “
WW
” - all weights equal to 1 including empty bins; error bars ignored.
‘Use range’ sets On/Off the option “
R
” - fit only data within the specified function range. Sliders settings are used if
this option is set to On. Users can change the function range values by pressing the left mouse button near to the
left/right slider edges. It is possible to change both values simultaneously by pressing the left mouse button near to the
slider center and moving it to a new position.
‘Improve fit results’ sets On/Off the option “M”- after minimum is found, search for a new one.
‘Add to list’ sets On/Off the option “
+
”- add function to the list without deleting the previous one. When fitting a
histogram, the function is attached to the histogram’s list of functions. By default, the previously fitted function is
deleted and replaced with the most recent one, so the list only contains one function. Setting this option to On will
add the newly fitted function to the existing list of functions for the histogram. Note that the fitted functions are
saved with the histogram when it is written to a ROOT file. By default, the function is drawn on the pad displaying
the histogram.
5.6.3 Draw Options
‘SAME’ sets On/Off function drawing on the same pad. When a fit is executed, the image of the function is drawn on
the current pad.
‘No drawing’ sets On/Off the option “0”- do not draw the fit results.
‘Do not store/draw’ sets On/Off option “N”- do not store the function and do not draw it.
5.6.4 Advances Options
The advance option button is enabled only after having performed the fit and provides additional drawing options that
can be used after having done the fit. These new drawing tools, which can be selected by the “Advanced Drawing Tool”
panel that pops up when clicking the “Advanced” button, are:
•
Contour: to plot the confidence contour of two chosen parameters. One can select the number of points to draw
the contour (more points might require more time to compute it), the parameters and the desired confidence
level .
•
Scan : to plot a scan of the minimization function (likelihood or chi-squared) around the minimum as function of
the chosen parameter.
•
Conf Interval : to plot the confidence interval of the fitted function as a filled coloured band around its central
value. One can select the desired confidence level for the band to be plotted.
5.6.5 Print Options
This set of options specifies the amount of feedback printed on the root command line after performed fits.
‘Verbose’ - prints fit results after each iteration.
‘Quiet’ - no fit information is printed.
‘Default’ - between Verbose and Quiet.
5.6.6 Command Buttons
Fit button - performs a fit taking different option settings via the Fit Panel interface.
Reset - sets the GUI elements and related fit settings to the default ones.
Close - closes the Fit panel window.
5.7. NEW ROOT::FIT CLASSES 129
5.6.7 Minimization Options
With this tab one can select specific options for minimization. These include
•The minimizer library ( Minuit,Minuit2,Fumili,GSL,Genetics )
•
The method (algorithm) for minimization. For example for Minuit one can choose between (Migrad,Simplex or
Scan)
•Error definition
•Minimization tolerance
•Number of iterations/function calls
•Print Level: (Default,Verbose or Quiet).
5.7 New ROOT::Fit classes
The fitting of the data objects in ROOT, histograms, graphs and tree is performed via some common classes, which are
defined in the ROOT::Fit namespace. These classes can be classified in the following groups:
•
User classes driving the fit:
ROOT::Fit::Fitter
for executing the fit,
ROOT::Fit::FitConfig
for configuring
the fit,
ROOT::Fit::ParameterSettings
to define the properties of the fit parameters (initial values, bounds,
etc..), ROOT::Fit::FitResult for storing the result of the fit.
•
Data classes containing the data sets used in the fitting. These classes are the
ROOT::Fit::BinData
for describing
bin data sets, thus data points containing both coordinates and a corresponding value/weight with optionally
an error on the value or the coordinate and the
ROOT::Fit::UnBinData
for un-binned data sets, which consisst
only of a vector of coordinate values. The coordinate values can be one-dimensional (i.e. one entry per event) or
multi-dimensional (N entries per event).
•Function classes defining the type of fit (the objective function used for fitting):
–ROOT::Fit::Chi2FCN for chi2 (least-square fits),
–ROOT::Fit::PoissonLikelihoodFCN for binned likelihood fits of histograms,
–ROOT::Fit::LogLikelihoodFCN
for generic un-binned likelihood fits. These classes are templated
on the type of function interface they implement (see later). User convenient typedefs are also
provided. They derive from the common generic interface multi-dimensional for function evaluation,
ROOT::Math::IBaseFunctionMultiDim.
In addition the fitter classes make uses of the generic interfaces for parametric function evaluations,
ROOT::Math::IParametricFunctionMultiDim
to define the fit model function and use the
ROOT::Math::Minimizer
interface to perform the minimization of the
objective function.
More information about the function interface and the multi-dimensional minimization in ROOT is given in the
Mathematical Library chapter.
Here we present a detailed description of the
ROOT::Fit
classes and how to use them. Using these classes instead of
the interface provided directly in the ROOT data objects, like
TH1::Fit
allow are more fine control to configure and
customise the fits. For example, using these classes a combined fit of several histograms can be performed.
To understand how these class work, let’s go through a simple example, such as fitting an histogram.
When fitting an histogram, instead of using
TH1::Fit
we will show in the following hot wo use the
ROOT::Fit
classes.
We will show how to perform the following different type of fits with the histogram data: * a least square fit using
the observed errors (Neyman chi-squared); * a least square fit using the expected errors from the function (Pearson
chi-squared); * a binned likelihood fit; * an extended unbinned likelihood fits, if the histogram has been set to store in
the buffer the original data used to fill it.
Let’s go through all the steps required for performing these fits using the ROOT::Fit::Fitter class. These steps are:
1. Create the input fit data object. 2. Create the input model function. 3. Configure the fit. 4. Perform the data
fitting. 5. Examine the result.
5.7.1 Creating the input fit data
We have two types of input data, binned data (class
ROOT::Fit::BinData
) used for least square (chi-square) fits of
histograms or
TGraph
objects or un-binned data (class
ROOT::Fit::UnBinData
) used for fitting vectors of data points
(e.g. from a TTree).
130 CHAPTER 5. FITTING HISTOGRAMS
5.7.1.1 Using Binned data
Let’s suppose we have an histogram, represented as a
TH1
type object (it can be one or multi-dimensional). The
following shows how to create and fill a ROOT:Fit::BinData object.
ROOT::Fit::DataOptions opt;
opt.fIntegral = true;
ROOT::Fit::BinData data(opt);
// fill the bin data using the histogram
// we can do this using the following helper function from the Hist library
TH1 * h1 = (TH1*) gDirectory->Get("myHistogram");
ROOT::Fit::FillData(data, h1);
In this code example, we have used the utility function of the Hist library,
ROOT::Fit::FillData
to fill the
BinData
object. The
ROOT::Fit::FillData
is defined in the headerfile
HFitInterface.h
and it has a signature for all different
ROOT objects, like
TH1
,
THnBase
,
TGraph
,
TGraph2D
and
TMultiGraph
It is possible to specify, when creating the
BinData
object, the data range we want to use and some fitting options we want to apply to fill in the object and
later when fitting. The fit data options are controlled by the
ROOT::Fit::DataOptions
class, the range by the
ROOT::Fit::DataRange class.
Here is an example how to specify the input option to use the integral of the function value in the bin instead of using
the function value evaluated at the bin center, when doing the fit and to use a range beween the ‘xmin’ and ‘xmax’
values.
ROOT::Fit::DataOptions opt;
opt.fIntegral = true;
ROOT::Fit::DataRange range(xmin,xmax);
ROOT::Fit::BinData data(opt,range);
// fill the bin data using the histogram
// we can do this using the following helper function from the Hist library
TH1 * h1 = (TH1*) gDirectory->Get("myHistogram");
ROOT::Fit::FillData(data, h1);
The list of possible fit options available is the following:
ROOT::Fit::DataOptions opt;
opt.fIntegral = true;// use integral of bin content instead of bin center (default is false).
opt.fBinVolume = true;// normalize data by the bin volume (default is false).
// This is for fitting density functions in histograms with variable bin sizes.
opt.fUseRange =true;// use the function range when creating the fit data (default is false).
opt.fExpErrors = true;// use the expected errors estimated from the function values
// assuming Poisson statistics and not the observed errors (default is false).
opt.fUseEmpty = true;// use empty bins when fitting (default is false). If fExpErrors
// is not set an arbitrary error = 1 is assigned to those bins.
opt.fErrors1 = true;// Set all measured errors to 1 (default is false).
opt.fCoordErrors = false;// When available coordinate errors are not used in the fit
// (default is true: the errors are used when they are available,
// e.g. fitting a TGraphErrors).
opt.fAsymErrors = false;// When available asymmetric errors are considered in the fit
// (default is true, the asymmetric errors are used when they are available,
// e.g. fitting a TGraphAsymmErrors).
The
ROOT::Fit::DataRange
class supports defining multiple rectangular ranges in each dimension, and supports
n-dimension. The function
DataRange::AddRange(icoord,xmin,xmax)
adds a range in the coordinate
icoord
with
lower value xmin and upper value xmax:
ROOT::Fit::DataRange range;
range.AddRange(icoordinate, xmin, xmax);
5.7. NEW ROOT::FIT CLASSES 131
5.7.1.2 Using Un-Binned data
The unbinned data sets are represented with the
ROOT::Fit::UnBinData
class. For creating un-binned data sets, a
ROOT::Fit::UnBinData
object, one has two possibilities: 1. Copy the data inside
ROOT::Fit::UnBinData
. One can
create an empty
UnBinData
object, iterate on the data and add the data point one by one, or directly create the
UnBinData
object from a data iterator. In this case an input
ROOT::Fit::DataRange
object is passed in order to copy
the data according to the given range. 2. Use
ROOT::Fit::UnBinData
as a wrapper to an external data storage. In
this case the
UnBinData
object is created from an iterator or pointers to the data and the data are not copied inside.
In this case the data cannot be selected according to a specified range. All the data points will be included in the fit.
The
ROOT::Fit::UnBinData
class supports also weighted data. In addition to the data points (coordinates), which
can be of arbitrary
k
dimensions, the class can be constructed from a vector of weights. This is an example of taking
data from an histogram buffer of a TH1 object:
double * buffer = histogram->GetBuffer();
// number of entry is first entry in the buffer
int n = buffer[0];
// when creating the data object it is important to create with the size of the data
ROOT::Fit::UnBinData data(n);
for (int i=0; i < n; ++i)
data.add(buffer[2*i+1]); // the buffer of 1D histogram contains nevt,x1,w1,x2,w2,......
Instead in this example we will create a 2-dim UnBinData object with the contents from a ROOT TTree
TFile * file = TFile::Open("hsimple.root");
TTree *ntuple = 0; file->GetObject("ntuple",ntuple);
// select from the tree the data we want to use for fitting
// we use TTree::Draw for this
int nevt = ntuple->Draw("px:py","","goff");
double * x = ntuple->GetV1();
double * y = ntuple->GetV2();
ROOT::Fit::UnBinData data(nevt, x, y );
5.7.2 Creating the Fit model
In order to fit a data sets we need a model to describe our data, e.g. a probability density function describing our
observed data or an hypothetical function describing the relation between the independent variables
X
and the single
dependent variable
Y
. We can have an arbitrary number
k
of independent variables. For example, when fitting a
k-dimensional histogram, the independent variables Xare the bin center coordinates and Yis the bin weight.
The model function needs to be expressed as function of some unknown parameters. The fitting will find the best
parameter value to describe the observed data.
We can use the ROOT
TF1
class, the parametric function class, to describe the model function. However
the
ROOT::Fit::Fitter
class, to be independent of the ROOT
Hist
library, takes as input a more general
parametric function object, the interface (abstract) class
ROOT::Math::IParametricFunctionMultiDim
, which
describe a generic one or multi-dimensional function with parameters. This interface extends the abstract class
ROOT::Math::IBaseFunctionMultiDim
, with methods to set/retrieve parameter values and to evaluate the function
given the independent vector of values
X
and vector of parameters
P
. More information about the different
ROOT::Math
function interfaces is available in the Mathematical Library chapter.
An end-user can convert a
TF1
object in a
ROOT::Math::IParametricFunctionMultiDim
, using the wrapper class
ROOT::Math::WrapperMultiTF1:
TF1 * f1 = new TF1("f1","gaus");
ROOT::Math::WrappedMultiTF1 fitFunction(f1, f1->GetNdim() );
ROOT::Fit::Fitter fitter;
fitter.SetFunction( fitFunction, false);
When creating the wrapper, the parameter values stored in
TF1
will be copied in the
ROOT::Math::WrappedMultiTF1
object. The function object representing the model function is given to the
ROOT::Fitter
class using the
Fitter::SetFunction method.
132 CHAPTER 5. FITTING HISTOGRAMS
The user has also the possibility to provide a function object, which implements the derivatives of the function
with respect to the parameters. This information might be useful for some types of fits. In this case he needs to
provide the function object as a class deriving from the
ROOT::Math::IParametricGradFunctionMultiDim
interface.
Note that the wrapper class
ROOT::Math::WrappedMultiTF1
implements also the gradient interface, using internally
TF1::GradientPar
, which is based on numerical differentiation, apart for the case of linear functions (i.e. when
TF1::IsLinear()
is
true
). The parameter derivatives of the model function can be useful to some minimization
algorithms, such as Fumili. However, in general is better to leave the minimization algorithm (e.g. Minuit) to compute
the needed derivatives using its own customised numerical differentiation algorithm. In order to not provide to the
fitter the parameter derivatives, we explicitly passed in Fitter::SetFunction afalse value.
5.7.3 Fit Configuration
The configuration of the fit is done via the
ROOT::Fit::FitConfig
class and its contained
ROOT::Fit::ParameterSettings
class. These are the possible allowed fit configurations:
•setting the initial values of the parameters;
•setting the parameter step sizes;
•setting eventual parameter bounds;
•setting the minimizer library and the particular algorithm to use;
•setting different minimization options (print level, tolerance, max iterations, etc. . . )
•
setting the type of parameter errors to compute (parabolic error, Minos errors, re-normalize errors using fitted
chi2 values)
The initial parameter values can be set directly in the input model function object. However, for setting pa-
rameter bounds and step sizes to values different than the automatically computed ones, one needs to use the
ROOT::Fit::ParameterSetting
class. This example code will set the lower/upper bounds for the first parameter and
a lower bound for the second parameter
fitter.SetFunction( fitFunction, false);
fitter.Config().ParSettings(0).SetLimits(0,1.E6);
fitter.Config().ParSettings(2).SetLowerLimit(0);
Note that a
ROOT::Fit::ParameterSettings
objects exists for each fit parameter and it created by the
ROOT::Fit::FitConfig
class, after the model function has been set in the Fitter. Only when the function is set, the
number of parameter is known and automatically the
FitConfig
creates the corresponding
ParameterSetting
objects.
When fitting, different minimizer can be used. The can be implemented in different libraries and loaded ar run time
by the plug-in manager system of ROOT. Each different minimizer (e.g. Minuit, Minuit2, Fumili, etc.) consists of a
different implementation of the
ROOT::Math::Minimizer
interface. Within the same minimizer, thus within the same
class implementing the
Minimizer
interface, different algorithms can exist. For example in the case of Minuit, we have
Migrad, Simplex or Minimize. The minimizer and its corresponding algorithm, when available, can be set by using
the function
FitConfig::SetMinimizer("minimizerName")
or by using directly the
ROOT:Math::MinimizerOptions
class.
If the requested minimizer is not available in ROOT, the default one is used. The default minimizer type and algorithm
can be specified by using the static function
ROOT::Math::MinimizerOptions::SetDefaultMinimizer("minimizerName")
5.7.4 Minimizer Libraries and Algorithms
The list of available minimizer libraries currently available in ROOT, with their corresponding available algorithms is
the following one. Some minimizers (e.g. Minuit) contain several algorithms that the user can choose. Others are
based on a single algorithm (e.g. Fumili)
•Minuit
(library libMinuit). Old version of Minuit, based on the
TMinuit
class. The list of possible algorithms
are:
–Migrad (default one)
–Simplex
–Minimize (it is a combination of Migrad and Simplex)
–MigradImproved
–Scan
5.7. NEW ROOT::FIT CLASSES 133
–Seek
•Minuit2 (library libMinuit2 ). New C++ version of Minuit. The list of possible algorithm is :
–Migrad (default)
–Simplex
–Minimize
–Scan
–Fumili . This is the same algorithm of TFumili, but implemented in the Minuit2 library.
•Fumili
. Implement a dedicated minimization algorithm for least-square and likelihood fits. It has requirements
on the type of method function to be used. No specific algorithm exists
•GSLMultiMin
(library libMathMore). Minimizer based on the Multidimensional Minimization routines of the Gnu
Scientific Library (GSL). The list of available algorithms is
–BFGS2 (default) : second version of the vector Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm;
–BFGS : old version of the vector Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm;
–ConjugateFR : Fletcher-Reeves conjugate gradient algorithm;
–ConjugatePR : Polak-Ribiere conjugate gradient algorithm;
–SteepestDescent : steepest descent algorithm;
•GSLMultiFit
(library libMathMore). Minimizer based on the Non-Linear Least-Square routines of GSL. This
minimizer can be used only for least-square fits.
•GSLSimAn (library libMathMore). Minimizer based on simulated annealing.
•Genetic (library libGenetic). Genetic minimizer based on an algorithm implemented in the TMVA package.
Each minimizer can be configured using the
ROOT::Math::MinimizerOptions
class. The list of possible option that
can be set are:
•Minimizer type (MinimizerOptions::SetMinimizerType(const char *)) .
•Minimizer algorithm (MinimizerOptions::SetMinimizerAlgorithm(const char *)).
•Print Level (MinimizerOptions::SetPrintLevel(int )) to set the verbose printing level (default is 0).
•Tolerance (MinimizerOptions::SetTolerance(double )) tolerance used to control the iterations.
•Maximum number of function calls (MinimizerOptions::SetMaxFunctionCalls(int )).
•
Maximum number of iterations (
MinimizerOptions::SetMaxIterations(int )
). Note that this is not used by
Minuit
•
FCN Upper value for Error Definition (
MinimizerOptions::SetMaxIterations(int )
). Value in the minimiza-
tion function used to compute the parameter errors. The default is to get the uncertainties at the 68% CL is a
value of 1 for a chi-squared function minimization and 0.5 for a log-likelihood function.
•
Strategy (
MinimizerOptions::SetStrategy(int )
), minimization strategy used. For each minimization strategy
Minuit uses different configuration parameters (e.g. different requirements in computing derivatives, computing
full Hessian (strategy = 2) or an approximate version. The default is a value of 1. In this case the full Hessian
matrix is computed only after the minimization.
•
Precision (
MinimizerOptions::SetTolerance(double )
). Precision value in the evaluation of the minimization
function. Default is numerical double precision.
Note that not all the options are implemented by all the minimizers. For example in Minuit is possible to set the
maximum number of function calls, but not the maximum number of iterations. The Strategy and the Precision options
apply instead only for Minuit (and Minuit2 ).
The class supports also setting different default values for the options, by using the static functions
MinimizerOptions::SetDefault...
(for example
MinimizerOptions::SetDefaultPrintLevel(int )
). The
list of the current option values can be inspected by using MinimizerOptions::Print.
ROOT::Math::MinimizerOptions() opt;
// print the default minimizer option values
opt.Print();
In addition it is possible to provide extra options which might apply for a particular minimizer
MinimizerOptions::SetExtraOptions(const
IOptions & )
. See the documentation of the particular minimizer to use for the list of possible additional options
available.
134 CHAPTER 5. FITTING HISTOGRAMS
5.7.5 Performing the Fit
Here we have now all the required input ingredients for the fit, the data and the function to fit. Depending on these we
have now several different way to perform the fit, using the corresponding methods of the
ROOT::Fit::Fitter
class
and depending on the type of input data.
5.7.5.1 Available fit methods
•Least-square fit
:
Fitter::LeastSquare(const BinData & )
or
Fitter::Fit(const Bindata &)
. It re-
quires the user to pass a
BinData
object. It should be used when the data values follow a Gaussian distribution.
This fit method is implemented using the class ROOT::Fit::Chi2FCN.
•Binned Likelihood fit
:
Fitter::LikelihoodFit(const Bindata & )
. The user needs to pass a
BinData
object. It should be used when the data values follow a Poisson or a multinomial distribution. The Poisson case
(extended fit) is the default and in this case the function normalization is also fit to the data. The Multi-nominal
case can be selected by passing the optional extended boolean flag as false. This method is implemented by the
class ROOT::Fit:::PoissonLikelihoodFCN.
•Un-Binned likelihood fit
:
Fitter::LikelihoodFit(const UnBindata &)
. The user needs to pass an
UnBinData
object. By default the fit is not extended (i.e. the normalization is not fitted to the data). As
above the user can select an extended likelihood fit by passing the optional extended boolean flag as true. This
methos is implemented using the class LogLikelihoodFCN
•Linear Fit
: A linear fit can be selected (no iterative minimization is needed in this case, but using linear algebra
algorithms from the Matrix library), if the model function is linear in the parameters.
5.7.5.2 Customised Fit methods
Above we described the pre-defined methods used for fitting. A user can also implement its own fitting methods, thus
its version of the chi-square or likelihood function he wants to minimize. In this cas, the user does not really need to
build as input a
ROOT::Fit
data set and model function as we described before. He can implements its own version of
the method function using on its own data set objects and functions.
In this case
ROOT::Fit::Fitter::SetFCN
is used to set the method function and
ROOT::Fit::FitFCN
is used for
fitting. The method function can be passed also in
ROOT::Fit::FitFCN
, but in this case a previously defined fitting
configuration is used.
The possible type of method functions that can be bassed in ROOT::Fit::Fitter::SetFCN are:
•
A generic functor object implementing
operator()(const double * p)
where
p
is the parameter vectors. In
this case one needs to pass the number of parameters, the function object and optionally a vector of initial
parameter values. Other optional parameter include the size of the data sets and a flag specifying if it is a chi2
(least-square fit). In the last two parameters are given, the chi2/ndf can be computed after fitting the data.
template <class Function>
bool Fitter::SetFCN(unsigned int npar, Function & f,
const double * initialParameters = 0,
unsigned int dataSize=0,bool isChi2Fit = false)
•A function object implementing the ROOT::Math::IBaseFunctionMultiDim interface:
bool Fitter::SetFCN(const ROOT::Math::IBaseFunctionMultiDim & f,
const double * initialParameters = 0,
unsigned int dataSize=0,bool isChi2Fit = false)
•
A function object implementing the
ROOT::Math::FitMethodFunction
interface. This is an interface class
extending the
ROOT::Math::IBaseFunctionMultiDim
with some extra functionality which can be used when
fitting. This extra functionality is required by dedicated fitting algorithms like Fumili or GSLMultiFit.
bool Fitter::SetFCN(const ROOT::Math::FitMethodFunction & f,
const double * initialParameters = 0,unsigned int dataSize=0)
•
A old-Minuit like FCN interface (i.e. a free function with the signature
fcn(int &npar, double *gin, double
&f, double *u, int flag).
typedef void(* MinuitFCN)(int &npar, double *gin, double &f, double *u, int flag)
bool Fitter::SetFCN(MinuitFCN fcn, int npar,
const double * initialParameters = 0,
unsigned int dataSize=0,bool isChi2Fit = false)
5.8. THE MINIMIZATION PACKAGES 135
5.7.6 Fit Result
The result of the fit is contained in the
ROOT::Fit::Result
object. A reference to the result object is obtained with
the function
Fitter::Result()
. The
ROOT::Fit::FitResult
class provides an API for retrieving parameter values,
errors, covariance and correlation matrix from the fit, minimum chi2/likelihood values, etc. . .
AFitResult::Print method is also available to print the result of the fit.
The class has a self-explanatory API so, see its reference documentation for the possible information available after the
fit.
One extra functionality offered by
ROOT::Fit::FitResult
is the possibility to compute the confidence intervals of
the function after the fit. The function
ROOT::Fit::FitResult::GetConfidenceInterval
given an input data sets
(e.g. a
BinData
object) and a confidence level value (e.g. 68%) computes the lower/upper band values of the model
function at the given data points.
5.7.7 TFitResult
TFitResult
is a class deriving from
ROOT::Fit::Result
and providing in addition some convenient methods to return
a covariance or correlation matrix as a
TMatrixDSym
object. In addition
TFitResult
derives from
TNamed
and can be
conveniently stored in a file.
When fitting an histogram ( a
TH1
object) or a graph (a
TGraph
object) it is possible to return a
TFitResult
via the
TFitResultPtr
object, which behaves as a smart pointer to a
TFitResult
.
TFitResultPtr
is the return object by
TH1::Fit
or
TGraph::Fit
. By default the TFitResultPtr contains only the status of the fit and can be obtained by an
automatic conversion of the TFitResultPtr to an integer.
If the fit option
S
is instead used,
TFitResultPtr
contains the
TFitResult
and behaves as a smart pointer to it. This
is an example:
int fitStatus = hist->Fit(myFunction); // TFitResultPtr contains only the fit status
TFitResultPtr r = hist->Fit(myFunction,"S"); // TFitResultPtr contains the TFitResult
TMatrixDSym cov = r->GetCovarianceMatrix(); // to access the covariance matrix
Double_t chi2 = r->Chi2(); // to retrieve the fit chi2
Double_t par0 = r->Parameter(0); // retrieve the value for the parameter 0
Double_t err0 = r->ParError(0); // retrieve the error for the parameter 0
r->Print("V"); // print full information of fit including covariance matrix
r->Write(); // store the result in a file
5.8 The Minimization packages
As explained before various minimization packages can be used when fitting in ROOT. We have seen before how
to configure the
Fitter
class to use different minimization packages and different minimization options. When
using the
Fit
method the minimization package (and its options) can be selected using the static methods of the
ROOT::Math::MinimizerOptions
class. For example to select
Minuit2
instead of
Minuit
for fitting an histogram do:
ROOT::Math::MinimizerOptions::SetDefaultMinimizer("Minuit2");
// fit the histogram histo with the gaussian pre-defined function
histo->Fit("gaus");
In the following we will give some brief description of the minimization packages. The packages all implement the
ROOT::Math::Minimizer
interface which can be use for finding the minimum of a multi-dimensional function. The
interface is documented in the Mathematical Library Chapter.
In addition packages like Minuit or Minuit2 provide their own interfaces.
5.9 MINUIT (Old TMInuit Version)
This package was originally written in FORTRAN by Fred James and part of
PACKLIB
(patch D506). It has been
converted to a C++ class by René Brun. The current implementation in C++ is a straightforward conversion of the
original FORTRAN version. The main changes are:
136 CHAPTER 5. FITTING HISTOGRAMS
•
The variables in the various
Minuit
labeled common blocks have been changed to the
TMinuit
class data members
•
The internal arrays with a maximum dimension depending on the maximum number of parameters are now data
members’ arrays with a dynamic dimension such that one can fit very large problems by simply initializing the
TMinuit constructor with the maximum number of parameters
•
The include file
Minuit.h
has been commented as much as possible using existing comments in the code or the
printed documentation
•The original Minuit subroutines are now member functions
•Constructors and destructor have been added
•
Instead of passing the
FCN
function in the argument list, the addresses of this function is stored as pointer in the
data members of the class. This is by far more elegant and flexible in an interactive environment. The member
function SetFCN can be used to define this pointer
•
The ROOT static function
Printf
is provided to replace all format statements and to print on currently defined
output file
•
The functions
SetObjectFit/GetObjectFit
can be used inside the
FCN
function to set/get a referenced object
instead of using global variables
•
By default
fGraphicsMode
is true. When calling the
Minuit
functions such as
mncont
,
mnscan
, or any
Minuit
command invoking
mnplot
,
TMinuit::mnplot()
produces a
TGraph
object pointed by
fPlot
. One can retrieve
this object with TMinuit::GetPlot(). For example:
h->Fit("gaus");
gMinuit->Command("SCAn 1");
TGraph *gr = (TGraph*)gMinuit->GetPlot();
gr->SetMarkerStyle(21);
gr->Draw("alp");
•To set Minuit in no graphics mode, call
gMinuit->SetGraphicsMode(kFALSE);
5.9.1 Basic Concepts of Minuit
The
Minuit
package acts on a multi parameter FORTRAN function to which one must give the generic name
FCN
. In
the ROOT implementation, the function
FCN
is defined via the
Minuit SetFCN
member function when a
HistogramFit
command is invoked. The value of FCN will in general depend on one or more variable parameters.
To take a simple example, in case of ROOT histograms (classes
TH1C
,
TH1S
,
TH1F
,
TH1D
) the
Fit
function de-
fines the
Minuit
fitting function as being
H1FitChisquare
or
H1FitLikelihood
depending on the options selected.
H1FitChisquare
calculates the chi-square between the user fitting function (Gaussian, polynomial, user defined, etc)
and the data for given values of the parameters. It is the task of
Minuit
to find those values of the parameters which
give the lowest value of chi-square.
5.9.2 The Transformation of Limited Parameters
For variable parameters with limits, Minuit uses the following transformation:
Pint = arcsin(2((Pext-a)/(b-a))-1)
Pext = a+((b-a)/(2))(sinPint+1)
so that the internal value
Pint
can take on any value, while the external value Pext can take on values only between
the lower limit a and the ext upper limit b. Since the transformation is necessarily non-linear, it would transform
a nice linear problem into a nasty non-linear one, which is the reason why limits should be avoided if not necessary.
In addition, the transformation does require some computer time, so it slows down the computation a little bit, and
more importantly, it introduces additional numerical inaccuracy into the problem in addition to what is introduced in
the numerical calculation of the FCN value. The effects of non-linearity and numerical round off both become more
important as the external value gets closer to one of the limits (expressed as the distance to nearest limit divided by
distance between limits). The user must therefore be aware of the fact that, for example, if they put limits of (0, 1010)
on a parameter, then the values 0.0 and 1. 0 will be indistinguishable to the accuracy of most machines.
5.9. MINUIT (OLD TMINUIT VERSION) 137
The transformation also affects the parameter error matrix, of course, so Minuit does a transformation of the error
matrix (and the ‘’parabolic” parameter errors) when there are parameter limits. Users should however realize that the
transformation is only a linear approximation, and that it cannot give a meaningful result if one or more parameters is
very close to a limit, where ∂P ext
∂P int 6= 0. Therefore, it is recommended that:
•
Limits on variable parameters should be used only when needed in order to prevent the parameter from taking
on unphysical values
•
When a satisfactory minimum has been found using limits, the limits should then be removed if possible, in order
to perform or re-perform the error analysis without limits
5.9.3 How to Get the Right Answer from Minuit
Minuit
offers the user a choice of several minimization algorithms. The
MIGRAD
algorithm is in general the best
minimized for nearly all functions. It is a variable-metric method with inexact line search, a stable metric updating
scheme, and checks for positive-definiteness. Its main weakness is that it depends heavily on knowledge of the first
derivatives, and fails miserably if they are very inaccurate.
If parameter limits are needed, in spite of the side effects, then the user should be aware of the following techniques to
alleviate problems caused by limits:
5.9.3.1 Getting the Right Minimum with Limits
If MIGRAD converges normally to a point where no parameter is near one of its limits, then the existence of limits has
probably not prevented
Minuit
from finding the right minimum. On the other hand, if one or more parameters is
near its limit at the minimum, this may be because the true minimum is indeed at a limit, or it may be because the
minimized has become ‘’blocked” at a limit. This may normally happen only if the parameter is so close to a limit
(internal value at an odd multiple of
±π
2
that
Minuit
prints a warning to this effect when it prints the parameter
values. The minimized can become blocked at a limit, because at a limit the derivative seen by the minimized
∂F
∂P int
is
zero no matter what the real derivative ∂F
∂P ext is.
∂F
∂P int =∂F
∂P ext ∂P ext
∂P int =∂F
∂P ext = 0
5.9.3.2 Getting the Right Parameter Errors with Limits
In the best case, where the minimum is far from any limits,
Minuit
will correctly transform the error matrix, and the
parameter errors it reports should be accurate and very close to those you would have got without limits. In other
cases (which should be more common, since otherwise you would not need limits), the very meaning of parameter
errors becomes problematic. Mathematically, since the limit is an absolute constraint on the parameter, a parameter
at its limit has no error, at least in one direction. The error matrix, which can assign only symmetric errors, then
becomes essentially meaningless.
5.9.3.3 Interpretation of Parameter Errors
There are two kinds of problems that can arise: the reliability of
Minuit
’s error estimates, and their statistical
interpretation, assuming they are accurate.
5.9.3.4 Statistical Interpretation
For discussion of basic concepts, such as the meaning of the elements of the error matrix, or setting of exact confidence
levels see the articles:
•
F.James. Determining the statistical Significance of experimental Results. Technical Report DD/81/02 and
CERN Report 81-03, CERN, 1981
•
W.T.Eadie, D.Drijard, F.James, M.Roos, and B.Sadoulet. Statistical Methods in Experimental Physics. North-
Holland, 1971
138 CHAPTER 5. FITTING HISTOGRAMS
5.9.4 Reliability of Minuit Error Estimates
Minuit
always carries around its own current estimates of the parameter errors, which it will print out on request, no
matter how accurate they are at any given point in the execution. For example, at initialization, these estimates are just
the starting step sizes as specified by the user. After a HESSE step, the errors are usually quite accurate, unless there
has been a problem.
Minuit
, when it prints out error values, also gives some indication of how reliable it thinks they
are. For example, those marked
CURRENT GUESS ERROR
are only working values not to be believed, and
APPROXIMATE
ERROR means that they have been calculated but there is reason to believe that they may not be accurate.
If no mitigating adjective is given, then at least
Minuit
believes the errors are accurate, although there is always a
small chance that Minuit has been fooled. Some visible signs that Minuit may have been fooled:
•Warning messages produced during the minimization or error analysis
•Failure to find new minimum
•Value of EDM too big (estimated Distance to Minimum)
•
Correlation coefficients exactly equal to zero, unless some parameters are known to be uncorrelated with the
others
•
Correlation coefficients very close to one (greater than 0.99). This indicates both an exceptionally difficult
problem, and one which has been badly parameterized so that individual errors are not very meaningful because
they are so highly correlated
•
Parameter at limit. This condition, signaled by a
Minuit
warning message, may make both the function minimum
and parameter errors unreliable. See the discussion above ‘Getting the right parameter errors with limits’
The best way to be absolutely sure of the errors is to use ‘’independent’‘calculations and compare them, or compare
the calculated errors with a picture of the function. Theoretically, the covariance matrix for a’‘physical” function must
be positive-definite at the minimum, although it may not be so for all points far away from the minimum, even for a
well-determined physical problem. Therefore, if
MIGRAD
reports that it has found a non-positive-definite covariance
matrix, this may be a sign of one or more of the following:
5.9.4.1 A Non-physical Region
On its way to the minimum,
MIGRAD
may have traversed a region that has unphysical behavior, which is of course not
a serious problem as long as it recovers and leaves such a region.
5.9.4.2 An Underdetermined Problem
If the matrix is not positive-definite even at the minimum, this may mean that the solution is not well defined, for
example that there are more unknowns than there are data points, or that the parameterization of the fit contains a
linear dependence. If this is the case, then
Minuit
(or any other program) cannot solve your problem uniquely. The
error matrix will necessarily be largely meaningless, so the user must remove the under determinedness by reformulating
the parameterization. Minuit cannot do this itself.
5.9.4.3 Numerical Inaccuracies
It is possible that the apparent lack of positive-definiteness is due to excessive round off errors in numerical calculations
(in the user function), or not enough precision. This is unlikely in general, but becomes more likely if the number
of free parameters is very large, or if the parameters are badly scaled (not all of the same order of magnitude), and
correlations are large. In any case, whether the non-positive-definiteness is real or only numerical is largely irrelevant,
since in both cases the error matrix will be unreliable and the minimum suspicious.
5.9.4.4 An Ill-posed Problem
For questions of parameter dependence, see the discussion above on positive-definiteness. Possible other mathematical
problems are the following:
•
Excessive numerical round off - be especially careful of exponential and factorial functions which get big very
quickly and lose accuracy.
•
Starting too far from the solution - the function may have unphysical local minima, especially at infinity in some
variables.

5.10. MINUIT2 PACKAGE 139
5.10 Minuit2 Package
Minuit2
is a new object-oriented implementation, written in C++, of the popular
MINUIT
minimization package.
Compared with the
TMinuit
class, which is a direct conversion from FORTRAN to C++,
Minuit2
is a complete
redesign and re-implementation of the package. This new version provides all the functionality present in the old
FORTRAN version, with almost equivalent numerical accuracy and computational performances. Furthermore, it
contains some fixes and small improvements and this new functionality: * The possibility to set single side parameter
limits * the FUMILI algorithm (see the next paragraph “FUMILI Minimization Package”), which is an optimized
method for least square and log likelihood minimizations.
Minuit2 has been originally developed by M. Winkler and F. James in the SEAL project. More information can be
found on the MINUIT Web Site and in particular at the following documentation page at http://www.cern.ch/minuit/
doc/doc.html.
A detailed User Guide for Minuit2 exists, describing the API of the internal classes. ROOT uses
Minuit2
for fitting
via the Minuit2Minimizer class which implements the ROOT::Math::Minimizer interface.
Minuit2
is also distributed as an independent package of ROOT and can be built without any other dependency on
the ROOT libraries.
Examples on how to use the
Minuit2
and
Fumili2
plug-ins are provided in the tutorials’ directory
$ROOTSYS/tutorials/fit
:
minuit2FitBench.C
,
minuit2FitBench2D.C
and
minuit2GausFit.C
. More information on the classes and functions
present in Minuit2 is available at online reference documentation.
Useful information on MINUIT and minimization in general is provided in the following documents:
F. James, Minuit Tutorial on Function Minimization (http://seal.cern.ch/documents/minuit/mntutorial.pdf); F.
James, The Interpretation of Errors in Minuit (http://seal.cern.ch/documents/minuit/mnerror.pdf);
5.11 FUMILI Minimization Package
FUMILI is used to minimize Chi-square function or to search maximum of likelihood function. Experimentally measured
values
Fi
are fitted with theoretical functions
fi
(
~xi,~
θ
), where
~xi
are coordinates, and
~
θ
- vector of parameters. For
better convergence Chi-square function has to be the following form
χ2
2=1
2
n
X
i=1 fi(~xi,~
θ)−Fi
σi!2
where σiare errors of the measured function. The minimum condition is:
∂χ2
∂θi
=
n
X
j=1
1
σ2
j
.∂fi
∂θih(~xj,~
θ)−Fji= 0, i = 1...m
where
m
is the quantity of parameters. Expanding left part of this equation over parameter increments and retaining
only linear terms one gets
∂χ2
θiθ=~
θ0
+X
k∂2χ2
∂θi∂θkθ=~
θ0
.(θk−θ0
k)=0
here ~
θ0is some initial value of parameters. In general case:
∂2χ2
∂θi∂θk
=
n
X
j=1
1
σ2
j
∂fj
θi
∂fj
θk
+
n
X
j=1
(fj−Fj)
σ2
j·∂2fj
∂θi∂θk
In FUMILI algorithm for second derivatives of Chi-square approximate expression is used when last term in previous
equation is discarded. It is often done, not always wittingly, and sometimes causes troubles, for example, if user wants
to limit parameters with positive values by writing down
θ2
i
instead of
θi
. FUMILI will fail if one tries minimize
χ2=g2(~
θ)where g is arbitrary function.
Approximate value is:

140 CHAPTER 5. FITTING HISTOGRAMS
∂2χ2
∂θi∂θk≈Zik =
n
X
j=1
1
σ2
j
∂fj
θi
∂fj
θk
Then the equations for parameter increments are:
∂χ2
∂θi~
θ=~
θ0
+X
k
Zik ·(θk−θ0
k)=0, i = 1 . . . m
Remarkable feature of algorithm is the technique for step restriction. For an initial value of parameter
~
θ0
a parallelepiped
P0
is built with the center at
~
θ0
and axes parallel to coordinate axes
θi
. The lengths of parallelepiped sides along i-th
axis is 2bi, where biis such a value that the functions fj(~
θ)are quasi-linear all over the parallelepiped.
FUMILI takes into account simple linear inequalities in the form:
θmin
i≤θi≤θmax
i
They form parallelepiped
P
(
P0
may be deformed by
P
). Very similar step formulae are used in FUMILI for negative
logarithm of the likelihood function with the same idea - linearization of function argument.
5.12 Neural Networks
5.12.1 Introduction
Neural Networks are used in various fields for data analysis and classification, both for research and commercial
institutions. Some randomly chosen examples are image analysis, financial movements’ predictions and analysis, or
sales forecast and product shipping optimization. In particles physics neural networks are mainly used for classification
tasks (signal over background discrimination). A vast majority of commonly used neural networks are multilayer
perceptrons. This implementation of multilayer perceptrons is inspired from the
MLPfit
package, which remains one of
the fastest tools for neural networks studies.
5.12.2 The MLP
The multilayer perceptron is a simple feed-forward network with the following structure showed on the left.
It is made of neurons characterized by a bias and weighted links in between - let’s call those links synapses. The
input neurons receive the inputs, normalize them and forward them to the first hidden layer. Each neuron in any
subsequent layer first computes a linear combination of the outputs of the previous layer. The output of the neuron is
then function of that combination with f being linear for output neurons or a sigmoid for hidden layers.
Such a structure is very useful because of two theorems:
1- A linear combination of sigmoids can approximate any continuous function.
2- Trained with
output=1
for the signal and 0 for the background, the approximated function of inputs
X
is the
probability of signal, knowing X.
5.12.3 Learning Methods
The aim of all learning methods is to minimize the total error on a set of weighted examples. The error is defined
as the sum in quadrate, divided by two, of the error on each individual output neuron. In all methods implemented
in this library, one needs to compute the first derivative of that error with respect to the weights. Exploiting the
well-known properties of the derivative, one can express this derivative as the product of the local partial derivative by
the weighted sum of the outputs derivatives (for a neuron) or as the product of the input value with the local partial
derivative of the output neuron (for a synapse). This computation is called “back-propagation of the errors”. Six
learning methods are implemented.
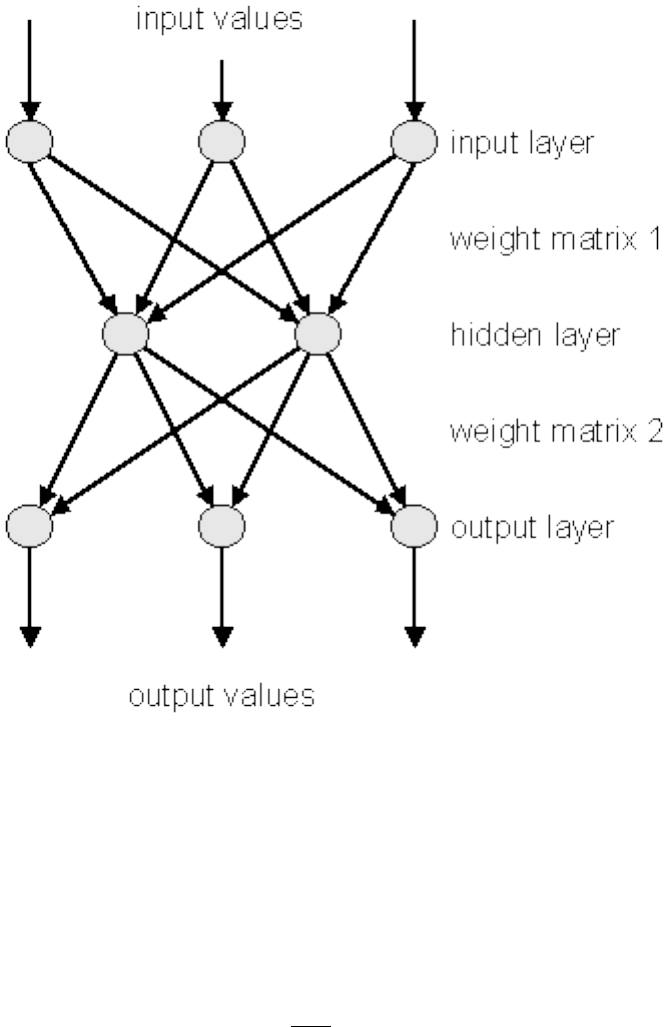
5.12. NEURAL NETWORKS 141
5.12.3.1 Stochastic Minimization
This is the most trivial learning method. The Robbins-Monro stochastic approximation is applied to multilayer
perceptrons. The weights are updated after each example according to the formula:
wij (t+ 1) = wij (t)+∆wij (t)
with:
∆wij (t) = −η∂ep
∂wij
+δ+∆wij (t−1)
The parameters for this method are Eta,EtaDecay,Delta and Epsilon.
5.12.3.2 Steepest Descent With Fixed Step Size (Batch Learning)
It is the same as the stochastic minimization, but the weights are updated after considering all the examples, with the
total derivative dEdw. The parameters for this method are Eta,EtaDecay,Delta and Epsilon.
5.12.3.3 Steepest Descent Algorithm
Weights are set to the minimum along the line defined by the gradient. The only parameter for this method is
Tau
.
Lower Tau = higher precision = slower search. A value Tau=3 seems reasonable.
5.12.3.4 Conjugate Gradients With the Polak-Ribiere Updating Formula
Weights are set to the minimum along the line defined by the conjugate gradient. Parameters are
Tau
and
Reset
, which
defines the epochs where the direction is reset to the steepest descent (estimated by using the Polak-Ribiere formula).
142 CHAPTER 5. FITTING HISTOGRAMS
5.12.3.5 Conjugate Gradients With the Fletcher-Reeves Updating Formula
Weights are set to the minimum along the line defined by the conjugate gradient. Parameters are
Tau
and
Reset
, which
defines the epochs where the direction is reset to the steepest descent (estimated by using the Fletcher-Reeves formula).
5.12.3.6 The Broyden, Fletcher, Goldfarb, Shanno (BFGS) Method
It implies the computation of a
NxN
matrix, but seems more powerful at least for less than 300 weights. Parameters are
Tau and Reset, which defines the epochs where the direction is reset to the steepest descent.
5.12.4 Using the Network
Neural network are build from a set of “samples”. A sample is a set of values defining the inputs and the corresponding
output that the network should ideally provide. In ROOT this is a
TTree
entry. The first thing to be decided is the
network layout. This layout is described in a string where the layers are separated by semicolons. The input/output
layers are defined by giving the expression for each neuron, separated by comas. Hidden layers are just described by
the number of neurons.
In addition, input and output layer formulas can be preceded by ‘@’ (e.g. “@out”) if one wants to normalize the
corresponding value. Also, if the string ends with ‘
!
’, output neurons are set up for classification, i.e. with a sigmoid (1
neuron) or softmax (more neurons) activation function.
Many questions on the good usage of neural network, including rules of dumb to determine the best network topology
are addressed at ftp://ftp.sas.com/pub/neural/FAQ.html
// a simple network: 2 inputs, 10 hidden and 1 normalized
// output neuron
TMultiLayerPerceptron network("r,z:10:@Br",tree);
Expressions are evaluated as for
TTree::Draw()
. Input and outputs are taken from the
TTree
associ-
ated with the network. This
TTree
can be given as argument of the constructor or defined later with
TMultiLayerPerceptron::SetData()
. Events can also be weighted. The weight expression can be given in
the constructor or set later with the method
SetWeight()
of the class
TMultiLayerPerceptron
. Two datasets must
be defined before learning the network: a training dataset that is used when minimizing the error, and a test dataset
that will avoid bias. Those two datasets can be build aside and then given to the network, or can be build from a
standard expression. By default, half of the events are put in both datasets.
// a more complex 4:8:1 network
// the ptsumf branch is used as weigh;
// default event lists are explicit
TMultiLayerPerceptron network("m,pt,acol,acopl:8:type","pt",tree,
"Entry$%2","Entry$/2");
The method TMultiLayerPerceptron::SetLearningMethod() defines the learning method. Learning methods are:
TMultiLayerPerceptron::kStochastic,
TMultiLayerPerceptron::kBatch,
TMultiLayerPerceptron::kSteepestDescent,
TMultiLayerPerceptron::kRibierePolak,
TMultiLayerPerceptron::kFletcherReeves,
TMultiLayerPerceptron::kBFGS // default
The training can start with
TMultiLayerPerceptron::Train(Int_t nepoch,Option_t* options).
The first argu-
ment is the number of epochs while option is a string that can contain “
text
” (simple text output), “
graph
” (evaluating
graphical training curves), “
update = X
” (step for the text/graph output update) or “
+
” (will skip the randomization
and start from the previous values). All combinations are available.
network.Train(1000,"text,graph,update=10"); // full output every
// 10 epochs
network.Train(100,"text,+"); // 100 more epochs
//starts with existing weights
5.12. NEURAL NETWORKS 143
The weights can be saved to a file (
DumpWeights
) and then reloaded (
LoadWeights
) to a new compatible network. The
output can also be evaluated (
Evaluate
) for a given output neuron and an array of double input parameters or the
network can be exported (
Export
) as a standalone code. Up to now, this is only as a C++ or PYTHON class, but
other languages could be implemented.
5.12.5 Examples
An example of how to use
TMultiLayerPerceptron
is the macro
mlpHiggs.C
in $ROOTSYS/tutorials. Using some
standard simulated information that could have been obtained at
LEP
, a neural network is build, which can make the
difference between
WW
events and events containing a Higgs boson. Starting with a
TFile
containing two
TTree
s: one
for the signal, the other for the background, a simple script is used:
void mlpHiggs(Int_t ntrain=100) {
if (!gROOT->GetClass("TMultiLayerPerceptron"))
gSystem->Load("libMLP");
// prepare inputs - the 2 trees are merged into one, and a
// "type" branch, equal to 1 for the signal and 0 for the
// background is added
TFile input("mlpHiggs.root");
TTree *signal = (TTree *)input.Get("sig_filtered");
TTree *background = (TTree *)input.Get("bg_filtered");
TTree *simu = new TTree("MonteCarlo",
"Filtered Monte Carlo Events");
...
Since the input is a
TTree
and we are starting from two different
TTree
s (with different names), they are first merged
into one, and a “
type
” branch is added, that says whether there is a signal or a background event. Those irrelevant
details are skipped here.
...
TMultiLayerPerceptron *mlp = new TMultiLayerPerceptron(
"msumf,ptsumf, acolin, acopl:8:type","ptsumf",simu,
"Entry$%2","Entry$/2");
mlp->Train(ntrain, "text,graph,update=10");
The neural network is instantiated and trained. “
ptsumf
” is used as a weight, and the standard event lists are explicit.
The network that is then build has four input neurons, eight additional ones in the only hidden layer and one single
output neuron.
// Use the NN to plot the results for each sample
TH1F *bg = new TH1F("bgh","NN output",50,-.5,1.5);
TH1F *sig = new TH1F("sigh","NN output",50,-.5,1.5);
bg->SetDirectory(0);
sig->SetDirectory(0);
Double_t params[4];
for (i=0; i < background->GetEntries(); i++) {
background->GetEntry(i);
params[0] = msumf; params[1] = ptsumf;
params[2] = acolin; params[3] = acopl;
bg->Fill(mlp->Evaluate(0,params));
}
for (i=0; i < signal->GetEntries(); i++) {
signal->GetEntry(i);
params[0] = msumf;
params[1] = ptsumf;
params[2] = acolin;
params[3] = acopl;
sig->Fill(mlp->Evaluate(0,params));
}
TCanvas *cv = new TCanvas("NNout_cv","Neural net output");
bg->SetFillStyle(3008);
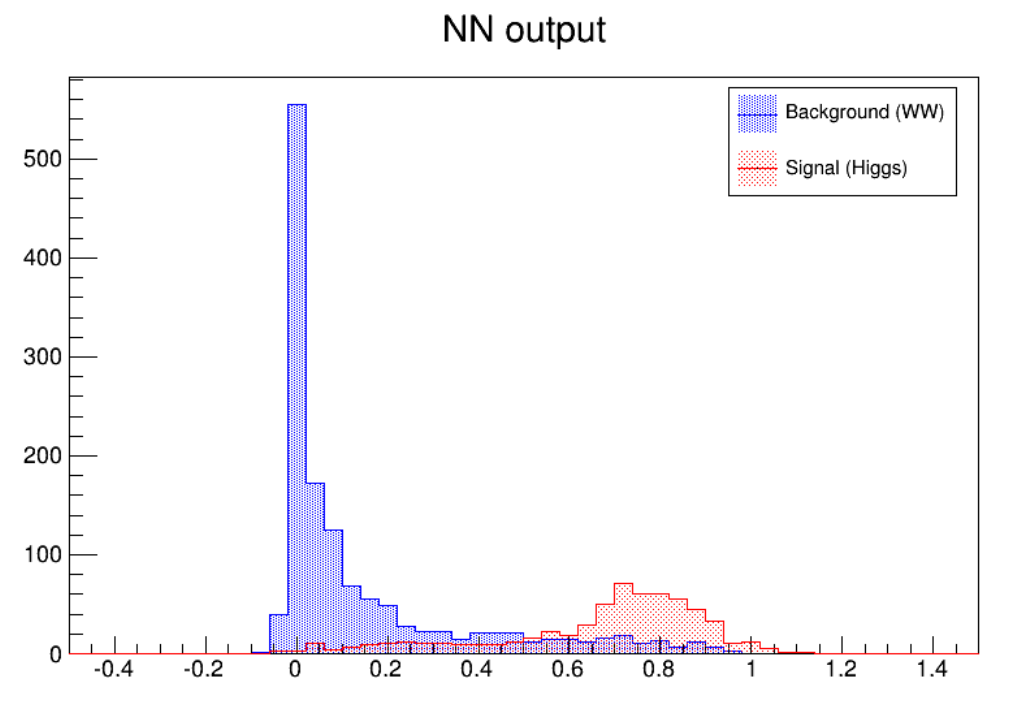
144 CHAPTER 5. FITTING HISTOGRAMS
bg->SetFillColor(kBlue);
sig->SetFillStyle(3003);
sig->SetFillColor(kRed);
bg->SetStats(0);
sig->SetStats(0);
bg->Draw();
sig->Draw("same");
TLegend *legend = new TLegend(.75,.80,.95,.95);
legend->AddEntry(bg,"Background(WW)");
legend->AddEntry(sig,"Signal(Higgs)");
legend->Draw();
The neural net output is then used to display the final difference between background and signal events. The figure
“The neural net output” shows this plot.
Figure 5.5: The neural net output
As it can be seen, this is a quite efficient technique. As mentioned earlier, neural networks are also used for fitting
function. For some application with a cylindrical symmetry, a magnetic field simulation gives as output the angular
component of the potential vector A, as well as the radial and zcomponents of the Bfield.
One wants to fit those distributions with a function in order to plug them into the
Geant
simulation code. Polynomial
fits could be tried, but it seems difficult to reach the desired precision over the full range. One could also use a
spline
interpolation between known points. In all cases, the resulting field would not be C-infinite.
An example of output (for Br) is shown. First the initial function can be seen as the target. Then, the resulting
(normalized) neural net output. In order to ease the learning, the “normalize output” was used here. The initial
amplitude can be recovered by multiplying by the original RMS and then shifting by the original mean.
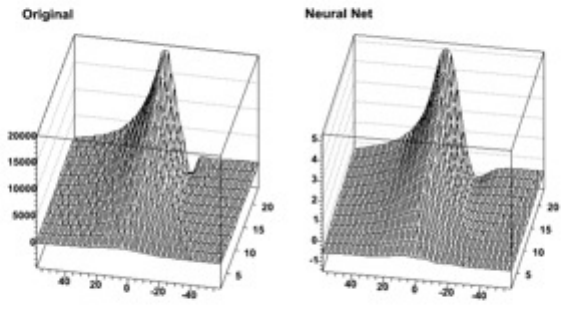
5.12. NEURAL NETWORKS 145
Figure 5.6: The original and the neural net for Br
146 CHAPTER 5. FITTING HISTOGRAMS
Chapter 6
A Little C++
This chapter introduces you to some useful insights into C++, to allow you to use of the most advanced features in
ROOT. It is in no case a full course in C++.
6.1 Classes, Methods and Constructors
C++ extends C with the notion of class. If you’re used to structures in C, a class is a
struct
that is a group of
related variables, which is extended with functions and routines specific to this structure (class). What is the interest?
Consider a struct that is defined this way:
struct Line {
float x1;
float y1;
float x2;
float y2;
}
This structure represents a line to be drawn in a graphical window.
(x1,y1)
are the coordinates of the first point,
(x2,y2)
the coordinates of the second point. In the standard C, if you want to draw effectively such a line, you first
have to define a structure and initialize the points (you can try this):
Line firstline;
firstline.x1 = 0.2;
firstline.y1 = 0.2;
firstline.x2 = 0.8;
firstline.y2 = 0.9;
This defines a line going from the point
(0.2,0.2)
to the point
(0.8,0.9)
. To draw this line, you will have to write a
function, say LineDraw(Line l) and call it with your object as argument:
LineDraw(firstline);
In C++, we would not do that. We would instead define a class like this:
class TLine {
Double_t x1;
Double_t y1;
Double_t x2;
Double_t y2;
TLine(int x1, int y1, int x2, int y2);
void Draw();
}
Here we added two functions, that we will call methods or member functions, to the
TLine
class. The first method is
used for initializing the line objects we would build. It is called a constructor. The second one is the
Draw
method
itself. Therefore, to build and draw a line, we have to do:
147
148 CHAPTER 6. A LITTLE C++
TLine l(0.2,0.2,0.8,0.9);
l.Draw();
The first line builds the object
l
by calling its constructor. The second line calls the
TLine::Draw()
method of this
object. You don’t need to pass any parameters to this method since it applies to the object l, which knows the
coordinates of the line. These are internal variables x1,y1,x2,y2 that were initialized by the constructor.
6.2 Inheritance and Data Encapsulation
We have defined a
TLine
class that contains everything necessary to draw a line. If we want to draw an arrow, is it so
different from drawing a line? We just have to draw a triangle at one end. It would be very inefficient to define the
class
TArrow
from scratch. Fortunately, inheritance allows a class to be defined from an existing class. We would write
something like:
class TArrow : public TLine {
int ArrowHeadSize;
void Draw();
void SetArrowSize(int arrowsize);
}
The keyword “
public
” will be explained later. The class
TArrow
now contains everything that the class
TLine
does,
and a couple of things more, the size of the arrowhead and a function that can change it. The Draw method of
TArrow
will draw the head and call the draw method of TLine. We just have to write the code for drawing the head!
6.2.1 Method Overriding
Giving the same name to a method (remember: method = member function of a class) in the child class (
TArrow
)
as in the parent (
TLine
) does not give any problem. This is called
overriding
a method. Draw in
TArrow
overrides
Draw in
TLine
. There is no possible ambiguity since, when one calls the
Draw()
method; this applies to an object
which type is known. Suppose we have an object
l
of type
TLine
and an object
a
of type
TArrow
. When you want to
draw the line, you do:
l.Draw();
Draw() from TLine is called. If you do:
a.Draw();
Draw() from TArrow is called and the arrow ais drawn.
6.2.2 Data Encapsulation
We have seen previously the keyword “
public
”. This keyword means that every name declared public is seen by the
outside world. This is opposed to “
private
” that means only the class where the name was declared private could see
this name. For example, suppose we declare in TArrow the variable ArrowHeadSize private.
private:
int ArrowHeadSize;
Then, only the methods (i.e. member functions) of
TArrow
will be able to access this variable. Nobody else will see it.
Even the classes that we could derive from
TArrow
will not see it. On the other hand, if we declare the method
Draw()
as public, everybody will be able to see it and use it. You see that the character public or private does not depend
of the type of argument. It can be a data member, a member function, or even a class. For example, in the case of
TArrow, the base class TLine is declared as public:
class TArrow : public TLine { ...
6.3. CREATING OBJECTS ON THE STACK AND HEAP 149
This means that all methods of
TArrow
will be able to access all methods of
TLine
, but this will be also true for
anybody in the outside world. Of course, this is true if
TLine
accepts the outside world to see its methods/data
members. If something is declared private in
TLine
, nobody will see it, not even
TArrow
members, even if
TLine
is
declared as a public base class.
What if
TLine
is declared “
private
” instead of “
public
” ? Well, it will behave as any other name declared private in
TArrow
: only the data members and methods of
TArrow
will be able to access
TLine
, its methods and data members,
nobody else. This may seem a little bit confusing and readers should read a good C++ book if they want more details.
Especially since, besides public and private, a member can be protected. Usually, one puts private the methods that the
class uses internally, like some utilities classes, and that the programmer does not want to be seen in the outside world.
With “good” C++ practice (which we have tried to use in ROOT), all data members of a class are private. This is
called data encapsulation and is one of the strongest advantages of Object Oriented Programming (OOP). Private data
members of a class are not visible, except to the class itself. So, from the outside world, if one wants to access those
data members, one should use so called “getters” and “setters” methods, which are special methods used only to get or
set the data members. The advantage is that if the programmers want to modify the inner workings of their classes,
they can do so without changing what the user sees. The user does not even have to know that something has changed
(for the better, hopefully). For example, in our
TArrow
class, we would have set the data member
ArrowHeadSize
private. The setter method is SetArrowSize(), we do not need a getter method:
class TArrow : public TLine {
private:
int ArrowHeadSize;
public:
void Draw();
void SetArrowSize(int arrowsize);
}
To define an arrow object you call the constructor. This will also call the constructor of
TLine
, which is the parent
class of TArrow, automatically. Then we can call any of the line or arrow public methods:
root[] TArrow *myarrow = new TArrow(1,5,89,124);
root[] myarrow->SetArrowSize(10);
root[] myarrow->Draw();
6.3 Creating Objects on the Stack and Heap
To explain how objects are created on the stack and on the heap we will use the
Quad
class. You can find the
definition in $ROOTSYS/tutorials/quadp/Quad.h and Quad.cxx. The Quad class has four methods. The constructor
and destructor,
Evaluate
that evaluates
ax**2 + bx +c
, and
Solve
which solves the quadratic equation
ax**2 + bx
+c = 0.
Quad.h :
class Quad {
public:
Quad(Float_t a, Float_t b, Float_t c);
~Quad();
Float_t Evaluate(Float_t x) const;
void Solve() const;
private:
Float_t fA;
Float_t fB;
Float_t fC;
};
Quad.cxx:
#include <iostream.h>
#include <math.h>
#include "Quad.h"
150 CHAPTER 6. A LITTLE C++
Quad::Quad(Float_t a, Float_t b, Float_t c) {
fA = a;
fB = b;
fC = c;
}
Quad::~Quad() {
Cout <<"deleting object with coeffts: "<< fA << "," << fB << ","
<< fC << endl;
}
Float_t Quad::Evaluate(Float_t x) const {
return fA*x*x + fB*x + fC;
}
void Quad::Solve() const {
Float_t temp = fB*fB - 4.*fA*fC;
if ( temp > 0.){
temp = sqrt( temp );
cout << "There are two roots: " << ( -fB - temp ) / (2.*fA)
<< "and"<< ( -fB + temp ) / (2.*fA) << endl;
}else {
if ( temp == 0.){
cout << "There are two equal roots: " << -fB / (2.*fA)
<< endl;
}else {
cout << "There are no roots" << endl;
}
}
}
Let us first look how we create an object. When we create an object by:
root[] Quad my_object(1.,2.,-3.);
We are creating an object on the stack. A FORTRAN programmer may be familiar with the idea; it is not unlike a
local variable in a function or subroutine. Although there are still a few old timers who do not know it, FORTRAN
is under no obligation to save local variables once the function or subroutine returns unless the SAVE statement is
used. If not then it is likely that FORTRAN will place them on the stack and they will “pop off” when the RETURN
statement is reached. To give an object more permanence it has to be placed on the heap.
root[] .L Quad.cxx
root[] Quad *my_objptr = new Quad(1.,2.,-3.);
The second line declares a pointer to
Quad
called
my_objptr
. From the syntax point of view, this is just like all the
other declarations we have seen so far, i.e. this is a stack variable. The value of the pointer is set equal to
new Quad(1.,2.,-3.);
new
, despite its looks, is an operator and creates an object or variable of the type that comes next,
Quad
in this case,
on the heap. Just as with stack objects it has to be initialized by calling its constructor. The syntax requires that the
argument list follow the type. This one statement has brought two items into existence, one on the heap and one on
the stack. The heap object will live until the delete operator is applied to it.
There is no FORTRAN parallel to a heap object; variables either come or go as control passes in and out of a function
or subroutine, or, like a COMMON block variables, live for the lifetime of the program. However, most people in HEP
who use FORTRAN will have experience of a memory manager and the act of creating a bank is a good equivalent of
a heap object. For those who know systems like ZEBRA, it will come as a relief to learn that objects do not move,
C++ does not garbage collect, so there is never a danger that a pointer to an object becomes invalid for that reason.
However, having created an object, it is the user’s responsibility to ensure that it is deleted when no longer needed, or
to pass that responsibility onto to some other object. Failing to do that will result in a memory leak, one of the most
common and most hard-to-find C++ bugs.
To send a message to an object via a pointer to it, you need to use the “->” operator e.g.:
6.3. CREATING OBJECTS ON THE STACK AND HEAP 151
root[] my_objptr->Solve();
Although we chose to call our pointer
my_objptr
, to emphasize that it is a pointer, heap objects are so common in an
object-oriented program that pointer names rarely reflect the fact - you have to be careful that you know if you are
dealing with an object or its pointer! Fortunately, the compiler won’t tolerate an attempt to do something like:
root[] my_objptr.Solve();
Although this is a permitted by the Cling shortcuts, it is one that you are strongly advised not to follow! As we have
seen, heap objects have to be accessed via pointers, whereas stack objects can be accessed directly. They can also be
accessed via pointers:
root[] Quad stack_quad(1.,2.,-3.);
root[] Quad *stack_ptr = &stack_quad;
root[] stack_ptr->Solve();
Here we have a
Quad
pointer that has been initialized with the address of a stack object. Be very careful if you take
the address of stack objects. As we shall see soon, they are deleted automatically, which could leave you with an illegal
pointer. Using it will corrupt and may well crash the program!
It is time to look at the destruction of objects. A destructor is a special C++ function that releases resources for
(or destroy) an object of a class. It is opposite of a constructor that create the object of a class when is called. The
compiler will provide a destructor that does nothing if none is provided. We will add one to our Quad class so that we
can see when it is called. The class names the destructor but with a prefix ~ which is the C++ one’s complement
i.e. bit wise complement, and hence has destruction overtones! We declare it in the .h file and define it in the
.cxx
file.
It does not do much except print out that it has been called (still a useful debug technique despite today’s powerful
debuggers!).
Now run root, load the Quad class and create a heap object:
root[] .L Quad.cxx
root[] Quad *my_objptr = new Quad(1.,2.,-3.);
To delete the object:
root[] delete my_objptr;
root[] my_objptr = 0;
You should see the print out from its destructor. Setting the pointer to zero afterwards is not strictly necessary (and
Cling does it automatically), but the object is no more accessible, and any attempt to use the pointer again will, as has
already been stated, cause grief. So much for heap objects, but how are stack objects deleted? In C++, a stack object
is deleted as soon as control leaves the innermost compound statement that encloses it. Therefore, it is singularly futile
to do something like:
root[] { Quad my_object(1.,2.,-3.); }
Cling does not follow this rule; if you type in the above line, you will not see the destructor message. As explained in
the Script lesson, you can load in compound statements, which would be a bit pointless if everything disappeared as
soon as it was loaded! Instead, to reset the stack you have to type:
root[] gROOT->Reset();
This sends the Reset message via the global pointer to the ROOT object, which, amongst its many roles, acts as a
resource manager. Start ROOT again and type in the following:
root[] .L Quad.cxx
root[] Quad my_object(1.,2.,-3.);
root[] Quad *my_objptr = new Quad(4.,5.,-6.);
root[] gROOT->Reset();
152 CHAPTER 6. A LITTLE C++
You will see that this deletes the first object but not the second. We have also painted ourselves into a corner, as
my_objptr was also on the stack. This command will fail.
root[] my_objptr->Solve();
Cling no longer knows what
my_objptr
is. This is a great example of a memory leak; the heap object exists but we
have lost our way to access it. In general, this is not a problem. If any object will outlive the compound statement in
which it was created then a more permanent pointer will point to it, which frequently is part of another heap object.
See Resetting the Interpreter Environment in the chapter “Cling the C++ Interpreter”.
Chapter 7
The C++ Interpreter Cling
ROOT has a C++ interpreter called cling built in. It is used for the prompt, both C++ and Python. It also serves as a
source of information to store C++ objects, and provides the back-end for ROOT’s signal/slot and plug-in mechanisms.
This chapter focuses on the parts of cling that you will encounter while interacting with ROOT.
7.1 The ROOT Prompt
Start up a ROOT session by typing root at the system prompt.
$ root
------------------------------------------------------------
| Welcome to ROOT 6.00/00 http://root.cern.ch |
| (c) 1995-2014, The ROOT Team |
| Built for linuxx8664gcc |
| From tag v6-00-00,30 May 2014 |
| Try '.help','.demo','.license','.credits','.quit'/'.q'|
------------------------------------------------------------
root [0]
Now we create a TLine object:
root [1] TLine l;
root [2] l.Print()
TLine X1=0.000000 Y1=0.000000 X2=0.000000 Y2=0.000000
root [3] l.SetX1(10)
root [4] l.SetY1(11)
root [5] l.Print()
TLine X1=10.000000 Y1=11.000000 X2=0.000000 Y2=0.000000
root [6] .g l
.g l
ROOT_prompt_0 1(address: NA) class TLine l, size = 72
root [7] l.GetX1();
root [8] l.GetX1()
(Double_t) 1.000000e+01
Note some of the features of the ROOT prompt: - Terminating with ‘
;
‘ is not required, see “C++ Extensions To Ease
Scripting” below. -
Emacs
style command line editing. - Raw interpreter commands start with a dot;
.g l
for instance
shows the interpreter information on the global called
l
. - To show the result of an expression just do not type the
trailing ;.
For the further examples we will “abbreviate” root [0] etc by root [].
root [] .class TLine
===========================================================================
153
154 CHAPTER 7. THE C++ INTERPRETER CLING
class TLine
SIZE: 72 FILE: TLine.h LINE: 39
Base classes: --------------------------------------------------------
0x20 public TAttBBox2D
List of member variables --------------------------------------------------
TLine.h 42 0x28 protected: Double_t fX1
TLine.h 43 0x30 protected: Double_t fY1
TLine.h 44 0x38 protected: Double_t fX2
TLine.h 45 0x40 protected: Double_t fY2
TLine.h 50 0x0 public:enum TLine::<anonymous at /home/axel/build/root/trunk/obj/include/TLine.h:49:4> kLineNDC
TLine.h 51 0x0 public:enum TLine::<anonymous at /home/axel/build/root/trunk/obj/include/TLine.h:49:4> kVertical
TLine.h 52 0x0 public:enum TLine::<anonymous at /home/axel/build/root/trunk/obj/include/TLine.h:49:4> kHorizontal
TLine.h 94 0x0 private:static class TClass *fgIsA
List of member functions :---------------------------------------------------
filename line:size busy function type and name
(compiled) (NA):(NA) 0public: TLine();
(compiled) (NA):(NA) 0public: TLine(Double_t x1, Double_t y1, Double_t x2, Double_t y2);
(compiled) (NA):(NA) 0public: TLine(const TLine &line);
(compiled) (NA):(NA) 0public:virtual ~TLine() noexcept;
(compiled) (NA):(NA) 0public:void Copy(class TObject &line) const;
(compiled) (NA):(NA) 0public:virtual Int_t DistancetoPrimitive(Int_t px, Int_t py);
(compiled) (NA):(NA) 0public:virtual class TLine *DrawLine(Double_t x1, Double_t y1, Double_t x2, Double_t y2);
(compiled) (NA):(NA) 0public:virtual class TLine *DrawLineNDC(Double_t x1, Double_t y1, Double_t x2, Double_t y2);
(compiled) (NA):(NA) 0public:virtual void ExecuteEvent(Int_t event, Int_t px, Int_t py);
(compiled) (NA):(NA) 0public: Double_t GetX1() const;
(compiled) (NA):(NA) 0public: Double_t GetX2() const;
(compiled) (NA):(NA) 0public: Double_t GetY1() const;
(compiled) (NA):(NA) 0public: Double_t GetY2() const;
(compiled) (NA):(NA) 0public: Bool_t IsHorizontal();
(compiled) (NA):(NA) 0public: Bool_t IsVertical();
(compiled) (NA):(NA) 0public:virtual void ls(Option_t *option = "")const;
(compiled) (NA):(NA) 0public:virtual void Paint(Option_t *option = "");
(compiled) (NA):(NA) 0public:virtual void PaintLine(Double_t x1, Double_t y1, Double_t x2, Double_t y2);
(compiled) (NA):(NA) 0public:virtual void PaintLineNDC(Double_t u1, Double_t v1, Double_t u2, Double_t v2);
(compiled) (NA):(NA) 0public:virtual void Print(Option_t *option = "")const;
(compiled) (NA):(NA) 0public:virtual void SavePrimitive(std::ostream &out, Option_t *option = "");
(compiled) (NA):(NA) 0public:virtual void SetNDC(Bool_t isNDC = kTRUE);
(compiled) (NA):(NA) 0public:void SetHorizontal(Bool_t set = kTRUE);
(compiled) (NA):(NA) 0public:void SetVertical(Bool_t set = kTRUE);
(compiled) (NA):(NA) 0public:virtual void SetX1(Double_t x1);
(compiled) (NA):(NA) 0public:virtual void SetX2(Double_t x2);
(compiled) (NA):(NA) 0public:virtual void SetY1(Double_t y1);
(compiled) (NA):(NA) 0public:virtual void SetY2(Double_t y2);
(compiled) (NA):(NA) 0public:virtual struct Rectangle_t GetBBox();
(compiled) (NA):(NA) 0public:virtual class TPoint GetBBoxCenter();
(compiled) (NA):(NA) 0public:virtual void SetBBoxCenter(const class TPoint &p);
(compiled) (NA):(NA) 0public:virtual void SetBBoxCenterX(const Int_t x);
(compiled) (NA):(NA) 0public:virtual void SetBBoxCenterY(const Int_t y);
(compiled) (NA):(NA) 0public:virtual void SetBBoxX1(const Int_t x);
(compiled) (NA):(NA) 0public:virtual void SetBBoxX2(const Int_t x);
(compiled) (NA):(NA) 0public:virtual void SetBBoxY1(const Int_t y);
(compiled) (NA):(NA) 0public:virtual void SetBBoxY2(const Int_t y);
(compiled) (NA):(NA) 0public:static class TClass *Class();
(compiled) (NA):(NA) 0public:static const char *Class_Name();
(compiled) (NA):(NA) 0public:static Version_t Class_Version();
(compiled) (NA):(NA) 0public:static void Dictionary();
(compiled) (NA):(NA) 0public:virtual class TClass *IsA() const;
(compiled) (NA):(NA) 0public:virtual void ShowMembers(class TMemberInspector &insp) const;
(compiled) (NA):(NA) 0public:virtual void Streamer(class TBuffer &);
(compiled) (NA):(NA) 0public:void StreamerNVirtual(class TBuffer &ClassDef_StreamerNVirtual_b);
(compiled) (NA):(NA) 0public:static const char *DeclFileName();
(compiled) (NA):(NA) 0public:static int ImplFileLine();
(compiled) (NA):(NA) 0public:static const char *ImplFileName();
7.2. FEEDING SOURCES FILES TO ROOT: C++ SCRIPTS 155
(compiled) (NA):(NA) 0public:static int DeclFileLine();
root [] .> test.log
root [] l.Dump();
root [] .>
root [] ?
Here we see:
•Use .class as quick help and reference
•Unix like I/O redirection using .> out.txt and unredirection with .>
•Use ?to get help on all “raw” interpreter commands
•Use @ to abort a multi-line command
Now let us execute a multi-line command:
root [] {
root [] ? TLine l;
root [] ? for (int i=0;i<5; i++) {
root [] ? l.SetX1(i);
root [] ? l.SetY1(i+1);
root [] ? l.Print();
root [] ? }
root [] ? }
TLine X1=0.000000 Y1=1.000000 X2=0.000000 Y2=0.000000
TLine X1=1.000000 Y1=2.000000 X2=0.000000 Y2=0.000000
TLine X1=2.000000 Y1=3.000000 X2=0.000000 Y2=0.000000
TLine X1=3.000000 Y1=4.000000 X2=0.000000 Y2=0.000000
TLine X1=4.000000 Y1=5.000000 X2=0.000000 Y2=0.000000
root [] .q
Here we note:
•A multi-line command starts with a { and ends with a }.
•Inside continuation, every line has to be correctly terminated with a ; (like in “real” C++).
•All objects are created in global scope.
•There is no way to back up; you are better off writing a script.
•Use .q to exit root.
7.2 Feeding Sources Files To ROOT: C++ Scripts
ROOT script files (often called “Macros”) contain pure C++ code. They can contain a simple sequence of statements
like in the multi command line example given above, but also arbitrarily complex class and function definitions.
The most frequent interaction with the ROOT prompt uses .x to “run” a file:
root [] .x myScript.C
This loads myScript.C into the interpreter and calls the function
myScript()
. You can pass arguments using
.x
myScript.C(12, "A String").
Alternatively you can load the script and then run a function explicitly:
root [] .L myScript.C
root [] myScript()
The above is equivalent to .x myScript.C.
In a named script, the objects created on the stack are deleted when the function exits. In a common scenario you
create a histogram in a named script on the stack. You draw the histogram, but when the function exits the canvas is
empty and the histogram has disappeared. To avoid the histogram from disappearing you can create it on the heap (by
using new). This will leave the histogram object intact, but the pointer in the named script scope will be “gone”. Since
histograms (and trees) are added to the list of objects in the current directory, you can always retrieve them to delete
them if needed.
156 CHAPTER 7. THE C++ INTERPRETER CLING
root[] TH1F *h = (TH1F*)gDirectory->Get("myHist"); // or
root[] TH1F *h = (TH1F*)gDirectory->GetList()->FindObject("myHist");
In addition, histograms and trees are automatically deleted when the current directory is closed. This will automatically
take care of the clean up. See “Input/Output”.
7.2.1 Executing a Script From a Script
You may want to execute a script conditionally inside another script. To do it you need to call the interpreter and
you can do that with
TROOT::ProcessLine()
. The example
$ROOTSYS/tutorials/tree/cernstaff.C
calls a script
to build the root file if it does not exist:
void cernstaff() {
if (gSystem->AccessPathName("cernstaff.root")) {
gROOT->ProcessLine(".x cernbuild.C");
}
ProcessLine
takes a parameter, which is a pointer to an
int
or to a
TInterpreter::EErrorCode
to let you
access the interpreter error code after an attempt to interpret. This will contain the error as defined in
enum
TInterpreter::EErrorCode with TInterpreter::kSuccess being the value for a successful execution.
7.2.2 Executing a Script From the Invocation
Instead if starting ROOT and running a script on the prompt you can also pass it to ROOT in its invocation:
$ root -l -b 'myCode.C("some String", 12)'
The exact kind of quoting depends on your shell; the one shown here works for bash-like shells.
ROOT can evaluate any expression as part of the invocation; another version of the previous example can be spelled
like this:
$ root -l -b -e 'gROOT->ProcessLine(".x myCode.C(\"some String\", 12)");'
7.3 C++ Extensions To Ease Scripting
In the next example, we demonstrate three of the most important extensions ROOT and Cling make to C++. Start
ROOT in the directory $ROOTSYS/tutorials (make sure to have first run .x hsimple.C):
root [0]f=new TFile("hsimple.root")
(class TFile *) 0x4045e690
root [1] f->ls()
TFile** hsimple.root
TFile* hsimple.root
KEY: TH1F hpx;1This is the px distribution
KEY: TH2F hpxpy;1py ps px
KEY: THProfile hprof;1Profile of pz versus px
KEY: TNtuple ntuple;1Demo ntuple
root [2] hpx->Draw()
Warning in <MakeDefCanvas>: creating a default canvas with name c1
root [3] .q
The
root [0]
command shows the first extension; the declaration of
f
may be omitted as a shortcut for
auto
.
Cling will correctly create
f
as pointer to object of class
TFile
. Nonetheless we recommend to use
auto f = new
TFile("hsimple.root").
The second extension is more important. In case Cling cannot find an object being referenced, it will ask ROOT
to search for an object with an identical name in the search path defined by
TROOT::FindObject()
. If ROOT finds
the object, it returns a pointer to this object to Cling and a pointer to its class definition and Cling will execute the
7.4. ACLIC: COMPILING SCRIPTS INTO LIBRARIES 157
requested member function. This shortcut is quite natural for an interactive system and saves much typing. In this
example, ROOT searches for hpx and finds it in hsimple.root.
The next, fundamental extension is shown below. There is no need to put a semicolon at the end of a line. When you
leave it off the value of the expression will be printed on the next line. For example:
root[] 23+5
(int)28
root[] 23+5;
root[] TMath::Sin
(Double_t (*)(Double_t)) Function @0x7ffff7ebb090
at include/TMath.h:418:
inline Double_t TMath::Sin(Double_t x)
{return sin(x); }
Be aware that these extensions do not work when a compiler replaces the interpreter. Your code will not compile,
hence when writing large scripts, it is best to stay away from these shortcuts. It will save you from having problems
compiling your scripts using a real C++ compiler.
7.4 ACLiC: Compiling Scripts Into Libraries
Instead of having Cling interpret your script there is a way to have your scripts compiled, linked and dynamically
loaded using the C++ compiler and linker. The advantage of this is that your scripts will run with the speed of
compiled C++ and that you can use language constructs that are not fully supported by Cling. On the other hand, you
cannot use any Cling shortcuts (see “C++ Extensions To Ease Scripting” above) and for small scripts, the overhead of
the compile/link cycle might be larger than just executing the script in the interpreter.
ACLiC will build a dictionary and a shared library from your C++ script, using the compiler and the compiler options
that were used to compile the ROOT executable. You do not have to write a Makefile remembering the correct compiler
options, and you do not have to exit ROOT.
7.4.1 Usage
Before you can compile your interpreted script you need to add include statements for the classes used in the script.
Once you did that, you can build and load a shared library containing your script. To load it use the command
.L
and
append the file name with a +.
root[] .L MyScript.C+
The + option generates the shared library and names it by taking the name of the file “filename” but replacing the
dot before the extension by an underscore and by adding the shared library extension for the current platform. For
example on most platforms, hsimple.cxx will generate hsimple_cxx.so.
The + command rebuild the library only if the script or any of the files it includes are newer than the library. When
checking the timestamp, ACLiC generates a dependency file which name is the same as the library name, just replacing
the ‘so’ extension by the extension ‘d’. For example on most platforms, hsimple.cxx will generate hsimple_cxx.d.
To ensure that the shared library is rebuilt you can use the ++ syntax:
root[] .L MyScript.C++
To build, load, and execute the function with the same name as the file you can use the
.x
command. This is the same
as executing a named script; you can also provide parameters. The only difference is you need to append a + or a ++.
root[] .x MyScript.C+(4000)
Creating shared library /home/./MyScript_C.so
You can select whether the script in compiled with debug symbol or with optimization by appending the letter ‘g’ or
‘O’ after the ‘+’ or ‘++’. Without the specification, the script is compiled with the same level of debugging symbol and
optimization as the currently running ROOT executable. For example:
158 CHAPTER 7. THE C++ INTERPRETER CLING
root[] .L MyScript.C++g
will compile MyScript.C with debug symbols; usually this means giving the -g option to compiler.
root[] .L MyScript.C++O
will compile MyScript.C with optimizations; usually this means giving the -O option to compiler. The syntax:
root[] .L MyScript.C++
is using the default optimization level. The initial default is to compile with the same level of optimization as the root
executable itself. The default can be changed by:
root[] gSystem->SetAclicMode(TSystem::kDebug);
root[] gSystem->SetAclicMode(TSystem::kOpt);
Note that the commands:
root[] .L MyScript.C+g
root[] .L MyScript.C+O
respectively compile
MyScript.C
with debug and optimization if the library does not exist yet; they will not change
the debug and the optimization level if the library already exist and it is up to date. To use ACLiC from compiled
code or from inside another macro, we recommend using
gROOT->ProcessLine()
. For example, in one script you can
use ACLiC to compile and load another script.
gROOT->ProcessLine(".L MyScript.C+")
gROOT->ProcessLine(".L MyScript.C++")
7.4.2 Setting the Include Path
You can get the include path by typing:
root[] .include
You can append to the include path by typing:
root[] .include $HOME/mypackage/include
In a script you can append to the include path:
gSystem->AddIncludePath(" -I$HOME/mypackage/include ")
You can also overwrite the existing include path:
gSystem->SetIncludePath(" -I$HOME/mypackage/include ")
The
$ROOTSYS/include
directory is automatically appended to the include path, so you do not have to worry about
including it. To add library that should be used during linking of the shared library use something like:
gSystem->AddLinkedLibs("-L/my/path -lanylib");
This is especially useful for static libraries. For shared ones you can also simply load them before trying to compile the
script:
gSystem->Load("mydir/mylib");
7.4. ACLIC: COMPILING SCRIPTS INTO LIBRARIES 159
ACLiC uses the directive
fMakeSharedLibs
to create the shared library. If loading the shared library fails, it tries to
output a list of missing symbols by creating an executable (on some platforms like OSF, this does not HAVE to be an
executable) containing the script. It uses the directive
fMakeExe
to do so. For both directives, before passing them
to
TSystem::Exec()
, it expands the variables
$SourceFiles
,
$SharedLib
,
$LibName
,
$IncludePath
,
$LinkedLibs
,
$ExeName
and
$ObjectFiles
. See
SetMakeSharedLib()
for more information on those variables. When the file being
passed to ACLiC is on a read only file system, ACLiC warns the user and creates the library in a temporary directory:
root[] .L readonly/t.C++
Warning in <ACLiC>: /scratch/aclic/subs/./readonly is not writable!
Warning in <ACLiC>: Output will be written to /tmp
Info in <TUnixSystem::ACLiC>: creating shared library
/tmp//scratch/aclic/subs/./readonly/t_C.so
To select the temporary directory ACLiC looks at
$TEMP
,
$TEMP_DIR
,
$TEMPDIR
,
$TMP
,
$TMPDIR
,
$TMP_DIR
or uses
/tmp (
or
C:/)
. Also, a new interface
TSystem::Get/SetBuildDir
is introduced to let users select an alterna-
tive ‘root’ for building of the ACLiC libraries. For
filename/full/path/name/macro.C
, the library is created as
fBuildDir/full/path/name/macro_C.so.
7.4.3 Dictionary Generation
You can direct what is added to the dictionary generated by ACLiC in two ways. The simplest way is to add at the
end of script (i.e. after the symbols have been defined) something like:
#if defined(__ROOTCLING__)
#pragma link C++ class MyOtherClass;
#endif
You can also write this portion of code in a file name
MyScript_linkdef.h
where the suffix
’_linkdef’
is the prefix de-
fined by the key
‘ACLiC.Linkdef
‘ in the currently used resource file (usually
.rootrc
or
$ROOTSYS/etc/system.rootrc
)
and the prefix is the name of your script.
The default behavior of
rootcling
is to not link in (i.e. generate the dictionary for) any of the symbols. In particular,
this means that the following lines are, in the general case, unnecessary.
#pragma link off all globals;
#pragma link off all classes;
#pragma link off all functions;
This also means that linking the instantiation of a class template:
#pragma link C++ class mytemplate<int>;
ONLY links this specific class. You need to request the generation of the iterators explicitly.
See the documentation of rootcling for details how pragma can be used.
NOTE: You should not call ACLiC with a script that has a function called main().
7.4.4 Intermediate Steps and Files
ACLiC executes two steps and a third one if needed. These are:
•Calling rootcling to create a dictionary using rootcling.
•Calling the compiler to build the shared library from the script.
•If there are errors, it calls the compiler to build a dummy executable to clearly report unresolved symbols.
ACLiC makes a shared library with a dictionary containing the classes and functions declared in the script. It also
adds the classes and functions declared in included files with the same name as the script file and any of the following
extensions:
.h
,
.hh
,
.hpp
,
.hxx
,
.hPP
,
.hXX
. This means that, by default, you cannot combine scripts from different
files into one library by using
#include
statements; you will need to compile each script separately. In a future release,
we plan to add the global variables declared in the script to the dictionary also. If you are curious about the specific
calls, you can raise the ROOT debug level: gDebug=3 and ACLiC will print these steps. If you need to keep the
intermediate files around, for example when debugging the script using gdb, use gDebug=7.
160 CHAPTER 7. THE C++ INTERPRETER CLING
7.4.5 Moving between Interpreter and Compiler
The best way to develop portable scripts is to make sure you can always run them with both, the interpreter and with
ACLiC. To do so, do not use the Cling extensions and program around the Cling limitations. When it is not possible
or desirable to program around the Cling limitations, you can use the C preprocessor symbols defined for Cling and
rootcling.
The preprocessor symbol
__CLING__
is defined for both ROOT and
rootcling
. The symbol
__ROOTCLING__
(and
__ROOTCLING__ for backward compatibility) is only defined in rootcling.
Use
!defined(__CLING__) || defined(__ROOTCLING__)
to bracket code that needs to be seen by the compiler and
rootcling, but will be invisible to the interpreter.
Use
!defined(__CLING__)
to bracket code that should be seen only by the compiler and not by Cling nor
rootcling.
For
example, the following will hide the declaration and initialization of the array
gArray
from both Cling and
rootcling
.
#if !defined(__CLING__)
int gArray[] = { 2,3,4};
#endif
Because ACLiC calls
rootcling
to build a dictionary, the declaration of
gArray
will not be included in the dictionary,
and consequently,
gArray
will not be available at the command line even if ACLiC is used. Cling and
rootcling
will ignore all statements between the
"#if !defined (__CLING__)"
and “
#endif"
. If you want to use
gArray
in
the same script as its declaration, you can do so. However, if you want use the script in the interpreter you have to
bracket the usage of
gArray
between
#if’s,
since the definition is not visible. If you add the following preprocessor
statements:
#if !defined(__CLING__)
int gArray[] = { 2,3,4};
#elif defined(__ROOTCLING__)
int gArray[];
#endif
gArray
will be visible to
rootcling
but still not visible to Cling. If you use ACLiC,
gArray
will be available at the
command line and be initialized properly by the compiled code.
We recommend you always write scripts with the needed include statements. In most cases, the script will still run
with the interpreter. However, a few header files are not handled very well by Cling.
These types of headers can be included in interpreted and compiled mode:
•The subset of standard C/C++ headers defined in $ROOTSYS/Cling/include.
•
Headers of classes defined in a previously loaded library (including ROOT own). The defined class must have a
name known to ROOT (i.e. a class with a ClassDef).
Hiding header files from
rootcling
that are necessary for the compiler but optional for the interpreter can lead to a
subtle but fatal error. For example:
#ifndef __CLING__
#include "TTree.h"
#else
class TTree;
#endif
class subTree : public TTree {
};
In this case,
rootcling
does not have enough information about the
TTree
class to produce the correct dictionary file.
If you try this,
rootcling
and compiling will be error free, however, instantiating a
subTree
object from the Cling
command line will cause a fatal error. In general, it is recommended to let
rootcling
see as many header files as
possible.
7.5. CLASSES DEFINED BY SCRIPTS 161
7.5 Classes Defined By Scripts
Lets create a small class
TMyClass
and a derived class
TChild
. The virtual method
TMyClass::Print()
is overridden
in TChild. Save this in file called script4.C.
#include <iostream.h>
class TMyClass {
private:
float fX; //x position in centimeters
float fY; //y position in centimeters
public:
TMyClass() { fX = fY = -1; }
virtual void Print() const;
void SetX(float x){fX=x;}
void SetY(float y){fY=y;}
};
void TMyClass::Print() const // parent print method
{
cout << "fX="<< fX << ",fY="<< fY << endl;
}
class TChild : public TMyClass {
public:
void Print() const;
};
void TChild::Print() const // child print metod
{
cout << "This is TChild::Print()" << endl;
TMyClass::Print();
}
To execute script4.C do:
root[] .L script4.C
root[] TMyClass *a = new TChild
root[] a->Print()
This is TChild::Print()
fX = -1,fY=-1
root[] a->SetX(10)
root[] a->SetY(12)
root[] a->Print()
This is TChild::Print()
fX=10,fY=12
root[] .class TMyClass
=====================================================
class TMyClass
size=0x8 FILE:script4.C LINE:3
List of base class-----------------------------------
List of member variable------------------------------
Defined in TMyClass
0x0 private:float fX
0x4 private:float fY
List of member function------------------------------
Defined in TMyClass
filename line:size busy function type and name
script4.C 16:5 0 public:class TMyClass TMyClass(void);
script4.C 22:4 0 public:void Print(void);
script4.C 12:1 0 public:void SetX(float x);
script4.C 13:1 0 public:void SetY(float y);
root[] .q
As you can see, an interpreted class behaves just like a compiled class. See “Adding a Class” for ways how to add a
class with a shared library and with ACLiC.
162 CHAPTER 7. THE C++ INTERPRETER CLING
7.6 Inspecting Objects
An object of a class inheriting from
TObject
can be inspected, with the
Inspect()
method. The
TObject::Inspect
method creates a window listing the current values of the objects members. For example, the next picture is of
TFile
.
root[] TFile f("staff.root")
root[] f.Inspect()
You can see the pointers are in red and can be clicked on to follow the pointer to the object. If you clicked on
fList
, the
list of objects in memory and there were none, no new canvas would be shown. On top of the page are the navigation
buttons to see the previous and next screen.
Figure 7.1: ROOT object inspector of TFile
7.6. INSPECTING OBJECTS 163
Figure 7.2: The object inspector of fKeys, the list of keys in the memory
164 CHAPTER 7. THE C++ INTERPRETER CLING
Chapter 8
Object Ownership
An object has ownership of another object if it has permission to delete it. Usually a collection or a parent object
such as a pad holds ownership. To prevent memory leaks and multiple attempts to delete an object, you need to know
which objects ROOT owns and which are owned by you.
The following rules apply to the ROOT classes.
•
Histograms, trees, and event lists created by the user are owned by current directory (
gDirectory
). When the
current directory is closed or deleted the objects it owns are deleted.
•
The
TROOT
master object (
gROOT
) has several collections of objects. Objects that are members of these collections
are owned by gROOT see “Ownership by the Master TROOT Object (gROOT).
•
Objects created by another object, for example the function object (e.g.
TF1
) created by the
TH1::Fitmethod is
owned by the histogram.
•An object created by DrawCopy methods, is owned by the pad it is drawn in.
If an object fits none of these cases, the user has ownership. The next paragraphs describe each rule and user ownership
in more detail.
8.1 Ownership by Current Directory (gDirectory)
When a histogram, tree, or event list (
TEventList
) is created, it is added to the list of objects in the current directory
by default. You can get the list of objects in a directory and retrieve a pointer to a specific object with the
GetList
method. This example retrieves a histogram.
TH1F *h = (TH1F*)gDirectory->GetList()->FindObject("myHist");
The method
TDirectory::GetList()
returns a
TList
of objects in the directory. It looks in memory, and is
implemented in all ROOT collections. You can change the directory of a histogram, tree, or event list with the
SetDirectory method. Here we use a histogram for an example, but the same applies to trees and event lists.
h->SetDirectory(newDir);
You can also remove a histogram from a directory by using
SetDirectory(0)
. Once a histogram is removed from the
directory, it will not be deleted when the directory is closed. It is now your responsibility to delete this histogram once
you have finished with it. To change the default that automatically adds the histogram to the current directory, you
can call the static function:
TH1::AddDirectory(kFALSE);
Not all histograms created here after will be added to the current directory. In this case, you own all histogram objects
and you will need to delete them and clean up the references. You can still set the directory of a histogram by calling
SetDirectory once it has been created as described above.
Note that, when a file goes out of scope or is closed all objects on its object list are deleted.
165
166 CHAPTER 8. OBJECT OWNERSHIP
8.2 Ownership by the Master TROOT Object (gROOT)
The master object
gROOT ,
maintains several collections of objects. For example, a canvas is added to the collection of
canvases and it is owned by the canvas collection.
TSeqCollection* fFiles List of TFile
TSeqCollection* fMappedFiles List of TMappedFile
TSeqCollection* fSockets List of TSocket and TServerSocket
TSeqCollection* fCanvases List of TCanvas
TSeqCollection* fStyles List of TStyle
TSeqCollection* fFunctions List of TF1, TF2, TF3
TSeqCollection* fTasks List of TTask
TSeqCollection* fColors List of TColor
TSeqCollection* fGeometries List of geometries
TSeqCollection* fBrowsers List of TBrowser
TSeqCollection* fSpecials List of special objects
TSeqCollection* fCleanups List of recursiveRemove collections
These collections are also displayed in the root folder of the
Object Browser
. Most of these collections are self
explanatory. The special cases are the collections of specials and cleanups.
8.2.1 The Collection of Specials
This collection contains objects of the following classes:
TCutG
,
TMultiDimFit
,
TPrincipal
,
TChains
. In addition it
contains the
gHtml
object,
gMinuit
objects, and the array of contours graphs (
TGraph
) created when calling the
Draw
method of a histogram with the "CONT,LIST" option.
8.2.2 Access to the Collection Contents
The current content for a collection listed above can be accessed with the corresponding
gROOT->GetListOf
method
(for example
gROOT->GetListOfCanvases
). In addition,
gROOT->GetListOfBrowsables
returns a collection of all
objects visible on the left side panel in the browser. See the image of the Object Browser in the next figure.
Figure 8.1: The ROOT Object Browser
8.3. OWNERSHIP BY OTHER OBJECTS 167
8.3 Ownership by Other Objects
When an object creates another, the creating object is the owner of the created one. For example:
myHisto->Fit("gaus")
The call to Fit copies the global
TF1
Gaussian function and attaches the copy to the histogram. When the histogram is
deleted, the copy is deleted also.
When a pad is deleted or cleared, all objects in the pad with the
kCanDelete
bit set are deleted automatically. Currently
the objects created by the DrawCopy methods, have the kCanDelete bit set and are therefore owned by the pad.
8.4 Ownership by the User
The user owns all objects not described in one of the above cases.
TObject
has two bits,
kCanDelete
and
kMustCleanup
,
that influence how an object is managed (in
TObject::fBits)
. These are in an enumeration in
TObject.h.
To set
these bits do:
MyObject->SetBit(kCanDelete)
MyObject->SetBit(kMustCleanup)
The bits can be reset and tested with the TObject::ResetBit and TObject::TestBit methods.
8.4.1 The kCanDelete Bit
The
gROOT
collections (see above) own their members and will delete them regardless of the
kCanDelete
bit. In all
other collections, when the collection
Clear
method is called (i.e.
TList::Clear())
, members with the
kCanDelete
bit set, are deleted and removed from the collection. If the
kCanDelete
bit is not set, the object is only removed from
the collection but not deleted.
If a collection
Delete
(
TList::Delete()
) method is called, all objects in the collection are deleted without considering
the
kCanDelete
bit. It is important to realize that deleting the collection (i.e. delete
MyCollection
), DOES NOT
delete the members of the collection.
If the user specified
MyCollection->SetOwner()
the collection owns the objects and delete
MyCollection
will delete
all its members. Otherwise, you need to:
// delete all member objects in the collection
MyCollection->Delete();
// and delete the collection object
delete MyCollection;
Note that
kCanDelete
is automatically set by the
DrawCopy
method and the user can set it for any object. For example,
the user must manage all graphics primitives. If you want
TCanvas
to delete the primitive you created you have to set
the kCanDelete bit.
The
kCanDelete
bit setting is displayed with
TObject::ls()
. The last number is either 1 or 0 and is the
kCanDelete
bit.
root[] TCanvas MyCanvas("MyCanvas")
root[] MyCanvas.Divide(2,1)
root[] MyCanvas->cd(MyCanvas_1)
root[] hstat.Draw() // hstat is an existing TH1F
root[] MyCanvas->cd(MyCanvas_2)
root[] hstat.DrawCopy() // DrawCopy sets the kCanDelete bit
(class TH1*)0x88e73f8
root[] MyCanvas.ls()
Canvas Name=MyCanvas ...
TCanvas ... Name= MyCanvas ...
TPad ... Name= MyCanvas_1 ...
168 CHAPTER 8. OBJECT OWNERSHIP
TFrame ...
OBJ: TH1F hstat Event Histogram : 0
TPaveText ... title
TPaveStats ... stats
TPad ... Name= MyCanvas_2 ...
TFrame ...
OBJ: TH1F hstat Event Histogram : 1
TPaveText ... title
TPaveStats ... stats
8.4.2 The kMustCleanup Bit
When the
kMustCleanup
bit is set, the object destructor will remove the object and its references from all collections
in the clean up collection (
gROOT ::fCleanups
). An object can be in several collections, for example if an object is in a
browser and on two canvases. If the
kMustCleanup
bit is set, it will be removed automatically from the browser and
both canvases when the destructor of the object is called.
The kMustCleanup bit is set:
•When an object is added to a pad (or canvas) in TObject::AppendPad.
•When an object is added to a TBrowser with TBrowser::Add.
•When an object is added to a TFolder withTFolder::Add.
•When creating an inspector canvas with TInspectCanvas::Inspector.
•When creating a TCanvas.
•When painting a frame for a pad, the frame’s kMustCleanup is set in TPad::PaintPadFrame
The user can add their own collection to the collection of clean ups, to take advantage of the automatic garbage
collection. For example:
// create two list
TList *myList1, *myList2;
// add both to of clean ups
gROOT->GetListOfCleanUps()->Add(myList1);
gROOT->GetListOfCleanUps()->Add(myList2);
// assuming myObject is in myList1 and myList2, when calling:
delete myObject;
// the object is deleted from both lists
Chapter 9
Graphics and the Graphical User
Interface
Graphical capabilities of ROOT range from 2D objects (lines, polygons, arrows) to various plots, histograms, and 3D
graphical objects. In this chapter, we are going to focus on principals of graphics and 2D objects. Plots and histograms
are discussed in a chapter of their own.
9.1 Drawing Objects
In ROOT, most objects derive from a base class
TObject
. This class has a virtual method
Draw()
so all objects are
supposed to be able to be “drawn”. The basic whiteboard on which an object is drawn is called a canvas (defined by
the class
TCanvas
). If several canvases are defined, there is only one active at a time. One draws an object in the active
canvas by using the statement:
object.Draw()
This instructs the object “
object
” to draw itself. If no canvas is opened, a default one (named “
c1
”) is instantiated
and is drawn.
root[] TLine a(0.1,0.1,0.6,0.6)
root[] a.Draw()
<TCanvas::MakeDefCanvas>: created default TCanvas with name c1
The first statement defines a line and the second one draws it. A default canvas is drawn since there was no opened one.
9.2 Interacting with Graphical Objects
When an object is drawn, one can interact with it. For example, the line drawn in the previous paragraph may be
moved or transformed. One very important characteristic of ROOT is that transforming an object on the screen will
also transform it in memory. One actually interacts with the real object, not with a copy of it on the screen. You can
try for instance to look at the starting X coordinate of the line:
root[] a.GetX1()
(double)1.000000000e-1
X1
is the
x
value of the starting coordinate given in the definition above. Now move it interactively by clicking with the
left mouse button in the line’s middle and try to do again:
root[] a.GetX1()
(Double_t)1.31175468483816005e-01
You do not obtain the same result as before, the coordinates of ‘
a
’ have changed. As said, interacting with an object
on the screen changes the object in memory.
169
170 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.2.1 Moving, Resizing and Modifying Objects
Changing the graphic objects attributes can be done with the GUI or programmatically. First, let’s see how it is done
in the GUI.
9.2.1.1 The Left Mouse Button
As was just seen moving or resizing an object is done with the left mouse button. The cursor changes its shape to
indicate what may be done:
Point the object or one part of it:
Rotate:
Resize (exists also for the other directions):
Enlarge (used for text):
Move:
Here are some examples of:
Moving: Resizing:
Rotating:
9.2.1.2 With C++ Statements (Programmatically)
How would one move an object in a script? Since there is a tight correspondence between what is seen on the screen
and the object in memory, changing the object changes it on the screen. For example, try to do:
root[] a.SetX1(0.9)
9.2. INTERACTING WITH GRAPHICAL OBJECTS 171
This should change one of the coordinates of our line, but nothing happens on the screen. Why is that? In short, the
canvas is not updated with each change for performance reasons. See “Updating the Pad”.
9.2.2 Selecting Objects
9.2.2.1 The Middle Mouse Button
Objects in a canvas, as well as in a pad, are stacked on top of each other in the order they were drawn. Some objects
may become “active” objects, which mean they are reordered to be on top of the others. To interactively make an
object “active”, you can use the middle mouse button. In case of canvases or pads, the border becomes highlighted
when it is active.
9.2.2.2 With C++ Statements (Programmatically)
Frequently we want to draw in different canvases or pads. By default, the objects are drawn in the active canvas. To
activate a canvas you can use the TPad::cd() method.
root[] c1->cd()
9.2.3 Context Menus: the Right Mouse Button
The context menus are a way to interactively call certain methods of an object. When designing a class, the programmer
can add methods to the context menu of the object by making minor changes to the header file.
9.2.3.1 Using Context Menus
On a ROOT canvas, you can right-click on any object and see the context menu for it. The script
hsimple.C
draws
a histogram. The image below shows the context menus for some of the objects on the canvas. Next picture shows
that drawing a simple histogram involves as many as seven objects. When selecting a method from the context menu
and that method has options, the user will be asked for numerical values or strings to fill in the option. For example,
TAxis::SetTitle will prompt you for a string to use for the axis title.
9.2.3.2 Structure of the Context Menus
The curious reader will have noticed that each entry in the context menu corresponds to a method of the class. Look
for example to the menu named
TAxis::xaxis
.
xaxis
is the name of the object and
TAxis
the name of its class. If we
look at the list of
TAxis
methods, for example in http://root.cern.ch/root/htmldoc/TAxis.html, we see the methods
SetTimeDisplay() andUnZoom(), which appear also in the context menu.
There are several divisions in the context menu, separated by lines. The top division is a list of the class methods; the
second division is a list of the parent class methods. The subsequent divisions are the methods other parent classes
in case of multiple inheritance. For example, see the TPaveText::title context menu. ATPaveText inherits from
TAttLine, which has the method SetLineAttributes().
9.2.3.3 Adding Context Menus for a Class
For a method to appear in the context menu of the object it has to be marked by
// *MENU*
in the header file. Below
is the line from TAttLine.h that adds the SetLineAttribute method to the context menu.
virtual void SetLineAttributes(); // *MENU*
Nothing else is needed, since Cling knows the classes and their methods. It takes advantage of that to create the
context menu on the fly when the object is clicking on. If you click on an axis, ROOT will ask the interpreter what are
the methods of the TAxis and which ones are set for being displayed in a context menu.
Now, how does the interpreter know this? Remember, when you build a class that you want to use in the ROOT
environment, you use
rootcling
that builds the so-called stub functions and the dictionary. These functions and
the dictionary contain the knowledge of the used classes. To do this,
rootcling
parses all the header files. ROOT
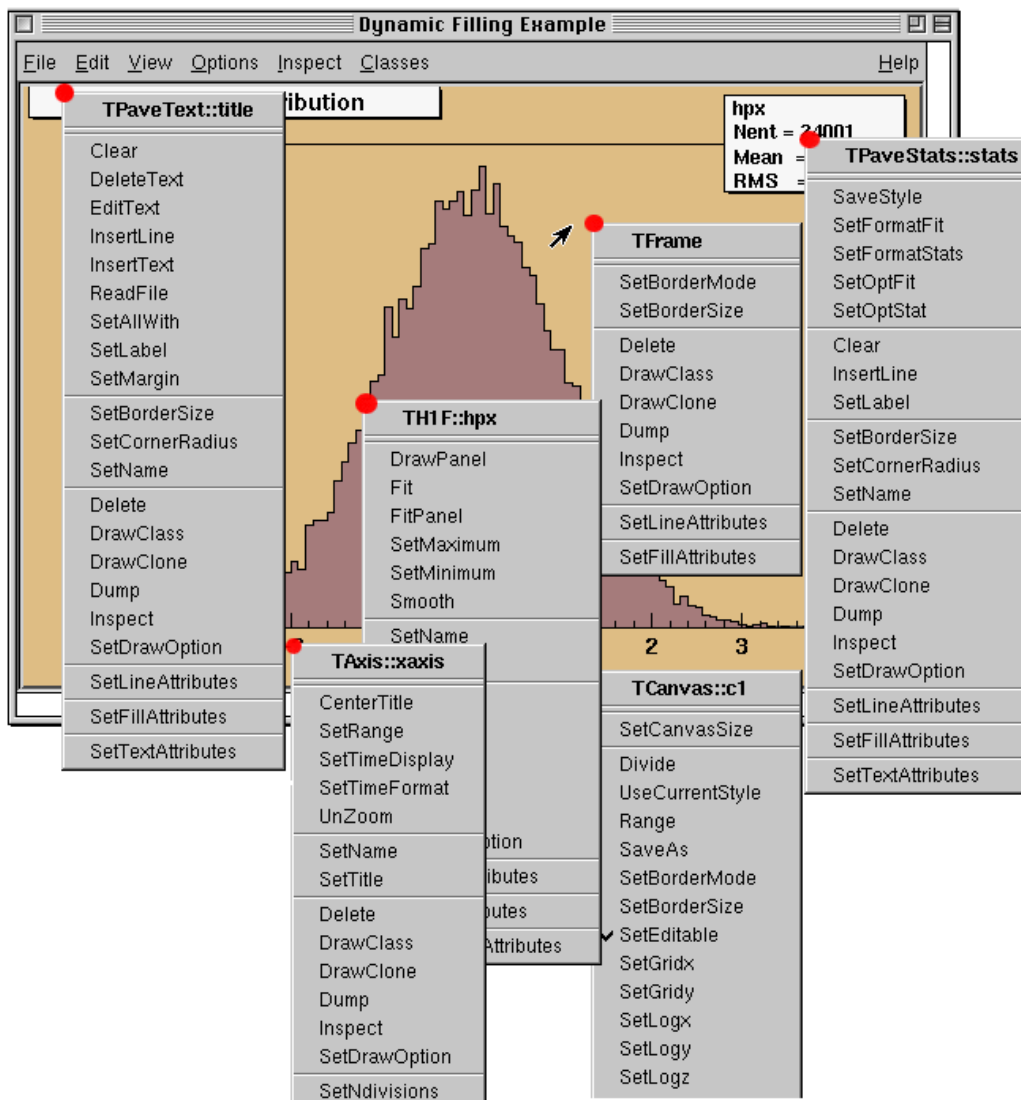
172 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
Figure 9.1: Context menus of different objects in a canvas
9.2. INTERACTING WITH GRAPHICAL OBJECTS 173
has defined some special syntax to inform Cling of certain things, this is done in the comments so that the code still
compiles with a C++ compiler.
For example, you have a class with a
Draw()
method, which will display itself. You would like a context menu to
appear when on clicks on the image of an object of this class. The recipe is the following:
•The class has to contain the ClassDef/ClassImp macros
•
For each method you want to appear in the context menu, put a comment after the declaration containing
*MENU*
or
*TOGGLE*
depending on the behavior you expect. One usually uses Set methods (setters). The
*TOGGLE*
comment is used to toggle a
boolean
data field. In that case, it is safe to call the data field
fMyBool
where
MyBool is the name of the setter SetMyBool. Replace MyBool with your own boolean variable.
•You can specify arguments and the data members in which to store the arguments.
For example:
class MyClass : public TObject {
private:
int fV1; // first variable
double fV2; // second variable
public:
int GetV1() {return fV1;}
double GetV2() {return fV2;}
void SetV1(int x1) { fV1 = x1;} // *MENU*
void SetV2(double d2) { fV2 = d2;} // *MENU*
void SetBoth(int x1, double d2) {fV1 = x1; fV2 = d2;}
ClassDef (MyClass,1)
}
To specify arguments:
void SetXXX(Int_t x1, Float_t y2); //*MENU* *ARGS={x1=>fV1}
This statement is in the comment field, after the *MENU*. If there is more than one argument, these arguments are
separated by commas, where fX1 and fY2 are data fields in the same class.
void SetXXX(Int_t x1, Float_t y2); //*MENU* *ARGS={x1=>fX1,y2=>fY2}
If the arguments statement is present, the option dialog displayed when selecting
SetXXX field
will show the values of
variables. We indicate to the system which argument corresponds to which data member of the class.
9.2.4 Executing Events when a Cursor Passes on Top of an Object
This paragraph is for class designers. When a class is designed, it is often desirable to include drawing methods for it.
We will have a more extensive discussion about this, but drawing an object in a canvas or a pad consists in “attaching”
the object to that pad. When one uses
object.Draw()
, the object is NOT painted at this moment. It is only attached
to the active pad or canvas.
Another method should be provided for the object to be painted, the
Paint()
method. This is all explained in the next
paragraph. As well as
Draw()
and
Paint()
, other methods may be provided by the designer of the class. When the
mouse is moved or a button pressed/released, the
TCanvas
function named
HandleInput()
scans the list of objects in
all it’s pads and for each object calls some standard methods to make the object react to the event (mouse movement,
click or whatever).
The second one is DistanceToPrimitive(px,py). This function computes a “distance” to an object from the mouse
position at the pixel position (
px
,
py
, see definition at the end of this paragraph) and returns this distance in pixel
units. The selected object will be the one with the shortest computed distance. To see how this works, select the
“
Event Status
” item in the canvas “
Options
” menu. ROOT will display one status line showing the picked object. If
the picked object is, for example, a histogram, the status line indicates the name of the histogram, the position
x,y
in
histogram coordinates, the channel number and the channel content.
174 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
It is nice for the canvas to know what the closest object from the mouse is, but it’s even nicer to be able to make this
object react. The third standard method to be provided is
ExecuteEvent()
. This method actually does the event
reaction. Its prototype is where
px
and
py
are the coordinates at which the event occurred, except if the event is a key
press, in which case px contains the key code.
void ExecuteEvent(Int_t event, Int_t px, Int_t py);
Where event is the event that occurs and is one of the following (defined in Buttons.h):
kNoEvent, kButton1Down, kButton2Down,
kButton3Down, kKeyDown, kButton1Up,
kButton2Up, kButton3Up, kButton1Motion,
kButton2Motion, kButton3Motion, kKeyPress,
kButton1Locate, kButton2Locate, kButton3Locate,
kKeyUp, kButton1Double, kButton2Double,
kButton3Double, kMouseMotion, kMouseEnter,
kMouseLeave
We hope the names are self-explanatory.
Designing an
ExecuteEvent
method is not very easy, except if one wants very basic treatment. We will not go into
that and let the reader refer to the sources of classes like
TLine
or
TBox
. Go and look at their
ExecuteEvent
method!
We can nevertheless give some reference to the various actions that may be performed. For example, one often wants
to change the shape of the cursor when passing on top of an object. This is done with the SetCursor method:
gPad->SetCursor(cursor)
The argument cursor is the type of cursor. It may be:
kBottomLeft, kBottomRight, kTopLeft,
kTopRight, kBottomSide, kLeftSide,
kTopSide, kRightSide, kMove,
kCross, kArrowHor, kArrowVer,
kHand, kRotate, kPointer,
kArrowRight, kCaret, kWatch
They are defined in
TVirtualX.h
and again we hope the names are self-explanatory. If not, try them by designing a
small class. It may derive from something already known like TLine.
Note that the
ExecuteEvent()
functions may in turn; invoke such functions for other objects, in case an object is
drawn using other objects. You can also exploit at best the virtues of inheritance. See for example how the class
TArrow (derived from TLine) use or redefine the picking functions in its base class.
The last comment is that mouse position is always given in pixel units in all these standard functions.
px=0
and
py=0
corresponds to the top-left corner of the canvas. Here, we have followed the standard convention in windowing systems.
Note that user coordinates in a canvas (pad) have the origin at the bottom-left corner of the canvas (pad). This is all
explained in the paragraph “The Coordinate Systems of a Pad”.
9.3 Graphical Containers: Canvas and Pad
We have talked a lot about canvases, which may be seen as windows. More generally, a graphical entity that contains
graphical objects is called a Pad. A Canvas is a special kind of Pad. From now on, when we say something about pads,
this also applies to canvases. A pad (class
TPad
) is a graphical container in the sense it contains other graphical objects
like histograms and arrows. It may contain other pads (sub-pads) as well. A Pad is a linked list of primitives of any
type (graphs, histograms, shapes, tracks, etc.). It is a kind of display list.
Drawing an object is nothing more than adding its pointer to this list. Look for example at the code of
TH1::Draw()
.
It is merely ten lines of code. The last statement is
AppendPad()
. This statement calls method of
TObject
that just
adds the pointer of the object, here a histogram, to the list of objects attached to the current pad. Since this is a
TObject’s method, every object may be “drawn”, which means attached to a pad.
When is the painting done then ? The answer is: when needed. Every object that derives from
TObject
has a
Paint()
method. It may be empty, but for graphical objects, this routine contains all the instructions to paint effectively it in
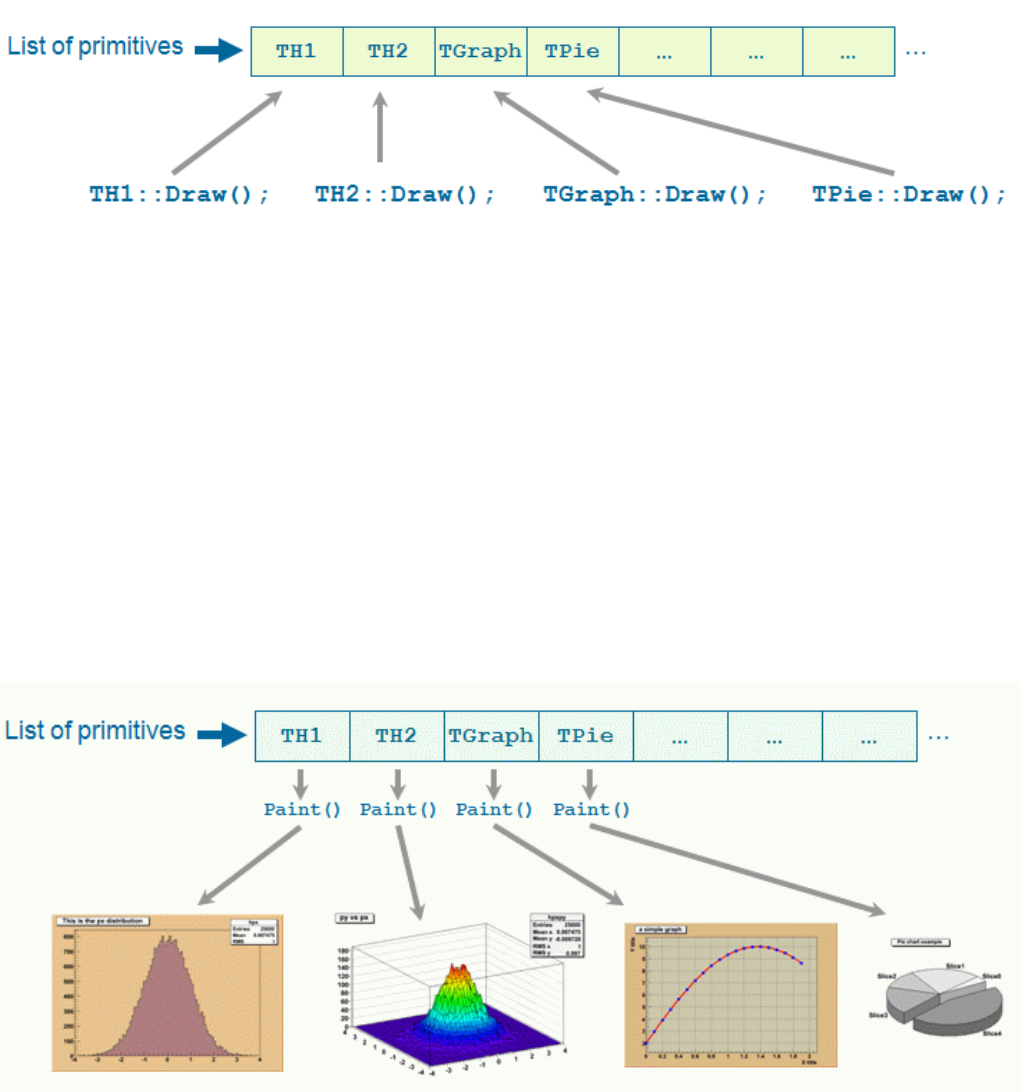
9.3. GRAPHICAL CONTAINERS: CANVAS AND PAD 175
Figure 9.2: The pad display list
Figure 9.3: Pad painting
176 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
the active pad. Since a Pad has the list of objects it owns, it will call successively the
Paint()
method of each object,
thus re-painting the whole pad on the screen. If the object is a sub-pad, its
Paint()
method will call the
Paint()
method of the objects attached, recursively calling Paint() for all the objects.
In some cases a pad need to be painted during a macro execution. To force the pad painting
gPad->Update()
(see
next section) should be performed.
The list of primitives stored in the pad is also used to pick objects and to interact with them.
9.3.1 The Global Pad: gPad
When an object is drawn, it is always in the so-called active pad. For every day use, it is comfortable to be able to
access the active pad, whatever it is. For that purpose, there is a global pointer, called
gPad
. It is always pointing to
the active pad. If you want to change the fill color of the active pad to blue but you do not know its name, do this.
root[] gPad->SetFillColor(38)
To get the list of colors, go to the paragraph “Color and color palettes” or if you have an opened canvas, click on the
View menu, selecting the Colors item.
9.3.1.1 Finding an Object in a Pad
Now that we have a pointer to the active pad,
gPad
and that we know this pad contains some objects, it is sometimes
interesting to access one of those objects. The method
GetPrimitive()
of
TPad
, i.e.
TPad::GetPrimitive(const
char* name)
does exactly this. Since most of the objects that a pad contains derive from
TObject
, they have a name.
The following statement will return a pointer to the object
myobjectname
and put that pointer into the variable
obj
.
As you can see, the type of returned pointer is TObject*.
root[] obj = gPad->GetPrimitive("myobjectname")
(class TObject*)0x1063cba8
Even if your object is something more complicated, like a histogram
TH1F
, this is normal. A function cannot return
more than one type. So the one chosen was the lowest common denominator to all possible classes, the class from
which everything derives,
TObject
. How do we get the right pointer then? Simply do a cast of the function output
that will transform the output (pointer) into the right type. For example if the object is a TPaveLabel:
root[] obj = (TPaveLabel*)(gPad->GetPrimitive("myobjectname"))
(class TPaveLabel*)0x1063cba8
This works for all objects deriving from
TObject
. However, a question remains. An object has a name if it derives
from
TNamed
, not from
TObject
. For example, an arrow (
TArrow
) doesn’t have a name. In that case, the “name” is
the name of the class. To know the name of an object, just click with the right button on it. The name appears at
the top of the context menu. In case of multiple unnamed objects, a call to
GetPrimitive("className")
returns the
instance of the class that was first created. To retrieve a later instance you can use
GetListOfPrimitives()
, which
returns a list of all the objects on the pad. From the list you can select the object you need.
9.3.1.2 Hiding an Object
Hiding an object in a pad can be made by removing it from the list of objects owned by that pad. This list is accessible
by the
GetListOfPrimitives()
method of
TPad
. This method returns a pointer to a
TList
. Suppose we get the
pointer to the object, we want to hide, call it obj (see paragraph above). We get the pointer to the list:
root[] li = gPad->GetListOfPrimitives()
Then remove the object from this list:
root[] li->Remove(obj)
The object will disappear from the pad as soon as the pad is updated (try to resize it for example). If one wants to
make the object reappear:
root[] obj->Draw()
Caution, this will not work with composed objects, for example many histograms drawn on the same plot (with the
option “same”). There are other ways! Try to use the method described here for simple objects.
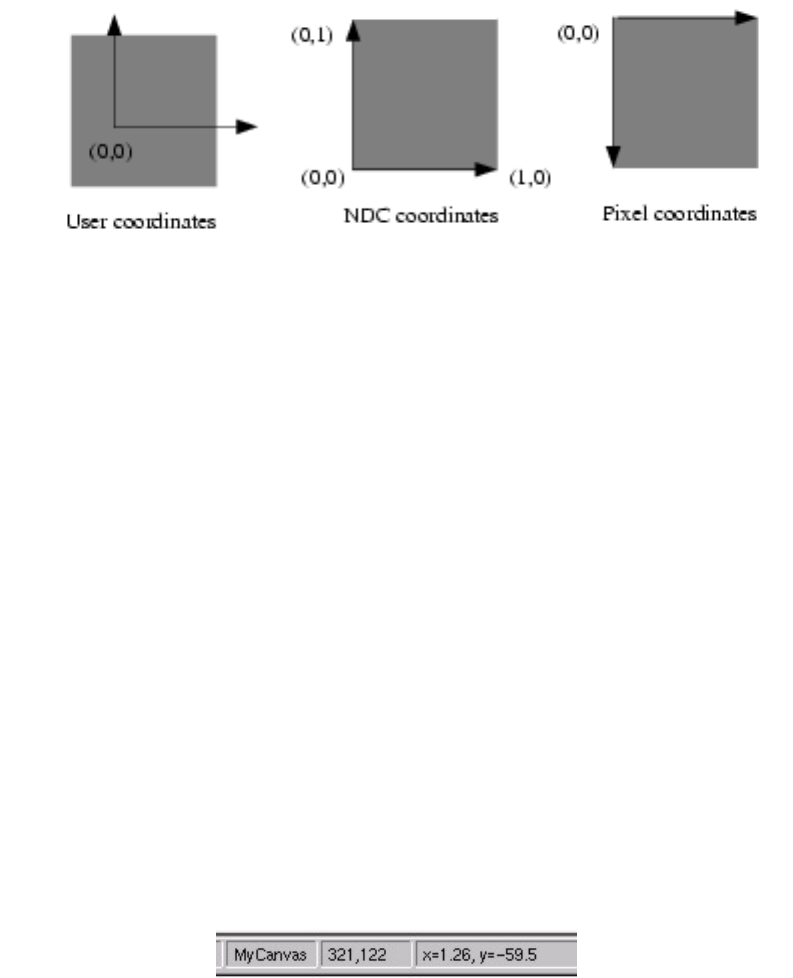
9.3. GRAPHICAL CONTAINERS: CANVAS AND PAD 177
9.3.2 The Coordinate Systems of a Pad
There are coordinate systems in a TPad: user coordinates, normalized coordinates (NDC), and pixel coordinates.
Figure 9.4: Pad coordinate systems
9.3.2.1 The User Coordinate System
The most common is the user coordinate system. Most methods of
TPad
use the user coordinates, and all graphic
primitives have their parameters defined in terms of user coordinates. By default, when an empty pad is drawn, the
user coordinates are set to a range from 0 to 1 starting at the lower left corner. At this point they are equivalent of the
NDC coordinates (see below). If you draw a high level graphical object, such as a histogram or a function, the user
coordinates are set to the coordinates of the histogram. Therefore, when you set a point it will be in the histogram
coordinates.
For a newly created blank pad, one may use
TPad::Range
to set the user coordinate system. This function is defined
as:
void Range(float x1,float y1,float x2,float y2)
The arguments
x1
,
x2
defines the new range in the x direction, and the
y1
,
y2
define the new range in the y-direction.
root[] TCanvas MyCanvas ("MyCanvas")
root[] gPad->Range(-100,-100,100,100)
This will set the active pad to have both coordinates to go from -100 to 100, with the center of the pad at (0,0). You
can visually check the coordinates by viewing the status bar in the canvas. To display the status bar select Event
Status entry in the View canvas menu.
Figure 9.5: The status bar
9.3.2.2 The Normalized Coordinate System (NDC)
Normalized coordinates are independent of the window size and of the user system. The coordinates range from 0 to 1
and (0, 0) corresponds to the bottom-left corner of the pad. Several internal ROOT functions use the NDC system (3D
primitives, PostScript, log scale mapping to linear scale). You may want to use this system if the user coordinates are
not known ahead of time.
9.3.2.3 The Pixel Coordinate System
The least common is the pixel coordinate system, used by functions such as
DistanceToPrimitive()
and
ExecuteEvent()
. Its primary use is for cursor position, which is always given in pixel coordinates. If (
px,py
) is the
cursor position,
px=0
and
py=0
corresponds to the top-left corner of the pad, which is the standard convention in
windowing systems.
178 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.3.2.4 Using NDC for a particular Object
Most of the time, you will be using the user coordinate system. But sometimes, you will want to use NDC. For example,
if you want to draw text always at the same place over a histogram, no matter what the histogram coordinates are.
There are two ways to do this. You can set the NDC for one object or may convert NDC to user coordinates. Most
graphical objects offer an option to be drawn in NDC. For instance, a line (
TLine
) may be drawn in NDC by using
DrawLineNDC(). A latex formula or a text may use TText::SetNDC() to be drawn in NDC coordinates.
9.3.3 Converting between Coordinate Systems
There are a few utility functions in
TPad
to convert from one system of coordinates to another. In the following table, a
point is defined by
(px,py)
in pixel coordinates,
(ux,uy)
in user coordinates,
(ndcx,ndcy)
in normalized coordinates,
(apx,apy) are in absolute pixel coordinates.
Conversion TPad’s Methods Returns
NDC to Pixel UtoPixel(ndcx)
VtoPixel(ndcy)
Int_t
Int_t
Pixel to User PixeltoX(px)
PixeltoY(py)
PixeltoXY(px,py,&ux,&uy)
Double_t
Double_t
Double_t ux,uy
User to Pixel XtoPixel(ux)
YtoPixel(uy)
XYtoPixel(ux,uy,&px,&py)
Int_t
Int_t
Int_t px,py
User to absolute pixel XtoAbsPixel(ux)
YtoAbsPixel(uy)
XYtoAbsPixel(ux,uy,&apx,&apy)
Int_t
Int_t
Int_t apx,apy
Absolute pixel to user AbsPixeltoX(apx)
AbsPixeltoY(apy)
AbsPixeltoXY(apx,apy,&ux,&uy)
Double_t
Double_t
Double_t ux,uy
Note: all the pixel conversion functions along the Y axis consider that
py=0
is at the top of the pad except
PixeltoY()
which assume that the position
py=0
is at the bottom of the pad. To make
PixeltoY()
converting the same way as
the other conversion functions, it should be used the following way (pis a pointer to a TPad):
p->PixeltoY(py - p->GetWh());
9.3.4 Dividing a Pad into Sub-pads
Dividing a pad into sub pads in order for instance to draw a few histograms, may be done in two ways. The first is to
build pad objects and to draw them into a parent pad, which may be a canvas. The second is to automatically divide a
pad into horizontal and vertical sub pads.
9.3.4.1 Creating a Single Sub-pad
The simplest way to divide a pad is to build sub-pads in it. However, this forces the user to explicitly indicate the size
and position of those sub-pads. Suppose we want to build a sub-pad in the active pad (pointed by
gPad
). First, we
build it, using a TPad constructor:
root[] spad1 = new TPad("spad1","The first subpad",.1,.1,.5,.5)
One gives the coordinates of the lower left point (0.1, 0.1) and of the upper right one (0.5, 0.5). These coordinates are
in NDC. This means that they are independent of the user coordinates system, in particular if you have already drawn
for example a histogram in the mother pad. The only thing left is to draw the pad:
root[] spad1->Draw()
If you want more sub-pads, you have to repeat this procedure as many times as necessary.
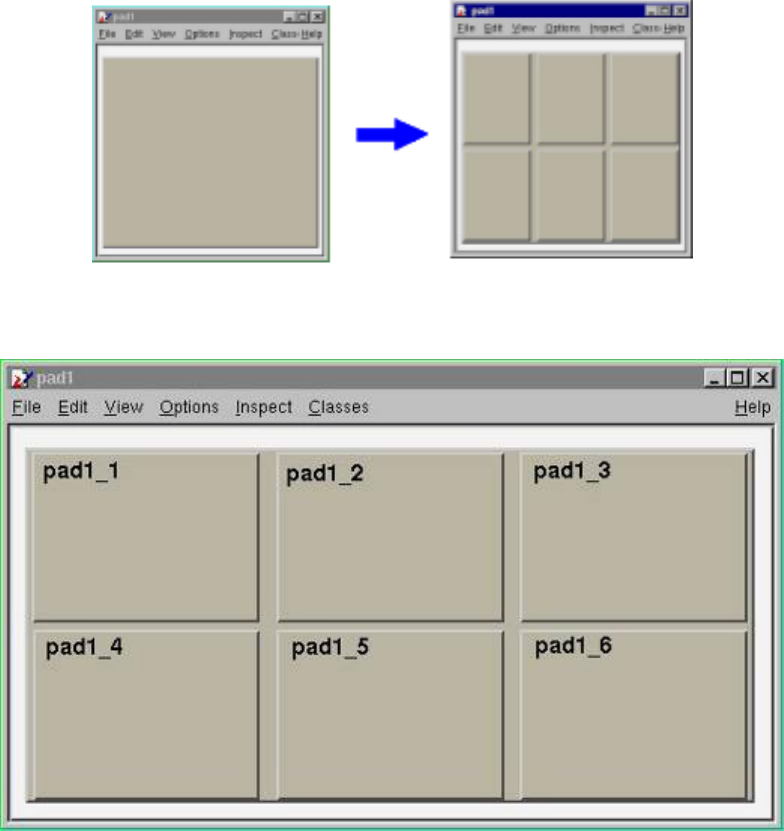
9.3. GRAPHICAL CONTAINERS: CANVAS AND PAD 179
9.3.4.2 Dividing a Canvas into Sub-Pads
The manual way of dividing a pad into sub-pads is sometimes very tedious. There is a way to automatically generate
horizontal and vertical sub-pads inside a given pad.
root[] pad1->Divide(3,2)
Figure 9.6: Dividing a pad into 6 sub-pads
Figure 9.7: Dividing a pad into 6 sub-pads
If
pad1
is a pad then, it will divide the pad into 3 columns of 2 sub-pads. The generated sub-pads get names
pad1_i
where the index
i=1
to
nxm
(in our case
pad1_1
,
pad1_2
. . .
pad1_6)
. The names
pad1_1
etc. . . correspond to new
variables in Cling, so you may use them as soon as the executed method was
pad->Divide()
. However, in a compiled
program, one has to access these objects. Remember that a pad contains other objects and that these objects may
themselves be pads. So we can use the GetPrimitive() method:
TPad* pad1_1 = (TPad*)(pad1->GetPrimitive("pad1_1"))
One question remains. In case one does an automatic divide, how one can set the default margins between pads? This
is done by adding two parameters to Divide(), which are the margins in xand y:
root[] pad1->Divide(3,2,0.1,0.1)
The margins are here set to 10% of the parent pad width.
180 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.3.5 Updating the Pad
For performance reasons, a pad is not updated with every change. For example, changing the coordinates of the pad
does not automatically redraw it. Instead, the pad has a “bit-modified” that triggers a redraw. This bit is automatically
set by:
•Touching the pad with the mouse - for example resizing it with the mouse.
•Finishing the execution of a script.
•Adding a new primitive or modifying some primitives for example the name and title of an object.
•You can also set the “bit-modified” explicitly with the Modified method:
// the pad has changed
root[] pad1->Modified()
// recursively update all modified pads:
root[] c1->Update()
A subsequent call to TCanvas::Update() scans the list of sub-pads and repaints the pads declared modified.
In compiled code or in a long macro, you may want to access an object created during the paint process. To do so, you
can force the painting with a
TCanvas::Update()
. For example, a
TGraph
creates a histogram (
TH1
) to paint itself. In
this case the internal histogram obtained with
TGraph::GetHistogram()
is created only after the pad is painted. The
pad is painted automatically after the script is finished executing or if you force the painting with
TPad::Modified()
followed by a
TCanvas::Update()
. Note that it is not necessary to call
TPad::Modified()
after a call to
Draw()
. The
“bit-modified” is set automatically by
Draw()
. A note about the “bit-modified” in sub pads: when you want to update
a sub pad in your canvas, you need to call
pad->Modified()
rather than
canvas->Modified()
, and follow it with a
canvas->Update()
. If you use
canvas->Modified()
, followed by a call to
canvas->Update()
, the sub pad has not
been declared modified and it will not be updated. Also note that a call to
pad->Update()
where pad is a sub pad of
canvas, calls canvas->Update() and recursively updates all the pads on the canvas.
9.3.6 Making a Pad Transparent
As we will see in the paragraph “Fill Attributes”, a fill style (type of hatching) may be set for a pad.
root[] pad1->SetFillStyle(istyle)
This is done with the
SetFillStyle
method where
istyle
is a style number, defined in “Fill Attributes”. A special
set of styles allows handling of various levels of transparency. These are styles number 4000 to 4100, 4000 being fully
transparent and 4100 fully opaque. So, suppose you have an existing canvas with several pads. You create a new pad
(transparent) covering for example the entire canvas. Then you draw your primitives in this pad. The same can be
achieved with the graphics editor. For example:
root[] .x tutorials/hist/h1draw.C
root[] TPad *newpad=new TPad("newpad","Transparent pad",0,0,1,1);
root[] newpad->SetFillStyle(4000);
root[] newpad->Draw();
root[] newpad->cd();
root[] // create some primitives, etc
9.3.7 Setting the Log Scale
Setting the scale to logarithmic or linear is an attribute of the pad, not the axis or the histogram. The scale is an
attribute of the pad because you may want to draw the same histogram in linear scale in one pad and in log scale in
another pad. Frequently, we see several histograms on top of each other in the same pad. It would be very inconvenient
to set the scale attribute for each histogram in a pad.
Furthermore, if the logic was set in the histogram class (or each object) the scale setting in each
Paint
method of all
objects should be tested.
If you have a pad with a histogram, a right-click on the pad, outside of the histograms frame will convince you. The
SetLogx()
,
SetLogy()
and
SetLogz()
methods are there. As you see,
TPad
defines log scale for the two directions
x
and yplus zif you want to draw a 3D representation of some function or histogram.
The way to set log scale in the x direction for the active pad is:
9.4. GRAPHICAL OBJECTS 181
root[] gPad->SetLogx(1)
To reset log in the z direction:
root[] gPad->SetLogz(0)
If you have a divided pad, you need to set the scale on each of the sub-pads. Setting it on the containing pad does not
automatically propagate to the sub-pads. Here is an example of how to set the log scale for the x-axis on a canvas with
four sub-pads:
root[] TCanvas MyCanvas("MyCanvas","My Canvas")
root[] MyCanvas->Divide(2,2)
root[] MyCanvas->cd(1)
root[] gPad->SetLogx()
root[] MyCanvas->cd(2)
root[] gPad->SetLogx()
root[] MyCanvas->cd(3)
root[] gPad->SetLogx()
9.3.8 WaitPrimitive method
When the
TPad::WaitPrimitive()
method is called with no arguments, it will wait until a double click or any key
pressed is executed in the canvas. A call to
gSystem->Sleep(10)
has been added in the loop to avoid consuming at all
the CPU. This new option is convenient when executing a macro. By adding statements like:
canvas->WaitPrimitive();
You can monitor the progress of a running macro, stop it at convenient places with the possibility to interact with the
canvas and resume the execution with a double click or a key press.
9.3.9 Locking the Pad
You can make the
TPad
non-editable. Then no new objects can be added, and the existing objects and the pad can not
be changed with the mouse or programmatically. By default the TPad is editable.
TPad::SetEditable(kFALSE)
9.4 Graphical Objects
In this paragraph, we describe the various simple 2D graphical objects defined in ROOT. Usually, one defines these
objects with their constructor and draws them with their
Draw()
method. Therefore, the examples will be very brief.
Most graphical objects have line and fill attributes (color, width) that will be described in “Graphical objects attributes”.
If the user wants more information, the class names are given and they may refer to the online developer documentation.
This is especially true for functions and methods that set and get internal values of the objects described here. By
default 2D graphical objects are created in User Coordinates with (0, 0) in the lower left corner.
9.4.1 Lines, Arrows and Polylines
The simplest graphical object is a line. It is implemented in the TLine class. The line constructor is:
TLine(Double_t x1,Double_t y1,Double_t x2,Double_t y2)
The arguments x1,y1,x2,y2 are the coordinates of the first and second point. It can be used:
root[] l = new TLine(0.2,0.2,0.8,0.3)
root[] l->Draw()
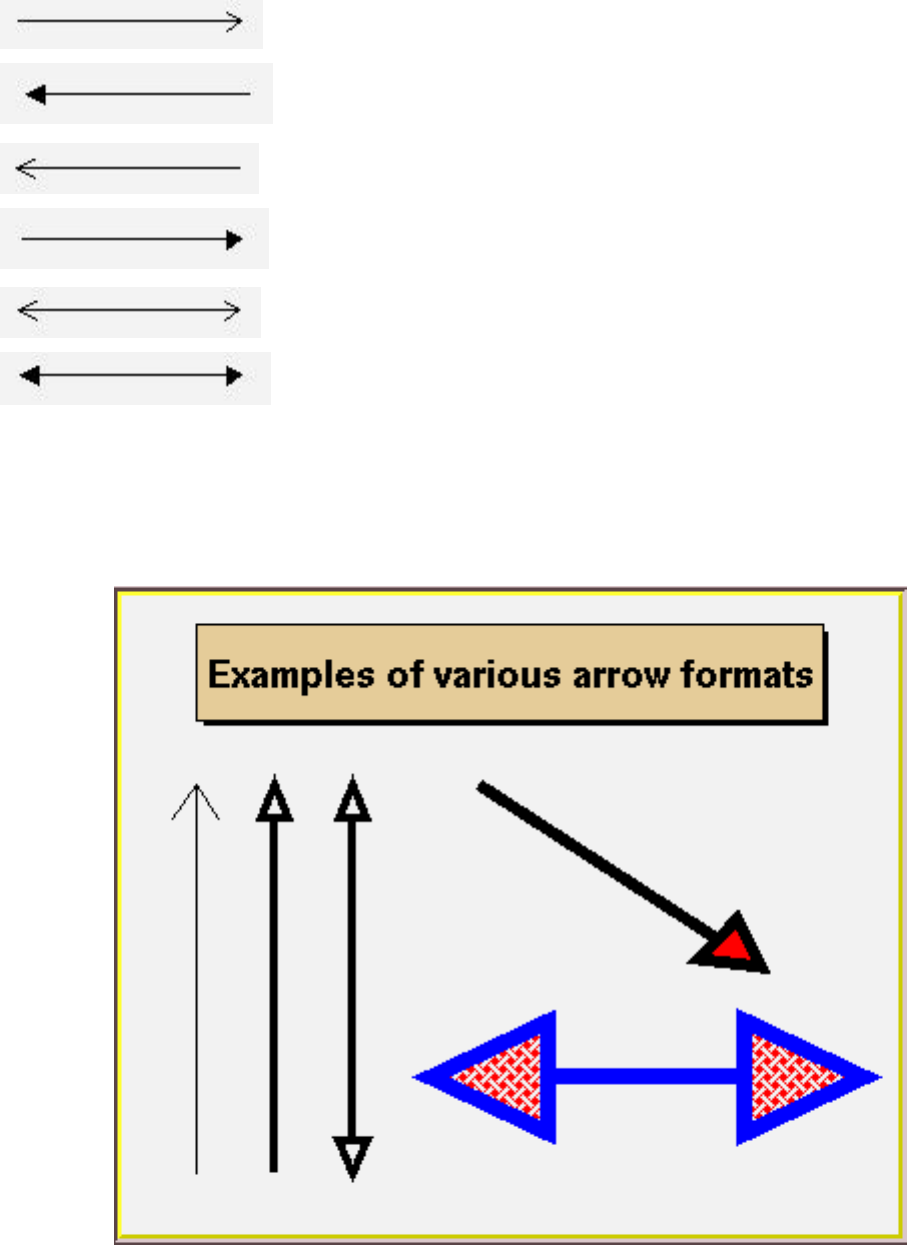
182 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
The arrow constructor is:
TArrow(Double_t x1, Double_t y1,
Double_t x2, Double_t y2,
Float_t arrowsize, Option_t *option)
It defines an arrow between points
x1,y1
and
x2,y2
. The arrow size is in percentage of the pad height. The
option
parameter has the following meanings:
“>”
“<|”
“<”
“|>”
“<>”
“<|>”
Once an arrow is drawn on the screen, one can:
•click on one of the edges and move this edge.
•click on any other arrow part to move the entire arrow.
Figure 9.8: Different arrow formats
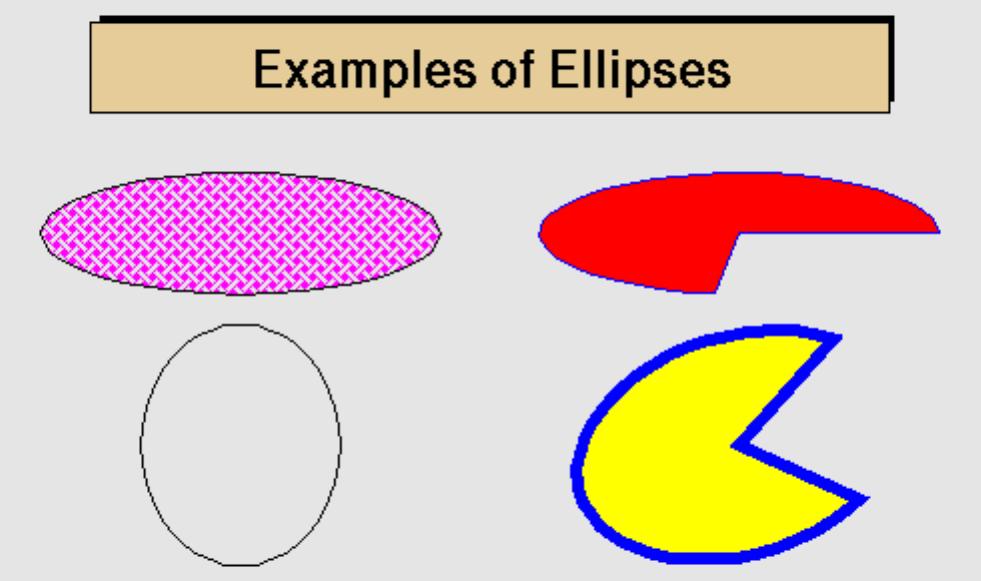
9.4. GRAPHICAL OBJECTS 183
If
FillColor
is 0, an open triangle is drawn; else a full triangle is filled with the set fill color. If
ar
is an arrow object,
fill color is set with:
ar.SetFillColor(icolor);
Where icolor is the color defined in “Color and Color Palettes”.
The default-opening angle between the two sides of the arrow is 60 degrees. It can be changed with the method
ar->SetAngle(angle), where angle is expressed in degrees.
A poly-line is a set of joint segments. It is defined by a set of N points in a 2D space. Its constructor is:
TPolyLine(Int_t n,Double_t* x,Double_t* y,Option_t* option)
Where
n
is the number of points, and
x
and
y
are arrays of
n
elements with the coordinates of the points.
TPolyLine
can be used by it self, but is also a base class for other objects, such as curly arcs.
9.4.2 Circles and Ellipses
An ellipse can be truncated and rotated. It is defined by its center
(x1,y1)
and two radii
r1
and
r2
. A minimum and
maximum angle may be specified
(phimin,phimax)
. The ellipse may be rotated with an angle
theta
. All these angles
are in degrees. The attributes of the outline line are set via
TAttLine
, of the fill area - via
TAttFill
class. They are
described in “Graphical Objects Attributes”.
Figure 9.9: Different types of ellipses
When an ellipse sector is drawn only, the lines between the center and the end points of the sector are drawn by default.
By specifying the drawn option “
only
”, these lines can be avoided. Alternatively, the method
SetNoEdges()
can be
called. To remove completely the ellipse outline, specify zero (0) as a line style.
The TEllipse constructor is:
TEllipse(Double_t x1, Double_t y1, Double_t r1, Double_t r2,
Double_t phimin, Double_t phimax, Double_t theta)
An ellipse may be created with:
root[] e = new TEllipse(0.2,0.2,0.8,0.3)
root[] e->Draw()
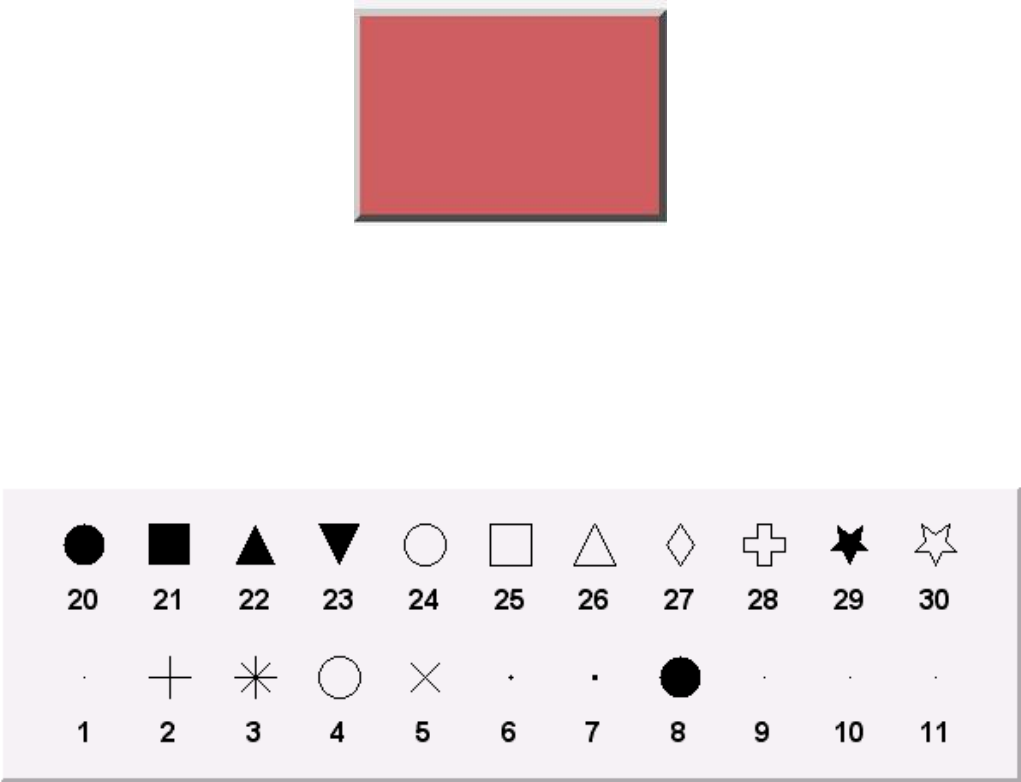
184 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.4.3 Rectangles
The class
TBox
defines a rectangle. It is a base class for many different higher-level graphical primitives. Its bottom left
coordinates x1,y1 and its top right coordinates x2,y2, defines a box. The constructor is:
TBox(Double_t x1,Double_t y1,Double_t x2,Double_t y2)
It may be used as in:
root[] b = new TBox(0.2,0.2,0.8,0.3)
root[] b->SetFillColor(5)
root[] b->Draw()
Figure 9.10: A rectangle with a border
A
TWbox
is a rectangle (
TBox
) with a border size and a border mode. The attributes of the outline line and of the fill
area are described in “Graphical Objects Attributes”
9.4.4 Markers
A marker is a point with a fancy shape! The possible markers are shown in the next figure.
Figure 9.11: Markers
The marker constructor is:
TMarker(Double_t x,Double_t y,Int_t marker)
The parameters
x
and
y
are the marker coordinates and
marker
is the marker type, shown in the previous figure.
Suppose the pointer
ma
is a valid marker. The marker size is set via
ma->SetMarkerSize(size)
, where
size
is the
desired size. Note, that the marker types 1, 6 and 7 (the dots) cannot be scaled. They are always drawn with the same
number of pixels.
SetMarkerSize
does not apply on them. To have a “scalable dot” a circle shape should be used
instead, for example, the marker type 20. The default marker type is 1, if
SetMarkerStyle
is not specified. It is the
most common one to draw scatter plots.
The user interface for changing the marker color, style and size looks like shown in this picture. It takes place in the
editor frame anytime the selected object inherits the class TAttMarker.
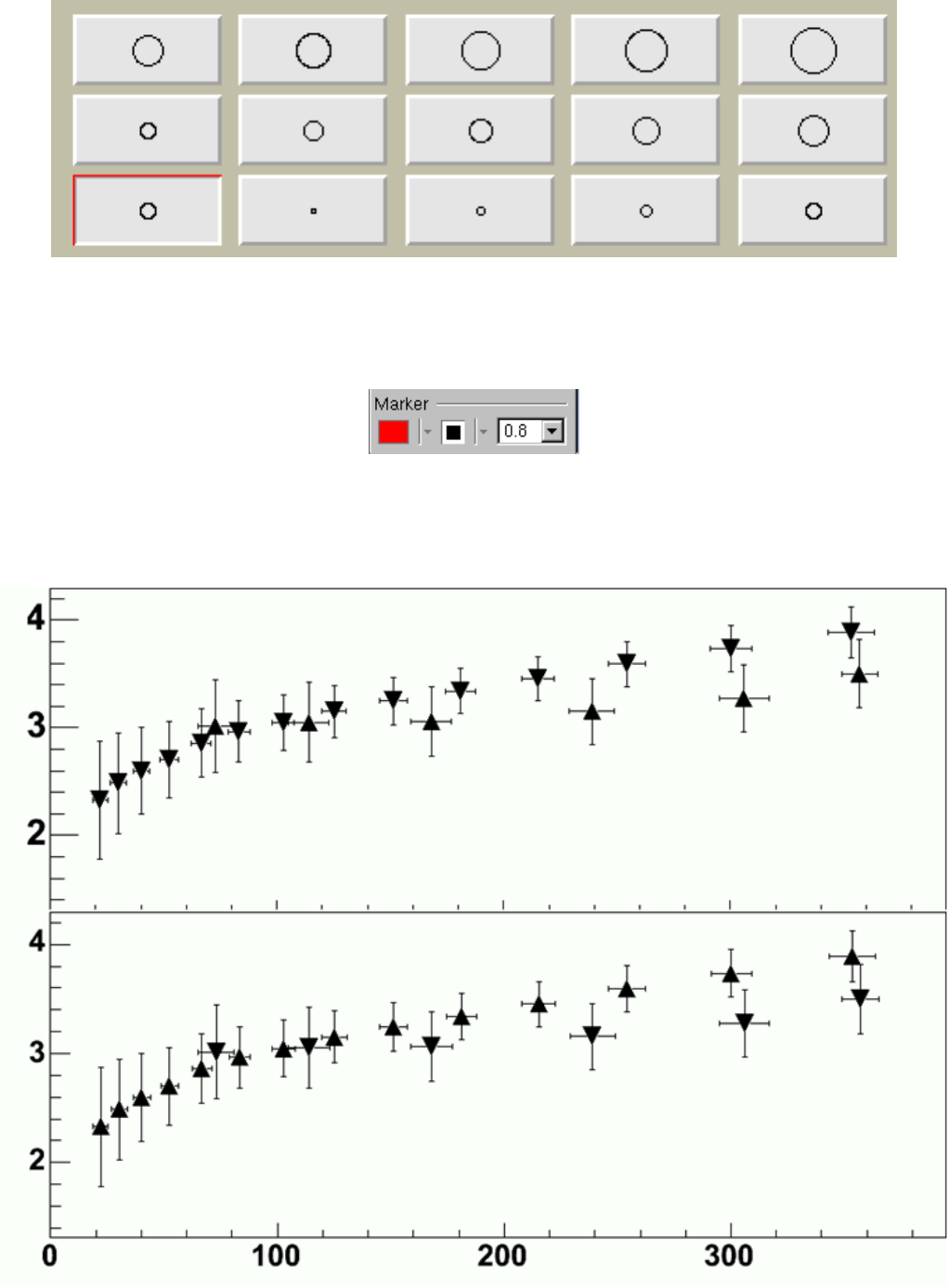
9.4. GRAPHICAL OBJECTS 185
Figure 9.12: Different marker sizes
Figure 9.13: Different marker sizes
Figure 9.14: The use of non-symmetric markers
186 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
Non-symmetric symbols should be used carefully in plotting. The next two graphs show how the misleading a careless
use of symbols can be. The two plots represent the same data sets but because of a bad symbol choice, the two on the
top appear further apart from the next example.
A
TPolyMaker
is defined by an array on N points in a 2D space. At each point
x[i]
,
y[i]
a marker is drawn. The list
of marker types is shown in the previous paragraph. The marker attributes are managed by the class
TAttMarker
and
are described in “Graphical Objects Attributes”. The TPolyMarker constructor is:
TPolyMarker(Int_t n,Double_t *x,Double_t *y,Option_t *option)
Where xand yare arrays of coordinates for the npoints that form the poly-marker.
9.4.5 Curly and Wavy Lines for Feynman Diagrams
This is a peculiarity of particle physics, but we do need sometimes to draw Feynman diagrams. Our friends working
in banking can skip this part. A set of classes implements curly or wavy poly-lines typically used to draw Feynman
diagrams. Amplitudes and wavelengths may be specified in the constructors, via commands or interactively from
context menus. These classes are
TCurlyLine
and
TCurlyArc
. These classes make use of
TPolyLine
by inheritance;
ExecuteEvent methods are highly inspired from the methods used in TPolyLine and TArc.
Figure 9.15: The picture generated by the tutorial macro feynman.C
The TCurlyLine constructor is:
TCurlyLine(Double_t x1, Double_t y1, Double_t x2, Double_t y2,
Double_t wavelength, Double_t amplitude)
The coordinates
(x1
,
y1)
define the starting point,
(x2
,
y2)
- the end-point. The
wavelength
and the
amplitude
are
given in percent of the pad height.
The TCurlyArc constructor is:
TCurlyArc(Double_t x1, Double_t y1, Double_t rad,
Double_t phimin, Double_t phimax,
Double_t wavelength, Double_t amplitude)
The curly arc center is
(x1
,
y1)
and the radius is
rad
. The wavelength and the amplitude are given in percent of the
line length. The parameters
phimin
and
phimax
are the starting and ending angle of the arc (given in degrees). Refer
to $ROOTSYS/tutorials/graphics/feynman.C for the script that built the figure above.
9.4. GRAPHICAL OBJECTS 187
9.4.6 Text and Latex Mathematical Expressions
Text displayed in a pad may be embedded into boxes, called paves (
TPaveLabel
), or titles of graphs or many other
objects but it can live a life of its own. All text displayed in ROOT graphics is an object of class
TText
. For a physicist,
it will be most of the time a
TLatex
expression (which derives from
TText
).
TLatex
has been conceived to draw
mathematical formulas or equations. Its syntax is very similar to the Latex in mathematical mode.
9.4.6.1 Subscripts and Superscripts
Subscripts and superscripts are made with the
_
and
ˆ
commands. These commands can be combined to make complex
subscript and superscript expressions. You may choose how to display subscripts and superscripts using the 2 functions
SetIndiceSize(Double_t)
and
SetLimitIndiceSize(Int_t)
. Examples of what can be obtained using subscripts
and superscripts:
The expression Gives The expression Gives The expression Gives
xˆ{2y} x2yxˆ{yˆ{2}} xy2x_{1}ˆ{y_{1}} xy1
1
x_{2y} x2yxˆ{y_{1}} xy1x_{1}ˆ{y} xy
1
9.4.6.2 Fractions
Fractions denoted by the / symbol are made in the obvious way. The
#frac
command is used for large fractions in
displayed formula; it has two arguments: the numerator and the denominator. For example, the equation x = y + z 2
y 2 + 1 is obtained by following expression x=#frac{y+z/2}{yˆ{2}+1}.
9.4.6.3 Roots
The #sqrt command produces the square ROOT of its argument; it has an optional first argument for other roots.
Example: #sqrt{10} #sqrt[3]{10}
9.4.6.4 Delimiters
You can produce three kinds of proportional delimiters.
#[]{....} or “à la” Latex
#left[.....#right]big square brackets
#{}{....} or #left{.....#right}big curly brackets
#||{....} or #left|.....#right|big absolute value symbol
#(){....} or #left(.....#right)big parenthesis
9.4.6.5 Changing Style in Math Mode
You can change the font and the text color at any moment using:
#font[font-number]{...} and #color[color-number]{...}
9.4.6.6 Line Splitting
A
TLatex
string may be split in two with the following command:
#splitline{top}{bottom}
.
TAxis
and
TGaxis
objects can take advantage of this feature. For example, the date and time could be shown in the time axis over two
lines with: #splitline{21 April 2003}{14:23:56}
188 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.4.7 Greek Letters
The command to produce a lowercase Greek letter is obtained by adding
#
to the name of the letter. For an uppercase
Greek letter, just capitalize the first letter of the command name.
#alpha #beta #chi #delta #varepsilon #phi
#gamma #eta #iota #varphi #kappa #lambda
#mu #nu #omicron #pi #theta #rho
#sigma #tau #upsilon #varomega #omega #xi
#psi #zeta #Alpha #Beta #Chi #Delta
#Epsilon #Phi #Gamma #Eta #Iota #Kappa
#vartheta #Lambda #Mu #Nu #Omicron #Pi
#Theta #Rho #Sigma #Tau #Upsilon #Omega
#varsigma #Xi #Psi #epsilon #varUpsilon #Zeta
9.4.8 Mathematical Symbols
TLatex
can make mathematical and other symbols. A few of them, such as
+
and
>
, are produced by typing the
corresponding keyboard character. Others are obtained with the commands as shown in the table above.
9.4.8.1 Accents, Arrows and Bars
Symbols in a formula are sometimes placed one above another. TLatex provides special commands for that.
#hat{a} =hat
#check =inverted hat
#acute =acute
#grave =accent grave
#dot =derivative
#ddot =double derivative
#tilde =tilde
#slash =special sign. Draw a slash on top of the text between brackets for example
#slash{E}_{T}generates “Missing ET”
a _ is obtained with #bar{a}
a -> is obtained with #vec{a}
9.4.8.2 Example 1
The script $ROOTSYS/tutorials/graphics/latex.C:
{
TCanvas c1("c1","Latex",600,700);
TLatex l;
l.SetTextAlign(12);
l.SetTextSize(0.04);
l.DrawLatex(0.1,0.8,"1) C(x) = d #sqrt{#frac{2}{#lambdaD}}
#int^{x}_{0}cos(#frac{#pi}{2}t^{2})dt");
l.DrawLatex(0.1,0.6,"2) C(x) = d #sqrt{#frac{2}{#lambdaD}}
#int^{x}cos(#frac{#pi}{2}t^{2})dt");
l.DrawLatex(0.1,0.4,"3) R = |A|^{2} =
#frac{1}{2}(#[]{#frac{1}{2}+C(V)}^{2}+
#[]{#frac{1}{2}+S(V)}^{2})");
l.DrawLatex(0.1,0.2,"4) F(t) = #sum_{i=
-#infty}^{#infty}A(i)cos#[]{#frac{i}{t+i}}");
}

9.4. GRAPHICAL OBJECTS 189

190 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE

9.4. GRAPHICAL OBJECTS 191
Figure 9.16: The picture generated by the tutorial macro latex.C
192 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.4.8.3 Example 2
The script $ROOTSYS/tutorials/graphics/latex2.C:
{
TCanvas c1("c1","Latex",600,700);
TLatex l;
l.SetTextAlign(23);
l.SetTextSize(0.1);
l.DrawLatex(0.5,0.95,"e^{+}e^{-}#rightarrowZ^{0}
#rightarrowI#bar{I}, q#bar{q}");
l.DrawLatex(0.5,0.75,"|#vec{a}#bullet#vec{b}|=
#Sigmaa^{i}_{jk}+b^{bj}_{i}");
l.DrawLatex(0.5,0.5,"i(#partial_{#mu}#bar{#psi}#gamma^{#mu}
+m#bar{#psi}=0
#Leftrightarrow(#Box+m^{2})#psi=0");
l.DrawLatex(0.5,0.3,"L_{em}=eJ^{#mu}_{em}A_{#mu} ,
J^{#mu}_{em}=#bar{I}#gamma_{#mu}I
M^{j}_{i}=#SigmaA_{#alpha}#tau^{#alphaj}_{i}");
}
Figure 9.17: The picture generated by the tutorial macro latex2.C
9.4.8.4 Example 3
The script $ROOTSYS/tutorials/graphics/latex3.C:
{
TCanvas c1("c1");
TPaveText pt(.1,.5,.9,.9);
pt.AddText("#frac{2s}{#pi#alpha^{2}}
#frac{d#sigma}{dcos#theta} (e^{+}e^{-}
#rightarrow f#bar{f} ) = ");
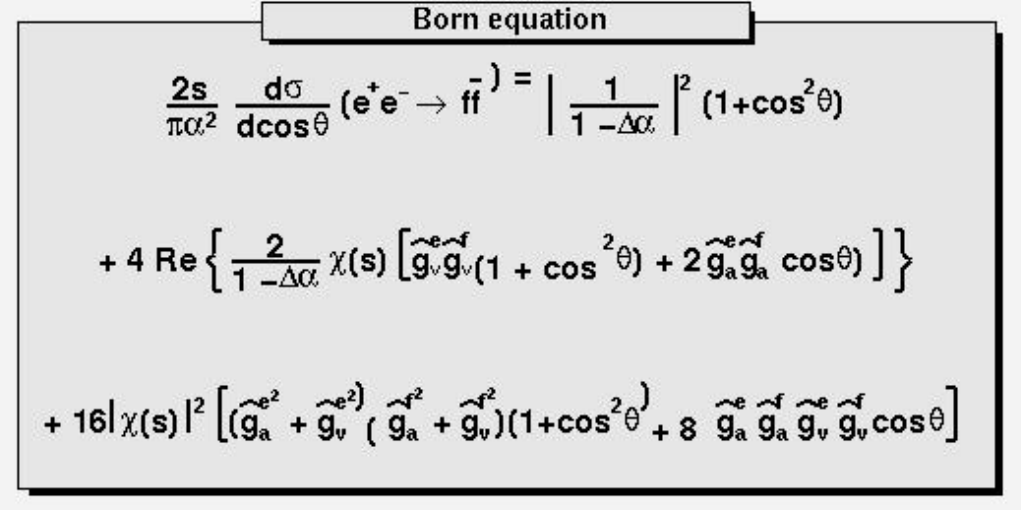
9.4. GRAPHICAL OBJECTS 193
pt.AddText("#left| #frac{1}{1 - #Delta#alpha} #right|^{2}
(1+cos^{2}#theta");
pt.AddText("+ 4 Re #left{ #frac{2}{1 - #Delta#alpha} #chi(s)
#[]{#hat{g}_{#nu}^{e}#hat{g}_{#nu}^{f}
(1+ cos^{2}#theta) + 2#hat{g}_{a}^{e}
#hat{g}_{a}^{f} cos#theta) } #right}");
pt.SetLabel("Born equation");
pt.Draw();
}
Figure 9.18: The picture generated by the tutorial macro latex3.C
9.4.9 Text in a Pad
Text displayed in a pad may be embedded into boxes, called paves, or may be drawn alone. In any case, it is
recommended to use a Latex expression, which is covered in the previous paragraph. Using
TLatex
is valid whether
the text is embedded or not. In fact, you will use Latex expressions without knowing it since it is the standard for all
the embedded text. A pave is just a box with a border size and a shadow option. The options common to all types of
paves and used when building those objects are the following:
option = "T" top frame
option = "B" bottom frame
option = "R" right frame
option = "L" left frame
option = "NDC" x1,y1,x2,y2 are given in NDC
option = "ARC" corners are rounded
We will see the practical use of these options in the description of the more functional objects like
TPaveLabels
. There
are several categories of paves containing text:
TPaveLabel
,
TPaveText
and
TPavesText
.
TPaveLabels
are panels
containing one line of text. They are used for labeling.
TPaveLabel(Double_t x1, Double_t y1, Double_t x2, Double_t y2,
const char *label, Option_t *option)
Where (
x1
,
y1
) are the coordinates of the bottom left corner,
(x2,y2)
- coordinates of the upper right corner. “
label
”
is the text to be displayed and “
option
” is the drawing option, described above. By default, the border size is 5 and the
option is “
br
”. If one wants to set the border size to some other value, one may use the method
SetBorderSize()
. For

194 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
example, suppose we have a histogram, which limits are (-100,100) in the x direction and (0, 1000) in the y direction.
The following lines will draw a label in the center of the histogram, with no border. If one wants the label position to
be independent of the histogram coordinates, or user coordinates, one can use the option “
NDC
”. See “The Coordinate
Systems of a Pad”.
root[] pl = new TPaveLabel(-50,0,50,200,"Some text")
root[] pl->SetBorderSize(0)
root[] pl->Draw()
Figure 9.19: PaveLabels drawn with different options
A
TPaveLabel
can contain only one line of text. A
TPaveText
may contain several lines. This is the only difference.
This picture illustrates and explains some of the points of
TPaveText
. Once a
TPaveText
is drawn, a line can be added
or removed by brining up the context menu with the mouse.
A
TPavesText
is a stack of text panels (see
TPaveText
). One can set the number of stacked panels at building time. It
has the following constructor: By default, the number of stacked panels is 5, option=“br”.
TPavesText(Double_t x1, Double_t y1, Double_t x2, Double_t y2,
Int_t npaves, Option_t* option)
9.4.10 The TeX Processor TMathText
TMathText’s purpose is to write mathematical equations, exactly as TeX would do it. The syntax is the same as the
TeX’s one.
The script $ROOTSYS/tutorials/graphics/tmathtex.C:
gives the following output:
TMathText
uses plain TeX syntax and uses “\” as control instead of “#”. If a piece of text containing “\” is given to
TLatex
then
TMathText
is automatically invoked. Therefore, as histograms’ titles, axis titles, labels etc . . . are drawn
using TLatex, the TMathText syntax can be used for them also.
9.5 Axis
The axis objects are automatically built by various high level objects such as histograms or graphs. Once build, one
may access them and change their characteristics. It is also possible, for some particular purposes to build axis on their
own. This may be useful for example in the case one wants to draw two axis for the same plot, one on the left and one
on the right.
For historical reasons, there are two classes representing axis.
TAxis
*
axis
is the axis object, which will be returned
when calling the TH1::GetAxis() method.
TAxis *axis = histo->GetXaxis()
Of course, you may do the same for
Y
and
Z
-axis. The graphical representation of an axis is done with the
TGaxis
class. The histogram classes and
TGraph
generate instances of this class. This is internal and the user should not have
to see it.

9.5. AXIS 195
Figure 9.20: PaveText examples
Figure 9.21: A PaveText example

196 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
Figure 9.22: A TMathText example
9.5.1 Axis Title
The axis title is set, as with all named objects, by
axis->SetTitle("Whatever title you want");
When the axis is embedded into a histogram or a graph, one has to first extract the axis object:
h->GetXaxis()->SetTitle("Whatever title you want")
9.5.2 Axis Options and Characteristics
The axis options are most simply set with the styles. The available style options controlling specific axis options are
the following:
TAxis *axis = histo->GetXaxis();
axis->SetAxisColor(Color_t color = 1);
axis->SetLabelColor(Color_t color = 1);
axis->SetLabelFont(Style_t font = 62);
axis->SetLabelOffset(Float_t offset = 0.005);
axis->SetLabelSize(Float_t size = 0.04);
axis->SetNdivisions(Int_t n = 510, Bool_t optim = kTRUE);
axis->SetNoExponent(Bool_t noExponent = kTRUE);
axis->SetTickLength(Float_t length = 0.03);
axis->SetTitleOffset(Float_t offset = 1);
axis->SetTitleSize(Float_t size = 0.02);
The getters corresponding to the described setters are also available. The general options, not specific to axis, as for
instance SetTitleTextColor() are valid and do have an effect on axis characteristics.
9.5. AXIS 197
9.5.3 Setting the Number of Divisions
Use
TAxis::SetNdivisions(ndiv,optim)
to set the number of divisions for an axis. The
ndiv
and
optim
are as
follows:
•ndiv = N1 + 100*N2 + 10000*N3
•N1 = number of first divisions.
•N2 = number of secondary divisions.
•N3 = number of tertiary divisions.
•optim = kTRUE (default), the divisions’ number will be optimized around the specified value.
•optim = kFALSE, or n < 0, the axis will be forced to use exactly n divisions.
For example:
ndiv = 0: no tick marks.
ndiv = 2: 2 divisions, one tick mark in the middle of the axis.
ndiv = 510: 10 primary divisions, 5 secondary divisions
ndiv = -10: exactly 10 primary divisions
9.5.4 Zooming the Axis
You can use TAxis::SetRange or TAxis::SetRangeUser to zoom the axis.
TAxis::SetRange(Int_t binfirst,Int_t binlast)
The
SetRange
method parameters are bin numbers. They are not axis. For example if a histogram plots the values
from 0 to 500 and has 100 bins,
SetRange(0,10)
will cover the values 0 to 50. The parameters for
SetRangeUser
are
user coordinates. If the start or end is in the middle of a bin the resulting range is approximation. It finds the low edge
bin for the start and the high edge bin for the high.
TAxis::SetRangeUser(Axis_t ufirst,Axis_t ulast)
Both methods,
SetRange
and
SetRangeUser
, are in the context menu of any axis and can be used interactively. In
addition, you can zoom an axis interactively: click on the axis on the start, drag the cursor to the end, and release the
mouse button.
9.5.5 Drawing Axis Independently of Graphs or Histograms
An axis may be drawn independently of a histogram or a graph. This may be useful to draw for example a supplementary
axis for a graph. In this case, one has to use the
TGaxis
class, the graphical representation of an axis. One may use
the standard constructor for this kind of objects:
TGaxis(Double_t xmin, Double_t ymin, Double_t xmax, Double_t ymax,
Double_t wmin, Double_t wmax, Int_t ndiv = 510,
Option_t* chopt,Double_t gridlength = 0)
The arguments
xmin, ymin
are the coordinates of the axis’ start in the user coordinates system,
and xmax, ymax
are the end coordinates. The arguments
wmin
and
wmax
are the minimum (at the start) and maximum (at the end)
values to be represented on the axis;
ndiv
is the number of divisions. The options, given by the “
chopt
” string are the
following:
•chopt = ’G’: logarithmic scale, default is linear.
•chopt = ’B’: Blank axis (it is useful to superpose the axis).
198 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
Instead of the
wmin,wmax
arguments of the normal constructor, i.e. the limits of the axis, the name of a
TF1
function
can be specified. This function will be used to map the user coordinates to the axis values and ticks.
The constructor is the following:
TGaxis(Double_t xmin, Double_t ymin, Double_t xmax, Double_t ymax,
const char* funcname, Int_t ndiv=510,
Option_t* chopt, Double_t gridlength=0)
In such a way, it is possible to obtain exponential evolution of the tick marks position, or even decreasing. In fact,
anything you like.
9.5.6 Orientation of Tick Marks on Axis
Tick marks are normally drawn on the positive side of the axis, however, if xmin = xmax, then negative.
•chopt = ’+’: tick marks are drawn on Positive side. (Default)
•chopt = ’-’: tick marks are drawn on the negative side.
•chopt = ’+-’: tick marks are drawn on both sides of the axis.
•chopt = ‘U’: unlabeled axis, default is labeled.
9.5.7 Labels
9.5.7.1 Position
Labels are normally drawn on side opposite to tick marks. However,
chopt = ’=’
: on Equal side. The function
TAxis::CenterLabels()
sets the bit
kCenterLabels
and it is visible from
TAxis
context menu. It centers the bin
labels and it makes sense only when the number of bins is equal to the number of tick marks. The class responsible for
drawing the axis TGaxis inherits this property.
9.5.7.2 Orientation
Labels are normally drawn parallel to the axis. However, if
xmin = xmax
, then they are drawn orthogonal, and if
ymin=ymax they are drawn parallel.
9.5.7.3 Labels for Exponents
By default, an exponent of the form 10ˆN is used when the label values are either all very small or very large. One can
disable the exponent by calling:
TAxis::SetNoExponent(kTRUE)
Note that this option is implicitly selected if the number of digits to draw a label is less than the
fgMaxDigits
global
member. If the property
SetNoExponent
was set in
TAxis
(via
TAxis::SetNoExponent)
, the
TGaxis
will inherit this
property.
TGaxis
is the class responsible for drawing the axis. The method
SetNoExponent
is also available from the
axis context menu.
9.5.7.4 Number of Digits in Labels
TGaxis::fgMaxDigits
is the maximum number of digits permitted for the axis labels above which the notation with
10ˆN is used. It must be greater than 0. By default
fgMaxDigits
is 5 and to change it use the
TGaxis::SetMaxDigits
method. For example to set fgMaxDigits to accept 6 digits and accept numbers like 900000 on an axis call:
TGaxis::SetMaxDigits(6)
9.5. AXIS 199
Figure 9.23: Y-axis with and without exponent labels
9.5.7.5 Tick Mark Positions
Labels are centered on tick marks. However, if xmin = xmax, then they are right adjusted.
•chopt = ’R’: labels are right adjusted on tick mark (default is centered)
•chopt = ’L’: labels are left adjusted on tick mark.
•chopt = ’C’: labels are centered on tick mark.
•chopt = ’M’: In the Middle of the divisions.
9.5.7.6 Label Formatting
Blank characters are stripped, and then the label is correctly aligned. The dot, if last character of the string, is also
stripped. In the following, we have some parameters, like tick marks length and characters height (in percentage of the
length of the axis, in user coordinates). The default values are as follows:
•Primary tick marks: 3.0 %
•Secondary tick marks: 1.5 %
•Third order tick marks: .75 %
•Characters height for labels: 4%
•Labels offset: 1.0 %
9.5.7.7 Stripping Decimals
Use the
TStyle::SetStripDecimals
to strip decimals when drawing axis labels. By default, the option is set to true,
and TGaxis::PaintAxis removes trailing zeros after the dot in the axis labels, e.g. {0, 0.5, 1, 1.5, 2, 2.5, etc.}
TStyle::SetStripDecimals (Bool_t strip=kTRUE)
If this function is called with
strip=kFALSE
,
TGaxis::PaintAxis()
will draw labels with the same number of digits
after the dot, e.g. {0.0, 0.5, 1.0, 1.5, 2.0, 2.5, etc.}
200 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.5.7.8 Optional Grid
chopt = ’W’: cross-Wire
9.5.7.9 Axis Binning Optimization
By default, the axis binning is optimized.
•chopt = ’N’: No binning optimization
•chopt = ’I’: Integer labeling
9.5.8 Axis with Time Units
Histograms’ axis can be defined as “time axis”. To do that it is enough to activate the
SetTimeDisplay
attribute on a
given axis. If his a histogram, it is done the following way:
h->GetXaxis()->SetTimeDisplay(1); // X axis is a time axis
Two parameters can be adjusted in order to define time axis: the time format and the time offset.
9.5.8.1 Time Format
It defines the format of the labels along the time axis. It can be changed using the
TAxis
method
SetTimeFormat
. The
time format is the one used by the C function
strftime()
. It is a string containing the following formatting characters:
For the date: %a abbreviated weekday name
%b abbreviated month name
%d day of the month (01-31)
%m month (01-12)
%y year without century
%Y year with century
For the time: %H hour (24-hour clock)
%I hour (12-hour clock)
%p local equivalent of AM or PM
%M minute (00-59)
%S seconds (00-61)
%% %
The other characters are output as is. For example to have a format like dd/mm/yyyy one should do:
h->GetXaxis()->SetTimeFormat("%d/%m/%Y");
If the time format is not defined, a default one will be computed automatically.
9.5.8.2 Time Offset
This is a time in seconds in the UNIX standard UTC format (the universal time, not the local one), defining the
starting date of a histogram axis. This date should be greater than 01/01/95 and is given in seconds. There are three
ways to define the time offset:
1- By setting the global default time offset:
TDatime da(2003,02,28,12,00,00);
gStyle->SetTimeOffset(da.Convert());
If no time offset is defined for a particular axis, the default time offset will be used. In the example above, notice the
usage of TDatime to translate an explicit date into the time in seconds required by SetTimeFormat.
2- By setting a time offset to a particular axis:
9.5. AXIS 201
TDatime dh(2001,09,23,15,00,00);
h->GetXaxis()->SetTimeOffset(dh.Convert());
3- Together with the time format using
SetTimeFormat
. The time offset can be specified using the control character
%F after the normal time format. %F is followed by the date in the format: yyyy-mm-dd hh:mm:ss.
h->GetXaxis()->SetTimeFormat("%d/%m/%y%F2000-02-28 13:00:01");
Notice that this date format is the same used by the
TDatime
function
AsSQLString
. If needed, this function can be
used to translate a time in seconds into a character string which can be appended after
%F
. If the time format is not
specified (before %F) the automatic one will be used. The following example illustrates the various possibilities.
{
gStyle->SetTitleH(0.08);
TDatime da(2003,02,28,12,00,00);
gStyle->SetTimeOffset(da.Convert());
ct = new TCanvas("ct","Time on axis",0,0,600,600);
ct->Divide(1,3);
ht1 = new TH1F("ht1","ht1",30000,0.,200000.);
ht2 = new TH1F("ht2","ht2",30000,0.,200000.);
ht3 = new TH1F("ht3","ht3",30000,0.,200000.);
for (Int_t i=1;i<30000;i++) {
Float_t noise = gRandom->Gaus(0,120);
ht1->SetBinContent(i,noise);
ht2->SetBinContent(i,noise*noise);
ht3->SetBinContent(i,noise*noise*noise);
}
ct->cd(1);
ht1->GetXaxis()->SetLabelSize(0.06);
ht1->GetXaxis()->SetTimeDisplay(1);
ht1->GetXaxis()->SetTimeFormat("%d/%m/%y%F2000-02-2813:00:01");
ht1->Draw();
ct->cd(2);
ht2->GetXaxis()->SetLabelSize(0.06);
ht2->GetXaxis()->SetTimeDisplay(1);
ht2->GetXaxis()->SetTimeFormat("%d/%m/%y");
ht2->Draw();
ct->cd(3);
ht3->GetXaxis()->SetLabelSize(0.06);
TDatime dh(2001,09,23,15,00,00);
ht3->GetXaxis()->SetTimeDisplay(1);
ht3->GetXaxis()->SetTimeOffset(dh.Convert());
ht3->Draw();
}
The output is shown in the figure below. If a time axis has no specified time offset, the global time offset will be stored
in the axis data structure. The histogram limits are in seconds. If
wmin
and
wmax
are the histogram limits, the time
axis will spread around the time offset value from
TimeOffset+wmin
to
TimeOffset+wmax
. Until now all examples had
a lowest value equal to 0. The following example demonstrates how to define the histogram limits relatively to the time
offset value.
{
// Define the time offset as 2003, January 1st
TDatime T0(2003,01,01,00,00,00);
int X0 = T0.Convert();
gStyle->SetTimeOffset(X0);
// Define the lowest histogram limit as 2002,September 23rd
TDatime T1(2002,09,23,00,00,00);
int X1 = T1.Convert()-X0;
// Define the highest histogram limit as 2003, March 7th
202 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
Figure 9.24: Time axis examples
9.5. AXIS 203
TDatime T2(2003,03,07,00,00,00);
int X2 = T2.Convert(1)-X0;
TH1F * h1 = new TH1F("h1","test",100,X1,X2);
TRandom r;
for (Int_t i=0;i<30000;i++) {
Double_t noise = r.Gaus(0.5*(X1+X2),0.1*(X2-X1));
h1->Fill(noise);
}
h1->GetXaxis()->SetTimeDisplay(1);
h1->GetXaxis()->SetLabelSize(0.03);
h1->GetXaxis()->SetTimeFormat("%Y/%m/%d");
h1->Draw();
}
The output is shown in the next figure. Usually time axes are created automatically via histograms, but one may also
want to draw a time axis outside a “histogram context”. Therefore, it is useful to understand how
TGaxis
works for
such axis. The time offset can be defined using one of the three methods described before. The time axis will spread
around the time offset value. Actually, it will go from
TimeOffset+wmin
to
TimeOffset+wmax
where
wmin
and
wmax
are the minimum and maximum values (in seconds) of the axis. Let us take again an example. Having defined “2003,
February 28 at 12h”, we would like to see the axis a day before and a day after.
Figure 9.25: A histogram with time axis X
ATGaxis can be created the following way (a day has 86400 seconds):
TGaxis *axis = new TGaxis(x1,y1,x2,y2,-100000,150000,2405,"t");
the “
t
” option (in lower case) means it is a “time axis”. The axis goes form 100000 seconds before
TimeOffset
and
150000 seconds after. So the complete macro is:
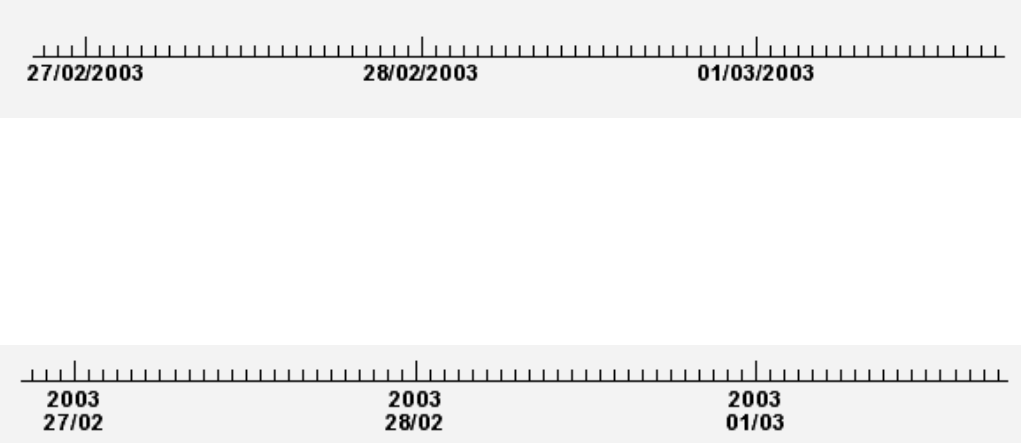
204 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
{
c1 = new TCanvas("c1","Examples of TGaxis",10,10,700,500);
c1->Range(-10,-1,10,1);
TGaxis *axis = new TGaxis(-8,-0.6,8,-0.6,-100000,150000,2405,"t");
axis->SetLabelSize(0.03);
TDatime da(2003,02,28,12,00,00);
axis->SetTimeOffset(da.Convert());
axis->SetTimeFormat("%d/%m/%Y");
axis->Draw();
}
The time format is specified with:
axis->SetTimeFormat("%d/%m/%Y");
The macro gives the following output:
Thanks to the
TLatex
directive
#splitline
it is possible to write the time labels on two lines. In the previous example
changing the SetTimeFormat line by:
axis->SetLabelOffset(0.02);
axis->SetTimeFormat("#splitline{%Y}{%d/%m}");
will produce the following axis:
9.5.9 Axis Examples
To illustrate what was said, we provide two scripts. The first one creates the picture shown in the next figure.
The first script is:
{
c1 = new TCanvas("c1","Examples of Gaxis",10,10,700,500);
c1->Range(-10,-1,10,1);
TGaxis *axis1 = new TGaxis(-4.5,-0.2,5.5,-0.2,-6,8,510,"");
axis1->SetName("axis1");
axis1->Draw();
TGaxis *axis2 = new TGaxis(4.5,0.2,5.5,0.2,0.001,10000,510,"G");
axis2->SetName("axis2");
axis2->Draw();
TGaxis *axis3 = new TGaxis(-9,-0.8,-9,0.8,-8,8,50510,"");
axis3->SetName("axis3");
axis3->Draw();
TGaxis *axis4 = new TGaxis(-7,-0.8,7,0.8,1,10000,50510,"G");
axis4->SetName("axis4");
axis4->Draw();
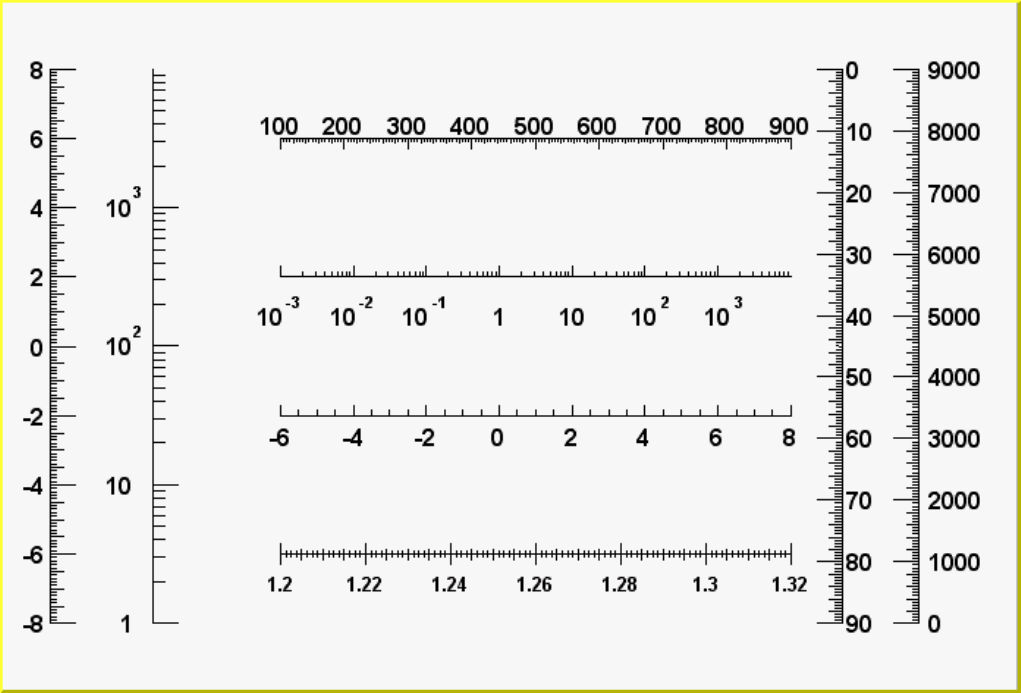
9.5. AXIS 205
Figure 9.26: The first axis example
TGaxis *axis5 = new TGaxis(-4.5,-6,5.5,-6,1.2,1.32,80506,"-+");
axis5->SetName("axis5");
axis5->SetLabelSize(0.03);
axis5->SetTextFont(72);
axis5->SetLabelOffset(0.025);
axis5->Draw();
TGaxis *axis6 = new TGaxis(-4.5,0.6,5.5,0.6,100,900,50510,"-");
axis6->SetName("axis6");
axis6->Draw();
TGaxis *axis7 = new TGaxis(8,-0.8,8,0.8,0,9000,50510,"+L");
axis7->SetName("axis7");
axis7->SetLabelOffset(0.01);
axis7->Draw();
// one can make axis top->bottom. However because of a problem,
// the two x values should not be equal
TGaxis *axis8 = new TGaxis(6.5,0.8,6.499,-0.8,0,90,50510,"-");
axis8->SetName("axis8");
axis8->Draw();
}
The second example shows the use of the second form of the constructor, with axis ticks position determined by a
function TF1:
void gaxis3a()
{
gStyle->SetOptStat(0);
TH2F *h2 = new TH2F("h","Axes",2,0,10,2,-2,2);
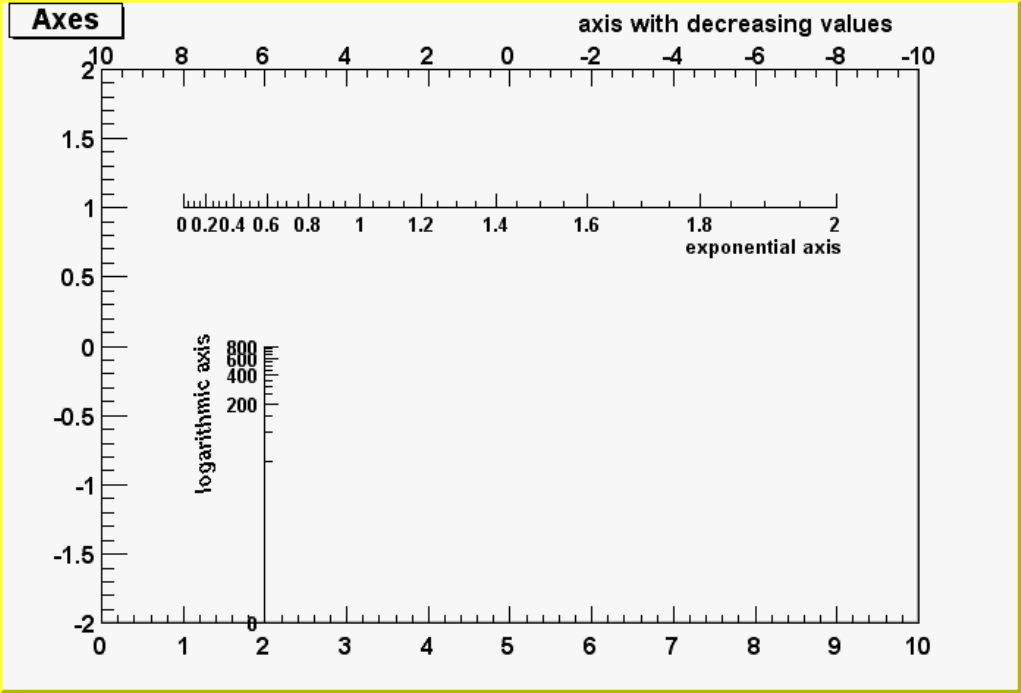
206 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
Figure 9.27: The second axis example
h2->Draw();
TF1 *f1=new TF1("f1","-x",-10,10);
TGaxis *A1 = new TGaxis(0,2,10,2,"f1",510,"-");
A1->SetTitle("axis with decreasing values");
A1->Draw();
TF1 *f2=new TF1("f2","exp(x)",0,2);
TGaxis *A2 = new TGaxis(1,1,9,1,"f2");
A2->SetTitle("exponential axis");
A2->SetLabelSize(0.03);
A2->SetTitleSize(0.03);
A2->SetTitleOffset(1.2);
A2->Draw();
TF1 *f3=new TF1("f3","log10(x)",0,800);
TGaxis *A3 = new TGaxis(2,-2,2,0,"f3",505);
A3->SetTitle("logarithmic axis");
A3->SetLabelSize(0.03);
A3->SetTitleSize(0.03);
A3->SetTitleOffset(1.2);
A3->Draw();
}
// strip chart example
void seism() {
TStopwatch sw; sw.Start();
//set time offset
TDatime dtime;
gStyle->SetTimeOffset(dtime.Convert());
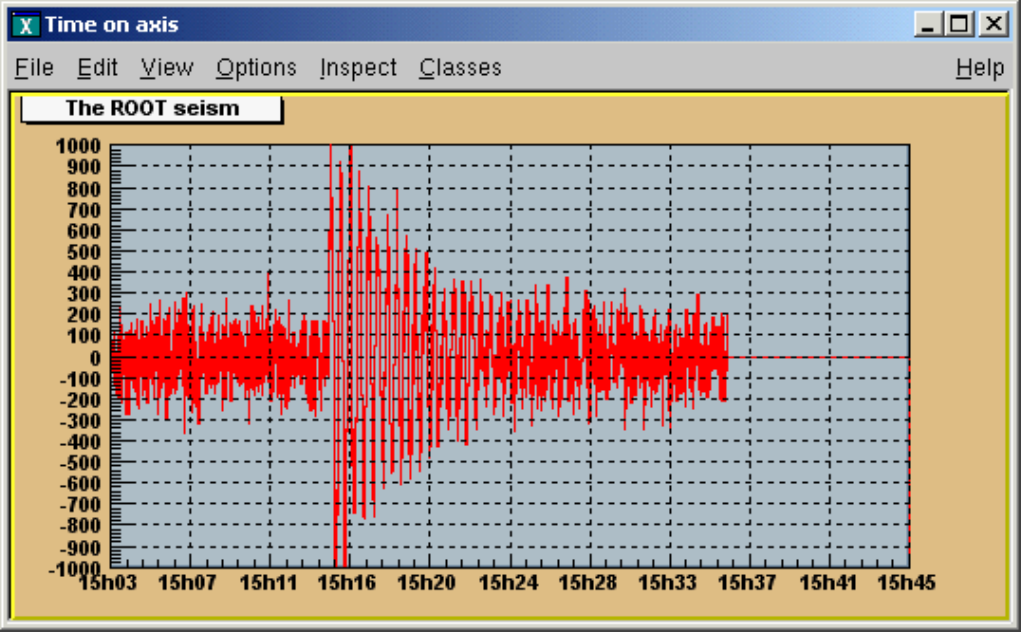
9.5. AXIS 207
Figure 9.28: An axis example with time display
TCanvas *c1 = new TCanvas("c1","Time on axis",10,10,1000,500);
c1->SetFillColor(42);
c1->SetFrameFillColor(33);
c1->SetGrid();
Float_t bintime = 1;
// one bin = 1 second. change it to set the time scale
TH1F *ht = new TH1F("ht","The ROOT seism",10,0,10*bintime);
Float_t signal = 1000;
ht->SetMaximum(signal);
ht->SetMinimum(-signal);
ht->SetStats(0);
ht->SetLineColor(2);
ht->GetXaxis()->SetTimeDisplay(1);
ht->GetYaxis()->SetNdivisions(520);
ht->Draw();
for (Int_t i=1;i<2300;i++) {
// Build a signal : noisy damped sine
Float_t noise = gRandom->Gaus(0,120);
if (i>700)
noise += signal*sin((i-700.)*6.28/30)*exp((700.-i)/300.);
ht->SetBinContent(i,noise);
c1->Modified();
c1->Update();
gSystem->ProcessEvents();
//canvas can be edited during the loop
}
printf("Real Time = %8.3fs,Cpu Time = %8.3fsn",sw.RealTime(),
sw.CpuTime());
}
208 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.6 Graphical Objects Attributes
9.6.1 Text Attributes
When a class contains text or derives from a text class, it needs to be able to set text attributes like font type, size,
and color. To do so, the class inherits from the
TAttText
class (a secondary inheritance), which defines text attributes.
TLatex and TText inherit from TAttText.
9.6.1.1 Setting Text Alignment
Text alignment may be set by a method call. What is said here applies to all objects deriving from
TAttText
, and
there are many. We will take an example that may be transposed to other types. Suppose “
la
” is a
TLatex
object.
The alignment is set with:
root[] la->SetTextAlign(align)
The parameter align is a short describing the alignment:
align = 10*HorizontalAlign + VerticalAlign
For horizontal alignment, the following convention applies:
•1 = left
•2 = centered
•3 = right
For vertical alignment, the following convention applies:
•1 = bottom
•2 = centered
•3 = top
For example, align: 11 = left adjusted and bottom adjusted; 32 = right adjusted and vertically centered.
9.6.1.2 Setting Text Angle
Use TAttText::SetTextAngle to set the text angle. The angle is the degrees of the horizontal.
root[] la->SetTextAngle(angle)
9.6.1.3 Setting Text Color
Use
TAttText::SetTextColor
to set the text color. The
color
is the color index. The colors are described in “Color
and Color Palettes”.
root[] la->SetTextColor(color)
9.6. GRAPHICAL OBJECTS ATTRIBUTES 209
9.6.1.4 Setting Text Font
Use
TAttText::SetTextFont
to set the font. The parameter font is the font code, combining the font and precision:
font = 10 * fontID + precision
root[] la->SetTextFont(font)
The table below lists the available fonts. The font IDs must be between 1 and 14. The precision can be:
•Precision = 0 fast hardware fonts (steps in the size)
•Precision = 1 scalable and rotate-able hardware fonts (see below)
•Precision = 2 scalable and rotate-able hardware fonts
When precision 0 is used, only the original non-scaled system fonts are used. The fonts have a minimum (4) and
maximum (37) size in pixels. These fonts are fast and are of good quality. Their size varies with large steps and they
cannot be rotated. Precision 1 and 2 fonts have a different behavior depending if True Type Fonts (TTF) are used
or not. If TTF are used, you always get very good quality scalable and rotate-able fonts. However, TTF are slow.
Precision 1 and 2 fonts have a different behavior for PostScript in case of TLatex objects:
•
With precision 1, the PostScript text uses the old convention (see
TPostScript
) for some special characters to
draw sub and superscripts or Greek text.
•
With precision 2, the “PostScript” special characters are drawn as such. To draw sub and superscripts it is highly
recommended to use TLatex objects instead.
For example: font = 62 is the font with ID 6and precision 2.
The available fonts are:
Font ID X11 True Type name Is italic “boldness”
1 times-medium-i-normal “Times New Roman” Yes 4
2 times-bold-r-normal “Times New Roman” No 7
3 times-bold-i-normal “Times New Roman” Yes 7
4 helvetica-medium-r-norma l “Arial” No 4
5 helvetica-medium-o-norma l “Arial” Yes 4
6 helvetica-bold-r-normal “Arial” No 7
7 helvetica-bold-o-normal “Arial” Yes 7
8 courier-medium-r-normal “Courier New” No 4
9 courier-medium-o-normal “Courier New” Yes 4
10 courier-bold-r-normal “Courier New” No 7
11 courier-bold-o-normal “Courier New” Yes 7
12 symbol-medium-r-normal “Symbol” No 6
13 times-medium-r-normal “Times New Roman” No 4
14 “Wingdings” No 4
This script makes the image of the different fonts:
{
textc = new TCanvas("textc","Example of text",1);
for (int i=1;i<15;i++) {
cid = new char[8];
sprintf(cid,"ID %d :",i);
cid[7]=0;
lid = new TLatex(0.1,1-(double)i/15,cid);
lid->SetTextFont(62);
lid->Draw();
l = new TLatex(.2,1-(double)i/15,
"The quick brown fox is not here anymore")
l->SetTextFont(i*10+2);
l->Draw();

210 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
Figure 9.29: Font’s examples
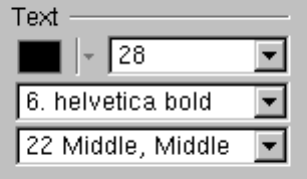
9.6. GRAPHICAL OBJECTS ATTRIBUTES 211
}
}
9.6.1.5 How to use True Type Fonts
You can activate the True Type Fonts by adding the following line in your .rootrc file.
Unix.*.Root.UseTTFonts: true
You can check that you indeed use the
TTF
in your Root session. When the
TTF
is active, you get the following
message at the start of a session: “Free Type Engine v1.x used to render TrueType fonts.” You can also check with the
command:
gEnv->Print()
9.6.1.6 Setting Text Size
Use TAttText::SetTextSize to set the text size.
root[] la->SetTextSize(size)
The size is the text size expressed in percentage of the current pad size.
The text size in pixels will be:
•If current pad is horizontal, the size in pixels = textsize * canvas_height
•If current pad is vertical, the size in pixels = textsize * canvas_width
The user interface for changing the text color, size, font and allignment looks like
shown in this picture. It takes place in the editor frame anytime the selected object inherits the class TAttText.
9.6.2 Line Attributes
All classes manipulating lines have to deal with line attributes: color, style and width. This is done by using secondary
inheritance of the class
TAttLine
. The line color may be set by a method call. What is said here applies to all objects
deriving from
TAttLine
, and there are many (histograms, plots). We will take an example that may be transposed to
other types. Suppose “li” is a TLine object. The line color is set with:
root[] li->SetLineColor(color)
The argument color is a color number. The colors are described in “Color and Color Palettes”
The line style may be set by a method call. What is said here applies to all objects deriving from
TAttLine
, and there
are many (histograms, plots). We will take an example that may be transposed to other types. Suppose “
li
” is a
TLine object. The line style is set with:
root[] li->SetLineStyle(style)
The argument style is one of: 1=solid, 2=dash, 3=dot, 4=dash-dot.
The line width may be set by a method call. What is said here applies to all objects deriving from
TAttLine
, and
there are many (histograms, plots). We will take an example that may be transposed to other types. Suppose “
li
” is a
TLine object. The line width is set with:
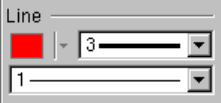
212 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
root[] li->SetLineWidth(width)
The width is the width expressed in pixel units.
The user interface for changing the line color, line width and style looks like shown in this
picture. It takes place in the editor frame anytime the selected object inherits the class TAttLine.
9.6.3 Fill Attributes
Almost all graphics classes have a fill area somewhere. These classes have to deal with fill attributes. This is done by
using secondary inheritance of the class
TAttFill
. Fill color may be set by a method call. What is said here applies to
all objects deriving from
TAttFill
, and there are many (histograms, plots). We will take an example that may be
transposed to other types. Suppose “h” is a TH1F (1 dim histogram) object. The histogram fill color is set with:
root[] h->SetFillColor(color)
The color is a color number. The colors are described in “Color and color palettes”
Fill style may be set by a method call. What is said here applies to all objects deriving from
TAttFill
, and there are
many (histograms, plots). We will take an example that may be transposed to other types. Suppose “
h
” is a
TH1F
(1
dim histogram) object. The histogram fill style is set with:
root[] h->SetFillStyle(style)
The convention for style is: 0:hollow, 1001:solid, 2001:hatch style, 3000+pattern number:patterns, 4000 to 4100:trans-
parency, 4000:fully transparent, 4100: fully opaque.
Fill styles >3100 and <3999 are hatches. They are defined according to the FillStyle=3ijk value as follows:
•i(1-9)
specifies the space between each hatch
(1=minimum space
,
9=maximum)
. The final spacing is set by
SetHatchesSpacing() method and it is*GetHatchesSpacing().
•j(0-9)
specifies the angle between 0 and 90 degres as follows:
0=0
,
1=10
,
2=20
,
3=30
,
4=45
,
5=not drawn
,
6=60
,
7=70,8=80 and 9=90.
•k(0-9)
specifies the angle between 0 and 90 degres as follows:
0=180
,
1=170
,
2=160
,
3=150
,
4=135
,
5=not drawn
,
6=120,7=110,8=100 and 9=90.
9.6.4 Color and Color Palettes
At initialization time, a table of basic colors is generated when the first Canvas constructor is called. This table is a
linked list, which can be accessed from the gROOT object (see TROOT::GetListOfColors()). Each color has an index
and when a basic color is defined, two “companion” colors are defined:
•the dark version (color index + 100)
•the bright version (color index + 150)
The dark and bright colors are used to give 3-D effects when drawing various boxes (see
TWbox
,
TPave
,
TPaveText
,
TPaveLabel, etc). If you have a black and white copy of the manual, here are the basic colors and their indices.
The list of currently supported basic colors (here dark and bright colors are not shown) are shown. The color numbers
specified in the basic palette, and the picture above, can be viewed by selecting the menu entry Colors in the View
canvas menu. The user may define other colors. To do this, one has to build a new TColor:
TColor(Int_t color,Float_t r,Float_t g,Float_t b,const char* name)
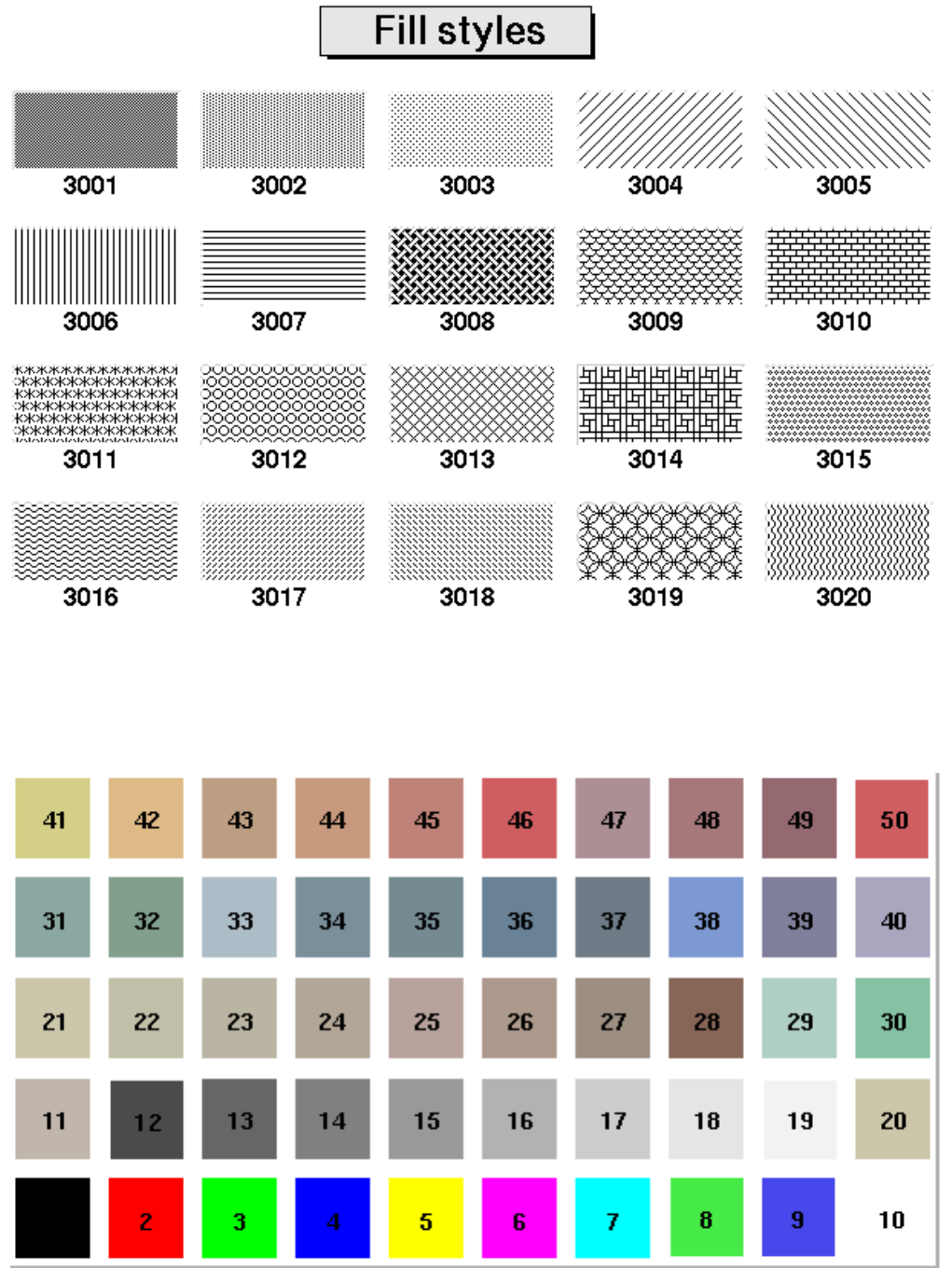
9.6. GRAPHICAL OBJECTS ATTRIBUTES 213
Figure 9.30: The various patterns
Figure 9.31: The basic ROOT colors

214 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
One has to give the color number and the three Red, Green, Blue values, each being defined from 0 (min) to 1(max).
An optional name may be given. When built, this color is automatically added to the existing list of colors. If the color
number already exists, one has to extract it from the list and redefine the RGB values. This may be done for example
with:
root[] color=(TColor*)(gROOT->GetListOfColors()->At(index_color))
root[] color->SetRGB(r,g,b)
Where r,gand bgo from 0 to 1 and index_color is the color number you wish to change.
The user interface for changing the fill color and style looks like shown in this picture. It
takes place in the editor frame anytime the selected object inherits the class TAttFill.
9.6.4.1 Color Palette (for Histograms)
Defining one color at a time may be tedious. The histogram classes (see Draw Options) use the color palette. For
example,
TH1::Draw("col")
draws a 2-D histogram with cells represented by a box filled with a color
CI
function of
the cell content. If the cell content is
N
, the color
CI
used will be the color number in
colors[N]
. If the maximum cell
content is
>ncolors
, all cell contents are scaled to
ncolors
. The current color palette does not have a class or global
object of its own. It is defined in the current style as an array of color numbers. The current palette can be changed
with:
TStyle::SetPalette(Int_t ncolors,Int_t*color_indexes).
By default, or if
ncolors <= 0
, a default palette (see above) of 50 colors is defined. The colors defined in this palette
are good for coloring pads, labels, and other graphic objects. If
ncolors > 0
and
colors = 0
, the default palette
is used with a maximum of
ncolors
. If
ncolors == 1 && colors == 0
, then a pretty palette with a spectrum
Violet->Red
is created. It is recommended to use this pretty palette when drawing lego(s), surfaces or contours. For
example, to set the current palette to the “pretty” one, do:
root[] gStyle->SetPalette(1)
A more complete example is shown below. It illustrates the definition of a custom palette. You can adapt it to suit
your needs. In case you use it for contour coloring, with the current color/contour algorithm, always define two more
colors than the number of contours.
void palette() {
// Example of creating new colors (purples)
const Int_t colNum = 10;// and defining of a new palette
Int_t palette[colNum];
for (Int_t i=0; i<colNum; i++) {
// get the color and if it does not exist create it
if (! gROOT->GetColor(230+i) ){
TColor *color =
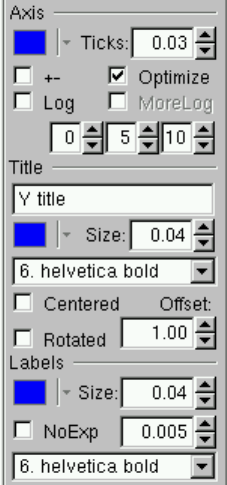
9.7. THE GRAPHICS EDITOR 215
new TColor(230+i,1-(i/((colNum)*1.0)),0.3,0.5,"");
}else {
TColor *color = gROOT->GetColor(230+i);
color->SetRGB(1-(i/((colNum)*1.0)),0.3,0.5);
}
palette[i] = 230+i;
}
gStyle->SetPalette(colNum,palette);
TF2 *f2 = new TF2("f2","exp(-(x^2)-(y^2))",-3,3,-3,3);
// two contours less than the number of colors in palette
f2->SetContour(colNum-2);
f2->Draw("cont");
}
9.7 The Graphics Editor
A new graphics editor took place in ROOT v4.0. The editor can be activated by selecting the Editor menu entry in the
canvas View menu or one of the context menu entries for setting line, fill, marker or text attributes. The following
object editors are available for the current ROOT version.
9.7.1 TAxisEditor
This user interface gives the possibility for changing the following axis attributes:
•color of the selected axis, the axis’ title and labels;
•the length of thick parameters and the possibility to set them on both axis sides (if +- is selected);
•to set logarithmic or linear scale along the selected axis with a choice for optimized or more logarithmic labels;
•primary, secondary and tertiary axis divisions can be set via the three number fields;
•the axis title can be added or edited and the title’s color, position, offset, size and font can be set interactively;
•
the color, size, and offset of axis labels can be set similarly. In addition, there is a check box for no exponent
choice, and another one for setting the same decimal part for all labels.
216 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.7.2 TPadEditor
•It provides the following user interface:
•Fixed aspect ratio - can be set for pad resizing.
•Edit - sets pad or canvas as editable.
•Cross-hair - sets a cross hair on the pad.
•TickX - set ticks along the X axis.
•TickY - set ticks along the Y axis.
•GridX - set a grid along the X axis.
•GridY - set a grid along the Y axis.
•The pad or canvas border size can be set if a sunken or a raised border mode is
•selected; no border mode can be set too.
9.8 Copy and Paste
You can make a copy of a canvas using
TCanvas::DrawClonePad
. This method is unique to
TCanvas
. It clones the
entire canvas to the active pad. There is a more general method
TObject::DrawClone
, which all objects descendent of
TObject
, specifically all graphic objects inherit. Below are two examples, one to show the use of
DrawClonePad
and
the other to show the use of DrawClone.
9.8.1 Using the GUI
In this example we will copy an entire canvas to a new one with DrawClonePad. Run the script draw2dopt.C.
root[] .x tutorials/hist/draw2dopt.C
This creates a canvas with 2D histograms. To make a copy of the canvas follow the steps:
•Right-click on it to bring up the context menu
•Select DrawClonePad
This copies the entire canvas and all its sub-pads to a new canvas. The copied canvas is a deep clone, and all the
objects on it are copies and independent of the original objects. For instance, change the fill on one of the original
histograms, and the cloned histogram retains its attributes.
DrawClonePad
will copy the canvas to the active pad; the
target does not have to be a canvas. It can also be a pad on a canvas.
If you want to copy and paste a graphic object from one canvas or pad to another canvas or pad, you can do so with
DrawClone
method inherited from
TObject
. All graphics objects inherit the
TObject::DrawClone
method. In this
example, we create a new canvas with one histogram from each of the canvases from the script draw2dopt.C.
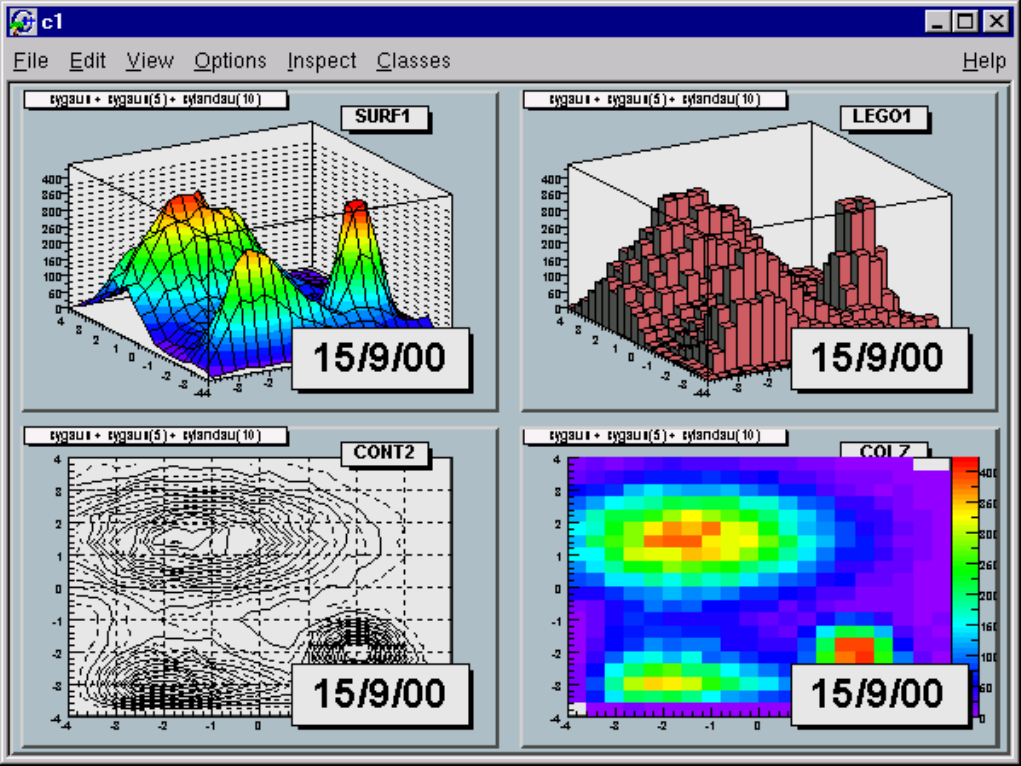
9.8. COPY AND PASTE 217
Figure 9.32: Different draw options
218 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
•Start a new ROOT session and execute the script draw2dopt.C
•Select a canvas displayed by the script, and create a new canvas c1 from the File menu.
•
Make sure that the target canvas (
c1
) is the active one by middle clicking on it. If you do this step right after
step 2, c1 will be active.
•Select the pad with the first histogram you want to copy and paste.
•Right click on it to show the context menu, and select DrawClone.
•Leave the option blank and hit OK.
Repeat these steps for one histogram on each of the canvases created by the script, until you have one pad from each
type. If you wanted to put the same annotation on each of the sub pads in the new canvas, you could use
DrawClone
to do so. Here we added the date to each pad. The steps to this are:
•Create the label in on of the pads with the graphics editor.
•Middle-click on the target pad to make it the active pad
•Use DrawClone method of the label to draw it in each of the other panels.
The option in the
DrawClone
method argument is the Draw option for a histogram or graph. A call to
TH1::DrawClone
can clone the histogram with a different draw option.
9.8.2 Programmatically
To copy and paste the four pads from the command line or in a script you would execute the following statements:
root[] .x tutorials/hist/draw2dopt.C
root[] TCanvas c1("c1","Copy Paste",200,200,800,600);
root[] surfaces->cd(1); // get the first pad
root[] TPad *p1 = gPad;
root[] lego->cd(2);// get the next pad
root[] TPad *p2 = gPad;
root[] cont->cd(3);// get the next pad
root[] TPad *p3 = gPad;
root[] c2h->cd(4);// get the next pad
root[] TPad *p4 = gPad;
root[] // to draw the four clones
root[] c1->cd();
root[] p1->DrawClone();
root[] p2->DrawClone();
root[] p3->DrawClone();
root[] p4->DrawClone();
Note that the pad is copied to the new canvas in the same location as in the old canvas. For example if you were to
copy the third pad of
surf
to the top left corner of the target canvas you would have to reset the coordinates of the
cloned pad.
9.9 Legends
Legends for a graph are obtained with a
TLegend
object. This object points to markers, lines, boxes, histograms,
graphs and represent their marker, line, fill attributes. Any object that has a marker or line or fill attribute may have
an associated legend. A
TLegend
is a panel with several entries (class
TLegendEntry
) and is created by the constructor
TLegend(Double_t x1, Double_t y1, Double_t x2, Double_t y2,
const char *header, Option_t *option)
The legend is defined with default coordinates, border size and option. The legend coordinates (NDC) in the current
pad are x1,y1,x2,y2. The default text attributes for the legend are:
9.10. THE POSTSCRIPT INTERFACE 219
•Alignment = 12 left adjusted and vertically centered
•Angle = 0 (degrees)
•Color = 1 (black)
•Size = calculate when number of entries is known
•Font = helvetica-medium-r-normal scalable font = 42, and bold = 62 for title
The title is a regular entry and supports
TLatex
. The default is no title (
header = 0
). The options are the same as
for
TPave
; by default, they are “
brand
”. Once the legend box is created, one has to add the text with the
AddEntry()
method:
TLegendEntry* TLegend::AddEntry(TObject *obj,
const char *label,
Option_t *option)
The parameters are:
•*objis a pointer to an object having marker, line, or fill attributes (a histogram, or a graph)
•label is the label to be associated to the object
•option:
•“L” draw line associated with line attributes of obj, if obj inherits from TAttLine.
•“P” draw poly-marker associated with marker attributes of obj, if obj inherits TAttMarker.
•“F” draw a box with fill associated with fill attributes of obj, if obj inherits TAttFill.
One may also use the other form of the method AddEntry:
TLegendEntry* TLegend::AddEntry(const char *name,
const char *label,
Option_t *option)
Here
name
is the name of the object in the pad. Other parameters are as in the previous case. Next example shows
how to create a legend:
leg = new TLegend(0.4,0.6,0.89,0.89);
leg->AddEntry(fun1,"One Theory","l");
leg->AddEntry(fun3,"Another Theory","f");
leg->AddEntry(gr,"The Data","p");
leg->Draw();
// oops we forgot the blue line... add it after
leg->AddEntry(fun2,
"#sqrt{2#pi} P_{T} (#gamma) latex formula","f");
// and add a header (or "title") for the legend
leg->SetHeader("The Legend Title");
leg->Draw();
Here
fun1
,
fun2
,
fun3
and
gr
are pre-existing functions and graphs. You can edit the
TLegend
by right clicking on it.
9.10 The PostScript Interface
To generate a PostScript (or encapsulated PostScript) file for a single image in a canvas, you can:
•
Select to print the canvas in the PostScript file format from the File menu / Save or Save As menu entries. By
default, a PostScript file is generated, if you do not specify the file format.
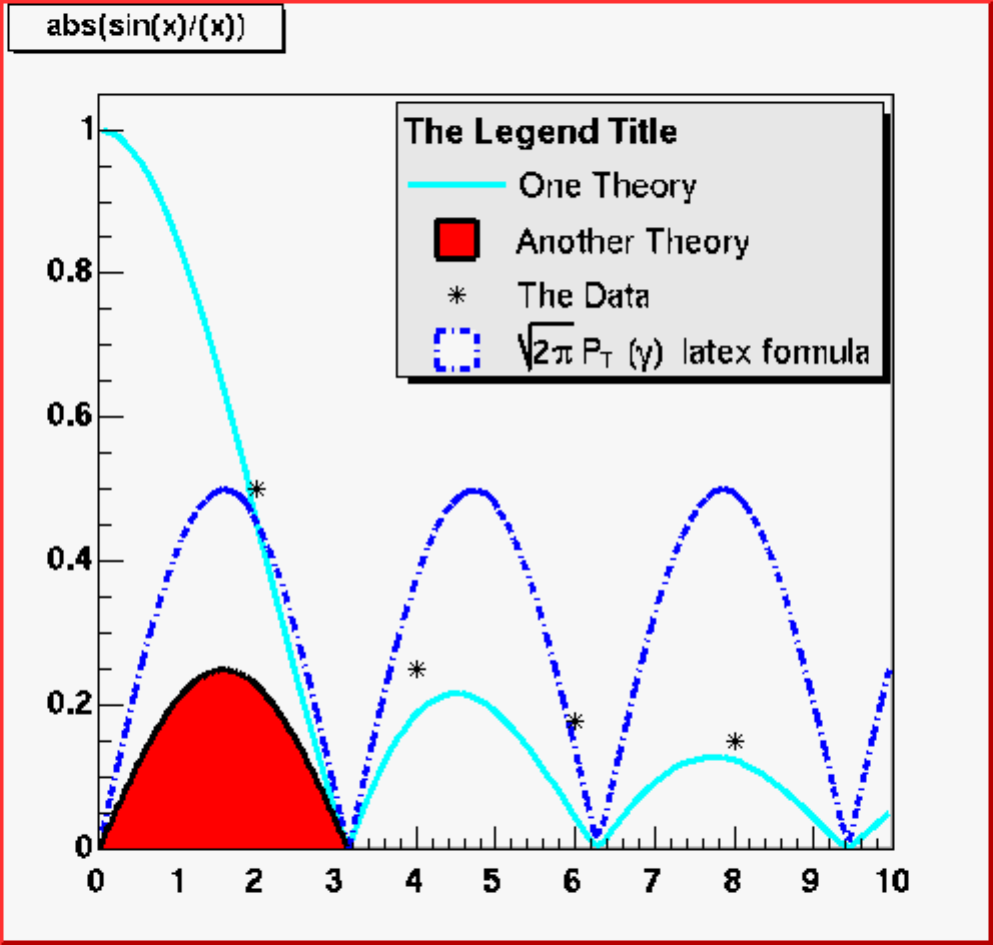
220 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
Figure 9.33: A legend example
9.10. THE POSTSCRIPT INTERFACE 221
•
Click in the canvas area, near the edges, with the right mouse button and select the Print context menu entry.
This will generate a file of canvas pointed to by c1. You can select the name of the PostScript file. If the file
name is
xxx.ps
, you will generate a PostScript file named
xxx.ps
. If the file name is
xxx.eps
, you generate an
encapsulated Postscript file instead. In your program (or script), you can type:
c1->Print("xxx.ps")// or
c1->Print("xxx.eps")
Next example prints the picture in the pad pointed by pad1.
pad1->Print("xxx.ps")
The TPad::Print method has a second parameter called option. Its value can be:
•0which is the default and is the same as “ps”
•“ps” a Postscript file is produced
•“Portrait” a Postscript file is produced with Portrait orientation
•“Landscape” a Postscript file is produced with Landscape orientation
•“eps”an Encapsulated Postscript file
•“Preview”an Encapsulated Postscript file with preview is produced
•“gif” a Graphics Interchange Format file
•“cxx” a C++ macro file is generated
•“pdf”a Portable Document Format file
•“xml” a eXtensible Mark-up Language file
•“jpg”a Joint Photographic Experts Group file
•“png” a Portable Network Graphics Format (PNG file)
•“xpm” a X11 Pixel Map Format
•“svg” a Scalable Vector Graphics file
•“tiff” a Tagged-Image File Format
•“root”a ROOT binary file is produced
You do not need to specify this second parameter; you can indicate by the filename extension what format you want to
save a canvas in (i.e. canvas.ps,canvas.gif,canvas.C, etc).
The size of the PostScript picture, by default, is computed to keep the aspect ratio of the picture on the screen, where
the size along
x
is always 20 cm. You can set the size of the PostScript picture before generating the picture with a
command such as:
TPostScript myps("myfile.ps",111)
myps.Range(xsize,ysize);
object->Draw();
myps.Close();
The first parameter in the TPostScript constructor is the name of the file; the second one is the format option:
•111 - ps portrait
•112 - ps landscape
•113 - eps
You can set the default paper size with:
gStyle->SetPaperSize(xsize,ysize);
You can resume writing again in this file with
myps.Open()
. Note that you may have several Post Script files opened
simultaneously. Use
TPostScript::Text(x,y,"string")
to add text to a postscript file. This method writes the
string in quotes into a PostScript file at position x, y in world coordinates.
222 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.10.1 Special Characters
The following characters have a special action on the PostScript file:
•‘- go to Greek
•’- go to special
•~- go to Zapf Dingbats
•?- go to subscript
•ˆ- go to superscript
•!- go to normal level of script
•&- backspace one character
•#- end of Greek or end of ZapfDingbats
These special characters are printed as such on the screen. To generate one of these characters on the PostScript file,
you must escape it with the escape character “@”. The use of these special characters is illustrated in several scripts
referenced by the TPostScript constructor.
9.10.2 Writing Several Canvases to the Same PostScript File
The following sequence writes the canvas to “c1.ps” and closes the postscript file:
TCanvas c1("c1");
h1.Draw();
c1.Print("c1.ps");
If the Postscript file name finishes with “
(
”, the file remains opened (it is not closed). If the Postscript file name
finishes with “)” and the file has been opened with “(”, the file is closed.
{
TCanvas c1("c1");
h1.Draw();
c1.Print("c1.ps("); // write canvas and keep the ps file open
h2.Draw();
c1.Print("c1.ps"); // canvas is added to "c1.ps"
h3.Draw();
c1.Print("c1.ps)"); // canvas is added to "c1.ps"
// and ps file is closed
}
The
TCanvas::Print("file.ps(")
mechanism is very useful, but it can be a little inconvenient to have the action of
opening/closing a file being atomic with printing a page. Particularly if pages are being generated in some loop, one
needs to detect the special cases of first and last page. The “
[
” and “
]
” can be used instead of “
(
” and “
)
” as shown in
the next example.
c1.Print("file.ps["); // no actual print; just open file.ps
for (i=0; i<10; ++i) {
// fill canvas for context i
...
c1.Print("file.ps"); // actually print canvas to file.ps
}// end loop
c1.Print("file.ps]"); // no actual print; just close file.ps
The following script illustrates how to open a postscript file and draw several pictures. The generation of a new
postscript page is automatic when TCanvas::Clear is called by object->Draw().
9.10. THE POSTSCRIPT INTERFACE 223
{
TFile f("hsimple.root");
TCanvas c1("c1","canvas",800,600);
//select PostScript output type
Int_t type = 111;//portrait ps
// Int_t type = 112; //landscape ps
// Int_t type = 113; //eps
//create a PostScript file and set the paper size
TPostScript ps("test.ps",type);
ps.Range(16,24); //set x,y of printed page
//draw 3 histograms from file hsimple.root on separate pages
hpx->Draw();
c1.Update(); //force drawing in a script
hprof->Draw();
c1.Update();
hpx->Draw("lego1");
c1.Update();
ps.Close();
}
The next example does the same:
{
TFile f("hsimple.root");
TCanvas c1("c1","canvas",800,600);
//set x,y of printed page
gStyle->SetPaperSize(16,24);
//draw 3 histograms from file hsimple.root on separate pages
hpx->Draw();
c1->Print("test1.ps(","Portrait");
hprof->Draw();
c1->Print("test1.ps");
hpx->Draw("lego1");
c1->Print("test1.ps)");
}
This following example shows two pages. The canvas is divided.
TPostScript::NewPage
must be called before starting
a new picture.
object->Draw
does not clear the canvas in this case because we clear only the pads and not the main
canvas. Note that c1->Update must be called at the end of the first picture.
{
TFile *f1 = new TFile("hsimple.root");
TCanvas *c1 = new TCanvas("c1");
TPostScript *ps = new TPostScript("file.ps",112);
// picture 1
c1->Divide(2,1);
ps->NewPage();
c1->cd(1);
hpx->Draw();
c1->cd(2);
hprof->Draw();
// picture 2
c1->Update();
ps->NewPage();
c1->cd(1);
224 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
hpxpy->Draw();
c1->cd(2);
ntuple->Draw("px");
c1->Update();
ps->Close();
// invoke PostScript viewer
gSystem->Exec("gs file.ps");
}
The next one does the same:
{
TFile *f1 = new TFile("hsimple.root");
TCanvas *c1 = new TCanvas("c1");
c1->Divide(2,1);
// picture 1
c1->cd(1);
hpx->Draw();
c1->cd(2);
hprof->Draw();
c1->Print("test2.ps(","Landscape");
// picture 2
c1->cd(1);
hpxpy->Draw();
c1->cd(2);
ntuple->Draw("px");
c1->Print("test2.ps)");
gSystem->Exec("gs file.ps"); // invoke PostScript viewer
}
9.10.3 The Color Models
TPostScript
(and
TPDF
) support two color models: RGB and CMYK. CMY and CMYK models are subtractive color
models unlike RGB which is an additive. They are mainly used for printing purposes. CMY means Cyan Magenta
Yellow to convert RGB to CMY it is enough to do:
C=1-R
,
M=1-G
and
Y=1-B
. CMYK has one more component K
(black). The conversion from RGB to CMYK is:
Double_t Black = TMath::Min(TMath::Min(1-Red,1-Green),1-Blue);
Double_t Cyan = (1-Red-Black)/(1-Black);
Double_t Magenta = (1-Green-Black)/(1-Black);
Double_t Yellow = (1-Blue-Black)/(1-Black);
CMYK
add the black component which allows to have a better quality for black printing.
TPostScript
(and
TPDF
)
support the CMYK model. To change the color model use:
gStyle->SetColorModelPS(c);
•c=0means TPostScript will use RGB color model (default)
•c=1means TPostScript will use CMYK color model
9.11 The PDF Interface
Like PostScript, PDF is a vector graphics output format allowing a very high graphics output quality. The functionnalities
provided by this class are very similar to those provided by TPostScript‘.
Compare to PostScript output, the PDF files are usually smaller because some parts of them can be compressed.
PDF also allows to define table of contents. This facility can be used in ROOT. The following example shows how to
proceed:
9.12. CREATE OR MODIFY A STYLE 225
{
TCanvas* canvas = new TCanvas("canvas");
TH1F* histo = new TH1F("histo","test 1",10,0.,10.);
histo->SetFillColor(2);
histo->Fill(2.);
histo->Draw();
canvas->Print("plots.pdf(","Title:One bin filled");
histo->Fill(4.);
histo->Draw();
canvas->Print("plots.pdf","Title:Two bins filled");
histo->Fill(6.);
histo->Draw();
canvas->Print("plots.pdf","Title:Three bins filled");
histo->Fill(8.);
histo->Draw();
canvas->Print("plots.pdf","Title:Four bins filled");
histo->Fill(8.);
histo->Draw();
canvas->Print("plots.pdf)","Title:The fourth bin content is 2");
}
Each character string following the keyword “Title:” makes a new entry in the table of contents.
9.12 Create or Modify a Style
All objects that can be drawn in a pad inherit from one or more attribute classes like
TAttLine
,
TAttFill
,
TAttText
,
TAttMarker
. When objects are created, their default attributes are taken from the current style. The current style
is an object of the class
TStyle
and can be referenced via the global variable
gStyle
(in
TStyle.h
). See the class
TStyle for a complete list of the attributes that can be set in one style.
ROOT provides several styles called:
•“Default” - the default style
•“Plain” - the simple style (black and white)
•“Bold” - bolder lines
•“Video” - suitable for html output or screen viewing
The “Default” style is created by:
TStyle *default =new TStyle("Default","Default Style");
The “
Plain
” style can be used if you want to get a “conventional” PostScript output or if you are working on a
monochrome display. The following example shows how to create it.
TStyle *plain = new TStyle("Plain",
"Plain Style(no colors/fill areas)");
plain->SetCanvasBorderMode(0);
plain->SetPadBorderMode(0);
plain->SetPadColor(0);
plain->SetCanvasColor(0);
plain->SetTitleColor(0);
plain->SetStatColor(0);
You can set the current style by:
gROOT->SetStyle(style_name);
You can get a pointer to an existing style by:
226 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
TStyle *style = gROOT->GetStyle(style_name);
You can create additional styles by:
TStyle *st1 = new TStyle("st1","my style");
st1->Set...
st1->cd(); // this becomes now the current style gStyle
In your rootlogon.C file, you can redefine the default parameters via statements like:
gStyle->SetStatX(0.7);
gStyle->SetStatW(0.2);
gStyle->SetLabelOffset(1.2);
gStyle->SetLabelFont(72);
Note that when an object is created, its attributes are taken from the current style. For example, you may have created
a histogram in a previous session and saved it in a file. Meanwhile, if you have changed the style, the histogram will be
drawn with the old attributes. You can force the current style attributes to be set when you read an object from a file
by calling ForceStyle before reading the objects from the file.
gROOT->ForceStyle();
When you call
gROOT->ForceStyle()
and read an object from a ROOT file, the object’s method
UseCurrentStyle
is called. The attributes saved with the object are replaced by the current style attributes. You call also call
myObject->UseCurrentStyle()
directly. For example if you have a canvas or pad with your histogram or any other
object, you can force these objects to get the attributes of the current style by:
canvas->UseCurrentStyle();
The description of the style functions should be clear from the name of the
TStyle
setters or getters. Some functions
have an extended description, in particular:
•TStyle::SetLabelFont
•TStyle::SetLineStyleString: set the format of dashed lines.
•TStyle::SetOptStat
•TStyle::SetPalette to change the colors palette
•TStyle::SetTitleOffset
•TStyle::SetOptDate(Int_t optdate)
to support several date formats. If
optdate
is non-null, the current
date/time will be printed in the canvas. The position of the date string can be controlled by:
optdate =
10*format+mode
•mode = 1 the date is printed in the bottom/left corner
•mode = 2 date is printed in the bottom/right corner
•mode = 3 date is printed in the top/right corner
•format = 0 (default) date format is like: “Wed Sep 25 17:10:35 2002”
•format = 1 date format is: “2002-09-25”
•format = 2 date format is: “2002-09-25 17:10:35”
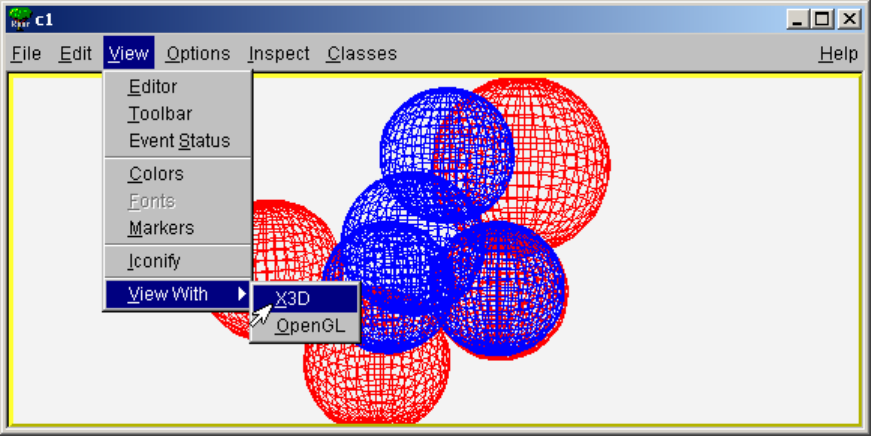
9.13. 3D VIEWERS 227
9.13 3D Viewers
ROOT provides several viewers capable of displaying 3D content:
•the Pad - simple line drawing using TPad and associated projection class TView;
•GL Viewer - high quality and performance viewer(See “The GL Viewer”);
•X3D viewer - simple legacy viewer (See “The X3D Viewer”);
•GL-in-pad - combination of basic GL viewer in TPad, with no hardware acceleration.
The X3D and GL viewers are created as external windows, associated with a pad, and displaying the same content
as it. Only these external viewers are detailed here - for Pad (
TPad
,
TView
classes) you should refer to “Graphical
Containers: Canvas and Pad” and the class definitions.
All viewers use a common architecture to publish 3D objects to the viewer - described in “Common 3D Viewer
Architecture” below. In most cases, you will
not
need to use this, working instead with a package, such as the “The
Geometry Package”, which provides comprehensive, high level functionality to create and place objects into complex
3D scenes, and uses the viewer architecture internally to show the result in your chosen viewer.
9.13.1 Invoking a 3D viewer
A 3D viewer can be created in a script by passing the appropriate option to
Draw()
when attaching the drawn object(s)
to a pad. For a fuller explanation of pads, attaching objects with
Draw()
etc. refer to “Graphical Containers: Canvas
and Pad”.
root[] myShapes->Draw("ogl");
Valid option strings are:
•“ogl” : external GL viewer
•“x3d”: external X3D viewer
•“pad”: pad viewer
If no option is passed to
Draw()
then the “
pad
” is used by default. If you already have content in a pad, which you
would like to display in one of the external viewers you can select from the canvas View menu / View With, and pick
the viewer type.
Figure 9.34: Invoking external 3D viewers from canvas menus
Note: A current limitation means that when an external viewer is created the pad is no longer redrawn. When the
external viewer is closed, clicking in the pad will refresh.

228 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.13.2 The GL Viewer
The GL Viewer uses (or compliant libraries such as ) to generate high quality, high-performance 3D renderings, with
sophisticated lighting, materials and rendering styles for 3D scenes. Many users will be able to take advantage of
hardware acceleration of the underlying OpenGL commands by their computer’s video card, resulting is considerable
performance gains - up to interactive manipulation of 1000’s of complex shapes in real-time.
The GL Viewer is supported on all official ROOT platforms (assuming you have suitable libraries), and is the main 3D
viewer, which development effort is concentrated upon. As OpenGL
®
is a trademark we refer to our viewer built on
this technology as the ‘GL Viewer’. The code for it can be found under $ROOTSYS/gl.
Figure 9.35: The GL 3D Viewer
You can manipulate the viewer via the GUI or via the base
TGLViewer
object behind the interface. These are detailed
below - see also $ROOTSYS/tutorials/gl/glViewerExercise.C.
9.13.2.1 Projections Modes (Cameras)
The GL Viewer supports two basic types of camera, which affect how the 3D world is projected onto the 2D render
area:
•
Perspective: Objects are drawn with characteristic ‘foreshortening’ effect, where distant objects appear smaller
than near ones. This is useful for obtaining a ‘real world’ views. The degree of foreshortening is affected by the
current camera field of view (focal length of its ‘lens’) - see “Adjusting Cameras”.
•
Orthographic: Distance from camera does not affect object size. These projections are useful for measurement or
checking alignments, as the sizes and angles between objects are preserved.
You can select the active camera from the viewer’s Camera menu on the top menu bar. There are three perspective
camera choices:
•Perspective (Floor XOZ) Default
•Perspective (Floor YOZ)
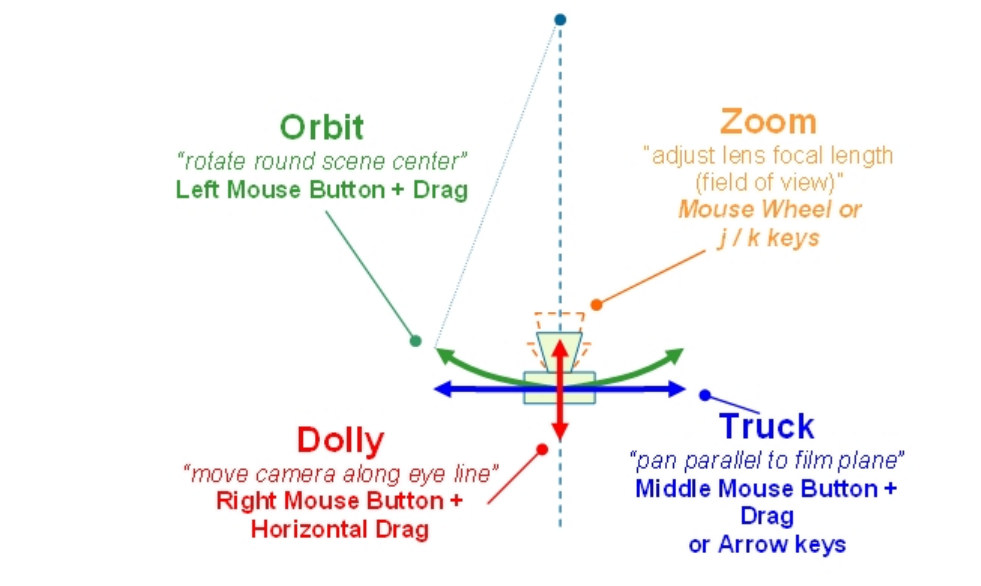
9.13. 3D VIEWERS 229
•Perspective (Floor XOY)
In each case the perspective camera is constrained to keep the chosen floor plane, defined by a pair of world axes,
appearing level at all times - i.e. there is no banking of the ‘horizon’ that you experience when a plane rolls. There are
also three orthographic camera choices:
•Orthographic (XOY)
•Orthographic (XOZ)
•Orthographic (ZOY)
Orthographic projections are generally constrained to look down one of the global axes of the world, with the other two
axes lying horizontal/vertical on the viewer window. Therefore, XOY has the X-axis horizontal, the Y-axis vertical.
You can always confirm the orientation and constraints of the camera in the world by enabling axis drawing in the
“Guides” tab - see sections “Guides” and “Clipping” below. For orthographic camera a ruler-depicting current scene
units is also available.
You can also pick the current camera by obtaining a handle to the GL Viewer object behind the interface:
TGLViewer * v = (TGLViewer *)gPad->GetViewer3D();
calling the method TGLViewer::SetCurrentCamera with one of the TGLViewer::ECameraType types:
v->SetCurrentCamera(TGLViewer::kCameraPerspXOZ);
See also $ROOTSYS/tutorials/gl/glViewerExercise.C.
9.13.2.2 Adjusting Cameras
The interactions with the camera are summarized above. In each case the interaction is listed, along with description
and user actions required to achieve it. For all cameras you can reset the original default view, framing the entire
scene, by double clicking any mouse button.
Figure 9.36: GL Viewer camera interactions
For the Zoom interaction you can use the following modifiers combinations to adjust the sensitivity:
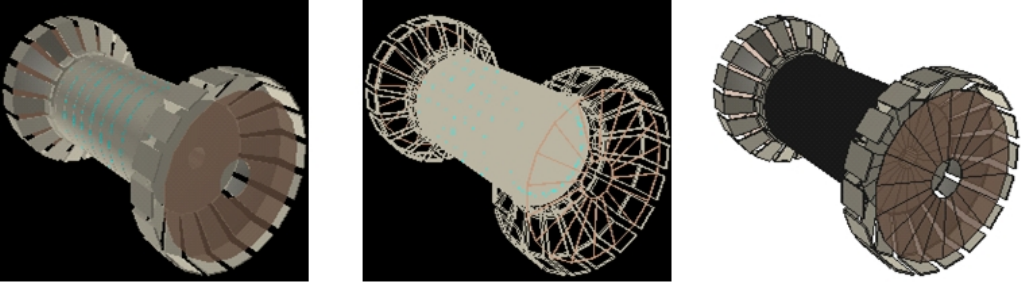
230 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
•Shiftx 10
•Ctrlx 0.1
•Shift + Ctrlx 0.01
The modifiers must be applied after the zoom action has started (right mouse button is down).
Note for orthographic cameras:
•There is no field of view of view/focal length - dollying and zooming producing an identical scaling action.
•There is a fixed eye direction - so the ‘Orbit’ action is disabled.
Note for perspective cameras:
•
Dollying (moving the camera backwards/forwards) and zooming are often confused, and may appear very similar.
•
When you dolly the camera the lens focal length does not change, hence the distortions associated with the
projections are unaffected. However the movement can result in objects coming ‘through the front’ of the camera
and disappearing.
•
When you zoom, the camera does not move - hence clipping of near objects is unaffected. However with extremely
small zooms (FOV large/focal length short) noticeable distortions, causing straight lines to become curved, can
be seen with objects near the camera - the ‘fisheye’ lens effect.
•
Generally dollying is more ‘natural’, but you may need to use both to achieve the desired perspective and eye
position - particularly when you are working inside or very close to 3D objects.
Configure the camera by calling the methods
SetPerspectiveCamera(
) or
SetOrthographicCamera()
of
TGLViewer
:
TGLViewer * v = (TGLViewer *)gPad->GetViewer3D();
v->SetOrthoCamera(TGLViewer::kCameraOrthoXOY,
left,right,top,bottom);
...
v->SetPerspectiveCamera (camera,fov,dolly,center,hRotate,vRotate);
Note - you can configure any of the six cameras in the viewer at any time, but you will not see the result until the
camera is made current.
9.13.2.3 Draw Styles
The GL Viewer supports three different rendering modes, which are applied to all the objects in your scene, but not
Clip Shapes and Guides (See “Clipping” and “Manipulators”). These are shown below, along with the key used to
activate the style.
Figure 9.37: GL Viewer draw styles
Filled Polygons Wireframe Outline
Enable with ‘r’ key Enable with ‘w’ key Enable with ‘t’ key Solid polygons,
with hidden surface Object edges in color, with Combination of Filled Polygons removal, color surface materials, no
surface filling/hiding. and Outline styles. Solid opacity, specular reflection etc. shapes with edges. Black background.
Black background. White background.
Call method TGLViewer::SetStyle with one of TGLRnrCtx::EDrawStyleflags kFill,kOutline,kWireFrame:
v->SetStyle(TGLRnrCtx::kFill);
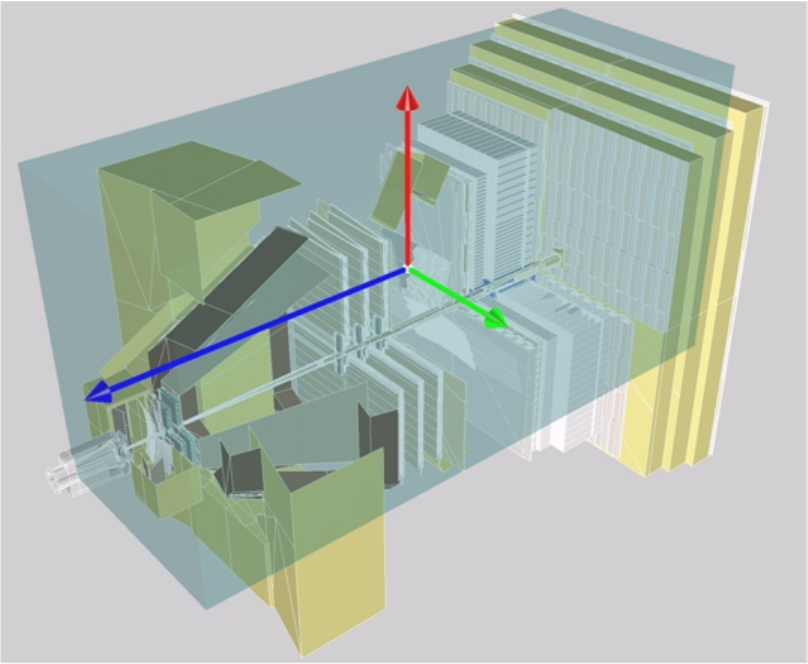
9.13. 3D VIEWERS 231
9.13.2.4 Lighting / Style
The GL viewer creates five diffuse lights (left, right, top, bottom, and front) arranged around the 3D scene. These
lights are carried with the camera - that is they are always in same position relative to your eye - the left light always
shines from the left.
Light controls are located: Viewer Controls Pane ‘Style’.
Each light has a checkbox to enable/disable it. Set lights on/off with TGLLightSet::SetLight e.g.
v->GetLightSet()->SetLight(TGLLightSet::kLightBottom, kFALSE);
9.13.2.5 Clipping
The GL viewer supports interactive clipping, enabling you to remove sections of your 3D scene and the shapes, revealing
internal details.
Figure 9.38: GL Viewer interactive box clipping
The controls for clipping can be found under: Viewer Controls Pane ‘Clipping’ tab.
Two clipping ‘shapes’ are currently supported:
•Single plane
•Box
Pick the type from the radio buttons - only one (or none) may be active at one time.
The clip object can be adjusted by:
•Adjusting the values in the properties panel GUI
•Directly manipulating the clip object in the viewer
232 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
To show and/or directly manipulate the object check the ‘Show / Edit in Viewer’ checkbox. The clip object is drawn in
semi-transparent light brown. The current manipulator is attached to it, allowing you direct control over its position,
scale and rotation. See “Manipulators” section below for details on using viewer manipulators.
The clip plane is described by the standard plane equation:
ax+by+cz+d=0
, where the factors
a
,
b
,
c
,
d
are entered
into the edit boxes, and applied using the ‘Apply’ button.
The clip box is described by its center position, entered in the ‘Center X’, ‘Center Y’ and ‘Center Z’ edit boxes, and its
lengths (extents) entered in the ‘Length X’, ‘Length Y’ and ‘Length Z’ edit boxes.
This clipping is achieved using OpenGL clip plane support; as such, there are certain limitations:
•Solid shapes are not capped - they appear hollow.
•
Only shapes, which can be described with combination of planes, can be rendered in this fashion - e.g. a clipping
tube is not possible.
•
Each additional clipping plane requires an additional render pass - so the more active planes the more time the
render will take.
Set the current clip object with TGLClipSet::SetClipType
v->GetClipSet()->SetClipType(TGLClipSet::kClipPlane);
Configure the clip object with TGLClipSet::SetClipState
Double_t planeEq[4]={0.5,1.0,-1.0,2.0};
v->GetClipSet()->SetClipState(TGLClipSet::kClipPlane, planeEq);
As with cameras, any clip can be configured at any time, but you must set the clip current to see the effect.
9.13.2.6 Manipulators
Manipulators are GUI ‘widgets’ or controls attached to a 3D object in the viewer, allowing a direct manipulation of
the object’s geometry. There are three manipulators for the three basic geometries transformations. In each case, the
manipulator consists of three components, one for each local axis of the object, shown in standard colors: red (X),
green (Y) and blue (Z).
Activate the manipulator by moving the mouse over one of these components (which turns yellow to indicate active
state). Click with left mouse and drag this active component to perform the manipulation. Toggle between the
manipulator types using the ‘x’, ‘c’, ‘v’ keys while the mouse cursoris above the manipulator. Note: Manipulators
cannot be controlled via the API at present.
9.13.2.7 Guides
Guides are visual aids drawn into the viewer world. Controls for these are under the “Guides” tab:
Viewer Controls Pane Guides Tab
Axes show the world (global) frame coordinatedirections: X (red), Y (green) and Z (blue). The negative portion of the
axis line is shown in dark color, the positive in bright. The axis name and minimum / maximum values are labeled in
the same color. There are three options for axes drawing - selected by radio buttons:
•None - not drawn (default).
•Edge - draw axes on the (minimum) edge of the scene extents box.
•Origin - drawn axes through the origin.
For edge axes, the zero value for each axis is marked on the axis line with a colored sphere. For origin axes, a single
white sphere is shown at the origin.
Edge axes are depth clipped - i.e. are obscured by 3D objects in front of them. Origin axes (which generally pass
through the middle of the 3D scene) are not depth clipped - so always visible.
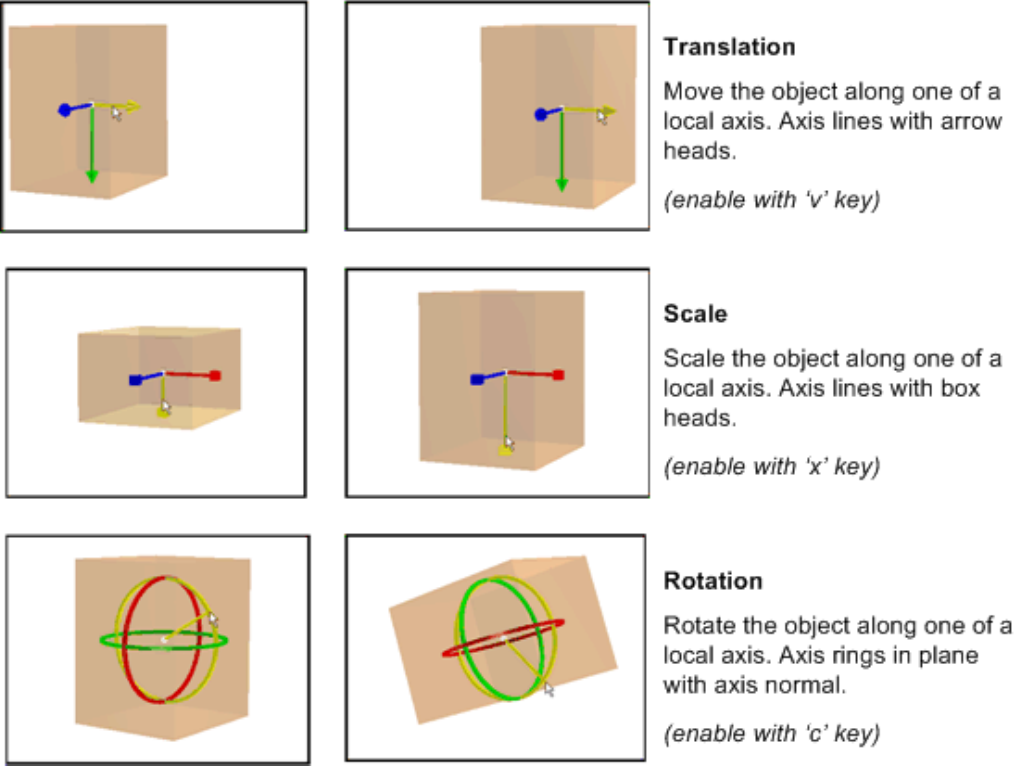
9.13. 3D VIEWERS 233
Figure 9.39: GL Viewer object manipulators
234 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
A single orange sphere of fixed view port (window) size can be shown at any arbitrary position. Enable / disable the
drawing with ‘Show’ checkbox. Enter X/Y/Z position in the edit boxes to set position. Initial position is at the center
of the scene.
Set the guides using
TGLViewer::SetGuideState
e.g. to enable edge axes, and enable a reference marker at world
position 50, 60, 100:
Double_t refPos[3]={50.0,60.0,100.0};
v->SetGuideState(TGLUtil::kAxesEdge, kTRUE, refPos);
9.13.2.8 Selecting Scene Shapes
You can select a single shape from your scene by pressing ‘Shift’ key, pointing and left clicking anywhere on the shape
in the viewer. Selection is currently shown by drawing the shape-bounding box (not depth clipped) in white (polygon
or wire frame render styles) or red (outline render style). Manipulators supported by the shape are drawn in red, green
and blue while the non-supported ones are drawn in grey. To deselect a shape, either select another, or shift/click
anywhere on the background (empty space) in the viewer. You cannot select Manipulators or Guides (Axes / Reference
Marker).
9.13.2.9 Editing Shapes
When a shape is selected, the viewer’s control pane shows the user interface that allows you to review and adjust the
color and geometry properties of the shape.
Note: At present modifications to the shapes are local to the viewer - they are not propagated back to external
objects/client that published to the viewer. The changes are preserved only until the viewer is closed. In some cases,
this will never be feasible as there is not a one-to-one correspondence between a shape in the viewer and a single
external object in which the modification could be stored.
9.13.2.10 Colors / Style
Viewer Controls Pane ‘Style’ tab.
A full description of OpenGL materials, colors and lighting is beyond the scope of this document. You should refer to
the OpenGL programming manual (Red Book) for a full discussion. In most cases adjustment of the Diffuse color
material + Opacity/Shine properties is sufficient to achieve desired results.
A shape has four-color materials (components):
•Diffuse
•Ambient
•Specular
•Emissive
For each of these you can select the component via the radio buttons. Each component can have the red, green and
blue values for the component adjusted via the sliders. You can apply this adjustment to the shape itself, or to all
shapes sharing a common ‘family’. Shapes of the same family have external objects with the same
TObject
name string.
You can also adjust the ‘Opacity’ and ‘Shine’ for the shapes materials via the sliders.
9.13.2.11 Geometry
Viewer Controls Pane ‘Geometry’ tab.
Review and modify the shapes X/Y/Z center and scaling factors via the edit boxes. Selection and editing of shapes is
not available via the API at present.
9.13.2.12 Outputting Viewer Contents
The current viewer rendering can be output to an external
EPS
or
PDF
, using the options under the ‘File’ menu on the
top menu bar. The file is named ‘viewer.eps’ or ‘viewer.pdf’ and written to the current ROOT directory.
9.13. 3D VIEWERS 235
9.13.3 The X3D Viewer
The X3D viewer is a fairly simple and limited viewer, capable of showing basic lines and polygons. It lacks the quality,
performance and more advanced features of the GL Viewer, and additionally is not supported on Windows. It is not
actively developed and you are encouraged to use the GL Viewer out of preference. The below table presents the main
interactions - these are repeated in the Help dialog of the viewer.
Action KeyActionKey
Wireframe Mode wRotate about xx a
Hidden Line Mode eRotate about yy b
Hidden Surface Mode rRotate about zz c
Move object down uAuto-rotate about x1 2 3
Move object up iAuto-rotate about y4 5 6
Move object left lAuto-rotate about z7 8 9
Move object right hToggle controls styleo
Move object forward jToggle stereo displays
Move object backward kToggle blue stereo viewd
Adjust focus (stereo mode) [ ] { }Toggle double bufferf
Rotate object Left mouse button down + move.
9.13.4 Common 3D Viewer Architecture
The 3D Viewer Architecture provides a common mechanism for viewer clients to publish 3D objects to it. It enables:
•
Decoupling of producers (geometry packages etc) who model collection of 3D objects from consumers (viewers)
which display them.
•Producer code free of explicit drawing commands & viewer specific branching.
•Support differing viewers and clients capabilities, e.g.
•Mix of native (in viewer) shapes and generic client side tessellation.
•Local/global frame object description
•Bounding boxes
•Placing copies sharing common geometry (logical/physical shapes).
The architecture consists of:
•TVirtualViewer3D
interface: An abstract handle to the viewer, allowing client to add objects, test preferences
etc.
•TBuffer3D
class hierarchy: Used to describe 3D objects (“shapes”) - filled /added by negotiation with viewer via
TVirtualViewer3D.
A typical interaction between viewer and client using these, taken from TGeoPainter is:
TVirtualViewer3D * viewer = gPad->GetViewer3D();
// Does viewer prefer local frame positions?
Bool_t localFrame = viewer->PreferLocalFrame();
// Perform first fetch of buffer from the shape and try adding it to the viewer
const TBuffer3D &buffer = shape.GetBuffer3D(TBuffer3D::kCore |
TBuffer3D::kBoundingBox |
TBuffer3D::kShapeSpecific,
localFrame);
Int_t reqSections = viewer->AddObject(buffer, &addDaughters);
236 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
// If the viewer requires additional sections fetch from the shape
// (if possible) and add again
if (reqSections != TBuffer3D::kNone)
shape.GetBuffer3D(reqSections, localFrame);
Together these allow clients to publish objects to any one of the 3D viewers free of viewer specific drawing code. They
allow our simple x3d viewer, and considerably more sophisticated OpenGL one to both work with both geometry
libraries (g3d and geom) efficiently.
In addition to external viewers, created in separate windows, this architecture is also used by internal
TPad
drawing
when it requires 3D projections. Publishing to a viewer consists of the following steps:
1- Create / obtain viewer handle.
2- Begin scene on viewer.
3- Fill mandatory parts of TBuffer3D describing object.
4- Add to viewer.
5- Fill optional parts of TBuffer3D as requested by viewer.
[ . . . . repeat 3/4/5 as required for other/child objects]
6- End scene on viewer.
You should attach the top-level node of your external geometry (or the manager) to a
TPad
object using
TObject::Draw(), and perform the publishing to the viewer in your object’s TObject::Paint() over-
loaded method. See “Scene Rebuilds”, and example scripts, for more details.
9.13.4.1 Creating / Obtaining Viewer Handle
External viewers are bound to a
TPad
object (this may be removed as a requirement in the future). You can create or
obtain the current viewer handle via the method:
TVirtualViewer3D * v = gPad->GetViewer3D("type");
Here the “type” string defines the viewer type - currently one of:
•“ogl” : External GL viewer
•“x3d”: External X3D viewer
•“pad”: Pad viewer
If no type is passed (null string), and there is no current viewer, then the type is defaulted to “
pad
”. If no type is passed
and there is a current viewer, then this is returned - hence once a viewer is created it can be obtained elsewhere by:
TVirtualViewer3D * v = gPad->GetViewer3D();
9.13.4.2 Opening / Closing Scenes
Objects must be added to viewer between BeginScene() and EndScene() calls e.g.
viewer->BeginScene();
// Add objects
viewer ->EndScene();
These calls enable the viewer to suspend redraws, and perform internal caching/setup. If the object you attach to the
pad derives from
TAtt3D
, then the pad will take responsibility for calling
BeginScene()
and
EndScene()
for you. You
can always test if the scene is already open for object addition with:
viewer->BuildingScene();
Note: the x3d viewer does not support rebuilding of scenes - objects added after the first Open/Close Scene pair will
be ignored.
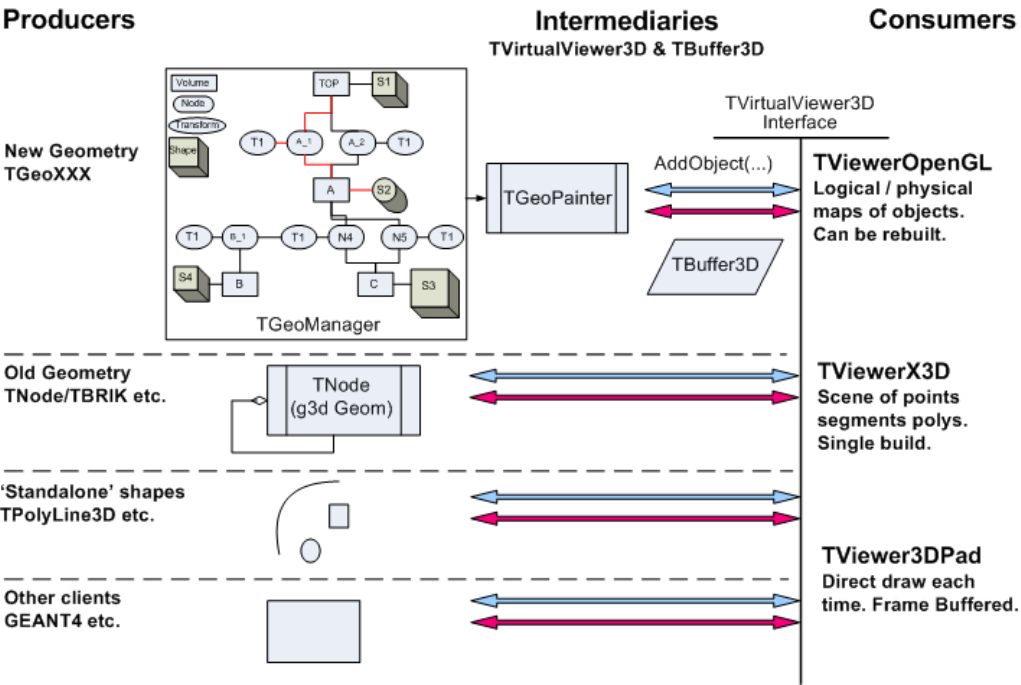
9.13. 3D VIEWERS 237
Figure 9.40: Overview of 3D viewer architecture
9.13.4.3 Describing Objects - Filling TBuffer3D
The viewers behind the TVirtualViewer3D interface differ greatly in their capabilities e.g.
•
Some support native shape (e.g. spheres/tubes in OpenGL) and can draw these based on an abstract description.
Others always require a tessellation description based on
TBuffer3D
’s
kRaw
/
kRawSizes
points/lines/segments
sections.
•
Some need the 3D object positions in the master (world) frame, others can cope with local frames and a translation
matrix to place the object.
•Some require bounding boxes for objects - others do not.
Similarly some viewer clients are only capable of providing positions in master frame, cannot provide bounding boxes
etc. Additionally we do not want to incur the cost of expensive tessellation operations if the viewer does not require
them. To cope with these variations the TBuffer3D objects are filled by negotiation with the viewer.
TBuffer3D
classes are conceptually divided into enumerated sections:
kCore
,
kBoundingBox
,
kRaw
- see the class
diagram and the file
TBuffer3D.h
for more details. The
TBuffer3D
methods
SectionsValid()
,
SetSectionsValid()
,
ClearSectionsValid() are used to test, set, clear these section validity flags e.g.
buffer.SetSectionsValid(TBuffer3D::kShapeSpecific);
...
if (buffer.SectionsValid(TBuffer3D:: kShapeSpecific)) {
...
}
The sections found in the base
TBuffer3D
(
kCore/kBoundingBox/kRawSizes/kRaw
) are sufficient to describe any
tessellated shape in a generic fashion. An additional
kShapeSpecific
section is added in
TBuffer3D
derived classes,
allowing a more abstract shape description (“a sphere of inner radius x, outer radius y”). This enables a viewer, which
knows how to draw (tessellate) the shape itself to do so, while providing a generic fallback suitable for all viewers. The
rules for client negotiation with the viewer are:
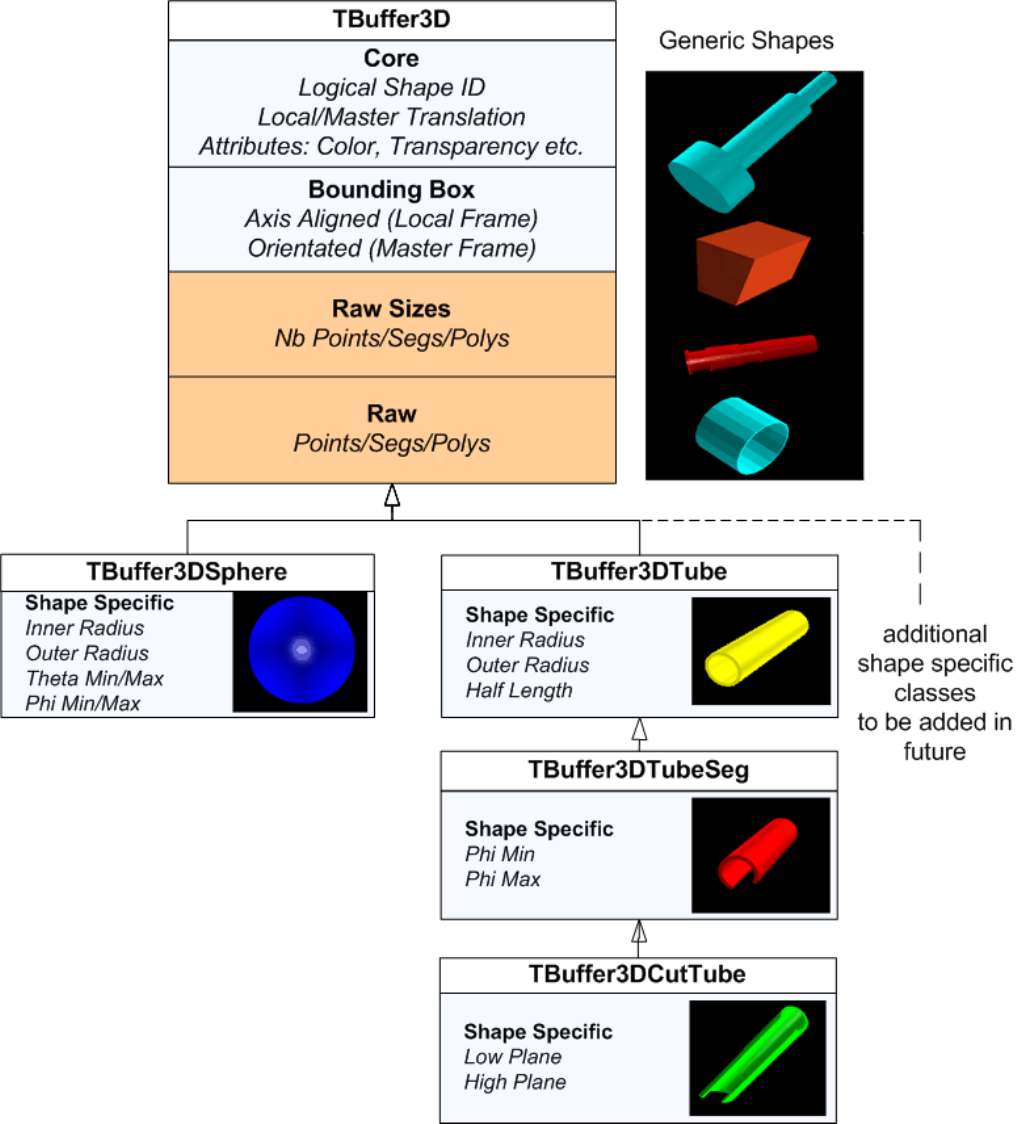
238 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
Figure 9.41: TBuffer3D class hierarchy
9.13. 3D VIEWERS 239
•If suitable specialized TBuffer3D class exists, use it, otherwise use TBuffer3D.
•Complete the mandatory kCore section.
•Complete the kShapeSpecific section if applicable.
•Complete the kBoundingBox if you can.
•Pass this buffer to the viewer using one of the TBuffer3D::AddObject() methods.
If the viewer requires more sections to be completed (
kRaw/kRawSizes
)
TBuffer3D::AddObject()
will return flags
indicating which ones, otherwise it returns
kNone
. If requested, you must fill the buffer, mark these sections valid, and
call
TBuffer3D::AddObject
again, to complete adding the object. For example, in out
TGeo
geometry package, in
TGeoPainter::PaintShape, we perform the negotiation with viewer:
TVirtualViewer3D * viewer = gPad->GetViewer3D();
if (shape.IsA() != TGeoCompositeShape::Class()) {
// Does viewer prefer local frame positions?
Bool_t localFrame = viewer->PreferLocalFrame();
// Perform first fetch of buffer from the shape and adding
// it to the viewer
const TBuffer3D &buffer = shape.GetBuffer3D(TBuffer3D::kCore |
TBuffer3D::kBoundingBox |
TBuffer3D::kShapeSpecific, localFrame);
Int_t reqSections = viewer->AddObject(buffer, &addDaughters);
// If the viewer requires additional sections fetch from the
// shape (if possible) and add again
if (reqSections != TBuffer3D::kNone) {
shape.GetBuffer3D(reqSections, localFrame);
viewer->AddObject(buffer, &addDaughters);
}
}
The buffer is supplied/filled by the appropriate
TShape::GetBuffer3D()
and
TShape::FillBuffer3D overloads
e.g. for a sphere in TGeoSphere.
const TBuffer3D &TGeoSphere::GetBuffer3D(Int_t reqSections,
Bool_t localFrame) const {
// Fills a static 3D buffer and returns a reference.
static TBuffer3DSphere buffer;
// Filling of kBoundingBox is defered to TGeoBBox, and
// kCore on up to TGeoShape
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
// Complete kShapeSpecific section for sphere
if (reqSections & TBuffer3D::kShapeSpecific) {
buffer.fRadiusInner = fRmin;
buffer.fRadiusOuter = fRmax;
...
buffer.SetSectionsValid(TBuffer3D::kShapeSpecific);
}
// Complete kRawSizes section
if (reqSections & TBuffer3D::kRawSizes) {
...
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
// Complete kRaw tesselation section
if ((reqSections & TBuffer3D::kRaw) &&
buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
// Transform points to master frame if viewer requires it
// The fLocalFrame flag and translation matrix will have
// already been set in TGeoShape::FillBuffer3D() as required
240 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
if (!buffer.fLocalFrame)
TransformPoints(buffer.fPnts, buffer.NbPnts());
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}
Note:
•we use a static TBuffer3D derived object for efficiency - once the object is added the buffer can be reused.
•kRawSize
(the calculation of tessellation sizing required in buffer) and
kRaw
(the actual filling of tessellation) is
split, as the X3D viewer requires two publication passes - one to establish the full tessellation capacity for all
shapes, and another to actually add them. Splitting avoids having to do the expensive tessellation on the first
pass.
9.13.4.4 Shape Specific TBuffer3D Derived Classes
Currently we provide the following shape specific classes, which the GL Viewer can take advantage of (see
TBuffer3D.h
and TBuffer3DTypes.h)
•TBuffer3DSphere
- solid, hollow and cut spheres (GL Viewer only supports solid spheres at present - cut / hollow
ones will be requested as tessellated objects by client.)
•TBuffer3DTube - basic tube with inner/outer radius and length.
•TBuffer3DTubeSeg - angle tube segment.
•TBuffer3DCutTube - angle tube segment with plane cut ends.
See the above example from
TGeoSphere::GetBuffer3D
and also equivalent functions in
TGeoTube
,
TGeoTubeSeg
and
TGeoCtub
. Anyone is free to add new
TBuffer3D
classes, but it should be clear that one or more viewers will require
updating to be able to take advantage of them. Hence we only provide classes which existing viewers can benefit from.
The number of native shapes in GL Viewer will be expanded in the future.
9.13.4.5 Master / Local Reference Frames
The Core section of TBuffer3D contains two members relating to reference frames:
•fLocalFrame
: indicates if any positions in the buffer (bounding box and tessellation vertexes) are in local or
master (world frame).
•fLocalMaster
: is a standard 4x4 translation matrix (OpenGL column major ordering) for placing the object
into the 3D master frame.
If
fLocalFrame
is false,
fLocalMaster
should contain an identity matrix. This is set by default, and can be reset
using the TBuffer3D::SetLocalMasterIdentity() method.
9.13.4.6 Bounding Boxes
You are not obliged to complete the
kBoundingBox
section, as any viewer requiring one internally (GL Viewer) will
build it if you do not provide. However to do this the viewer will force you to provide the (expensive) raw tessellation,
and the resulting box will be axis aligned with the overall scene, which is non-ideal for rotated shapes. As we need
to support orientated (rotated) bounding boxes,
TBuffer3D
requires the 6 vertices of the box. We also provide a
convenience function,
TBuffer::SetAABoundingBox()
, for simpler case of setting an axis aligned bounding box. The
bounding box should be filled in same frame (local / master) as the rest of the
TBuffer3D
, and inaccordance with
fLocalFrame flag.
A typical example from TGeoBBox::FillBuffer3D:
9.13. 3D VIEWERS 241
if (reqSections & TBuffer3D::kBoundingBox) {
Double_t halfLengths[3] = { fDX, fDY, fDZ };
buffer.SetAABoundingBox(fOrigin, halfLengths);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fBBVertex[0], 8);
}
buffer.SetSectionsValid(TBuffer3D::kBoundingBox);
}
9.13.4.7 Logical and Physical Objects
Some viewers can support two types of object placement:
•Add object as a single independent entity in the world reference frame - e.g. a sphere, radius r, at x,y,z.
•
Repeated placement (copying) in world frame of this locally unique piece of geometry (described in local reference
frame) e.g. define a sphere S(radius r), place copy at x1,y1,z1, another copy at x2,y2,z2 etc.
The second case is very typical in geometry packages, e.g. ROOT’s
TGeo
package, GEANT4 etc, where we have very
large number repeated placements of relatively few unique “shapes”.
Some viewers (GL Viewer only at present) are able to take advantage of this by identifying unique logical shapes from
the
fID
logical ID member of
TBuffer3D
. If repeated addition of the same
fID
is found, the shape is cached already -
and the costly tessellation does not need to be sent again. The viewer can also perform internal GL specific caching
(display lists) with considerable performance gains in these cases. For this to work correctly the logical object in must
be described in
TBuffer3D
in the local reference frame, complete with the local
/
master translation. In some cases you
will not have a real object you can reasonably set
TBuffer3D::fID to, or the object is recycled or temporary.
To suppress internal caching in the GL Viewer in these cases, set TBuffer3D::fID to 0 (null).
The viewer indicates it can support local frame objects through the
TVirtualViewer3D
interface method:
PreferLocalFrame()
. If this returns
kTRUE
you can make repeated calls to
AddObject()
, with
TBuffer3D
containing
the same fID, and different fLocalMaster placements.
For viewers supporting logical/physical objects, the TBuffer3D content refers to the properties of the logical object,
with the exception of:
•fLocalMaster transform
•fColor
•fTransparency
attributes, which can be varied for each physical object.
As
a minimum requirement
all clients must be capable of filling the raw tessellation of the object buffer, in the
master reference frame. Conversely viewers must always be capable of displaying the object described by this buffer. If
either does not meet this requirement the object may not be displayed.
9.13.4.8 Scene Rebuilds
TBuffer3D::AddObject is not an explicit command to the viewer - it may for various reasons decide to ignore it:
•It already has the object internally cached.
•The object falls outside some ‘interest’ limits of the viewer camera.
•The object is too small to be worth drawing.
In all these cases
TBuffer3D::AddObject()
returns kNone, as it does for successful addition, indicating it does not
require further information about this object. Hence you should not try to make any assumptions about what the
viewer did with the object. The viewer may decide to force the client to rebuild (republish) the scene, obtaining a
different collection of objects, if the internal viewer state changes .e.g. significant camera move. It does this presently
by forcing a repaint on the attached
TPad
object - hence you should attach you master geometry object to the pad (via
TObject::Draw()), and perform the publishing to the viewer in response to TObject::Paint().
242 CHAPTER 9. GRAPHICS AND THE GRAPHICAL USER INTERFACE
9.13.4.9 Physical IDs
TVirtualViewer3D provides for two methods of object addition:
virtual Int_t AddObject(const TBuffer3D &buffer,
Bool_t * addChildren = 0)
virtual Int_t AddObject(UInt_t physicalID,
const TBuffer3D & buffer,
Bool_t *addChildren = 0)
If you use the first (simple) case a viewer using logical/physical pairs will generate sequential IDs for each physical
object internally. Scene rebuilds will require destruction and recreation of all physical objects. For the second you
can specify an identifier from the client side, which must be unique and stable - i.e. the IDs of a published object is
consistent, regardless of changes in termination of contained child geometry branches. In this case the viewer can safely
cache the physical objects across scene rebuilds, discarding those no longer of interest.
9.13.4.10 Child Objects
In many geometries there is a rigid containment hierarchy, and so if the viewer is not interested in a certain object due
to limits/size then it will also not be interest in any of the contained branch of siblings. Both
TBuffer3D::AddObject()
methods have an
addChildren
return parameter. The viewer will complete this (if passed) indicating if children of the
object just sent are worth sending.
9.13.4.11 Recycling TBuffer3D
Once add TBuffer3D::AddObject() has been called, the contents are copied to the viewer’s internal data structures.
You are free to destroy this TBuffer3D, or recycle it for the next object if suitable.
9.13.4.12 Examples
For an example of a simple geometry, working in master reference frame examine the code under $ROOTSYS/g3d. For
a more complex example, which works in both master and local frames, and uses logical
/
physical division of shape
geometry and placement, examine the code under
$ROOTSYS/geom
- in particular
TGeoShape
hierarchy, and the painter
object TGeoPainter (under geopainter) where the negotiation with the viewer is performed.
Chapter 10
Folders and Tasks
10.1 Folders
A
TFolder
is a collection of objects visible and expandable in the ROOT object browser. Folders have a name and a
title and are identified in the folder hierarchy by an “UNIX-like” naming convention. The base of all folders is
//root
.
It is visible at the top of the left panel in the browser. The browser shows several folders under //root.
New folders can be added and removed to/from a folder.
10.2 Why Use Folders?
One reason to use folders is to reduce class dependencies and improve modularity. Each set of data has a producer
class and one or many consumer classes. When using folders, the producer class places a pointer to the data into a
folder, and the consumer class retrieves a reference to the folder.
The consumer can access the objects in a folder by specifying the path name of the folder.
Here is an example of a folder’s path name:
//root/Event/Hits/TCP
One does not have to specify the full path name. If the partial path name is unique, it will find it; otherwise it will
return the first occurrence of the path.
The first diagram shows a system without folders. The objects have pointers to each other to access each other’s data.
Pointers are an efficient way to share data between classes. However, a direct pointer creates a direct coupling between
classes. This design can become a very tangled web of dependencies in a system with a large number of classes.
In the second diagram, a reference to the data is in the folder and the consumers refer to the folder rather than
each other to access the data. The naming and search service provided by the ROOT folders hierarchy provides an
alternative. It loosely couples the classes and greatly enhances I/O operations. In this way, folders separate the data
from the algorithms and greatly improve the modularity of an application by minimizing the class dependencies.
In addition, the folder hierarchy creates a picture of the data organization. This is useful when discussing data design
issues or when learning the data organization. The example below illustrates this point.
10.3 How to Use Folders
Using folders means to build a hierarchy of folders, posting the reference to the data in the folder by the producer, and
creating a reference to the folder by the user.
10.3.1 Creating a Folder Hierarchy
To create a folder hierarchy you add the top folder of your hierarchy to
//root
. Then you add a folder to an existing
folder with the
TFolder::AddFolder
method. This method takes two parameters: the name and title of the folder to
be added. It returns a pointer of the newly created folder.
The code below creates the folder hierarchy shown in the browser. In this macro, the folder is also added to the list of
browsable. This way, it is visible in the browser on the top level.
243
244 CHAPTER 10. FOLDERS AND TASKS
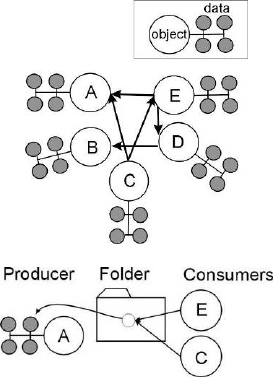
10.3. HOW TO USE FOLDERS 245
{
// Add the top folder of my hierary to //root
TFolder *aliroot=gROOT->GetRootFolder()->AddFolder("aliroot",
"aliroot top level folders");
// Add the hierarchy to the list of browsables
gROOT->GetListOfBrowsables()->Add(aliroot,"aliroot");
// Create and add the constants folder
TFolder *constants=aliroot->AddFolder("Constants",
"Detector constants");
// Create and add the pdg folder to pdg
TFolder *pdg = constants->AddFolder("DatabasePDG","PDG database");
// Create and add the run folder
TFolder *run = aliroot->AddFolder("Run","Run dependent folders");
// Create and add the configuration folder to run
TFolder *configuration = run->AddFolder("Configuration",
"Run configuration");
// Create and add the run_mc folder
TFolder *run_mc = aliroot->AddFolder("RunMC",
"MonteCarlo run dependent folders");
// Create and add the configuration_mc folder to run_mc
TFolder *configuration_mc = run_mc->AddFolder("Configuration",
"MonteCarlo run configuration");
}
10.3.2 Posting Data to a Folder (Producer)
A
TFolder
can contain other folders as shown above or any
TObject
descendents. In general, users will not post a
single object to a folder; they will store a collection or multiple collections in a folder. For example, to add an array to
a folder:
TObjArray *array;
run_mc->Add(array);
10.3.3 Reading Data from a Folder (Consumer)
One can search for a folder or an object in a folder using the
TROOT::FindObjectAny
method. It analyzes the string
passed as its argument and searches in the hierarchy until it finds an object or folder matching the name. With
FindObjectAny
, you can give the full path name, or the name of the folder. If only the name of the folder is given, it
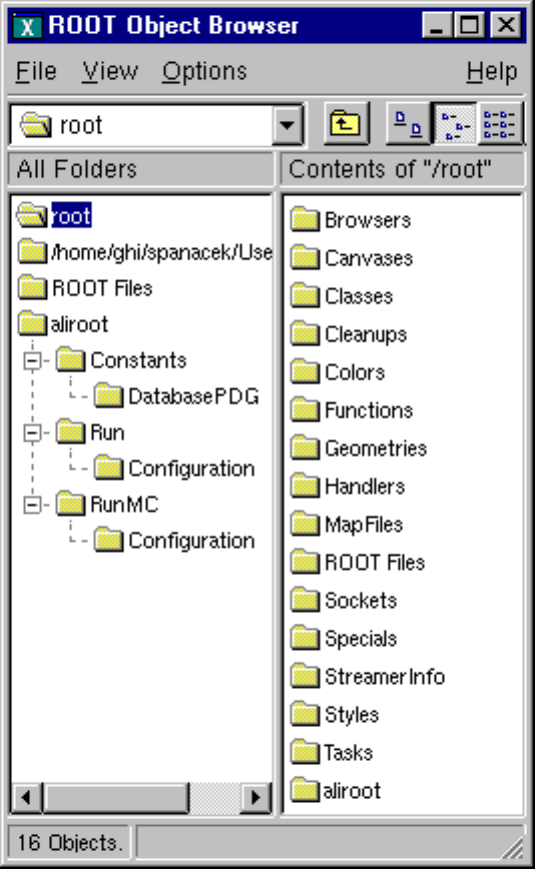
246 CHAPTER 10. FOLDERS AND TASKS
10.4. TASKS 247
will return the first instance of that name. A string-based search is time consuming. If the retrieved object is used
frequently or inside a loop, you should save a pointer to the object as a class data member. Use the naming service
only in the initialization of the consumer class. When a folder is deleted, any reference to it in the parent or other
folder is deleted also.
conf=(TFolder*)gROOT->FindObjectAny("/aliroot/Run/Configuration");
// or ...
conf=(TFolder*)gROOT->FindObjectAny("Configuration");
By default, a folder does not own the object it contains. You can overwrite that with
TFolder::SetOwner
. Once
the folder is the owner of its contents, the contents are deleted when the folder is deleted. Some ROOT objects are
automatically added to the folder hierarchy. For example, the following folders exist on start up:
//root/ROOT Files with the list of open Root files
//root/Classes with the list of active classes
//root/Geometries with active geometries
//root/Canvases with the list of active canvases
//root/Styles with the list of graphics styles
//root/Colors with the list of active colors
For example, if a file
myFile.root
is added to the list of files, one can retrieve a pointer to the corresponding
TFile
object with a statement like:
TFile *myFile = (TFile*)gROOT->FindObjectAny(
"/ROOTFiles/myFile.root");
//or...
TFile *myFile = (TFile*)gROOT->FindObjectAny("myFile.root");
10.4 Tasks
Tasks can be organized into a hierarchy and displayed in the browser. The
TTask
class is the base class from which
the tasks are derived. To give task functionality, you need to subclass the TTask class and override the Exec method.
An example of
TTask
subclasses
is $ROOTSYS/tutorials/MyTasks.cxx
. The script that creates a task hierarchy and
adds it to the browser is $
ROOTSYS/tutorials/tasks.C
. Here is a part of
MyTasks.cxx
that shows how to subclass
from TTask.
// A set of classes deriving from TTask see macro tasks.C. The Exec
// function of each class prints one line when it is called.
#include "TTask.h"
class MyRun : public TTask {
public:
MyRun() { ; }
MyRun(const char *name,const char *title);
virtual ~MyRun() { ; }
void Exec(Option_t *option="");
ClassDef(MyRun,1)// Run Reconstruction task
};
class MyEvent : public TTask {
public:
MyEvent() { ; }
MyEvent(const char *name,const char *title);
virtual ~MyEvent() { ; }
void Exec(Option_t *option="");
ClassDef(MyEvent,1)// Event Reconstruction task
};
Later in MyTasks.cxx, we can see examples of the constructor and overridden Exec() method:
248 CHAPTER 10. FOLDERS AND TASKS
ClassImp(MyRun)
MyRun::MyRun(const char *name,const char *title):TTask(name,title)
{
...
}
void MyRun::Exec(Option_t *option)
{
printf("MyRun executingn");
}
Each
TTask
derived class may contain other
TTasks
that can be executed recursively. In this way, a complex program
can be dynamically built and executed by invoking the services of the top level task or one of its subtasks. The
constructor of
TTask
has two arguments: the name and the title. This script creates the task defined above, and
creates a hierarchy of tasks.
// Show the tasks in a browser. To execute a Task, select
// "ExecuteTask" in the context menu see also other functions in the
// TTask context menu, such as:
// -setting a breakpoint in one or more tasks
// -enabling/disabling one task, etc
void tasks() {
gROOT->ProcessLine(".L MyTasks.cxx+");
TTask *run = new MyRun("run","Process one run");
TTask *event = new MyEvent("event","Process one event");
TTask *geomInit = new MyGeomInit("geomInit",
"Geometry Initialisation");
TTask *matInit = new MyMaterialInit("matInit",
"MaterialsInitialisation");
TTask *tracker = new MyTracker("tracker","Tracker manager");
TTask *tpc = new MyRecTPC("tpc","TPC Reconstruction");
TTask *its = new MyRecITS("its","ITS Reconstruction");
TTask *muon = new MyRecMUON("muon","MUON Reconstruction");
TTask *phos = new MyRecPHOS("phos","PHOS Reconstruction");
TTask *rich = new MyRecRICH("rich","RICH Reconstruction");
TTask *trd = new MyRecTRD("trd","TRD Reconstruction");
TTask *global = new MyRecGlobal("global","Global Reconstruction");
// Create a hierarchy by adding sub tasks
run->Add(geomInit);
run->Add(matInit);
run->Add(event);
event->Add(tracker);
event->Add(global);
tracker->Add(tpc);
tracker->Add(its);
tracker->Add(muon);
tracker->Add(phos);
tracker->Add(rich);
tracker->Add(trd);
// Add the top level task
gROOT->GetListOfTasks()->Add(run);
// Add the task to the browser
gROOT->GetListOfBrowsables()->Add(run);
new TBrowser;
}
Note that the first line loads the class definitions in
MyTasks.cxx
with ACLiC. ACLiC builds a shared library and
adds the classes to the Cling dictionary. See “Adding a Class with ACLiC”.
To execute a TTask, you call the ExecuteTask method. ExecuteTask will recursively call:
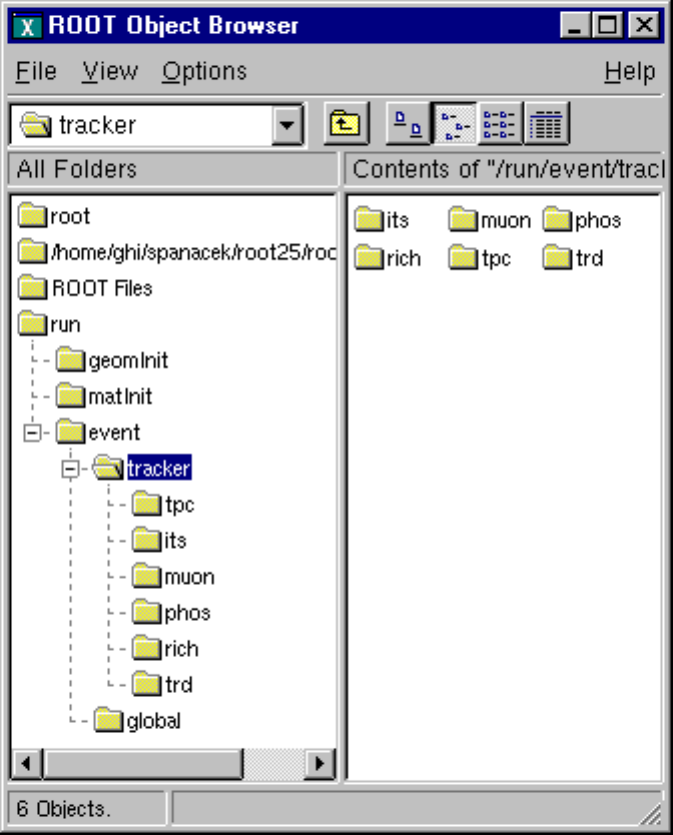
10.4. TASKS 249
Figure 10.1: Tasks in the ROOT browser
250 CHAPTER 10. FOLDERS AND TASKS
•the TTask::Execmethod of the derived class;
•the TTask::ExecuteTasks to execute for each task the list of its subtasks;
If the top level task is added to the list of ROOT browseable objects, the tree of tasks can be seen in the ROOT
browser. To add it to the browser, get the list of browseable objects first and add it to the collection.
gROOT->GetListOfBrowsables()->Add(run);
The first parameter of the
Add
method is a pointer to a
TTask
, the second parameter is the string to show in the
browser. If the string is left out, the name of the task is used.
After executing, the script above the browser will look like in this figure.
10.5 Execute and Debug Tasks
The browser can be used to start a task, set break points at the beginning of a task or when the task has completed.
At a breakpoint, data structures generated by the execution up this point may be inspected asynchronously and then
the execution can be resumed by selecting the “Continue” function of a task.
A task may be active or inactive (controlled by
TTask::SetActive
). When a task is inactive, its sub tasks are not
executed. A task tree may be made persistent, saving the status of all the tasks.
Chapter 11
Input/Output
This chapter covers the saving and reading of objects to and from ROOT files. It begins with an explanation of the
physical layout of a ROOT file. It includes a discussion on compression, and file recovery. Then we explain the logical
file, the class
TFile
and its methods. We show how to navigate in a file, how to save objects and read them back. We
also include a discussion on
Streamers
.
Streamers
are the methods responsible to capture an objects current state to
save it to disk or send it over the network. At the end of the chapter is a discussion on the two specialized ROOT files:
TNetFile and TWebFile.
11.1 The Physical Layout of ROOT Files
A ROOT file is like a UNIX file directory. It can contain directories and objects organized in unlimited number of
levels. It also is stored in machine independent format (ASCII, IEEE floating point, Big Endian byte ordering). To
look at the physical layout of a ROOT file, we first create one. This example creates a ROOT file and 15 histograms,
fills each histogram with 1000 entries from a Gaussian distribution, and writes them to the file.
{
char name[10], title[20];
TObjArray Hlist(0); // create an array of Histograms
TH1F* h; // create a pointer to a histogram
// make and fill 15 histograms and add them to the object array
for (Int_t i = 0;i<15; i++) {
sprintf(name,"h%d",i);
sprintf(title,"histo nr:%d",i);
h = new TH1F(name,title,100,-4,4);
Hlist.Add(h);
h->FillRandom("gaus",1000);
}
// open a file and write the array to the file
TFile f("demo.root","recreate");
Hlist.Write();
f.Close();
}
The example begins with a call to the
TFile
constructor. This class is describing the ROOT file (that has the extension
“
.root
”). In the next section, we will cover
TFile
in details. The last line of the example closes the file. To view its
contents we need to open it again, and to create a TBrowser object by:
root[] TFile f("demo.root")
root[] TBrowser browser;
You can check if the file is correctly opened by:
TFile f("demo.root");
if (f.IsZombie()) {
cout << "Error opening file" << endl;
251
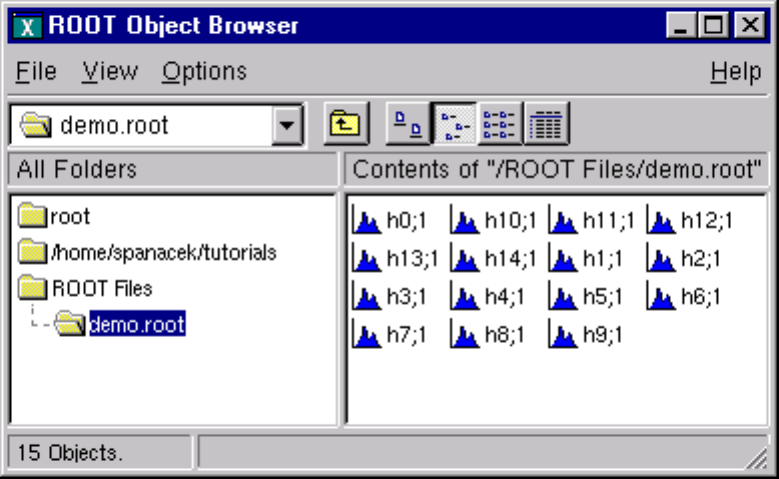
252 CHAPTER 11. INPUT/OUTPUT
Figure 11.1: The browser with 15 created histograms
exit(-1);
}else {
...
}
Once we have the
TFile
object, we can call the
TFile::Map()
method to view the physical layout. The output prints
the date/time, the start record address, the number of bytes in the record, the class name of the record and the
compression factor.
root[] f.Map()
20051208/124502 At:100 N=114 TFile
20051208/124502 At:214 N=413 TH1F CX = 2.35
20051208/124502 At:627 N=410 TH1F CX = 2.36
20051208/124502 At:1037 N=396 TH1F CX = 2.45
20051208/124502 At:1433 N=400 TH1F CX = 2.42
20051208/124502 At:1833 N=402 TH1F CX = 2.41
20051208/124502 At:2235 N=416 TH1F CX = 2.33
20051208/124502 At:2651 N=406 TH1F CX = 2.39
20051208/124502 At:3057 N=403 TH1F CX = 2.40
20051208/124502 At:3460 N=411 TH1F CX = 2.36
20051208/124502 At:3871 N=400 TH1F CX = 2.42
20051208/124502 At:4271 N=409 TH1F CX = 2.38
20051208/124502 At:4680 N=409 TH1F CX = 2.38
20051208/124502 At:5089 N=420 TH1F CX = 2.32
20051208/124502 At:5509 N=406 TH1F CX = 2.40
20051208/124502 At:5915 N=405 TH1F CX = 2.40
20051208/124503 At:6320 N=3052 StreamerInfo CX = 3.16
20051208/124503 At:9372 N=732 KeysList
20051208/124503 At:10104 N=53 FreeSegments
20051208/124503 At:10157 N=1END
Here we see the fifteen histograms (
TH1F
’s) with the first one starting at byte 148. We also see an entry
TFile
. You
may notice that the first entry starts at byte 100. The first 100 bytes are taken by the file header.
11.1.1 The File Header
This table shows the file header information. When fVersion is greater than 1000000, the file is a large file (> 2 GB)
and the offsets will be 8 bytes long. The location in brackets are the location in the case of a large file.
11.1. THE PHYSICAL LAYOUT OF ROOT FILES 253
Byte Value Name Description
1-> 4 “root” Root file identifier
5-> 8fVersion File format version
9-> 12 fBEGIN Pointer to first data record
13 -> 16 [13->20] fEND Pointer to first free word at the EOF
17 -> 20 [21->28] fSeekFree Pointer to FREE data record
21 -> 24 [29->32] fNbytesFree Number of bytes in FREE data record
25 -> 28 [33->36] nfree Number of free data records
29 -> 32 [37->40] fNbytesName Number of bytes in TNamed at creation time
33 -> 33 [41->41] fUnits Number of bytes for file pointers
34 -> 37 [42->45] fCompress Zip compression level
34 -> 37 [46->53] fSeekInfo Pointer to TStreamerInfo record
34 -> 37 [54->57] fNBytesInfo Number of bytes in TStreamerInfo record
34 -> 37 [58->75] fCompress Universal Unique ID
The first four bytes of the file header contain the string “root” which identifies a file as a ROOT file. Because of this
identifier, ROOT is not dependent on the “
.root
” extension. It is still a good idea to use the extension, just for us
to recognize them easier. The
nfree
and value is the number of free records. This variable along with
FNBytesFree
keeps track of the free space in terms of records and bytes. This count also includes the deleted records, which are
available again.
11.1.2 The Top Directory Description
The 84 bytes after the file header contain the top directory description, including the name, the date and time it was
created, and the date and time of the last modification.
20010404/092347 At:64 N=84 TFile
11.1.3 The Histogram Records
What follows are the 15 histograms, in records of variable length.
20010404/092347 At:148 N=380 TH1F CX = 2.49
20010404/092347 At:528 N=377 TH1F CX = 2.51
The first 4 bytes of each record is an integer holding the number of bytes in this record. A negative number flags the
record as deleted, and makes the space available for recycling in the next writing. The rest of bytes in the header
contain all the information to identify uniquely a data block on the file. It is followed by the object data.
The next table explains the values in each individual record. If the key is located past the 32 bit file limit (> 2 GB)
then some fields will be 8 bytes instead of 4 bytes (values between the brackets):
Byte Value Name Description
1-> 4Nbytes Length of compressed object (in bytes)
5-> 6Version TKey version identifier
7-> 10 ObjLen Length of uncompressed object
11 -> 14 Datime Date and time when object was written to file
15 -> 16 KeyLen Length of the key structure (in bytes)
17 -> 18 Cycle Cycle of key
19 -> 22 [19->26] SeekKey Pointer to record itself (consistency check)
23 -> 26 [27->34] SeekPdir Pointer to directory header
27 -> 27 [35->35] lname Number of bytes in the class name
28 -> . . . [36->.. .] | ClassName | Object Class Name
. . . -> . . . | lname | Number of bytes in the object name
. . . -> . . . | Name |lName bytes with the name of the object
. . . -> . . . | lTitle | Number of bytes in the object title
. . . -> . . . | Title | Title of the object
. . . -> . . . | DATA | Data bytes associated to the object
You see a reference to TKey. It is explained in detail in the next section.
254 CHAPTER 11. INPUT/OUTPUT
11.1.4 The Class Description List (StreamerInfo List)
The histogram records are followed by the
StreamerInfo
list of class descriptions. The list contains the description of
each class that has been written to file.
20010404/092347 At:5854 N=2390 StreamerInfo CX = 3.41
The class description is recursive, because to fully describe a class, its ancestors and object data members have to be
described also. In demo.root, the class description list contains the description for:
•TH1F
•all classes in the TH1F inheritance tree
•all classes of the object data members
•all classes in the object data members’ inheritance tree.
This description is implemented by the
TStreamerInfo
class
,
and is often referred to as simply
StreamerInfo
. You
can print a file’s
StreamerInfo
list with the
TFile::ShowStreamerInfo
method. Below is an example of the output.
Only the first line of each class description is shown. The
demo.root
example contains only
TH1F
objects. Here we see
the recursive nature of the class description; it contains the StreamerInfoof all the classes needed to describe TH1F.
root[] f.ShowStreamerInfo()
StreamerInfo for class: TH1F, version=1
BASE TH1 offset=0type= 0 1-Dim histogram base class
BASE TArrayF offset=0type= 0Array of floats
StreamerInfo for class: TH1, version=3
BASE TNamed offset=0type=67 The basis for named object(name,title)
BASE TAttLine offset=0type=0Line attributes
BASE TAttFill offset=0type=0Fill area attributes
BASE TAttMarker offset=0type=0Marker attributes
Int_t fNcells offset=0type=3number bins(1D),cells(2D)+U/Overflows
TAxis fXaxis offset=0type=61 X axis descriptor
TAxis fYaxis offset=0type=61 Y axis descriptor
TAxis fZaxis offset=0type=61 Z axis descriptor
Short_t fBarOffset offset=0type=2(1000*offset) for barcharts or legos
Short_t fBarWidth offset=0type=2(1000*width) for bar charts or legos
Stat_t fEntries offset=0type=8Number of entries//continued...
Stat_t fTsumw offset=0type=8Total Sum of weights
Stat_t fTsumw2 offset=0type=8Total Sum of squares of weights
Stat_t fTsumwx offset=0type=8Total Sum of weight*X
Stat_t fTsumwx2 offset=0type=8Total Sum of weight*X*X
Double_t fMaximum offset=0type=8Maximum value for plotting
Double_t fMinimum offset=0type=8Minimum value for plotting
Double_t fNormFactor offset=0type=8Normalization factor
TArrayD fContour offset=0type=62 Array to display contour levels
TArrayD fSumw2 offset=0type=62 Array of sum of squares of weights
TString fOption offset=0type=65 histogram options
TList* fFunctions offset=0type=63 ->Pointer to list of functions(fits,user)
StreamerInfo for class: TNamed, version=1
...
StreamerInfo for class: TAttLine, version=1
...
StreamerInfo for class: TAttFill, version=1
...
StreamerInfo for class: TAttMarker, version=1
...
StreamerInfo for class: TArrayF, version=1
...
StreamerInfo for class: TArray, version=1
11.2. THE LOGICAL ROOT FILE: TFILE AND TKEY 255
...
StreamerInfo for class: TAxis, version=6
...
StreamerInfo for class: TAttAxis, version=4
...
ROOT allows a class to have multiple versions, and each version has its own description in form of a
StreamerInfo
.
Above you see the class name and version number. The
StreamerInfo
list has only one description for each class/version
combination it encountered. The file can have multiple versions of the same class, for example objects of old and new
versions of a class can be in the same file. The StreamerInfois described in detail in the section on Streamers.
11.1.5 The List of Keys and the List of Free Blocks
The last three entries on the output of
TFile::Map()
are the list of keys, the list of free segments, and the address
where the data ends.. When a file is closed, it writes a linked list of keys at the end of the file. This is what we see in
the third to the last entry. In our example, the list of keys is stored in 732 bytes beginning at byte# 8244.
20010404/092347 At:8244 N=732 KeysList
20010404/092347 At:8976 N=53 FreeSegments
20010404/092347 At:9029 N=1END
The second to last entry is a list of free segments. In our case, this starts 8976 and is not very long, only 53 bytes,
since we have not deleted any objects. The last entry is the address of the last byte in the file.
11.1.6 File Recovery
A file may become corrupted or it may be impossible to write it to disk and close it properly. For example if the file
is too large and exceeds the disk quota, or the job crashes or a batch job reaches its time limit before the file can
be closed. In these cases, it is imperative to recover and retain as much information as possible. ROOT provides an
intelligent and elegant file recovery mechanism using the redundant directory information in the record header.
If a file that has been not properly closed is opened again, it is scanned and rebuilt according to the information in
the record header. The recovery algorithm reads the file and creates the saved objects in memory according to the
header information. It then rebuilds the directory and file structure. If the file is opened in write mode, the recovery
makes the correction on disk when the file is closed; however if the file is opened in read mode, the correction can not
be written to disk. You can also explicitly invoke the recovery procedure by calling the
TFile::Recover()
method.
You can recover the directory structure, but you cannot save what you recovered to the file on disk. In the following
example, we interrupted and aborted the previous ROOT session, causing the file not to be closed. When we start a
new session and attempt to open the file, it gives us an explanation and status on the recovery attempt.
root[] TFile f("demo.root")
Warning in <TFile::TFile>: file demo.root probably not closed, trying to recover successfully recovered 15 keys
11.2 The Logical ROOT File: TFile and TKey
We saw that the
TFile::Map()
method reads the file sequentially and prints information about each record while
scanning the file. It is not feasible to support only sequential access and hence ROOT provides random or direct access,
i.e. reading a specified object at a time. To do so,
TFile
keeps a list of
TKeys
, which is essentially an index to the
objects in the file. The
TKey
class describes the record headers of objects in the file. For example, we can get the list of
keys and print them. To find a specific object on the file we can use the TFile::Get() method.
root[] TFile f("demo.root")
root[] f.GetListOfKeys()->Print()
TKey Name = h0, Title = histo nr:0, Cycle = 1
TKey Name = h1, Title = histo nr:1, Cycle = 1
TKey Name = h2, Title = histo nr:2, Cycle = 1
TKey Name = h3, Title = histo nr:3, Cycle = 1
TKey Name = h4, Title = histo nr:4, Cycle = 1
TKey Name = h5, Title = histo nr:5, Cycle = 1
256 CHAPTER 11. INPUT/OUTPUT
TKey Name = h6, Title = histo nr:6, Cycle = 1
TKey Name = h7, Title = histo nr:7, Cycle = 1
TKey Name = h8, Title = histo nr:8, Cycle = 1
TKey Name = h9, Title = histo nr:9, Cycle = 1
TKey Name = h10, Title = histo nr:10, Cycle = 1
TKey Name = h11, Title = histo nr:11, Cycle = 1
TKey Name = h12, Title = histo nr:12, Cycle = 1
TKey Name = h13, Title = histo nr:13, Cycle = 1
TKey Name = h14, Title = histo nr:14, Cycle = 1
root[] TH1F *h9 = (TH1F*)f.Get("h9");
The
TFile::Get()
finds the
TKey
object with name “
h9
”. Using the
TKey
info it will import in memory the object in
the file at the file address #3352 (see the output from the
TFile::Map
above). This is done by the
Streamer
method
that is covered in detail in a later section. Since the keys are available in a
TList
of
TKeys we can iterate over the
list of keys:
{
TFile f("demo.root");
TIter next(f.GetListOfKeys());
TKey *key;
while ((key=(TKey*)next())) {
printf("key: %s points to an object of class: %s at %dn",
key->GetName(),
key->GetClassName(),key->GetSeekKey());
}
}
The output of this script is:
root[] .x iterate.C
key: h0 points to an object of class: TH1F at 150
key: h1 points to an object of class: TH1F at 503
key: h2 points to an object of class: TH1F at 854
key: h3 points to an object of class: TH1F at 1194
key: h4 points to an object of class: TH1F at 1539
key: h5 points to an object of class: TH1F at 1882
key: h6 points to an object of class: TH1F at 2240
key: h7 points to an object of class: TH1F at 2582
key: h8 points to an object of class: TH1F at 2937
key: h9 points to an object of class: TH1F at 3293
key: h10 points to an object of class: TH1F at 3639
key: h11 points to an object of class: TH1F at 3986
key: h12 points to an object of class: TH1F at 4339
key: h13 points to an object of class: TH1F at 4694
key: h14 points to an object of class: TH1F at 5038
In addition to the list of keys,
TFile
also keeps two other lists:
TFile::fFree
is a
TList
of free blocks used to recycle
freed up space in the file. ROOT tries to find the best free block. If a free block matches the size of the new object to
be stored, the object is written in the free block and this free block is deleted from the list. If not, the first free block
bigger than the object is used.
TFile::fListHead
contains a sorted list (
TSortedList
) of objects in memory. The
diagram below illustrates the logical view of the TFile and TKey.
11.2.1 Viewing the Logical File Contents
TFile
is a descendent of
TDirectory
, which means it behaves like a
TDirectory
. We can list the contents, print the
name, and create subdirectories. In a ROOT session, you are always in a directory and the directory you are in is
called the current directory and is stored in the global variable
gDirectory
. Let us look at a more detailed example of
a ROOT file and its role as the current directory. First, we create a ROOT file by executing a sample script.
root[] .x $ROOTSYS/tutorials/hsimple.C
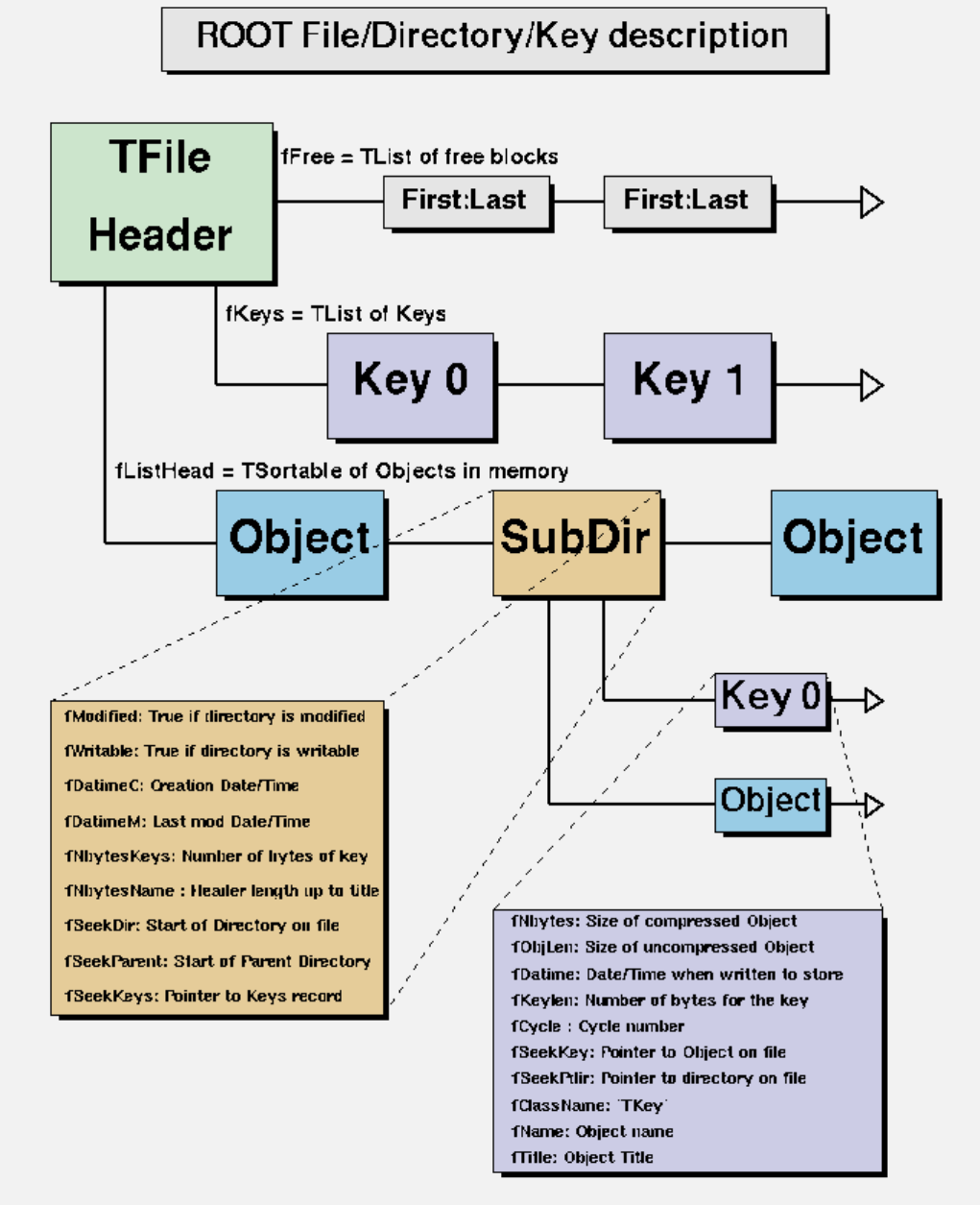
11.2. THE LOGICAL ROOT FILE: TFILE AND TKEY 257
Figure 11.2: ROOT File/Directory/Key description
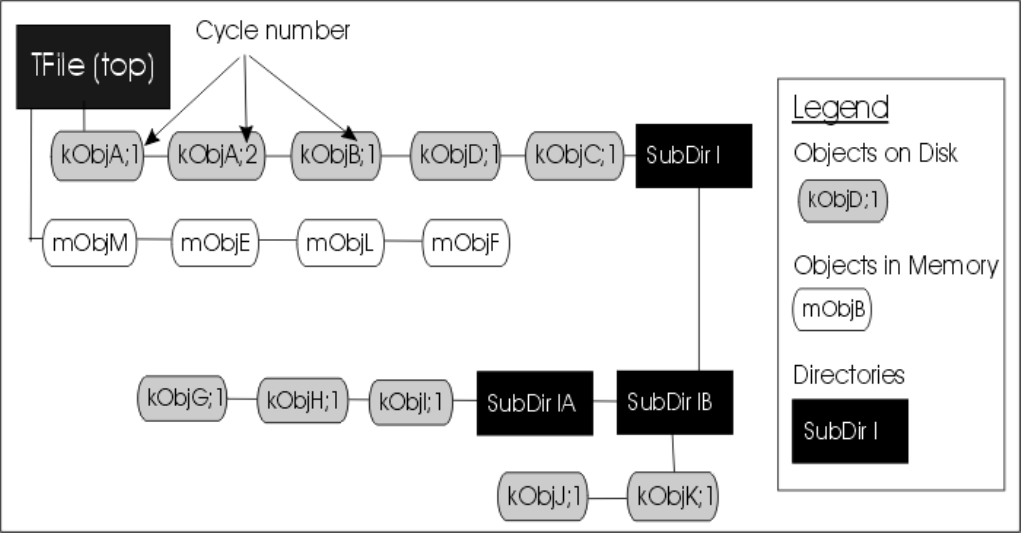
258 CHAPTER 11. INPUT/OUTPUT
Now you should have
hsimple.root
in your directory. The file was closed by the script so we have to open it again to
work with it. We open the file with the intent to update it, and list its contents.
root[] TFile f ("hsimple.root","UPDATE")
root[] f.ls()
TFile** hsimple.root
TFile* hsimple.root
KEY: TH1F hpx;1This is the px distribution
KEY: TH2F hpxpy;1py vs px
KEY: TProfile hprof;1Profile of pz versus px
KEY: TNtuple ntuple;1Demo ntuple
It shows the two lines starting with
TFile
followed by four lines starting with the word “
KEY
”. The four keys tell us
that there are four objects on disk in this file. The syntax of the listing is:
KEY: <class> <variable>;<cycle number> <title>
For example, the first line in the list means there is an object in the file on disk, called
hpx
. It is of the class
TH1F
(one-dimensional histogram of floating numbers). The object’s title is “This is the
px
distribution”. If the line starts
with
OBJ
, the object is in memory. The <class> is the name of the ROOT class (T-something). The <variable> is the
name of the object. The cycle number along with the variable name uniquely identifies the object. The <title> is the
string given in the constructor of the object as title.
Figure 11.3: The structure of TFile
The figure shows a
TFile
with five objects in the top directory
(kObjA;1, kObjA;2, kObjB;1, kObjC;1
and
kObjD;1)
.
ObjA
is on file twice with two different cycle numbers. It also shows four objects in memory (
mObjE
,
mObjeF
,
mObjM
,
mObjL). It also shows several subdirectories.
11.2.2 The Current Directory
When you create a
TFile
object, it becomes the current directory. Therefore, the last file to be opened is always the
current directory. To check your current directory you can type:
root[] gDirectory->pwd()
Rint:/
This means that the current directory is the ROOT session (
Rint
). When you create a file, and repeat the command
the file becomes the current directory.
11.2. THE LOGICAL ROOT FILE: TFILE AND TKEY 259
root[] TFile f1("AFile1.root");
root[] gDirectory->pwd()
AFile1.root:/
If you create two files, the last becomes the current directory.
root[] TFile f2("AFile2.root");
root[] gDirectory->pwd()
AFile2.root:/
To switch back to the first file, or to switch to any file in general, you can use the
TDirectory::cd
method. The next
command changes the current directory back to the first file.
root[] f1.cd();
root[] gDirectory->pwd()
AFile1.root:/
Note that even if you open the file in “READ” mode, it still becomes the current directory. Cling also offers a shortcut
for gDirectory->pwd() and gDirectory->ls(), you can type:
root[] .pwd
AFile1.root:/
root[] .ls
TFile** AFile1.root
TFile* AFile1.root
To return to the home directory where we were before:
root[] gROOT->cd()
(unsigned char)1
root[] gROOT->pwd()
Rint:/
11.2.3 Objects in Memory and Objects on Disk
The
TFile::ls()
method has an option to list the objects on disk (“
-d
”) or the objects in memory (“
-m
”). If no
option is given it lists both, first the objects in memory, then the objects on disk. For example:
root[] TFile *f = new TFile("hsimple.root");
root[] gDirectory->ls("-m")
TFile** hsimple.root
TFile* hsimple.root
Remember that
gDirectory
is the current directory and at this time is equivalent to “
f
”. This correctly states that no
objects are in memory.
The next command lists the objects on disk in the current directory.
root[] gDirectory->ls("-d")
TFile** hsimple.root
TFile* hsimple.root
KEY: TH1F hpx;1This is the px distribution
KEY: TH2F hpxpy;1py vs px
KEY: TProfile hprof;1Profile of pz versus px
KEY: TNtuple ntuple;1Demo ntuple
To bring an object from disk into memory, we have to use it or “Get” it explicitly. When we use the object, ROOT
gets it for us. Any reference to
hprof
will read it from the file. For example drawing
hprof
will read it from the file
and create an object in memory. Here we draw the profile histogram, and then we list the contents.
260 CHAPTER 11. INPUT/OUTPUT
root[] hprof->Draw()
<TCanvas::MakeDefCanvas>: created default TCanvas with name c1
root[] f->ls()
TFile** hsimple.root
TFile* hsimple.root
OBJ: TProfile hprof Profile of pz versus px : 0
KEY: TH1F hpx;1This is the px distribution
KEY: TH2F hpxpy;1py vs px
KEY: TProfile hprof;1Profile of pz versus px
KEY: TNtuple ntuple;1Demo ntuple
We now see a new line that starts with OBJ. This means that an object of class
TProfile
, called
hprof
has been
added in memory to this directory. This new
hprof
in memory is independent from the
hprof
on disk. If we make
changes to the
hprof
in memory, they are not propagated to the
hprof
on disk. A new version of
hprof
will be saved
once we call Write.
You may wonder why
hprof
is added to the objects in the current directory.
hprof
is of the class
TProfile
that
inherits from
TH1D
, which inherits from
TH1
.
TH1
is the basic histogram. All histograms and trees are created in the
current directory (also see “Histograms and the Current Directory”). The reference to “all histograms” includes objects
of any class descending directly or indirectly from
TH1
. Hence, our
TProfile hprof
is created in the current directory
f.There was another side effect when we called the TH1::Draw method. ROOT printed this statement:
<TCanvas::MakeDefCanvas>: created default TCanvas with name c1
It tells us that a
TCanvas
was created and it named it
c1
. This is where ROOT is being nice, and it creates a canvas
for drawing the histogram if no canvas was named in the draw command, and if no active canvas exists. The newly
created canvas, however, is NOT listed in the contents of the current directory. Why is that? The canvas is not added
to the current directory, because by default ONLY histograms and trees are added to the object list of the current
directory. Actually,
TEventList
objects are also added to the current directory, but at this time, we don’t have to
worry about those. If the canvas is not in the current directory then where is it? Because it is a canvas, it was added
to the list of canvases.
This list can be obtained by the command
gROOT->GetListOfCanvases()->ls()
. The
ls()
will print the contents of
the list. In our list, we have one canvas called c1. It has a TFrame, a TProfile, and a TPaveStats.
root[] gROOT->GetListOfCanvases()->ls()
Canvas Name=c1 Title=c1
Option=TCanvas fXlowNDC=0fYlowNDC=0fWNDC=1fHNDC=1
Name= c1 Title= c1
Option=TFrame X1= -4.000000 Y1=0.000000 X2=4.000000 Y2=19.384882
OBJ: TProfile hprof Profile of pz versus px : 0
TPaveText X1=-4.900000 Y1=20.475282 X2=-0.950000 Y2=21.686837 title
TPaveStats X1=2.800000 Y1=17.446395 X2=4.800000 Y2=21.323371 stats
Lets proceed with our example and draw one more histogram, and we see one more OBJ entry.
root[] hpx->Draw()
root[] f->ls()
TFile** hsimple.root
TFile* hsimple.root
OBJ: TProfile hprof Profile of pz versus px : 0
OBJ: TH1F hpx This is the px distribution : 0
KEY: TH1F hpx;1This is the px distribution
KEY: TH2F hpxpy;1py vs px
KEY: TProfile hprof;1Profile of pz versus px
KEY: TNtuple ntuple;1Demo ntuple
TFile::ls()
loops over the list of objects in memory and the list of objects on disk. In both cases, it calls the
ls()
method of each object. The implementation of the
ls
method is specific to the class of the object, all of these objects
are descendants of
TObject
and inherit the
TObject::ls()
implementation. The histogram classes are descendants of
TNamed
that in turn is a descent of
TObject
. In this case,
TNamed::ls()
is executed, and it prints the name of the
class, and the name and title of the object. Each directory keeps a list of its objects in the memory. You can get this
list by TDirectory::GetList(). To see the lists in memory contents you can do:
11.2. THE LOGICAL ROOT FILE: TFILE AND TKEY 261
root[]f->GetList()->ls()
OBJ: TProfile hprof Profile of pz versus px : 0
OBJ: TH1F hpx This is the px distribution : 0
Since the file fis the current directory (gDirectory ), this will yield the same result:
root[] gDirectory->GetList()->ls()
OBJ: TProfile hprof Profile of pz versus px : 0
OBJ: TH1F hpx This is the px distribution : 0
11.2.4 Saving Histograms to Disk
At this time, the objects in memory (OBJ) are identical to the objects on disk (KEY). Let’s change that by adding a
fill to the hpx we have in memory.
root[] hpx->Fill(0)
Now the
hpx
in memory is different from the histogram (
hpx
) on disk. Only one version of the object can be in memory,
however, on disk we can store multiple versions of the object. The
TFile::Write
method will write the list of objects
in the current directory to disk. It will add a new version of hpx and hprof.
root[] f->Write()
root[] f->ls()
TFile** hsimple.root
TFile* hsimple.root
OBJ: TProfile hprof Profile of pz versus px : 0
OBJ: TH1F hpx This is the px distribution : 0
KEY: TH1F hpx;2This is the px distribution
KEY: TH1F hpx;1This is the px distribution
KEY: TH2F hpxpy;1py vs px
KEY: TProfile hprof;2Profile of pz versus px
KEY: TProfile hprof;1Profile of pz versus px
KEY: TNtuple ntuple;1Demo ntuple
The
TFile::Write
method wrote the entire list of objects in the current directory to the file. You see that it added
two new keys:
hpx;2
and
hprof;2
to the file. Unlike memory, a file is capable of storing multiple objects with the
same name. Their cycle number, the number after the semicolon, differentiates objects on disk with the same name. If
you wanted to save only
hpx
to the file, but not the entire list of objects, you could use the
TH1::Write
method of
hpx
:
root[] hpx->Write()
A call to
obj->Write
without any parameters will call
obj->GetName()
to find the name of the object and use it to
create a key with the same name. You can specify a new name by giving it as a parameter to the Write method.
root[] hpx->Write("newName")
If you want to re-write the same object, with the same key, use the overwrite option.
root[] hpx->Write("",TObject::kOverwrite)
If you give a new name and use the
kOverwrite
, the object on disk with the matching name is overwritten if such an
object exists. If not, a new object with the new name will be created.
root[] hpx->Write("newName",TObject::kOverwrite)
The Write method did not affect the objects in memory at all. However, if the file is closed, the directory is emptied
and the objects on the list are deleted.
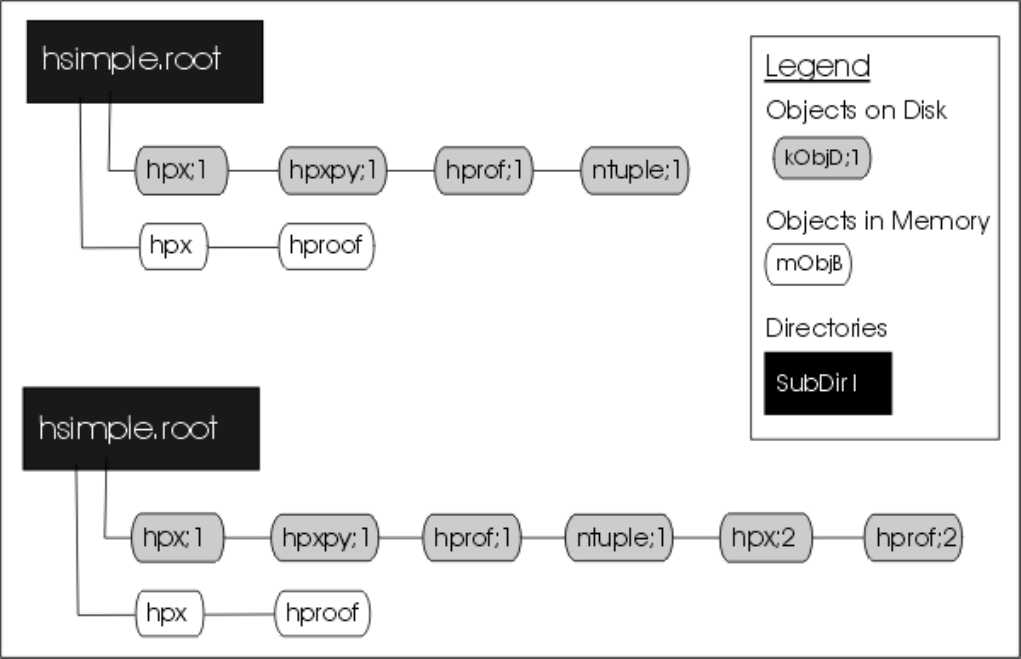
262 CHAPTER 11. INPUT/OUTPUT
Figure 11.4: The file before and after the call to Write
root[] f->Close()
root[] f->ls()
TFile** hsimple.root
TFile* hsimple.root
In the code snipped above, you can see that the directory is now empty. If you followed along so far, you can see that
c1 which was displaying hpx is now blank. Furthermore, hpx no longer exists.
root[] hpx->Draw()
Error: No symbol hpx in current scope
This is important to remember, do not close the file until you are done with the objects or any attempt to reference the
objects will fail.
11.2.5 Histograms and the Current Directory
When a histogram is created, it is added by default to the list of objects in the current directory. You can get the list
of histograms in a directory and retrieve a pointer to a specific histogram.
TH1F *h = (TH1F*)gDirectory->Get("myHist"); // or
TH1F *h = (TH1F*)gDirectory->GetList()->FindObject("myHist");
The method
TDirectory::GetList()
returns a
TList
of objects in the directory. You can change the directory of a
histogram with the SetDirectory method.
h->SetDirectory(newDir);
If the parameter is 0, the histogram is no longer associated with a directory.
11.2. THE LOGICAL ROOT FILE: TFILE AND TKEY 263
h->SetDirectory(0);
Once a histogram is removed from the directory, it will no longer be deleted when the directory is closed. It is now your
responsibility to delete this histogram object once you are finished with it. To change the default that automatically
adds the histogram to the current directory, you can call the static function:
TH1::AddDirectory(kFALSE);
In this case, you will need to do all the bookkeeping for all the created histograms.
11.2.6 Saving Objects to Disk
In addition to histograms and trees, you can save any object in a ROOT file. For example to save a canvas to the
ROOT file you can use either TObject::Write() or TDirectory::WriteTObject(). The example:
root[] c1->Write()
This is equivalent to:
root[] f->WriteTObject(c1)
For objects that do not inherit from TObject use:
root[] f->WriteObject(ptr,"nameofobject")
Another example:
root[] TFile *f = new TFile("hsimple.root","UPDATE")
root[] hpx->Draw()
<TCanvas::MakeDefCanvas>: created default TCanvas with name c1
root[] c1->Write()
root[] f->ls()
TFile** hsimple.root
TFile* hsimple.root
OBJ: TH1F hpx This is the px distribution : 0
KEY: TH1F hpx;2This is the px distribution
KEY: TH1F hpx;1This is the px distribution
KEY: TH2F hpxpy;1py vs px
KEY: TProfile hprof;2Profile of pz versus px
KEY: TProfile hprof;1Profile of pz versus px
KEY: TNtuple ntuple;1Demo ntuple
KEY: TCanvas c1;1c1
11.2.7 Saving Collections to Disk
All collection classes inherit from
TCollection
and hence inherit the
TCollection::Write() method. When you
call TCollection::Write()
each object in the container is written individually into its own key in the file. To write
all objects into one key you can specify the name of the key and use the optionTObject::kSingleKey. For example:
root[] TList * list = new TList;
root[] TNamed * n1, * n2;
root[] n1 = new TNamed("name1","title1");
root[] n2 = new TNamed("name2","title2");
root[] list->Add(n1);
root[] list->Add(n2);
root[] gFile->WriteObject(list,"list",TObject::kSingleKey);
264 CHAPTER 11. INPUT/OUTPUT
11.2.8 A TFile Object Going Out of Scope
There is another important point to remember about
TFile::Close
and
TFile::Write
. When a variable is declared
on the stack in a function such as in the code below, it will be deleted when it goes out of scope.
void foo() {
TFile f("AFile.root","RECREATE");
}
As soon as the function
foo
has finished executing, the variable
f
is deleted. When a
TFile
object is deleted an
implicit call to
TFile::Close
is made. This will save only the file descriptor to disk. It contains the file header, the
StreamerInfo
list, the key list, the free segment list, and the end address. See “The Physical Layout of ROOT Files”.
The
TFile::Close
does not make a call to
Write()
, which means that the objects in memory will not be saved in the
file. You need to explicitly call TFile::Write() to save the object in memory to file before the exit of the function.
void foo() {
TFile f("AFile.root","RECREATE");
... stuff ...
f.Write();
}
To prevent an object in a function from being deleted when it goes out of scope, you can create it on the heap instead
of on the stack. This will create a
TFile
object
f
, that is available on a global scope, and it will still be available when
exiting the function.
void foo() {
TFile *f = new TFile("AFile.root","RECREATE");
}
11.2.9 Retrieving Objects from Disk
If you have a ROOT session running, please quit and start fresh.
We saw that multiple versions of an object with the same name could be in a ROOT file. In our example, we saved a
modified histogram
hpx
to the file, which resulted in two
hpx’s
uniquely identified by the cycle number:
hpx;1
and
hpx;2
. The question is how we can retrieve the right version of
hpx
. When opening the file and using
hpx
, Cling
retrieves the one with the highest cycle number. To read the
hpx;1
into memory, rather than the
hpx:2
we would get
by default, we have to explicitly get it and assign it to a variable.
root[] TFile *f1 = new TFile("hsimple.root")
root[] TH1F *hpx1; f1->GetObject("hpx;1",hpx)
root[] hpx1->Draw()
11.2.10 Subdirectories and Navigation
The
TDirectory
class lets you organize its contents into subdirectories, and
TFile
being a descendent of
TDirectory
inherits this ability. Here is an example of a ROOT file with multiple subdirectories as seen in the ROOT browser.
To add a subdirectory to a file use
TDirectory::mkdir
. The example below opens the file for writing and creates a
subdirectory called “Wed011003”. Listing the contents of the file shows the new directory in the file and the
TDirectory
object in memory.
root[] TFile *f = new TFile("AFile.root","RECREATE")
root[] f->mkdir("Wed011003")
(class TDirectory*)0x1072b5c8
root[] f->ls()
TFile** AFile.root
TFile* AFile.root
TDirectory* Wed011003 Wed011003
KEY: TDirectory Wed011003;1Wed011003
11.2. THE LOGICAL ROOT FILE: TFILE AND TKEY 265
We can change the current directory by navigating into the subdirectory, and after changing directory; we can see that
gDirectory is now “Wed011003”.
root[] f->cd("Wed011003")
root[] gDirectory->pwd()
AFile.root:/Wed011003
In addition to
gDirectory
we have
gFile
, another global that points to the current file. In our example,
gDirectory
points to the subdirectory, and gFile points to the file (i.e. the files’ top directory).
root[] gFile->pwd()
AFile.root:/
Use cd() without any arguments to return to the file’s top directory.
root[] f->cd()
AFile.root:/
Change to the subdirectory again, and create a histogram. It is added to the current directory, which is the subdirectory
“Wed011003”.
root[] f->cd("Wed011003")
root[] TH1F *histo = new TH1F("histo","histo",10,0,10)
root[] gDirectory->ls()
TDirectory* Wed011003 Wed011003
OBJ: TH1F histo histo : 0
If you are in a subdirectory and you want to have a pointer to the file containing the subdirectory, you can do:
root[] gDirectory->GetFile()
If you are in the top directory
gDirectory
is the same as
gFile
. We write the file to save the histogram on disk, to
show you how to retrieve it later.
root[] f->Write()
root[] gDirectory->ls()
TDirectory* Wed011003 Wed011003
OBJ: TH1F histo histo : 0
KEY: TH1F histo;1histo
When retrieving an object from a subdirectory, you can navigate to the subdirectory first or give it the path name
relative to the file. The read object is created in memory in the current directory. In this first example, we get
histo
from the top directory and the object will be in the top directory.
root[] TH1 *h; f->GetObject("Wed011003/histo;1",h)
If file is written, a copy of
histo
will be in the top directory. This is an effective way to copy an object from one
directory to another. In contrast, in the code box below,
histo
will be in memory in the subdirectory because we
changed the current directory.
root[] f->cd("Wed011003")
root[] TH1 *h; gDirectory->GetObject("histo;1",h)
Note that there is no warning if the retrieving was not successful. You need to explicitly check the value of h, and if it
is null, the object could not be found. For example, if you did not give the path name the histogram cannot be found
and the pointer to h is null:
266 CHAPTER 11. INPUT/OUTPUT
root[] TH1 *h; gDirectory->GetObject("Wed011003/histo;1",h)
root[] h
(class TH1*)0x10767de0
root[] TH1 *h; gDirectory->GetObject("histo;1",h)
root[] h
(class TH1*)0x0
To remove a subdirectory you need to use
TDirectory::Delete
. There is no
TDirectory::rmdir
. The Delete method
takes a string containing the variable name and cycle number as a parameter.
void Delete(const char *namecycle)
The namecycle string has the format name;cycle. The next are some rules to remember:
•name = * means all, but don’t remove the subdirectories
•cycle =* means all cycles (memory and file)
•cycle =“” means apply to a memory object
•cycle = 9999 also means apply to a memory object
•namecycle = “” means the same as namecycle =“T*”
•namecycle =T* delete subdirectories
For example to delete a directory from a file, you must specify the directory cycle:
root[] f->Delete("Wed011003;1")
Some other examples of namecycle format are:
•foo:delete the object named foo from memory
•foo;1: delete the cycle 1 of the object named foo from the file
•foo;*: delete all cycles of foo from the file and also from memory
•*;2: delete all objects with cycle number 2 from the file
•*;*: delete all objects from memory and from the file
•T*;*: delete all objects from memory and from the file including all subdirectories
11.3 Streamers
To follow the discussion on
Streamers
, you need to know what a simple data type is. A variable is of a simple data
type if it cannot be decomposed into other types. Examples of simple data types are longs, shorts, floats, and chars. In
contrast, a variable is of a composite data type if it can be decomposed. For example, classes, structures, and arrays are
composite types. Simple types are also called primitive types, basic types, and Cling sometimes calls them fundamental
types.
When we say, “writing an object to a file”, we actually mean writing the current values of the data members. The most
common way to do this is to decompose (also called the serialization of) the object into its data members and write
them to disk. The decomposition is the job of the
Streamer
. Every class with ambitions to be stored in a file has a
Streamerthat decomposes it and “streams” its members into a buffer.
The methods of the class are not written to the file, it contains only the persistent data members. To decompose the
parent classes, the
Streamer
calls the
Streamer
of the parent classes. It moves up the inheritance tree until it reaches
an ancestor without a parent. To serialize the object data members it calls their
Streamer
. They in turn move up
their own inheritance tree and so forth. The simple data members are written to the buffer directly. Eventually the
buffer contains all simple data members of all the classes that make up this particular object. Data members that are
references (as
MyClass &fObj;
) are never saved, it is always the responsibility of the object’s constructor to set them
properly.
11.3. STREAMERS 267
11.3.1 Automatically Generated Streamers
A
Streamer
usually calls other
Streamers
: the
Streamer
of its parents and data members. This architecture depends on
all classes having
Streamers
, because eventually they will be called. To ensure that a class has a
Streamer
,
rootcling
automatically creates one in the
ClassDef
macro that is defined in
$ROOTSYS/include/Rtypes.h
.
ClassDef
defines
several methods for any class, and one of them is the
Streamer
. The automatically generated
Streamer
is complete
and can be used as long as no customization is needed.
The
Event
class is defined in
$ROOTSYS/test/Event.h
. Looking at the class definition, we find that it inherits from
TObject. It is a simple example of a class with diverse data members.
class Event : public TObject {
private:
TDirectory *fTransient; //! current directory
Float_t fPt; //! transient value
char fType[20];
Int_t fNtrack;
Int_t fNseg;
Int_t fNvertex;
UInt_t fFlag;
Float_t fTemperature;
EventHeader fEvtHdr; //|| don't split
TClonesArray *fTracks; //->
TH1F *fH; //->
Int_t fMeasures[10];
Float_t fMatrix[4][4];
Float_t *fClosestDistance; //[fNvertex]
...
The Event class is added to the dictionary by the
rootcling
utility. This is the
rootcling
statement in the
$ROOTSYS/test/Makefile:
@rootcling -f EventDict.cxx -c Event.h EventLinkDef.h
The EventDict.cxx file contains the automatically generated Streamerfor Event:
void Event::Streamer(TBuffer &R__b){
// Stream an object of class Event.
if (R__b.IsReading()) {
Event::Class()->ReadBuffer(R__b, this);
}else {
Event::Class()->WriteBuffer(R__b, this);
}
}
When writing an
Event
object,
TClass::WriteBuffer
is called.
WriteBuffer
writes the current version number of
the
Event class,
and its contents into the buffer
R__b
. The
Streamer
calls
TClass::ReadBuffer
when reading an
Event object. The ReadBuffer method reads the information from buffer R__b into the Event object.
11.3.2 Transient Data Members (//!)
To prevent a data member from being written to the file, insert a “
!
” as the first character after the comment marks.
It tells ROOT not to save that data member in a root file when saving the class. For example, in this version of Event,
the fPt and fTransient data members are not persistent.
class Event : public TObject {
private:
TDirectory *fTransient; //! current directory
Float_t fPt; //! transient value
...
268 CHAPTER 11. INPUT/OUTPUT
11.3.3 The Pointer to Objects (//->)
The string “
->
” in the comment field of the members
*fH
and
*fTracks
instruct the automatic
Streamer
to assume
these will point to valid objects and the
Streamer
of the objects can be called rather than the more expensive
R__b <<
fH
. It is important to note that no check is done on the validity of the pointer value. In particular if the pointer points,
directly or indirectly, back to the current object, this will result in an infinite recursion and the abrupt end of the
process.
TClonesArray *fTracks; //->
TH1F *fH; //->
11.3.4 Variable Length Array
When the
Streamer
comes across a pointer to a simple type, it assumes it is an array. Somehow, it has to know how
many elements are in the array to reserve enough space in the buffer and write out the appropriate number of elements.
This is done in the class definition. For example:
class Event : public TObject {
private:
char fType[20];
Int_t fNtrack;
Int_t fNseg;
Int_t fNvertex;
...
Float_t *fClosestDistance; //[fNvertex]
The array
fClosestDistance
is defined as a pointer of floating point numbers. A comment mark (//), and the number
in square brackets tell the Streamerthe length of the array for this object. In general the syntax is:
<simple type> *<name>//[<length>]
The length cannot be an expression. If a variable is used, it needs to be an integer data member of the class. It must
be defined ahead of its use, or in a base class.
The same notation also applies to variable length array of object and variable length array of pointer to objects.
MyObject *obj; //[fNojbs]
MyObject **objs; //[fDatas]
11.3.5 Double32_t
Math operations very often require double precision, but on saving single usually precision is sufficient. For this purpose
we support the typedef Double32_t which is stored in memory as a double and on disk as a float or interger. The actual
size of disk (before compression) is determined by the parameter next to the data member declartion. For example:
Double32_t m_data; //[min,max<,nbits>]
If the comment is absent or does not contain min,max,nbit, the member is saved as a float.
If min
and
max
are present, they are saved as a 32 bits precision.
min
and
max
can be explicit values or be expressions
of values known to Cling (e.g. “pi").
If nbits is present, the member is saved as int with ‘nbit’. For more details see the io tutorials double32.C.
11.3.6 Prevent Splitting (//|| )
If you want to prevent a data member from being split when writing it to a tree, append the characters || right after
the comment string. This only makes sense for object data members. For example:
EventHeader fEvtHdr; //|| do not split the header
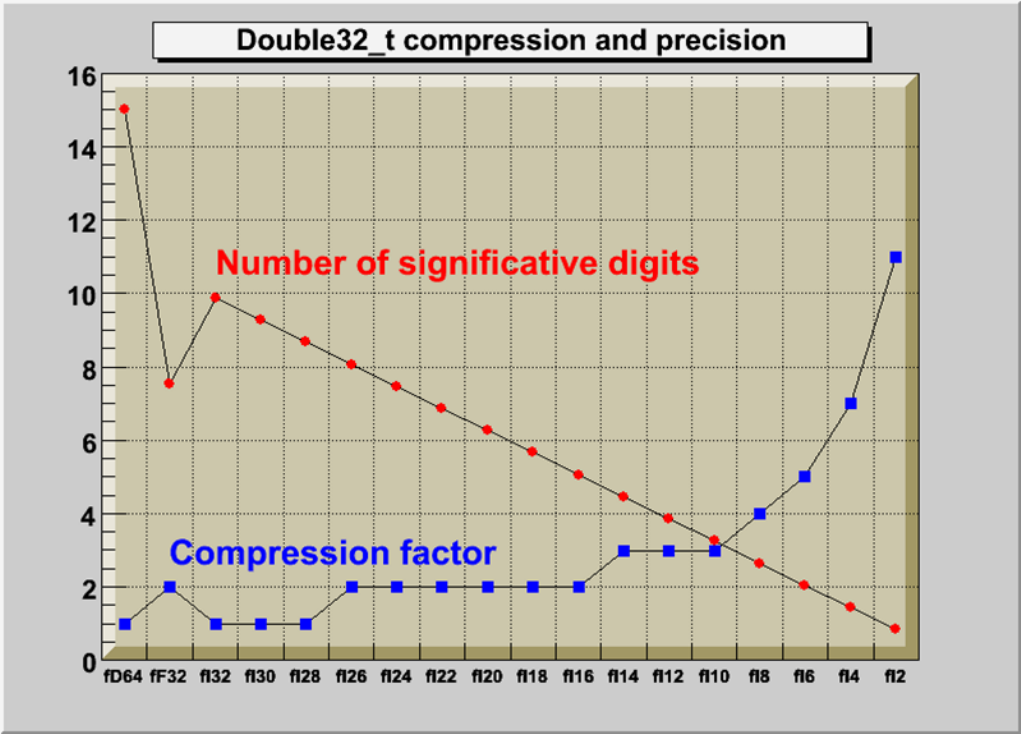
11.3. STREAMERS 269
Figure 11.5: Compression and precision of Double32_t
270 CHAPTER 11. INPUT/OUTPUT
11.3.7 Streamers with Special Additions
Most of the time you can let
rootcling
generate a
Streamer
for you. However if you want to write your own
Streamer
you can do so. For some classes, it may be necessary to execute some code before or after the read or
write block in the automatic
Streamer
. For example after the execution of the read block, one can initialize some
non persistent members. There are two reasons why you would need to write your own Streamer: 1) if you have a
non-persistent data member that you want to initialize to a value depending on the read data members; 2) if you
want or need to handle the schema evolution on your own. In addition, the automatic
Streamer
does not support
C-structures. It is best to convert the structure to a class definition.
First, you need to tell
rootcling
not to build a
Streamer
for you. The input to the
rootcling
command (in
the
makefile
) is a list of classes in a
LinkDef.h
file. For example, the list of classes for
Event
is listed in
$ROOTSYS/test/EventLinkDef.h
. The “
-
” at the end of the class name tells
rootcling
not to generate a
Streamer
.
In the example, you can see the
Event
class is the only one for which
rootcling
is instructed not to generate a
Streamer.
#ifdef __ROOTCLING__
#pragma link off all globals;
#pragma link off all classes;
#pragma link off all functions;
#pragma link C++ class EventHeader+;
#pragma link C++ class Event-;
#pragma link C++ class HistogramManager+;
#pragma link C++ class Track+;
#endif
#pragma link C++ class EventHeader+;
The “
+
” sign tells
rootcling
to use the new
Streamer
system introduced in ROOT 3.0. The following is an example of
a customized
Streamer
for
Event
. The
Streamer
takes a
TBuffer
as a parameter, and first checks to see if this is a
case of reading or writing the buffer.
void Event::Streamer(TBuffer &R__b) {
if (R__b.IsReading()) {
Event::Class()->ReadBuffer(R__b, this);
fTransient = gDirectory; //save current directory
fPt= TMath::Sqrt(fPx*fPx + fPy*fPy + fPz*fPz);
}else {
Event::Class()->WriteBuffer(R__b, this);
}
}
11.3.8 Writing Objects
The
Streamer
decomposes the objects into data members and writes them to a buffer. It does not write the buffer to a
file, it simply populates a buffer with bytes representing the object. This allows us to write the buffer to a file or do
anything else we could do with the buffer. For example, we can write it to a socket to send it over the network. This is
beyond the scope of this chapter, but it is worthwhile to emphasize the need and advantage of separating the creation
of the buffer from its use. Let us look how a buffer is written to a file. The dictionary for a class needs to be loaded
before any object of that type can be saved.
The TObject::Write method does the following:
•Creates a TKey object in the current directory
•Creates a TBuffer object which is part of the newly created TKey
•Fills the TBuffer with a call to the class::Streamer method
•Creates a second buffer for compression, if needed
•Reserves space by scanning the TFree list. At this point, the size of the buffer is known.
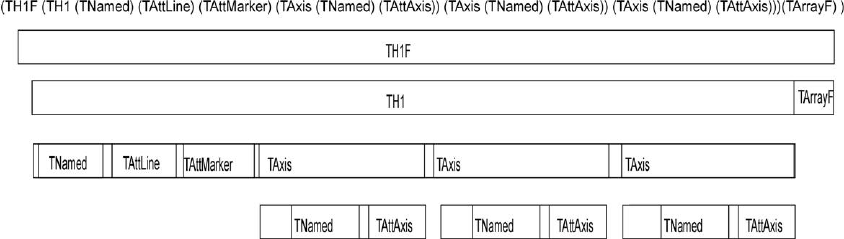
11.4. POINTERS AND REFERENCES IN PERSISTENCY 271
•Writes the buffer to the file
•Releases the TBuffer part of the key
In other words, the
TObject::Write
calls the
Streamer
method of the class to build the buffer. The buffer is in the
key and the key is written to disk. Once written to disk the memory consumed by the buffer part is released. The key
part of the TKey is kept.
Figure 11.6: A diagram of a streamed TH1F in the buffer
The key consumes about 60 bytes, whereas the buffer, since it contains the object data, can be very large.
11.3.9 Ignore Object Streamers
Your class can ignore the
TObject Streamer
with the
MyClass->Class::IgnoreObjectStreamer()
method. When the
class
kIgnoreTObjectStreamer
bit is set (by calling the
IgnoreTObjectStreamer
method
)
, the automatically generated
Streamer
will not call
TObject::Streamer
, and the
TObject
part of the class is not streamed to the file. This is useful
in case you do not use the
TObject fBits
and
fUniqueID
data members. You gain space on the file, and you do not
loose functionality if you do not use the
fBits
and
fUniqueID.
See “The Role of TObject” on the use of
fBits
and
fUniqueID.
11.3.10 Streaming a TClonesArray
When writing a
TClonesArray
it bypasses by default the
Streamer
of the member class and uses a more efficient
internal mechanism to write the members to the file. You can override the default and specify that the member class
Streameris used by setting the TClonesArray::BypassStreamer bit to false:
TClonesArray *fTracks;
fTracks->BypassStreamer(kFALSE); // use the member Streamer
When the
kBypassStreamer
bit is set, the automatically generated
Streamer
can call directly the method
TClass::WriteBuffer
. Bypassing the
Streamer
improves the performance when writing/reading the objects in the
TClonesArray
. However, the drawback is when a
TClonesArray
is written with
split=0
bypassing the
Streamer
, the
StreamerInfo
of the class in the array being optimized, one cannot later use the
TClonesArray
with
split > 0
. For
example, there is a problem with the following scenario: a class
Foo
has a
TClonesArray
of
Bar
objects the
Foo
object
is written with split=0 to Tree T1. In this case the StreamerInfo for the class Bar is created in optimized mode in
such a way that data members of the same type are written as an array improving the I/O performance. In a new
program, T1 is read and a new Tree T2 is created with the object Foo in split > 1.
When the
T2
branch is created, the
StreamerInfo
for the class
Bar
is created with no optimization (mandatory for
the split mode). The optimized Bar
StreamerInfo
is going to be used to read the
TClonesArray
in
T1
. The result
will be
Bar
objects with data member values not in the right sequence. The solution to this problem is to call
BypassStreamer(kFALSE)
for the
TClonesArray
. In this case, the normal
Bar::Streamer
function will be called. The
Bar::Streamer
function works OK independently if the
Bar StreamerInfo
had been generated in optimized mode or
not.
11.4 Pointers and References in Persistency
An object pointer as a data member presents a challenge to the streaming software. If the object pointed to is saved
every time, it could create circular dependencies and consume a large amount of disk space. The network of references
must be preserved on disk and recreated upon reading the file.
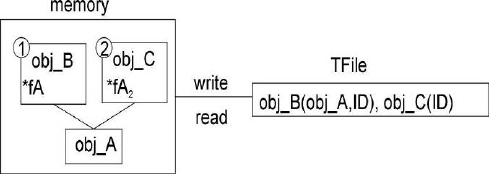
272 CHAPTER 11. INPUT/OUTPUT
If you use independent I/O operations for pointers and their referenced objects you can use the
TRef
class. Later in
this section is an example that compares disk space, memory usage, and I/O times of C++ pointers and
TRefs
. In
general, a TRef is faster than C++ but the advantage of a C++ pointer is that it is already C++.
11.4.1 Streaming C++ Pointers
When ROOT encounters a pointer data member it calls the
Streamer
of the object and labels it with a unique object
identifier. The object identifier is unique for one I/O operation. If there is another pointer to the object in the same
I/O operation, the first object is referenced i.e. it is not saved again. When reading the file, the object is rebuilt and
the references recalculated.
Figure 11.7: Streaming object pointers
In this way, the network of pointers and their objects is rebuilt and ready to use the same way it was used before it
was persistent. If the pointer hold the address of an object which in embedded in another object (as opposed to being
pointed to by a pointer), the object will be duplicate at read time. To avoid this, make the pointer a transient data
member.
11.4.2 Motivation for the TRef Class
If the object is split into several files or into several branches of one or more
TTrees
, standard C++ pointers cannot
be used because each I/O operation will write the referenced objects, and multiple copies will exist. In addition, if
the pointer is read before the referenced object, it is null and may cause a run time system error. To address these
limitations, ROOT offers the TRef class.
TRef
allows referencing an object in a different branch and/or in a different file.
TRef
also supports the complex
situation where a
TFile
is updated multiple times on the same machine or a different machine. When a
TRef
is read
before its referenced object, it is null. As soon as the referenced object is read, the
TRef
points to it. In addition, one
can specify an action to be taken by
TRef
in the case it is read before its reference object (see“Action on Demand”
below).
11.4.3 Using TRef
A
TRef
is a lightweight object pointing to any
TObject
. This object can be used instead of normal C++ pointers in
case:
•The referenced object R and the pointer P are not written to the same file
•P is read before R
•R and P are written to different Tree branches
Below is a line from the example in $ROOTSYS/test/Event.cxx.
TRef fLastTrack; //pointer to last track
...
Track *track = (Track*)fTracks->ConstructedAt(fNtrack++);
track->Set(random);
// Save reference to last Track in the collection of Tracks
fLastTrack = track;
The
track
and its reference
fLastTrack
can be written with two separate I/O calls in the same or in different files, in
the same or in different branches of a
TTree
. If the
TRef
is read and the referenced object has not yet been read,
TRef
will return a null pointer. As soon as the referenced object will be read, TRef will point to it.
11.4. POINTERS AND REFERENCES IN PERSISTENCY 273
11.4.4 How Does It Work?
A
TRef
is itself a
TObject
with an additional transient pointer
fPID
. When a
TRef
is used to point to a
TObject*R
,
for example in a class with
TRef P;
one can do:
P = R; //to set the pointer
When the statement P=Ris executed, the following happens:
•The pointer fPID is set to the current TProcessID (see below).
•The current ObjectNumber (see below) is incremented by one.
•R.fUniqueID is set to ObjectNumber.
•In the fPID object, the element fObjects[ObjectNumber] is set to R
•P.fUniqueID is also set to ObjectNumber.
After having set
P
, one can immediately return the value of
R
using
P.GetObject()
. This function returns the
fObjects[fUniqueID] from the fPID object.
When the
TRef
is written, the process id number
pidf
of
fPID
is written in addition to the
TObject
part of the
TRef
(
fBits,fUniqueID
). When the
TRef
is read, its pointer
fPID
is set to the value stored in the
TObjArray
of
TFile::fProcessIDs(fProcessIDs[pidf]).
When a referenced object is written,
TObject::Streamer
writes the
pidf
in addition to the standard
fBits and
fUniqueID
. When
TObject::Streamer
reads a reference object, the
pidf
is read. At this point, the referenced object
is entered into the table of objects of the TProcessID corresponding to pidf.
WARNING: If
MyClass
is the class of the referenced object, The
TObject
part of
MyClass
must be streamed. One
should not call MyClass::Class()->IgnoreTObjectStreamer().
11.4.4.1 TProccessID and TUUID
A
TProcessID
uniquely identifies a ROOT job. The
TProcessID
title consists of a
TUUID
object, which provides a
globally unique identifier. The
TUUID
class implements the UUID (Universally Unique Identifier), also known as GUID
(Globally Unique Identifier). A UUID is 128 bits long, and if generated according to this algorithm, is either guaranteed
to be different from all other UUID generated until 3400 A.D. or extremely likely to be different.
The
TROOT
constructor automatically creates a
TProcessID
. When a
TFile
contains referenced objects, the
TProcessID
object is written to the file. If a file has been written in multiple sessions (same machine or not), a
TProcessID
is
written for each session. The TProcessID objects are used by TRef to uniquely identify the referenced TObject.
When a referenced object is read from a file (its bit
kIsReferenced
is set), this object is entered into the objects
table of the corresponding
TProcessID
. Each
TFile
has a list of
TProcessIDs
(see
TFile::fProcessIDs
) also
accessible
from
TProcessID::fgPIDs
(for all files). When this object is deleted, it is removed from the
table via the cleanup mechanism invoked by the **
TObject
** destructor. Each **
TProcessID
** has a
table (
TObjArray *fObjects
) that keeps track of all referenced objects. If a referenced object has
a
fUniqueID
, a pointer to this unique object may be found using
fObjects->At(fUniqueID)
. In the same
way, when a **
TRef::GetObject
** is called,
GetObject
uses its own
fUniqueID
to find the pointer to the
referenced object. SeeTProcessID::GetObjectWithIDandPutObjectWithID‘.
11.4.4.2 Object Number
When an object is referenced, a unique identifier is computed and stored in both the
fUniqueID
of the referenced and
referencing object. This
uniqueID
is computed by incrementing by one the static global in
TProcessID::fgNumber
. The
fUniqueID
is the serial object number in the current session. One can retrieve the current
fgNumber
value by calling the
static function
TProcessID::GetObjectCount
at any time or can set this number by
TProcessID::SetObjectCount
.
To avoid a growing table of
fObjects
in
TProcessID
, in case, for example, one processes many events in a loop,
it might be necessary to reset the object number at the end of processing of one event. See an example in
$ROOTSYS/test/Event.cxx
(look at function
Build
). The value of
ObjectNumber
may be saved at the beginning
of one event and reset to this original value at the end of the event. These actions may be nested.
274 CHAPTER 11. INPUT/OUTPUT
saveNumber = TProcessID::GetObjectCount();
...
TProcessID::SetObjectCount(savedNumber);
11.4.5 Action on Demand
The normal behavior of a
TRef
has been described above. In addition,
TRef
supports “Actions on Demand”. It may
happen that the referenced object is not yet in the memory, on a separate file or not yet computed. In this case,
TRef
is able to execute automatically an action:
•Call to a compiled function (static function of member function)
•Call to an interpreted function
•Execution of a Cling script
11.4.5.1 How to Select This Option?
In the definition of the TRef data member in the original class, do:
TRef fRef; //EXEC:execName points to something
When the special keyword
"EXEC:"
is found in the comment field of the member, the next string is assumed to be
the name of a TExec object. When a file is connected, the dictionary of the classes on the file is read in memory (see
TFile::ReadStreamerInfo). When the TStreamerElement
object is read, a
TExec
object is automatically created
with the name specified after the keyword "EXEC:" in case a TExec with a same name does not already exist.
The action to be executed via this TExec can be specified with:
•A call to the TExec constructor, if the constructor is called before
•Opening the file.
•A call to TExec::SetAction at any time.
One can compute a pointer to an existing TExec with a name with:
TExec *myExec = gROOT->GetExec(execName);
myExec->SetAction(actionCommand);
The parameter actionCommand is a string containing a Cling instruction. Examples:
myExec->SetAction("LoadHits()");
myExec->SetAction(".x script.C");
When a
TRef
is de-referenced via
TRef::GetObject, its TExec
** is automatically executed. The
TExec
function/script
can do one or more of the following:**
•Load a file containing the referenced object. This function typically looks in the file catalog.
•
Compute a pointer to the referenced object and communicate this pointer back to the calling function
TRef::SetObject via:
TRef::SetObject(object)
As soon as an object is returned to
GetObject
, the
fUniqueID
of the
TRef
is set to the
fUniqueID
of the referenced
object. At the next call to
GetObject
, the pointer stored in
fPid:fObjects[fUniqueID]
will be returned directly. An
example of action on demand is in $ROOTSYS/test/Event.h:
TRef fWebHistogram; //EXEC:GetWebHistogram
11.5. SCHEMA EVOLUTION 275
When calling
fWebHistogram.GetObject()
, the function
GetObject
will automatically invoke the script
GetWebHistogram.C via the interpreter. An example of a GetWebHistogram.C script is shown below:
void GetWebHistogram() {
TFile *f=TFile::Open("http://root.cern.ch/files/pippa.root");
f->cd("DM/CJ");
TH1 *h6 = (TH1*)gDirectory->Get("h6");
h6->SetDirectory(0);
delete f;
TRef::SetObject(h6);
}
In the above example, a call to
fWebHistogram.GetObject()
executes the script with the function
GetWebHistogram
.
This script connects a file with histograms:
pippa.root
on the ROOT Web site and returns the object
h6
to
TRef::GetObject.
TRef fWebHistogram; //EXEC:GetWebHistogram()
Note that if the definition of the
TRef fWebHistogram
had been changed the compiled or interpreted function
GetWebHistogram() would have been called instead of the Cling script GetWebHistogram.C.
11.4.6 Array of TRef
When storing multiple
TRef
s, it is more efficient to use a
TRefArray
. The efficiency is due to having a single pointer
fPID
for all
TRefs
in the array. It has a dynamic compact table of
fUniqueIDs
. We recommend that you use a
TRefArray rather then a collection of TRefs.
Example:
•Suppose a TObjArray *mytracks containing a list of Track objects.
•
Suppose a
TRefArray *pions
containing pointers to the pion tracks in
mytracks
. This list is created with
statements like: pions->Add(track);
•Suppose a TRefArray *muons containing pointers to the muon tracks in mytracks.
The 3 arrays mytracks,pions and muons may be written separately.
11.5 Schema Evolution
Schema evolution is a problem faced by long-lived data. When a schema changes, existing persistent data can become
inaccessible unless the system provides a mechanism to access data created with previous versions of the schema. In
the lifetime of collaboration, the class definitions (i.e. the schema) are likely to change frequently. Not only can the
class itself change, but any of its parent classes or data member classes can change also. This makes the support for
schema evolution necessary.
ROOT fully supports schema evolution. The next figure below illustrates some of the scenarios.
The top half represents different versions of the shared library with the class definitions. These are the in-memory class
versions. The bottom half represents data files that contain different versions of the classes.
•An old version of a shared library and a file with new class definitions - this can be the case when someone has
not updated the library and is reading a new file.
•Reading a file with a shared library that is missing a class definition (i.e. missing class D).
•
Reading a file without any class definitions. This can be the case where the class definition is lost, or unavailable.
•The current version of a shared library and an old file with old class versions (backward compatibility). This is
often the case when reading old data.
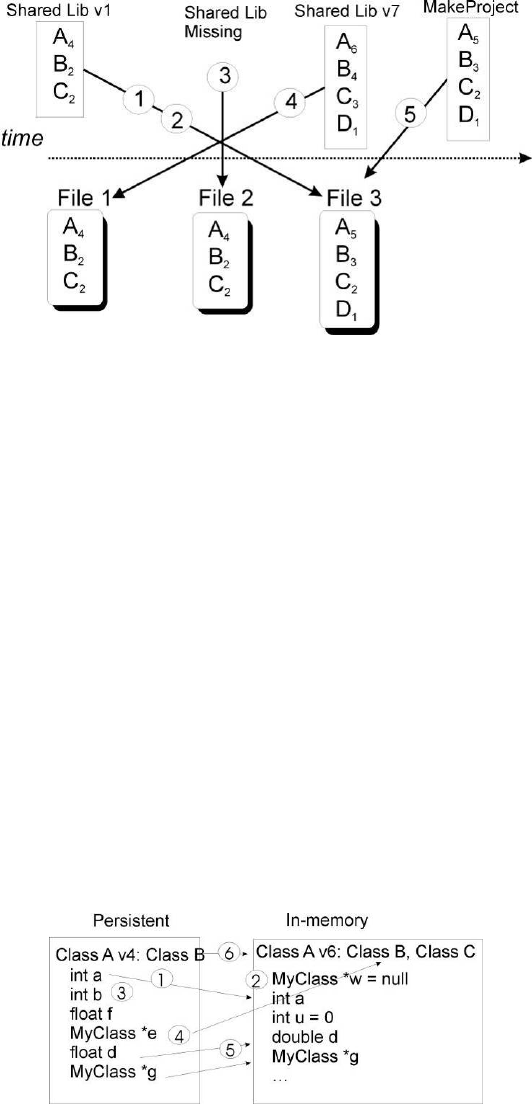
276 CHAPTER 11. INPUT/OUTPUT
Figure 11.8: The ROOT schema evolution
•
Reading a file with a shared library built with
MakeProject
. This is the case when someone has already read the
data without a shared library and has used ROOT
MakeProject
feature to reconstruct the class definitions and
shared library (MakeProject is explained in detail later on).
In case of a mismatch between the in-memory version and the persistent version of a class, ROOT maps the persistent
one to the one in memory. This allows you to change the class definition at will, for example:
•Change the order of data members in the class.
•
Add new data members. By default, the value of the missing member will be 0 or in case of an object it will be
set to null.
•Remove data members.
•Move a data member to a base class or vice-versa.
•
Change the type of a member if it is a simple type or a pointer to a simple type. If a loss of precision occurs, a
warning is given.
•Add or remove a base class
Figure 11.9: The schema evolution for objects written on disk and in memory
ROOT supports schema evolution by keeping a class description of each version of the class that was ever written to
disk, with the class. When it writes an object to file, it also writes the description of the current class version along
with it. This description is implemented in the StreamerInfoclass.
11.5.1 The TStreamerInfo Class
Each class has a list of
StreamerInfo
objects, one for each version of the class if that version was written to disk at
least once. When reading an object from a file, the system uses the
StreamerInfo
list to decode an object into the
current version. The
StreamerInfo
is made up of
TStreamerElements
. Each describes one persistent data member of
the class. By default, all data members of a class are persistent. To exclude a data member (i.e. make it not persistent),
add a “!” after the comment marks. For example the pointer *fPainter of a TH1 is not persistent:
TVirtualHistPainter* fPainter //!pointer to histogram painter
11.5. SCHEMA EVOLUTION 277
11.5.2 The TStreamerElement Class
A
TStreamerElement
describes a data member of a simple type, object, array, pointer, or container. The offset in the
TStreamerElement is the starting address of the data for that data member.
BASE TNamed offset= 0type=67 The basis for a named object
BASE TAttLine offset= 28 type= 0Line attributes
In this example, the
TNamed
data starts at byte 0, and
TAttLine
starts at byte 28. The offset is machine and compiler
dependent and is computed when the
StreamerInfo
is analyzed. The types are defined in the file
TStreamerInfo.h
and listed here:
enum EReadWrite {
kBase=0, kChar=1,kShort=2,kInt=3,kLong=4,
kFloat=5, kCounter=6,kCharStar=7, kDouble=8,kUChar=11,
kUShort=12, kUInt=13,kULong=14,kBits=15,kOffsetL=20,
kOffsetP=40, kObject=61,kAny=62,kObjectp=63,kObjectP=64,
kTString=65, kTObject=66,kTNamed=67,kSkip=100,kSkipL=120,
kSkipP=140, kConv=200, kConvL=220,kConvP=240,kStreamer=500,
kStreamLoop=501, kMissing=99999
};
The method
TClass::GetStreamerInfo
analyzes the
StreamerInfo
the same way it would be analyzed by refer-
ring to the class. While analyzing the
StreamerInfo
, it computes the offsets. The type field is the type of the
TStreamerElement. It is specific to the StreamerInfo definition.
11.5.3 Example: TH1 StreamerInfo
In the
StreamerInfo
of the
TH1
class we see the four base classes:
TNamed
,
TAttLine
,
TAttFill
,
andTAttMarker
.
These are followed by a list of the data members. Each data member is implemented by a
TStreamerElement
object.
root[] TH1::Class()->GetStreamerInfo()->ls()
StreamerInfo for class: TH1, version=3
BASE TNamed offset= 0type=67 The basis for a named object
BASE TAttLine offset= 28 type= 0Line attributes
BASE TAttFill offset= 40 type= 0Fill area attributes
BASE TAttMarker offset= 48 type= 0Marker attributes
Int_t fNcells offset= 60 type= 3number of bins(1D
TAxis fXaxis offset= 64 type=61 X axis descriptor
TAxis fYaxis offset=192 type=61 Y axis descriptor
TAxis fZaxis offset=320 type=61 Z axis descriptor
Short_t fBarOffset offset=448 type= 2(1000*offset)for bar charts or legos
Short_t fBarWidth offset=450 type= 2(1000*width)for bar charts or legos
Stat_t fEntries offset=452 type= 8Number of entries
Stat_t fTsumw offset=460 type= 8Total Sum of weights
Stat_t fTsumw2 offset=468 type= 8Total Sum of squares of weights
Stat_t fTsumwx offset=476 type= 8Total Sum of weight*X
Stat_t fTsumwx2 offset=484 type= 8Total Sum of weight*X*X
Double_t fMaximum offset=492 type= 8Maximum value for plotting
Double_t fMinimum offset=500 type= 8Minimum value for plotting
Double_t fNormFactor offset=508 type= 8Normalization factor
TArrayD fContour offset=516 type=62 Array to display contour levels
TArrayD fSumw2 offset=528 type=62 Array of sum of squares of weights
TString fOption offset=540 type=65 histogram options
TList* fFunctions offset=548 type=63 ->Pointer to list of functions
i= 0, TNamed type= 67, offset= 0, len=1, method=0
i= 1, TAttLine type= 0, offset= 28, len=1, method=142484480
i= 2, TAttFill type= 0, offset= 40, len=1, method=142496992
i= 3, TAttMarker type= 0, offset= 48, len=1, method=142509704
i= 4, fNcells type= 3, offset= 60, len=1, method=0
i= 5, fXaxis type= 61, offset= 64, len=1, method=1081287424
278 CHAPTER 11. INPUT/OUTPUT
i= 6, fYaxis type= 61, offset=192, len=1, method=1081287548
i= 7, fZaxis type= 61, offset=320, len=1, method=1081287676
i= 8, fBarOffset type= 22, offset=448, len=2, method=0
i= 9, fEntries type= 28, offset=452, len=8, method=0
i=10, fContour type= 62, offset=516, len=1, method=1081287804
i=11, fSumw2 type= 62, offset=528, len=1, method=1081287924
i=12, fOption type= 65, offset=540, len=1, method=1081288044
i=13, fFunctions type= 63, offset=548, len=1, method=1081288164
11.5.4 Optimized StreamerInfo
The entries starting with “
i=0
” is the optimized format of the
StreamerInfo
. Consecutive data members of the
same simple type and size are collapsed and read at once into an array for performance optimization.
i= 0, TNamed type= 67, offset= 0, len=1, method=0
i= 1, TAttLine type= 0, offset= 28, len=1, method=142484480
i= 2, TAttFill type= 0, offset= 40, len=1, method=142496992
i= 3, TAttMarker type= 0, offset= 48, len=1, method=142509704
For example, the five data members beginning with
fEnties
and the three data members beginning with
fMaximum
,
are put into an array called fEntries (i=9) with the length 8.
i= 9, fEntries type= 28, offset=452, len=8, method=0
Only simple type data members are combined, object data members are not combined. For example the three axis
data members remain separate. The “method” is a handle to the method that reads the object.
11.5.5 Automatic Schema Evolution
When a class is defined in ROOT, it must include the
ClassDef
macro as the last line in the header file inside the
class definition. The syntax is:
ClassDef(<ClassName>,<VersionNumber>)
The version number identifies this particular version of the class. When a class has version 0 it is not stored in a root
file but its base class(es) is(are). The reason can be that this class has no data members worth saving or all real info is
in the base classes. The version number is written to the file in the
Streamer
by the call
TBuffer::WriteVersion
.
You, as the designer of the class, do not need to do any manual modification in the
Streamer
. ROOT schema evolution
mechanism is automatic and handled by the StreamerInfo.
11.5.6 Manual Data Model Evolution Capabilities
The automatic data model schema evolution implemented in ROOT makes it possible to read back the serialized
data object in the situation when the definition of the classes those objects represent changed slightly (some of the
data members were removed or some new ones added). It is also possible to manually specify the rules for more
sophisticated data transformations done while reading to load the serialized objects into data structures that changed
quite significantly.
ROOT provides two interface enabling users to specify the conversion rules. The first way is to define a rule in the
dictionary file and the second way is to insert it to the TClass object using the C++ API.
There are two types of conversion rules. The first of them, the normal rules, are the ones that should be used in the
most of the cases. They provide a buffered input data and an address of the in-memory target object and allow user to
specify the conversion function mapping the data being read to the output format. The second type of the rules, the
raw rules, also provide the pointer to the target object but the input is a raw TBuffer object containing the input data
member declared as an input to the rule. This type of a rule is provided mainly to handle the file format changes that
couldn’t have been handled otherwise and in general should not be used unless there is no other option.
11.5. SCHEMA EVOLUTION 279
11.5.6.1 The dictionaries
The most convenient place to specify the conversion rules is a dictionary. One can do that either in a LinkDef file or in
the selection xml file being fed to genreflex. The syntax of the rules is the following:
•For dictionaries created from a LinkDef file:
#pragma read \
sourceClass="ClassA" \
source="double m_a; double m_b; double m_c" \
version="[4-5,7,9,12-]" \
checksum="[12345,123456]" \
targetClass="ClassB" \
target="m_x" \
embed="true" \
include="iostream,cstdlib" \
code="{m_x = onfile.m_a * onfile.m_b * onfile.m_c; }" \
#pragma readraw \
sourceClass="TAxis" \
source="fXbins" \
targetClass="TAxis" \
target="fXbins" \
version="[-5]" \
include="TAxis.h" \
code="\
{\
Float_t * xbins=0; \
Int_t n = buffer.ReadArray( xbins ); \
fXbins.Set( xbins ); \
}"
•For REFLEX dictionaries:
<ioread sourceClass="ClassA"
source="double m_a; double m_b; double m_c"
version="[4-5,7,9,12-]"
checksum="[12345,123456]"
targetClass="ClassB"
target="m_x"
embed="true"
include="iostream,cstdlib">
<![CDATA[
m_x = onfile.m_a * onfile.m_b * onfile.m_c;
]] >
</ioread>
<ioreadraw sourceClass="TAxis"
source="fXbins"
targetClass="TAxis"
target="fXbins"
version="[-5]"
include="TAxis.h">
<![CDATA[
Float_t *xbins = 0;
Int_t n = buffer.ReadArray( xbins ) ;
fXbins.Set( xbins );
]] >
</ioreadraw>
The variables in the rules have the following meaning:
280 CHAPTER 11. INPUT/OUTPUT
•sourceClass
–The field defines the on-disk class that is the input for the rule.
•source
–
A semicolon-separated list of values defining the source class data members that need to be cached and
accessible via object proxy when the rule is executed. The values are either the names of the data members
or the type-name pairs (separated by a space). If types are specified then the ondisk structure can be
generated and used in the code snippet defined by the user.
•version
–
A list of versions of the source class that can be an input for this rule. The list has to be enclosed in a square
bracket and be a comma-separated list of versions or version ranges. The version is an integer number,
whereas the version range is one of the following:
–“a-b”: a and b are integers and the expression means all the numbers between and including a and b
–“-a”: a is an integer and the expression means all the version numbers smaller than or equal to a
–“a-”: a is an integer and the expression means all the version numbers greater than or equal to a
•checksum
–
A list of checksums of the source class that can be an input for this rule. The list has to be enclosed in a
square brackets and is a comma-separated list of integers.
•targetClass
–The field is obligatory and defines the name of the in-memory class that this rule can be applied to.
•target
–A semicolon-separated list of target class data member names that this rule is capable of calculating.
•embed
–
This property tells the system if the rule should be written in the output file is some objects of this class are
serialized.
•include
–
A list of header files that should be included in order to provide the functionality used in the code snippet;
the list is comma delimited.
•code
–An user specified code snippet
The user can assume that in the provided code snippet the following variables will be defined:
The user provided code snippets have to consist of valid C++ code. The system can do
some preprocessing before wrapping the code into function calls and declare some variables to facilitate the rule
definitions. The user can expect the following variables being predeclared:
•newObj
–variable representing the target in-memory object, its type is that of the target object
•oldObj
–
in normal conversion rules, an object of TVirtualObject class representing the input data, guaranteed to
hold the data members declared in the source property of the rule
•buffer
–
in raw conversion rules, an object of TBuffer class holding the data member declared in source property of
the rule
•
names of the data members of the target object declared in the target property of the rule declared to be the
appropriate type
•onfile.xxx
–
in normal conversion rules, names of the variables of basic types declared in the source property of the rule
11.5. SCHEMA EVOLUTION 281
11.5.6.2 The C++ API
The schema evolution C++ API consists of two classes:
ROOT::TSchemaRuleSet
and
ROOT::TSchemaRule
. Objects of
the TSchemaRule class represent the rules and their fields have exactly the same meaning as the ones of rules specified
in the dictionaries.
TSchemaRuleSet
objects manage the sets of rules and ensure their consistency. There can be no
conflicting rules in the rule sets. The rule sets are owned by the
TClass
objects corresponding to the target classes
defined in the rules and can be accessed using TClass::{Get|Adopt}SchemaRules.
11.5.7 Manual Schema Evolution
If you have written your own
Streamer
as described in the section “Streamers with Special Additions”, you will
have to manually add code for each version and manage the evolution of your class. When you add or remove data
members, you must modify the
Streamer
by hand. ROOT assumes that you have increased the class version number
in the
ClassDef
statement and introduced the relevant test in the read part of the Streamer. For example, if a new
version of the
Event
class above includes a new member:
Int_t fNew
the
ClassDef
statement should be changed to
ClassDef(Event,2) and the following lines should be added to the read part of the Streamer:
if (R__v > 1) R__b >> fNew;
else fNew = 0;// set to some default value
If, in the same new version 2 you remove the member
fH
, you must add the following code to read the histogram object
into some temporary object and delete it:
if (R__v) < 2{
TH1F *dummy = 0;
R__b >> dummy;
delete dummy;
}
Our experience with manual schema evolution shows that it is easy to make and mismatches between
Streamer
writers
and readers are frequent and increase as the number of classes increase. We recommend you use
rootcling
generated
Streamers whenever you can, and profit from the automatic schema evolution.
11.5.8 Building Class Definitions with the StreamerInfo
A ROOT file’s
StreamerInfo
list contains the description of all versions of all classes in the file. When a file is
opened the
StreamerInfo
is read into memory and it provides enough information to make the file browsable. The
TStreamerInfo
enables us to recreate a header file for the class in case the compiled class is not available. This is
done with the
TFile::MakeProject
method. It creates a directory with the header files for the named classes and a
makefile to compile a shared library with the class definitions.
11.5.9 Example: MakeProject
To explain the details, we use the example of the
ATLFast
project that is a fast simulation for the ATLAS experiment.
The complete source for
ATLFast
can be down loaded at ftp://root.cern.ch/root/atlfast.tar.gz. Once we compile and
run
ATLFast
we get a ROOT file called
atlfast.root
, containing the
ATLFast
objects. When we open the file, we get
a warning that the file contains classes that are not in the dictionary. This is correct since we did not load the class
definitions.
root[] TFile f("atlfast.root")
Warning in <TClass::TClass>: no dictionary for class TMCParticle is available
Warning in <TClass::TClass>: no dictionary for class ATLFMuon available
We can see the StreamerInfofor the classes:
root[] f.ShowStreamerInfo()
...
StreamerInfo for class: ATLFMuon, version=1
BASE TObject offset= 0type=66 Basic ROOT object
282 CHAPTER 11. INPUT/OUTPUT
BASE TAtt3D offset= 0type= 03D attributes
Int_t m_KFcode offset= 0type= 3Muon KF-code
Int_t m_MCParticle offset= 0type= 3Muon position in MCParticles list
Int_t m_KFmother offset= 0type= 3Muon mother KF-code
Int_t m_UseFlag offset= 0type= 3Muon energy usage flag
Int_t m_Isolated offset= 0type= 3Muon isolation (1for isolated)
Float_t m_Eta offset= 0type= 5Eta coordinate
Float_t m_Phi offset= 0type= 5Phi coordinate
Float_t m_PT offset= 0type= 5Transverse energy
Int_t m_Trigger offset= 0type= 3Result of trigger...
However, when we try to use a specific class we get a warning because the class is not in the dictionary. We can create
a class using gROOT->GetClass() which makes a fake class from the StreamerInfo.
// Build a 'fake'class
root[] gROOT->GetClass("ATLFMuon")
(const class TClass*)0x87e5c08
// The fake class has a StreamerInfo
root[] gROOT->GetClass("ATLFMuon")->GetStreamerInfo()->ls()
StreamerInfo for class: ATLFMuon, version=1
BASE TObject offset= 0type=66 Basic ROOT object
BASE TAtt3D offset= 0type= 03D attributes
Int_t m_KFcode offset= 16 type= 3Muon KF-code
Int_t m_MCParticle offset= 20 type= 3Muon position in MCParticles list
Int_t m_KFmother offset= 24 type= 3Muon mother KF-code
Int_t m_UseFlag offset= 28 type= 3Muon energy usage flag
Int_t m_Isolated offset= 32 type= 3Muon isolation
Float_t m_Eta offset= 36 type= 5Eta coordinate
Float_t m_Phi offset= 40 type= 5Phi coordinate
Float_t m_PT offset= 44 type= 5Transverse energy
Int_t m_Trigger offset= 48 type= 3Result of trigger
i= 0, TObject type= 66, offset= 0, len=1, method=0
i= 1, TAtt3D type= 0, offset= 0, len=1, method=142684688
i= 2, m_KFcode type= 23, offset= 16, len=5, method=0
i= 3, m_Eta type= 25, offset= 36, len=3, method=0
i= 4, m_Trigger type= 3, offset= 48, len=1, method=0
MakeProject has three parameters:
MakeProject(const char *dirname,const char *classes,Option_t *option)
The first is the directory name in which to place the generated header files. The second parameter is the name of
the classes to include in the project. By default, all classes are included. It recognizes the wild card character *, for
example, “ATLF*” includes all classes beginning with ATLF. The third parameter is an option with the following
values:
•“new” If the directory does not exist, it is created.
•
“
recreate
” If the directory does not exist, it is creates as in “new”, in addition if the directory does exist, all
existing files are deleted before creating the new files.
•
“
update
” The new classes are added to the existing directory and the existing classes are replaced with the new
definition. If the directory does not exist, it creates it as in “new”.
•
“+”: This option can be used in combination with the other three. It will create the necessary files to easily
build a shared library containing the class definitions.Specifically it will:
•
Generate a script called
MAKE
that builds the shared library containing the definition of all classes in the directory.
•Generate a LinkDef.hfiles to use with rootcling in MAKE.
•Run rootcling to generate a <dirname>ProjectDict.cxx file.
•Compile the <dirname>ProjectDict.cxxwith the current options in compiledata.h.
11.5. SCHEMA EVOLUTION 283
•Build a shared library<dirname>.so.
•
“++”:This option can be used instead of the single “+”. It does everything the single “+” does, and dynamically
loads the shared library <dirname>.so.
This example makes a directory called
MyProject
that will contain all class definitions from the
atlfast.root
file.
The necessary
makefile
to build a shared library are also created, and since the ‘++’ is appended, the shared library
is also loaded.
root[] f.MakeProject("MyProject","*","recreate++")
MakeProject has generated 0classes in MyProject
MyProject/MAKE file has been generated
Shared lib MyProject/MyProject.so has been generated
Shared lib MyProject/MyProject.so has been dynamically linked
The contents of MyProject:
root[] .! ls MyProject
ATLFCluster.h ATLFJet.h ATLFMiscMaker.h ATLFTrack.h
TMCParticle.h ATLFClusterMaker.h ATLFJetMaker.h ATLFMuon.h
ATLFElectron.h ATLFMCMaker.h ATLFMuonMaker.h ATLFElectronMaker.h
ATLFMaker.h ATLFPhoton.h ATLFHistBrowser.h ATLFMisc.h
ATLFPhotonMaker.h ATLFTrackMaker.h ATLFTrigger.h ATLFTriggerMaker.h
LinkDef.h MAKE MyProject.so MyProjectProjectDict.h
MyProjectProjectDict.cxx MyProjectProjectDict.o
Now you can load the shared library in any consecutive root session to use the atlfast classes.
root[]gSystem->Load("MyProject/MyProject")
root[]ATLFMuon muon
This is an example of a generated header file:
//////////////////////////////////////////////////////////
// This class has been generated by TFile::MakeProject
// (Thu Apr 5 10:18:37 2001 by ROOT version 3.00/06)
// from the TStreamerInfo in file atlfast.root
//////////////////////////////////////////////////////////
#ifndef ATLFMuon_h
#define ATLFMuon_h
#include "TObject.h"
#include "TAtt3D.h"
class ATLFMuon : public TObject , public TAtt3D {
public:
Int_t m_KFcode; //Muon KF-code
Int_t m_MCParticle; //Muon position in MCParticles list
Int_t m_KFmother; //Muon mother KF-code
Int_t m_UseFlag; //Muon energy usage flag
Int_t m_Isolated; //Muon isolation (1 for isolated)
Float_t m_Eta; //Eta coordinate
Float_t m_Phi; //Phi coordinate
Float_t m_PT; //Transverse energy
Int_t m_Trigger; //Result of trigger
ATLFMuon() {;}
virtual ~ATLFMuon() {;}
ClassDef(ATLFMuon,1)//
};
ClassImp(ATLFMuon)
#endif
284 CHAPTER 11. INPUT/OUTPUT
11.6 Migrating to ROOT 3
We will distinguish the following cases:
Case A
: You have your own
Streamer
method in your class implementation file. This also means that you have
specified MyClass in the LinkDef.h file.
•Keep MyClass - unchanged.
•Increment your class version id in ClassDef by 1, e.g. ClassDef(MyClass, 2)
•
Change your
Streamer
function in the following way: The old write block can be replaced by the new standard
Write. Change the read block to use the new scheme for the new versions and the old code for the old versions.
void MyClass::Streamer(TBuffer &R__b) {
// Stream an object of class MyClass.
if (R__b.IsReading()) {
UInt_t R__s, R__c;
Version_t R__v = R__b.ReadVersion(&R__s, &R__c);
if (R__v > 1) {
MyClass::Class()->ReadBuffer(R__b, this, R__v, R__s, R__c);
return;
}
// process old versions before automatic schema evolution
R__b >> xxxx;
R__b >> .. etc
R__b.CheckByteCount(R__s, R__c, MyClass::IsA()); // end of old versions
}else
MyClass::Class()->WriteBuffer(R__b,this);
}
Case B: You use the automatic Streamer in the dictionary file.
•
Move the old Streamer from the file generated by
rootcling
to your class implementation file, then modify the
Streamer function as in Case A above.
•Increment your class version id in ClassDef by 1, i.e.ClassDef(MyClass, 2)
•Add option “-” in the pragma line of LinkDef.
Case C
: You use the automatic
Streamer
in the dictionary file and you already use the option “+” in the
LinkDef
file. If the old automatic
Streamer
does not contain any statement using the function
WriteArray
, you have nothing
to do, except running
rootcling
again to regenerate the new form of the
Streamer
function, otherwise proceed like
for case B.
11.7 Compression and Performance
ROOT uses a compression algorithm based on the well-known
gzip
algorithm. It supports nine levels of compression.
The default for ROOT is one. The compression level can be set with the method
TFile::SetCompressionLevel
. The
experience with this algorithm shows that a compression level of 1.3 for raw data files and around two on most DST
files is the optimum. The choice of one for the default is a compromise between the time it takes to read and write the
object vs. the disk space savings.
To specify no compression, set the level to zero.
We recommend using compression when the time spent in I/O is small compared to the total processing time. If the
I/O operation is increased by a factor of 5 it is still a small percentage of the total time and it may compress the data
by a factor of 10. On the other hand if the time spend on I/O is large, compression may have a large impact on the
program’s performance.
The compression factor, i.e. the savings of disk space, varies with the type of data. A buffer with a same value array is
compressed so that the value is only written once. For example, a track has the mass of a pion that it is always the
same, and the charge of the pion that is either positive or negative. For 1000 pions, the mass will be written only
once, and the charge only twice (positive and negative). When the data is sparse, i.e. when there are many zeros, the
compression factor is also high.
11.8. REMOTELY ACCESS TO ROOT FILES VIA A ROOTD 285
Compression level Bytes Write Time (sec) Read Time (sec.)
0 1,004,998 4.77 0.07
1 438,366 6.67 0.05
5 429,871 7.03 0.06
9 426,899 8.47 0.05
The time to uncompress an object is small compared to the compression time and is independent of the selected
compression level. Note that the compression level may be changed at any time, but the new compression level will
only apply to newly written objects. Consequently, a ROOT file may contain objects with different compression levels.
This table shows four runs of the demo script that creates 15 histograms with different compression parameters. To
make the numbers more significant, the macro was modified to create 1000 histograms. We have included two more
examples to show the impact of compression on Trees in the next chapter.
11.8 Remotely Access to ROOT Files via a rootd
Reading and writing ROOT files over the net can be done by creating a
TNetFile
object instead of a
TFile
object.
Since the
TNetFile
class inherits from the
TFile
class, it has exactly the same interface and behavior. The only
difference is that it reads and writes to a remote rootd daemon.
11.8.1 TNetFile URL
TNetFile file names are in standard URL format with protocol “root”. The following are valid TNetFile URL’s:
root://hpsalo/files/aap.root
root://hpbrun.cern.ch/root/hsimple.root
root://pcna49a:5151/~na49/data/run821.root
root://pcna49d.cern.ch:5050//v1/data/run810.root
The only difference with the well-known http URL’s is that the root of the remote file tree is the remote user’s home
directory. Therefore an absolute pathname requires a
//
after the host or port (as shown in the last example above).
Further the expansion of the standard shell characters, like
~
,
$
,
..
, etc. is handled as expected. The default port
on which the remote
rootd
listens is 1094 and
TNetFile
(actually by
TUrl
that is used by
TNetFile
) assumes this
default port. The port number has been allocated by the IANA and is reserved for ROOT.
11.8.2 Remote Authentication
Connecting to a
rootd
daemon requires a remote user id and password.
TNetFile
supports several ways for you to
provide your login information:
•Setting it globally via the static methods TNetFile::SetUser and TNetFile::SetPasswd
•Via the ~/.netrc file (same format and file as used by ftp)
•Via command line prompt
•
Setting the SPR password file via the option
-P FILE
, i.e. the next line will start the
rootd
daemon using the files
$HOME/.srootdpass2.conf
and
$HOME/.srootdpass2
for SPR authentication:
rootd -P $HOME/.srootdpass2
11.8.3 A Simple Session
root[] TFile *f1 = TFile::Open("local/file.root","update")
root[] TFile *f2 = TFile::Open("root://pcna49a.cern.ch/data/file.root","new")
Name (pcna49a:rdm):
Password:
root[] TFile *f3 = TFile::Open("http://root.cern.ch/~rdm/hsimple.root")
root[] f3.ls()
TWebFile** http://root.cern.ch/~rdm/hsimple.root
TWebFile* http://root.cern.ch/~rdm/hsimple.root
KEY: TH1F hpx;1This is the px distribution
286 CHAPTER 11. INPUT/OUTPUT
KEY: TH2F hpxpy;1py vs px
KEY: TProfile hprof;1Profile of pz versus px
KEY: TNtuple ntuple;1Demo ntuple
root[] hpx.Draw()
11.8.4 The rootd Daemon
The
rootd
daemon works with the
TNetFile
class. It allows remote access to ROOT database files in read or read/write
mode. The
rootd
daemon can be found in the directory
$ROOTSYS/bin
. It can be started either via
inetd
or by hand
from the command line (no need to be super user). Its performance is comparable with NFS but while NFS requires all
kind of system permissions to setup,
rootd
can be started by any user. The simplest way to start
rootd
is by starting
it from the command line while being logged in to the remote machine. Once started
rootd
goes immediately in the
background (does not need
&
) and you can log out from the remote node. The only required argument is the range
of ports (specified using
-p port1-port2
).
rootd
will listen on the first available port in this range. You can also
specify
-p 0-N
to search relative to the service port specified in
/etc/services.
If a single port is specified (
rootd
-p 1094)
then no search is made. Unless started by
inetd (rootd -i)
, it prints information about the found port,
something like:
ROOTD_PORT=5151, ROOTD_PID=14433
before spawning the daemon. This way the user knows what
was used (eval ‘rootd‘ will set these as variables in Bourne-like shells). Also, rootd shows an error message (as well
as sending the syslog message) if there is any problem binding the port or forking the daemon.
Using TNetFile you can now read and write files on the remote machine.
In the example below,
rootd
runs on the remote node under user id
minuser
and searches for an available port into
the range 1094-1098. It finds and listens to port 1094. When creating a
TNetFile
object you have to specify the same
port number 1094 and use
minuser
(and corresponding password) as login id. When
rootd
is started in this way, you
can only login with the user id under which rootd was started on the remote machine.
hpsalo[] telnet fsgi02.fnal.gov
login: minuser
Password:
<fsgi02> rootd -p 1094-1098
ROOTD_PORT=1094
ROOTD_PID=14433
<fsgi02> exit
hpsalo[] root
root[] TFile *f = TFile::Open("root://fsgi02.fnal.gov:1094/file.root","new")
Name (fsgi02.fnal.gov:rdm): minuser
Password:
root[] f.ls()
However, you can make many connections since the original
rootd
will fork (spawn) a new
rootd
that will service the
requests from the
TNetFile
. The original
rootd
keeps listening on the specified port for other connections. Each time
a
TNetFile
makes a connection; it gets a new private
rootd
that will handle its requests. At the end of a ROOT,
session when all TNetFiles are closed only the original rootd will stay alive ready to service future TNetFiles.
11.8.5 Starting rootd via inetd
If you expect to often connect via
TNetFile
to a remote machine, it is more efficient to install
rootd
as a service of
the
inetd
super daemon. In this way, it is not necessary for each user to run a private
rootd
. However, this requires a
one-time modification of two system files (and super user privileges to do so). Add to
/etc/services
the line:
rootd
1094/tcp. To /etc/inetd.conf the line:
rootd stream tcp nowait root /usr/local/root/bin/rootd rootd -i
After these changes force
inetd
to reread its configuration file with: “
kill -HUP <pid inetd>
”. It is not necessary to
specify a port number in the URL given to
TNetFile
when the setup done this way.
TNetFile
assumes the default
port to be 1094 as specified above in the /etc/services file.
11.8.6 Command Line Arguments for rootd
rootd supports the following arguments:
11.9. READING ROOT FILES VIA APACHE WEB SERVER 287
•-i says that rootd is started by inetd
•-p port#-port# specifies the range of ports to be searched
•-p 0-N the service ports range in /etc/services
•-d level level of debug info written to syslogd
0 = no debug (default) 1 = minimum
2 = medium3 = maximum
11.9 Reading ROOT Files via Apache Web Server
By adding one ROOT specific module to your Apache web server, you can distribute ROOT files to any ROOT user.
There is no longer a need to send your files via FTP and risking (out of date) histograms or other objects. Your
latest up-to-date results are always accessible to all your colleagues. To access ROOT files via a web server, create a
TWebFile object instead of a TFile object with a standard URL as file name. For example:
root[] TWebFile f("http://root.cern.ch/~rdm/hsimple.root")
root[] f.ls()
TWebFile** http://root.cern.ch/~rdm/hsimple.root
TWebFile* http://root.cern.ch/~rdm/hsimple.root
KEY: TH1F hpx;1This is the px distribution
KEY: TH2F hpxpy;1py vs px
KEY: TProfile hprof;1Profile of pz versus px
KEY: TNtuple ntuple;1Demo ntuple
root[] hpx.Draw()
Since
TWebFile
inherits from
TFile
all
TFile
operations work as expected. However, due to the nature of a web server
a
TWebFile
is a read-only file. A
TWebFile
is ideally suited to read relatively small objects (like histograms or other
data analysis results). Although possible, you don’t want to analyze large TTree’s via a TWebFile.
Here follows a step-by-step recipe for making your Apache 1.1 or 1.2 web server ROOT aware:
•
Go to your Apache source directory and add the file ftp://root.cern.ch/root/mod_root.c or ftp://root.cern.ch/
root/mod_root133.c when your Apache server is >1.2 (rename the file mod_root.c).
•Add to the end of the Configuration file the line: Module root_module mod_root.o
•Run the Configure script
•Type make
•Copy the new httpd to its expected place
•Go to the conf directory and add at the end of the srm.conf file the line:AddHandler root-action root
•Restart the httpd server
11.9.1 Using the General Open Function of TFile
To make life simple we provide a general function to open any type of file (except shared memory files of class
TMapFile
).
This functionality is provided by the static TFile::Open() function:
TFile *TFile::Open(const Text_t *name,Option_t *option="",
const Text_t *title="",Int_t compress,Int_t netopt)
Depending on the
name
argument, the function returns a
TFile
, a
TNetFile
or a
TWebFile
object. In case a
TNetFile
URL specifies a local file, a
TFile
object will be returned (and of course no login information is needed). The arguments
of the Open() function are the same as the ones for the TFile constructor.
Using
ReOpen()
method it is possible to reopen a file with a different access mode, like from READ to UPDATE
or from NEW, CREATE, RECREATE, UPDATE to READ. Thus the mode argument can be either “READ” or
“UPDATE”. The method returns:
288 CHAPTER 11. INPUT/OUTPUT
•0 in case the mode was successfully modified;
•1 in case the mode did not change (it was already as requested or there were wrong input arguments);
•-1 in case of failure. In the last case the file cannot be used anymore.
11.10 XML Interface
A new module
xml
as implemented by Sergey Linev (GSI). It is an optional package that can be used to save a canvas
into
file.xml
file format instead of
file.root
. XML files do not have any advantages compared to the normal ROOT
files, except that the information in these files can be edited via a normal editor. The main motivation for this new
format is to facilitate the communication with other non ROOT applications. Currently writing and reading XML files
is limited to ROOT applications. It is our intention to develop a simple reader independent of the ROOT libraries that
could be used as an example for real applications.
The XML format should be used only for small data volumes, typically histogram files, pictures, geometries, calibrations.
The XML file is built in memory before being dumped to disk. Like for normal ROOT files, XML files use the same
I/O mechanism exploiting the ROOT/Cling dictionary. Any class having a dictionary can be saved in XML format.
This first implementation does not support subdirectories or trees.
The shared library
libRXML.so
may be loaded dynamically via
gSystem->Load("libRXML")
. This library is also
automatically loaded by the plug-in manager as soon a XML file is created. To create an XTM file, simply specify
a filename with an .xml extension when calling
TFile::Open
.
TFile::Open
will recognize that you are trying to
open an XML file and return a
TXMLFile
object. When a XML file is open in write mode, one can use the normal
TObject::Write to write an object in the file.
// example of a session saving a histogram to a XML file
TFile *f = TFile::Open("Example.xml","recreate");
TH1F *h = new TH1F("h","test",1000,-2,2)
h->FillRandom("gaus");
h->Write();
delete f;
// example of a session saving a histogram to a XML file
TFile *f = TFile::Open("Example.xml");
TH1F *h = (TH1F*)f->Get("h");
h->Draw();
The canvas can be saved as a XML file format via File menu / Save or Save As menu entries. One can do also:
canvas->Print("Example.xml");
Chapter 12
Trees
12.1 Why Should You Use a Tree?
In the “Input/Output” chapter, we saw how objects can be saved in ROOT files. In case you want to store large
quantities of same-class objects, ROOT has designed the
TTree
and
TNtuple
classes specifically for that purpose. The
TTree
class is optimized to reduce disk space and enhance access speed. A
TNtuple
is a
TTree
that is limited to only
hold floating-point numbers; a
TTree
on the other hand can hold all kind of data, such as objects or arrays in addition
to all the simple types.
When using a
TTree
, we fill its branch buffers with leaf data and the buffers are written to disk when it is full. Branches,
buffers, and leafs, are explained a little later in this chapter, but for now, it is important to realize that each object is
not written individually, but rather collected and written a bunch at a time.
This is where the
TTree
takes advantage of compression and will produce a much smaller file than if the objects were
written individually. Since the unit to be compressed is a buffer, and the
TTree
contains many same-class objects, the
header of the objects can be compressed.
The
TTree
reduces the header of each object, but it still contains the class name. Using compression, the class name
of each same-class object has a good chance of being compressed, since the compression algorithm recognizes the bit
pattern representing the class name. Using a
TTree
and compression the header is reduced to about 4 bytes compared
to the original 60 bytes. However, if compression is turned off, you will not see these large savings.
The
TTree
is also used to optimize the data access. A tree uses a hierarchy of branches, and each branch can be read
independently from any other branch. Now, assume that
Px
and
Py
are data members of the event, and we would like
to compute Px2 + Py2 for every event and histogram the result.
If we had saved the million events without a TTree we would have to:
•read each event in its entirety into memory
•extract the Px and Py from the event
•compute the sum of the squares
•fill a histogram
We would have to do that a million times! This is very time consuming, and we really do not need to read the entire
event, every time. All we need are two little data members (
Px
and
Py
). On the other hand, if we use a tree with one
branch containing
Px
and another branch containing
Py
, we can read all values of
Px
and
Py
by only reading the
Px
and Py branches. This makes the use of the TTree very attractive.
12.2 A Simple TTree
This script builds a
TTree
from an ASCII file containing statistics about the staff at CERN. This script,
staff.C
and
its input file staff.dat are in $ROOTSYS/tutorials/tree.
{
// example of macro to read data from an ascii file and
// create a root file with an histogram and a TTree
gROOT->Reset();
289
290 CHAPTER 12. TREES
// the structure to hold the variables for the branch
struct staff_t {
Int_t cat;
Int_t division;
Int_t flag;
Int_t age;
Int_t service;
Int_t children;
Int_t grade;
Int_t step;
Int_t nation;
Int_t hrweek;
Int_t cost;
};
staff_t staff;
// continued...
// open the ASCII file
FILE *fp = fopen("staff.dat","r");
char line[81];
// create a new ROOT file
TFile *f = new TFile("staff.root","RECREATE");
// create a TTree
TTree *tree = new TTree("T","staff data from ascii file");
// create one branch with all information from the stucture
tree->Branch("staff",&staff.cat,"cat/I:division:flag:age:service:
children:grade:step:nation:hrweek:cost");
// fill the tree from the values in ASCII file
while (fgets(&line,80,fp)) {
sscanf(&line[0],"%d%d%d%d",&staff.cat,&staff.division,
&staff.flag,&staff.age);
sscanf(&line[13],"%d%d%d%d",&staff.service,&staff.children,
&staff.grade,&staff.step);
sscanf(&line[24],"%d%d%d",&staff.nation,&staff.hrweek,
&staff.cost);
tree->Fill();
}
// check what the tree looks like
tree->Print();
fclose(fp);
f->Write();
}
The script declares a structure called
staff_t
, with several integers representing the relevant attribute of a staff
member. It opens the ASCII file, creates a ROOT file and a
TTree
. Then it creates one branch with the
TTree::Branch
method. The first parameter of the
Branch
method is the branch name. The second parameter is the address from
which the first leaf is to be read. In this example it is the address of the structure
staff
. Once the branch is defined,
the script reads the data from the ASCII file into the
staff_t
structure and fills the
tree
. The ASCII file is closed,
and the ROOT file is written to disk saving the
tree
. Remember, trees and histograms are created in the current
directory, which is the file in our example. Hence an f->Write()saves the tree.
12.3 Show an Entry with TTree::Show
An easy way to access one entry of a tree is the use the
TTree::Show
method. For example to look at the 10th entry
in the staff.root tree:
root[] TFile f("staff.root")
root[] T->Show(10)
======> EVENT:10
Category = 361
12.4. PRINT THE TREE STRUCTURE WITH TTREE::PRINT 291
Flag = 15
Age = 51
Service = 29
Children = 0
Grade = 7
Step = 13
Hrweek = 40
Cost = 7599
Division = PS
Nation = FR
12.4 Print the Tree Structure with TTree::Print
A helpful command to see the tree structure meaning the number of entries, the branches and the leaves, is
TTree::Print
.
root[] T->Print()
**********************************************************************
*Tree :T : staff data from ascii file *
*Entries :3354 : Total = 245417 bytes File Size = 59945*
* Tree compression factor = 2.90 *
**********************************************************************
*Br 0:staff :Category/I:Flag:Age:Service:Children:Grade:... *
* | Cost *
*Entries :3354 : Total Size = 154237 bytes File Size = 32316 *
*Baskets : 3: Basket Size = 32000 bytes Compression= 2.97 *
12.5 Scan a Variable the Tree with TTree::Scan
The TTree::Scan method shows all values of the list of leaves separated by a colon.
root[] T->Scan("Cost:Age:Children")
************************************************
* Row * Cost * Age * Children *
************************************************
*0*11975 *58 *0*
*1*10228 *63 *0*
*2*10730 *56 *2*
*3*9311 *61 *0*
*4*9966 *52 *2*
*5*7599 *60 *0*
*6*9868 *53 *1*
*7*8012 *60 *1*
...
12.6 The Tree Viewer
The tree viewer is a quick and easy way to examine a tree. To start the tree viewer, open a file and object browser.
Right click on a
TTree
and select
StartViewer
. You can also start the tree viewer from the command line. First load
the viewer library.
root[] TFile f("staff.root")
root[] T->StartViewer()
If you want to start a tree viewer without a tree, you need to load the tree player library first:
root[] gSystem->Load("libTreeViewer.so")
root[] new TTreeViewer()
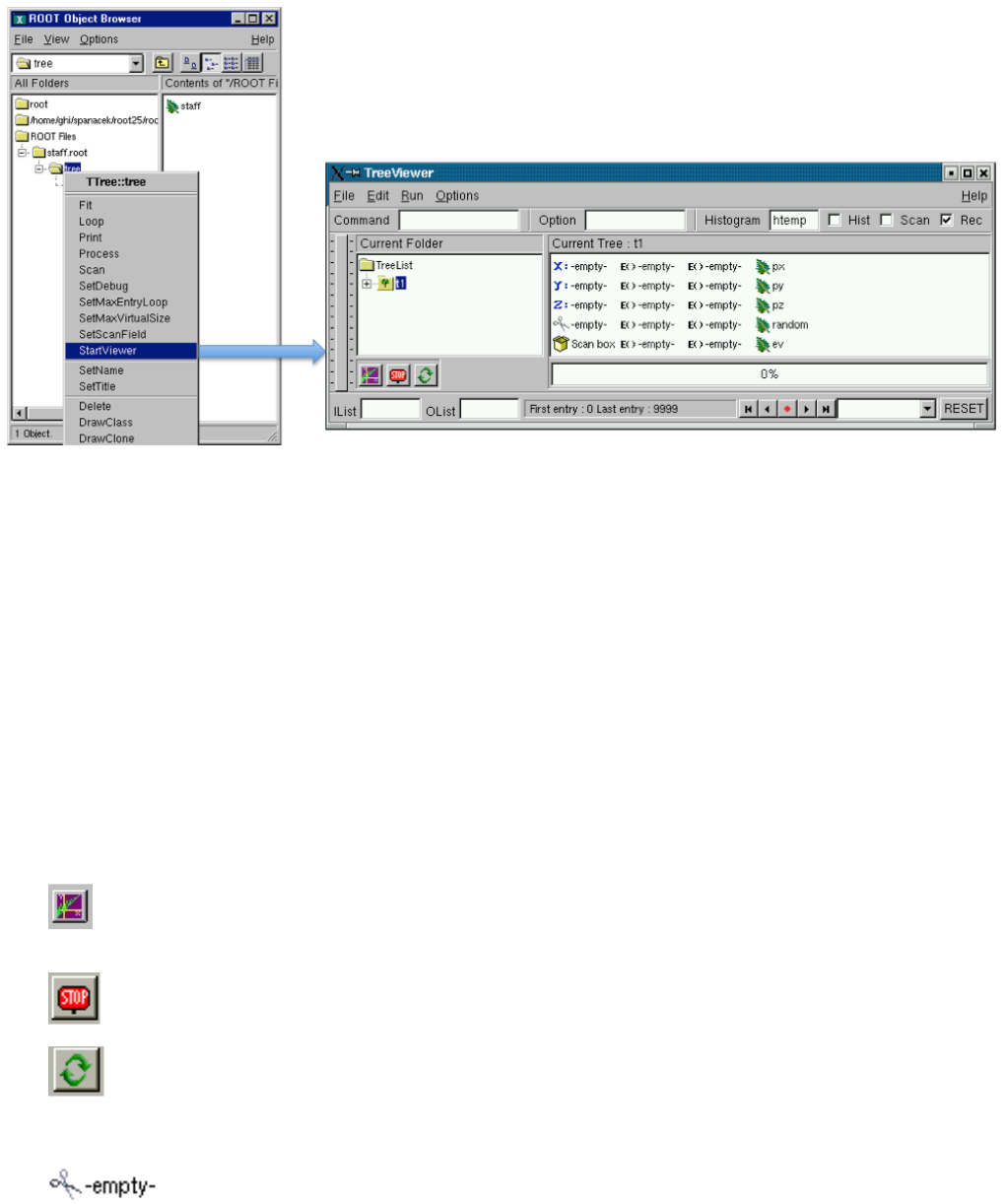
292 CHAPTER 12. TREES
Figure 12.1: Activating the tree viewer
The figure above shows how the tree viewer looks like for the example file
staff.root
. The left panel contains the list
of trees and their branches; in this case there is only one tree. You can add more trees with the File-Open command to
open the file containing the new tree, then use the context menu on the right panel, select
SetTreeName
and enter the
name of the tree to add. On the right are the leaves or variables in the tree. You can double click on any leaf to a
histogram it.
The toolbar in the upper part can be used for user commands, changing the drawing option and the histogram name.
The lower part contains three picture buttons that draw a histogram, stop the current command, and refresh the tree.
The three check buttons toggle the following:
Hist- the histogram drawing mode;
Scan- enables redirecting of TTree::Scancommand in an ASCII file;
Rec - enables recording of the last issued command.
•
To draw more than one dimension you can drag and drop any leaf to the
X,Y,Z
boxes“. Then push the
Draw button, witch is marked with the purple icon on the bottom left.
•All commands can be interrupted at any time by pressing this button.
•
The method
TTree::Refresh
is called by pressing the refresh button in
TTreeViewer
. It redraws the
current exposed expression. Calling
TTree::Refresh
is useful when a tree is produced by a writer process and
concurrently analyzed by one or more readers.
•
To add a cut/weight to the histogram, enter an expression in the “cut box”. The cut box is the
one with the scissor icon.
Below them there are two text widgets for specifying the input and output event lists. A Tree Viewer session is made
by the list of user-defined expressions and cuts, applying to a specified tree. A session can be saved using File /
SaveSource
menu or the
SaveSource
method from the context menu of the right panel. This will create a macro
having as default name treeviewer.C that can be ran at any time to reproduce the session.
Besides the list of user-defined expressions, a session may contain a list of RECORDS. A record can be produced in
the following way: dragging leaves/expression on X/Y/Z; changing drawing options; clicking the RED button on the
bottom when happy with the histogram
NOTE that just double clicking a leaf will not produce a record: the histogram must be produced when clicking the
DRAW button on the bottom-left. The records will appear on the list of records in the bottom right of the tree viewer.
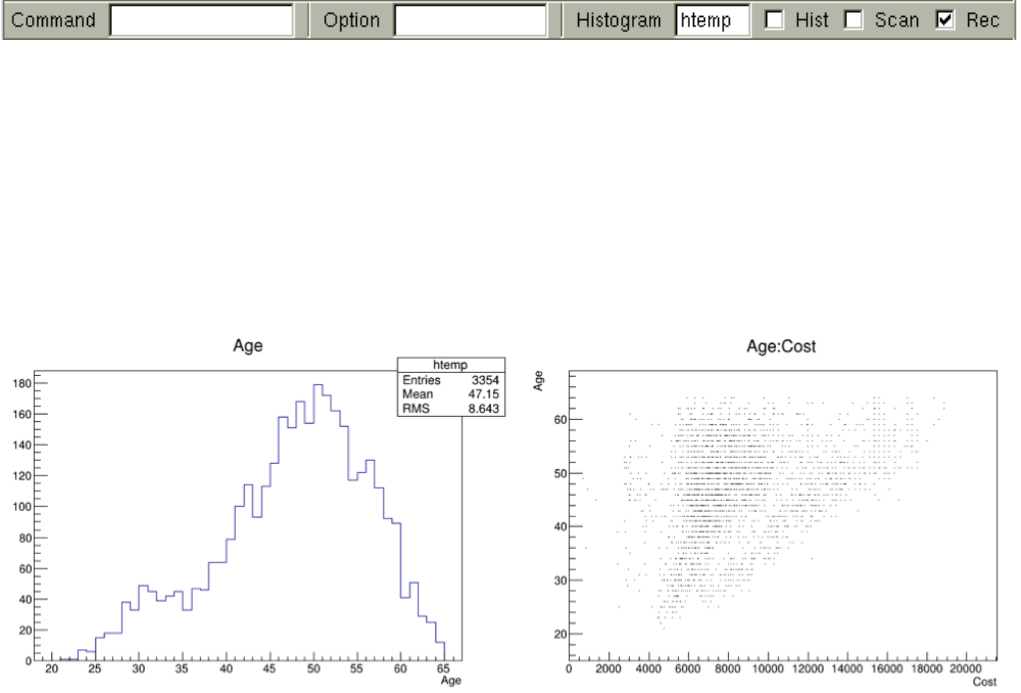
12.7. CREATING AND SAVING TREES 293
Selecting a record will draw the corresponding histogram. Records can be played using the arrow buttons near to the
record button. When saving the session, the list of records is being saved as well.
Records have a default name corresponding to the Z: Y: X selection, but this can be changed using
SetRecordName()
method from the right panel context menu. You can create a new expression by right clicking on any of the
E()
boxes.
The expression can be dragged and dropped into any of the boxes (
X, Y, Z, Cut
, or
Scan
). To scan one or more
variables, drop them into the Scan box, then double click on the box. You can also redirect the result of the scan to a
file by checking the Scan box on top.
When the “
Rec
” box is checked, the
Draw
and
Scan
commands are recorded in the history file and echoed on the
command line. The “Histogram” text box contains the name of the resulting histogram. By default it is
htemp
. You
can type any name, if the histogram does not exist it will create one. The Option text box contains the list of Draw
options. See “Draw Options”. You can select the options with the Options menu. The Command box lets you enter
any command that you could also enter on the command line. The vertical slider on the far left side can be used to
select the minimum and maximum of an event range. The actual start and end index are shown in on the bottom in
the status window.
There is an extensive help utility accessible with the Help menu. The
IList
and
OList
are to
specify
an input list of
entry indices and a name for the output list respectively. Both need to be of type
TList
and contain integers of entry
indices. These lists are described below in the paragraph “Error! Reference source not found.”.
Figure 12.2: A couple of graphs
The first one is a plot of the age distribution, the second a scatter plot of the cost vs. age. The second one was generated
by dragging the age leaf into the Y-box and the cost leaf into the X-box, and pressing the Draw button. By default,
this will generate a scatter plot. Select a different option, for example "lego" to create a 2D histogram.
12.7 Creating and Saving Trees
This picture shows the TTree class:
To create a
TTree
we use its constructor. Then we design our data layout and add the branches. A tree can be created
by giving a name and title:
TTree t("MyTree","Example Tree");
12.7.1 Creating a Tree from a Folder Hierarchy
An alternative way to create a tree and organize it is to use folders (see “Folders and Tasks”). You can build a folder
structure and create a tree with branches for each of the sub-folders:
TTree folder_tree("MyFolderTree","/MyFolder");
The second argument
"/MyFolder"
is the top folder, and the “/” signals the
TTree
constructor that this is a folder not
just the title. You fill the tree by placing the data into the folder structure and calling TTree::Fill.
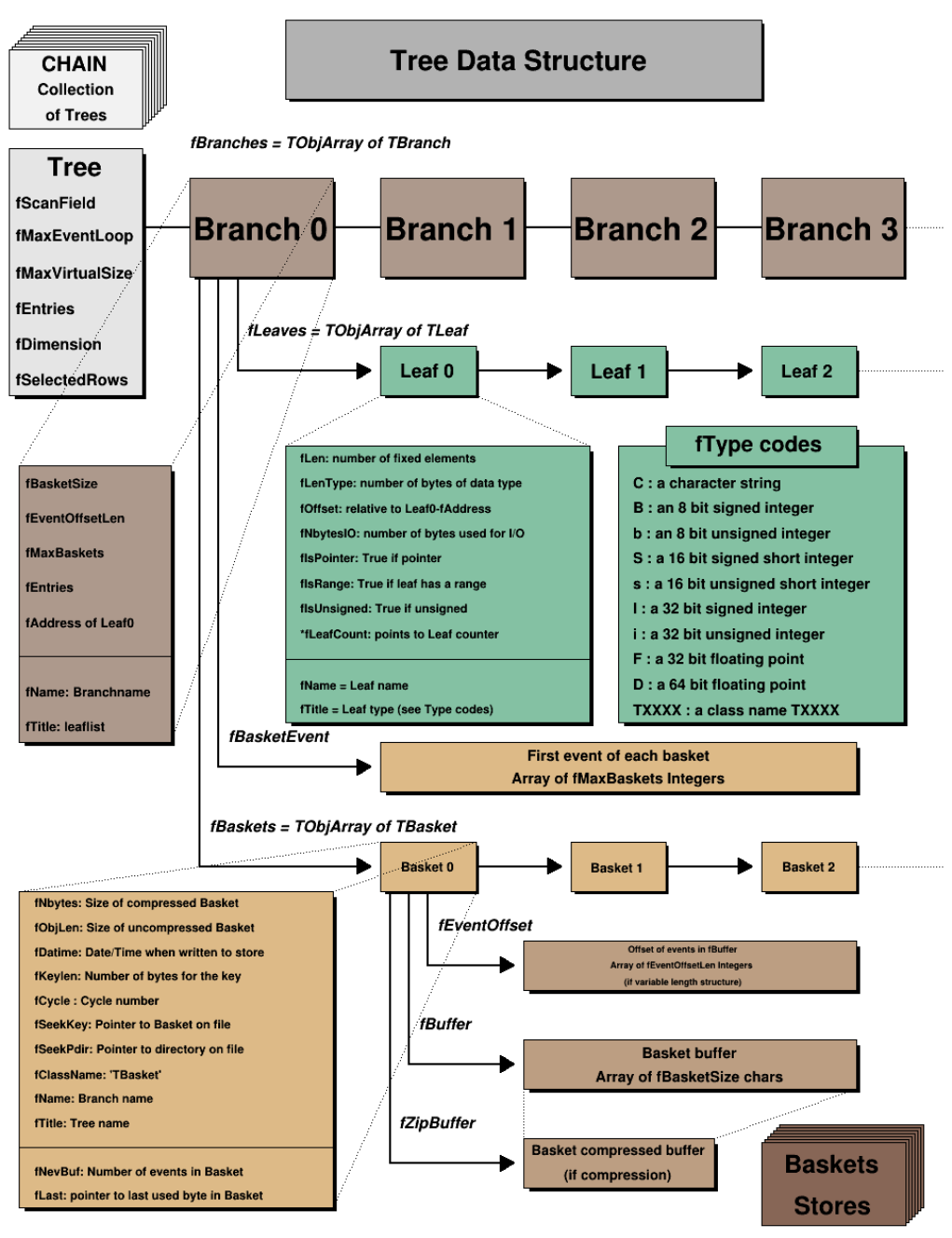
294 CHAPTER 12. TREES
Figure 12.3: The TTree class
12.7. CREATING AND SAVING TREES 295
12.7.2 Tree and TRef Objects
MyTree->BranchRef();
This call requests the construction of an optional branch supporting table of references (
TRefTable
). This branch
(
TBranchRef
) will keep all the information needed to find the branches containing referenced objects at each
Tree::Fill
,
the branch numbers containing the referenced objects are saved in the table of references. When the Tree header is
saved (via
TTree::Write
for example), the branch is saved, keeping the information with the pointers to the branches
having referenced objects. Enabling this optional table, allow
TTree::Draw
to automatically load the branches needed
to dereference a TRef (or TRefArray) object.
12.7.3 Autosave
Autosave
gives the option to save all branch buffers every
n
byte. We recommend using
Autosave
for large acquisitions.
If the acquisition fails to complete, you can recover the file and all the contents since the last
Autosave
. To set the number
of bytes between
Autosave
you can use the
TTree::SetAutosave()
method. You can also call
TTree::Autosave in
the acquisition loop every nentry.
12.7.4 Trees with Circular Buffers
When a
TTree
is memory resident, you set it up so that it retains retain only the last few entries. For example, this
can be very useful for monitoring purpose.
void TTree::SetCircular(Long64_t maxEntries);
where
maxEntries
is the maximum number of entries to be kept in the buffers. When the number of entries exceeds
this value, the first entries in the
Tree
are deleted and the buffers used again. An example of a script using a circular
buffer is shown below:
void circular() {
gROOT->cd(); //make sure that the Tree is memory resident
TTree *T = new TTree("T","test circular buffers");
TRandom r;
Float_t px,py,pz;
Double_t random;
UShort_t i;
T->Branch("px",&px,"px/F");
T->Branch("py",&py,"py/F");
T->Branch("pz",&pz,"pz/F");
T->Branch("random",&random,"random/D");
T->Branch("i",&i,"i/s");
T->SetCircular(20000);
for (i=0;i<65000; i++) {
r.Rannor(px,py);
pz = px*px + py*py;
random = r.Rndm();
T->Fill();
}
T->Print();
}
12.7.5 Size of TTree in the File
When writing a
TTree
to a file, if the file size reaches the value stored in the
TTree::GetMaxTreeSize()
, the current
file is closed and a new file is created. If the original file is named “
myfile.root
”, subsequent files are named
“myfile_1.root”, “myfile_2.root”, etc.
Currently, the automatic change of file is restricted to the case where the tree is in the top level directory. The file
should not contain sub-directories. Before switching to a new file, the tree header is written to the current file, then
the current file is closed. To process the multiple files created by ChangeFile(), one must use a TChain.
296 CHAPTER 12. TREES
The new file name has a suffix “
_N
” where
N
is equal to
fFileNumber+1
. By default a Root session starts with
fFileNumber=0
. One can set
fFileNumber
to a different value via
TTree::SetFileNumber()
. In case a file named
“
_N
” already exists, the function will try a file named “
__N
”, then “
___N
”, etc. The maximum tree size can be set
via the static function
TTree::SetMaxTreeSize()
. The default value of
fgMaxTreeSize
is 1.9 GB. If the current file
contains other objects (like TH1 and TTree), these objects are automatically moved to the new file.
12.7.6 User Info Attached to a TTree Object
The function
TTree::GetUserInfo()
allows adding any object defined by a user to the tree that is not depending on
the entry number. For example:
tree->GetUserInfo()->Add(myruninfo);
12.7.7 Indexing a Tree
Use TTree::BuildIndex(), to build an index table using expressions depending on the value in the leaves.
tree->BuildIndex(majorname, minorname);
The index is built in the following way:
•a pass on all entries is made like in TTree::Draw()
•var1 = majorname
•var2 = minorname
•sel = 231 ×majorname +minorname
•for each entry in the tree the sel expression is evaluated and the results array is sorted into fIndexValues
Once the index is computed, using the
TTree::GetEntryWithIndex(majornumber, minornumber)
one entry can be
retrieved. Example:
// to create an index using leaves Run and Event
tree.BuildIndex("Run","Event");
// to read entry corresponding to Run=1234 and Event=56789
tree.GetEntryWithIndex(1234,56789);
Note that
majorname
and
minorname
may be expressions using original tree variables e.g.: “
run-90000
”, “
event +3*xx
”.
In case an expression is specified, the equivalent expression must be computed when calling
GetEntryWithIndex()
.
To build an index with only majorname, specify minorname="0" (default).
Note that once the index is built, it can be saved with the TTree object with:
tree.Write(); //if the file has been open in "update" mode
The most convenient place to create the index is at the end of the filling process just before saving the tree header. If a
previous index was computed, it is redefined by this new call.
Note that this function can also be applied to a
TChain
. The return value is the number of entries in the Index (< 0
indicates failure).
12.8 Branches
The organization of branches allows the designer to optimize the data for the anticipated use. The class for a branch is
called
TBranch
. If two variables are independent, and the designer knows the variables will not be used together, they
should be placed on separate branches. If, however, the variables are related, such as the coordinates of a point, it is
most efficient to create one branch with both coordinates on it. A variable on a
TBranch
is called a leaf (yes -
TLeaf
).
Another point to keep in mind when designing trees is that branches of the same
TTree
can be written to separate
files. To add a
TBranch
to a
TTree
we call the method
TTree::Branch()
. Note that we DO NOT use the
TBranch
constructor.
The
TTree::Branch
method has several signatures. The branch type differs by what is stored in it. A branch can hold
an entire object, a list of simple variables, contents of a folder, contents of a
TList
, or an array of objects. Let’s see
some examples. To follow along you will need the shared library
libEvent.so
. First, check if it is in
$ROOTSYS/test
.
If it is, copy it to your own area. If it is not there, you have to build it by typing make in $ROOTSYS/test.
12.9. ADDING A BRANCH TO HOLD A LIST OF VARIABLES 297
12.9 Adding a Branch to Hold a List of Variables
As in the very first example (
staff.root
) the data we want to save is a list of simple variables, such as integers or
floats. In this case, we use the following TTree::Branch signature:
tree->Branch("Ev_Branch",&event,
"temp/F:ntrack/I:nseg:nvtex:flag/i");
The first parameter is the branch name.
The second parameter is the address from which the first variable is to be read. In the code above, “event” is a
structure with one float and three integers and one unsigned integer. You should not assume that the compiler aligns
the elements of a structure without gaps. To avoid alignment problems, you need to use structures with same length
members. If your structure does not qualify, you need to create one branch for each element of the structure.
The leaf name is NOT used to pick the variable out of the structure, but is only used as the name for the leaf. This
means that the list of variables needs to be in a structure in the order described in the third parameter.
This third parameter is a string describing the leaf list. Each leaf has a name and a type separated by a “/” and it is
separated from the next leaf by a “:”.
<Variable>/<type>:<Variable>/<type>
The example on the next line has two leafs: a floating-point number called temp and an integer named ntrack.
"temp/F:ntrack/I:"
The type can be omitted and if no type is given, the same type as the previous variable is assumed. This leaf list has
three integers called ntrack,nseg, and nvtex.
"ntrack/I:nseg:nvtex"
There is one more rule: when no type is given for the very first leaf, it becomes a
float
(F). This leaf list has three
floats called temp,mass, and px.
"temp:mass:px"
The symbols used for the type are:
•C: a character string terminated by the 0 character
•B: an 8 bit signed integer
•b: an 8 bit unsigned integer
•S: a 16 bit signed integer
•s: a 16 bit unsigned integer
•I: a 32 bit signed integer
•i: a 32 bit unsigned integer
•L: a 64 bit signed integer
•l: a 64 bit unsigned integer
•F: a 32 bit floating point
•D: a 64 bit floating point
•O: [the letter ‘o’, not a zero] a boolean (Bool_t)
The type is used for a byte count to decide how much space to allocate. The variable written is simply the block of
bytes starting at the starting address given in the second parameter. It may or may not match the leaf list depending
on whether or not the programmer is being careful when choosing the leaf address, name, and type.
By default, a variable will be copied with the number of bytes specified in the type descriptor symbol. However, if the
type consists of two characters, the number specifies the number of bytes to be used when copying the variable to the
output buffer. The line below describes ntrack to be written as a 16-bit integer (rather than a 32-bit integer).
"ntrack/I2"
298 CHAPTER 12. TREES
With this Branch method, you can also add a leaf that holds an entire array of variables. To add an array of floats use
the f[n] notation when describing the leaf.
Float_t f[10];
tree->Branch("fBranch",f,"f[10]/F");
You can also add an array of variable length:
{
TFile *f = new TFile("peter.root","recreate");
Int_t nPhot;
Float_t E[500];
TTree* nEmcPhotons = new TTree("nEmcPhotons","EMC Photons");
nEmcPhotons->Branch("nPhot",&nPhot,"nPhot/I");
nEmcPhotons->Branch("E",E,"E[nPhot]/F");
}
See “Example 2: A Tree with a C Structure” below (
$ROOTSYS/tutorials/tree/tree2.C
) and
staff.C
at the
beginning of this chapter.
12.10 Adding a TBranch to Hold an Object
To write a branch to hold an event object, we need to load the definition of the
Event
class, which is in
$ROOTSYS/test/libEvent.so
(if it doesn’t exist type make in
$ROOTSYS/test
). An object can be saved in a tree if a
ROOT dictionary for its class has been generated and loaded.
root[] .L libEvent.so
First, we need to open a file and create a tree.
root[] TFile *f = new TFile("AFile.root","RECREATE")
root[] TTree *tree = new TTree("T","A Root Tree")
We need to create a pointer to an
Event
object that will be used as a reference in the
TTree::Branch
method. Then
we create a branch with the TTree::Branch method.
root[] Event *event = new Event()
root[] tree->Branch("EventBranch","Event",&event,32000,99)
To add a branch to hold an object we use the signature above. The first parameter is the name of the branch. The
second parameter is the name of the class of the object to be stored. The third parameter is the address of a pointer to
the object to be stored.
Note that it is an address of a pointer to the object, not just a pointer to the object.
The fourth parameter is the buffer size and is by default 32000 bytes. It is the number of bytes of data for that branch
to save to a buffer until it is saved to the file. The last parameter is the split-level, which is the topic of the next
section. Static class members are not part of an object and thus not written with the object. You could store them
separately by collecting these values in a special “status” object and write it to the file outside of the tree. If it makes
sense to store them for each object, make them a regular data member.
12.10.1 Setting the Split-level
To split a branch means to create a sub-branch for each data member in the object. The split-level can be set to 0 to
disable splitting or it can be set to a number between 1 and 99 indicating the depth of splitting.
If the split-level is set to zero, the whole object is written in its entirety to one branch. The
TTree
will look like the
one on the right, with one branch and one leaf holding the entire event object.
When the split-level is 1, an object data member is assigned a branch. If the split-level is 2, the data member objects
will be split also, and a split level of 3 its data members objects, will be split. As the split-level increases so does the
splitting depth. The ROOT default for the split-level is 99. This means the object will be split to the maximum.
12.10. ADDING A TBRANCH TO HOLD AN OBJECT 299
Figure 12.4: A split and not split tree
12.10.1.1 Memory Considerations when Splitting a Branch
Splitting a branch can quickly generate many branches. Each branch has its own buffer in memory. In case of many
branches (say more than 100), you should adjust the buffer size accordingly. A recommended buffer size is 32000 bytes
if you have less than 50 branches. Around 16000 bytes if you have less than 100 branches and 4000 bytes if you have
more than 500 branches. These numbers are recommended for computers with memory size ranging from 32MB to
256MB. If you have more memory, you should specify larger buffer sizes. However, in this case, do not forget that your
file might be used on another machine with a smaller memory configuration.
12.10.1.2 Performance Considerations when Splitting a Branch
A split branch is faster to read, but slightly slower to write. The reading is quicker because variables of the same type
are stored consecutively and the type does not have to be read each time. It is slower to write because of the large
number of buffers as described above. See "
Performance Benchmarks" for performance impact of split and non-split mode.
12.10.1.3 Rules for Splitting
When splitting a branch, variables of different types are handled differently. Here are the rules that apply when splitting
a branch.
•If a data member is a basic type, it becomes one branch of class TBranchElement.
•A data member can be an array of basic types. In this case, one single branch is created for the array.
•
A data member can be a pointer to an array of basic types. The length can vary, and must be specified in the
comment field of the data member in the class definition. See “Input/Output”.
•
Pointer data member are not split, except for pointers to a
TClonesArray
. The
TClonesArray
(pointed to) is
split if the split level is greater than two. When the split level is one, the TClonesArray is not split.
•
If a data member is a pointer to an object, a special branch is created. The branch will be filled by calling the
class Streamer function to serialize the object into the branch buffer.
•
If a data member is an object, the data members of this object are split into branches according to the split-level
(i.e. split-level > 2).
•Base classes are split when the object is split.
•Abstract base classes are never split.
•All STL containers are supported.
300 CHAPTER 12. TREES
// STL vector of vectors of TAxis*
vector<vector<TAxis *> > fVectAxis;
// STL map of string/vector
map<string,vector<int> > fMapString;
// STL deque of pair
deque<pair<float,float> > fDequePair;
•
As of ROOT 4.01/00, only
std::vector
of objects can be split. Support for splitting the other type of STL
containers will be introduced in the near future.
•C-structure data members are not supported in split mode.
•An object that is not split may be slow to browse.
•A STL container that is not split will not be accessible in the browser.
12.10.2 Exempt a Data Member from Splitting
If you are creating a branch with an object and in general you want the data members to be split, but you want to
exempt a data member from the split. You can specify this in the comment field of the data member:
class Event : public TObject {
private:
EventHeader fEvtHdr; //|| Don't split the header
12.10.3 Adding a Branch to Hold a TClonesArray
ROOT has two classes to manage arrays of objects. The
TObjArray
can manage objects of different classes, and the
TClonesArray
that specializes in managing objects of the same class (hence the name Clones Array).
TClonesArray
takes advantage of the constant size of each element when adding the elements to the array. Instead of allocating
memory for each new object as it is added, it reuses the memory. Here is an example of the time a
TClonesArray
can save over a
TObjArray
. We have 100,000 events, and each has 10,000 tracks, which gives 1,000,000,000 tracks.
If we use a
TObjArray
for the tracks, we implicitly make a call to new and a corresponding call to delete for each
track. The time it takes to make a pair of new/delete calls is about 7 s (10-6). If we multiply the number of tracks
by 7 s, (1,000,000,000 * 7 * 10-6) we calculate that the time allocating and freeing memory is about 2 hours. This is
the chunk of time saved when a
TClonesArray
is used rather than a
TObjArray
. If you do not want to wait 2 hours
for your tracks (or equivalent objects), be sure to use a
TClonesArray
for same-class objects arrays. Branches with
TClonesArrays
use the same method (
TTree::Branch
) as any other object described above. If splitting is specified
the objects in the TClonesArray are split, not the TClonesArray itself.
12.10.4 Identical Branch Names
When a top-level object (say
event
), has two data members of the same class the sub branches end up with identical
names. To distinguish the sub branch we must associate them with the master branch by including a “
.
” (a dot) at
the end of the master branch name. This will force the name of the sub branch to be
master.sub
branch instead of
simply
sub
branch. For example, a tree has two branches
Trigger
and
MuonTrigger
, each containing an object of the
same class (Trigger). To identify uniquely the sub branches we add the dot:
tree->Branch("Trigger.","Trigger",&b1,8000,1);
tree->Branch("MuonTrigger.","Trigger",&b2,8000,1);
If
Trigger
has three members,
T1
,
T2
,
T3
, the two instructions above will generate sub branches called:
Trigger.T1
,
Trigger.T2,Trigger.T3,MuonTrigger.T1,MuonTrigger.T2, andMuonTrigger.T3.
12.11 Adding a Branch with a Folder
Use the syntax below to add a branch from a folder:
tree->Branch("/aFolder");
This method creates one branch for each element in the folder. The method returns the total number of branches
created.
12.12. ADDING A BRANCH WITH A COLLECTION 301
12.12 Adding a Branch with a Collection
This Branch method creates one branch for each element in the collection.
tree->Branch(*aCollection, 8000,99);
// Int_t TTree::Branch(TCollection *list, Int_t bufsize,
// Int_t splitlevel, const char *name)
The method returns the total number of branches created. Each entry in the collection becomes a top level branch
if the corresponding class is not a collection. If it is a collection, the entry in the collection becomes in turn top
level branches, etc. The split level is decreased by 1 every time a new collection is found. For example if
list
is a
TObjArray*
•If splitlevel = 1, one top level branch is created for each element of the TObjArray.
•
If
splitlevel = 2
, one top level branch is created for each array element. If one of the array elements is a
TCollection, one top level branch will be created for each element of this collection.
In case a collection element is a
TClonesArray
, the special Tree constructor for
TClonesArray
is called. The collection
itself cannot be a TClonesArray. If name is given, all branch names will be prefixed with name_.
IMPORTANT NOTE1: This function should not be called if
splitlevel<1
.IMPORTANT NOTE2: The branches
created by this function will have names corresponding to the collection or object names. It is important to give names
to collections to avoid misleading branch names or identical branch names. By default collections have a name equal to
the corresponding class name, e.g. the default name of TList is “TList”.
12.13 Examples for Writing and Reading Trees
The following sections are examples of writing and reading trees increasing in complexity from a simple tree with
a few variables to a tree containing folders and complex Event objects. Each example has a named script in the
$ROOTSYS/tutorials/tree directory. They are called tree1.C to tree4.C. The examples are:
•tree1.C: a tree with several simple (integers and floating point) variables.
•tree2.C
: a tree built from a C structure (
struct
). This example uses the
Geant3
C wrapper as an example of a
FORTRAN common block ported to C with a C structure.
•tree3.C: in this example, we will show how to extend a tree with a branch from another tree with the Friends
feature. These trees have branches with variable length arrays. Each entry has a variable number of tracks, and
each track has several variables.
•tree4.C:
a tree with a class (
Event
). The class Event is defined in
$ROOTSYS/test
. In this example we first
encounter the impact of splitting a branch.
Each script contains the main function, with the same name as the file (i.e.
tree1
), the function to write -
tree1w
,
and the function to read -
tree1r
. If the script is not run in batch mode, it displays the tree in the browser and tree
viewer. To study the example scripts, you can either execute the main script, or load the script and execute a specific
function. For example:
// execute the function that writes, reads, shows the tree
root[] x tree1.C
// use ACLiC to build shared library, check syntax, execute
root[] x tree1.C++
// Load the script and select a function to execute
root[] L tree1.C
root[] tree1w()
root[] tree1r()
12.14 Example 1: A Tree with Simple Variables
This example shows how to write, view, and read a tree with several simple (integers and floating-point) variables.
302 CHAPTER 12. TREES
12.14.1 Writing the Tree
Below is the function that writes the tree (
tree1w
). First, the variables are defined (
px, py, pz, random
and
ev
).
Then we add a branch for each of the variables to the tree, by calling the TTree::Branch method for each variable.
void tree1w(){
// create a tree file tree1.root - create the file, the Tree and
// a few branches
TFile f("tree1.root","recreate");
TTree t1("t1","a simple Tree with simple variables");
Float_t px, py, pz;
Double_t random;
Int_t ev;
t1.Branch("px",&px,"px/F");
t1.Branch("py",&py,"py/F");
t1.Branch("pz",&pz,"pz/F");
t1.Branch("ev",&ev,"ev/I");
// fill the tree
for (Int_t i=0; i<10000; i++) {
gRandom->Rannor(px,py);
pz = px*px + py*py;
random = gRandom->Rndm();
ev = i;
t1.Fill();
}
// save the Tree heade; the file will be automatically closed
// when going out of the function scope
t1.Write();
}
12.14.1.1 Creating Branches with A single Variable
This is the signature of TTree::Branch to create a branch with a list of variables:
TBranch* TTree::Branch(const char* name,void* address,
const char* leaflist,
Int_t bufsize = 32000)
The first parameter is the branch name. The second parameter is the address from which to read the value. The third
parameter is the leaf list with the name and type of each leaf. In this example, each branch has only one leaf. In the
box below, the branch is named px and has one floating point type leaf also called px.
t1.Branch("px",&px,"px/F");
12.14.1.2 Filling the Tree
First we find some random values for the variables. We assign
px
and
py
a Gaussian with mean = 0 and sigma = 1
by calling
gRandom->Rannor(px,py)
, and calculate
pz
. Then we call the
TTree::Fill()
method. The call
t1.Fill()
fills all branches in the tree because we have already organized the tree into branches and told each branch where to
get the value from. After this script is executed we have a ROOT file called
tree1.root
with a tree called
t1
. There
is a possibility to fill branches one by one using the method
TBranch::Fill()
. In this case you do not need to call
TTree::Fill()
method. The entries can be set by
TTree::SetEntries(Double_t n)
. Calling this method makes
sense only if the number of existing entries is null.
12.14.2 Viewing the Tree
In the right panel of the ROOT object browse are the branches:
ev
,
px
,
py
,
pz
, and
random
. Note that these are shown
as leaves because they are “end” branches with only one leaf. To histogram a leaf, we can simply double click on it in
the browser. This is how the tree
t1
looks in the Tree Viewer. Here we can add a cut and add other operations for
histogramming the leaves. See “The Tree Viewer”. For example, we can plot a two dimensional histogram.
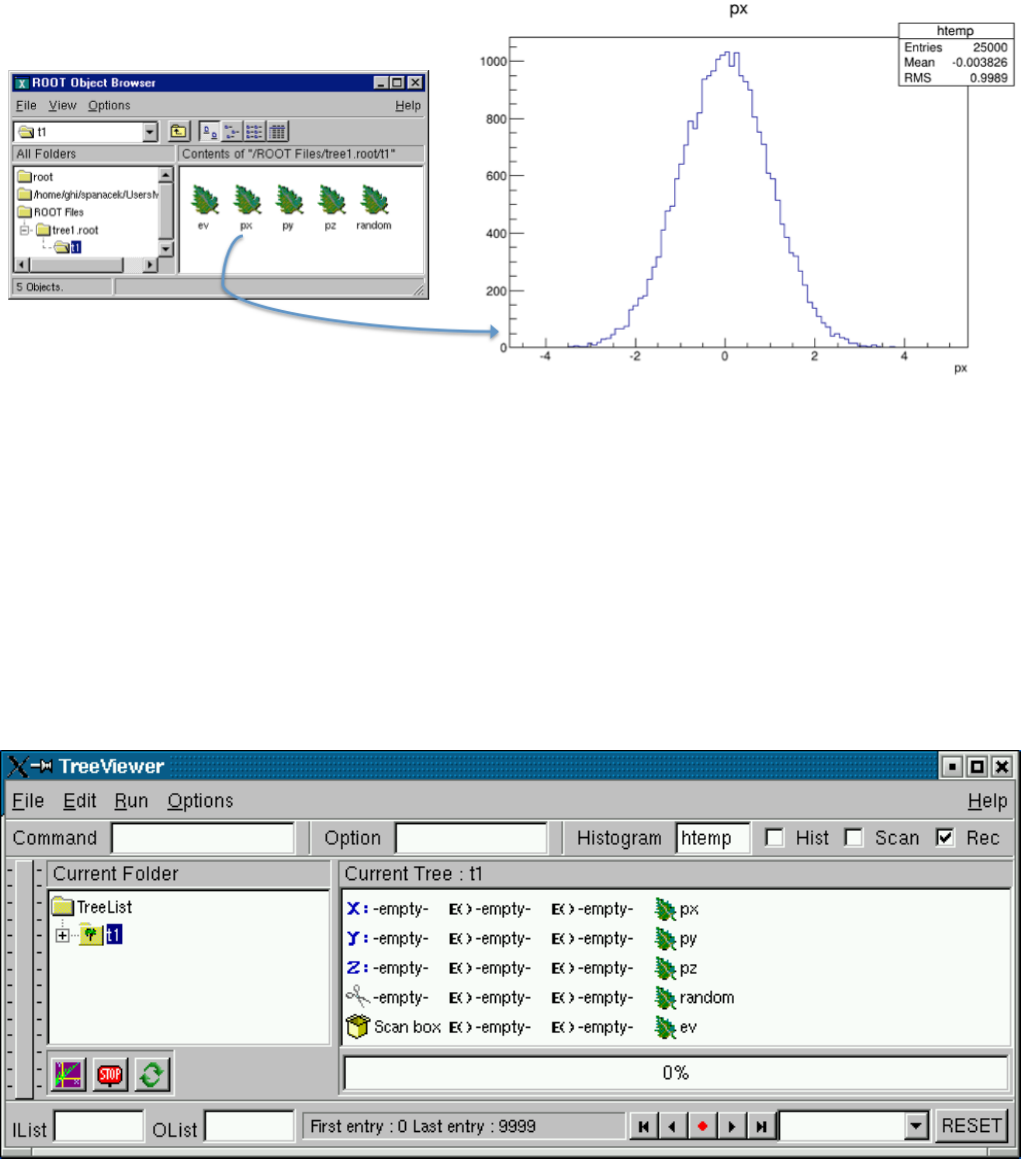
12.14. EXAMPLE 1: A TREE WITH SIMPLE VARIABLES 303
Figure 12.5: The tree1.root file and its tree in the browser and a leaf histogram
Figure 12.6: The tree viewer
304 CHAPTER 12. TREES
12.14.3 Reading the Tree
The
tree1r
function shows how to read the tree and access each entry and each leaf. We first define the variables to
hold the read values.
Float_t px, py, pz;
Then we tell the tree to populate these variables when reading an entry. We do this with the method
TTree::SetBranchAddress
. The first parameter is the branch name, and the second is the address of the variable
where the branch data is to be placed. In this example, the branch name is
px
. This name was given when the tree
was written (see tree1w). The second parameter is the address of the variable px.
t1->SetBranchAddress("px",&px);
12.14.3.1 GetEntry
Once the branches have been given the address, a specific entry can be read into the variables with the method
TTree::GetEntry(n)
. It reads all the branches for entry (n) and populates the given address accordingly. By default,
GetEntry()
reuses the space allocated by the previous object for each branch. You can force the previous object to be
automatically deleted if you call mybranch.SetAutoDelete(kTRUE) (default is kFALSE).
Consider the example in $ROOTSYS/test/Event.h. The top-level branch in the tree Tis declared with:
Event *event = 0;
// event must be null or point to a valid object;
// it must be initialized
T.SetBranchAddress("event",&event);
When reading the Tree, one can choose one of these 3 options:
Option 1:
for (Int_t i = 0; i<nentries; i++) {
T.GetEntry(i);
//the object event has been filled at this point
}
This is the default and recommended way to create an object of the class Event.It will be pointed by event.
At the following entries,
event
will be overwritten by the new data. All internal members that are
TObject
* are
automatically deleted. It is important that these members be in a valid state when
GetEntry
is called. Pointers must
be correctly initialized. However these internal members will not be deleted if the characters “
->
” are specified as the
first characters in the comment field of the data member declaration.
The pointer member is read via the
pointer->Streamer(buf)
if “
->
” is specified. In this case, it is assumed that
the pointer is never null (see pointer
TClonesArray *fTracks
in the
$ROOTSYS/test/Event
example). If “
->
” is not
specified, the pointer member is read via
buf >> pointer
. In this case the pointer may be null. Note that the option
with “->” is faster to read or write and it also consumes less space in the file.
Option 2 - the option AutoDelete is set:
TBranch *branch = T.GetBranch("event");
branch->SetAddress(&event);
branch->SetAutoDelete(kTRUE);
for (Int_t i=0; i<nentries; i++) {
T.GetEntry(i); // the object event has been filled at this point
}
At any iteration, the GetEntry deletes the object event and a new instance of Event is created and filled.
Option 3 - same as option 1, but you delete the event yourself:
12.15. EXAMPLE 2: A TREE WITH A C STRUCTURE 305
for (Int_t i=0; i<nentries; i++) {
delete event;
event = 0;//EXTREMELY IMPORTANT
T.GetEntry(i);
// the objrect event has been filled at this point
}
It is strongly recommended to use the default option 1. It has the additional advantage that functions like
TTree::Draw
(internally calling
TTree::GetEntry
) will be functional even when the classes in the file are not available. Reading
selected branches is quicker than reading an entire entry. If you are interested in only one branch, you can use the
TBranch::GetEntry method and only that branch is read. Here is the script tree1r:
void tree1r(){
// read the Tree generated by tree1w and fill two histograms
// note that we use "new" to create the TFile and TTree objects,
// to keep them alive after leaving this function.
TFile *f = new TFile("tree1.root");
TTree *t1 = (TTree*)f->Get("t1");
Float_t px, py, pz;
Double_t random;
Int_t ev;
t1->SetBranchAddress("px",&px);
t1->SetBranchAddress("py",&py);
t1->SetBranchAddress("pz",&pz);
t1->SetBranchAddress("random",&random);
t1->SetBranchAddress("ev",&ev);
// create two histograms
TH1F *hpx = new TH1F("hpx","px distribution",100,-3,3);
TH2F *hpxpy = new TH2F("hpxpy","py vs px",30,-3,3,30,-3,3);
//read all entries and fill the histograms
Int_t nentries = (Int_t)t1->GetEntries();
for (Int_t i=0; i<nentries; i++) {
t1->GetEntry(i);
hpx->Fill(px);
hpxpy->Fill(px,py);
}
// We do not close the file. We want to keep the generated
// histograms we open a browser and the TreeViewer
if (gROOT->IsBatch()) return;
new TBrowser ();
t1->StartViewer();
//In the browser, click on "ROOT Files", then on "tree1.root"
//You can click on the histogram icons in the right panel to draw
//them in the TreeViewer, follow the instructions in the Help.
}
12.15 Example 2: A Tree with a C Structure
The executable script for this example is $ROOTSYS/tutorials/tree/tree2.C.In this example we show:
•how to build branches from a C structure
•how to make a branch with a fixed length array
•how to make a branch with a variable length array
•how to read selective branches
•how to fill a histogram from a branch
•how to use TTree::Draw to show a 3D plot
A C structure (
struct
) is used to build a ROOT tree. In general we discourage the use of C structures
,
we recommend
using a class instead. However, we do support them for legacy applications written in C or FORTRAN. The example
306 CHAPTER 12. TREES
struct
holds simple variables and arrays. It maps to a Geant3 common block
/gctrak/.
This is the definition of the
common block/structure:
const Int_t MAXMEC = 30;
// PARAMETER (MAXMEC=30)
// COMMON/GCTRAK/VECT(7),GETOT,GEKIN,VOUT(7)
// + ,NMEC,LMEC(MAXMEC)
// + ,NAMEC(MAXMEC),NSTEP
// + ,PID,DESTEP,DESTEL,SAFETY,SLENG
// + ,STEP,SNEXT,SFIELD,TOFG,GEKRAT,UPWGHT
typedef struct {
Float_t vect[7];
Float_t getot;
Float_t gekin;
Float_t vout[7];
Int_t nmec;
Int_t lmec[MAXMEC];
Int_t namec[MAXMEC];
Int_t nstep;
Int_t pid;
Float_t destep;
Float_t destel;
Float_t safety;
Float_t sleng;
Float_t step;
Float_t snext;
Float_t sfield;
Float_t tofg;
Float_t gekrat;
Float_t upwght;
} Gctrak_t;
When using Geant3, the common block is filled by Geant3 routines at each step and only the
TTree::Fill
method
needs to be called. In this example we emulate the Geant3 step routine with the
helixStep
function. We also emulate
the filling of the particle values. The calls to the Branch methods are the same as if Geant3 were used.
void helixStep(Float_t step, Float_t *vect, Float_t *vout)
{
// extrapolate track in constant field
Float_t field = 20;// field in kilogauss
enum Evect {kX,kY,kZ,kPX,kPY,kPZ,kPP};
vout[kPP] = vect[kPP];
Float_t h4 = field*2.99792e-4;
Float_t rho = -h4/vect[kPP];
Float_t tet = rho*step;
Float_t tsint = tet*tet/6;
Float_t sintt = 1- tsint;
Float_t sint = tet*sintt;
Float_t cos1t = tet/2;
Float_t f1 = step*sintt;
Float_t f2 = step*cos1t;
Float_t f3 = step*tsint*vect[kPZ];
Float_t f4 = -tet*cos1t;
Float_t f5 = sint;
Float_t f6 = tet*cos1t*vect[kPZ];
vout[kX] = vect[kX] + (f1*vect[kPX] - f2*vect[kPY]);
vout[kY] = vect[kY] + (f1*vect[kPY] + f2*vect[kPX]);
vout[kZ] = vect[kZ] + (f1*vect[kPZ] + f3);
vout[kPX] = vect[kPX] + (f4*vect[kPX] - f5*vect[kPY]);
vout[kPY] = vect[kPY] + (f4*vect[kPY] + f5*vect[kPX]);
12.15. EXAMPLE 2: A TREE WITH A C STRUCTURE 307
vout[kPZ] = vect[kPZ] + (f4*vect[kPZ] + f6);
}
12.15.1 Writing the Tree
void tree2w() {
// write tree2 example
//create a Tree file tree2.root
TFile f("tree2.root","recreate");
//create the file, the Tree
TTree t2("t2","a Tree with data from a fake Geant3");
// declare a variable of the C structure type
Gctrak_t gstep;
// add the branches for a subset of gstep
t2.Branch("vect",gstep.vect,"vect[7]/F");
t2.Branch("getot",&gstep.getot,"getot/F");
t2.Branch("gekin",&gstep.gekin,"gekin/F");
t2.Branch("nmec",&gstep.nmec,"nmec/I");
t2.Branch("lmec",gstep.lmec,"lmec[nmec]/I");
t2.Branch("destep",&gstep.destep,"destep/F");
t2.Branch("pid",&gstep.pid,"pid/I");
//Initialize particle parameters at first point
Float_t px,py,pz,p,charge=0;
Float_t vout[7];
Float_t mass = 0.137;
Bool_t newParticle = kTRUE;
gstep.step = 0.1;
gstep.destep = 0;
gstep.nmec = 0;
gstep.pid = 0;
//transport particles
for (Int_t i=0; i<10000; i++) {
//generate a new particle if necessary (Geant3 emulation)
if (newParticle) {
px = gRandom->Gaus(0,.02);
py = gRandom->Gaus(0,.02);
pz = gRandom->Gaus(0,.02);
p = TMath::Sqrt(px*px+py*py+pz*pz);
charge = 1;
if (gRandom->Rndm() < 0.5) charge = -1;
gstep.pid += 1;
gstep.vect[0]=0;
gstep.vect[1]=0;
gstep.vect[2]=0;
gstep.vect[3] = px/p;
gstep.vect[4] = py/p;
gstep.vect[5] = pz/p;
gstep.vect[6] = p*charge;
gstep.getot = TMath::Sqrt(p*p + mass*mass);
gstep.gekin = gstep.getot - mass;
newParticle = kFALSE;
}
// fill the Tree with current step parameters
t2.Fill();
//transport particle in magnetic field (Geant3 emulation)
helixStep(gstep.step, gstep.vect, vout);
308 CHAPTER 12. TREES
//make one step
//apply energy loss
gstep.destep = gstep.step*gRandom->Gaus(0.0002,0.00001);
gstep.gekin -= gstep.destep;
gstep.getot = gstep.gekin + mass;
gstep.vect[6]= charge*TMath::Sqrt(gstep.getot*gstep.getot
- mass*mass);
gstep.vect[0] = vout[0];
gstep.vect[1] = vout[1];
gstep.vect[2] = vout[2];
gstep.vect[3] = vout[3];
gstep.vect[4] = vout[4];
gstep.vect[5] = vout[5];
gstep.nmec = (Int_t)(5*gRandom->Rndm());
for (Int_t l=0; l<gstep.nmec; l++) gstep.lmec[l] = l;
if (gstep.gekin < 0.001) newParticle = kTRUE;
if (TMath::Abs(gstep.vect[2])>30) newParticle = kTRUE;
}
//save the Tree header. The file will be automatically
// closed when going out of the function scope
t2.Write();
}
12.15.1.1 Adding a Branch with a Fixed Length Array
At first, we create a tree and create branches for a subset of variables in the C structure
Gctrak_t
. Then we add several
types of branches. The first branch reads seven floating-point values beginning at the address of
’gstep.vect’
. You
do not need to specify
&gstep.vect
, because in C and C++ the array variable holds the address of the first element.
t2.Branch("vect",gstep.vect,"vect[7]/F");
t2.Branch("getot",&gstep.getot,"getot/F");
t2.Branch("gekin",&gstep.gekin,"gekin/F");
12.15.1.2 Adding a Branch with a Variable Length Array
The next two branches are dependent on each other. The first holds the length of the variable length array and the
second holds the variable length array. The
lmec
branch reads
nmec
number of integers beginning at the address
gstep.lmec.
t2.Branch("nmec",&gstep.nmec,"nmec/I");
t2.Branch("lmec",gstep.lmec,"lmec[nmec]/I");
The variable nmec is a random number and is reset for each entry.
gstep.nmec = (Int_t)(5*gRandom->Rndm());
12.15.1.3 Filling the Tree
In this emulation of Geant3, we generate and transport particles in a magnetic field and store the particle parameters
at each tracking step in a ROOT tree.
12.15.2 Analysis
In this analysis, we do not read the entire entry we only read one branch. First, we set the address for the branch
to the file
dstep
, and then we use the
TBranch::GetEntry
method. Then we fill a histogram with the
dstep
branch
entries, draw it and fit it with a Gaussian. In addition, we draw the particle’s path using the three values in the vector.
Here we use the
TTree::Draw
method. It automatically creates a histogram and plots the 3 expressions (see Trees in
Analysis).
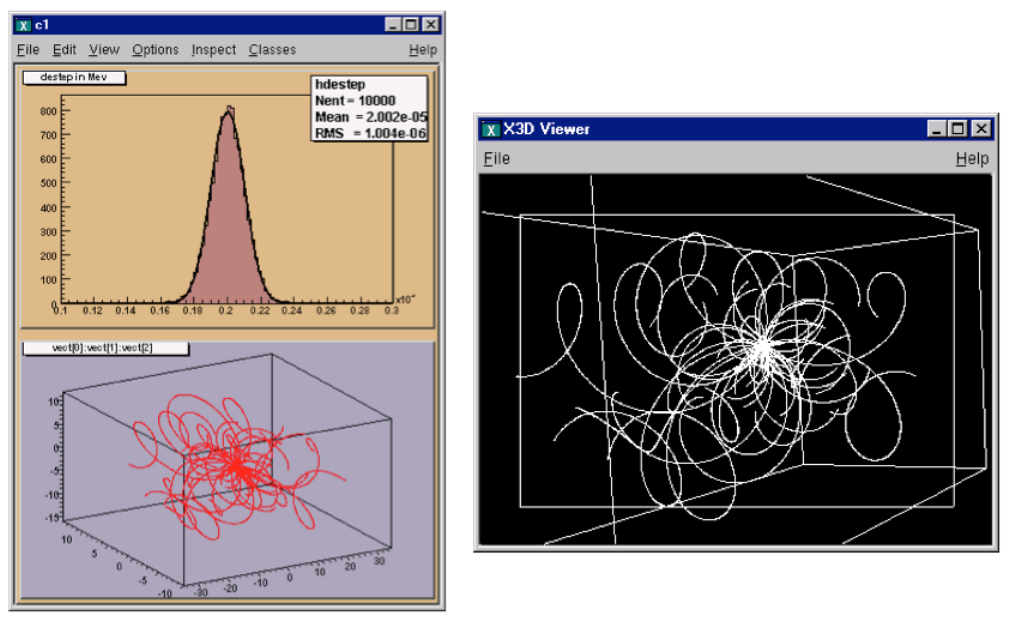
12.15. EXAMPLE 2: A TREE WITH A C STRUCTURE 309
void tree2r() {
// read the Tree generated by tree2w and fill one histogram
// we are only interested by the destep branch
// note that we use "new" to create the TFile and TTree objects because we
// want to keep these objects alive when we leave this function
TFile *f = new TFile("tree2.root");
TTree *t2 = (TTree*)f->Get("t2");
static Float_t destep;
TBranch *b_destep = t2->GetBranch("destep");
b_destep->SetAddress(&destep);
//create one histogram
TH1F *hdestep = new TH1F("hdestep","destep in Mev",100,1e-5,3e-5);
//read only the destep branch for all entries
Int_t nentries = (Int_t)t2->GetEntries();
for (Int_t i=0;i<nentries;i++) {
b_destep->GetEntry(i);
// fill the histogram with the destep entry
hdestep->Fill(destep);
}
// we do not close the file; we want to keep the generated histograms;
// we fill a 3-d scatter plot with the particle step coordinates
TCanvas *c1 = new TCanvas("c1","c1",600,800);
c1->SetFillColor(42);
c1->Divide(1,2);
c1->cd(1);
hdestep->SetFillColor(45);
hdestep->Fit("gaus");
c1->cd(2);
gPad->SetFillColor(37); // continued...
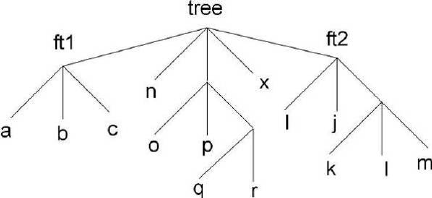
310 CHAPTER 12. TREES
t2->SetMarkerColor(kRed);
t2->Draw("vect[0]:vect[1]:vect[2]");
if (gROOT->IsBatch()) return;
// invoke the x3d viewer
gPad->GetViewer3D("x3d");
}
12.16 Example 3: Adding Friends to Trees
In this example, we will show how to extend a tree with a branch from another tree with the Friends feature.
12.16.1 Adding a Branch to an Existing Tree
You may want to add a branch to an existing tree. For example, if one variable in the tree was computed with a certain
algorithm, you may want to try another algorithm and compare the results. One solution is to add a new branch, fill it,
and save the tree. The code below adds a simple branch to an existing tree. Note that the
kOverwrite
option in the
Write method overwrites the existing tree. If it is not specified, two copies of the tree headers are saved.
void tree3AddBranch() {
TFile f("tree3.root","update");
Float_t new_v;
TTree *t3 = (TTree*)f->Get("t3");
TBranch *newBranch = t3-> Branch("new_v",&new_v,"new_v/F");
//read the number of entries in the t3
Int_t nentries = (Int_t)t3->GetEntries();
for (Int_t i = 0; i < nentries; i++){
new_v= gRandom->Gaus(0,1);
newBranch->Fill();
}
t3->Write("",TObject::kOverwrite); // save only the new version of
// the tree
}
Adding a branch is often not possible because the tree is in a read-only file and you do not have permission to save
the modified tree with the new branch. Even if you do have the permission, you risk loosing the original tree with an
unsuccessful attempt to save the modification. Since trees are usually large, adding a branch could extend it over the
2GB limit. In this case, the attempt to write the tree fails, and the original data is may also be corrupted. In addition,
adding a branch to a tree enlarges the tree and increases the amount of memory needed to read an entry, and therefore
decreases the performance. For these reasons, ROOT offers the concept of friends for trees (and chains). We encourage
you to use TTree::AddFriend rather than adding a branch manually.
12.16.2 TTree::AddFriend
A tree keeps a list of friends. In the context of a tree (or a chain), friendship means unrestricted access to the friends
data. In this way it is much like adding another branch to the tree without taking the risk of damaging it. To add a
friend to the list, you can use the
TTree::AddFriend
method. The
TTree
(
tree
) below has two friends (
ft1
and
ft2
)
and now has access to the variables a,b,c,i,j,k,l and m.
The
AddFriend
method has two parameters, the first is the tree name and the second is the name of the ROOT file
where the friend tree is saved.
AddFriend
automatically opens the friend file. If no file name is given, the tree called
ft1 is assumed to be in the same file as the original tree.
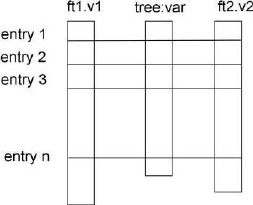
12.16. EXAMPLE 3: ADDING FRIENDS TO TREES 311
tree.AddFriend("ft1","friendfile1.root");
If the friend tree has the same name as the original tree, you can give it an alias in the context of the friendship:
tree.AddFriend("tree1 = tree","friendfile1.root");
Once the tree has friends, we can use
TTree::Draw
as if the friend’s variables were in the original tree. To specify
which tree to use in the Draw method, use the syntax:
<treeName>.<branchname>.<varname>
If the variablename is enough to identify uniquely the variable, you can leave out the tree and/or branch name.
For example, these commands generate a 3-d scatter plot of variable “
var
” in the
TTree tree
versus variable
v1
inTTree ft1versus variablev2in **TTree**ft2‘.
tree.AddFriend("ft1","friendfile1.root");
tree.AddFriend("ft2","friendfile2.root");
tree.Draw("var:ft1.v1:ft2.v2");
The picture illustrates the access of the tree and its friends with a Draw command.
When
AddFriend
is called, the ROOT file is automatically opened and the friend tree (
ft1)
header is read into memory.
The new friend (
ft1
) is added to the list of friends of
tree
. The number of entries in the friend must be equal or
greater to the number of entries of the original tree. If the friend tree has fewer entries, a warning is given and the
missing entries are not included in the histogram.
Use TTree::GetListOfFriends to retrieve the list of friends from a tree.
When the tree is written to file (
TTree::Write
), the friends list is saved with it. Moreover, when the tree is retrieved,
the trees on the friends list are also retrieved and the friendship restored. When a tree is deleted, the elements of the
friend list are also deleted. It is possible to declare a friend tree that has the same internal structure (same branches
and leaves) as the original tree, and compare the same values by specifying the tree.
tree.Draw("var:ft1.var:ft2.var");
The example code is in $ROOTSYS/tutorials/tree/tree3.C. Here is the script:
void tree3w() {
// Example of a Tree where branches are variable length arrays
// A second Tree is created and filled in parallel.
// Run this script with .x tree3.C
// In the function treer, the first Tree is open.
// The second Tree is declared friend of the first tree.
// TTree::Draw is called with variables from both Trees.
const Int_t kMaxTrack = 500;
Int_t ntrack;
Int_t stat[kMaxTrack];
Int_t sign[kMaxTrack];
Float_t px[kMaxTrack];
Float_t py[kMaxTrack];
Float_t pz[kMaxTrack];
Float_t pt[kMaxTrack];
Float_t zv[kMaxTrack];
Float_t chi2[kMaxTrack];
312 CHAPTER 12. TREES
Double_t sumstat;
// create the first root file with a tree
TFile f("tree3.root","recreate");
TTree *t3 = new TTree("t3","Reconst ntuple");
t3->Branch("ntrack",&ntrack,"ntrack/I");
t3->Branch("stat",stat,"stat[ntrack]/I");
t3->Branch("sign",sign,"sign[ntrack]/I");
t3->Branch("px",px,"px[ntrack]/F");
t3->Branch("py",py,"py[ntrack]/F");
t3->Branch("pz",pz,"pz[ntrack]/F");
t3->Branch("zv",zv,"zv[ntrack]/F");
t3->Branch("chi2",chi2,"chi2[ntrack]/F");
// create the second root file with a different tree
TFile fr("tree3f.root","recreate");
TTree *t3f = new TTree("t3f","a friend Tree");
t3f->Branch("ntrack",&ntrack,"ntrack/I");
t3f->Branch("sumstat",&sumstat,"sumstat/D");
t3f->Branch("pt",pt,"pt[ntrack]/F");
// Fill the trees
for (Int_t i=0;i<1000;i++) {
Int_t nt = gRandom->Rndm()*(kMaxTrack-1);
ntrack = nt;
sumstat = 0;
// set the values in each track
for (Int_t n=0;n<nt;n++) {
stat[n] = n%3;
sign[n] = i%2;
px[n] = gRandom->Gaus(0,1);
py[n] = gRandom->Gaus(0,2);
pz[n] = gRandom->Gaus(10,5);
zv[n] = gRandom->Gaus(100,2);
chi2[n] = gRandom->Gaus(0,.01);
sumstat += chi2[n];
pt[n] = TMath::Sqrt(px[n]*px[n] + py[n]*py[n]);
}
t3->Fill();
t3f->Fill();
}
// Write the two files
t3->Print();
f.cd();
t3->Write();
fr.cd();
t3f->Write();
}
// Function to read the two files and add the friend
void tree3r() {
TFile *f = new TFile("tree3.root");
TTree *t3 = (TTree*)f->Get("t3");
// Add the second tree to the first tree as a friend
t3->AddFriend("t3f","tree3f.root");
// Draw pz which is in the first tree and use pt
// in the condition. pt is in the friend tree.
t3->Draw("pz","pt>3");
}
// This is executed when typing .x tree3.C
void tree3() {
tree3w();
12.17. EXAMPLE 4: A TREE WITH AN EVENT CLASS 313
tree3r();
}
12.17 Example 4: A Tree with an Event Class
This example is a simplified version of
$ROOTSYS/test/MainEvent.cxx
and where Event objects are saved in a
tree. The full definition of
Event
is in
$ROOTSYS/test
/
Event.h
. To execute this macro, you will need the library
$ROOTSYS/test/libEvent.so
. If it does not exist you can build the test directory applications by following the
instruction in the $ROOTSYS/test/README file.
In this example we will show
•the difference in splitting or not splitting a branch
•how to read selected branches of the tree,
•how to print a selected entry
12.17.1 The Event Class
Event is a descendent of TObject. As such it inherits the data members of TObject and its methods such as Dump()
and
Inspect()
and
Write()
. In addition, because it inherits from
TObject
it can be a member of a collection. To
summarize, the advantages of inheriting from a TObject are:
•Inherit the Write,Inspect, and Dump methods
•Enables a class to be a member of a ROOT collection
•Enables RTTI
Below is the list of the
Event
data members. It contains a character array, several integers, a floating-point number,
and an
EventHeader
object. The
EventHeader
class is described in the following paragraph.
Event
also has two
pointers, one to a
TClonesArray
of tracks and one to a histogram. The string “
->
” in the comment field of the
members
*fTracks
and
*fH
instructs the automatic
Streamer
to assume that the objects
*fTracks
and
*fH
are never
null pointers and that fTracks->Streamer can be used instead of the more time consuming form R__b << fTracks.
class Event : public TObject {
private:
char fType[20];
Int_t fNtrack;
Int_t fNseg;
Int_t fNvertex;
UInt_t fFlag;
Float_t fTemperature;
EventHeader fEvtHdr;
TClonesArray *fTracks; //->
TH1F *fH; //->
Int_t fMeasures[10];
Float_t fMatrix[4][4];
Float_t *fClosestDistance; //[fNvertex]
static TClonesArray *fgTracks;
static TH1F *fgHist;
// ... list of methods
ClassDef(Event,1)//Event structure
};
12.17.2 The EventHeader Class
The
EventHeader
class (also defined in
Event.h
) does not inherit from
TObject
. Beginning with ROOT 3.0, an object
can be placed on a branch even though it does not inherit from
TObject
. In previous releases branches were restricted
to objects inheriting from the
TObject
. However, it has always been possible to write a class not inheriting from
TObject to a tree by encapsulating it in a TObject descending class as is the case in EventHeader and Event.
314 CHAPTER 12. TREES
class EventHeader {
private:
Int_t fEvtNum;
Int_t fRun;
Int_t fDate;
// ... list of methods
ClassDef(EventHeader,1)//Event Header
};
12.17.3 The Track Class
The
Track
class descends from
TObject
since tracks are in a
TClonesArray
(i.e. a ROOT collection class) and contains
a selection of basic types and an array of vertices. Its TObject inheritance enables Track to be in a collection and in
Event is a TClonesArray of Tracks.
class Track : public TObject {
private:
Float_t fPx; //X component of the momentum
Float_t fPy; //Y component of the momentum
Float_t fPz; //Z component of the momentum
Float_t fRandom; //A random track quantity
Float_t fMass2; //The mass square of this particle
Float_t fBx; //X intercept at the vertex
Float_t fBy; //Y intercept at the vertex
Float_t fMeanCharge; //Mean charge deposition of all hits
Float_t fXfirst; //X coordinate of the first point
Float_t fXlast; //X coordinate of the last point
Float_t fYfirst; //Y coordinate of the first point
Float_t fYlast; //Y coordinate of the last point
Float_t fZfirst; //Z coordinate of the first point
Float_t fZlast; //Z coordinate of the last point
Float_t fCharge; //Charge of this track
Float_t fVertex[3]; //Track vertex position
Int_t fNpoint; //Number of points for this track
Short_t fValid; //Validity criterion
// method definitions ...
ClassDef(Track,1)//A track segment
};
12.17.4 Writing the Tree
We create a simple tree with two branches both holding
Event
objects. One is split and the other is not. We also
create a pointer to an Event object (event).
void tree4w() {
// check to see if the event class is in the dictionary
// if it is not load the definition in libEvent.so
if (!TClassTable::GetDict("Event")) {
gSystem->Load("$ROOTSYS/test/libEvent.so");
}
// create a Tree file tree4.root
TFile f("tree4.root","RECREATE");
// create a ROOT Tree
TTree t4("t4","A Tree with Events");
// create a pointer to an Event object
Event *event = new Event();
// create two branches, split one
t4.Branch("event_branch","Event", &event,16000,2);
t4.Branch("event_not_split","Event", &event,16000,0);
12.17. EXAMPLE 4: A TREE WITH AN EVENT CLASS 315
// a local variable for the event type
char etype[20];
// fill the tree
for (Int_t ev = 0; ev <100; ev++) {
Float_t sigmat, sigmas;
gRandom->Rannor(sigmat,sigmas);
Int_t ntrack = Int_t(600 +600 *sigmat/120.);
Float_t random = gRandom->Rndm(1);
sprintf(etype,"type%d",ev%5);
event->SetType(etype);
event->SetHeader(ev, 200,960312, random);
event->SetNseg(Int_t(10*ntrack+20*sigmas));
event->SetNvertex(Int_t(1+20*gRandom->Rndm()));
event->SetFlag(UInt_t(random+0.5));
event->SetTemperature(random+20.);
for(UChar_t m = 0;m<10; m++) {
event->SetMeasure(m, Int_t(gRandom->Gaus(m,m+1)));
}
// continued...
// fill the matrix
for(UChar_t i0 = 0;i0<4; i0++) {
for(UChar_t i1 = 0;i1<4; i1++) {
event->SetMatrix(i0,i1,gRandom->Gaus(i0*i1,1));
}
}
// create and fill the Track objects
for (Int_t t = 0; t < ntrack; t++) event->AddTrack(random);
t4.Fill(); // Fill the tree
event->Clear(); // Clear before reloading event
}
f.Write(); // Write the file header
t4.Print(); // Print the tree contents
}
12.17.5 Reading the Tree
First, we check if the shared library with the class definitions is loaded. If not we load it. Then we read two branches,
one for the number of tracks and one for the entire event. We check the number of tracks first, and if it meets our
condition, we read the entire event. We show the fist entry that meets the condition.
void tree4r() {
// check if the event class is in the dictionary
// if it is not load the definition in libEvent.so
if (!TClassTable::GetDict("Event")) {
gSystem->Load("$ROOTSYS/test/libEvent.so");
}
// read the tree generated with tree4w
// note that we use "new" to create the TFile and TTree objects, because we
// want to keep these objects alive when we leave this function.
TFile *f = new TFile("tree4.root");
TTree *t4 = (TTree*)f->Get("t4");
// create a pointer to an event object for reading the branch values.
Event *event = new Event();
// get two branches and set the branch address
TBranch *bntrack = t4->GetBranch("fNtrack");
TBranch *branch = t4->GetBranch("event_split");
branch->SetAddress(&event);
Int_t nevent = t4->GetEntries();
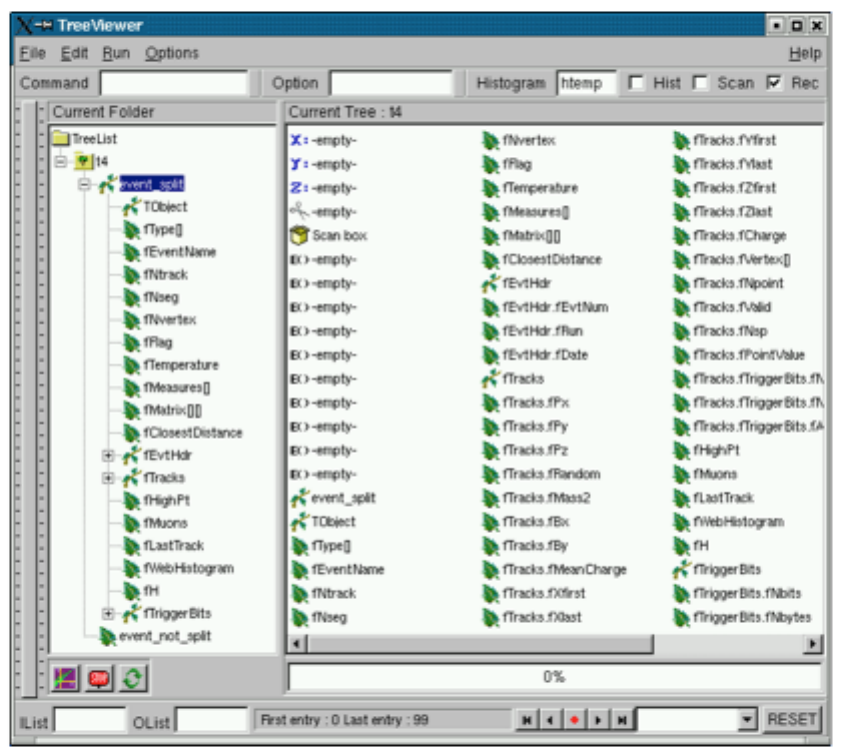
316 CHAPTER 12. TREES
Int_t nselected = 0;
Int_t nb = 0;
for (Int_t i=0; i<nevent; i++) {
//read branch "fNtrack"only
bntrack->GetEntry(i);
// reject events with more than 587 tracks
if (event->GetNtrack() > 587)continue;
// read complete accepted event in memory
nb += t4->GetEntry(i);
nselected++;
// print the first accepted event
if (nselected == 1) t4->Show();
// clear tracks array
event->Clear();
}
if (gROOT->IsBatch()) return;
new TBrowser();
t4->StartViewer();
}
Now, let’s see how the tree looks like in the tree viewer.
Figure 12.7: The tree viewer with tree4 example
You can see the two branches in the tree in the left panel: the event branch is split and hence expands when clicked on.
The other branch event not split is not expandable and we can not browse the data members.
12.18. EXAMPLE 5: IMPORT AN ASCII FILE INTO A TTREE 317
The
TClonesArray
of tracks
fTracks
is also split because we set the split level to 2. The output on the command line
is the result of tree4->Show(). It shows the first entry with more than 587 tracks:
======> EVENT:26
event_split =
fUniqueID = 0
fBits = 50331648
fType[20] = 11612111210149000000000000000
fNtrack = 585
fNseg = 5834
fNvertex = 17
fFlag = 0
fTemperature = 20.044315
fEvtHdr.fEvtNum = 26
fEvtHdr.fRun = 200
fEvtHdr.fDate = 960312
fTracks = 585
fTracks.fUniqueID = 0,0,0,0,0,0,0,0,0,0
...
12.18 Example 5: Import an ASCII File into a TTree
The method
TTree::ReadFile
can be used to automatic define the structure of the
TTree
and read the data from a
formatted ascii file.
Long64_t TTree::ReadFile(const char *filename,
const char *branchDescriptor)
Creates or simply read branches from the file named whose name is passed in ’filename’.
{
gROOT->Reset();
TFile *f = new TFile("basic2.root","RECREATE");
TH1F *h1 = new TH1F("h1","x distribution",100,-4,4);
TTree *T = new TTree("ntuple","data from ascii file");
Long64_t nlines = T->ReadFile("basic.dat","x:y:z");
printf(" found %lld pointsn",nlines);
T->Draw("x","z>2");
T->Write();
}
If
branchDescriptor
is set to an empty string (the default), it is assumed that the
Tree
descriptor is given in the first
line of the file with a syntax like: A/D:Table[2]/F:Ntracks/I:astring/C.
Otherwise branchDescriptor must be specified with the above syntax.Lines in the input file starting with “#” are
ignored. A
TBranch
object is created for each variable in the expression. The total number of rows read from the file is
returned.
12.19 Trees in Analysis
The methods
TTree::Draw
,
TTree::MakeClass
and
TTree::MakeSelector
are available for data analysis using trees.
The
TTree::Draw
method is a powerful yet simple way to look and draw the trees contents. It enables you to plot a
variable (a leaf) with just one line of code. However, the Draw method falls short once you want to look at each entry
and design more sophisticated acceptance criteria for your analysis. For these cases, you can use
TTree::MakeClass
.
It creates a class that loops over the trees entries one by one. You can then expand it to do the logic of your analysis.
The
TTree::MakeSelector
is the recommended method for ROOT data analysis. It is especially important for large
data set in a parallel processing configuration where the analysis is distributed over several processors and you can
specify which entries to send to each processor. With
MakeClass
the user has control over the event loop, with
MakeSelectorthe tree is in control of the event loop.
318 CHAPTER 12. TREES
12.20 Simple Analysis Using TTree::Draw
We will use the tree in staff.root that was made by the macro in $ROOTSYS/tutorials/tree/staff.C.
First, open the file and lists its contents.
root[] TFile f ("staff.root")
root[] f.ls()
TFile** staff.root
TFile* staff.root
KEY: TTree T;1staff data from ascii file
We can see the
TTree
“
T
” in the file. We will use it to experiment with the
TTree::Draw
method, so let’s create a
pointer to it:
root[] TTree *MyTree = T
Cling allows us to get simply the object by using it. Here we define a pointer to a
TTree
object and assign it the value
of “
T
”, the
TTree
in the file. Cling looks for an object named “
T
” in the current ROOT file and returns it (this assumes
that “T” has not previously been used to declare a variable or function).
In contrast, in compiled code, you can use:
TTree *MyTree;f.GetObject("T",MyTree);
To show the different
Draw
options, we create a canvas with four sub-pads. We will use one sub-pad for each
Draw
command.
root[] TCanvas *myCanvas = new TCanvas()
root[] myCanvas->Divide(2,2)
We activate the first pad with the TCanvas::cd statement:
root[] myCanvas->cd(1)
We then draw the variable Cost:
root[] MyTree->Draw("C
As you can see, the last call
TTree::Draw
has only one parameter. It is a string containing the leaf name. A histogram
is automatically created as a result of a
TTree::Draw
. The style of the histogram is inherited from the
TTree
attributes
and the current style (
gStyle
) is ignored. The
TTree
gets its attributes from the current
TStyle
at the time it was
created. You can call the method
TTree::UseCurrentStyle
to change to the current style rather than the
TTree
style.
(See gStyle ; see also “Graphics and the Graphical User Interface” )
In the next segment, we activate the second pad and draw a scatter plot variables:
root[] myCanvas->cd(2)
root[] MyTree->Draw("Cost:Age")
This signature still only has one parameter, but it now has two dimensions separated by a colon
("x:y")
. The item
to be plotted can be an expression not just a simple variable. In general, this parameter is a string that contains
up to three expressions, one for each dimension, separated by a colon (“
e1:e2:e3
”). A list of examples follows this
introduction.
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 319
12.20.1 Using Selection with TTree:Draw
Change the active pad to 3, and add a selection to the list of parameters of the draw command.
root[] myCanvas->cd(3)
root[] MyTree->Draw("Cost:Age","Nation == "FR"")
This will draw the
Cost
vs.
Age
for the entries where the nation is equal to “
FR
”. You can use any C++ operator, and
some functions defined in
TFormula
, in the selection parameter. The value of the selection is used as a weight when
filling the histogram. If the expression includes only Boolean operations as in the example above, the result is 0 or 1. If
the result is 0, the histogram is not filled. In general, the expression is:
Selection = "weight *(boolean expression)"
If the Boolean expression evaluates to true, the histogram is filled with a weight. If the weight is not explicitly specified
it is assumed to be 1.
For example, this selection will add 1 to the histogram if x is less than y and the square root of z is less than 3.2.
"x<y && sqrt(z)>3.2"
On the other hand, this selection will add x+y to the histogram if the square root of z is larger than 3.2.
"(x+y)*(sqrt(z)>3.2)"
The
Draw
method has its own parser, and it only looks in the current tree for variables. This means that any variable
used in the selection must be defined in the tree. You cannot use an arbitrary global variable in the
TTree::Draw
method.
12.20.2 Using TCut Objects in TTree::Draw
The
TTree::Draw
method also accepts
TCutG
objects. A
TCut
is a specialized string object used for
TTree
selections.
A
TCut
object has a name and a title. It does not have any data members in addition to what it inherits from
TNamed
.
It only adds a set of operators to do logical string concatenation. For example, assume:
TCut cut1 = "x<1"
TCut cut2 = "y>2"
then
cut1 && cut2
//result is the string "(x<1)&&(y>2)"
Operators =, +=, +, *, !, &&, || are overloaded, here are some examples:
root[] TCut c1 = "x < 1"
root[] TCut c2 = "y < 0"
root[] TCut c3 = c1 && c2
root[] MyTree.Draw("x", c1)
root[] MyTree.Draw("x",c1||"x>0")
root[] MyTree.Draw("x", c1 && c2)
root[] MyTree.Draw("x","(x + y)" * (c1 && c2))
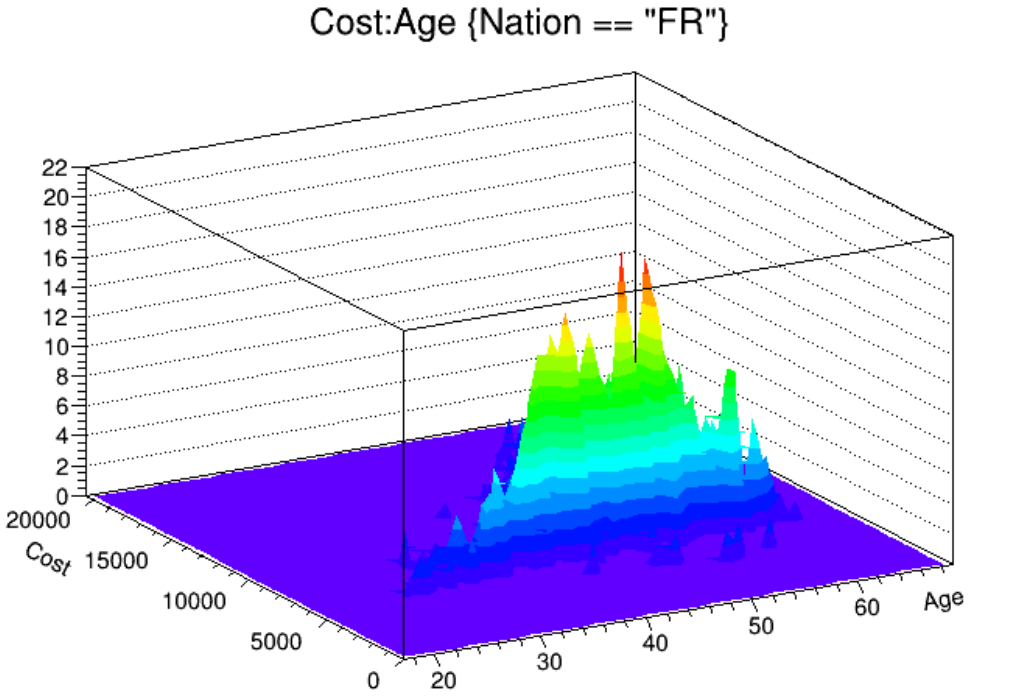
320 CHAPTER 12. TREES
12.20.3 Accessing the Histogram in Batch Mode
The
TTree::Draw
method creates a histogram called
htemp
and puts it on the active pad. In a batch program, the
histogram htemp created by default, is reachable from the current pad.
// draw the histogram
nt->Draw("x","cuts");
// get the histogram from the current pad
TH1F *htemp = (TH1F*)gPad->GetPrimitive("htemp");
// now we have full use of the histogram
htemp->GetEntries();
If you pipe the result of the
TTree::Draw
into a histogram, the histogram is also available in the current directory.
You can do:
// Draw the histogram and fill hnew with it
nt->Draw("x>>hnew","cuts");
// get hnew from the current directory
TH1F *hnew = (TH1F*)gDirectory->Get("hnew");
// or get hnew from the current Pad
TH1F *hnew = (TH1F*)gPad->GetPrimitive("hnew");
12.20.4 Using Draw Options in TTree::Draw
The next parameter is the draw option for the histogram:
root[] MyTree->Draw("Cost:Age","Nation == \"FR\"","surf2");
Figure 12.8: Using draw options in trees
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 321
The draw options are the same as for
TH1::Draw
. See “Draw Options” where they are listed. In addition to the draw
options defined in
TH1
, there are three more. The
’prof’
and
’profs’
draw a profile histogram (
TProfile
) rather
than a regular 2D histogram (
TH2D
) from an expression with two variables. If the expression has three variables, a
TProfile2D is generated.
The ‘
profs
’ generates a
TProfile
with error on the spread. The ‘
prof
’ option generates a
TProfile
with error on the
mean. The “
goff
” option suppresses generating the graphics. You can combine the draw options in a list separated by
commas. After typing the lines above, you should now have a canvas that looks this.
12.20.5 Superimposing Two Histograms
When superimposing two 2-D histograms inside a script with
TTree::Draw
and using the “
same
” option, you will need
to update the pad between Draw commands.
{
// superimpose two 2D scatter plots
// Create a 2D histogram and fill it with random numbers
TH2 *h2 = new TH2D ("h2","2D histo",100,0,70,100,0,20000);
for (Int_t i = 0;i<10000; i++)
h2->Fill(gRandom->Gaus(40,10),gRandom->Gaus(10000,3000));
// set the color to differentiate it visually
h2->SetMarkerColor(kGreen);
h2->Draw();
// Open the example file and get the tree
TFile f("staff.root");
TTree *myTree = (TTree*)f.Get("T");
// the update is needed for the next draw command to work properly
gPad->Update();
myTree->Draw("Cost:Age","","same");
}
In this example,
h2->Draw
is only adding the object h2 to the pad’s list of primitives. It does not paint the object
on the screen. However,
TTree::Draw
when called with option “
same
” gets the current pad coordinates to build an
intermediate histogram with the right limits. Since nothing has been painted in the pad yet, the pad limits have not
been computed. Calling
pad->Update()
forces the painting of the pad and allows
TTree::Draw
to compute the right
limits for the intermediate histogram.
12.20.6 Setting the Range in TTree::Draw
There are two more optional parameters to the
TTree::Draw
method: one is the number of entries and the second one
is the entry to start with. For example, this command draws 1000 entries starting with entry 100:
myTree->Draw("Cost:Age","","",1000,100);
12.20.7 TTree::Draw Examples
The examples below use the
Event.root
file generated by the
$ROOTSYS/test/Event
executable and the
Event
,
Track
,
and
EventHeader
class definitions are in
$ROOTSYS/test/Event.h
. The commands have been tested on the split-levels
0, 1, and 9. Each command is numbered and referenced by the explanations immediately following the examples.
// Data members and methods
1tree->Draw("fNtrack");
2tree->Draw("event.GetNtrack()");
3tree->Draw("GetNtrack()");
4tree->Draw("fH.fXaxis.fXmax");
5tree->Draw("fH.fXaxis.GetXmax()");
6tree->Draw("fH.GetXaxis().fXmax");
7tree->Draw("GetHistogram().GetXaxis().GetXmax()");
// Expressions in the selection parameter
8tree->Draw("fTracks.fPx","fEvtHdr.fEvtNum%10 == 0");
322 CHAPTER 12. TREES
9tree->Draw("fPx","fEvtHdr.fEvtNum%10 == 0");
// Two dimensional arrays defined as:
// Float_t fMatrix[4][4] in Event class
10 tree->Draw("fMatrix");
11 tree->Draw("fMatrix[ ][ ]");
12 tree->Draw("fMatrix[2][2]");
13 tree->Draw("fMatrix[ ][0]");
14 tree->Draw("fMatrix[1][ ]");
// using two arrays... Float_t fVertex[3]; in Track class
15 tree->Draw("fMatrix - fVertex");
16 tree->Draw("fMatrix[2][1] - fVertex[5][1]");
17 tree->Draw("fMatrix[ ][1] - fVertex[5][1]");
18 tree->Draw("fMatrix[2][ ] - fVertex[5][ ]");
19 tree->Draw("fMatrix[ ][2] - fVertex[ ][1]");
20 tree->Draw("fMatrix[ ][2] - fVertex[ ][ ]");
21 tree->Draw("fMatrix[ ][ ] - fVertex[ ][ ]");
// variable length arrays
22 tree->Draw("fClosestDistance");
23 tree->Draw("fClosestDistance[fNvertex/2]");
// mathematical expressions
24 tree->Draw("sqrt(fPx*fPx + fPy*fPy + fPz*fPz))");
// external function call
25 tree->Draw("TMath::BreitWigner(fPx,3,2)");
// strings
26 tree->Draw("fEvtHdr.fEvtNum","fType=="type1" ");
27 tree->Draw("fEvtHdr.fEvtNum","strstr(fType,"1" ");
// Where fPoints is defined in the track class:
// Int_t fNpoint;
// Int_t *fPoints; [fNpoint]
28 tree->Draw("fTracks.fPoints");
29 tree->Draw("fTracks.fPoints - fTracks.fPoints[][fAvgPoints]");
30 tree->Draw("fTracks.fPoints[2][]- fTracks.fPoints[][55]");
31 tree->Draw("fTracks.fPoints[][] - fTracks.fVertex[][]");
// selections
32 tree->Draw("fValid&0x1","(fNvertex>10) && (fNseg<=6000)");
33 tree->Draw("fPx","(fBx>.4) || (fBy<=-.4)");
34 tree->Draw("fPx","fBx*fBx*(fBx>.4) + fBy*fBy*(fBy<=-.4)");
35 tree->Draw("fVertex","fVertex>10");
36 tree->Draw("fPx[600]");
37 tree->Draw("fPx[600]","fNtrack>600");
// alphanumeric bin histogram
// where Nation is a char* indended to be used as a string
38 tree->Draw("Nation");
// where MyByte is a char* intended to be used as a byte
39 tree->Draw("MyByte + 0");
// where fTriggerBits is a data member of TTrack of type TBits
40 tree->Draw("fTracks.fTriggerBits");
// using alternate values
41 tree->Draw("fMatrix-Alt$(fClosestDistance,0)");
// using meta information about the formula
42 tree->Draw("fMatrix:Iteration$")
43 T->Draw("fLastTrack.GetPx():fLastTrack.fPx");
44 T->Scan("((Track*)(fLastTrack@.GetObject())).GetPx()","","");
45 tree->Draw("This->GetReadEntry()");
46 tree->Draw("mybr.mystring");
47 tree->Draw("myTimeStamp");
12.20.7.1 Explanations:
1. tree->Draw("fNtrack");
It fills the histogram with the number of tracks for each entry. fNtrack is a member of event.
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 323
2. tree->Draw("event.GetNtrack()");
Same as case 1, but use the method of event to get the number of tracks. When using a method, you can include
parameters for the method as long as the parameters are literals.
3. tree->Draw("GetNtrack()");
Same as case 2, the object of the method is not specified. The command uses the first instance of the
GetNtrack
method found in the objects stored in the tree. We recommend using this shortcut only if the method name is unique.
4. tree->Draw("fH.fXaxis.fXmax");
Draw the data member of a data member. In the tree, each entry has a histogram. This command draws the maximum
value of the X-axis for each histogram.
5. tree->Draw("fH.fXaxis.GetXmax()");
Same as case 4, but use the method of a data member.
6. tree->Draw("fH.GetXaxis().fXmax");
The same as case 4: a data member of a data member retrieved by a method.
7. **tree->Draw("GetHistogram().GetXaxis().GetXmax()");**
Same as case 4, but using methods.
8. tree->Draw("fTracks.fPx","fEvtHdr.fEvtNum%10 == 0");
Use data members in the expression and in the selection parameter to plot
fPx
or all tracks in every 10th entry. Since
fTracks is a TClonesArray of Tracks, there will be d values of fPx for each entry.
9. tree->Draw("fPx","fEvtHdr.fEvtNum%10 == 0");
Same as case 8, use the name of the data member directly.
10. tree->Draw("fMatrix");
When the index of the array is left out or when empty brackets are used
[]
, all values of the array are selected. Draw
all values of
fMatrix
for each entry in the tree. If
fMatrix
is defined as:
Float_t fMatrix[4][4]
, all 16 values are
used for each entry.
11. tree->Draw("fMatrix[ ][ ]");
The same as case 10, all values of fMatrix are drawn for each entry.
12. tree->Draw("fMatrix[2][2]");
The single element at fMatrix[2][2] is drawn for each entry.
13. tree->Draw("fMatrix[][0]");
Four elements of fMatrix are used: fMatrix[1][0],fMatrix[2][0],fMatrix[3][0],fMatrix[4][0].
14. tree->Draw("fMatrix[1][ ]");
Four elements of fMatrix are used: fMatrix[1][0],fMatrix[1][2],fMatrix[1][3],fMatrix[1][4].
324 CHAPTER 12. TREES
15. tree->Draw("fMatrix - fVertex");
With two arrays and unspecified element numbers, the number of selected values is the minimum of the first dimension
times the minimum of the second dimension. In this case
fVertex
is also a two dimensional array since it is a data
member of the tracks array. If
fVertex
is defined in the track class as:
Float_t *fVertex[3]
, it has
fNtracks
x 3
elements.
fMatrix
has 4 x 4 elements. This case, draws 4 (the smaller of
fNtrack
and 4) times 3 (the smaller of 4 and
3), meaning 12 elements per entry. The selected values for each entry are:
fMatrix[0][0] - fVertex[0][0]
fMatrix[0][1] - fVertex[0][1]
fMatrix[0][2] - fVertex[0][2]
fMatrix[1][0] - fVertex[1][0]
fMatrix[1][1] - fVertex[1][1]
fMatrix[1][2] - fVertex[1][2]
fMatrix[2][0] - fVertex[2][0]
fMatrix[2][1] - fVertex[2][1]
fMatrix[2][2] - fVertex[2][2]
fMatrix[3][0] - fVertex[3][0]
fMatrix[3][1] - fVertex[3][1]
fMatrix[3][2] - fVertex[3][2]
16. tree->Draw("fMatrix[2][1] - fVertex[5][1]");
This command selects one value per entry.
17. tree->Draw("fMatrix[ ][1] - fVertex[5][1]");
The first dimension of the array is taken by the fMatrix.
fMatrix[0][1] - fVertex[5][1]
fMatrix[1][1] - fVertex[5][1]
fMatrix[2][1] - fVertex[5][1]
fMatrix[3][1] - fVertex[5][1]
18. tree->Draw("("fMatrix[2][ ] - fVertex[5][ ]");
The first dimension minimum is 2, and the second dimension minimum is 3 (from
fVertex
). Three values are selected
from each entry:
fMatrix[2][0] - fVertex[5][0]
fMatrix[2][1] - fVertex[5][1]
fMatrix[2][2] - fVertex[5][2]
19. tree->Draw("fMatrix[ ][2] - fVertex[ ][1]")
This is similar to case 18. Four values are selected from each entry:
fMatrix[0][2] - fVertex[0][1]
fMatrix[1][2] - fVertex[1][1]
fMatrix[2][2] - fVertex[2][1]
fMatrix[3][2] - fVertex[3][1]
20. tree->Draw("fMatrix[ ][2] - fVertex[ ][ ]")
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 325
This is similar to case 19. Twelve values are selected (4x3) from each entry:
fMatrix[0][2] - fVertex[0][0]
fMatrix[0][2] - fVertex[0][1]
fMatrix[0][2] - fVertex[0][2]
fMatrix[1][2] - fVertex[1][0]
fMatrix[1][2] - fVertex[1][1]
fMatrix[1][2] - fVertex[1][2]
fMatrix[2][2] - fVertex[2][0]
fMatrix[2][2] - fVertex[2][1]
fMatrix[2][2] - fVertex[2][2]
fMatrix[3][2] - fVertex[3][0]
fMatrix[3][2] - fVertex[3][1]
fMatrix[3][2] - fVertex[3][2]
21. tree->Draw("fMatrix[ ][ ] - fVertex[ ][ ]")
This is the same as case 15. The first dimension minimum is 4 (from
fMatrix
), and the second dimension minimum is
3 (from fVertex). Twelve values are selected from each entry.
22. tree->Draw("fClosestDistance")
This event data member fClosestDistance is a variable length array:
Float_t *fClosestDistance; //[fNvertex]
This command selects all elements, but the number per entry depends on the number of vertices of that entry.
23. tree->Draw("fClosestDistance[fNvertex/2]")
With this command the element at
fNvertex/2
of the
fClosestDistance
array is selected. Only one per entry is
selected.
24. tree->Draw("sqrt(fPx*fPx + fPy*fPy + fPz*fPz)")
This command shows the use of a mathematical expression. It draws the square root of the sum of the product.
25. tree->Draw("TMath::BreitWigner(fPx,3,2)")
The formula can contains call to a function that takes numerical arguments and returns a numerical value. The function
needs to be declared to the dictionary and need to be available from the global namespace. In particular, global
functions and public static member functions can be called.
26. tree->Draw("fEvtHdr.fEvtNum","fType=="type1" ")
You can compare strings, using the symbols == and !=, in the first two parameters of the
Draw
command (
TTreeFormula
).
In this case, the event number for ‘type1’ events is plotted.
27. tree->Draw("fEvtHdr.fEvtNum","strstr(fType,"1") ")
To compare strings, you can also use strstr. In this case, events having a ‘1’ in fType are selected.
28. tree->Draw("fTracks.fPoints")
326 CHAPTER 12. TREES
If fPoints is a data member of the Track class declared as:
Int_t fNpoint;
Int_t *fPoints; [fNpoint]
The size of the array
fPoints
varies with each track of each event. This command draws all the value in the
fPoints
arrays.
29. tree->Draw("fTracks.fPoints - fTracks.fPoints[][fAvgPoints]");
When fAvgPoints is a data member of the Event class, this example selects:
fTracks[0].fPoints[0] - fTracks[0].fPoint[fAvgPoints]
fTracks[0].fPoints[1] - fTracks[0].fPoint[fAvgPoints]
fTracks[0].fPoints[2] - fTracks[0].fPoint[fAvgPoints]
fTracks[0].fPoints[3] - fTracks[0].fPoint[fAvgPoints]
fTracks[0].fPoints[4] - fTracks[0].fPoint[fAvgPoints]
...
fTracks[0].fPoints[max0]- fTracks[0].fPoint[fAvgPoints]
...
fTracks[1].fPoints[0] - fTracks[1].fPoint[fAvgPoints]
fTracks[1].fPoints[1] - fTracks[1].fPoint[fAvgPoints]
fTracks[1].fPoints[2] - fTracks[1].fPoint[fAvgPoints]
fTracks[1].fPoints[3] - fTracks[1].fPoint[fAvgPoints]
fTracks[1].fPoints[4] - fTracks[1].fPoint[fAvgPoints]
...
fTracks[1].fPoints[max1]- fTracks[1].fPoint[fAvgPoints]
...
fTracks[fNtrack-1].fPoints[0] - fTracks[fNtrack-1].fPoint[fAvgPoints]
fTracks[fNtrack-1].fPoints[1] - fTracks[fNtrack-1].fPoint[fAvgPoints]
fTracks[fNtrack-1].fPoints[2] - fTracks[fNtrack-1].fPoint[fAvgPoints]
fTracks[fNtrack-1].fPoints[3] - fTracks[fNtrack-1].fPoint[fAvgPoints]
fTracks[fNtrack-1].fPoints[4] - fTracks[fNtrack-1].fPoint[fAvgPoints]
...
fTracks[fNtrack-1].fPoints[maxn] - fTracks[fNtrack-1].fPoint[fAvgPoints]
Wheremax0,max1,... max n, is the size of thefPointsarray for the respective track.
30. tree->Draw("fTracks.fPoints[2][]- fTracks.fPoints[][55]")
For each event, this expression is selected:
fTracks[2].fPoints[0] - fTracks[0].fPoints[55]
fTracks[2].fPoints[1] - fTracks[1].fPoints[55]
fTracks[2].fPoints[2] - fTracks[2].fPoints[55]
fTracks[2].fPoints[3] - fTracks[3].fPoints[55]
...
fTracks[2].fPoints[max] - fTracks[max].fPoints[55]
where max is the minimum of fNtrack and fTracks[2].fNpoint.
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 327
31. tree->Draw("fTracks.fPoints[][] - fTracks.fVertex[][]")
For each event and each track, this expression is selected. It is the difference between
fPoints
and of
fVertex
. The
number of elements used for each track is the minimum of fNpoint and 3 (the size of the fVertex array).
fTracks[0].fPoints[0] - fTracks[0].fVertex[0]
fTracks[0].fPoints[1] - fTracks[0].fVertex[1]
fTracks[0].fPoints[2] - fTracks[0].fVertex[2]
// with fTracks[1].fNpoint==7
fTracks[1].fPoints[0] - fTracks[1].fVertex[0]
fTracks[1].fPoints[1] - fTracks[1].fVertex[1]
fTracks[1].fPoints[2] - fTracks[1].fVertex[2]
// with fTracks[1].fNpoint==5
fTracks[2].fPoints[0] - fTracks[1].fVertex[0]
fTracks[2].fPoints[1] - fTracks[1].fVertex[1]
// with fTracks[2].fNpoint==2
fTracks[3].fPoints[0] - fTracks[3].fVertex[0]
// with fTracks[3].fNpoint==1
fTracks[4].fPoints[0] - fTracks[4].fVertex[0]
fTracks[4].fPoints[1] - fTracks[4].fVertex[1]
fTracks[4].fPoints[2] - fTracks[4].fVertex[2]
// with fTracks[4].fNpoint==3
32. tree->Draw("fValid&0x1","(fNvertex>10) && (fNseg<=6000)")
You can use bit patterns (&,|,<<) or Boolean operation.
33. tree->Draw("fPx","(fBx>.4) || (fBy<=-.4)");
34. tree->Draw("fPx","fBx*fBx*(fBx>.4) + fBy*fBy*(fBy<=-.4)");
The selection argument is used as a weight. The expression returns a multiplier and in case of a Boolean the multiplier
is either 0 (for false) or 1 (for true). The first command draws
fPx
for the range between 0.4 and -0.4, the second
command draws fPx for the same range, but adds a weight using the result of the second expression.
35. tree->Draw("fVertex","fVertex>10")
When using arrays in the selection and the expression, the selection is applied to each element of the array.
if (fVertex[0]>10) fVertex[0]
if (fVertex[1]>10) fVertex[1]
if (fVertex[2]>10) fVertex[2]
36. tree->Draw("fPx[600]")
37. tree->Draw("fPx[600]","fNtrack > 600")
When using a specific element for a variable length array the entries with fewer elements are ignored. Thus these two
commands are equivalent.
38. tree->Draw("Nation")
Nation
is a
char*
branch. When drawing a
char*
it will plot an alphanumeric histogram, of the different value of the
string Nation. The axis will have the Nation values. See “Histograms”.
328 CHAPTER 12. TREES
39. tree->Draw("MyChar +0")
If you want to plot a char* variable as a byte rather than a string, you can use the syntax above.
40. tree->Draw("fTracks.fTriggerBits")
fTriggerBits
is a data member of
TTrack
of type
TBits
. Objects of class
TBits
can be drawn directly. This command
will create a 1D histogram from 0 to nbits which is filled for each non-null bit-number.
41. tree->Draw("fMatrix-Alt$(fClosestDistance,0)")
Alt$(primary,alternate)
returns the value of “
primary
” if it is available for the current iteration; otherwise return
the value of “
alternate
”. Assuming that
fClosestDistance
is a smaller array than
fMatrix
. This example will draw
fMatrix[i]+fClosestDistance[i]
for
i
less than the size of
fClosestDistance
, and will draw
fMatrix[i]+0
for
the other value of i.
42. tree->Draw("fClosestDistance:Iteration$")
This example draws a 2D plot with, for all entries,
fClosestDistance[i]:i
for each value of
i
between 0 and the size
of
fClosestDistance
.
Iterations$
is one of four special variables giving some indications of the state of the loops
implied by the formula:
Entry$ : return the current entry number (TTree::GetReadEntry())
Entries$ : return the total number of entries (TTree::GetEntries())
Length$ : return the total number of element of this formula for this entry
Iteration$: return the current iteration over this formula for this entry (i.e. varies from 0 to Length$).
43. T->Draw(“fLastTrack.GetPx():fLastTrack.fPx”);‘**
TRef
and
TRefArray
are automatically deferenced and this shows the value of the
fPx
of the track referenced by
fLastTrack
. To access the
TRef
object itself use the ‘
@
’ notation (see next example). This auto dereferencing can be
extended (via an implementation of TVirtualRefProxy) to any reference type.
44. T->Scan(“((Track*)(fLastTrack@.GetObject())).GetPx()“,”“,”“);‘**
Will cast the return value of
GetObject()
(which happens to be
TObject*
in this case) before requesting the
GetPx()
member functions.
45. tree->Draw("This->GetReadEntry()");
You can refer to the tree (or chain) containing the data by using the string ‘
This
’. You can also call any
TTree
methods.
Next example will display the name of the first ‘user info’ object:
tree->Draw("This->GetUserInfo()->At(0)->GetName()");
46. tree->Draw("mybr.mystring");
TString
and
std::string
object are plotted directly. The example 45 draws the same results - i.e. an histogram
whose labels are the string value of ‘mystring’:
tree->Draw("mybr.mystring.c_str()");
or
tree->Draw("mybr.mytstring.Data()");
47. tree->Draw("myTimeStamp");
You can plot plot objects of any class which has either
AsDouble
or
AsString
(
AsDouble
has priority). For such a
class (for example TTimeStamp), the line 46 will plot the same as:
tree->Draw("myTimeStamp.AsDouble");
AsString can be returning either a char*, or a TString or an std::string.
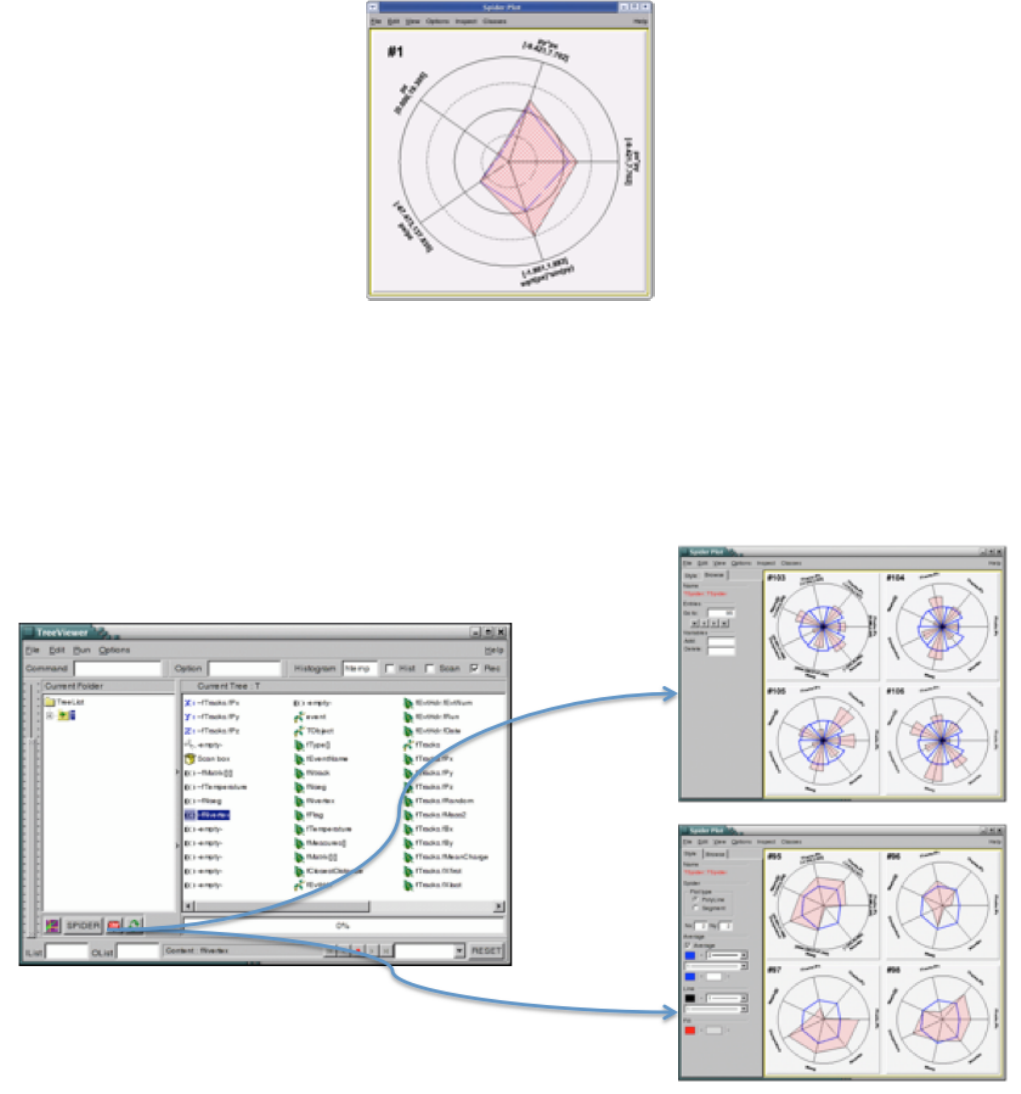
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 329
12.20.8 Multiple variables visualisation
This section presents the visualization technique available in ROOT to represent multiple variables (>4) data sets.
12.20.8.1 Spider (Radar) Plots
Spider plots (sometimes called “web-plots” or “radar plots”) are used to compare series of data points (events). They
use the human ability to spot un-symmetry.
Figure 12.9: Example of spider plot.
Variables are represented on individual axes displayed along a circle. For each variable the minimum value sits on the
circle’s center, and the maximum on the circle’s radius. Spider plots are not suitable for an accurate graph reading
since, by their nature, it can be difficult to read out very detailed values, but they give quickly a global view of an
event in order to compare it with the others. In ROOT the spider plot facility is accessed from the tree viewer GUI.
The variables to be visualized are selected in the tree viewer and can be scanned using the spider plot button.
Figure 12.10: The tree viewer Graphical User Interface and the Spider Plot Editor.
The spider plot graphics editor provides two tabs to interact with the spider plots’ output: the tab “Style” defining the
spider layout and the tab “Browse” to navigate in the tree.
330 CHAPTER 12. TREES
12.20.8.2 Parallel Coordinates Plots
The Parallel Coordinates Plots are a common way of studying and visualizing multiple variables data sets. They were
proposed by in A.Inselberg in 1981 as a new way to represent multi-dimensional information. In traditional Cartesian
coordinates, axes are mutually perpendicular. In Parallel coordinates, all axes are parallel which allows representing
data in much more than three dimensions. To show a set of points in Parallel Coordinates, a set of parallel lines is
drawn, typically vertical and equally spaced. A point in n-dimensional space is represented as a polyline with vertices
on the parallel axes. The position of the vertex on the i-th axis corresponds to the i-th coordinate of the point. The
three following figures show some very simple examples:
Figure 12.11: The Parallel Coordinates representation of the six dimensional point (-5,3,4,2,0,1).
Figure 12.12: The line y = -3x+20 and a circle in Parallel Coordinates.
The Parallel Coordinates technique is good at: spotting irregular events, seeing the data trend, finding correlations
and clusters. Its main weakness is the cluttering of the output. Because each “point” in the multidimensional space
is represented as a line, the output is very quickly opaque and therefore it is difficult to see the data clusters. Most
of the work done about Parallel Coordinates is to find techniques to reduce the output’s cluttering. The Parallel
Coordinates plots in ROOT have been implemented as a new plotting option “PARA” in the
TTree::Draw()method
.
To demonstrate how the Parallel Coordinates works in ROOT we will use the tree produced by the following “pseudo
C++” code:
void parallel_example() {
TNtuple *nt = new TNtuple("nt","Demo ntuple","x:y:z:u:v:w:a:b:c");
for (Int_t i=0; i<3000; i++) {
nt->Fill( rnd, rnd, rnd, rnd, rnd, rnd, rnd, rnd, rnd );
nt->Fill( s1x, s1y, s1z, s2x, s2y, s2z, rnd, rnd, rnd );
nt->Fill( rnd, rnd, rnd, rnd, rnd, rnd, rnd, s3y, rnd );
nt->Fill( s2x-1, s2y-1, s2z, s1x+.5, s1y+.5, s1z+.5, rnd, rnd, rnd );
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 331
nt->Fill( rnd, rnd, rnd, rnd, rnd, rnd, rnd, rnd, rnd );
nt->Fill( s1x+1, s1y+1, s1z+1, s3x-2, s3y-2, s3z-2, rnd, rnd, rnd );
nt->Fill( rnd, rnd, rnd, rnd, rnd, rnd, s3x, rnd, s3z );
nt->Fill( rnd, rnd, rnd, rnd, rnd, rnd, rnd, rnd, rnd );
}
The data set generated has:
•9 variables: x, y, z, u, v, w, a, b, c.
•3000*8 = 24000 events.
•3 sets of random points distributed on spheres: s1, s2, s3
•Random values (noise): rnd
•
The variables a,b,c are almost completely random. The variables a and c are correlated via the 1st and 3rd
coordinates of the 3rd “sphere” s3.
The command used to produce the Parallel Coordinates plot is:
nt->Draw("x:a:y:b:z:u:c:v:w","","PARA");
Figure 12.13: Cluttered output produced when all the tree events are plotted.
If the 24000 events are plotted as solid lines and no special techniques are used to clarify the picture, the result is the
previous picture which is very cluttered and useless. To improve the readability of the Parallel Coordinates output and
to explore interactively the data set, many techniques are available. We have implemented a few in ROOT. First of all,
in order to show better where the clusters on the various axes are, a 1D histogram is associated to each axis. These
histograms (one per axis) are filled according to the number of lines passing through the bins.
These histograms can be represented which colors (get from a palette according to the bin contents) or as bar charts.
Both representations can be cumulated on the same plot. This technique allows seeing clearly where the clusters are on
an individual axis but it does not give any hints about the correlations between the axes.
Avery simple technique allows to make the clusters appearing: Instead of painting solid lines we paint dotted lines. The
cluttering of each individual line is reduced and the clusters show clearly as we can see on the next figure. The spacing
between the dots is a parameter which can be adjusted in order to get the best results.
Interactivity is a very important aspect of the Parallel Coordinates plots. To really explore the data set it is essential
to act directly with the events and the axes. For instance, changing the axes order may show clusters which were not
visible in a different order. On the next figure the axes order has been changed interactively. We can see that many
more clusters appear and all the “random spheres” we put in the data set are now clearly visible. Having moved the
variables u,v,w after the variables x,y,z the correlation between these two sets of variables is clear also.
To pursue further data sets exploration we have implemented the possibility to define selections interactively. A
selection is a set of ranges combined together. Within a selection, ranges along the same axis are combined with logical
OR, and ranges on different axes with logical AND. A selection is displayed on top of the complete data set using its
own color. Only the events fulfilling the selection criteria (ranges) are displayed. Ranges are defined interactively using
332 CHAPTER 12. TREES
Figure 12.14: The histogram’s axis can be represented with colors or as bar charts.
Figure 12.15: Using dotted lines is a very simple method to reduce the cluttering.
Figure 12.16: Axis order is very important to show clusters.
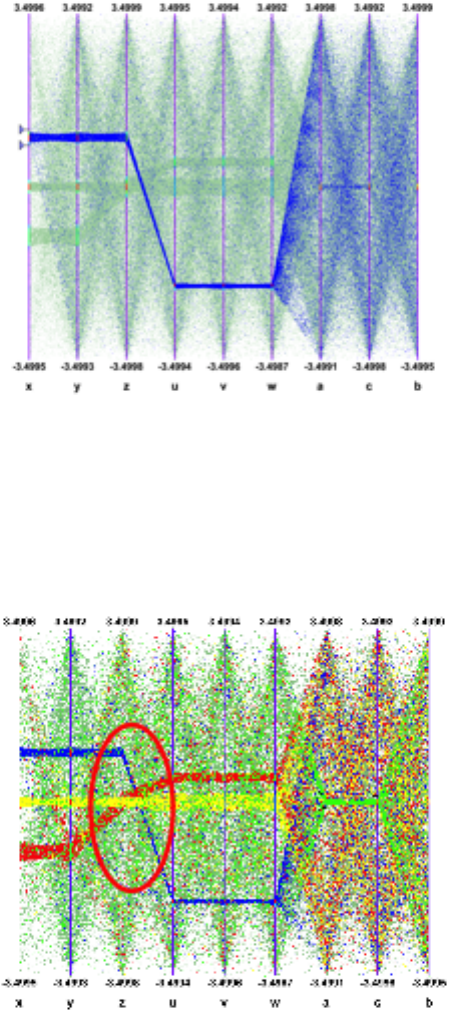
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 333
Figure 12.17: Selections are set of ranges which can be defined interactively.
cursors, like on the first axis on the figure. Several selections can be defined at the same time, each selection having its
own color.
Several selections can been defined. Each cluster is now clearly visible and the zone with crossing clusters is now
understandable whereas, without any selection or with only a single one, it was not easy to understand.
Figure 12.18: Several selections can be defined each of them having its own color.
Interactive selections on Parallel Coordinates are a powerful tool because they can be defined graphically on many
variables (graphical cuts in ROOT can be defined on two variables only) which allow a very accurate events filtering.
Selections allow making precise events choices: a single outlying event is clearly visible when the lines are displayed as
“solid” therefore it is easy to make cuts in order to eliminate one single event from a selection. Such selection (to filter
one single event) on a scatter plot would be much more difficult.
Once a selection has been defined, it is possible to use it to generate a
TEntryList
which is applied on the tree and
used at drawing time. In our example the selection we defined allows to select exactly the two correlated “random
spheres”.
Another technique has been implemented in order to show clusters when the picture is cluttered. A weight is assigned
to each event. The weight value is computed as:
weight =
n
X
i=1
bi
Where:
•bi is the content of bin crossed by the event on the i-th axis.
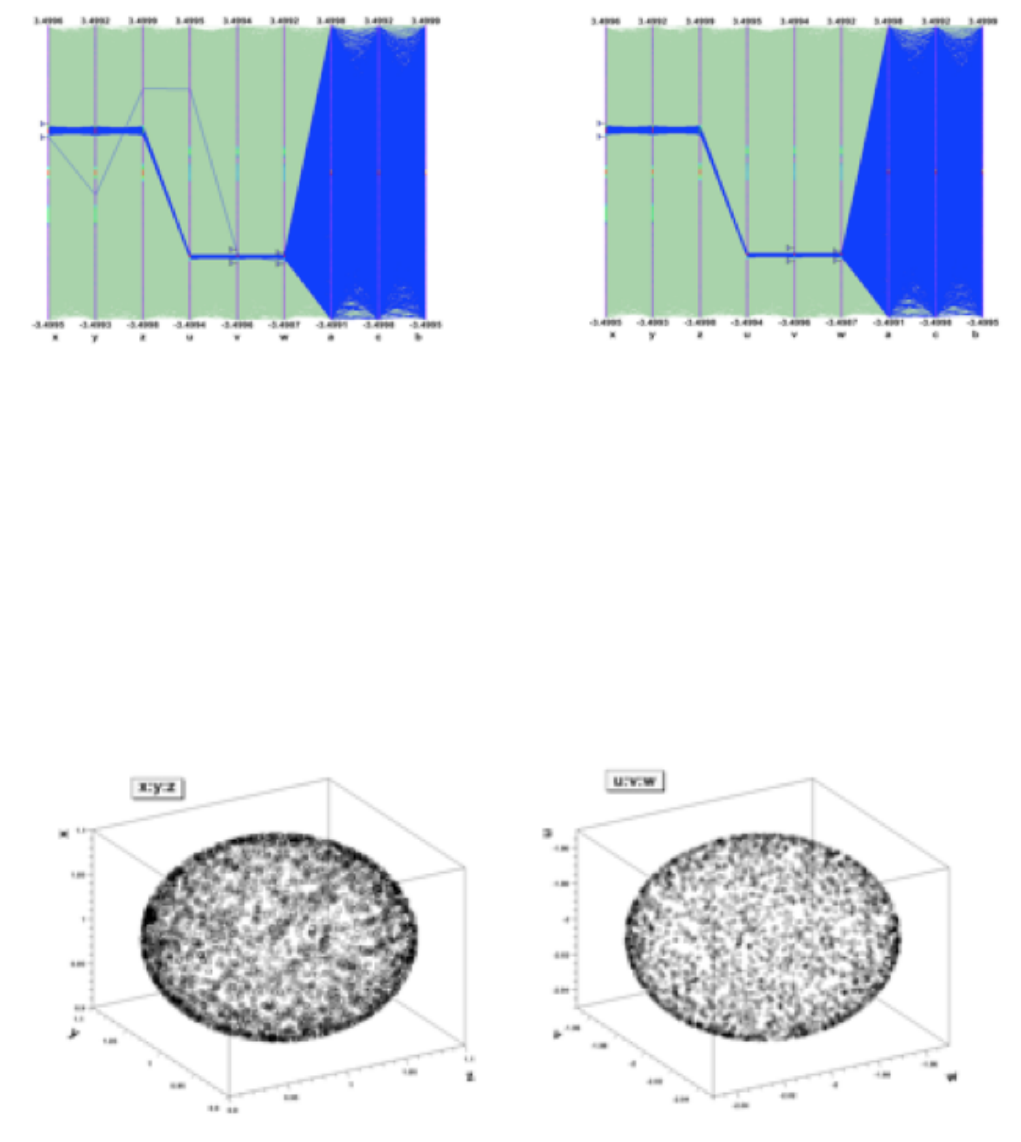
334 CHAPTER 12. TREES
Figure 12.19: Selections allow to easily filter one single event.
Figure 12.20: Output of nt->Draw(“x:y:z”) and nt->Draw(“u:v:w”) after applying the selection.
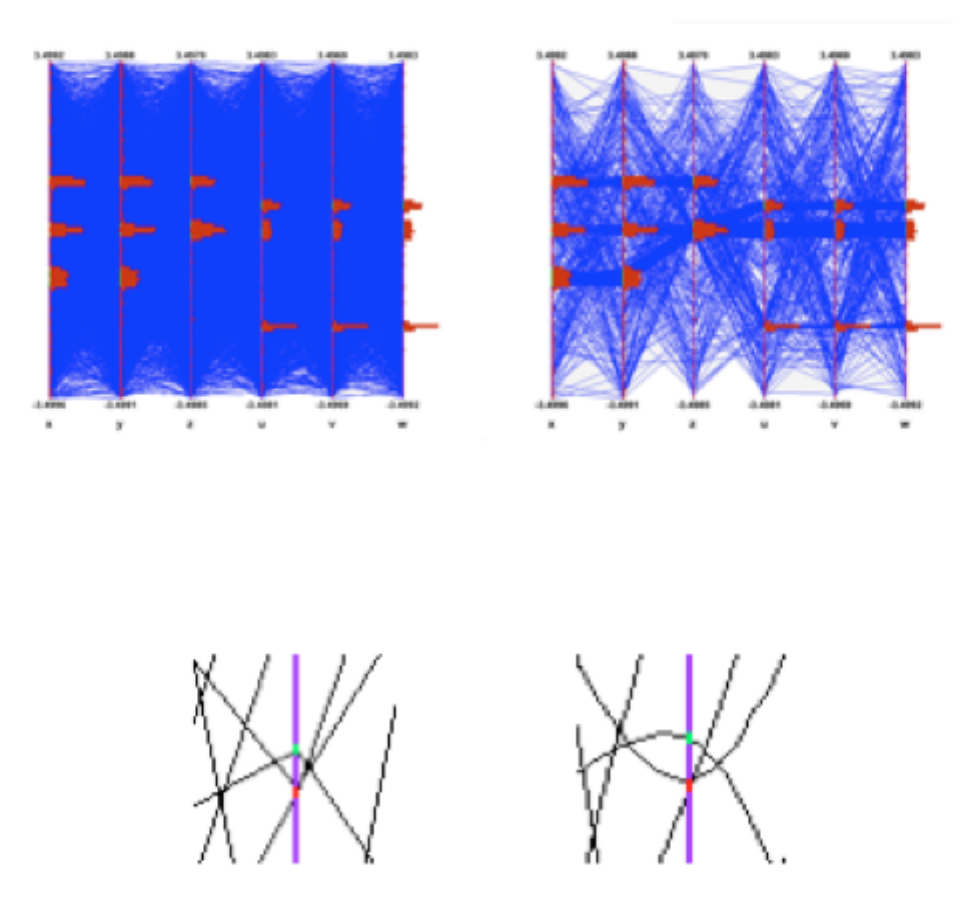
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 335
•n is the number of axis.
The events having the bigger weights are those belonging to clusters. It is possible to paint only the events having a
weight above a given value and the clusters appear. The next example “weight cut” applied on the right plot is 50.
Only the events with a weight greater than 50 are displayed.
Figure 12.21: Applying a “weight cut” makes the clusters visible.
In case only a few events are displayed, drawing them as smooth curves instead of straight lines helps to differentiate
them.
Figure 12.22: Zoom on a Parallel Coordinates plot detail: curves differentiate better events.
Interactivity and therefore the Graphical User Interface are very important to manipulate the Parallel Coordinates
plots. The ROOT framework allows to easily implement the direct interactions on the graphical area and the graphical
editor facility provides dedicated GUI.
Tranparency is very useful with parallel coordinates plots. It alows to show cleraly the clusters.
12.20.8.3 Box (Candle) Plots
A Box Plot (also known as a “box-and whisker” plot or “candle stick” plot) is a convenient way to describe graphically
a data distribution (D) with only the five numbers. It was invented in 1977 by John Tukey. The five numbers are:
1. The minimum value of the distribution D (Min).
2. The lower quartile (Q1): 25% of the data points in D are less than Q1.
3. The median (M): 50% of the data points in D are less than M.
4. The upper quartile (Q3): 75% of the data points in D are less than Q3.
5. The maximum value of the distribution D (Max).
336 CHAPTER 12. TREES
Figure 12.23: Parallel Coordinates graphical editors.
Figure 12.24: Parallel Coordinates with transparency.
Figure 12.25: A box plot describes a distribution with only five numbers.
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 337
In ROOT Box Plots (Candle Plots) can be produced from a TTree using the “candle” option in TTree::Draw().
tree->Draw(“px:cos(py):sin(pz)”,””,”candle”);
12.20.9 Using TTree::Scan
TTree::Scan can be used to print the content of the tree’s entries optional passing a selection.
root[] MyTree->Scan();
will print the first 8 variables of the tree.
root[] MyTree->Scan("*");
will print all the variable of the tree.
Specific variables of the tree can be explicit selected by list them in column separated list:
root[] MyTree->Scan("var1:var2:var3");
will print the values of var1,var2 and var3. A selection can be applied in the second argument:
root[] MyTree->Scan("var1:var2:var3","var1==0");
will print the values of var1,var2 and var3 for the entries where var1 is exactly 0.
TTree::Scan
returns the number of entries passing the selection. By default 50 rows are shown before
TTree::Scan
pauses and ask you to press the Enter key to see the next 50 rows. You can change the default number of rows to be
shown before <CR> via
mytree->SetScanfield(maxrows)
where maxrows is 50 by default. If maxrows is set to 0 all
rows of the
Tree
are shown. This option is interesting when dumping the contents of a Tree to an ascii file, eg from the
command line:
root[] tree->SetScanField(0);
root[] tree->Scan("*"); >tree.log
will create a file tree.log.
Arrays (within an entry) are printed in their linear forms. If several arrays with multiple dimensions are printed
together, they will NOT be synchronized. For example, with a tree containing arr1[4][2]and arr2[2][3],
root[] MyTree("arr1:arr2");
will results in a printing similar to:
************************************************
* Row * Instance * arr1 * arr2 *
***********************************************
*x*0* arr1[0][0]* arr2[0][0]*
*x*1* arr1[0][1]* arr2[0][1]*
*x*2* arr1[1][0]* arr2[0][2]*
*x*3* arr1[1][1]* arr2[1][0]*
*x*4* arr1[2][0]* arr2[1][1]*
*x*5* arr1[2][1]* arr2[1][2]*
*x*6* arr1[3][0]* *
*x*7* arr1[3][1]* *
However, if there is a selection criterium which is an array, then all the formulas will be synchronized with the selection
criterium (see TTree::Draw for more information).
The third parameter of TTree::Scan can be use to specific the layout of the table:
338 CHAPTER 12. TREES
•lenmax=dd
- where ‘dd’ is the maximum number of elements per array that should be printed. If ‘dd’ is 0, all
elements are printed (this is the default).
•colsize=ss
- where ‘ss’ will be used as the default size for all the column. If this options is not specified, the
default column size is 9.
•precision=pp - where ‘pp’ will be used as the default ‘precision’ for the printing format.
•col=xxx
- where ‘
xxx
’ is colon (:) delimited list of printing format for each column if no format is specified for a
column, the default is used.
For example:
tree->Scan("a:b:c","","colsize=30 precision=3 col=::20.10");
will print 3 columns, the first 2 columns will be 30 characters long, the third columns will be 20 characters long. The
printf format for the columns (assuming they are numbers) will be respectively: %30.3g %30.3g %20.10g.
12.20.10 TEventList and TEntryList
The
TTree::Draw
method can also be used to build a list of the entries. When the first argument is preceded by
">>"
ROOT knows that this command is not intended to draw anything, but to save the entries in a list with the name
given by the first argument. As a result, a
TEventList
or a
TEntryList
object is created in the current directory. For
example, to create a TEventList of all entries with more than 600 tracks, do:
root[] TFile *f = new TFile("Event.root");
root[] T->Draw(">> myList","fNtrack > 600");
To create a TEntryList, use the option “entrylist”.
root[] T->Draw(">>myList","fNtrack>600","entrylist");
This list contains the entry number of all entries with more than 600 tracks. To see the entry numbers use the
Print("all") command.
root[] myList->Print("all");
When using the “
>>
” whatever was in the list is overwritten. The list can be grown by using the “
>>+
” syntax. For
example to add the entries, with exactly 600 tracks:
root[] T->Draw(">>+ myList","fNtrack == 600","entrylist");
If the Draw command generates duplicate entries, they are not added to the list.
root[] T->Draw(">>+ myList"," fNtrack > 610","entrylist");
This command does not add any new entries to the list because all entries with more than 610 tracks have already
been found by the previous command for entries with more than 600 tracks.
12.20.10.1 Main Differences between TEventList and TEntryList
The functionality is essentialy the same: both are used to store entry numbers.
TEntryList
, however, uses considerably
less memory for storage, and is optimized for both very high and very low selectivity of cuts (see
TEntryListBlock
class description for the details of internal storage). Unlike the
TEventList
,
TEntryList
makes a distinction between
indices from a
TChain
and from a
TTree
. While a
TEntryList
for a
TTree
can be seen as just a list of numbers, a
TEntryList
for a
TChain
is a collection of
TEntryList
(s) for the
TTree
(s) that constitute this
TChain
. Such “sub-lists”
can be extracted by calling the function
TEntryList::GetEntryList(const char *treename, const char *filename)
and then be used to construct a new
TEntryList
for a new
TChain
, or processed independently as normal
TEntryList
(s)
for TTree(s). This modularity makes TEntryList much better suited for PROOF processing than the TEventList.
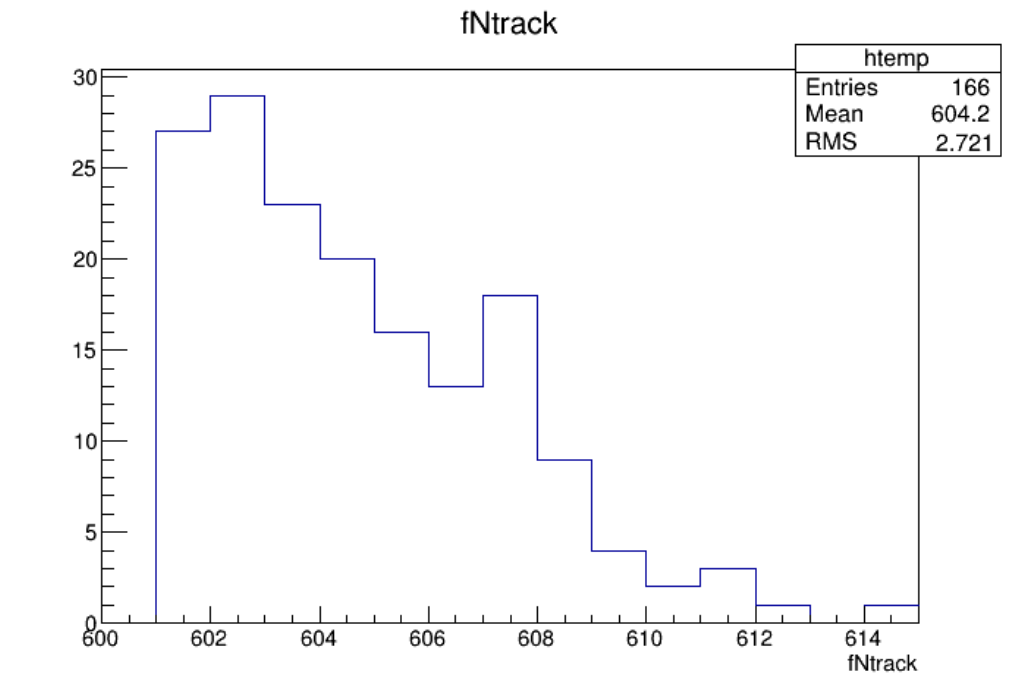
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 339
12.20.10.2 Using an Event List
A
TEventList
or a
TEntryList
can be used to limit the
TTree
to the events in the list. The methods
SetEventList
and
SetEntryList
tell the tree to use the list and hence limit all subsequent calls to
Draw
,
Scan
,
Process
,
Query
,
Principal
and
CopyTree
methods to the entries in the list. In general, it affects the
GetEntryNumber
method and all
functions using it for looping over the tree entries. The
GetEntry
and
GetEntries
methods are not affected. Note,
that in the
SetEventList
method, the
TEventList
argument is internally transformed into a
TEntryList
, and this
operation, in case of a
TChain
, requires loading of all the tree headers. In this example, we create a list with all entries
with more than 600 tracks and then set it so that the tree will use this list. To reset the
TTree
to use all events use
SetEventList(0) or SetEntryList(0).
1. Let’s look at an example. First, open the file and draw the fNtrack.
root[] TFile *f = new TFile("Event.root");
root[] TTree *T = (TTree*)f->Get("T");
root[] T->Draw("fNtrack");
2.
Now, put the entries with over 600 tracks into a
TEntryList
called
myList
. We get the list from the current
directory and assign it to a variable list.
root[] T->Draw(">>myList","fNtrack > 600","entrylist");
root[] TEntryList *list=(TEntryList*)gDirectory->Get("myList");
3.
Instruct the tree
T
to use the new list and draw it again. Note that this is exactly the same
Draw
command. The
list limits the entries.
root[] T->SetEntryList(list);
root[] T->Draw("fNtrack");
You should now see a canvas similar to this one.
340 CHAPTER 12. TREES
12.20.10.3 Operations on TEntryLists
If you have entry lists that were created using different cuts, you can combine the lists to get a new list, with entries
passing at least one of the cuts. Example:
root[] T->Draw(">>list1","fNtrack>600","entrylist");
root[] TEntryList *list1 = (TEntryList*)gDirectory->Get("list1");
root[] T->Draw(">>list2","fNtrack<590","entrylist");
root[] TEntryList *list2 = (TEntryList*)gDirectory->Get("list2");
root[] list1->Add(list2);
list1 now contains entries with more than 600 or less than 590 tracks. Check this by calling:
root[] T->SetEntryList(list1);
root[] T->Draw("fNtrack");
You can also subtract
TEntryList
from each other, so that the first list contains only the entries, passing the selection
of the first list and not present in the second list.
To add some individual entries, use
TEntryList::Enter()
function. To remove the entries you don’t like, use
TEntryList::Remove()
. To see if the entry is in the list, use
TEntryList::Contains()
. Remember, that all operation
in a TEntryList for a TChain are on the TTree level. This is illustrated by the following example:
root[] TEntryList *list1 = new TEntryList("list1","list1");
root[] list1->SetTree("tree1","file1")
root[] list1->Enter(0);
root[] list1->Enter(2);
root[] TEntryList *list2 = new TEntryList("list2","list2");
root[] list2->SetTree("tree2","file2");
root[] list2->Enter(0);
root[] list2->Enter(3);
root[] list1->Add(list2);
root[] list1->Print("all")
tree1 file1
0
2
tree2 file2
0
3
The result is a
TEntryList
for a
TChain
of
tree1
and
tree2
. If the second list was for the same
TTree
in the same
file as the first list, the result would be as follows:
root[] TEntryList *list2_2 = new TEntryList("list2_2","list2_2");
root[] list2_2->SetTree("tree2","file2");
root[] list2_2->Enter(1);
root[] list2_2->Enter(2);
root[] list2->Add(list2_2);
root[] list2->Print("all")
tree2 file2
0
1
2
3
12.20.10.4 TEntryListFromFile
This is a special kind of
TEntryList
, used only when processing
TChain
objects (see the method
TChain::SetEntryListFile()
).
It is used in the case, when the entry lists, corresponding to the trees of this chain, are stored in separate files. It
allows to load the entry lists in memory one by one, keeping only the list for the currently processed tree loaded.
For more details on entry lists, see
TEntryList
,
TEntryListBlock
and
TEntryListFromFile
class descriptions, func-
tions
TChain::SetEntryList()
,
TChain::SetEntryListFile()
, and the macro
$ROOTSYS/test/stressEntryList.C
.
12.20. SIMPLE ANALYSIS USING TTREE::DRAW 341
12.20.11 Filling a Histogram
The TTree::Draw method can also be used to fill a specific histogram. The syntax is:
root[] TFile *f = new TFile("Event.root")
root[] T->Draw("fNtrack >> myHisto")
root[] myHisto->Print()
TH1.Print Name= myHisto, Entries= 100, Total sum= 100
As we can see, this created a
TH1
, called
myHisto
. If you want to append more entries to the histogram, you can use
this syntax:
root[] T->Draw("fNtrack >>+ myHisto")
If you do not create a histogram ahead of time, ROOT will create one at the time of the Draw command (as is the case
above). If you would like to draw the variable into a specific histogram where you, for example, set the range and bin
number, you can define the histogram ahead of time and use it in the Draw command. The histogram has to be in the
same directory as the tree.
root[] TH1 *h1 = new TH1("h1","h1",50,0.,150.);
root[] T->Draw("fNtrack>> h1");
When you project a
TTree
into a histogram, the histogram inherits the
TTree
attributes and not the current style
attributes. This allows you to project two Trees with different attributes into the same picture. You can call the
method
TTree::UseCurrentStyle
to change the histogram to use the current style
gStyle
. See “Graphics and the
Graphical User Interface.
The binning of the newly created histogram can be specified in two ways. You can set a default in the
.rootrc
and/or
you can add the binning information in the TTree::Draw command.
To set number of bins default for the 1-D, 2-D, 3-D histograms can be specified in the
.rootrc
file via the environment
variables, e.g.:
# default binnings Hist.Binning.1D.x: 100
Hist.Binning.2D.x: 40
Hist.Binning.2D.y: 40
Hist.Binning.2D.Prof: 100
Hist.Binning.3D.x: 20
Hist.Binning.3D.y: 20
Hist.Binning.3D.z: 20
Hist.Binning.3D.Profx: 100
Hist.Binning.3D.Profy: 100
To set the number of bins for a specific histogram when using
TTree::Draw,
add up to nine numbers following the
histogram name. The numbers meaning is:
1 bins in x-direction
2 lower limit in x-direction
3upper limit in x-direction
4-6 same for y-direction
7-9 same for z-direction
When a bin number is specified, the value becomes the default. Any of the numbers can be skipped. For example:
tree.Draw("sqrt(x)>>hsqrt(500,10,20)";
// plot sqrt(x) between 10 and 20 using 500 bins
tree.Draw("sqrt(x):sin(y)>>hsqrt(100,10,,50,.1,.5)";
// plot sqrt(x) against sin(y) 100 bins in x-direction;
// lower limit on x-axis is 10; no upper limit
// 50 bins in y-direction; lower limit on y-axis is .1;
// upper limit is .5
342 CHAPTER 12. TREES
When the name is followed by binning information, appending the histogram with a “+”, will not reset
hsqrt
, but will
continue to fill it.
tree.Draw("sqrt(x)>>+hsqrt","y>0");
This works for 1-D, 2-D and 3-D histograms.
12.20.11.1 Projecting a Histogram
If you would like to fill a histogram, but not draw it you can use the TTree::Project() method.
root[] T->Project("quietHisto","fNtrack")
12.20.11.2 Making a Profile Histogram
In case of a two dimensional expression, you can generate a
TProfile
histogram instead of a two dimensional histogram
by specifying the
’prof’
or ’
profs’
option. The
prof
option is automatically selected when the output is redirected
into a TProfile. For example y:x>>pf where pfis an existing TProfile histogram.
12.20.11.3 Tree Information
Once we have drawn a tree, we can get information about the tree. These are the methods used to get information
from a drawn tree TTree:
•GetSelectedRows
: Returns the number of entries accepted by the selection expression. In case where no selection
was specified, it returns the number of entries processed.
•GetV1: Returns a pointer to the float array of the first variable.
•GetV2: Returns a pointer to the float array of second variable
•GetV3: Returns a pointer to the float array of third variable.
•GetW
: Returns a pointer to the float array of Weights where the weight equals the result of the selection expression.
To read the drawn values of
fNtrack
into an array, and loop through the entries follow the lines below. First, open the
file and draw the fNtrack variable:
root[] TFile *f = new TFile("Event.root")
root[] T->Draw("fNtrack")
Then declare a pointer to a float and use the GetV1 method to retrieve the first dimension of the tree. In this example
we only drew one dimension (fNtrack) if we had drawn two, we could use GetV2 to get the second one.
root[] Float_t *a
root[] a = T->GetV1()
Loop through the first 10 entries and print the values of fNtrack:
root[] for (int i=0;i<10; i++)
root[] cout << a[i] << ""<< endl // need an endl to see the values
594 597 606 595 604 610 604 602 603 596
By default,
TTree::Draw
creates these arrays with
fEstimate
words where
fEstimate
can be set via
TTree::SetEstimate
. If you have more entries than
fEstimate
only the first
fEstimate
selected entries
will be stored in the arrays. The arrays are used as buffers. When
fEstimate
entries have been processed, ROOT
scans the buffers to compute the minimum and maximum of each coordinate and creates the corresponding histograms.
You can use these lines to read all entries into these arrays:
root[] Int_t nestimate = (Int_t)T->GetEntries();
root[] T->SetEstimate(nestimate);
Obviously, this will not work if the number of entries is very large. This technique is useful in several cases, for example
if you want to draw a graph connecting all the
x
,
y(or z)
points. Note that you may have a tree (or chain) with 1
billion entries, but only a few may survive the cuts and will fit without problems in these arrays.
12.21. USING TTREE::MAKECLASS 343
12.21 Using TTree::MakeClass
The
TTree::Draw
method is convenient and easy to use; however it falls short if you need to do some programming
with the variable.
For example, for plotting the masses of all oppositely changed pairs of tracks, you would need to write a program that
loops over all events, finds all pairs of tracks, and calculates the required quantities. We have shown how to retrieve
the data arrays from the branches of the tree in the previous section, and you could just write that program from
scratch. Since this is a very common task, ROOT provides a utility that generates a skeleton class designed to loop
over the entries of the tree.
This is the
TTree::MakeClass
method. We will now go through the steps of using
MakeClass
with a simplified example.
The methods used here obviously work for complex event loop calculations.
These are our assumptions: we would like to do selective plotting and loop through each entry of the tree and tracks.
We chose a simple example: we want to plot
fPx
of the first 100 tracks of each entry. We have a ROOT tree with a
branch for each data member in the “
Event
” object. To build this file and tree follow the instructions on how to build
the examples in
$ROOTSYS/test
. Execute
Event
and instruct it to split the object with this command (from the UNIX
command line).
> $ROOTSYS/test/Event 400 1 2 1
This creates an Event.root file with 400 events, compressed, split, and filled.
See $ROOTSYS/test/MainEvent.cxx for more info.
The person who designed the tree makes a shared library available to you, which defines the classes needed. In this case,
the classes are Event,
EventHeader
, and Track and they are defined in the shared library
libEvent.so
. The designer
also gives you the
Event.h
file to see the definition of the classes. You can locate
Event.h
in
$ROOTSYS/test
, and if
you have not yet built
libEvent.so
, please see the instructions of how to build it (typing make in $ROOTSYS/test is
enough). If you have already built it, you can now use it again.
12.21.1 Creating a Class with MakeClass
First, we load the shared library and open Event.root.
root[] .L libEvent.so
root[] TFile *f = new TFile("Event.root");
root[] f->ls();
TFile** Event.root TTree benchmark ROOT file
TFile* Event.root TTree benchmark ROOT file
KEY: TH1F htime;1Real-Time to write versus time
KEY: TTree T;1An example of a ROOT tree
We can see there is a tree “
T
”, and just to verify that we are working with the correct one, we print the tree, which will
show us the header and branches.
root[] T->Print();
From the output of print we can see that the tree has one branch for each data member of
Event
,
Track
, and
EventHeader
. Now we can use
TTree::MakeClass
on our tree “
T
”.
MakeClass
takes one parameter, a string containing
the name of the class to be made. In the command below, the name of our class will be “MyClass”.
root[] T->MakeClass("MyClass")
Files: MyClass.h and MyClass.C generated from Tree: T
Cling informs us that it has created two files.
MyClass.
h contains the class definition and
MyClass.C
contains the
MyClass::Loop()
method.
MyClass
has more methods than just
Loop()
. The other methods are a constructor, a
destructor,
GetEntry()
,
LoadTree()
,
Notify()
,
Cut()
and
Show()
. The implementations of these methods are in the
.h file. This division of methods was done intentionally. The .C file is kept as short as possible, and contains only
code that is intended for you to customize. The .h file contains all the other methods. It is clear that you want to be
as independent as possible of the header file (i.e.
MyClass.h
) generated by
MakeClass
. The solution is to implement
a derived class, for example
MyRealClass
deriving from
MyClass
such that a change in your
Tree
or regeneration of
MyClass.h
does not force you to change
MyRealClass.h
. You can imagine deriving several classes from
MyClass.h
,
each with a specific algorithm. To understand both files, let’s start with MyClass.h and the class declaration:
344 CHAPTER 12. TREES
12.21.2 MyClass.h
class MyClass {
public :
// Pointer to the analyzed TTree or TChain
TTree *fChain;
// Current Tree number in a TChain
Int_t fCurrent;
// Declaration of leaves types
UInt_t fUniqueID;
UInt_t fBits;
Char_t fType[20];
Int_t fNtrack;
Int_t fNseg;
Int_t fNvertex;
UInt_t fFlag;
Float_t fTemperature;
Int_t fEvtHdr_fEvtNum;
// List of branches
TBranch *b_fUniqueID;
TBranch *b_fBits;
TBranch *b_fType;
TBranch *b_fNtrack;
TBranch *b_fNseg;
TBranch *b_fNvertex;
TBranch *b_fFlag;
TBranch *b_fTemperature;
TBranch *b_fEvtHdr_fEvtNum;
...
MyClass(TTree *tree=0);
~MyClass();
Int_t Cut(Int_t entry);
Int_t GetEntry(Int_t entry);
Int_t LoadTree(Int_t entry);
void Init(TTree *tree);
void Loop();
Bool_t Notify();
void Show(Int_t entry = -1);
};
We can see data members in the generated class. The first data member is
fChain
. Once this class is instantiated,
fChain
will point to the original tree or chain this class was made from. In our case, this is “T” in “
Event.root
”. If
the class is instantiated with a tree as a parameter to the constructor,
fChain
will point to the tree named in the
parameter. Next is
fCurrent
, which is also a pointer to the current tree/chain. Its role is only relevant when we have
multiple trees chained together in a
TChain
. The class definition shows us that this tree has one branch and one leaf
per data member. The methods of MyClass are:
•MyClass(TTree *tree=0) -
this constructor has an optional tree for a parameter. If you pass a tree,
MyClass
will use it rather than the tree from which it was created.
•void Init(TTree *tree) -
it is called by the constructor to initialize the tree for reading. It associates each
branch with the corresponding leaf data member.
•~MyClass() -the destructor, nothing special.
•Int_t GetEntry(Int_t entry) -
it loads the class with the entry specified. Once you have executed
GetEntry
,
the leaf data members in
MyClass
are set to the values of the entry. For example,
GetEntry(12)
loads the 13th
event into the event data member of
MyClass
(note that the first entry is 0).
GetEntry
returns the number of
bytes read from the file. In case the same entry is read twice, ROOT does not have to do any I/O. In this case
GetEntry
returns 1. It does not return 0, because many people assume a return of 0 means an error has occurred
while reading.
•Int_t LoadTree(Int_t entry)
and
void Notify()
- these two methods are related to chains.
LoadTree
will
load the tree containing the specified entry from a chain of trees. Notify is called by
LoadTree
to adjust the
branch addresses.
12.21. USING TTREE::MAKECLASS 345
•void Loop()
- it is the skeleton method that loops through each entry of the tree. This is interesting to us,
because we will need to customize it for our analysis.
12.21.3 MyClass.C
MyClass::Loop
consists of a for-loop calling
GetEntry
for each entry. In the template, the numbers of bytes are added
up, but it does nothing else. If we were to execute it now, there would be no output.
void MyClass::Loop() {
if (fChain == 0)return;
Int_t nentries = Int_t(fChain->GetEntries());
Int_t nbytes = 0,nb=0;
for (Int_t jentry=0; jentry<nentries;jentry++) {
Int_t ientry = LoadTree(jentry);
// in case of a TChain , ientry is the entry number in the
// current file
nb = fChain->GetEntry(jentry); nbytes += nb;
// if (Cut(ientry) < 0) continue;
}
}
At the beginning of the file are instructions about reading selected branches. They are not reprinted here, but please
read them from your own file
12.21.4 Modifying MyClass::Loop
Let us continue with the goal of going through the first 100 tracks of each entry and plot
Px
. To do this we change the
Loop method.
...
if (fChain == 0)return;
Int_t nentries = Int_t(fChain->GetEntries());
TH1F *myHisto = new TH1F("myHisto","fPx",100, -5,5);
TH1F *smallHisto = new TH1F("small","fPx",100, -5,5);
...
In the for-loop, we need to add another for-loop to go over all the tracks. In the outer for-loop, we get the entry
and the number of tracks. In the inner for-loop, we fill the large histogram (
myHisto
) with all tracks and the small
histogram (smallHisto) with the track if it is in the first 100.
...
for (Int_t jentry=0; jentry<nentries;jentry++) {
GetEntry(jentry);
for (Int_t j = 0;j<100; j++) {
myHisto->Fill(fTracks_fPx[j]);
if (j<100) {
smallHisto->Fill(fTracks_fPx[j]);
}
}
}
...
Outside of the for-loop, we draw both histograms on the same canvas.
...
myHisto->Draw();
smallHisto->Draw("Same");
...
Save these changes to
MyClass.C
and start a fresh root session. We will now load
MyClass
and experiment with its
methods.
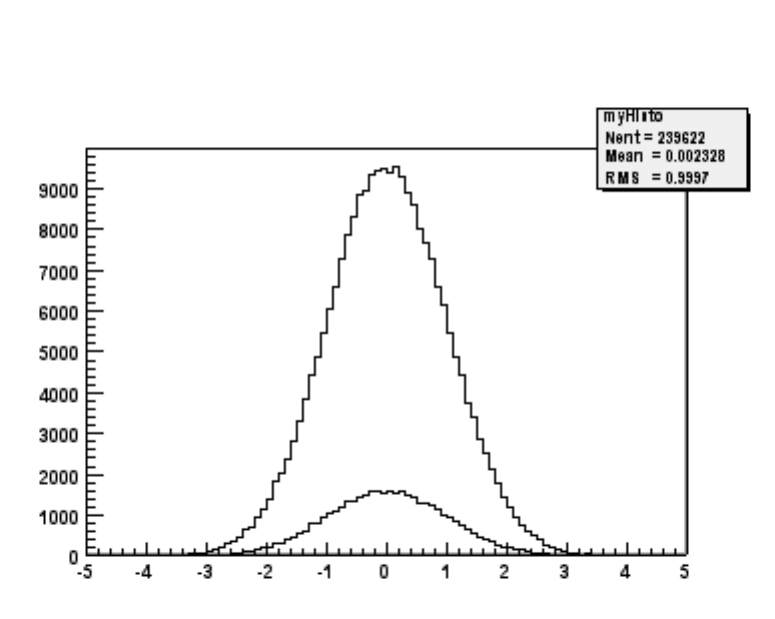
346 CHAPTER 12. TREES
12.21.5 Loading MyClass
The first step is to load the library and the class file. Then we can instantiate a MyClass object.
root[] .L libEvent.so
root[] .L MyClass.C
root[] MyClass m
Now we can get a specific entry and populate the event leaf. In the code snipped below, we get entry 0, and print the
number of tracks (594). Then we get entry 1 and print the number of tracks (597).
root[] m.GetEntry(0)
(int)57503
root[] m.fNtrack()
(Int_t)594
root[] m.GetEntry(1)
(int)48045
root[] m.fNtrack()
(Int_t)597
Now we can call the Loop method, which will build and display the two histograms.
root[] m.Loop()
You should now see a canvas that looks like this.
To conclude the discussion on MakeClass let us lists the steps that got us here.
•Call TTree::MakeClass, which automatically creates a class to loop over the tree.
•Modify the MyClass::Loop() method in MyClass.C to fit your task.
•Load and instantiate MyClass, and run MyClass::Loop().
12.22. USING TTREE::MAKESELECTOR 347
12.22 Using TTree::MakeSelector
With a
TTree
we can make a selector and use it to process a limited set of entries. This is especially important in a
parallel processing configuration where the analysis is distributed over several processors and we can specify which
entries to send to each processor. The
TTree::Process
method is used to specify the selector and the entries. Before
we can use
TTree::Process
we need to make a selector. We can call the
TTree::MakeSelector
method. It creates
two files similar to TTree::MakeClass.
In the resulting files is a class that is a descendent of TSelector and implements the following methods:
•TSelector::Begin() -
this method is called every time a loop over the tree starts. This is a convenient place to
create your histograms.
•TSelector::Notify() - it is called at the first entry of a new tree in a chain.
•TSelector::Process() -
it is called to process an event. It is the user’s responsibility to read the corresponding
entry in memory (may be just a partial read). Once the entry is in memory one can apply a selection and if
the event is selected histograms can be filled. Processing stops when this function returns
kFALSE
. It combines
the methods
TSelector::ProcessCut() and TSelector::ProcessFill()
in one, avoiding the necessity to
maintain the state in the class to communicate between these two functions. It reduces the information that
needs to be shared between them and promotes a more granular data access by reading branches as they are
needed.
•TSelector::Terminate() -
it is called at the end of a loop on a
TTree
. This is a convenient place to draw and
fit your histograms.
•TSelector::Version() -
this function provides backward compatibility for old versions and support for the
future upgrades.
•
The
TSelector
, unlike the resulting class from
MakeClass
, separates the processing into a
ProcessCut()
and
ProcessFill(), so we can limit reading of branches to the ones we need.
•
When a selector is used with a
TChain
in methods
Process()
,
ProcessFill()
,
ProcessCut()
, you must use
the pointer to the current
TTree
to call the method
GetEntry(entry)
. The parameter
entry
is always the local
entry number in the current tree. Assuming that fChain is the pointer to the TChain being processed, use
fChain->GetTree()->GetEntry(entry);
To create a selector call:
root[] T->MakeSelector("MySelector");
Where
T
is the
TTree
and
MySelector
is the name of created class and the name of the
.h
and
.C
files. The resulting
TSelector
is the argument to
TTree::Process
. The argument can be the file name or a pointer to the selector object.
root[] T->Process("MySelector.C","",1000,100);
This call will interpret the class defined in
MySelector.C
and process 1000 entries beginning with entry 100. The file
name can be appended with a “+” or a “++” to use ACLiC.
root[] T->Process("MySelector.C++","",1000,100);
When appending a “++”, the class will be compiled and dynamically loaded.
root[] T->Process("MySelector.C+","",1000,100);
When appending a “+”, the class will also be compiled and dynamically loaded. When it is called again, it recompiles
only if the macro (
MySelector.C
) has changed since it was compiled last. If not, it loads the existing library. The next
example shows how to create a selector with a pointer:
MySelector *selector = (MySelector *)TSelector::GetSelector("MySelector.C+");
T->Process(selector);
348 CHAPTER 12. TREES
Using this form, you can do things like:
selector->public_attribute1 = init_value;
for (int i=0; i<limit; i++) {
T->Process(selector);
selector->public_attribute1 =
function(selector->public_attribute2);
}
TTree::Process()
is aware of PROOF, ROOT parallel processing facility. If PROOF is setup, it divides the processing
amongst the slave CPUs.
12.22.1 Performance Benchmarks
The program
$ROOTSYS/test/bench.cxx
compares the I/O performance of STL vectors to the ROOT native
TClonesArrays
collection class. It creates trees with and without compression for the following cases:
vector<THit>
,
vector<THit*>,TClonesArray(TObjHit)not split TClonesArray(TObjHit)split.
The next graphs show the two columns on the right which represent the split and non-split
TClonesArray
, are
significantly lower than the vectors. The most significant difference is in reading a file without compression.
The file size with compression, write times with and without compression and the read times with and without
compression all favor the TClonesArray.
12.23 Impact of Compression on I/O
This benchmark illustrates the pros and cons of the compression option. We recommend using compression when the
time spent in I/O is small compared to the total processing time. In this case, if the I/O operation is increased by a
factor of 5 it is still a small percentage of the total time and it may very well save a factor of 10 on disk space. On the
other hand if the time spend on I/O is large, compression may slow down the program’s performance. The standard
test program
$ROOTSYS/test/Event
was used in various configurations with 400 events. The data file contains a
TTree
.
The program was invoked with:
Event 400 comp split
•comp = 0 means: no compression at all.
•comp = 1 means: compress everything if split = 0.
•comp = 1 means: compress only the tree branches with integers if split = 1.
•comp = 2 means: compress everything if split=1.
•split = 0 : the full event is serialized into one single buffer.
•
split = 1 : the event is split into branches. One branch for each data member of the Event class. The list of
tracks (a TClonesArray) has the data members of the Track class also split into individual buffers.
These tests were run on Pentium III CPU with 650 MHz.
Event
Parameters
File Size Total Time to
Write (MB/sec)
Effective Time to
Write (MB/sec)
Total Time to
Read All (MB/sec)
Total Time to
Read Sample
(MB/sec)
Comp = 0
Split = 1
19.75 MB 6.84 s.(2.8 MB/s) 3.56 s.(5.4 MB/s) 0.79s.(24.2 MB/s) 0.79 s.(24.2 MB/s)
Comp = 1
Split = 1
17.73 MB 6.44 s.(3.0 MB/s) 4.02 s.(4.8 MB/s) 0.90 s.(21.3 MB/s) 0.90 s.(21.3 MB/s)
Comp = 2
Split = 1
13.78 MB
11.34s.(1.7 MB/s)
9.51 s.(2.0 MB/s) 2.17 s.(8.8 MB/s) 2.17 s.(8.8 MB/s)
The
Total Time
is the real time in seconds to run the program.
Effective time
is the real time minus the time spent
in non I/O operations (essentially the random number generator). The program
Event
generates in average 600 tracks
per event. Each track has 17 data members. The read benchmark runs in the interactive version of ROOT. The ‘Total
Time to Read All’ is the real time reported by the execution of the script &ROOTSYS/test/eventa.
12.24. CHAINS 349
We did not correct this time for the overhead coming from the interpreter itself. The
Total time to read sample
is
the execution time of the script
$ROOTSYS/test/eventb
. This script loops on all events. For each event, the branch
containing the number of tracks is read. In case the number of tracks is less than 585, the full event is read in memory.
This test is obviously not possible in non-split mode. In non-split mode, the full event must be read in memory. The
times reported in the table correspond to complete I/O operations necessary to deal with
machine independent
binary files
. On
Linux
, this also includes byte-swapping operations. The ROOT file allows for direct access to any
event in the file and direct access to any part of an event when split=1.
Note also that the uncompressed file generated with split=0 is 48.7 Mbytes and only 47.17 Mbytes for the option
split=1. The difference in size is due to the object identification mechanism overhead when the event is written to a
single buffer. This overhead does not exist in split mode because the branch buffers are optimized for homogeneous
data types. You can run the test programs on your architecture. The program
Event
will report the write performance.
You can measure the read performance by executing the scripts
eventa
and
eventb
. The performance depends not
only of the processor type, but also of the disk devices (local, NFS, AFS, etc.).
12.24 Chains
A
TChain
object is a list of ROOT files containing the same tree. As an example, assume we have three files called
file1.root, file2.root, file3.root
. Each file contains one tree called “
T
”. We can create a chain with the
following statements:
TChain chain("T"); // name of the tree is the argument
chain.Add("file1.root");
chain.Add("file2.root");
chain.Add("file3.root");
The name of the
TChain
will be the same as the name of the tree; in this case it will be
"T". Note that two
objects
can have the same name as long as they are not histograms in the same directory, because there, the histogram names
are used to build a hash table. The class
TChain
is derived from the class
TTree
. For example, to generate a histogram
corresponding to the attribute “
x
” in tree “
T
” by processing sequentially the three files of this chain, we can use the
TChain::Draw method.
chain.Draw("x");
When using a TChain, the branch address(es) must be set with:
chain.SetBranchAdress(branchname,...) // use this for TChain
rather than:
branch->SetAddress(...); // this will not work
The second form returns the pointer to the branch of the current
TTree
in the chain, typically the first one. The
information is lost when the next
TTree
is loaded. The following statements illustrate how to set the address of the
object to be read and how to loop on all events of all files of the chain.
{
TChain chain("T"); // create the chain with tree "T"
chain.Add("file1.root"); // add the files
chain.Add("file2.root");
chain.Add("file3.root");
TH1F *hnseg = new TH1F("hnseg",
"Number of segments for selected tracks",
5000,0,5000);
// create an object before setting the branch address
Event *event = new Event();
// Specify the address where to read the event object
chain.SetBranchAddress("event", &event);
// Start main loop on all events In case you want to read only a few
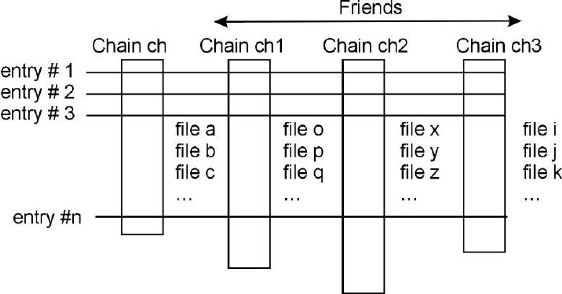
350 CHAPTER 12. TREES
// branches, use TChain::SetBranchStatus to activate a branch.
Int_t nevent = chain.GetEntries();
for (Int_t i=0;i<nevent;i++) {
// read complete accepted event in memory
chain.GetEvent(i);
// Fill histogram with number of segments
hnseg->Fill(event->GetNseg());
}
// Draw the histogram
hnseg->Draw();
}
12.24.1 TChain::AddFriend
ATChain
has a list of friends similar to a tree (see
TTree::AddFriend)
. You can add a friend to a chain with the
TChain::AddFriend
method. With
TChain::GetListOfFriends
you can retrieve the list of friends. The next example
has four chains each has 20 ROOT trees from 20 ROOT files.
TChain ch("t"); // a chain with 20 trees from 20 files
TChain ch1("t1");
TChain ch2("t2");
TChain ch3("t3");
Now we can add the friends to the first chain.
ch.AddFriend("t1");
ch.AddFriend("t2");
ch.AddFriend("t3");
The parameter is the name of friend chain (the name of a chain is always the name of the tree from which it was
created). The original chain has access to all variables in its friends. We can use the
TChain::Draw
method as if the
values in the friends were in the original chain. To specify the chain to use in the Draw method, use:
<chainname>.<branchname>.<varname>
If the variable name is enough to identify uniquely the variable, you can leave out the chain and/or branch name. For
example, this generates a 3-d scatter plot of variable “
var
” in the
TChain ch
versus variable
v1 inTChain t1 versus
variable v2 in TChaint2.
ch.Draw("var:t1.v1:t2.v2");
When a
TChain::Draw
is executed, an automatic call to
TTree::AddFriend
connects the trees in the chain. When a
chain is deleted, its friend elements are also deleted.
The number of entries in the friend must be equal or greater to the number of entries of the original chain. If the friend
has fewer entries a warning is given and the resulting histogram will have missing entries. For additional information see
TTree::AddFriends()
. A full example of a tree and friends is in Example #3
($ROOTSYS/tutorials/tree/tree3.C
)
in the Trees section above.
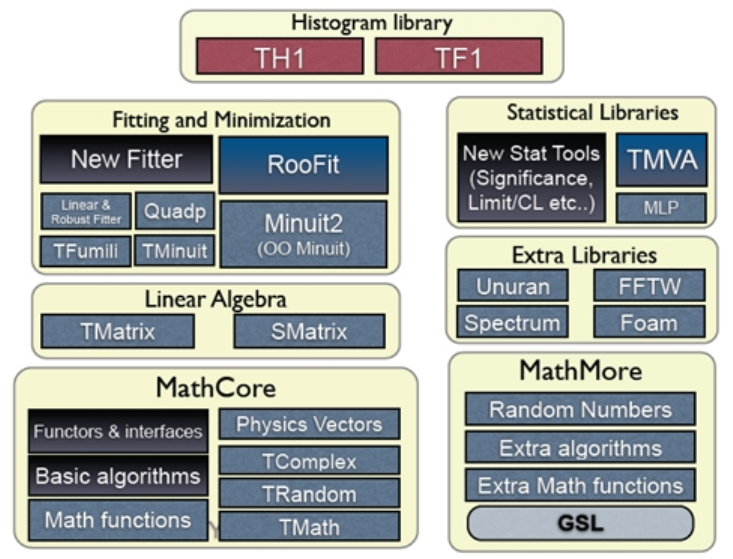
Chapter 13
Math Libraries in ROOT
The aim of Math libraries in ROOT is to provide and to support a coherent set of mathematical and statistical functions.
The latest developments have been concentrated in providing first versions of the
MathCore
and
MathMore
libraries,
included in ROOT v5.08. Other recent developments include the new version of
MINUIT
, which has been re-designed
and re-implemented in the C++ language. It is integrated in ROOT. In addition, an optimized package for describing
small matrices and vector with fixed sizes and their operation has been developed (
SMatrix
). The structure is shown
in the following picture.
Figure 13.1: Math libraries and packages
13.1 MathCore Library
MathCore
provides a collection of functions and C++ classes for numerical computing. This library includes only the
basic mathematical functions and algorithms and not all the functionality required by the physics community. A more
advanced mathematical functionality is provided by the
MathMore
library. The current set of included classes, which
are provided in the ROOT::Math namespace are:
•Basic special functions like the gamma, beta and error function.
•
Mathematical functions used in statistics, such as the probability density functions and the cumulative distributions
functions (lower and upper integral of the pdf’s).
351
352 CHAPTER 13. MATH LIBRARIES IN ROOT
•
Generic function classes and interfaces for evaluating one-dimensional (
ROOT::Math::IBaseFunctiononeDim
)
and multi-dimensional functions (
ROOT::Math::IBaseFunctionMultiDim
) and parametric function interfaces
for evaluating functions with parameters in one (
ROOT::Math::IParametricFunctionOneDim
) or multi di-
mensions (
ROOT::Math::IParametricFunctionMultiDim
). A set of user convenient wrapper classes, such as
ROOT::Math::Functor
is provided for wrapping user-classes in the needed interface, required to use the algorithms
of the ROOT Mathematical libraries.
•Numerical algorithms interfaces and in same cases default implementations for:
–numerical integration;
–numerical differentiation;
–one dimensional root-finding;
–one-dimensional minimization;
–multi-dimensional minimization (only the ROOT::Math::Minimizer interface)
•
Fitting classes: set of classes for fitting generic data sets. These classes are provided in the namespace
ROOT::Fit
.
They are describing separately in the Fitting chapter.
The sets described above is independednt of ROOT libraries and can be built as a set of standalone classes. In addition
MathCore provides the following classes (depending on ROOT libCore library):
•TMath: namespace with mathematical functions and basic function algorithms.
•TComplex: class for complex numbers.
•
Random classes: the base class
TRandom
and the derived classes
TRandom1
,
TRandom2
and
TRandom3
, implementing
the pseudo-random number generators.
A detailed description for all MathCore classes is available in the Doxygen online reference documentation.
13.2 MathMore Library
The
MathMore
library provides an advanced collection of functions and C++ classes for numerical computing. This is
an extension of the functionality provided by the
MathCore
library. The
MathMore
library is implemented wrapping in
C++ the GNU Scientific Library (GSL). The current set, provided in the ROOT::Math namespace include:
•Special mathematical functions (like Bessel functions, Legendre polynomials, etc.. )
•
Additional mathematical functions used in statistics such as probability density functions, cumulative distributions
functions and their inverse which are not in MathCore but present in the GSL library.
•
Numerical algorithms for one dimensional functions based on implementation of the GNU Scientific Library
(GSL):
•
Numerical integration classes implementing the interface
ROOT::Math::Integrator
which is based on the
Adaptive integration algorithms of QUADPACK
•Numerical differentiation via ROOT::Math::GSLDerivator
•Root finder implementing the ROOT::Math::RootFinder interface, using different solver algorithms from GSL
•one-dimensional Minimization implementing the interfaceROOT::Math::IMinimizer1D
•Interpolation via ROOT::Math::Interpolation. All the GSL interpolation types are supported
•Function approximation based on Chebyshev polynomials via the class ROOT::Math::Chebyshev
•
Random number generators and distributions based on GSL using the
ROOT::Math::Random<Engine_type>
class.
•Polynomial evaluation and root solvers
13.3. TMATH 353
The mathematical functions are implemented as a set of free functions in the namespace
ROOT::Math
. The naming
used for the special functions is the same proposed for the C++ standard (see C++ standard extension proposal
document).The
MathMore
library is implemented wrapping in C++ the GNU Scientific Library ( ). Building
MathMore
requires a version of GSL larger or equal 1.8. The source code of
MathMore
is distributed under the GNU General
Public License.
MathMore
(and its ROOT Cling dictionary) can be built within ROOT whenever a GSL library is found in the system.
The GSL library and header file location can be specified in the ROOT configure script, by doing:
./configure --with-gsl-incdir=... --with-gsl-libdir=...
MathMore
can be built also a stand-alone library (without requiring ROOT) downloding the tar file from the Web at
this link. In this case the library will not contain the dictionary information and therefore cannot be used interactively
More information on the classes and functions present in
MathMore
is available in the online reference documentation.
13.3 TMath
In the namespace, TMath, a collection of free functions is provided for the following functionality:
•numerical constants (like pi,e,h, etc.);
•trigonometric and elementary mathematical functions;
•functions to work with arrays and collections (e.g. functions to find min and max of arrays);
•statistic functions to work on array of data (e.g. mean and RMS of arrays);
•algorithms for binary search/hashing sorting;
•special mathematical functions like Bessel,Erf,Gamma, etc.;
•statistical functions, like common probability and cumulative (quantile) distributions
•geometrical functions.
For more details, see the reference documentation of TMath at http://root.cern.ch/root/htmldoc/TMath.html.
13.3.1 Numerical Constants
TMath
offers a wide range of constants in the form of inline functions. Notice that they are not defined as C/C++
preprocessor macros. This set of functions includes one or more definitions for the following constants:
•Pi.
•Base of natural logarithm.
•Velocity of light.
•Gravitational constant (G).
•Standard acceleration of gravity (g).
•Standard acceleration of Gravity.
•Plank’s contant.
•Boltzmann’s and Steffan-Boltzmann’s constants.
•Avogadro’s number.
•Universal gas constant.
•Molecular weight of dry air.
•Dry air gas constant.
•Euler-Mascheroni Constant.
•Elementary charge.
354 CHAPTER 13. MATH LIBRARIES IN ROOT
13.3.2 Elementary Functions
A set of miscellaneous elementary mathematical functions is provided along with a set of basic trigonometrical functions.
Some of this functions refer to basic mathematical functions like the square root, the power to a number of the calculus
of a logarithm, while others are used for number treatment, like rounding.
Although there are some functions that are not in the standard C math library (like
Factorial
), most of the functionality
offered here is just a wrapper of the first ones. Nevertheless, some of the them also offer some security checks or a
better precision, like the trigonometrical functions ASin(x),ACos(x) or ATan(x).
“‘{.cpp} // Generate a vector with 10 random numbers vector v(10); std::generate(v.begin(), v.end(), rand);
// Find the minumum value of the vector (iterator version) vector::iterator it; it = TMath::LocMin(v.begin(), v.end());
std::cout << *it << std::endl;
// The same with the old-style version int i; i = TMath::LocMin(10, &v[0]); std::cout << v[i] << std::endl; “‘
Another example of these functions can be found in $ROOTSYS/tutorials/permute.C.
13.3.3 Statistic Functions Operating on Arrays.
This set of functions processes arrays to calculate:
•Mean.
•Median.
•Geometrical mean.
•Sample Standard Deviation (RMS).
•The kth smallest element.
These functions, as the array algorithms, have two different interfaces. An old-style one where the size of the array is
passed as a first argument followed by a pointer to the array itself and a modern C++-like interface that receives two
iterators to it.
“‘{.cpp} // Size of the array const int n = 100;
// Vector v with random values vector v(n); std::generate(v.begin(), v.end(), rand);
// Weight vector w vector w(n); std::fill(w.begin(), w.end, 1);
double mean;
// Calculate the mean of the vector // with iterators mean = TMath::Mean(v.begin(), v.end());
// old-style mean = TMath::Mean(n, &v[0]);
// Calculate the mean with a weight vector // with iterators mean = TMath::Mean(v.begin(), v.end(), w.begin());
// old-style mean = TMath::Mean(n, &v[0], &w[0]); “‘
13.3.4 Special and Statistical Functions.
TMath
also provides special functions like Bessel, Error functions, Gamma or similar plus statistical mathematical
functions, including probability density functions, cumulative distribution and their inverse.
The majority of the special functions and the statitical distributions are provided also as free functions in the
ROOT::Math
namespace. See one of the next paragraph for the complete description of the functions provided in
ROOT::Math
. The
user is encourage to use those versions of the algorithms rather than the ones in TMath.
Functions not present in ROOT::Math and provided only by TMath are:
•Special functions:
•DiLogarithm
•Struve
•Statistical functions:
•KolmogorovProb
13.4. RANDOM NUMBERS 355
•Voigt function
•LaplaceDist
•Vavilov
The example tutorial
GammaFun.C
and
mathBeta.C
in
$ROOTSYS/tutorials
shows an example of use of the
ROOT::Math
special functions
13.4 Random Numbers
In ROOT pseudo-random numbers can be generated using the
TRandom
classes. 4 different types exist:
TRandom
,
TRandom1
,
TRandom2
and
TRandom3
. All they implement a different type of random generators.
TRandom
is the base
class used by others. It implements methods for generating random numbers according to pre-defined distributions,
such as Gaussian or Poisson.
13.4.1 TRandom
Pseudo-random numbers are generated using a linear congruential random generator. The multipliers used are the
same of the BSD rand() random generator. Its sequence is:
xn+1 = (axn+c) mod mwith a= 1103515245,c= 12345 and m= 231.
This type of generator uses a state of only a 32 bit integer and it has a very short period, 2
31
,about 10
9
, which can be
exhausted in just few seconds. The quality of this generator is therefore BAD and it is strongly recommended to NOT
use for any statistical study.
13.4.2 TRandom1
This random number generator is based on the Ranlux engine, developed by M. Lüsher and implemented in Fortran by
F. James. This engine has mathematically proven random proprieties and a long period of about 10
171
. Various luxury
levels are provided
(1,2,3,4)
and can be specified by the user in the constructor. Higher the level, better random
properties are obtained at a price of longer CPU time for generating a random number. The level 3 is the default,
where any theoretical possible correlation has very small chance of being detected. This generator uses a state of 24
32-bits words. Its main disadvantage is that is much slower than the others (see timing table). For more information
on the generator see the following article:
•
F. James, “RANLUX: A Fortran implementation of the high quality pseudo-random number generator of Lüscher”,
Computer Physics Communication, 79 (1994) 111.
13.4.3 TRandom2
This generator is based on the maximally equidistributed combined Tausworthe generator by L’Ecuyer. It uses only 3
32-bits words for the state and it has a period of about 10
26
. It is fast and given its small states, it is recommended for
applications, which require a very small random number size. For more information on the generator see the following
article:
•
P. L’Ecuyer, “Maximally Equidistributed Combined Tausworthe Generators”, Mathematics of Computation, 65,
213 (1996), 203-213.
13.4.4 TRandom3
This is based on the Mersenne and Twister pseudo-random number generator, developed in 1997 by Makoto Matsumoto
and Takuji Nishimura. The newer implementation is used, referred in the literature as MT19937. It is a very fast and
very high quality generator with a very long period of 10
6000
. The disadvantage of this generator is that it uses a state
of 624 words. For more information on the generator see the following article:
•
M. M. Matsumoto and T. Nishimura, “Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-
random number generator”, ACM Trans. on Modeling and Computer Simulations, 8, 1, (1998), 3-20.
TRandom3
is the recommended random number generator, and it is used by default in ROOT using the global
gRandom
object (see chapter gRandom).
356 CHAPTER 13. MATH LIBRARIES IN ROOT
13.4.5 Seeding the Generators
The seeds for the generators can be set in the constructor or by using the
SetSeed
method. When no value is given
the generator default seed is used, like 4357 for
TRandom3
. In this case identical sequence will be generated every time
the application is run. When the 0 value is used as seed, then a unique seed is generated using a
TUUID
, for
TRandom1
,
TRandom2
and
TRandom3
. For
TRandom
the seed is generated using only the machine clock, which has a resolution of
about 1 sec. Therefore identical sequences will be generated if the elapsed time is less than a second.
13.4.6 Examples of Using the Generators
The method
Rndm()
is used for generating a pseudo-random number distributed between 0 and 1 as shown in the
following example:
// use default seed
// (same random numbers will be generated each time)
TRandom3 r; // generate a number in interval ]0,1] (0 is excluded)
r.Rndm();
double x[100];
r.RndmArray(100,x); // generate an array of random numbers in ]0,1]
TRandom3 rdm(111); // construct with a user-defined seed
// use 0: a unique seed will be automatically generated using TUUID
TRandom1 r1(0);
TRandom2 r2(0);
TRandom3 r3(0);
// seed generated using machine clock (different every second)
TRandom r0(0);
13.4.7 Random Number Distributions
The
TRandom
base class provides functions, which can be used by all the other derived classes for generating random
variates according to predefined distributions. In the simplest cases, like in the case of the exponential distribution, the
non-uniform random number is obtained by applying appropriate transformations. In the more complicated cases,
random variates are obtained using acceptance-rejection methods, which require several random numbers.
TRandom3 r;
// generate a gaussian distributed number with:
// mu=0, sigma=1 (default values)
double x1 = r.Gaus();
double x2 = r.Gaus(10,3); // use mu = 10, sigma = 3;
The following table shows the various distributions that can be generated using methods of the
TRandom
classes. More
information is available in the reference documentation for
TRandom
. In addition, random numbers distributed according
to a user defined function, in a limited interval, or to a user defined histogram, can be generated in a very efficient way
using TF1::GetRandom() or TH1::GetRandom().
Distributions Description
Double_t Uniform(Double_t x1,Double_t x2 ) Uniform random numbers between x1,x2
Double_t Gaus(Double_t mu,Double_t sigma ) Gaussian random numbers.
Default values: mu=0,sigma=1
Double_t Exp(Double_t tau) Exponential random numbers with mean tau.
Double_t Landau(Double_t mean,Double_t s igma) Landau distributed random numbers.
Default values: mean=0,sigma=1
Double_t BreitWigner(Double_t mean,
Double_t gamma)
Breit-Wigner distributed random numbers.
Default values mean=0,gamma=1
Int_t Poisson(Double_t mean)
Double_t PoissonD(Double_t mean)
Poisson random numbers
Int_t Binomial(Int_t ntot,Double_t prob ) Binomial Random numbers
Circle(Double_t &x,Double_t &y,Double_t r) Generate a random 2D point (x,y) in
a circle of radius r
Sphere(Double_t &x,Double_t &y,
Double_t &z,Double_t r)
Generate a random 3D point (x,y,z) in
a sphere of radius r
Rannor(Double_t &a,Double_t &b) Generate a pair of Gaussian random
numbers with mu=0 and sigma=1
13.4. RANDOM NUMBERS 357
13.4.8 UNURAN
An interface to a new package, UNU.RAN, (Universal Non Uniform Random number generator for generating
non-uniform pseudo-random numbers) was introduced in ROOT v5.16.
UNU.RAN is an ANSI C library licensed under GPL. It contains universal (also called automatic or black-box)
algorithms that can generate random numbers from large classes of continuous (in one or multi-dimensions), discrete
distributions, empirical distributions (like histograms) and also from practically all standard distributions. An extensive
online documentation is available at the UNU.RAN Web Site http://statmath.wu-wien.ac.at/unuran/
The ROOT class TUnuran is used to interface the UNURAN package. It can be used as following:
•
With the UNU.RAN native, string API for pre-defined distributions (see UNU.RAN documentation for the
allowed string values at http://statistik.wu-wien.ac.at/unuran/doc/unuran.html ):
TUnuran unr;
// initialize unuran to generate normal random numbers using
// a "arou" method
unr.Init("normal()","method=arou");
...
// sample distributions N times (generate N random numbers)
for (int i=0; i<N; ++i)
double x = unr.Sample();
•
For continuous 1D distribution object via the class
TUnuranContDist
that can be created for example from a
TF1
function providing the pdf (probability density function) . The user can optionally provide additional information
via TUnuranContDist::SetDomain(min,max) like the domain() for generating numbers in a restricted region.
// 1D case: create a distribution from two TF1 object
// pointers pdfFunc
TUnuranContDist dist( pdfFunc);
// initialize unuran passing the distribution and a string
// defining the method
unr.Init(dist, "method=hinv");
// sample distribution N times (generate N random numbers)
for (int i=0; i < N; ++i)
double x = unr.Sample();
•
For multi-dimensional distribution via the class
TUnuranMultiContDist
, which can be created from a the
multi-dimensional pdf.
// Multi- dimensional case from a TF1 (TF2 or TF3) objects
TUnuranMultiContDist dist( pdfFuncMulti);
// the recommended method for multi-dimensional function is "hitro"
unr.Init(dist,"method=hitro");
// sample distribution N times (generate N random numbers)
double x[NDIM];
for (int i=0; i<N; ++i)
unr.SampleMulti(x);
•
For discrete distribution via the class
TUnuranDiscrDist
, which can be initialized from a
TF1
or from a vector of
probabilities.
// Create distribution from a vector of probabilities
double pv[NSize] = {0.1,0.2,...};
TUnuranDiscrDist dist(pv,pv+NSize);
// the recommended method for discrete distribution is
unr.Init(dist, "method=dgt");
// sample N times (generate N random numbers)
for (int i=0; i < N; ++i)
int k = unr.SampleDiscr();

358 CHAPTER 13. MATH LIBRARIES IN ROOT
•
For empirical distribution via the class
TUnuranEmpDist
. In this case one can generate random numbers from a
set of un-bin or bin data. In the first case the parent distribution is estimated by UNU.RAN using a gaussian
kernel smoothing algorithm. The
TUnuranEmpDist
distribution class can be created from a vector of data or from
TH1 (using the bins or from its buffer for un-binned data).
// Create distribution from a set of data
// vdata is an std::vector containing the data
TUnuranEmpDist dist(vdata.begin(),vdata.end());
unr.Init(dist);
// sample N times (generate N random numbers)
for (int i=0; i<N; ++i)
double x = unr.Sample();
•
For some predefined distributions, like
Poisson
and
Binomial
, one can use directly a function in the
TUnuran
class. This is more convenient in passing distribution parameters than using directly the string interface.
TUnuran unr;
// Initialize unuran to generate normal random numbers from the
// Poisson distribution with parameter mu
unr.InitPoisson(mu);
...
// Sample distributions N times (generate N random numbers)
for (int i=0; i<N; ++i)
int k = unr.SampleDiscr();
Functionality is also provided via the C++ classes for using a different random number generator by passing a TRandom
pointer when constructing the TUnuran class (by default the ROOT gRandom is passed to UNURAN).
13.4.9 Performances of Random Numbers
Here are the CPU times obtained using the four random classes on an
lxplus
machine with an Intel 64 bit architecture
and compiled using gcc 3.4:
TRandom (ns/call) TRandom1 (ns/call) TRandom2 (ns/call) TRandom3 (ns/call)
Rndm() • • 6 9
Gaus() 31 161 35 42
Rannor() 116 216 126 130
Poisson(m-10) 147 1161 162 239
Poisson(m=10)
UNURAN
80 294 89 99
13.5 Mathematical Functions
The mathematical functions are present in both
MathCore
and
MathMore
libraries. All mathematical functions are
implemented as free functions in the namespace
ROOT::Math
. The most used functions are in the
MathCore
library
while the others are in the
MathMore
library. The functions in
MathMore
are all using the implementation of the GNU
Scientific Library (GSL). The naming of the special functions is the same defined in the C++ Technical Report on
Standard Library extensions. The special functions are defined in the header file Math/SpecFunc.h.
13.5.1 Special Functions in MathCore
•ROOT::Math::beta(double x,double y) -evaluates the beta function:
B(x, y) = Γ(x)Γ(y)
Γ(x+y)
•double ROOT::Math::erf(double x)
- evaluates the error function encountered in integrating the normal
distribution:
erf(x) = 2
√πZx
0
e−t2dt

13.5. MATHEMATICAL FUNCTIONS 359
•double ROOT::Math::erfc(double x) - evaluates the complementary error function:
erfc(x)=1−erf(x) = 2
√πZ∞
x
e−t2dt
•double ROOT::Math::tgamma(double x) - calculates the gamma function:
Γ(x) = Z∞
0
tx−1e−tdt
13.5.2 Special Functions in MathMore
•double ROOT::Math::assoc_legendre(unsigned l,unsigned m,double x) -
computes the associated Legen-
dre polynomials (with m>=0,l>=m and |x|<1):
Pm
l(x) = (1 −x2)m/2dm
dxmPl(x)
•double ROOT::Math::comp_ellint_1(double k)
- calculates the complete elliptic integral of the first kind
(with 0≤k2≤1:
K(k) = F(k, π/2) = Zπ/2
0
dθ
p1−k2sin2θ
•double ROOT::Math::comp_ellint_2(double k)
- calculates the complete elliptic integral of the second kind
(with 0≤k2≤1):
E(k) = E(k, π/2) = Zπ/2
0p1−k2sin2θdθ
•double ROOT::Math::comp_ellint_3(double n,double k)
- calculates the complete elliptic integral of the
third kind (with 0≤k2≤1):
Π(n, k, π/2) = Zπ/2
0
dθ
(1 −nsin2θ)p1−k2sin2θ
•double ROOT::Math::conf_hyperg(double a,double b,double z)
- calculates the confluent hyper-geometric
functions of the first kind:
1F1(a;b;z) = Γ(b)
Γ(a)
∞
X
n=0
Γ(a+n)
Γ(b+n)
zn
n!
•double ROOT::Math::conf_hypergU(double a,double b,double z)
- calculates the confluent hyper-geometric
functions of the second kind, known also as Kummer function of the second type. It is related to the confluent
hyper-geometric function of the first kind:
U(a, b, z) = π
sin πb 1F1(a, b, z)
Γ(a−b+ 1) −z1−b1F1(a−b+ 1,2−b, z)
Γ(a)
•double ROOT::Math::cyl_bessel_i(double nu,double x)
- calculates the modified Bessel function of the first
kind, also called regular modified (cylindrical) Bessel function:
Iν(x) = i−νJν(ix) =
∞
X
k=0
(1
2x)ν+2k
k!Γ(ν+k+ 1)
•double ROOT::Math::cyl_bessel_j(double nu,double x)
- calculates the (cylindrical) Bessel function of the
first kind, also called regular (cylindrical) Bessel function:
Jν(x) =
∞
X
k=0
(−1)k(1
2x)ν+2k
k!Γ(ν+k+ 1)
•double ROOT::Math::cyl_bessel_k(double nu,double x)
- calculates the modified Bessel function of the
second kind, also called irregular modified (cylindrical) Bessel function for x > 0,v > 0:
Kν(x) = π
2iν+1(Jν(ix) + iN (ix)) = (π
2
I−ν(x)−Iν(x)
sin νπ for non-integral ν
π
2lim µ→νI−µ(x)−Iµ(x)
sin µπ for integral ν
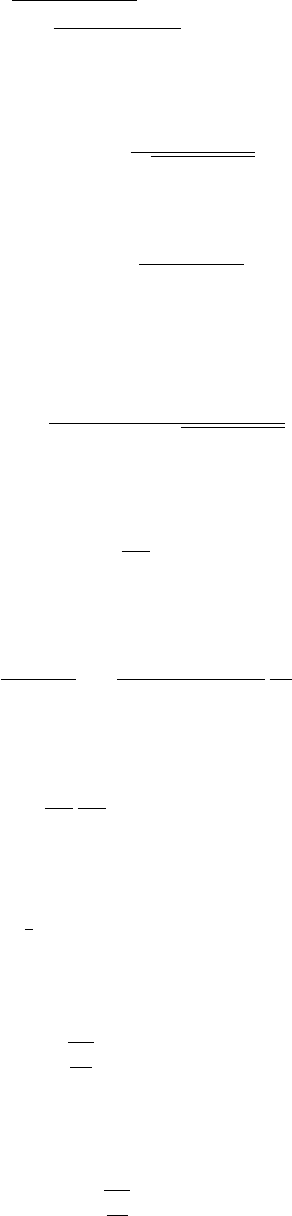
360 CHAPTER 13. MATH LIBRARIES IN ROOT
•double ROOT::Math::cyl_neumann(double nu,double x)
- calculates the (cylindrical) Bessel function of the
second kind, also called irregular (cylindrical) Bessel function or (cylindrical) Neumann function:
Nν(x) = Yν(x) = (Jνcos νπ−J−ν(x)
sin νπ for non-integral ν
lim µ→νJµcos µπ−J−µ(x)
sin µπ for integral ν
•double ROOT::Math::ellint_1(double k,double phi)
- calculates incomplete elliptic integral of the first kind
(with 0≤k2≤1):
K(k) = F(k, π/2) = Zπ/2
0
dθ
p1−k2sin2θ
•double ROOT::Math::ellint_2(double k,double phi)
- calculates the complete elliptic integral of the second
kind (with 0≤k2≤1):
E(k) = E(k, π/2) = Zπ/2
0p1−k2sin2θdθ
•double ROOT::Math::ellint_3(double n,double k,double phi)
- calculates the complete elliptic integral of
the third kind (with 0≤k2≤1):
Π(n, k, π/2) = Zπ/2
0
dθ
(1 −nsin2θ)p1−k2sin2θ
•double ROOT::Math::expint(double x) - calculates the exponential integral:
Ei(x) = −Z∞
−x
e−t
tdt
•double ROOT::Math::hyperg(double a,double b,double c,double x)
- calculates Gauss’ hyper-geometric
function:
2F1(a, b;c;x) = Γ(c)
Γ(a)Γ(b)
∞
X
n=0
Γ(a+n)Γ(b+n)
Γ(c+n)
xn
n!
•double ROOT::Math::legendre(unsigned l,double x)
- calculates the Legendre polynomials for
l≥
0,
|x| ≤
1
in the Rodrigues representation:
Pl(x) = 1
2ll!
dl
dxl(x2−1)l
•double ROOT::Math::riemann_zeta(double x) - calculates the Riemann zeta function:
ζ(x) = P∞
k=1 k−xfor x > 1
2xπx−1sin (1
2πx)Γ(1 −x)ζ(1 −x)for x < 1
•double ROOT::Math::sph_bessel(unsigned n,double x)
- calculates the spherical Bessel functions of the first
kind (also called regular spherical Bessel functions):
jn(x) = rπ
2xJn+1/2(x)
•double ROOT::Math::sph_neumann(unsigned n,double x)
- calculates the spherical Bessel functions of the
second kind (also called irregular spherical Bessel functions or spherical Neumann functions):
nn(x) = yn(x) = rπ
2xNn+1/2(x)
13.5.3 Probability Density Functions (PDF)
Probability density functions of various distributions. All the functions, apart from the discrete ones, have the extra
location parameter
x0
, which by default is zero. For example, in the case of a gaussian
pdf
,
x0
is the
mean
,
mu
, of the
distribution. All the probability density functions are defined in the header file
Math/DistFunc.h
and are part of the
MathCore libraries. The definition of these functions is documented in the reference doc for statistical functions:

13.5. MATHEMATICAL FUNCTIONS 361
double ROOT::Math::beta_pdf(double x,double a, double b);
double ROOT::Math::binomial_pdf(unsigned int k,double p,unsigned int n);
double ROOT::Math::breitwigner_pdf(double x,double gamma,double x0=0);
double ROOT::Math::cauchy_pdf(double x,double b=1,double x0=0);
double ROOT::Math::chisquared_pdf(double x,double r,double x0=0);
double ROOT::Math::exponential_pdf(double x,double lambda,double x0=0);
double ROOT::Math::fdistribution_pdf(double x,double n,double m,double x0=0);
double ROOT::Math::gamma_pdf(double x,double alpha,double theta,double x0=0);
double ROOT::Math::gaussian_pdf(double x,double sigma,double x0=0);
double ROOT::Math::landau_pdf(double x,double s,double x0=0);
double ROOT::Math::lognormal_pdf(double x,double m,double s,double x0=0);
double ROOT::Math::normal_pdf(double x,double sigma,double x0=0);
double ROOT::Math::poisson_pdf(unsigned int n,double mu);
double ROOT::Math::tdistribution_pdf(double x,double r,double x0=0);
double ROOT::Math::uniform_pdf(double x,double a,double b,double x0=0);
13.5.4 Cumulative Distribution Functions (CDF)
For all the probability density functions, we have the corresponding cumulative distribution functions and their
complements. The functions with extension _cdf calculate the lower tail integral of the probability density function:
D(x) = Zx
−∞
p(x0)dx0
while those with the
cdf_c
extension calculate the upper tail of the probability density function, so-called in statistics
the survival function. For example, the function:
double ROOT::Math::gaussian_cdf(double x,double sigma,double x0=0);
evaluates the lower tail of the Gaussian distribution:
D(x) = Zx
−∞
1
√2πσ2e−(x0−x0)2/2σ2dx0
while the function:
double ROOT::Math::gaussian_cdf_c(double x, double sigma, double x0=0);
evaluates the upper tail of the Gaussian distribution:
D(x) = Z+∞
x
1
√2πσ2e−(x0−x0)2/2σ2dx0
The cumulative distributions functions are defined in the header file
Math/ProbFunc.h
. The majority of the CDF’s are
present in the
MathCore
, apart from the
chisquared
,
fdistribution
,
gamma
and
tdistribution
, which are in the
MathMore library.
13.5.4.1 Inverse of the Cumulative Distribution Functions(Quantiles)
For almost all the cumulative distribution functions (
_cdf
) and their complements (
_cdf_c
) present in the library, we
provide the inverse functions. The inverse of the cumulative distribution function is called in statistics quantile function.
The functions with the extension
_quantile
calculate the inverse of the cumulative distribution function (lower tail
integral of the probability density function), while those with the
quantile_c
extension calculate the inverse of the
complement of the cumulative distribution (upper tail integral). All the inverse distributions are in the MathMore
library and are defined in the header file Math/ProbFuncInv.h.
The following picture illustrates the available statistical functions (PDF, CDF and quantiles) in the case of the normal
distribution.
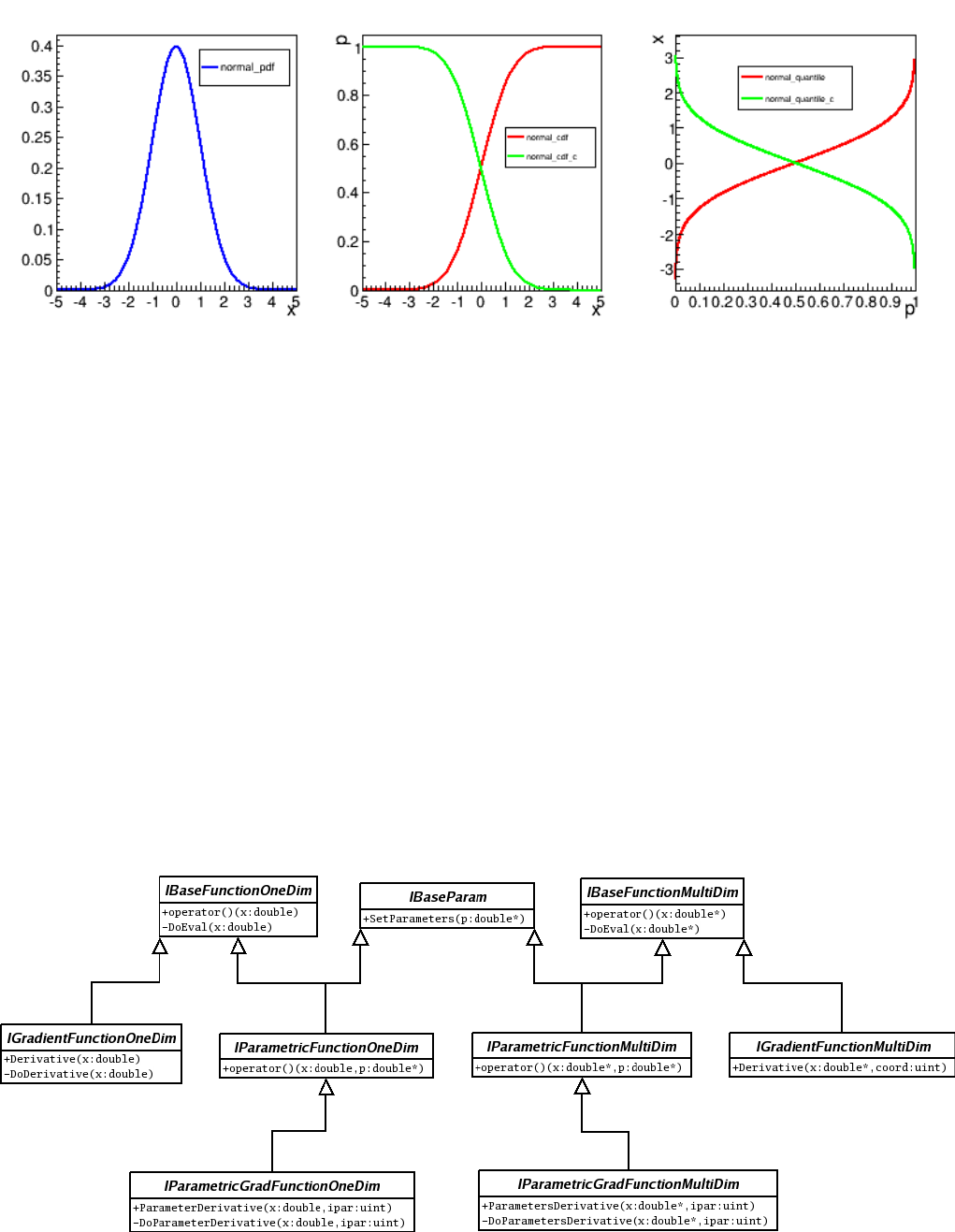
362 CHAPTER 13. MATH LIBRARIES IN ROOT
Figure 13.2: PDF, CDF and quantiles in the case of the normal distribution
13.6 Numerical Algorithms
ROOT provides C++ classes implementing numerical algorithms to solve a wide set of problem, like:
•Evaluation of function derivatives.
•Evaluation of integrals.
•Finding the roots of a function
•Finding the minimum/maximum of a function
In order to use these algorithm the user needs to provide a function. ROOT provides a common way of specifying
them via some interfaces
13.7 ROOT::Math Function interfaces
To get a consistency in the mathematical methods within ROOT, there exists a set of interfaces to define the basic
behaviour of a mathematical function. In order to use the classes presented in this chapter, the mathematical functions
defined by the user must inherit from any of the classes seen in the figure:
Figure 13.3: ROOT::Math Function interface structure
13.7.1 One-dimensional Function Interfaces
These interfaces are used for numerical algorithms operating only on one-dimensional functions and cannot be applied
to multi-dimensional functions.
13.7. ROOT::MATH FUNCTION INTERFACES 363
For this case the users needs to define a function object which evaluates in one dimension, and the object will have to
derivate from the following:
•ROOT::Math::IBaseFunctionOneDim
: This class is the most basic function. Provides a method to evaluate the
function given a value (simple double) by implementing
double operator() (const double )
. The user class
defined only needs to reimplement the pure abstract method
double DoEval(double x)
, that will do the work
of evaluating the function at point x.
Example on how to create a class that represents a mathematical function. The user only has to override two methods
from IBaseFunctionOneDim:
#include "Math/IFunction.h"
class MyFunction: public ROOT::Math::IBaseFunctionOneDim
{
double DoEval(double x) const
{
return x*x;
}
ROOT::Math::IBaseFunctionOneDim* Clone() const
{
return new MyFunction();
}
};
•ROOT::Math::IGradientFunctionOneDim
: Some of the numerical algorithm will need to calculate the derivatives
of the function. In these cases, the user will have to provide the neccesary code for this to happen. The interface
defined in
IGradientFunctionOneDim
introduced the method
double Derivative(double x)
that will return
the derivative of the function at the point
x
. The class inherit by the user will have to implement the abstract
method double DoDerivative(double x), leaving the rest of the class untouched.
Example for implementing a gradient one-dimensional function:
#include "Math/IFunction.h"
class MyGradientFunction: public ROOT::Math::IGradientFunctionOneDim
{
public:
double DoEval(double x) const
{
return sin(x);
}
ROOT::Math::IBaseFunctionOneDim* Clone() const
{
return new MyGradientFunction();
}
double DoDerivative(double x) const
{
return -cos(x);
}
};
13.7.2 Multi-dimensional Function Interfaces
The most generic case of a multidimensional function has similar approach. Some examples will be shown next. It
is important to notice, that one dimensional functions can be also implemented through the interfaces that will be
presented here. Nevertheless, the user needs to implement those following the indications of the previous chapter,
for algorithm woring exclusivly on one-dimensional functions. For algorithms working on both one-dimensional and
multi-dimensional functions they should instead use this interface.
364 CHAPTER 13. MATH LIBRARIES IN ROOT
•ROOT::Math::IBaseFunctionMultiDim
: This interface provides the
double operator() (const double*)
that
takes an array of doubles with all the values for the different dimensions. In this case, the user has to provide
the functionality for two different functions:
double DoEval(const double*)
and
unsigned int NDim()
. The
first ones evaluates the function given the array that represents the multiple variables. The second returns the
number of dimensions of the function.
Example of implementing a basic multi-dimensional function:
#include "Math/IFunction.h"
class MyFunction: public ROOT::Math::IBaseFunctionMultiDim
{
public:
double DoEval(const double*x)const
{
return x[0] + sin(x[1]);
}
unsigned int NDim() const
{
return 2;
}
ROOT::Math::IBaseFunctionMultiDim* Clone() const
{
return new MyFunction();
}
};
•ROOT::Math::IGradientFunctionMultiDim
: This interface offers the same functionality as the base function
plus the calcualtion of the derivative. It only adds the
double Derivative(double* x, uint ivar)
method for
the user to implement. This method must implement the derivative of the function with respect to the variable
indicated with the second parameter.
Example of implementing a multi-dimensional gradient function
#include "Math/IFunction.h"
class MyGradientFunction: public ROOT::Math::IGradientFunctionMultiDim
{
public:
double DoEval(const double*x)const
{
return x[0] + sin(x[1]);
}
unsigned int NDim() const
{
return 2;
}
ROOT::Math::IGradientFunctionMultiDim* Clone() const
{
return new MyGradientFunction();
}
double DoDerivative(const double*x,unsigned int ipar) const
{
if ( ipar == 0)
return sin(x[1]);
else
13.7. ROOT::MATH FUNCTION INTERFACES 365
return x[0] + x[1] * cos(x[1]);
}
};
13.7.3 Parametric Function Interfaces
These interfaces, for evaluating multi-dimensional functions are used for fitting. These interfaces are defined in the
header file
Math/IParamFunction.h
. See also the documentation of the
ROOT::Fit
classes in the Fitting chaper for
more information.
•ROOT::Math::IParametricFunctionMultiDim
: Describes a multi dimensional parametric function. Similarly to
the one dimensional version, the user needs to provide the method
void SetParameters(double* p)
as well
as the getter methods
const double * Parameters()
and
uint NPar()
. Example of creating a parametric
function:
#include "Math/IFunction.h"
#include "Math/IParamFunction.h"
class MyParametricFunction: public ROOT::Math::IParametricFunctionMultiDim
{
private:
const double* pars;
public:
double DoEvalPar(const double*x,const double*p)const
{
return p[0] * x[0] + sin(x[1]) + p[1];
}
unsigned int NDim() const
{
return 2;
}
ROOT::Math::IParametricFunctionMultiDim* Clone() const
{
return new MyParametricFunction();
}
const double* Parameters() const
{
return pars;
}
void SetParameters(const double* p)
{
pars = p;
}
unsigned int NPar() const
{
return 2;
}
};
•ROOT::Math::IParametricGradFunctionMultiDim
: Provides an interface for parametric gradient multi-
dimensional functions. In addition to function evaluation it provides the gradient with respect to the parameters,
via the method
ParameterGradient()
. This interface is only used in case of some dedicated fitting algorithms,
when is required or more efficient to provide derivatives with respect to the parameters. Here is an example:
366 CHAPTER 13. MATH LIBRARIES IN ROOT
#include "Math/IFunction.h"
#include "Math/IParamFunction.h"
class MyParametricGradFunction:
public ROOT::Math::IParametricGradFunctionMultiDim
{
private:
const double* pars;
public:
double DoEvalPar(const double*x,const double*p)const
{
return p[0] * x[0] + sin(x[1]) + p[1];
}
unsigned int NDim() const
{
return 2;
}
ROOT::Math::IParametricGradFunctionMultiDim* Clone() const
{
return new MyParametricGradFunction();
}
const double* Parameters() const
{
return pars;
}
void SetParameters(const double* p)
{
pars = p;
}
unsigned int NPar() const
{
return 2;
}
double DoParameterDerivative(const double*x,const double* p,
unsigned int ipar) const
{
if ( ipar == 0)
return sin(x[1]) + p[1];
else
return p[0] * x[0] + x[1] * cos(x[1]) + p[1];
}
};
13.7.4 Wrapper Functions
To facilitate the user to insert their own type of function in the needed function interface, helper classes, wrapping the
user interface in the
ROOT::Math
function interfaces are provided. this will avoid the user to re-implement dedicated
funcition classes, following the code example shown in the previous paragraphs.
There is one possible wrapper for every interface explained in the previous section. The following table indicates the
wrapper for the most basic ones:
Interface Function Wrapper
ROOT::Math::IBaseFunctionOneDim ROOT::Math::Functor1D
ROOT::Math::IGradientFunctionOneDim ROOT::Math::GradFunctor1D
ROOT::Math::IBaseFunctionMultiDim ROOT::Math::Functor
13.7. ROOT::MATH FUNCTION INTERFACES 367
Interface Function Wrapper
ROOT::Math::IGradientFunctionMultiDim ROOT::Math::GradFunctor
Thee functor wrapper are defined in the header file Math/Functor.h.
13.7.4.1 Wrapping One Dimensional Functions
The
ROOT::Math::Functor1D
is used to wrap one-dimensional functions It can wrap all the following types: * A free
C function of type
double ()(double )
. * Any C++ callable object implemention
double operator()( double )
.
* A class member function with the correct signature like
double Foo::Eval(double )
. In this case one pass the
object pointer and a pointer to the member function (&Foo::Eval).
Example:
#include "Math/Functor.h"
class MyFunction1D {
public:
double operator()(double x) const {
return x*x;
}
double Eval(double x) const {return x+x; }
};
double freeFunction1D(double x){
return 2*x;
}
int main()
{
// wrapping a free function
ROOT::Math::Functor1D f1(&freeFunction1D);
MyFunction1D myf1;
// wrapping a function object implementing operator()
ROOT::Math::Functor1D f2(myf1);
// wrapping a class member function
ROOT::Math::Functor1D f3(&myf1,&MyFunction1D::Eval);
cout << f1(2) << endl;
cout << f2(2) << endl;
cout << f3(2) << endl;
return 0;
}
13.7.4.2 Wrapping One Dimensional Gradient Functions
The
ROOT::Math::GradFunctor1D
class is used to wrap one-dimensional gradient functions. It can be constructed
in three different ways: * Any object implementing both
double operator()( double)
for the function evaluation
and
double Derivative(double)
for the function derivative. * Any object implementing any member function like
Foo::XXX(double )
for the function evaluation and any other member function like
Foo::YYY(double )
for the
derivative. * Any two function objects implementing
double operator()( double )
. One object provides the
function evaluation, the other the derivative. One or both function object can be a free C function of type
double
()(double ).
368 CHAPTER 13. MATH LIBRARIES IN ROOT
13.7.4.3 Wrapping Multi-dimensional Functions
The class
ROOT::Math::Functor
is used to wrap in a very simple and convenient way multi-dimensional function
objects. It can wrap all the following types: * Any C++ callable object implementing
double operator()( const
double * )
. * A free C function of type
double ()(const double * )
. * A member function with the correct
signature like
Foo::Eval(const double * )
. In this case one pass the object pointer and a pointer to the member
function (&Foo::Eval).
The function dimension is required when constructing the functor.
Example of using Functor:
#include "Math/Functor.h"
class MyFunction {
public:
double operator()(const double *x) const {
return x[0]+x[1];
}
double Eval(const double *x)const {return x[0]+x[1]; }
};
double freeFunction(const double *x)
{
return x[0]+x[1];
}
int main()
{
// test directly calling the function object
MyFunction myf;
// test from a free function pointer
ROOT::Math::Functor f1(&freeFunction,2);
// test from function object
ROOT::Math::Functor f2(myf,2);
// test from a member function
ROOT::Math::Functor f3(&myf,&MyFunction::Eval,2);
double x[] = {1,2};
cout << f1(x) << endl;
cout << f2(x) << endl;
cout << f3(x) << endl;
return 0;
}
13.7.4.4 Wrapping Multi-dimensional Gradient Functions
The class
ROOT::Math::GradFunctor
is used to wrap in a very C++ callable object to make gradient functions. It
can be constructed in three different way: * From an object implementing both
double operator()( const double
* )
for the function evaluation and
double Derivative(const double *, int icoord)
for the partial derivatives.
* From an object implementing any member function like
Foo::XXX(const double *)
for the function evaluation and
any member function like
Foo::XXX(const double *, int icoord)
for the partial derivatives. * From an function
object implementing
double operator()( const double * )
for the function evaluation and another function object
implementing double operator() (const double *, int icoord) for the partial derivatives.
The function dimension is required when constructing the functor.
13.8. NUMERICAL INTEGRATION 369
13.7.4.5 Special case: Wrapping TF1 objects in Parametric Function interfaces
In many cases, the user works with the
TF1
class. The mathematical library in ROOT provides some solutions to wrap
these into the interfaces needed by other methods. If the desired interface to wrap is one-dimensional, the class to
use is
ROOT::Math::WrappedTF1
. The default constructor takes a
TF1
reference as an argument, that will be wrapped
with the interfaces of a ROOT::Math::IParametricGradFunctionOneDim. Example:
#include "TF1.h"
#include "Math/WrappedTF1.h"
int main()
{
TF1 f("Sin Function","sin(x)+y",0,3);
ROOT::Math::WrappedTF1 wf1(f);
cout << f(1) << endl;
cout << wf1(1) << endl;
return 0;
}
For a TF1 defining a multidimensional function or in case we need to wrap in a multi-dimensional function interface, the
class to use is
ROOT::Math::WrappedMultiTF1
. Following the usual procedure, setting the
TF1
though the constructor,
will wrap it into a ROOT::Math::IParametricGradFunctionMultiDim. Example:
#include "TF1.h"
#include "Math/WrappedMultiTF1.h"
int main()
{
TF2 f("Sin Function","sin(x) + y",0,3,0,2);
ROOT::Math::WrappedMultiTF1 wf1(f);
double x[] = {1,2};
cout << f(x) << endl;
cout << wf1(x) << endl;
return 0;
}
13.8 Numerical Integration
The algorithms provided by ROOT for numerical integration are implemented following the hierarchy shown
in the next image.
ROOT::Math::VirtualIntegrator
defines the most basic functionality while the specific
behaviours for one or multiple dimensions are implemented in
ROOT::Math::VirtualIntegratorOneDim
and
ROOT::Math::VirtualIntegratorMultiDim
. These interfaces define the integrator functionality with abstract meth-
ods to set the function, to compute the integral or to set the integration tolerance. These methods must be implemented
in the concrete classes existing for the different integration algorithms. The user cannot create directly these virtual
integrator interfaces. He needs to create the
ROOT::Math::IntegratorOneDim
class for integrating one-dimensional
functions and
ROOT::Math::IntegratorMultiDim
for multi-dimensional functions. Through the ROOT Plug-In
Manager, the user can initialize
ROOT::Math::IntegratorOneDim
or
ROOT::Math::IntegratorMultiDim
with any of
the concrete integration classes without dealing with them directly. These two classes provide the same interface as in
VirtualIntegratorOneDim
and
VirtualIntegratorMultiDim
, but with the possibility to choose in the constructor,
which method will be used to perform the integration.
The method to set the function to be integrated, must be of the function interface type described before.
ROOT::Math::IBaseFunctionOneDimFunction
is used for
ROOT::Math::IBaseFunctionMultiDim
and The only
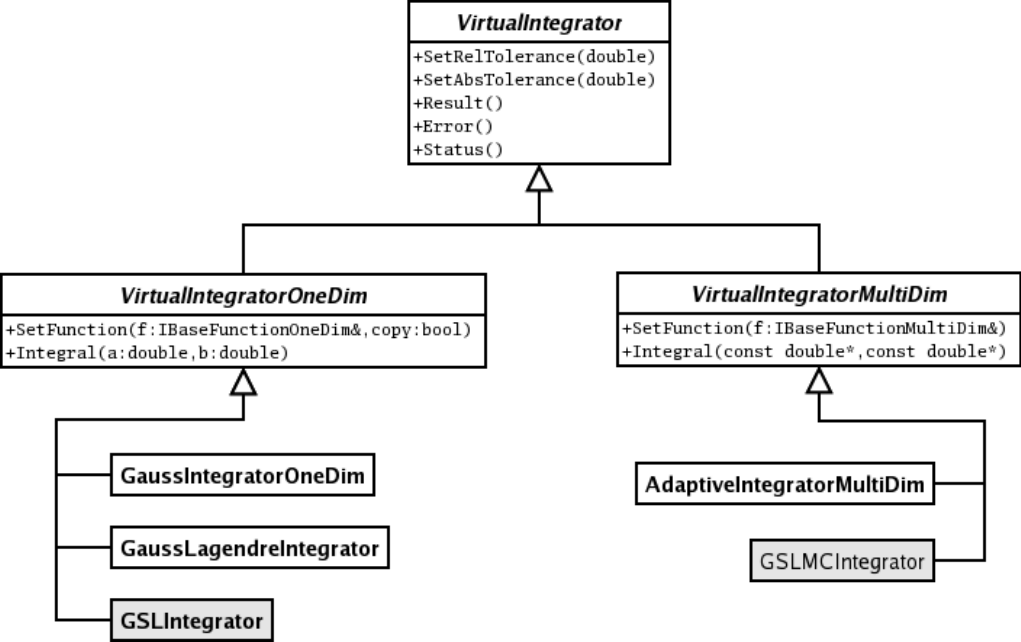
370 CHAPTER 13. MATH LIBRARIES IN ROOT
difference between the
ROOT::Math::IntegratorOneDim
and
ROOT::Math::IntegratorMultiDim
resides in the
dimensionality of that function and some specific that will be seen afterwards for the one dimensional one.
Figure 13.4: ROOT::Math Numerical Integrator classes
The rest of the classes shown above in the diagram are the specialized classes provided. Each one implements a
different method that will be explained in detail. It is important to notice that the two grayed classes (the one which
name starts by GSL) are part of the MathMore library. We will later show in more detail the differences between the
implementations.
13.8.1 Integration of One-dimensional Functions
13.8.1.1 Using ROOT::Math::IntegratorOneDim
Here is a code example on how to use the
ROOT::Math::IntegratorOneDim
class (note that the class is defined in
the header file
Math/Integrator.h
). In this example we create different instance of the class using some of the
available algorithms in ROOT. If no algorithm is specified, the default one is used. The default Integrator together
with other integration options such as relative and absolute tolerance, can be specified using the static method of the
ROOT::Math::IntegratorOneDimOptions
#include "Math/Integrator.h"
const double ERRORLIMIT = 1E-3;
double f(double x) {
return x;
}
double f2(const double * x) {
return x[0] + x[1];
}
int testIntegration1D() {
13.8. NUMERICAL INTEGRATION 371
const double RESULT = 0.5;
int status = 0;
// set default tolerances for all integrators
ROOT::Math::IntegratorOneDimOptions::SetDefaultAbsTolerance(1.E-6);
ROOT::Math::IntegratorOneDimOptions::SetDefaultRelTolerance(1.E-6);
ROOT::Math::Functor1D wf(&f);
ROOT::Math::Integrator ig(ROOT::Math::IntegrationOneDim::kADAPTIVESINGULAR);
ig.SetFunction(wf);
double val = ig.Integral(0,1);
std::cout << "integral result is " << val << std::endl;
status += std::fabs(val-RESULT) > ERRORLIMIT;
ROOT::Math::Integrator ig2(ROOT::Math::IntegrationOneDim::kNONADAPTIVE);
ig2.SetFunction(wf);
val = ig2.Integral(0,1);
std::cout << "integral result is " << val << std::endl;
status += std::fabs(val-RESULT) > ERRORLIMIT;
ROOT::Math::Integrator ig3(wf, ROOT::Math::IntegrationOneDim::kADAPTIVE);
val = ig3.Integral(0,1);
std::cout << "integral result is " << val << std::endl;
status += std::fabs(val-RESULT) > ERRORLIMIT;
ROOT::Math::Integrator ig4(ROOT::Math::IntegrationOneDim::kGAUSS);
ig4.SetFunction(wf);
val = ig4.Integral(0,1);
std::cout << "integral result is " << val << std::endl;
status += std::fabs(val-RESULT) > ERRORLIMIT;
ROOT::Math::Integrator ig4(ROOT::Math::IntegrationOneDim::kLEGENDRE);
ig4.SetFunction(wf);
val = ig4.Integral(0,1);
std::cout << "integral result is " << val << std::endl;
status += std::fabs(val-RESULT) > ERRORLIMIT;
return status;
}
13.8.2 One-dimensional Integration Algorithms
Here we provide a brief description of the different integration algorithms, which are also implemented as separate
classes. The algorithms can be instantiated using the following enumeration values:
Enumeration name Integrator class
ROOT::Math::IntegratorOneDim::kGAUSS ROOT::Math::GaussianIntegrator
ROOT::Math::IntegratorOneDim::kLEGENDRE ROOT::Math:::GausLegendreIntegrator
ROOT::Math::Integration::kNONADAPTIVE ROOT::Math:::GSLIntegrator
ROOT::Math::Integration::kADAPTIVE ROOT::Math:::GSLIntegrator
ROOT::Math::Integration::kADAPTIVESINGULAR ROOT::Math:::GSLIntegrator
13.8.2.1 ROOT::Math:::GaussIntegrator
It uses the most basic Gaussian integration algorithm, it uses the 8-point and the 16-point Gaussian quadrature
approximations. It is derived from the DGAUSS rountine of the CERNLIB by S. Kolbig. This class
Here is an example of using directly the GaussIntegrator class
#include "TF1.h"
#include "Math/WrappedTF1.h"
#include "Math/GaussIntegrator.h"
372 CHAPTER 13. MATH LIBRARIES IN ROOT
int main()
{
TF1 f("Sin Function","sin(x)",0, TMath::Pi());
ROOT::Math::WrappedTF1 wf1(f);
ROOT::Math::GaussIntegrator ig;
ig.SetFunction(wf1, false);
ig.SetRelTolerance(0.001);
cout << ig.Integral(0, TMath::PiOver2()) << endl;
return 0;
}
13.8.2.2 ROOT::Math::GaussLegendreIntegrator
This class implementes the Gauss-Legendre quadrature formulas. This sort of numerical methods requieres that the
user specifies the number of intermediate function points used in the calculation of the integral. It will automatically
determine the coordinates and weights of such points before performing the integration. We can use the example above,
but replacing the creation of a
ROOT::Math::GaussIntegrator
object with
ROOT::Math::GaussLegendreIntegrator
.
13.8.2.3 ROOT::Math::GSLIntegrator
This is a wrapper for the QUADPACK integrator implemented in the GSL library. It supports several integration
methods that can be chosen in construction time. The default type is adaptive integration with singularity applying a
Gauss-Kronrod 21-point integration rule. For a detail description of the GSL methods visit the GSL user guide This
class implements the best algorithms for numerical integration for one dimensional functions. We encourage the use it
as the main option, bearing in mind that it uses code from the GSL library, wich is provided in the MathMore library
of ROOT.
The interface to use is the same as above. We have now the possibility to specify a different integration algorithm in
the constructor of the ROOT::Math::GSLIntegrator class.
ROOT::Math::GSLIntegrator ig(ROOT::Math::Integration::kADAPTIVE, ROOT::Math::Integration::kGAUSS51); // create the adaptive integrator with the 51 point rule
ig.SetRelTolerance(1.E-6); // set relative tolerance
ig.SetAbsTolerance(1.E-6); // set absoulte tolerance
The algorithm is controlled by the given absolute and relative tolerance. The iterations are continued until the following
condition is satisfied
absErr <=max(epsAbs, epsRel ∗Integral)
Where absErr is an estimate of the absolute error (it can be retrieved with
GSLIntegrator::Error()
) and Integral is
the estimate of the function integral (it can be obtained with GSLIntegrator::Result())
The possible integration algorithm types to use with the GSLIntegrator are the following. More information is provided
in the
GSL
users documentation. *
ROOT::Math::Integration::kNONADAPTIVE
: based on
gsl_integration_qng
. It
is a non-adaptive procedure which uses fixed Gauss-Kronrod-Patterson abscissae to sample the integrand at a maximum
of 87 points. It is provided for fast integration of smooth functions. *
ROOT::Math::Integration::kADAPTIVE
: based
on
gsl_integration_qag
. It is an adaptiva Gauss-Kronrod integration algorithm, the integration region is divided
into subintervals, and on each iteration the subinterval with the largest estimated error is bisected. It is possible to
specify the integration rule as an extra enumeration parameter. The possible rules are *
Integration::kGAUSS15
: 15 points Gauss-Konrod rule (value = 1) *
Integration::kGAUSS21
: 21 points Gauss-Konrod rule (value
= 2) *
Integration::kGAUSS31
: 31 points Gauss-Konrod rule (value = 3) *
Integration::kGAUSS41
: 41
points Gauss-Konrod rule (value = 4) *
Integration::kGAUSS51
: 51 points Gauss-Konrod rule (value = 5) *
Integration::kGAUSS61
: 61 points Gauss-Konrod rule (value = 6) The higher-order rules give better accuracy for
smooth functions, while lower-order rules save time when the function contains local difficulties, such as discontinuities.
If no integration rule is passed, the 31 points rule is used as default.
•ROOT::Math::Integration::kADAPTIVESINGULAR
: based on
gsl_integration_qags
. It is an integration type
which can be used in the case of the presence of singularities.It uses the Gauss-Kronrod 21-point integration rule.
This is the default algorithm
13.8. NUMERICAL INTEGRATION 373
Note that when using the common
ROOT::Math::IntegratorOneDIm
class the enumeration type defining the
algorithm must be defined in the namespace
ROOT::Math::IntegrationOneDim
(to distinguish from the multi-
dimensional case) and the rule enumeration (or its corresponding integer) can be passed in the constructor of the
ROOT::Math::IntegratorOneDIm.
13.8.3 Multi-dimensional Integration
The multi-dimensional integration algorithm should be applied to functions with dimension larger than one. Adaptive
multi-dimensional integration works for low function dimension, while MC integration can be applied to higher
dimensions.
13.8.3.1 Using ROOT::Math::IntegratorMultiDim
Here is a code example on how to use the
ROOT::Math::IntegratorOneDim
class (note that the class is defined in the
header file Math/Integrator.h). In this example we create different instance of the class using some of the available
algorithms in ROOT.
#include "Math/IntegratorMultiDim.h"
#include "Math/Functor.h"
double f2(const double * x) {
return x[0] + x[1];
}
int testIntegrationMultiDim() {
const double RESULT = 1.0;
const double ERRORLIMIT = 1E-3;
int status = 0;
ROOT::Math::Functor wf(&f2,2);
double a[2]={0,0};
double b[2]={1,1};
ROOT::Math::IntegratorMultiDim ig(ROOT::Math::IntegrationMultiDim::kADAPTIVE);
ig.SetFunction(wf);
double val = ig.Integral(a,b);
std::cout << "integral result is " << val << std::endl;
status += std::fabs(val-RESULT) > ERRORLIMIT;
ROOT::Math::IntegratorMultiDim ig2(ROOT::Math::IntegrationMultiDim::kVEGAS);
ig2.SetFunction(wf);
val = ig2.Integral(a,b);
std::cout << "integral result is " << val << std::endl;
status += std::fabs(val-RESULT) > ERRORLIMIT;
ROOT::Math::IntegratorMultiDim ig3(wf,ROOT::Math::IntegrationMultiDim::kPLAIN);
val = ig3.Integral(a,b);
std::cout << "integral result is " << val << std::endl;
status += std::fabs(val-RESULT) > ERRORLIMIT;
ROOT::Math::IntegratorMultiDim ig4(wf,ROOT::Math::IntegrationMultiDim::kMISER);
val = ig4.Integral(a,b);
std::cout << "integral result is " << val << std::endl;
status += std::fabs(val-RESULT) > ERRORLIMIT;
return status;
}
374 CHAPTER 13. MATH LIBRARIES IN ROOT
13.8.3.2 Multi-dimensions Integration Algorithms
Here is the types, that can be specified as enumeration and the corresponding classes
Enumeration name Integrator class
ROOT::Math::IntegratorMultiDim::kADAPTIVE ROOT::Math::AdaptiveIntegratorMultiDim
ROOT::Math::IntegratorMultiDim::kVEGAS ROOT::Math:::GSLMCIntegrator
ROOT::Math::IntegratorMultiDim::kMISER ROOT::Math:::GSLMCIntegrator
ROOT::Math::IntegratorMultiDim::kPLAIN ROOT::Math:::GSLMCIntegrator
The control parameters for the integration algorithms can be specified using the
ROOT::Math::IntegratorMultiDimOptions
class. Static methods are provided to change the default values. It is possible to print the list of default control
parameters using the ROOT::Math::IntegratorMultiDimOptions::Print function. Example:
ROOT::Math::IntegratorMultiDimOptions opt;
opt.Print();
Integrator Type : ADAPTIVE
Absolute tolerance : 1e-09
Relative tolerance : 1e-09
Workspace size : 100000
(max) function calls : 100000
Depending on the algorithm, some of the control parameters might have no effect.
13.8.3.3 ROOT::Math::AdaptiveIntegratorMultiDim
This class implements an adaptive quadrature integration method for multi dimensional functions. It is described
in this paper Genz, A.A. Malik, An adaptive algorithm for numerical integration over an N-dimensional rectangular
region, J. Comput. Appl. Math. 6 (1980) 295-302. It is part of the MathCore library. The user can control the relative
and absolute tolerance and the maximum allowed number of function evaluation.
13.8.3.4 ROOT::Math::GSLMCIntegrator
It is a class for performing numerical integration of a multidimensional function. It uses the numerical integration
algorithms of GSL, which reimplements the algorithms used in the QUADPACK, a numerical integration package written
in Fortran. Plain MC, MISER and VEGAS integration algorithms are supported for integration over finite (hypercubic)
ranges. For a detail description of the GSL methods visit the GSL users guide. Specific configuration options (documented
in the GSL user guide) for the
ROOT::Math::GSLMCIntegration
can be set directly in the class, or when using it via the
ROOT::Math::IntegratorMultiDim interface, can be defined using the ROOT::Math::IntegratorMultiDimOptions.
13.9 Function Derivation
There are in ROOT only two classes to perform numerical derivation. One of them is in the MathCore library
while the other is in the MathMore wrapping an integration function from the GSL library. * RichardsonDerivator:
Implements the Richardson method for numerical integration. It can calculate up to the third derivative of a function.
* GSLDerivator of MathMore based on GSL.
13.10 Numerical Minimization
The algorithms provided by ROOT for numerical integration are implemented following the hierarchy shown in
the next image. The left branch of classes are used for one dimensional minimization, while the right one is
used for multidimensional minimization. In the case of multidimensional minimization we have also the classes
TMinuitMinimizer
implemented using
TMinuit
,
TFumiliMinimizer
implemented using
TFumili
for least square or
likelihood minimizations. We encourage the use of the GSL algorithms for one dimensional minimization and
Minuit2
(or the old versionMinuit) for multi dimensional minimization.
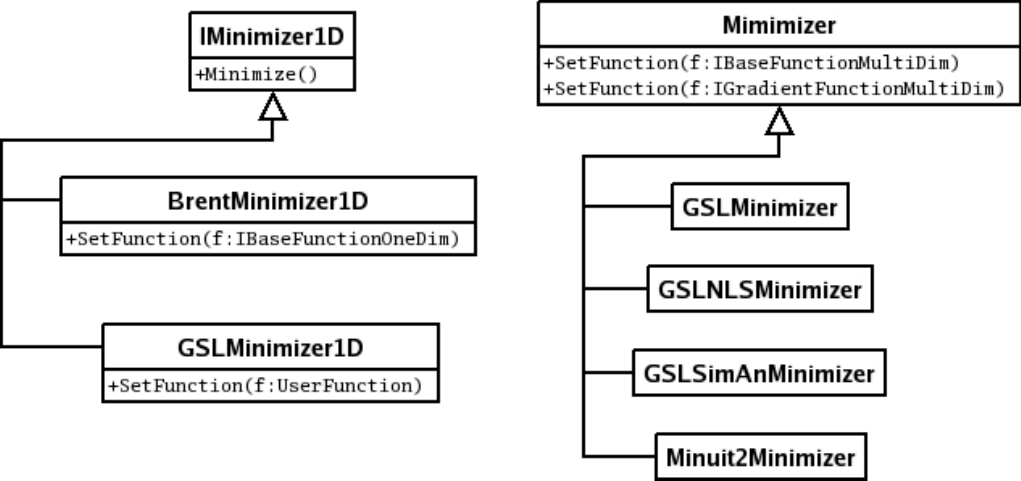
13.10. NUMERICAL MINIMIZATION 375
Figure 13.5: Numerical Minimization classes
13.10.1 One-Dimensional Minimization
These algorithms are for finding the minimum of a one-dimensional minimization function. The function to minimize
must be given to the class implementing the algorithm as a
ROOT::Math::IBaseFunctionOneDim
object. The algorithms
supported are only bracketing algorithm which do not use derivatives information.
Two classes exist. One in the MathCore library implementing the Brent method (not using the derivatives) and one in
the MathMore library implementing several different methods, using in some case the derivatives.
13.10.1.1 ROOT::Math::BrentMinimizer1D
This class implements the Brent method to minimize one-dimensional function. An interval containing the function
minimum must be provided. Here is an example where we define the function to minimize as a lambda func-
tion (requires C++11). The function to minimize must be given to the class implementing the algorithm as a
ROOT::Math::IBaseFunctionOneDim object.
ROOT::Math::Functor1D func( [](double x){ return 1+ -4*x+1*x*x; } );
ROOT::Math::BrentMinimizer1D bm;
bm.SetFunction(func, -10,10);
bm.Minimize(10,0,0);
cout << "Minimum: f(" << bm.XMinimum() << ")="<<bm.FValMinimum() << endl;
Note that when setting the function to minimize, one needs to provide the interval range to find the minimum. In the
Minimize call, the maximum number of function calls, the relative and absolute tolerance must be provided.
13.10.1.2 ROOT::Math::GSLMInimizer1D
This class wraps two different methods from the GSL. The algorithms which can be choosen at construction time are
GOLDENSECTION, which is the simplest method but the slowest and BRENT (the default one) which combines the
golden section with a parabolic interpolation. The algorithm can be chosen as a different enumeration in the constructor:
*
ROOT::Math::Minim1D::kBRENT
for the Brent algorithm (default) *
ROOT::Math::Minim1D::kGOLDENSECTION
for
the golden section algorithm
// this makes class with the default Brent algorithm
ROOT::Math::GSLMinimizer1D minBrent;
// this make the class with the Golden Section algorithm
ROOT::Math::GSLMinimizer1D minGold(ROOT::Math::Minim1D::kGOLDENSECTION);
The interface to set the function and to minimize is the same as in the case of the BrentMinimizer1D.
376 CHAPTER 13. MATH LIBRARIES IN ROOT
13.10.1.3 Using the TF1 class
It is possible to perform the one-dimensional minimization/maximization of a function by using directly the function class
in ROOT,
TF1
of the Hist library. The minmization is implemented in
TF1
using the BrentMInimizer1D and available
with the class member functions *
TF1::GetMinimum
/
TF1::GetMaximum
to find the function minimum/maximum value
*TF1::GetMinimumX/TF1::GetMaximumX to find the x value corresponding at the function minimum.
The interval to search for the minimum (the default is the
TF1
range), tolerance and maximum iterations can be
provided as optional parameters of the TF1::GetMinimum/Maximum functions.
13.10.2 Multi-Dimensional Minimization
All the algorithms for multi-dimensional minimization are implementing the
ROOT::Math::Minimizer
interface and
they can be used in the same way and one can switch between minimizer at run-time. The minimizer concrete class
can be in different ROOT libraries and they can be instantiate using the ROOT plug-in manager. More information on
multi-dimensional minimization is provided in the Fitting Histogram chapter.
13.11 ROOT Finder Algorithms
The function must be given to the class implementing the algorithm as a
ROOT::Math::IBaseFunctionOneDim
object.
Some of the algorithm requires the derivatives of the function. In that case a
ROOT::Math::IGradientFunctionOneDim
object must be provided.
13.12 Generic Vectors for 2, 3 and 4 Dimensions (GenVector)
GenVector
is a package intended to represent vectors and their operations and transformations, such as rotations and
Lorentz transformations, in 3 and 4 dimensions. The 3D space is used to describe the geometry vectors and points,
while the 4D space-time is used for physics vectors representing relativistic particles. These 3D and 4D vectors are
different from vectors of the linear algebra package, which describe generic N-dimensional vectors. Similar functionality
is currently provided by the CLHEP and packages and the ROOT Physics vector classes (See “Physics Vectors”). It
also re-uses concepts and ideas from the CMS Common Vector package. In contrast to CLHEP or the ROOT physics
libraries,
GenVector
provides class templates for modeling the vectors. The user can control how the vector is internally
represented. This is expressed by a choice of coordinate system, which is supplied as a template parameter when
the vector is constructed. Furthermore, each coordinate system is itself a template, so that the user can specify the
underlying scalar type.
The
GenVector
classes do not inherit from
TObject
, therefore cannot be used as in the case of the physics vector
classes in ROOT collections.
In addition, to optimize performances, no virtual destructors are provided. In the following paragraphs, the main
characteristics of
GenVector
are described. A more detailed description of all the
GenVector
classes is available also at
http://seal.cern.ch/documents/mathlib/GenVector.pdf
13.12.1 Main Characteristics
13.12.1.1 Optimal Runtime Performances
We try to minimize any overhead in the run-time performance. We have deliberately avoided the use of any virtual
function and even virtual destructors in the classes. In addition, as much as possible functions are defined as inline.
For this reason, we have chosen to use template classes to implement the
GenVector
concepts instead of abstract or
base classes and virtual functions. It is then recommended to avoid using the
GenVector
classes polymorphically and
developing classes inheriting from them.
13.12.1.2 Points and Vector Concept
Mathematically vectors and points are two distinct concepts. They have different transformations, as vectors only
rotate while points rotate and translate. You can add two vectors but not two points and the difference between two
points is a vector. We then distinguish for the 3 dimensional case, between points and vectors, modeling them with
different classes:
13.12. GENERIC VECTORS FOR 2, 3 AND 4 DIMENSIONS (GENVECTOR) 377
•ROOT::Math::DisplacementVector2D
and
ROOT::Math::DisplacementVector3D
template classes describing 2
and 3 component direction and magnitude vectors, not rooted at any particular point;
•ROOT::Math::PositionVector2D
and
ROOT::Math::PositionVector3D
template classes modeling the points in
2 and 3 dimensions.
For the 4D space-time vectors, we use the same class to model them,
ROOT::Math::LorentzVector
, since we have
recognized a limited need for modeling the functionality of a 4D point.
13.12.1.3 Generic Coordinate System
The vector classes are based on a generic type of coordinate system, expressed as a template parameter of the class.
Various classes exist to describe the various coordinates systems:
2D coordinate system classes:
•ROOT::Math::Cartesian2D, based on (x,y);
•ROOT::Math::Polar2D, based on (r,phi);
3D coordinate system classes:
•ROOT::Math::Cartesian3D, based on (x,y,z);
•ROOT::Math::Polar3D, based on (r,theta,phi);
•ROOT::Math::Cylindrical3D, based on (rho,z,phi)
•ROOT::Math::CylindricalEta3D, based on (rho,eta,phi), where eta is the pseudo-rapidity;
4D coordinate system classes:
•ROOT::Math::PxPyPzE4D, based on based on (px,py,pz,E);
•ROOT::Math::PxPyPzM4D, based on based on (px,py,pz,M);
•ROOT::Math::PtEtaPhiE4D, based on based on (pt,eta,phi,E);
•ROOT::Math::PtEtaPhiM4D, based on based on (pt,eta,phi,M);
Users can define the vectors according to the coordinate type, which is the most efficient for their use. Transformations
between the various coordinate systems are available through copy constructors or the assignment (=) operator. For
maximum flexibility and minimize memory allocation, the coordinate system classes are templated on the scalar type.
To avoid exposing templated parameter to the users, typedefs are defined for all types of vectors based on doubles.
See in the examples for all the possible types of vector classes, which can be constructed by users with the available
coordinate system types.
13.12.1.4 Coordinate System Tag
The 2D and 3D points and vector classes can be associated to a tag defining the coordinate system. This can be used to
distinguish between vectors of different coordinate systems like global or local vectors. The coordinate system tag is a tem-
plate parameter of the
ROOT::Math::DisplacementVector3D
and
ROOT::Math::PositionVector3D
(and also for 2D
classes). A default tag exists for users who do not need this functionality,
ROOT::Math::DefaultCoordinateSystemTag
.
13.12.1.5 Transformations
The transformations are modeled using simple (non-template) classes, using double as the scalar type to avoid too
large numerical errors. The transformations are grouped in rotations (in 3 dimensions), Lorentz transformations and
Poincare transformations, which are translation
/
rotation combinations. Each group has several members which may
model physically equivalent transformations but with different internal representations. Transformation classes can
operate on all type of vectors by using the operator
()
or the operator
*
and the transformations can be combined via
the operator *. The available transformations are:
378 CHAPTER 13. MATH LIBRARIES IN ROOT
•3D rotation classes
•rotation described by a 3x3 matrix (ROOT::Math::Rotation3D)
•rotation described by Euler angles (ROOT::Math::EulerAngles)
•rotation described by a direction axis and an angle (ROOT::Math::AxisAngle)
•rotation described by a quaternion (ROOT::Math::Quaternion)
•
optimized rotation around
x
(
ROOT::Math::RotationX
),
y
(
ROOT::Math::RotationY
) and
z
(
ROOT::Math::RotationZ
)
and described by just one angle.
•
3D transformation: we describe the transformations defined as a composition between a rotation and a translation
using the class
ROOT::Math::Transform3D
. It is important to note that transformations act differently on vectors
and points. The vectors only rotate, therefore when applying a transformation (rotation + translation) on a
vector, only the rotation operates while the translation has no effect. The
Transform3D
class interface is similar
to the one used in the CLHEP Geometry package (class ).
•Lorentz rotation:
•
generic Lorentz rotation described by a
4x4
matrix containing a 3D rotation part and a boost part (class
ROOT::Math::LorentzRotation)
•
a pure boost in an arbitrary direction and described by a 4x4 symmetric matrix or 10 numbers (class
ROOT::Math::Boost)
•boost along the axis:x(ROOT::Math::BoostX), y(ROOT::Math::BoostY) and z(ROOT::Math::BoostZ).
13.12.1.6 Minimal Vector Classes Interface
We have tried to keep the interface to a minimal level by:
•Avoiding methods that provide the same functionality but use different names (like getX() and x()).
•
Minimizing the number of setter methods, avoiding methods, which can be ambiguous and can set the vector
classes in an inconsistent state. We provide only methods which set all the coordinates at the same time or set
only the coordinates on which the vector is based, for example
SetX()
for a Cartesian vector. We then enforce
the use of transformations as rotations or translations (additions) for modifying the vector contents.
•
The majority of the functionality, which is present in the CLHEP package, involving operations on two vectors,
is moved in separated helper functions (see
ROOT::Math::VectorUtil
). This has the advantage that the basic
interface will remain more stable with time while additional functions can be added easily.
13.12.1.7 Naming Convention
As part of ROOT, the
GenVector
package adheres to the prescribed ROOT naming convention, with some (approved)
exceptions, as described here:
•Every class and function is in the ROOT::Math namespace.
•
Member function names start with upper-case letter, apart some exceptions (see the next section about CLHEP
compatibility).
13.12.1.8 Compatibility with CLHEP Vector Classes
•
For backward compatibility with CLHEP the vector classes can be constructed from a CLHEP
HepVector
or
HepLorentzVector
, by using a template constructor, which requires only that the classes implement the
accessorsx(),y(), and z() (and t() for the 4D).
•
We provide vector member function with the same naming convention as CLHEP for the most used functions like
x(),y() and z().
13.12. GENERIC VECTORS FOR 2, 3 AND 4 DIMENSIONS (GENVECTOR) 379
13.12.1.9 Connection to Linear Algebra Package
In some use cases, like in track reconstruction, it is needed to use the content of the vector and rotation classes in
conjunction with linear algebra operations. We prefer to avoid any direct dependency to any linear algebra package.
However, we provide some hooks to convert to and from linear algebra classes. The vector and the transformation
classes have methods which allow to get and set their data members (like
SetCoordinates
and
GetCoordinates
)
passing either a generic iterator or a pointer to a contiguous set of data, like a C array. This allows an easy connection
with the linear algebra package, which in turn, allows creation of matrices using C arrays (like the ROOT
TMatrix
classes) or iterators (
SMatrix
classes). Multiplication between linear algebra matrices and
GenVector
vectors is possible
by using the template free functions
ROOT::Math::VectorUtil::Mult
. This function works for any linear algebra
matrix, which implements the operator (i,j) and with first matrix element at i=j=0.
13.12.2 Example: 3D Vector Classes
To avoid exposing template parameter to the users, typedef’s are defined for all types of vectors based on dou-
ble’s and float’s. To use them, one must include the header file
Math/Vector3D.h
. The following typedef’s, de-
fined in the header file
Math/Vector3Dfwd.h
, are available for the different instantiations of the template class
ROOT::Math::DisplacementVector3D:
•ROOT::Math::XYZVector vector based on x,y,z coordinates (Cartesian) in double precision
•ROOT::Math::XYZVectorF vector based on x,y,z coordinates (Cartesian) in float precision
•ROOT::Math::Polar3DVector vector based on r,theta,phi coordinates (polar) in double precision
•ROOT::Math::Polar3DVectorF vector based on r,theta,phi coordinates (polar) in float precision
•ROOT::Math::RhoZPhiVector vector based on rho,z,phi coordinates (cylindrical) in double precision
•ROOT::Math::RhoZPhiVectorF vector based on rho,z,phi coordinates (cylindrical) in float precision
•ROOT::Math::RhoEtaPhiVector
vector based on
rho,eta,phi
coordinates (cylindrical using
eta
instead of
z
)
in double precision
•ROOT::Math::RhoEtaPhiVectorF
vector based on
rho,eta,phi
coordinates (cylindrical using
eta
instead of
z
)
in float precision
13.12.2.1 Constructors and Assignment
The following declarations are available:
XYZVector v1; //an empty vector (x=0, y=0, z=0)
XYZVector v2(1,2,3); //vector with x=1, y=2, z=3;
Polar3DVector v3(1,PI/2,PI); //vector with r=1, theta=PI/2, phi=PI
RhoEtaPHiVector v4(1,2, PI); //vector with rho=1, eta=2, phi=PI
Note that each vector type is constructed by passing its coordinate representation, so a
XYZVector(1,2,3)
is different
from a
Polar3DVector(1,2,3)
. In addition, the vector classes can be constructed by any vector, which implements
the accessors
x()
,
y()
and
z()
. This can be another 3D vector based on a different coordinate system type. It can be
even any vector of a different package, like the CLHEP HepThreeVector that implements the required signature.
XYZVector v1(1,2,3);
RhoEtaPhiVector r2(v1);
CLHEP::HepThreeVector q(1,2,3);
XYZVector v3(q);
380 CHAPTER 13. MATH LIBRARIES IN ROOT
13.12.2.2 Coordinate Accessors
All coordinate accessors are available through the class ROOT::Math::DisplacementVector3D:
//returns cartesian components for the cartesian vector v1
v1.X(); v1.Y(); v1.Z();
//returns cylindrical components for the cartesian vector v1
v1.Rho(); v1.Eta(); v1.Phi();
//returns cartesian components for the cylindrical vector r2
r2.X(); r2.Y(); r2.Z()
In addition, all the 3 coordinates of the vector can be retrieved with the GetCoordinates method:
double d[3];
//fill d array with (x,y,z) components of v1
v1.GetCoordinates(d);
//fill d array with (r,eta,phi) components of r2
r2.GetCoordinates(d);
std::vector vc(3);
//fill std::vector with (x,y,z) components of v1
v1.GetCoordinates(vc.begin(),vc.end());
See the reference documentation of
ROOT::Math::DisplacementVector3D
for more details on all the coordinate
accessors.
13.12.2.3 Setter Methods
One can set only all the three coordinates via:
v1.SetCoordinates(c1,c2,c3); // (x,y,z) for a XYZVector
r2.SetCoordinates(c1,c2,c3); // r,theta,phi for a Polar3DVector
r2.SetXYZ(x,y,z); // 3 cartesian components for Polar3DVector
Single coordinate setter methods are available for the basic vector coordinates, like
SetX()
for a
XYZVector
or
SetR()
for a polar vector. Attempting to do a SetX() on a polar vector will not compile.
XYZVector v1;
v1.SetX(1); //OK setting x for a Cartesian vector
Polar3DVector v2;
v2.SetX(1); //ERROR: cannot set X for a Polar vector.
//Method will not compile
v2.SetR(1); //OK setting r for a Polar vector
In addition, there are setter methods from C arrays or iterator
double d[3]={1.,2.,3.};
XYZVector v;
// set (x,y,z) components of v using values from d
v.SetCoordinates(d);
or, for example, from an std::vector using the iterator
std::vector w(3);
// set (x,y,z) components of v using values from w
v.SetCoordinates(w.begin(),w.end());
13.12. GENERIC VECTORS FOR 2, 3 AND 4 DIMENSIONS (GENVECTOR) 381
13.12.2.4 Arithmetic Operations
The following operations are possible between vector classes, even of different coordinate system types: (
v1,v2
are any
type of ROOT::Math::DisplacementVector3D classes, v3 is the same type of v1;ais a scalar value)
v1 += v2;
v1 -= v2;
v1 = - v2;
v1 *= a;
v1 /= a;
v2 = a * v1;
v2 = v1 / a;
v2 = v1 * a;
v3 = v1 + v2;
v3 = v1 - v2;
13.12.2.5 Comparison
For v1 and v2 of the same type (same coordinate system and same scalar type):
v1 == v2;
v1 != v2;
13.12.2.6 Dot and Cross Product
We support the dot and cross products, through the
Dot()
and
Cross()
method, with any vector (
q
) implementing
x(),y() and z().
XYZVector v1(x,y,z);
double s = v1.Dot(q);
XYZVector v2 = v1.Cross(q);
Note that the multiplication between two vectors using the operator *is not supported because it is ambiguous.
13.12.2.7 Other Methods
XYZVector u = v1.Unit(); //return unit vector parallel to v1
13.12.3 Example: 3D Point Classes
To use all possible types of 3D points one must include the header file
Math/Point3D.h
. The following type-
def’s defined in the header file
Math/Point3Dfwd.h
, are available for different instantiations of the template class
ROOT::Math::PositionVector3D:
•ROOT::Math::XYZPoint point based on x,y,zcoordinates (Cartesian) in double precision
•ROOT::Math::XYZPointF point based on x,y,zcoordinates (Cartesian) in float precision
•ROOT::Math::Polar3DPoint point based on r,theta,phi coordinates (polar) in double precision
•ROOT::Math::Polar3DPointF point based on r,theta,phi coordinates (polar) in float precision
•ROOT::Math::RhoZPhiPoint point based on rho,z,phi coordinates (cylindrical using z) in double precision
•ROOT::Math::RhoZPhiPointF point based on rho,z,phi coordinates (cylindrical using z) in float precision
•ROOT::Math::RhoEtaPhiPoint
point based on
rho
,
eta
,
phi
coordinates (cylindrical using eta instead of
z
) in
double precision
•ROOT::Math::RhoEtaPhiPointF
point based on
rho
,
eta
,
phi
coordinates (cylindrical using eta instead of
z
) in
float precision
382 CHAPTER 13. MATH LIBRARIES IN ROOT
13.12.3.1 Constructors and Assignment
The following declarations are available:
XYZPoint p1; //an empty vector (x=0, y=0, z=0)
XYZPoint p2(1,2,3); //
Note that each point type is constructed by passing its coordinate representation, so a
XYZPoint(1,2,3)
is different
from a
Polar3DPoint(1,2,3)
. In addition the point classes can be constructed by any vector, which implements the
accessors
x()
,
y()
and
z()
. This can be another 3D point based on a different coordinate system type or even any
vector of a different package, like the CLHEP HepThreePoint that implements the required signatures.
XYZPoint p1(1,2,3);
RhoEtaPHiPoint r2(v1);
CLHEP::HepThreePoint q(1,2,3);
XYZPoint p3(q);
13.12.3.2 Coordinate Accessors and Setter Methods
For the points classes we have the same getter and setter methods as for the vector classes. See “Example: 3D Vector
Classes”.
13.12.3.3 Point-Vector Operations
The following operations are possible between points and vector classes: (
p1
,
p2
and
p3
are instanti-
ations of the
ROOT::Math::PositionVector3D
objects with
p1
and
p3
of the same type;
v1
and
v2
are
ROOT::Math::DisplacementVector3D objects).
p1 += v1;
p1 -= v1;
p3 = p1 + v1; // p1 and p3 are the same type
p3 = v1 + p1; // p3 is based on the same coordinate system as v1
p3 = p1 - v1;
p3 = v1 - p1;
v2 = p1 - p2; // difference between points returns a vector v2
// based on the same coordinate system as p1
Note that the addition between two points is NOT possible and the difference between points returns a vector.
13.12.3.4 Other Operations
Exactly as for the 3D Vectors, the following operations are allowed:
•comparison of points
•scaling and division of points with a scalar
•dot and cross product with any type of vector
13.12.4 Example: LorentzVector Classes
As in the 3D case, typedef’s are defined for user convenience. and can be used by including the header file
Math/Vector4D.h
. The following typedef’s, defined in the header file
Math/Vector4Dfwd.h
, are available for the
different instantiations of the template class ROOT::Math::LorentzVector:
•ROOT::Math::XYZTVector vector based on x,y,z,tcoordinates (Cartesian) in double precision
•ROOT::Math::XYZTVectorF vector based on x,y,z,tcoordinates (Cartesian) in float precision
•ROOT::Math::PtEtaPhiEVector vector based on pt(rho),eta,phi and E(t) coordinates in double precision
13.12. GENERIC VECTORS FOR 2, 3 AND 4 DIMENSIONS (GENVECTOR) 383
•ROOT::Math::PtEtaPhiMVector vector based on pt(rho),eta,phi and M(t) coordinates in double precision
•ROOT::Math::PxPyPzMVector vector based on px,py,pz and M(mass) coordinates in double precision
The metric used for all the LorentzVector is (-,-,-,+) .
13.12.4.1 Constructors and Assignment
The following declarations are available:
// create an empty vector (x=0, y=0, z=0, t=0)
XYZTVector v1;
// vector with x=1, y=2, z=3, t=4
XYZTVector v2(1,2,3,4);
// vector with pt=1, eta=2, phi=PI, E=5
PtEtaPhiEVector v3(1,2,PI,5);
Note that each type of vector is constructed by passing its coordinate representation, so a
XYZTVector(1,2,3,4)
is
different from a
PtEtaPhiEVector(1,2,3,4)
. In addition, the Vector classes can be constructed by any vector, which
implements the accessors x(),y(),z() and t().
This can be another
ROOT::Math::LorentzVector
based on a different coordinate system or any vector of a different
package, like the CLHEP HepLorentzVector that implements the required signature.
XYZTVector v1(1,2,3,4);
PtEtaPhiEVector v2(v1);
CLHEP::HepLorentzVector q(1,2,3,4);
XYZTVector v3(q);
13.12.4.2 Coordinate Accessors
All the same coordinate accessors are available through the interface of ROOT::Math::LorentzVector. For example:
//returns cartesian components for the cartesian vector v1
v1.X(); v1.X(); v1.Z(); v1.T();
//returns cartesian components for the cylindrical vector v2
v2.Px(); v2.Py(); v2.Pz(); v2.E();
//returns other components for the cartesian vector v1
v1.Pt(); v1.Eta(); v1.Phi(); v1.M()
In addition, all 4 vector coordinates can be retrieved with the GetCoordinates method:
double d[4];
//fill d array with (x,y,z,t) components of v1
v1.GetCoordinates(d);
//fill d array with (pt,eta,phi,e) components of v2
v2.GetCoordinates(d);
std::vector w(4);
//fill std::vector with (x,y,z,t)
v1.GetCoordinates(w.begin(),w.end());
//components of v1
To get information on all the coordinate accessors see the ROOT::Math::LorentzVector reference documentation.
384 CHAPTER 13. MATH LIBRARIES IN ROOT
13.12.4.3 Setter Methods
One can set only all the three coordinates via:
//sets the (x,y,z,t) for a XYZTVector
v1.SetCoordinates(c1,c2,c3,c4);
//sets pt,eta,phi,e for a PtEtaPhiEVector
v2.SetCoordinates(c1,c2,c3,c4);
//sets cartesian components for PtEtaPhiEVector
v2.SetXYZ(x,y,z,t);
Single coordinate setter methods are available for the basic vector coordinates, like
SetX()
for a
XYZTVector
or
SetPt()
for a PtEtaPhiEVector. Attempting to do a SetX() on a non-Cartesian vector will not compile.
XYZTVector v1;
v1.SetX(1); //OK setting x for a cartesian vector
PtEtaPhiEVector v2;
v2.SetX(1); //ERROR: cannot set X for a non-cartesian
//vector. Method will not compile.
v2.SetR(1)// OK setting Pt for a PtEtaPhiEVector vector
In addition, there are setter methods from C arrays or iterators.
double d[4]={1.,2.,3.,4.};
XYZTVector v;
//set (x,y,z,t) components of v using values from d
v.SetCoordinates(d);
or for example from an std::vectorusing the iterators
std::vector w(4);
//set (x,y,z,t) components of v using values from w
v.SetCoordinates(w.begin(),w.end());
13.12.4.4 Arithmetic Operations
The following operations are possible between Lorentz vectors classes, even of different coordinate system types: (
v
and
w
are two Lorentz vector of the same type,
q
is a generic Lorentz vector implementing
x()
,
y()
,
z()
and
t()
, and
a
is a generic scalar type: double, float, int, etc.) .
v += q;
v -= q;
v = -q;
v *= a;
v /= a;
w=v+q;
w=v-q;
w=v*a;
w=a*v;
w=v/a;
13.12.4.5 Comparison
v == w;
v != w;
13.12. GENERIC VECTORS FOR 2, 3 AND 4 DIMENSIONS (GENVECTOR) 385
13.12.4.6 Other Methods
a = v.Dot(q); //dot product in metric(+,+,+,-) of 2 LorentzVectors
XYZVector s = v.Vect() //return the spatial components (x,y,z)
v.Beta(); //return beta and gamma value (vector must
v.Gamma() // be time-like otherwise result is meaningless)
XYZVector b = v.BoostToCM(); //return boost vector which will bring
//the Vector in its mas frame (P=0)
13.12.5 Example: Vector Transformations
Transformation classes are grouped in rotations (in three dimensions), Lorentz transformations and Poincarre transfor-
mations, which are translation
/
rotation combinations. Each group has several members which may model physically
equivalent transformations but with different internal representations. All the classes are non-template and use double
precision as the scalar type. The following types of transformation classes are defined:
3D rotations:
•ROOT::Math::Rotation3D, rotation described by a 3x3 matrix of doubles
•ROOT::Math::EulerAngles
rotation described by the three Euler angles (
phi
,
theta
and
psi
) following the
GoldStein definition.
•ROOT::Math::RotationZYX
rotation described by three angles defining a rotation first along the
Z
axis, then
along the rotated Y’ axis and then along the rotated X” axis.
•ROOT::Math::AxisAngle, rotation described by a vector (axis) and an angle
•ROOT::Math::Quaternion, rotation described by a quaternion (4 numbers)
•ROOT::Math::RotationX, specialized rotation along the X axis
•ROOT::Math::RotationY, specialized rotation along the Y axis
•ROOT::Math::RotationZ, specialized rotation along the Z axis
3D transformations (rotations + translations)
•ROOT::Math::Transform3D, (rotations and then translation) described by a 3x4 matrix (12 double numbers)
•ROOT::Math::Translation3D (only translation) described by a 3D Vector
Lorentz rotations and boosts
•ROOT::Math::LorentzRotation, 4D rotation (3D rotation plus a boost) described by a 4x4 matrix
•ROOT::Math::Boost
, a Lorentz boost in an arbitrary direction and described by a 4x4 symmetrix matrix (10
numbers)
•ROOT::Math::BoostX, a boost in the X axis direction
•ROOT::Math::BoostY, a boost in the Y axis direction
•ROOT::Math::BoostZ, a boost in the Z axis direction
13.12.5.1 Constructors
All rotations and transformations are default constructible (giving the identity transformation). All rotations are
constructible taking a number of scalar arguments matching the number (and order of components).
Rotation3D rI; //a summy rotation (Identity matrix)
RotationX rX(PI); //a RotationX with an angle PI
EulerAngles rE(phi,theta,psi); //an Euler rotation with phi,
//theta,psi angles
XYZVector u(ux,uy,uz);
AxisAngle rA(u,delta); //a rotation based on direction u,
//angle delta
386 CHAPTER 13. MATH LIBRARIES IN ROOT
In addition, all rotations and transformations (other than the axial rotations) and transformations are constructible
from (begin,end) iterators or from pointers behave like iterators.
double data[9];
//create a rotation from a rotation matrix
Rotation3D r(data,data+9);
std::vector w(12);
//create Transform3D from std::vector content
Transform3D t(w.begin(),w.end());
All rotations, except the axial rotations, are constructible and assigned from any other type of rotation (including the
axial):
//create a rotation 3D from a rotation along X axis of angle PI
Rotation3D r(ROOT::Math::RotationX(PI));
//construct an Euler rotation from A Rotation3D
EulerAngles r2(r);
//assign an Axis rotation from an Euler Rotation
AxisAngle r3; r3 = r2;
Transform3D (rotation + translation) can be constructed from a rotation and a translation vector:
Rotation3D r;
XYZVector v;
Transform3D t1(r,v); //construct from rotation and then
//translation
Transform3D t2(v,r); //construct inverse from first translation
//then rotation
Transform3D t3(r); //construct from only a rotation
//(zero translation)
Transform3D t4(v); //construct from only translation
//(identity rotation)
13.12.5.2 Operations
All transformations can be applied to vector and points using the operator * or using the operator()
XYZVector v1(...);
Rotation3D r(...);
XYZVector v2 = r*v1; //rotate vector v1 using r
v2 = r(v1); //equivalent
Transformations can be combined using the operator
*
. Rotation, translation and
Transform3D
classes can be all
combined with the operator *. The result of a combination of a rotation and a translation will be a
Transform3D
class.
Note that the rotations are not commutative, the order is then important.
Rotation3D r1(...);
Rotation3D r2(...);
Rotation3D r3 = r2*r1; //a combine rotation r3 by
//applying first r1 then r2
We can combine rotations of different types, like
Rotation3D
with any other type of rotations. The product of two
different axial rotations returns a Rotation3D:
RotationX rx(1.);
RotationY ry(2.);
Rotation3D r = ry * rx; //rotation along X and then Y axis
13.12. GENERIC VECTORS FOR 2, 3 AND 4 DIMENSIONS (GENVECTOR) 387
It is also possible to invert all the transformation or return their inverse:
Rotation3D r1(...);
r1.Invert(); //invert the rotation modifying its content
Rotation3D r2 =r1.Inverse(); //return the inverse in a new
//rotation class
We have used rotation as examples, but all these operations can be applied to all the transformation classes.
13.12.5.3 Set/GetComponents Methods
Common methods to all transformations are
Get
and
SetComponents
. They can be used to retrieve all the scalar
values on which the transformation is based.
RotationX rx;
rx.SetComponents(1.); //set agle of the X rotation
double d[9] = {........};
Rotation3D r;
r.SetComponents(d,d+9); //set 9 components of 3D rotation
double d[16];
LorentzRotation lr;
lr.GetComponents(d,d+16); //get 16 components of a LorentzRotation
TMatrixD(3,4) m;
Transform3D t;
t.GetComponens(m); //fill 3x4 matrix with components of t
The
GetComponents
and
SetComponents
methods can be used with a signature based iterators or by using any foreign
matrix which implements the
operator(i,j)
or a different signatures depending on the transformation type. For more
details on all methods see the reference documentation of any specific transformation class.
13.12.6 Example with External Packages
13.12.6.1 Connection to Linear Algebra Classes
It is possible to use the vector and rotation classes together with the linear algebra classes and to set and get the
contents of any 3D or 4D vector from a linear algebra vector class which implements an iterator or something which
behaves like an iterator. For example a pointer to a C array (double
*
) behaves like an iterator. It is then assumed that
the coordinates, like (x,y,z) will be stored contiguously.
TVectorD r2(N); //ROOT Linear Algebra Vector containing
//many vectors
XYZVector v2;
//construct vector from x=r[INDEX], y=r[INDEX+1], z=r[INDEX+2]
v2.SetCoordinates(&r2[INDEX],&r2[index]+3);
To fill a linear algebra vector from a 3D or 4D vector, with
GetCoordinates()
one can get the internal coordinate
data.
HepVector c(3); //CLHEP Linear algebra vector
//fill HepVector c with c[0]=x, c[1]=y, c[2]=z
v2.GetCoordinates(&c[0],&c[index]+3)
or using TVectorD:
double *data[3];
v2.GetCoordinates(data,data+3);
TVectorD r1(3,data); //create a new Linear Algebra vector
//copying the data
In the case of transformations, constructor and method to set
/
get components exist with linear algebra matrices. The
requisite is that the matrix data are stored, for example in the case of a Lorentz rotation, from (0,0) thru (3,3)
TMatrixD(4,4) m;
LorentzRotation r(m); //create Lorentz r
388 CHAPTER 13. MATH LIBRARIES IN ROOT
13.12.6.2 Connection to Other Vector Classes
The 3D and 4D vectors of the
GenVector
package can be constructed and assigned from any vector which satisfies the
following requisites:
•for 3D vectors implementing the x(),y() and z() methods
•for Lorentz vectors implementing the x(),y(),z() and t() methods.
CLHEP::Hep3Vector hv;
XYZVector v1(hv); //create 3D vector from
//CLHEP 3D Vector
HepGeom::Point3D hp;
XYZPoint p1(hp); //create a 3D p
13.13 Linear Algebra: SMatrix Package
The ROOT Linear algebra package is documented in a separate chapter (see “Linear Algebra in ROOT”).
SMatrix
is a C++ package, for high performance vector and matrix computations. It has been introduced in ROOT v5.08.
It is optimized for describing small matrices and vectors and It can be used only in problems when the size of the
matrices is known at compile time, like in the tracking reconstruction of physics experiments. It is based on a C++
technique, called expression templates, to achieve an high level optimization. The C++ templates can be used to
implement vector and matrix expressions such that these expressions can be transformed at compile time to code which
is equivalent to hand optimized code in a low-level language like FORTRAN or C (see for example T. Veldhuizen,
Expression Templates, C++ Report, 1995).
The
SMatrix
has been developed initially by T. Glebe in Max-Planck-Institut, Heidelberg, as part of the
HeraB
analysis
framework. A subset of the original package has been now incorporated in the ROOT distribution, with the aim to
provide a stand-alone and high performance matrix package. The API of the current package differs from the original
one, in order to be compliant to the ROOT coding conventions.
SMatrix
contains the generic
ROOT::Math::SMatrix
and
ROOT::Math::SVector
classes for describing matrices and
vectors of arbitrary dimensions and of arbitrary type. The classes are templated on the scalar type and on the size, like
number of rows and columns for a matrix . Therefore, the matrix/vector dimension has to be known at compile time.
An advantage of using the dimension as template parameters is that the correctness of dimension in the matrix/vector
operations can be checked at compile time.
SMatrix
supports, since ROOT v5.10, symmetric matrices using a storage class (
ROOT::Math::MatRepSym
) which
contains only the
N*(N+1)/2
independent element of a
NxN
symmetric matrix. It is not in the mandate of this package
to provide complete linear algebra functionality. It provides basic matrix and vector functions such as matrix-matrix,
matrix-vector, vector-vector operations, plus some extra functionality for square matrices, like inversion and determinant
calculation. The inversion is based on the optimized Cramer method for squared matrices of size up to 6x6.
The
SMatrix
package contains only header files. Normally one does not need to build any library. In the ROOT
distribution a library,
libSmatrix
is produced with the C++ dictionary information for squared and symmetric
matrices and vectors up to dimension 7 and based on
Double_t
,
Float_t
and
Double32_t
. The following paragraphs
describe the main characteristics of the matrix and vector classes. More detailed information about the
SMatrix
classes
API is available in the online reference documentation.
13.13.1 Example: Vector Class (SVector)
The template class
ROOT::Math::SVector
represents
n
-dimensional vectors for objects of arbitrary type. This class
has 2 template parameters, which define at compile time, its properties: 1) type of the contained elements (for example
float or double); 2) size of the vector. The use of this dictionary is mandatory if one want to use
Smatrix
in Cling and
with I/O.
13.13.1.1 Creating a Vector
The following constructors are available to create a vector:
•Default constructor for a zero vector (all elements equal to zero).
13.13. LINEAR ALGEBRA: SMATRIX PACKAGE 389
•
Constructor (and assignment) from a vector expression, like
v=p*q+w
. Due to the expression template technique,
no temporary objects are created in this operation.
•Constructor by passing directly the elements. This is possible only for vectors up to size 10.
•
Constructor from an iterator copying the data referred by the iterator. It is possible to specify the begin and end
of the iterator or the begin and the size. Note that for the Vector the iterator is not generic and must be of type
T*, where Tis the type of the contained elements.
In the following example we assume that we are using the namespace ROOT::Math
//create an empty vector of size 3 ( v[0]=v[1]=v[2]=0)
SVector<double,3> v;
double d[3]={1,2,3};
SVector<double,3> v(d,3); //create a vector from a C array
13.13.1.2 Accessing and Setting Methods
The single vector elements can be set or retrieved using the
operator[i]
,
operator(i)
or the iterator interface. Notice
that the index starts from zero and not from one as in FORTRAN. Also no check is performed on the passed index.
The full vector elements can be set also by using the SetElements function passing a generic iterator.
double x = m(i); // return the i-th element
x = *(m.begin()+i); // return the i-th element
v[0]=1;// set the first element
v(1)=2;// set the second element
*(v.begin()+3)=3;// set the third element
std::vector<double> w(3);
// set vector elements from a std::vector<double>::iterator
v.SetElements(w.begin(),w.end());
In addition there are methods to place a sub-vector in a vector. If the size of the sub-vector is larger than the vector
size a static assert (a compilation error) is produced.
SVector>double,N> v;
SVector>double,M> w;
// M <= N otherwise a compilation error is obtained later
// place a vector of size M starting from
// element ioff, v[ioff+i]=w[i]
v.Place_at(w,ioff);
// return a sub-vector of size M starting from
// v[ioff]: w[i]=v[ioff+i]
w = v.Sub < SVector>double,M> > (ioff);
For the vector functions see later in the Matrix and Vector Operators and Functions paragraph.
13.13.2 Example: Matrix Class (SMatrix)
The template class
ROOT::Math::SMatrix
represents a matrix of arbitrary type with
nrows x ncol
dimension. The
class has 4 template parameters, which define at compile time, its properties:
•type of the contained elements, T, for example float or double;
•number of rows;
•number of columns;
•
representation type. This is a class describing the underlined storage model of the Matrix. Presently exists only
two types of this class:
390 CHAPTER 13. MATH LIBRARIES IN ROOT
•ROOT::Math::MatRepStd
for a general
nrows x ncols
matrix. This class is itself a template on the contained
type
T
, the number of rows and the number of columns. Its data member is an array
T[nrows*ncols]
containing
the matrix data. The data are stored in the row-major C convention. For example, for a matrix
M
, of size
3x3
,
the data {a0,a1,...,a8} are stored in the following order:
M=
a0a1a2
a3a4a5
a6a7a8
•ROOT::Math::MatRepSym
for a symmetric matrix of size
NxN
. This class is a template on the contained type and
on the symmetric matrix size
N
. It has as data member an array of type
T
of size
N*(N+1)/2
, containing the lower
diagonal block of the matrix. The order follows the lower diagonal block, still in a row-major convention. For
example for a symmetric 3x3 matrix the order of the 6independent elements {a0,a1,...,a5} is:
M=
a0a1a3
a1a2a4
a3a4a5
13.13.2.1 Creating a Matrix
The following constructors are available to create a matrix:
•Default constructor for a zero matrix (all elements equal to zero).
•Constructor of an identity matrix.
•
Copy constructor (and assignment) for a matrix with the same representation, or from a different one when
possible, for example from a symmetric to a general matrix.
•
Constructor (and assignment) from a matrix expression, like
D=A*B+C
. Due to the expression template technique,
no temporary objects are created in this operation. In the case of an operation like
A=A*B+C
, a temporary object
is needed and it is created automatically to store the intermediary result in order to preserve the validity of this
operation.
•
Constructor from a generic STL-like iterator copying the data referred by the iterator, following its order. It
is both possible to specify the begin and end of the iterator or the begin and the size. In case of a symmetric
matrix, it is required only the triangular block and the user can specify whether giving a block representing the
lower (default case) or the upper diagonal part.
Here are some examples on how to create a matrix. We use typedef’s in the following examples to avoid the full
C++ names for the matrix classes. Notice that for a general matrix the representation has the default value,
ROOT::Math::MatRepStd
, and it is not needed to be specified. Furthermore, for a general square matrix, the number
of column may be as well omitted.
// typedef definitions used in the following declarations
typedef ROOT::Math::SMatrix<double,3> SMatrix33;
typedef ROOT::Math::SMatrix<double,2> SMatrix22;
typedef ROOT::Math::SMatrix<double,3,3,
ROOT::Math::MatRepSym<double,3>> SMatrixSym3;
typedef ROOT::Math::SVector>double,2> SVector2;
typedef ROOT::Math::SVector>double,3> SVector3;
typedef ROOT::Math::SVector>double,6> SVector6;
SMatrix33 m0; // create a zero 3x3 matrix
// create an 3x3 identity matrix
SMatrix33 i = ROOT::Math::SMatrixIdentity();
double a[9]={1,2,3,4,5,6,7,8,9}; // input matrix data
// create a matrix using the a[] data
SMatrix33 m(a,9); // this will produce the 3x3 matrix
// ( 1 2 3 )
// ( 4 5 6 )
// ( 7 8 9 )
13.13. LINEAR ALGEBRA: SMATRIX PACKAGE 391
Example to fill a symmetric matrix from an std::vector:
std::vector<double> v(6);
for (int i=0; i<6; ++i) v[i] = double(i+1);
SMatrixSym3 s(v.begin(),v.end()) // this will produce the
// symmetric matrix
// ( 1 2 4 )
// ( 2 3 5 )
// ( 4 5 6 )
//create a general matrix from a symmetric matrix (the opposite
// will not compile)
SMatrix33 m2 = s;
13.13.2.2 Accessing and Setting Methods
The matrix elements can be set using the
operator()(irow,icol)
, where
irow
and
icol
are the row and column
indexes or by using the iterator interface. Notice that the indexes start from zero and not from one as in FORTRAN.
Furthermore, all the matrix elements can be set also by using the SetElements function passing a generic iterator. The
elements can be accessed by the same methods as well as by using the function
ROOT::Math::SMatrix::apply
. The
apply(i)
has exactly the same behavior for general and symmetric matrices; in contrast to the iterator access methods
which behave differently (it follows the data order).
SMatrix33 m;
m(0,0)=1;// set the element in first row and first column
*(m.begin()+1)=2;// set the second element (0,1)
double d[9]={1,2,3,4,5,6,7,8,9};
m.SetElements(d,d+9); // set the d[] values in m
double x = m(2,1); // return the element in 3
x = m.apply(7); // return the 8-th element (row=2,col=1)
x = *(m.begin()+7); // return the 8-th element (row=2,col=1)
// symmetric matrices
//(note the difference in behavior between apply and the iterators)
x = *(m.begin()+4)// return the element (row=2,col=1)
x = m.apply(7); // returns again the (row=2,col=1) element
There are methods to place and/or retrieve
ROOT::Math::SVector
objects as rows or columns in (from) a matrix.
In addition one can put (get) a sub-matrix as another
ROOT::Math::SMatrix
object in a matrix. If the size of the
sub-vector or sub-matrix is larger than the matrix size a static assert (a compilation error) is produced. The non-const
methods are:
SMatrix33 m;
SVector2 v2(1,2);
// place a vector in the first row from
// element (0,1) : m(0,1)=v2[0]
m.Place_in_row(v2,0,1);
// place the vector in the second column from
// (0,1) : m(0,1) = v2[0]
m.Place in_col(v2,0,1);
SMatrix22 m2;
// place m2 in m starting from the
// element (1,1) : m(1,1) = m2(0,0)
m.Place_at(m2,1,1);
SVector3 v3(1,2,3);
// set v3 as the diagonal elements
// of m : m(i,i) = v3[i] for i=0,1,2
m.SetDiagonal(v3)
The const methods retrieving contents (getting slices of a matrix) are:
a={1,2,3,4,5,6,7,8,9};
SMatrix33 m(a,a+9);
392 CHAPTER 13. MATH LIBRARIES IN ROOT
SVector3 irow = m.Row(0); // return as vector the first row
SVector3 jcol = m.Col(1); // return as vector the second column
// return a slice of the first row from
// (0,1): r2[0]= m(0,1); r2[1]=m(0,2)
SVector2 r2 = m.SubRow<SVector2> (0,1);
// return a slice of the second column from
// (0,1): c2[0] = m(0,1); c2[1] = m(1,1)
SVector2 c2 = m.SubCol<SVector2> (1,0);
// return a sub-matrix 2x2 with the upper left corner at(1,1)
SMatrix22 subM = m.Sub<SMatrix22> (1,1);
// return the diagonal element in a SVector
SVector3 diag = m.Diagonal();
// return the upper(lower) block of the matrix m
SVector6 vub = m.UpperBlock(); // vub = [ 1, 2, 3, 5, 6, 9 ]
SVector6 vlb = m.LowerBlock(); // vlb = [ 1, 4, 5, 7, 8, 9 ]
13.13.2.3 Linear Algebra Matrix Functions (Inversion, Determinant)
Only limited linear algebra functionality is available for
SMatrix
. It is possible for squared matrices
NxN
, to find the
inverse or to calculate the determinant. Different inversion algorithms are used if the matrix is smaller than
6x6
or if
it is symmetric. In the case of a small matrix, a faster direct inversion is used. For a large
(N>6)
symmetric matrix
the Bunch-Kaufman diagonal pivoting method is used while for a large
(N>6)
general matrix an LU factorization is
performed using the same algorithm as in the CERNLIB routine dinv.
// Invert a NxN matrix.
// The inverted matrix replaces the existing one if the
// result is successful
bool ret = m.Invert(); // return the inverse matrix of m.
// If the inversion fails ifail is different than zero ???
int ifail = 0;
ifail = m.Inverse(ifail);
// determinant of a square matrix - calculate the determinant
// modyfing the matrix content and returns it if the calculation
// was successful
double det;
bool ret = m.Det(det);
// calculate determinant by using a temporary matrix; preserves
// matrix content
bool ret = n.Det2(det);
13.13.3 Example: Matrix and Vector Functions and Operators
13.13.3.1 Matrix and Vector Operators
The
ROOT::Math::SVector
and
ROOT::Math::SMatrix
classes define the following operators described below. The
m1
,
m2,m3 are vectors or matrices of the same type (and size) and ais a scalar value:
m1 == m2 // returns whether m1 is equal to m2
// (element by element comparison)
m1 != m2 // returns whether m1 is NOT equal to m2
// (element by element comparison)
m1 < m2 // returns whether m1 is less than m2
// (element wise comparison)
m1 > m2 // returns whether m1 is greater than m2
13.13. LINEAR ALGEBRA: SMATRIX PACKAGE 393
// (element wise comparison)
// in the following m1 and m3 can be general and m2 symmetric,
// but not vice-versa
m1 += m2 // add m2 to m1
m1 -= m2 // subtract m2 to m1
m3 = m1 + m2 // addition
m1 - m2 // subtraction
// Multiplication and division via a scalar value a
m3 = a*m1; m3 = m1*a; m3 = m1/a;
Vector-Vector multiplication:
The operator
*
defines an element by element multiplication between vectors.
For the standard vector-vector algebraic multiplication returning a scalar,
vTv
(dot product), one must use the
ROOT::Math::Dot function. In addition, the Cross (only for vector sizes of 3), ROOT::Math::Cross
, and the
Tensor product, ROOT::Math::TensorProd, are defined.
Matrix - Vector multiplication:
The operator
*
defines the matrix-vector multiplication:
yi
=
PjMi,j xj
. The
operation compiles only if the matrix and the vectors have the right sizes.
//M is a N1xN2 matrix, x is a N2 size vector, y is a N1 size vector
y=M*x
Matrix - Matrix multiplication: The operator *defines the matrix-matrix multiplication: Ci,j =PkAi,kBk,j .
// A is a N1xN2 matrix, B is a N2xN3 matrix and C is a N1xN3 matrix
C=A*B
The operation compiles only if the matrices have the right size. In the case that
A
and
B
are symmetric matrices,
C
is a
general one, since their product is not guaranteed to be symmetric.
13.13.4 Matrix and Vector Functions
The most used matrix functions are:
•ROOT::Math::Transpose(M) returns the transpose matrix MT
•ROOT::Math::Similarity(v,M) returns the scalar value resulting from the matrix-vector product vTMv
•ROOT::Math::Similarity(U,M)
returns the matrix resulting from the product:
U M UT
. If
M
is symmetric, the
returned resulting matrix is also symmetric
•ROOT::Math::SimilarityT(U,M)
returns the matrix resulting from the product:
UT M U
. If
M
is symmetric, the
returned resulting matrix is also symmetric
The major vector functions are:
•ROOT::Math::Dot(v1,v2) returns the scalar value resulting from the vector dot product
•ROOT::Math::Cross(v1,v2)
returns the vector cross product for two vectors of size 3. Note that the
Cross
product is not defined for other vector sizes
•ROOT::Math::Unit(v) returns unit vector. One can use also the v.Unit()method.
•ROOT::Math::TensorProd(v1,v2)
returns a general matrix
M
of size
N1xN2
resulting from the tensor product
between the vector v1 of size N1 and v2 of size N2:
For a list of all the available matrix and vector functions see the SMatrix online reference documentation.
394 CHAPTER 13. MATH LIBRARIES IN ROOT
13.13.4.1 Matrix and Vector I/O
One can print (or write in an output stream) Vectors and Matrices) using the Print method or the << operator:
// m is a SMatrix or a SVector object
m.Print(std::cout);
std::cout << m << std::endl;
In the ROOT distribution, the Cling dictionary is generated for
SMatrix
and
SVector
for for
Double_t
,
Float_t
and
Double32_t up to dimension 7. This allows the possibility to store them in a ROOT file.
13.14 ROOT Statistics Classes
13.14.1 Classes for Computing Limits and Confidence Levels
TFeldmanCousins
class calculates the
CL
upper/lower limit for a Poisson process using the Feldman-Cousins method
(as described in PRD V57 #7, p3873-3889). No treatment is provided in this method for the uncertainties in the signal
or the background.
TRolke
computes confidence intervals for the rate of a Poisson process in the presence of background and efficiency,
using the profile likelihood technique for treating the uncertainties in the efficiency and background estimate. The
signal is always assumed to be Poisson; background may be Poisson, Gaussian, or user-supplied; efficiency may be
Binomial, Gaussian, or user-supplied. See publication at Nucl. Instrum. Meth. A551:493-503,2005.
TLimit
class computes 95% C.L. limits using the Likelihood ratio semi-Bayesian method ( method; see e.g. T. Junk,
NIM A434, p. 435-443, 1999). It takes signal background and data histograms wrapped in a
TLimitDataSource
as
input, and runs a set of Monte Carlo experiments in order to compute the limits. If needed, inputs are fluctuated
according to systematic.
13.14.2 Specialized Classes for Fitting
TFractionFitter
fits Monte Carlo (MC) fractions to data histogram (a la HMCMLL, R. Barlow and C. Beeston, Comp.
Phys. Comm. 77 (1993) 219-228). It takes into account both data and Monte Carlo statistical uncertainties through a
likelihood fit using Poisson statistics. However, the template (MC) predictions are also varied within statistics, leading
to additional contributions to the overall likelihood. This leads to many more fit parameters (one per bin per template),
but the minimization with respect to these additional parameters is done analytically rather than introducing them as
formal fit parameters. Some special care needs to be taken in the case of bins with zero content.
TMultiDimFit
implements multi-dimensional function parameterization for multi-dimensional data by fitting them to
multi-dimensional data using polynomial or Chebyshev or Legendre polynomial
TSpectrum
contains advanced spectra processing functions for 1- and 2-dimensional background estimation, smoothing,
deconvolution, peak search and fitting, and orthogonal transformations.
RooFit
is a complete toolkit for fitting and data analysis modeling (see the RooFit User Guide at ftp://root.cern.ch/root/doc/RooFit_Users_Manual_2.07-
29.pdf)
TSplot
to disentangle signal from background via an extended maximum likelihood fit and with a tool to access the
quality and validity of the fit producing distributions for the control variables. (see M. Pivk and F.R. Le Diberder,
Nucl. Inst. Meth.A 555, 356-369, 2005).
13.14.3 Multi-variate Analysis Classes
TMultiLayerPerceptron is a Neural Network class (see for more details the chapter “Neural Networks”).
TPrincipal provides the Principal Component Analysis.
TRobustEstimator is a robust method for minimum covariance determinant estimator (MCD).
TMVA
is a package for multivariate data analysis (see http://tmva.sourceforge.net/docu/TMVAUsersGuide.pdf the
User’s Guide).
Chapter 14
Linear Algebra in ROOT
The linear algebra package is supposed to give a complete environment in ROOT to perform calculations like equation
solving and eigenvalue decompositions. Most calculations are performed in double precision. For backward compatibility,
some classes are also provided in single precision like
TMatrixF
,
TMatrixFSym
and
TVectorF
. Copy constructors exist
to transform these into their double precision equivalent, thereby allowing easy access to decomposition and eigenvalue
classes, only available in double precision.
The choice was made not to provide the less frequently used complex matrix classes. If necessary, users can always
reformulate the calculation in 2 parts, a real one and an imaginary part. Although, a linear equation involving complex
numbers will take about a factor of 8 more computations, the alternative of introducing a set of complex classes in this
non-template library would create a major maintenance challenge.
Another choice was to fill in both the upper-right corner and the bottom-left corner of a symmetric matrix. Although
most algorithms use only the upper-right corner, implementation of the different matrix views was more straightforward
this way. When stored only the upper-right part is written to file.
For a detailed description of the interface, the user should look at the root reference guide at: http://root.cern.ch/root/
Reference.html
14.1 Overview of Matrix Classes
The figure below shows an overview of the classes available in the linear algebra library,
libMatrix.so
. At the
center is the base class
TMatrixDBase
from which three different matrix classes,
TMatrixD
,
TMatrixDSym
and
TMatrixDFSparse
derive. The user can define customized matrix operations through the classes
TElementActionD
and TElementsPosActionD.
Reference to different views of the matrix can be created through the classes on the right-hand side, see “Matrix Views”.
These references provide a natural connection to vectors.
Matrix decompositions (used in equation solving and matrix inversion) are available through the classes on the left-hand
side (see “Matrix Decompositions”). They inherit from the
TDecompBase
class. The Eigen Analysis is performed
through the classes at the top, see “Matrix Eigen Analysis”. In both cases, only some matrix types can be analyzed.
For instance,
TDecompChol
will only accept symmetric matrices as defined
TMatrixDSym
. The assignment operator
behaves somewhat different than of most other classes. The following lines will result in an error:
TMatrixD a(3,4);
TMatrixD b(5,6);
b = a;
It required to first resize matrix b to the shape of a.
TMatrixD a(3,4);
TMatrixD b(5,6);
b.ResizeTo(a);
b = a;
395
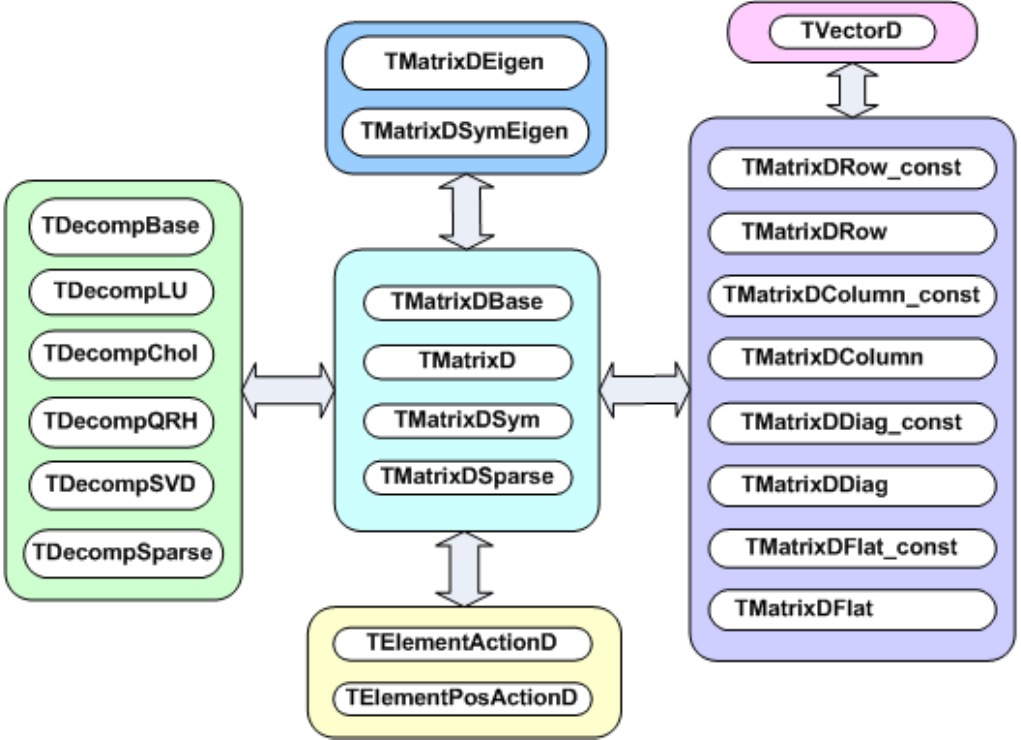
396 CHAPTER 14. LINEAR ALGEBRA IN ROOT
Figure 14.1: Overview of matrix classes
14.2. MATRIX PROPERTIES 397
14.2 Matrix Properties
A matrix has five properties, which are all set in the constructor:
•precision
- float or double. In the first case you will use the
TMatrixF
class family, in the latter case the
TMatrixD one;
•type - general (TMatrixD), symmetric (TMatrixDSym) or sparse (TMatrixDSparse);
•size - number of rows and columns;
•index - range start of row and column index. By default these start at zero;
•sparse map - this property is only relevant for a sparse matrix. It indicates where elements are unequal zero.
14.2.1 Accessing Properties
The following table shows the methods to access the information about the relevant matrix property:
Method Descriptions
Int_t GetRowLwb () row lower-bound index
Int_t GetRowUpb () row upper-bound index
Int_t GetNrows () number of rows
Int_t GetColLwb () column lower-bound index
Int_t GetColUpb () column upper-bound index
Int_t GetNcols () number of columns
Int_t GetNoElements () number of elements, for a dense matrix this equals: fNrows x
fNcols
Double_t GetTol () tolerance number which is used in decomposition operations
Int_t *GetRowIndexArray () for sparse matrices, access to the row index of fNrows+1 entries
Int_t *GetColIndexArray () for sparse matrices, access to the column index of fNelems entries
The last two methods in this table are specific to the sparse matrix, which is implemented according to the Harwell-
Boeing format. Here, besides the usual shape/size descriptors of the matrix like
fNrows
,
fRowLwb
,
fNcols
and
fColLwb
,
we also store a row index, fRowIndex and column index, fColIndex for the elements unequal zero:
fRowIndex[0,..,fNrows]:
Stores for each row the index range of the elements in the data and
column array
fColIndex[0,..,fNelems-1]: Stores the column number for each data element != 0.
The code to print all matrix elements unequal zero would look like:
TMatrixDSparse a;
const Int_t *rIndex = a.GetRowIndexArray();
const Int_t *cIndex = a.GetColIndexArray();
const Double_t *pData = a.GetMatrixArray();
for (Int_t irow = 0; irow < a.getNrows(); irow++) {
const Int_t sIndex = rIndex[irow];
const Int_t eIndex = rIndex[irow+1];
for (Int_t index = sIndex; index < eIndex; index++) {
const Int_t icol = cIndex[index];
const Double_t data = pData[index];
printf("data(%d,%d) = %.4en",irow+a.GetfRowLwb(),
icol+a.GetColLwb(),data);
}
}
14.2.2 Setting Properties
The following table shows the methods to set some of the matrix properties. The resizing procedures will maintain the
matrix elements that overlap with the old shape. The optional last argument
nr_zeros
is only relevant for sparse
398 CHAPTER 14. LINEAR ALGEBRA IN ROOT
matrices. If supplied, it sets the number of non-zero elements. If it is smaller than the number overlapping with the old
matrix, only the first (row-wise)nr_zeros are copied to the new matrix.
Method Descriptions
SetTol (Double_t tol) set the tolerance number
ResizeTo (Int_t nrows,Int_t ncols,
Int_t nr_nonzeros=-1)
change matrix shape to
nrows
x
ncols
. Index will
start at zero
ResizeTo(Int_t row_lwb,Int_t row_upb,
Int_t col_lwb,Int_t col_upb,
Int_t nr_nonzeros=-1)
change matrix shape to
row_lwb:row_upb xcol_lwb:col_upb
SetRowIndexArray (Int_t *data) for sparse matrices, set the row index. The array
data should contains at leastfNrows+1 entries
column lower-bound index
SetColIndexArray (Int_t *data) for sparse matrices, set the column index. The
array data should contains at least
fNelems
entries
SetSparseIndex (Int_t nelems new) allocate memory for a sparse map of nelems_new
elements and copy (if exists) at most nelems_new
matrix elements over to the new structure
SetSparseIndex (const TMatrixDBase &a) copy the sparse map from matrix aNote that this
can be a dense matrix!
SetSparseIndexAB (const TMatrixDSparse &a, const
TMatrixDSparse &b)
set the sparse map to the same of the map of
matrix aand b
The second half of the table is only relevant for sparse matrices. These methods define the sparse structure. It should
be clear that a call to any of these methods has to be followed by a
SetMatrixArray
(. . . ) which will supply the
matrix data, see the next chapter “Creating and Filling a Matrix”.
14.3 Creating and Filling a Matrix
The matrix constructors are listed in the next table. In the simplest ones, only the number of rows and columns is
given. In a slightly more elaborate version, one can define the row and column index range. Finally, one can also define
the matrix data in the constructor. In Matrix Operators and Methods we will encounter more fancy constructors that
will allow arithmetic operations.
TMatrixD(Int_t nrows,Int_t ncols)
TMatrixD(Int_t row_lwb,Int_t row_upb,Int_t col_lwb,Int_t col_upb)
TMatrixD(Int_t nrows,Int_t ncols,const Double_t *data, Option_t option= "")
TMatrixD(Int_t row_lwb,Int_t row_upb,Int_t col_lwb,Int_t col_upb,
const Double_t *data,Option_t *option="")
TMatrixDSym(Int_t nrows)
TMatrixDSym(Int_t row_lwb,Int_t row_upb)
TMatrixDSym(Int_t nrows,const Double_t *data,Option_t *option="")
TMatrixDSym(Int_t row_lwb,Int_t row_upb,const Double_t *data, Option_t *opt="")
TMatrixDSparse(Int_t nrows,Int_t ncols)
TMatrixDSparse(Int_t row_lwb,Int_t row_upb,Int_t col_lwb, Int_t col_upb )
TMatrixDSparse(Int_t row_lwb,Int_t row_upb,Int_t col_lwb,Int_t col_upb,
Int_t nr_nonzeros,Int_t *row,Int_t *col,Double_t *data)
If only the matrix shape is defined in the constructor, matrix data has to be supplied and possibly the sparse structure.
In “Setting Properties” was discussed how to set the sparse structure.
Several methods exist to fill a matrix with data:
SetMatrixArray(const Double_t*data,Option_t*option="")
, copies the array data. If option
="F"
, the array fills
the matrix column-wise else row-wise. This option is only implemented for
TMatrixD
and
TMatrixDSym
. It is expected
that the array data contains at least fNelems entries.
SetMatrixArray(Int_t nr,Int_t *irow,Int_t *icol,Double_t *data)
, is only available for sparse matrices. The
three arrays should each contain
nr
entries with row index, column index and data entry. Only the entries with
non-zero data value are inserted!
operator()
or
operator[]
, these operators provide the easiest way to fill a matrix but are in particular for a sparse
matrix expensive. If no entry for slot (
i,j
) is found in the sparse index table it will be entered, which involves some
memory management! Therefore, before invoking this method in a loop it is wise to set the index table first through a
call to the SetSparseIndex method.
14.4. MATRIX OPERATORS AND METHODS 399
SetSub(Int_t row_lwb,Int_t col_lwb,const TMatrixDBase &source)
, the matrix to be inserted at position
(row_lwb,col_lwb) can be both, dense or sparse.
Use(...)
allows inserting another matrix or data array without actually copying the data. Next table shows the
different flavors for the different matrix types.
Use(TMatrixD &a)
Use(Int_t row_lwb,Int_t row_upb,Int_t col_lwb,Int_t col_upb,Double_t *d ata)
Use(Int_t nrows,Int_t ncols,Double_t *data)
Use(TMatrixDSym &a)
Use(Int_t nrows,Double_t *data)
Use(Int_t row_lwb,Int_t row_upb,Double_t *data)
Use(TMatrixDSparse &a)
Use(Int_t row_lwb,Int_t row_upb,Int_t col_lwb,Int_t col_upb,Int_t nr_no nzeros,
Int_t *pRowIndex,Int_t *pColIndex,Double_t *pData)
Use(Int_t nrows,Int_t ncols,Int_t nr_nonzeros,Int_t *pRowIndex,
Int_t *pColIndex,Double_t *pData)
Below follow a few examples of creating and filling a matrix. First we create a Hilbert matrix by copying an array.
TMatrixD h(5,5);
TArrayD data(25);
for (Int_t = 0;i<25; i++) {
const Int_t ir = i/5;
const Int_t ic = i%5;
data[i] = 1./(ir+ic);
}
h.SetMatrixArray(data.GetArray());
We also could assign the data array to the matrix without actually copying it.
TMatrixD h; h.Use(5,5,data.GetArray());
h.Invert();
The array data now contains the inverted matrix. Finally, create a unit matrix in sparse format.
TMatrixDSparse unit1(5,5);
TArrayI row(5),col(5);
for (Int_t i = 0;i<5; i++) row[i] = col[i] = i;
TArrayD data(5); data.Reset(1.);
unit1.SetMatrixArray(5,row.GetArray(),col.GetArray(),data.GetArray());
TMatrixDSparse unit2(5,5);
unit2.SetSparseIndex(5);
unit2.SetRowIndexArray(row.GetArray());
unit2.SetColIndexArray(col.GetArray());
unit2.SetMatrixArray(data.GetArray());
14.4 Matrix Operators and Methods
It is common to classify matrix/vector operations according to BLAS (Basic Linear Algebra Subroutines) levels, see
following table:
BLAS level operations example floating-point operations
1 vector-vector xT y n
2 matrix-vector matrix Ax n2
3 matrix-matrix AB n3
Most level 1, 2 and 3 BLAS are implemented. However, we will present them not according to that classification
scheme it is already boring enough.
400 CHAPTER 14. LINEAR ALGEBRA IN ROOT
14.4.1 Arithmetic Operations between Matrices
Description Format Comment
element
wise sum
C=A+B
A+=B
Add (A,alpha,B)
TMatrixD(A,TMatrixD::kPlus,B)
overwrites A
A=A+αB constructor
element wise subtraction C=A-B A-=B
TMatrixD(A,TMatrixD::kMinus,B)
overwrites A
constructor
matrix multiplication C=A*B
A*=B
C.Mult(A,B)
overwrites A
TMatrixD(A,TMatrixD::kMult,B) constructor of A.B
TMatrixD(A, TMatrixD::kTransposeMult,B) constructor of AT.B
TMatrixD(A, TMatrixD::kMultTranspose,B) constructor of A.BT
element wise multiplication
element wise division
ElementMult(A,B)
ElementDiv(A,B)
A(i,j)*= B(i,j)
A(i,j)/= B(i,j)
14.4.2 Arithmetic Operations between Matrices and Real Numbers
Description Format Comment
element wise sum C=r+A C=A+r A+=r overwrites A
element wise subtraction C=r-A C=A-r A-=r overwrites A
matrix multiplication C=r*A C=A*r A*=r overwrites A
14.4.3 Comparisons and Boolean Operations
The following table shows element wise comparisons between two matrices:
Format Output Description
A == B Bool_t equal to
A != B
A>B
A >= B
A<B
A <= B
matrix
matrix
matrix
matrix
matrix
Not equal
Greater than
Greater than or equal to
Smaller than
Smaller than or equal to
AreCompatible(A,B)
Compare(A,B)
VerifyMatrixIdentity(A,B,verb, maxDev)
Bool_t
Bool_t
Compare matrix properties
return summary of comparison
Check matrix identity within maxDev
tolerance
The following table shows element wise comparisons between matrix and real:
Format Output Description
A == r
A != r
A > r
A >= r
A < r
A <= r
Bool_t
Bool_t
Bool_t
Bool_t
Bool_t
Bool_t
equal to
Not equal
Greater than
Greater than or equal to
Smaller than
Smaller than or equal to
VerifyMatrixValue(A,r,verb, maxDev) Bool_t Compare matrix value with r within
maxDev tolerance
14.4.4 Matrix Norms
Format Output Description

14.5. MATRIX VIEWS 401
A.RowNorm()
A.NormInf()
A.ColNorm()
A.Norm1()
A.E2Norm()
A.NonZeros()
A.Sum()
A.Min()
A.Max()
Double_t
Double_t
Double_t
Double_t
Double_t
Int_t
Double_t
Double_t
Double_t
norm induced by the infinity vector norm, maxi
Pi|Aij |
maxiPi|Aij |
norm induced by the 1 vector norm, maxjPi|Aij |
maxjPi|Aij |
Square of the Euclidean norm,
Pji(A2
ij )
number of elements unequal zero
Pji(Aij )
minij (Aij )
maxij (Aij )
A.NormByColumn (v,"D")
A.NormByRow (v,"D")
TMatrixD
TMatrixD
Aij /=νi, divide each matrix column by vector v. If
the second argument is “M”, the column is multiplied.
Aij /=νj, divide each matrix row by vector v. If the
second argument is “M”, the row is multiplied.
14.4.5 Miscellaneous Operators
Format Output Description
A.Zero() TMatrixX Aij = 0
A.Abs() TMatrixX Aij =|Aij |
A.Sqr() TMatrixX Aij =A2
ij
A.Sqrt() TMatrixX Aij =p(Aij )
A.UnitMatrix() TMatrixX Aij = 1 for i ==j else 0
A.Randomize
(alpha,beta,seed)
TMatrixX Aij = (β−α)S(0,1) + αa random matrix is generated
with elements uniformly distributed between αand β
A.T() TMatrixX Aij =Aji
A.Transpose(B) TMatrixX Aij =Bji
A.Invert(&det) TMatrixX Invert matrix A. If the optional pointer to the Double_t
argument det is supplied, the matrix determinant is
calculated.
A.InvertFast(&det) TMatrixX like Invert but for matrices i =(6x6)a faster but less
accurate Cramer algorithm is used
A.Rank1Update(v,alpha) TMatrixX Perform with vector v a rank 1 operation on the matrix:
A=A+α.ν.νT
A.RandomizePD(alpha,beta,seed)‘ TMatrixX Aij = (β−α)S(0,1) + αa random symmetric
positive-definite matrix is generated with elements
uniformly distributed between αand β
Output
TMatrixX
indicates that the returned matrix is of the same type as
A
, being
TMatrixD
,
TMatrixDSym
or
TMatrixDSparse. Next table shows miscellaneous operations for TMatrixD.
Format Output Description
A.Rank1Update(v1,v2,alpha) TMatrixD Perform with vector v1 and v2, a rank 1
operation on the matrix: A=A+α.ν.ν2T
14.5 Matrix Views
Another way to access matrix elements is through the matrix-view classes,
TMatrixDRow
,
TMatrixDColumn
,
TMatrixDDiag
and
TMatrixDSub
(each has also a const version which is obtained by simply appending const to the
class name). These classes create a reference to the underlying matrix, so no memory management is involved. The
next table shows how the classes access different parts of the matrix:
class view
TMatrixDRow const(X,i) TMatrixDRow(X,i)
x00 x0n
xi0... xij ... xin
xn0xnn
402 CHAPTER 14. LINEAR ALGEBRA IN ROOT
TMatrixDColumn const(X,j)
TMatrixDColumn(X,j)
x00 x0jx0n
...
xij
...
xn0xnj xnn
TMatrixDDiag const(X) TMatrixDDiag(X)
x00 x0n
...
...
...
xn0xnn
TMatrixDSub const(X,i,l,j,k)
TMatrixDSub(X,i,l,j,k)
x00 x0n
xij ... xik
xlj ... xlk
xn0xnn
14.5.1 View Operators
For the matrix views
TMatrixDRow
,
TMatrixDColumn
and
TMatrixDDiag
, the necessary assignment operators are
available to interact with the vector class
TVectorD
. The sub matrix view
TMatrixDSub
has links to the matrix classes
TMatrixD
and
TMatrixDSym
. The next table summarizes how the access individual matrix elements in the matrix
views:
Format Comment
TMatrixDRow(A,i)(j) TMatrixDRow(A,i)[j] element Aij
TMatrixDColumn(A,j)(i) TMatrixDColumn(A,j)[i] element Aij
TMatrixDDiag(A(i) TMatrixDDiag(A[i] element Aij
TMatrixDSub(A(i) TMatrixDSub(A,rl,rh,cl,ch)(i,j) element Aij
element Arl+i,cl+j
The next two tables show the possible operations with real numbers, and the operations between the matrix views:
Description Format Comment
assign real TMatrixDRow(A,i) = r row i
TMatrixDColumn(A,j) = r column j
TMatrixDDiag(A) = r matrix diagonal
TMatrixDSub(A,i,l,j,k) = r sub matrix
add real TMatrixDRow(A,i) += r row i
TMatrixDColumn(A,j) += r column j
TMatrixDDiag(A) += r matrix diagonal
TMatrixDSub(A,i,l,j,k) +=r sub matrix
multiply with real TMatrixDRow(A,i) *= r row i
TMatrixDColumn(A,j) *= r column j
TMatrixDDiag(A) *= r matrix diagonal
TMatrixDSub(A,i,l,j,k) *= r sub matrix
Description Format Comment
TMatrixDRow(A,i1) +=
TMatrixDRow const(B,i2)
add row i2to row i1
add matrix slice TMatrixDColumn(A,j1) +=
TMatrixDColumn const(A,j2)
add column j2to column j1
TMatrixDDiag(A) += TMatrixDDiag
const(B)
add Bdiagonal to Adiagonal
14.6. MATRIX DECOMPOSITIONS 403
TMatrixDRow(A,i1) *=
TMatrixDRow const(B,i2)
multiply row i2with row i1element wise
TMatrixDColumn(A,j1) *=
TMatrixDColumn const(A,j2)
multiply column
j
2with column
j
1element
wise
multiply matrix slice TMatrixDDiag(A) *= TMatrixDDiag
const(B)
multiply Bdiagonal with Adiagonal
element wise
TMatrixDSub(A,i1,l1,j1,k1) *=
TMatrixDSub(B,i2,l2,j2,k2)
multiply sub matrix of Awith sub matrix
of B
TMatrixDSub(A,i,l,j,k) *= B multiply sub matrix of Awith matrix of B
In the current implementation of the matrix views, the user could perform operations on a symmetric matrix that
violate the symmetry. No checking is done. For instance, the following code violates the symmetry.
TMatrixDSym A(5);
A.UnitMatrix();
TMatrixDRow(A,1)[0]=1;
TMatrixDRow(A,1)[2]=1;
14.5.2 View Examples
Inserting row i1into rowi2 of matrix Acan easily accomplished through:
TMatrixDRow(A,i1) = TMatrixDRow(A,i2)
Which more readable than:
const Int_t ncols = A.GetNcols();
Double_t *start = A.GetMatrixArray();
Double_t *rp1 = start+i*ncols;
const Double_t *rp2 = start+j*ncols;
while (rp1 < start+ncols) *rp1++ = *rp2++;
Check that the columns of a Haar -matrix of order order are indeed orthogonal:
const TMatrixD haar = THaarMatrixD(order);
TVectorD colj(1<<order);
TVectorD coll(1<<order);
for (Int_t j = haar.GetColLwb(); j <= haar.GetColUpb(); j++) {
colj = TMatrixDColumn_const(haar,j);
Assert(TMath::Abs(colj*colj-1.0)<=1.0e-15);
for (Int_t l = j+1; l <= haar.GetColUpb(); l++) {
coll = TMatrixDColumn_const(haar,l);
Assert(TMath::Abs(colj*coll) <= 1.0e-15);
}
}
Multiplying part of a matrix with another part of that matrix (they can overlap)
TMatrixDSub(m,1,3,1,3) *= m.GetSub(5,7,5,7);
14.6 Matrix Decompositions
The linear algebra package offers several classes to assist in matrix decompositions. Each of the decomposition methods
performs a set of matrix transformations to facilitate solving a system of linear equations, the formation of inverses as
well as the estimation of determinants and condition numbers. More specifically the classes
TDecompLU
,
TDecompBK
,
TDecompChol
,
TDecompQRH
and
TDecompSVD
give a simple and consistent interface to the LU, Bunch-Kaufman, Cholesky,
QR and SVD decompositions. All of these classes are derived from the base class
TDecompBase
of which the important
methods are listed in next table:
404 CHAPTER 14. LINEAR ALGEBRA IN ROOT
Method Action
Bool_t Decompose() perform the matrix decomposition
Double_t Condition() calculate ||A||1 ||A-1||1, see “Condition
number”
void Det(Double_t &d1,Double_t &d2) the determinant is d1 2d2. Expressing the
determinant this way makes under/over-flow
very unlikely
Bool_t Solve(TVectorD &b) solve Ax=b; vectorbis supplied through the
argument and replaced with solution x
TVectorD Solve(const TVectorD &b,Bool_t &ok) solve Ax=b; x is returned
Bool_t Solve(TMatrixDColumn &b) solve Ax=column(B,j);column(B,j) is
supplied through the argument and replaced
with solution x
Bool_t TransSolve(TVectorD &b) solve ATx=b;vector bis supplied through
the argument and replaced with solution x
TVectorD TransSolve(const TVectorD b, Bool_t &ok) solve ATx=b;vector xis returned
Bool_t TransSolve(TMatrixDColumn &b) solve ATx=column(B,j); column(B,j) is
supplied through the argument and replaced
with solution x
Bool_t MultiSolve(TMatrixD &B) solve ATx=b;. matrix Bis supplied through
the argument and replaced with solution X
void Invert(TMatrixD &inv) call to MultiSolve with as input argument
the unit matrix. Note that for a matrix (
m
x
n
)
-
A
with
m>n
, a pseudo-inverse is calculated
TMatrixD Invert() call to MultiSolve with as input argument
the unit matrix. Note that for a matrix (
m
x
n
)
-
A
with
m>n
, a pseudo-inverse is calculated
Through
TDecompSVD
and
TDecompQRH
one can solve systems for a (
m
x
n
) -
A
with
m>n
. However, care has to be taken
for methods where the input vector/matrix is replaced by the solution. For instance in the method
Solve(b)
, the
input vector should have length m but only the first n entries of the output contain the solution. For the
Invert(B)
method, the input matrix B should have size (mxn) so that the returned (mxn) pseudo-inverse can fit in it.
The classes store the state of the decomposition process of matrix
A
in the user-definable part of
TObject::fBits
, see
the next table. This guarantees the correct order of the operations:
kMatrixSet
kDecomposed
kDetermined
kCondition
kSingular
Aassigned
Adecomposed, bit kMatrixSet must have been set.
det Acalculated, bit kDecomposed must have been set.
||A||1 ||A-1||1 is calculated bit kDecomposed must have been set.
Ais singular
The state is reset by assigning a new matrix through
SetMatrix(TMatrixD &A)
for
TDecompBK
and
TDecompChol
(actually SetMatrix(TMatrixDSym &A) and SetMatrix(TMatrixDSparse &A) for TMatrixDSparse).
As the code example below shows, the user does not have to worry about the decomposition step before calling a solve
method, because the decomposition class checks before invoking Solve that the matrix has been decomposed.
TVectorD b = ..;
TMatrixD a = ..;
.
TDecompLU lu(a);
Bool_t ok;
lu.Solve(b,ok);
In the next example, we show again the same decomposition but now performed in a loop and all necessary steps are
manually invoked. This example also demonstrates another very important point concerning memory management! Note
that the vector, matrix and decomposition class are constructed outside the loop since the dimensions of vector/matrix
are constant. If we would have replaced
lu.SetMatrix(a)
by
TDecompLU lu(a)
, we would construct/deconstruct the
array elements of lu on the stack.
TVectorD b(n);
TMatrixD a(n,n);
TDecompLU lu(n);
14.6. MATRIX DECOMPOSITIONS 405
Bool_t ok;
for (....) {
b = ..;
a = ..;
lu.SetMatrix(a);
lu.Decompose();
lu.Solve(b,ok);
}
14.6.1 Tolerances and Scaling
The tolerance parameter
fTol
(a member of the base class
TDecompBase
) plays a crucial role in all operations of the
decomposition classes. It gives the user a tool to monitor and steer the operations its default value is
ε
where 1 +
ε
= 1.
If you do not want to be bothered by the following considerations, like in most other linear algebra packages, just set
the tolerance with
SetTol
to an arbitrary small number. The tolerance number is used by each decomposition method
to decide whether the matrix is near singular, except of course SVD that can handle singular matrices. This will be
checked in a different way for any decomposition. For instance in LU, a matrix is considered singular in the solving
stage when a diagonal element of the decomposed matrix is smaller than
fTol
. Here an important point is raised. The
Decompose()
method is successful as long no zero diagonal element is encountered. Therefore, the user could perform
decomposition and only after this step worry about the tolerance number.
If the matrix is flagged as being singular, operations with the decomposition will fail and will return matrices or vectors
that are invalid. If one would like to monitor the tolerance parameter but not have the code stop in case of a number
smaller than fTol, one could proceed as follows:
TVectorD b = ..;
TMatrixD a = ..;
.
TDecompLU lu(a);
Bool_t ok;
TVectorD x = lu.Solve(b,ok);
Int_t nr = 0;
while (!ok) {
lu.SetMatrix(a);
lu.SetTol(0.1*lu.GetTol());
if (nr++ > 10)break;
x = lu.Solve(b,ok);
}
if (x.IsValid())
cout << "solved with tol =" << lu.GetTol() << endl;
else
cout << "solving failed " << endl;
The observant reader will notice that by scaling the complete matrix by some small number the decomposition will
detect a singular matrix. In this case, the user will have to reduce the tolerance number by this factor. (For CPU time
saving we decided not to make this an automatic procedure).
14.6.2 Condition number
The numerical accuracy of the solution
x
in
Ax = b
can be accurately estimated by calculating the condition number
k
of matrix A, which is defined as:
k=||A||1||A−1||1where ||A||1=max
j(Pi|Aij |)
A good rule of thumb is that if the matrix condition number is 10n, the accuracy in
x
is
15
-
n
digits for double
precision.
Hager devised an iterative method (W.W. Hager, Condition estimators, SIAM J. Sci. Stat. Comp., 5 (1984), pp. 311-316)
to determine ||A−1||1without actually having to calculate A−1. It is used when calling Condition().
A code example below shows the usage of the condition number. The matrix
A
is a (10x10) Hilbert matrix that is
badly conditioned as its determinant shows. We construct a vector
b
by summing the matrix rows. Therefore, the
406 CHAPTER 14. LINEAR ALGEBRA IN ROOT
components of the solution vector
x
should be exactly 1. Our rule of thumb to the 2.1012 condition number predicts
that the solution accuracy should be around
15-12=3
digits. Indeed, the largest deviation is 0.00055 in component 6.
TMatrixDSym H = THilbertMatrixDSym(10);
TVectorD rowsum(10);
for (Int_t irow = 0; irow < 10; irow++)
for (Int_t icol = 0; icol < 10; icol++)
rowsum(irow) += H(irow,icol);
TDecompLU lu(H);
Bool_t ok;
TVectorD x = lu.Solve(rowsum,ok);
Double_t d1,d2;
lu.Det(d1,d2);
cout << "cond:" << lu.Condition() << endl;
cout << "det :" << d1*TMath:Power(2.,d2) << endl;
cout << "tol :" << lu.GetTol() << endl;
x.Print();
cond:3.9569e+12
det :2.16439e-53
tol :2.22045e-16
Vector 10 is as follows
|1|
------------------
0|1
1|1
2|0.999997
3|1.00003
4|0.999878
5|1.00033
6|0.999452
7|1.00053
8|0.999723
9|1.00006
14.6.3 LU
Decompose an nxn matrix A.
PA = LU
Ppermutation matrix stored in the index array
fIndex
:
j=fIndex[i]
indicates that row j and row
i
should be swapped.
Sign of the permutation, −1n, where nis the number of interchanges in the permutation, stored in fSign.
Lis lower triangular matrix, stored in the strict lower triangular part of
fLU.
The diagonal elements of Lare unity
and are not stored.
Uis upper triangular matrix, stored in the diagonal and upper triangular part of fU.
The decomposition fails if a diagonal element of fLU equals 0.
14.6.4 Bunch-Kaufman
Decompose a real symmetric matrix A
A = UDUT
Dis a block diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks Dk.
Uis product of permutation and unit upper triangular matrices:
14.6. MATRIX DECOMPOSITIONS 407
U = Pn-1Un-1
· · ·
PkUk
· · ·
where kdecreases from n- 1 to 0 in steps of 1 or 2. Permutation matrix Pk is stored
in fIpiv.Uk is a unit upper triangular matrix, such that if the diagonal block Dk is of order s(s= 1, 2), then
Uk=
1v0
0 1 0
0 0 1
k−ssn−k
k−s
s
n−k
If s= 1, Dk overwrites A(k, k), and v overwrites A(0: k - 1, k).
If s= 2, the upper triangle of
Dk
overwrites
A
(k-1, k-1),
A
(k-1,k), and
A
(k, k), and v overwrites
A
(0 : k - 2, k - 1 : k).
14.6.5 Cholesky
Decompose a symmetric, positive definite matrix A
A = UTU
Uis an upper triangular matrix. The decomposition fails if a diagonal element of
fU<=0
, the matrix is not positive
negative.
14.6.6 QRH
Decompose a (mxn) - matrix Awith m >= n.
A = QRH
Qorthogonal (mxn) - matrix, stored in fQ;
Rupper triangular (nxn) - matrix, stored in fR;
H(nxn) - Householder matrix, stored through;
fUp n - vector with Householder up’s;
fW n - vector with Householder beta’s.
The decomposition fails if in the formation of reflectors a zero appears, i.e. singularity.
14.6.7 SVD
Decompose a (mxn) - matrix Awith m >= n.
A = USVT
U(mxm) orthogonal matrix, stored in fU;
Sis diagonal matrix containing the singular values. Diagonal stored in vector
fSig
which is ordered so that
fSig[0]
>= fSig[1] >= ... >= fSig[n-1];
V(nxn) orthogonal matrix, stored in fV.
The singular value decomposition always exists, so the decomposition will (as long as m >= n) never fail. If m<n,
the user should add sufficient zero rows to
A
, so that m== n. In the
SVD
,
fTol
is used to set the threshold on the
minimum allowed value of the singular values: min singular = fTol maxi(Sii).
408 CHAPTER 14. LINEAR ALGEBRA IN ROOT
14.7 Matrix Eigen Analysis
Classes
TMatrixDEigen
and
TMatrixDSymEigen
compute eigenvalues and eigenvectors for general dense and symmetric
real matrices, respectively. If matrix
A
is symmetric, then
A
=
V.D.V T
, where the eigenvalue matrix
D
is diagonal
and the eigenvector matrix
V
is orthogonal. That is, the diagonal values of
D
are the eigenvalues, and
V.V T
=
I
,
where
I
- is the identity matrix. The columns of
V
represent the eigenvectors in the sense that
A.V
=
V.D
. If
A
is
not symmetric, the eigenvalue matrix
D
is block diagonal with the real eigenvalues in 1-by-1 blocks and any complex
eigenvalues, a+i*b, in 2-by-2 blocks, [a,b;-b,a]. That is, if the complex eigenvalues look like:
u+iv . . . . .
. u −iv . . . .
. . a +ib . . .
. . . a −ib . .
. . . . x .
. . . . . y
then Dlooks like:
u v . . . .
−v u . . . .
. . a b . .
. . . −b a .
. . . . x .
. . . . . y
This keeps
V
a real matrix in both symmetric and non-symmetric cases, and
A.V
=
V.D
. The matrix
V
may be badly
conditioned, or even singular, so the validity of the equation A=V.D.V −1depends upon the condition number of V.
Next table shows the methods of the classes
TMatrixDEigen
and
TMatrixDSymEigen
to obtain the eigenvalues and
eigenvectors. Obviously, MatrixDSymEigen constructors can only be called with TMatrixDSym:
Format Output Description
eig.GetEigenVectors () TMatrixD eigenvectors for both TMatrixDEigen and
TMatrixDSymEigen
eig.GetEigenValues () TVectorD eigenvalues vector for TMatrixDSymEigen
eig.GetEigenValues() TMatrixD eigenvalues matrix for TMatrixDEigen
eig.GetEigenValuesRe () TVectorD real part of eigenvalues for TMatrixDEigen
eig.GetEigenValuesIm () TVectorD imaginary part of eigenvalues for
TMatrixDEigen
Below, usage of the eigenvalue class is shown in an example where it is checked that the square of the singular values of
a matrix care identical to the eigenvalues of cT.c:
const TMatrixD m = THilbertMatrixD(10,10);
TDecompSVD svd(m);
TVectorD sig = svd.GetSig(); sig.Sqr();
// Symmetric matrix EigenVector algorithm
TMatrixDSym mtm(TMatrixDBase::kAtA,m);
const TMatrixDSymEigen eigen(mtm);
const TVectorD eigenVal = eigen.GetEigenValues();
const Bool_t ok = VerifyVectorIdentity(sig,eigenVal,1,1.-e-14);
14.8 Speed Comparisons
Speed of four matrix operations have been compared between four matrix libraries,
GSL CLHEP
,
ROOT v3.10
and
ROOT
v4.0. Next figure shows the CPU time for these four operations as a function of the matrix size:
1. A*B
The execution time is measured for the sum of A * Bsym, Bsym* A and A * B. Notice the matrix_size3
dependence of execution time.
CLHEP
results are hampered by a poor implementation of symmetric matrix
multiplications. For instance, for general matrices of size 100x100, the time is 0.015 sec. while A * Bsym takes
0.028 sec and Bsym* A takes 0.059 sec.
14.8. SPEED COMPARISONS 409
Both
GSL
and
ROOT v4.0
can be setup to use the hardware-optimized multiplication routines of the
BLAS
libraries. It
was tested on a G4 PowerPC. The improvement becomes clearly visible around sizes of (50x50) were the execution
speed improvement of the Altivec processor becomes more significant than the overhead of filling its pipe.
2. A−1Here, the time is measured for an in-place matrix inversion.
Except for
ROOT v3.10
, the algorithms are all based on an
LU
factorization followed by forward/back-substitution.
ROOT
v3.10 is using the slower Gaussian elimination method. The numerical accuracy of the CLHEP routine is poor:
•
up to 6x6 the numerical imprecise Cramer multiplication is hard-coded. For instance, calculating
U=H*H-1
, where
H
is a (5x5) Hilbert matrix, results in off-diagonal elements of 10
−7
instead of the 10
−13
using an
LU
according to
Crout.
•
scaling protection is non-existent and limits are hard-coded, as a consequence inversion of a Hilbert matrix for
sizes>(12x12)
fails. In order to gain speed the
CLHEP
algorithm stores its permutation info of the pivots points
in a static array, making multi-threading not possible.
GSL
uses LU decomposition without the implicit scaling of
Crout
. Therefore, its accuracy is not as good. For instance
a (10x10) Hilbert matrix has errors 10 times larger than the
LU Crout
result. In
ROOT v4.0
, the user can choose
between the
Invert()
and
IvertFast()
routines, where the latter is using the Cramer algorithm for
sizes<7x7
. The
speed graph shows the result for InvertFast().
3. A*x=b
the execution time is measured for solving the linear equation
A*x=b
. The same factorizations are used
as in the matrix inversion. However, only 1 forward/back-substitution has to be used instead of msize as in
the inversion of (msize x msize) matrix. As a consequence the same differences are observed but less amplified.
CLHEP shows the same numerical issues as in step the matrix inversion. Since ROOT3.10 has no dedicated
equation solver, the solution is calculated through x=A-1*b. This will be slower and numerically not as stable.
4.
(
AT∗A
)
−1∗AT
timing results for calculation of the pseudo inverse of matrix a. The sequence of operations
measures the impact of several calls to constructors and destructors in the
C++
packages versus a
C
library like
GSL.
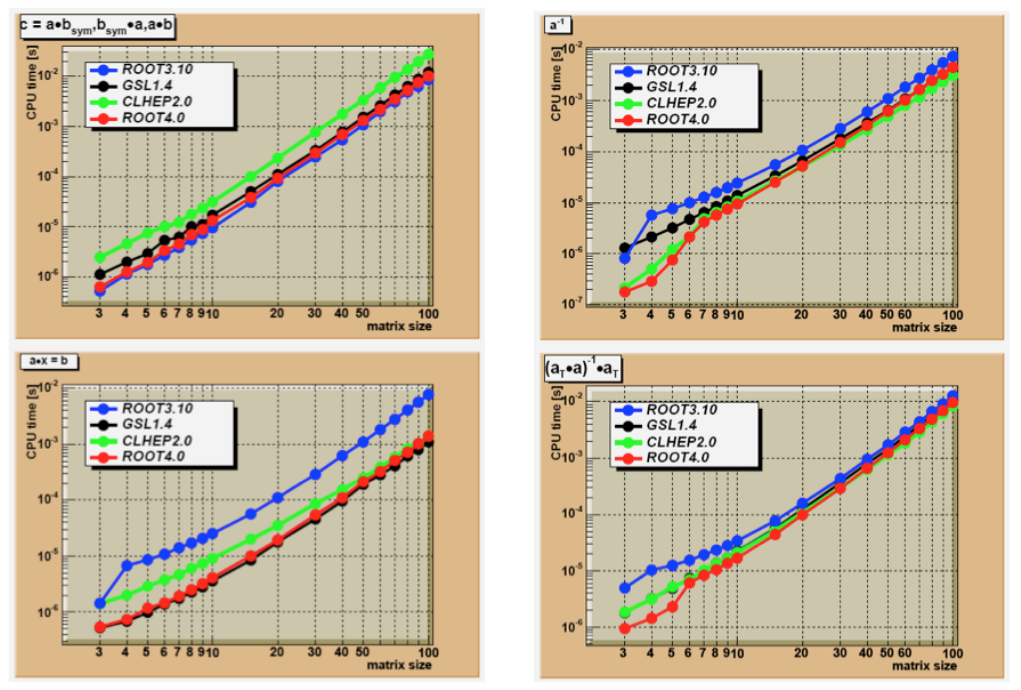
410 CHAPTER 14. LINEAR ALGEBRA IN ROOT
Figure 14.2: Speed comparison between the different matrix packages
Chapter 15
Adding a Class
15.1 The Role of TObject
The light-weight
TObject
class provides the default behavior and protocol for the objects in the ROOT system.
Specifically, it is the primary interface to classes providing object I/O, error handling, inspection, introspection, and
drawing. The interface to this service is via abstract classes.
15.1.1 Introspection, Reflection and Run Time Type Identification
Introspection, which is also referred to as reflection, or run time type identification (RTTI) is the ability of a class
to reflect upon itself or to “look inside itself. ROOT implements reflection with the
TClass
class. It provides all the
information about a class, a full description of data members and methods, including the comment field and the method
parameter types. A class with the ClassDef macro has the ability to obtain a TClass with the IsA method.
TClass *cl = obj->IsA();
It returns a TClass. In addition, an object can directly get the class name and the base classes by:
const char* name = obj->ClassName();
If the class is a descendent of
TObject
, you can check if an object inherits from a specific class, you can use the
InheritsFrom method. This method returns kTrue if the object inherits from the specified class name or TClass.
Bool_t b = obj->InheritsFrom("TLine");
Bool_t b = obj->InheritsFrom(TLine::Class());
ROOT and
Cling
rely on reflection and the class dictionary to identify the type of a variable at run time. With
TObject
inheritance come some methods that use Introspection to help you see the data in the object or class. For
instance:
obj->Dump(); // lists all data members and their current valsue
obj->Inspect(); // opens a window to browse data members
obj->DrawClass(); // Draws the class inheritance tree
For an example of obj->Inspect(), see “Inspecting Objects”.
15.1.2 Collections
To store an object in a ROOT collection, it must be a descendent of
TObject
. This is convenient if you want to store
objects of different classes in the same collection and execute the method of the same name on all members of the
collection. For example, the list of graphics primitives are in a ROOT collection called
TList
. When the canvas is
drawn, the
Paint
method is executed on the entire collection. Each member may be a different class, and if the
Paint
method is not implemented, TObject::Paint will be executed.
411
412 CHAPTER 15. ADDING A CLASS
15.1.3 Input/Output
The
TObject::Write
method is the interface to the ROOT I/O system. It streams the object into a buffer using the
Streamer method. It supports cycle numbers and automatic schema evolution. See “Input/Output”.
15.1.4 Paint/Draw
These graphics methods are defaults; their implementation in
TObject
does not use the graphics subsystem. The
TObject::Draw
method is simply a call to
AppendPad
. The
Paint
method is empty. The default is provided so that
one can call
Paint
in a collection. The method
GetDrawOption
returns the draw option that was used when the object
was drawn on the canvas. This is especially relevant with histograms and graphs.
15.1.5 Clone/DrawClone
Two useful methods are
Clone
and
DrawClone
. The
Clone
method takes a snapshot of the object with the
Streamer
and creates a new object. The DrawClone method does the same thing and in addition draws the clone.
15.1.6 Browse
This method is called if the object is browse-able and is to be displayed in the object browser. For example the
TTree
implementation of
Browse
, calls the Browse method for each branch. The
TBranch::Browse
method displays the name
of each leaf. For the object’s
Browse
method to be called, the
IsFolder()
method must be overridden to return true.
This does not mean it has to be a folder, it just means that it is browse-able.
15.1.7 SavePrimitive
This method is called by a canvas on its list of primitives, when the canvas is saved as a script. The purpose of
SavePrimitve
is to save a primitive as a C++ statement(s). Most ROOT classes implement the
SavePrimitive
method. It is recommended that the
SavePrimitive
is implemented in user defined classes if it is to be drawn on
a canvas. Such that the command
TCanvas::SaveAs(Canvas.C)
will preserve the user-class object in the resulting
script.
15.1.8 GetObjectInfo
This method is called when displaying the event status in a canvas. To show the event status window, select the
Options
menu and the
EventStatus
item. This method returns a string of information about the object at position
(x, y). Every time the cursor moves, the object under the cursor executes the
GetObjectInfo
method. The string is
then shown in the status bar. There is a default implementation in
TObject
, but it is typically overridden for classes
that can report peculiarities for different cursor positions (for example the bin contents in a TH1).
15.1.9 IsFolder
By default an object inheriting from
TObject
is not brows-able, because
TObject::IsFolder()
returns
kFALSE
. To
make a class browse-able, the
IsFolder
method needs to be overridden to return
kTRUE
. In general, this method
returns kTRUE if the object contains browse-able objects (like containers or lists of other objects).
15.1.10 Bit Masks and Unique ID
A
TObject
descendent inherits two data members:
fBits
and
fUniqueID
.
fBits
is 32-bit data member used with a
bit mask to get object information. Bits 0 - 13 are reserved as global bits, bits 14 - 23 can be used in different class
hierarchies.
enum EObjBits {
kCanDelete = BIT(0), // if can be deleted
kMustCleanup = BIT(3), // if destructor must call RecursiveRemove()
kObjInCanvas = BIT(3), // for backward compatibility only
kIsReferenced = BIT(4), // if referenced by TRef or TRefArray
15.2. MOTIVATION 413
kHasUUID = BIT(5), // if has a TUUID, fUniqueID=UUIDNumber
kCannotPick = BIT(6), // if cannot be picked in a pad
kNoContextMenu = BIT(8), // if does not want a context menu
kInvalidObject = BIT(13)// object ctor succeeded but the object should not be used
};
For example, the bits
kMustCleanup
and
kCanDelete
are used in
TObject
. See “The kCanDelete Bit” and “The
kMustCleanup Bit”. They can be set by any object and should not be reused. Make sure to no overlap in any given
hierarchy them. The bit 13 (
kInvalidObject
) is set when an object could not be read from a ROOT file. It will check
this bit and will skip to the next object on the file.
The
TObject
constructor initializes the
fBits
to zero depending if the object is created on the stack or allocated on
the heap. When the object is created on the stack, the
kCanDelete
bit is set to false to protect from deleting objects
on the stack. The high 8 bits are reserved for the system usage; the low 24 bits are user settable.
fUniqueID
is a data
member used to give a unique identification number to an object. It is initialized to zero by the
TObject
constructor.
ROOT does not use this data member. The two data members (
fBits
and
fUniqueID
) are streamed out when writing
an object to disk. If you do not use them, you can save some space and time by specifying:
MyClass::Class()->IgnoreTObjectStreamer();
This sets a bit in the
TClass
object. If the file is compressed, the savings are minimal since most values are zero;
however, it saves some space when the file is not compressed. A call to
IgnoreTObjectStreamer
also prevents the
creation of two additional branches when splitting the object. If left alone, two branches called
fBits
and
fUniqueID
will appear.
15.2 Motivation
If you want to integrate and use your classes with ROOT, to enjoy features like, extensive RTTI (Run Time Type
Information) and ROOT object I/O and inspection, you have to add the following line to your class header files:
ClassDef(ClassName,ClassVersionID); //The class title
For example in TLine.h we have:
ClassDef(TLine,1); //A line segment
The
ClassVersionID
is used by the ROOT I/O system. It is written on the output stream and during reading you
can check this version ID and take appropriate action depending on the value of the ID. See “Streamers”. Every time
you change the data members of a class, you should increase its
ClassVersionID
by one. The
ClassVersionID
should
be
>=1
. Set
ClassVersionID=0
in case you don’t need object I/O. To be able to generate properly documentation for
your classes using THtml you must add the statement:
ClassImp(ClassName)
For example in TLine.cxx:
ClassImp(TLine)
Note that you should provide a default constructor for your classes, i.e. a constructor with zero parameters or with
one or more parameters all with default values in case you want to use object I/O. If do not provide such a default
contructor, you MUST implement an I/O constructor. If not you will get a compile time error. See the “The Default
Constructor” paragraph in this chapter. The
ClassDef
and
ClassImp
macros are defined in the file
Rtypes.h
. This
file is referenced by all ROOT include files, so you will automatically get them if you use a ROOT include file.
414 CHAPTER 15. ADDING A CLASS
15.2.1 Template Support
In ROOT version 3.03 and older, ROOT provided special
ClassDef
and
ClassImp
macros for classes with two and
three template arguments. In ROOT version 3.04 and above, the macros
ClassDef
and
ClassImp
can be used directly
even for a class template.
ClassImp
is used to register an implementation file in a class. For class templates, the
ClassImp can only be used for a specific class template instance.
ClassImp(MyClass1<double>);
For multiple template arguments, you will need to use an intermediary typedef:
typedef MyClass2<int,float> myc_i_f;
ClassImp(myc_i_f);
You can also register an implementation for all instances of a class template by using templateClassImp:
templateClassImp(MyClass3);
Here are examples of a header and a LinkDef file:
// in header file MyClass.h
template <typename T> class MyClass1 {
private:
T fA;
...
public:
...
ClassDef(MyClass1,1)
};
template <typename T1, typename T2> class MyClass2 {
private:
T1 fA;
T2 fB;
public:
...
ClassDef(MyClass2,1)
};
template <typename T1, typename T2, typename T3> class MyClass3 {
private:
T1 fA;
T2 fB;
T3 fC;
...
public:
...
ClassDef(MyClass3,1)
};
// A LinkDef.h file with all the explicit template instances
// that will be needed at link time
#ifdef __CLING__
#pragma link C++ class MyClass1<float>+;
#pragma link C++ class MyClass1<double>+;
#pragma link C++ class MyClass2<float,int>+;
#pragma link C++ class MyClass2<float,double>+;
#pragma link C++ class MyClass3<float,int,TObject*>+;
#pragma link C++ class MyClass3<float,TEvent*,TObject*>+;
#endif
15.3. THE DEFAULT CONSTRUCTOR 415
15.3 The Default Constructor
ROOT object I/O requires every class to have either a default constructor or an I/O constructor. A default constructor
is a constructor with zero parameters or with one or more parameters all with default values. An I/O constructor is a
constructor with exactly one parameter which type is a pointer to one of the type marked as an ‘io constructor type’.
We will come back to this context in a few paragraphs. This default or I/O constructor is called whenever an object is
being read from a ROOT database. Be sure that you do not allocate any space for embedded pointer objects in this
constructor. This space will be lost (memory leak) while reading in the object. For example:
class T49Event : public TObject {
private:
Int_t fId;
TCollection *fTracks;
...
public:
// Error space for TList pointer will be lost
T49Event() { fId = 0; fTrack = new TList; }
// Correct default initialization of pointer
T49Event() { fId = 0; fTrack = 0; }
...
};
The memory will be lost because during reading of the object the pointer will be set to the object it was pointing to at
the time the object was written. Create the
fTrack
list when you need it, e.g. when you start filling the list or in a
not-default constructor.
...
if (!fTrack) fTrack = new TList;
...
The constructor actually called by the ROOT I/O can be customized by using the rootcling pragma:
#pragma link C++ ioctortype UserClass;
For example, with this pragma and a class named MyClass, the ROOT I/O will call the first of the following 3
constructors which exists and is public:
MyClass(UserClass*);MyClass(TRootIOCtor*);
MyClass(); // Or a constructor with all its arguments defaulted.
When more than one pragma ioctortype is used, the first seen as priority. For example with:
#pragma link C++ ioctortype UserClass1;
#pragma link C++ ioctortype UserClass2;
We look for the first existing public constructor in the following order:
MyClass(UserClass1*);
MyClass(UserClass2*);
MyClass(TRootIoCtor*);
MyClass(); // Or a constructor with all its arguments defaulted.
15.4 rootcling: The Cling Dictionary Generator
A way in which dictionaries can be generated is via the
rootcling
utility. This tool generates takes as input a set of
headers and generates in output the dictionary C++ code and a
pcm
file. This latter file is fundamental for the correct
functioning of the dictionary at runtime. It should be located in the directory where the shared library is installed in
which the compiled dictionary resides.
416 CHAPTER 15. ADDING A CLASS
NOTA BENE: the dictionaries that will be used within the same project must have unique names. In other words,
compiled object files relative to dictionary source files cannot reside in the same library or in two libraries loaded by the
same application if the original source files have the same name. This loose limitation is imposed by the registration
mechanism ROOT has in place to keep track of dynamically loaded libraries.
In the following example, we walk through the steps necessary to generate a dictionary, I/O, and inspect member
functions. Let’s start with a TEvent class, which contains a collection of TTracks.
The TEvent.h header is:
#ifndef __TEvent__
#define __TEvent__
#include "TObject.h"
class TCollection;
class TTrack;
class TEvent : public TObject {
private:
Int_t fId; // event sequential id
Float_t fTotalMom; // total momentum
TCollection *fTracks; // collection of tracks
public:
TEvent() { fId = 0; fTracks = 0; }
TEvent(Int_t id);
~TEvent();
void AddTrack(TTrack *t);
Int_t GetId() const {return fId; }
Int_t GetNoTracks() const;
void Print(Option_t *opt="");
Float_t TotalMomentum();
ClassDef(TEvent,1); //Simple event class
};
The things to notice in these header files are:
•The usage of the ClassDef macro
•The default constructors of the TEvent and TTrack classes
•Comments to describe the data members and the comment after the ClassDef macro to describe the class
These classes are intended for you to create an event object with a certain id, and then add tracks to it. The track
objects have a pointer to their event. This shows that the I/O system correctly handles circular references.
The TTrack.h header is:
#ifndef __TTrack__
#define __TTrack__
#include "TObject.h"
class TEvent;
class TTrack : public TObject {
private:
Int_t fId; //track sequential id
TEvent *fEvent; //event to which track belongs
Float_t fPx; //x part of track momentum
Float_t fPy; //y part of track momentum
Float_t fPz; //z part of track momentum
public:
TTrack() { fId = 0; fEvent = 0;fPx=fPy=fPz=0; }
TTrack(Int_t id, Event *ev, Float_t px,Float_t py,Float_t pz);
Float_t Momentum() const;
TEvent *GetEvent() const {return fEvent; }
15.4. ROOTCLING: THE CLING DICTIONARY GENERATOR 417
void Print(Option_t *opt="");
ClassDef (TTrack,1); //Simple track class
};
#endif
Next is the implementation of these two classes.
TEvent.cxx:
#include <iostream.h>
#include "TOrdCollection.h"
#include "TEvent.h"
#include "TTrack.h"
ClassImp(TEvent)
...
TTrack.cxx:
#include <iostream.h>
#include "TMath.h"
#include "Track.h"
#include "Event.h"
ClassImp(TTrack)
...
Now using rootcling we can generate the dictionary file.
rootcling eventdict.cxx -c TEvent.h TTrack.h
Looking in the file
eventdict.cxx
we can see, the
Streamer()
and
ShowMembers()
methods for the two classes.
Streamer()
is used to stream an object to/from a
TBuffer
and
ShowMembers()
is used by the
Dump()
and
Inspect()
methods of TObject. Here is the TEvent::Streamer method:
void TEvent::Streamer(TBuffer &R__b) {
// Stream an object of class TEvent.
if (R__b.IsReading()) {
Version_t R__v = R__b.ReadVersion();
TObject::(R__b);
R__b >> fId;
R__b >> fTotalMom;
R__b >> fTracks;
}else {
R__b.WriteVersion(TEvent::IsA());
TObject::Streamer(R__b);
R__b << fId;
R__b << fTotalMom;
R__b << fTracks;
}
}
The
TBuffer
class overloads the
operator<<()
and
operator>>()
for all basic types and for pointers to objects.
These operators write and read from the buffer and take care of any needed byte swapping to make the buffer machine
independent. During writing, the
TBuffer
keeps track of the objects that have been written and multiple references to
the same object are replaced by an index. In addition, the object’s class information is stored.
TEvent
and
TTracks
418 CHAPTER 15. ADDING A CLASS
need manual intervention. Cut and paste the generated
Streamer()
from the
eventdict.cxx
into the class’ source file
and modify as needed (e.g. add counter for array of basic types) and disable the generation of the
Streamer()
when
using the
LinkDef.h
file for next execution of
rootcling
. In case you do not want to read or write this class (no I/O)
you can tell rootcling to generate a dummy Streamer()by changing this line in the source file:
ClassDef(TEvent,0);
If you want to prevent the generation of Streamer(), see the section “Adding a Class with a Shared Library”.
15.4.1 Dictionaries for STL
Usually, headers are passed to rootcling at the command line. To generate a dictionary for a class from the STL, e.g.
std::vector<MyClass>
, you would normally pass the header defining
MyClass
and
std::vector
. The latter is a
compiler specific header and cannot be passed to rootcling directly. Instead, create a little header file that includes
both headers, and pass that to rootcling.
Often ROOT knows where
MyClass
and the templated class (e.g. vector) are defined, for example because the files got
#included
. Knowing these header files ROOT can automatically generate the dictionary for any template combination
(e.g.
vector<myClass>
) when it is needed, by generating files starting with
AutoDict*
. You can toggle this feature
on or off at the ROOT prompt by executing .autodict.
15.5 Adding a Class with a Shared Library
Step 1:
Define your own class in
SClass.h
and implement it in
SClass.cxx
. You must provide a default constructor
or an I/O constructor for your class. See the “The Default Constructor” paragraph in this chapter.
#include <iostream.h>
#include "TObject.h"
class SClass : public TObject {
private:
Float_t fX; //x position in centimeters
Float_t fY; //y position in centimeters
Int_t fTempValue; //! temporary state value
public:
SClass() { fX = fY = -1; }
void Print() const;
void SetX(float x){fX=x;}
void SetY(float y){fY=y;}
ClassDef(SClass, 1)
};
Step 2:
Add a call to the
ClassDef
macro to at the end of the class definition (in the
SClass.h
file).
ClassDef(SClass,1)
. Add a call to the
ClassImp
macro in the implementation file (
SClass.cxx
):
ClassImp(SClass)
.
// SClass.cxx:
#include "SClass.h"
ClassImp(SClass);
void SClass::Print() const {
cout << "fX="<< fX << ",fY="<< fY << endl;
}
You can add a class without using the
ClassDef
and
ClassImp
macros; however, you will be limited. Specifically the
object I/O features of ROOT will not be available to you for these classes. See “Cling the C++ Interpreter”. The
ShowMembers
and
Streamer
method, as well as the
>>
operator overloads, are implemented only if you use
ClassDef
and
ClassImp
. See
$ROOTSYS/include/Rtypes.h
for the definition of
ClassDef
and
ClassImp
. To exclude a data
member from the Streamer, add a !as the first character in the comments of the field:
Int_t fTempValue; //! temporary state value
15.5. ADDING A CLASS WITH A SHARED LIBRARY 419
15.5.1 The LinkDef.h File
Step 3: The LinkDef.h file tells rootcling which classes should be added to the dictionary.
#ifdef __CLING__
#pragma link C++ class SClass;
#endif
Three options can trail the class name:
•-
: tells
rootcling not
to generate the
Streamer
method for this class. This is necessary for those classes that
need a customized Streamer method.
#pragma link C++ class SClass-; // no streamer
•!
: tells
rootcling not
to generate the
operator>>(TBuffer &b,MyClass *&obj)
method for this class. This
is necessary to be able to write pointers to objects of classes not inheriting from TObject.
#pragma link C++ class SClass!; // no >> operator
// or
#pragma link C++ class SClass-!; // no streamer, no >> operator
•+
: in ROOT version 1 and 2 tells
rootcling
to generate a
Streamer
with extra byte count information. This
adds an integer to each object in the output buffer, but it allows for powerful error correction in case a
Streamer
method is out of sync with data in the file. The +option is mutual exclusive with both the -and !options.
IMPORTANT NOTE: In ROOT Version 3 and later, a “+” after the class name tells
rootcling
to use the new I/O
system. The byte count check is always added. The new I/O system has many advantages including support automatic
schema evolution, full support for STL collections and better run-time performance. We strongly recommend using it.
#pragma link C++ class SClass+; // add byte count
For information on
Streamers
see “Input/Output”. To get help on
rootcling
type on the UNIX command line:
rootcling -h
15.5.1.1 The Order Matters
When using template classes, the order of the pragma statements matters. For example, here is a template class
Tmpl
and a normal class Norm, which holds a specialized instance of a Tmpl:
class Norm {
private:
Tmpl<int>* fIntTmpl;
public:
...
};
Then in
Linkdef.h,
the pragma statements must be ordered by listing all specializations before any classes that need
them:
// Correct Linkdef.h ordering
...
#pragma link C++ class Tmpl<int>;
#pragma link C++ class Norm;
...
And not vice versa:
420 CHAPTER 15. ADDING A CLASS
// Bad Linkdef.h ordering
...
#pragma link C++ class Norm;
#pragma link C++ class Tmpl<int>;
...
In this case,
rootcling
generates
Norm::Streamer()
that makes reference to
Tmpl<int>::Streamer()
. Then
rootcling
gets to process
Tmpl<int>
and generates a specialized
Tmpl<int>::Streamer()
function. The prob-
lem is, when the compiler finds the first
Tmpl<int>::Streamer()
, it will instantiate it. However, later in the file it
finds the specialized version that
rootcling
generated. This causes the error. However, if the
Linkdef.h
order is
reversed then
rootcling
can generate the specialized
Tmpl<int>::Streamer()
before it is needed (and thus never
instantiated by the compiler).
15.5.1.2 Other Useful Pragma Statements
The complete list of pragma statements currently supported by Cling is:
#pragma link [C|C++|off] all [class|function|global|typedef];
#pragma link [C|C++|off]
[class|struct|union|enum|namespace|protected][name];
#pragma link [C|C++|off] [global|typedef][name];
#pragma link [C|C++|off] [nestedclass|nestedtypedef];
#pragma link [C++|C|off|MACRO] function [name]<(argtypes)>;
#pragma link
[C++|C|off|MACRO] function [classname]::[name]<(argtypes)>;
#pragma link off all methods;
#pragma link [C|C++|off] defined_in [filename];
#pragma link
[C|C++|off] defined_in [class|struct|namespace] [name];
#pragma link [C|C++|off] all_function [classname];
#pragma link [C|C++|off] all_datamember [classname];
The [classname] and the [name] can also contain wildcards. For example:
#pragma link C++ class MyClass*;
This will request the dictionary for all the class whose name start with
’MyClass’
and are already known to Cling
(class templates need to have already been instantiated to be considered).
#pragma link [C|C++|off] all [class|function|global|typedef];
This pragma statement turns on or off the dictionary generation for all classes, structures, namespaces, global variables,
global functions and typedefs seen so far by Cling. Example:
// some C++ header definition
#ifdef __ROOTCLING__
// turns off dictionary generation for all
#pragma link off all class;
#pragma link off all function;
#pragma link off all global;
#pragma link off all typedef;
#endif
The next pragma statement selectively turns on or off the dictionary generation for the specified
classs
,
struct
,
union,enum or namespace:
#pragma link
[C|C++|off][class|class+protected|
struct|union|enum|namespace][name];
15.5. ADDING A CLASS WITH A SHARED LIBRARY 421
The Dictionary of all public members of class and struct will be generated. If the ‘
class+protected
’ flag is used, the
dictionary for protected members will also be generated. However, dictionary for protected constructor and destructor
will not be generated. This ‘
class+protected
’ flag will help you only for plain protected member access, but not for
virtual function resolution.
If you use the ‘namespace’ flag, it is recommended to add also:
#pragma link nestedclass;
#pragma link nestedtypedef;
The behavior of ‘class’, ‘struct’ and ‘namespace’ flag are identical. Example:
// some C++ header definition
#ifdef __ROOTCLING__
#pragma link off all class;
#pragma link C++ class A;
#pragma link C++ class B;
#pragma link C++ class C<int>;
#pragma link C++ class+protected D;
#pragma link C++ namespace project1;
#pragma link C++ nestedclass;
#pragma link C++ nestedtypedef;
#endif
The next pragma statement selectively turns on or off the dictionary generation for global variables and typedef.
#pragma link [C|C++|off] [global|typedef] [name];
Example:
// some C/C++ header definition
#ifdef __ROOTCLING__
#pragma link off all global;
#pragma link off all typedef;
#pragma link C++ global a;
#pragma link C++ typedef Int_t;
#endif
This pragma statement turns on the dictionary generation for nested classes and nested typedefs.
#pragma link [C|C++|off] [nestedclass|nestedtypedef];
Example:
// some C/C++ header definition
#ifdef __ROOTCLING__
#pragma link off all global;
#pragma link off all typedef;
#pragma link C++ global a;
#pragma link C++ typedef Int_t;
#endif
The next pragma statements turn on or off the dictionary generation for the specified function(s) or member function(s).
The list of arguments’ type is optional. If you omit argument types, all function with specified [
name
] will be affected.
If the list of arguments’ type is specified, only the function that has exactly same argument list will be affected.
#pragma link [C++|C|off|MACRO] function [fname]<(argtypes)>;
#pragma link
[C++|C|off|MACRO] function [classname]::[fname]<(argtypes)>;
422 CHAPTER 15. ADDING A CLASS
The ‘
#pragma link [C++|C] function
’ and ‘
#pragma link MACRO function
’ behaves similarly. The ‘
#pragma link
[C++|C] function
’ assumes the target to be a real function which has pointer to it. A pointer to registered function
is registered. On the other hand, ‘
#pragma link MACRO function
’ assumes target to be macro function. Pointer to
function cannot be referenced in this case.
For the next example:
void f(int a);
void f(double a);
int g(int a,double b);
int g(double x);
#define max(a,b) (a>b?a:b)
class A {
public:
int h(double y);
int h(int a,double b);
};
The pragma statements are:
#ifdef __ROOTCLING__
#pragma link off all functions;
#pragma link C++ function f;
#pragma link C++ function g(int,double);
#pragma link C++ MACRO max;
#pragma link C++ class A;
#pragma link off function A::h(double);
#endif
Until Cling version 5.15.60, in order to generate dictionary for a member function, not only the member function but
also the class itself has to be turned on for the linkage. There was an inconvenience when generating dictionary for
template member function afterwards.
From Cling v.5.15.61, a new behavior is introduced. If link for a member function is specified, dictionary is generated
even if link to the belonging class is off. For example, if you originally have A.h as follows:
// A.h
template<class T> class A {
public:
template<class E> void f(E& x) { ... }
};
And generate dictionary for that:
#ifdef __ROOTCLING__
#pragma link C++ class A<int>;
#endif
Then prepare another header file and instantiate the template member function of A.:
// B.h
#include "A.h"
class B {
...
};
You can generate dictionary for the newly instantiated template member function only.
15.5. ADDING A CLASS WITH A SHARED LIBRARY 423
#ifdef __ROOTCLING__
#pragma link off defined_in A.h;
#pragma link C++ function A<int>::f(B&);
#endif
The next pragma turns off the dictionary generation of all the member functions in all classes.
#pragma link off all methods;
Example:
#ifdef __ROOTCLING__
#pragma link off all methods;
#endif
The next pragma statements control the linking of all the member functions or data members for a specified class.
#pragma link [C|C++|off] all_function [classname];
#pragma link [C|C++|off] all_datamember [classname];
At this moment, there should be no needs to use those statements. Example:
#ifdef __ROOTCLING__
#pragma link off all_function A;
#pragma link off all_datamember A;
#endif
See also: #pragma link function.
The next pragma statement turns on/off dictionary generation of the object defined in specific file. The filename has to
be the full pathname of the file.
#pragma link [C|C++|off] defined_in [filename];
Example:
// file1.h
// any C++ header definition
// file2.h
#ifdef __ROOTCLING__
#pragma link off all classes;
#pragma link off all functions;
#pragma link off all globals;
#pragma link off all typedef;
#pragma link C++ defined_in file1.h;
#endif
The next pragma statements turn on or off the dictionary generation of the object defined in a specific scope. The
[
scope_name
] should be
class
name,
struct
name or
namespace
name. When using these pragmas, it is recommended
to use also:
#pragma link C++ nestedclass
Otherwise, definitions in enclosed scope do not appear in the dictionary.
#pragma link [C|C++|off] defined_in [scope_name];
#pragma link [C|C++|off] defined_in
[class|struct|namespace] [scope_name];
424 CHAPTER 15. ADDING A CLASS
Example:
namespace ns {
int a;
double b;
};
The pragma statements are:
#ifdef __ROOTCLING__
#pragma link C++ defined_in ns;
#pragma link C++ nestedclass;
#endif
This statements controls default link mode for rootcling.
#pragma link default [on|off]
By turning default ‘on’, all language constructs in given header files will be included in generated Cling dictionary
(interface method source file). If default is set to ‘off’, nothing will be included in the generated dictionary. The next
statement explicitly set linkage to each item:
#pragma link [C|C++|off] [class|function|global]
This pragma statement must be given before rootcling reads any C/C++ definitions from header files. Example:
#ifdef __ROOTCLING__
#pragma link default off;
#endif
class A {
int a;
double b;
};
class B {
int d;
double e;
};
#ifdef __ROOTCLING__
#pragma link C++ class A; // only class A is linked, not B
#endif
15.5.1.2.1 Compilation Step 4:
Compile the class using the
Makefile.
In the
Makefile
call
rootcling
to make
the dictionary for the class. Call it
SClassDict.cxx
. The
rootcling
utility generates the methods
Streamer
,
TBuffer
&operator>>() and ShowMembersfor ROOT classes.
gmake -f Makefile
Load the shared library:
root[] .L SClass.so
root[] SClass *sc = new SClass()
root[] TFile *f = new TFile("Afile.root","UPDATE");
root[] sc->Write();
For more information on
rootcling
see the
$ROOTSYS/test
directory
Makefile
,
Event.cxx
, and
Event.h
for an
example, or follow this link: http://root.cern.ch/root/RootCintMan.html
15.6. GENREFLEX: A COMFORTABLE INTERFACE TO ROOTCLING 425
15.6 genreflex: A Comfortable Interface to rootcling
Version 5 supported both
Cint
and
Reflex
dictionaries. The tool to create
Reflex
dictionaries was a Python script
called
genreflex
and was very successful in the user community. Even if version 6 has only one type of dictionaries,
cling
dictionaries, a re-implementation of
genreflex
is provided. More precisely, in ROOT6,
genreflex
is nothing
but a wrapper around
rootcling
, which offers an identical CLI and behaviour to the old Python tool. The input to
genreflex
is a C++ header file, a set of switches and a selection XML file. The output, as for
rootcling
, is a C++
dictionary source and a
pcm
files. An exhaustive documentation of the CLI switches of
genreflex
can be inspected
with the genreflex --help command.
The entity corresponding to the
LinkDef
file for
genreflex
is the selection XML file, also called selection XML or
simply selection file. A selection XML file allows to describe a list of classes for which the dictionaries are to be created.
In addition, it allows to specify properties of classes or data members, without the need to add comments in the source
code. This is of primary importance when dictionaries must be created for classes residing in code which cannot be
modified. For a complete description of the structure of the selection XML files and the way in which attributes can be
set, refer to the genreflex --help command.
It is important to observe that selection XML files can be used in presence of
rootcling
invocations instead of
LinkDef
files.
15.6.1 The ROOT::Meta::Selection namespace
Not only
LinkDef
and
selection
files allow to select the classes for which the dictionaries must be created: a third
method is available. This is represented by the
ROOT::Meta::Selection
namespace. The idea behind this technique is
that all the classes which are located in this special namespace are automatically selected for dictionary generation. All
the properties and annotations allowed by
LinkDef
and
selection XML
files are possible. For a detailed documentation
of the features of the ROOT::Meta::Selection namespace, refer to its online documentation.
15.7 Adding a Class with ACLiC
Step 1: Define your class
#include "TObject.h"
// define the ABC class and make it inherit from TObject so that
// we can write ABC to a ROOT file
class ABC : public TObject {
public:
Float_t a, b, c, p;
ABC() : a(0), b(0), c(0), p(0){};
// Define the class for the dictionary
ClassDef (ABC,1)
};
// Call the ClassImp macro to give the ABC class RTTI and
// full I/O capabilities.
#if !defined(__CLING__)
ClassImp(ABC);
#endif
Step 2: Load the ABC class in the script.
// Check if ABC is already loaded
if (!TClass::GetDict("ABC")) {
gROOT->ProcessLine(".L ABCClass.C++");
}
// Use the Class
426 CHAPTER 15. ADDING A CLASS
ABC *v = new ABC;
v->p = (sqrt((v->a * v->a)+ (v->b * v->b)+(v->c * v->c)));
Chapter 16
Collection Classes
Collections are a key feature of the ROOT system. Many, if not most, of the applications you write will use collections.
If you have used parameterized C++ collections or polymorphic collections before, some of this material will be review.
However, much of this chapter covers aspects of collections specific to the ROOT system. When you have read this
chapter, you will know
•How to create instances of collections
•The difference between lists, arrays, hash tables, maps, etc.
•How to add and remove elements of a collection
•How to search a collection for a specific element
•How to access and modify collection elements
•How to iterate over a collection to access collection elements
•How to manage memory for collections and collection elements
•How collection elements are tested for equality (IsEqual())
•How collection elements are compared (Compare()) in case of sorted collections
•How collection elements are hashed (Hash()) in hash tables
16.1 Understanding Collections
A collection is a group of related objects. You will find it easier to manage a large number of items as a collection. For
example, a diagram editor might manage a collection of points and lines. A set of widgets for a graphical user interface
can be placed in a collection. A geometrical model can be described by collections of shapes, materials and rotation
matrices. Collections can themselves be placed in collections. Collections act as flexible alternatives to traditional data
structures of computers science such as arrays, lists and trees.
16.1.1 General Characteristics
The ROOT collections are polymorphic containers that hold pointers to TObjects, so:
•They can only hold objects that inherit from TObject
•They return pointers to TObjects, that have to be cast back to the correct subclass
Collections are dynamic; they can grow in size as required. Collections themselves are descendants of
TObject
so can
themselves be held in collections. It is possible to nest one type of collection inside another to any level to produce
structures of arbitrary complexity.
Collections do not own the objects they hold for the very good reason that the same object could be a member of more
than one collection. Object ownership is important when it comes to deleting objects; if nobody owns the object it
could end up as wasted memory (i.e. a memory leak) when no longer needed. If a collection is deleted, its objects are
not. The user can force a collection to delete its objects, but that is the user’s choice.
427
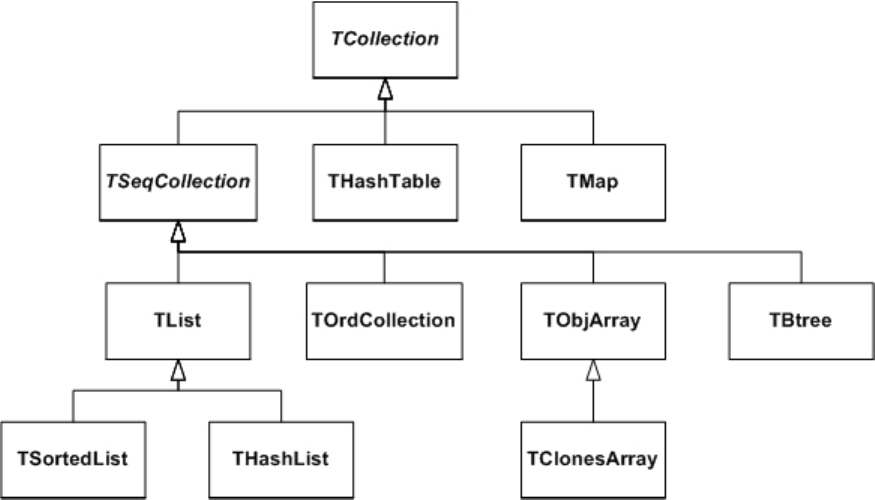
428 CHAPTER 16. COLLECTION CLASSES
16.1.2 Determining the Class of Contained Objects
Most containers may hold heterogeneous collections of objects and then it is left to the user to correctly cast the
TObject
pointer to the right class. Casting to the wrong class will give wrong results and may well crash the program!
Therefore, the user has to be very careful. Often a container only contains one class of objects, but if it really contains
a mixture, it is possible to ask each object about its class using the InheritsFrom method.
For example if myObject is a TObject pointer:
if (myObject->InheritsFrom("TParticle") {
printf("myObject is a TParticlen");
}
As the name suggests, this test works even if the object is a subclass of
TParticle
. The member function
IsA()
can
be used instead of
InheritsFrom
to make the test exact. The
InheritsFrom
and
IsA
methods use the extensive Run
Time Type Information (RTTI) available via the ROOT meta-classes.
16.1.3 Types of Collections
The ROOT system implements the following basic types of collections: unordered collections, ordered collections and
sorted collections. Next figure shows the inheritance hierarchy for the primary collection classes. All primary collection
classes derive from the abstract base class TCollection.
Figure 16.1: The inheritance hierarchy of the primary collection classes
16.1.4 Ordered Collections (Sequences)
Sequences are collections that are externally ordered because they maintain internal elements according to the order in
which they were added. The following sequences are available:
•TList
•THashList
•TOrdCollection
•TObjArray
•TClonesArray
16.2. ITERATORS: PROCESSING A COLLECTION 429
The
TOrdCollection
,
TObjArray
as well as the
TClonesArray
can be sorted using their Sort() member function (for
this, the stored objects must provide a comparison function by overriding TObject::Compare() and also must enable
sorting by overriding TObject::IsSortable() to return true). Ordered collections all derive from the abstract base class
TSeqCollection
. Sorted collections are ordered by an internal (automatic) sorting mechanism. The following sorted
collections are available (the stored items must be sortable):
•TSortedList
•TBtree
Unordered collections don’t maintain the order in which the elements were added, i.e. when you iterate over an
unordered collection, you are not likely to retrieve elements in the same order they were added to the collection. The
following unordered collections are available:
•THashTable
•TMap
16.2 Iterators: Processing a Collection
The concept of processing all the members of a collection is generic, i.e. independent of any specific representation of a
collection. To process each object in a collection one needs some type of cursor that is initialized and then steps over
each member of the collection in turn. Collection objects could provide this service but there is a snag: as there is only
one collection object per collection there would only be one cursor. Instead, to permit the use of as many cursors as
required, they are made separate classes called iterator. For each collection class there is an associated iterator class
that knows how to sequentially retrieve each member in turn. The relationship between a collection and its iterator is
very close and may require that the iterator has full access to the collection (i.e. it is a friend class). In general iterator
will be used via the TIter wrapper class. For example:
•TList TListIter
•TMap TMapIter
16.3 Foundation Classes
All collections are based on the fundamental classes:
TCollection
and
TIterator
. They are so generic that it is not
possible to create objects from them; they are only used as base classes for other classes (i.e. they are abstract base
classes).
The
TCollection
class provides the basic protocol (i.e. the minimum set of member functions) that all collection
classes have to implement. These include:
•Add Adds another object to the collection.
•GetSize Returns the number of objects in the collection.
•Clear Clears out the collection, but does not delete the removed objects.
•Delete Clears out the collection and deletes the removed objects. This should only be used
if the collection owns its objects (which are not normally the case).
•FindObject Finds an object given either its name or address.
•MakeIterator Returns an iterator associated with the collection.
•Remove Removes an object from the collection.
The code example below shows a class containing three lists, where the
fTracks
list is the owning collection and the
other two lists are used to store a sub-set of the track objects. In the destructor of the class, the method
Delete
is
called for the owning collection to delete correctly its entire track objects. To delete the objects in the container use
fTrack->Delete(). To delete the container itself, do ’delete fTracks’.
430 CHAPTER 16. COLLECTION CLASSES
class TEvent : public TObject {
private:
TList *fTracks; //list of all tracks
TList *fVertex1; //subset of tracks part of vertex1
TList *fVertex2; //subset of tracks part of vertex2
};
TEvent::~TEvent()
{
fTracks->Delete();
delete fTracks;
delete fVertex1;
delete fVertex2;
}
The TIterator class defines the minimum set of member functions that all iterators must support. These include:
•Next Returns the next member of the collection or 0 if no more members.
•Reset Resets the iterator so that Next returns the first object.
16.4 A Collectable Class
By default, all objects of
TObject
derived classes can be stored in ROOT containers. However, the
TObject
class
provides some member functions that allow you to tune the behavior of objects in containers. For example, by default
two objects are considered equal if their pointers point to the same address. This might be too strict for some classes
where equality is already achieved if some or all of the data members are equal. By overriding the following TObject
member functions, you can change the behavior of objects in collections:
•IsEqual()
is used by the
FindObject()
collection method. By default,
IsEqual()
compares the two object
pointers.
•Compare()
returns -1, 0 or 1 depending if the object is smaller, equal or larger than the other object. By default,
aTObject has not a valid Compare() method.
•IsSortable()
returns true if the class is sort able (i.e. if it has a valid
Compare(
) method). By default, a
TObject
is not sort able.
•Hash()
returns a hash value. It needs to be implemented if an object has to be stored in a collection using a
hashing technique, like
THashTable
,
THashList
and
TMap
. By default,
Hash(
) returns the address of the object.
It is essential to choose a good hash function.
The example below shows how to use and override these member functions.
class TObjNum : public TObject {
private:
Int_t num; // TObjNum is a simple container for an integer.
public:
TObjNum(Int_t i = 0) : num(i) { }
~TObjNum() { }
void SetNum(Int_t i) { num = i; }
Int_t GetNum() const {return num; }
void Print(Option_t *) const
{ printf("num = %dn", num); }
Bool_t IsEqual(TObject *obj) const
{return num == ((TObjNum*)obj)->num; }
Bool_t IsSortable() const {return kTRUE; }
Int_t Compare(const TObject *obj) const
{if (num < ((TObjNum*)obj)->num) return -1;
else if (num > ((TObjNum*)obj)->num) return 1;
else return 0; }
ULong_t Hash() const {return num; }
};
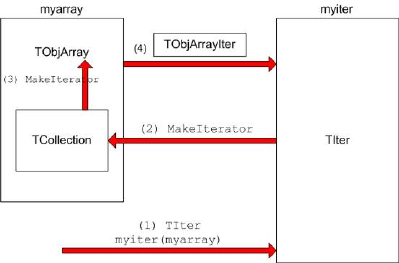
16.5. THE TITER GENERIC ITERATOR 431
16.5 The TIter Generic Iterator
As stated above, the
TIterator
class is abstract; it is not possible to create
TIterator
objects. However, it should be
possible to write generic code to process all members of a collection so there is a need for a generic iterator object. A
TIter
object acts as generic iterator. It provides the same
Next()
and
Reset()
methods as
TIterator
although it
has no idea how to support them! It works as follows:
•
To create a
TIter
object its constructor must be passed an object that inherits from
TCollection
. The
TIter
constructor calls the
MakeIterator()
method of this collection to get the appropriate iterator object that inherits
from TIterator.
•
The
Next()
and
Reset()
methods of
TIter
simply call the
Next()
and
Reset()
methods of the iterator object.
Therefore, TIter simply acts as a wrapper for an object of a concrete class inheriting from TIterator.
To see this working in practice, consider the
TObjArray
collection. Its associated iterator is
TObjArrayIter
. Suppose
myarray is a pointer to a TObjArray that contains MyClass objects, i.e.
TObjArray *myarray;
To create a TIter object called myiter:
TIter myiter(myarray);
As shown in the diagram, this results in several methods being called:
•The TIter constructor is passed a TObjArray
•TIter asks embedded TCollection to make an iterator
•TCollection asks TObjArray to make an iterator
•TObjArray returns a TObjArrayIter.
Now define a pointer for MyClass objects and set it to each member of the TObjArray:
MyClass *myobject;
while ((myobject = (MyClass *)myiter.Next())) {
// process myobject
}
The heart of this is the myiter.Next() expression which does the following:
•The Next() method of the TIter object myiter is called
•The TIter forwards the call to the TIterator embedded in the TObjArrayIter
•TIterator forwards the call to the TObjArrayIter
•TObjArrayIter finds the next MyClass object and returns it
•TIter passes the MyClass object back to the caller
Sometimes the
TIter
object is called next, and then instead of writing:
next.Next()
which is legal, but looks rather
odd, iteration is written as next(). This works because the function operator() is defined for the TIter class to be
equivalent to the Next() method.
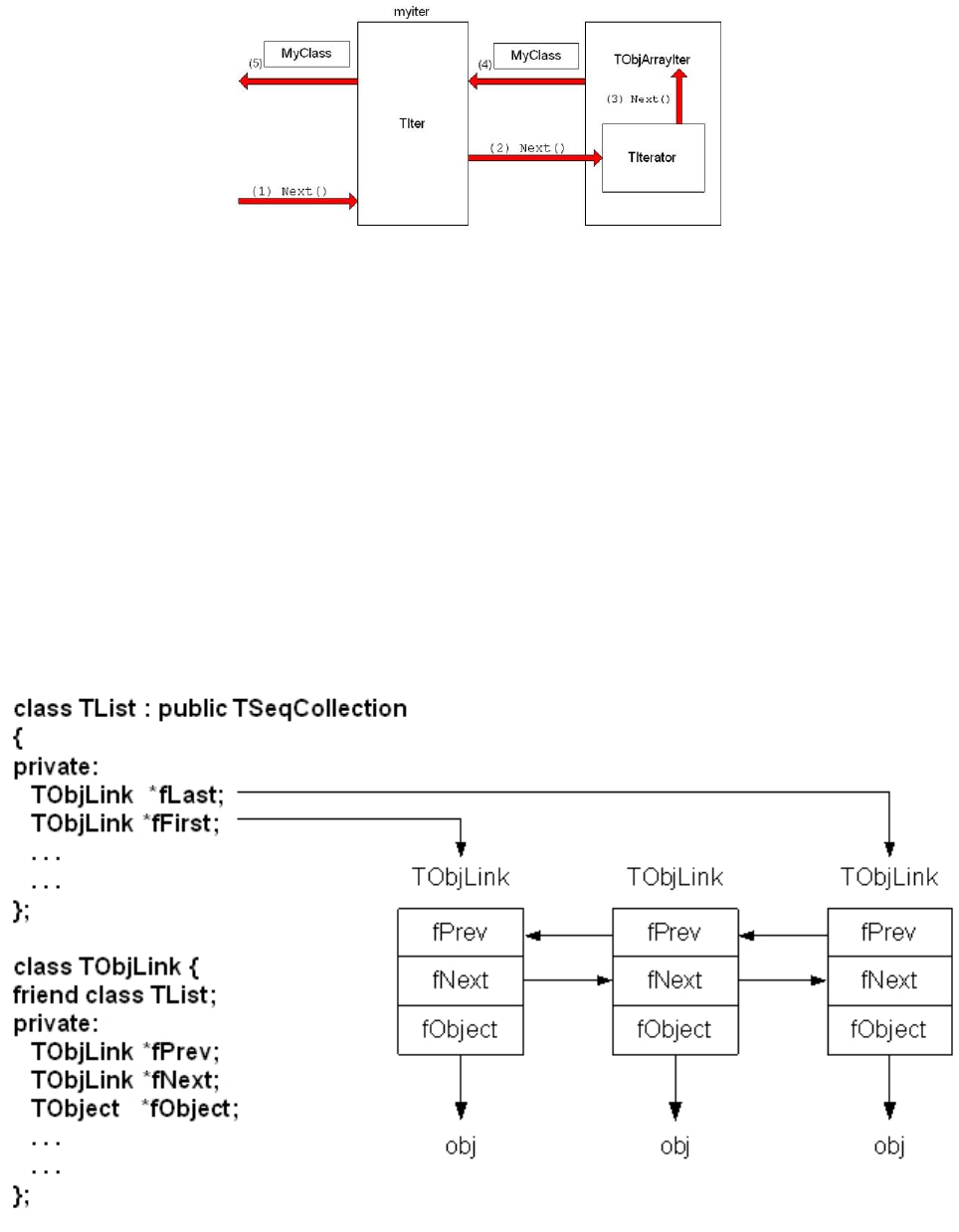
432 CHAPTER 16. COLLECTION CLASSES
16.6 The TList Collection
A
TList
is a doubly linked list. Before being inserted into the list the object pointer is wrapped in a
TObjLink
object
that contains, besides the object pointer also a previous and next pointer.
Objects are typically added using:
•Add()
•AddFirst(), AddLast()
•AddBefore(), AddAfter()
Main features ofTList: very low cost of adding/removing elements anywhere in the list.
Overhead per element: 1 TObjLink, i.e. two 4 (or 8) byte pointers + pointer to vtable = 12 (or 24) bytes.
Next figure shows the internal data structure of a TList.
Figure 16.2: The internal data structure of a TList
16.6.1 Iterating Over a TList
There are four ways to iterate over a TList:
•Using the ForEach script:
GetListOfPrimitives()->ForEach(TObject,Draw)();
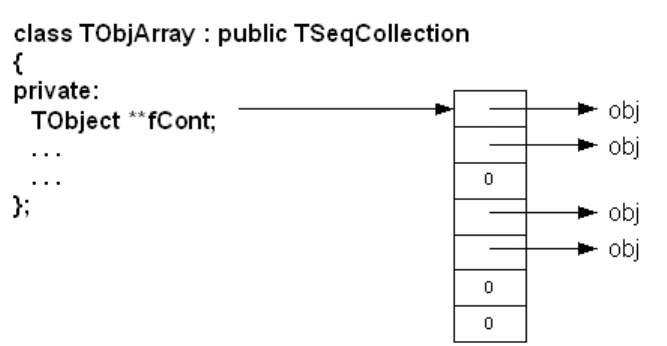
16.7. THE TOBJARRAY COLLECTION 433
•Using the TList iterator TListIter (via the wrapper class TIter):
TIter next(GetListOfTracks());
while ((TTrack *obj = (TTrack *)next()))
obj->Draw();
•Using the TObjLink list entries (that wrap the TObject*):
TObjLink *lnk = GetListOfPrimitives()->FirstLink();
while (lnk) {
lnk->GetObject()->Draw();
lnk = lnk->Next();
}
•Using the TList’s After() and Before() member functions:
TFree *idcur = this;
while (idcur) {
...
idcur = (TFree*)GetListOfFree()->After(idcur);
}
Method 1 uses internally method 2.
Method 2 works for all collection classes. TIter overloads operator().
Methods 3 and 4 are specific for TList.
Methods 2, 3 and 4 can also easily iterate backwards using either a backward
TIter
(using argument
kIterBackward
)
or by using LastLink() and lnk>Prev() or by using the Before() method.
16.7 The TObjArray Collection
A
TObjArray
is a collection which supports traditional array semantics via the overloading of
operator[]
. Objects
can be directly accessed via an index. The array expands automatically when objects are added. At creation time one
specifies the default array size (default = 16) and lower bound (default = 0). Resizing involves a re-allocation and a
copy of the old array to the new. This can be costly if done too often. If possible, set initial size close to expected
final size. Index validity is always checked (if you are 100% sure and maximum performance is needed you can use
UnCheckedAt()
instead of
At()
or
operator[]
). If the stored objects are sort able the array can be sorted using
Sort()
. Once sorted, efficient searching is possible via the
BinarySearch()
method. The figure shows the internal
data structure of a TObjArray:
Figure 16.3: The internal data structure of a TObjArray
Iterating can be done using a TIter iterator or via a simple for loop:
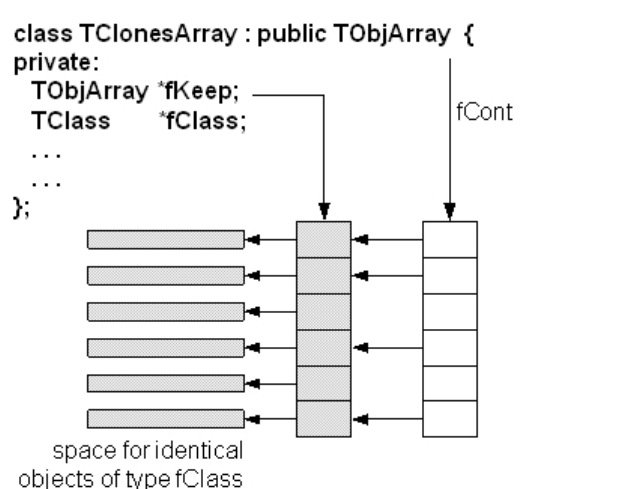
434 CHAPTER 16. COLLECTION CLASSES
for (int i=0; i <= fArr.GetLast(); i++)
if ((track = (TTrack*)fArr[i])) // or fArr.At(i)
track->Draw();
Main features of
TObjArray
are simple, well-known array semantics.
Overhead per element
: none, except possible
over sizing of fCont.
16.8 TClonesArray An Array of Identical Objects
A
TClonesArray
is an array of identical (clone) objects. The memory for the objects stored in the array is allocated
only once in the lifetime of the clones array. All objects must be of the same class. For the rest this class has the same
properties as a TObjArray.
Figure 16.4: The internal data structure of a TClonesArray
The figure above shows the internal data structure of a
TClonesArray
. The class is specially designed for repetitive
data analysis tasks, where in a loop many times the same objects, are created and deleted. The only supported way to
add objects to a
TClonesArray
is via the
new
with placement method. The different
Add()
methods of
TObjArray
and its base classes are not supported.
16.8.1 The Idea Behind TClonesArray
To reduce the very large number of new and delete calls in large loops like this (O(100000) x O(10000) times new/delete):
TObjArray a(10000);
while (TEvent *ev = (TEvent *)next()) { // O(100000)
for (int i=0; i < ev->Ntracks; i++) { // O(10000)
a[i] = new TTrack(x,y,z,...);
...
}
...
a.Delete();
}
You better use a TClonesArray which reduces the number of new/delete calls to only O(10000):
TClonesArray a("TTrack",10000);
while (TEvent *ev = (TEvent *)next()) { // O(100000)
16.9. TEMPLATE CONTAINERS AND STL 435
for (int i=0; i < ev->Ntracks; i++) { // O(10000)
TTrack *track = (Track*)a.ConstructedAt(i);
track->Set(x,y,z,...);
...
}
...
a.Clear(); // Or Clear("C") if the track objects must be returned (via Track::Clear) to a default state.
}
Considering that a pair of new/delete calls on average cost about 70 ms, O(109) new/deletes will save about 19 hours.
For the other collections, see the class reference guide on the web and the test program
$ROOTSYS/test/tcollex.cxx.
16.9 Template Containers and STL
Some people dislike polymorphic containers because they are not truly “type safe”. In the end, the compiler leaves it
the user to ensure that the types are correct. This only leaves the other alternative: creating a new class each time a
new (container organization) / (contained object) combination is needed. To say the least this could be very tedious.
Most people faced with this choice would, for each type of container:
Define the class leaving a dummy name for the contained object type. When a particular container was needed, copy
the code and then do a global search and replace for the contained class. C++ has a built in template scheme that
effectively does just this. For example:
template<class T>
class ArrayContainer {
private:
T *member[10];
...
};
This is an array container with a 10-element array of pointers to T, it could hold up to 10 T objects. This array is
flawed because it is static and hard-coded, it should be dynamic. However, the important point is that the template
statement indicates that T is a template, or parameterized class. If we need an
ArrayContainer
for Track objects, it
can be created by:
ArrayContainer<Track> MyTrackArrayContainer;
C++ takes the parameter list and substitutes Track for T throughout the definition of the class
ArrayContainer
, then
compiles the code so generated, effectively doing the same we could do by hand, but with a lot less effort.
This produces code that is type safe, but does have different drawbacks:
•Templates make code harder to read.
•At the time of writing this documentation, some compilers can be very slow when dealing with templates.
•It does not solve the problem when a container has to hold a heterogeneous set of objects.
•
The system can end up generating a great deal of code; each container/object combination has its own code, a
phenomenon that is sometimes referred to as code bloat.
•The Standard Template Library (STL) is part on ANSI C++, and includes a set of template containers.
436 CHAPTER 16. COLLECTION CLASSES

Chapter 17
Physics Vectors
The physics vector classes describe vectors in three and four dimensions and their rotation algorithms. The classes
were ported to root from CLHEP see:
http://wwwinfo.cern.ch/asd/lhc++/clhep/manual/UserGuide/Vector/vector.html
17.1 The Physics Vector Classes
In order to use the physics vector classes you will have to load the Physics library:
gSystem.Load("libPhysics.so");
There are four classes in this package. They are:
TVector3
is a general three-vector. A
TVector3
may be expressed in Cartesian, polar, or cylindrical coordinates.
Methods include dot and cross products, unit vectors and magnitudes, angles between vectors, and rotations and
boosts. There are also functions of particular use to HEP, like pseudo-rapidity, projections, and transverse part of a
TVector3, and kinetic methods on 4-vectors such as Invariant Mass of pairs or containers of particles.
TLorentzVector
is a general four-vector class, which can be used either for the description of position and time (
x
,
y
,
z
,
t
) or momentum and energy (
px
,
py
,
pz
,
E
).
TRotation
is a class describing a rotation of a
TVector3
object.
TLorentzRotation
is a class to describe the Lorentz transformations including Lorentz boosts and rotations. In
addition, a
TVector2
is a basic implementation of a vector in two dimensions and is not part of the CLHEP translation.
17.2 TVector3
TVector3
is a general three-vector class, which can be used for description of different vectors in 3D. Components of
three vectors:
•x,y,z= basic components
•θ= azimuth angle
•φ= polar angle
•magnitude = mag =px2+y2+z2
•transverse component = perp =px2+y2
Using the
TVector3
class, you should remember that it contains only common features of three vectors and lacks
methods specific for some particular vector values. For example, it has no translated function because translation has
no meaning for vectors.
437
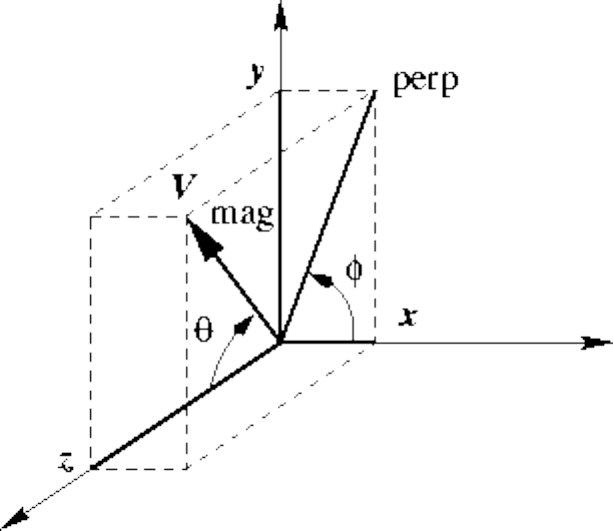
438 CHAPTER 17. PHYSICS VECTORS
17.2.1 Declaration / Access to the Components
TVector3
has been implemented as a vector of three
Double_t
variables, representing the Cartesian coordinates. By
default the values are initialized to zero, however you can change them in the constructor:
TVector3 v1; // v1 = (0,0,0)
TVector3 v2(1); // v2 = (1,0,0)
TVector3 v3(1,2,3); // v3 = (1,2,3)
TVector3 v4(v2); // v4 = v2
It is also possible (but not recommended) to initialize a
TVector3
with a
Double_t
or
Float_t C
array. You can get
the components by name or by index:
xx = v1.X(); or xx = v1(0);
yy = v1.Y(); yy = v1(1);
zz = v1.Z(); zz = v1(2);
The methods SetX(),SetY(),SetZ() and SetXYZ() allow you to set the components:
v1.SetX(1.); v1.SetY(2.); v1.SetZ(3.);
v1.SetXYZ(1.,2.,3.);
17.2.2 Other Coordinates
To get information on the
TVector3
in spherical (
rho
,
phi
,
theta
) or cylindrical (
z
,
r
,
theta
) coordinates, the following
methods can be used.
Double_t m = v.Mag();
// get magnitude (=rho=Sqrt(x*x+y*y+z*z)))
Double_t m2 = v.Mag2(); // get magnitude squared
Double_t t = v.Theta(); // get polar angle
Double_t ct = v.CosTheta();// get cos of theta
Double_t p = v.Phi(); // get azimuth angle
Double_t pp = v.Perp(); // get transverse component
Double_t pp2= v.Perp2(); // get transverse squared
It is also possible to get the transverse component with respect to another vector:
17.2. TVECTOR3 439
Double_t ppv1 = v.Perp(v1);
Double_t pp2v1 = v.Perp2(v1);
The pseudo-rapidity (eta = -ln (tan (theta/2))) can be obtained by Eta() or PseudoRapidity():
Double_t eta = v.PseudoRapidity();
These setters change one of the non-Cartesian coordinates:
v.SetTheta(.5); // keeping rho and phi
v.SetPhi(.8); // keeping rho and theta
v.SetMag(10.); // keeping theta and phi
v.SetPerp(3.); // keeping z and phi
17.2.3 Arithmetic / Comparison
The TVector3 class has operators to add, subtract, scale and compare vectors:
v3 = -v1;
v1 = v2+v3;
v1 += v3;
v1 = v1 - v3;
v1 -= v3;
v1 *= 10;
v1 = 5*v2;
if(v1 == v2) {...}
if(v1 != v2) {...}
17.2.4 Related Vectors
v2 = v1.Unit(); // get unit vector parallel to v1
v2 = v1.Orthogonal(); // get vector orthogonal to v1
17.2.5 Scalar and Vector Products
s = v1.Dot(v2); // scalar product
s = v1 * v2; // scalar product
v = v1.Cross(v2); // vector product
17.2.6 Angle between Two Vectors
Double_t a = v1.Angle(v2);
17.2.7 Rotation around Axes
v.RotateX(.5);
v.RotateY(TMath::Pi());
v.RotateZ(angle);
17.2.8 Rotation around a Vector
v1.Rotate(TMath::Pi()/4, v2); // rotation around v2
440 CHAPTER 17. PHYSICS VECTORS
17.2.9 Rotation by TRotation Class
TVector3
objects can be rotated by
TRotation
objects using the
Transform()
method, the operator
*=
, or the operator
*of the TRotation class. See the later section on TRotation.
TRotation m;
...
v1.Transform(m);
v1 = m*v1;
v1 *= m; // v1 = m*v1
17.2.10 Transformation from Rotated Frame
This code transforms v1 from the rotated frame (z’ parallel to direction, x’ in the theta plane and y’ in the
xy
plane as
well as perpendicular to the theta plane) to the (x, y, z) frame.
TVector3 direction = v.Unit()
v1.RotateUz(direction); // direction must be TVector3 of unit length
17.3 TRotation
The TRotation class describes a rotation of TVector3 object. It is a 3 * 3 matrix of Double_t:
xx xy xz
yx yy yz
zx zy zz
It describes a so-called active rotation, i.e. a rotation of objects inside a static system of coordinates. In case you want
to rotate the frame and want to know the coordinates of objects in the rotated system, you should apply the inverse
rotation to the objects. If you want to transform coordinates from the rotated frame to the original frame you have
to apply the direct transformation. A rotation around a specified axis means counterclockwise rotation around the
positive direction of the axis.
17.3.1 Declaration, Access, Comparisons
TRotation r; // r initialized as identity
TRotation m(r); //m=r
There is no direct way to set the matrix elements - to ensure that a
TRotation
always describes a real rotation. But
you can get the values by with the methods XX()..ZZ() or the (,) operator:
Double_t xx = r.XX(); // the same as xx=r(0,0)
xx = r(0,0);
if (r==m) {...} // test for equality
if (r!=m) {..} // test for inequality
if (r.IsIdentity()) {...} // test for identity
17.3.2 Rotation around Axes
The following matrices describe counter-clockwise rotations around the coordinate axes and are implemented in:
RotateX(),RotateY() and RotateZ():
Rx(a) =
1 0 0
0cos(a)−sin(a)
0sin(a)cos(a)
Ry(a) =
cos(a) 0 sin(a)
0 1 0
−sin(a) 0 cos(a)
Rz(a) =
cos(a)−sin(a) 0
sin(a)cos(a) 0
0 0 1
r.RotateX(TMath::Pi()); // rotation around the x-axis
17.3. TROTATION 441
17.3.3 Rotation around Arbitrary Axis
The
Rotate()
method allows you to rotate around an arbitrary vector (not necessary a unit one) and returns the
result.
r.Rotate(TMath::Pi()/3,TVector3(3,4,5));
It is possible to find a unit vector and an angle, which describe the same rotation as the current one:
Double_t angle;
TVector3 axis;
r.GetAngleAxis(angle,axis);
17.3.4 Rotation of Local Axes
The RotateAxes()method adds a rotation of local axes to the current rotation and returns the result:
TVector3 newX(0,1,0);
TVector3 newY(0,0,1);
TVector3 newZ(1,0,0);
a.RotateAxes(newX,newX,newZ);
Methods
ThetaX()
,
ThetaY()
,
ThetaZ()
,
PhiX()
,
PhiY()
,
PhiZ()
return azimuth and polar angles of the rotated
axes:
Double_t tx,ty,tz,px,py,pz;
tx= a.ThetaX();
...
pz= a.PhiZ();
17.3.5 Inverse Rotation
TRotation a,b;
...
b = a.Inverse();// b is inverse of a, a is unchanged
b = a.Invert();// invert a and set b = a
17.3.6 Compound Rotations
The
operator *
has been implemented in a way that follows the mathematical notation of a product of the two
matrices which describe the two consecutive rotations. Therefore, the second rotation should be placed first:
r = r2 * r1;
17.3.7 Rotation of TVector3
The
TRotation
class provides an
operator *
which allows expressing a rotation of a
TVector3
analog to the
mathematical notation:
x0
y0
z0
=
xx xy xz
yx yy yz
zx zy zz ×
x
y
z
TRotation r;
TVector3 v(1,1,1);
v=r*v;
You can also use the Transform() method or the operator *= of the TVector3 class:
TVector3 v;
TRotation r;
v.Transform(r);
442 CHAPTER 17. PHYSICS VECTORS
17.4 TLorentzVector
TLorentzVector
is a general four-vector class, which can be used either for the description of position and time (
x
,
y
,
z,t) or momentum and energy (px,py,pz,E).
17.4.1 Declaration
TLorentzVector
has been implemented as a set a
TVector3
and a
Double_t
variable. By default, all components are
initialized by zero.
TLorentzVector v1; // initialized by (0.,0.,0.,0.)
TLorentzVector v2(1.,1.,1.,1.);
TLorentzVector v3(v1);
TLorentzVector v4(TVector3(1.,2.,3.),4.);
For backward compatibility there are two constructors from a Double_t and Float_t array.
17.4.2 Access to Components
There are two sets of access functions to the components of a
TLorentzVector
:
X()
,
Y()
,
Z()
,
T()
and
Px()
,
Py()
,
Pz()
and
E()
. Both sets return the same values but the first set is more relevant for use where
TLorentzVector
describes a combination of position and time and the second set is more relevant where
TLorentzVector
describes
momentum and energy:
Double_t xx =v.X();
...
Double_t tt = v.T();
Double_t px = v.Px();
...
Double_t ee = v.E();
The components of TLorentzVector can also accessed by index:
xx = v(0);orxx = v[0];
yy = v(1);yy = v[1];
zz = v(2);zz = v[2];
tt = v(3);tt = v[3];
You can use the Vect() method to get the vector component of TLorentzVector:
TVector3 p = v.Vect();
For setting components there are two methods: SetX(),.., SetPx(),..:
v.SetX(1.); orv.SetPx(1.);
......
v.SetT(1.);v.SetE(1.);
To set more the one component by one call you can use the
SetVect()
function for the
TVector3
part or
SetXYZT()
,
SetPxPyPzE(). For convenience there is also a SetXYZM():
v.SetVect(TVector3(1,2,3));
v.SetXYZT(x,y,z,t);
v.SetPxPyPzE(px,py,pz,e);
v.SetXYZM(x,y,z,m); // v = (x,y,z,e = Sqrt(x*x+y*y+z*z+m*m))
17.4. TLORENTZVECTOR 443
17.4.3 Vector Components in Non-Cartesian Coordinates
There are a couple of methods to get and set the TVector3 part of the parameters in spherical coordinate systems:
Double_t m, theta, cost, phi, pp, pp2, ppv2, pp2v2;
m = v.Rho();
t = v.Theta();
cost = v.CosTheta();
phi = v.Phi();
v.SetRho(10.);
v.SetTheta(TMath::Pi()*.3);
v.SetPhi(TMath::Pi());
or get information about the r-coordinate in cylindrical systems:
Double_t pp, pp2, ppv2, pp2v2;
pp = v.Perp(); // get transverse component
pp2 = v.Perp2(); // get transverse component squared
ppv2 = v.Perp(v1); // get transverse component with respect
// to another vector
pp2v2 = v.Perp(v1);
there are two more set functions SetPtEtaPhiE(pt,eta,phi,e) and SetPtEtaPhiM(pt,eta,phi,m) for convenience.
17.4.4 Arithmetic and Comparison Operators
The TLorentzVector class provides operators to add subtract or compare four-vectors:
v3 = -v1;
v1 = v2+v3;
v1+= v3;
v1 = v2 + v3;
v1-= v3;
if (v1 == v2) {...}
if (v1 != v3) {...}
17.4.5 Magnitude/Invariant mass, beta, gamma, scalar product
The scalar product of two four-vectors is calculated with the (-,-,-,+)metric:
s = v1*v2 = t1*t2-x1*x2-y1*y2-z1*z2
The magnitude squared mag2 of a four-vector is therefore:
mag2 = v*v = t*t-x*x-y*y-z*z
If mag2 is negative: mag = -Sqrt(-mag*mag). The methods are:
Double_t s, s2;
s = v1.Dot(v2);// scalar product
s = v1*v2;// scalar product
s2 = v.Mag2();ors2 = v.M2();
s = v.Mag();s = v.M();
Since in case of momentum and energy the magnitude has the meaning of invariant mass
TLorentzVector
pro-
vides the more meaningful aliases
M2()
and
M()
. The methods
Beta()
and
Gamma()
returns
beta
and
gamma =
1/Sqrt(1-beta*beta).
444 CHAPTER 17. PHYSICS VECTORS
17.4.6 Lorentz Boost
A boost in a general direction can be parameterized with three parameters which can be taken as the components of a
three vector
b=(bx,by,bz)
. With
x=(x,y,z)
and
gamma=1/Sqrt(1-beta*beta)
(beta being the module of vector b)
,
an arbitrary active Lorentz boost transformation (from the rod frame to the original frame) can be written as:
x = x’ + (gamma-1)/(beta*beta)*(b*x’)*b + gamma*t’*b
t = gamma(t’+ b*x’)
The
Boost()
method performs a boost transformation from the rod frame to the original frame.
BoostVector()
returns a TVector3 of the spatial components divided by the time component:
TVector3 b;
v.Boost(bx,by,bz);
v.Boost(b);
b = v.BoostVector();// b=(x/t,y/t,z/t)
17.4.7 Rotations
There are four sets of functions to rotate the TVector3 component of a TLorentzVector:
Around Axes:
v.RotateX(TMath::Pi()/2.);
v.RotateY(.5);
v.RotateZ(.99);
Around an arbitrary axis:
v.Rotate(TMath::Pi()/4., v1); // rotation around v1
Transformation from rotated frame:
v.RotateUz(direction); // direction must be a unit TVector3
Rotation by TRotation:
TRotation r;
v.Transform(r);//or v *= r; (v = r*v)
17.4.8 Miscellaneous
Angle between two vectors:
Double_t a = v1.Angle(v2);// get angle between v1 and v2
Methods Plus() and Minus() return the positive and negative light-cone components:
Double_t pcone = v.Plus();
Double_t mcone = v.Minus();
A general Lorentz transformation (see class
TLorentzRotation)
can be used by the
Transform()
method, the
*=, or
*operator of the TLorentzRotation class:
TLorentzRotation l;
v.Transform(l);
v = l*v;orv *= l;// v = l*v
17.5. TLORENTZROTATION 445
17.5 TLorentzRotation
The
TLorentzRotation
class describes Lorentz transformations including Lorentz boosts and rotations (see
TRotation
)
lambda =
xx xy xz xt
yx yy yz yt
zx zy zz zt
tx ty tz tt
17.5.1 Declaration
By default it is initialized to the identity matrix, but it may also be initialized by other
TLorentzRotation
, by a pure
TRotation or by a boost:
TLorentzRotation l; // l is initialized as identity
TLorentzRotation m(l);//m=l
TRotation r;
TLorentzRotation lr(r);
TLorentzRotation lb1(bx,by,bz);
TVector3 b;
TLorentzRotation lb2(b);
The Matrix for a Lorentz boosts is:
1 + gamma0∗bx ∗bx gamma0∗bx ∗by gamma0∗bx ∗bz gamma ∗bx
gamma0∗bx ∗bz 1 + gamma0∗by ∗by gamma0∗by ∗by gamma ∗by
gamma0∗bz ∗bx gamma0∗bz ∗by 1 + gamma0∗bz ∗bz gamma ∗bz
gamma ∗bx gamma ∗by gamma ∗bz gamma
with the boost vector b=(bx,by,bz);gamma=1/Sqrt(1-beta*beta);gamma’=(gamma-1)/beta*beta.
17.5.2 Access to the Matrix Components/Comparisons
The access to the matrix components is possible with the methods
XX()
,
XY()
...
TT()
, and with the operator
(int,int)
:
Double_t xx;
TLorentzRotation l;
xx = l.XX(); // gets the xx component
xx = l(0,0); // gets the xx component
if (l == m) {...} // test for equality
if (l != m) {...} // test for inequality
if (l.IsIdentity()) {...} // test for identity
17.5.3 Transformations of a Lorentz Rotation
There are four possibilities to find the product of two TLorentzRotation transformations:
TLorentzRotation a,b,c;
c = b*a; // product
c = a.MatrixMultiplication(b); // a is unchanged
a *= b; // a=a*b
c = a.Transform(b) // a=b*a then c=a
Lorentz boosts:
Double_t bx, by, bz;
TVector3 v(bx,by,bz);
TLorentzRotation l;
l.Boost(v);
l.Boost(bx,by,bz);
446 CHAPTER 17. PHYSICS VECTORS
Rotations:
TVector3 axis;
l.RotateX(TMath::Pi()); // rotation around x-axis
l.Rotate(.5,axis); // rotation around specified vector
Inverse transformation: use the method
Inverse()
to return the inverse transformation keeping the current one
unchanged.The method Invert() inverts the current TLorentzRotation:
l1 = l2.Inverse(); // l1 is inverse of l2, l2 unchanged
l1 = l2.Invert(); // invert l2, then l1=l2
The matrix for the inverse transformation of a TLorentzRotation is as follows:
xx xy xz −tx
yx yy yz −ty
zx zy zz −tz
−xt −yt −zt tt
17.5.4 Transformation of a TLorentzVector
To apply
TLorentzRotation
to
TLorentzVector
you can use either the
VectorMultiplication()
method or the
*
operator. You can also use the Transform() function and the *=operator of the class TLorentzVector.
TLorentzVector v;
TLorentzRotation l;
...
v = l.VectorMultiplication(v);
v=l*v;
v.Transform(l);
v *= l; // v = l*v
17.5.5 Physics Vector Example
The test file
$ROOTSYS/test/TestVectors.cxx is
an example of using physics vectors. The vector classes are not
loaded by default, and to run it, you will need to load libPhysics.so first:
root[] .L $ROOTSYS/lib/libPhysics.so
root[] .x TestVectors.cxx
To load the physics vector library in a ROOT application use:
gSystem->Load("libPhysics");
The example
$ROOTSYS/test/TestVectors.cxx
does not return much, especially if all went well, but when you look
at the code you will find examples for many calls.
Chapter 18
The Geometry Package
The new ROOT geometry package is a tool for building, browsing, navigating and visualizing detector geometries. The
code works standalone with respect to any tracking Monte-Carlo engine; therefore, it does not contain any constraints
related to physics. However, the navigation features provided by the package are designed to optimize particle transport
through complex geometries, working in correlation with simulation packages such as GEANT3, GEANT4 and FLUKA.
18.1 Quick Start: Creating the “world”
This chapter will provide a detailed description on how to build valid geometries as well as the ways to optimize them.
There are several components gluing together the geometrical model, but for the time being let us get used with the
most basic concepts.
The basic bricks for building-up the model are called
volumes.
These represent the un-positioned pieces of the geometry
puzzle. The difference is just that the relationship between the pieces is not defined by neighbors, but by
containment
.
In other words, volumes are put one inside another making an in-depth hierarchy. From outside, the whole thing looks
like a big pack that you can open finding out other smaller packs nicely arranged waiting to be opened at their turn.
The biggest one containing all others defines the “
world
” of the model. We will often call this
master reference
system (MARS)
. Going on and opening our packs, we will obviously find out some empty ones, otherwise, something is
very wrong. . . We will call these leaves (by analogy with a tree structure).
On the other hand, any volume is a small world by itself - what we need to do is to take it out and to ignore all the
rest since it is a self-contained object. In fact, the modeller can act like this, considering a given volume as temporary
MARS, but we will describe this feature later on. Let us focus on the biggest pack - it is mandatory to define one.
Consider the simplest geometry that is made of a single box. Here is an example on how to build it:
18.1.1 Example 1: Creating the World
We first need to load the geometry library. This is not needed if one does make map in root folder.
root[] gSystem->Load("libGeom");
Second, we have to create an instance of the geometry manager class. This takes care of all the modeller components,
performing several tasks to insure geometry validity and containing the user interface for building and interacting with
the geometry. After its creation, the geometry manager class can be accessed with the global gGeoManager :
root[] new TGeoManager("world","the simplest geometry");
We want to create a single volume in our geometry, but since any volume needs to have an associated medium, we will
create a dummy one. You can safely ignore the following lines for the time being, since materials and media will be
explained in detail later on.
root[] TGeoMaterial *mat = new TGeoMaterial("Vacuum",0,0,0);
root[] TGeoMedium *med = new TGeoMedium("Vacuum",1,mat);
447
448 CHAPTER 18. THE GEOMETRY PACKAGE
We can finally make our volume having a box shape. Note that the world volume does not need to be a box - it can be
any other shape. Generally, boxes and tubes are the most recommendable shapes for this purpose due to their fast
navigation algorithms.
root[] TGeoVolume *top=gGeoManager->MakeBox("Top",med,10.,10.,10.);
The default units are in centimeters. Now we want to make this volume our world. We have to do this operation
before closing the geometry.
root[] gGeoManager->SetTopVolume(top);
This should be enough, but it is not since always after defining some geometry hierarchy,
TGeo
needs to build some
optimization structures and perform some checks. Note the messages posted after the statement is executed. We will
describe the corresponding operations later.
root[] gGeoManager->CloseGeometry();
Now we are really done with geometry building stage, but we would like to see our simple world:
root[] top->SetLineColor(kMagenta);
root[] gGeoManager->SetTopVisible(); // the TOP is invisible
root[] top->Draw();
18.1.2 Example 2: A Geometrical Hierarchy Look and Feel
Before going further, let us get a look and feel of interacting with the modeller. For this, we will use one of the examples
illustrating the geometry package. To get an idea on the geometry structure created in this example, just look at the
link: http://root.cern.ch/root/html/tutorials/geom/rootgeom.C.html. You will notice that this is a bit more complex
that just creating the “world” since several other volumes are created and put together in a hierarchy. The purpose
here is just to learn how to interact with a geometry that is already built, but just few hints on the building steps in
this example might be useful. The geometry here represents the word ROOT that is replicated in some symmetric
manner. You might for instance ask some questions after having a first look:
Q: "OK, I understand the first lines that load the libGeom library and create a geometry manager
object. I also recognize from the previous example the following lines creating some materials
and media, but what about the geometrical transformations below?"
A:
As explained before, the model that we are trying to create is a hierarchy of volumes based on
containment
. This
is accomplished by
positioning
some volumes
inside
others. Any volume is an un-positioned object in the sense
that it defines only a
local frame
(matching the one of its
shape
). In order to fully define the mother-daughter
relationship between two volumes one has to specify how the daughter will be positioned inside. This is accomplished
by defining a
local geometrical transformation
of the daughter with respect to the mother coordinate system.
These transformations will be subsequently used in the example.
Q: "I see the lines defining the top level volume as in the previous example, but what about the
other volumes named REPLICA and ROOT?"
A: You will also notice that several other volumes are created by using lines like:
TGeoVolume *someVolume = gGeoManager->MakeXXX("someName",
ptrMedium, /* parameters coresponding to XXX ...*/ )
In the method above
XXX
represent some shape name (Box, Tube, etc.). This is just a simple way of creating a volume
having a given shape in one-step (see also section: “Creating and Positioning Volumes”). As for REPLICA and ROOT
volumes, they are just some
virtual volumes
used for grouping and positioning together other
real volumes
. See
“Positioned Volumes (Nodes)”. The same structure represented by (a real or) a virtual volume can be
replicated
several times in the geometry.
Q: "Fine, so probably the real volumes are the ones composing the letters R, O and T. Why one
have to define so many volumes to make an R?"
A:
Well, in real life some objects have much more complex shapes that an
R
. The modeller cannot just know all of them;
the idea is to make a complex object by using elementary building blocks that have known shapes (called
primitive
shapes ). Gluing these together in the appropriate way is the user responsibility.
18.1. QUICK START: CREATING THE “WORLD” 449
Q: "I am getting the global picture but not making much out of it... There are also a lot of
calls to TGeoVolume::AddNode() that I do not understand."
A:
A volume is positioned inside another one by using this method. The relative geometrical transformation as
well as a copy number must be specified. When positioned, a volume becomes a
node
of its container and a new
object of the class
TGeoNode
is automatically created. This method is therefore the key element for the creation of a
hierarchical link between two volumes. As it will be described further on in this document, there are few other methods
performing similar actions, but let us keep things simple for the time being. In addition, notice that there are some
visualization-related calls in the example followed by a final
TGeoVolume::Draw()
call for the top volume. These are
explained in details in the section “Visualization Settings and Attributes”. At this point, you will probably like to see
how this geometry looks like. You just need to run the example and you will get the following picture that you can
rotate using the mouse; or you can zoom / move it around (see what the Help menu of the GL window displays).
% root rootgeom.C
Now let us browse the hierarchy that was just created. Start a browser and double-click on the item simple1 representing
the
gGeoManager
object. Note that right click opens the context menu of the manager class where several global
methods are available.
root[] new TBrowser;
The folders
Materials
,
Media
and
Local transformations
are in fact the containers where the geometry manager
stores the corresponding objects. The
Illegal overlaps
folder is empty but can be filled after performing a geometry
validity check (see section: “Checking the Geometry”). If tracking is performed using
TGeo
, the folder
Tracks
might
contain user-defined tracks that can be visualized/animated in the geometry context (see section: “Creating and
Visualizing Tracks”). Since for the time being we are interested more in the geometrical hierarchy, we will focus on the
last two displayed items TOPand TOP_1. These are the top volume and the corresponding top node in the hierarchy.
Double clicking on the
TOP
volume will unfold all different volumes contained by the top volume. In the right panel, we
will see all the volumes contained by
TOP
(if the same is positioned 4 times we will get 4 identical items). This rule will
apply to any clicked volume in the hierarchy. Note that right clicking a volume item activates the volume context
menu containing several specific methods. We will call the volume hierarchy developed in this way as the
logical
geometry graph
. The volume objects are nodes inside this graph and the same volume can be accessed starting from
different branches.
450 CHAPTER 18. THE GEOMETRY PACKAGE
On the other hand, the real geometrical objects that are seen when visualizing or tracking the geometry are depicted in
the
TOP_1
branch. These are the nodes of the
physical tree
of positioned volumes represented by
TGeoNode
objects.
This hierarchy is a tree since a node can have only one parent and several daughters. For a better understanding of the
hierarchy, have a look at http://root.cern.ch/root/htmldoc/TGeoManager.html.
Just close now the
X3D
window and focus at the wire frame picture drawn in a pad. Activate Options/Event Status.
Moving the mouse in the pad, you will notice that objects are sometimes changing color to red. Volumes are highlighted
in this way whenever the mouse pointer is close enough to one of its vertices. When this happens, the corresponding
volume is selected and you will see in the bottom right size of the ROOT canvas its name, shape type and corresponding
path in the physical tree. Right clicking on the screen when a volume is selected will also open its context menu
(picking). Note that there are several actions that can be performed both at view (no volume selected) and volume
level.
TView (mouse not selecting any volume):
•Click-and-drag rotates the view.
•Pressing some keys perform different actions:
•J/K - zoom / unzoom
•H, L, U, I - move the viewpoint
•Right click + SetParallel ()/SetPerspective () - switch from parallel to perspective view.
•Right click + ShowAxis() - show coordinate axes.
•Right click + Centered/Left/Side/Top - change view direction.
TGeoVolume (mouse selecting a volume):
•Double click will focus the corresponding volume.
•Right click + CheckOverlaps() - run overlap checker on current volume.
•Right click + Draw () - draw that volume according current global visualization options
•Right click + DrawOnly()-draw only the selected volume.
•Right click + InspectShape/Material() - print info about shape or material.
•Right click + Raytrace() - initiate a ray tracing algorithm on current view.
•
Right click +
RandomPoints/Rays()
- shoot random points or rays inside the bounding box of the clicked volume
and display only those inside visible volumes.
•Right click + Weight() - estimates the weight of a volume within a given precision.
Note that there are several additional methods for visibility and line attributes settings.
18.2 Materials and Tracking Media
We have mentioned that volumes are the building blocks for geometry, but they describe real objects having well
defined properties. In fact, there are just two of them: the material they are made from and their geometrical shape.
These have to be created before creating the volume itself, so we will describe the bits and pieces needed for making
the geometry before moving to an architectural point of view.
As far as materials are concerned, they represent the physical properties of the solid from which a volume is made.
Materials are just a support for the data that has to be provided to the tracking engine that uses this geometry package.
Due to this fact, the
TGeoMaterial
class is more like a thin data structure needed for building the corresponding
native materials of the Monte-Carlo tracking code that uses TGeo.
18.2.1 Elements, Materials and Mixtures
In order to make easier material and mixture creation, one can use the pre-built table of elements owned by
TGeoManager
class:
TGeoElementTable *table = gGeoManager->GetElementTable();
TGeoElement *element1 = table->GetElement(Int_t Z);
TGeoElement *element2 = table->FindElement("Copper");
Materials made of single elements can be defined by their atomic mass (
A
), charge (
Z
) and density (
rh
o). One can also
create a material by specifying the element that it is made of. Optionally the radiation and absorption lengths can be
also provided; otherwise they can be computed on-demand [G3]. The class representing them is TGeoMaterial:
18.2. MATERIALS AND TRACKING MEDIA 451
TGeoMaterial(const char *name,Double_t a,Double_t z,
Double_t density, Double_t radlen=0,Double_t intlen=0);
TGeoMaterial(const char *name, TGeoElement *elem,
Double_t density);
TGeoMaterial(const char* name, Double_t a, Double_t z,
Double_t rho,
TGeoMaterial::EGeoMaterialState state,
Double_t temperature = STP_temperature,
Double_t pressure = STP_pressure)
Any material or derived class is automatically indexed after creation. The assigned index is corresponding to the last
entry in the list of materials owned by
TGeoManager
class. This can be changed using the
TGeoMaterial::SetIndex()
method, however it is not recommended while using the geometry package interfaced with a transport MC. Radiation
and absorption lengths can be set using:
TGeoMaterial::SetRadLen(Double_t radlen, Double_t intlen);
•radlen: radiation length. If radlen<=0 the value is computed using GSMATE algorithm in GEANT3
•intlen: absorption length
Material state, temperature and pressure can be changed via setters. Another material property is transparency. It can
be defined and used while viewing the geometry with OpenGL.
void SetTransparency (Char_t transparency = 0)
•transparency: between 0 (opaque default) to 100 (fully transparent)
One can attach to a material a user-defined object storing Cerenkov properties. Another hook for material shading
properties is currently not in use. Mixtures are materials made of several elements. They are represented by the class
TGeoMixture, deriving from TGeoMaterial and defined by their number of components and the density:
TGeoMixture(const char *name,Int_t nel,Double_t rho);
Elements have to be further defined one by one:
void TGeoMixture::DefineElement(Int_t iel,Double_t a,Double_t z,
Double_t weigth);
void TGeoMixture::DefineElement(Int_t iel, TGeoElement *elem,
Double_t weight);
void TGeoMixture::DefineElement(Int_t iel, Int_t z, Int_t natoms);
or:
void AddElement(TGeoMaterial* mat, Double_t weight);
void AddElement(TGeoElement* elem, Double_t weight);
void AddElement(TGeoElement* elem, Int_t natoms);
void AddElement(Double_t a, Double_t z, Double_t weight)
•iel: index of the element[0,nel-1]
•aand z: the atomic mass and charge
•weight: proportion by mass of the elements
•natoms: number of atoms of the element in the molecule making the mixture
The radiation length is automatically computed when all elements are defined. Since tracking MC provide several
other ways to create materials/mixtures, the materials classes are likely to evolve as the interfaces to these engines
are being developed. Generally in the process of tracking material properties are not enough and more specific media
properties have to be defined. These highly depend on the MC performing tracking and sometimes allow the definition
of different media properties (e.g. energy or range cuts) for the same material.
452 CHAPTER 18. THE GEOMETRY PACKAGE
18.2.2 Radionuclides
A new class
TGeoElementRN
was introduced in this version to provide support for radioactive nuclides and their decays.
A database of 3162 radionuclides can be loaded on demand via the table of elements (
TGeoElementTable
class). One
can make then materials/mixtures based on these radionuclides and use them in a geometry
root[] TGeoManager *geom = new TGeoManager("geom","radionuclides");
root[] TGeoElementTable *table = geom->GetElementTable();
root[] TGeoElementRN *c14 = table->GetElementRN(14,6); // A,Z
root[] c14->Print();
6-C-014 ENDF=60140; A=14; Z=6; Iso=0; Level=0[MeV]; Dmass=3.0199[MeV];
Hlife=1.81e+11[s] J/P=0+; Abund=0; Htox=5.8e-10; Itox=5.8e-10; Stat=0
Decay modes:
BetaMinus Diso: 0BR: 100.000% Qval: 0.1565
One can make materials or mixtures from radionuclides:
root[] TGeoMaterial *mat = new TGeoMaterial("C14", c14, 2.0);
The following properties of radionulides can be currently accessed via getters in the TGeoElementRN class:
Atomic number and charge (from the base class TGeoElement)
•Isomeric number (ISO)
•ENDF code - following the convention: ENDF=10000*Z+100*A+ISO
•Isomeric energy level [MeV]
•Mass excess [MeV]
•Half life [s]
•Spin/Parity - can be retrieved with: TGeoElementRN::GetTitle()
•Hynalation and ingestion toxicities
•List of decays - TGeoElementRN::GetDecays()
The radioactive decays of a radionuclide are represented by the class
TGeoDecayChannel
and they are stored in a
TObjArray. Decay provides:
•Decay mode
•Variation of isomeric number
•Qvalue for the decay [GeV]
•Parent element
•Daughter element
Radionuclides are linked one to each other via their decays, until the last element in the decay chain which must be
stable. One can iterate decay chains using the iterator TGeoElemIter:
root[] TGeoElemIter next(c14);
root[] TGeoElementRN *elem;
root[] while ((elem=next())) next.Print();
6-C-014 (100% BetaMinus) T1/2=1.81e+11
7-N-014 stable
To create a radioactive material based on a radionuclide, one should use the constructor:
TGeoMaterial(const char *name, TGeoElement *elem, Double_t density)
To create a radioactive mixture, one can use radionuclides as well as stable elements:
TGeoMixture(const char *name, Int_t nelements, Double_t density);
TGeoMixture::AddElement(TGeoElement *elem,
Double_t weight_fraction);
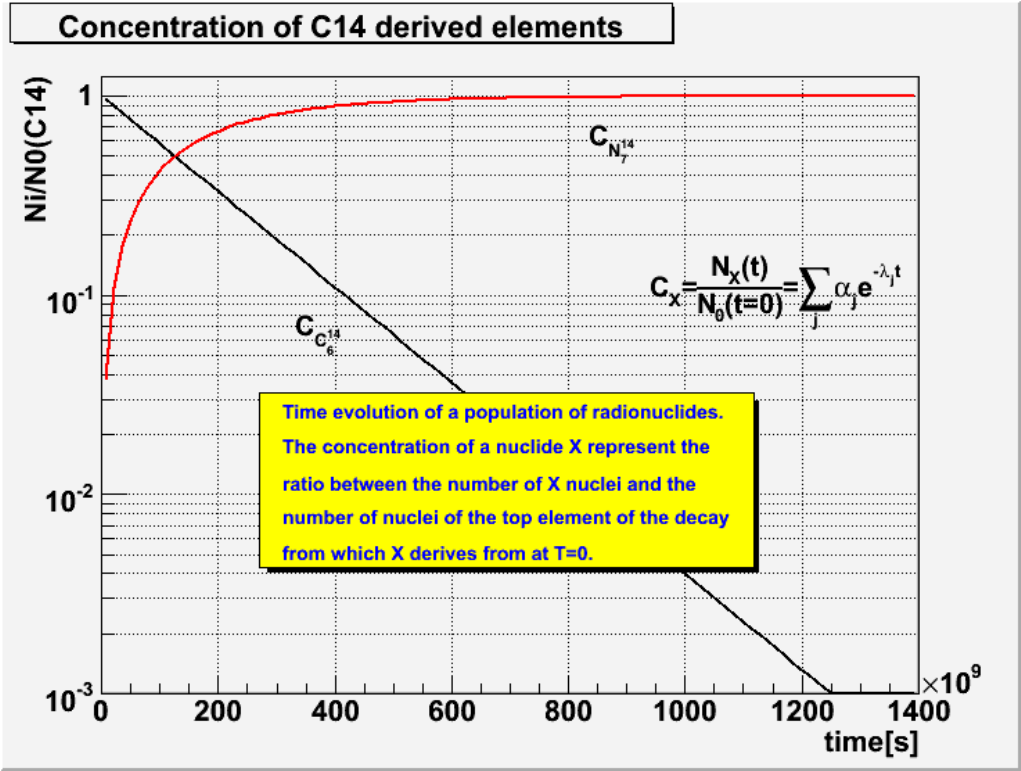
18.2. MATERIALS AND TRACKING MEDIA 453
Once defined, one can retrieve the time evolution for the radioactive materials/mixtures by using one of the next two
methods:
1. TGeoMaterial::FillMaterialEvolution(TObjArray *population, Double_t precision=0.001)
To use this method, one has to provide an empty
TObjArray
object that will be filled with all elements coming from
the decay chain of the initial radionuclides contained by the material/mixture. The precision represent the cumulative
branching ratio for which decay products are still considered.
Figure 18.1: Concentration of C14 derived elements
The population list may contain stable elements as well as radionuclides, depending on the initial elements. To test if
an element is a radionuclide:
Bool_t TGeoElement::IsRadioNuclide() const
All radionuclides in the output population list have attached objects that represent the time evolution of their fraction
of nuclei with respect to the top radionuclide in the decay chain. These objects (Bateman solutions) can be retrieved
and drawn:
TGeoBatemanSol *TGeoElementRN::Ratio();
void TGeoBatemanSol::Draw();
Another method allows to create the evolution of a given radioactive material/mixture at a given moment in time:
2. TGeoMaterial::DecayMaterial(Double_t time, Double_t precision=0.001)
The method will create the mixture that result from the decay of a initial material/mixture at time, while all resulting
elements having a fractional weight less than precision are excluded.
A demo macro for radioactive material features is
$ROOTSYS/tutorials/geom/RadioNuclides.C
It demonstrates also
the decay of a mixture made of radionuclides.
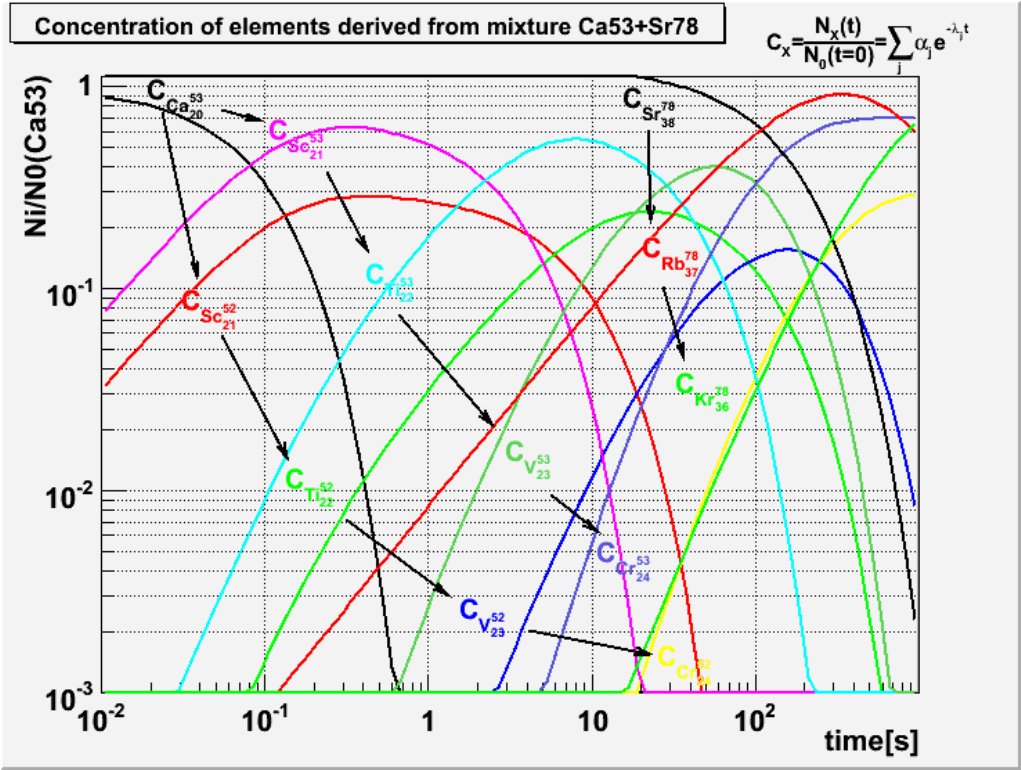
454 CHAPTER 18. THE GEOMETRY PACKAGE
Figure 18.2: Concentracion of elements derived fromCa53+Sr78
18.3. SHAPES 455
18.2.3 Tracking Media
The class
TGeoMedium
describes tracking media properties. This has a pointer to a material and the additional data
members representing the properties related to tracking.
TGeoMedium(const char *name,Int_t numed,TGeoMaterial *mat,
Double_t *params=0);
•name: name assigned to the medium
•mat: pointer to a material
•params: array of additional parameters
Another constructor allows effectively defining tracking parameters in GEANT3 style:
TGeoMedium(const char *name,Int_t numed,Int_t imat,Int_t ifield,
Double_t fieldm,Double_t tmaxfd,Double_t stemax,
Double_t deemax,Double_t epsil,Double_t stmin);
This constructor is reserved for creating tracking media from the VMC interface [. . . ]:
•numed: user-defined medium index
•imat: unique ID of the material
•others: see G3 documentation
Looking at our simple world example, one can see that for creating volumes one needs to create tracking media before.
The way to proceed for those not interested in performing tracking with external MC’s is to define and use only one
dummy tracking medium as in the example (or a NULL pointer).
18.2.4 User Interface for Handling Materials and Media
The TGeoManager class contains the API for accessing and handling defined materials:
TGeoManager::GetMaterial(name);
18.3 Shapes
Shapes are geometrical objects that provide the basic modeling functionality. They provide the definition of the
local
coordinate system of the volume. Any volume must have a shape. Any shape recognized by the modeller has to derive
from the base TGeoShape class, providing methods for:
•Finding out if a point defined in their local frame is contained or not by the shape;
•Computing the distance to enter/exit the shape from a local point, given a known direction;
•
Computing the maximum distance in any direction from a local point that does NOT result in a boundary
crossing of the shape (safe distance);
•
Computing the cosines of the normal vector to the crossed shape surface, given a starting local point and an
ongoing direction.
All the features above are globally managed by the modeller in order to provide navigation functionality. In addition to
those, shapes have also to implement additional specific abstract methods:
•
Computation of the minimal box bounding the shape, given that this box have to be aligned with the local
coordinates;
•Algorithms for dividing the shape along a given axis.
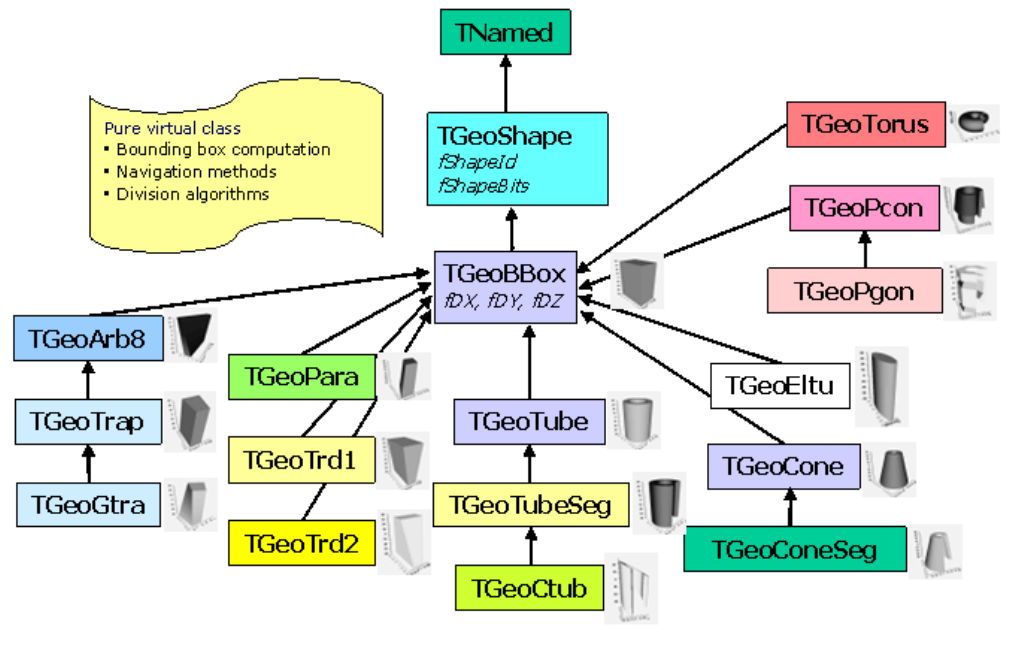
456 CHAPTER 18. THE GEOMETRY PACKAGE
Figure 18.3: Primitive Shapes - the general inheritance scheme
The modeller currently provides a set of 20 basic shapes, which we will call
primitives
. It also provides a special
class allowing the creation of shapes as a result of Boolean operations between primitives. These are called
composite
shapes
and the composition operation can be recursive (combined composites). This allows the creation of a
quite large number of different shape topologies and combinations. You can have a look and run the tutorial:
http://root.cern.ch/root/html/examples/geodemo.C.html
Shapes are named objects and all primitives have constructors like:
TGeoXXX(const char *name,<type> param1,<type> param2, ...);
TGeoXXX(<type> param1,<type> param2, ...);
Naming shape primitive is mandatory only for the primitives used in Boolean composites (see “Composite Shapes”).
For the sake of simplicity, we will describe only the constructors in the second form.
18.3.1 Units
The length units used in the geometry are
arbitrary
. However, there are certain functionalities that work with the
assumption that the used lengths are expressed in centimeters. This is the case for shape capacity or volume weight
computation. The same is valid when using the ROOT geometry as navigator for an external transport MC package
(e.g. GEANT) via the VMC interface.
Other units in use: All angles used for defining rotation matrices or some shape parameters are expressed in
degrees
.
Material density is expressed in [g/cm3].
18.3.2 Primitive Shapes
18.3.2.1 Boxes - TGeoBBox Class
Normally a box has to be build only with 3 parameters:
DX,DY,DZ
representing the half-lengths on X, Y and Z-axes.
In this case, the origin of the box will match the one of its reference frame and the box will range from:
-DX
to
DX
on
X-axis, from
-DY
to
DY
on Y and from
-DZ
to
DZ
on Z. On the other hand, any other shape needs to compute and store

18.3. SHAPES 457
the parameters of their minimal bounding box. The bounding boxes are essential to optimize navigation algorithms.
Therefore all other primitives derive from
TGeoBBox
. Since the minimal bounding box is not necessary centered in
the origin, any box allows an origin translation
(Ox
,
Oy
,
Oz)
. All primitive constructors automatically compute the
bounding box parameters. Users should be aware that building a translated box that will represent a primitive shape
by itself would affect any further positioning of other shapes inside. Therefore it is highly recommendable to build
non-translated boxes as primitives and translate/rotate their corresponding volumes only during positioning stage.
TGeoBBox(Double_t dx,Double_t dy,Double_t dz,Double_t *origin=0);
Figure 18.4: TGeoBBox class
18.3.2.2 Parallelepiped - TGeoPara class
A parallelepiped is a shape having 3 pairs of parallel faces out of which one is parallel with the XY plane (Z faces). All
faces are parallelograms in the general case. The Z faces have 2 edges parallel with the X-axis.
Figure 18.5: TGeoPara class
The shape has the center in the origin and it is defined by:
•dX, dY, dZ:
half-lengths of the projections of the edges on X, Y and Z. The lower Z face is positioned at
-dZ
,
while the upper at +dZ.
•alpha:
angle between the segment defined by the centers of the X-parallel edges and Y axis
[-90,90]
in degrees
•theta: theta angle of the segment defined by the centers of the Z faces;
•phi: phi angle of the same segment
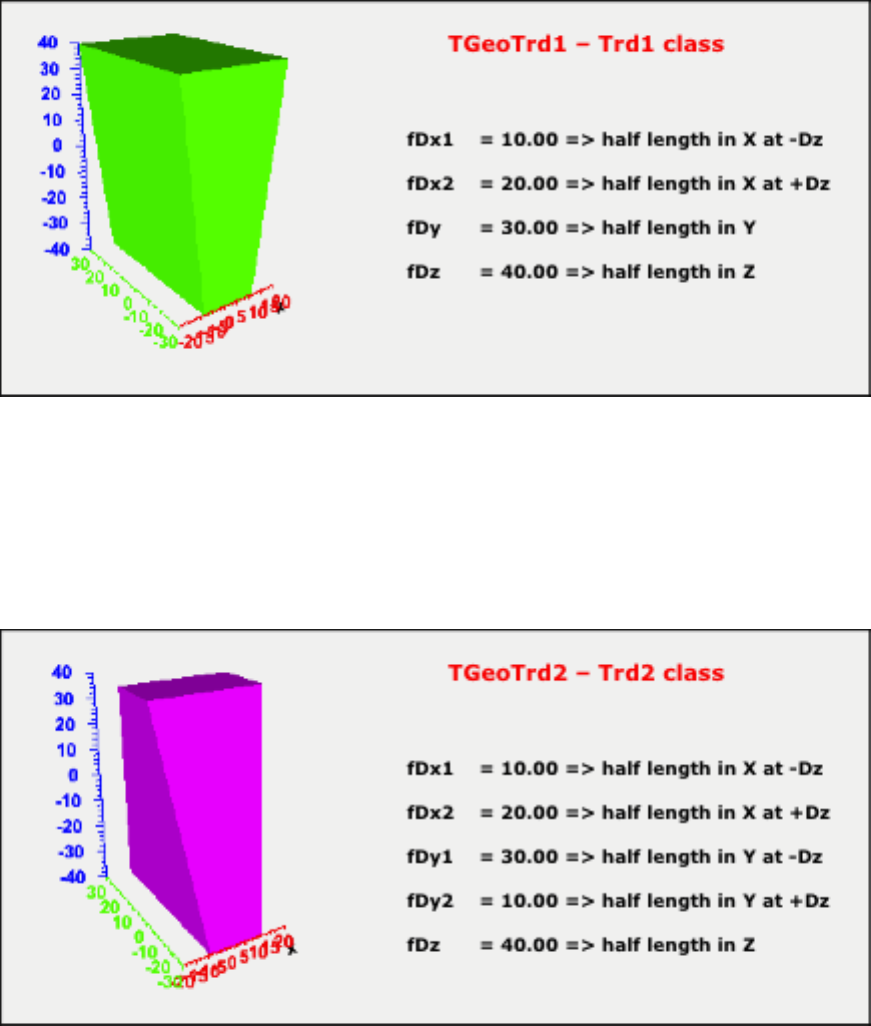
458 CHAPTER 18. THE GEOMETRY PACKAGE
TGeoPara(dX,dY,dZ,alpha,theta,phi);
A box is a particular parallelepiped having the parameters: (dX,dY,dZ,0.,0.,0.).
18.3.2.3 Trapezoids
In general, we will call trapezoidall shapes having 8 vertices and up to 6 trapezoid faces. Besides that, two of the
opposite faces are parallel to XY plane and are positioned at
dZ
. Since general trapezoids are seldom used in detector
geometry descriptions, there are several primitives implemented in the modeller for particular cases.
Trd1
is a trapezoid with only X varying with Z. It is defined by the half-length in Z, the half-length in X at the lowest
and highest Z planes and the half-length in Y:
TGeoTrd1(Double_t dx1,Double_t dx2,Double_t dy,Double_t dz);
Figure 18.6: TGeoTrd1 class
Trd2
is a trapezoid with both X and Y varying with Z. It is defined by the half-length in Z, the half-length in X at the
lowest and highest Z planes and the half-length in Y at these planes:
TGeoTrd2(Double_t dx1,Double_t dx2,Double_t dy1,Double_t dy2, Double_t dz);
Figure 18.7: TGeoTrd2 class

18.3. SHAPES 459
18.3.2.4 General Trapezoid - TGeoTrap Class
A general trapezoid is one for which the faces perpendicular to z are trapezes but their centers are not necessary at the
same x, y coordinates.
Figure 18.8: TGeoTrap Class
It has eleven parameters: the half length in z, the polar angles from the center of the face at low z to that at high z,
H1
the half length in y at low z,
LB1
the half length in x at low z and y low edge,
LB2
the half length in x at low z and y
high edge,
TH1
the angle with respect to the y axis from the center of low y edge to the center of the high y edge, and
H2,LB2,LH2,TH2, the corresponding quantities at high z.
TGeoTrap(Double_t dz,Double_t theta,Double_t phi,
Double_t h1,Double_t bl1,Double_t tl1,Double_t alpha1,
Double_t h2,Double_t bl2,Double_t tl2,Double_t alpha2);
18.3.2.5 Twisted Trapezoid - TGeoGtra class
A twisted trapezoid is a general trapezoid defined in the same way but that is twisted along the Z-axis. The twist is
defined as the rotation angle between the lower and the higher Z faces.
TGeoGtra(Double_t dz,Double_t theta,Double_t phi,Double_t twist,
Double_t h1,Double_t bl1,Double_t tl1,Double_t alpha1,
Double_t h2,Double_t bl2,Double_t tl2,Double_t alpha2 );
18.3.2.6 Arbitrary 8 vertices shapes - TGeoArb8 class
An
Arb8
is defined by two quadrilaterals sitting on parallel planes, at
dZ
. These are defined each by 4 vertices having
the coordinates
(Xi,Yi,+/-dZ)
,
i=0
,
3
. The lateral surface of the
Arb8
is defined by the 4 pairs of edges corresponding
to vertices (
i,i+1
) on both
-dZ
and
+dZ
. If M and M’ are the middles of the segments
(i,i+1)
at
-dZ
and
+dZ
, a
lateral surface is obtained by sweeping the edge at
-dZ
along MM’ so that it will match the corresponding one at
+dZ
.
Since the points defining the edges are arbitrary, the lateral surfaces are not necessary planes - but twisted planes
having a twist angle linear-dependent on Z.
TGeoArb8::TGeoArb8(Double_t dz,Double_t ivert);
•dz: half-length in Z;
•ivert = [0,7]
Vertices have to be defined clockwise in the XY pane, both at
+dz
and
-dz
. The quadrilateral at
-dz
is defined by
indices [0,3], whereas the one at
+dz
by vertices [4,7]. The vertex with
index=7
has to be defined last, since it triggers
the computation of the bounding box of the shape. Any two or more vertices in each Z plane can have the same (X,Y)
coordinates. It this case, the top and bottom quadrilaterals become triangles, segments or points. The lateral surfaces
are not necessary defined by a pair of segments, but by pair segment-point (making a triangle) or point-point (making
a line). Any choice is valid as long as at one of the end-caps is at least a triangle.
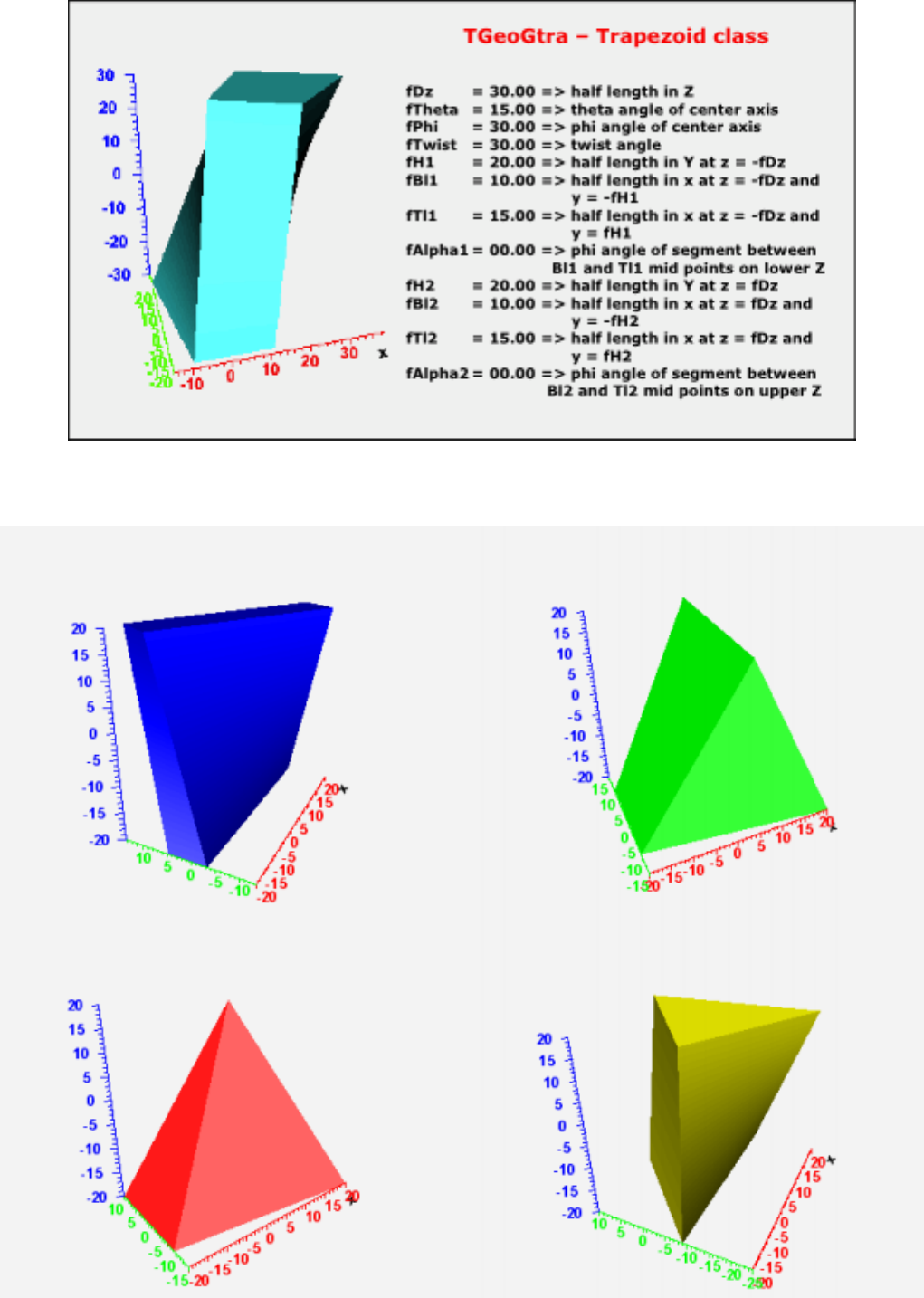
460 CHAPTER 18. THE GEOMETRY PACKAGE
Figure 18.9: TGeoGtra class
Figure 18.10: TGeoArb8 class

18.3. SHAPES 461
18.3.2.7 Tubes - TGeoTube Class
Tubes have Z as their symmetry axis. They have a range in Z, a minimum and a maximum radius:
TGeoTube(Double_t rmin,Double_t rmax,Double_t dz);
The full Z range is from -dz to +dz.
Figure 18.11: TGeoTube Class
18.3.2.8 Tube Segments - TGeoTubeSeg Class
A tube segment is a tube having a range in phi. The tube segment class derives from
TGeoTube
, having 2 extra
parameters: phi1 and phi2.
TGeoTubeSeg(Double_t rmin,Double_t rmax,Double_t dz,
Double_t phi1,Double_t phi2);
Here
phi1
and
phi2
are the starting and ending
phi
values in degrees. The
general phi convention
is that the shape
ranges from
phi1
to
phi2
going counterclockwise. The angles can be defined with either negative or positive values.
They are stored such that phi1 is converted to [0,360] and phi2 > phi1.
Figure 18.12: TGeoTubeSeg Class
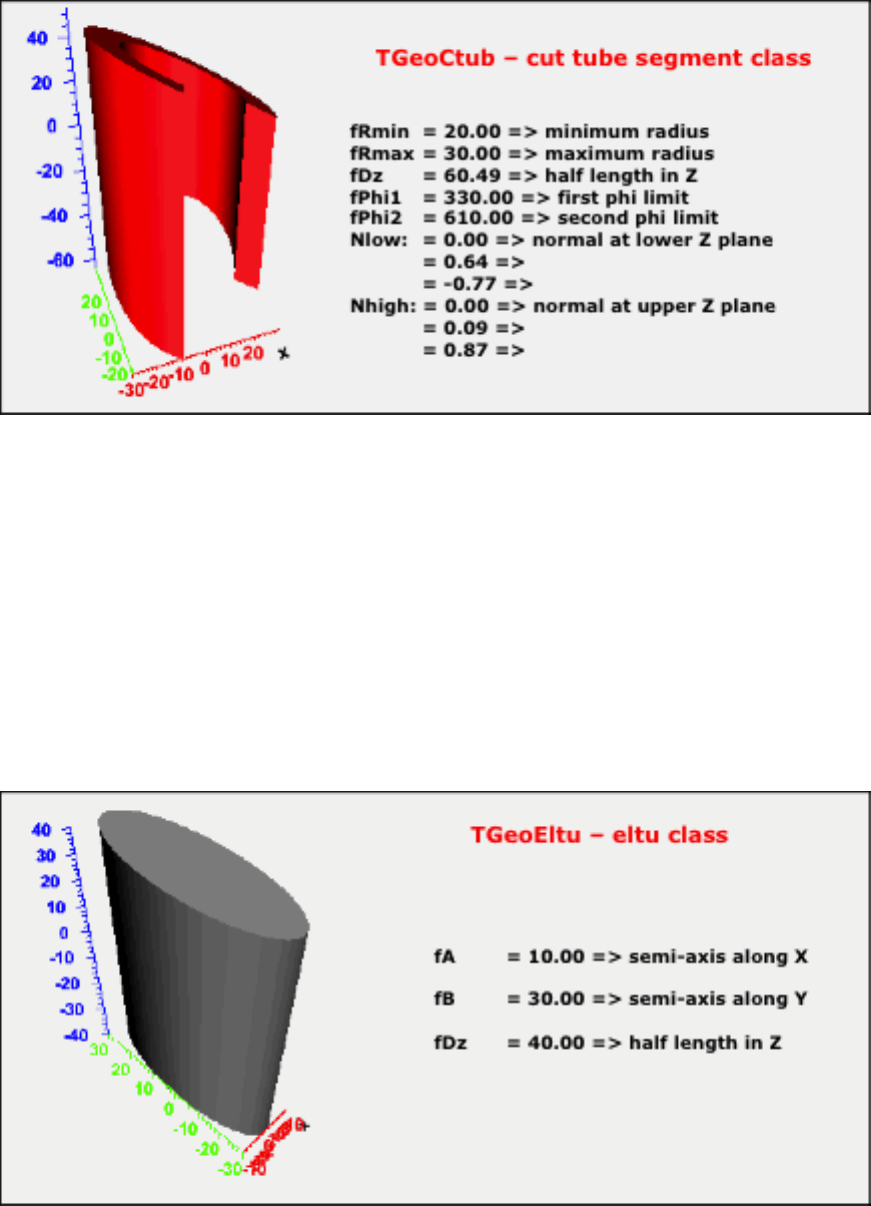
462 CHAPTER 18. THE GEOMETRY PACKAGE
18.3.2.9 Cut Tubes - TGeoCtub Class
The cut tubes constructor has the form:
TGeoCtub(Double_t rmin,Double_t rmax,Double_t dz,
Double_t phi1,Double_t phi2,
Double_t nxlow,Double_t nylow,Double_t nzlow, Double_t nxhi,
Double_t nyhi,Double_t nzhi);
Figure 18.13: TGeoCtub Class
A cut tube is a tube segment cut with two planes. The centers of the 2 sections are positioned at
dZ
. Each cut plane is
therefore defined by a point (0,0,dZ) and its normal unit vector pointing outside the shape:
Nlow=(Nx,Ny,Nz<0),Nhigh=(Nx’,Ny’,Nz’>0).
18.3.2.10 Elliptical Tubes - TGeoEltu Class
An elliptical tube is defined by the two semi-axes A and B. It ranges from -dZ to +dZ as all other tubes:
TGeoEltu(Double_t a,Double_t b,Double_t dz);
Figure 18.14: TGeoEltu Class

18.3. SHAPES 463
18.3.2.11 Hyperboloids - TGeoHype Class
A hyperboloid is represented as a solid limited by two planes perpendicular to the Z axis (top and bottom planes) and
two hyperbolic surfaces of revolution about Z axis (inner and outer surfaces). The class describing hyperboloids is
TGeoHype has 5 input parameters:
TGeoHype(Double_t rin,Double_t stin,Double_t rout,
Double_t stout,Double_t dz);
Figure 18.15: TGeoHype Class
The hyperbolic surface equation is taken in the form:
r2 - z2tan2() = r2min
•r,z: cylindrical coordinates for a point on the surface
•:stereo angle between the hyperbola asymptotic lines and Z axis
•r2min: minimum distance between hyperbola and Z axis (at z=0)
The input parameters represent:
•rin, stin: minimum radius and tangent of stereo angle for inner surface
•rout, stout: minimum radius and tangent of stereo angle for outer surface
•dz: half length in Z (bounding planes positions at +/-dz)
The following conditions are mandatory in order to avoid intersections between the inner and outer hyperbolic surfaces
in the range +/-dz:
•rin<rout
•rout>0
•rin2 + dz2*stin2 > rout2 + dz2*stout2
Particular cases:
•rin=0, stin0: the inner surface is conical
•stin=0 / stout=0: cylindrical surface(s)
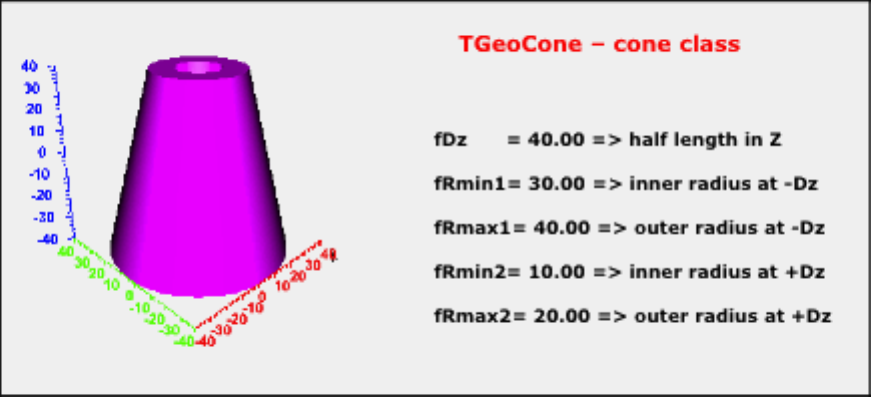
464 CHAPTER 18. THE GEOMETRY PACKAGE
18.3.2.12 Cones - TGeoCone Class
The cones are defined by 5 parameters:
TGeoCone(Double_t dz,Double_t rmin1,Double_t rmax1,
Double_t rmin2,Double_t rmax2);
•rmin1: internal radius at Z is -dz
•rmax1: external radius at Z is -dz
•rmin2: internal radius at Z is +dz
•rmax2: external radius at Z is +dz
•dz: half length in Z (a cone ranges from -dz to +dz)
A cone has Z-axis as its symmetry axis.
Figure 18.16: TGeoCone Class
18.3.2.13 Cone Segments - TGeoConeSeg Class
A cone segment is a cone having a range in
phi.
The cone segment class derives from
TGeoCone
, having two extra
parameters: phi1 and phi2.
TGeoConeSeg(Double_t dz,Double_t rmin1,Double_t rmax1,
Double_t rmin2,Double_t rmax2,Double_t phi1,Double_t phi2);
Parametersphi1 and phi2 have the same meaning and convention as for tube segments.
18.3.2.14 Sphere - TGeoSphere Class
Spheres in
TGeo
are not just balls having internal and external radii, but sectors of a sphere having defined theta and
phi ranges. The TGeoSphere class has the following constructor.
TGeoSphere(Double_t rmin,Double_t rmax,Double_t theta1,
Double_t theta2,Double_t phi1, Double_t phi2);
•rmin: internal radius of the spherical sector
•rmax: external radius
•theta1: starting theta value [0, 180) in degrees
•theta2: ending theta value (0, 180] in degrees (theta1<theta2)
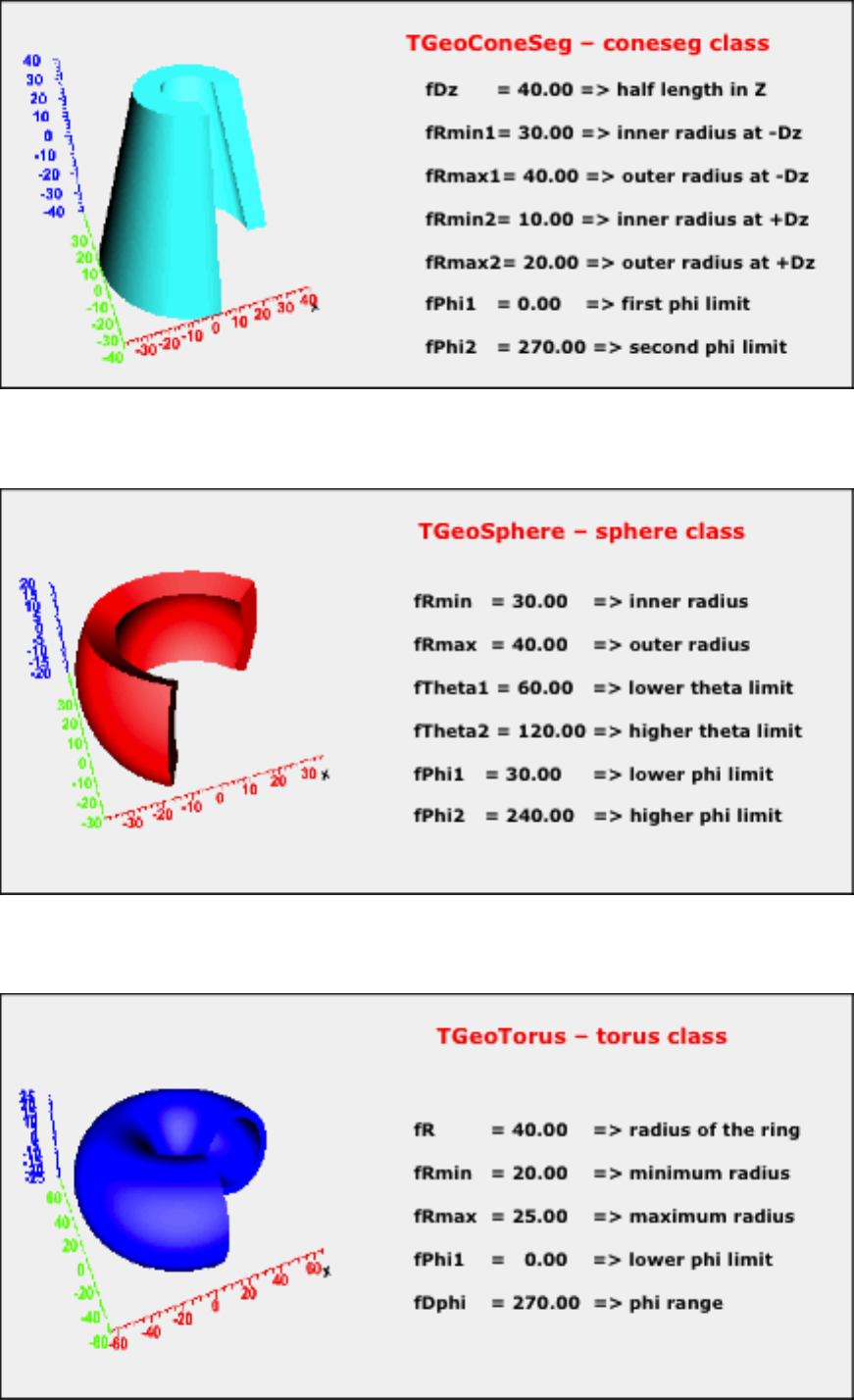
18.3. SHAPES 465
Figure 18.17: TGeoConeSeg Class
Figure 18.18: TGeoSphere Class
Figure 18.19: TGeoTorus Class

466 CHAPTER 18. THE GEOMETRY PACKAGE
18.3.2.15 Torus : TGeoTorus Class
The torus is defined by its axial radius, its inner and outer radius.
It may have a phirange:
TGeoTorus(Double_t R,Double_t Rmin,Double_t Rmax,Double_t Phi1,
Double_t Dphi);
•R: axial radius of the torus
•Rmin: inner radius
•Rmax: outer radius
•Phi1: starting phi angle
•Dphi: total phi range
18.3.2.16 Paraboloid : TGeoParaboloid Class
A paraboloid is defined by the revolution surface generated by a parabola and is bounded by two planes perpendicular
to Z axis. The parabola equation is taken in the form:
z=a·r2 + b
, where:
r2 = x2 + y2
. Note the missing linear
term (parabola symmetric with respect to Z axis).
The coefficients a and b are computed from the input values which are the radii of the circular sections cut by the
planes at +/-dz:
•-dz = a*r2low + b
•dz = a*r2high + b
TGeoParaboloid(Double_t rlo,Double_t rhi,Double_t dz);
Figure 18.20: TGeoParaboloid Class
18.3.2.17 Polycone : TGeoPcon Class
A polycone is represented by a sequence of tubes/cones, glued together at defined Z planes. The polycone might have a
phi segmentation, which globally applies to all the pieces. It has to be defined in two steps:
1. First call the TGeoPcon constructor to define a polycone:
TGeoPcon(Double_t phi1,Double_t dphi,Int_t nz

18.3. SHAPES 467
•phi1: starting phi angle in degrees
•dphi: total phi range
•nz: number of Z planes defining polycone sections (minimum 2)
2. Define one by one all sections [0, nz-1]
void TGeoPcon::DefineSection(Int_t i,Double_t z,
Double_t rmin, Double_t rmax);
•i: section index [0, nz-1]
•z: z coordinate of the section
•rmin: minimum radius corresponding too this section
•rmax: maximum radius.
The first section (i=0) has to be positioned always the lowest Z coordinate. It defines the radii of the first cone/tube
segment at its lower Z. The next section defines the end-cap of the first segment, but it can represent also the beginning
of the next one. Any discontinuity in the radius has to be represented by a section defined at the same Z coordinate as
the previous one. The Z coordinates of all sections must be sorted in increasing order. Any radius or Z coordinate of a
given plane have corresponding getters:
Double_t TGeoPcon::GetRmin(Int_t i);
Double_t TGeoPcon::GetRmax(Int_t i);
Double_t TGeoPcon::GetZ(Int_t i);
Note that the last section should be defined last, since it triggers the computation of the bounding box of the polycone.
Figure 18.21: TGeoPcon Class
18.3.2.18 Polygon: TGeoPgon Class
Polygons are defined in the same way as polycones, the difference being just that the segments between consecutive Z
planes are regular polygons. The phi segmentation is preserved and the shape is defined in a similar manner, just that
rmin and rmax represent the radii of the circles inscribed in the inner/outer polygon.
The constructor of a polygon has the form:
TGeoPgon(Double_t phi1,Double_t dphi,Int_t nedges,Int_t nz);
The extra parameter nedges represent the number of equal edges of the polygons, between phi1 and phi1+dphi.

468 CHAPTER 18. THE GEOMETRY PACKAGE
Figure 18.22: TGeoPgon Class
18.3.2.19 Polygonal extrusion: TGeoXtru Class
A
TGeoXtru
shape is represented by the extrusion of an arbitrary polygon with fixed outline between several Z sections.
Each Z section is a scaled version of the same “blueprint” polygon. Different global XY translations are allowed from
section to section. Corresponding polygon vertices from consecutive sections are connected.
An extruded polygon can be created using the constructor:
TGeoXtru::TGeoXtru(Int_t nplanes);
•nplanes:number of Z sections (minimum 2)
Figure 18.23: TGeoXtru Class
The lists of X and Y positions for all vertices have to be provided for the “blueprint” polygon:
18.3. SHAPES 469
TGeoXtru::DefinePolygon (Int_t nvertices, Double_t *xv,
Double_t *yv);
•nvertices:number of vertices of the polygon
•xv,yv:arrays of X and Y coordinates for polygon vertices
The method creates an object of the class
TGeoPolygon
for which the convexity is automatically determined . The
polygon is decomposed into convex polygons if needed.
Next step is to define the Z positions for each section plane as well as the XY offset and scaling for the corresponding
polygons.
TGeoXtru::DefineSection(Int_t snum,Double_t zsection,Double_t x0,
Double_t y0, Double_t scale);
•snum:
Z section index (0, nplanes-1). The section with
snum = nplanes-1
must be defined last and triggers the
computation of the bounding box for the whole shape
•zsection:
Z position of section
snum
. Sections must be defined in increasing order of Z (e.g.
snum=0
correspond
to the minimum Z and snum=nplanes-1 to the maximum one).
•x0,y0:offset of section snum with respect to the local shape reference frame T
•scale:factor that multiplies the X/Y coordinates of each vertex of the polygon at section snum:
•x[ivert] = x0 + scale*xv[ivert]
•y[ivert] = y0 + scale*yv[ivert]
18.3.2.20 Half Spaces: TGeoHalfSpace Class
•
A half space is limited just by a plane, defined by a point and the normal direction. The point lies on the plane
and the normal vector points outside the half space. The half space is the only shape which is infinite and can
be used only in Boolean operations that result in non-infinite composite shapes (see also “Composite Shapes”
below). A half space has to be defined using the constructor:
TGeoHalfSpace (const char *name, Double_t *point[3],
Double_t *norm[3]);
18.3.3 Composite Shapes
Composite shapes are Boolean combinations of two or more shape components. The supported Boolean operations
are union (+), intersection (*) and subtraction(-). Composite shapes derive from the base
TGeoShape
class, therefore
providing all shape features: computation of bounding box, finding if a given point is inside or outside the combination,
as well as computing the distance to entering/exiting. They can be directly used for creating volumes or used in the
definition of other composite shapes.
Composite shapes are provided in order to complement and extend the set of basic shape primitives. They have a
binary tree internal structure, therefore all shape-related geometry queries are signals propagated from top level down
to the final leaves, while the provided answers are assembled and interpreted back at top. This
CSG (composite solid
geometry)
hierarchy is effective for small number of components, while performance drops dramatically for large
structures. Building a complete geometry in this style is virtually possible but highly not recommended.
18.3.3.1 The Structure of Composite Shapes
A composite shape can always be looked as the result of a Boolean operation between only two shape components. All
information identifying these two components as well as their positions with respect to the frame of the composite is
represented by an object called Boolean node. A composite shape has a pointer to such a Boolean node. Since the
shape components may also be composites, they will also contain binary Boolean nodes branching out other two shapes
in the hierarchy. Any such branch ends-up when the final leaves are no longer composite shapes, but basic primitives.
The figure shows the composite shapes structure.
Suppose that A, B, C and D represent basic shapes, we will illustrate how the internal representation of few combinations
look like. We do this only for understanding how to create them in a proper way, since the user interface for this
purpose is in fact very simple. We will ignore for the time being the positioning of components. The definition of a
composite shape takes an expression where the identifiers are shape names. The expression is parsed and decomposed
in 2 sub-expressions and the top-level Boolean operator.
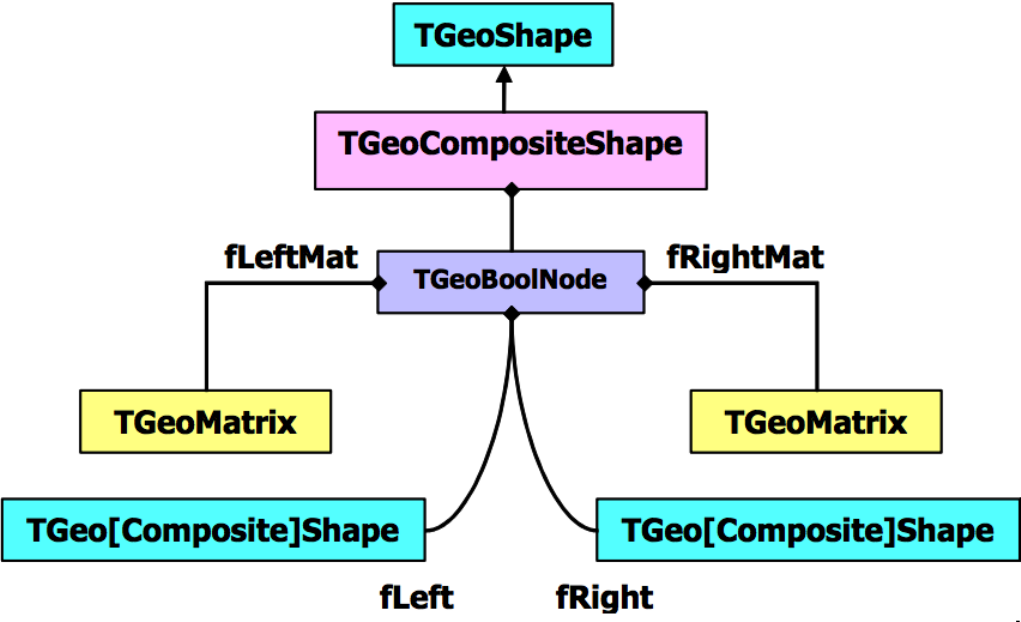
470 CHAPTER 18. THE GEOMETRY PACKAGE
Figure 18.24: The composite shapes structure
1. Union: A+B+C
Just to illustrate the Boolean expression parsing and the composite shape structure, let’s take a simple example. We
will describe the union of A, B and C. Both union operators are at the same level. Since:
A+B+C = (A+B)+C = A+(B+C)
The first
(+)
is taken as separator, hence the expression split in:
A
and
(B+C)
. A Boolean node of type
TGeoUnion("A","B+C")
is created. This tries to replace the 2 expressions by actual pointers to corresponding shapes.
The first expression (A) contains no operators therefore is interpreted as representing a shape. The shape named
“A” is searched into the list of shapes handled by the manager class and stored as the “left” shape in the Boolean
union node. Since the second expression is not yet fully decomposed, the “right” shape in the combination is created
as a new composite shape. This will split at its turn B+C into B and C and create a
TGeoUnion("B","C")
. The B
and C identifiers will be looked for and replaced by the pointers to the actual shapes into the new node. Finally, the
composite “A+B+C” will be represented as shown in Fig.17-23.**
To build this composite shape:
TGeoCompositeShape *cs1 = new TGeoCompositeShape("CS1","A+B+C");
Any shape entering a Boolean combination can be prior positioned. In order to do so, one has to attach a matrix name
to the shape name by using a colon (:). As for shapes, the named matrix has to be prior defined:
TGeoMatrix *mat;
// ... code creating some geometrical transformation
mat->SetName("mat1");
mat->RegisterYourself(); // see Geometrical transformations
An identifier
shape:matrix
have the meaning:
shape
is translated or rotated with
matrix
with respect to the Boolean
combination it enters as operand. Note that in the expression A+B+C no matrix identifier was provided, therefore the
identity matrix was used for positioning the shape components. The next example will illustrate a more complex case.
2. (A:m1+B):m2-(C:m3*D:m4):m5
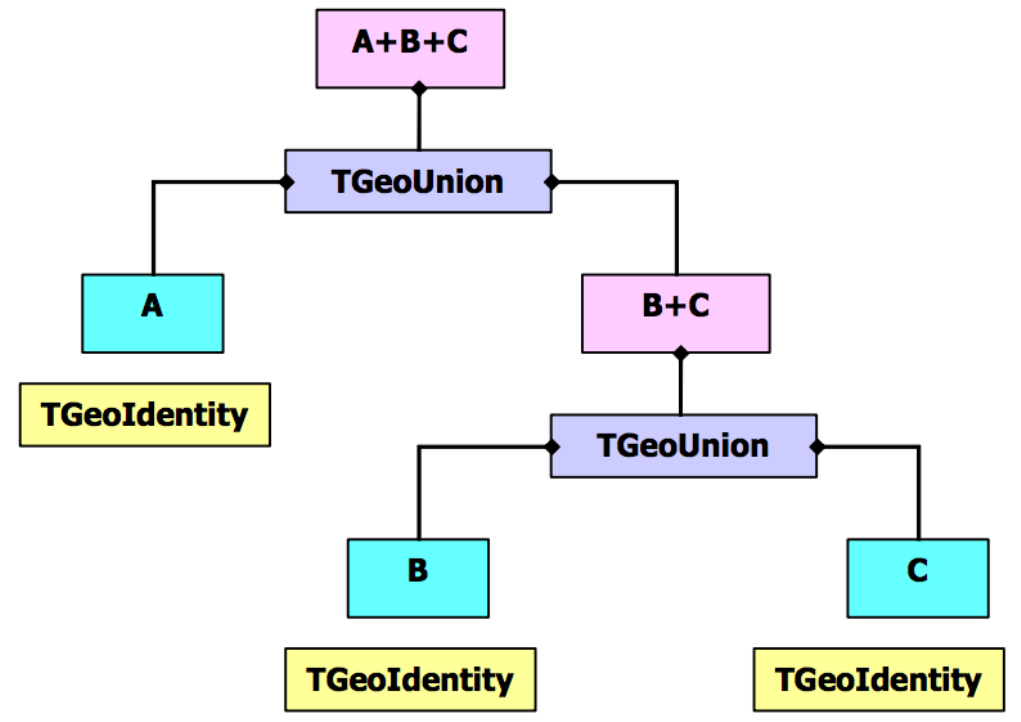
18.3. SHAPES 471
Figure 18.25: Representation of A+B+C
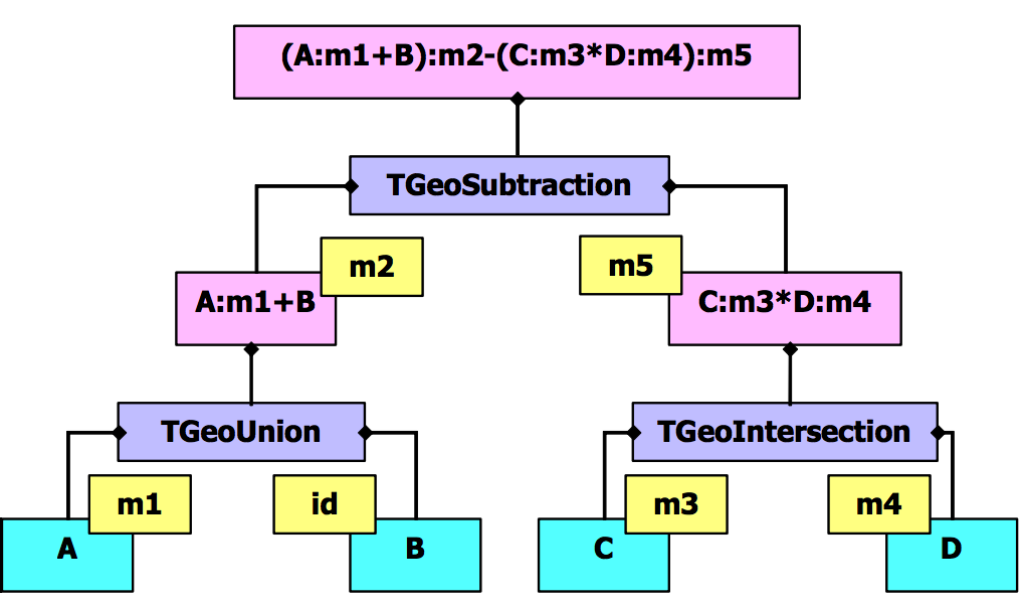
472 CHAPTER 18. THE GEOMETRY PACKAGE
Let’s try to understand the expression above. This expression means: subtract the intersection of Cand Dfrom the
union of
A
and
B
. The usage of parenthesis to force the desired precedence is always recommended. One can see that
not only the primitive shapes have some geometrical transformations, but also their intermediate compositions.
Figure 18.26: Internal representation for composite shapes
TGeoCompositeShape *cs2 = new TGeoCompositeShape("CS2",
"(A:m1+B):m2-(C:m3*D:m4):m5");
Building composite shapes as in the first example is not always quite useful since we were using un-positioned shapes.
When supplying just shape names as identifiers, the created Boolean nodes will assume that the shapes are positioned
with an identity transformation with respect to the frame of the created composite. In order to provide some positioning
of the combination components, we have to attach after each shape identifier the name of an existing transformation,
separated by a colon. Obviously all transformations created for this purpose have to be objects with unique names in
order to be properly substituted during parsing.
18.3.3.2 Composite Shape Example
One should have in mind that the same shape or matrix identifiers can be used many times in the same expression, as
in the following example:
const Double_t sq2 = TMath::Sqrt(2.);
gSystem->Load("libGeom");
TGeoManager *mgr =
new TGeoManager("Geom","composite shape example");
TGeoMedium *medium = 0;
TGeoVolume *top = mgr->MakeBox("TOP",medium,100,250,250);
mgr->SetTopVolume(top);
// make shape components
TGeoBBox *sbox = new TGeoBBox("B",100,125*sq2,125*sq2);
TGeoTube *stub = new TGeoTube("T",0,100,250);
TGeoPgon *spgon = new TGeoPgon("P",0.,360.,6,2);
spgon->DefineSection(0,-250,0,80);
spgon->DefineSection(1,250,0,80);
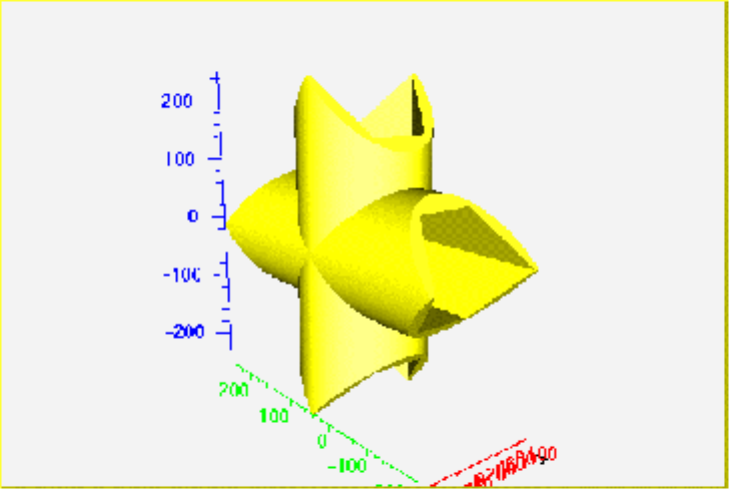
18.3. SHAPES 473
// define some rotations
TGeoRotation *r1 = new TGeoRotation("r1",90,0,0,180,90,90);
r1->RegisterYourself();
TGeoRotation *r2 = new TGeoRotation("r2",90,0,45,90,45,270);
r2->RegisterYourself();
// create a composite
TGeoCompositeShape *cs = new TGeoCompositeShape("cs",
"((T+T:r1)-(P+P:r1))*B:r2");
TGeoVolume *comp = new TGeoVolume("COMP",cs);
comp->SetLineColor(5);
// put it in the top volume
top->AddNode(comp,1);
mgr->CloseGeometry();
// visualize it with ray tracing
top->Raytrace();
Figure 18.27: A composite shape example
Composite shapes can be subsequently used for defining volumes. Moreover, these volumes contain other volumes,
following the general criteria. Volumes created based on composite shapes cannot be divided.
18.3.4 Navigation Methods Performed By Shapes
Shapes are named objects and register themselves to the
manager class
at creation time. This is responsible for their
final deletion. Shapes can be created without name if their retrieval by name is no needed. Generally shapes are
objects that are useful only at geometry creation stage. The pointer to a shape is in fact needed only when referring to
a given volume and it is always accessible at that level. Several volumes may reference a single shape; therefore its
deletion is not possible once volumes were defined based on it.
The navigation features related for instance to tracking particles are performed in the following way: Each shape
implement its specific algorithms for all required tasks in its local reference system. Note that the manager class
handles global queries related to geometry. However, shape-related queries might be sometimes useful:
Bool_t TGeoShape::Contains(Double_t *point[3]);
The method above returns
kTRUE
if the point *point is actually inside the shape. The point has to be defined in the
local shape reference. For instance, for a box having DX,DY and DZhalf-lengths a point will be considered inside if:
-DX <= point[0] <= DX
474 CHAPTER 18. THE GEOMETRY PACKAGE
-DY <= point[1] <= DY
-DZ <= point[2] <= DZ
Double_t TGeoShape::DistFromInside(Double_t *point[3],
Double_t *dir[3], Int_t iact,Double_t step,Double_t *safe);
The method computes the distance to exiting a shape from a given point
inside
, along a given direction. This direction
is given by its director cosines with respect to the local shape coordinate system. This method provides additional
information according the value of iact input parameter:
•iact = 0computes only safe distance and fill it at the location given by SAFE;
•iact = 1
a proposed STEP is supplied. The safe distance is computed first. If this is bigger than STEP than the
proposed step is approved and returned by the method since it does not cross the shape boundaries. Otherwise,
the distance to exiting the shape is computed and returned;
•iact = 2computes both safe distance and distance to exiting, ignoring the proposed step;
•iact > 2computes only the distance to exiting, ignoring anything else
Double_t TGeoShape::DistFromOutside(Double_t *point[3],
Double_t *dir[3],Int_t iact,Double_t step,Double_t *safe);
This method computes the distance to entering a shape from a given point
outside
. It acts in the same way as the
previous method.
Double_t TGeoShape::Safety(Double_t *point[3],Bool_t inside);
This computes the maximum shift of a point in any direction that does not change its
inside/outside
state (does not
cross shape boundaries). The state of the point has to be properly supplied.
Double_t *TGeoShape::ComputeNormal(Double_t *point[3],
Double_t *dir[3],Double_t *norm[3]);
The method above computes the director cosines of normal to the crossed shape surface from a given point towards
direction. This is filled into the
norm
array, supplied by the user. The normal vector is always chosen such that its dot
product with the direction is positive defined.
18.3.5 Creating Shapes
Shape objects embeds only the minimum set of parameters that are fully describing a valid physical shape. For instance,
the half-length, the minimum and maximum radius represent a tube. Shapes are used together with media in order to
create volumes, which in their turn are the main components of the geometrical tree. A specific shape can be created
stand-alone:
TGeoBBox *box = new TGeoBBox("s_box",halfX,halfY,halfZ); // named
TGeoTube *tub = new TGeoTube(rmin,rmax,halfZ); // no name
//... (See all specific shape constructors)
Sometimes it is much easier to create a volume having a given shape in one step, since shapes are not directly linked in
the geometrical tree but volumes are:
TGeoVolume *vol_box = gGeoManager->MakeBox("BOX_VOL",pmed,halfX,
halfY,halfZ);
TGeoVolume *vol_tub = gGeoManager->MakeTube("TUB_VOL",pmed,rmin,
rmax,halfZ);
// ...(See MakeXXX() utilities in TGeoManager class)
18.4. GEOMETRY CREATION 475
18.3.6 Dividing Shapes
Shapes can generally be divided along a given axis. Supported axes are:
X
,
Y
,
Z
,
Rxy
,
Phi
,
Rxyz
. A given shape cannot
be divided however on any axis. The general rule is that that divisions are possible on whatever axis that produces still
known shapes as slices. The division of shapes are performed by the call
TGeoShape::Divide()
, but this operation
can be done only via
TGeoVolume::Divide()
method. In other words, the algorithm for dividing a specific shape is
known by the shape object, but is always invoked in a generic way from the volume level. Details on how to do that
can be found in the paragraph ‘Dividing volumes’. One can see how all division options are interpreted and which their
result inside specific shape classes is.
18.3.7 Parametric Shapes
Shapes generally have a set of parameters that is well defined at build time. In fact, when the final geometrical hierarchy
is assembled and the geometry is closed, all constituent shapes
MUST
**have well defined and valid parameters. In order
to ease-up geometry creation, some parameterizations are however allowed.
For instance let’s suppose that we need to define several volumes having exactly the same properties but different sizes.
A way to do this would be to create as many different volumes and shapes. The modeller allows however the definition
of a single volume having undefined shape parameters.
TGeoManager::Volume(const char *name,const char *shape,Int_t nmed);
•name: the name of the newly created volume;
•shape:
the type of the associated shape. This has to contain the case-insensitive first 4 letters of the corresponding
class name (e.g. “tubs” will match TGeoTubeSeg, “bbox” will match TGeoBBox)
•nmed: the medium number.
This will create a special volume that will not be directly used in the geometry, but whenever positioned will require
a list of actual parameters for the current shape that will be created in this process. Such volumes having shape
parameters known only when used have to be positioned only with
TGeoManager::Node() method (see ‘Creating
and Positioning Volumes’).
Other case when shape parameterizations are quite useful is scaling geometry structures. Imagine that we would like
to enlarge/shrink a detector structure on one or more axes. This happens quite often in real life and is handled by
“fitting mother” parameters. This is accomplished by defining shapes with one or more invalid (negative) parameters.
For instance, defining a box having
dx=10.
,
dy=10.
, and
dz=-1
will not generate an error but will be interpreted in
a different way: A special volume
TGeoVolumeMulti
will be created. Whenever positioned inside a mother volume,
this will create a normal
TGeoVolume
object having as shape a box with
dz
fitting the corresponding
dz
of the mother
shape. Generally, this type of parameterization is used when positioning volumes in containers having a matching
shape, but it works also for most reasonable combinations.
18.4 Geometry Creation
A given geometry can be built in various ways, but one has to follow some mandatory steps. Even if we might use
some terms that will be explained later, here are few general rules:
•Volumes need media and shapes in order to be created.
•
Both containers and contained volumes must be created before linking them together, and the relative transfor-
mation matrix must be provided.
•Any volume have to be positioned somewhere otherwise it will not be considered as part of the geometry.
•
Visibility or tracking properties of volumes can be provided both at build time or after geometry is closed, but
global visualization settings (see section: “The Drawing Package”) should not be provided at build time, otherwise
the drawing package will be loaded.
There is also a list of specific rules:
•
Positioned volumes should not extrude their container or intersect with others within this unless it is specified
(see section: Overlapping Volumes).
•
The top volume (containing all geometry trees) must be specified before closing the geometry and must not be
positioned - it represents the global reference frame.
476 CHAPTER 18. THE GEOMETRY PACKAGE
•
After building the full geometry tree, the geometry must be closed (see the method
TGeoManager::CloseGeometry()
).
Voxelization can be redone per volume after this process.
The list is much bigger and we will describe in more detail the geometry creation procedure in the following sections.
Provided that geometry was successfully built and closed, the
TGeoManager
class will register itself to ROOT and the
logical/physical structures will become immediately browsable.
18.4.1 The Volume Hierarchy
The basic components used for building the logical hierarchy of the geometry are the positioned volumes called
nodes
.
Volumes are fully defined geometrical objects having a given shape and medium and possibly containing a list of nodes.
Nodes represent just positioned instances of volumes inside a container volume but users do not directly create them.
They are automatically created as a result of adding one volume inside other or dividing a volume. The geometrical
transformation held by nodes is always defined with respect to their mother (relative positioning). Reflection matrices
are allowed.
A hierarchical element is not fully defined by a node since nodes are not directly linked to each other, but through
volumes (a node points to a volume, which at its turn points to a list of nodes):
NodeTop VolTop NodeA VolA ...
One can therefore talk about “the node or volume hierarchy”, but in fact, an element is made by a pair volume-node.
In the line above is represented just a single branch, but of course from any volume other branches can also emerge.
The index of a node in such a branch (counting only nodes) is called depth. The top node have always depth=0.
Volumes need to have their daughter nodes defined when the geometry is closed. They will build additional structures
(called
voxels
) in order to fasten-up the search algorithms. Finally, nodes can be regarded as bi-directional links
between containers and contained volumes.
The structure defined in this way is a graph structure since volumes are replicable (same volume can become daughter
node of several other volumes), every volume becoming a branch in this graph. Any volume in the logical graph
can become the actual top volume at run time (see
TGeoManager::SetTopVolume()). All functionalities of the
modeller will behave in this case as if only the corresponding branch starting from this volume is the
active geometry.
Nodes are never instantiated directly by users, but created as a result of volume operations. Adding a volume named A
with a given
user id
inside a volume B will create a node named
A_id.
This will be added to the list of nodes stored
by B. In addition, when applying a division operation in N slices to a volume A, a list of nodes
B_1
,
B_2
, . . . ,
B_N
is
also created. A node
B_i
does not represent a unique object in the geometry because its container A might be at its
turn positioned as node inside several other volumes. Only when a complete branch of nodes is fully defined up to the
top node in the geometry, a given path:
/TOP_1/
...
/A_3/B_7
will represent a unique object. Its global transformation
matrix can be computed as the pile-up of all local transformations in its branch. We will therefore call
logical graph
the hierarchy defined by nodes and volumes. The expansion of the logical graph by all possible paths defines a tree
structure where all nodes are unique “touchable” objects. We will call this the “physical tree”. Unlike the logical graph,
the physical tree can become a huge structure with several millions of nodes in case of complex geometries; therefore,
it is not always a good idea to keep it transient in memory. Since the logical and physical structures are correlated,
the modeller rather keeps track only of the current branch, updating the current global matrix at each change of the
level in geometry. The current physical node is not an object that can be asked for at a given moment, but rather
represented by the combination: current node/current global matrix. However, physical nodes have unique ID’s that
can be retrieved for a given modeller state. These can be fed back to the modeller in order to force a physical node to
become current. The advantage of this comes from the fact that all navigation queries check first the current node;
therefore the location of a point in the geometry can be saved as a starting state for later use.
Nodes can be declared as
overlapping
in case they do overlap with other nodes inside the same container or extrude
this container (see also ‘Checking the Geometry’). Non-overlapping nodes can be created with:
TGeoVolume::AddNode(TGeoVolume *daughter,Int_t copy_No,
TGeoMatrix *matr);
The creation of overlapping nodes can be done with a similar prototype:
TGeoVolume::AddNodeOverlap(/*same arguments*/ );
When closing the geometry, overlapping nodes perform a check of possible overlaps with their neighbors. These are
stored and checked all the time during navigation; therefore, navigation is slower when embedding such nodes into
geometry. Nodes have visualization attributes as the volume has. When undefined by users, painting a node on a pad
will take the corresponding volume attributes.
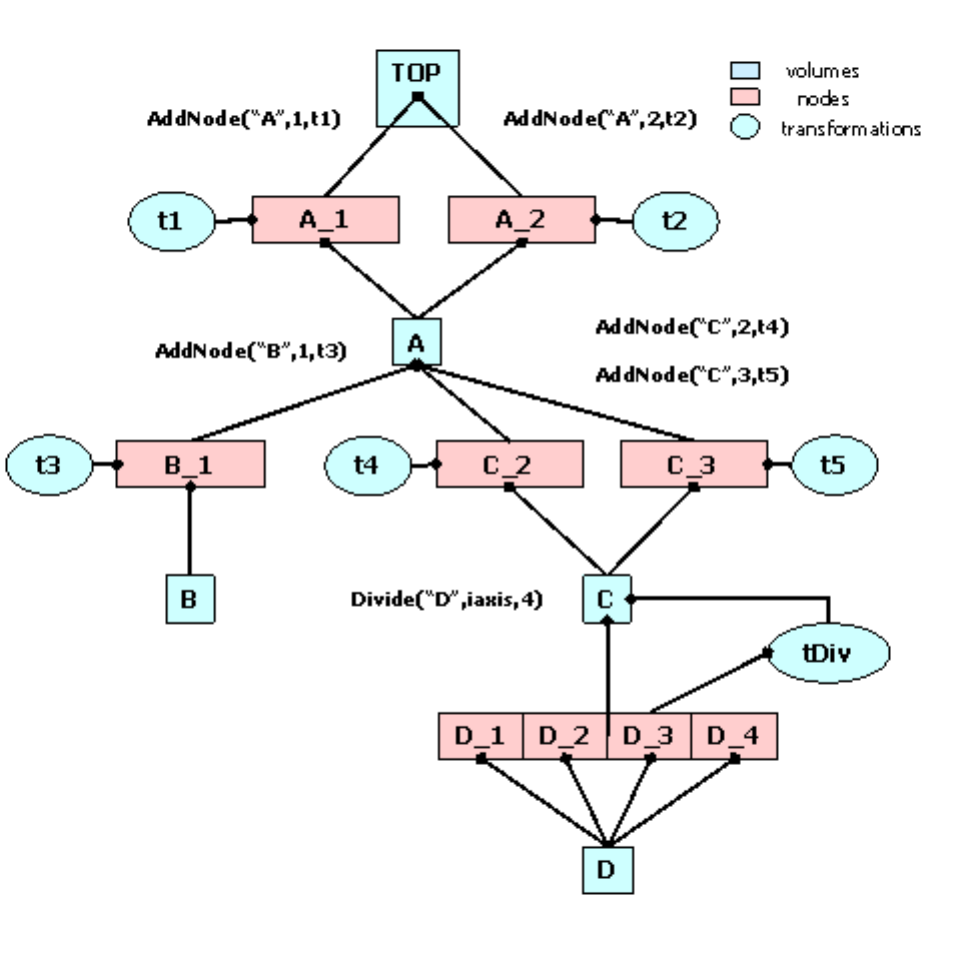
18.4. GEOMETRY CREATION 477
Figure 18.28: A geometry hierarchy in memory
478 CHAPTER 18. THE GEOMETRY PACKAGE
18.4.2 Creating and Positioning Volumes
18.4.2.1 Making Volumes
As mentioned before, volumes are the basic objects used in building the geometrical hierarchy. They represent objects
that are not positioned, but store all information about the placement of the other volumes they may contain. Therefore
a volume can be replicated several times in the geometry. As it was explained, in order to create a volume, one has to
put together a shape and a medium, which are already defined.
Volumes have to be named by users at creation time. Every different name may represent a unique volume object,
but may also represent more general a family (class) of volume objects having the same shape type and medium, but
possibly different shape parameters. It is the user’s task to provide different names for different volume families in
order to avoid ambiguities at tracking time.
A generic family rather than a single volume is created only in two cases: when a parametric shape is used or when a
division operation is applied. Each volume in the geometry stores a unique ID corresponding to its family. In order to
ease-up their creation, the manager class is providing an API that allows making a shape and a volume in a single step.
18.4.2.2 Example of Volume Creation
// Making a volume out of a shape and a medium.
TGeoVolume *vol = new TGeoVolume("VNAME",ptrShape,ptrMed);
// Making a volume out of a shape but without a defined medium.
TGeoVolume *vol = new TGeoVolume("VNAME",ptrShape);
// Making a volume with a given shape in one step
TGeoVolume *vol = gGeoManager->MakeBox("VNAME",ptrMed,dx,dy,dz);
TGeoVolume *vol = gGeoManager->MakeTubs("VNAME",ptrMed,rmin,rmax,
dz,phi1,phi2);
// See class TGeoManager for the rest of shapes.
// Making a volume with a given shape with a unique prototype
TGeoVolume *vol = gGeoManager->Volume("VNAME","XXXX",nmed,upar,
npar);
// Where XXXX stands for the first 4 letters of the specific shape
// classes, nmed is the medium number, upar is an Double_t * array
// of the shape parameters and npar is the number of parameters.
// This prototype allows (npar = 0) to define volumes with shape
// defined only at positioning time (volumes defined in this way
// need to be positioned using TGeoManager::Node() method)
18.4.2.3 Positioned Volumes (Nodes)
Geometrical modeling is a difficult task when the number of different geometrical objects is 106-108. This is more or
less the case for detector geometries of complex experiments, where a ‘flat’ CSG model description cannot scale with
the current CPU performances. This is the reason why models like GEANT [1] introduced an additional dimension
(depth) in order to reduce the complexity of the problem. This concept is also preserved by the ROOT modeller and
introduces a pure geometrical constraint between objects (volumes in our case) - containment. This means in fact that
any positioned volume has to be contained by another. Now what means contained and positioned?
•
We will say that a volume
contains
a point if this is inside the shape associated to the volume. For instance, a
volume having a box shape will contain all points
P=(X,Y,Z)
verifying the conditions:
Abs(Pi)dXi
. The points
on the shape boundaries are considered as inside the volume. The volume contains a daughter if it contains all
the points contained by the daughter.
•
The definition of containment works of course only with points defined in the local coordinate system of the
considered volume.
Positioning
a volume inside another have to introduce a geometrical transformation between
the two. If
M
defines this transformation, any point in the daughter reference can be converted to the mother
reference by: Pmother = MPdaughter
When creating a volume one does not specify if this will contain or not other volumes. Adding daughters to a volume
implies creating those and adding them one by one to the list of daughters. Since the volume has to know the position
18.4. GEOMETRY CREATION 479
of all its daughters, we will have to supply at the same time a geometrical transformation with respect to its local
reference frame for each of them.
TGeoVolume::AddNode(TGeoVolume *daughter,Int_t usernumber,
TGeoMatrix *matrix=gGeoIdentity)
The objects referencing a volume and a transformation are called
NODES
and their creation is fully handled by the
modeller. They represent the link elements in the hierarchy of volumes. Nodes are unique and distinct geometrical
objects ONLY from their container point of view. Since volumes can be replicated in the geometry, the same node may
be found on different branches.
In order to provide navigation features, volumes have to be able to find the proper container of any point defined in
the local reference frame. This can be the volume itself, one of its positioned daughter volumes or none if the point
is actually outside. On the other hand, volumes have to provide also other navigation methods such as finding the
distances to its shape boundaries or which daughter will be crossed first. The implementation of these features is done
at shape level, but the local mother-daughters management is handled by volumes. These build additional optimization
structures upon geometry closure. In order to have navigation features properly working one has to follow some rules
for building a valid geometry.
•
The daughter volume(s) must not extrude the mother shape. They are allowed however to have a common
boundaries.
•
The volumes positioned in the same container must not overlap with each other. They may touch on one
boundaries or shape vertex.
The daughter nodes of a volume can be also removed or replaced with other nodes:
void RemoveNode(TGeoNode* node)
TGeoNode*ReplaceNode(TGeoNode* nodeorig, TGeoShape* newshape = 0,
TGeoMatrix* newpos = 0, TGeoMedium* newmed = 0)
The last method allows replacing an existing daughter of a volume with another one. Providing only the node to be
replaced will just create a new volume for the node but having exactly the same parameters as the old one. This helps
in case of divisions for decoupling a node from the logical hierarchy so getting new content/properties. For non-divided
volumes, one can change the shape and/or the position of the daughter.
18.4.2.4 Virtual Containers and Assemblies of Volumes
Virtual containers are volumes that do not represent real objects, but they are needed for grouping and positioning
together other volumes. Such grouping helps not only geometry creation, but also optimizes tracking performance;
therefore, it is highly recommended. Virtual volumes need to inherit material/medium properties from the volume they
are placed into in order to be “invisible” at tracking time.
Let us suppose that we need to group together two volumes
A
and
B
into a structure and position this into several
other volumes
D,E,
and
F
. What we need to do is to create a virtual container volume
C
holding
A
and
B
, then position
Cin the other volumes.
Note that
C
is a volume having a determined medium. Since it is not a real volume, we need to manually set its
medium the same as that of
D,E
or
F
in order to make it ‘invisible’ (same physics properties). In other words, the
limitation in proceeding this way is that
D,E,
and
F
must point to the same medium. If this was not the case, we
would have to define different virtual volumes for each placement:
C
,
C’
and
C"
, having the same shape but different
media matching the corresponding containers. This might not happen so often, but when it does, it forces the creation
of several extra virtual volumes. Other limitation comes from the fact that any container is directly used by navigation
algorithms to optimize tracking. These must geometrically contain their belongings (positioned volumes) so that these
do not extrude its shape boundaries. Not respecting this rule generally leads to unpredictable results. Therefore
A
and
B
together must fit into
C
that has to fit also into
D,E,
and
F
. This is not always straightforward to accomplish,
especially when instead of Aand Bwe have many more volumes.
In order to avoid these problems, one can use for the difficult cases the class
TGeoVolumeAssembly
, representing an
assembly of volumes. This behaves like a normal container volume supporting other volumes positioned inside, but it
has neither shape nor medium. It cannot be used directly as a piece of the geometry, but just as a temporary structure
helping temporary assembling and positioning volumes.
If we define now
C
as an assembly containing
A
and
B
, positioning the assembly into
D,E
and
F
will actually position
only
A
and
B
directly into these volumes, taking into account their combined transformations
A/B
to
C
and
C
to
D/E/F
.
480 CHAPTER 18. THE GEOMETRY PACKAGE
This looks much nicer, is it? In fact, it is and it is not. Of course, we managed to get rid of the ‘unnecessary’ volume
C
in our geometry, but we end-up with a more flat structure for
D,E
and
F
(more daughters inside). This can get much
worse when extensively used, as in the case: assemblies of assemblies.
For deciding what to choose between using virtual containers or assemblies for a specific case, one can use for both
cases, after the geometry was closed:
gGeoManager->SetTopVolume(ptr_D);
gGeoManager->Test();
gGeoManager->RestoreMasterVolume();
The
ptr_D
is a pointer to volume
D
containing the interesting structure. The test will provide the timing for classifying
1 million random points inside D.
18.4.2.5 Examples of Volume Positioning
Now let us make a simple volume representing a copper wire. We suppose that a medium is already created (see
TGeoMedium class on how to create media).
We will create a TUBE shape for our wire, having Rmin=0cm,Rmax=0.01cm and a half-length dZ=1cm:
TGeoTube *tube = new TGeoTube("wire_tube",0,0.01,1);
One may omit the name for the shape
wire_tube,
if no retrieving by name is further needed during geometry building.
Different volumes having different names and materials can share the same shape.
Now let’s make the volume for our wire:
TGeoVolume *wire_co = new TGeoVolume("WIRE_CO",tube,
ptrCOPPER); //(*)
(*)
Do not bother to delete the media, shapes or volumes that you have created since all will be automatically cleaned
on exit by the manager class.
If we would have taken a look inside
TGeoManager::MakeTube()
method, we would have been able to create our wire
with a single line:
TGeoVolume *wire_co = gGeoManager->MakeTube("WIRE_CO",ptrCOPPER,
0,0.01,1); //(*)
(*)
The same applies for all primitive shapes, for which there can be found corresponding
MakeSHAPE()
methods. Their
usage is much more convenient unless a shape has to be shared between more volumes.
Let us make now an aluminum wire having the same shape, supposing that we have created the copper wire with the
line above:
TGeoVolume *wire_al = new TGeoVolume("WIRE_AL",wire_co>GetShape(),
ptrAL);
We would like now to position our wire in the middle of a gas chamber. We need first to define the gas chamber:
TGeoVolume *chamber = gGeoManager->MakeTube("CHAMBER",ptrGAS,
0,1,1);
Now we can put the wire inside:
chamber->AddNode(wire_co,1);
If we inspect now the chamber volume in a browser, we will notice that it has one daughter. Of course, the gas has
some container also, but let us keeps it like that for the sake of simplicity. Since we did not supply the third argument,
the wire will be positioned with an identity transformation inside the chamber.
18.4. GEOMETRY CREATION 481
18.4.2.6 Overlapping Volumes
Positioning volumes that does not overlap their neighbors nor extrude their container is sometimes quite strong
constraint. Having a limited set of geometric shapes might force sometimes overlaps. Since overlapping is contradictory
to containment, a point belonging to an overlapping region will naturally belong to all overlapping partners. The
answer provided by the modeller to “Where am I?” is no longer deterministic if there is no priority assigned.
There are two ways out provided by the modeller in such cases and we will illustrate them by examples.
•
Suppose we have 2 crossing tubes that we have to describe. Such a structure cannot be decomposed in a
containment schema. This is a typical example of simple structure that can be handled by using composite
shapes. What we have to do is to define as shapes the inner and outer parts of the tubes (tubes having
Rmin=0,Rmax=inner/outer radius), then to make a composite:
•C = (Tub1out+Tub2out)-(Tub1in+Tub2in)
•
On the other hand, if we have an EM calorimeter having a honeycomb structure, Boolean combinations do not
help anymore. Here the problem is that we usually have a very large number of cells that are naturally belonging
to the same container. This result in a very flat and slow structure for that particular container, which we
would very much want to avoid by introducing additional levels in depth. We can describe the basic cell as a
hexahedron that we can represent by using a polygon primitive shape. Instead of putting one by one all cells
in the same container, we can define rows of such elements, fitting in box-shaped containers. Then we can put
row-beside-row inside the container, making life much easier for its navigation algorithms. The problem is that in
order to reproduce the honeycomb structure out of rows of cells, we have to overlap row containers. Woops - we
have not obeyed rule No. 2 in positioning. The way out is to position our rows with a special prototype:
ptrCAL->AddNodeOverlap("ROW",nRow,matrixRow);
This will instruct the modeller that the daughter ROW inside CAL overlaps with something else. The modeller will
check this at closure time and build a list of possibly overlapping candidates. This option is equivalent with the option
MANY in GEANT3.
The modeller supports such cases only if user declares the overlapping nodes. In order to do that, one should use
TGeoVolume::AddNodeOverlap()
instead of
TGeoVolume::AddNode()
. When two or more positioned volumes are
overlapping, not all of them have to be declared so, but at least one. A point inside an overlapping region equally
belongs to all overlapping nodes, but the way these are defined can enforce the modeller to give priorities.
The general rule is that the deepest node in the hierarchy containing a point has the highest priority. For the same
geometry level, non-overlapping is prioritized over overlapping. In order to illustrate this, we will consider few examples.
We will designate non-overlapping nodes as ONLY and the others MANY as in GEANT3, where this concept was
introduced:
1.
The part of a MANY node B extruding its container A will never be “seen” during navigation, as if B was in fact
the result of the intersection of A and B.
2.
If we have two nodes A (ONLY) and B (MANY) inside the same container, all points in the overlapping region of
A and B will be designated as belonging to A.
3.
If A an B in the above case were both MANY, points in the overlapping part will be designated to the one defined
first. Both nodes must have the same medium.
4. The slices of a divided MANY will be as well MANY.
One needs to know that navigation inside geometry parts MANY nodes is much slower. Any overlapping part can be
defined based on composite shapes - might be in some cases a better way out.
18.4.2.7 Replicating Volumes
What can we do if our chamber contains two identical wires instead of one? What if then we would need 1000 chambers
in our detector? Should we create 2000 wires and 1000 chamber volumes? No, we will just need to replicate the ones
that we have already created.
chamber->AddNode(wire_co,1,new TGeoTranslation(0.2,0,0));
chamber->AddNode(wire_co,2,new TGeoTranslation(0.2,0,0));
482 CHAPTER 18. THE GEOMETRY PACKAGE
The 2 nodes that we have created inside chamber will both point to a
wire_co
object, but will be completely distinct:
WIRE_CO_1
and
WIRE_CO_2
. We will want now to place symmetrically 1000 chambers on a pad, following a pattern of
20 rows and 50 columns. One way to do this will be to replicate our chamber by positioning it 1000 times in different
positions of the pad. Unfortunately, this is far from being the optimal way of doing what we want. Imagine that we
would like to find out which of the 1000 chambers is containing a
(x,y,z)
point defined in the pad reference. You
will never have to do that, since the modeller will take care of it for you, but let’s guess what it has to do. The most
simple algorithm will just loop over all daughters, convert the point from mother to local reference and check if the
current chamber contains the point or not. This might be efficient for pads with few chambers, but definitely not
for 1000. Fortunately the modeller is smarter than that and creates for each volume some optimization structures
called
voxels
to minimize the penalty having too many daughters, but if you have 100 pads like this in your geometry
you will anyway loose a lot in your tracking performance. The way out when volumes can be arranged according
to simple patterns is the usage of divisions. We will describe them in detail later on. Let’s think now at a different
situation: instead of 1000 chambers of the same type, we may have several types of chambers. Let’s say all chambers
are cylindrical and have a wire inside, but their dimensions are different. However, we would like all to be represented
by a single volume family, since they have the same properties.
18.4.2.8 Volume Families
A volume family is represented by the class
TGeoVolumeMulti
. It represents a class of volumes having the same shape
type and each member will be identified by the same name and volume ID. Any operation applied to a
TGeoVolumeMulti
equally affects all volumes in that family. The creation of a family is generally not a user task, but can be forced in
particular cases:
TGeoManager::Volume(const char *vname,const char *shape,
Int_t nmed);
Where: vname is the family name, nmed is the medium number and shape is the shape type that can be:
•boxfor TGeoBBox
•trd1for TGeoTrd1
•trd2for TGeoTrd2
•trapfor TGeoTrap
•gtrafor TGeoGtra
•parafor TGeoPara
•tube,tubsfor TGeoTube,TGeoTubeSeg
•cone,consfor TGeoCone,TGeoCons
•eltufor TGeoEltu
•ctubfor TGeoCtub
•pconfor TGeoPcon
•pgonfor TGeoPgon
Volumes are then added to a given family upon adding the generic name as node inside other volume:
TGeoVolume *box_family = gGeoManager->Volume("BOXES","box",nmed);
// ...
gGeoManager->Node("BOXES",Int_t copy_no,"mother_name",Double_t x,
Double_t y,Double_t z,Int_t rot_index,Bool_t is_only,
Double_t *upar,Int_t npar);
•BOXES- name of the family of boxes
•copy_no- user node number for the created node
•mother_name- name of the volume to which we want to add the node
•x,y,z- translation components
•rot_index- index of a rotation matrix in the list of matrices
•upar- array of actual shape parameters
•npar- number of parameters
The parameters order and number are the same as in the corresponding shape constructors. Another particular case
where volume families are used is when we want that a volume positioned inside a container to match one ore more
container limits. Suppose we want to position the same box inside 2 different volumes and we want the Z size to match
the one of each container:
18.4. GEOMETRY CREATION 483
TGeoVolume *container1 = gGeoManager->MakeBox("C1",imed,10,10,30);
TGeoVolume *container2 = gGeoManager->MakeBox("C2",imed,10,10,20);
TGeoVolume *pvol = gGeoManager->MakeBox("PVOL",jmed,3,3,-1);
container1->AddNode(pvol,1);
container2->AddNode(pvol,1);
Note that the third parameter of
PVOL
is negative, which does not make sense as half-length on Z. This is interpreted
as: when positioned, create a box replacing all invalid parameters with the corresponding dimensions of the container.
This is also internally handled by the TGeoVolumeMulti class, which does not need to be instantiated by users.
18.4.2.9 Dividing Volumes
Volumes can be divided according a pattern. The simplest division can be done along one axis that can be:
X,Y,Z,Phi,Rxy or Rxyz
. Let’s take a simple case: we would like to divide a box in N equal slices along X co-
ordinate, representing a new volume family. Supposing we already have created the initial box, this can be done
like:
TGeoVolume *slicex = box->Divide("SLICEX",1,N);
Here
SLICEX
is the name of the new family representing all slices and 1 is the slicing axis. The meaning of the axis
index is the following: for all volumes having shapes like
box
,
trd1
,
trd2
,
trap
,
gtra
or
para -
1, 2, 3 mean X, Y, Z;
for
tube
,
tubs
,
cone
,
cons -
1 means
Rxy
, 2 means
phi
and 3 means Z; for
pcon
and
pgon
- 2 means
phi
and 3 means
Z; for spheres 1 means Rand 2 means phi.
In fact, the division operation has the same effect as positioning volumes in a given order inside the divided container -
the advantage being that the navigation in such a structure is much faster. When a volume is divided, a volume family
corresponding to the slices is created. In case all slices can be represented by a single shape, only one volume is added
to the family and positioned N times inside the divided volume, otherwise, each slice will be represented by a distinct
volume in the family.
Divisions can be also performed in a given range of one axis. For that, one has to specify also the starting coordinate
value and the step:
TGeoVolume *slicex = box->Divide("SLICEX",1,N,start,step);
A check is always done on the resulting division range: if not fitting into the container limits, an error message is
posted. If we will browse the divided volume we will notice that it will contain N nodes starting with index 1 up to N.
The first one has the lower X limit at
START
position, while the last one will have the upper X limit at
START+N*STEP
.
The resulting slices cannot be positioned inside another volume (they are by default positioned inside the divided one)
but can be further divided and may contain other volumes:
TGeoVolume *slicey = slicex->Divide("SLICEY",2,N1);
slicey->AddNode(other_vol,index,some_matrix);
When doing that, we have to remember that
SLICEY
represents a family, therefore all members of the family will be
divided on Y and the other volume will be added as node inside all.
In the example above all the resulting slices had the same shape as the divided volume (box). This is not always the
case. For instance, dividing a volume with
TUBE
shape on
PHI
axis will create equal slices having
TUBESEG
shape. Other
divisions can also create slices having shapes with different dimensions, e.g. the division of a TRD1 volume on Z.
When positioning volumes inside slices, one can do it using the generic volume family (e.g.
slicey
). This should be
done as if the coordinate system of the generic slice was the same as the one of the divided volume. The generic slice
in case of
PHI
division is centered with respect to X-axis. If the family contains slices of different sizes, any volume
positioned inside should fit into the smallest one.
Examples for specific divisions according to shape types can be found inside shape classes.
TGeoVolume::Divide(N,Xmin,Xmax,"X");
Create a new volume by dividing an existing one (GEANT3 like).
Divides
MOTHER
into
NDIV
divisions called
NAME
along axis
IAXIS
starting at coordinate value
START
and having size
STEP. The created volumes will have tracking media ID=NUMED (if NUMED=0 -> same media as MOTHER).
The behavior of the division operation can be triggered using OPTION (case insensitive):
484 CHAPTER 18. THE GEOMETRY PACKAGE
•Ndivide all range in NDIV cells (same effect as STEP<=0) (GSDVN in G3)
•NXdivide range starting with START in NDIV cells (GSDVN2 in G3)
•S
divide all range with given
STEP
;
NDIV
is computed and divisions will be centered in full range (same effect as
NDIV<=0) (GSDVS, GSDVT in G3)
•SXsame as DVS, but from START position (GSDVS2, GSDVT2 in G3)
18.4.2.10 Volume Assemblies
In general, geometry contains structures of positioned volumes that have to be grouped and handled together, for
different possible reasons. One of these is that the structure has to be replicated in several parts of the geometry, or it
may simply happen that they really represent a single object, too complex to be described by a primitive shape.
Usually handling structures like these can be easily done by positioning all components in the same container volume,
then positioning the container itself. However, there are many practical cases when defining such a container is not
straightforward or even possible without generating overlaps with the rest of the geometry. There are few ways out of
this:
•Defining the container for the structure as “overlapping” (see also " Overlapping Volumes **“**)
•
Representing the container as a composite shape - the Boolean union of all components (see also " Composite
Shapes “)
•Using an assembly volume - this will be described in the following.
The first two approaches have the disadvantage of penalizing the navigation performance with a factor increasing
more than linear of the number of components in the structure. The best solution is the third one because it uses all
volume-related navigation optimizations. The class
TGeoVolumeAssembly
represents an assembly volume. Its shape is
represented by TGeoShapeAssembly class that is the union of all components. It uses volume voxelization to perform
navigation tasks.
An assembly volume creates a hierarchical level and it geometrically insulates the structure from the rest (as a normal
volume). Physically, a point that is INSIDE a
TGeoShapeAssembly
is always inside one of the components, so a
TGeoVolumeAssembly
does not need to have a medium. Due to the self-containment of assemblies, they are very
practical to use when a container is hard to define due to possible overlaps during positioning. For instance, it is
very easy creating honeycomb structures. A very useful example for creating and using assemblies can be found at:
http://root.cern.ch/root/html/examples/assembly.C.html.
Creation of an assembly is very easy: one has just to create a
TGeoVolumeAssembly
object and position the components
inside as for any volume:
TGeoVolume *vol = new TGeoVolumeAssembly(name);
vol->AddNode(vdaughter1, cpy1, matrix1);
vol->AddNode(vdaughter2, cpy2, matrix2);
Note that components cannot be declared as “overlapping” and that a component can be an assembly volume. For
existing flat volume structures, one can define assemblies to force a hierarchical structure therefore optimizing the
performance. Usage of assemblies does NOT imply penalties in performance, but in some cases, it can be observed
that it is not as performing as bounding the structure in a container volume with a simple shape. Choosing a normal
container is therefore recommended whenever possible.
18.4.3 Geometrical Transformations
All geometrical transformations handled by the modeller are provided as a built-in package. This was designed
to minimize memory requirements and optimize performance of point/vector master-to-local and local-to-master
computation. We need to have in mind that a transformation in
TGeo
has two major use-cases. The first one is for
defining the placement of a volume with respect to its container reference frame. This frame will be called ‘master’
and the frame of the positioned volume - ‘local’. If
T
is a transformation used for positioning volume daughters, then:
MASTER = T * LOCAL
Therefore
T
is used to perform a local to master conversion, while
T-1
for a master to local conversion. The second
use case is the computation of the global transformation of a given object in the geometry. Since the geometry is
built as ‘volumes-inside-volumes’, the global transformation represents the pile-up of all local transformations in the
corresponding branch. Once a given object in the hierarchy becomes the current one, the conversion from master to
local coordinates or the other way around can be done from the manager class.

18.4. GEOMETRY CREATION 485
Figure 18.29: Assemblies of volumes
A general homogenous transformation is defined as a 4x4 matrix embedding a rotation, a translation and a scale. The
advantage of this description is that each basic transformation can be represented as a homogenous matrix, composition
being performed as simple matrix multiplication.
Rotation:
r11 r12 r13 0
r21 r22 r23 0
r31 r32 r33 0
0 0 0 1
Translation:
1 0 0 0
0 1 0 0
0 0 1 0
txtytz1
Scale:
sx0 0 0
0sy0 0
0 0 sz0
0 0 0 1
Inverse rotation:
r11 r21 r31 0
r12 r22 r32 0
r13 r23 r33 0
0 0 0 1
Inverse translation:
1 0 0 0
0 1 0 0
0 0 1 0
−tx−ty−tz1
Inverse scale:
1
sx0 0 0
01
sy0 0
0 0 1
sz0
0 0 0 1
•rij are the 3x3 rotation matrix components
•tx,ty,tzare the translation components
•sx,sy,szare arbitrary scale constants on each axis
The disadvantage in using this approach is that computation for 4x4 matrices is expensive. Even combining two
translations would become a multiplication of their corresponding matrices, which is quite an undesired effect. On
the other hand, it is not a good idea to store a translation as a block of 16 numbers. We have therefore chosen to
implement each basic transformation type as a class deriving from the same basic abstract class and handling its
specific data and point/vector transformation algorithms.
The base class TGeoMatrix defines abstract methods for:
•
Translation, rotation and scale getters. Every derived class stores only its specific data, e.g. a translation stores
an array of 3 doubles and a rotation an array of 9. However, getting the
TGeoTranslation
rotation array through
the base
TGeoMatrix
interface is a legal operation. The answer in this case is a pointer to a global constant array
representing an identity rotation.
Double_t *TGeoMatrix::GetTranslation() const;
Double_t *TGeoMatrix::GetRotation() const;
Double_t *TGeoMatrix::GetScale() const;
•Master-to-local and local-to-master point and vector transformations :
void TGeoMatrix::MasterToLocal(const Double_t *master,
Double_t *local)
486 CHAPTER 18. THE GEOMETRY PACKAGE
void TGeoMatrix::LocalToMaster(const Double_t *local,
Double_t *master)
void TGeoMatrix::MasterToLocalVect(const Double_t *master,
Double_t *local)
void TGeoMatrix::LocalToMasterVect(const Double_t *local,
Double_t *master)
Here master and local are arrays of size 3. These methods allow correct conversion also for reflections.
•Transformation type finding:
Bool_t TGeoMatrix::IsIdentity() const;
Bool_t TGeoMatrix::IsTranslation() const;
Bool_t TGeoMatrix::IsRotation() const;
Bool_t TGeoMatrix::IsScale() const;
Bool_t TGeoMatrix::IsCombi() const;// (tr. + rot.)
Bool_t TGeoMatrix::IsGeneral() const;// (tr. + rot. + scale)
Specific classes deriving from
TGeoMatrix
represent combinations of basic transformations. In order to define a matrix
as a combination of several others, a special class TGeoHMatrix is provided. Here is an example of matrix creation:
18.4.3.1 Matrix Creation Example
TGeoRotation r1,r2;
r1.SetAngles(90,0,30); //rotation defined by Euler angles
r2.SetAngles(90,90,90,180,0,0); //rotation defined by GEANT3 angles
TGeoTranslation t1(-10,10,0);
TGeoTranslation t2(10,-10,5);
TGeoCombiTrans c1(t1,r1);
TGeoCombiTrans c2(t2,r2);
TGeoHMatrix h = c1 * c2; // composition is done via TGeoHMatrix
TGeoHMatrix *ph = new TGeoHMatrix(hm); // class it is what we want
// to use for positioning
// a volume
ph->Print();
...
pVolume->AddNode(pVolDaughter,id,ph) // now ph is owned by
the manager
18.4.3.2 Rule for Creation of Transformations
Unless explicitly used for positioning nodes
(TGeoVolume::AddNode())
all matrices deletion have to be managed by
users. Matrices passed to geometry have to be created by using
new()
operator and
TGeoManager
class is responsible
for their deletion. Matrices that are used for the creation of composite shapes have to be named and registered to the
manager class:
transf->SetName(name); // if not already named in the constructor
transf->RegisterYourself();
Generally, it is advisable to create all intermediate transformations used for making the final combined one on the heap:
TGeoRotation r1(...);
TGeoRotation r2(...);
TGeoHMatrix *mat = new TGeoHMatrix("name"); // we want to use only
// this one in geometry
*mat = r1 * r2;
18.4. GEOMETRY CREATION 487
18.4.3.3 Available Geometrical Transformations
•
Translations (
TGeoTranslation
class) represent a
(dx,dy,dz)
translation. The only data member is:
Double_t
fTranslation[3]. Translations can be added or subtracted.
TGeoTranslation t1;
t1->SetTranslation(-5,10,4);
TGeoTranslation *t2 = new TGeoTranslation(4,3,10);
t2->Subtract(&t1);
•
Rotations (
TGeoRotation
class) represent a pure rotation. Data members are
Double_t fRotationMatrix[3*3]
.
Rotations can be defined either by Euler angles, either, by GEANT3 angles:
TGeoRotation *r1 = new TGeoRotation();
r1->SetAngles(phi,theta,psi); // all angles in degrees
This represents the composition of: first a rotation about Z axis with angle phi, then a rotation with theta about the
rotated X axis, and finally a rotation with psiabout the new Z axis.
r1->SetAngles(th1,phi1,th2,phi2,th3,phi3)
This is a rotation defined in GEANT3 style. Theta and phi are the spherical angles of each axis of the rotated coordinate
system with respect to the initial one. This construction allows definition of malformed rotations, e.g. not orthogonal.
A check is performed and an error message is issued in this case.
Specific utilities: determinant, inverse.
•
Scale transformations (
TGeoScale
class) - represent a scaled shrinking/enlargement, possibly different on all axes.
Data members: Double_t fScale[3]. Not implemented yet.
•
Combined transformations - represent a rotation followed by a translation. Data members:
Double_t
fTranslation[3],TGeoRotation *fRotation.
TGeoRotation *rot = new TGeoRotation("rot",10,20,30);
TGeoTranslation trans;
...
TGeoCombiTrans *c1 = new TGeoCombiTrans(trans,rot);
TGeoCombiTrans *c2 = new TGeoCombiTrans("somename",10,20,30,rot)
•General transformations: (TGeoHMatrix class) represent combined transformations in any order.
•
Identity transformation: (
TGeoIdentity
class) is a generic identity transformation represented by a singleton
class object gGeoIdentity.
18.4.4 Ownership of Geometry Objects
The class
TGeoManager
class contains the entire API needed for building and tracking geometry. It defines a global
pointer
gGeoManager
in order to be fully accessible from external code. The manager class is the owner of all geometry
objects defined in a session; therefore, users must not try to control their deletion. It contains lists of media, materials,
transformations, shapes and volumes. A special case is the one of geometrical transformations. When creating
a matrix or a translation, this is by default owned by external objects. The manager class becomes owner of all
transformations used for positioning volumes. In order to force the ownership for other transformations, one can use
TGeoMatrix::RegisterYourself()
method. Do not be therefore surprised that some transformations cannot be found
by name when creating a composite shape for instance if you did not register them after creation.
Logical nodes (positioned volumes) are created and destroyed by the
TGeoVolume
class. Physical nodes and their global
transformations are subjected to a caching mechanism due to the sometimes very large memory requirements of logical
graph expansion. The total number of physical instances of volumes triggers the caching mechanism and the cache
manager is a client of
TGeoManager
. The manager class also controls the drawing/checking package (
TGeoPainter
client). This is linked with ROOT graphical libraries loaded on demand in order to control visualization actions.
488 CHAPTER 18. THE GEOMETRY PACKAGE
18.5 Navigation and Tracking
Tracking is the feature allowing the transport of a given particle knowing its kinematics. A state is determined by any
combination of the position
~r
and direction
~n
with respect to the world reference frame. The direction
~n
must be a
unit vector having as components the director cosines. The full classification of a given state will provide the following
information: the deepest physical node containing the position vector, the distance to the closest boundary along the
direction vector, the next physical node after propagating the current point with this distance and the safety distance
to the nearest boundary. This information allows the propagation of particles inside a detector geometry by taking into
account both geometrical and physical constraints.
We will hereby describe the user interface of
TGeo
to access tracking functionality. This allows either developing a
tracker for simple navigation within a given geometry, either interfacing to an external tracking engine such as GEANT.
Note that the abstract interface for external trackers can be found in
$ROOTSYS/vmc
folder and it can be used to run
GEANT3, GEANT4 and FLUKA-based simulations (*) by using directly a geometry described with ROOT.
The interface methods related to tracking are incorporated into
TGeoManager
class and implemented in the navigator
class
TGeoNavigator
. In order to be able to start tracking, one has to define the initial state providing the starting
point ~r0and direction ~n0. There are several ways of doing that.
18.5.1 TGeoNavigator Class
One geometry may have several independent navigators to query to localize points or compute distances. The geometry
manager holds a list of active navigators accessible via:
TObjArray *navigators = gGeoManager->GetListOfNavigators();
Upon closing the geometry a default navigator is provided as first one in this list, but one may add its own via:
TGeoNavigator *navig = new TGeoNavigator(gGeoManager);
// Store the index of the user navigator
Int_t inav = gGeoManager->AddNavigator(navig);
// Make its own navigator the active one
gGeoManager->SetCurrentNavigator(inav);
// Switch between navigators
gGeoManager->SetCurrentNavigator(0);
A navigator holds several variables describing the current navigation state: current point position, current direction
distance to next boundary, isotropic safety, pointer to current and next nods as well as several tracking flags related to
volume boundary conditions or other properties required for track propagation in geometry. Each geometry query affects
these variables, so the only way in testing several navigation alternatives and remembering the active navigation state is
to use parallel navigation. The following paragraphs will describe the usage of a single navigator. All setters/getters for
navigation state parameters as well as navigation queries provided by
TGeoNavigator
are interfaced by
TGeoManager
and will act on the current navigator.
18.5.2 Initializing the Starting Point
The current point (
x,y,z
) known by the modeller is stored as
Double_t fCurrentPoint[3]
by the navigator class.
This array of the three coordinates is defined in the current global reference system and can be retrieved any time:
Const Double_t *cpoint = gGeoManager->GetCurrentPoint();
Initializing this point can be done like:
gGeoManager->SetCurrentPoint(x,y,z);
// or:
gGeoManager->SetCurrentPoint(Double_t *point[3]);
18.5. NAVIGATION AND TRACKING 489
18.5.3 Initializing the Direction
In order to move inside geometry starting with the current point, the modeller needs to know the current direction
(nx,ny,nz)
. This direction is stored as
Double_t fCurrentDirection[3]
by the navigator and it represents a
direction in the global frame. It can be retrieved with:
Const Double_t *cdir = gGeoManager->GetCurrentDirection();
The direction can be initialized in a similar manner as the current point:
gGeoManager->SetCurrentDirection(nx,ny,nz);
// or:
gGeoManager->SetCurrentDirection(Double_t *dir);
18.5.4 Initializing the State
Setting the initial point and direction is not enough for initializing tracking. The modeller needs to find out where the
initial point is located in the geometrical hierarchy. Due to the containment based architecture of the model, this is the
deepest positioned object containing the point. For illustrating this, imagine that we have a simple structure with a top
volume
A
and another one
B
positioned inside. Since
A
is a top volume, its associated node
A_1
will define
MARS
and our
simple hierarchy of nodes (positioned volumes) will be:
/A_1/B_1
. Suppose now that the initial point is contained by
B_1
. This implies by default that the point is also contained by
A_1
, since
B_1
have to be fully contained by this. After
searching the point location, the modeller will consider that the point is located inside
B_1
, which will be considered as
the representative object (node) for the current state. This is stored as:
TGeoNode
*
TGeoManager::fCurrentNode
and
can be asked from the manager class only after the ’Where am I?’ was completed:
TGeoNode *current = gGeoManager->GetCurrentNode();
In order to find the location of the current point inside the hierarchy of nodes, after setting this point it is mandatory
to call the ‘Where am I?’ method:
gGeoManager->FindNode();
In order to have more flexibility, there are in fact several alternative ways of initializing a modeller state:
// Setting the point and finding the state in one step:
gGeoManager->FindNode(Double_t x,Double_t y,Double_t z);
gGeoManager->FindNode(Double_t *point[3]);
// Setting both initial point and direction and finding the state:
gGeoManager->InitTrack(Double_t x,Double_t y,Double_t z,
Double_t nx, Double_t ny, Double_t nz);
gGeoManager->InitTrack(Double_t *point[3],Double_t *dir[3]);
Note that the current point coordinates can be changed and the state re-initialized at any time. This represents the
‘Where am I?’ geometrical query representing the basic navigation functionality provided by the modeller.
18.5.5 Checking the Current State
The current state and all variables related to this are essential during tracking and have to be checked several times.
Besides the current point and direction, the following additional information can be retrieved from
TGeoManager
interface:
•
The
current path
. This represents a string containing the names and copy numbers of all positioned objects in
the current
branch
written in the /folder/folder/. . . /folder/file fashion. The final node pointed by the path is the
deepest object containing the current point and is representative for the current state. All intermediate
folders
in the path are in fact also nodes “touched” by the current point, but having some “touched” containment. The
current path can be retrieved only after the state was initialized and is useful for getting an idea of the current
point location.
490 CHAPTER 18. THE GEOMETRY PACKAGE
const char *path = gGeoManager->GetPath();
cout << "Current path is: " << path << endl;
/A_1/B_34/C_3/D_1
•
The
current node,volume
and
material
. In order to take decisions on post-step or further stepping actions,
one has to know these. In order to get a pointer to the current node one can do:
TGeoNode *cnode = gGeoManager->GetCurrentNode();
// then:
TGeoVolume *cvol = gGeoManager->GetCurrentVolume();
// or:
cvol = cnode->GetVolume(); // (*)
// then:
TGeoMaterial *cmat = cvol->GetMedium()->GetMaterial();
(*) Note: If the current point is in fact outside the geometry, the current node pointer will not be NULL, but pointing
to the top node.
In order to take decisions in such case one needs always to test:
if (gGeoManager->IsOutside()) {
// current point is actually outside
... // corresponding action
}
Specific information related to the current volume/node like ID’s or shape can be then retrieved from the corresponding
objects.
•
Current state
index
. The number of possible different states of the modeller corresponds to the number of
different objects/paths in the geometry. This has nothing to do with the number of nodes, since the same node
can be found on different branches. In other words, the number of states corresponds to the number of nodes in
the
expanded geometry tree
. Since unfortunately this expansion from logical to physical hierarchy cannot be
stored on regular basis due to the large size of the latter, one cannot directly assign state numbers. If the size of
the expansion proves however to be small enough (less than about 50 million objects), a parallel structure storing
these state indices is built and stored in memory. In such case each state automatically gets an index that can be
retrieved after any state initialization. These indices can prove to be quite useful for being able to keep track of
the navigation history and force certain states. Let’s illustrate how this works with a simple example:
•
Suppose we have a simple geometry with a volume B positioned twice inside a container A. Then A is positioned
twice in a top container T. The complete list of logical nodes is:
T_1
,
A_1
,
A_2
,
B_1
,
B_2
. On the other hand we
will have more states than logical nodes:
•/T_1- 1 state at level = 0
•/T_1/A_1,/T_1/A_2- 2 states at level = 1
•/T_1/A_1/B_1,/T_1/A_1/B_2,/T_1/A_2/B_1,/T_1/A_2/B_2 - 4 states at level = 2
•
All these states will get automatic numbers, starting with 0 corresponding to the top-level state and ending
with an integer corresponding to Ntotal_states-1. The mapping from a given logical node to a state number is
generally not possible, as for the node B_1 that appears as current node for 2 different states. The numbering
order of states is therefore not important, but it can be used as in the following lines:
gGeoManager->InitTrack(pt,dir); // anything to initialize a state
Int_t istate = gGeoManager->GetCurrentNodeId(); // in fact state Id
{
//... code changing the current state
}
gGeoManager->CdNode(istate); // forces state's re-initialization
•
Current
global transformation
. This represents the transformation from
MARS
to the local reference of
the current node, being the product of all local mother-daughter transformations in the branch. The global
transformation can be referenced or copied:
const TGeoHMatrix *global = gGeoManager->GetCurrentMatrix();
TGeoHMatrix *copy = new TGeoHMatrix(*global);
18.5. NAVIGATION AND TRACKING 491
•
One often needs to perform
master-to-local
and
local-to-master
point and vector conversions to get from
MARS
to the local node coordinates. This can be done by using the global transformation or directly the
TGeoManager corresponding interfaces:
Double_t *glob_pt = gGeoManager->GetCurrentPoint();
Double_t *glob_dir = gGeoManager->GetCurrentDirection();
Double_t loc_pt[3], loc_dir[3];
// Go from MARS to local coordinates:
gGeoManager->MasterToLocal(glob_pt,loc_pt); // or:
global->MasterToLocal(glob_pt,loc_pt); // will be omitted from now
18.5.6 Saving and Restoring the Current State
As we already described, saving and restoring modeller states can be quite useful during tracking and is a feature
extensively used by external tracking engines. We will call this navigation history management, which in most of
the cases can be performed by handling the state identifiers. For quite big geometries, state indexing is not possible
anymore and will be automatically disabled by the modeller. Fortunately there is a backup solution working in any
condition: the modeller maintains a stack of states that is internally used by its own navigation algorithms, but user
code is also allowed to access it. This works on any stack principle by using PUSH and POP calls and user code is
responsible for popping the pushed states in order to keep the stack clean.
// push the current state in the stack
Int_t index = gGeoManager->PushPath();
// push state and current point
Int_t index = gGeoManager->PushPoint();
// retrieves the last pushed state (decrements stack index)
gGeoManager->PopPath();
// the same but retrieves also the point location
gGeoManager->PopPoint();
// just decrement stack index without changing state
gGeoManager->PopDummy();
// retrieves a state at given index without changing stack index
gGeoManager->PopPath(Int_t index);
18.5.7 Navigation Queries
After initializing the current state related to a given point and direction defined in
MARS (‘Where am I?’)
, one can
query for several geometrical quantities. All the related algorithms work in the assumption that the current point has
been localized inside the geometry (by the methods
TGeoManager::FindNode()
or
TGeoManager::InitTrack()
) and
the current node or path has not been changed by the user.
18.5.7.1 Finding If Current State Is Changed For a New Point
One can find fast if a point different from the current one has or not the same location inside the geometry tree. To
do that, the new point should not be introduced by using
TGeoManager::SetCurrentPoint()
method, but rather by
calling the specific method:
Bool_t TGeoManager::IsSameLocation(Double_t x,Double_t y,
Double_t z,Bool_t change=kFALSE);
In the prototype above,
x, y
and
z
are the coordinates of the new point. The modeller will check whether the current
volume still contains the new point or its location has changed in the geometry hierarchy. If the new location is different,
two actions are possible according to the value of change:
•change = kFALSE
(default) - the modeller does not change the current state but just inform the caller about this
change.
•change = kTRUE
- the modeller will actually perform a new
‘Where am I?’
search after finding out that the
location has changed. The current state will be actualized accordingly.
492 CHAPTER 18. THE GEOMETRY PACKAGE
Note that even when performing a normal search on the current state after changing the current point coordinates
(e.g.
gGeoManager->FindNode(newX,newY,newZ)
), users can always query if the previous state has changed by using
a method having the same name but without parameters:
Bool_t TGeoManager::IsSameLocation();
18.5.7.2 Finding the Distance to the Next Boundary
All tracking engines need to compare the currently proposed physical step with the maximum allowed distance in the
current material. The modeller provides this information by computing the distance to the first boundary starting from
the current point along a straight line. The starting point and direction for this procedure are the ones corresponding
to the current state. The boundary search is initialized inside the current volume and the crossed boundary can belong
either to the current node or to one of its daughters. The full prototype of the method is:
TGeoNode *TGeoManager::FindNextBoundary(Double_t step=kBig);
In the prototype above, besides the current point and direction that are supposed already initialized, the only input
parameter is
step
. This represents the maximum step allowed by the tracking algorithm or the
physical step
. The
modeller will search for a boundary crossing only up to a distance equal to this value. If a boundary is found, a pointer
to the object (node) having it is returned; otherwise the method returns NULL.
The computed value for the computed distance can be subsequently retrieved from the manager class:
Double_t snext = gGeoManager->GetStep();
Double_t safety = gGeoManager->GetSafeDistance();
According the step value, two use cases are possible:
•step = TGeoShape::kBig
(default behavior;
kBig = 1030
). In this case, there is no limitation on the search
algorithm, the first crossed node is returned and the corresponding distance computed. If the current point is
outside geometry and the top node is not crossed, the corresponding distance will be set to
kBig
and a
NULL
pointer returned. No additional quantity will be computed.
•step < kBig
. In this case, the progressive search starting from the current point will be stopped after a distance
equal with the supplied step. In addition to the distance to the first crossed boundary, the
safety radius
is
also computed. Whenever the information regarding the maximum required step is known it is recommended to
be provided as input parameter in order to speed-up the search.
In addition to the distance computation, the method sets an additional flag telling if the current track will enter inside
some daughter of the current volume or it will exit inside its container:
Bool_t TGeoManager::IsStepEntering() const;
A combined task is to first find the distance to the next boundary and then extrapolate the current point/direction
with this distance making sure that the boundary was crossed. Finally the goal would be to find the next state after
crossing the boundary. The problem can be solved in principle using FindNextBoundary, but the boundary crossing can
give unpredictable results due to numerical roundings. The manager class provides a method that allows this combined
task and ensures boundary crossing. This should be used instead of the method
FindNextBoundary()
whenever the
tracking is not imposed in association with an external MC transport engine (which provide their own algorithms for
boundary crossing).
TGeoNode *TGeoManager::FindNextBoundaryAndStep(Double_t stepmax,
Bool_t comp_safe=kFALSE);
The meaning of the parameters here is the same as for FindNextBoundary, but the safety value is triggered by an
input flag. The output is the node after the boundary crossing.
18.5. NAVIGATION AND TRACKING 493
18.5.7.3 Computing the Safe Radius
Other important navigation query for tracking is the computation of the safe distance. This represents the
maximum
step
that can be made from the current point in
any direction
that assures that no boundary will be crossed. Knowing
this value gives additional freedom to the stepping algorithm to propagate the current track on the corresponding
range
without checking
if the current state has changed. In other words, the modeller insures that the current state
does not change in any point within the safety radius around the current point.
The computation of the safe radius is
automatically
computed any time when the next boundary is queried within a
limited step:
TGeoNode *crossed = gGeoManager->FindNextBoundary(pstep);
Double_t safety = gGeoManager->GetSafeDistance();
Otherwise, the computation of safety can always be forced:
Double_t safety = gGeoManager->Safety();
18.5.7.4 Making a Step
The modeller is able to make steps starting from the current point along the current direction and having the current
step length. The new point and its corresponding state will be automatically computed:
TGeoNode *TGeoManager::Step(Bool_t is_geom = kTRUE,
Bool_t cross = kTRUE);
We will explain the method above by its use cases. The input flag
is_geom
allows specifying if the step is limited by
geometrical reasons (a boundary crossing) or is an arbitrary step. The flag cross can be used in case the step is made
on a boundary and specifies if user wants to cross or not the boundary. The returned node represents the new current
node after the step was made.
•
Making a geometrically contained step with boundary crossing (
is_geom=kTRUE
,
cross=kTRUE
) - This is
the default method behavior. In this case, the step size is supposed to be already set by a previous
TGeoManager::FindNextBoundary()
call. Due to floating-point boundary uncertainties, making a step
corresponding
exactly
to the distance to next boundary does not insure boundary crossing. If the method is
called with this purpose, an extra small step will be made in order to make the crossing the most probable event
(
epsil=10-6cm
). Even with this extra small step cannot insure 100% boundary crossing for specific crossed
shapes at big incident angles. After such a step is made, additional cross-checks become available:
gGeoManager->FindNextBoundary(pstep);
Double_t snext = gGeoManager->GetStep();
// The geometrical step is taken
TGeoNode *newNode = gGeoManager->Step();
// The step=snext+epsil is made
Bool_t hasCrossed = gGeoManager->IsEntering();
// Is the boundary crossed or not?
Bool_t isOnBoundary = gGeoManager->IsOnBoundary(); // The proposed
// geometrically limited step to be made was smaller
// than epsil value.
Bool_t isOutside = gGeoManager->IsOutside();
//Did we exit geometry ?
In case the desired end-point of the step should be in the same starting volume, the input flag
cross
should be set to
kFALSE. In this case, the epsil value will be subtracted from the current step.
•
Making a step of arbitrary value (
is_geom=kFALSE
,
cross=
no matter). In this case, the step to be made can be
either resulting from a next computation, either set by hand:
gGeoManager->SetStep(stepvalue);
gGeoManager->Step(kFALSE);
The step value in this case will
exactly
match the desired step. In case a boundary crossing failed after geometrically
limited stepping, one can force as many small steps as required to really cross the boundary. This is not what generally
happens during the stepping, but sometimes small rounding of boundary positions may occur and cause problems.
These have to be properly handled by the stepping code.
494 CHAPTER 18. THE GEOMETRY PACKAGE
18.5.7.5 The Normal Vector to the Next Crossed Surface at Crossing Point
Supposing we have found out that a particle will cross a boundary during the next step, it is sometimes useful to
compute the normal to the crossed surface. The modeller uses the following convention: we define as
normal
(
~n
) the
unit vector perpendicular to a surface in the
next crossing point
, having the orientation such that:
~n.~
d >
0. Here
~
d
represents the current direction. The next crossing point represents the point where a ray shot from the current point
along the current direction crosses the surface.
Double_t *TGeoManager::FindNormal(Bool_t forward=kTRUE);
The method above computes the normal to the next crossed surface in forward or backward direction (i.e. the current
one), assuming the state corresponding to a current arbitrary point is initialized. An example of usage of normal
computation is ray tracing.
The two most important features of the geometrical modeller concerning tracking are scalability and performance as
function of the total number of physical nodes. The first refers to the possibility to make use of the available memory
resources and at the same time be able to resolve any geometrical query, while the second defines the capability of
the modeller to respond quickly even for huge geometries. These parameters can become critical when simulating big
experiments like those at LHC.
18.5.8 Creating and Visualizing Tracks
In case the modeller is interfaced with a tracking engine, one might consider quite useful being able to store and
visualize at least a part of the tracks in the context of the geometry. The base class
TVirtualGeoTrack
provides this
functionality. It currently has one implementation inside the drawing package (
TGeoTrack
class). A track can be
defined like:
TVirtualGeoTrack(Int_t id,Int_t pdg,TVirtualGeoTrack *parent=0,
TObject *particle=0);
Where:
id
is user-defined id of the track,
pdg
-
pdg
code,
parent
- a pointer to parent track,
particle
- a pointer to
an arbitrary particle object (may be a TParticle).
A track has a list of daughters that have to be filled using the following method:
TVirtualGeoTrack *TVirtualGeoTrack::AddDaughter(Int_t id,Int_t pdg,
TObject *particle=0);
The method above is pure virtual and have to create a track daughter object. Tracks are fully customizable objects
when inheriting from
TVirtualGeoTrack
class. We will describe the structure and functionality provided by the default
implementation of these, which are TGeoTrack objects.
A
TGeoTrack
is storing a list of
control points (x,y,z)
belonging to the track, having also time information
(t)
.
The painting algorithm of such tracks allows drawing them in any time interval after their creation. The track position
at a given time is computed by interpolation between control points.
myTrack->AddPoint(x,y,z,t);
The creation and management of tracks is in fact fully controlled by the
TGeoManager
class. This holds a list of
primary tracks
that is also visible during browsing as
Tracks
folder. Primary tracks are tracks having no parent
in the tracking history (for instance the output of particle generators may be considered as primaries from tracking
point of view). The manager class holds in
TGeoManager::fCurrentTrack a pointer to the current track. When
starting tracking a particle, one can create a track object like:
Int_t track_index = gGeoManager->AddTrack(id,pdg,ptrParticle);
Here
track_index
is the index of the newly created track in the array of primaries. One can get the pointer of this
track and make it known as current track by the manager class:
18.6. CHECKING THE GEOMETRY 495
TVirtualGeoTrack *track = gGeoManager->GetTrack(track_index);
gGeoManager->SetCurrentTrack(track);
// or directly
gGeoManager->SetCurrentTrack(track_index);
TVirtualGeoTrack *current = gGeoManager->GetCurrentTrack();
One can also look for a track by user id or track index:
ptrTrack = gGeoManager->GetTrackOfId(user_id);
ptrParent = gGeoManager->GetParentTrackOfId(user_id);
ptrTrack = gGeoManager->GetTrack(index);
Supposing a particle represented by a primary track decays or interacts, one should not create new primaries as
described before, but rather add them as secondary:
TVirtualGeoTrack *secondary =
ptrTrack->AddTrack(secondId,pdg,secondParticle);
At any step made by the current track, one is able to add control points to either primary or secondary:
track->AddPoint(x,y,z,t);
After tracks were defined and filled during tracking, one will be able to browse directly the list of tracks held by the
manager class. Any track can be drawn using its
Draw()
and
Animate()
methods, but there are also global methods
for drawing or animation that can be accessed from TGeoManager context menu:
TGeoManager::DrawTracks(Option_t *option);
TGeoManager::AnimateTracks(Double_t tmin=0.,Double_t tmax=1E-8,
Int_t nframes=200,Option_t *option="");
The drawing/animation time range is a global variable that can be directly set:
gGeoManager->SetTminTmax(tmin, tmax);
// without arguments resets the time range to the maximum value
Once set, the time range will be active both for individual or global track drawing. For animation, this range is divided
to the desired number of frames and will be automatically updated at each frame in order to get the animation effect.
The option provided to all track-drawing methods can trigger different track selections:
default:A track (or all primary tracks) drawn without daughters
/D: Track and first level descendents only are drawn
/*: Track and all descendents are drawn
/Ntype: All tracks having name=type are drawn
Generally several options can be concatenated in the same string (E.g. "/D /Npion-").
For animating tracks, additional options can be added:
/G:
Geometry animate. Generally when drawing or animating tracks, one has to first perform a normal drawing of the
geometry as convenient. The tracks will be drawn over the geometry. The geometryitself will be animated (camera
moving and rotating in order to “catch” the majority of current track segments.)
/S:
Save all frames in gif format in the current folder. This option allows creating a movie based on individual frames.
18.6 Checking the Geometry
Several checking methods are accessible from the context menu of volume objects or of the manager class. They generally
apply only to the visible parts of the drawn geometry in order to ease geometry checking, and their implementation is
in the
TGeoChecker
class. The checking package contains an overlap checker and several utility methods that generally
have visualization outputs.
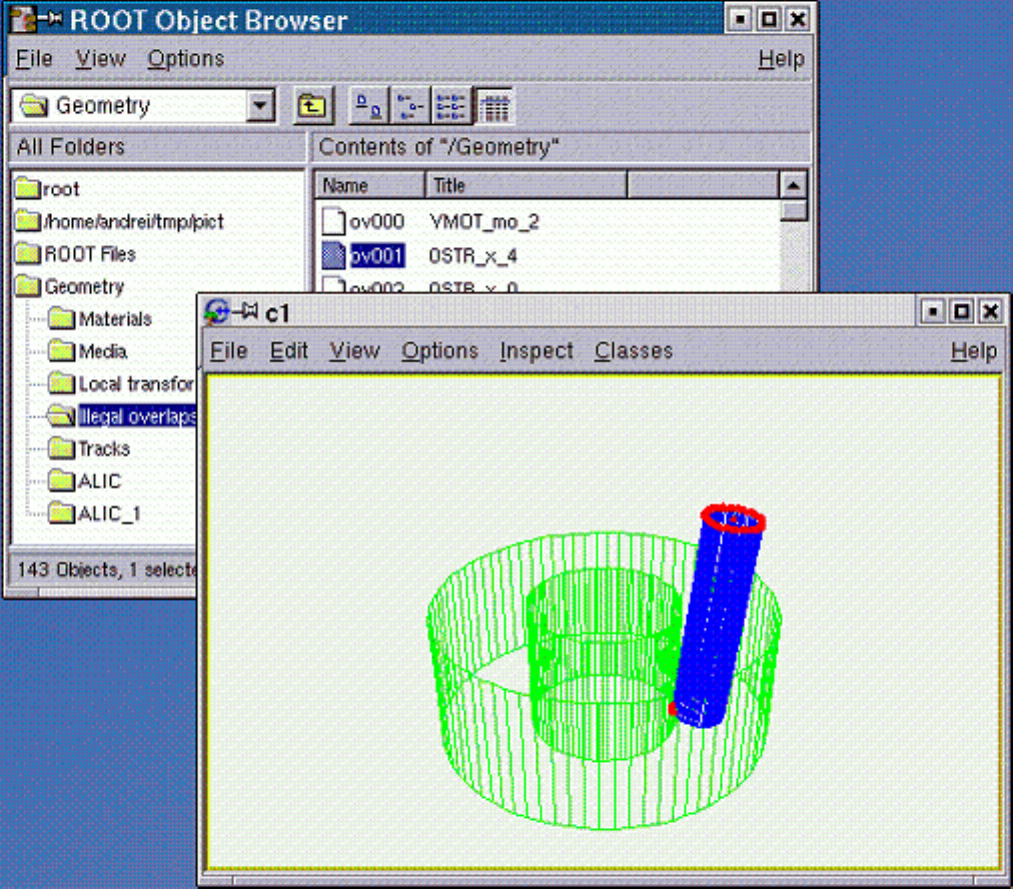
496 CHAPTER 18. THE GEOMETRY PACKAGE
18.6.1 The Overlap Checker
An overlap is any region in the Euclidian space being contained by more than one positioned volume. Due to the
containment scheme used by the modeller, all points inside a volume have to be also contained by the mother therefore
are overlapping in that sense. This category of overlaps is ignored due to the fact that any such point is treated as
belonging to the deepest node in the hierarchy.
Figure 18.30: Extruding volumes
A volume containment region is in fact the result of the subtraction of all daughters. On the other hand, there are two
other categories of overlaps that are considered illegal since they lead to unpredictable results during tracking.
A)
If a positioned volume contains points that are not also contained by its mother, we will call the corresponding
region as an
extrusion
. When navigating from outside to inside (trying to enter such a node) these regions are
invisible since the current track has not yet reached its mother. This is not the case when going the other way
since the track has first to exit the extruding node before checking the mother. In other words, an extrusion
behavior is dependent on the track parameters, which is a highly undesirable effect.
B)
We will call
overlaps
only the regions in space contained by more than one node inside the same container.
The owner of such regions cannot be determined based on hierarchical considerations; therefore they will be
considered as belonging to the node from which the current track is coming from.
When coming from their container, the ownership is totally unpredictable. Again, the ownership of overlapping regions
highly depends on the current track parameters.
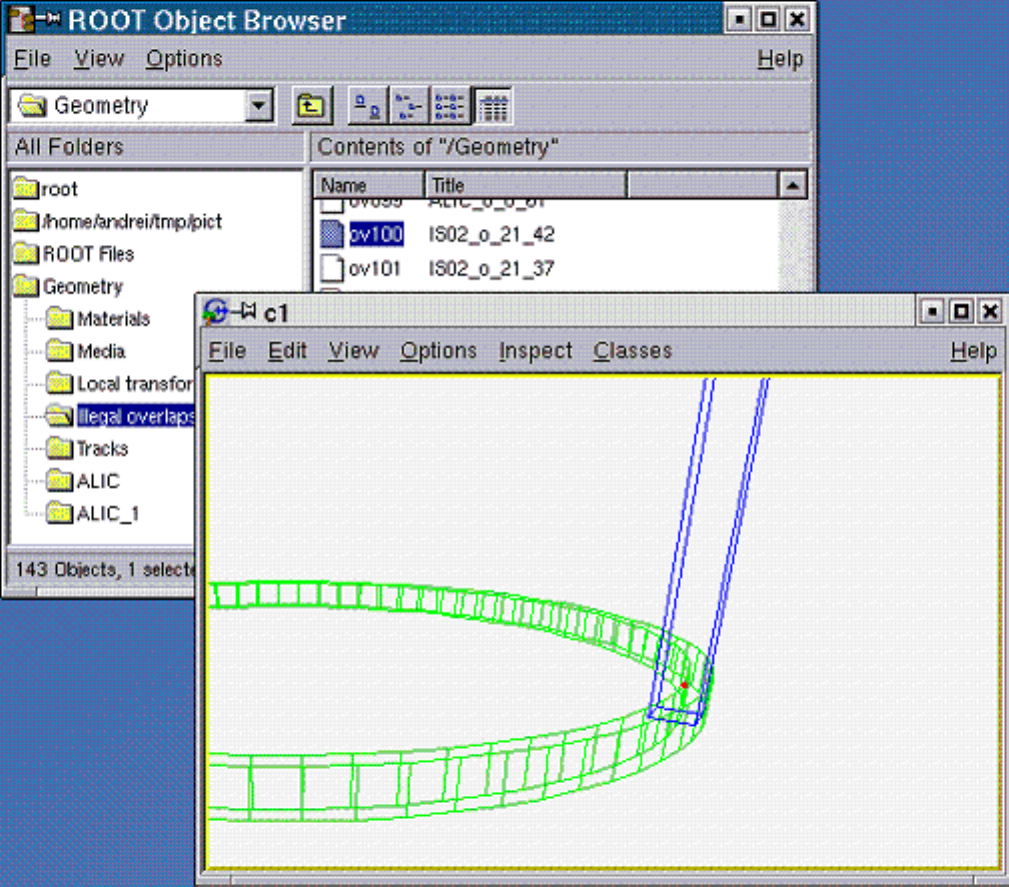
18.6. CHECKING THE GEOMETRY 497
We must say that even the overlaps of type A) and B) are allowed in case the corresponding nodes are created
using
TGeoVolume::AddNodeOverlap()
method. Navigation is performed in such cases by giving priority to the
non-overlapping nodes. The modeller has to perform an additional search through the overlapping candidates. These
are detected automatically during the geometry closing procedure in order to optimize the algorithm, but we will stress
that extensive usage of this feature leads to a drastic deterioration of performance. In the following we will focus on
the non-declared overlaps of type A) and B) since this is the main source of errors during tracking. These are generally
non-intended overlaps due to coding mistakes or bad geometry design. The checking package is loaded together with
the painter classes and contains an automated overlap checker.**
Figure 18.31: Overlap checking
This can be activated both at volume level (checking for illegal overlaps only one level inside a given volume) and from
the geometry manager level (checking full geometry):
myVolume->CheckOverlaps(precision, option);
gGeoManager->CheckOverlaps(precision);
myNode->CheckOverlaps(precision);
Here precision represents the desired maximum accepted overlap value in centimeters (default value is 0.1). This
tool checks all possible significant pairs of candidates inside a given volume (not declared as overlapping or division
volumes). The check is performed by verifying the mesh representation of one candidate against the shape of the other.
This sort of check cannot identify all possible overlapping topologies, but it works for more than 95% and is much
faster than the usual shape-to-shape comparison. For a 100% reliability, one can perform the check at the level of
a single volume by using
option
=“
d
” or
option
=“
d<number>
” to perform overlap checking by sampling the volume
498 CHAPTER 18. THE GEOMETRY PACKAGE
with <
number
> random points (default 1 million). This produces also a picture showing in red the overlapping region
and estimates the volume of the overlaps.
An extrusion A) is declared in any of the following cases:
•
At least one of the vertices of the daughter mesh representation is outside the mother volume (in fact its shape)
and having a safety distance to the mother greater than the desired value;
•At least one of the mother vertices is contained also by one of its daughters, in the same conditions.
An overlap B) is declared if:
•
At least one vertex of a positioned volume mesh is contained (having a safety bigger than the accepted maximum
value) by other positioned volume inside the same container. The check is performed also by inverting the
candidates.
The code is highly optimized to avoid checking candidates that are far away in space by performing a fast check on
their bounding boxes. Once the checking tool is fired-up inside a volume or at top level, the list of overlaps (visible as
Illegal overlaps inside a
TBrowser
) held by the manager class will be filled with
TGeoOverlap
objects containing a full
description of the detected overlaps. The list is sorted in the decreasing order of the overlapping distance, extrusions
coming first. An overlap object name represents the full description of the overlap, containing both candidate node
names and a letter (x-extrusion, o-overlap) representing the type. Double-clicking an overlap item in a
TBrowser
produces a picture of the overlap containing only the two overlapping nodes (one in blue and one in green) and having
the critical vertices represented by red points. The picture can be rotated/zoomed or drawn in X3d as any other view.
Calling gGeoManager->PrintOverlaps() prints the list of overlaps.
18.6.2 Graphical Checking Methods
Figure 18.32: Safety computation checking
In order to check a given point,
CheckPoint(x,y,z)
method of
TGeoManager
draws the daughters of the volume
containing the point one level down, printing the path to the deepest physical node holding this point. It also computes
the closest distance to any boundary.

18.6. CHECKING THE GEOMETRY 499
Figure 18.33: Random points
A method to check the validity of a given geometry is shooting random points. This can be called with the method
TGeoVolume::RandomPoints()
and it draws a volume with the current visualization settings. Random points are
generated in the bounding box of the drawn volume. The points are drawn with the color of their deepest container.
Only points inside visible nodes are drawn.
A ray tracing method can be called
TGeoVolume::RandomRays()
. This shoots rays from a given point in the local
reference frame with random directions. The intersections with displayed nodes appear as segments having the color of
the touched node.

500 CHAPTER 18. THE GEOMETRY PACKAGE
Figure 18.34: Random rays
18.7. THE DRAWING PACKAGE 501
18.7 The Drawing Package
The
modeller provides a powerful drawing package, supporting several different options of visualization. A library separated
from the main one provides all functionality being linked with the underlying ROOT visualization system. This library
is dynamically loaded by the plug-in manager only when drawing features are requested. The geometrical structures
that can be visualized are volumes and volume hierarchies.
The main component of the visualization system is volume primitive painting in a ROOT pad. Starting from this one,
several specific options or subsystems are available, like: X3D viewing using hidden line and surface removal algorithms,
OpenGL viewing* or ray tracing.
The method TGeoManager::GetGeomPainter()loads the painting library in memory.
This is generally not needed since it is called automatically by
TGeoVolume::Draw()
as well as by few other methods
setting visualization attributes.
18.7.1 Drawing Volumes and Hierarchies of Volumes
The first thing one would like to do after building some geometry is to visualize the volume tree. This provides the
fastest validation check for most common coding or design mistakes. As soon as the geometry is successfully closed,
one should draw it starting from the top-level volume:
//... code for geometry building
root[] gGeoManager->CloseGeometry();
root[] gGeoManager->GetMasterVolume()->Draw();
Doing this ensures that the original top-level volume of the geometry is drawn, even if another volume is currently the
geometry
root
. OK, I suppose you already did that with your simple geometry and immediately noticed a new ROOT
502 CHAPTER 18. THE GEOMETRY PACKAGE
canvas popping-up and having some more or less strange picture inside. Here are few questions that might come:
•Q: "The picture is strangely rotated; where are the coordinate axes?"
A:
If drawn in a new canvas, any view has some default viewpoint, center of view and size. One can then perform
mouse/keyboard actions to change them:
•Mouse left-click and drag will rotate the view;
•
Some keys can be pressed when the view canvas is selected: J/K zoom/un-zoom, U/I move up/down, L/H move
left/right. The coordinate axes display as well as changing top or side viewpoints can be activated from the
TView context menu: right-click on the picture when no object is selected;
•Q: "Every line is black! I cannot figure out what is what..."
A:
Volumes can have different colors (those known by ROOT of course). Think at using them after each volume
creation: myvolume->SetLineColor(Int_t color); otherwise everything is by default black.
•Q: "The top volume of my geometry is a box but I see only its content."
A:
By default the drawn volume is not displayed just because we do not want to hide its content when changing the view to
HLR or solid mode. In order to see it in the default wire frame picture one has to call
TGeoManager::SetTopVisible().
•Q: "I do not see all volumes in my tree but just something inside."
A:
By default,
TGeoVolume::Draw()
paints the content of a given volume three levels down. You can change this by
using: gGeoManager ::SetVisLevel(n);
Not only that, but none of the volumes at intermediate levels (0-2) are visible on the drawing unless they are
final ‘leaves’ on their branch (e.g. have no other volumes positioned inside). This behavior is the default one and
corresponds to ‘leaves’ global visualization mode (
TGeoManager::fVisOption = 1). In order to see on the screen
the intermediate containers, one can change this mode: gGeoManager->SetVisOption(0).
•Q: "Volumes are highlighted when moving the mouse over their vertices. What does it mean?"
A:
Indeed, moving the mouse close to some volume vertices selects it. By checking the
Event Status
entry in the
root canvas
Options
menu, you will see exactly which is the selected node in the bottom right. Right-clicking when a
volume is selected will open its context menu where several actions can be performed (e.g. drawing it).
•Q: "OK, but now I do not want to see all the geometry, but just a particular volume and its
content. How can I do this?"
A:
Once you have set a convenient global visualization option and level, what you need is just call the
Draw()
method of your interesting volume. You can do this either by interacting with the expanded tree of volumes in a
ROOT browser (where the context menu of any volume is available), either by getting a pointer to it (e.g. by name):
gGeoManager->GetVolume("vol_name")->Draw();
18.7.2 Visualization Settings and Attributes
Supposing you now understand the basic things to do for drawing the geometry or parts of it, you still might be not
happy and wishing to have more control on it. We will describe below how you can tune some fine settings. Since the
corresponding attributes are flags belonging to volume and node objects, you can change them at any time (even when
the picture is already drawn) and see immediately the result.
18.7.2.1 Colors and Line Styles
We have already described how to change the line colors for volumes. In fact, volume objects inherit from TAttLine
class so the line style or width can also be changed:
myVolume->SetLineColor(kRed);
myVolume->SetLineWith(2);
myVolume->SetLineStyle(kDotted);
When drawing in solid mode, the color of the drawn volume corresponds to the line color.
18.7. THE DRAWING PACKAGE 503
18.7.2.2 Visibility Settings
The way geometry is build forces the definition of several volumes that does not represent real objects, but just virtual
containers used for grouping and positioning volumes together. One would not want to see them in the picture. Since
every volume is by default visible, one has to do this sort of tuning by its own:
myVolumeContainer->SetVisibility(kFALSE);
As described before, the drawing package supports two main global options: 1 (default) - only final volume leaves; 0
- all volumes down the drawn one appear on the screen. The global visible level put a limitation on the maximum
applied depth. Combined with visibility settings per volume, these can tune quite well what should appear on the
screen. However, there are situations when users want to see a volume branch displayed down to the maximum depth,
keeping at the same time a limitation or even suppressing others. In order to accomplish that, one should use the
volume attribute:
Visible daughters
. By default, all daughters of all volumes are displayed if there is no limitation
related with their level depth with respect to the top drawn volume.
18.7.3 Ray Tracing
Ray tracing is a quite known drawing technique based on tracking rays from the eye position through all pixels of a
view port device. The pixel color is derived from the properties of the first crossed surface, according some illumination
model and material optical properties. While there are currently existing quite sophisticated ray tracing models,
TGeo
is
currently using a very simple approach where the light source is matching the eye position (no shadows or back-tracing
of the reflected ray). In future we are considering providing a base class in order to be able to derive more complex
models.
Due to the fact that the number of rays that have to be tracked matches the size in pixels of the pad, the time required
by this algorithm is proportional to the pad size. On the other hand, the speed is quite acceptable for the default
ROOT pad size and the images produced by using this technique have high quality. Since the algorithm is practically
using all navigation features, producing ray-traced pictures is also a geometry validation check. Ray tracing can be
activated at volume level as the normal Draw().
Figure 18.35: Ray-traced view in a pad
myVolume->Raytrace()
Once ray-tracing a view, this can be zoomed or rotated as a usual one. Objects on the screen are no longer highlighted
when picking the vertices but the corresponding volumes is still accessible.
18.7.3.1 Clipping Ray-traced Images
A ray-traced view can be
clipped
with any shape known by the modeller. This means that the region inside the
clipping shape is subtracted from the current drawn geometry (become invisible). In order to activate clipping, one has
to first define the clipping shape(s):
1. TGeoShape *clip1, *clip2, ...
504 CHAPTER 18. THE GEOMETRY PACKAGE
One might switch between several clipping shapes. Note that these shapes are considered defined in the current
MARS
.
Composite shapes may be used.
2. gGeoManager->SetClippingShape(clip1);
One can activate or deactivate clipping at any time: gGeoManager->SetClipping(flag);
3. Perform ray-tracing:gGeoManager->GetTopVolume()->Raytrace();
One can redo the steps 2-3 as many times as needed. Let us look how the
rootgeom
example looks clipped with a tube.
Figure 18.36: Ray-tracing example with box-clipping
18.8 Representing Misalignments of the Ideal Geometry
The ideal positioning of a detector does not match its position in the experimental hall. This generally happens not only
for the detector modules, but also for their components. The accurate knowledge of the detector real misalignments
can be extremely important for getting close to its designed resolution and the expected tracking efficiency.
TGeo
offers
tools for representing positioning misalignments, applying them to the ideal geometry and performing navigation under
these conditions. Detector tracking algorithms can then directly query the geometry for navigation purposes or for
retrieving actual misalignment information.
18.8.1 Physical Nodes
Physical nodes are the actual “touchable” objects in the geometry, representing actually a path of positioned volumes
starting witrh the top node:
path=/TOP/A_1/B_4/C_3
, where
A
,
B
,
C
represent names of volumes. The number of
physical nodes is given by the total number of possible of branches in the geometry hierarchy. In case of detector
geometries and specially for calorimeters this number can be of the order 106-109, therefore it is impossible to create
all physical nodes as objects in memory. In
TGeo
, physical nodes are represented by the class
TGeoPhysicalNode
and
can be created on demand for alignment purposes:
18.8. REPRESENTING MISALIGNMENTS OF THE IDEAL GEOMETRY 505
TGeoPhysicalNode(const char* path)
The knowledge of the path to the objects that need to be misaligned is essential since there is no other way of identifying
them. One can however create “symbolic links” to any complex path to make it more representable for the object it
designates:
TGeoPNEntry(const char* unique_name, const char* path)
void TGeoPNEntry::SetPhysicalNode(TGeoPhysicalNode *node)
Such a symbolic link hides the complexity of the path to the align object and replaces it with a more meaningful name.
In addition,
TGeoPNEntry
objects are faster to search by name and they may optionally store an additional user matrix.
// Creating a symlink object.
TGeoPNEntry *TGeoManager::SetAlignableEntry(const char *unique_n,
const char*path)
// Retrieving an existing alignable object.
TGeoPNEntry *TGeoManager::GetAlignableEntry(const char *name)
// Retrieving an existing alignable object at a given index.
TGeoPNEntry *GetAlignableEntry(Int_t index)
Physical nodes store internally the full list of logical nodes corresponding to the elements from the string path, as well
as the global transformation matrix for each of them. The top node corresponds to the level 0 in the stored array,
while the last node will correspond to level
n
. For each level, the node, volume and global matrix can be retrieved
using corresponding getters:
TGeoHMatrix *GetMatrix(Int_t level=-1)const
TGeoNode *GetNode(Int_t level=-1)const
TGeoShape *GetShape(Int_t level=-1)const
TGeoVolume *GetVolume(Int_t level=-1)const
By default the object at level n is retrieved (the alignable object).
Once created, a physical node can be misaligned, meaning that its positioning matrix or even the shape.:
void Align(TGeoMatrix* newmat=0, TGeoShape* newshape=0,
Bool_t check=kFALSE)
The convention used is that newmat represents the new local matrix of the last node in the branch with respect to its
mother volume. The
Align()
method will actually duplicate the corresponding branch within the logical hierarchy,
creating new volumes and nodes. This is mandatory in order to avoid problems due to replicated volumes and can
create exhaustive memory consumption if used abusively.
Once aligned, a physical node is ready to be tracked. The operation can be done only after the geometry was closed.
Important NOTE: Calling the
Align()
method for a physical node changes the node pointers for the stored node
branch in the active geometry, Due to this the other defined physical nodes containing elements of this path will be
invalid. Example:
TGeoPhysicalNode *pn1 =
gGeoManager->MakePhysicalNode("/A_1/B_1/C_2");
TGeoPhysicalNode *pn2 =
gGeoManager->MakePhysicalNode("/A_1/B_1/C_3");
...
pn1->Align(...);
The call to
pn1->Align()
will invalidate the pointer to the node
B_1
in
pn2
object.. The way out is to either call
pn1->Align() before the creation of pn2, eithr to use a global method that will correct all existing physical nodes:
void RefreshPhysicalNodes(Bool_t lock = kTRUE)
The method above will optionally lock the possibility of doing any further misalignment.
506 CHAPTER 18. THE GEOMETRY PACKAGE
18.9 Geometry I/O
Once geometry is successfully built, it can be saved in a root file, as C++ macro or as GDML file by calling:
TGeoManager::Export(const char *filename,const char*keyname="",
Option_t *opt="vg")
•Filename
is the name of the file to be written (mandatory). Depending on the extension of the file, the geometry
is exported either as ,root file or .C(.cxx) macro or GDML file in case extension is .gdml.
•keynameis the name of the key in the file (default “”)
•opt
=
"v"
is an export voxelization (default), otherwise voxelization is recomputed after loading the geometry,
"g"
this option (default) is taken into account only for exporting to gdml file and it ensures compatibility with
Geant4 (e.g. it adds extra plane to incorrectly set polycone, it checks whether offset of Phi division is in (-360;0>
range, . . . ), for this gdml export there are two more option, that are not set by default:
"f"
and
"n"
. If none
of this two options are set, then names of solids and volumes in resulting gdml file will have incremental suffix
(e.g. TGeoBBox_0x1, TGeoBBox_0x2, . . . ). If
"f"
option is set then then suffix will contain pointer of object
(e.g. TGeoBBox_0xAAAAA01, . . . ). Finally if option
"n"
is set then no suffix will be added, though in this case
uniqness of the names is not ensured and it can cause that file will be invalid.
Loading geometry from a root file can be done in the same way as for any other ROOT object, but a static method is
also provided:
TGeoManager::Import(const char *filename,const char *keyname="",
Option_t *opt="")
Example:
// Writing to a file geometry definition ending with:
root[] gGeoManager->CloseGeometry();
// geometry is ready
root[] gGeoManager->Export("MyGeom.root");
// file MyGeom.root produced
root[] gGeoManager->Export("MyGeom.C");
// C++ macro MyGeom.C produced
root[] gGeoManager->Export("MyGeom.gdml");
// GDML file MyGeom.gdml produced
root[] myVolume->SaveAs("MyVolume.C");
// C++ macro for the branch starting
// with MyVolume
// Reading from a file
root[] gSystem->Load("libGeom");
root[] TGeoManager::Import("MyGeom.root"); // geometry is ready
Note that not all-current information held by the modeller is written on the file. For instance, the painter and checker
objects are not written, as well as the temporary current navigation properties: current node path, point or direction.
On the other hand, all objects belonging to the geometrical hierarchy will always be written. The idea is to be able to
retrieve the geometry in a ready state, ignoring what the state variables that can be always re-initialized. When the
code is generated for a given
TGeoVolume
in the geometry, just the branch starting with that volume will be saved in
the file. Executing the generated code will create a geometry that has
MyVolume
as top volume. In this case, only the
materials/media/matrices used effectively in the MyVolume branch are exported to file.
Volumes can be made persistent in the same way the full geometry is. Exporting is straightforward (module1, 2 are
pointers to TGeoVolume objects):
module1->Export("file.root");
// by default file is overwritten
module2->Export("file.root","","update");
// to the same file
Importing will append the volume to the current TGeoManager or will create one:
18.10. NAVIGATION ALGORITHMS 507
TGeoManager *geom = new TGeoManager("myGeom","");
TGeoVolume *top = geom->MakeBox(...);
geom->SetTopVolume(top);
//name of volume or key (depending on export usage)
TGeoVolume *module1 = TGeoVolume::Import("file.root","MOD1");
TGeoVolume *module2 = TGeoVolume::Import("file.root","MOD2");
top->AddNode(module1, 1,new TGeoTranslation(0,0,100));
top->AddNode(module2, 1,new TGeoTranslation(0,0,-100));
// One should close oneself the geometry
geom->CloseGeometry();
18.9.1 GDML
Few lines above word GDML was used. GDML stands for
G
eometry
D
escription
M
arkup
L
anguage. It is an
application-indepedent geometry description format based on XML. It is mainly used for geometry interchange between
ROOT and Geant4 framework. More details about this project can be found http://gdml.web.cern.ch. This feature
(importing/exporting from/to gdml file format) is disabled by default in ROOT installation. To enable this feature add
--enable-gdml option to ./configure script call.
18.10 Navigation Algorithms
This section will describe the main methods and algorithms used for implementing the navigation features within the
geometrical modeller. This includes navigation queries at shape level, global geometrical queries and optimization
mechanisms.
18.10.1 Finding the State Corresponding to a Location (x,y,z)
For reminder, a geometry state is a ‘touchable’ object in the geometry hierarchy. It is represented by a path like:
/TOP_1/A_1/B_3/C_1
, where
B_3
for instance is a copy of volume
B
positioned inside volume
A
. A state is
always associated to a transformation matrix
M
of the touchable with respect to the global reference frame (obtained
by piling-up all local transformations of nodes in the branch with respect to their containers). The current state and
the corresponding global matrix are updated whenever the geometry depth is modified. The global transformations
corresponding to all nodes in the current branch are kept in an array: (MTOP_1, MA_1, MB_3, . . . ).
The elementary operations for changing the state are:
TGeoManager::CdUp();
TGeoManager::CdDown(i);
TGeoManager::CdTop()
The current state accounting and global matrix handling after these operations are depicted in the figure below. Now
let us suppose that we have a particle at position P(x,y,z). The first thing needed for transporting it is the current
object our particle is into, so that we can retrieve its material properties. This task is done by:
TGeoNode *TGeoManager::FindNode(x,y,z)
Note that the current particle position can be set using
SetCurrentPosition(x,y,z)
method of the manager class,
in which case
FindNode()
can be called without arguments. The method returns a pointer to the deepest node that
geometrically contains P(in our case let us suppose it is B_3 ). Since a node is just a positioned volume, we can then
get a pointer to the volume, medium or material objects related to it. Deepest means that B_3 still contains point P
(as well as A_1 and TOP_1 ), but none of the daughters of volume
B
does. After finding out the node containing the
particle, one can check if the geometry state is different compared to the last located point:
Bool_t *TGeoManager::IsSameLocation()
The algorithm for finding where a point is located in geometry is presented in the figure 17-36.
It always starts by checking if the last computed modeller state is the answer. This optimizes the search when
continuously tracking a particle. The main actions performed are:
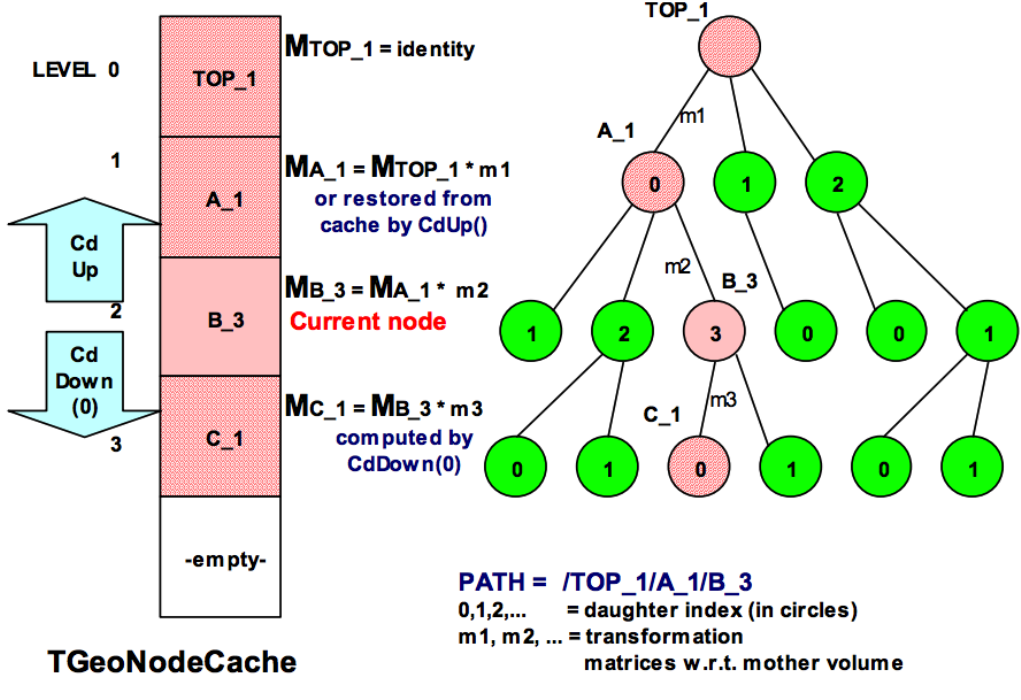
508 CHAPTER 18. THE GEOMETRY PACKAGE
Figure 18.37: Navigation in the geometry hierarchy
•moving up and down in the logical node tree while updating the current node and its global matrix
•converting the global position into the local frame of the current node/volume
•
checking whether the local position lies within the geometrical shape of the current volume - if this is the case
continue the search downwards for the daughters of the current node, otherwise search upwards its containers
until the top level is reached.
•
the number of candidate nodes to be checked at a given level is minimized by an additional optimization structure:
voxels. This is effective even in case there is only one daughter of the current volume.
•
in case the current node is declared as possibly overlapping, the method FindInCluster() is invoked. This method
checks all different possibilities within the cluster of overlapping candidates. One of the candidates is prioritized
if one of the following conditions id fulfilled (in order):
•Is declared as non-overlapping (these are anyway searched first)
•Has at least one daughter that contains the current point
•Was already declared as containing the point at a previous step
18.10.2 Finding the Distance to Next Crossed Boundary
The most important feature provided by the modeller related to track propagation is the computation of the distance
to the next boundary along a straight line.
The relevant state parameters used for this task are:
•Current particle position and direction (x,y,z,nx,ny,nz), where ni is the direction cosine with axis (i).
•
Current node (and path) in geometry must be set by calling
TGeoManager::FindNode(x,y,z)
beforehand The
method computing the distance to next boundary is:
TGeoNode *TGeoManager::FindNextBoundary(stepmax, path)
The output node returned by the method is the object which shape boundary will be crossed first. The distance to the
next crossing can be retrieved after the call:
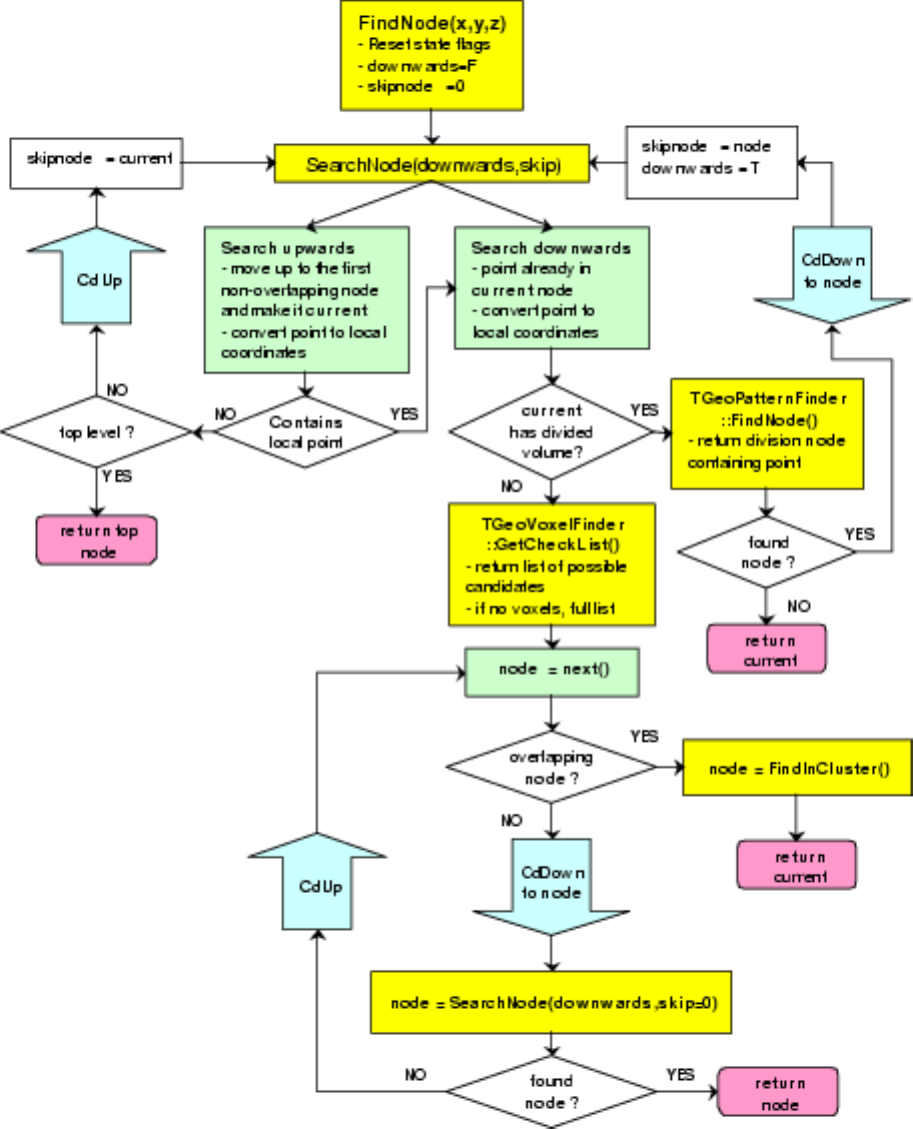
18.10. NAVIGATION ALGORITHMS 509
Figure 18.38: Finding the location of a point in the geometry hierarchy
510 CHAPTER 18. THE GEOMETRY PACKAGE
Double_t TGeoManager::GetStep()
•
The main input parameter is
stepmax,
which act as a trigger for different features. The absolute value of this
parameter represents the step value proposed by the user. The algorithm will never try o search for boundaries
further than this distance. In case no boundary is found the returned node will be the current one and the
computed step to boundary will be equal to abs (
stepmax
) having the meaning “step approved”. The default
value for stepmax is TGeoShape::Bigwith the meaning that boundaries are looked for without limitation.
According the values of the input parameters the method will perform additional optional tasks:
|stepmax| < TGeoShape::Big() ‘ ‘
The safe distance in the current volume is also computed. Moving the particle from its current location with this
distance in any direction is safe in the sense that will never change the current state.
stepmax < 0
The global matrix for the object that will have the next crossed boundary is also computed. This can be retrieved for
masterlocal point or vector conversions: TGeoManager::GetNextMatrix()
In case the computation of the normal vector to the next crossed surface is required, using a negative stepmax value is
recommended. In this case one can subsequently call a method for fast normal computation:
Double_t *TGeoManager::FindNormalFast()
path 0
In case a path to a given physical object is specified, the distance to its boundary is computed ignoring the rest of the
geometry
18.10.2.1 Output Values
TGeoManager::GetStep(): distance to next boundary.
TGeoManager::GetSafeDistance(): safe distance (in case it was computed).
TGeoManager::IsOnBoundary()
: the initial point
(x,y,z)
was (or was not) on a boundary within
TGeoShape::Tolerance()
.
The algorithm checks first if the computation of safety was required. If this is the case and the global point coordinates
did not change from the last query, the last computed safety is taken. Otherwise, the method
TGeoManager::Safety
()
is invoked. A safety value less than
TGeoShape::Tolerance()
will set the flag IsOnBoundary to true. On the
other hand, a safety value bigger than the proposed step will stop the computation of the distance to next boundary,
returning the current geometry location with the meaning that the proposed step is safe.
The next stage is to check if computation of the distance to a give physical object specified by a path was required.
If this is the case, the modeller changes the state to point to the required object, converts the current point and
direction coordinates to the local frame of this object and c omputes the distance to its shape. The node returned is
the one pointed by the input path in case the shape is crossed; otherwise the returned value is NULL. In case the
distance to next crossed boundary is required, the current point has to be physically INSIDE the shape pointed by
the current volume. This is only insured in case a call to
TGeoManager::FindNode()
was performed for the current
point. Therefore, the first step is to convert the global current point and direction in the local reference frame of the
current volume and to compute the distance to exit its shape from inside. The returned value is again compared to
the maximum allowed step (the proposed one) and in case the distance is safe no other action is performed and the
proposed step is approved. In case the boundary is closer, the computed distance is taken as maximum allowed step.
For optimization purposed, for particles starting very close to the current volume boundary (less than 0.01 microns)
and exiting the algorithm stops here.
After computing the distance to exit the current node, the distance to the daughter of the current volume which
is crossed next is computed by
TGeoManager::FindNextDaughterBoundary().
This computes the distance to all
daughter candidates that can be possibly crossed by using volume voxelization. The algorithm is efficient in average
only in case the number of daughters is greater than 4. For fewer nodes, a simple loop is performed and the minimum
distance (from a point outside each shape) is taken and compared to the maximum allowed step. The step value is
again updated if step<stepmax .
A special case is when the current node is declared as possibly overlapping with something else. If this is the case, the
distance is computed for all possibly overlapping candidates, taking into account the overlapping priorities (see also: "
Overlapping volumes “).
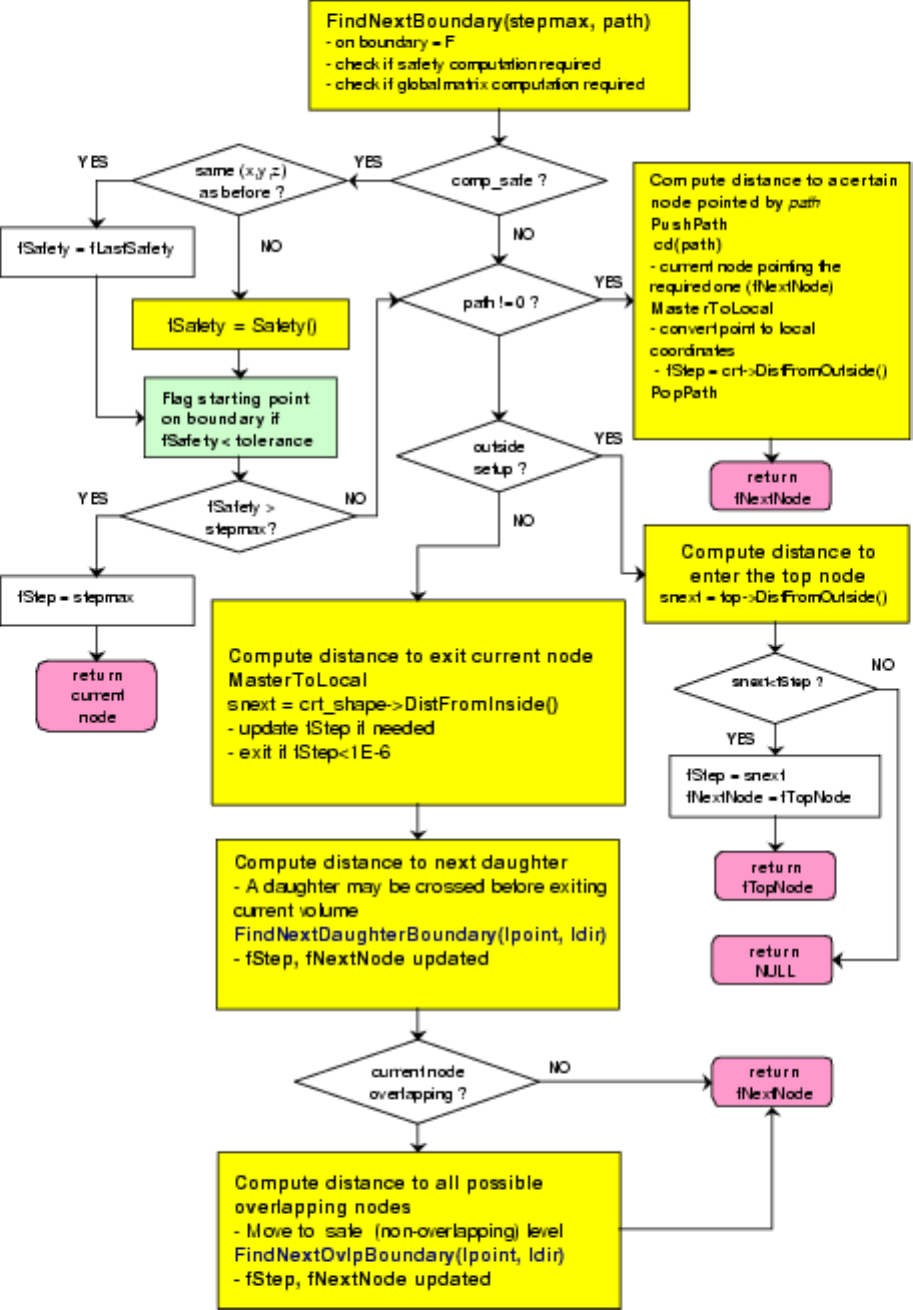
18.10. NAVIGATION ALGORITHMS 511
Figure 18.39: Finding the distance to the next crossed boundary
512 CHAPTER 18. THE GEOMETRY PACKAGE
The global matrix describing the next crossed physical node is systematically computed in case the value of the proposed
step is negative. In this case, one can subsequently call
TGeoManager::ComputeNormalFast()
to get the normal vector
to the crossed surface, after propagating the current point with the
TGeoManager::GetStep()
value. This propagation
can be done like:
Double_t *current_point = gGeoManager->GetCurrentPoint();
Double_t *current_dir = gGeoManager->GetCurrentDirection();
for (Int_t i=0; i<3; i++)
current_point[i] += step * current_dir[I];
Note: The method
TGeoManager::FindNextBoundary()
does not modify the current point/direction nor the current
volume/state. The returned node is the next crossed one, but the physical path (state) AFTER crossing the boundary
is not determined. In order to find out this new state, one has to propagate the point with a distance slightly bigger
that the computed step value (which is accurate within numerical precision). A method that performs this task finding
the next location is
TGeoManager::Step()
, described in " Making a Step “, but users may implement more precise
methods to insure post-step boundary crossing.
18.11 Geometry Graphical User Interface
The geombuilder package allows you to create and edit geometries. The package provides a library of all GUI classes
related to geometry. Each editable geometry class
TGeoXXX
have a correspondent editor
TGeoXXXEditor
that provides
a graphics user interface allowing to edit some (or all) parameters of a geometry object. The editable objects are
geometry manager, volumes, nodes, shapes, media, materials and matrices. The interfaces provide also access to specific
functionality of geometry objects. The editing mechanism is based on ROOT GED (Graphics Editors) functionality
and the library is loaded using the plug-in mechanism.
18.11.1 Editing a Geometry
There are two different use cases having different ways of invoking the geometry editors. The first one applies when
starting with geometry from scratch and using the builder functionality to create new geometry objects. In this case,
one should use the sequence:
root[] TGeoManager *geom = new TGeoManager("MyGeom",
"Test builder");
root[] geom->Edit(Option_t *option="");
The lines above will create a new
TGeoManager
class, create an empty canvas and start the editor in the left-sided
editor frame attached to the canvas. To open the editor in a separate frame one should provide a non-empty string as
option to the Edit() method.
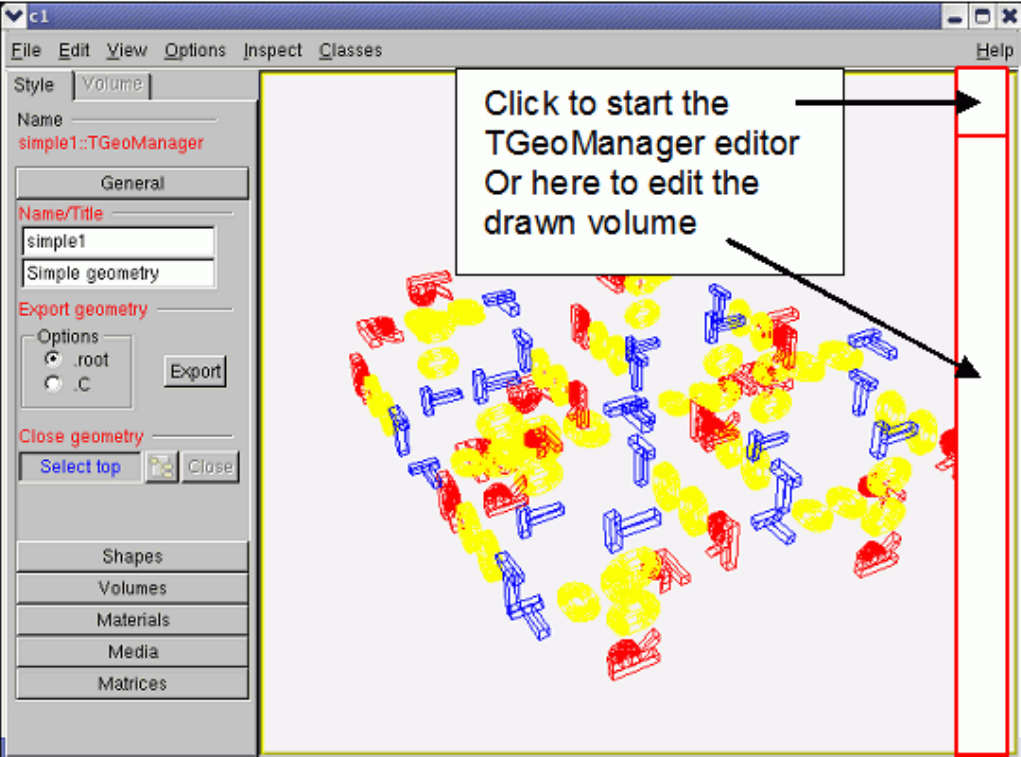
18.11. GEOMETRY GRAPHICAL USER INTERFACE 513
Figure 18.40: The geometry manager editor
514 CHAPTER 18. THE GEOMETRY PACKAGE
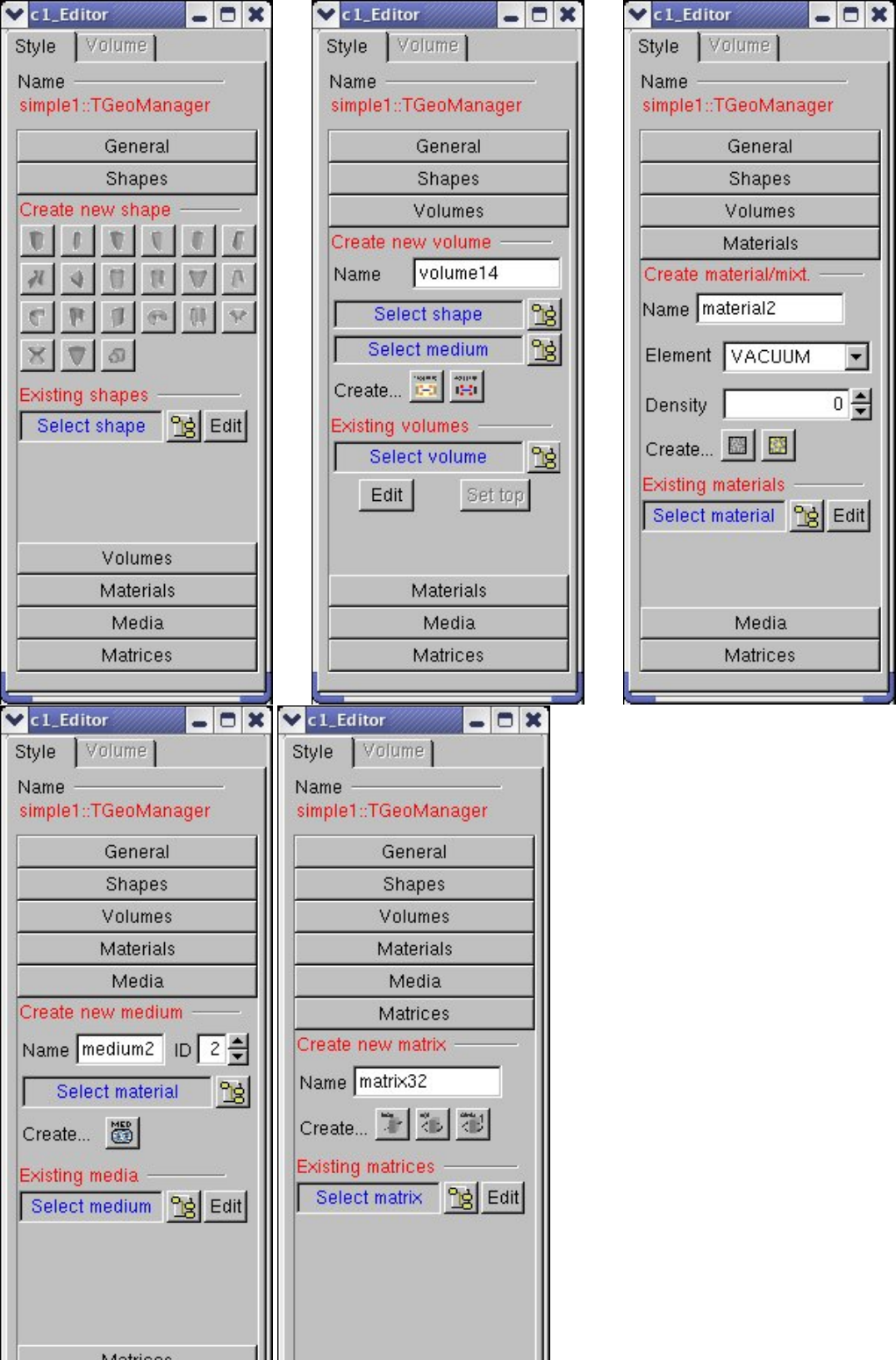
18.11. GEOMETRY GRAPHICAL USER INTERFACE 515
18.11.2 The Geometry Manager Editor
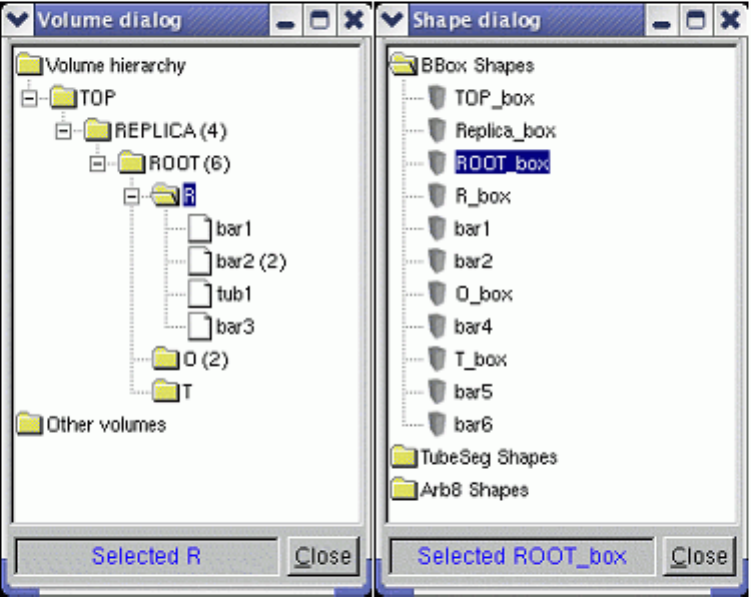
516 CHAPTER 18. THE GEOMETRY PACKAGE
The second use case applies when starting to edit an existing geometry. Supposing the geometry was loaded into
memory, besides the first method that still applies one can also edit drawn geometry objects. For this, the menu entry
View/Editor of the canvas containing for instance a drawn volume must be activated. For starting the volume editor
one can click on a volume. The GUI of the
TGeoManager
class can be started by clicking on the top-right
40x40
pixels
corner of the pad with a drawn geometry.
This is the main entry point for editing the geometry or creating new objects. Once the interface is created (using one
of the methods described above), several categories can be accessed via a shutter GUI widget:
•
General. This allows changing the name/title of the geometry, setting the top volume, closing the geometry and
saving the geometry in a file. The file name is formed by
geometry_name.C
or
.root
depending if the geometry
need to be saved as a Cmacro or a .root file.
•
Shapes. The category provides buttons for creation of all supported shapes. The new shape name is chosen by
the interface, but can be changed from the shape editor GUI. Existing shapes can be browsed and edited from
the same category.
•
Volumes. The category allows the creation of a new volume having a given name, shape and medium. For creating
a volume assembly only the name is relevant. Existing volumes can be browsed or edited from this category.
•Materials. Allows creation of new materials/mixtures or editing existing ones.
•
Media. The same for creation/editing of tracking media (materials having a set of properties related to tracking)
•
Matrices. Allows creation of translations, rotations or combined transformations. Existing matrices can also be
browser/edited.
18.11.3 Editing Existing Objects
For editing an existing object from one of the categories described above, the interface imposes first a selection among
all objects of the corresponding type stored in the geometry. This can be done by clicking the button next to the blue
label Select <object>. The dialog interfaces are generally different for different types of objects. The volume selection
dialog offers the possibility to select either a volume already connected to the geometry hierarchy or non-connected
ones. Selection for shapes and matrices is split into categories represented by top-level list tree items for: boxes, tubes,
translations, rotations, etc.
Figure 18.41: Selection dialogs for different TGeo objects
Once a selection is made and the dialog is closed, the selected item name will appear in the corresponding label and
the button Edit will start the object editor in a transient frame. Closing these transient frames will not delete, but just
hide existing opened editors for later reuse. Their lifetime is determined by the canvas to which the manager editor is
attached to, since these will be destroyed together.
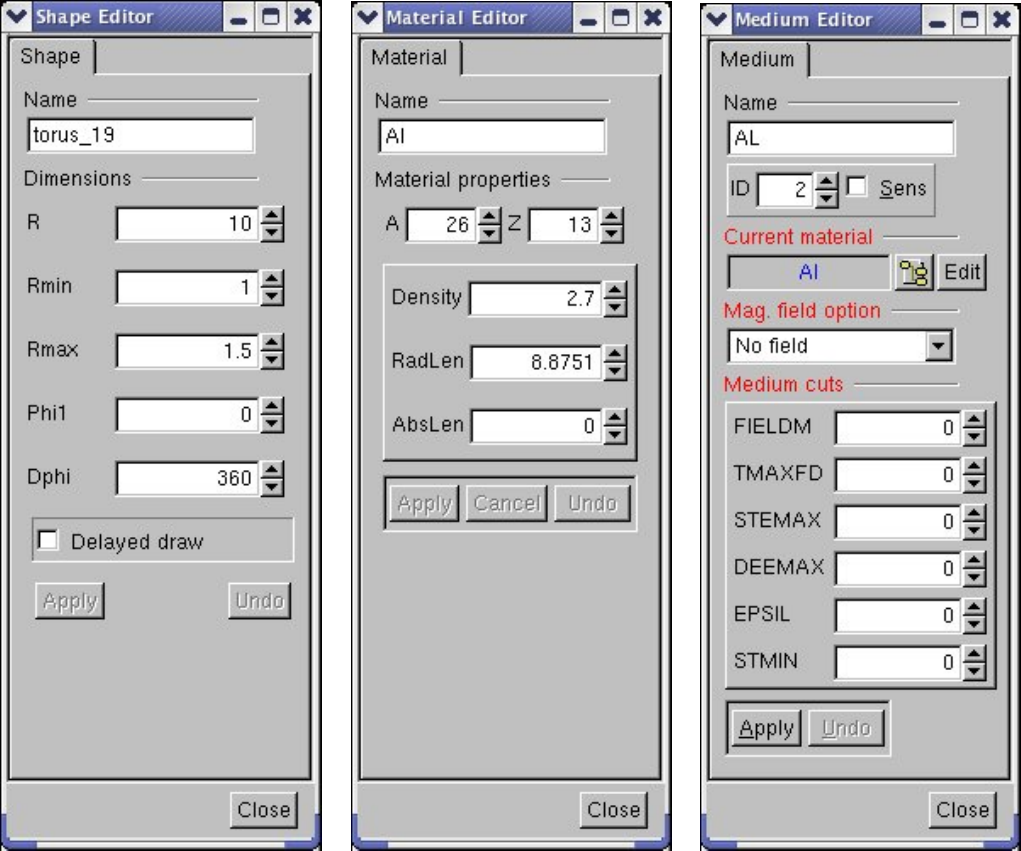
18.11. GEOMETRY GRAPHICAL USER INTERFACE 517
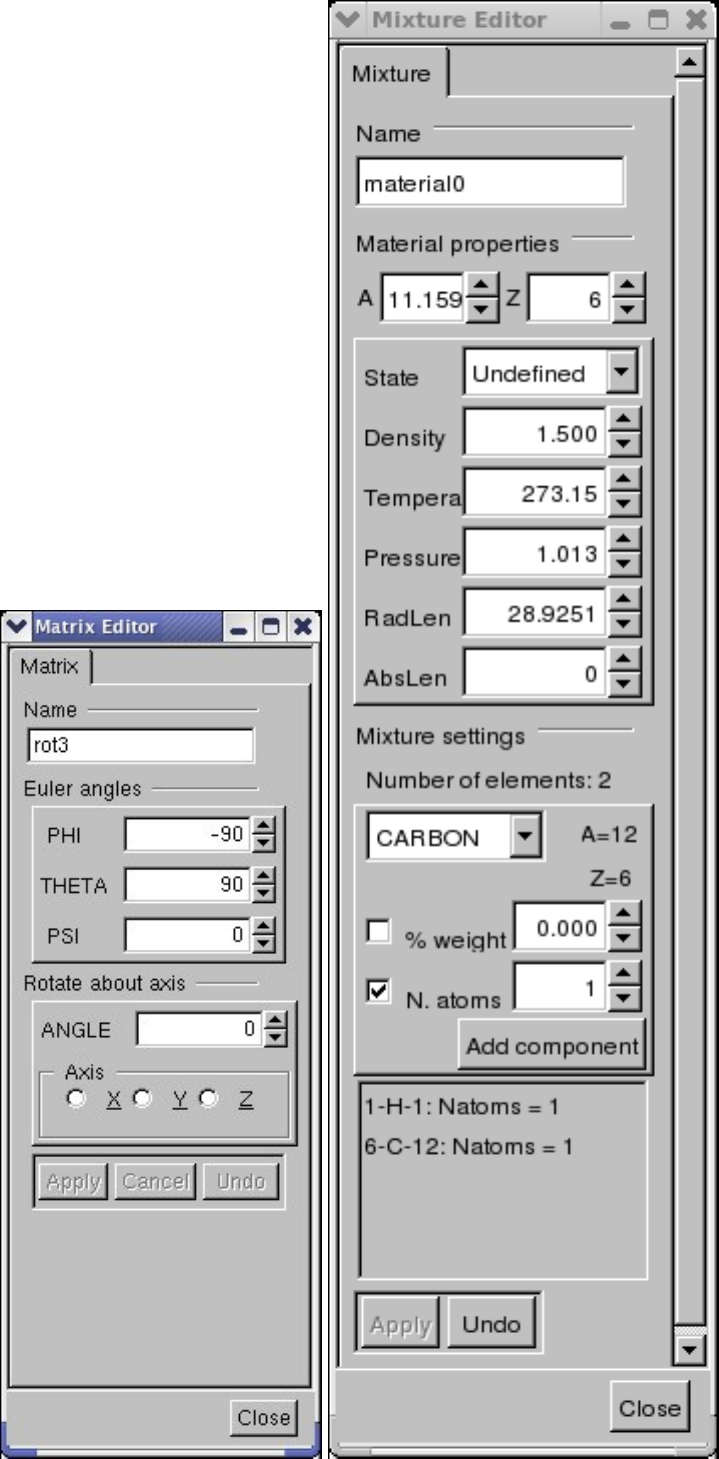
518 CHAPTER 18. THE GEOMETRY PACKAGE
For most editors, the functionalities Apply and Undo are provided.
18.11. GEOMETRY GRAPHICAL USER INTERFACE 519
For shapes, changing any of the shape parameters will activate the “Apply” button only if the check button “Delayed
draw” is checked, otherwise the changes are immediately applied. Once the apply button is pressed, the changes are
applied to the edited shape and drawn. The “Undo” button becomes active after the first modification has been applied.
It allows restoring the initial parameters of the shape.
NOTE: In this version the “Undo” does not allow restoring an intermediate state of the parameters that was applied -
it will always restore the parameters at the moment the shape was edited.
All material properties changes are undoable. The mixture editor currently allows adding elements one by one in the
mixture composition. This can be done either by element weight fraction or by number of atoms. Once an element was
added using one method the other mehod is not selectable anymore. Summing component fractions up to 1 in the final
mixture is the user responsability. Adding materials as components of a mixture is not supported in this version.
The elements that were added to the mixture appear in the bottom of the mixture editor. The operations performed
on mixture are not undoable.
18.11.4 Creation of New Objects
As described above, all geometry object creators are accessible within the geometry manager editor frame. Generally,
if the new object that needs to be created does not depend on other objects, it will be built with a set of default
parameters. This is the case for all shapes (except composite shapes) and matrices. For all the other objects the
interface forces the selection of components before creating the object.
18.11.5 Editing Volumes
Volumes are hierarchical components in the geometry, therefore their editor is more complex. It provides the following
functionalities:
•
General. This category allows changing the name of the volume and selecting other shape or medium among
existing ones.
•
Daughters. The category allows removing existing daughter nodes or adding new ones. The button “Position”
allows editing the positioning matrix of a given node.
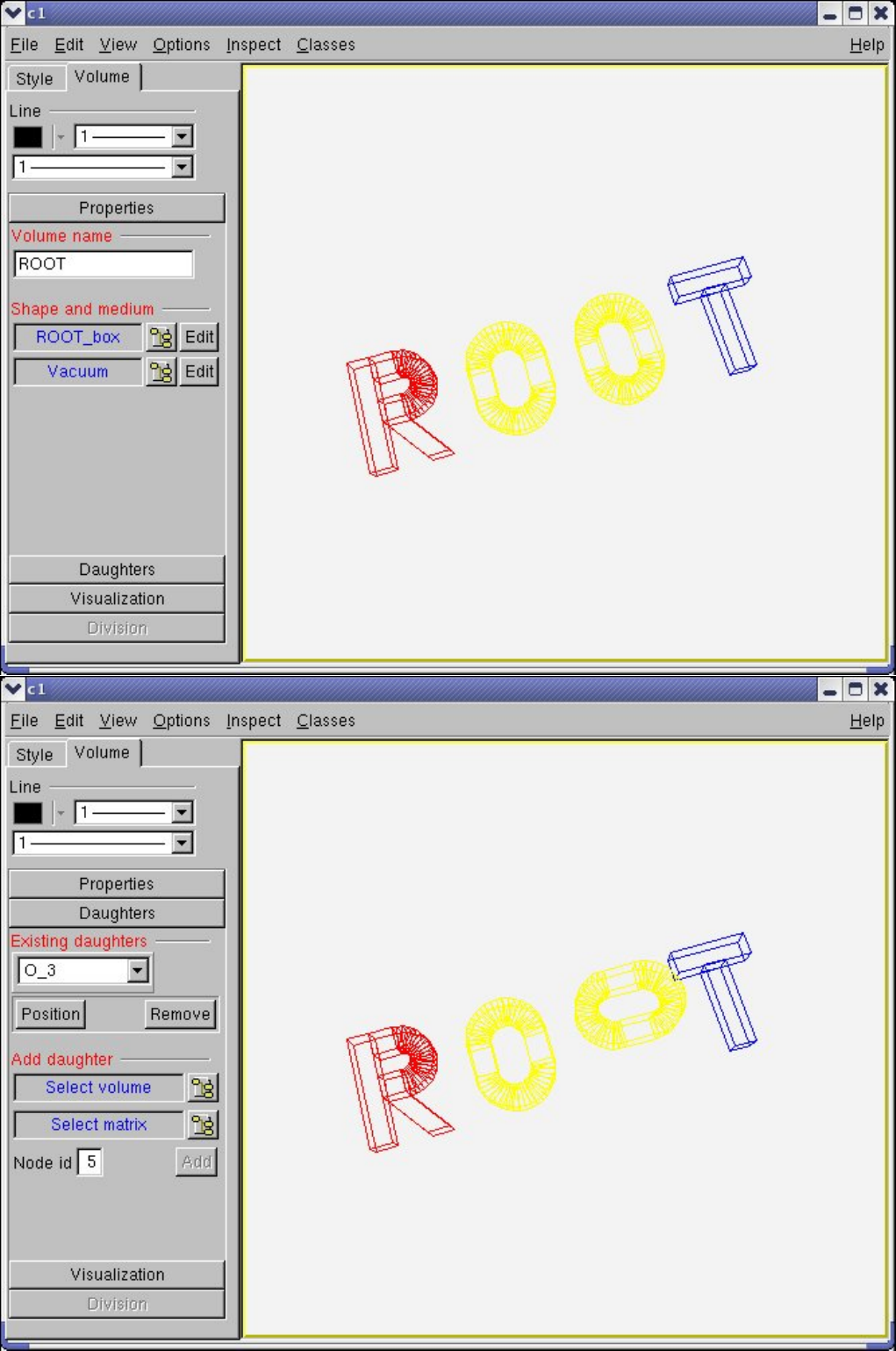
520 CHAPTER 18. THE GEOMETRY PACKAGE
18.11. GEOMETRY GRAPHICAL USER INTERFACE 521
•
Visualization. This category allows changing the visibility of the edited volume or for its daughters, as well
as other visualization settings. The radio button “All” allows viewing all volumes down to the selected depth.
“Leaves” will draw only the deepest nodes that have the selected depth or lower level ones that have no daughters
inside. “Only” will allow drawing only the edited volume. The check button “Raytrace” will just draw the current
selection in solid mode using the ray-tracing algorithm provided by TGeo.
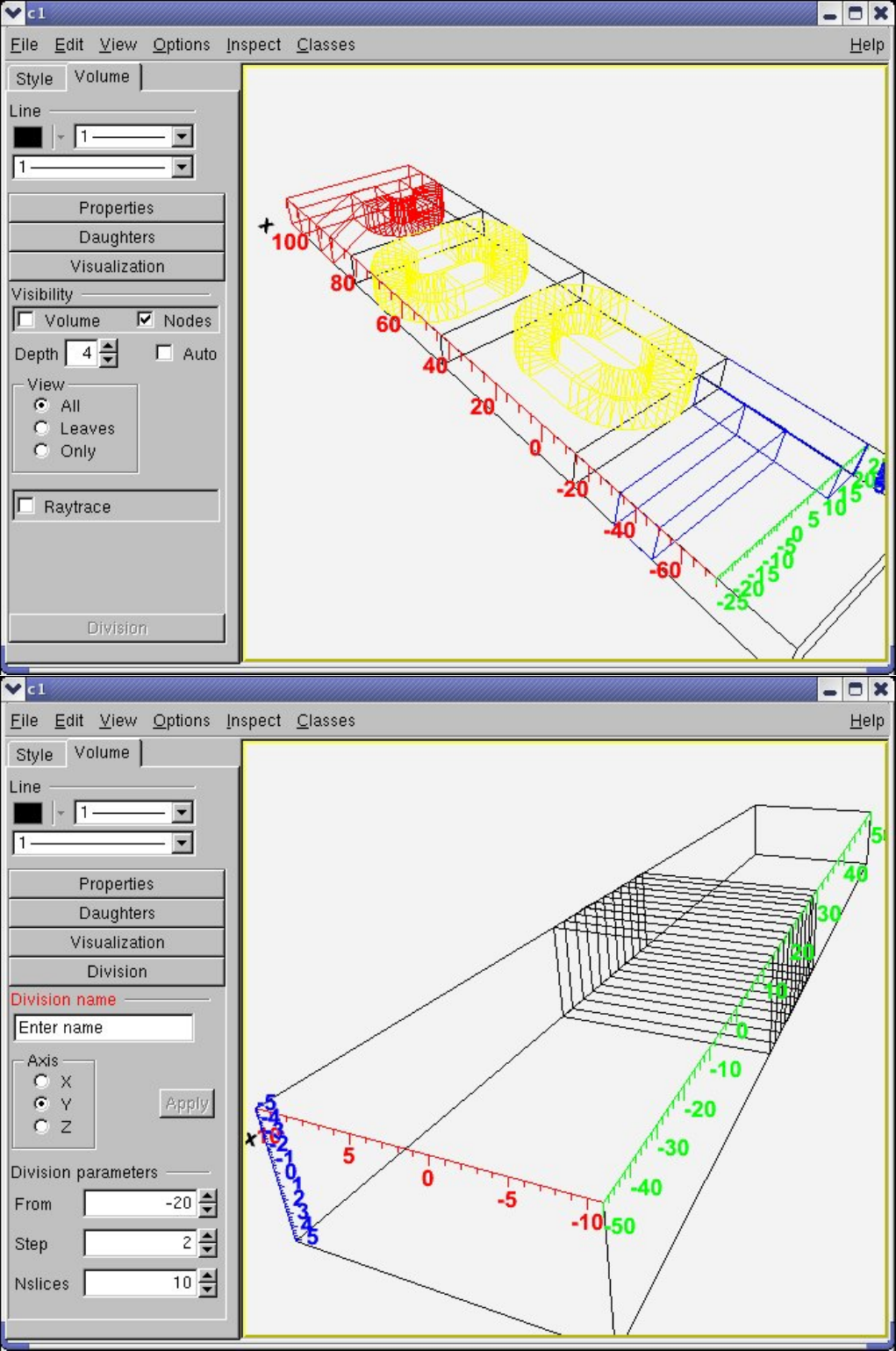
522 CHAPTER 18. THE GEOMETRY PACKAGE
18.11. GEOMETRY GRAPHICAL USER INTERFACE 523
•
Division. Allows dividing the edited volume according a given pattern. The division axes that are allowed are
presented in a radio-button group. The number entries labeled “From”, “Step” and “Nslices” correspond to the
divisioning parameters on the selected axis. The range of the division is between
start
and
start+ndiv*step
values and its validity is checked upon changing one of the values.
NOTE: When changing a value in a number entry by typing a number, press ENTER at the end to validate. This
applies for taking into account and validation of any number change in the geometry editors.
18.11.6 How to Create a Valid Geometry with Geometry Editors
1. Create a new geometry manager and start the editor as described at the beginning.
2.
Create at least one material from the “Materials” shutter item category. Generally, for creating objects, the
interface is always in the
TGeoManagerEditor
in different categories - one should just provide a name and
requested parameters.
3.
Create a shape that will be used for the top volume within the “Shapes” category. For the moment, the shapes
that have editors are Box, Para, Trd1, Trd2, Tube, Tube segment, Cone, Cone segment, Hype, Pcon, Torus and
Sphere.
4.
Create a medium from one of the existing materials from the “Medium” category. You will notice that some
categories as “Volume” and “Medium” are inactive at the beginning because at that time there is no material yet
(for making a medium) and no shape (for making a volume). These categories are dynamically activated once all
the required components are defined.
5.
Create a volume from the “Volumes” category. You will notice that contrary to the other editors, the volume
editor is opened in a tab, not transient - this is because it is more complex.
6.
Go back to “General” category and select the newly created volume as the top one (you can do it also from the
volume category). This is just for starting. To create some hierarchy, one has to create several other volumes and
the matrices to position them. Once this is done, use the volume editor interface to:
•add/remove daughters, change shape, edit position of daughters
•change visualization settings
•divide the volume (only if there are no daughters yet)
7. Close the geometry from the “General” category.
524 CHAPTER 18. THE GEOMETRY PACKAGE
Chapter 19
Python and Ruby Interfaces
Python is a popular, open-source, dynamic programming language with an interactive interpreter. Its interoperability
with other programming languages, both for extending Python as well as embedding it, is excellent and many existing
third-party applications and libraries have therefore so-called “Python bindings.” PyROOT provides Python bindings
for ROOT: it enables cross-calls from ROOT/Cling into Python and vice versa, the intermingling of the two interpreters,
and the transport of user-level objects from one interpreter to the other. PyROOT enables access from ROOT to any
application or library that itself has Python bindings, and it makes all ROOT functionality directly available from the
python interpreter.
19.1 PyROOT Overview
The Python scripting language is widely used for scientific programming, including high performance and distributed
parallel code (see http://www.scipy.org). It is the second most popular scripting language (after Perl) and enjoys a
wide-spread use as a “glue language”: practically every library and application these days comes with Python bindings
(and if not, they can be easily written or generated).
PyROOT
, a Python extension module, provides the bindings for the ROOT class library in a generic way using the Cling
dictionary. This way, it allows the use of any ROOT classes from the Python interpreter, and thus the “glue-ing” of
ROOT libraries with any non-ROOT library or applications that provide Python bindings. Further,
PyROOT
can be
loaded into the Cling interpreter to allow (as of now still rudimentary) access to Python classes. The best way to
understand the benefits of PyROOT is through a few examples.
19.1.1 Glue-ing Applications
The
PyQt
library, see http://www.riverbankcomputing.co.uk/pyqt, provides Python bindings for the Qt cross-platform
GUI framework ( http://www.trolltech.com). With
PyROOT
and
PyQt
, adding ROOT application layer code to a Qt
GUI, becomes children play. The following example shows how a Python class can be used to have ROOT code respond
to a click on a Qt widget.
# Glue-ing Qt and ROOT through Python
import sys, ROOT
from qt import *
theApp = QApplication( sys.argv)
box = QVBox()
box.resize(QSize(40,10).expandedTo(box.minimumSizeHint()))
class myButton(QPushButton):
def __init__( self,label,master):
QPushButton.__init__(self,label,master)
self.setFont( QFont('Times',18,QFont.Bold))
def browse(self):
self.b = ROOT.TBrowser()
bb = myButton('browser',box)
525
526 CHAPTER 19. PYTHON AND RUBY INTERFACES
QObject.connect( bb,SIGNAL('clicked()'),bb.browse)
theApp.setMainWidget(box)
box.show()
theApp.exec_loop()
When the example is run, a Qt button is displayed, and when the button is clicked, a
TBrowser
instance is created and
will appear on the screen.
PyROOT
takes care of feeding system events to ROOT widgets, so the
TBrowser
instance and
the button behave properly when users interact with them.
19.1.2 Access to ROOT from Python
There are several tools for scientific analysis that come with bindings that allow the use of these tools from the Python
interpreter.
PyROOT
provides this for users who want to do analysis in Python with ROOT classes. The following
example shows how to fill and display a ROOT histogram while working in Python. Of course, any actual analysis
code may come from somewhere else through other bindings, e.g. from a C++ program.
When run, the next example will display a 1-dimensional histogram showing a Gaussian distribution. More examples
like the one above are distributed with ROOT under the $ROOTSYS/tutorials directory.
# Example: displaying a ROOT histogram from Python
from ROOT import gRandom,TCanvas,TH1F
c1 = TCanvas('c1','Example',200,10,700,500)
hpx = TH1F('hpx','px',100,-4,4)
for i in xrange(25000):
px = gRandom.Gaus()
hpx.Fill(px)
hpx.Draw()
c1.Update()
19.1.3 Access to Python from ROOT
Access to Python objects from Cling is not completely fleshed out. Currently, ROOT objects and built-in types can
cross the boundary between the two interpreters, but other objects are much more restricted. For example, for a
Python object to cross, it has to be a class instance, and its class has to be known to Cling first (i.e. the class has to
cross first, before the instance can). All other cross-coding is based on strings that are run on the Python interpreter
and vise-versa.
With the ROOT v4.00/06 and later, the
TPython
class will be loaded automatically on use, for older editions,
the
libPyROOT.so
needs to be loaded first before use. It is possible to switch between interpreters by calling
TPython::Prompt()
on the ROOT side, while returning with
ˆD
(
EOF
). State is preserved between successive switches,
and string based cross calls can nest as long as shared resources are properly handled.
// Example: accessing the Python interpreter from ROOT
// either load PyROOT explicitly or rely on auto-loading
root[] gSystem->Load( "libPyROOT" );
root[] TPython::Exec("print1+1");
2
// create a TBrowser on the Python side, and transfer it back and forth
root[] TBrowser* b = (void*)TPython::Eval("ROOT.TBrowser()");
(class TObject*)0x8d1daa0
root[] TPython::Bind(b,"b");
// builtin variables can cross-over (after the call i==2)
root[] int i = TPython::Eval( "1+1" );
root[] i
(int)2
19.1. PYROOT OVERVIEW 527
19.1.4 Installation
There are several ways of obtaining
PyROOT
, and which is best depends on your specific situation. If you work at CERN,
you can use the installation available on
afs
. Otherwise, you will want to build from source, as
PyROOT
is not build
by default in the binaries distributed from the ROOT project site. If you download the ROOT binaries, take care to
download and install the Python distribution from http://www.python.org/ against which they were built.
19.1.4.1 Environment Settings
ROOT installations with the build of
PyROOT
enabled are available from the CERN
afs
cell
/afs/cern.ch/sw/root/<version>/<platform>
.
To use them, simply modify your shell environment accordingly. For Unix:
export PATH=$ROOTSYS/bin:$PYTHONDIR/bin:$PATH
export LD_LIBRARY_PATH=$ROOTSYS/lib:$PYTHONDIR/lib:$LD_LIBRARY_PATH
export PYTHONPATH=$ROOTSYS/lib:$PYTHONPATH
For Windows:
set PATH=%ROOTSYS%/bin;%PYTHONDIR%/bin;%PATH%
set PYTHONPATH=%ROOTSYS%/bin;%PYTHONPATH%
where
$ROOTSYS
should be set to
/afs/cern.ch/sw/root/<version>/<platform>
, and
PYTHONDIR
to
/afs/cern.ch/sw/lcg/external/Python/2.3.4/<platform>
with <version> and <platform> as appropriate. Note that the latest version of Python is 2.4.1.
19.1.4.2 Building from Source
The standard installation instructions for building ROOT from source apply, with the addition that the build of
PyROOT
needs to be enabled at the configuration step. First, follow the instructions for obtaining and unpacking the source,
and setting up the build environment.
Then, use the following command to configure the build process (of course, feel free to add any additional flags you
may need):
$ ./configure <arch> [--with-python-incdir=<dir>][--with-python-libdir=>dir>]
For details on
<arch>
see the official build pages, the Python include directory should point to the directory that
contains
Python.h
and the library directory should point to the directory containing
libpythonx.y.so
, where ‘
x
’ and
‘
y
’ are the major and minor version number, respectively. If you do not specify include and library directories explicitly,
the configuration process will try the PYTHONDIR environment variable or, alternatively, the standard locations.
A recent distribution of Python is required: version 2.4.3 is preferred, but the older 2.2.x and 2.3.x versions suffice and
are supported as well. Versions older than 2.2 are not supported and will not work. Note that one problem with 2.2 is
that the shared library of the
Python
interpreter core is not build by default and the ‘–enable-shared’ flag should thus
be used when building
Python
from source. If the
Python
interpreter that is installed on your system is too old, please
obtain a new version from http://www.python.org.
Once configured, you continue the build process the normal way:
$ make
$ make install
After some time, a library called
libPyROOT.so
(or
libPyROOT.dll
, on Windows) will be created in the
$ROOTSYS/lib
(
$ROOTSYS/bin on Windows
) directory and a top Python module,
ROOT.py
, will be copied into the
same place. The final step is to setup the shell environment, which is similar to what is described in the chapter
‘Environment Settings’. Note that the
$ROOTSYS
entries are probably already there if you followed the standard
instructions, and that the
PYTHONDIR
entries should be replaced as appropriate by your choice at configuration time, or
be left out if you had the configuration script pick up them up from a default location.
19.1.5 Using PyROOT
Since it is an extension module, the usage of
PyROOT
probably comes naturally if you’re used to Python. In general,
PyROOT
attempts to allow working in both Python and ROOT style, and although it is succeeding, it isn’t perfect: there
are edges. The following sections explain in some detail what you can expect, and what you need to watch out for.
528 CHAPTER 19. PYTHON AND RUBY INTERFACES
19.1.5.1 Access to ROOT Classes
Before a ROOT class can be used from Python, its dictionary needs to be loaded into the current process. Starting
with ROOT version 4.00/06, this happens automatically for all classes that are declared to the auto-loading mechanism
through so-called
rootmap
files. Effectively, this means that all classes in the ROOT distributions are directly available
for import. For example:
from ROOT import TCanvas # available at startup
c = TCanvas()
from ROOT import TLorentzVector # triggers auto-load of libPhysics
l = TLorentzVector()
Although it is not recommended, a simple way of working with PyROOT is doing a global import:
from ROOT import *
c = TCanvas()
l = TLorentzVector()
Keeping the ROOT namespace (“
import ROOT
”), or only importing from ROOT those classes that you will actually
use (see above), however, will always be cleaner and clearer:
import ROOT
c = ROOT.TCanvas()
l = ROOT.TLorentzVector()
Since it is foreseen that most people will use the simple approach anyway, the request to copy all from module ROOT
will not actually result in copying all ROOT classes into the current namespace. Instead, classes will still be bound
(and possibly loaded) on an as-needed basis. Note carefully how this is different from other Python (extension) modules,
and what to expect if you use the normal inspection tools (such as e.g. ‘
dir()
’). This feature prevents the inspection
tools from being swamped by an enormous amount of classes, but they can no longer be used to explore unknown parts
of the system (e.g. to find out which classes are available). Furthermore, because of this approach, <
tab
>-completion
will usually not be available until after the first use (and hence creation) of a class.
Access to class static functions, public data members, enums, etc. is as expected. Many more example uses of ROOT
classes from Python can be found in the tutorials directory in the ROOT distribution. The recipes section contains a
description on working with your own classes (see “Using Your Own Classes”).
19.1.5.2 Access to STL Classes
The STL classes live in the ROOT.std namespace (or, if you prefer to get them from there, in the ROOT module
directly, but doing so makes the code less clear, of course). Be careful in their use, because Python already has types
called “string” and “list.”
In order to understand how to get access to a templated class, think of the general template as a meta class. By
instantiating the meta class with the proper parameters, you get an actual class, which can then be used to create
object instances. An example usage:
>>> from ROOT import std
>>> v = std.vector(int)()
>>> for i in range(0,10):
... v.push_back(i)
...
>>> for i in v:
... print(i, end=' ')
123456789
>>>
>>> list(v)
[0,1,2,3,4,5,6,7,8,9]
>>>
19.1. PYROOT OVERVIEW 529
The parameters to the template instantiation can either be an actual type or value (as is used here, “int”), or a
string representation of the parameters (e.g. “ ‘double’ ”), or a mixture of both (e.g. “ ‘TCanvas, 0’ ” or “ ‘double’, 0”
). The “std::vector<int>” class is one of the classes builtin by default into the Cling extension dlls. You will get a
non-functional class (instances of which can still be passed around to C++) if the corresponding dictionary doesn’t
exist.
19.1.5.3 Access to ROOT Globals
Most globals and global functions can be imported directly from the ROOT.py module, but some common ones (most
notably
gMinuit
, although that variable now exists at startup from release 5.08 onward) do not exist yet at program
startup, as they exist in modules that are loaded later (e.g. through the auto-loading mechanims). An example session
should make this clear:
>>> from ROOT import *
>>> gROOT # directly available
<ROOT.TROOT object at 0x399c30>
>>> gMinuit # library not yet loaded: not available
Traceback (most recent call last):
File "<stdin>", line 1, in ?
NameError: name 'gMinuit'is not defined
>>> TMinuit # use of TMinuit class forces auto-loading
<class '__main__.TMinuit'>
>>> gMinuit # now gMinuit is available
<__main__.TMinuit object at 0x1458c70>
>>> not not gMinuit # but it is the null pointer, until set
False
>>> g = TMinuit()
>>> not not gMinuit
True
It is also possible to create globals interactively, either by executing a Cling macro, or by a call to
gROOT.ProcessLine()
.
These globals are made available in the same way: either use them directly after creation in ‘from ROOT import *’
more, or get them from the ROOT namespace after an ‘import ROOT’.
As of 5.08, the behaviour of ROOT globals is the same as python globals, which is sometimes counterintuitive: since
they are references, they can be changed only if done so directly through their containing module. The following session
shows that in detail:
>>> from ROOT import *
>>> print(gDebug)
0
>>> gROOT.ProcessLine( 'gDebug = 7;')
>>> print(gDebug)
0# local gDebug is unchanged
>>> gDebug = 5# changes _local_ reference only
>>> print(gDebug)
5# locally correct, but ...
>>> gROOT.ProcessLine( 'cout << gDebug << endl;')
7# ... ROOT global unchanged
>>> import ROOT
>>> print(ROOT.gDebug)
7# still the old value (not '5')
>>> ROOT.gDebug = 3# changes ROOT module reference
>>> gROOT.ProcessLine( 'cout << gDebug << endl;')
3# ROOT global properly changed
>>>
The above is another good reason to prefer ‘import ROOT’ over ‘from ROOT import *’.
19.1.5.4 Access to Python
The access to Python from Cling goes through the
TPython
class, or directly if a Python object or class has crossed
the border. The TPython class, which looks approximately like this:
530 CHAPTER 19. PYTHON AND RUBY INTERFACES
class TPython {
public:
// load a Python script as if it were a macro
static void LoadMacro(const char* name);
// execute a Python statement (e.g. "import ROOT")
static void Exec(const char* cmd);
// evaluate a Python expression (e.g. "1+1")
static const TPyReturn& Eval(const char* expr);
// bind a ROOT object with, at the Python side, the name "label"
static bool Bind(TObject* obj,const char* label);
// enter an interactive Python session (exit with ^D)
static void Prompt();
};
LoadMacro(const char* name)
- the argument is a name of a Python file that is to be executed (
’execfile’
), after
which any new classes are automatically made available to Cling. Since it is non-selective, use with care.
ExecScript(const char* name,int argc=0,const char** argv=0)
- the argument is a name of a python file that
is to be executed (‘execfile’) in a private namespace to minimize side-effects. Optionally, you can add CLI-style
arguments which are handed to the script through ‘sys.argv’ in the normal way.
Exec(const char* cmd)
- the argument is a string of Python code that is executed as a statement. There is no return
value, but an error message will be printed if there are problems such as syntax errors.
Eval(const char* expr)
- the argument is a string of Python code that is evaluated as an expression. The result of
the expression is returned, if it is either a builtin type (int, long, float, double, and
const char*
are supported), a
Python type that can cross, or a ROOT type. If a ROOT type is returned, an explicit cast to void* is needed to assign
the return value to a local pointer (which may have a different type), whereas builtin types will be cast implicitly, if
possible, to the type of the local variable to which they are assigned.
Bind(TObject* obj,const char* label)
- transfer a ROOT object from the Cling to the Python interpreter, where
it will be referenced with a variable called “label”.
Prompt() - Transfer the interactive prompt to Python.
With the ROOT v4.00/06 and later, the
TPython
class will be loaded automatically on use, for older editions, the
libPyROOT.so
needs to be loaded first with
gSystem->Load()
before use. Refer back to the other example of the use
of TPython that was given in “Access to Python from ROOT”.
To show in detail how Python access can be used, an example Python module is needed, as follows:
print('creating class MyPyClass ... ')
class MyPyClass:
def __init__(self):
print('in MyPyClass.__init__')
self._browser = None
def gime(self, what):
return what
This module can now be loaded into a Cling session, the class used to instantiate objects, and their member functions
called for showing how different types can cross:
root[] TPython::LoadMacro("MyPyClass.py");
creating class MyPyClass ...
root[] MyPyClass m;
in MyPyClass.__init__
root[] char* s = m.gime("aap");
root[] s
(char*0x41ee7754)"aap"
Note that the
LoadMacro()
call makes the class automatically available, such that it can be used directly. Otherwise,
agROOT->GetClass() call is required first.
19.1. PYROOT OVERVIEW 531
19.1.5.5 Callbacks
The simplest way of setting a callback to Python from Cling, e.g. for a button, is by providing the execution string.
See for example tutorials/pyroot/demo.py that comes with the ROOT installation:
# [..]
bar = ROOT.TControlBar('vertical','Demos')
bar.AddButton('Help on Demos',r'TPython::Exec("execfile('demoshelp.py')");','Click Here For Help on Running the Demos')
bar.AddButton('browser',r'TPython::Exec("b = Tbrowser()");','Start the ROOT browser')
# [..]
Here, the callback is a string that will be interpreted by Cling to call
TPython::Exec()
, which will, in turn, interpret
and execute the string given to it. Note the use of raw strings (the ‘
r
’ in front of the second argument string), in order
to remove the need of escaping the backslashes.
19.1.5.6 Cling Commands
In interactive mode, the Python exception hook is used to mimic some of the Cling commands available. These are:
.q
,
.!
,
.x
,
.L
,
.cd
,
.ls
,
.pwd
,
.?
and
.help
. Note that
.x
translates to Python ‘
execfile()
’ and thus accepts only
Python files, not Cling macros.
19.1.6 Memory Handling
The Python interpreter handles memory for the user by employing reference counting and a garbage collector (for
new-style objects, which includes
PyROOT
objects). In C++, however, memory handling is done either by hand, or
by an application specific, customized mechanism (as is done in ROOT). Although
PyROOT
is made aware of ROOT
memory management, there are still a few boundary conditions that need to be dealt with by hand. Also, the heuristics
that
PyROOT
employs to deal with memory management are not infallible. An understanding in some detail of the
choices that are made is thus important.
19.1.6.1 Automatic Memory Management
There are two global policies that can be set: heuristics and strict. By default, the heuristic policy is used, in which
the following rules are observed:
•
A ROOT object created on the Python interpreter side is owned by Python and will be deleted once the last
Python reference to it goes away. If, however, such an object is passed by non-const address as a parameter to a
C++ function (with the exception of the use as “self” to a member function), ownership is relinquished.
•
A ROOT object coming from a ROOT call is not owned, but before it passes to the Python interpreter, its “must
cleanup” bit is set if its type is a class derived from
TObject
. When the object goes out of scope on the C++
side, the Python object will change type into an object that largely behaves like None.
The strict policy differs in that it will never relinquish ownership when passing an object as a parameter to a function.
It is then up to the developer to prevent double deletes. Choosing one or the other policy is done by:
ROOT.SetMemoryPolicy( ROOT.kMemoryStrict )
for the strict policy, or for the heuristic policy:
ROOT.SetMemoryPolicy( ROOT.kMemoryHeuristics )
Care must be taken in the case of graphic objects: when drawn on the current pad, a reference to the graphics is kept
that
PyROOT
isn’t currently aware of, and it is up to the developer to keep at lease one Python reference alive. See
$ROOTSYS/tutorials/pyroot/zdemo.py
(available in the latest release) for an example. Alternatively, one can tell
python to give up ownership for individual instances:
o = ROOT.TObject()
ROOT.SetOwnership( o, False ) # True to own, False to release
532 CHAPTER 19. PYTHON AND RUBY INTERFACES
19.1.6.2 Memory Management by Hand
If needed, you can explicitly destroy a ROOT object that you own through its associated TClass:
myobject.IsA().Destructor(myobject)
which will send out the deletion notification to the system (thus you do not need to care anymore at this point about
Python reference counting, the object will go, even if it’s reference count it non-zero), and free the memory.
19.1.7 Performance
The performance of
PyROOT
when programming with ROOT in Python is similar to that of Cling. Differences occur
mainly because of differences in the respective languages: C++ is much harder to parse, but once parsed, it is much
easier to optimize. Consequently, individual calls to ROOT are typically faster from
PyROOT
, whereas loops are typically
slower.
When programming in Python, the modus operandi is to consider performance generally “good enough” on the outset,
and when it turns out that, it is not good enough; the performance critical part is converted into C/C++ in an
extension module. The school of thought where pre-mature optimization is the root of all evil should find this way
of working very satisfying. In addition, if you look at their history, you will see that many of the standard Python
modules have followed this path.
Your code should always make maximum use of ROOT facilities; such that most of the time is spending in compiled
code. This goes even for very simple things: e.g. do not compute invariant masses in Python, use
TLorentzVector
instead. Moreover, before you start optimizing, make sure that you have run a profiler to find out where the bottlenecks
are. Some performance, without cost in terms of programmer effort, may be gained by using
psyco
, see the next link:
http://psyco.sourceforge.net, a Python just in time compiler (JIT). Note, however, that
psyco
is limited to Intel i386
CPUs. Since
psyco
optimizes Python, not
PyROOT
calls; it generally does not improve performance that much if most
of your code consists of ROOT API calls. Mathematical computations in Python, on the other hand, benefit a lot.
Every call to a Python member function results in a lookup of that member function and an association of this method
with
’self’
. Furthermore, a temporary object is created during this process that is discarded after the method call. In
inner loops, it may be worth your while (up to 30%), to short-cut this process by looking up and binding the method
before the loop, and discarding it afterwards. Here is an example:
hpx = TH1F('hpx','px',100,-4,4)
hpxFill = hpx.Fill # cache bound method
for i in xrange(25000):
px = gRandom.Gaus()
hpxFill(px) # use bound method: no lookup needed
del hpxFill # done with cached method
Note that if you do not discard the bound method, a reference to the histogram will remain outstanding, and it will
not be deleted when it should be. It is therefore important to delete the method when you’re done with it.
19.1.8 Use of Python Functions
It is possible to mix Python functions with ROOT and perform such operations as plotting and fitting of histograms
with them. In all cases, the procedure consists of instantiating a ROOT
TF1
,
TF2
, or
TF3
with the Python function
and working with that ROOT object. There are some memory issues, so it is for example not yet possible to delete
a
TF1
instance and then create another one with the same name. In addition, the Python function, once used for
instantiating the TF1, is never deleted.
Instead of a Python function, you can also use callable instances (e.g., an instance of a class that has implemented
the
__call__
member function). The signature of the Python callable should provide for one or two arrays. The first
array, which must always be present, shall contain the
x
,
y
,
z
, and t values for the call. The second array, which is
optional and its size depends on the number given to the
TF1
constructor, contains the values that parameterize the
function. For more details, see the TF1 documentation and the examples below.
19.1. PYROOT OVERVIEW 533
19.1.8.1 Plotting Python Function
This is an example of a parameter less Python function that is plotted on a default canvas:
from ROOT import TF1, TCanvas
def identity( x ):
return x[0]
# create an identity function
f = TF1('pyf1', identity, -1., 1.)
# plot the function
c = TCanvas()
f.Draw()
Because no number of parameters is given to the
TF1
constructor, ‘
0
’ (the default) is assumed. This way, the ‘
identity’
function need not handle a second argument, which would normally be used to pass the function parameters. Note
that the argument’
x
’ is an array of size 4. The following is an example of a parameterized Python callable instance
that is plotted on a default canvas:
from ROOT import TF1, TCanvas
class Linear:
def __call__( self, x, par ):
return par[0] + x[0]*par[1]
# create a linear function with offset 5, and pitch 2
f = TF1('pyf2',Linear(),-1.,1.,2)
f.SetParameters(5.,2.)
# plot the function
c = TCanvas()
f.Draw()
Note that this time the constructor is told that there are two parameters, and note in particular how these parameters
are set. It is, of course, also possible (and preferable if you only use the function for plotting) to keep the parameters
as data members of the callable instance and use and set them directly from Python.
19.1.8.2 Fitting Histograms
Fitting a histogram with a Python function is no more difficult than plotting: instantiate a
TF1
with the Python
callable and supply that
TF1
as a parameter to the
Fit()
member function of the histogram. After the fit, you can
retrieve the fit parameters from the TF1 instance. For example:
from ROOT import TF1, TH1F, TCanvas
class Linear:
def __call__( self, x, par ):
return par[0] + x[0]*par[1]
# create a linear function for fitting
f = TF1('pyf3',Linear(),-1.,1.,2)
# create and fill a histogram
h = TH1F('h','test',100,-1.,1.)
f2 = TF1('cf2','6.+x*4.5',-1.,1.)
h.FillRandom('cf2',10000)
# fit the histo with the python 'linear'function
h.Fit(f)
534 CHAPTER 19. PYTHON AND RUBY INTERFACES
# print results
par = f.GetParameters()
print('fit results: const =', par[0], ',pitch =', par[1])
19.1.9 Working with Trees
Next to making histograms, working with trees is probably the most common part of any analysis. The
TTree
implementation uses pointers and dedicated buffers to reduce the memory usage and to speed up access. Consequently,
mapping
TTree
functionality to Python is not straightforward, and most of the following features are implemented in
ROOT release 4.01/04 and later only, whereas you will need 5.02 if you require all of them.
19.1.9.1 Accessing an Existing Tree
Let us assume that you have a file containing
TTrees
,
TChains
, or
TNtuples
and want to read the contents for use in
your analysis code. This is commonly the case when you work with the result of the reconstruction software of your
experiment (e.g. the combined ntuple in ATLAS). The following example code outlines the main steps (you can run it
on the result of the tree1.C macro):
from ROOT import TFile
# open the file
myfile = TFile('tree1.root')
# retrieve the ntuple of interest
mychain = myfile.Get('t1')
entries = mychain.GetEntriesFast()
for jentry in xrange(entries):
# get the next tree in the chain and verify
ientry = mychain.LoadTree(jentry)
if ientry < 0:
break
# copy next entry into memory and verify
nb = mychain.GetEntry(jentry)
if nb<=0:
continue
# use the values directly from the tree
nEvent = int(mychain.ev)
if nEvent<0:
continue
print(mychain.pz, '=', mychain.px*mychain.px, '+', mychain.py*mychain.py)
Access to arrays works the same way as access to single value tree elements, where the size of the array is determined
by the number of values actually read from the file. For example:
# loop over array tree element
for d in mychain.mydoubles:
print(d)
# direct access into an array tree element
i5 = mychain.myints[5]
19.1.9.2 Writing a Tree
Writing a ROOT
TTree
in a Python session is a little convoluted, if only because you will need a C++ class to make
sure that data members can be mapped, unless you are working with built-in types. Here is an example for working
with the latter only:
19.1. PYROOT OVERVIEW 535
from ROOT import TFile, TTree
from array import array
h = TH1F('h1','test',100,-10.,10.)
f = TFile('test.root','recreate')
t = TTree('t1','tree with histos')
maxn = 10
n = array('i',[0])
d = array('f',maxn*[0.])
t.Branch('mynum',n,'mynum/I')
t.Branch('myval',d,'myval[mynum]/F')
for i in range(25):
n[0] = min(i,maxn)
for j in range(n[0]):
d[j] = i*0.1+j
t.Fill()
f.Write()
f.Close()
The use of arrays is needed, because the pointer to the address of the object that is used for filling must be given
to the
TTree::Branch()
call, even though the formal argument is declared a ’
void*’
. In the case of ROOT objects,
similar pointer manipulation is unnecessary, because the full type information is available, and
TTree::Branch()
has
been Pythonized to take care of the call details. However, data members of such objects that are of built-in types, still
require something extra since they are normally translated to Python primitive types on access and hence their address
cannot be taken. For that purpose, there is the AddressOf() function. As an example:
from ROOT import TFile, TTree
from ROOT import gROOT, AddressOf
gROOT.ProcessLine(
"struct MyStruct { Int_t fMyInt1; Int_t fMyInt2; Int_t fMyInt3; Char_t fMyCode[4]; };" );
from ROOT import MyStruct
mystruct = MyStruct()
f = TFile('mytree.root','RECREATE')
tree = TTree('T','Just A Tree')
tree.Branch('myints',mystruct,'MyInt1/I:MyInt2:MyInt3')
tree.Branch('mycode',AddressOf(mystruct,'fMyCode'),'MyCode/C')
for i in range(0,10):
mystruct.fMyInt1 = i
mystruct.fMyInt2 = i*i
mystruct.fMyInt3 = i*i*i
mystruct.fMyCode = "%03d" % i # note string assignment
tree.Fill()
f.Write()
f.Close()
The C++ class is defined through the
gROOT.ProcessLine()
call, and note how the
AddressOf()
function is used for
data members of built-in type. Most of the above is for ROOT version 5.02 and later only. For older releases, and
without further support, here is an example as to how you can get hold of a pointer-to-pointer to a ROOT object:
h = TH1F()
addressofobject = array('i',[h.IsA().DynamicCast(h.IsA(),h)])
19.1.10 Using Your Own Classes
A user’s own classes can be accessed after loading, either directly or indirectly, the library that contains the dictionary.
One easy way of obtaining such a library, is by using ACLiC:
536 CHAPTER 19. PYTHON AND RUBY INTERFACES
$ cat MyClass.C
class MyClass {
public:
MyClass(int value = 0) {
m_value = value;
}
void SetValue(int value) {
m_value = value;
}
int GetValue() {
return m_value;
}
private:
int m_value;
};
$ echo .L MyClass.C+ | root.exe -b
[...]
Info in <TUnixSystem::ACLiC>: creating shared library [..]/./MyClass_C.so
$
Then you can use it, for example, like so:
from ROOT import gSystem
# load library with MyClass dictionary
gSystem.Load('MyClass_C')
# get MyClass from ROOT
from ROOT import MyClass
# use MyClass
m = MyClass(42)
print(m.GetValue())
You can also load a macro directly, but if you do not use ACLiC, you will be restricted to use the default constructor
of your class, which is otherwise fully functional. For example:
from ROOT import gROOT
# load MyClass definition macro (append '+'to use ACLiC)
gROOT.LoadMacro('MyClass.C')
# get MyClass from ROOT
from ROOT import MyClass
# use MyClass
m = MyClass()
m.SetValue(42)
print(m.GetValue())
19.2 How to Use ROOT with Ruby
Ruby ROOT is a Ruby extension module that allows the user to interact with any ROOT class from the Ruby scripting
language. The Ruby module resolves ROOT Classes and Methods at run-time using the Cling API, so there is no need
for wrapping specific Classes to be used in Ruby. The Ruby module, also, contains a
TRuby
class to execute Ruby
statements via Cling and export C++ Objects to Ruby objects, interactively.
19.2. HOW TO USE ROOT WITH RUBY 537
19.2.1 Building and Installing the Ruby Module
The Ruby extension module is not built by default when building ROOT from sources. The user should follow the
standard installation instructions and enable the build of the Ruby module. Ruby version >= 1.8 is required.
./configure <arch> --enable-ruby --enable-explicitlink
[--with-ruby-incdir=<dir>] [--with-ruby-libdir=<dir>]
gmake
If you do not specify include and library directories configure will use Ruby to grab the directories where Ruby’s
headers and library are located. A library called
libRuby.so [libRuby.dll]
will be created in the
$ROOTSYS/lib
[$ROOTSYS/bin].
19.2.1.1 Setting up the Environment
For working with the Ruby module, the
LD_LIBRARY_PATH [PATH]
and
RUBYLIB,
need to be set in addition to the
standard $ROOTSYS.
For UNIX Platforms:
export LD_LIBRARY_PATH=$ROOTSYS/lib:$LD_LIBRARY_PATH
export RUBYLIB=$ROOTSYS/lib:$RUBYLIB
For Windows:
set PATH=%ROOTSYS%/bin;%PATH%
set RUBYLIB=%ROOTSYS%/bin;%RUBYLIB%
19.2.1.2 Running ROOT scripts from Ruby
The user should make sure that the ruby command is the one of the installation that has been used to build the Ruby
extension module. If the RUBYLIB environment variable is set correctly, the user can execute a Ruby script with
ROOT functionality in the following way:
ruby -rlibRuby foo.rb
Another way is to start the Ruby script with the Ruby require command:
require ’libRuby’
An example is as follows:
require 'libRuby'
gROOT.Reset
c1 = TCanvas.new('c1','Example with Formula',200,10,700,500)
#
# Create a one dimensional function and draw it
#
fun1 = TF1.new('fun1','abs(sin(x)/x)',0,10)
c1.SetGridx
c1.SetGridy
fun1.Draw
c1.Update
The user can find a number of examples in the
$ROOTSYS/tutorials
. To run them you need to execute the command:
cd $ROOTSYS/tutorials
ruby demo.rb
538 CHAPTER 19. PYTHON AND RUBY INTERFACES
19.2.1.3 Invoking the Ruby Module from Cling Interpreter
A ROOT user can run any Ruby command and eventually to run
IRB
, the Interactive Ruby Shell. The commands to
execute are:
root[] TRuby::Exec("require '/usr/local/lib/root/libRuby'");
root[] TRuby::Exec("c1 = TBrowser.new");
root[] TRuby::Eval("c1.GetName");
root[] TRuby::Eval("puts c1.GetName");
Browser
root[] TCanvas *c2 = new TCanvas("ruby test","test",10,10,100,100);
root[] TRuby::Bind(c2, "$c");
root[] TRuby::Eval("puts $c.GetTitle");
test
root[] TRuby::Prompt();
root[] TRuby::Prompt();
irb(main):001:0> print 1
1=> nil
irb(main):002:0>
Notice that whenever you bind a ROOT Object in the Ruby side, you need to use a global Ruby variable, that is a
variable with a leading “$”.
Chapter 20
The Tutorials and Tests
This chapter is a guide to the examples that come with the installation of ROOT. They are located in two directories:
$ROOTSYS/tutorials and $ROOTSYS/test.
20.1 $ROOTSYS/tutorials
The tutorials directory contains many example scripts. To have all examples working you must have write permission
and you will need to execute
hsimple.C
first. If you do not have write permission in the directory
$ROOTSYS/tutorials
,
copy the entire directory to your area. The script
hsimple.C
displays a histogram as it is being filled, and creates a
ROOT file used by the other examples.
To execute it type:
$ cd $ROOTSYS/tutorials
$ root
------------------------------------------------------------
| Welcome to ROOT 6.00/00 http://root.cern.ch |
| (c) 1995-2014, The ROOT Team |
| Built for linuxx8664gcc |
| From tag v6-00-00,30 May 2014 |
| Try '.help','.demo','.license','.credits','.quit'/'.q'|
------------------------------------------------------------
root [0] .x hsimple.C
Now execute
demos.C
, which brings up the button bar shown on the left. You can click on any button to execute
another example. To see the source, open the corresponding source file (for example
fit1.C
). Once you are done, and
want to quit the ROOT session, you can do so by typing .q.
root[] .x demos.C
root[] .q
20.2 $ROOTSYS/test
The test directory contains a set of examples that represent all areas of the framework. When a new release is cut, the
examples in this directory are compiled and run to test the new release’s backward compatibility.
We see these source files:
Makefile Makefile to build all test programs.
hsimple.cxx Simple test program that creates and saves some histograms
MainEvent.cxx
Simple test program that creates a ROOT Tree object and fills it with some simple
structures but also with complete histograms. This program uses the files
Event.cxx,EventCint.cxx and Event.h. An example of a procedure to link this
program is in
bind_Event
. Note that the
Makefile
invokes the
rootcling
utility
to generate the Cling interface EventCint.cxx
539
540 CHAPTER 20. THE TUTORIALS AND TESTS
Event.cxx Implementation for classes Event and Track
minexam.cxx Simple test program for data fitting
tcollex.cxx Example usage of the ROOT collection classes
tcollbm.cxx Benchmarks of ROOT collection classes
ctorture.cxx Test program for the class TComplex
tstring.cxx Example usage of the ROOT string class
vmatrix.cxx Verification program for the TMatrix class
vvector.cxx Verification program for the TVectorclass
vlazy.cxx Verification program for lazy matrices
hworld.cxx Small program showing basic graphics
guitest.cxx Example usage of the ROOT GUI classes
gui viewer .cxx Another ROOT GUI example program
Hello.cxx Dancing text example
Aclock.cxx Analog clock (a la X11 xclock)
Tetris.cxx The known Tetris game based on the ROOT graphics
stress.cxx Important ROOT stress testing program
stress*.cxx Stress testing of different ROOT classes
bench.cxx STL and ROOT container test and benchmarking program
QpRandomDriver.cx x Verfication program for Quadratic programming classes in Quadp library
DrawTest.sh Entry script to extensive TTree query test suite
dt_* Scripts used by DrawTest.sh
The
$ROOTSYS/test
directory is a gold mine of root-wisdom nuggets, and we encourage you to explore and exploit it.
These instructions will compile all programs in $ROOTSYS/test:
If you do not have write permission in the
$ROOTSYS/test
directory, copy the entire
$ROOTSYS/test
directory to your
area. The
Makefile
is a useful example of how ROOT applications are linked and built. Edit the
Makefile
to specify
your architecture by changing the ARCH variable, for example, on an SGI machine type:ARCH =sgikcc.
Now compile all programs:
%gmake
This will build several applications and shared libraries. We are especially interested in Event, stress, and guitest.
20.2.1 Event - An Example of a ROOT Application
Event is created by compiling
MainEvent.cxx
, and
Event.cxx
. It creates a ROOT file with a tree and two histograms.
When running Event we have four optional arguments with defaults:
Argument Default
1 Number of Events (1 . . . n) 400
2 Compression level:
0: no compression at all.
1: If the split level is set to zero, everything is compressed according to the
gzip
level 1. If split level is set to 1, leaves that are not floating point numbers
are compressed using the gzip level 1.
2: If the split level is set to zero, everything is compressed according to the
gzip level 2. If split level is set to 1, all non floating point leaves are
compressed according to the gzip level 2 and the floating point leaves are
compressed according to the gzip level 1 (gzip level -1).
Floating point numbers are compressed differently because the gain when
compressing them is about 20 - 30%. For other data types it is generally better
and around 100%.
1
3 Split or not Split
0: only one single branch is created and the complete event is serialized in one
single buffer
1: a branch per variable is created.
1
(Split)
4 Fill
0: read the file
1: write the file, but don’t fill the histograms
2: don’t write, don’t fill the histograms
10: fill the histograms, don’t write the file
11: fill the histograms, write the file
20: read the file sequentially
25: read the file at random
1
(Write, no fill)

20.2. $ROOTSYS/TEST 541
542 CHAPTER 20. THE TUTORIALS AND TESTS
20.2.1.1 Effect of Compression on File Size and Write Times
You may have noticed that a ROOT file has up to nine compression level, but here only levels 0, 1, and 2 are described.
Compression levels above 2 are not competitive. They take up to much write time compared to the gain in file space.
Below are three runs of Event on a Pentium III 650 MHz and the resulting file size and write and read times.
No Compression:
> Event 400 0 1 1
400 events and 19153182 bytes processed.
RealTime=6.840000 seconds, CpuTime=3.560000 seconds
compression level=0, split=1, arg4=1
You write 2.800173 Mbytes/Realtime seconds
You write 5.380107 Mbytes/Cputime seconds
> ls -l Event.root
... 19752171 Feb 23 18:26 Event.root
> Event 400 0 1 20
400 events and 19153182 bytes processed.
RealTime=0.790000 seconds, CpuTime=0.790000 seconds
You read 24.244533 Mbytes/Realtime seconds
You read 24.244533 Mbytes/Cputime seconds
We see the file size without compression is 19.75 MB, the write time is 6.84 seconds and the read time is 0.79 seconds.
Compression = 1: event is compressed:
> Event 400 1 1 1
400 events and 19153182 bytes processed.
RealTime=6.440000 seconds, CpuTime=4.020000 seconds
compression level=1, split=1, arg4=1
You write 2.974096 Mbytes/Realtime seconds
You write 4.764473 Mbytes/Cputime seconds
> ls -l Event.root
... 17728188 Feb 23 18:28 Event.root
> Event 400 1 1 20
400 events and 19153182 bytes processed.
RealTime=0.900000 seconds, CpuTime=0.900000 seconds
You read 21.281312 Mbytes/Realtime seconds
You read 21.281312 Mbytes/Cputime seconds
We see the file size 17.73, the write time was 6.44 seconds and the read time was 0.9 seconds.
Compression = 2: Floating point numbers are compressed with level 1:
> Event 400 2 1 1
400 events and 19153182 bytes processed.
RealTime=11.340000 seconds, CpuTime=9.510000 seconds
compression level=2, split=1, arg4=1
You write 1.688993 Mbytes/Realtime seconds
You write 2.014004 Mbytes/Cputime seconds
> ls -l Event.root
... 13783799 Feb 23 18:29 Event.root
> Event 400 2 1 20
400 events and 19153182 bytes processed.
RealTime=2.170000 seconds, CpuTime=2.170000 seconds
You read 8.826351 Mbytes/Realtime seconds
You read 8.826351 Mbytes/Cputime seconds
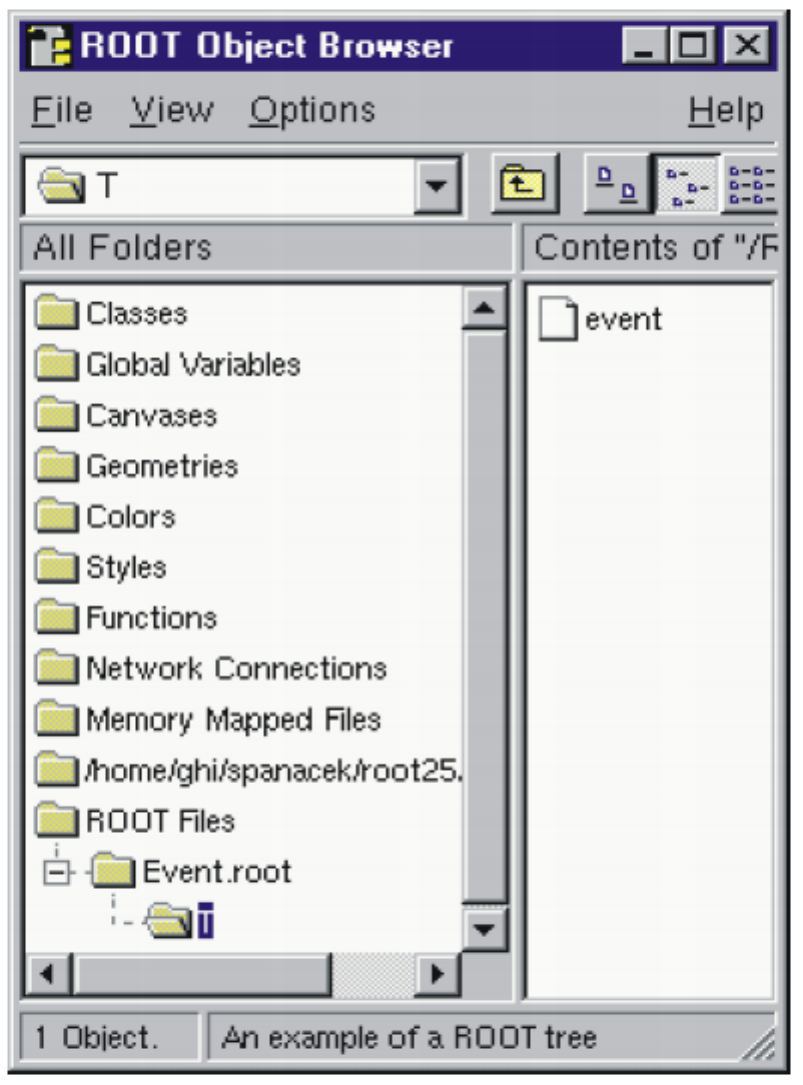
20.2. $ROOTSYS/TEST 543
The file size is 13.78 MB, the write time is 11.34 seconds and the read time is 2.17 seconds.
This table summarizes the findings on the impact of compressions:
Compression File Size Write Times Read Times
0 19.75 MB 6.84 sec. 0.79 sec.
1 17.73 MB 6.44 sec. 0.90 sec.
2 13.78 MB 11.34 sec. 2.17 sec.
20.2.1.2 Setting the Split Level
Split Level = 0:
Now we execute Event with the split parameter set to 0:
> Event 400 1 0 1
> root
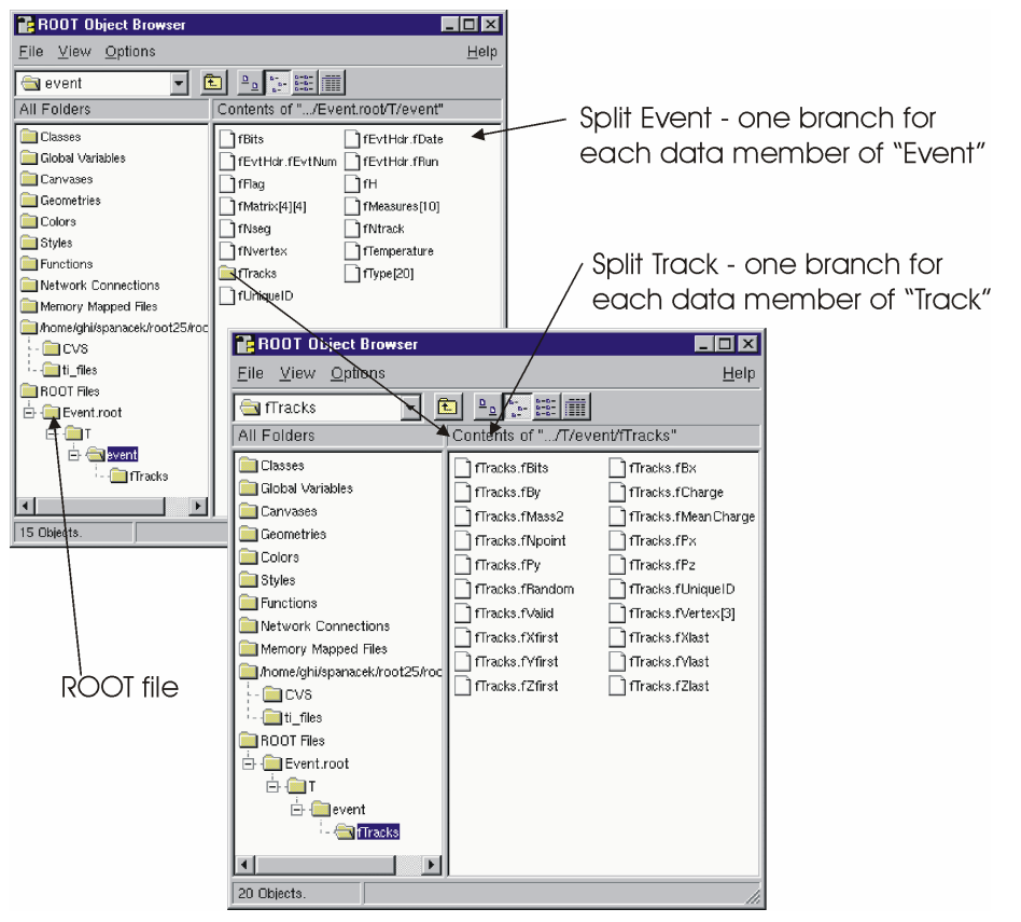
544 CHAPTER 20. THE TUTORIALS AND TESTS
root[] TFile f("Event.root")
root[] TBrowser T
We notice that only one branch is visible (event). The individual data members of the
Event
object are no longer
visible in the browser. They are contained in the event object on the event branch, because we specified no splitting.
Split Level = 1:
Setting the split level to 1 will create a branch for each data member in the Event object. First we execute
Event
and
set the split level to 1 and start the browser to examine the split tree:
> Event 400 1 1 1
> root
root[] TFile f("Event.root")
root[] TBrowser browser
20.2.2 stress - Test and Benchmark
The executable stress is created by compiling
stress.cxx
. It completes sixteen tests covering the following capabilities
of the ROOT framework.
•Functions, Random Numbers, Histogram Fits
20.2. $ROOTSYS/TEST 545
•Size & compression factor of a ROOT file
•Purge, Reuse of gaps in TFile
•2D Histograms, Functions, 2D Fits
•Graphics & PostScript
•Subdirectories in a ROOT file
•TNtuple, Selections, TCutG,TEventList
•Split and Compression modes for Trees
•Analyze Event.root file of stress 8
•Create 10 files starting from Event.root
•Test chains of Trees using the 10 files
•Compare histograms of test 9 and 11
•Merging files of a chain
•Check correct rebuilt of Event.root in test 13
•Divert Tree branches to separate files
•Cling test (3 nested loops) with LHCb trigger
The program stress takes one argument, the number of events to process. The default is 1000 events. Be aware that
executing stress with 1000 eventswill create several files consuming about 100 MB of disk space; running stress with 30
events will consume about 20 MB. The disk space is released once stress is done.
There are two ways to run stress:
From the system prompt or from the ROOT prompt using the interpreter.
> cd $ROOTSYS/test
> stress // default 1000 events
> stress 30 // test with 30 events
Start ROOT with the batch mode option (-b) to suppress the graphic output.
> root -b
root[] .L stress.cxx
root[] stress(1000)// test with 1000 events
root[] stress(30)// test with 30 events
The output of stress includes a pass/fail conclusion for each test, the total number of bytes read and written, and the
elapsed real and CPU time. It also calculates a performance index for your machine relative to a reference machine a
DELL Inspiron 7500 (Pentium III 600 MHz) with 256 MB of memory and 18GB IDE disk in ROOTMARKS. Higher
ROOTMARKS means better performance. The reference machine has 200 ROOTMARKS, so the sample run below
with 53.7 ROOTMARKS is about four times slower than the reference machine.
Here is a sample run:
% root -b
root[] .x stress.cxx(30)
Test 1: Functions, Random Numbers, Histogram Fits............. OK
Test 2: Check size & compression factor of a Root file........ OK
Test 3: Purge, Reuse of gaps in TFile......................... OK
Test 4: Test of 2-d histograms, functions, 2-d fits........... OK
Test 5: Test graphics & PostScript ............................OK
Test 6: Test subdirectories in a Root file.................... OK
Test 7: TNtuple, selections, TCutG, TEventList.......... OK
Test 8: Trees split and compression modes..................... OK

546 CHAPTER 20. THE TUTORIALS AND TESTS
Test 9: Analyze Event.root file of stress 8................... OK
Test 10 : Create 10 files starting from Event.root.............. OK
Test 11 : Test chains of Trees using the 10 files............... OK
Test 12 : Compare histograms of test 9and 11................... OK
Test 13 : Test merging files of a chain......................... OK
Test 14 : Check correct rebuilt of Event.root in test 13........ OK
Test 15 : Divert Tree branches to separate files................ OK
Test 16 : Cling test (3nested loops) with LHCb trigger.......... OK
******************************************************************
* IRIX64 fnpat1 6.5 01221553 IP27
******************************************************************
stress : Total I/O = 75.3 Mbytes, I = 59.2,O= 16.1
stress : Compr I/O = 75.7 Mbytes, I = 60.0,O= 15.7
stress : Real Time = 307.61 seconds Cpu Time = 292.82 seconds
******************************************************************
* ROOTMARKS = 53.7 * Root2.25/00 20000710/1022
20.2.3 guitest - A Graphical User Interface
The
guitest
example, created by compiling
guitest.cxx
, tests and illustrates the use of the native GUI widgets
such as cascading menus, dialog boxes, sliders and tab panels. It is a very useful example to study when designing a
GUI. Some examples of the output of
guitest
are shown next. To run it type
guitest
at the system prompt in the
$ROOTSYS/test
directory. We have included an entire chapter on this subject where we explore
guitest
in detail and
use it to explain how to build our own ROOT application with a GUI. See “Writing a Graphical User Interface”.
Figure 20.1: Native GUI widgets
Chapter 21
Example Analysis
This chapter is an example of a typical physics analysis. Large data files are chained together and analyzed using the
TSelector class.
21.1 Explanation
This script uses four large data sets from the H1 collaboration at DESY Hamburg. One can access these data sets (277
Mbytes) from the ROOT web site at: ftp://root.cern.ch/root/h1analysis/
The physics plots generated by this example cannot be produced using smaller data sets.
There are several ways to analyze data stored in a ROOT Tree
•Using TTree::Draw:
•
This is very convenient and efficient for small tasks. A
TTree
::Draw call produces one histogram at the time.
The histogram is automatically generated. The selection expression may be specified in the command line.
•Using the TTreeViewer:
•This is a graphical interface to TTree::Draw with the same functionality.
•Using the code generated by TTree::MakeClass:
•
In this case, the user creates an instance of the analysis class. They have the control over the event loop and can
generate an unlimited number of histograms.
•
Using the code generated by
TTree::MakeSelector
: Like for the code generated by
TTree::MakeClass
, the
user can do complex analysis. However, they cannot control the event loop. The event loop is controlled by
TTree::Process
called by the user. This solution is illustrated by the code below. The advantage of this method
is that it can be run in a parallel environment using PROOF (the Parallel Root Facility).
A chain of four files (originally converted from PAW ntuples) is used to illustrate the various ways to loop on ROOT data
sets. Each contains a ROOT Tree named “
h42
”. The class definition in h1analysis.h has been generated automatically
by the ROOT utility TTree::MakeSelector using one of the files with:
h42->MakeSelector("h1analysis");
This produces two files: h1analysis.h and
h1analysis.C
. A skeleton of
h1analysis.C
file is made for you to customize.
The h1analysis class is derived from the ROOT class
TSelector
. The following members functions of h1analyhsis (i.e.
TSelector) are called by the TTree::Process method.
•Begin
: This function is called every time a loop over the tree starts. This is a convenient place to create your
histograms.
•Notify(): This function is called at the first entry of a new tree in a chain.
•ProcessCut
: This function is called at the beginning of each entry to return a flag true if the entry must be
analyzed.
547
548 CHAPTER 21. EXAMPLE ANALYSIS
•ProcessFill: This function is called in the entry loop for all entries accepted by Select.
•Terminate
: This function is called at the end of a loop on a
TTree
. This is a convenient place to draw and fit
your histograms.
To use this program, try the following session.
First, turn the timer on to show the real and CPU time per command.
root[] gROOT->Time();
Step A: create a
TChain
with the four H1 data files. The chain can be created by executed this short script
h1chain.C
below. $H1 is a system symbol pointing to the H1 data directory.
{
TChain chain("h42");
chain.Add("$H1/dstarmb.root");
//21330730 bytes, 21920 events
chain.Add("$H1/dstarp1a.root");
//71464503 bytes, 73243 events
chain.Add("$H1/dstarp1b.root");
//83827959 bytes, 85597 events
chain.Add("$H1/dstarp2.root");
//100675234 bytes, 103053 events
}
Run the above script from the command line:
root[] .x h1chain.C
Step B: Now we have a directory containing the four data files. Since a
TChain
is a descendent of
TTree
we can call
TChain::Process
to loop on all events in the chain. The parameter to the
TChain::Process
method is the name of
the file containing the created TSelector class (h1analysis.C).
root[] chain.Process("h1analysis.C")
Step C : Same as step B, but in addition fill the event list with selected entries. The event list is saved to a file “
elist.root
”
by the
TSelector::Terminate
method. To see the list of selected events, you can do
elist->Print("all")
. The
selection function has selected 7525 events out of the 283813 events in the chain of files. (2.65 per cent)
root[] chain.Process("h1analysis.C","fillList")
Step D: Process only entries in the event list. The event list is read from the file in elist.root generated by step C.
root[] chain.Process("h1analysis.C","useList")
Step E: The above steps have been executed with the interpreter. You can repeat the steps B, C, and D using ACLiC
by replacing “h1analysis.C” by “h1analysis.C+” or “h1analysis.C++”.
Step F: If you want to see the differences between the interpreter speed and ACLiC speed start a new session, create
the chain as in step 1, then execute
root[] chain.Process("h1analysis.C+","useList")
The commands executed with the four different methods B, C, D and E produce two canvases shown below:
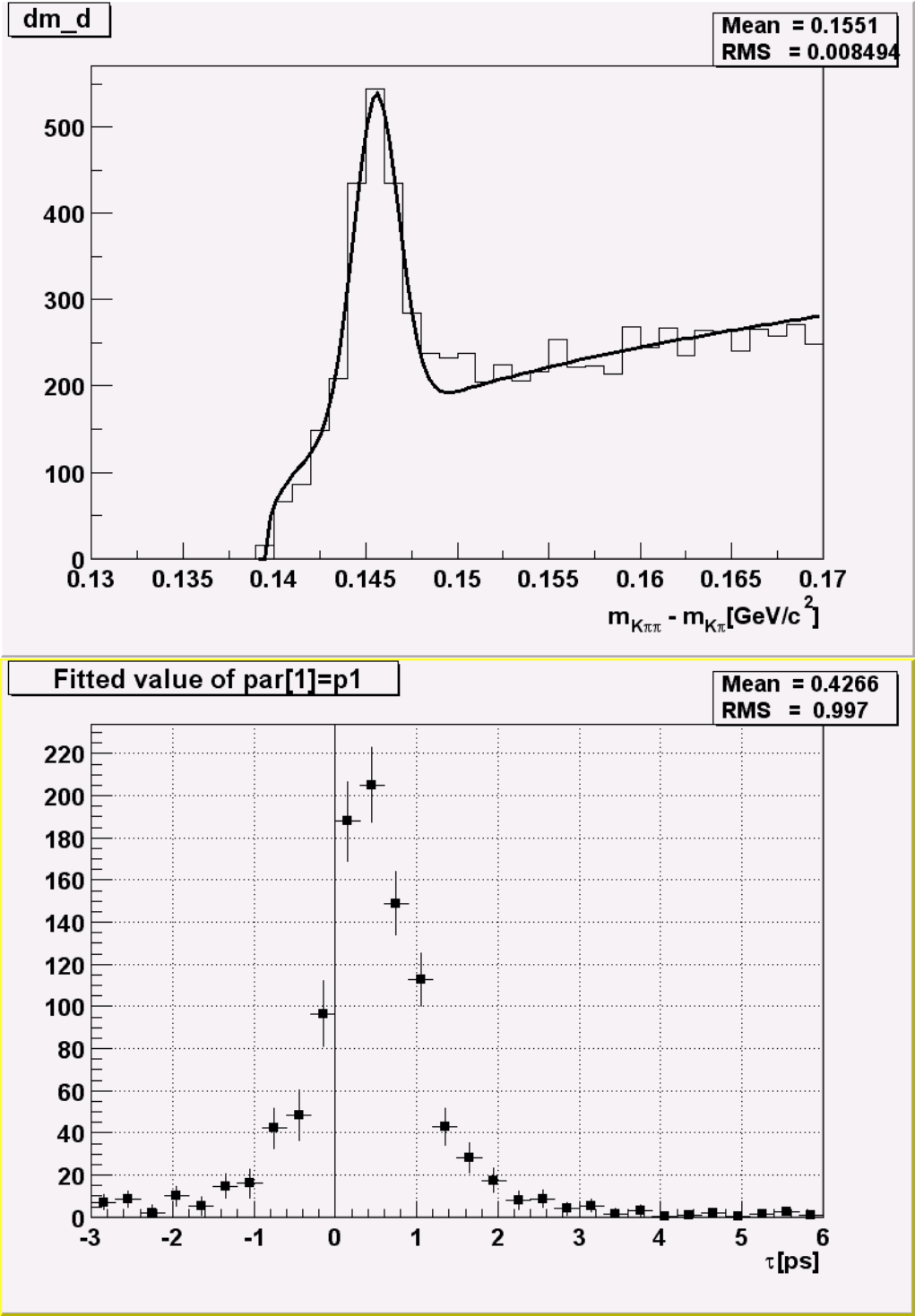
21.1. EXPLANATION 549
550 CHAPTER 21. EXAMPLE ANALYSIS
21.2 Script
This is the
h1analsysis.C
file that was generated by
TTree::MakeSelector
and then modified to perform the analysis.
#include "h1analysis.h"
#include "TH2.h"
#include "TF1.h"
#include "TStyle.h"
#include "TCanvas.h"
#include "TLine.h"
#include "TEventList.h"
const Double_t dxbin = (0.17-0.13)/40;// Bin-width
const Double_t sigma = 0.0012;
TEventList *elist = 0;
Bool_t useList, fillList;
TH1F *hdmd;
TH2F *h2;
//_________________________________________________________
Double_t fdm5(Double_t *xx, Double_t *par)
{
Double_t x = xx[0];
if (x <= 0.13957)return 0;
Double_t xp3 = (x-par[3])*(x-par[3]);
Double_t res = dxbin*(par[0]*TMath::Power(x-0.13957,par[1])
+ par[2]/2.5066/par[4]*TMath::Exp(-xp3/2/par[4]/par[4]));
return res;
}
//_________________________________________________________
Double_t fdm2(Double_t *xx, Double_t *par)
{
Double_t x = xx[0];
if (x <= 0.13957)return 0;
Double_t xp3 = (x-0.1454)*(x-0.1454);
Double_t res = dxbin*(par[0]*TMath::Power(x-0.13957,0.25)
+ par[1]/2.5066/sigma*TMath::Exp(-xp3/2/sigma/sigma));
return res;
}
//_________________________________________________________
void h1analysis::Begin(TTree *tree)
{
// function called before starting the event loop
// -it performs some cleanup
// -it creates histograms
// -it sets some initialization for the event list
//initialize the Tree branch addresses
Init(tree);
//print the option specified in the Process function
TString option = GetOption();
printf("Starting h1analysis with process option: %sn",option.Data());
//Some cleanup in case this function had already been executed
//Delete any previously generated histograms or functions
gDirectory->Delete("hdmd");
gDirectory->Delete("h2*");
delete gROOT->GetFunction("f5");
delete gROOT->GetFunction("f2");
21.2. SCRIPT 551
//create histograms
hdmd = new TH1F("hdmd","dm_d",40,0.13,0.17);
h2 = new TH2F("h2","ptD0 vs dm_d",30,0.135,0.165,30,-3,6);
//process cases with event list
fillList = kFALSE;
useList = kFALSE;
fChain->SetEventList(0);
delete gDirectory->GetList()->FindObject("elist");
// case when one creates/fills the event list
if (option.Contains("fillList")) {
fillList = kTRUE;
elist = new TEventList("elist","selection from Cut",5000);
}
// case when one uses the event list generated in a previous call
if (option.Contains("useList")) {
useList = kTRUE;
TFile f("elist.root");
elist = (TEventList*)f.Get("elist");
if (elist) elist->SetDirectory(0);
//otherwise the file destructor will delete elist
fChain->SetEventList(elist);
}
}
//_________________________________________________________
Bool_t h1analysis::ProcessCut(Int_t entry)
{// Selection function to select D* and D0.
//in case one event list is given in input,
//the selection has already been done.
if (useList) return kTRUE;
// Read only the necessary branches to select entries.
// return as soon as a bad entry is detected
b_md0_d->GetEntry(entry);
if (TMath::Abs(md0_d-1.8646)>=0.04)return kFALSE;
b_ptds_d->GetEntry(entry);
if (ptds_d <= 2.5)return kFALSE;
b_etads_d->GetEntry(entry);
if (TMath::Abs(etads_d) >= 1.5)return kFALSE;
b_ik->GetEntry(entry); ik--;
//original ik used f77 convention starting at 1
b_ipi->GetEntry(entry);
ipi--;
b_ntracks->GetEntry(entry);
b_nhitrp->GetEntry(entry);
if (nhitrp[ik]*nhitrp[ipi] <= 1)return kFALSE;
b_rend->GetEntry(entry);
b_rstart->GetEntry(entry);
if (rend[ik]-rstart[ik] <= 22)return kFALSE;
if (rend[ipi]-rstart[ipi] <= 22)return kFALSE;
b_nlhk->GetEntry(entry);
if (nlhk[ik] <= 0.1)return kFALSE;
b_nlhpi->GetEntry(entry);
if (nlhpi[ipi] <= 0.1)return kFALSE;
b_ipis->GetEntry(entry);
ipis--;
if (nlhpi[ipis] <= 0.1)return kFALSE;
b_njets->GetEntry(entry);
if (njets < 1)return kFALSE;
// if option fillList, fill the event list
if (fillList) elist->Enter(fChain->GetChainEntryNumber(entry));
552 CHAPTER 21. EXAMPLE ANALYSIS
return kTRUE;
}
//_________________________________________________________
void h1analysis::ProcessFill(Int_t entry)
{// Function called for selected entries only
// read branches not processed in ProcessCut
b_dm_d->GetEntry(entry);
//read branch holding dm_d
b_rpd0_t->GetEntry(entry);
//read branch holding rpd0_t
b_ptd0_d->GetEntry(entry);
//read branch holding ptd0_d //continued...
//fill some histograms
hdmd->Fill(dm_d);
h2->Fill(dm_d,rpd0_t/0.029979*1.8646/ptd0_d);
}
//_________________________________________________________
void h1analysis::Terminate()
{// Function called at the end of the event loop
//create the canvas for the h1analysis fit
gStyle->SetOptFit();
TCanvas *c1 = new TCanvas("c1","h1analysis analysis",10,10,800,600);
c1->SetBottomMargin(0.15);
hdmd->GetXaxis()->SetTitle("m_{K#pi#pi}-m_{K#pi}[GeV/c^{2}]");
hdmd->GetXaxis()->SetTitleOffset(1.4);
//fit histogram hdmd with function f5 using
//the loglikelihood option
TF1 *f5 = new TF1("f5",fdm5,0.139,0.17,5);
f5->SetParameters(1000000,.25,2000,.1454,.001);
hdmd->Fit("f5","lr");
//create the canvas for tau d0
gStyle->SetOptFit(0);
gStyle->SetOptStat(1100);
TCanvas *c2 = new TCanvas("c2","tauD0",100,100,800,600);
c2->SetGrid();
c2->SetBottomMargin(0.15);
// Project slices of 2-d histogram h2 along X ,
// then fit each slice with function f2 and make a
// histogram for each fit parameter.
// Note that the generated histograms are added
// to the list of objects in the current directory.
TF1 *f2 = new TF1("f2",fdm2,0.139,0.17,2);
f2->SetParameters(10000,10);
h2->FitSlicesX(f2,0,0,1,"qln");
TH1D *h2_1 = (TH1D*)gDirectory->Get("h2_1");
h2_1->GetXaxis()->SetTitle("#tau[ps]");
h2_1->SetMarkerStyle(21);
h2_1->Draw();
c2->Update();
TLine *line = new TLine(0,0,0,c2->GetUymax());
line->Draw();
// save the event list to a Root file if one was produced
if (fillList) {
21.2. SCRIPT 553
TFile efile("elist.root","recreate");
elist->Write();
}
}
554 CHAPTER 21. EXAMPLE ANALYSIS
Chapter 22
Networking
In this chapter, you will learn how to send data over the network using the ROOT socket classes.
22.1 Setting-up a Connection
On the serverside, we create a
TServerSocket
to wait for a connection request over the network. If the request is
accepted, it returns a full-duplex socket. Once the connection is accepted, we can communicate to the client that we
are ready to go by sending the string “go”, and we can close the server socket.
{// server
TServerSocket *ss = new TServerSocket(9090,kTRUE);
TSocket *socket = ss->Accept();
socket->Send("go");
ss->Close();
}
On the clientside, we create a socket and ask the socket to receive input.
{// client
TSocket *socket = new TSocket("localhost",9090);
Char str[32];
socket->Recv(str,32);
}
22.2 Sending Objects over the Network
We have just established a connection and you just saw how to send and receive a string with the example “go”. Now
let’s send a histogram.
To send an object (in our case on the client side) it has to derive from
TObject
class because it uses the
Streamers
to
fill a buffer that is then sent over the connection. On the receiving side, the
Streamers
are used to read the object
from the message sent via the socket. For network communication, we have a specialized
TBuffer
, a descendant of
TBuffer
called
TMessage
. In the following example, we create a
TMessage
with the intention to store an object, hence
the constant
kMESS_OBJECT
in the constructor. We create and fill the histogram and write it into the message. Then
we call TSocket::Send to send the message with the histogram.
...
// create an object to be sent
TH1F *hpx = new TH1F("hpx","px distribution",100,-4,4);
hpx->FillRandom("gaus",1000);
// create a TMessage to send the object
TMessage message(kMESS_OBJECT);
555
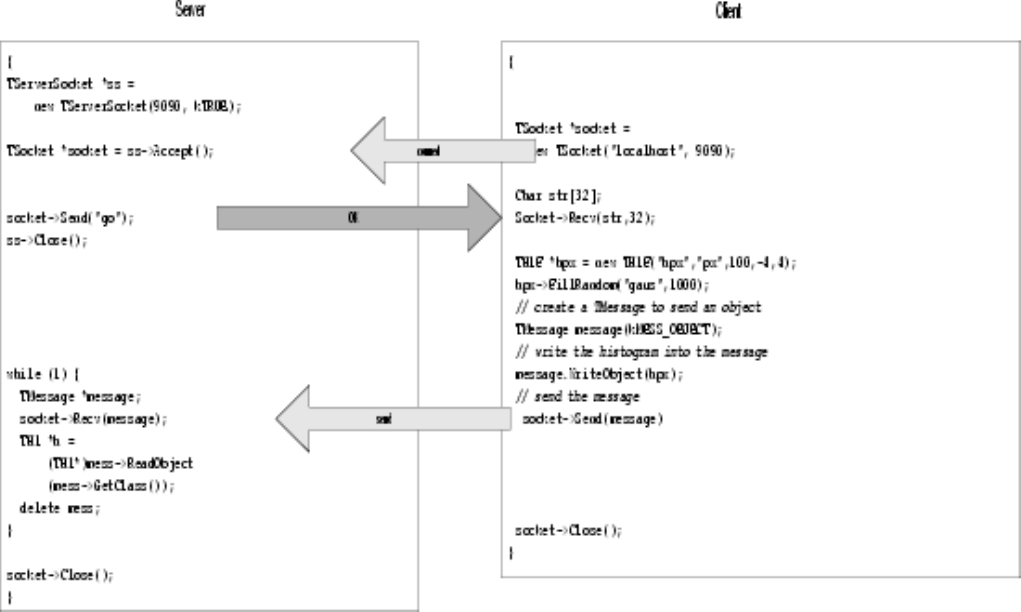
556 CHAPTER 22. NETWORKING
// write the histogram into the message buffer
message.WriteObject(hpx);
// send the message
socket->Send(message);
...
On the receiving end (in our case the server side), we write a while loop to wait and receive a message with a histogram.
Once we have a message, we call
TMessage::ReadObject
, which returns a pointer to
TObject
. We have to cast it to a
TH1
pointer, and now we have a histogram. At the end of the loop, the message is deleted, and another one is created
at the beginning.
while (1) {
TMessage *message;
socket->Recv(message);
TH1 *h = (TH1*)message->ReadObject(message->GetClass());
delete message;
}
22.3 Closing the Connection
Once we are done sending objects, we close the connection by closing the sockets at both ends.
Socket->Close();
This diagram summarizes the steps we just covered:
Figure 22.1: Server - Client setting-up and closing the connection
22.4 A Server with Multiple Sockets
Chances are that your server has to be able to receive data from multiple clients. The class we need for this is
TMonitor
.
It lets you add sockets and the
TMonitor::Select
method returns the socket with data waiting. Sockets can be added,
removed, or enabled and disabled. Here is an example of a server that has a TMonitor to manage multiple sockets:
22.4. A SERVER WITH MULTIPLE SOCKETS 557
{
TServerSocket *ss = new TServerSocket (9090, kTRUE);
// Accept a connection and return a full-duplex communication socket.
TSocket *s0 = ss->Accept();
TSocket *s1 = ss->Accept();
// tell the clients to start
s0->Send("go 0");
s1->Send("go 1");
// Close the server socket (unless we will use it
// later to wait for another connection).
ss->Close();
TMonitor *mon = new TMonitor;
mon->Add(s0);
mon->Add(s1);
while (1) {
TMessage *mess;
TSocket *s;
s = mon->Select();
s->Recv(mess);
...
}
}
The full code for the example above is in $ROOTSYS/tutorials/net/hserv.C and
$ROOTSYS/tutorials/net/hclient.C.
558 CHAPTER 22. NETWORKING
Chapter 23
Threads
A thread is an independent flow of control that operates within the same address space as other independent flows of
controls within a process. In most UNIX systems, thread and process characteristics are grouped into a single entity
called a process. Sometimes, threads are called “lightweight processes”.
Note: This introduction is adapted from the AIX 4.3 Programmer’s Manual.
23.1 Threads and Processes
In traditional single-threaded process systems, a process has a set of properties. In multi-threaded systems, these
properties are divided between processes and threads.
23.1.1 Process Properties
A process in a multi-threaded system is the changeable entity. It must be considered as an execution frame. It has all
traditional process attributes, such as:
•Process ID, process group ID, user ID, and group ID
•Environment
•Working directory
A process also provides a common address space and common system resources:
•File descriptors
•Signal actions
•Shared libraries
•Inter-process communication tools (such as message queues, pipes, semaphores, or shared memory)
23.1.2 Thread Properties
A thread is the schedulable entity. It has only those properties that are required to ensure its independent flow of
control. These include the following properties:
•Stack
•Scheduling properties (such as policy or priority)
•Set of pending and blocked signals
•Some thread-specific data (TSD)
559
560 CHAPTER 23. THREADS
An example of thread-specific data is the error indicator,
errno
. In multi-threaded systems,
errno
is no longer a global
variable, but usually a subroutine returning a thread-specific
errno
value. Some other systems may provide other
implementations of
errno
. With respect to ROOT, a thread specific data is for example the
gPad
pointer, which is
treated in a different way, whether it is accessed from any thread or the main thread.
Threads within a process must not be considered as a group of processes (even though in Linux each thread receives an
own process id, so that it can be scheduled by the kernel scheduler). All threads share the same address space. This
means that two pointers having the same value in two threads refer to the same data. Also, if any thread changes one
of the shared system resources, all threads within the process are affected. For example, if a thread closes a file, the file
is closed for all threads.
23.1.3 The Initial Thread
When a process is created, one thread is automatically created. This thread is called the initial thread or the main
thread. The initial thread executes the main routine in multi-threaded programs.
Note: At the end of this chapter is a glossary of thread specific terms
23.2 Implementation of Threads in ROOT
The TThread class has been developed to provide a platform independent interface to threads for ROOT.
23.2.1 Installation
For the time being, it is still necessary to compile a threaded version of ROOT to enable some very special treatments
of the canvas operations. We hope that this will become the default later.
To compile ROOT, just do (for example on a debian Linux):
./configure linuxdeb2 --with-thread=/usr/lib/libpthread.so
gmake depend
gmake
This configures and builds ROOT using /usr/lib/libpthread.so as the Pthread library, and defines R__THREAD.
This enables the thread specific treatment of gPad, and creates $ROOTSYS/lib/libThread.so.
Note: The parameter linuxdeb2 has to be replaced with the appropriate ROOT keyword for your platform.
23.2.2 Classes
TThread
class implements threads . The platform dependent implementation is in the
TThreadImp
class and its
descendant classes (e.g. TPosixThread ).
TMutex
class implements
mutex
locks. A mutex is a mutually exclusive lock. The platform dependent implementation
is in the TMutexImp class and its descendant classes (e.g. TPosixMutex)
TCondition
class implements a condition variable. Use a condition variable to signal threads. The platform dependent
implementation is in the TConditionImp and TPosixCondition classes .
TSemaphore
class implements a counting semaphore. Use a semaphore to synchronize threads. The platform dependent
implementation is in the TMutexImp and TConditionImp classes.
23.2.3 TThread for Pedestrians
To run a thread in ROOT, follow these steps:
1. Initialization
Add these lines to your rootlogon.C:
23.2. IMPLEMENTATION OF THREADS IN ROOT 561
{
...
// The next line may be unnecessary on some platforms
gSystem->Load("/usr/lib/libpthread.so");
gSystem->Load("$ROOTSYS/lib/libThread.so");
...
}
This loads the library with the TThread class and the pthread specific implementation file for Posix threads.
2. Coding
Define a function (e.g.
void* UserFun(void* UserArgs))
that should run as a thread. The code for the examples is
at the web site of the authors (Jörn Adamczewski, Marc Hemberger). After downloading the code from this site, you
can follow the example below:
http://www-linux.gsi.de/~go4/HOWTOthreads/howtothreadsbody.html
3. Loading
Start an interactive ROOT session. Load the shared library:
root[] gSystem->Load("mhs3.so"); // or
root[] gSystem->Load("CalcPiThread.so");
4. Creating
Create a thread instance (see also example RunMhs3.CorRunPi.C) with:
root[] TThread *th = new TThread(UserFun,UserArgs);
When called from the interpreter, this gives the name “
UserFun
” to the thread. This name can be used to retrieve the
thread later. However, when called from compiled code, this method does not give any name to the thread. So give a
name to the thread in compiled use:
root[] TThread *th = new TThread("MyThread", UserFun, UserArgs);
You can pass arguments to the thread function using the
UserArgs
-pointer. When you want to start a method of a
class as a thread, you have to give the pointer to the class instance as UserArgs.
5. Running
root[] th->Run();
root[] TThread::Ps(); // like UNIX ps c.ommand;
With the
mhs3
example, you should be able to see a canvas with two pads on it. Both pads keep histograms updated
and filled by three different threads. With the
CalcPi
example, you should be able to see two threads calculating Pi
with the given number of intervals as precision.
23.2.4 TThread in More Details
Cling is not thread safe yet, and it will block the execution of the threads until it has finished executing.
562 CHAPTER 23. THREADS
23.2.4.1 Asynchronous Actions
Different threads can work simultaneously with the same object. Some actions can be dangerous. For example, when
two threads create a histogram object, ROOT allocates memory and puts them to the same collection. If it happens at
the same time, the results are undetermined. To avoid this problem, the user has to synchronize these actions with:
TThread::Lock() // Locking the following part of code
... // Create an object, etc...
TThread::UnLock() // Unlocking
The code between
Lock()
and
UnLock()
will be performed uninterrupted. No other threads can perform actions or
access objects/collections while it is being executed. The methods
TThread::Lock()
and
TThread::UnLock()
internally
use a global TMutex instance for locking.
The user may also define their own
TMutex MyMutex
instance and may locally protect their asynchronous actions by
calling MyMutex.Lock() and MyMutex.UnLock().
23.2.4.2 Synchronous Actions: TCondition
To synchronize the actions of different threads you can use the
TCondition
class, which provides a signaling mechanism.
The
TCondition
instance must be accessible by all threads that need to use it, i.e. it should be a global object (or a
member of the class which owns the threaded methods, see below). To create a
TCondition
object, a
TMutex
instance
is required for the Wait and
TimedWait
locking methods. One can pass the address of an external mutex to the
TCondition constructor:
TMutex MyMutex;
TCondition MyCondition(&MyMutex);
If zero is passed, TCondition creates and uses its own internal mutex:
TCondition MyCondition(0);
You can now use the following methods of synchronization:
•TCondition::Wait()
waits until any thread sends a signal of the same condition instance:
MyCondition.Wait()
reacts on MyCondition.Signal() or MyCondition.Broadcast().MyOtherCondition.Signal() has no effect.
•
If several threads wait for the signal from the same
TCondition MyCondition
, at
MyCondition.Signal()
only
one thread will react; to activate a further thread another MyCondition.Signal() is required, etc.
•
If several threads wait for the signal from the same
TCondition MyCondition
, at
MyCondition.Broadcast()
all
threads waiting for MyCondition are activated at once.
In some tests of
MyCondition
using an internal mutex,
Broadcast()
activated only one thread (probably depending
whether MyCondition had been signaled before).
•MyCondition.TimedWait(secs,nanosecs)
waits for
MyCondition
until the absolute time in seconds and nanosec-
onds since beginning of the epoch (January, 1st, 1970) is reached; to use relative timeouts “delta’‘, it is required
to calculate the absolute time at the beginning of waiting “now”; for example:
Ulong_t now,then,delta; // seconds
TDatime myTime; // root daytime class
myTime.Set(); // myTime set to "now"
now=myTime.Convert(); // to seconds since 1970
•
Return value wait of
MyCondition.TimedWait
should be 0, if
MyCondition.Signal()
was received, and should
be nonzero, if timeout was reached.
The conditions example shows how three threaded functions are synchronized using
TCondition
: a ROOT script
condstart.C starts the threads, which are defined in a shared library (conditions.cxx, conditions.h).
23.2. IMPLEMENTATION OF THREADS IN ROOT 563
23.2.4.3 Xlib Connections
Usually
Xlib
is not thread safe. This means that calls to the X could fail, when it receives X-messages from different
threads. The actual result depends strongly on which version of
Xlib
has been installed on your system. The only
thing we can do here within ROOT is calling a special function
XInitThreads()
(which is part of the
Xlib
), which
should (!) prepare the Xlib for the usage with threads.
To avoid further problems within ROOT some redefinition of the
gPad
pointer was done (that’s the main reason for the
recompilation). When a thread creates a
TCanvas
, this object is actually created in the main thread; this should be
transparent to the user. Actions on the canvas are controlled via a function, which returns a pointer to either thread
specific data (TSD) or the main thread pointer. This mechanism works currently only for
gPad
,
gDirectory
,
gFile
and will be implemented soon for other global Objects as e.g. gVirtualX .
23.2.4.4 Canceling a TThread
Canceling of a thread is a rather dangerous action. In
TThread
canceling is forbidden by default. The user can change
this default by calling TThread::SetCancelOn(). There are two cancellation modes: deferred and asynchronous.
23.2.4.5 Deferred
Set by
TThread::SetCancelDeferred()
(default): When the user knows safe places in their code where a thread can
be canceled without risk for the rest of the system, they can define these points by invoking
TThread::CancelPoint()
.
Then, if a thread is canceled, the cancellation is deferred up to the call of
TThread::CancelPoint()
and then the
thread is canceled safely. There are some default cancel points for
pthreads
implementation, e.g. any call of the
TCondition::Wait(),TCondition::TimedWait(),TThread::Join().
23.2.4.6 Asynchronous
Set by TThread::SetCancelAsynchronous(): If the user is sure that their application is cancel safe, they could call:
TThread::SetCancelAsynchronous();
TThread::SetCancelOn();
// Now cancelation in any point is allowed.
...
// Return to default
TThread::SetCancelOff();
TThread::SetCancelDeferred();
To cancel a thread TThread* th call:
th->Kill();
To cancel by thread name:
TThread::Kill(name);
To cancel a thread by ID:
TThread::Kill(tid);
To cancel a thread and delete th when cancel finished:
th->Delete();
Deleting of the thread instance by the operator delete is dangerous. Use
th->Delete()
instead. C++ delete is safe
only if thread is not running. Often during the canceling, some clean up actions must be taken. To define clean up
functions use:
564 CHAPTER 23. THREADS
void UserCleanUp(void *arg) {
// here the user cleanup is done
...
}
TThread::CleanUpPush(&UserCleanUp,arg);
// push user function into cleanup stack"last in, first out"
TThread::CleanUpPop(1); // pop user function out of stack and
// execute it, thread resumes after this call
TThread::CleanUpPop(0); // pop user function out of stack
// _without_ executing it
Note:
CleanUpPush
and
CleanUpPop
should be used as corresponding pairs like brackets; unlike
pthreads
cleanup
stack (which is not implemented here), TThread does not force this usage.
23.2.4.7 Finishing thread
When a thread returns from a user function the thread is finished. It also can be finished by
TThread::Exit()
. Then,
in case of
thread
-detached mode, the thread vanishes completely. By default, on finishing
TThread
executes the most
recent cleanup function (CleanUpPop(1) is called automatically once).
23.3 Advanced TThread: Launching a Method in a Thread
Consider a class Myclass with a member function that shall be launched as a thread.
void* Myclass::Thread0((void* arg)
To start Thread0 as a TThread, class Myclass may provide a method:
Int_t Myclass::Threadstart(){
if(!mTh){
mTh= new TThread("memberfunction",
(void(*)(void *))&Thread0,(void*) this);
mTh->Run();
return 0;
}
return 1;
}
Here
mTh
is a
TThread*
pointer which is member of
Myclass
and should be initialized to 0 in the constructor. The
TThread constructor is called as when we used a plain C function above, except for the following two differences.
First, the member function Thread0 requires an explicit cast to
(void(*) (void *)
). This may cause an annoying
but harmless compiler warning:
Myclass.cxx:98: warning:
converting from "void (Myclass::*)(void *)"to "void *" )
Strictly speaking,
Thread0
must be a static member function to be called from a thread. Some compilers, for example
gcc version 2.95.2, may not allow the (void(*) (void*))s cast and just stop if Thread0 is not static. On the other
hand, if
Thread0
is static, no compiler warnings are generated at all. Because the
’this’
pointer is passed in
’arg’
in the call to
Thread0(void *arg),
you have access to the instance of the class even if
Thread0
is static. Using the
’this’
pointer, non static members can still be read and written from
Thread0
, as long as you have provided Getter
and Setter methods for these members. For example:
Bool_t state = arg->GetRunStatus();
arg->SetRunStatus(state);
23.4. THE SIGNALS OF ROOT 565
Second, the pointer to the current instance of
Myclass
, i.e. (void*) this, has to be passed as first argument of the
threaded function Thread0 (C++ member functions internally expect this pointer as first argument to have access to
class members of the same instance).
pthreads
are made for simple C functions and do not know about Thread0 being
a member function of a class. Thus, you have to pass this information by hand, if you want to access all members of
the Myclass instance from the Thread0 function.
Note: Method Thread0 cannot be a virtual member function, since the cast of
Thread0
to
void(*)
in the
TThread
constructor may raise problems with C++ virtual function table. However, Thread0 may call another virtual member
function virtual void
Myclass::Func0()
which then can be overridden in a derived class of
Myclass
. (See example
TMhs3).
Class Myclass may also provide a method to stop the running thread:
Int_t Myclass::Threadstop() {
if (mTh) {
TThread::Delete(mTh);
delete mTh;
mTh=0;
return 0;
}
return 1;
}
Example
TMhs3:
Class
TThreadframe
(
TThreadframe.h, TThreadframe.cxx
) is a simple example of a framework
class managing up to four threaded methods. Class
TMhs3
(
TMhs3.h, TMhs3.cxx)
inherits from this base class, showing
the
mhs3
example 8.1
(mhs3.h, mhs3.cxx)
within a class. The
Makefile
of this example builds the shared libraries
libTThreadframe.so
and
libTMhs3.so
. These are either loaded or executed by the ROOT script
TMhs3demo.C,
or
are linked against an executable: TMhs3run.cxx.
23.3.1 Known Problems
Parts of the ROOT framework, like the interpreter, are not yet thread-safe. Therefore, you should use this package
with caution. If you restrict your threads to distinct and ‘simple’ duties, you will able to benefit from their use. The
TThread
class is available on all platforms, which provide a POSIX compliant thread implementation. On Linux,
Xavier Leroy’s Linux Threads implementation is widely used, but the
TThread
implementation should be usable on all
platforms that provide pthread.
Linux Xlib on SMP machines
is not yet thread-safe. This may cause crashes during threaded graphics operations;
this problem is independent of ROOT.
Object instantiation:
there is no implicit locking mechanism for memory allocation and global ROOT lists. The
user has to explicitly protect their code when using them.
23.4 The Signals of ROOT
The list of default signals handled by ROOT is:
kSigChildkSigPipe
kSigBuskSigAlarm
kSigSegmentationViolationkSigUrgent
kSigIllegalInstructionkSigFloatingException
kSigSystemkSigWindowChanged
The signals
kSigFloatingException
,
kSigSegmentationViolation
,
kSigIllegalInstruction
, and
kSigBus
cause
the printing of the
*** Break ***
message and make a long jump back to the ROOT prompt. No other custom
TSignalHandler can be added to these signals.
The
kSigAlarm
signal handles asynchronous timers. The
kSigWindowChanged
signal handles the resizing of the terminal
window. The other signals have no other behavior then that to call any registered TSignalHandler::Notify() .
When building in interactive application the use of the
TRint
object handles the
kSigInterrupt
signal. It causes the
printing of the message:
*** Break *** keyboard interrupt
and makes a long jump back to the ROOT command
prompt. If no
TRint
object is created, there will be no
kSigInterrupt
handling. All signals can be reset to their default
566 CHAPTER 23. THREADS
UNIX behavior via the call of
TSytem::ResetSignal()
. All signals can be ignored via
TSytem::IgnoreSignal()
.
The
TSytem::IgnoreInterrupt()
is a method to toggle the handling of the interrupt signal. Typically it is called to
prevent a SIGINT to interrupt some important call (like writing to a ROOT file).
If
TRint
is used and the default ROOT interrupt handler is not desired, you should use
GetSignalHandler()
of
TApplication to get the interrupt handler and to remove it by RemoveSignalHandler()of TSystem .
23.5 Glossary
The following glossary is adapted from the description of the Rogue Wave Threads.h++ package.
A
process
is a program that is loaded into memory and prepared for execution. Each process has a private address
space. Processes begin with a single thread.
A
thread
is a sequence of instructions being executed in a program. A thread has a program counter and a private
stack to keep track of local variables and return addresses. A multithreaded process is associated with one or more
threads. Threads execute independently. All threads in a given process share the private address space of that process.
Concurrency
exists when at least two threads are in progress at the same time. A system with only a single processor
can support concurrency by switching execution contexts among multiple threads.
Parallelism
arises when at least two threads are executing simultaneously. This requires a system with multiple
processors. Parallelism implies concurrency, but not vice-versa.
A function is
reentrant
if it will behave correctly even if a thread of execution enters the function while one or more
threads are already executing within the function. These could be the same thread, in the case of recursion, or different
threads, in the case of concurrency.
Thread-specific data
(
TSD
) is also known as thread-local storage (TLS). Normally, any data that has lifetime beyond
the local variables on the thread’s private stack are shared among all threads within the process. Thread-specific data
is a form of static or global data that is maintained on a per-thread basis. That is, each thread gets its own private
copy of the data.
Left to their own devices, threads execute independently.
Synchronization
is the work that must be done when there
are, in fact, interdependencies that require some form of communication among threads. Synchronization tools include
mutexes, semaphores, condition variables, and other variations on locking.
A
critical section
is a section of code that accesses a non-sharable resource. To ensure correct code, only one
thread at a time may execute in a critical section. In other words, the section is not reentrant.
A
mutex
, or mutual exclusion lock, is a synchronization object with two states locked and unlocked. A mutex is usually
used to ensure that only one thread at a time executes some critical section of code. Before entering a critical section,
a thread will attempt to lock the mutex, which guards that section. If the mutex is already locked, the thread will
block until the mutex is unlocked, at which time it will lock the mutex, execute the critical section, and unlock the
mutex upon leaving the critical section.
A
semaphore
is a synchronization mechanism that starts out initialized to some positive value. A thread may ask to
wait on a semaphore in which case the thread blocks until the value of the semaphore is positive. At that time the
semaphore count is decremented and the thread continues. When a thread releases semaphore, the semaphore count is
incremented. Counting semaphores are useful for coordinating access to a limited pool of some resource.
Readers/Writer Lock
- a multiple-reader, single-writer lock is one that allows simultaneous read access by many
threads while restricting write access to only one thread at a time. When any thread holds the lock for reading, other
threads can also acquire the lock reading. If one thread holds the lock for writing, or is waiting to acquire the lock for
writing, other threads must wait to acquire the lock for either reading or writing.
Use a
condition variable
in conjunction with a mutex lock to automatically block threads until a particular condition
is true.
Multithread Safe Levels - a possible classification scheme to describe thread-safety of libraries:
•
All public and protected functions are reentrant. The library provides protection against multiple threads trying
to modify static and global data used within a library. The developer must explicitly lock access to objects shared
between threads. No other thread can write to a locked object unless it is unlocked. The developer needs to lock
local objects. The spirit, if not the letter of this definition, requires the user of the library only to be familiar with
the semantic content of the objects in use. Locking access to objects that are being shared due to extra-semantic
details of implementation (for example, copy-on-write) should remain the responsibility of the library.
23.5. GLOSSARY 567
•
All public and protected functions are reentrant. The library provides protection against multiple threads trying
to modify static and global data used within the library. The preferred way of providing this protection is to use
mutex locks. The library also locks an object before writing to it. The developer is not required to explicitly
lock or unlock a class object (static, global or local) to perform a single operation on the object. Note that even
multithread safe level II hardly relieves the user of the library from the burden of locking.
A thread suffers from
deadlock
if it is blocked waiting for a condition that will never occur. Typically, this occurs
when one thread needs to access a resource that is already locked by another thread, and that other thread is trying to
access a resource that has already been locked by the first thread. In this situation, neither thread is able to progress;
they are deadlocked.
Amultiprocessor is a hardware system with multiple processors or multiple, simultaneous execution units.
•
Examples can be found at http://www-linux.gsi.de/~go4/HOWTOthreads/howtothreadsbody.html (the thread
authors’ web site - Jörn Adamczewski and Marc Hemberger).
568 CHAPTER 23. THREADS

Chapter 24
PROOF: Parallel Processing
The Parallel ROOT Facility, PROOF, is an extension of ROOT allowing transparent analysis of large sets of ROOT
files in parallel on remote computer clusters or multi-core computers. The main design goals for the PROOF system
are:
Transparency : there should be as little difference as possible between a local ROOT based analysis session and a
remote parallel PROOF session, both being interactive and giving the same results.
Scalability : the basic architecture should not put any implicit limitations on the number of computers that can be
used in parallel.
Adaptability : the system should be able to adapt itself to variations in the remote environment (changing load on the
cluster nodes, network interruptions, etc.).
Being an extension of the ROOT system, PROOF is designed to work on objects in ROOT data stores, though, for the
time being, it mainly addresses the case of TTree based object collections.
PROOF is primarily meant as an interactive alternative to batch systems for Central Analysis Facilities and departmental
workgroups (Tier-2’s). However, thanks to a multi-tier architecture allowing multiple levels of masters, it can be easily
adapted to wide range virtual clusters distributed over geographically separated domains and heterogeneous machines
(GRIDs).
While pure interactivity might not always be possible when performing a complicated analysis on a very large data
set, PROOF still tries to give the user the interactive experience with something we call “interactive batch”. With
“interactive batch” the user can start very long running queries, disconnect the client and at any time, any location
and from any computer reconnect to the query to monitor its progress or retrieve the results. This feature gives it a
distinct advantage over purely batch based solutions, that only provide an answer once all sub-jobs have been finished.
Details about the PROOF system and the way to use it can be found at 1
The PROOF development is a joint effort between CERN and MIT.
1http://root.cern.ch/twiki/bin/view/ROOT/PROOF
569
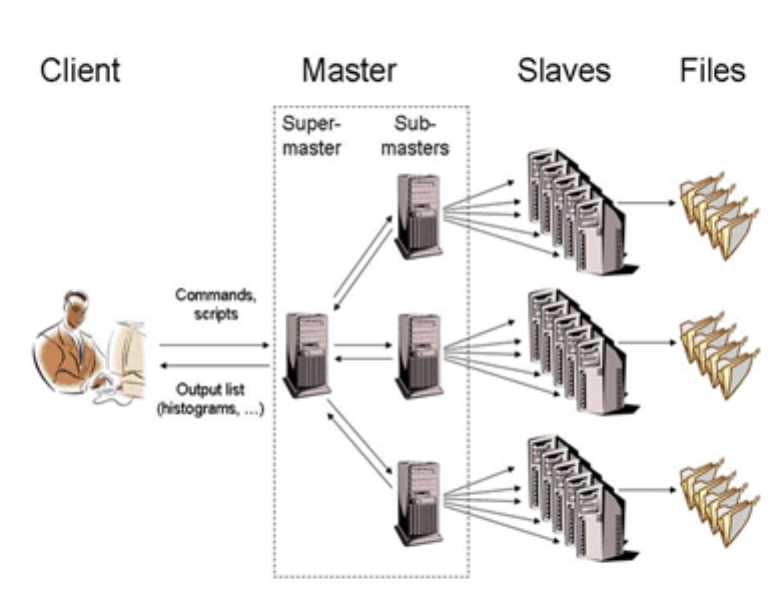
570 CHAPTER 24. PROOF: PARALLEL PROCESSING
Figure 24.1: The Multi-tier structure of a PROOF cluster
Chapter 25
Writing a Graphical User Interface
The ROOT GUI classes support an extensive and rich set of widgets with the Windows 95 look and feel. The widget
classes interface to the underlying graphics system via a single abstract class. Concrete versions of this abstract class
have been implemented for X11 and Win32, thereby making the ROOT GUI fully cross-platform. Originally the GUI
classes were based on Hector Peraza’s Xclass’95 widget library http://xclass.sourceforge.net/
25.1 The ROOT GUI Classes
Features of the GUI classes in a nutshell:
•Originally based on the Xclass’95 widget library
•A rich and complete set of widgets
•Win’95 look and feel
•All machine dependent graphics calls abstracted via the TVirtualX “abstract” class
•Completely scriptable via the C++ interpreter (fast prototyping)
•Supports signal/slot event handling as pioneered by Trolltech’s Qt
•Full class documentation is generated automatically (as for all ROOT classes)
•Code generation for variety of GUI’s
25.2 Widgets and Frames
The ROOT GUI classes provide of set of components that allow an easy way to develop cross-platform GUI applications
with a Windows look and feel.
The main widgets are:
•
Simple widgets: labels, icons, push buttons, either with text or pixmaps, check buttons, radio buttons, menu bars
and popup menus, scroll bars, list boxes, combo boxes, group frames, text entry widgets, tab widgets, progress
bars, sliders, tool tips
•Complex widgets: shutter, toolbar, status bar, list view, list tree
•Common dialogs: File Open/Save, File Properties, Font Selection, Color Selection, About
•The widgets are shown in frames:
•frame, composite frame, main frame, transient frame, group frame
•Arranged by layout managers:
•horizontal layout, vertical layout, row layout, list layout, tile layout, matrix layout
571
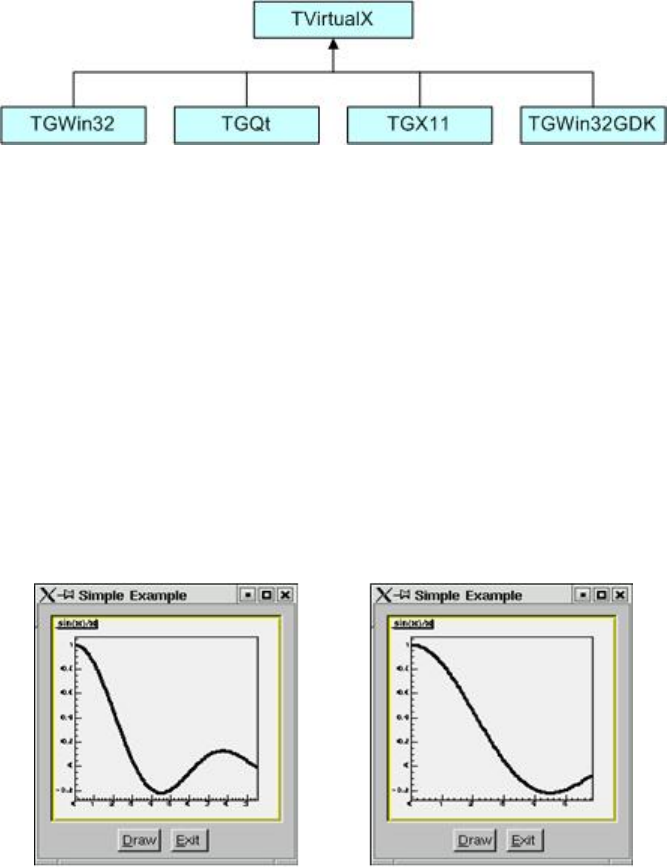
572 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
Using a combination of layout hints:
•left, right, center x, center y, top, bottom, expand x, expand y, fixed offsets
Event handling by signals/slots and messaging (as opposed to callbacks):
•in response to actions widgets send messages and emit signals
•associated frames process these messages or the slot methods connected to the signals are executed
25.3 TVirtualX
The GUI classes interface to the platform dependent low level graphics system via the semi-abstract graphics base class
TVirtualX
. Currently concrete implementations exist for X11 and Win32 (MacOS X is fully supported via Apple’s X11
implementation). Thanks to this single graphics interface, porting the ROOT GUI to a new platform requires only the
implementation of TVirtualX.
The TGQt interface is currently still under development.
25.4 A Simple Example
We will start with a simple example that builds a small application containing a canvas and two buttons: Draw and
Exit. Its functionality will be very simple: every time you click on Draw button, the graphics of the function
sin(x)/x
will be drawn in randomly chosen interval in the canvas window, if you click on Exit - you close the application. This
example shows the basic concepts for almost any GUI-application in ROOT and it is important to understand how it is
constructed. The example program is written as a named script. See “Cling the C++ Interpreter”. Remember that the
named script can be executed via
root[] .x example.C
only if the filename (without extension) and the function entry point are both the same.
We need to say a few words about the parent-children relationship between the widgets before going through the real
code. The widgets’ behaviors are based on this relationship. Every parent widget is responsible for where the children
are and it ensures all properties and behavior for them. For example, if you want to hide several widgets, it will be
enough to hide their parent widget. Later you can show the parent and the children will appear too. Writing your code
you have to specify the parent-child relationship. Usually in a child constructor the address of the parent is passed
as an argument. In general frames are parents of simple widgets. In this example you will see how we organize the
parent-children relationship by using frame widgets in addition to the canvas window and button widgets.
25.4. A SIMPLE EXAMPLE 573
Let’s now go through the code of the example.C.
The first lines include ROOT header files. The header file names are almost always as the class names (
TApplication
,
TF1
,
TCanvas
), but there are cases when similar classes are grouped together in one header file: all frames are declared
in TGFrame.h, all buttons - in TGButton.h, etc. Our small example is based on an object of the class MyMainFrame.
new MyMainFrame(gClient->GetRoot(),200,200);
The first parameter
gClient->GetRoot()
makes the initial connection to the window server. It is a pointer to the root
window of the screen, which is obtained from
gClient
. The next two parameters initialize the width and height of the
application window in pixels. Let see what
MyMainFrame
is. The three arguments pass to the
TGMainFrame
constructor
when we create the fMain object.
The first thing to note is the inclusion of the
RQ_OBJECT
macro in the class declaration of
MyMainFrame
. It is necessary
to provide a standalone class signal/slot capability. The signal/slot communication mechanism is described in a separate
chapter. See “Event Processing: Signals and Slots”.
// example.C
#include <TGClient.h>
#include <TCanvas.h>
#include <TF1.h>
#include <TRandom.h>
#include <TGButton.h>
#include <TGFrame.h>
#include <TRootEmbeddedCanvas.h>
#include <RQ_OBJECT.h>
class MyMainFrame {
RQ_OBJECT("MyMainFrame")
private:
TGMainFrame *fMain;
TRootEmbeddedCanvas *fEcanvas;
public:
MyMainFrame(const TGWindow *p,UInt_t w,UInt_t h);
virtual ~MyMainFrame();
void DoDraw();
};
MyMainFrame::MyMainFrame(const TGWindow *p,UInt_t w,UInt_t h) {
// Create a main frame
fMain = new TGMainFrame(p,w,h);
// Create canvas widget
fEcanvas = new TRootEmbeddedCanvas("Ecanvas",fMain,200,200);
fMain->AddFrame(fEcanvas, new TGLayoutHints(kLHintsExpandX |
kLHintsExpandY, 10,10,10,1));
// Create a horizontal frame widget with buttons
TGHorizontalFrame *hframe = new TGHorizontalFrame(fMain,200,40);
TGTextButton *draw = new TGTextButton(hframe,"&Draw");
draw->Connect("Clicked()","MyMainFrame",this,"DoDraw()");
hframe->AddFrame(draw, new TGLayoutHints(kLHintsCenterX,
5,5,3,4));
TGTextButton *exit = new TGTextButton(hframe,"&Exit",
"gApplication->Terminate(0)");
hframe->AddFrame(exit, new TGLayoutHints(kLHintsCenterX,
5,5,3,4));
fMain->AddFrame(hframe, new TGLayoutHints(kLHintsCenterX,
2,2,2,2));
// Set a name to the main frame
fMain->SetWindowName("Simple Example");
// Map all subwindows of main frame
fMain->MapSubwindows();
574 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
// Initialize the layout algorithm
fMain->Resize(fMain->GetDefaultSize());
// Map main frame
fMain->MapWindow();
}
void MyMainFrame::DoDraw() {
// Draws function graphics in randomly chosen interval
TF1 *f1 = new TF1("f1","sin(x)/x",0,gRandom->Rndm()*10);
f1->SetLineWidth(3);
f1->Draw();
TCanvas *fCanvas = fEcanvas->GetCanvas();
fCanvas->cd();
fCanvas->Update();
}
MyMainFrame::~MyMainFrame() {
// Clean up used widgets: frames, buttons, layout hints
fMain->Cleanup();
delete fMain;
}
void example() {
// Popup the GUI...
new MyMainFrame(gClient->GetRoot(),200,200);
}
The
TGMainFrame
class defines a top level window that interacts with the system window manager. Its method
CloseWindow()
is invoked when Alt+F4 are pressed or a window manager close/exit command is used. To terminate the
application when this happens you need to override the
CloseWindow()
method and call
gApplication->Terminate(0)
.
The main frame can be considered as a container where all widgets of the application are organized with respect to
their parent-child relationship. After the main frame we create
fEcanvas
- an object of class
TRootEmbeddedCanvas
.
It is a quite complex widget and we will explain it in detail later. For the moment keep in mind only its main purpose -
to create a TCanvas - the ROOT basic whiteboard for drawing and editing different graphical objects.
fEcanvas = new TRootEmbeddedCanvas("Ecanvas",fMain,200,200);
In the
TRootEmbeddedCanvas
constructor we pass the address of the main frame widget
fMain
as a second parameter.
This pass is important because it makes
fMain
the parent of the canvas window. The first parameter
Ecanvas
is the
name of the
TCanvas
, the last two parameters give the width and height of canvas window in pixels. Next step is to
add
fEcanvas
to the parent frame defining its appearance inside the parent window. We use the method
AddFrame():
fMain->AddFrame(fEcanvas,new TGLayoutHints(kLHintsExpandX |
kLHintsExpandY, 10,10,10,1));
It adds the
fEcanvas
into the list of children widgets of the main frame
fMain
. The specification of how it
should be placed inside the parent frame is made by the
TGLayoutHints
object. Setting its first parameter to
kLHintsExpandX|kLHintsExpandY
we define the canvas window as expanded on x and y in the frame. The next four
parameters define amounts of padding in left, right, top and bottom in pixels. This means that the canvas window will
be expanded when the parent window expands, but it will keep around a frame of 10 pixels on left, right, top and 1
pixel on bottom.
The laying out is always made with respect to the parent-children relationship. There is a special chapter presenting
the different layout managers, but we will quickly introduce the concept here. The layout process will apply not to the
embedded canvas window but to its parent - the main frame. A popular layout manager and the one used in this case
is the vertical layout manager which arranges its widgets vertically in a column.
The next widget we create as a child of the main frame is the horizontal frame hframe:
TGHorizontalFrame *hframe=new TGHorizontalFrame(fMain,200,40);
The first parameter of its constructor is again the address of its parent,
fMain
. The next ones define the frame width
and height in pixels. The name of the class
TGHorizontalFrame
gives a hint that a horizontal layout will apply on its
children widgets. The Draw and Exit buttons will be laid out horizontally. Here are their constructors:
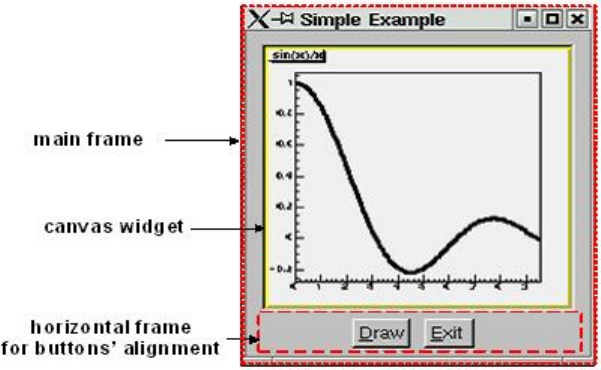
25.4. A SIMPLE EXAMPLE 575
TGTextButton *draw = new TGTextButton(hframe,"&Draw");
hframe ->AddFrame(draw, new TGLayoutHints(kLHintsCenterX,5,5,3,4));
TGTextButton *exit = new TGTextButton(hframe,"&Exit",
"gApplication->Terminate(0)");
hframe ->AddFrame(exit,new TGLayoutHints(kLHintsCenterX,5,5,3,4));
They are created as objects of the TGTextButton class that represent the command buttons with a text label. When
you click on a command button it performs the action shown on its label. These buttons are well known as “push
buttons” or just “buttons”. The parent address
hframe
is passed as first parameter. The second one defines the button
label and normally indicates the action to be taken when the button is clicked. It is possible to define a hot key for
the button at that point using the hot string for its label. A hot string is a string with a “hot” character underlined.
This character we call the button hot key. It shows the assigned keyboard mnemonic for the button choice. Following
our example, this means that you can use
Alt+D
to click on Draw button and
Alt+E
to click on Exit. There is a
possibility to specify a command string as third parameter of the button constructor. We use it to assign the command
gApplication->Terminate(0). The application will be terminated when you click on the Exit button.
We call again
AddFrame()
to add the buttons to their parent widget giving layout hints for each of them. This time we
would like to have centered buttons with an amount of 5 pixels on the left, 5 on the right, 3 on the top and 4 on the
bottom. You can feel already that the same steps are repeated three times: to create a new widget with passing a
parent address as a parameter, to define layout hints for it and to add it in the parent list. The next line is something
new:
draw->Connect("Clicked()","MyMainFrame",this,"DoDraw()");
Here we connect a signal to a slot. Whenever the draw button is clicked, it emits a signal that something has happened
(it is clicked) to whom might be interesting in the outside world. The widget does not know who will use this information.
On the other side of the program world there is some code which should be executed when the button is clicked. This
code is called a slot. Think about slots as normal C++ functions or class methods. The line above specifies that the slot
MyMainFrame::DoDraw()
will be executed when the draw button is clicked. Our slot draws the graphics of
sin(x)/x
in randomly chosen interval every time the draw button sends a signal “I am clicked”. The signal/slot communication
mechanism originally featured in Qt by TrollTech(see http://doc.trolltech.com/3.1/signalsandslots.html). ROOT
supports its own version of signals/slots. We will return to that point in details later. We specified all child widgets of
the horizontal frame (the Draw and Exit buttons in our case). Next, we need to add their parent frame to the main
frame:
fMain->AddFrame(hframe,new TGLayoutHints(kLHintsCenterX,2,2,2,2));
The last thing to do is to set the main window title and to make all widgets visible. Commonly in all systems windows
are assigned by name to be identified by users. This name is displayed in the application’s title bar and can be set by:
fMain->SetWindowName("Simple Example");
The next lines make the widgets visible. The first one maps all child frames of the top-level frame; the last one - the
main frame itself, i.e. makes it appear on the screen.
576 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
fMain->MapSubwindows();
fMain->Resize(fMain->GetDefaultSize());
fMain->MapWindow();
The line in between has an important mission - to execute all layout specifications for the widgets before the top-level
window itself is shown on the screen. We can run the named script via the Cling interpreter with the command:
root[].x example.C
The event processing starts. If you change the state of a widget, it emits a signal and the corresponding slot is executed
ensuring the functionality we want for this small example.
The steps we passed can be generalized as follows:
•Opening of the connection to the system
•Definition of main frame (top level window)
•Creation of widgets as children of the top-level frame; assign them desired properties following the steps:
•Create a new widget passing its parent in the constructor
•Connect widget’s signals with desired slots to ensure desired functionality
•Define widget’s layout and add it to the parent list of children
•Set main window attributes
•Map all sub windows
•Initialize the layout algorithm via Resize(GetDefaultSize()) method
•Map the main frame
•Execution of the even-processing loop
25.4.1 A Standalone Version
As usual a standalone program in C++ has to contain a main() function - the starting point for the application
execution. In this case it is better to separate the program code creating a program header file example2a.h with
the
MyMainFrame
class declaration and
example2a.cxx
- with the class methods implementation. To run our simple
example as a standalone application we need to create in addition an object of class
TApplication
. It will make a
correct initialization of the dictionaries if it is not yet done. It will be responsible for holding everything together
and to handle all events in the application. Its environment provides an interface to the ROOT graphics system and
by calling the
Run()
method the event loop starts and the application program is waiting for the user action. The
application exits only if the top level window is not closed. Two header files are used in addition:
TApplication.h
-
for the class
TApplication
and
TGClient.h
that is used to make initial connection to the graphics system. The class
TApplication
must be instantiated only once in any given application. The original list of argument options can be
retrieved via the Argc() and Argv() methods.
Note: to have signals/slots working we need to create a dictionary for the class
MyMainFrame
, i.e. we create the file
ex2aLinkDef.h containing the line:
#pragma link C++ class MyMainFrame;
We compile the example:
rootcling -f ex2aDict.cxx -c example2a.h ex2aLinkDef.h
g++ -o example2a example2a.cxx ex2aDict.cxx `root-config --cflags --glibs`
example2a.h
25.4. A SIMPLE EXAMPLE 577
#include <TQObject.h>
#include <RQ_OBJECT.h>
class TGWindow;
class TGMainFrame;
class TRootEmbeddedCanvas;
class MyMainFrame {
RQ_OBJECT("MyMainFrame")
private:
TGMainFrame *fMain;
TRootEmbeddedCanvas *fEcanvas;
public:
MyMainFrame(const TGWindow *p,UInt_t w,UInt_t h);
virtual ~MyMainFrame();
void DoDraw();
};
example2a.cxx
#include <TApplication.h>
#include <TGClient.h>
#include <TCanvas.h>
#include <TF1.h>
#include <TRandom.h>
#include <TGButton.h>
#include <TRootEmbeddedCanvas.h>
#include "example2a.h"
MyMainFrame::MyMainFrame(const TGWindow *p,UInt_t w,UInt_t h) {...}
MyMainFrame::~MyMainFrame() { ... }
void MyMainFrame::DoDraw() { ... }
void example() { ... }
int main(int argc, char **argv) {
TApplication theApp("App",&argc,argv);
example();
theApp.Run();
return 0;
}
The class
MyMainFrame
could derive from
TGMainFrame
. In that case the
RQ_OBJECT
macro is not needed anymore, since
the functionality it provides is obtained now via inheritance from
TGMainFrame
. This will reflect in the
MyMainFrame
class declaration and in the code of the MyMainFrame::MyMainFrame constructor as follows:
example2b.h
#include <TGFrame.h>
class MyMainFrame : public TGMainFrame {
private:
TRootEmbeddedCanvas *fEcanvas;
public:
MyMainFrame(const TGWindow *p,UInt_t w,UInt_t h);
virtual ~MyMainFrame() { ... }
void DoDraw(){ ... }
ClassDef(MyMainFrame,0)
};
example2b.cxx
#include <TApplication.h>
#include <TGClient.h>
578 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
#include <TCanvas.h>
#include <TF1.h>
#include <TRandom.h>
#include <TGButton.h>
#include <TRootEmbeddedCanvas.h>
#include "example2b.h"
MyMainFrame::MyMainFrame(const TGWindow *p,UInt_t w,UInt_t h)
: TGMainFrame(p,w,h) {
// Creates widgets of the example
fEcanvas = new TRootEmbeddedCanvas ("Ecanvas",this,200,200);
AddFrame(fEcanvas, new TGLayoutHints(kLHintsExpandX |
kLHintsExpandY, 10,10,10,1));
TGHorizontalFrame *hframe=new TGHorizontalFrame(this,200,40);
TGTextButton *draw = new TGTextButton(hframe,"&Draw");
draw->Connect("Clicked()","MyMainFrame",this,"DoDraw()");
hframe->AddFrame(draw, new TGLayoutHints(kLHintsCenterX,
5,5,3,4));
TGTextButton *exit = new TGTextButton(hframe,"&Exit ",
"gApplication->Terminate()");
hframe->AddFrame(exit, new TGLayoutHints(kLHintsCenterX,
5,5,3,4));
AddFrame(hframe,new TGLayoutHints(kLHintsCenterX,2,2,2,2));
// Sets window name and shows the main frame
SetWindowName("Simple Example");
MapSubwindows();
Resize(GetDefaultSize());
MapWindow();
}
25.5 Widgets Overview
The word widget is a contraction of windows and gadget. Almost all GUI elements are widgets. A button is a widget,
a menu item is a widget, a scrollbar is a widget, and a complete dialog box is a widget too. Some widgets may have
sub widgets. For example, a dialog box can contain buttons, text fields, a combo-box, etc.
On the screen widgets look like rectangular areas with special behaviors. In terms of the object-oriented programming
we can define a widget in ROOT as an object of a class deriving from TGObject.
This section presents all currently supported widgets in ROOT and their most useful methods. All of them can be consid-
ered as building blocks for an application, and most of them can be found in dialogs. Provided snippets of the code will
give you practical guidelines where and how to use certain widgets. The macro
$ROOTSYS/tutorials/gui/guitest.C
contains the complete source code.
Any custom widget can be created by sub classing existing widgets. To achieve a better understanding of the widgets’
properties they are separated by their type and their inheritance. As all of them inherit from
TGObject
and most from
TGWidget, these base classes are described first.
25.5.1 TGObject
TGObject
is the base class for all ROOT GUI classes. It inherits from
TObject
. The two data members of this
class contain important information about X11/Win32 window identifier and the connection to the host’s graphics
system. Every GUI element, which derives from
TGObject
has access to the
TGClient
via the data member
fClient
of
TGObject. TGClient
creates the connection with the host’s graphics system and sets up the complete graphics
system for all widgets.
25.5.2 TGWidget
The widgets base class
TGWidget
is typically used as a mix-in class via multiple inheritances. Its properties are
available for all deriving widgets:
TGButton
,
TGComboBox
,
TGTab
,
TGColorPalette
,
TGColorPick
,
TGDoubleSlider
,
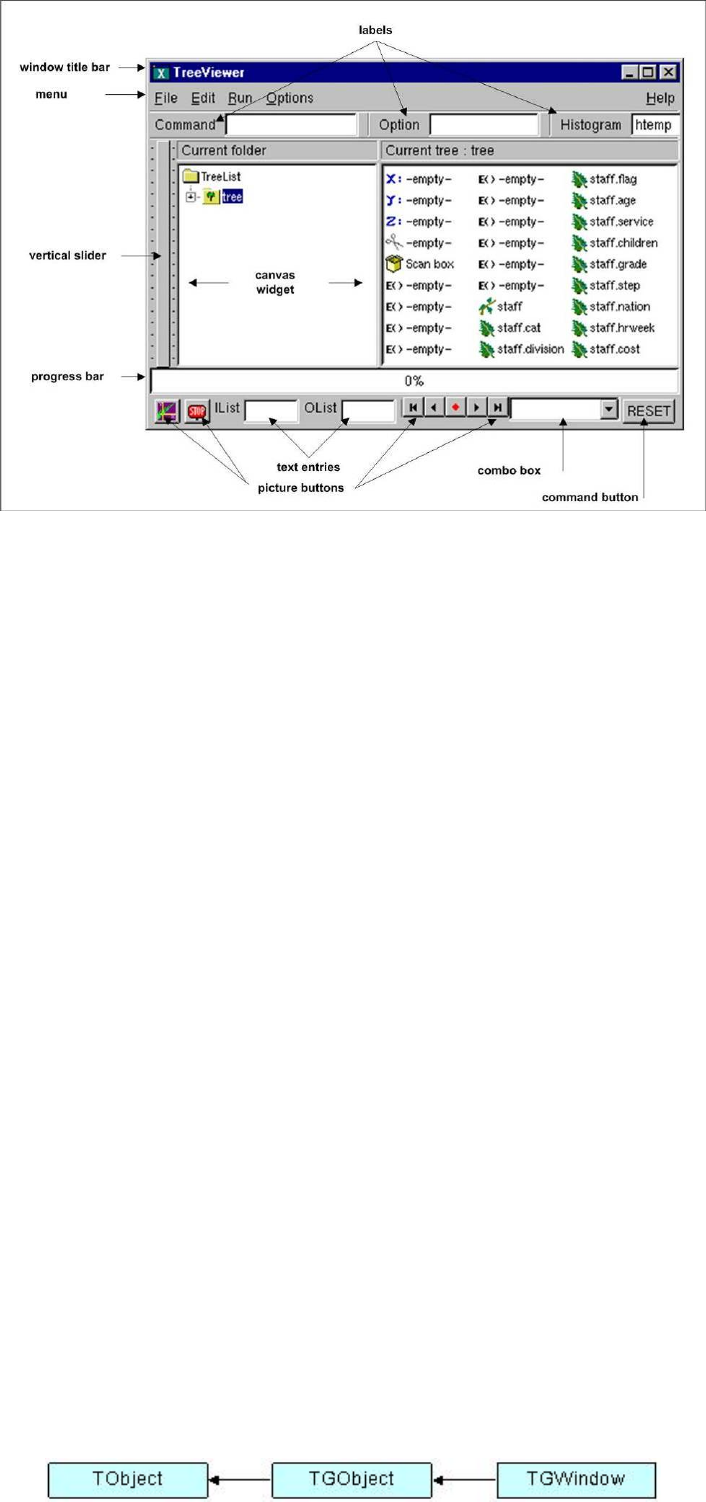
25.5. WIDGETS OVERVIEW 579
Figure 25.1: Widgets created by ROOT GUI classes
TGListTree,TGNumberEntry,TGScrollBar,TGShutterItem,TGTextEntry,TGSlider,TGListBox,TGView.
This class has four data members keeping information about the widget id - important for event processing, the
window which handles the widget’s events, the widget status flags and the assigned command (if there is any). The
general properties of
TGWidget
are specified by
SetFlags(Int_t flags)
and
ClearFlags(Int_t flags)
methods.
The status flags are:
kWidgetWantFocus
,
kWidgetHasFocus
, and
kWidgetIsEnabled
. The method
Associate(const
TGWindow* w)
- sets the window which handles the widget events.
SetCommand(const char* command)
- sets the
command to be executed. The command string can be gathering via
GetCommand()
method. For example, the third
parameter in TGTextButton constructor can be omitted and set later in your program, i.e. instead of:
TGTextButton *exit = new TGTextButton(hframe,"&Exit",
"gApplication->Terminate()");
You will have the following the two lines:
TGTextButton *exit = new TGTextButton(hframe,"&Exit");
exit->SetCommand("gApplication->Terminate()");
The method
IsEnabled()
- returns
kTRUE
if the widget has flag
kWidgetIsEnabled
and it accepts user events. This
method is very important for creating a good user interface because it allows you to disable or enable a widget depending
on the situation of your application. As a standard all disabled widgets are displayed “grayed out”.
HasFocus()
-
returns
kTRUE
if the widget has the input focus (i.e. flag
kWidgetHasFocus
is set). Remember that only one item in a
complex widget as a dialog can have the value of
HasFocus()
sets as true.
WantFocus()
- returns
kTRUE
if the flag
kWidgetWantFocus is set.
25.5.3 TGWindow
TGWindow
is a ROOT GUI window base class. It inherits from
TGObject
and
TGFrame
derives from it. The application
does not use it directly. It creates and registers a new window within the system. This window has common
characteristics: existing parent, location, size in height and width (it has a default minimum size 1, 1 under which it
cannot shrink), border with particular view, state, specific attributes. If there are no specified arguments their values
will be taken from the parent. It receives events from the window system and can paint a representation of itself on the
screen.
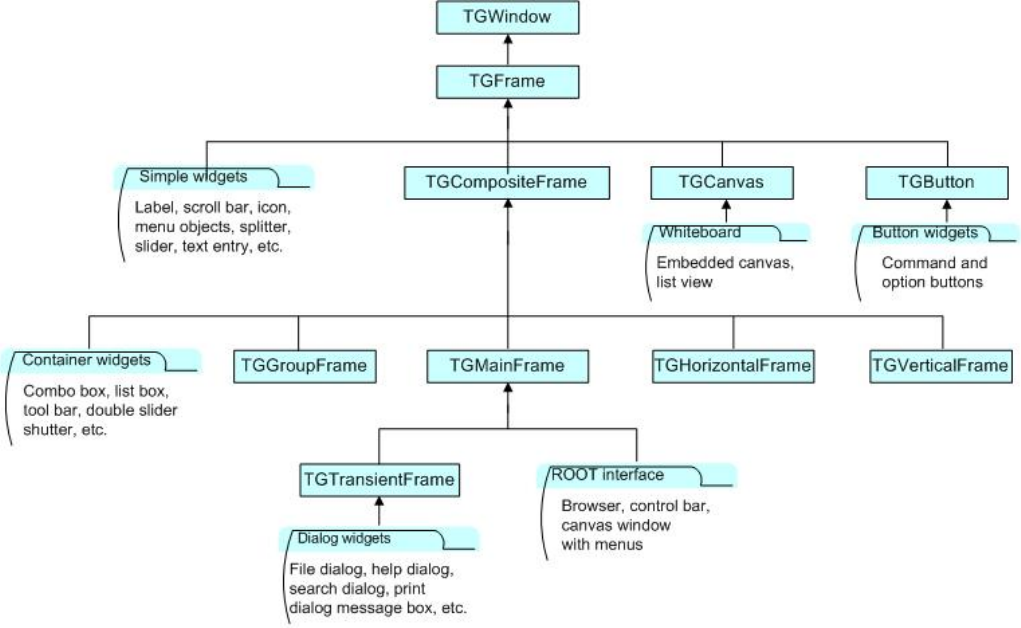
580 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
25.5.4 Frames
Most of the frame classes are mainly created for arranging widgets in a window. The class
TGFrame
is a subclass of
TGWindow
providing additional window characteristics and overriding some methods of
TGWindow
. It is a base class for
the simple widgets as buttons, labels, etc. Its only purpose is to draw a frame around widgets that do not have a frame
of their own. The main groups of TGFrame member functions are:
•Window’s functions: DoRedraw(),DeleteWindow(),Activate(), etc.
•Geometry functions: Move(),Resize(),SetSize(), etc.
•Graphics handlers: ChangeBackground(),ChangeOptions(), etc.
•Mouse and keyboard functions: HandleButton(),HandleFocusChange(),HandleKey(),HandleMotion(), etc.
•
Event handlers:
HandleEvent()
,
ProcessEvent()
,
GetSender()
,
SendMessage()
,
ProcessMessage()
,
GetLastClick(), etc.
Figure 25.2: The GUI classes hierarchy
Ones of
TGFrame
member functions provide direct functionality; others - will be overridden by
TGFrame
subclasses to
ensure particular widget’s functionality. There are two constructors provided in
TGFrame
class. One creates a frame
using an externally created window:
TGFrame(TGClient *c,Window_t id,const TGWindow *parent = 0);
For example, it can register the root window (called by
TGClient
), or a window created via
TVirtualX::InitWindow()
(window id is obtained by TVirtualX::GetWindowID() method). The other TGFrame constructor is:
TGFrame(const TGWindow *p,UInt_t w,UInt_t h,UInt_t options=0,
ULong_t back = GetDefaultBackground());
The options parameter is the bitwise OR between defined frame types. Here is a short description of these types:
Frame Type Description
25.5. WIDGETS OVERVIEW 581
kChildFrame a frame embedded in a parent
kMainFrame a main frame interacting with the system Window Manager
kTransientFrame a top level dialog’s frame
kVerticalFrame a frame that layouts its children in a column
kHorizontalFrame a frame that layouts its children in a row
kSunkenFrame a frame with a sunken board appearance
kRaisedFrame a frame with a raised board appearance
kFitWidth a frame with dynamically scaled width
kFitHeight a frame with dynamically scaled height
kFixedWidth a frame with fixed width
kFixedHeight a frame with fixed height
kFixedSize =kFixedWidth |kFixedHeight
a frame with fixed width and height
kDoubleBorder a frame having a double line border
kOwnBackground a frame having own background
kTempFrame
a temporary frame shown in certain circumstances; for example, it is used for
creation of tool tip widget
The method
ChangeOpton(UInt_t options)
allows you to change frame options. Next example shows you how to
change kVerticalFrame option to kHorizontalFrame:
frame->ChangeOptions((frame->GetOptions()& ~kVerticalFrame) |
kHorizontalFrame);
The class
TGCompositeFrame
is the base class of all composite widgets as a menu bar, a list box, a combo box, etc.
It subclasses
TGFrame
and has in addition a layout manager and a list of child frames/widgets. There are two steps
to do the design using a composite frame widget. First you put all widgets you need within this frame and assign
them desired properties using
AddFrame(),
then you lay them out by the
Layout()
method according to the assigned
layout manager. The method
AddFrame()
creates an instance of
TGFrameElement
class for every child widget of a
composite frame. This class has three public data members: the child pointer, its layout hints, and a status variable
showing if the child is visible or hidden. If no hints are specified, the default layout hints are used. Because the layout
is very important part of any design we include a special section about layout management and layout hints.
You can set a layout manager for the composite frame via:
compFrame->SetLayoutManager(TGLayoutManager *l);
The child widgets cannot be added to different composite frames.
Any child frame can be removed from the parent list by:
compFrame->RemoveFrame(TGFrame *f);
You can hide or show a child frame of a composite frame using the methods:
HideFrame(TGFrame *f)
or
ShowFrame(TGFrame *f).
You should call, for example
HideFrame(TGFrame *f),
only after the frames have been
laid out and the sub windows of the composite frame have been mapped via method MapSubwindows(), i.e.
frame->AddFrame(hFrame1,fLayout1);
frame->AddFrame(hFrame2,fLayout2);
frame->Resize(frame->GetDefaultSize()); // lays out frames
frame->MapSubwindows(); // maps subwindows
frame->HideFrame(hFrame2); // hides frame hFrame2
frame->MapWindow(); // maps main frame
The state information about a child frame can be obtained from the methods
GetState(TGframe *f)
,
IsArranged(TGFrame *f), and IsVisible(TGFrame *f).
The method
Cleanup()
deletes all objects of the composite frame added via
AddFrame()
. All
TGFrameElement
objects
(frames and layout hints) must be unique, i.e. cannot be shared.
We already mentioned that
TGMainFrame
class defines top level windows interacting with the system window manager.
It handles applications with a menu bar, toolbar, text entry fields and other widgets surrounding a central area (e.g. a
canvas widget). It lays out a set of related widgets and provides the typical application main window behavior. As you
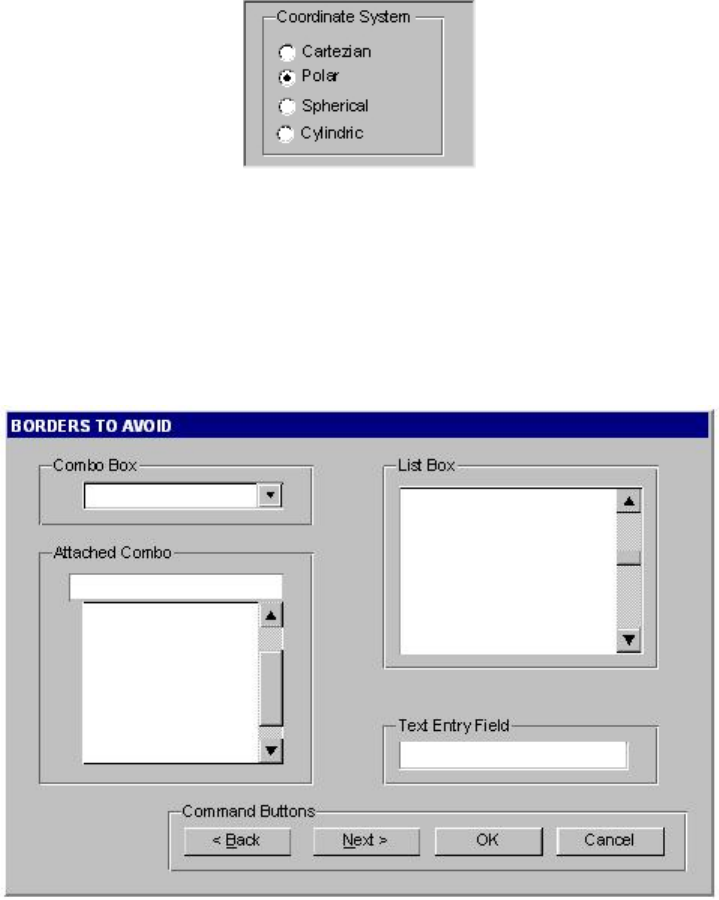
582 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
can see from the Figure above, it inherits from
TGCompositeFrame
and is inherited by
TGTransientFrame
and several
ROOT interface classes: TViewerX3D,TRootBrowser,TRootCanvas,TRootControlBar,TTreeViewer.
To fix the size of a top level window you have to use the method
TGMainFrame::SetWMSize().
This call tells the
Window Manager that it should not resize the window. The option
kFixedSize
works only for embedded frames like
TGCompositeFrame and derived classes (in combination with layout hints).
The
TGVerticalFrame
and
TGHorizontalFrame
are composite frames that lay out their child frames in vertical or
horizontal way in the same order as they were added and according to their hints preferences.
The
TGTransientFrame
class defines transient windows that typically are used for dialogs. They extend and complete
an interaction within a limited context. Always transient frames are displayed from another window or another dialog.
They may appear because of a command button being activated or a menu item being selected. They may also present
automatically when an additional input and the user attention are required by a certain condition.
The
TGGroupFrame
class presents a very convenient frame which surrounds visually a group of logically connected
widgets: radio buttons, related check boxes, two or more functionally related controls.
It is a composite frame with a border and a title. The title explains the purpose of the group and should be a noun or
noun phrase. Here is an example taken from guitest.C:
groupFrame = new TGGroupFrame(tf,"Options",kVerticalFrame);
groupFrame->SetTitlePos(TGGroupFrame::kLeft);
The second line sets the title position on the left. You can change it to be centered or right aligned if you use
TGGroupFrame::kCenter or TGGroupFrame::kRight as a parameter.
Be conservative in the use of borders because of the potential for clutter. Do not place them around single entry fields,
single combo boxes, list boxes and groups of command buttons. The design of these widgets provides them with a
border. The picture above provides kind of borders to avoid.
25.6 Layout Management
The layout process is an integral part of any GUI. When you create a simple message window, laying out its few
buttons and text widgets is quite simple. However, this process becomes increasingly difficult if you have to implement
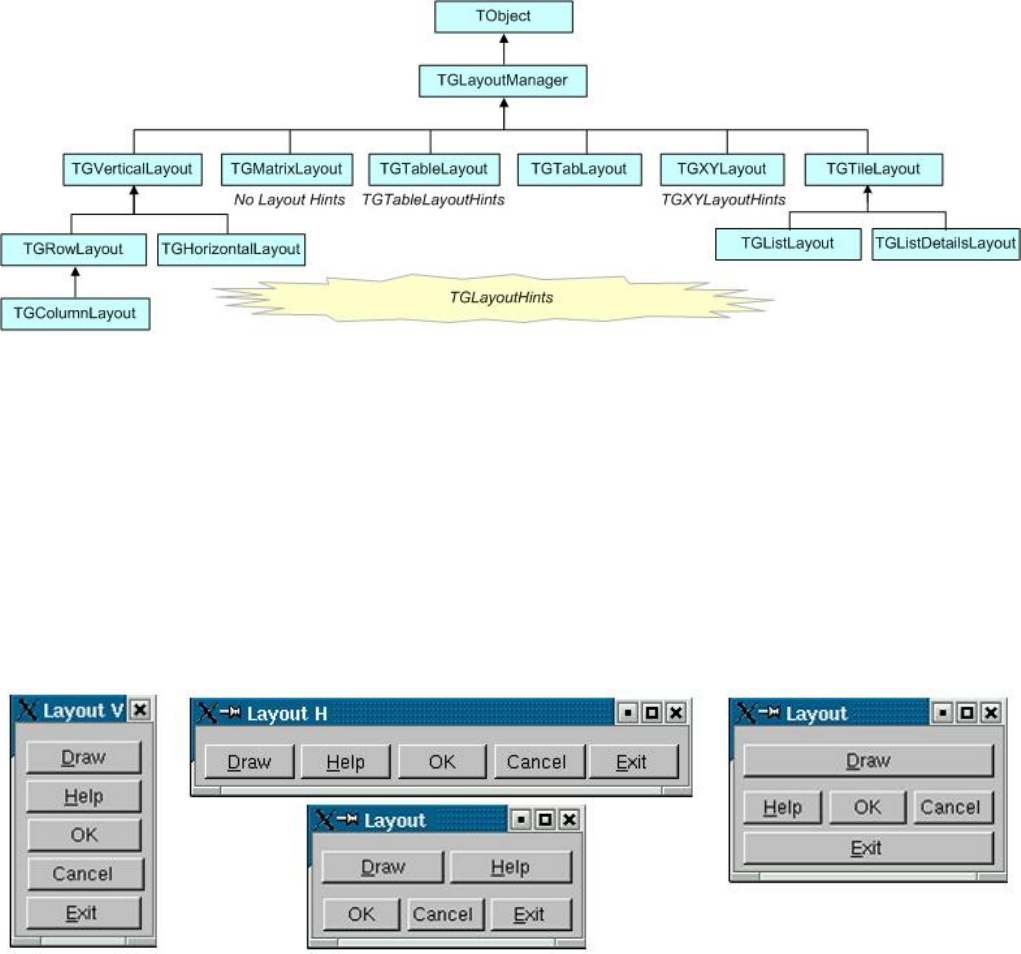
25.6. LAYOUT MANAGEMENT 583
large GUI’s with many widgets that should behave properly when the GUI is resized or uses a different font type or
size. Layout management is the process of determining the size and position of every widget in a container.
A layout manager is an object that performs layout management for the widgets within a container. You already know
that when adding a component (child widget) to a container (parent widget) you can provide alignment hints (or rely
on the default ones). These hints are used by the layout manager to correctly position the widgets in the container.
The TGLayoutManager is an abstract class providing the basic layout functionality.
Figure 25.3: The layout classes hierarchy
The base “container” class is
TGCmpositeFrame
. You can easily change the layout manager using the
SetLayoutManager(TGLayoutManager *l)
method. Setting the proper layout manager for each container is
the first step you have to do. The container uses that layout manager to position and size the components before they
are painted. ROOT currently provides the layout managers shown on the picture above.
The next important step is to provide hints about every widget in the container, i.e. to provide positions and right
amount of space between the components. The
TGLayoutHints
objects set hints by specifying the white space in pixels
around every widget.
Let’s see an example with five buttons. First you put them in a container, assign them desired properties, and then
you lay them out according to the layout manager. This process can be repeated: you go back and add, remove or
change some of the widgets and lay them out again.
Once created, you can consider these widgets as elementary objects even though they are compound ones. The pictures
above present four different layouts of five buttons. The first one shows laid out vertically buttons. Almost everywhere
you can find this vertical orientation. Looking at dialogs you see that often they consist of number of rows laid out
below each other. Some of the rows could have an internal vertical structure as well. The second picture shows the
same buttons laid out horizontally - the next common orientation. The other two show different layouts based on
mixed use of the vertical and horizontal orientation. You might recognize their pattern: two (third picture) and three
(last picture) rows that are vertically laid out.
As we already explained the layout process is always applying to a container. It will be enough to define the container
frame with vertical or horizontal layout to have buttons as in the first and second pictures.
To design them in several rows we need to use additional frames as invisible containers: two horizontal frames, children
of a vertical parent frame; or one horizontal frame laid out vertically with the Draw and Exit buttons. For widgets in a
group it is obvious to use a vertical layout.
The layout hints data member of TGLayoutHints is the bit wise OR between the hints:
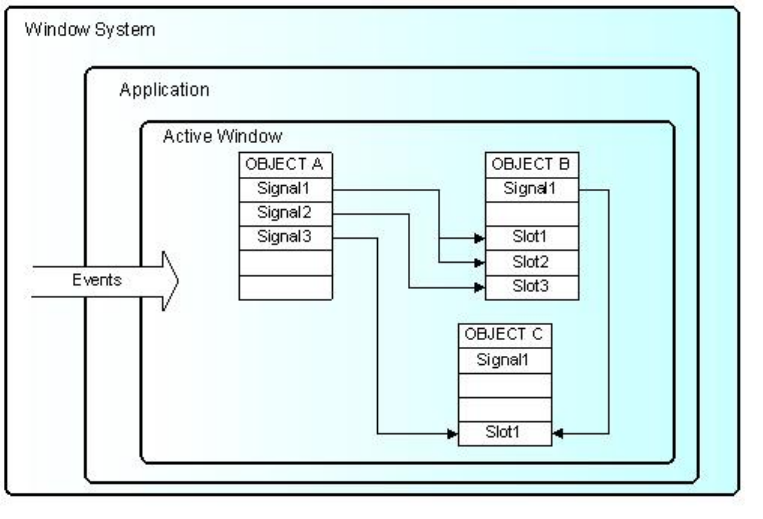
584 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
Hints Description
kLHintsNoHints no specified layout hints, the default ones will be used
kLHintsLeft
specifies the frame position to the left of the container frame after other frames with
the same hint into the list
kLHintsCenterX specifies the frame position centered horizontally (with vertical containers only)
kLHintsRight
specifies the frame position to the right of the container frame before any other laid
out frames with the same hint into the list
kLHintsTop specifies the frame position to the top of the container frame, below any laid out
frames with the same hint
kLHintsCenterY specifies the frame position centered vertically (with horizontal containers only)
kLHintsBottom
specifies the frame position to the bottom of the container frame, above any laid out
frames with the same hint
kLHintsExpandX specifies the frame to be expanded up to the width of the container frame. If the
container frame is a vertical frame - it will fit the whole width. If it is a horizontal
frame - after the positioning of all frames the available “free” width space is shared
between the frames having this hint
kLHintsExpandY specifies the frame to be expanded up to the height of the container frame. If the
container frame is a horizontal frame - it will fit the whole height. If the container
frame is a vertical frame - after the arrangement of all frames the available “free”
height space is shared between the frames having this hint
kLHintsNormal =kLHintsLeft | kLHintsTop - default hints
Layout policy:
Child frames never modify their container frame. The container frame can (or cannot) adapt its size in the layout
process. It can show all or a part of its frames. Every
TGFrame
object has a default minimum size (1, 1) assured by
TGWindow.
25.7 Event Processing: Signals and Slots
Event handling covers the interaction between different objects and between the user and the objects in an application.
There are two general ways for the user to interact with an application: the keyboard and the mouse. The Graphical
User Interface is as a bridge between the user and the program - it provides methods to detect the user actions and
instruments that do something as a reaction of these actions. The user communicates with an application through the
window system. The window system reports interaction events to the application. The application in turn forwards
them to the currently active window. The objects/widgets receive the events and react to them according to the
application functionality.
The signals/slot communication mechanism is an advanced object communication concept; it largely replaces the
concept of callback functions to handle actions in GUI’s. Signals and slots are just like any object-oriented methods
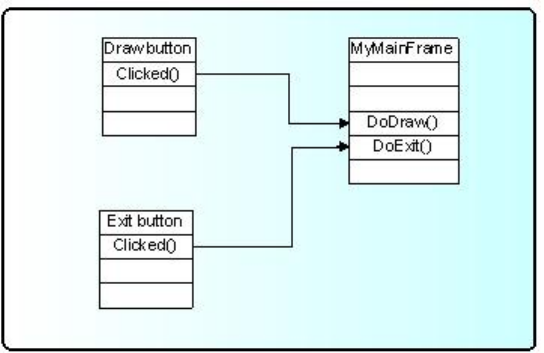
25.7. EVENT PROCESSING: SIGNALS AND SLOTS 585
implemented in C++. The objects are the instances of classes that don’t know anything about each other. They
interact and allow method calls of other object’s methods. The idea is simple: any object can send out (emit) a signal
in certain situations saying that something happened. This is all it does to communicate and it does not know whether
anything is interested in this information. On the other side there might be an object waiting for that signal and ready
to react to it. This object disposes of special instruments to listen to the sent out signals. To have a communication we
need a message transmission between the objects. In this simple example we use signals and slots. The code of the
method TGButton::Clicked() is:
virtual void Clicked() { Emit("Clicked()"); } // *SIGNAL*
I.e. any button emits the signal
Clicked()
any time someone clicks on it. As you can see this method is virtual and
could be overridden if you need to. In our simple example we call the
Connect()
method to connect the
Clicked()
signal of Draw button with MyMainFrame::DoDraw():
draw->Connect("Clicked()","MyMainFrame",this,"DoDraw()");
In the same way we can connect to the signal
Clicked()
of the Exit button with the system call
gApplication->Terminate(0).
We declare a new slot
DoExit(),
implement it to invoke the termination call and associate this slot with the signal
Clicked() of the Exit button.
The code of example.C can be changed as follows:
public:
...
void DoExit(); // a new slot is added
}
void MyMainFrame::DoExit() {
gApplication->Terminate(0);
}
MyMainFrame::MyMainFrame(const TGWindow *p,UInt_t w,UInt_t h) {
...
TGTextButton *exit = new TGTextButton(hframe,"&Exit ");
// connects signal Clicked() with slot DoExit()
exit->Connect("Clicked()","MyMainFrame",this,"DoExit()");
...
}
Here is an abstract view of the signal/slots connections in example.C:
To benefit from this mechanism your classes must inherit from
TQObject
or otherwise the class definition must start
with
RQ_OBJECT("ClassName")
macro. This macro allows the signals/slots communication mechanism to be applied
between compiled and interpreted classes in an interactive ROOT session without having the class derive from
TQObject
.
Every signal method declaration is followed by a comment
"*SIGNAL*".
Only instances of a class that defines a signal
or instances of its subclasses can emit the signal. The ROOT implementation of a popular example presenting signals
and slots is the next. Let’s have a minimal class declaration:
586 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
class MyClass {
private:
Int_t fValue;
public:
MyClass() { fValue=0; }
Int_t GetValue() const {return fValue; }
void SetValue(Int_t);
};
It will become the following as interpreted:
class MyClass {
RQ_OBJECT("MyClass")
private:
Int_t fValue;
public:
MyClass() { fValue=0; }
Int_t GetValue() const {return fValue; }
void SetValue(Int_t); // *SIGNAL*
};
Both class declarations have the same data member and public methods to access the value. By placing the
RQ_OBJECT("MyClass")
macro inside the
MyClass
body (
MyClass
is not inherited from
TQObject
) we allow this class
to use the signal/slot communication. Any instance of this class can tell the outside world that the state of its data
member has changed by emitting a signal
SetValue(Int_t).
A possible implementation of
MyClass::SetValue()
can be:
void MyClass::SetValue(Int_t v) {
if (v != fValue) {
fValue = v;
Emit("SetValue(Int_t)",v);
}
}
The line
Emit("SetValue(Int_t)",v)
activates the signal
SetValue(Int_t)
with argument v. You can use any of the
methods
TQObject::Emit("full_method_name",arguments)
to emit a signal. We create two instances of
MyClass
and connect them together:
MyClass *objA = new MyClass();
MyClass *objB = new MyClass();
objA->Connect("SetValue(Int_t)","MyClass",objB,"SetValue(Int_t)");
objB->SetValue(11);
objA->SetValue(79);
objB->GetValue(); // the value is 79
By calling the method
objA->Connect()
,
objA
connects its signal “
SetValue(Int_t)
” to the “
MyClass::SetValue(Int_t)
”
method (slot) of
objB
. Next, when you call
objA->SetValue(79)
object
objA
emits a signal which
objB
receives and
objB->SetValue(79)is invoked.
It is executed immediately, just like a normal function call.
objB
will emit the same signal in turn, but nobody is
interested in this signal, since no slot has been connected to it. Signals are currently implemented for all ROOT GUI
classes, event handlers (
TFileHandler
,
TSignalHandler
, etc.), timers (
TTimer)
and pads (
TPad
,
TCanvas
, etc.). To
find all defined signals you just do: grep ‘*SIGNAL*’ $ROOTSYS/include/*.h
As a programmer you build the sender-receiver part of object connections using the
TQObject::Connect()
method.
You can connect one signal to many different slots. The slots will be activated in order they were connected to the
signal. You can change this order using the methods
LowPriority()
and
HightPriority()
of
TQObject
. Also, many
signals can be connected to one slot of a particular object or a slot can be connected to a signal for all objects of
a specific class. It is even possible to connect a signal directly to another signal - this will emit the second signal
immediately after the first one is emitted.
All signals and slots are normal class methods and can take any number of arguments of any type. The common
methods of TQObject that activate a signal with any number and type of parameters are:
25.7. EVENT PROCESSING: SIGNALS AND SLOTS 587
Emit(signal_name,param);
With no parameters param the method will be:
ApplyButton->Emit("Clicked()");
param can be a single parameter or an array of Long_t parameters as it is shown below:
TQObject *processor; // data processor
TH1F *hist; // filled with processor results
...
processor->Connect("Evaluated(Float_t, Float_t)","TH1F", hist,
"Fill(Axis_t x, Axis_t y)");
...
Long_t args[2];
args[0]=(Long_t)processor->GetValue(1);
args[0]=(Long_t)processor->GetValue(2);
...
processor->Emit("Evaluated(Float_t, Float_t)", args);
...
To use signals and slot you need something that brings them together. The class
TQObject
has several methods creating
sender-receiver connections. Some of them are static and can be called without having an instance of the class. The
ROOT implementation of signals and slots allows connections to any known Cling object. The class name parameter in
the Connect() methods must be a class with a dictionary (interpreted classes have an implicit dictionary).
TGButton *button;
TH2 *hist;
...
TQObject::Connect(button,"Clicked()","TH2",hist,"Draw(Option_t*)");
You can replace it with 0 (zero) and in this case the slot string defines a global or interpreted function name. The
receiver parameter should be zero too. For example:
TQObject::Connect(button, "Clicked()",0,0,"hsimple()");
To make a single connection from all objects of a class you should write:
TQObject::Connect("Channel","AllarmOn()","HandlerClass",handler,
"HandleAllarm()");
The first argument specifies the class name Channel. The signal
AllarmOn()
of any object of the class Channel is
connected to the HandleAllarm() method of the handler object of the class HandlerClass.
In example.C we have used the not-static Connect()method:
Bool_t Connect(const char *signal, const char *receiver_class,
void *receiver, const char *slot);
It needs to know four things: the signal that should be connected, the receiver class, the object that will receive the
signal, and the slot that will be connected to the signal. Because this method is non-static we can write this as a
receiver parameter.
In all methods you have to specify the signal and the slot with their names and parameter types. Do not write values
instead of types in that place. It is possible to pass a parameter by value to a slot method in the following way:
Connect(myButton, "Pressed()","TH1",hist, "SetMaximum(=123) ");
Connect(myButton, "Pressed()","TH1",hist, "Draw(="LEGO")");
588 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
As you see the parameter’s value is preceded by the equation symbol (=).
You have the possibility to destroy a signal/slot connection by using
Disconnect()
methods. There are three ways to
do this:
1/ to destroy all connections to an object’s signals;
2/ to destroy all connections to a particular object’s signal; 3/ to detach an object from a specific receiver:
Disconnect(myObgect); // case 1
Disconnect(myObgect, "mySignal"); // case 2
Disconnect(myObgect,0,myReceiver,0); // case 3
Three parameters of these methods could be replaced by 0. The meaning in these cases would be “any signal”, “any
receiving object”, “any slot of the receiving object”, i.e. 0 is used as a wildcard. The sender parameter cannot be 0,
because you can disconnect signals from one given object. If the signal parameter is 0, the receiver and the slot are
disconnected from any signal. Giving the name of the signal you disconnect this signal.
In addition to all Qt features the ROOT version of signals/slots gives you the possibility to connect slots to a class.
The slots will be executed every time the specified signal is emitted by any object of this class. A slot can have default
arguments and it can be either a class method or stand-alone function (compiled or interpreted).
The method
TQObject::HasConnection(signale_name)
checks if there is an object connected to this signal and
returns true if it is the case.
Using
TQObject::NumberOfConnections()
,
TQObject::NumberOfSignals()
you can check how many signals or
connections has the object.
The rules for using signals/slots mechanism in a standalone executable program do not differ from what was described
previously. Let’s remind that
•a slot can be any class method with a generated Cling dictionary
•a slot can be a function with a dictionary
Detailed information how to generate a dictionary can be found on http://root.cern.ch/root/CintGenerator.html
The following example demonstrates how to use signals/slots mechanism in a standalone executable program on
linux
platform with the gcc compiler.
tst.C
#include <TQObject.h>
#include <RQ_OBJECT.h>
class A {
RQ_OBJECT("A")
private:
Int_t fValue;
public:
A() : fValue(0){}
~A() { }
void SetValue(Int_t value); // *SIGNAL*
void PrintValue() const { printf("value = %d\n", fValue); }
};
void A::SetValue(Int_t value) { // Set new value
// Emit signal "SetValue(Int_t)" with a single parameter
if (value != fValue) {
fValue = value;
Emit("SetValue(Int_t)", fValue);
}
}
// Main program
#ifdef STANDALONE
int main(int argc, char **argv) {
A* a = new A();
A* b = new A();

25.8. WIDGETS IN DETAIL 589
a->Connect("SetValue(Int_t)","A",b,"SetValue(Int_t)");
printf("n******* Test of SetValue(Int_t) signal *******n");
b->SetValue(10);
printf("nt***** b before ******n");
b->PrintValue();
a->SetValue(20);
printf("t***** b after a->SetValue(20) ******n");
b->PrintValue();
return 0;
}
#endif
ACLiC simplifies this procedure and allows the dictionary generation by:
root[] .L tst.C++
It will create the shared library tst_C.so.
The next line will create an executable:
g++ -otst tst.C ‘root-config --cflags --libs‘ ./tst_C.so -DSTANDALONE
The library
tst_C.so
is a dynamically loaded library and should be located in
$LD_LIBRARY_PATH
. The current working
directory should be added to $LD_LIBRARY_PATH via:
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:./
To run it, you just do:
./tst
25.8 Widgets in Detail
25.8.1 Buttons
Buttons are a popular group of widgets designed to provide specific interfaces for user interaction.
TGButton
is an
abstract class defining the general button behavior: width, height, state, its group, tool tip text, etc.
There are two main groups of buttons: command buttons with a text or graphics inside that indicate the action to be
accomplished and option buttons well known as radio and check buttons that select or change properties. The first
group is presented in ROOT by
TGPictureButton
and
TGTextButton
classes. They yield an action as soon as they are
clicked. It can be opening/closing a dialog box or invoking a specific function in an application. Remember the Draw
button from the example. The radio and check buttons from the second group are used to select an option. There is a
visual difference between these two groups: the text buttons appear “pressed in” only while they are clicked, while the
radio and check buttons change their appearance when they are selected and keep that appearance afterwards.
A text button is represented by the class
TGTextButton
. We already used its constructor in the example. The button
label indicates the action to be taken when the button is selected or pressed. The text can be a hot string defining a
hot key (known as shortcut key also) for this selection. The hot key is an underlined character in a button label that
shows the assigned keyboard mnemonic for its choice. A button that prompts more information for users has the label
generally followed by ellipsis (. . . ).
As we saw the hot strings “&Draw” and “&Exit” define the text labels “Draw” and “Exit” and keyboard mnemonics
Alt+D
,
Alt+E
for their selection. The letter D and E appear underlined on the screen. All text buttons should have a
unique shortcut key with the exception of OK and Cancel.
These buttons are usually placed within a window to provide fast access to frequently used or critical commands. They
help in situations where a command is not available through the menu bar. You already know that a command string
can be passed in the text button via the constructor:
TGTextButton(const TGWindow *p, const char *s, const char *cmd,
Int_t id, GContext_t norm, FontStruct_t font,
UInt_t options);
590 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
A button label can be changed by
SetText(new_label).
There are important guidelines to be followed about a button
label. The text has to provide a meaningful description of the performed action. The single-word label should be used
whenever possible, only two-three words for clarity, if necessary. Do not number labels. Always follow all platform
presentation and usage guidelines for standard button functions. Let’s remember a few standard names and definitions
of well known buttons:
OK - any changed information in a window is accepted and the window is closed;
Cancel - closes window without implementing submitted changes;
Reset - resets defaults and cancels any changed information that has not be submitted;
Apply - any changed information is accepted and again displayed in the window that remains open;
Close - closes the window;
Help - opens online Help.
Below are examples of text buttons. Note the two placement methods. The first example should be used when there
are one to three command buttons; the second one when there are more than three buttons.
Picture buttons are usually rectangular in shape with an icon or graphics label. These buttons may appear alone or
placed in a group at the window’s top or side. They are most frequently used to quickly access commands, many of
which are normally accessed through the tool bar. For example, the picture buttons below can be used to provide
different styles of a histogram drawing.
Here is the example how to create the first button:
TGPictureButton *fPicture = new TGPictureButton(parent,
gClient->GetPicture("h1_s.xpm"), 11);
The picture of file h1_s.xpm is used in the button. All
.xpm
files are located in the directory
$ROOTSYS/icons
. You
can assign a command directly as a parameter of the picture button constructor. The picture of
TGPictureButton
can
be changed by:
fPicture->SetPicture("h2_s.xpm");
The advantage of command buttons is that they are always visible, providing a reminder of their existence. They
can be inscribed with a meaningful description of what they do by
TGToolTip("Some describing text").
Their
activation is much easier and faster than using a two-step menu bar/pull-down sequence. The only disadvantage of
the text and picture buttons is that they consume considerable screen space if they are many. Having no more than
six command buttons per window or dialog box helps to appropriately balance the application’s effectiveness, its real
efficiency, and the operational simplicity.
The classes
TGRadioButton
and
TGCheckButton
present the option buttons in ROOT. Like the text buttons, they
have text or hot string as a label. Radio buttons are grouped in logical sets of two or more and appear with a text label
to the right. The choices are mutually exclusive and only one setting is permitted at one time. They represent visually
all alternatives and it is easy to access and compare choices. They facilitate the situations where all alternatives cannot
be easily remembered or where displaying the alternatives together helps to understand and select the proper choice. It
is very useful to provide a default setting whenever it is possible. When it is not possible to establish a default setting
because of the nature of the information, it is better to leave all radio buttons blank.
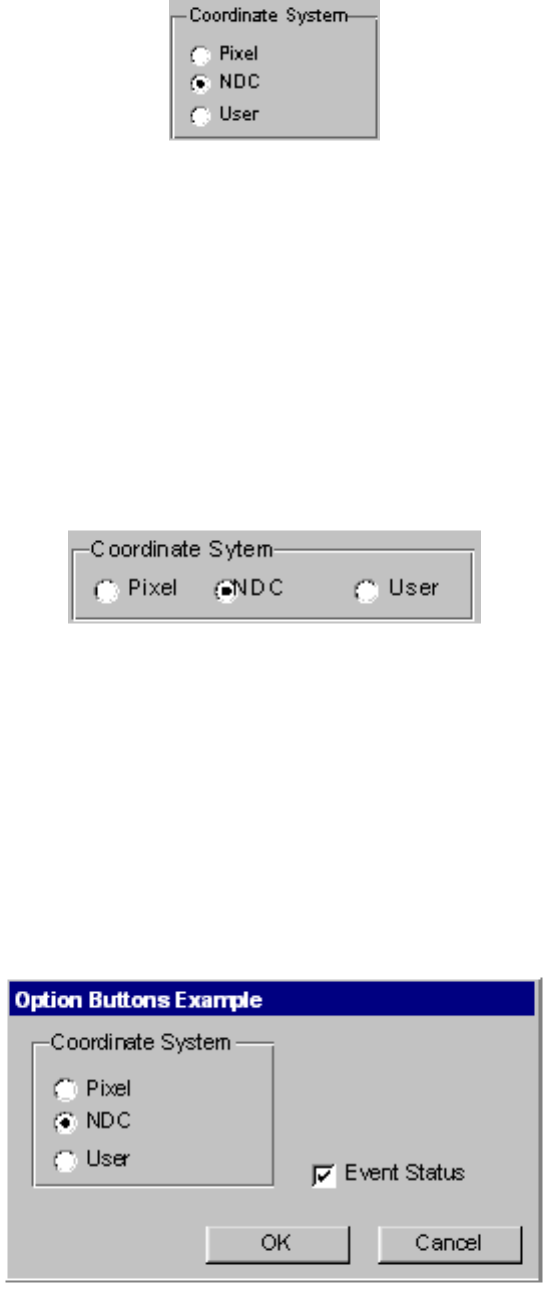
25.8. WIDGETS IN DETAIL 591
A columnar orientation is the preferred manner of radio buttons presentation. If the vertical space on the window
is limited, they can be oriented horizontally. Selection choices should be organized logically in groups. Here is the
example that produces the image above:
br = new TGButtonGroup(p,"Coordinate system",kVerticalFrame);
fR[0] = new TGRadioButton(bg,new TGHotString("&Pixel"));
fR[1] = new TGRadioButton(bg,new TGHotString("&NDC "));
fR[2] = new TGRadioButton(bg,new TGHotString("&User "));
fR[1]->SetState(kButtonDown);
br->Show();
It is enough to change
kVerticalFrame
to
kHorizontalFrame
in
TGButtonGroup
constructor and you will have radio
buttons aligned horizontally:
The class
TGButtonGroup
will help you to organize button widgets in a group. There is no need to call
AddFrame()
since the buttons are added automatically with a default layout hint to their parent by
TGButtonGroup::Show()
as
shown in the previous example. The buttons in the group have assigned identifiers. Any button in a group emits a
Clicked()
signal with this identifier when it is clicked. This giving an ideal solution to connect several
Clicked()
signals to one slot.
An exclusive button group switches off all toggle buttons except the selected one. The group is by default non-exclusive
but its entire radio buttons will be mutually exclusive.
TGHButtonGroup
and
TGVButtonGroup
are convenience classes that offer you a thin layer on top of
TGButtonGroup
.
TGHButtonGroup
organize button widgets in a group of one horizontal row,
TGVButtonGroup
in a group of one column.
You can also organize buttons in rows and columns using the provided constructor and TGMatrixLayout.
Do not use a radio button to indicate the presence or absence of a state - use a check box instead.
To have the check button “Event Status” and to set it as selected we need to write:
TGCheckButton *estat = new TGCheckButton(p, "Event Status",1);
estat->SetState(kButtonDown);
Check boxes show the selected choices and any number of them can be selected, including none. Their proper usage is
for setting attributes, properties or values; also for data or choices that are discrete, small and fixed in number, not
easily remembered. With check boxes all alternatives are visible: it is easy to access and compare choices because they

592 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
can all be seen together. Each option acts as a switch and can be either “on” or “off”. It is never changed in contents.
Checkboxes differ from radio buttons in that they permit selection of more than one alternative. Each box can be
switched on or off independently. These buttons can be used alone or grouped in sets. It is good practice to provide
default settings for check boxes whenever it is possible.
This can be done by:
SetState(EButtonState state)
The parameter state can be one of kButtonUp,kButtonDown,kButtonEngaged,kButtonDisabled.
Check boxes can be used to affect other controls. The contents of a list can, for example, be filtered by setting a check
box. In any case, use a check box only when both states of a choice are clearly opposite and unambiguous. If opposite
states are not clear, it is better to use two radio buttons.
Choice description, i.e. check box label, must be clear, meaningful, fully spelled out, and displayed in mixed-type text.
Whenever the use of a given button is inappropriate, for whatever reason, that button should be disabled:
button->SetState(kButtonDisabled);
Never make a button appear and disappear.
In general, option buttons should not offer more than eight choices. If the number of choices exceeds this maximum, it
is better to use a multiple selection list box.
The method
IsToggleButton()
gives the information whether a radio button or a check button is selected. An option
button can be set or unset via its method PSetState(EButtonState state).
The method
HandleKey(event)
is called when the defined hotkey is hit for any button. It sets the selected option
button or clicks the selected text button and invokes its defined action.
25.8.2 Text Entries
A
TGTextEntry
is a one-line text input widget. It contains text that is entered or modified through the keyboard. This
text may be displayed in different way according to the set echo mode. Users can control them by
SetEchoMode()
,
GetEchoMode() methods.
•kNormal - display characters as they are entered (default);
•kNoEcho - do not display anything;
•kPassword - display asterisks instead of the characters actually entered.
The way in which typed characters are inserted in the text entry is defined by
TGTextEntry::EInsertMode
and can
be toggled by the Insert key:
•kInsert - typed character are inserted (cursor has shape of short line)
•kReplace - entered characters substitute already typed ones (cursor has the shape of filled rectangle).
There ate different text alignment modes defined by
TGWidget::ETextJustification
. They are valid until text fits
the frame width of the text entry field.
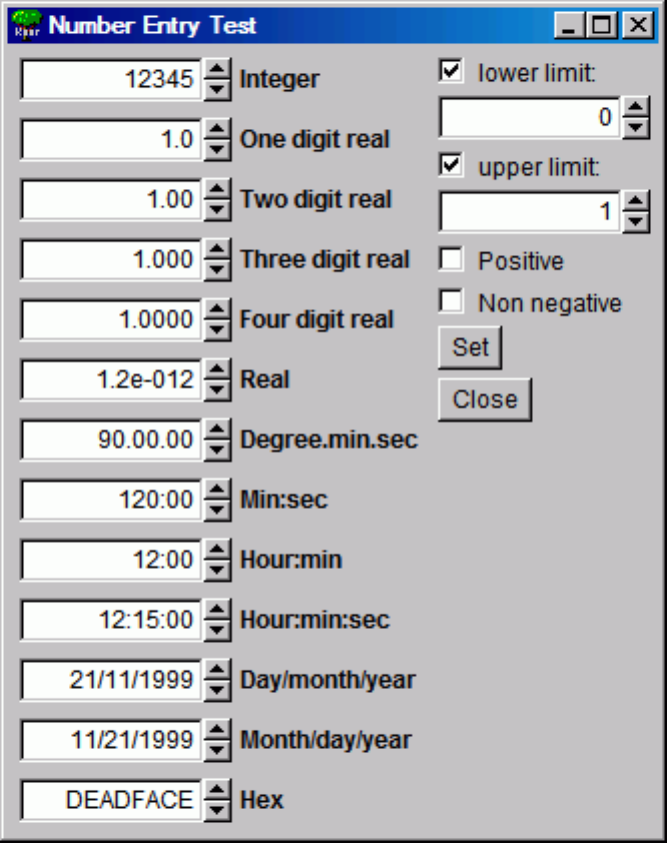
25.8. WIDGETS IN DETAIL 593
•kTextLeft - left-side text alignment
•kTextRight - right-side text alignment
•kTextCenterX - center text alignment along x direction
•kTextTop - top-side text alignment
•kTextBottom - bottom-side text alignment
•kTextCenterY - center text alignment along y direction
25.8.3 Number Entries
The
TGNumberEntry
class present number entry widgets. A number entry is a single-line field followed by two small,
vertically arranged up-down buttons. Its purpose is to make a selection by either scrolling through a small set of
meaningful predefined choices or typing numbers. The
TGNumberFormat
class contains
enum
types to specify the
numeric format. The number entry widget is based on
TGTextEntry
. It allows only numerical input. The widget
supports numerous formats including integers, hex numbers, real numbers, fixed fraction real and time/date formats.
It also allows to restrict input values to non-negative or positive numbers and to specify explicit limits.
The following styles are supported:
•kNESInteger - integer number
•kNESRealOne - real number with one digit (no exponent)
•kNESRealTwo - real number with two digits (no exponent)
594 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
•kNESRealThree - real number with three digits (no exponent)
•kNESRealFour - real number with four digits (no exponent)
•kNESReal - arbitrary real number
•kNESDegree - angle in degree:minutes:seconds format
•kNESMinSec - time in minutes:seconds format
•kNESHourMin - time in hour:minutes format
•kNESHourMinSec - time in hour:minutes:seconds format
•kNESDayMYear - date in day/month/year format
•kNESMDayYear - date in month/day/year format
•kNESHex- hexadecimal number
The following attributes can be specified:
•kNEAAnyNumber - any number is allowed
•kNEANonNegative - only non-negative numbers are allowed
•kNEAPositive - only positive numbers are allowed
Explicit limits can be specified individually:
•kNELNoLimits - no limits
•kNELLimitMin - lower limit only
•kNELLimitMax - upper limit only
•kNELLimitMinMax - both lower and upper limits
fN1 = new TGNumberEntry(parent, 0.005,9, kENTRY1,
TGNumberFormat::kNESRealThree, //style
TGNumberFormat::kNEAAnyNumber, //input value filter
TGNumberFormat::kNELLimitMinMax, //specify limits
-1.,1.); //limit values
TGNumberEntryField is a number entry input widget.
Nent = new TGNumberEntryField(hgrunf2, kNENT_ID, 0.6,
TGNumberFormat::kNESRealThree,
TGNumberFormat::kNEAAnyNumber);
TGNumberEntryField
is a plain vanilla entry field, whereas
TGNumberEntry
adds two small buttons to increase and
decrease the numerical value in the field. The number entry widgets also support using the up and down cursor keys to
change the numerical values. The step size can be selected with control and shift keys:
•–small step (1 unit/factor of 3)
•Shift medium step (10 units/factor of 10)
•Controllarge step (100 units/factor of 30)
•Shift+Controlhuge step (1000 units/factor of 100)
The steps are either linear or logarithmic. The default behavior is set when the entry field is created, but it can be
changed by pressing the alt key at the same time.
25.8. WIDGETS IN DETAIL 595
25.8.4 Menus
Menus provide a list of commands or options helping the user to select and to perform a task. The menu system classes
are TGMenuBar,TGMenuTitle,TGPopupMenu, and TGMenuEntry.
The
TGMenuBar
class implements a menu bar widget. It is used to specify and provide access to common and frequently
used application actions described in menu titles, implemented by
TGMenuTitle
class. The menu bar is the highest-level
of the menu system and it is a starting point for all interactions. Also, it is always visible and allows using the keyboard
equivalents. The geometry of the menu bar is automatically set to the parent widget, i.e. the menu bar automatically
resizes itself so that it has the same width as its parent (typically TGMainFrame).
The menu bar is as a container for its menus - objects of the type
TGPopupMenu.
Popup menus can appear in a menu
bar. They can be a sub-menu of another popup menu (cascading menus) or can be standalone (as a context menu).
They are made of one or more menu items choices. When displayed, the menu items are arranged in a vertical list.
Usually they correspond to actions (e.g.
Open)
. These items can be labeled with text, graphics or a combination of both.
Each of them should have a character defined as its unique key for access. Grouped logically by their functionality,
they are separated visually by menu separators in groups. For example, The
File
menu is a common menu title for
tasks that apply to a file, as Open,Save,Close,Print. . .
// a popup menu
fMenuFile = new TGPopupMenu(gClient->GetRoot());
// adding menu entries
fMenuFile->AddEntry("&Open...",M_FILE_OPEN);
fMenuFile->AddEntry("&Save",M_FILE_SAVE);
fMenuFile->AddEntry("S&ave as...",M_FILE_SAVEAS);
fMenuFile->AddEntry("&Close", -1);
// adding separator
fMenuFile->AddSeparator();
// next group of menu entries
fMenuFile->AddEntry("&Print",M_FILE_PRINT);
fMenuFile->AddEntry("P&rint setup...",M_FILE_PRINTSETUP);
...
fMenuFile->AddSeparator();
fMenuFile->AddEntry("E&xit",M_FILE_EXIT);
First we create the File menu by creating an object of class
TGPopupMenu
and adding menu entries with
AddEntry
method. Its first parameter is a hot string, the second - a menu ID. The ampersand character (&) denotes shortcut for
each menu entry; you can use the letter after it to manage the menu via keyboard. There are three groups of menu
entries separated visually by two separators.
You can add a sub-menu by using the method
TGPopupMenu::AddPopup
. Its first parameter is again a string, the
second one - a pointer to a
TGPopupMenu
object that will appear as a sub-menu when the menu entry will be selected.
The often used visual indicator of a sub- menu is a right-facing arrow to the right of the parent menu item. Generally
only one level of cascading menus is recommended and you should be careful in using more. Next lines show how to
create a menu bar with File,Test and Help menus:
// menu bar item layout hints
fMBItemLayout = new TGLayoutHints(kLHintsTop|kLHintsLeft,0,4,0,0);
fMBHelpLayout = new TGLayoutHints(kLHintsTop|kLHintsRight);
// menu bar
fMenuBar = new TGMenuBar(fMain,100,20,kHorizontalFrame);
// adding popup menus
fMenuBar->AddPopup("&File", fMenuFile, fMBItemLayout);
fMenuBar->AddPopup("&Test", fMenuTest, fMBItemLayout);
fMenuBar->AddPopup("&Help", fMenuHelp, fMBHelpLayout);
Using the method
TGMenuBar::AddPopup
we add three
TGPopupMenu
objects to the menu bar
fMenuBar
. The first
parameter is a hot string used by
TGMenuTitle
object. When you add a popup menu to the menu bar, a
TGMenuTitle
object is created by the menu bar. It is the name of the popup menu. A menu title should have a one-word name

596 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
that reflects the purpose of all items within the corresponding popup menu. It should also have a defined character as
its unique access key. The second parameter is the popup menu we would like to add. The third one is an object of
TGLayoutHints
type that defines how the menu title will be laid out in the menu bar. In our example the
File
and
Test
menus will be laid out to the left of the menu bar with 4 pixels distance in between, the
Help
menu - will be laid
out to the right.
The menu classes provide a very flexible menu system: you can enable, disable, add or remove menu items dynamically.
The method
HideEntry(menuID)
hides the menu entry (the entry will not be shown in the popup menu). To
enable a hidden entry you should call
EnableEntry(menuID)
method. By default all entries are enabled. The method
DisableEntry(menuID)
helps you to disable a menu entry - it will appear in sunken relieve. The
DeleteEntry(menuID)
method will delete the specified entry from the menu.
A few words about the menu design. A menu should be kept consistent and simple. All related items need to be in a
popup menu. The cascade menus should be used judiciously. Try to limit them to one, maximum two levels.
There are some rules for naming the menu objects:
•Define unique names within a menu
•Use capitalized one-word names allowing the quick scan of the menu
•Define unique access key for any menu item
•Indicate by ellipsis (. . . ) after the title with no space when a menu item will pop-up a dialog box
The proper kind of graphical menus is a critical point to every application success and depends of three main factors:
•number of presented items in the menu
•how often the menu is used
•how often the menu contents may change
25.8.5 Toolbar
A toolbar (
TGToolBar
) is a composite frame that contains
TGPictureButton
objects. It provides an easy and fast
access to most frequently used commands or options across multiple application screens. Also, it invokes easily a sub
application within an application. All its functions can be obtained by application menus. It is located horizontally at
the top of the main window just below the menu bar. All other subtask and sub-feature bars are positioned along sides
of window.
// toolbar icon files
const char *xpms[] = {
"x_pic.xpm",
"y_pic.xpm",
"z_pic.xpm",
0
};
// toolbar tool tip text
const char *tips[] = {
"X Settings",
"Y Settings",
"Z Settings",
0
};
// toolbar button separator
int separator = 5;

25.8. WIDGETS IN DETAIL 597
// structure containing toolbar button information
ToolBarData_t t[3];
// creation of a toolbar object as a child of main frame
TGToolBar *tb = new TGToolBar(fMain,520,80);
for (int i=0;i<3; i++) {
// filling the ToolBarData_t with information
t[i].fPixmap = xpms[i]; // icon file
t[i].fTipText = tips[i]; // tool tip text
t[i].fStayDown = kFALSE; // button behavior if clicked
t[i].fId = i+1;// button id
t[i].fButton = NULL; // button pointer
if (strlen(xpms[i]) == 0) {
separator = 5;
continue;
}
tb->AddButton(fMain,&t[i],separator);
separator = 0;
}
// adding the tool bar to the main frame
fMain->AddFrame(tb, new TGLayoutHints(kLHintsTop|kLHintsExpandX));
// adding a horizontal line as a separator
TGHorizontal3DLine *lh = new TGHorizontal3DLine(fMain);
fMain->AddFrame(lh, new TGLayoutHints(kLHintsTop|kLHintsExpandX));
To have a tool bar in your application you do not need to do anything special - only to create objects: a tool bar and
its picture buttons. This sample code creates the following three toolbar buttons:
First we need to complete a ToolBarData_t structure for each tool bar button before adding it to the tool bar. This
structure contains:
•the icon file name “filename.xpm”
•the tool tip text - a short help message explaining the button purpose
•the Boolean variable defining the button behavior when is clicked
•kFALSE - do not stay down
•kTRUE - to stay down
•the button ID
•the button pointer (TGButton *) - should be NULL
We create an array
*xpms[]
containing the icon file names that will be used for a picture button creation. If you write
only the file names here ROOT will search these files in
$ROOTSYS/icons
directory. If the icon files are not there, you
should provide the full path name also. The array
*tips[]
contains the tool tip texts for buttons. The integer variable
separator is used to set the distance between two groups of toolbar buttons. It defines the amount of pixels to the left
for each button.
We create a tool bar object and add the buttons using the
AddButton
method. The variable separator helps us to
define no space between the buttons in a group (0), and 5 pixels extra-space before and after. All buttons added via
this method will be deleted by the toolbar. On return the
TGButton
field of the
ToolBarData_t
structure is filled in
(if the icon pixmap was valid). The first parameter is the window to which the button messages will be sent. Lastly, we
create an object of class
TGHorizontal3DLine
- a horizontal 3D line. It will separate the toolbar from the menu bar
because the layout hints we define as kLHintsTop |kLHintsExpandX.
It is user friendly to allow the possibility for the tool bar to be turned on or off (via a menu). If you use a single tool
bar, it should fill the complete width of its parent. When using more than one, you should also think about setting the
bar size to the end of the most right button. This way other bars can be displayed in the same row below the menu bar.
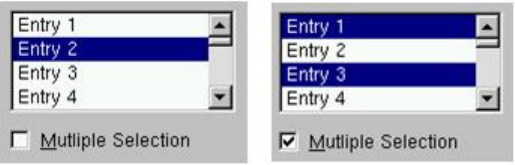
598 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
Tool bar buttons should have equal size, meaningful and unique icons, and short meaningful tool tip text. The related
buttons should be grouped together by frequency or sequence of use, or importance. Potentially destructive buttons
must be separated from them to avoid accidental activation and potentially catastrophic results. Temporarily not
available items should be displayed grayed out.
25.8.6 List Boxes
The purpose of a list box is to display a collection of items from which single or multiple selection can be made. It
is always visible, having a scroll bar when the displayed area is not enough to show all items. The choices may be
mutually exclusive (a list box with single selection) or not mutually exclusive (a list box with multiple selection).
The proper usage of the list boxes is for selecting values, or objects, or setting attributes. You have to create them to
display 4 to 8 choices at one time (3 is a required minimum in case of lack of screen space). The list should contain not
more than 40 items accessible by scrolling view (vertical scroll bar). If more are required, you should provide a method
for using search criteria or scoping the options. The best list boxes use is for textual data or choices. They should be
wide enough to display fully all items. When it is not possible, break the long items with ellipsis and provide tool tip
that displays the full item text.
The list box widget is represented by
TGListBox
,
TGLBContainer
,
TGLBEntry
and
TGTextLBEntry
classes. Currently
entries are simple text strings (
TGTextLBEntry
). A
TGListBox
looks a lot like a
TGCanvas
. It has a
TGViewPort
containing a
TGLBContainer
which contains the entries and it also has a vertical scrollbar which becomes visible if
there are more items than fit in the visible part of the container. The
TGListBox
is user callable. The other classes are
service classes of the list box. Here is a sample code showing how to create a list box with ten entries:
// list box widget containing 10 entries
int fFirstEntry = 0, fLastEntry = 10;
char tmp[20];
TGListBox *fListBox = new TGListBox(parent, 90);
for (i = fFirstEntry; i < fLastEntry; i++) {
sprintf(tmp, "Entry %i", i+1);
fListBox->AddEntry(tmp, i);
}
fListBox->Resize(150,80);
parent->AddFrame(fListBox,new TGLayoutHints(kLHintsTop|kLHintsLeft,
5,5,5,5));
We create the list box widget passing the parent window pointer and giving an ID number. Next we add entries
with specified string and ID to the list box. Before adding the list box to its parent widget, it should be resized via
Resize(width, height)
method. The list box width and height are in pixels. The default entry layout hints are
kLHintsExpandX | kLHintsTop. If you want to add entries using different ones, call the method:
TGListBox::AddEntry(TGLBEntry *lbe, TGLayoutHints *lhints);
It adds the specified
TGLBEntry
and
TGLayoutHints
to the list box. There are several methods providing a flexible
entry manipulation: you can insert, add or remove list box items dynamically. The list box entry IDs are used in these
methods and also in event processing routines. In our example the integer variables
fFirstEntry
and
fLastEntry
contain the information about the first and last entry IDs. You can add or remove a list box entry using them in the
following way:
// adding an entry
fLastEntry++;
sprintf(tmp, "Entry %i", fLastEntry);
fListBox->AddEntry(tmp, fLastEntry);
fListBox->MapSubwindows();
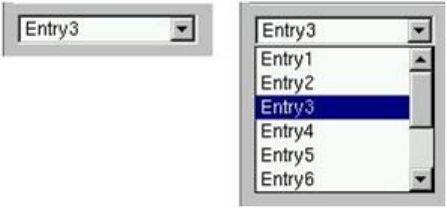
25.8. WIDGETS IN DETAIL 599
fListBox->Layout();
...
// removing an entry
if (fFirstEntry < fLastEntry) {
fListBox->RemoveEntry(fFirstEntry);
fListBox->Layout();
fFirstEntry++;
}
A single-selection list box is used for selecting only one item in a list.
A multiple-selection list box permits selection of more than one item. The selected choices should be visible - you have
several choices to do this:
•to mark selected choices with a check mark or highlight them
•to provide a summary list box to the right of the list box, containing the selected choices
•
to provide a display-only text control indicating the number of selected choices (its position should be justified
upper-right above the list box)
•if the actions Select All or Deselect All must be quickly or frequently performed, use command buttons
25.8.7 Combo Boxes
A combo box is as single-selection list box that shows only the currently selected entry and a prompt button displayed
as a downward arrow. The prompt button provides a visual cue that a list box is hidden. Its main advantage is
consuming of quite a bit of screen space. When the user clicks on it, a list pops up, from which a new choice can be
made. After a new item is chosen the combo box folds again showing the new selection.
The combo box widget is represented by the user callable class
TGComboBox
. The class
TGComboBoxPopup
is a service
class. The combo box constructor is very similar to the list box one. The first parameter is a parent widget pointer
again, the second - an integer value that will be used as combo box ID. The method used for adding entries is very
similar to the list box method we used before. The method Select(entryID) sets the current combo box entry.
char tmp[20];
// combo box layout hints
fLcombo = new TGLayoutHints(kLHintsTop | kLHintsLeft,5,5,5,5);
// combo box widget
TGComboBox *fCombo = new TGComboBox(parent,100);
for (i=0;i<10; i++) {
sprintf(tmp, "Entry%i", i+1);
fCombo->AddEntry(tmp, i+1);
}
fCombo->Resize(150,20);
// Entry3 is selected as current
fCombo->Select(2);
parent->AddFrame(fCombo, fLcombo);
You have the same flexibility to add, insert or remove entries. As with list boxes you can retrieve the information
for currently selected item via
GetSelected
or
GetSelectedEntry
methods. The first one returns the entry ID, the
second - the current entry pointer (TGLBEntry *).

600 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
25.8.8 Sliders
A slider is a scale with an indicator (slider) that you can drag to choose a value from a predefined range. It may be
oriented horizontally or vertically. In both cases it provides an excellent indication of where a value exists within a
range of values.
The class
TGHSlider
represents the horizontal slider;
TGVSlider
- the vertical one. Both inherit from the base class
TGSlider
that creates the main slider parameters: the range of values within a value can be selected; the indicator
type; the tick mark scale. Using its methods
SetRange
,
SetPosition
and
SetScale
you can set these parameters. To
retrieve the set slider value you can call GetPosition method.
Next sample code creates a horizontal slider
hslider
with a tick mark of type
kSlider1
. Its width is 150 pixels, and
its scale is placed down (
kScaleDownRight
). The last parameter in the
TGHSlider
constructor is the slider ID. It
will be used for event processing. The methods
SetRange
and
SetPosition
set the range and the current tick mark
position of the slider.
hslider = new TGHSlider(parent,150,kSlider1|kScaleDownRight,sID);
hslider->SetRange(0,50);
hslider->SetPosition(39);
Slider values can be set by using the mouse to drag the slider across the scale until the desired value is reached. Another
way is to click in the slider trough instead of dragging.
25.8.8.1 Double Slider
Double slider widgets allow easy selection of a min and a max value out of a range. They can be either horizon-
tal or vertical oriented. There is a choice of different types of tick marks:
kDoubleScaleNo
,
kScaleDownRight
,
kDoubleScaleBoth.
To change the
min
value you should press the left mouse button near to the left (
TGDoubleHSlider
) or bottom
(
TGDoubleHSlider
) edge of the slider. Alternatively, to change the
max
value you need to press the mouse near to the
right (
TGDoubleHSlider
) or top (
TGDoubleHSlider
) edge of the slider. To change both values simultaneously you
should press the left mouse button near to the center of the slider.
TGDoubleSlider
is an abstract base class that creates the main slider parameters. The concrete class to use for a
vertical double slider is
TGDoubleVSlider
and
TGDoubleHSlider
for a horizontal one. The double slider constructors
are similar to those of the other sliders. If you set
kDoubleScaleNo
as a scale parameter no scale will be drawn. Here
is an example:
vDslider = new TGDoubleVSlider(p,100,kDoubleScaleNo,dsliderID);
vDslider->SetRange(-10,10);
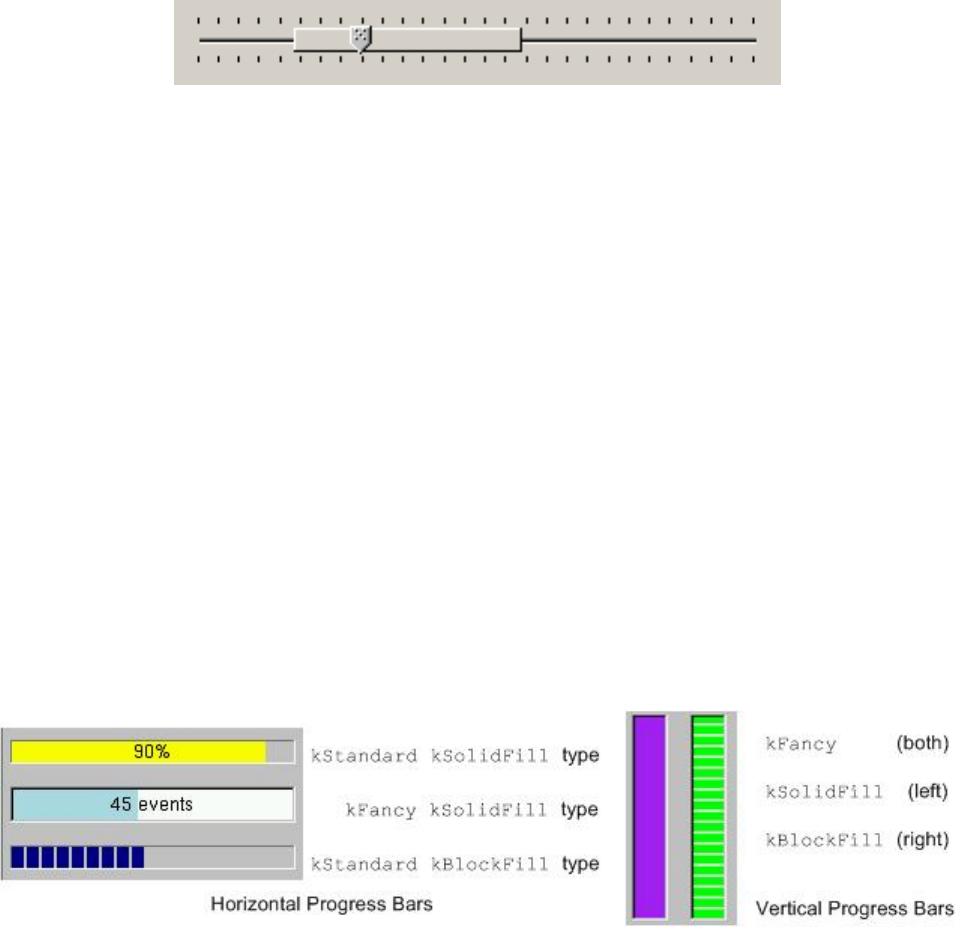
25.8. WIDGETS IN DETAIL 601
25.8.9 Triple Slider
The new
TGTripleHSlider
and
TGTripleVSlider
classes inherit from the double slider widgets and allow easy selection
of a range and a pointer value. The pointer position can be constrained into the selected range or can be relative to it.
To change the slider range value press the left mouse button near to the left/right (top/bottom) edges of the slider. To
change both values simultaneously press the mouse button near to the slider center. To change pointer value press the
mouse on the pointer and drag it to the desired position.
fSlider = new TGTripleHSlider(parent,100,kDoubleScaleBoth,kSLD_ID,
kHorizontalFrame);
parent->AddFrame(fSlider,new TGLayoutHints(kLHintsExpandX,5,5,5,5));
fSlider->SetConstrained(kTRUE);
fSlider->SetRange(rmin, rmax);
fSlider->SetPosition(pmin, pmax);
fSlider ->SetPointerPosition(pvalue);
25.8.10 Progress Bars
A progress bar is a widget that shows that an operation is in progress and how much time is left. It is a long rectangular
bar, initially empty, that fills with a color as a process is being performed. The filled-in area indicates the percentage
of the process that has been completed. You should use this widget for waits exceeding
one minute
. For a very time
consuming operation it is better to break the operation into subtasks and provide a progress bar for each of them.
A progress bar may be oriented horizontally or vertically. The horizontally oriented progress bar fills with a color
from left to right; the vertically oriented - from bottom to top. A percent complete message provides an indication of
the completed part of the process. It is a good practice to include some descriptive text of the process to keep users
informed and entertained while they are waiting for process completion.
The picture below shows the progress bars you can create using the classes
TGProgressBar
,
TGHProgressBar
, and
TGHProgressBar.
// vertical frame with three horizontal progressive bars
TGVerticalFrame *vframe = new TGVerticalFrame(fMain, 10,10);
fHProg1 = new TGHProgressBar(vframe,TGProgressBar::kStandard,300);
fHProg1->ShowPosition();
fHProg1->SetBarColor("yellow");
fHProg2 = new TGHProgressBar(vframe,TGProgressBar::kFancy,300);
fHProg2->SetBarColor("lightblue");
fHProg2->ShowPosition(kTRUE,kFALSE,"%.0f events");
fHProg3 = new TGHProgressBar(vframe,TGProgressBar::kStandard,300);
fHProg3->SetFillType(TGProgressBar::kBlockFill);
vframe->AddFrame(fHProg1,new TGLayoutHints(kLHintsTop|kLHintsLeft|
kLHintsExpandX,5,5,5,10));
vframe->AddFrame(fHProg2,new TGLayoutHints(kLHintsTop|kLHintsLeft|
kLHintsExpandX,5,5,5,10));
vframe->AddFrame(fHProg3,new TGLayoutHints(kLHintsTop|kLHintsLeft|
602 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
kLHintsExpandX,5,5,5,10));
vframe->Resize(200,200);
25.8.11 Static Widgets
The classes
TGLabel
and
TGIcon
show some information - text or graphics. The line below creates a label object. The
syntax is very simple: you specify the parent widget and a string object holding the desired text.
TGLabel *label = new TGLabel(parentWidget, "Label's string");
Next sample creates an icon object. First we create an object of type
TGPicture
. The
TGPicture
objects are never
created directly by the application code. We call
TGClient
telling it the pixmap’s file name to create a
TGPicture
object and, in turn, it will return a pointer to the created object. If the pixmap file cannot be found the returned
pointer will be
NULL
. As usual, the first parameter of a
TGIcon
constructor is the parent frame. The second one is the
TGPicture
object holding the pixmap we want to show. Last two parameters define the width and height of pixmap in
pixels. In the end we add the created icon object to its parent.
// icon widget
const TGPicture *ipic=(TGPicture *)gClient->GetPicture("leaf.xpm");
TGIcon *icon = new TGIcon(parent,ipic,40,40);
parent->AddFrame(icon,new TGLayoutHints(kLHintsLeft|kLHintsBottom,
1,15,1,1));
The
TGPicture
objects are cached by
TGClient
in order to keep the resource usage low and to improve the efficiency
of the client-server windowing systems.
TGClient
will check whether a pixmap with the same name was already loaded
before to register a new picture object. If it finds it, it will return a pointer to the existing object. Also, it will increase
the usage counter for the object.
All
TGPicture
objects are managed by the class
TGPicturePool
.
TGClient
creates an object of this type upon
initialization. Normally your application program does not deal directly with this class because all manipulations go
through TGClient class.
Once you have finished with using of the
TGPicture
object, you should call the method
TGClient::FreePicture(const
TGPicture *pic)
to free it. The usage counter of the picture object will be decreased and when it reaches zero - the
TGPicture object will be deleted.
25.8.12 Status Bar
The status bar widget is used to display some information about the current application state: what is being viewed in
the window, a descriptive message about selected objects, or other no interactive information. It may also be used to
explain highlighted menu and tool bar items.
An application can only have one status bar at a time.
There is nothing special to create a status bar in your application. You should decide how many fields you need to
present the current application state to the user. By default a status bar consists of one part. Multiple parts can be
created by
SetParts
method. Its first parameter is an array of integers that give the percentage size of each part. The
second parameter gives the number of status bar parts. Using SetText method you can set a text for any part.
// status bar
Int_t parts[] = {33,10,10,47};
fStatusBar = new TGStatusBar(fMain,50,10,kHorizontalFrame);
25.8. WIDGETS IN DETAIL 603
fStatusbar->SetParts(parts,4);
fMain->AddFrame(fStatusBar, new TGLayoutHints(kLHintsBottom |
kLHintsLeft | kLHintsExpandX, 0,0,2,0));
...
// fill status bar fields with information; selected is the object
// below the cursor; atext contains pixel coordinates info
fStatusBar->SetText(selected->GetTitle(),0);
fStatusBar->SetText(selected->GetName(),1);
fStatusBar->SetText(atext,2);
fStatusBar->SetText(selected->GetObjectInfo(px,py),3);
25.8.13 Splitters
A window can be split into two parts (panes) by using a horizontal or a vertical splitter. A horizontal splitter resizes
the frames above and below of it; a vertical splitter resizes the frames left and right of it.
This widget is represented by
TGSplitter
,
TGHSplitter
, and
TGVSplitter
classes. Currently there is no special
graphics representation for splitter widgets; only the cursor changes when crossing a splitter.
There is nothing special to create a splitter - two lines of code only:
TGHSplitter *hsplitter = new TGHSplitter(fVf);
hsplitter->SetFrame(fH1,kTRUE);
You call a horizontal
TGHSplitter
or a vertical
TGVSplitter
splitter constructor and after you set the frame to be
resized via
SetFrame
method. In spite of that, there are rules to be followed when you create a splitter in your
application.
For a horizontal splitter they are:
•the parent of a horizontal splitter must inherit from TGCompoziteFrame and must have a vertical layout
•the above resized frame must have kFixedHeight option set
•use layout hints kLHintsTop | kLHintsExpandX when adding the above resized frame to its parent
•
use layout hints
kLHintsBottom | kLHintsExpandX | kLHintsExpandY
when adding the bottom resized frame
to its parent
•set the above frame to be resized using SetFrame method; the second parameter should be kTRUE
You can see these rules in the code below:
// Create horizontal splitter
fVf = new TGVerticalFrame(fMain,10,10);
fH1 = new TGHorizontalFrame(fVf,10,10, kFixedHeight);
fH2 = new TGHorizontalFrame(fVf,10,10);
fFtop = new TGCompositeFrame(fH1,10,10, kSunkenFrame);
fFbottom = new TGCompositeFrame(fH2,10,10,kSunkenFrame);
fLtop = new TGLabel(fFtop,"Top Frame");
fLbottom = new TGLabel(fFbottom,"Bottom Frame");
604 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
fFtop->AddFrame(fLtop, new TGLayoutHints(kLHintsLeft |
kLHintsCenterY,3,0,0,0));
fFbottom->AddFrame(fLbottom, new TGLayoutHints(kLHintsLeft |
kLHintsCenterY,3,0,0,0));
fH1->AddFrame(fFtop, new TGLayoutHints(kLHintsTop |
kLHintsExpandY | kLHintsExpandX,0,0,1,2));
fH2->AddFrame(fFbottom,new TGLayoutHints(kLHintsTop |
kLHintsExpandY | kLHintsExpandX,0,0,1,2));
fH1->Resize(fFtop->GetDefaultWidth(),fH1->GetDefaultHeight()+20);
fH2->Resize(fFbottom->GetDefaultWidth(),fH2->GetDefaultHeight()+20);
fVf->AddFrame(fH1, new TGLayoutHints(kLHintsTop | kLHintsExpandX));
TGHSplitter *hsplitter = new TGHSplitter(fVf);
hsplitter->SetFrame(fH1,kTRUE);
fVf->AddFrame(hsplitter,new TGLayoutHints(kLHintsTop |
kLHintsExpandX));
fVf->AddFrame(fH2, new TGLayoutHints(kLHintsBottom |
kLHintsExpandX | kLHintsExpandY));
For a vertical splitter the rules are:
•the parent of a vertical splitter must inherit from TGCompoziteFrame and must have a horizontal layout
•the left resized frame must have kFixedWidth option set
•use layout hints kLHintsLeft | kLHintsExpandY when adding the left resized frame to the parent
•
use layout hints
kLHintsRight|kLHintsExpandX |kLHintsExpandY
when adding the right resized frame to the
parent
•set the left frame to be resized using SetFrame method; the second parameter should be kTRUE
Next is a sample code for a vertical splitter:
// Create vertical splitter
fHf = new TGHorizontalFrame(fMain, 50,50);
fV1 = new TGVerticalFrame(fHf, 10,10, kFixedWidth);
fV2 = new TGVerticalFrame(fHf, 10,10);
fFleft = new TGCompositeFrame(fV1, 10,10, kSunkenFrame);
fFright = new TGCompositeFrame(fV2, 10,10, kSunkenFrame);
fLleft = new TGLabel(fFleft, "Left Frame");
fLright = new TGLabel(fFright, "Right Frame");
fFleft->AddFrame(fLleft, new TGLayoutHints(kLHintsLeft |
kLHintsCenterY,3,0,0,0));
fFright->AddFrame(fLright, new TGLayoutHints(kLHintsLeft |
kLHintsCenterY,3,0,0,0));
fV1->AddFrame(fFleft,new TGLayoutHints(kLHintsTop |
kLHintsExpandX | kLHintsExpandY,0,0,5,5));
fV2->AddFrame(fFright,new TGLayoutHints(kLHintsTop |
kLHintsExpandX | kLHintsExpandY, 0,0,5,5));
fV1->Resize(fFleft->GetDefaultWidth()+20, fV1->GetDefaultHeight());
fV2->Resize(fFright->GetDefaultWidth(), fV1->GetDefaultHeight());
fHf->AddFrame(fV1,new TGLayoutHints(kLHintsLeft | kLHintsExpandY));
splitter = new TGVSplitter(fHf,2,30);
splitter->SetFrame(fV1, kTRUE);
fHf->AddFrame(splitter,new TGLayoutHints(kLHintsLeft |
kLHintsExpandY));
fHf->AddFrame(fV2,new TGLayoutHints(kLHintsRight | kLHintsExpandX |
kLHintsExpandY));
25.8. WIDGETS IN DETAIL 605
25.8.14 TGCanvas, ViewPort and Container
When all display information cannot be presented in a window, the additional information must be found and made
visible. A
TGCanvas
is a frame containing two scrollbars (horizontal and vertical) and a viewport (
TGViewPort
).
The viewport acts as the window through which we look at the contents of the container frame. A
TGContainer
frame manages a content area. It can display and control a hierarchy of multi-column items, and provides the ability
to add new items at any time. By default it doesn’t map sub-windows, which are items of the container. In this
case sub-window must provide
DrawCopy
method, see for example
TGLVEntry
class. It is also possible to use option
which allows mapping sub-windows. This option has much slower drawing speed in case of more than 1000 items
placed in container. To activate this option the fMapSubwindows data member must be set to
kTRUE
(for example
TTVLVContainer class).
A scroll bar only is available when scrolling is necessary. It consists of three elements: a slider box and two directional
scroll arrows (buttons).
fCanvas = new TGCanvas(parent, w, h);
fContents = new TGListTree(fCanvas, kHorizontalFrame);
fContents->Associate(parent);
parent->AddFrame(fCanvas, new TGLayoutHints(kLHintsExpandX |
kLHintsExpandY));
// or
fCanvas = new TGCanvas(parent, w, h);
fContents = new TGListTree(fCanvas->GetViewPort(),100,100,
kHorizontalFrame);
fContents->SetCanvas(fCanvas);
fContents->Associate(parent);
fCanvas->SetContainer(fContents);
parent->AddFrame(fCanvas, new TGLayoutHints(kLHintsExpandX |
kLHintsExpandY));
The TGContainer class can handle the following keys:
F7, Ctnrl-Factivate a search dialog
F3, Ctnrl-Gcontinue to search
Endgo to the last item in container
Homego to the first item in container
PageUpnavigate up
PageDownnavigate down
arrow keysnavigate inside container
Return/Enterequivalent to double click of the mouse button
Contrl-Aselect all items
Spaceinvert selection.
25.8.15 Embedded Canvas
This class creates a
TGCanvas
in which a well known ROOT
TCanvas
is embedded. A pointer to the
TCanvas
can be
obtained via the GetCanvas() member function.
fEc1 = new TRootEmbeddedCanvas("ec1",fParent,100,100);
fParent ->AddFrame(fEc1, new TGLayoutHints(kLHintsExpandX |
kLHintsExpandY));
fEc2 = new TRootEmbeddedCanvas("ec2",fParent,100,100);
fParent ->AddFrame(fEc2, new TGLayoutHints(kLHintsExpandX |
kLHintsExpandY));
fEc1->GetCanvas()->SetBorderMode(0);
fEc2->GetCanvas()->SetBorderMode(0);
fEc1->GetCanvas()->SetBit(kNoContextMenu);
fEc1->GetCanvas()->Connect("ProcessedEvent(Int_t,Int_t,Int_t,TObject*)",
"MyClass",this,"HandleMyCanvas(Int_t,Int_t,Int_t,TObject*)");
606 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
To embed a canvas derived from a TCanvas do the following:
TRootEmbeddedCanvas *embed = new TRootEmbeddedCanvas(0, p, w, h);
// note name must be 0, not null string ""
Int_t wid = embed->GetCanvasWindowId();
TCanvas *myc = new TCanvas("myname",10,10,wid);
embed->AdoptCanvas(myc);
// the TCanvas is adopted by the embedded canvas and will be
// destroyed by it
25.9 The ROOT Graphics Editor (GED)
Everything drawn in a ROOT canvas is an object. There are classes for all objects, and they fall into hierarchies. In
addition, the ROOT has fully cross-platform GUI classes and provides all standard components for an application
environment with common ‘look and feel’. The object-oriented, event-driven programming model supports the modern
signals/slots communication mechanism. It handles user interface actions and allows total independence of interacting
objects and classes. This mechanism uses the ROOT dictionary information and the Cling the C++ Interpreter to
connect signals to slots methods.
Therefore, all necessary elements for an object-oriented editor design are in place. The editor complexity can be reduced
by splitting it into discrete units of so-called
object editors
. Any object editor provides an object specific GUI. The
main purpose of the ROOT graphics editor is the organization of the object editors’ appearance and the task sequence
between them.
25.9.1 Object Editors
Every object editor follows a simple naming convention: to have as a name the object class name concatenated with
‘
Editor
’ (e.g. for
TGraph
objects the object editor is
TGraphEditor
). Thanks to the signals/slots communication
mechanism and to the method
DistanceToPrimitive()
that computes a “distance’‘to an object from the mouse
position, it was possible to implement a signal method of the canvas that says which is the selected object and to which
pad it belongs. Having this information the graphics editor loads the corresponding object editor and the user interface
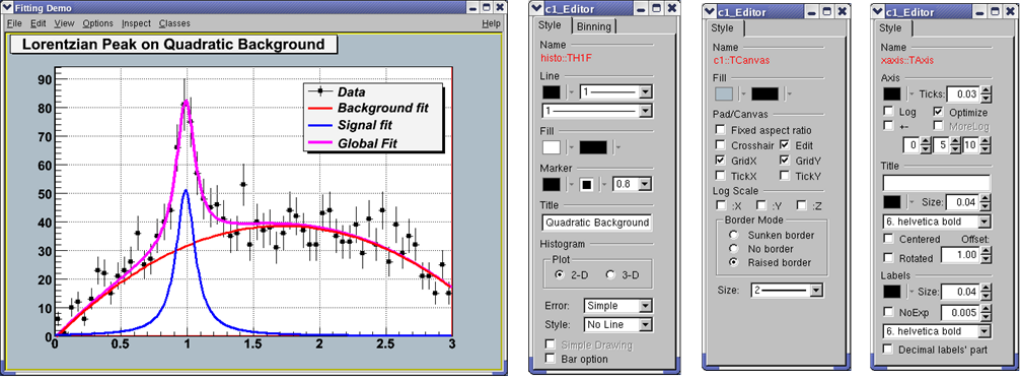
25.9. THE ROOT GRAPHICS EDITOR (GED) 607
is ready for use. This way after a click on ‘axis’—the axis editor is active; a click on a ‘pad’ activates the pad editor,
etc.
The algorithm in use is simple and is based on the object-oriented relationship and communication. When the user
activates the editor, according to the selected object
<obj>
in the canvas it looks for a class name
<obj>Editor
. For
that reason, the correct naming is very important. If a class with this name is found, the editor verifies that this class
derives from the base editor class
TGedFrame
. If all checks are satisfied, the editor makes an instance of the object
editor. Then, it scans all object base classes searching the corresponding object editors. When it finds one, it makes an
instance of the base class editor too.
Once the object editor is in place, it sets the user interface elements according to the object’s status. After that, it is
ready to interact with the object following the user actions.
The graphics editor gives an intuitive way to edit objects in a canvas with immediate feedback. Complexity of some
object editors is reduced by hiding GUI elements and revealing them only on users’ requests.
An object in the canvas is selected by clicking on it with the left mouse button. Its name is displayed on the top of the
editor frame in red color. If the editor frame needs more space than the canvas window, a vertical scroll bar appears
for easy navigation.
Figure 25.4: Histogram, pad and axis editors
25.9.2 Editor Design Elements
The next rules describe the path to follow when creating your own object editor that will be recognized and loaded by
the graphics editor in ROOT, i.e. it will be included as a part of it.
(a) Derive the code of your object editor from the base editor class TGedFrame.
(b)
Keep the correct naming convention: the name of the object editor should be the object class name concatenated
with the word ‘Editor’.
(c) Provide a default constructor.
(d) Use the signals/slots communication mechanism for event processing.
(e)
Implement the virtual method
SetModel(TObject *obj)
where all widgets are set with the current object’s
attributes. This method is called when the editor receives a signal from the canvas saying that an object is the
selected.
(f)
Implement all necessary slots and connect them to appropriate signals that GUI widgets send out. The GUI
classes in ROOT are developed to emit signals whenever they change a state that others might be interested. As
we noted already, the signals/slots communication mechanism allows total independence of the interacting classes.
25.9.2.1 Creation and Destruction
GED-frames are constructed during traversal of class hierarchy of the selected object, executed from method
TGedEditor::SetModel()
. When a new object of a different class is selected, the unneeded GED-frames are cached in
memory for potential reuse. The frames are deleted automatically when the editor is closed.
608 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
Note: A deep cleanup is assumed for all frames put into the editor. This implies:
•do not share the layout-hints among GUI components;
•do not delete child widgets in the destructor as this is done automatically.
25.9.2.2 Using Several Tabs
Sometimes you might need to use several tabs to organize properly your class-editor. Each editor tab is a resource
shared among all the class-editors. Tabs must be created from the constructor of your editor-class by using the method:
TGVerticalFrame* TGedFrame::CreateEditorTabSubFrame(const Text_t *name),
It returns a pointer to a new tab container frame ready for use in your class. If you need to hide/show this frame
depending on the object’s status, you should store it in a data member. See for examples: TH1Editor,TH2Editor.
25.9.2.3 Base-Class Editors Control
Full control over base-class editors can be achieved by re-implementing virtual method void
TGedFrame::ActivateBaseClassEditors(TClass
*cl)
. It is called during each compound editor rebuild and the default implementation simply offers all base-classes to
the publishing mechanism.
To prevent inclusion of a base-class into the compound editor, call:
void TGedEditor::ExcludeClassEditor(TClass* class, Bool_t recurse)
Pointer to the compound GED-editor is available in TGedFrame‘s data-member:
TGedEditor *fGedEditor
Ordering of base-class editor frames follows the order of the classes in the class hierarchy. This order can be changed
by modifying the value of
TGedFrame
’s data member
Int_t fPriority
. The default value is 50; smaller values move
the frame towards to the top. This priority should be set in the editor constructor.
25.10 Drag and Drop
Drag and Drop support is introduced for Linux (via Xdnd - the drag and drop protocol for X window system) and for
Windows (via Clipboard). Users can selects something in ROOT with a mouse press, drags it (moves the mouse while
keeping the mouse button pressed) and releases the mouse button someplace else. When the button is released the
selected data is “dropped” at that location. This way, a histogram from an opened ROOT file in the browser can be
dragged to any TCanvas.
A script file from the browser can be dropped to a TGTextView or TGTextEdit widget in TGTextEditor.
On Linux, it is possible to drag objects between ROOT and an external application. For example to drag a macro file
from the ROOT browser to the Kate editor. On Windows, drag and drop works only within a single ROOT application
(for the time being), but works also from Windows Explorer to TCanvas ot to TGTextEdit.
25.10. DRAG AND DROP 609
25.10.1 Drag and Drop Data Class
The Drag and Drop Cata class
TDNDdata
is used to describe and handle the transferred data during an drag and drop
operation. It consists of:
Atom_t fDataType: atom describing the data type.
Atom_t fAction: atom describing the action (copy, move, link); currently, only copy is used.
void *fData: actual data (buffer).
Int_t fDataLength: length (size) of data buffer.
Currently two types are recognized by ROOT: “application/root” for ROOT objects and “text/uri-list” for path/filenames
(uri comes from Unique Resource Identifier). A text/uri-list is a standard file listing format for drag and drop that
specifies a list of files (each file per line). Each line ends with a carriage return and newline
rn
. File names have to be
valid, url-encoded URI’s as shown below:
file://localhost/usr/bin/opera or file://localhost/c:/programs/myfile.txt
file://server/data/software.xml or http://root.cern.ch/root/images/ftpstats.gif
The atoms and the drag and drop manager (
TGDNDManager
), are created at the main application creation time (class
TGMainFrame).
Setting a Drag Source - first, create and fill data:
TH1F *h = new TH1F("h","h",1000,-3,3);
h->FillRandom("gaus",50000);
TDNDdata data;
TBufferFile *buf = new TBufferFile(TBuffer::kWrite);
buf->WriteObject(h);
data.fData = buf->Buffer();
data.fDataLength = buf->Length();
data.fDataType = gVirtualX->InternAtom("application/root");
Then, set a GUI widget as DND Source, and associate the data. Source widget can be any class inheriting from
TGFrame.
SourceWidget=new TGIcon(this,gClient->GetPicture("f1_s.xpm"),32,32);
SourceWidget->SetDNDSource(kTRUE);
SourceWidget->SetDNDdata(&data);
Setting A Drop Target - set the widget as DND Target, and set the DND types it must be aware of: as
SourceWidget
,
TargetWidget can be any class inheriting from TGFrame.
TargetWidget = new TRootEmbeddedCanvas("Target",this,700,400);
TargetWidget->SetDNDTarget(kTRUE);
gVirtualX->SetDNDAware(TargetWidget->GetId(),
gDNDManager->GetTypeList());
gDNDManager->GetTypeList() returns the list of types recognized by ROOT.
Note that the Widget may receive drag and drop messages with drop-data it does not understand, and thus it should
only accept drops of the proper type.
25.10.2 Handling Drag and Drop Events
Once a widget has been set as DND Target, it has to handle Drag and Drop events.
Atom_t HandleDNDenter(Atom_t *typelist)
- this method is used to handle a drag operation entering the widget.
The typelist parameter is the list of types the data contains. If the list contains one type the widget understands, it
should return this type to notify the manager that the drop would be accepted, i.e. :
610 CHAPTER 25. WRITING A GRAPHICAL USER INTERFACE
for (int i=0; typelist[i] != kNone; ++i) {
if (typelist[i] == gVirtualX->InternAtom("application/root"))
// accept "application/root" DND type
return typelist[i];
}
// other type not accepted
return kNone;
Atom_t HandleDNDposition(Int_t x,Int_t y,Atom_t action,Int_t xroot, Int_t yroot)-
this method should
be used to handle the drag position in widget coordinates (x,y) or in root coordinates (xroot,yroot).
// get the pad over which the cursor is
TPad *pad = fCanvas->Pick(x, y, 0);
if (pad) {
pad->cd();
gROOT->SetSelectedPad(pad);
}
return action;
Bool_t HandleDNDdrop(
TDNDdata *data
) - this is the place where the widget actually receives the
data. First, check the data format (see description of **
TDNDData‘** - Drag and Drop data class) and
then use it accordingly. In the case of ROOT object, here is an example of how to retrieve it:
if (data->fDataType == gVirtualX->InternAtom("application/root")) {
TBufferFile buf(TBuffer::kRead, data->fDataLength,
(void *)data->fData);
buf.SetReadMode();
TObject *obj = (TObject *)buf.ReadObjectAny(TObject::Class());
if (obj->IsA()->GetMethodAllAny("Draw"))
obj->Draw();
}
In the case of URI/list, the use is:
if (data->fDataType == gVirtualX->InternAtom("text/uri-list")) {
TString sfname((char *)data->fData);
TUrl uri(sfname.Data());
if (sfname.EndsWith(".jpg")
TImage *img = TImage::Open(uri.GetFile());
}
Bool_t HandleDNDleave()
is used if a specific action has to be performed when the drag operation leaves the widget.
Chapter 26
ROOT/Qt Integration Interfaces
26.1 Qt-ROOT Implementation of TVirtualX Interface (BNL)
Qt-ROOT implementation of
TVirtualX
(Qt-layer) is to provide a convenient way of creating the complex end-user
applications that require both Qt GUI and ROOT features. The primary goal is to allow “embedding” the ROOT
classes like
TCanvas
and
TPad
into the arbitrary Qt widgets and using it seamlessly with other Qt-based components
and Qt-based third party libraries.
TGQt
ROOT class, a Qt-based implementation of
TVirtualX
interface is an optional
ROOT component. The implementation was developed and is supported by the collaboration at Brookhaven National
Laboratory.
26.1.1 Installation
26.1.1.1 Qt Package Installation and Configuration
ROOT Qt-layer requires a “good” properly configured Qt package version. To install it, one has to:
1.
Make sure the adequate version of Qt system. Even though Qt ROOT implementation theoretically can work with
any Qt release version 3.xx, we found the earlier versions of the package not reliable and recommend installing
the Qt version 3.3 or higher. The package was tested against Qt 4.3 also (Qt 4.3 and higher versions contain
some features introduced by TrollTech to back the ROOT applications).
2.
Check the Qt package configuration and its compilation options are consistent with those used to compile and
install ROOT alone. For Qt 3.x, we recommend configuring Qt as follows:
./configure -thread -no-xft -qt-gif -no-exeptions
I.e. one is required to build the Qt version with the “
thread
” support and with “
no exceptions
”. Generally, you are
free to select the remaining Qt options like the types of the different image formats provided etc. You can check the Qt
installation parameters by looking up the file:
more $QTDIR/config.status
No special flag for Qt 4.3 build and higher have been set yet to make QtRoot working.
3.
Attention. The Qt port for 4.3 and above versions should be considered as an experimental one. Most examples
in this manual are for Qt version 3.3 and they need to be adjusted for Qt 4.3.x.
26.1.1.2 Qt-layer Installation
The Qt-layer is included into the ROOT distribution kit. To install it one has to configure ROOT. The installation
does not change any other components of the ROOT package. It produces several extra-shared libraries that may be
dynamically loaded into the ROOT session at start time with the regular ROOT plug-in mechanism to replace the
“native” GUI interface. To install Qt-layer one should follow the ROOT installation procedure providing the QTDIR
environment variable points to the proper version of Qt system. Many Linux flavors come with the pre-installed Qt.
May sure you are not going to pick the obsolete version.
611
612 CHAPTER 26. ROOT/QT INTEGRATION INTERFACES
% cd root
% ./configure <target> --enable-qt
% gmake
% gmake install
26.1.1.3 Qt Main C++ Classes Cling Dictionary
The ROOT Cling dictionary allows to call the Qt main classes directly from the ROOT command prompt is an optional
component and it is not created during the “Qt-layer installation”. To build / re-build the Qt main classes ROOT
dictionary one can invoke the make
% cd root
% gmake qtcint
The dictionary contains so-called Qt main classes as defined by TrollTech on the Web page: http://doc.trolltech.com/3.
3/mainclasses.html. The dictionary is NOT loaded automatically and it should be loaded by the user ROOT macro as
needed.
26.1.1.4 Qt-layer Configuration
Any ROOT-based application should be configured to use Qt-layer using ROOT “Environment Setup”. The correct
QTDIR
environment variable to locate the proper version of Qt package should be provided as well. There are several
ways to customize the ROOT setup environment to activate Qt-layer.
Look up at $ROOTSYS/etc/system.rootrc. Find there the definition of Gui.Backend and Gui.Factory:
# GUI specific settings
Gui.Backend: native
Gui.Factory: native
Now you can either edit the file
$ROOTSYS/etc/system.rootrc
or provide your own custom
.rootrc
redefine the
options:
# GUI specific settings
Gui.Backend: qt
Gui.Factory: qt
If you need to switch often from native layer to qt one back and force you may find convenient to define the type of
GUI using some external environment variable defining options indirectly:
# GUI specific settings
Gui.Backend: $(GUI)
Gui.Factory: $(GUI)
The last step is to make sure your
LD_LIBRARY_PATH
variable point to the
$QTDIR/lib
directory. Optionally, you can
define the Qt Widget “look and feel” using the option
Gui.Style
option. The number of different styles to choose
from is defined by your local Qt installation. Usually you can choose from “
window
”, “
motif
”, “
cde
”, “
motifplus
”,
“
platinum
”, “
sgi
”, “
compact
”, “
windowsxp
”, “
aqua
” or “
macintosh
”. For example, the option defined below will force
the “windows” look and feel on any platform.
# Qt GUI style setting
Gui.Style: windows
The default style is so-called “native” style. That is defined by the current application environment.
26.1.2 Applications
As soon as you customize ROOT “Environment Setup” to use Qt-layer you can start any ROOT session or stand-alone
ROOT-based applications and . . . even though your applications will be using the Qt package you should not see any
difference. This merely means if the only thing you want to do is just use ROOT or some ROOT-based stand-alone
application “as is” then you probably do not need to switch to Qt-layer and should skip this section entirely. It is
recommended you communicate the lower graphical layer via the generic
TVirtualX
interface provided by the global
gVirtualX .
26.1. QT-ROOT IMPLEMENTATION OF TVIRTUALX INTERFACE (BNL) 613
26.1.2.1 Qt-based ROOT Applications
“ROOT application” is the application that either instantiates the ROOT
TApplication
/
TRint
class and enters
the ROOT event loop or is the shared library that can be loaded into the already running ROOT application via
TSystem::Load
method or via ROOT plug-in mechanism. You must neither initialize Qt
QApplication
nor enter the
Qt event loop. Qt-layer takes care about these two steps. What you need is to instantiate the Qt object of your choice
and to keep playing ROOT rules.
#include <TRint.h>
#include <qpushbutton.h>
int main( int argc, char **argv ) {
// Create an interactive ROOT application
TRint *theApp = new TRint("Rint", &argc, argv);
// Create Qt object within ROOT application
QPushButton hello( "Hello world!",0);
hello.resize( 100,30 );
hello.show();
// and enter the ROOT event loop...
theApp->Run();
}
Under UNIX, you can build the stand-alone ROOT HelloWord Qt-based application with the command
g++ `root-config --cflags --glibs`-I$QTDIR/include -L$QTDIR/lib
-lqt-mt HelloWord.cxx -o HelloWord
26.1.2.2 ROOT-based Qt Applications
“Qt application” is the application that either instantiates the Qt
QApplication
and enters the Qt event loop or is the
shared library that can be loaded into the already running Qt application via Qt plug-in mechanism. You must neither
initialize ROOT
TApplication
/
TRint
nor enter the ROOT event loop. Qt-layer takes care about both of these steps.
What you need is just to instantiate the embedded and regular ROOT objects of your choice and keep playing Qt rules.
ROOT-based Qt applications treat the “native” style of the ROOT
Gui.Backend
and
Gui.Factory
parameters as “qt”.
For example,
// Minimal ROOT based Qt example
#include <qapplication.h>
#include "TGraph.h"
#include "TQtWidget.h"
#include "TCanvas.h"
int main( int argc, char **argv ) {
QApplication *app = new QApplication(argc, argv);
TQtWidget *MyWidget= new TQtWidget(0,"MyWidget");
// Create any other Qt-widget here
MyWidget->show();
MyWidget->GetCanvas()->cd();
TGraph *mygraph;
float x[3]={1,2,3};
float y[3]={1.5,3.0,4.5};
mygraph = new TGraph(3,x,y);
mygraph->SetMarkerStyle(20);
mygraph->Draw("AP");
MyWidget->GetCanvas()->Update();
app->exec();
return 0;
}
The code above can be converted into the running application using qmake, TrollTech provided, build utility. As soon
as you have qmake project file HelloCanvas.pro:
614 CHAPTER 26. ROOT/QT INTEGRATION INTERFACES
# Automatically generated by qmake (1.07a) Sun Jun 26 02:03:47 2005
# Adjusted by hand to include $ROOTSYS/include/rootcling.pri file
TEMPLATE = app thread
CONFIG -= moc
INCLUDEPATH += .
# include "by hand" the qmake include file from
# ROOT distribution to define
# 1. include path to the ROOT system header files
# 2. the list of the ROOT shared libraries to link
# Qt application against of
# 3. qmake rules to generate ROOT/Cint dictionaries
include("$(ROOTSYS)/include/rootcling.pri")
# Input
SOURCES += HelloCanvas.cxx
You can get the running ROOT-based Qt application with the Unix shell commands:
qmake HelloCanvas.pro
make
HelloCanvas
26.1.2.3 Qt Project for Creation of ROOT Shared Libraries with Qt Components and ROOT Dictio-
naries
It is possible and desirable to create the ROOT-based Qt application with TrollTech provided qmake utility. To do
that one should include one qmake include file, namely,
$ROOTSYS/include/rootcling.pri
with one extra line in the
project file (as the example above has revealed). The include file defines all necessary components one needs to compile
and link the healthy Qt application against of the ROOT shared libraries. It contains the qmake rules to create the
ROOT/Cling dictionary from the list of the provided header files.
For example, we may convert the stand-alone Qt-based ROOT application above into C++ class with
RootCint
dictionary, that one loads into the interactive ROOT session and invokes interactively. This task requires four simple
files.
1. Class dictionary definition file LinkDef.h:
#ifdef __CLING__
#pragma link off all globals;
#pragma link off all classes;
#pragma link off all functions;
#pragma link C++ class TMyQButton;
#endif
2. Class header file TMyQButton.h:
#ifndef ROOT_TMyQButton
#define ROOT_TMyQButton
#include "Rtypes.h"
class QPushButton;
class TVirtualPad;
class TMyQButton {
private:
QPushButton *fMyButton;
26.1. QT-ROOT IMPLEMENTATION OF TVIRTUALX INTERFACE (BNL) 615
public:
TMyQButton(const char*name="");
virtual ~TMyQButton();
void SetSize(UInt_t w, UInt_t h);
void Show(Bool_t show=kTRUE);
void SetText(const char *text);
void SetOn(Bool_t on=kTRUE);
void SetStyle(const char * style);
};
#endif
3. Class implementation file TMyQButton.cxx:
#include "TMyQButton.h"
#include <qpushbutton.h>
// This class allow you to create and manipulate the QPushButton
// interactively
TMyQButton::TMyQButton(const char *name) {
// Create Qt QPushButton interactively
fMyButton = new QPushButton(name,0);
}
TMyQButton::~TMyQButton() { delete fMyButton; }
void TMyQButton::SetSize(UInt_t w, UInt_t h) {
// Resize the Qt button
fMyButton->resize(w,h);
}
void TMyQButton::Show(Bool_t show) {
// Show / hide the button
if (show) fMyButton->show();
else fMyButton->hide();
}
void TMyQButton::SetText(const char *text) {
// Set / change the button text
fMyButton->setText(text);
}
void TMyQButton::SetOn(Bool_t on) {
fMyButton->setOn(on);
}
void TMyQButton::SetStyle(const char * style) {
// Set button's look and feel
// The possible styles are defined by the local Qt installation.
// For example the possible style can be: "window","motif",
// "cde","sgi","motifplus","platinum","compact","windowsxp",
// "aqua","macintosh"
fMyButton->setStyle(style);
}
4. qmake project file MyQButton.pro:
TEMPLATE = lib dll thread
# Input
HEADERS += TMyQButton.h
SOURCES += TMyQButton.cxx
CREATE_ROOT_DICT_FOR_CLASSES = $$HEADERS LinkDef.h
include("$(ROOTSYS)/include/rootcling.pri")
At this point, you are ready to produce the class-shared library with the ROOT/Cling dictionary by invoking two shell
commands (as above):
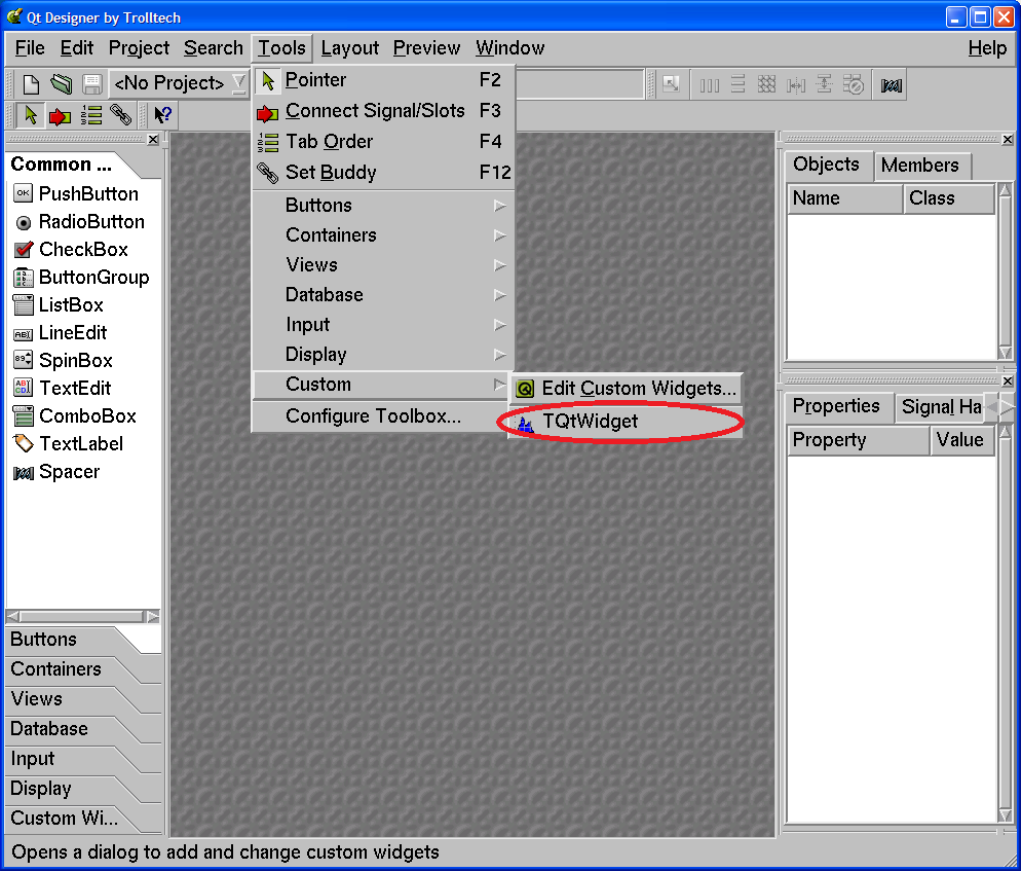
616 CHAPTER 26. ROOT/QT INTEGRATION INTERFACES
qmake MyQButton.pro
make
In addition, get you class into the interactive Root session:
root[] gSystem->Load("lib
Please, pay your attention that class implementation does not contain any Qt system initialization call. Since
the above example is a ROOT application, do not forget, one needs the
.rootrc
file to assign “
qt
” value for the
optionsGui.Backend and Gui.Factory.
Note: Do not mix the ROOT GUI and Qt GUI API within the same class implementation.
26.1.2.4 Using Qt “Designer” to Create Qt GUI with Embedded ROOT Objects
Qt package is equipped with Qt designer - a powerful tool to create the high quality, robust GUI interfaces for your
applications. It is possible and desirable to use this utility to create the ROOT-based Qt GUI. To do that one should
add the
$ROOTSYS/include/rootcling.pri
in the project file generated by designer and configure Qt designer to use
the so-called “custom widget” defined by
$ROOTSYS/include/TQtWidget.cw
. The file defines the custom
TQtWidget
Qt widget to back the embedded
TCanvas
objects. To customize your designer start
designer
and select “Edit Custom
Widget” menu:
Open “Edit Custom Widget” dialog and load the
TQtWidget
(“embedded”
TCanvas
) widget definition into the designer.
One should do this at once. Designer will remember the last configuration and will be restoring it for all subsequent
designer sessions.
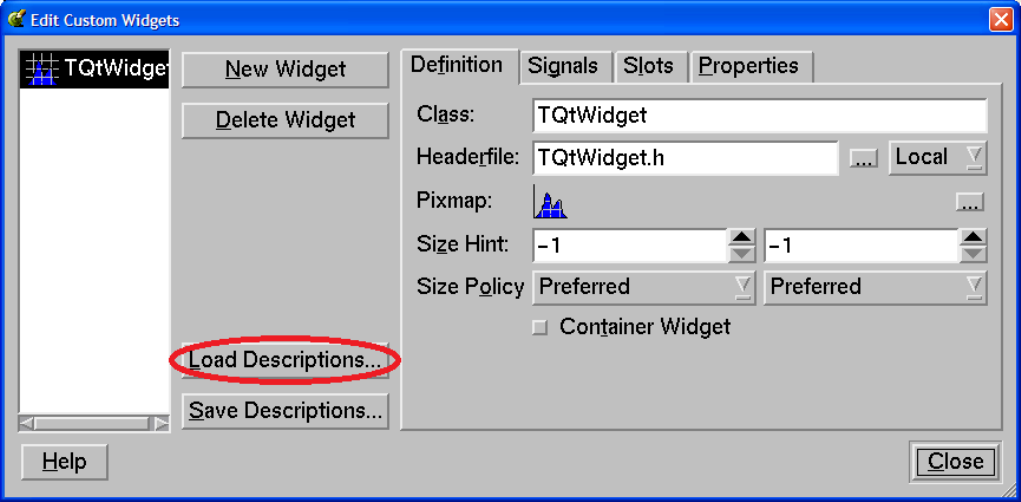
26.1. QT-ROOT IMPLEMENTATION OF TVIRTUALX INTERFACE (BNL) 617
Now, you can create your shining GUI interface that contains
TCanvas
/
TPad
object with all features of these famous
ROOT classes.
We strongly recommend you to read the “Quick Start” section of the Qt designer manual http://doc.trolltech.com/3.
3/designer-manual.html. One can find further information, the examples of the working ROOT-based Qt projects
including all examples of this section as well as the list of the references and publications on the Qt project Web site
http://root.bnl.gov
26.1.2.5 Using Qt Class Library from the ROOT C++ Interpreter
Since the Qt package is a regular C++ class library to use it within ROOT C++ interpreter environment one should
either load the dedicated RootCint dictionary or apply ACLiC mode.
For example, the following ROOT interactive session is to popup the “Open File” Qt dialog box and print out the file
name selected by the user via the dialog.
root[] gSystem->Load("qtcint");
root[] cout << QFileDialog::getOpenFileName() << endl;
The ROOT session:
root[] gSystem->Load("qtcint");
root[] QPrinter p;
root[] p.setup(); // Display the Qt "Setup printer" dialog box
root[] Int_t id = gPad->GetPixmapID();
root[] QPixmap *pix = (QPixmap *)(TGQt::iwid(id));
root[] QPainter pnt(&p);
root[] pnt.drawPixmap(0,0,*pix);
is to display the Qt “Setup Printer” dialog and use QPrinter object to print the current
TPad
image to the selected
printer. To use the more complex Qt-related code one is advised to apply “ACLiC - Automatic Compiler of Libraries
for Cling” (see Cling the C++ Interpreter). For example:
#ifndef __CLING__
# include <qfiledialog.h>
# include <qstringlist.h>
# include <qstring.h>
#endif
void FileDialog() {
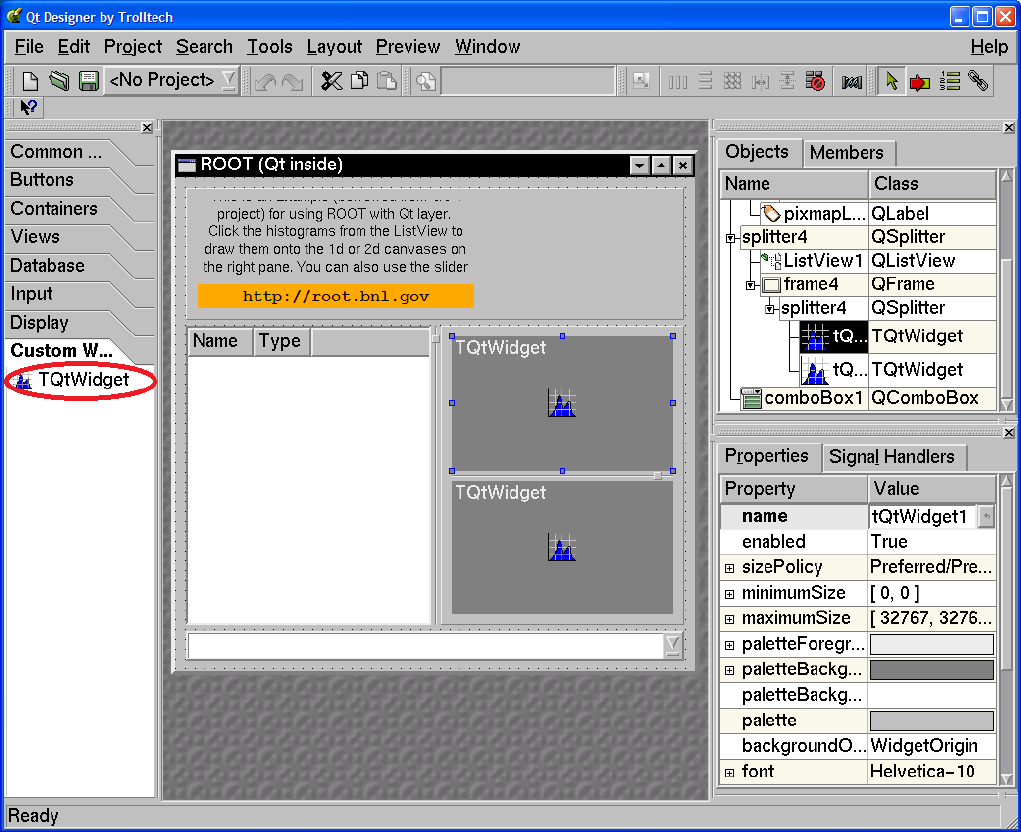
618 CHAPTER 26. ROOT/QT INTEGRATION INTERFACES
26.1. QT-ROOT IMPLEMENTATION OF TVIRTUALX INTERFACE (BNL) 619
// This is small AClIC wrapper to use Qt 3.3 QFileDialog class
// See: http://doc.trolltech.com/3.3/qfiledialog.html#getOpenFileNames
// To use, invoke ACLiC from the ROOT prompt:
// root [] .x FileDialog .C++
QStringList files = QFileDialog::getOpenFileNames ();
QStringList::Iterator it = files.begin();
while ( it != files.end() ) {
printf ("Next file selected: %sn", (const char *)(*it));
++it;
}
}
With the ROOT ACLiC session:
root [0] .x FileDialog.C++
Info in <TUnixSystem::ACLiC>: creating shared library macros/./FileDialog_C.so
Next file selected: macros/QtFileDialog.C
Next file selected: macros/QtMultiFileDialog.C
Next file selected: macros/QtMultiFileDialog_C.so
Next file selected: macros/QtPrintDialog.C
Next file selected: macros/QtPrintDialog_C.so
the Qt generated “Open File Dialog” pops up and prints out the list of the selected files.
26.1.3 TQtWidget Class, Qt Signals / Slots and TCanvas Interface
TQtWidget
is a
QWidget
with the
QPixmap
double buffer. It is designed to back the ROOT
TCanvasImp
class interface
and it can be used as a regular Qt Widget to create Qt-based GUI with the embedded
TCanvas
objects. It was
mentioned the class can used as a “custom widget” to create the advanced GUI with the TrollTech “designer” utility.
To do that
TQtWidget
class can emit the set of the “Qt signals” and it is equipped with the collection of the dedicated
“Qt slots”.
26.1.3.1 TQtWidget Public Qt Slots
TQtWidget
class inherits all slots of its base QWidget class (see: http://doc.trolltech.com/3.3/qwidget.html). In
addition, it is in possession of two groups of the dedicated slots.
620 CHAPTER 26. ROOT/QT INTEGRATION INTERFACES
virtual void cd();
virtual void cd(int subpadnumber);
Make the associated
TCanvas
/
TPad
the current one, the proxy interface to the embedded
TCanvas::cd()
and
TCanvas::cd(int subpadnumber) methods.
virtual bool Save(const QString &fileName) const
virtual bool Save(const char *fileName) const
virtual bool Save(const QString &fileName,const char *format,
int quality=60)const
virtual bool Save(const char *fileName,const char *format,
int quality=60)const
The slots are to save the double buffer of the
TQtWidget
object using the default or specified save format. The default
save format is defined either by the “known” file extension or by the “default” file format.
The default format can be changed by
TQtWidget::SetSaveFormat
method and it is set to be “
PNG
” at the class
constructor.
26.1.3.2 TQtWidget Qt Signals
The class object emits the different signals that can be used to create the sophisticated GUI applications.
The signal
CanvasPainted()
is emitted to notify the GUI that the double buffer of the widget has been filled and
buffer has been painted onto the screen. In the other words, this signal means that all
TObject
objects of the embedded
TCanvas have been visualized on the screen. The signal:
Saved(bool ok)
is emitted to notify the GUI that a TCanvas has been saved into the file:
RootEventProcessed(TObject *selected, unsigned int event, TCanvas *c)
This signal notifies the Qt framework that the Qt mouse/keyboard event has been process by ROOT. The
signal is disabled by default, i.e. the connected slot is not called unless the signal is explicitly enabled with
TQtWidget::EnableSignalEvents method.
For example, to create a custom response to the mouse crossing of a
TCanvas
, you need to connect the
RootEventProsecced signal with your qt slot. The next piece of the code demonstrates that:
connect(tQtWidget,SIGNAL(RootEventProcessed(TObject *,
unsigned int, TCanvas *)),
this,SLOT(CanvasEvent(TObject *, unsigned int, TCanvas *)));
...
void qtrootexample1::CanvasEvent(TObject *obj, unsigned int event,
TCanvas *)
{
TQtWidget *tipped = (TQtWidget *)sender();
const char *objectInfo = obj->GetObjectInfo(tipped->GetEventX(),
tipped->GetEventY());
QString tipText ="You have ";
if (tipped == tQtWidget1)
tipText +="clicked";
else
tipText +="passed";
tipText += " the object <";
tipText += obj->GetName();
tipText += "> of class ";
tipText += obj->ClassName();
tipText += ":";
tipText += objectInfo;
QWhatsThis::display(tipText)
}
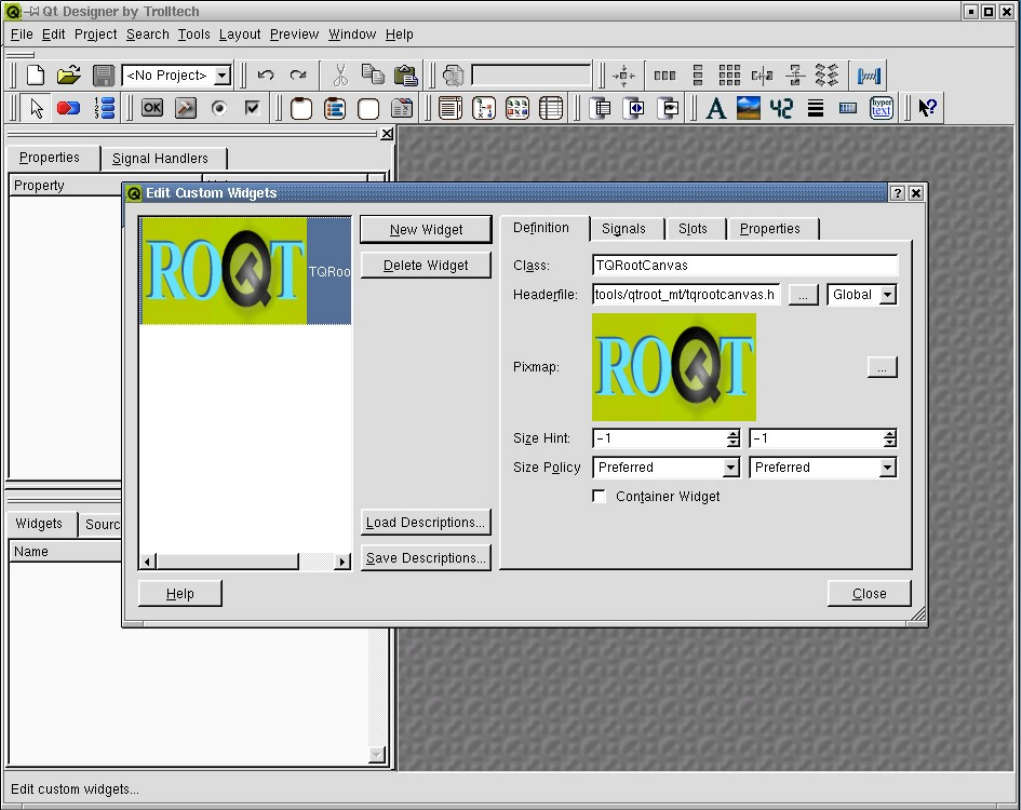
26.2. GSI QTROOT 621
26.2 GSI QtROOT
The Qt Interface developed at Darmstadt GSI is a lightweight interface that enables the user to write a Qt 3 application,
which can use ROOT. The Native Qt 4 support is planned and will be available in the near future. Furthermore,
existing Qt 3 Application can use this interface to have almost full access to the Root functionality (see “Create the
Main file for the project” below). Using this interface a full access to both ROOT and Qt widgets is possible in one
application.
An Embedded Root canvas can be set inside any Qt widget by C++ calls or using the Qt designer. To use the Qt 3.x
designer to make ROOT applications with Qt GUI’s follow the steps described below:
1) Add the TQRootCanvas to the Qt Designer:
•Start the designer
•In the designer menu choose tools->custom->Edit Custom Widget
•In the Edit Custom Widget window choose “Load Description”
•From GSI Qt-Root interface directory load the file “TQRootCanvas.cw”
Now you will see the
TQRootCanvas
in the Class field, you will also see all other parameters, signals, slots and properties
of the TQRootCanvas.
Now we are ready use the TQRootCanvas within the Qt 3.x designer.
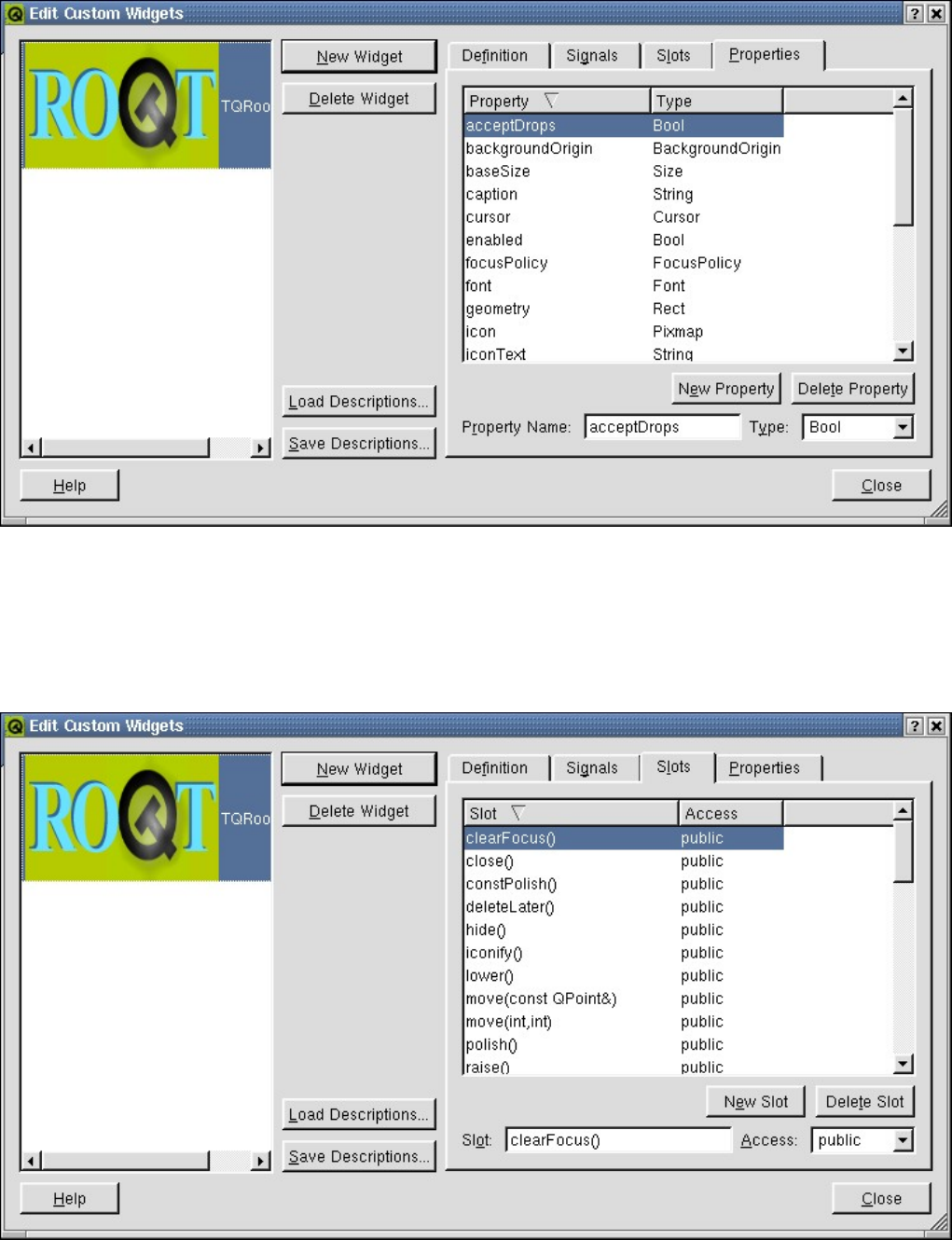
622 CHAPTER 26. ROOT/QT INTEGRATION INTERFACES
26.2. GSI QTROOT 623
26.2.1 Create a New Project in the Designer
1). Choose “File->New”
2). Select C++ Project
3). Create the Project in a directory of your choice.
4). In the project settings (Project->Setting from the designer main window) select the C++ tab. Add ROOT and
GSI Qt-Root libraries into the Libs entry field. For example:
-L(ROOTSYS)/lib -lCore -lCint -lHist -lGraf -lGraf3d -lGpad -lTree -lRint -lPostscript -lMatrix
-lPhysics -lnsl -lm -ldl -rdynamic -lqtgsi
Add $(ROOTSYS)/include into Includepath entry field.
These setting will be saved in project.pro file and qmake will generate the Makefile according to them.
Now you can create your own widgets in the designer and add them to the project.
26.2.2 main()
The main file should look like:
#include "TQtApplication.h"
#include "TQtRootApplication.h"
#include "MyWidget1.h"
int main( int argc, char ** argv ){
TQRootApplication a( argc, argv, 0);
TQApplication app("uno",&argc,argv);
MyWidget1 *w = new Mywidget1;
w->show();
a.connect(&a, SIGNAL(lastWindowClosed()), &a, SLOT(quit()));
return a.exec();
}
624 CHAPTER 26. ROOT/QT INTEGRATION INTERFACES
Chapter 27
Automatic HTML Documentation
THtml
is ROOT’s documentation engine. It can be used to document your classes in a reference guide, and to convert
your text or source files to HTML.
27.1 Reference Guide
The Reference Guide for the ROOT classes at http://root.cern.ch/root/html/ has been generated by ROOT’s
THtml
class. Just as for ROOT’s classes, it can generate (and update) a reference guide for your classes, too. You document
your classes using source code comments. All comments will be automatically put into a
<pre></pre>
environment to
keep the indentation and line length. You can write “raw” HTML by enclosing comments in the keywords
Begin_Html
and End_Html.
To generate documentation for the class TObject you could run the following commands:
root[] THtml h
root[] h.SetInputDir("$(ROOTSYS)");
root[] h.MakeClass("TObject");
root[] h.CreateJavascript();
root[] h.CreateStylesheet();
The comments following the first comment of the form //____________________, before any method, is
assumed to be the
class description
. As with any other documentation part, it has to be a continuous block of
comments.
Any documented class will have an
class index entry
in the
ClassIndex.html
, showing their name with a link to
their documentation page and a miniature description. This description for e.g. the class
MyClass
has to be given in
MyClass’s header file as documentation.
Amethod description block starts immediately after ‘{’ and looks like this:
void TWorld::HelloWorldFunc(string *text)
{
// This is a documentation example of the function TWorld::HelloWorldFunc
helloWorld.Print(text);
}
Like in a class description block, everything until the first non-commented line is considered as a valid member function
description block.
Data members are documented by putting a C++ comment behind their declaration in the header file, e.g.
Int_t fIAmADataMember; // this is a data member
When documenting a class,
THtml
creates both a “beautified” version of the source file and a web page containing the
class documentation. The documentation also shows the
author
and a
copyright statement
. This information is
extracted from the source file. The author can be in the format
625
626 CHAPTER 27. AUTOMATIC HTML DOCUMENTATION
// Author: Enrico Fermi
for people that have an entry in CERN’s XWho database, and for those who have not:
// Author: Enrico Fermi <mailto:enrico@fnal.gov>
The copyright statement is introduced by the string “* Copyright” inside a comment.
You should read the class reference page at http://root.cern.ch/root/html/THtml.html to learn about all of
THtml
’s
features.
27.1.1 Product and Module Documentation
For
THtml
, a product like ROOT is a combination of several modules. It can include user-provided document for
both products and modules. The name of the product can be set by calling
THtml::SetProductName()
. By default,
the documentation is searched for in the
doc/
subdirectory of the source tree, and in the
../doc
directory, relative
to the directory of first source file of a module. This can be set by calls to
THtml::SetProductDocDir()
and
THtml::SetModuleDocPath().
The documentation is generated as an index page with links to further files. This index page includes the file
index.txt
converted to HTML (via
THtml::Convert()
) or the file index.html (without conversion to HTML, of course), if any of
these files exist. The index page will also contain a list of links to all files in the directory that end on
.html
or
.txt
.
Files ending on
.txt
will be converted to HTML before they are copied to the output directory. For each file, the
link’s text will be the file name without extension, with underscores replaced by spaces.
You can see an example of the module documentation including links, the corresponding
index.html
, and the module
class index at http://root.cern.ch/root/html/HIST_Index.html.
27.2 Converting Sources (and Other Files) to HTML
THtml can take a file (C++ or text) and convert it to HTML. There are two main use cases:
The output of a
macro
converted to HTML will almost look like the beautified source file of a class reference. The
Begin_Html/End_Html
keywords are supported; comments, strings, and keywords are colored like in
THtml
’s output
for source code.
The macro
Event.cxx
in
$ROOTSYS/test
can be seen as an example of documented ROOT macros at http://root.cern.
ch/root/html/examples/Event.cxx.html
THtml::Convert()
converts a single text file to HTML. For example, it can be run on a change log. Each known class
name will be linked to its documentation page. An example is ROOT’s change log at http://root.cern.ch/root/html/
examples/V5.16.txt.html
To convert the source file MyCode.C to HTML, you can run
root[] THtml h
root[] h.Convert("MyCode.C","Look At My Code","htmlout/");
This will create the file htmlout/MyCode.C.html. The HTML page will have the title “Look At My Code”.
27.3 Special Documentation Elements: Directives
A common documentation problem is the inclusion of images. They are usually generated externally, which poses
problems with where to keep the images, and how to keep them up to date.
THtml
solves this by offering a few special
documentation elements: macro and latex directives.
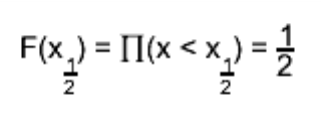
27.3. SPECIAL DOCUMENTATION ELEMENTS: DIRECTIVES 627
27.3.1 Latex Directive
Documentation surrounded by the keywords
BEGIN_LATEX / END_LATEX
will be passed to ROOT Latex engine
TLatex
.
The keywords can be written with small or capital letters (case insensitive). The output will be stored to an image file,
which gets automatically included in the documentation.
// This function calculates BEGIN_LATEX
// F(x_{#frac{1}{2}}) = #prod(x < x_{#frac{1}{2}}) = #frac{1}{2}
// END_LATEX
THtml will inject the following picture:
The image file name is generated from the formula and will be unique for all the documentation. It is stored along-side
the documentation, and it will be automatically regenerated when the documentation is updated. The handling of the
Latex directive is done by the class TDocLatexDirective.
The BEGIN_LATEX keyword can take the following parameters:
•fontsize: sets the TLatex font size. The default value is 16.
•separator
: sets a list of characters for which a new column will be started. This allows aligned, multi-line,
multi-column layout, which can be useful for e.g. mathematical derivations. It is unset by default, meaning the
Latex directive will only generate one column.
•rseparator
: like separator, but a regular expression. Columns start with a match of this regular expression.
Only one of separator or rseparator can be given.
•align: defines the alignment of the columns. Note that the column delimiter counts as a column itself!
Example invocation, where the font size is set to 10, new columns are started by the characters ‘
=
’ and ‘
,
’, and the two
columns are left aligned with the separator column centered:
Begin_Latex(fontsize=10, separator=’=,’, align=lcl)
27.3.2 Macro Directive
A more general approach is offered by the Macro directive, enclosed in the keywords
BEGIN_MACRO / END_MACRO
. The
keywords can be written with small or capital letters (case insensitive). If the text enclosed by these keywords contains
the character ‘
{
’ the text is assumed to be source code. Otherwise it is assumed to be a file name relative to the current
file’s path, and taking into account the paths specified by
THtml::AddMacroPath(). The macro file or the C++
source is executed when generating the documentation. It is expected to return a TObject*, which will
be saved to a GIF file, by calling the virtual function TObject::SaveAs().****
The BEGIN_MACRO keyword can take the following parameters:
•GUI
: will end batch mode. This is needed e.g. for creating screen shots of GUI elements, where the call to
TObject::SaveAs() will invoke TGObject::SaveAs() which needs the graphics system to be initialized.
•source
: requests the source of the macro to be shown in a second tab on the HTML page. This is useful e.g. for
example macros, showing how the image was generated. Lines that should be executed but not shown in the
source tab can be hidden by ending them with
*HIDE*
(most probably as a comment). Lines may be hidden
because they are not needed for the understanding of the macro or because they only make sense in the context
of the documentation, like the statement returning the TObject*.
Example invocation, with enabled ROOT graphics system and a source tab:
Begin_Macro(gui, source)
628 CHAPTER 27. AUTOMATIC HTML DOCUMENTATION
27.4 Customizing HTML
THtml
allows a vast amount of customizations, from a custom style to custom links, to customized java scripts. By
default, the style sheet is taken from
$ROOTSYS/etc/html/ROOT.css
when the documentation is generated. The path
for
ROOT.css
can be changed by calling
THtml::SetEtcDir()
; it should contain the same CSS classes and entity
IDs as the original
ROOT.css
. This style sheet is an easy means of customizing the layout and appearance of the
documentation pages. Many of
THtml
setting can be customized by calls to
THtml
member functions or by settings in
.rootrc, as documented in the
THtml
class reference page http://root.cern.ch/root/html/THtml. The following will
enumerate some of the highlights.
27.4.1 Referencing Documentation for other Libraries
When
THtml
generates documentation for classes it recognizes all class names known to ROOT. If
THtml
does not
have sources for a class it determines the class’s library name. This has to be set by means of
rootmap
files, see
Library Autoloading of this User’s Guide. Given the library name,
THtml
searches for an entry in its map of libraries to
documentation URLs. If it finds it, it will create a link to the documentation at that URL for all occurrences of a given
class name. One can set the URL
../mylib/
for a library name
MyLib
by setting
Root.Html.MyLib: ../mylib/
or by
calling
THtml::SetLibURL("MyLib", "../mylib/")
. Occurrences of class
MyClass
of
MyLib
will now be referenced
as ../mylib/MyClass.html.
27.4.2 Search Engine
THtml can invoke external search engines. The ROOT reference guide sets Root.Html.Search to http://www.google.
com/search?q=%s+site%3A%u. Calling
THtml::SetSearchStemURL()
will set the same. If this URL stem is set,
THtml
will create search fields in the index pages. It will send the words entered in these search fields as %s in the
URL; %u will be replaced by the current document’s path, allowing a site- and directory-specific search.
27.4.3 ViewCVS
Most code is managed in a version control system like CVS. ViewCVS is a WWW reader interface to the versioning
control system that allows e.g. tracking a file’s changes.
THtml
will reference these pages automatically if the
.rootrc
variable
Root.Html.ViewCVS
is set to the URL stem of the ViewCVS. installation. Alternatively, one can call
THtml::SetViewCVS().
27.4.4 Wiki Pages
In some contexts it might be desirable to let users comment on classes, e.g. for suggestions of use or alternatives,
details of behavior, and cross references to other relevant classes. A successful example of this is the PHP.net
documentation with its user annotations.
THtml
can include a link to a class’s Wiki page by setting the Wiki base
URL via Root.Html.WikiURL or THtml::SetWikiURL().
27.5 Tutorial
You can run the tutorial
htmlex.C
to see how
THtml
converts a script to HTML and how it creates the corresponding
class reference:
root[] .x $(ROOTSYS)/tutorials/htmlex.C+
Have a look at the HTML version of the macro in
htmldoc/htmlex.C.html
(which should be the same as the one at
http://root.cern.ch/root/html/examples/htmlex.C.html).
It demonstrates how to generate documentation for your classes and for ROOT classes and how to “beautify” a macro.
Chapter 28
Appendix A: Install and Build ROOT
28.1 License
ROOT is made available under the LGPL v2.1 license. For full details see the file LICENSE in the ROOT distribution.
28.2 Installing ROOT
To install ROOT you will need to go to the ROOT website at: http://root.cern.ch/drupal/content/downloading-root
You have a choice to download the binaries or the source. The source is quicker to transfer since it is only 31 MB, but
you will need to compile and link it. The binaries range from 50 MB to 100 MB depending on the target platform.
28.3 Choosing a Version
The ROOT developers follow the principle of “release early and release often”, however a very large portion of a user
base requires a stable product therefore generally three versions of the system is available for download - new, old and
pro:
•
The new version evolves quickly, with weekly or bi-weekly releases. Use this to get access to the latest and
greatest, but it may not be stable. By trying out the new version you can help us converge quickly to a stable
version that can then become the new pro version. If you are a new user we would advice you to try the new
version.
•
The pro (production) version is a version we feel comfortable with to exposing to a large audience for serious
work. The change rate of this version is much lower than for the new version, it is about 3 to 6 months.
•
The old version is the previous pro version that people might need for some time before switching the new pro
version. The old change rate is the same as for pro.
28.4 Installing Precompiled Binaries
The binaries are available for downloading from http://root.cern.ch/drupal/content/downloading-root. Once down-
loaded you need to unzip and de-tar the file. For example, if you have downloaded ROOT v5.30 for Linux-SLC5:
% gunzip root_v5.30.00.Linux-slc5-gcc4.3.tar.gz
% tar xvf root_v5.30.00.Linux-slc5-gcc4.3.tar
This will create the directory root. Before getting started read the file README/README. Also, read the Introduction
chapter for an explanation of the directory structure.
629
630 CHAPTER 28. APPENDIX A: INSTALL AND BUILD ROOT
28.5 Installing the Source
You have a choice to download a compressed (tar ball) file containing the source, or you can use the Subversion (svn)
source code change control system and check out the most recent source. The compressed file is a one time only choice;
every time you would like to upgrade you will need to download the entire new version. Choosing the CVS option will
allow you to get changes as they are submitted by the developers and you can stay up to date.
28.5.1 Installing and Building the Source from a Compressed File
To install the ROOT source you can download the tar file containing all the source files from the ROOT website. The
first thing you should do is to get the latest version as a tar file. Unpack the source tar file, this creates directory ‘root’:
% tar zxvf root_v5.30.xx.source.tar.gz
Type the build commands:
% cd root
% ./configure --help
% ./configure [<arch>]
% (g)make
Add bin/ to PATH and lib/ to LD_LIBRARY_PATH. For the sh shell family do:
% . bin/thisroot.sh
and for the csh shell family do:
% source bin/thisroot.csh
Try running root:
% root
It is also possible to setup and build ROOT in a fixed location. Please check README/INSTALL for more a detailed
description of this procedure.
28.5.1.1 Target directory
By default, ROOT will be built in the
$ROOTSYS
directory. In that case the whole system (binaries, sources, tutorials,
etc.) will be located under the $ROOTSYS directory.
28.5.1.2 Makefile targets
The
Makefile
is documented in details in the README/BUILDSYSTEM file. It explains the build options and
targets.
28.5.2 More Build Options
To build the library providing thread support you need to define either the environment variable ‘
THREAD=-lpthread’
or
the configure flag
‘--with-thread=-lpthread
’ (it is the default for the
linuxegcs
architecture). [Note: this
is only tested on Linux for the time being.] To build the library providing CERN RFIO (remote I/O) sup-
port you need to define either the environment variable
‘ RFIO=<path>/libshift.a
’ or the configure flag
‘--with-rfio=<path>/libshift.a’. For pre-built version of libshift.a see ftp://root.cern.ch/root/shift/
To build the PAW and Geant3 conversion programs h2root and g2root you need to define either the environment
variable ‘CERNLIB=<cernlibpath>‘or the configure flag ‘--with-cern-libdir=<cernlibpath>’.
To build the
MySQL
interface library you need to install
MySQL
first. Visit http://www.mysql.com/ for the latest versions.
28.6. FILE SYSTEM.ROOTRC 631
To build the strong authentication module used by
rootd
, you first have to install the SRP (Secure Remote Password)
system. Visit http://srp.stanford.edu
To use the library you have to define either the environment variable ‘
SRP=<srpdir>
’ or the configure flag
‘--with-srp=<srpdir>’.
To build the event generator interfaces for Pythia and Pythia6, you first have to get the Pythia libraries available from
ftp: ftp://root.cern.ch/root/pythia6.tar.gz.
To use the libraries you have to define either ‘
PYTHIA=<pythiadir>
’ or the configure flag
‘--with-pythia=<pythiadir>
’.
The same applies for Pythia6.
28.5.2.1 Installing the Source from Subversion
This paragraph describes how to checkout and build ROOT from Subversion for Unix systems. For description
of a checkout for other platforms, please see ROOT installation web page: http://root.cern.ch/drupal/content/
installing-root-source.
% svn co http://root.cern.ch/svn/root/trunk root
U root/...
U ...
% cd root
% ./configure --help
% ./configure [<arch>]
% (g)make
If you are a part of collaboration, you may need to use setup procedures specific to the particular development
environment prior to running (g)make. For more install instructions and options, see the file README/INSTALL.
28.5.2.2 Subversion for Windows
Although there exists a native version of Subversion for Windows, we only support the build process under the
Cygwin
environment. You must have svn version 1.6 or newer. The checkout and build procedure is similar to that for UNIX.
For detailed install instructions, see the file REAMDE/INSTALL.
28.5.2.3 Staying up-to-date
To keep your local ROOT source up-to-date with the Subversion repository you should regularly run the command:
% svn up
28.6 File system.rootrc
ROOT Environment settings are handled via the class
TEnv
.
gEnv->Print()
shows which values are active. Any
settings can be obtained by
TEnv::GetValue
methods that return an integer, double or character value for a named
resource. If the resource is not found, the default value (given as the second parameter) is returned.
fShowEventStatus = gEnv->GetValue("Canvas.ShowEventStatus",kFALSE);
Via the method TEnv::SetValue allows you can set the value of a resource or create a new resource:
gEnv->SetValue("Root.ObjectStat",1);
Path used by dynamic loader to find shared libraries and macros. Paths are different for Unix and Windows. The
example shows the defaults for all ROOT applications for either Unix or Windows:
Unix.*.Root.DynamicPath: .:$(ROOTSYS)/lib
Unix.*.Root.MacroPath: .:$(ROOTSYS)/macros
WinNT.*.Root.DynamicPath: .;$(ROOTSYS)/bin;$(PATH)
WinNT.*.Root.MacroPath: .;$(ROOTSYS)/macros
632 CHAPTER 28. APPENDIX A: INSTALL AND BUILD ROOT
Path where to look for TrueType fonts:
Unix.*.Root.UseTTFonts: true
*.*.Root.TTFontPath: $(ROOTSYS)/fonts
Use Net* API functions:
WinNT.UseNetAPI: true
Use thread library (if exists).
Unix.*.Root.UseThreads: false
Select the compression algorithm (0=old zlib, 1=new zlib). Setting this to ‘0’ may be a security vulnerability.
Root.ZipMode: 1
Show where item is found in the specified path:
Root.ShowPath: false
Activate memory statistics (size and cnt are used to trap allocation of blocks of a certain size after cnt attempts).
Root.MemStat: 0
Root.MemStat.size: -1
Root.MemStat.cnt: -1
Root.ObjectStat: 0
Activate memory leak checker (use in conjunction with
$ROOTSYS/bin/memprobe
). Currently only works on Linux with
gcc.
Root.MemCheck: 0
Root.MemCheckFile: memcheck.out
Global debug mode. When >0 turns on progressively more details debugging.
Root.Debug: 0
Root.Stacktrace: yes
Settings for X11 behaviour.
X11.Sync: no
X11.FindBestVisual: yes
Default editor in use.
Unix.*.Editor: vi
WinNT.*.Editor: notepad
Default 3d Viewer. By default 3-D views are shown in the pad, if the next line is activated, the default viewer will be
OpenGL.
Viewer3D.DefaultDrawOption: ogl
Default Fitter (current choices are Minuit,Minuit2,Fumili and Fumili2).
Root.Fitter: Minuit
Specify list of file endings which TTabCom (TAB completion) should ignore.
TabCom.FileIgnore: .cpp:.h:.cmz
28.6. FILE SYSTEM.ROOTRC 633
28.6.1 TCanvas Specific Settings
Opaque move and resize show full pad during the operation instead of only the outline. Especially for resize you will
need serious CPU power.
UseScreenFactor=true
means to size canvas according to size of screen, so a canvas still
looks good on a low resolution laptop screen without having to change canvas size in macros.
Canvas.MoveOpaque: false
Canvas.ResizeOpaque: false
Canvas.UseScreenFactor: true
Hight color 2 is the red one.
Canvas.HighLightColor: 2
Next three settings are related to different user interface parts of canvas window. If they are set to true, the corresponding
event status bar, tool bar, graphics editor to beactivated by default.
Canvas.ShowEventStatus: false
Canvas.ShowToolBar: false
Canvas.ShowEditor: false
AutoExec allows TExec objects to be executed on mouse and key events.
Canvas.AutoExec: true
Canvas print directory is set to the current one by default:
Canvas.PrintDirectory .
Printer settings:
WinNT.*.Print.Command: AcroRd32.exe
#Unix.*.Print.Command: a2ps -P%p --landscape --columns=2 --margin=30 -rf8.0 %f
Print.Printer: 32-rb20-hp
Print.Directory: .
Print.FileType: pdf
Default histogram binnings used by TTree::Draw() method.
Hist.Binning.1D.x: 100
Hist.Binning.2D.x: 40
Hist.Binning.2D.y: 40
Hist.Binning.2D.Prof: 100
Hist.Binning.3D.x: 20
Hist.Binning.3D.y: 20
Hist.Binning.3D.z: 20
Hist.Binning.3D.Profx: 100
Hist.Binning.3D.Profy: 100
Default statistics names used for parameters in TPaveStats:
Hist.Stats.Entries Entries
Hist.Stats.Mean Mean
Hist.Stats.MeanX Mean x
Hist.Stats.MeanY Mean y
Hist.Stats.RMS RMS
Hist.Stats.RMSX RMS x
Hist.Stats.RMSY RMS y
Hist.Stats.Underflow Underflow
634 CHAPTER 28. APPENDIX A: INSTALL AND BUILD ROOT
Hist.Stats.Overflow Overflow
Hist.Stats.Integral Integral
Hist.Stats.Skewness Skewness
Hist.Stats.SkewnessX Skewness x
Hist.Stats.SkewnessY Skewness y
Hist.Stats.Kurtosis Kurtosis
Hist.Stats.KurtosisX Kurtosis x
Hist.Stats.KurtosisY Kurtosis y
28.6.2 THtml Specific Settings
See the reference guide documentation of
THtml
class at http://root.cern.ch/root/htmldoc/THtml.html for more
details.
XHTML content charset (see http://www.w3.org/TR/2002/REC-xhtml1-20020801, default: ISO-8859-1) is set by:
Root.Html.Charset:
Stem of a search engine for the documentation, where
%s
is replaced by the term entered in the search text box
(example: http://www.google.com/search?q=%s+site%3Aroot.cern.ch%2Froot%2Fhtml, default is "")
Root.Html.Search:
Link to the site’s search engine (default: "", example: http://root.cern.ch/root/Search.phtml)
Root.Html.SearchEngine:
String to prepend to
TClass::GetImplFileName()
names containing directories when looking for source files (default:
"",example: ../root)
Root.Html.SourcePrefix:
Link stem to
ViewCVS
entry for classes, where a class name is assumed to match a file name (default:
""
, example:
http://root.cern.ch/viewcvs).
Root.Html.ViewCVS:
Stem of the CERN XWho system (default: http://consult.cern.ch/xwho/people?)
Root.Html.XWho:
If set to Doc++, allow method documentation in front of method even for methods in the source file (default: "")
Root.Html.DescriptionStyle:
Search path for the source and header files with their default settings:
Unix.*.Root.Html.SourceDir: .:src:include
WinNT.*.Root.Html.SourceDir: .;src;include
URL stem for ROOT documentation pages (default is "").
Root.Html.Root: http://root.cern.ch/root/html
Filesystem output directory for generated web pages (default: htmldoc).
Root.Html.OutputDir: htmldoc/
28.6. FILE SYSTEM.ROOTRC 635
Address of the package’s home page (default: http://root.cern.ch):
Root.Html.HomePage:
Location of user defined header and footer files, see http://root.cern.ch/root/html/THtml#conf:header (defaults are
"", example: ../header.txt,../footer.txt):
Root.Html.Header:
Root.Html.Footer:
Tag for detecting class description comments (default value is set below).
Root.Html.Description: //____________________
Tag for detecting “Author” comment (default value is set below).
Root.Html.Author: // Author:
Tag for detecting “last updated” comment.
THtml
uses the current date if this tag is not found in a class source file
(default value is set below).
Root.Html.LastUpdate: // @(#)
Tag for detecting “Copyright” comment (default value is set below).
Root.Html.Copyright: * Copyright
28.6.3 GUI Specific Settings
Set the “
native
” ROOT GUI interface to be used in a ROOT session. If set to “
qt
”, the “
native
” GUI interface is
replaced with one based on Qt by the regular ROOT plug-in mechanism.
Gui.Backend: native
Gui.Factory: native
GUI default fonts in use:
Gui.DefaultFont: -adobe-helvetica-medium-r-*-*-12-*-*-*-*-*-iso8859-1
Gui.MenuFont: -adobe-helvetica-medium-r-*-*-12-*-*-*-*-*-iso8859-1
Gui.MenuHiFont: -adobe-helvetica-bold-r-*-*-12-*-*-*-*-*-iso8859-1
Gui.DocFixedFont: -adobe-courier-medium-r-*-*-12-*-*-*-*-*-iso8859-1
Gui.DocPropFont: -adobe-helvetica-medium-r-*-*-12-*-*-*-*-*-iso8859-1
Gui.IconFont: -adobe-helvetica-medium-r-*-*-10-*-*-*-*-*-iso8859-1
Gui.StatusFont: -adobe-helvetica-medium-r-*-*-10-*-*-*-*-*-iso8859-1
Regular background and foreground colors in use:
Gui.BackgroundColor: #c0c0c0
Gui.ForegroundColor: black
Selection background and foreground colors in use:
Gui.SelectBackgroundColor: #000080
Gui.SelectForegroundColor: white
Document background and foreground colors in use:
636 CHAPTER 28. APPENDIX A: INSTALL AND BUILD ROOT
Gui.DocumentBackgroundColor: white
Gui.DocumentForegroundColor: black
Tooltip background and foreground colors in use:
Gui.TooltipBackgroundColor: LightYellow
Gui.TooltipForegroundColor: black
Path where all GUI icons in use can be found:
Gui.IconPath: $(HOME)/icons:$(ROOTSYS)/icons:.
Mime type file setting:
Gui.MimeTypeFile: $(HOME)/.root.mimes
If $(HOME)/.root.mimes does not exists, defaults to this:
#Gui.MimeTypeFile: $(ROOTSYS)/etc/root.mimes
28.6.4 TBrowser Settings
Current icon style selection - can be either small,big,list,details:
Browser.IconStyle: small
Current sorting rule applied on the browser objects - can be name,type,size,date:
Browser.SortBy: name
Number of items in a group view:
Browser.GroupView: 10000
Show or not hidden items:
Browser.ShowHidden: no
Create a thumbnail view after executing the macro (default is yes).
Browser.AutoThumbnail: yes
28.6.5 TRint Specific Settings
Rint (interactive ROOT executable) specific alias, logon and logoff macros.
Rint.Load: rootalias.C
Rint.Logon: rootlogon.C
Rint.Logoff: rootlogoff.C
Record ROOT session commands in a given history file (default is
$(HOME)/.root_hist
). If set to “
-
”, it turn off the
command recording.
Rint.History: $(HOME)/.root_hist
Next two lines set the history file size handling. Once
HistSize
is reached, the last
HistSave
entries are removed.
If
HistSize
is set to 0, it turns off command recording. Both values can be overridden by environment variable
ROOT_HIST=size[:save], where the “:save” part is optional.
Rint.HistSize: 500
Rint.HistSave: 400
28.6. FILE SYSTEM.ROOTRC 637
28.6.6 ACLiC Specific Settings
ACLiC.Linkdef
specifies the suffix that will be added to the script name to try to locate a custom linkdef file when
generating the dictionary.
ACLiC.Linkdef: _linkdef
The top directory for storing the libraries produced by ACLiC is set by:
ACLiC.BuildDir: /where/I/would/like/my/compiled/scripts
The additional include directives for ACLiC compilations are set by:
ACLiC.IncludePaths: -I/where/the/includes/are
28.6.7 PROOF Related Variables
PROOF debug options.
Proof.DebugLevel: 0
Proof.DebugMask:-1
PROOF GDB hooks allows a debugger to be attached early in the startup phase of
proofserv:
0 - don’t wait; 1 -
master proofserv enters wait loop; 2 - slave proofserv enters wait loop; 3 - any proofserv enters wait loop
Proof.GdbHook: 0
On the master to enable the parallel startup of workers using threads set next to “yes” (default is “no”):
Proof.ParallelStartup: no
Proof.StatsHist: no
Proof.StatsTrace: no
Proof.SlaveStatsTrace: no
Proof.CondorHome: /opt/condor
Proof.CondorConfig: /opt/condor/etc/condor_config
PEAC.GmUrl: http://somewhere:8080/clarens/
PEAC.LmUrl: http://elsewhere:8080/clarens/
Certificate and key
Clarens.CertFile: $(HOME)/.globus/usercert.pem
Clarens.KeyFile: $(HOME)/.globus/userkey.pem
28.6.7.1 Settings Related to Authentication for rootd and proofd
Default authentication method for
rootd
and
proofd
. These are supported for backward compatibility but have a
very low priority. System defaults are generated by configure as a list in
system.rootauthrc
in
$ROOTSYS/etc/
or
/etc/root; the file $HOME/.rootauthrc can be used to override the system defaults.
The value meaning: 0=UsrPwd,1=SRP,2=Krb5,3=Globus,4=SSH,5=UidGid.
Rootd.Authentication: 0
Proofd.Authentication: 0
638 CHAPTER 28. APPENDIX A: INSTALL AND BUILD ROOT
Connection is shutdown at timeout expiration. Timeout is in seconds. Negotiation cannot be attempted at low
level (i.e. inside TAuthenticate::Authenticate()) because of synchronization problems with the server. At higher level,
TAuthenticate::HasTimedOut() gives information about timeout: 0 = no timeout; 1 = timeout, no methods left; 2 =
timeout, still methods to be tried. Caller should decide about an additional attempt. Timeout is disabled by default
(< 0). It can be changed on-the-fly with the method TAuthenticate::SetTimeOut(to_value).
Auth.Timeout: -1
Password dialog box is set to 0 if you do not want a dialog box to be popped-up when a password is requested. Default
setting is 1.
Auth.UsePasswdDialogBox: 0
Set the following to 1 if you want full SRP authentication in PROOF (Client-to-Master and Master-to-Slave).
Proofd.SendSRPPwd: 0
Set next to 1 to use SSH authentication in PROOF servers (Master-to-Slave or Slaves-to-DataServers). This is switched
off by default because credentials forwarding for SSH is not controlled by the system; however the user may have other
ways to guarantee it, so it may want to switch it on.
ProofServ.UseSSH: 0
Default login name (if not defined it is taken from $(HOME)).
UsrPwd.Login: qwerty
SRP.Login: qwerty
Krb5.Login: qwerty@LOCAL.DOM.AIN
Globus.Login: cd:~/.globus cf:usercert.pem kf:userkey.pem
ad:/etc/grid-security/certificates
SSH.Login: qwerty
UidGid.Login: qwerty
To be prompted for login information.
UsrPwd.LoginPrompt: yes
SRP.LoginPrompt: yes
Krb5.LoginPrompt: yes
Globus.LoginPrompt: yes
SSH.LoginPrompt: yes
UidGid.LoginPrompt: yes
To reuse established security context.
UsrPwd.ReUse: yes
SRP.ReUse: no
Krb5.ReUse: no
Globus.ReUse: yes
SSH.ReUse: yes
Duration validity of the sec context for UsrPwd, SRP and SSH. Format: <hours>:<minutes> (default 24:00)
#UsrPwd.Valid: 24:00
#SRP.Valid: 24:00
#SSH.Valid: 24:00
To control password encryption for UsrPwd authentication.
UsrPwd.Crypt: yes
28.6. FILE SYSTEM.ROOTRC 639
Globus Miscellaneous - Globus Proxy duration:
HH:MM
(ex
12:15
for 12 hours and 15 min); ‘
default
’ for system
default.
Globus.ProxyDuration: default
#Globus.ProxyDuration: 12:15
Number of bits for the initial key.
Globus.ProxyKeyBits: 1024
Path to alternative ‘ssh’ (to override $PATH if ever needed).
SSH.ExecDir: /usr/bin
In case of error,
SSH
returns 1 (or
256=0x100
). To trap those errors for which one should retry, error printouts must be
parsed; any substring found under the
TEnv SSH.ErrorRetry
triggers a retry condition; strings can be added here in
the form (including double quotes):
+SSH.ErrorRetry: "<error_string>"
This is what one usually gets if the server has reached the maximum number of sshd daemons (defined by
MaxStartups
in sshd_config); this is a typical case in which one should retry.
SSH.ErrorRetry: "Connection closed by remote host"
Max number of retries for SSH in case of retry error (see above).
SSH.MaxRetry: 100
Type of key to be used for RSA encryption: 0=local;1=SSL (default if openssl available).
RSA.KeyType: 1
In case of
’RSA.KeyType: 1
’ this specifies the number of bits to be used for the Blowfish key used to encrypt the
exchanged information: default - 256, minimum - 128, maximum - 15912.
SSL.BFBits: 256
28.6.7.2 Server Authentication in TServerSocket
General setting: file with server access rules
SrvAuth.DaemonRc: /etc/root/system.daemonrc
Check of host equivalence via /etc/hosts.equiv or $HOME/.rhosts.
SrvAuth.CheckHostsEquivalence: 1
SRP: pass file (default $HOME/.srootdpass).
SrvAuth.SRPpassfile: $HOME/.srootdpass
Globus/GSI: hostcert configuration file.
SrvAuth.HostCert: /etc/root/hostcert.conf
Globus/GSI: gridmap file.
640 CHAPTER 28. APPENDIX A: INSTALL AND BUILD ROOT
SrvAuth.GridMap: /etc/grid-security/grid-mapfile
SSH: port for the sshd daemon.
SrvAuth.SshdPort: 22
Force file opening via
TNetFile
(
TXNetFile
) if a hostname is specified in the Url. By default, for local files
TFile::Open() invokes directly TFile.
TFile.ForceRemote: yes
Special cases for the
TUrl
parser, where the special cases are parsed in a protocol + file part, like rfio:host:/path/file.root,
castor:/path/file.root or /alien/path/file.root. In case the file namespace descriptor ends with - the namespace is not a
part of the filename. Extend in private .rootrc with a +Url.Special line.
Url.Special: file: rfio: hpss: castor: gfal: dcache:
+Url.Special: /alien/- /castor/
28.6.7.3 PROOF XRD Client Variables
Debug level (if <=0 : none, 1 : low, 2 : medium, 3 : high)
XProof.Debug: 0
Socket read timeout [in secs: default 10 secs]
XProof.ReadTimeout: 10
The following env vars are handled by TXNetFile and related classes (module netx,libNetx.so).
XNet.ConnectTimeout - maximum time to wait before server’s response on a connect [10 s]
XNet.RequestTimeout - maximum time to wait before considering a read/write failure [60 s]
XNet.ConnectDomainAllowRE
- sequence of
TRegexp
regular expressions separated by a
|
. A domain is granted access
to for the first connection if it matches one of these regexps. Example:
slac.stanford.edu|pd.infn.it|fe.infn.it
XNet.ConnectDomainDenyRE
- sequence of TRegexp regular expressions separated by a
|
. A domain is denied access
to for the first connection if it matches one of these regexps.
XNet.RedirDomainAllowRE
- sequence of TRegexp regular expressions separated by a
|
. A domain is granted access
to for a redirection if it matches one of these regexps. Example:
XNet.RedirDomainDenyRE
- sequence of TRegexp regular expressions separated by a
|
. A domain is granted access to
for a redirection if it matches one of these regexps.
XNet.MaxRedirectCount - maximum number of redirections from server [default - 255]
XNet.Debug
- log verbosity level (0=nothing,1=messages of interest to the user, 2=messages of interest to the developers
(includes also user messages), 3=dump of all sent/received data buffers (includes also user and developers messages).
[default - 0]
XNet.ReconnectTimeout
- sleep-time before going back to the load balancer (or rebouncing to the same failing host)
after a read/write error [default - 10s]
XNet.StartGarbageCollectorThread
- for test/development purposes. Normally nonzero (true), but as workaround
for external causes someone could be interested in not having the garbage collector thread around. [experimental!]
XNet.GoAsynchronous - default is 0. When activated, XTNetFile works in async mode, allowing input buffering and
unsolicited responses [experimental!]
XNet.TryConnect - Number of tries connect to a single server before giving up.
XNet.TryConnectServersList - number of connect retries to the whole server list given [default - 240]
28.7. DOCUMENTATION TO DOWNLOAD 641
XNet.PrintTAG
- Print a particular string the developers can choose to quickly recognize the version at run time
[default - 0]
Example of custom setting for the Rint application (root.exe). This overrides the default specified above for a generic
application. Color 5 is yellow.
Rint.Canvas.HighLightColor: 5
28.7 Documentation to Download
•The latest ROOT Users Guide
•http://root.cern.ch/root/doc/RootDoc.html
•ROOT Reference Guide
•http://root.cern.ch/root/Reference.html
Index
A
adding a class
ACLiC..........................................425
shared library...................................418
B
benchmarks .........................................348
box-and whisker plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335
C
C++................................................147
candle plot..........................................335
candle stick plot.....................................335
cling.................................................153
D
documentation
class............................................625
G
Geometry ........................................... 447
Graphical User Interface . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 571
GUI application.....................................546
H
histogram ............................................ 53
profile .......................................... 342
rebin..................................55,56,93,95
I
I/O..................................................251
install ROOT....................................25,629
L
list
entry ........................................... 338
event ........................................... 338
P
parallel poordinates . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 330
parallel processing...................................569
PROOF.............................................569
Python..............................................525
Q
Qt...................................................611
R
Ruby................................................525
T
TPad................................................174
transparency
parallel coordinates . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335
tree
chains...........................................349
friend...........................................350
MakeClass......................................343
MakeSelector....................................347
scan ............................................337
642